TS Inter 1st Year

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions

Question 1.
Prove that sin^-1\(\frac{4}{5}\) + sin^-1\(\frac{7}{25}\) = sin^-1\(\frac{117}{125}\). [Mar. ’16(TS), ’13]
Answer:
Let sin^-1\(\frac{4}{5}\) = A and sin^-1\(\frac{7}{25}\) = B
Then sin A = \(\frac{4}{5}\) and sin B = \(\frac{7}{25}\)
∴ cos A = \(\frac{3}{5}\) and cos B = \(\frac{24}{25}\)
∴ sin (A + B) = sin A cos B + cos A sin B

Question 2.
Prove that sin^-1\(\frac{3}{5}\) + sin^-1\(\frac{8}{17}\) = cos^-1\(\frac{36}{85}\). [Mar. ’19(TS); May ’12, ’09]
Answer:
Let sin^-1\(\left(\frac{3}{5}\right)\)

sin A = \(\frac{3}{5}\);
cot A = \(\frac{4}{5}\)

Let sin^-1\(\left(\frac{8}{17}\right)\) = B
sin B = \(\frac{8}{17}\);
cos B = \(\frac{15}{17}\)

Let cos^-1\(\left(\frac{36}{85}\right)\) = C
cos C = \(\frac{36}{85}\)
∴ A + B = C
cos (A + B) = cos C
L.H.S = cos (A + B) = cos A cos B – sin A sin B
= \(\frac{4}{5} \cdot \frac{15}{17}-\frac{3}{5} \cdot \frac{8}{17}=\frac{60}{85}-\frac{24}{85}=\frac{36}{85}\)
= RHS
∴ sin^-1\(\left(\frac{3}{5}\right)\) + sin^-1\(\left(\frac{8}{17}\right)\) = cos^-1\(\left(\frac{36}{85}\right)\)

Question 3.
Prove that cos^-1\(\left(\frac{4}{5}\right)\) + sin^-1\(\left(\frac{3}{\sqrt{34}}\right)\) = tan^-1\(\left(\frac{27}{11}\right)\). [May ’13]
Answer:
Let cos^-1\(\left(\frac{4}{5}\right)\) = A and sin^-1\(\left(\frac{3}{\sqrt{34}}\right)\) = B
Then cos A = \(\frac{4}{5}\) and
sin B = \(\left(\frac{3}{\sqrt{34}}\right)\)

tan A = \(\sqrt{\sec ^2 A-1}=\sqrt{\frac{25}{16}-1}\)
= \(\frac{3}{4}\)
and
cos²B

Question 4.
Find the value of
tan \(\left(\sin ^{-1}\left(\frac{3}{5}\right)+\cos ^{-1}\left(\frac{5}{\sqrt{34}}\right)\right)\). [Mar. ’13]
Answer:
Let sin^-1\(\left(\frac{3}{5}\right)\) = A and
cos^-1\(\left(\frac{5}{\sqrt{34}}\right)\)

Question 5.
Find the value of cos(sin^-1\(\frac{3}{5}\) + sin^-1\(\frac{5}{13}\)).
Answer:
Let sin^-1\(\left(\frac{3}{5}\right)\) = A and sin^-1\(\left(\frac{5}{13}\right)\) = B then
sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\)

∴ cos A = \(\frac{4}{5}\) and
cos B = \(\frac{12}{13}\)

∴ cos (A + B) = cos A cos B – sin A sin B
= \(\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)-\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)\)
= \(\frac{33}{65}\)

Question 6.
Prove that tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{5}\right)\) + tan^-1\(\left(\frac{1}{4}\right)\) = \(\frac{\pi}{4}\). [Mar. ’18(TS); Mar. ’19, ’17, ’15 (AP), May ’15(AP); May ’11, ’10, ’06, ’03; Mar. ’11]
Answer:

Question 7.
Find the value of tan(cos^-1\(\frac{4}{5}\) + tan^-1\(\frac{2}{3}\)). [Mar. ’12]
Answer:

Question 8.
Prove that 2sin^-1\(\left(\frac{3}{5}\right)\) – cos^-1\(\left(\frac{5}{13}\right)\) = cos^-1\(\left(\frac{323}{325}\right)\). [May, ’14; Mar. ’14, ’08]
Answer:

Question 9.
Prove that sin^-1\(\frac{4}{5}\) + 2tan^-1\(\frac{1}{3}\) = \(\frac{\pi}{2}\). [Mar. ’10, Mar. ’15(TS)]
Answer:

Question 10.
Show that cot (sin^-1\(\sqrt{\frac{13}{17}}\)) = sin(tan^-1\(\left(\frac{2}{3}\right)\))). [Mar. ’17(TS); May ’97]
Answer:

Question 11.
Prove that
cos(2stan^-1\(\frac{1}{7}\)) = sin(3tan^-1\(\frac{3}{4}\)). [B.P]
Answer:
L.H.S = cos(2stan^-1\(\frac{1}{7}\))
Let tan^-1\(\frac{1}{7}\) = A
⇒ tan A = \(\frac{1}{7}\)

Question 12.
Prove that [Mar. ’04]
sin[cot^-1\(\left(\frac{2 x}{1-x^2}\right)\) + cos^-1\(\left(\frac{1-x^2}{1+x^2}\right)\)] = 1
Answer:
Put x = tan θ then
= sin[cot^-1\(\left(\frac{2 \tan \theta}{1-\tan ^2 \theta}\right)\) + cos^-1\(\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)\)]
= sin[cot^-1(tan 2θ) + cos^-1(cos 2θ)]
= sin[cot^-1(cot(\(\frac{\pi}{2}\) – 2θ)) + cos^-1(cos 2θ)]
= sin[\(\frac{\pi}{2}\) – 2θ + 2θ] = sin\(\frac{\pi}{2}\) = 1 = R.H.S

Question 13.
If cos^-1p + cos^-1q + cos^-1r = π then prove that p² + q² + r² + 2pqr = 1. [Mar ’04; Mar. ’01, ’99]
Answer:
Given cos^-1p + cos^-1q + cos^-1r = π
Let cos^-1p = A ⇒ cos A = p
Let cos^-1q = B ⇒ cos B = q
Let cos^-1r = C ⇒ cos C = r
A + B + C = π ⇒ A + B = π – C
cos(A + B) = cos (π – C)
⇒ cos A. cos B – sin A . sin B = – cos C
cos A cos B – \(\sqrt{1-\cos ^2 \mathrm{~A}} \cdot \sqrt{1-\cos ^2 \mathrm{~B}}\) = -cos C
pq – \(\sqrt{1-p^2} \sqrt{1-q^2}\) = -r
pq + r = \(\sqrt{1-p^2} \sqrt{1-q^2}\)

Squaring on both sides
(pq + r)² = (1 – p²)(1 – q²)
p²q² + r² + 2pqr = 1 – q² – p² + p²q²
∴ p² + q² + r² + 2pqr = 1.

Question 14.
If sin^-1\(\left(\frac{2 p}{1+p^2}\right)\) – cos^-1\(\left(\frac{1-q^2}{1+q^2}\right)\) = tan^-1\(\left(\frac{2 x}{1-x^2}\right)\) then prove that x = \(\frac{\mathbf{p}-\mathbf{q}}{1+\mathbf{p q}}\). [May ’98]
Answer:

Question 15.
If sin^-1x + sin^-1y + sin^-1z = π, then prove that x\(\sqrt{1-x^2}\) + y\(\sqrt{1-y^2}\) + z\(\sqrt{1-z^2}\) = 2xyz. [Mar. ’06; May ’05, ’97]
Answer:
Given sin^-1x + sin^-1y + sin^-1z = π
Let sin^-1x = A ⇒ sin A = x
sin^-1y = B ⇒ sin B = y
sin^-1z = C ⇒ sin C = z
∴ A + B + C = π
= 2sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + sin 2C

= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (π – C) cos (A – B) + sin 2C
= 2 sin C cos (A – B) + 2 sin C cos C
= 2 sin C [cos (A – B) + cos C]
= 2 sin C [cos(A – B) + cos (π – (A + B))]
= 2 sin C [cos (A – B) – cos (A + B)]
= 2 sin C (2 sin A. sin B)
= 4 sin A sin B sin C
∴ sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
⇒ 2 sin A cos A + 2 sin B cos B + 2 sin C cos C = 4 sin A sin B sin C
⇒ sin A cos A + sin B cos B + sin C cos C = 2 sin A sin B sin C
⇒ sin\(\sqrt{1-\sin ^2 \mathrm{~A}}\) + sin B\(\sqrt{1-\sin ^2 \mathrm{~B}}\) + sin C\(\sqrt{1-\sin ^2 \mathrm{~C}}\) = 2sin A sin B sin C
∴ x\(\sqrt{1-x^2}\) + y\(\sqrt{1-y^2}\) + z\(\sqrt{1-z^2}\) = 2xyz

Question 16.
If tan^-1x + tan^-1y + tan^-1z = π, then prove that x + y + z = xyz. [Mar. ’03]
Answer:
Given tan^-1x + tan^-1y + tan^-1z = π
Let tan^-1x = A ⇒ tan A = x
Let tan^-1y = B ⇒ tan B = y
Let tan^-1z = C ⇒ tan B = y
∴ A + B + C = π ⇒ A + B = π – C
tan (A + B) = tan(π – C) ⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\)
= -tan C
\(\frac{x+y}{1-x y}\) = -z ⇒ x + y = -z + xyz
∴ x + y + z = xyz

Question 17.
Solve tan^-1\(\left(\frac{x-1}{x-2}\right)\) + tan^-1\(\left(\frac{x+1}{x+2}\right)=\frac{\pi}{4}\).
Answer:

Question 18.
Solve 3sin^-1\(\left(\frac{2 x}{1+x^2}\right)\) – 4cos^-1\(\left(\frac{1-x^2}{1+x^2}\right)\) + 2tan^-1\(\left(\frac{2 x}{1-x^2}\right)=\frac{\pi}{3}\). [Mar. ’09]
Answer:

3sin^-1(sin 2θ) – 4cos^-1(cos 2θ) + 2tan^-1(tan 2θ) = \(\frac{\pi}{3}\)
3(2θ) – 4(2θ) + 2(2θ) = \(\frac{\pi}{3}\)
⇒ 6θ – 8θ + 4θ = \(\frac{\pi}{3}\)
2θ = \(\frac{\pi}{3}\) ⇒ θ = \(\frac{\pi}{6}\)
⇒ tan θ = tan \(\frac{\pi}{6}\)
∴ x = \(\frac{1}{\sqrt{3}}\)

Some More Maths 1A Inverse Trigonometric Functions Important Questions

Question 1.
Prove that sin^-1\(\left(\frac{4}{5}\right)\) + sin^-1\(\left(\frac{5}{13}\right)\) + sin^-1\(\left(\frac{16}{65}\right)=\frac{\pi}{2}\). [Mar ’18(AP)]
Answer:
Let sin^-1\(\left(\frac{4}{5}\right)\) = A and sin^-1\(\left(\frac{5}{13}\right)\) = B
∴ sin A = \(\frac{4}{5}\) and sin B = \(\frac{5}{13}\)
∴ cos A = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)

Also cos (α + β) = cos α cos β – sin α sin β
= \(\frac{3}{5} \cdot \frac{12}{13}-\frac{4}{5} \cdot \frac{5}{13}=\frac{16}{65}\)
∴ α + β = cos^-1\(\left(\frac{16}{65}\right)\) ⇒ sin^-1\(\left(\frac{4}{5}\right)\) + sin^-1\(\left(\frac{5}{13}\right)\) = cos^-1\(\left(\frac{16}{65}\right)\)

L.H.S = sin^-1\(\left(\frac{4}{5}\right)\) + sin^-1\(\left(\frac{5}{13}\right)\) + sin^-1\(\left(\frac{16}{65}\right)\) = cos^-1\(\left(\frac{16}{65}\right)\) + sin^-1\(\left(\frac{16}{65}\right)\) = \(\frac{\pi}{2}\)

Question 2.
Prove that cot^-19 + cosec^-1\(\frac{\sqrt{41}}{4}=\frac{\pi}{4}\).
Answer:
Let cot^-19 = α
Let cosec^-1\(\frac{\sqrt{41}}{4}\) = β
⇒ cot α = 9 ⇒ cosec β = \(\frac{\sqrt{41}}{4}\)
⇒ tan α = \(\frac{1}{9}\) ⇒ tan β = \(\frac{4}{5}\)

From the figure
Take tan (α + β) = \(\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \cdot \tan \beta}\)

Question 3.
Prove that sin^-1\(\left(\frac{4}{5}\right)\) + 2tan^-1\(\left(\frac{1}{3}\right)=\frac{\pi}{2}\)
Answer:
Let sin^-1\(\left(\frac{4}{5}\right)\) = A then sin A = \(\frac{4}{5}\) and
tan^-1\(\left(\frac{1}{3}\right)\) = B then tan B = \(\frac{1}{3}\)

Question 4.
If cos^-1\(\frac{p}{a}\) + cos^-1\(\frac{q}{b}\) = α, then prove that \(\frac{p^2}{a^2}-\frac{2 p q}{a b}\)cos α + \(\frac{q^2}{b^2}\) = sin²α
Answer:
Given cos^-1\(\frac{p}{a}\) + cos^-1\(\frac{q}{b}\) = α

Question 5.
Solve sin^-1\(\left(\frac{5}{x}\right)\) + sin^-1\(\left(\frac{12}{x}\right)=\frac{\pi}{2}\), (x > 0)
Answer:
Let sin^-1\(\left(\frac{5}{x}\right)\) = A and sin^-1\(\left(\frac{12}{x}\right)\) = B then
sin A = \(\frac{5}{x}\) and sin B = \(\frac{12}{x}\)(x > 0)
∴ Now α + β = \(\frac{\pi}{2}\) ⇒ sin α = sin(\(\frac{\pi}{2}\) – β)
= cos β ⇒ \(\frac{5}{x}=\sqrt{1-\frac{144}{x^2}}\)

⇒ \(\frac{25}{x^2}=1-\frac{144}{x^2} \Rightarrow \frac{169}{x^2}\) = 1 ⇒ x² = 169
⇒ x = ±13 But x = 13(∵ x > 0)

Question 6.
Prove that sin^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{12}{13}\right)\) = cos^-1\(\left(\frac{33}{65}\right)\).
Answer:
Let sin^-1\(\left(\frac{3}{5}\right)\) = A and cos^-1\(\left(\frac{12}{13}\right)\) = B then
A + B ∈ (0, π)
∴ sin A = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)
cos A = \(\frac{4}{5}\) and sin B = \(\frac{5}{13}\)

Consider cos(A + B) = cos A cos B – sin A sin B
= \(\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)-\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)=\frac{48}{65}-\frac{15}{65}=\frac{33}{65}\)
A + B = cos^-1\(\left(\frac{33}{65}\right)\)
⇒ sin^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{12}{13}\right)\) = cos^-1\(\left(\frac{33}{65}\right)\)

Question 7.
Find the values of sin(cos^-1\(\frac{3}{5}\) + cos^-1\(\frac{12}{13}\)).
Answer:
Let cos^-1\(\left(\frac{3}{5}\right)\) = A and cos^-1\(\left(\frac{12}{13}\right)\) = B then
cos A = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)
∴ sin A = \(\frac{4}{5}\) and sin B = \(\frac{5}{13}\)
∴ sin(A + B) = sin A cos B + cos A sin B
= \(\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)+\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)=\frac{63}{65}\)
∴ sin(cos^-1\(\frac{3}{5}\) + cos^-1\(\frac{12}{13}\))

Question 8.
Prove that cos(2tan^-1\(\frac{1}{7}\)) = sin(2tan^-1\(\frac{3}{4}\))
Answer:
Let α = tan^-1(\(\frac{1}{7}\)) then tan α = \(\frac{1}{7}\)

Question 9.
Prove that tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{13}\) – tan^-1\(\frac{2}{9}\) = 0
Answer:
L.H.S = (tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{13}\)) – tan^-1\(\frac{2}{9}\)
[we have x > 0, y > 0, xy > 1 then tan^-1x + tan^-1y + tan^-1z = tan^-1\(\left(\frac{x+y}{1-x y}\right)\)]

Question 10.
Prove that tan^-1\(\frac{3}{4}\) + tan^-1\(\frac{3}{5}\) – tan^-1\(\frac{8}{19}\) = \(\frac{\pi}{4}\)
Answer:
LHS = tan^-1\(\frac{3}{4}\) + tan^-1\(\frac{3}{5}\) – tan^-1\(\frac{8}{19}\)

Question 11.
Show that tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{8}\) = cot^-1\(\frac{201}{43}\) + cot^-118.
Answer:

Question 12.
Show that sec² (tan^-12) + cosec² (cot^-12) = 10.
Answer:
Let a = tan^-12 ⇒ tan α = 2
sec²α = 1 + tan²α = 1 + 4 = 5
Let β = cot^-12 ⇒ cot β = 2
∴ cosec²β = 1 + cot²β = 1 + 4 = 5
∴ sec² (tan^-12) + cosec² (cot^-12)
= sec²α + cosec²β = 5 + 5 = 10

Question 13.
If α = tan^-1\(\left[\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right]\), then prove that x² = sin 2α.
Answer:

Question 14.
If tan^-1x + tan^-1y + tan^-1z = \(\frac{\pi}{2}\), prove that xy + yz + zx = 1.
Answer:
Given tan^-1x + tan^-1y + tan^-1z = \(\frac{\pi}{2}\)
tan^-1x + tan^-1y = \(\frac{\pi}{2}\) – tan^-1z
tan^-1\(\left[\frac{x+y}{1-x y}\right]\) = \(\frac{\pi}{2}\) – tan^-1z

⇒ (x + y)z = 1 – xy
⇒ xz + yz = 1 – xy
⇒ xy + yz + zx = 1

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Functions Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Functions Important Questions Very Short Answer Type

Question 1.
If the function f is defined by

then find the 2x +1, x < -3 values if exist of f(4), f(2.5), f(- 2), f(- 4), f(0), f(- 7). [Mar 14]
Answer:
(i) f(4) For x > 3, f(x) = 3x – 2
f(4) = 3 (4) – 2 = 12 – 2 = 10

(ii) f(2.5) is not defined.

(iii) f(-2)
For – 2 ≤ x ≤ 2, f(x) = x² – 2
f(- 2) = (- 2)² – 2 = 4 – 2 = 2

(iv) f(-4)
For x < – 3, f(x) = 2x + 1
f(- 4) = 2(- 4) + 1 = – 8 + 1 = – 7

(v) f(0)
For – 2 ≤ x ≤ 2, f(x) = x² – 2
f(0) = 0² – 2 = – 2

(vi) f(- 7)
For x < – 3, f(x) = 2x + 1
f(- 7) = 2 (- 7) + 1 = – 14 + 1 = – 13

If the function f is defined by

then find the values of
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(-2)
(v) f(- 5).
Answer:
(i) 5
(ii) 2
(iii) – 2.5
(iv) 1
(v) not defined

Question 2.
If A = \(\left\{0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2}\right\}\) and f: A → B is a surjection defined by f(x) = cos x then find B. [Mar. (TS) 17, 16 (AP), 11 May 15 (AP), 15 (TS), 11]
Answer:
Given A = \(\left\{0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2}\right\}\)
f(x) = cos x
Since f: A → B is a surjection then f(A) = B
f(0) = cos 0 = 1

∴ B = Range . f(A) = {1, \(\frac{\sqrt{3}}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}\), o}

If A = {- 2, – 1, 0, 1, 2} and f: A → B is a surjection defined by f(x) = x² + x + 1, then find B. [Mar. (AP) 19, 17] [Mar 16 (TS): May 14, 10]
Answer:
{3, 1, 7}

If A = {1, 2, 3, 4} and f: A → R is a function defined by f(x) = \(\frac{x^2-x+1}{x+1}\), then find the range of f.
Answer:
\(\left\{1, \frac{1}{2}, \frac{7}{4}, \frac{13}{5}\right\}\)

Question 3.
Determine whether the function f: R → R defined by

is an injection or a surjection or a bijection.
Answer:
Given f: R → R

If x = 3 > 2 then f(3) = 3
If x = 1 <2 then f(1) = 5(1) – 2 = 5 – 2 = 3
∴ 1 and 3 have same f image,
∴ f is not an injection.
If y ∈ R (co-domain) then y = x
x = y
then f (x) = x
f(x) = y
If y ∈ R (co-domain) then y = 5x – 2
y + 2 = 5x
x = \(\frac{y+2}{5}\)
then f (x) = 5x – 2

= y + 2 – 2 = y
∴ f is a surjection since f is not an injection then it is not a bijection.

Question 4.
If f: R → R, g : R → R are defined by f(x) = 4x – 1 and g(x) = x² + 2 then find [May 09. Mar. 05, 04]
(i)(gof) (x)
(ii) (gof) \(\left(\frac{a+1}{4}\right)\)
(iii) (fof) (x)
(iv) [go (fof)] (0)
Answer:
Given f: R → R, g: R → R
f(x) = 4x – 1 and g(x) = x² + 2

(i) (gof) (x) = g [f(x)] = g[4x – 1]
= (4x – 1)² + 2
= 16x² + 1 – 8x + 2
= 16x² – 8x + 3

(ii) (gof) \(\left(\frac{a+1}{4}\right)\) = g \(\left[\mathrm{f}\left(\frac{\mathrm{a}+1}{4}\right)\right]\)
= g\(\left[4\left(\frac{a+1}{4}\right)-1\right]\)
= g[a + 1 – 1 ]
= g(a) = a² + 2

(iii) (fof) (x) = f [f(x)] = f[4x – 1]
= 4 (4x – 1) – 1
= 16x – 4 – 1
= 16x – 5

(iv) [go (fof)] (0)
Now (fof) (0) = f[f(0)] = f[4(0) – 1] = f(- 1)
= 4( – 1) – 1 = – 4 – 1 = – 5
[go (fof)] (0) = go [(fof)(0)]
= g [- 5] = (- 5)² + 2
= 25 + 2 = 27

Question 5.
If f: Q → Q is defined by f(x) = 5x + 4 for all x ∈ Q, show that ‘f is a bijection and find f^-1. [Mar. 17 (TS). 16 (AP)]
Answer:
Given f: Q → Q, f(x) = 5x + 4, ∀ x ∈ Q
Let a₁, a₂ ∈ Q
f(a₁) = f(a₂)
5a₁ + 4 = 5a₂ + 4
5a₁ = 5a₂
a₁ = a₂
∴ f: Q → Q is an one – one function.
Let y ∈ Q (co-domain) then y = 5x + 4
y – 4 = 5x

f(x) = y
∴ f: Q → Q is an onto function.
∴ f: Q → Q is a bijection.
∴ f^-1: Q → Q is a bijection.

Question 6.
If f : R → R, g : R → R are defined by f(x) = 3x – 1, g(x) = x² + 1, then find (fog) (2). [Mar. 18 (AP) May 13; Mar 13]
Answer:
Given f: R → R and g : R → R defined by
f(x) = 3x – 1 ; g(x) = x² + 1
(fog) (2) = f[g(2)] = f(2² + 1)
= f(5) = 3(5) – 1 = 14

Question 7.
If f(x) = \(\frac{1}{x}\), g (x) = √x for all x ∈ (0, ∞), x then find (gof) (x).
Answer:
Given
f(x) = \(\frac{1}{x}\), g(x) = √x ∀ x ∈ (0, ∞)
Now (gof) (x) = g[f(x)] = g \(\left[\frac{1}{x}\right]\) = \(\sqrt{\frac{1}{x}}=\frac{1}{\sqrt{x}}\)

Question 8.
If f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) for all x ∈ R, then find (gof) (x). [Mar 19 (AP); Sep 92]
Answer:
Given f(x) = 2x – 1, g(x) \(\frac{x+1}{2}\) ∀ x ∈ R
Now (gof) (x) = g[f(x)] = g(2x – 1)
= \(\frac{2 \mathrm{x}-1+1}{2}\) = \(\frac{2 x}{2x}\) = x

Question 9.
If f(x) = 2, g(x) = x², h(x) = 2x for all x ∈ R, then find [fo(goh)] (x). [Mar. 17 (TS); July 01]
Answer:
Given f(x) = 2, g(x) = x², h(x) = 2x ∀ x ∈ R.
Now (goh) (x) = g[h(x)] = g[2x] = (2x)² = 4x²
[fo(goh)](x) = f[(goh) (x)] = f[4x²] = 2

Question 10.
Find the inverse function of f(x) = ax + b, (a ≠ 0); a, b ∈ R [Mar. 18 (TS); Mar. 13]
Answer:
Given, a, b ∈ R, f: R → R and
f(x) = ax + b
Let y = f(x) = ax + b
y = f(x) ⇒ x = f ^-1 (y) …………….. (1)
y = ax + b ⇒ ax = y – b ⇒ x = \(\frac{\mathrm{y}-\mathrm{b}}{\mathrm{a}}\) ……………… (2)
From (1) and (2)
f^-1(y) = \(\frac{y-b}{a}\) ⇒ f^-1(x) = \(\frac{x-b}{a}\)

If f: Q → Q is defined by f(x) = 5x + 4, for all x ∈ Q, find f^-1. [Mar. 12, 10]
Answer:
\(\frac{x-4}{5}\)

Question 11.
Find the inverse function of f(x) = 5^x [Mar. 15 (AP); Mar. ’11’, 06]
Answer:
Given f(x) = 5^x
Let y = f(x) = 5^x
y = f(x) ⇒ x = f^-1(y) …………………. (1)
y = 5x ⇒ x = log₅y ……………………. (2)
From (1) and (2),
f^-1(y) = log₅y ⇒ f^-1 (x) = log₅x

Question 12.
If f: R → R, g: R → R defined by f(x) = 3x – 2, g(x) = x² + 1, then find (i) (gof^-1) (2) (ii) (gof) (x – 1). [Mar. 08; May 06]
Answer:
Given f: R → R, g: R → R, f(x) = 3x – 2, g(x) = x² – 1
Let y = f(x) = 3x – 2
y = f(x) ⇒ x = f^-1 ……………. (1)
y = 3x – 2 ⇒ y + 2 = 3x
x = \(\frac{\mathrm{y}+2}{3}\) ………………….. (2)
From (1) & (2)
f^-1(y) = \(\frac{\mathrm{y}+2}{3}\)
⇒ f^-1 (x) = \(\frac{\mathrm{x}+2}{3}\)

(i) (gof^-1) (2)
= g[f^-1 (2)]

(ii) (gof) (x – 1)
= g[f(x -1)]
= g[3(x – 1) – 2]
= g[3x – 3 – 2]
= g(3x – 5)
= (3x – 5)² + 1
= 9x² + 25 – 30x + 1
= 9x² – 30x + 26

Question 13.
If f(x) = \(\frac{x+1}{x-1}\) (x ≠ ± 1), then find (fofof) (x) [Mar. 05]
Answer:
Given f(x) = \(\frac{x+1}{x-1}\) (x ≠ ± 1)

If f(x) = \(\) (x ≠ ± 1), then find (fofofof) (x)
Answer:
x

Question 14.
Find the domain of the real valued function f(x) = \(\sqrt{a^2-x^2}\) [June 04]
Answer:
Given f(x) = \(\sqrt{a^2-x^2}\) ∈ R
⇒ a² – x² ≥ 0
⇒ x² – a² ≤ 0
⇒ (x + a) (x – a) ≤ 0
– a ≤ x ≤ a

⇒ x ∈ [-a, a]
∴ Domain of ‘f is [-a, a]

Find the domain of the real valued function f(x) = \(\sqrt{16-x^2}\).
Answer:
[- 4, 4]

Find the domain of the real valued function f(x) = \(\sqrt{9-x^2}\).
Answer:
[-3, 3]

Question 15.
Find the domain of the real valued function
f(x) = \(\frac{1}{\left(x^2-1\right)(x+3)}\). [May 14, 93; Mar. 14]
Answer:
Given f(x) = \(\frac{1}{\left(x^2-1\right)(x+3)}\)
f(x) = \(\frac{1}{\left(x^2-1\right)(x+3)}\) ∈ R
⇒ (x² – 1) (x + 3) ≠ 0
x² – 1 ≠ 0, x + 3 ≠ 0
x² ≠ 1, x ≠ – 3
x ≠ ± 1
∴ x ≠ -3, -1, 1
∴ Domain of ‘f is R – {-3, -1, 1}

Find the domain of the real valued function f(x) = \(\frac{1}{6 x-x^2-5}\).
Answer:
R – {1, 5}

Find the domain of the real valued function f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\)
Answer:
R- {1, 2, 3}

Question 16.
Find the domain of the real valued function f(x) = \(\sqrt{4 x-x^2}\). [May 12, 10] [Mar; 18 (TS)]
Answer:
Given, f(x) = \(\sqrt{4 x-x^2}\) ∈ R
⇒ x(4 – x) ≥ 0

⇒ x(4 – x) ≥ 0
⇒ x(x-4) ≤ 0
⇒ (x – 0) (x – 4) ≤ 0
⇒ 0 ≤ x ≤ 4
∴ Domain of ‘f’ is [0, 4].

Question 17.
Find the domain of the real valued function f(x) = \(\frac{1}{\sqrt{1-x^2}}\)
Answer:
Given f(x) = \(\frac{1}{\sqrt{1-x^2}}\) ∈ R

⇔ 1 – x² > 0 “
⇔ (1 + x) (1 – x) > 0
⇔ x ∈ (-1, 1)
∴ Domain of T = {x/x ∈ (-1, 1)}

Question 18.
Find the domain of the real valued function f(x) = \(\sqrt{\mathbf{x}^2-25}\) [May 15 (AP); Mar. 12]
Answer:
Given f(x) = \(\sqrt{x^2-25}\) ∈ R
⇒ x² – 25 ≥ 0
⇒ (x + 5) (x – 5) ≥ 0
⇒ x < -5 or x > 5
⇒ x ∈ (- α, -5] ∪ [5, α)
∴ Domain of T is (-α, -5] ∪ [5, α).

Question 19.
Find the domain of the real valued function f(x) = log (x² – 4x + 3) [Mar. 16 (TS), 10, ‘08 ; May 11, 07]
Answer:
Given f(x) = log (x² – 4x + 3) ∈ R
⇒ x² – 4x + 3 > 0
⇒ x² – 3x – x + 3 > 0
⇒ x (x – 3) – 1 (x – 3) > 0
⇒ (x – 1) (x – 3) > 0
⇒ x < 1 or x > 3
⇒ x ∈ (- α, 1) ∪ (3, α)

Question 20.
Find the domain of the real valued function f(x) = \(\frac{\sqrt{3+x}+\sqrt{3-x}}{x}\)
Answer:
Given f(x) = \(\frac{\sqrt{3+x}+\sqrt{3-x}}{x}\) ∈ R
⇒ 3 + x ≥ 0 and 3 – x ≥ 0, x ≠ 0
x ≥ – 3 and 3 ≥ x, x ≠ 0, x ≤ 3
x ∈ [- 3, ∝) ∩ (-∝, 3) – {0}
⇒ x ∈ [- 3, 3] – {0}
(or)
⇒ x ∈ [- 3, 0) ∪ (0, 3]
∴ Domain of ‘f is [- 3, 3] – {0}

Find the domain of the real valued function f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\).
Answer:
[- 2, 0) ∪ (0, 2]

Question 21.
Find the range of the reed valued function, log |4 – x²|.
Answer:
Let y = f(x) = log |4 – x²|
f(x) ∈ R ⇒ 4 – x² ≠ 0
x² ≠ 4 ⇒ x ≠ ± 2
∴ Domain of ‘f is R – {- 2, 2}
∴ y = log_e |4 – x²|
|4 – x²| = e^y
⇒ e^y > 0, ∀ y ∈ R
∴ Range of T is R.

Question 22.
Find the range of the real valued function. \(\frac{x^2-4}{x-2}\) [May 03, 97]
Answer:
Let y = f(x) = \(\frac{x^2-4}{x-2}\)
f(x) ∈ R ⇒ x – 2 ≠ 0 ⇒ x ≠ 2
∴ Domain of ‘f is R – {2}
Let y = \(\frac{x^2-4}{x-2}\), if x ≠ 2 then y = x + 2
If x = 2, then y = 2 + 2 = 4
y is not defined at x = 2, then y cannot be equal to 4.
∴ Range of T is R – {4}.

Question 23.
Find the domain and range of the function f(x) = \(\frac{x}{2-3 x}\)
Answer:
Given f(x) = \(\frac{x}{2-3 x}\) ∈ R
⇒ 2 – 3x ≠ 0
⇒ 2 ≠ 3x
⇒ x ≠ \(\frac{2}{3}\)
∴ Domain of ‘f’ is R – \(\left\{\frac{2}{3}\right\}\)
Let y = f(x) = \(\frac{x}{2-3 x}\)
∴ y = \(\frac{x}{2-3 x}\)
2y – 3xy = x ⇒ 2y = x + 3x ⇒ 2y = x(1 + 3y)

Question 24.
If f = {(4, 5), (5, 6), (6, – 4)} and g = {(4, -4), (6, 5), (8, 5)}, then find
(i) f + 4
(ii) fg
(iii) √f
(iv) f².
Answer:
(i) f + 4
Domain of f + 4 = A = {4, 5, 6}
(f + 4) (x) = f(x) + 4
(f + 4) (4) = f(4) + 4 = 5 + 4 = 9
(f + 4) (5) = f(5) + 4 = 6 + 4= 10
(f + 4) (6) = f(6) + 4 = -4 + 4 = 0
∴ f + 4 = {(4, 9), (5, 10), (6, 0)}

(ii) fg
Domain of fg = A ∩ B = {4, 6}
(fg) (x) = f(x) . g(x)
(fg) (4) = f(4) . g(4) = 5(-4) = -20
(fg) (6) = f(6) . g(6) = (-4) (5) = -20
∴ fg = {(4, -20), (6, – 20)}

(iii) √f
Domain of √f = {4, 5, 6} = A
√f (x) = √f(x)
√f(4) = √f(4) = √5
√f (5) = √f(5) = √6
√f (6) = √f(6) = √-4 (does not exist)
∴ √f = {(4, √5), (5, √6)}

(iv) f²
Domain of f² = A = {4, 5, 6}
f²(x) = [f(x)]²
f²(4) = [f(4)]² = (5)² = 25
f²(5) = [f(5)]² = (6)² = 36
f²(6) = [f(6)]² = (- 4)² = 16
∴ f² = {(4, 25), (5, 36), (6, 16)}

If f = {(1, 2), (2, -3), (3, -1)}, then find
(i) 2f [Mar. 12; 94, 90; May 94]
(ii) 2 + f [Mar. 12; May 08]
(iii) f² [Mar. 08, May. 95, 90]
(iv) √f
Answer:
(i) {(1, 4), (2, -6), (3, -2)}
(ii) {(1, 4), (2, -1), (3, 1)}
(iii) {(1, 4), (2, 9), (3, 1)}
(iv) {(1, √2)}

Here you will find Telangana TSBIE State Board Syllabus TS Inter 1st Year English Study Material, Keep Going Interactive English Intermediate 1st Year English Textbook Solutions Pdf Download according to the latest exam curriculum. The chapter-wise TS Inter 1st Year Study Material will allow students to practice a wide range of questions, which will help them gain more knowledge and develop control over the subject.

TS Intermediate 1st Year English Study Material Pdf Download | TS Inter 1st Year English Textbook Solutions Telangana

Here, the students can access the links of chapter-wise Keep Going Interactive English Intermediate First Year English Textbook Solutions Pdf Download provides answers to all the textbook questions in simple language with the main aim of helping students ace the examinations.

TS Inter 1st Year English Textbook Answers

TS Intermediate 1st Year English Textbook Solutions – Poetry

• Chapter 1 Happiness
• Chapter 2 A Red Red Rose
• Chapter 3 The Beggar
• Chapter 4 The Nobel Nature
• Chapter 5 Keep Going

Inter 1st Year English Textbook Answers Telangana – Prose

• Chapter 6 Two Sides of Life
• Chapter 7 Father, Dear Father
• Chapter 8 The Green Champion – Thimmakka
• Chapter 9 The First Four Minutes
• Chapter 10 Box and Cox (One-act Play)

TS Inter 1st Year English Short Stories

• Chapter 11 Playing the Game
• Chapter 12 The Five Booms of Life
• Chapter 13 The Short-sighted Brothers
• Chapter 14 Sanghala Panthulu
• Chapter 15 The Dinner Party

TS Inter 1st Year English Reading Comprehension

• Reading Comprehension Passages from Short Stories
• Reading Comprehension Unseen Passages

TS Inter 1st Year English Grammar with Answers

• Matching Meanings
• Parts of Speech
• Articles
• Prepositions
• Tenses
• Transformation of Sentences
• Correction of Errors in Sentences
• Spelling: Missing Letters
• Silent Letters
• Phonetic Transcription
• Odd Sound Out
• Syllables
• Information Transfer

TS Inter 1st Year English Revision Tests I-V

• Revision Test-I
• Revision Test-II
• Revision Test-III
• Revision Test-IV
• Revision Test-V

We hope this TS Intermediate 1st Year English Textbook Solutions Pdf Download will be useful for students to get an idea of answering textbook questions efficiently. If there is any trouble in grasping the concepts related to TS Inter 1st Year English Textbook Answers Telangana, drop your questions in the comment and we will get back to you with a solution in time.

Telangana TSBIE TS Inter 1st Year Physics Study Material 6th Lesson Work, Energy and Power Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 6th Lesson Work, Energy and Power

Very Short Answer Type Questions

Question 1.
If a bomb at rest explodes into two pieces, the pieces must travel in opposite directions. Explain.
Answer:
Explosion is due to internal forces. In law of conservation of linear momentum internal forces cannot change the momentum of the system. So after explosion m₁v₁ + m₂v₂ = 0 or m₁v₁ = – m₂v₂ ⇒ they will fly in opposite directions.

Question 2.
State the conditions under which a force does no work.
Answer:

1. When force (F) and displacement (S) are mutually perpendicular then work done is zero.
   ∵ W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\) = |F| |S| cos θ when θ = 90° work W = 0
2. Even though force is applied if displacement is zero then work done W = 0.

Question 3.
Define Work, Power and Energy. State their S.I. units.
Answer:
Work :
The product of force and displacement along the direction of force is called work.
Work done W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\)
= \(|\overline{\mathrm{F}}||\overline{\mathrm{S}}|\) cos θ
S.I. unit of work is Joule.
Dimensional formula : ML²T^-2.

Power :
The rate of doing work is called power.

S.I. unit: Watt;
D.F. : ML²T^-3

Energy :
It is the capacity or ability of the body to do work. By spending energy we can do work or by doing work energy contentment of the body will increase.
S.I. unit: Joule ; D.F. : MML²T^-2

Question 4.
State the relation between the kinetic energy and momentum of a body.
Answer:
Kinetic energy K.E = \(\frac{1}{2}\)mv² ;
momentum \(\overline{\mathrm{p}}\) = mv
Relation between P and KE is
K.E = p²/2m. ⇒ P = \(\sqrt{K.E.2m}\)

Question 5.
State the sign of work done by a force in the following.
a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
b) Work done by gravitational force in the above case.
Answer:
a) When a bucket is lifted out of well work is done against gravity so work done is negative.

b) Work done by gravitational force is positive.

Question 6.
State the sign of work done by a force in the following.
a) work done by friction on a body sliding down an inclined plane.
b) work done gravitational force in the above case.
Answer:
a) Work done by friction while sliding down is negative. Because it opposes downward motion of the body.

b) Work done by gravitational force when a body is sliding down is positive.

Question 7.
State the sign of work done by a force in the following.
a) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
b) work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Answer:
a) Work done against the direction of motion of a body moving on a horizontal plane is negative.

b) In pendulum a∝ – y. So work done by air resistance to bring it to rest is considered as positive.

Question 8.
State if each of the following statements is true or false. Give reasons for your answer.
a) Total energy of a system is always conserved, no matter what internal and external forces on the body are present
b) The work done by earth’s gravitational force in keeping the moon in its orbit for its one revolution is zero.
Answer:
a) Law of conservation of energy states that energy can be neither created nor destroyed. This rule is applicable to internal forces and also for external forces when they are conservative forces.

b) Gravitational forces are conservative forces. Work done by conservative force around a closed path is zero.

Question 9.
Which physical quantity remains constant (i) in an elastic collision (ii) in an inelastic collision?
Answer:
In elastic collision :
P and K.E. are conserved, (remains constant)

In inelastic collision :
only momentum is conserved, (remains constant)

Question 10.
A body freely falling from a certain height ‘h’, after striking a smooth floor rebounds and h rises to a height h/2. What is the coefficient of restitution between the floor and the body?
Answer:
Given that, h₁ = h and h₂ = \(\frac{h}{2}\)
We know that coefficient of restitution.

Question 11.
What is the total displacement of freely falling body, after successive rebounds from the same place of ground, before it comes to stop? Assume that V is the coefficient of restitution between the body and the ground.
Answer:
Total displacement of a freely falling body after successive rebounds from the same place of ground, before it comes to stop is equal to height (h) from which the body is dropped.

Short Answer Questions

Question 1.
What is potential energy? Derive an expression for the gravitational potential energy.
Answer:
Potential energy :
It is the energy possessed by a body by the virtue of its position.
Ex: Energy stored in water a over head tank, wound spring.

Equation for potential energy :
Let a body of mass m is lifted through a height ‘h’ above the ground. Where ground is taken as refe-rence. In this process we are doing some work.

Work done against gravity W = m.g.h.
i. e., Force × displacement along the direction of force applied. This work done is stored in the body in the form of potential energy. Because work and energy can be interchanged.
∴ Potential Energy P.E. = mgh.

Question 2.
A lorry and a car moving with the same momentum are brought to rest by the application of brakes, which provide equal retarding forces. Which of them will come to rest in shorter time? Which will come to rest in less distance?
Answer:
Momentum (\(\overline{\mathrm{P}}\) = mv) is same for both lorry and car.
Work done to stop a body = Kinetic energy stored
∴ W = F. S = \(\frac{1}{2}\) mv² = K.E. But force applied by brakes is same for lorry and car.
Relation between \(\overline{\mathrm{P}}\) on K.E. is

So lighter body (car) will travel longer distance when P, F are same.
Then mS = constant.
∴ So car travels longer distance than lorry before it is stopped.

Question 3.
Distinguish between conservative and non-conservative forces with one example each.
Answer:
i) Conservative forces :
If work done by the force around a closed path is zero and it is independent of the path then such forces are called conservative forces.

Example:

1. Work done in lifting a body in gravitational field. When the body returns to its original position work done on it is zero.
   So gravitational forces are conservative forces.
2. Let a charge ‘q’ is moved in an electric field on a closed path then change in its electric potential i.e., static forces are conservative forces.

ii) Non-conservative forces :
For non-conservative forces work done by a force around a closed path is not equal to zero and it is dependent on the path.
Ex: Work done to move a body against friction. While taking a body between two points say A & B. We have to do work to move the body from A to B and also work is done to move the body from B to A. As result, the work done in moving the body in a closed path is not equals to zero. So frictional forces are non-conservative forces.

Question 4.
Show that in the case of one dimensional elastic collision, the relative velocity of approach of two colliding bodies before collision is equal to the relative velocity of separation after collision.
Answer:
To show relative velocity of approach of two colliding bodies before collision is equal to relative velocity of separation after collision.

Let two bodies of masses m₁, m₂ are moving with velocities u₁, u₂ along the straight line in same direction collided elastically.

Let their velocities after collision be v₁ and v₂.

According to the law of conservation of linear momentum
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ or m₁(u₁ – v₁) = m₂(v₂ – u₂) ………… (1)

According to law of conservation of kinetic energy
\(\frac{1}{2}\)m₁u²₁ + \(\frac{1}{2}\)m₂u²2 = \(\frac{1}{2}\)m₁v²₂ + \(\frac{1}{2}\)m₂v²₂
m₁(u²₁ – v²₁) = m₂(v²₂ – u²₂) ………. (2)
Dividing eqn. (2) by (1)

u₁ + v₁ = v₂ + u₂ ⇒ u₁ – u₂ = v₂ – v₁ ……. (3)
i.e., relative velocity of approach of the two bodies before collision = relative velocity of separation of the two bodies after collision. So coefficient of restitution is equal to ‘1’.

Question 5.
Show that two equal masses undergo oblique elastic collision will move at right angles after collision, if the second body initially at rest.
Answer:
Consider two bodies possess equal mass (m) and they undergo oblique elastic collision.

Let the first body moving with initial velocity ‘u’ collides with the second body at rest.

In elastic collision, momentum is conserved. So, conservation of momentum along X-axis yields.
mu = mv₁ cos θ₁ + mv₂ cos θ₂.
(i.e.) u = v₁ cos θ₁ + v₂ cos θ₂ ……. (1)
along Y-axis
0 = v₁ sin θ₁ – v₂ sin θ₂ ……… (2)
squaring and adding eq. (1) and (2) we get
u² = v²₁ + v²₂ + 2v₁v₂ cos (θ₁ + θ₂) …. (3)
As the collision is elastic,
Kinetic Energy (K.E.) is also conserved.

From eq. (3) and (4) 2v₁v₂ cos(θ₁ + θ₂) = 0
As it is given that v₁ ≠ 0 and v₂ ≠ 0
∴ cos(θ₁ + θ₂) = 0 or θ₁ + θ₂ = 90°.
The two equal masses undergoing oblique elastic collision will move at right angles after collision, if the second body initially at rest.

Question 6.
Derive an expression for the height attained by a freely falling body after ‘n’ number of rebounds from the floor.
Answer:
Let a small ball be dropped from a height ‘h’ on a horizontal smooth plate. Let it rebounds to a height ‘h₁‘.

Velocity with which it strikes the plate u₁ = \(\sqrt{2gh}\)
Velocity with which it leaves the plate v₁ = \(\sqrt{2gh_1}\)

The velocity of plate before and after collision is zero i.e., u₂ = 0, v₂ = 0
Coefficient of restitution,

For 2nd rebound it goes to a height
h₂ = e²h₁ = e²e²h = e⁴h

For 3rd rebound it goes to a height
h₃ = e²h₂ = e²e⁴h = e⁶h

For nth rebound height attained
h_n = e²ⁿh.

Question 7.
Explain the law of conservation of energy.
Answer:
Law of conservation of energy:
Wien forces doing work on a system are conservative then total energy of the system is constant i.e., energy can neither be created nor destroyed.
i.e., Total energy = (K + u) = constant form.

Explanation :
Consider a body undergoes small displacement ∆x under the action of conservative force F. According to work energy theorem.
Change in K.E = work done
∆K = F(x)∆x ………….. (1)
but Potential energy Au = -F(x)∆x ………….. (2)
from (1) and (2) = ∆K = – ∆u
⇒ ∆(K + u) = 0
Hence (K + u) = constant
i.e., sum of the kinetic energy and potential energy of the body is a constant

Since the universe may be considered as an isolated system, the total energy of the universe is constant.

Long Answer Questions

Question 1.
Develop the notions of work and kinetic energy and show that it leads to work- energy theorem. State the conditions under which a force does no work. [AP Mar. I 7, 15, May 1 7; TS Mar. 15]
Answer:
Work :
The product of component of force in the direction of displacement and the magnitude of displacement is called work.
W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\)
When \(\overline{\mathrm{F}}\) and \(\overline{\mathrm{S}}\) are parallel W = \(|\overline{\mathrm{F}}|\times|\overline{\mathrm{S}}|\)
When \(\overline{\mathrm{F}}\) and \(\overline{\mathrm{S}}\) has some angle 6 between them
W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\) cos θ

Kinetic energy :
Energy possessed by a moving body is called kinetic energy (k)

The kinetic energy of an object is a measure of the work that an object can do by the virtue of its motion.

Kinetic energy can be measured with equation K = \(\frac{1}{2}\)mv²
Ex : All moving bodies contain kinetic energy.

Work energy theorem (For variable force):
Work done by a variable force is always equal to the change in kinetic energy of the body.
Work done W = \(\frac{1}{2}\)mV² – \(\frac{1}{2}\)mV²₀? = K_f – K_i

Proof :
Kinetic energy of a body K = \(\frac{1}{2}\)mv²
Time rate of change of kinetic energy is

When force is conservative force F = F(x)
∴ On integration over initial position (x₁) and final position x₂

i.e., work done by a conservative force is equal to change in kinetic energy of the body.
Condition for Force not to do any work.

When Force (\(\overline{\mathrm{F}}\)) and displacement (\(\overline{\mathrm{S}}\)) are perpendicular work done is zero, i.e., when
θ = 90° then W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\) = 0

Question 2.
What are collisions? Explain the possible types of collisions? Develop the theory of one dimensional elastic collision. [TS Mar.’ 18; AF Mar. 19. May 14]
Answer:
A process in which the motion of a system of particles changes but keeping the total momentum conserved is called collision.

Collisions are two types :

1. elastic
2. inelastic.

To show relative velocity of approach before collision is equal to relative velocity of separation after collision.

Let two bodies of masses m₁, m₂ are moving with velocities u₁, u₂ along the same line in same direction collided elastically.

Let their velocities after collision are v₁ and v₂.

According to the law of conservation of linear momentum
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
or m₁ ( u₁ – v₁ ) = m₂ ( v₂ – u₂ ) ……… (1)

According to law of conservation of kinetic energy

i.e., In elastic collisions relative velocity of approach of the two bodies before collision = relative velocity of separation of the two bodies after collision.

Velocities of two bodies after elastic collision:

Question 3.
State and prove law of conservation of energy in case of a freely falling body. [TS Mar. ’19, ’17, ’16, May ’18, ’17, ’16, June ’15; AP Mar. ’18, ’16, ’15, May ’18, ’16, June ’15, May ’13]
Answer:
Law of conservation of energy :
Energy can neither be created nor destroyed. But it can be converted from one form into the another form so that the total energy will remains constant in a closed system.

Proof : In case of a freely fidling body :
Let a body of mass is dropped from a height H’ at point A.

Forces due to gravitational field are conservative forces, so total mechanical energy (E = P.E + K.E.) is constant i.e., neither destroyed nor created.

The conversion of potential energy to kinetic energy for a ball of mass ra dropped from a height H

1. At point H : Velocity of body v = 0
⇒ K = 0
Potential energy (u) = mgH
where H=height above the ground
T.E = u + K = mgH (1)

2. At point 0 :
i.e., just before touching the ground :
A constant force is a special case of specially dependent force F(x) so mechanical energy is conserved.
So energy at H = Energy at 0 = mgH

Proof:
At point ‘0’ height h = 0 ⇒
⇒ v = \(\sqrt{2gH}\) ; u = 0
K₀ = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) m2gH = mgH
Total energy E = mgH + 0 = mgH ………….. (2)

3. At any point h:
Let height above ground = h
u = mgh, K_h = \(\frac{1}{2}\)mV²
where v = \(\sqrt{2g(h – x)}\)
∴ Velocity of the body when it falls through a height (h – x) is \(\sqrt{2g(h – x)}\)
∴ Total energy =mgh + \(\frac{1}{2}\)m2g(H – h)
⇒ E = mgh + mgH – mgh = mgH ………… (3)
From eq. 1, 2 & 3 total energy at any point is constant.
Hence, law of conservation of energy is proved.

Conditions to apply law of conservation of energy:

1. Work done by internal forces is conservative.
2. No work is done by external force.

When the above two conditions are satisfied then total mechanical energy of a system will remain constant.

Problems

Question 1.
A test tube of mass 10 grams closed with a cork of mass 1 gram contains some ether. When the test tube is heated the cork flies out under the presssure of the ether gas. The test tube is suspended horizontally by a weight less rigid bar of length 5 cm. What is the minimum velocity with which the cork should fly out of the tube, so that test tube describing a full vertical circle about the point O. Neglect the mass of ether.
Solution:
Length of bar, L = 5 cm, = \(\frac{5}{100}\), g = 10m/s²
For the cork not to come out minimum velocity at lowest point is, v = \(\sqrt{5gL}\). At this condition centrifugal and centripetal forces are balanced.

Question 2.
A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 ms^-1. If the mass of each bullet is 5 gm, find the power of the machine gun? [AP May ’16, ’13, June ’15, Mar. ’14; AP Mar. ’18. ’16; TS May ’18]
Solution:
Number of bullets, n = 360
Time, t = 1 minute = 60s
Velocty of the bullet, v = 600 ms^-1 ; Mass of each bullet, m = 5gm = 5 × 10^-3 kg

⇒ P = 5400W = 5.4KW

Question 3.
Find the useful power used in pumping 3425 m³ of water per hour from a well 8 m deep to the surface, supposing 40% of the horse power during pumping is wasted. What is the horse power of the engine?
Solution:
Mass of water pumped, m = 3425 m³
= 3425 × 10³ kg.
Mass of lm³ water = 1000 kg
Depth of well d = 8 m., Power wasted = 40%
∴ efficiency, η = 60%
time, t = 1 hour = 3600 sec.

Question 4.
A pump is required to lift 600 kg of water per minute from a well 25m deep and to eject it with a speed of 50 ms^-1. Calculate the power required to perform the above task? (g = 10 m sec^-2) [TS Mar. ’19, ’16; AP May 18, Mar. 15, June 15]
Solution:
Mass of water m = 600 kg; depth = h = 25 m
Speed of water v = 25 m/s; g = 10 m/s², time t = 1 min = 60 sec.
Power of motor P = Power to lift water (P₁) + Kinetic energy of water (K.E) per second.
Power to lift water

∴ Power of motor P = 2500 + 3125 = 5625 watt 5.625 K.W.

Question 5.
A block of mass 5 kg initially at rest at the origin is acted on by a force along the X-positive direction represented by F=(20 + 5x)N. Calculate the work done by the force during the displacement of the block from x = 0 to x = 4m.
Solution:
Mass of block, m = 5 kg
Force acting on the block, F = (20 + 5x) N
If ‘w’ is the total amount of work done to displace the block from x = 0 to x = 4m then,

Question 6.
A block of mass 5 kg is sliding down a smooth inclined plane as shown. The spring arranged near the bottom of the inclined plane has a force constant 600 N/m. Find the compression in the spring at the moment the velocity of the block is maximum?

Solution:
Mass of the block, m = 5kg
Force constant, K = 600 N m^-1
From figure, sin θ = \(\frac{3}{5}\)
Force produced by the motion in the block,
F = mg sin0 ⇒ F = 5 × 9.8 × \(\frac{3}{5}\) = 29.4 N
But force constant K = \(\frac{F}{x}\) x
∴ x = \(\frac{F}{K}=\frac{29.5}{600}\) = 0.05m = 5cm

Question 7.
A force F = – \(\frac{K}{x^2}\) (x ≠ 0) acts on a particle along the X-axis. Find the work done by the force in displacing the particle from x = + a to x = + 2a. Take K as a positive constant.
Solution:
Force acting on the particle, F = –\(\frac{K}{x^2}\)
Total amount of work done to displace the particle from x = + a to x = + 2a is,

Question 8.
A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x = – a to x = + 2a?

Solution:
Average force acting on the particle, F = \(\frac{F}{K}\)

Amount of work done by the force to displace the particle from x = -a to x = +2a is,

Question 9.
From a height of 20 m above a horizontal floor, a ball is thrown down with initial velocity 20 m/s. After striking the floor, the ball bounces to the same height from which it was thrown. Find the coefficient of restitution for the collision between the ball and the floor? (g = 10 m/s²)
Solution:
Initial velocity = u¹ = 20 m/s, h – 20 m,
g = 10 m/s²

Velocity of approach,
u² = u^1² = u^1² +2as = 400+ 2 × 10 × 20
⇒ u² = 400 + 400 = 800 ⇒ u = 20√2
Height of rebounce = h = 20 m.
∴ Velocity of separation

Question 10.
A ball falls from a height of 10 m on to a hard horizontal floor and repeatedly bounces. If the coefficient of restitution is \(\frac{1}{\sqrt{2}\), then what is the total distance travelled by the ball before it ceases to rebound?
Solution:
Height from which the ball is allowed to fall, h = 10 m
Coefficient of restitution between the hard horizontal floor and the ball, e = \(\frac{1}{\sqrt{2}\)
∴ Total distance travelled by the ball before it ceases to rebound,

Question 11.
In a ballistics demonstration, a police officer fires a bullet of mass 50g with speed 200 msr1 on soft plywood of thickness 2 cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet?
Answer:
Mass of bullet m = 50g = 0.05 kg
Initial velocity V₀ = 200 m/s

Question 12.
Find the total energy of a body of 5 kg mass, which is at a height of 10 in from the earth and foiling downwards straightly with a velocity of 20 m/s. (Take the acceleration due to gravity as 10 m/s²) [TS May ’16]
Answer:
Mass m = 5 kg; Height h = 10 m ; g = 10 m/s²
Velocity v = 20 m/s.

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Hyperbolic Functions Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Hyperbolic Functions Important Questions

Question 1.
Show that sin h(x + y) = sin x cos hy + cos hx sin hy. [Mar ’98]
Answer:
R.H.S = sin x cos hy + cos hx sin hy

∴ sin h(x + y) = sin hx cos hy – cos hx. sinhy

Question 2.
Show that cos h(x + y) = cos hx cos hy + sin hx sin hy. [Mar. ’98, ’92]
Answer:
R.H.S = cos hx cos hy + sin hx sin hy

∴ cos h(x + y) = cos hx cos hy + sin hx sin hy.

Question 3.
Prove that sinh 2x = \(\frac{2 \tan h x}{1-\tan h^2 x}\). [May ’00]
Answer:

Question 4.
Show that cosh 2x – 1 = 2sinh²x. [Mar. ’08]
Answer:
L.H.S = cosh 2x – 1 = \(\frac{\mathrm{e}^{2 x}+\mathrm{e}^{-2 x}}{2}\) – 1
= \(\frac{\mathrm{e}^{2 x}+\mathrm{e}^{-2 \mathrm{x}}-2}{2}=\frac{\left(\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}\right)^2}{2}\)
= \(2\left[\frac{\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}}{2}\right]^2\) = 2sinh²x = RHS

Question 5.
Show that sinh^-1x = log_e(x + \(\sqrt{x^2+1}\)) [May ’03, ’97, ’95, ’91; Mar. ’95]
Answer:
Let sinh^-1x = y
sinh y = x ⇒ \(\frac{e^y-e^{-y}}{2}\) = x
⇒ e^y – e^-y = 2x
⇒ e^y – \(\frac{1}{\mathrm{e}^{\mathrm{y}}}\) = 2x
⇒ (e^y)² – 1 = 2xe^y
⇒ (e^y)² – 2xe^y – 1 = 0

This is a quadratic equation in e^y then
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
⇒ e = \(\frac{-(-2 x) \pm \sqrt{(-2 x)^2-4(1)(-1)}}{2.1}=\frac{2 x \pm \sqrt{4 x^2+4}}{2}\)
= x ± \(\sqrt{x^2+1}\)

Since e^y > 0 then, e^y = x + \(\sqrt{x^2+1}\)
y = log_e(x + \(\sqrt{x^2+1}\)
∴ sinh^-1x = log_e(x + \(\sqrt{x^2+1}\))

Question 6.
Show that cosh^-1x = log_e(x + \(\sqrt{x^2-1}\)) [Mar. ’03; May. ’96]
Answer:
Let cosh^-1x = y
cosh y = x ⇒ \(\frac{\mathrm{e}^{\mathrm{y}}+\mathrm{e}^{-\mathrm{y}}}{2}\) = x
⇒ e^y + e^-y = 2x
⇒ e^y + \(\frac{1}{\mathrm{e}^{\mathrm{y}}}\) = 2x
⇒ (e^y)² + 1 = 2xe^y
⇒ (e^y)² – 2xe^y + 1 = 0

This is a quadratic equation in e^y then
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\) e^y
= \(\frac{-(-2 \mathrm{x}) \pm \sqrt{(-2 \mathrm{x})^2-4(1)(1)}}{2.1}=\frac{2 \mathrm{x} \pm \sqrt{4 \mathrm{x}^2-4}}{2}\)
= x ± \(\sqrt{x^2-1}\)

Since e^y > 0 then e^y = x + \(\sqrt{x^2-1}\)
y = log_e (x + \(\sqrt{x^2-1}\))
∴ cosh^-1x = log_e(x + \(\sqrt{x^2-1}\))

Question 7.
Show that tanh^-1x = \(\frac{1}{2}\)log_e\(\left(\frac{1+x}{1-x}\right)\). [May ’97, ’93]
Answer:
Let tanh^-1x = y

Question 8.
If cosh x = \(\frac{5}{2}\), find the values of (i) cosh (2x) (ii) sinh (2x). [Mar. ’19, ’17 (TS), 16′ (AP), ’11, ’10, ’01; May ’15(TS), ’11, ’06]
Answer:
Given cosh x = \(\frac{5}{2}\)
(i) cosh (2x) = 2 cosh²x – 1 = 2\(\left(\frac{5}{2}\right)^2\) – 1
= 2\(\left(\frac{25}{4}\right)\) – 1 = \(\frac{25-2}{2}=\frac{23}{2}\)
∴ cosh (2x) = \(\frac{23}{2}\)

(ii) We know that cosh²(2x) – sinh²(2x) = 1
\(\left(\frac{23}{2}\right)^2\) – sinh²(2x) = 1
⇒ \(\frac{529}{4}\) – sinh² (2x) = 1
⇒ sinh²(2x) = \(\frac{529}{4}\) – 1
= \(\frac{525}{4}\) sinh (2x) = \(\pm \sqrt{\frac{525}{4}}=\pm \frac{5 \sqrt{21}}{2}\)

Question 9.
If cos hx = \(\frac{3}{2}\), then prove that tanh²\(\frac{x}{2}\) = tan² \(\frac{θ}{2}\). [May ’13; Mar. ’13]
Answer:
Given cosh x = sec θ
LHS = tanh²(\(\frac{x}{2}\)) = \(\frac{\cosh x-1}{\cosh x+1}=\frac{\sec \theta-1}{\sec \theta+1}=\frac{1-\cos \theta}{1+\cos \theta}\) = tan²(\(\frac{θ}{2}\)) = RHS

Question 10.
If sinh x = \(\frac{3}{4}\), find cosh (2x) and sinh (2x) [Mar. ’14; ’12; May ’14, ’09]
Answer:
Given sinh x = \(\frac{3}{4}\)
(i) cosh (2x) = 1 + 2 sinh²x = 1 + 2\(\left(\frac{3}{4}\right)^2\)
= 1 + 2\(\left(\frac{9}{16}\right)=\frac{8+9}{8}=\frac{17}{8}\)
∴ cosh (2x) = \(\frac{17}{8}\)

(ii) We know that cosh²(2x) – sinh²(2x) = 1
\(\left(\frac{17}{8}\right)^2\) – sinh(2x) = 1 ⇒ \(\frac{289}{64}\) – sinh²(2x) = 1
sinh²(2x) = \(\frac{289}{64}-1=\frac{289-64}{64}=\frac{225}{64}\)
∴ sinh²(2x) =±\(\frac{15}{8}\)

Question 11.
If sinh x = 3, then show that x = log_e(3 + \(\sqrt{10}\)) [May ’10; B.P]
Answer:
Given sin hx = 3 ⇒ x = sinh^-1(3) = log_e(3 + \(\sqrt{3^2+1}\)) [∵ sinh^-1x = log_e(x + \(\sqrt{\mathrm{x}^2+1}\))]
∴ x = log_e(3 + \(\sqrt{10}\))

Question 12.
Show that tanh^-1(\(\frac{1}{2}\)) = \(\frac{1}{2}\)log_e 3. [Mar. ’19, ’17, ’15(AP), ’08, ’05, ’02 May ’15(AP), ’07, ’05]
Answer:
L.H.S = tanh^-1(\(\frac{1}{2}\))
We know that tanh^-1(x) = \(\frac{1}{2}\)log_e\(\left(\frac{1+\mathrm{x}}{1-\mathrm{x}}\right)\)
Put x = \(\frac{1}{2}\)
⇒ tanh^-1(\(\frac{1}{2}\)) = \(\frac{1}{2}\)log_e\(\left(\frac{1+\frac{1}{2}}{1-\frac{1}{2}}\right)\) = \(\frac{1}{2}\)log_e\(\left(\frac{2+1}{2-1}\right)\)
∴ tanh^-1(\(\frac{1}{2}\)) = \(\frac{1}{2}\)log_e (3)

Question 13.
Prove that (cosh x – sinh x)ⁿ = cosh (nx) – sinh (nx). [Mar. ’15(TS); Mar. ’07, ’06]
Answer:

∴ L.H.S = R.H.S
∴ (cosh x – sinh x)ⁿ = cosh (nx) – sinh (nx).

Question 14.
Find the domain and range of the function y = tanh x. [May . ’04]
Answer:
Domain = R
Range = (-1, 1)

Question 15.
Show that f(x) = cosh x is an even function. [Mar. ’04]
Answer:
Given f(x) = cosh x = \(\frac{e^x+e^{-x}}{2}\)
Now, f(x) = \(\frac{\mathrm{e}^{-\mathrm{x}}+\mathrm{e}^{-(-\mathrm{x})}}{2}=\frac{\mathrm{e}^{-\mathrm{x}}+\mathrm{e}^{\mathrm{x}}}{2}\) = f(x)
∴ f(x) is an even function.

Some More Maths 1A Hyperbolic Functions Important Questions

Question 1.
Show that sinh (x – y) = sinh x cosh y – cosh x sinh y
Answer:
RHS = sinh x cosh y – cosh x sinh y

∴ sinh (x – y) = sinh x cosh y – cosh x sinh y

Question 2.
Show that cosh(x – y) = cosh x cosh y – sinh x sinh y
Answer:
RHS = cosh x cosh y – sinh x sinh y = \(\left[\frac{\mathrm{e}^{\mathrm{x}}+\mathrm{e}^{-\mathrm{x}}}{2}\right]\left[\frac{\mathrm{e}^{\mathrm{y}}+\mathrm{e}^{-\mathrm{y}}}{2}\right]-\left[\frac{\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}}{2}\right]\left[\frac{\mathrm{e}^{\mathrm{y}}-\mathrm{e}^{-\mathrm{y}}}{2}\right]\)

∴ cosh(x – y) = cosh x cosh y – sinh x sinh y

Question 3.
If cosh x = \(\frac{3}{2}\), then find the values of
(i) cosh 2x
(ii) sinh 2x
Answer:
Given cosh x = \(\frac{3}{2}\)
i) cosh 2x = 2cosh²x – 1 = 2\(\left(\frac{3}{2}\right)^2\) – 1 = 2.\(\frac{9}{4}\) – 1 = \(\frac{9}{2}\) – 1 = \(\frac{7}{2}\)
∴ cosh 2x = \(\frac{7}{2}\)

ii) We know that cosh²2x – sinh²2y = 1
\(\left(\frac{7}{2}\right)^2\) – sinh²2x = 1 = \(\frac{49}{4}\) = sinh²2x = \(\frac{49}{4}\) – 1 = \(\frac{45}{4}\)
⇒ sinh 2x = \(\frac{3 \sqrt{5}}{2}\)

Question 4.
If sin hx = 5, then show that x = log_e(5 + \(\sqrt{26}\))
Answer:
Given sin hx = 5 ⇒ x = sinh^-1x ⇒ sinh^-1(5)
We know that sinh^-1x = log_e(x + \(\sqrt{\mathrm{x}^2+1}\))
⇒ sinh^-1(5) = log_e(5 + \(\sqrt{5^2+1}\))
⇒ x = log_e(5 + \(\sqrt{25+1}\)) = log (5 + \(\sqrt{26}\))
∴ x = log_e(5 + \(\sqrt{26}\))

Question 5.
If tan hx = \(\frac{1}{4}\), then prove that x = \(\frac{1}{2}\)log_e\(\left(\frac{5}{3}\right)\)
Answer:
Given tan hx = \(\frac{1}{4}\)
⇒ x = tan h^-1\(\left(\frac{1}{4}\right)\)
We know that tan h^-1x = \(\frac{1}{2}\)log_e\(\left(\frac{1+\mathrm{x}}{1-\mathrm{x}}\right)\) ⇒ tan h^-1\(\left(\frac{1}{4}\right)\) = \(\frac{1}{2}\)log_e\(\left(\frac{1+\frac{1}{4}}{1-\frac{1}{4}}\right)\)
⇒ x = \(\frac{1}{2}\)log_e\(\left(\frac{4+1}{4-1}\right)\) = \(\frac{1}{2}\)log_e\(\left(\frac{5}{3}\right)\)
∴ x = \(\frac{1}{2}\)log_e\(\left(\frac{5}{3}\right)\)

Question 6.
Prove that (cosh x + sinh x)ⁿ = cosh(nx) + sinh (nx)
Answer:

∴ L.H.S = R.H.S
∴ (cosh x + sinh x)ⁿ = cosh(nx) + sinh (nx)

Question 7.
Prove that cosh²x – sinh²x = 1
Answer:
L.H.S = cosh²x – sinh²x

Question 8.
For any x ∈ R show that cosh 2x = 2cosh²x – 1.
Answer:
LHS = cosh 2x = \(\frac{\mathrm{e}^{2 \mathrm{x}}+\mathrm{e}^{-2 \mathrm{x}}}{2}\)
RHS = 2cosh²x – 1

∴ LHS = RHS
∴ cosh 2x = 2cosh²x – 1

Question 9.
Prove that sinh (3x) = 3sin hx + 4 sinh³x
Answer:
RHS = 3sin hx + 4 sinh³x

= sinh (3x) = LHS
∴ sinh (3x) = 3sin hx + 4 sinh³x

Question 10.
Prove that cos h(3x) = 4cos h³x – 3 cos hx
Answer:
RHS = 4cos h³x – 3 cos hx

= cos h(3x) = LHS
∴ cos h(3x) = 4cos h³x – 3 cos hx

Question 11.
Prove that tanh 3x = \(\frac{3 \tanh x+\tanh ^3 x}{1+3 \tanh ^2 x}\)
Answer:

Question 12.
Prove that tanh(x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh \times \tanh y}\)
Answer:
LHS = tanh(x – y)

Dividing numerator and denominator by cos hx cos hy we get = \(\frac{\tanh x-\tanh y}{1-\tanh \times \tanh y}\) = RHS
∴ tanh(x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh \times \tanh y}\)

Question 13.
Prove that coth(x – y) = \(\frac{{coth} x \cdot {coth} y-1}{{coth} y-{coth} x}\)
Answer:
LHS = coth(x – y)

Dividing by sinh x sinh y we get = \(\frac{{coth} x {coth} y-1}{{coth} y-{coth} x}\) = RHS
∴ coth(x – y) = \(\frac{{coth} x \cdot {coth} y-1}{{coth} y-{coth} x}\)

Here you will find Telangana TSBIE State Board Syllabus TS Inter 1st Year Telugu Study Material Pdf free download  నవోదయం & కథాలహరి, TS Intermediate 1st Year Telugu Textbook Solutions Questions and Answers according to the latest exam curriculum. The chapter-wise TS Inter 1st Year Study Material will allow students to practice a wide range of questions, which will help them gain more knowledge and develop control over the subject.

TS Intermediate 1st Year Telugu Study Material Pdf Download | TS Inter 1st Year Telugu Textbook Solutions Telangana

Here, the students can access the links of chapter-wise TS Inter 1st Year Telugu Study Material నవోదయం & కథాలహరి provides answers to all the textbook questions in simple language with the main aim of helping students ace the examinations.

TS Inter 1st Year Telugu Poems పద్య భాగం

• Poem 1 విద్యాలక్ష్యం
• Poem 2 మిత్రధర్మం
• Poem 3 శతక సుధ
• Poem 4 అచలం
• Poem 5 నాపేరు ప్రజాకోటి
• Poem 6 మహైక

TS Inter 1st Year Telugu Textbook Lessons గద్య భాగం

• Chapter 1 పాల్కురికి సోమనాథుడు
• Chapter 2 తెలంగాణ తెలుగుపదాలు – ఉర్దూ మూలాలు
• Chapter 3 ప్రాచీన సాహిత్యంలో మానవతావాదం
• Chapter 4 బతుకమ్మ పండుగ
• Chapter 5 తెలంగాణ జాతీయాలు
• Chapter 6 రాజాబహద్దుర్ వేంకట రామారెడ్డి సేవాతత్పరత

TS Inter 2nd Year Telugu Non-Detailed ఉపవాచకం : కథాలహరి

• Chapter 1 గొల్ల రామవ్వ
• Chapter 2 బిచ్చగాడు?
• Chapter 3 స్నేహలతాదేవి లేఖ
• Chapter 4 ఇన్సానియత్

TS Inter 1st Year Telugu Grammar వ్యాకరణాంశాలు

• సంధులు
• సమాసాలు
• లేఖారచన
• సాధారణ వ్యాసాలు
• స్థూల అవగాహన
• అనువాదం

We hope this TS Intermediate 1st Year Telugu Study Material Pdf Download నవోదయం & కథాలహరి will be useful for students to get an idea of answering textbook questions efficiently. If there is any trouble in grasping the concepts related to TS Inter 1st Year Telugu Textbook Solutions Telangana, drop your questions in the comment and we will get back to you with a solution in time.

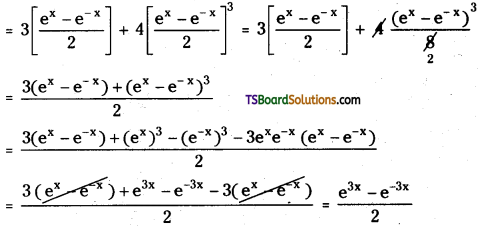
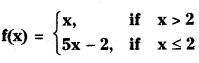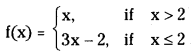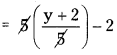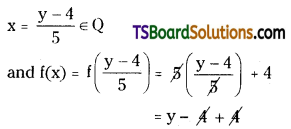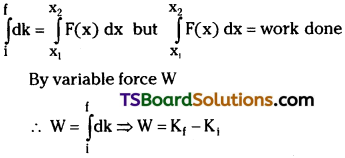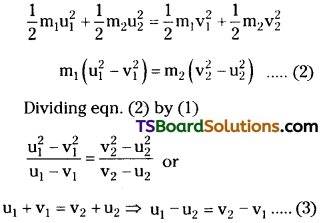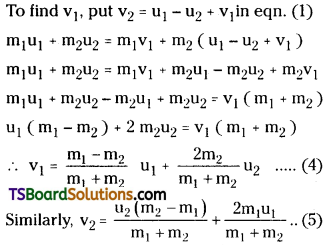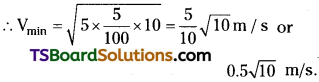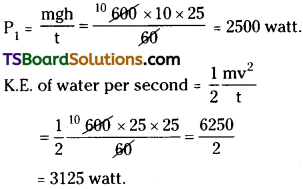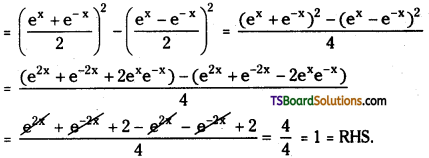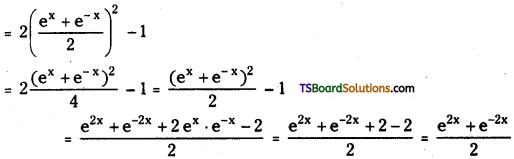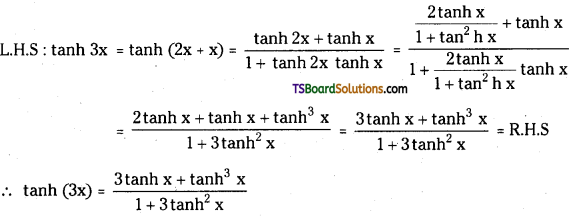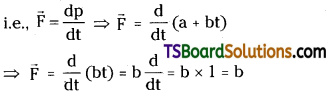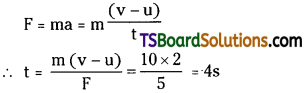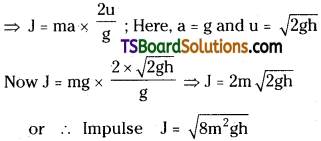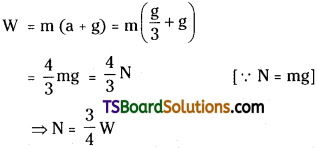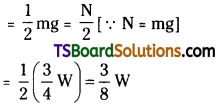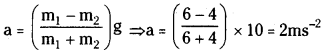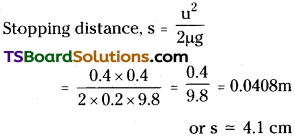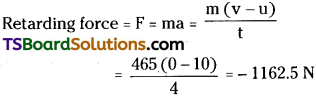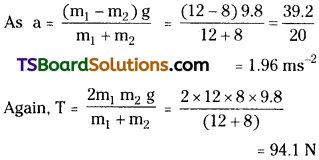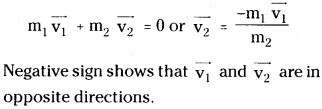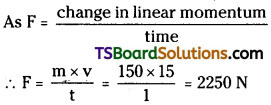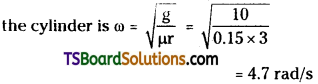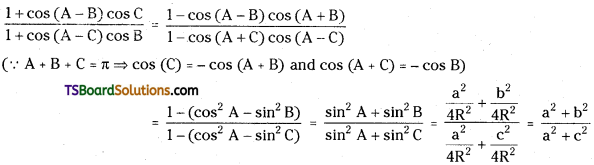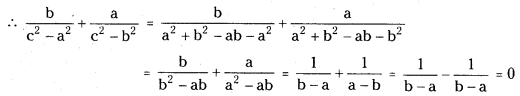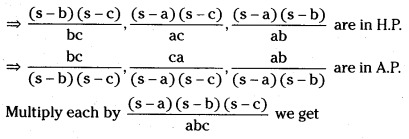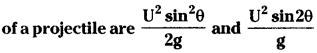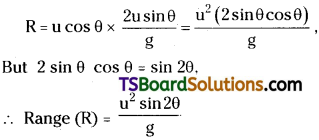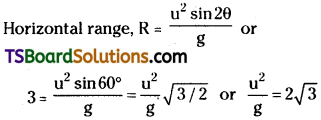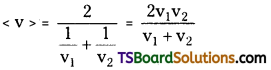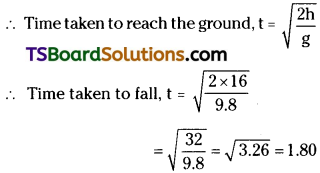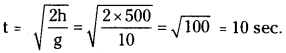Telangana TSBIE TS Inter 1st Year Physics Study Material 5th Lesson Laws of Motion Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 5th Lesson Laws of Motion

Very Short Answer Type Questions

Question 1.
Why are spokes provided in a bicycle wheel? [AP May ’14. ’13]
Answer:
The spokes of cycle wheel increase its moment of inertia. The greater the moment of inertia, the greater is the opposition to any change in uniform rotational motion. As a result the cycle runs smoother and steadier. If the cycle wheel had no spokes, the cycle would be driven with jerks and hence unsafe.

Question 2.
What is inertia? What gives the measure of inertia? [TS ‘Mar. 17; AP Mar. 19, 14]
Answer:
The inability of a body to change its state by itself is known as inertia.

Mass of a body is a measure for its Inertia.
Types of inertia

1. Inertia of rest
2. Inertia of motion
3. Inertia of direction.

Question 3.
According to Newton’s third law, every force is accompanied by an equal and opposite force. How can a movement ever take place? [AP May 17, June 15]
Answer:
From Newton’s third law action = – reaction. But action and reaction are not working on the same system. So they will not cancel each other. Hence, motion is possible.

Question 4.
When a bullet is fired from a gun, the gun gives a kick in the backward direction. Explain. [AP Mar. ’15]
Answer:
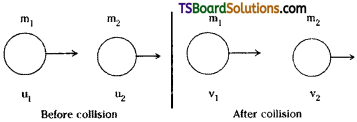
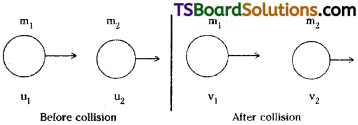
Firing of a gun is due to internal forces. Internal forces do not change the momentum of the system. Before firing m₁u₁ + m₂u₂ = 0. Since system is at rest after firing m₁v₁ + m₂v₂ = 0 (or) m₁v₁ = – m₂v₂. So gun and bullet will move in opposite directions to satisfy law of conservation of linear momentum.

Question 5.
Why does a heavy rifle not recoil as strongly as a light rifle using the same cartridges?
Answer:
Velocity (or) recoil v = \(\frac{mv}{M}\) i.e., ratio of momentum of bullet to mass of gun. If mass of gun is high then velocity of recoil is less with same cartridge.

Question 6.
If a bomb at rest explodes into two pieces, the pieces must travel in opposite directions. Explain. [TS Mar. 16, 15, June 15]
Answer:
Explosion is due to internal forces. From law of conservation of linear momentum, internal forces cannot change the momentum of the system. So after explosion m₁v₁ + m₂v₂ = 0 (or) m₁v₁ = – m₂v₂. According to law of conservation of linear momentum they will fly in opposite directions.

Question 7.
Define force. What are the basic forces in nature?
Answer:
Force is that which changes (or) tries to change the state of a body.

The basic forces in nature are :

1. Gravitational forces,
2. Electromagnetic forces,
3. Nuclear forces.

Question 8.
Can the coefficient of friction be greater than one?
Answer:
Yes. Generally coefficient of friction between the surfaces is always less than one. But under some special conditions like on extreme rough surfaces coefficient of friction may be greater than one.

Question 9.
Why does the car with a flattened tyre stop sooner than the one with inflated tyres?
Answer:
Due to flattening of tyres, frictional force increases. Because rolling frictional force between the surfaces is proportional to area of contact. Area of contact increases for flattened tyres. So rolling frictional force increases and the car will be stopped quickly.

Question 10.
A horse has to pull harder during the start of the motion than later. Explain. [AP Mar. 18, May 16, Mar. 13]
Answer:
To start motion in a body we must apply force to overcome static friction (F_s = µ_smg). When once motion is started between the bodies then kinetic frictional force comes into act. Kinetic friction (F_k = µ_kmg) is always less than static friction. So it is tough to start a body from rest than to keep it in motion.

Question 11.
WHat happens to the coefficient of friction if the weight of the body is doubled? [TS Mar. 19; AP Mar. 16, May 14]
Answer:
When weight of the body is doubled still then there is no change in coefficient of friction. Because frictional force cc normal reaction. So when weight of a body is doubled then frictional force and normal reaction will also becomes doubled and coefficient of friction remains constant.

Short Answer Questions

Question 1.
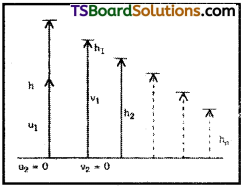
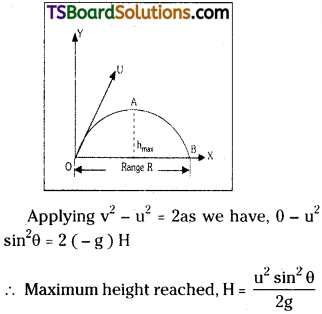
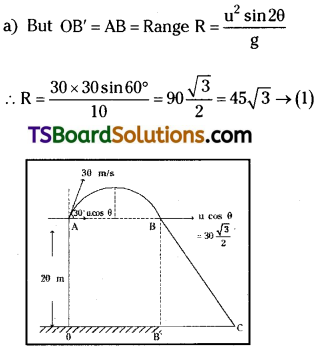
A stone of mass 0.1 kg is thrown vertically upwards. Give the magnitude and direction of the net force on the stone (a) during its upward motion, (b) during its downward motion, (c) at the highest point, where it momentarily comes to rest.
Answer:
Mass of stone, m = 0.1 kg.
a) During upward motion force acts downwards due to acceleration due to gravity.
Magnitude of force F = mg = 0.1 × 9.8
= 0.98 N (↓)
b) During downward motion force acts downward. Magnitude of force F = mg
= 0.1 × 9.8 = 0.98N (↓)

c) At highest point velocity v = 0. But still g will act on it only in downward motion so resultant force F = 0.98 N. downward.
Note : In the entire journey of the body force due to gravitational pull acts only in downward direction.

d) If the body is thrown with an angle of 30° with horizontal then vertical component of gravitational force does not change, hence in this case downward force F = mg = 0.1 × 9.8
= 0. 98 newton.

Question 2.
Define the terms momentum and impulse. State and explain the law of conservation of linear momentum. Give examples. [TS May 18, June 15]
Answer:
Momentum (\(\overline{\mathrm{P}}\)) : It is the product of mass and velocity of a body.

Momentum (\(\overline{\mathrm{P}}\)) = mass (m) × velocity (v)
∴ (\(\overline{\mathrm{P}}\)) = m\(\overline{\mathrm{v}}\)

Impulse (J) :
When a large force (F) acts on a body for small time (t) then the product of force and time is called Impulse.
Impulse (J) = Force (F) × time (t)
∴ Impulse (J) = F × t

Law of conservation of linear momentum:
There is no external force act on the system. The total linear momentum of the isolated system remains constant.

Proof :
Let two bodies of masses say A and B are moving with initial momenta PA and PB collided with each other. During collision they are in contact for a small time say ∆t. During this time of contact they will exchange their momenta. Let final momenta of the bodies are P¹_A and P¹_B. Let force applied by A on B is F_AB and force applied by B on A is F_BA.

From Newton’s 3rd Law F_AB = F_BA or F_AB ∆t = F_BA ∆t

From 2nd Law F_AB∆t = P¹_A – P_A change in momentum of A.
F_BA ∆t = P¹_B – P_B change in momentum of B.
∴ P¹_B – P_A = P¹_B – P_B or P_A + P_B = P¹_B + P¹_B
i. e., sum of momentum before collision is equals to sum of momentum after collision.

Question 3.
Why are shock absorbers used in motor cycles and cars? [AP June ’15]
Answer:
When vehicles are passing over the vertocies and depressions of a rough road they will collides with them for a very short period. This causes impulse effect. Due to large mass and high speed of the vehicles the magnitude of impulse is also high. Impulse may cause damage to the car or even to the passengers in it.

The bad effects of impulse is less if time of contact is more. Impulse J = F.t. For the same magnitude of impulse (change in momentum) if time of contact is high force acting on the vehicle is less. Shock absorbers will absorb the impulse and releases the same force slowly. This is due to large time constant of the springs.

So shock absorbers are used in vehicles to reduce impulse effects.

Question 4.
Explain the terms limiting friction, dynamic friction and rolling friction.
Answer:
Limiting friction :
Frictional forces always oppose relative motion between the bodies. These forces are self adjusting forces. Their magnitude will increase upto some extent with the value of applied force.

The maximum frictional force between the bodies at rest is called “limiting friction”.

Dynamic (or) kinetic friction :
When applied force is equal to or greater than limiting friction then the body will move. When once motion is started then frictional , force will abruptly falls to a minimum value.

Frictional force between moving bodies is called dynamic (or) kinetic friction. Kinetic friction is always less than limiting friction.

Rolling friction :
The resistance encountered by a rolling body on a surface is called rolling friction.

Question 5.
Explain the advantages and disadvantages of friction. [TS Mar. ’17, ’15; AF Mar. ’15]
Answer:
Advantages of friction :

1. We are able to walk because of friction.
2. It is impossible for a car to move on a slippery road.
3. Breaking system of vehicles works with the help of friction.
4. Friction between roads and tyres provides the necessary external force to accelerate the car.
5. Transmission of power to various parts of a machine through belts is possible by friction.

Disadvantages of friction:

1. In many cases we will try to reduce friction because it dissipates energy into heat.
2. It causes wear and tear to machine parts which causes frequent replacement of machine parts.

Question 6.
Explain Friction. Mention the methods used to decrease friction. [TS May, ’17, ’16; Mar. ’19, ’16; AP Mar. ’18. ’14; May ’18, ’14)
Answer:
Friction :
It is a contact force parallel to the surfaces in contact Friction will always oppose relative motion between the bodies.

Friction is a necessary evil. Friction is a must at some places and it must be reduced at some places.

Methods to reduce friction :
1) Polishing :
Friction causes due to surface irregularities. So by polishing friction can be reduced to some extent.

2) Lubricants :
By using lubricants friction can be reduced. Lubricants will spread as an ultra thin layer between the surfaces in contact and in friction decreases.

3) A thin cushion of air maintained between solid surfaces reduces friction.
Ex : Air pressure in tyres.

4) Ball bearings :
Ball bearings are used to reduce friction between machine parts.

Ball bearings will convert sliding motion into rolling motion. As a result friction is reduced.

Question 7.
State the laws of rolling friction.
Answer:
When a body is rolling over the other, then friction between the bodies is known as rolling friction.

Rolling friction coefficient,

Laws of rolling friction :

1. Rolling friction will develop a point contact between the surface and the rolling sphere. For objects like wheels line of contact will develop.
2. Rolling friction(f_r) has least value for given normal reaction when compared with static friction (f_s) or kinetic friction (f_k)
3. Rolling friction is directly proportional
   to normal reaction, f_r ∝ N.
4. In rolling friction the surfaces in contact will get momentarily deformed a little.
5. Rolling friction depends on area of contact. Due to this reason friction increases when air pressure is less in tyres (Flattened tyres).
6. Rolling friction is inversely proportional to radius of rolling body µ_r ∝ \(\frac{1}{r}\)

Question 8.
Why is pulling the lawn roller preferred to pushing it?
Answer:
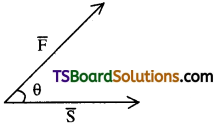
Let a lawn roller is pulled by means of a force F with some angle θ to the horizontal. By resolving the force into two components.

1. Horizontal component F cos θ is useful to pull the body.
2. The vertical component F sin θ opposes the weight

So N.R. = mg – F sin θ
But frictional force = µ. N.R.
∴ Frictional force [µ(mg – F sin θ)] decreases.

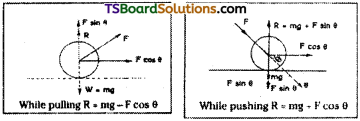
So it is easier to pull the body.
When the lawn roller is pushed by a force, the vertical component F sin θ causes the apparent increase of weight of the object. So the normal reaction N.R. = mg + F sin θ.
∴ Frictional force [µ(mg + F sin θ)] increases and it will be difficult to pull the body.

Long Answer Questions

Question  1.
a) State Newton’s second law of motion. Hence, derive the equation of motion F = ma from it. [AP Mar. ’19, ’17, ’16; AP May ’17. ’16; May ’13]
b) A body is moving along a circular path such that its speed always remains constant. Should there be a force acting on the body?
Answer:
a) Newton’s 2nd law :
The rate of change of momentum of a body is proportional to external force and acts along the direction of force applied.
i.e., \(\frac{dp}{dt}\) ∝ F

Derivation of equation F = ma:
According Newton’s 2nd law.
We know


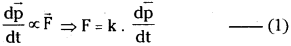
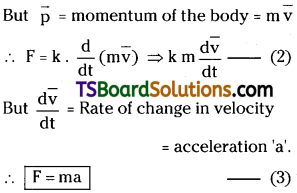
Here, k = constant.
The proportional constant is made equal to one, by properly selecting the unit of force.
∴ F = ma

b) Force on a body moving in a circular path :
Let a body of mass’m’ is moving in a circular path of radius V with constant speed. The velocity of the body is given by the tangent drawn at that point. Since velocity is changing continuously the body will have acceleration.

So the body will experience some acceleration. This is called normal acceleration (or) centripetal acceleration.

Question 2.
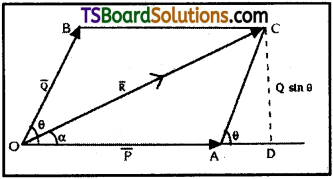
Define Angle of friction and Angle of repose. Show that angle of friction is equal to angle of repose for a rough inclined plane.
A block of mass 4 kg is resting on a rough horizontal plane and is about to move when a horizontal force of 30 N is applied on it. If g = 10 m/s². Find the total contact force exerted by the plane on the block.
Answer:
Angle of friction :
The angle made by the resultant of the Normal reaction and the limiting friction with Normal reaction is called angle of friction (Φ).

Angle of reppse :
Let a body of mass m is placed on a rough inclined plane. Let the angle with the horizontal ‘θ’ is gradually increased then fora particular angle of inclination (say α) the body will just slide down without acceleration. This angle θ = α is called angle of repose. At this stage the forces acting on the body are in equilibrium.

Equation for angle of repose :
Force acting on the body in vertically downward direction = W = mg.
By resolving this force into two components.

1. Force acting along the inclined plane in downward direction = mg sin θ.
   This component is responsible for downward motion.
2. The component mg cos θ . which is balanced by the normal reaction.

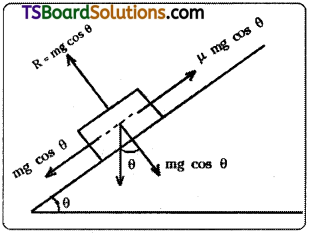
If the body slides down without acceleration resultant force on the body is zero, then
mg sin θ = Frictional force (f_k)
mg cos θ = Normal reaction (N.R.)
But coefficient friction

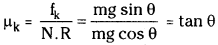
Hence θ = α is called angle of repose.
∴ µ_k = tan α

Hence tangent of angle of repose (tan θ) is equal to coefficient of friction (f_k) between the bodies.

b) When the block rests on the horizontal surface, it is in equilibrium under the action of four forces. They are
i) Normal reaction (N)
ii) Weight of the block (mg)
iii) Horizontal force (30 N)
iv) Limiting frictional force (f_L)

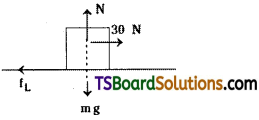
If the applied horizontal force is equal to the limiting frictional force, then only the block will be ready to move on the rough horizontal surface, i.e., f_L = horizontal force applied.
∴ Total contact force = 30 N.

Problems

Question 1.
The linear momentum of a particle as a function of time ‘t’ is given by, p = a + bt, where a and b are positive constants. What is the force acting on the particle?
Solution:
Linear momentum of a particle, p = a + bt
We know that force acting on a particle is equal to rate of change of linear momentum.

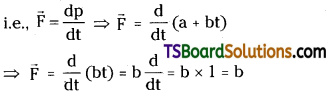
Question 2.
Calculate the time needed for a net force of 5 N to change the velocity of a 10 kg mass by 2 m/s. [TS May ’16]
Solution:
Force, F = 5N
Change in velocity, v – u = 2ms ^-1
Mass, m= 10 kg
From Newton’s second law of motion,

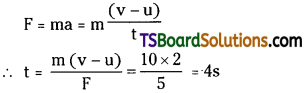
Question 3.
A ball of mass ‘m’ is thrown vertically upward from the ground and reaches a height ‘h’ before momentarily coming to rest, If ‘g’ is acceleration due to gravity. What is the impulse received by the ball due to gravity force during its flight?
Solution:
Impulse, J = force × time

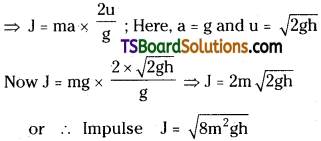
Question 4.
A constant force acting on a body of mass 3.0 kg changes its speed from 2.0 m s^-1 to 3.5 m s^-1 in 25 s. The direction of motion of the body remains unchanged. What is the magnitude and direction of the force?
Solution:
Mass of the body, m = 3.0 kg ;
Initial velocity of the body, u = 2.0 ms^-1
Final velocity of the body, v = 3.5 ms^-1
Time, t = 25 s
From Newton s second law of motion,

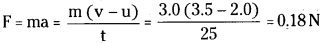
∴ Magnitude of force acting on the body, F = 0.18 N. The direction of force acting on the body is along the direction of motion of the body because force is positive.

Question 5.
A man in a lift feels an apparent weight ‘W’ when the lift is moving up with a uniform acceleration of 1/3^rd of the acceleration due to gravity. If the same man was in the same lift now moving down with a uniform acceleration that is 1/2 of the acceleration due to gravity, then what is his apparent weight?
Solution:
Case (i) :
When lift is moving upwards :
Apparent weight of the man = W
Acceleration, a = g/3
Apparent weight of the man when the lift is moving upwards is,

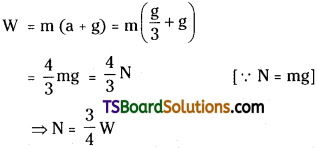
Case (ii) : When lift is moving downwards:
Let W’ be the apparent weight of the man Acceleration, a = g/2
Apparent weight of the man when the lift is moving downwards is,
W’ = m(g – a) = m (g – g/2)

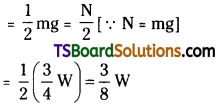
Question 6.
A container of mass 200 kg rests on the back of an open truck. If the truck accelerates at 1.5 m/s², what is the minimum coefficient of static friction between the container and the bed of the truck required to prevent the container from sliding off the back of the truck?
Solution:
Mass of the container, m = 200 kg
Acceleration of truck, a = 1.5 ms^-2
Coefficient of static friction, µ_s = \(\frac{a}{g}\)
\(\frac{1.5}{9.8}\) = 0.153

Question 7.
A bomb initially at rest at a height of 40 m above the ground suddenly explodes into two identical fragments. One of them starts moving vertically downwards with an initial speed of 10m/s. If acceleration due to gravity is 10m/s², What is the separation between the fragments 2s after the explosion?
Solution:
Case (i): (for downward moving fragment)
Initial velocity, u = 10 ms^-1
Acceleration, a = +g = 10 ms^-2
Time, t = 2s
From the equation of motion, s = ut + \(\frac{1}{2}\) at²
the distance moved in downward direction is,
s₁ = 10 × 2 + \(\frac{1}{2}\) × 10 × (2)² = 40 m

Case (ii) (for upward moving fragment)
Given that two fragments are identical hence, after explosion the fragments move in opposite directions. Here the first fragment moves in downward direction, hence, second fragment moves upward direction.
Again from s = ut = \(\frac{1}{2}\)at² we can write,
s₂ = – 10 × 2 + \(\frac{1}{2}\) × 10 × 4 = -20 + 20 = 0m
∴ Separation between the fragments 2s after the explosion = S₁ ~ S₂ = 40 – 0 = 40m

Question 8.
A fixed pulley with a smooth grove has a light string passing over it with a 4 kg attached on one side and a 3 kg on the other side. Another 3 kg is hung from the other 3 kg as shown with another light string. If the system is released from rest, find the common acceleration? (g = 10 m/s²)

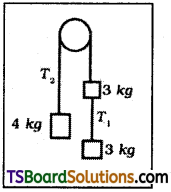
Solution:
Here, m₁ = 3 + 3 = 6 kg; m₂ = 4 kg ;
g = 10 ms^-2

Acceleration of the system,

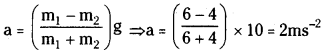
Question 9.
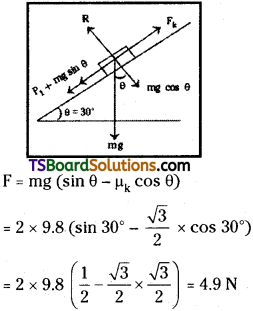
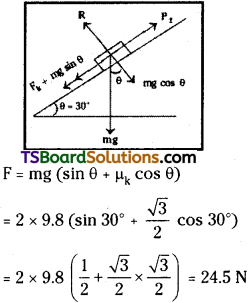
A block of mass of 2 kg slides on an inclined plane that makes an angle of 30° with the horizontal. The coefficient of friction between the block and the surface is √3/2.
a) What force should be applied to the block so that it moves down without any acceleration?
b) What force should be applied to the block so that it moves up without any acceleration?
Solution:
Mass of the block, m = 2kg
Angle of inclination, θ = 30°
Coefficient of friction between the block and the surface, µ = \(\frac{\sqrt{3}}{2}\)

a) The required force to move the block down without acceleration is,

b) The required force to move the block up without any acceleration is,

Question 10.
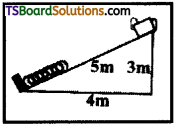
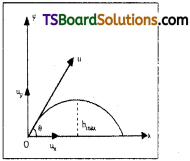
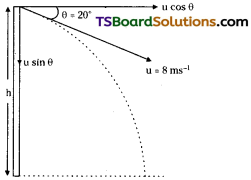
A block is placed on a ramp of parabolic shape given by the equation y = x²/20, sec Figure.

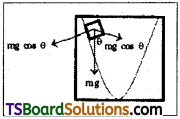
If µ_s = 0.5, what is the maximum height above the ground at which the block can be placed without slipping?
(tan θ = µ_s = \(\frac{dy}{dx}\))
Solution:
For the body not to drop
mg cos θ = µ mg sin θ
⇒ tan θ = µ given µ = 0.5 dy
But tan θ = \(\frac{dy}{dx}\) slope of parabolic region
⇒ \(\frac{dy}{dx}\) = µ = 0.5 …………… (1)

Question 11.
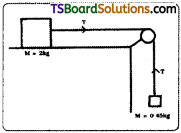
A block of metal of mass 2 kg on a horizontal table is attached to a mass of 0.45 kg by a light string passing over a frictionless pulley at the edge of the table. The block is subjected to a horizontal force by allowing the 0.45 kg mass to fall. The coefficient of sliding friction between the block and table is 0.2.
Calculate (a) the initial acceleration, (b) the tension in the string, (c) the distance the block would continue to move if, after 2 s of motion, the string should break.

Solution:
Mass of first block, m₁ = 0.45kg
Mass of second block, m₂ = 2 kg
coefficient of slidding friction between the block and table, µ = 0.2

b) Tension in the string

c) Velocity of string after 2 sec = u in this case; u’ = 0
∴ u = u’ + at = 0 + 0.2 × 2 = 0.4 m/s

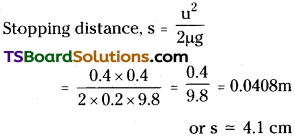
Question 12.
On a smooth horizontal surface, a block A of mass 10 kg is kept. On this block, a second block B of mass 5 kg is kept. The coefficient of friction between the two blocks is 0.4. A horizontal force of 30 N is applied on the lower block as shown. The force of friction between the blocks is (take g = 10 m/s²)

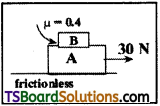
Solution:
Mass of block ‘A’ is, m_A = 10 kg
Mass of block ‘B’ is, m_B = 5 kg
Applied horizontal force, F = 30 N
Coefficient of friction between two blocks, µ = 0.4

Frictional force of block ‘B’ is f = µmg
⇒ f = 0.4 × 5 × 10 = 20N
∴ The frictional force acting between the two blocks, = F – f = 30 – 20 = 10 N

Question 13.
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 ms^-1. If the mass of the ball is 0.15 kg., determine the impulse imparted to the ball. (Assume linear motion of the ball). [AP Mar. ’17]
Solution:
Impulse = change in momentum
= (0.15 × 12) – (- 0.15 × 12) = 3.6 NS
in the direction from the batsman to the bowler.

Question 14.
A force \(2\overline{\mathrm{i}}+\overline{\mathrm{j}}-\overline{\mathrm{k}}\) Newton acts on a body which is initially at rest. At the end of 20 seconds the velocity of the body is \(4\overline{\mathrm{i}}+2\overline{\mathrm{j}}-2\overline{\mathrm{k}}\) m/s. What is the mass of the body? [AP May ’16]
Answer:
Force F = \(2\overline{\mathrm{i}}+\overline{\mathrm{j}}-\overline{\mathrm{k}}\), time t = 20 sec.
Initial velocity u₀ = 0.
Final velocity U = \(4\overline{\mathrm{i}}+2\overline{\mathrm{j}}-2\overline{\mathrm{k}}\)

Additional Problems

Question 1.
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms-1. How long does the body take to stop?
Solution:
Here, F = – 50N, m = 20 kg
u = 15 ms^-1, v = 0, t = ?

Question 2.
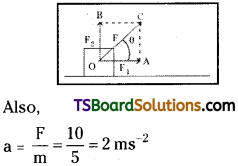
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.
Solution:

This is the direction of resultant force and hence the direction of acceleration of the body as shown in figure.

Question 3.
The driver of a three-wheeler moving with a speed of 36 km / h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0 s just in time to save the child. What is the average retarding force on the vehicle ? The mass of the three wheeler is 400 kg and the mass of the driver is 65 kg.
Solution:
Here, u = 36 km/h = 10 m/s, v = 0, t = 4s
m = 400 + 65 = 465 kg

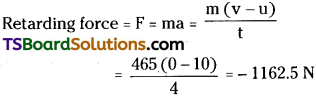
Question 4.
A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0 ms^-2. Calculate the initial thrust (force) of the blast.
Solution:
Here, m = 20000 kg = 2 × 10⁴ kg
Initial acceleration, a = 5 ms^-2;
Thrust, F = ?

Clearly, the thrust should be such that it overcomes the force of gravity besides giving it an upward acceleration of 5 ms^-2.

Thus the force should produce a net acceleration of 9.8 + 5.0 = 14.8 ms^-2.
As thrust = force = mass × acceleration
∴ F = 2 × 10⁴ × 14.8 = 2.96 × 10⁵N

Question 5.
A man of mass 70 kg stands on a weighing scale in a lift which is moving
a) upwards with a uniform speed of 10 ms^-1,
b) downwards with a uniform acceleration of 5 ms^-2,
c) upwards with a uniform acceleration of 5 ms^-2,
What would be the readings on the scale in each case?
d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
Solution:
Here, m = 70 kg, g = 10 m/s²
The weighing machine in each case measures the reaction R i.e., the apparent weight.
a) When the lift moves upwards with a uniform speed, its acceleration is zero.
R = mg = 70 × 10 = 700 N

b) When the lift moves downwards with a = 5 ms^-2
R = m(g – a) = 70 (10 – 5) = 350 N

c) When the lift moves upwards with a = 5 ms^-2
R = m (g + a) = 70 (10 + 5) = 1050 N

d) If the lift were to come down freely under gravity, downward acceleration. a = g
∴ R = m (g – a) = m (g – g) = Zero.

Question 6.
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string, a horizontal force F = 600 N is applied to (i) A, (ii) B along the direction of string. What is the tension in the string in each case?
Solution:
Here, F = 600 N m₁= 10 kg, m2 = 20 kg

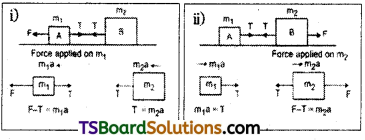
Let T be the tension in the string and a be the acceleration of the system, in the direction of force applied.
∴ a = \(\frac{F}{m_1+m_2}=frac{600}{10+20}\) = 20 m/s²

i) When force is applied on lighter block A, Fig (i).
T = m₂ a = 20 × 20 N’= 400 N

ii) When force is applied on heavier block B, Fig (ii).
T = m₁a = 10 × 20 NT = 200 N
Which is different from value of T in case (i). Hence our answer depends on which mass end, the force is applied.

Question 7.
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.

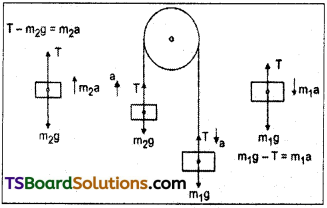
Solution:
Here, m₂ = 8kg, ; m₁ = 12 kg

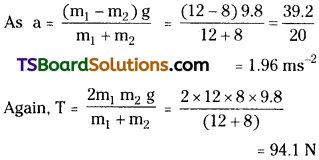
Question 8.
A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei the products must move in opposite directions.
Solution:
Let m₁, m₂ be the masses of products and \(\overrightarrow{\mathrm{v_1}},\overrightarrow{\mathrm{v_2}}\) be their respective velocities. Therfore, total linear momentum after disintegration = \(m_1\overrightarrow{\mathrm{v_1}}+m_2\overrightarrow{\mathrm{v_2}}\). Before disintegra-tion, the nucleus is at rest. Therefore, its linear momentum before disintegration is zero.

According to the principle of conservation of linear momentum,

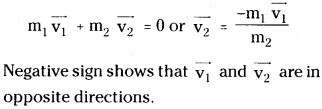
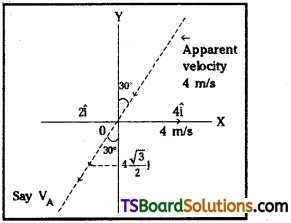
Question 9.
Two billiard balls each of mass 0.05 kg moving in opposite directions with speed 6 ms^-1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other?
Solution:
Here, initial momentum of the ball
A = 0.05 (6) = 0.3 kg ms^-1

As the speed is reversed on collision, final momentum of the ball A = 0.05 (-6)
= – 0.3 kg ms^-1

Impulse imparted to ball A = change in momentum of ball A = final momentum – initial momentum = – 0.3 – 0.3 = – 0.6 kg ms^-1.

Question 10.
A shell of mass 0.02 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is 80 ms^-1, what is the recoil speed of the gun?
Solution:
Here, mass of shell, m = 0.02 kg
mass of gun, M = 100 kg
muzzle speed of shell, V = 80 ms^-1
recoil speed of gun, v = ?
According to the principle of conservation of linear momentum, mV + Mυ = 0

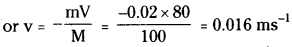
Question 11.
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev./min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
Solution:
Here, m = 0.25 kg, r = 1.5 m ;

Question 12.
Explain why
a) a horse cannot pull a cart and run in empty space,
b) passengers are thrown forward from their seats when a speeding bus stops suddenly,
c) it is easier to pull a lawn mover than to push it,
d) a cricketer moves his hands backwards while holding a catch.
Solution:
a) While trying to pull a cart, a horse pushes the ground backwards with a certain force at an angle. The ground offers an equal reaction in the opposite direction, on the feet of the horse. The forward component of this reaction is responsible for motion of the cart. In empty space, there is no reaction and hence, a horse cannot pull the cart and run.

b) This is due to “inertia of motion”.
When the speeding bus stops suddenly, lower part of the bodies in contact with the seats stop. The upper part of the bodies of the passengers tend to maintain the uniform motion. Hence, the passengers are thrown forward.

c) While pulling a lawn mover, force is applied upwards along the handle. The vertical component of this force is upwards and reduces the effective weight of the mover, Fig (a). While pushing a lawn mover, force is applied downwards along the handle. The vertical component of this force is downwards and increases the effective weight of the mover, Fig (b). As the effective weight is lesser in case of pulling than in case of pushing, therefore, “pulling is easier than pushing”.

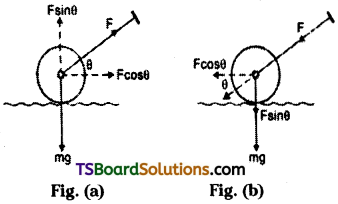
d) While holding a catch, the impulse received by the hands, F × t = change in linear momentum of the ball is constant. By moving his hands backwards, the cricketer increases the time of impact (t) to complete the catch. As t increases, F decreases and as a reaction, his hands are not hurt severely.

Question 13.
A stream of water flowing horizontally with a speed of 15 ms^-1 pushes out of a tube of cross-sectional area 10^-2 m², and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water, assuming it does not rebound?
Solution:
Here, v = 15 ms^-1
Area of cross section, a = 10^-2 m²
Volume of water pushing out/sec = a × v
= 10^-2 × 15 m³ s^-1

As density of water is 10³ kg/m³, therefore, mass of water striking the wall per sec.
m = (15 × 10^-2) × 10³ = 150 kg/s.

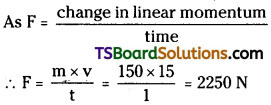
Question 14.
Ten one-rupee coins are put on top of each other on a table. Each coin has a mass m.
Give the magnitude and direction of
a) the force on the 7^th coin (counted from the bottom) due to all the coins on its top,
b) the force on the 7^th coin by the eighth coin,
c) the reaction of the 6^th coin on the 7^th coin.
Solution:
a) The force on 7^th coin is due to weight of the three coins lying above it. Therefore,
F = (3 m) kgf = (3 mg) N
where g is acceleration due to gravity. This force acts vertically downwards.

b) The eighth coin is already under the weight of two coins above it and it has its own weight too. Hence force on 7^th coin due to 8^th coin is sum of the two forces i.e.
F = 2m + m = (3m) kgf = (3 mg) N
The force acts vertically downwards.

c) The sixth coin is under the weight of four coins above it.
Reaction, r = -F = -4m (kgf) = – (4 mg) N

Minus sign indicates that the reaction acts vertically upwards, opposite to the weight.

Question 15.
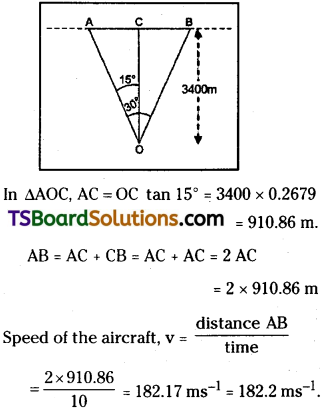
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
Solution:
Here θ = 15°

Question 16.
A train runs along an unbanked circular track of radius 30 m at a speed of 54 km/h. The mass of the train is 10⁶ kg. What provides the centripetal force required for this purpose – The engine or the rails? What is the angle of banking required to prevent wearing out of the rail?
Solution:
The centripetal force is provided by the lateral thrust exerted by the rails on the wheels. By Newton’s 3rd law, the train exerts an equal and opposite thrust on the rails causing its wear and tear.

Obviously, the outer rail will wear out faster due to the larger force exerted by the train on it.

Question 17.
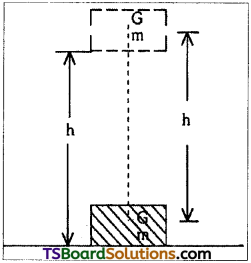
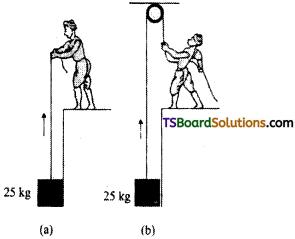
A block of mass 25 kg is raised by a 50 kg man in two different ways as shown in Fig. What is the action on the floor by the man in the two cases? If the floor yields to a normal force of 700 N, which mode should the man adopt to lift the block without the floor yielding?

Solution:
Here, mass of block, m = 25 kg
Mass of man, M = 50 kg
Force applied to lift the block
F = mg = 25 × 9.8 = 245 N
Weight of man W = Mg = 50 × 9.8 = 490 N.

a) When block is raised by man as shown in Fig. (a), force is applied by the man in the upward direction. This increases the apparent weight of the man. Hence action on the floor.
W’ = W + F = 490 + 245 = 735 N

b) When block is raised by man as shown in Fig. (b), force is applied by the man in the downward direction. This decreases the apparent weight of the man. Hence, action on the floor in this case would be W’ = W – F = 490 – 245 = 245 N.

As the floor yields to a normal force 700 N, the mode (b) has to be adopted by the man to lift the block.

Question 18.
A monkey of mass 40 kg climbs on a rope (Fig) which can stand a maximum tension of 600 N. In which of the following cases will the rope break : the monkey {LAWS OF MOTION )
a) climbs up with an acceleration of 6 ms^-2
b) climbs down with an acceleration of 4 ms^-2
c) climbs up with a uniform speed of 5 ms^-1
d) falls down the rope nearly freely under gravity?
(Ignore the mass of the rope).
Solution:
Here, mass of monkey, m = 40 kg
Maximum tension the rope can stand, T = 600 N.
In each case, actual tension in the rope will be equal to apparent weight of monkey (R), The rope will break when R exceeds T.
a) When monkey climbs up with a = 6 ms^-2,
R = m (g + a) = 40 (10 + 6) = 640 N (which is greater than T).
Hence the rope will break.

b) When monkey climbs down with a = 4 ms^-2
R = m (g – a) = 40 (10 – 4) = 240 N, which is less than T
∴ The rope will not break.

c) When monkey climbs up with a uniform speed v = 5 ms^-1,
its acceleration a = 0 ∴ R = mg = 40 × 10 = 400 N, which is less than T
∴ The rope will not break.

d) When monkey falls down the rope nearly freely under gravity, a = g
∴ R = m (g – a) = m (g – g) = 0 (Zero.)
Hence the rope will not break.

Question 19.
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 in rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Solution:
Here, m = 70 kg, r = 3 m
n = 200, rpm = \(\frac{200}{60}\) rps, p = 0.15, ω = ?

The horizontal force N by the wall on the man provides the necessary centripetal force = m r ω². The frictional force (f) in this case is vertically upwards opposing the weight (mg) of the man.

After the floor is removed, the man will remain stuck to the wall, when mg = f < µ N, i.e. mg < µ m r ω² or g < µ r ω²
∴ Minimum angular speed of rotation of

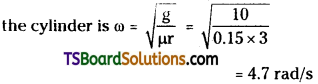
Question 20.
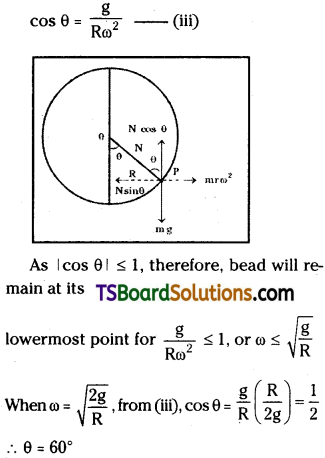
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for to ω ≤ √g/R. What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for to ω = √2g/R? Neglect friction.
Solution:
In Figure we have shown that radius vector joining the bead to the centre of the wire makes an angle 0 with the verticle downward direction. If N is normal reaction, then as is clear from the figure,
mg = N cos θ —- (i)
m r ω² = N sin θ —- (ii)
or m (R sin θ) ω² = N sin θ or m R ω² = N
from (i), mg = m R ω² cos θ or

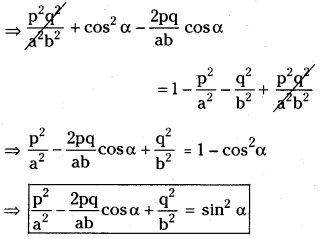
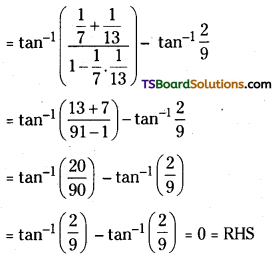
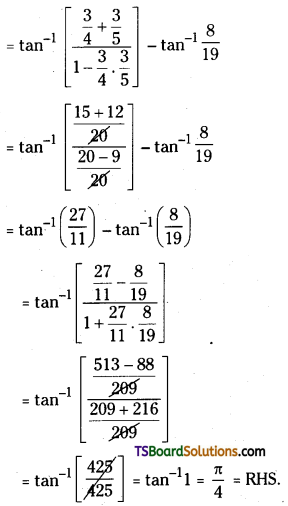
Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Long Answer Type

Question 1.
In ΔABC, show that b² = c² + a² – 2ca cos B. [Mar. ’02]
Answer:
LHS = b² = (2R sin B)² = 4R² sin² B = 4R²[sin (A + C)]² = 4R² (sin A cos C + cos A sin C)²
= 4R² (sin² A cos² C + cos² A sin² C + 2 sin A sin C cos A cos C)
= 4R² [sin² A (1 – sin² C) + (1 – sin² A) sin²C + 2 sin A sin C cos A cos C]
= 4R² (sin² A – sin²A sin²C + sin²C – sin²A sin²C + 2 sin A sin C cos A cos C)
= 4R² (sin²A + sin²C – 2 sin² A sin² C + 2 sin A sin C cos A cos C)
= 4R² [sin²A + sin²C + 2 sin A sin C (cos A cos C – sin A sin C)]
= 4R² [sin² A + sin² C + 2 sin A sin C cos (A + C)]
= 4R² sin² A + 4R² sin² C – 8R² sin A sin C cos B = a² + c² – 2ac cos B = RHS.

Question 2.
In ΔABC, show that [Mar ’94]
(i) sin\(\frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{b c}}\)
Answer:

(ii) cos\(\frac{A}{2}=\sqrt{\frac{s(s-a)}{b c}}\)
Answer:

(iii) tan\(\frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}}\)
Answer:

Question 3.
If a = (b – c)sec θ, prove that tan θ = \(\frac{2 \sqrt{b c}}{b-c}\)sin\(\frac{A}{2}\). [Mar; ’18(AP); Mar. ’16(TS); ’11]
Answer:
Given a = (b – c) sec θ
sec θ = \(\frac{a}{b-c}\)
tan²θ = sec²θ – 1 = \(\left(\frac{a}{b-c}\right)^2\) – 1 = \(\frac{a^2}{(b-c)^2}\) – 1 = \(\frac{a^2-(b-c)^2}{(b-c)^2}\)
= \(\frac{(a+b-c)(a-b+c)}{(b-c)^2}=\frac{(2 s-2 c)(2 s-2 b)}{(b-c)^2}=\frac{4 .(s-b)(s-c)}{(b-c)^2}\) = 4.\(\frac{(s-b)(s-c)}{(b-c)^2} \cdot \frac{b c}{b c}\)
tan²θ = 4.\(\frac{b c}{(b-c)^2}\)sin²\(\frac{A}{2}\)
tan θ = \(\frac{2 \sqrt{b c}}{b-c}\)sin\(\frac{A}{2}\)

Question 4.
Show that a cos²\(\frac{A}{2}\) + b cos²\(\frac{B}{2}\) + c cos²\(\frac{C}{2}\) = s + \(\frac{\Delta}{R}\) [May ’15(TS); Mar. ’03, ’00]
Answer:
L.H.S = a cos²\(\frac{A}{2}\) + b cos²\(\frac{B}{2}\) + c cos²\(\frac{C}{2}\)
= a\(\left[\frac{1+\cos A}{2}\right]\) + b\(\left[\frac{1+\cos B}{2}\right]\) + c\(\left[\frac{1+\cos C}{2}\right]\)
= \(\frac{\mathrm{a}}{2}+\frac{\mathrm{a}}{2}\) cos A + \(\frac{\mathrm{b}}{2}+\frac{\mathrm{b}}{2}\) cos B + \(\frac{\mathrm{c}}{2}+\frac{\mathrm{c}}{2}\) cos C
= \(\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{2}+\frac{\mathrm{c}}{2}+\frac{1}{2}\)(a cos A + b cos B + c cos C)
= \(\frac{a+b+c}{2}+\frac{1}{2}\)[2R sin A cos A + 2R sin B cos B + 2R sin C cos C]
= \(\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{2}+\frac{\mathrm{c}}{2}+\frac{1}{2}\)[sin 2A + sin 2B + sin 2C] = s + \(\frac{\mathrm{R}}{2}\)[sin 2A + sin 2B + sin 2C] …………(1)
Now sin 2A + sin2B + sin2C
= 2sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2
\mathrm{~B}}{2}\right)\) + sin2C
= 2 sin (A + B) cos (A – B) + sin 2C
= 2sin(180° – C)cos(A – B) + sin2C
= 2sin C cos (A – B) + 2sin C cos C
= 2sin C[cos(A – B) + cos C]
= 2sinC[cos(A – B) + cos[180° – (A + B)]
= 2sinC[cos(A – B) – cos(A + B)]
= 2sinC [2sin A sin B]
= 4 sin A sin B sin C
From (1) ⇒ s + \(\frac{\mathrm{R}}{2}\)[4sinA sinB sinC]
= s + 2R sin A sin B sin C
= s + \(\frac{2 \mathrm{R}^2}{\mathrm{R}}\) sin A sin B sin C = s + \(\frac{\Delta}{R}\) = R.H.S.

Question 5.
Prove that a³cos(B – C) + b³cos (C – A) + c²cos(A – B) = 3abc. [Mar. ’08; May ’00, ’98]
Answer:
L.H.S = a³ cos (B – C) + b³ cos (C – A) + c³ cos (A – B)
= Σa³ cos (B – C) = Ea². a cos (B – C) = Σa².2R sin A . cos (B – C)
= Σa² .2R sin (180° – (B + C)) cos (B – C) = Σa².2R sin(B + C) cos (B – C)
= Σa² . R[sin (B + C + B – C) + sin (B + C – B + C)] = Σa². R(sin 2B + sin 2C)
= Σa² . R (2 sin B cos B + 2 sin C cos C) = Σa² (2R sin B cos B + 2R sin C cos
= Σa² (b cos B + c cos C) = Σ(a²b cos B + a2c cos C)
= ab cos B + a c cos C + bc cos C + b a cos A + ca cos A + cb cos B
= ab(a cos B + b cos A) + bc(b cos C + c cos B) + ac (a cos C + c cos A)
= ab(c) + bc(a) + ac(b) = 3abc = RHS.

Question 6.
Prove that cot\(\frac{A}{2}\) + cot\(\frac{B}{2}\) + cot\(\frac{C}{2}\) = \(\frac{s^2}{\Delta}\). [Mar. ’09]
Answer:

Question 7.
Prove that tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\) + tan\(\frac{C}{2}\) = \(\frac{b c+c a+a b-s^2}{\Delta}\). [May ’98, ’97]
Answer:
L.H.S = tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\) + tan\(\frac{C}{2}\)

Question 8.
If sin θ = \(\frac{a}{b+c}\), then show that cos θ = \(\frac{2 \sqrt{b c}}{b+c}\)cos\(\frac{A}{2}\). [Mar. ’16(AP), ’12; May ’14]
Answer:
Given sin θ = \(\frac{a}{b+c}\)

Question 9.
If a = (b + c)cos θ, then prove that sin θ = \(\frac{2 \sqrt{b c}}{b+c}\)cos\(\frac{A}{2}\). [Mar. ’19(AP); May ’11]
Answer:
Given cos θ = \(\frac{a}{b+c}\)

sin θ = \(\frac{2 \sqrt{b c}}{b+c}\)cos\(\frac{A}{2}\)

Question 10.
If a² + b² + c² = 8R², then prove that the triangle Is right angled. [Mar ’01]
Answer:
Given a² + b² + c² = 8R²
(2R sin A)² + (2R sin B)² + (2R sin C)² = 8R²
4R² sin² A + 4R² sin² B + 4R² sin²C = 8R²
sin²A + sin²B + sin²C = 2
1 – cos²A + sin²B + sin²C = 2
1 – (cos²A – sin²B) + sin²C = 2
1 – cos (A + B). cos (A – B) sin²C = 2
1 – cos(180°- C)cos(A – B) + sin2C = 2
1 + cos C cos(A – B) + 1 – cos²C = 0
cos C [cos (A – B) – cos C] = 0
cosC[cos(A – B) – cos(180° – (A + B)] = 0
cos C [cos (A – B) + cos (A + B)] = 0
cos C (2 cos A cos B) = 0
2 cos A cos B cos C = 0
cos A. cos B cos C = 0
cos A = 0 or cos B = 0 or cos C = 0
A = 90° or B = 90° or C = 900
∴ The triangle is right angled.

Question 11.
Show that \(\frac{r_1}{b c}+\frac{r_2}{c a}+\frac{r_3}{a b}=\frac{1}{r}-\frac{1}{2 R}\). [May; 14, ’09, ’07, ’01, ’99, ’95; Mar. ’99, ’95, ’93]
Answer:

Question 12.
Show that (r₁ + r₂)sec²\(\frac{C}{2}\) = (r₂ + r₃)sec²\(\frac{A}{2}\) = (r₃ + r₁)sec²\(\frac{B}{2}\). [Mar. ’01]
Answer:

Question 13.
In ΔABC, if r₁ = 8, r₂ = 12, r₃ = 24; Find a, b and c. [Mar. ’17(AP). ’02; May ’15(AP), ’13]
Answer:
We have \(\frac{1}{\mathrm{r}}=\frac{1}{\mathrm{r}_1}+\frac{1}{\mathrm{r}_2}+\frac{1}{\mathrm{r}_3} \Rightarrow \frac{1}{\mathrm{r}}=\frac{1}{8}+\frac{1}{12}+\frac{1}{24}=\frac{3+2+1}{24}=\frac{6}{24}=\frac{1}{4}\) = r = 4
Also \(\sqrt{\mathrm{rr}_1 \mathrm{r}_2 \mathrm{r}_3}=\sqrt{4(8)(12)(24)}\) = 96
Since s = \(\frac{\Delta}{r}=\frac{96}{4}\) = 24
r₁ = \(\frac{\Delta}{s-a}\) ⇒ s – a = \(\frac{\Delta}{r_1}=\frac{96}{8}\) = 12 ⇒ a = s – 12 = 24 – 12 = 12
r₂ = \(\frac{\Delta}{s-b}\) ⇒ s – b = \(\frac{\Delta}{r_2}=\frac{96}{12}\) = 8 ⇒ b = s – 8 = 24 – 8 = 16
r₃ = \(\frac{\Delta}{s-c}\) ⇒ s – c = \(\frac{\Delta}{r_3}=\frac{96}{24}\) = 4 ⇒ b = s – 4 = 24 – 4 = 20
∴ The required values are a = 12, b = 16, c = 20

Question 14.
Show that \(\frac{a b-r_1 r_2}{r_3}=\frac{b c-r_2 r_3}{r_1}=\frac{c a-r_3 r_1}{r_2}\). [Mar. ’08]
Answer:

Question 15.
Prove that 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)². [Mar. ’97]
Answer:
L.H.S = 4(r₁r₂ + r₂r₃ + r₃r₁) = 4\(\left[\frac{\Delta}{s-a} \cdot \frac{\Delta}{s-b}+\frac{\Delta}{s-b} \cdot \frac{\Delta}{s-c}+\frac{\Delta}{s-c} \cdot \frac{\Delta}{s-a}\right]\)
= 4\(\left[\frac{\Delta^2}{(s-a)(s-b)}+\frac{\Delta^2}{(s-b)(s-c)}+\frac{\Delta^2}{(s-c)(s-a)}\right]\)
= 4\(\left[\frac{s(s-a)(s-b)(s-c)}{(s-a)(s-b)}+\frac{s(s-a)(s-b)(s-c)}{(s-b)(s-c)}+\frac{s(s-a)(s-b)(s-c)}{(s-c)(s-a)}\right]\)
= 4s[s – c + s – a + s – b] = 4s[3s – (a + b + c)] = 4s(3s – 2s) = 4s.s = 4s² = (2s)²
= (a + b + c)² = R.H.S

Question 16.
Show that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) + cos²\(\frac{C}{2}\) = 2 + \(\frac{r}{2R}\). [Mar ’15(TS); Mar. ’05]
Answer:

Question 17.
If P₁, P₂, P₃ are altitudes drawn from vertices A, B, C to the opposite sides of a triangle respectively, then show that
(i) \(\frac{1}{P_1}+\frac{1}{P_2}+\frac{1}{P_3}=\frac{1}{r}\) [Mar. ’18(TS); Mar. ’10]
(ii) P₁P₂P₃ = \(\frac{(a b c)^2}{8 R^3}=\frac{8 \Delta^3}{a b c}\). [Mar. ’10. ’91]
Answer:
Since P₁, P₂, P₃ are altitudes drawn from the vertices A, B, C to the opposite sides of a triangle respectively, then

Area of triangle ABC is Δ = \(\frac{1}{2}\) BC.AD = \(\frac{1}{2}\)aP₁ ⇒ P₁ = \(\frac{2 \Delta}{a}\)
AreaoftriangleABCls Δ = \(\frac{1}{2}\)AC.BE = \(\frac{1}{2}\)bP₂ ⇒ P₂ = \(\frac{2 \Delta}{b}\)
AreaoftriangleAßCls Δ = \(\frac{1}{2}\)AB.CF = \(\frac{1}{2}\)cP₃ ⇒ P₃ = \(\frac{2 \Delta}{c}\)

Question 18.
If a = 13, b = 14, c = 15, show that R = \(\frac{65 }{8}\), r = 4, r₁ = \(\frac{21}{2}\), r₂ = 12 and r₃ = 14. [Mar. ’19, ’16(AP), ’15(AP), ’14, ’04; May ’12, ’11, ’10; B.P]
Answer:
Given a = 13, b = 14, c = 15
s = \(\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}=\frac{13+14+15}{2}=\frac{42}{2}\) = 21

Question 19.
If r₁ = 2, r₂ = 3, r₃ = 6 and r = 1, then prove that a = 3 b = 4 and c = 5
Answer:
Given r = 1, r₁ = 2, r₂ = 3, r₃ = 6
We have Δ = \(\) = 6
Δ = 6
r = 1 ⇒ \(\frac{\Delta}{\mathrm{s}}\) = 1 ⇒ \(\frac{6}{s}\) = 1 ⇒ s = 6
r₁ = 2 ⇒ \(\frac{\Delta}{\mathrm{s-a}}\) = 2 ⇒ \(\frac{6}{6-a}\) = 2 ⇒ 6 – a = 3 ⇒ a = 3
r₂ = 3 ⇒ \(\frac{\Delta}{s-b}\) = 3 ⇒ \(\frac{6}{6-b}\) = 3 ⇒ 6 – b = 2 ⇒ b = 4
r₃ = 6 ⇒ \(\frac{\Delta}{s-c}\) = 6 ⇒ \(\frac{6}{6-c}\) = 6 ⇒ 6 – c = 1 ⇒ c = 5

Some More Maths 1A Properties of Triangles Important Questions

Question 1.
In a ΔABC, prove that \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) where R is the circum radius.
Answer:
Case -I:
∠A is acute
‘s’ is the centre of the circumcircle and CD is its diameter then CS = SD = R and CD = 2R. Join BD then ∠DBC = 90° and DBC is a right angled triangle then ∠BAC = ∠BDC [ v angles in the same segment]

sin ∠BAC = sin ∠BDC ⇒ sin A = \(\frac{B C}{C D}=\frac{a}{2 R} \Rightarrow \frac{a}{\sin A}\) = 2R
Similarly \(\frac{b}{\sin B}\) = 2R, \(\frac{b}{\sin C}\) = 2R
∴ \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) = 2R

Case – II:
∠A is right angled then a = BC = 2R = 2R.1 = 2R sin 90° = 2R sin A

\(\frac{a}{\sin A}\) = 2R
Similarly \(\frac{b}{\sin B}\) = 2R, \(\frac{c}{\sin C}\) = 2R
∴ \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) = 2R

Case – III:
∠A is obtuse
∠DBC is right angled (∵ angle in the semi circle)

In cyclic quadrilateral BACD
∠BDC + ∠BAC = 180° ⇒ ∠BDC = 180° – ∠BAC
∠BDC = 180° – A
sin ∠BDC = sin(180° – A) ⇒ \(\frac{\mathrm{BC}}{\mathrm{CD}}\) = sin A
sin A = \(\frac{a}{2 R} \Rightarrow \frac{a}{\sin A}\) = 2R ⇒ Similarly \(\frac{b}{\sin B}\) = 2R, \(\frac{c}{\sin C}\) = 2R
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) = 2R

Question 2.
Show that a² cot A + b² cot B + c² cot C = \(\frac{abc}{R}\). [Mar. ’14]
Answer:
L.H.S. = Σ a² cot A = Σ 4R² sin²A = Σ4R²sin A cos A = 2R²Σsin 2A
= 2R² (sin 2A + sin 2B + sin 2C) = 2R² [sin 2A + 2 sin (B + C) cos (B – C]
= 2R²[2 sin A cos A + 2 sin A cos (B – C)] = 4R² sin A [cos A + cos (B – C)]
= 4R² sin A [cos (B – C) – cos (B + C)] = 4R² sin A (2 sin B sin C)
= 2R² (4 sin A sin B sin C) = 8R²\(\frac{a}{2 R} \frac{b}{2 R} \frac{c}{2 R}=\frac{a b c}{R}\) = R.H.S

Question 3.
In ΔABC, if \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\) show that C = 60°
Answer:
\(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c} \Rightarrow \frac{b+c+a+c}{(a+c)(b+c)}=\frac{3}{a+b+c}\)
⇒ 3(a + c)(b + c) = (a + b + 2c)(a + b + c)
⇒ 3(ab + ac + bc + c²) = a² + b² + 2ab + 3c(a + b) + 2c²

⇒ ab = a² + b² – c² = ab = 2ab cos C (from cosine rule)
⇒ cos c = \(\frac{1}{2}\) ⇒ C = 60

Question 4.
In ΔABC, show that (a + b + c)(tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\)) = 2c cot\(\frac{C}{2}\)
Answer:
LHS = (a + b + c)(tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\)) = 2s\(\left[\frac{\Delta}{s(s-a)}+\frac{\Delta}{s(s-b)}\right]\) = 2Δ\(\left[\frac{1}{s-a}+\frac{1}{s-b}\right]\)

Question 5.
Show that b² sin 2C + c² sin 2B = 2bc sin A.
Answer:
L.H.S. = b² (2 sin C cos C) + c² (2sin B cos B)
= 2b² \(\frac{c}{2 R}\) cos C + 2c² \(\frac{b}{2 R}\) cos B = \(\frac{1}{R}\) (b²c cos C + c²b cos B)
= \(\frac{bc}{R}\) (b cos C + c cos B) = \(\frac{abc}{2}\) = 4Δ = 4 (\(\frac{1}{2}\)bc sin A) = 2bc sin A = R.H.S.

Question 6.
The angle of elevation of the top point P of the vertical tower PQ of height h from a point A is 45° and from a point B is 60°, where B is a point at a distance 30 meters from the point A measured along the line AB which makes an angle 30° with AQ. Find the height of the tower.
Answer:
Let the height of the tower PQ = h

∠PAQ = 45°, ∠BAQ = 30° and ∠PBC = 60°
Given AB = 30 mts.
∴ ∠BAP = ∠APB = 15°
Hence BP = AB = 30 and h = PC + CQ
sin 60° = \(\frac{\mathrm{PC}}{\mathrm{PB}}=\frac{\mathrm{PC}}{30}\) and sin30° = \(\frac{B D}{A B}=\frac{B D}{30}\)
∴ PC = 30 sin 60° = 30.\(\left(\frac{\sqrt{3}}{2}\right)\) = 15√3 and BD = 30.sin30° = 30.\(\left(\frac{1}{2}\right)\) = 15
∴ Height of the tower h = PC + CQ = 15(√3 + 1) mts.

Question 7.
Two trees A and B are on the same side of a river. From a point C in the river the distances of the trees A and B are 250 m and 300 m respectively. If the angle C is 45°, find the distance between the trees (use √2 = 1.414).
Answer:
Given AC = 300 m and BC = 250.m and in the ΔABC, using cosine rule

AB² = AC² + BC² – 2AC.BC.cos 45° = (300)² + (250)² – 2 (300) (250)\(\frac{1}{\sqrt{2}}\)
= 46450
∴ AB = 215.5 m (approximately)

Question 8.
Prove that \(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^2+b^2}{a^2+c^2}\)
Answer:

Question 9.
If C = 60°, then show that \(\frac{b}{c^2-a^2}+\frac{a}{c^2-b^2}\) = 0.
Answer:
C = 60° ⇒ c² = a² + b² – 2ab cos C = a² + b² – 2ab(cos 60°) = a² + b² – 2ab(1/2)
= a² + b² – ab …………..(1)

Question 10.
Prove that \(\frac{\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}}{\cot A+\cot B+\cot C}=\frac{(a+b+c)^2}{\left(a^2+b^2+c^2\right)}\).
Answer:

Question 11.
If \(\frac{a^2+b^2}{a^2-b^2}=\frac{\sin C}{\sin (A-B)}\), prove that ΔABC is either isosceles or right angled.
Answer:
Given \(\frac{a^2+b^2}{a^2-b^2}=\frac{\sin C}{\sin (A-B)} \Rightarrow \frac{a^2+b^2}{a^2-b^2}=\frac{\sin (A+B)}{\sin (A-B)}\)
By componendo and dividedo
⇒ \(\frac{a^2+b^2+a^2-b^2}{a^2+b^2-\left(a^2-b^2\right)}=\frac{\sin (A+B)+\sin (A-B)}{\sin (A+B)-\sin (A-B)} \Rightarrow \frac{2 a^2}{2 b^2}=\frac{2 \sin A \cos B}{2 \cos A \sin B}\)
⇒ \(\frac{a^2}{b^2}=\frac{2 R \sin A \cos B}{2 R \cos A \sin B}=\frac{a \cos B}{b \cos A} \Rightarrow \frac{a}{b}=\frac{\cos B}{\cos A}\)
⇒ 2R sin A cos A = 2R sin B cos B ⇒ R sin 2A = R sin 2B
⇒ sin 2A – sin 2B = 0 ⇒ A = B
∴ ΔABC is isosceles. (or) 2A = 180° – 2B ⇒ A + B = 90°
Hence A ≠ B ⇒ ΔABC is a right angled triangle.
∴ ΔABC is either isosceles or right angled.

Question 12.
If cos²A + cos²B + cos²C = 1, then show that AABC is right angled.
Answer:
Given cos²A + cos²B + cos²C = 1 …. (1)
∴ cos²A + cos²B + cos²C = cos²A + cos²B + 1 – sin²C = 1 + cos²A + cos (B + C) cos (B – C)
= 1 + cos²A – cos A cos (B – C) = 1 + cos A [cos A – cos (B – C)] = 1 – cos A [cos (B + C) + cos (B – C)] = 1 – 2cos A cos B cos C (∵ A + B + C = π, cos (B + C) = – cos A)
∴ 1 – 2 cos A cos B cos C = 1 ⇒ 2 cos A cos B cos C = 0 ⇒ A = 90° or B = 90° or C = 90°
∴ ΔABC is right angled.

Question 13.
If cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are in A.P., then prove that a, b, c are in A.P.
Answer:
cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are in A.P.
⇒ \(\frac{s(s-a)}{\Delta}, \frac{s(s-b)}{\Delta}, \frac{s(s-c)}{\Delta}\) are in A.P.
⇒ (s – a), (s – b), (s – c) are in A.P ⇒ -a, -b, -c are in A.P ⇒ a, b, c are in A.P.

Question 14.
If sin²\(\frac{A}{2}\), sin²\(\frac{B}{2}\), sin²\(\frac{C}{2}\) are in H.P., then show that a, b, c are in H.P.
Answer:
Given sin²\(\frac{A}{2}\), sin²\(\frac{B}{2}\), sin²\(\frac{C}{2}\) are in H.P.

⇒ \(\frac{s-a}{a}, \frac{s-b}{b}, \frac{s-c}{c}\) are in A.P. ⇒ \(\frac{s}{a}, \frac{s}{b}, \frac{s}{c}\) are in A.P ⇒ \(\frac{1}{\mathrm{a}}, \frac{1}{\mathrm{~b}}, \frac{1}{\mathrm{c}}\) are in A.P
∴ a, b, c are in H.P.

Question 15.
Two ships leave a port at the same time. One goes 24 km per hour in the direction N 45° E and other travel 32 kms per hour in the direction S 75° E. Find the distance between the ships at the end of 3 hours.
Answer:
The first ship goes 24 km/hr.
∴ After 3 hrs. first ship goes 72 kms.

The second ship goes 32 km/hr.
∴ After 3 hrs. second ship goes 96 kms.
Let AB = x be the distance between the ships.
From the geometry of the figure ∠AOB = 60°
Using cosine rule in ΔAOB we have
cos 60° = \(\frac{(72)^2+(96)^2-x^2}{2(72)+(96)} \Rightarrow \frac{1}{2}=\frac{5184+9216-x^2}{13824}\)
⇒ 13824 = 28800 – 2x² ⇒ 2x² = 14976 ⇒ x² = 7488 ⇒ x = 86.4 (approximately)
At the end of 3 hours the difference between the ships is 86.4 kms.

Question 16.
The upper 374th portion of a vertical pole subtends an angle tan-13/5 at a point in the horizontal plane through its foot and at a distance of 40 m from the foot. Given that the vertical pole is at a height less than 100 m from the ground, find its height.
Answer:
From the figure AB is the vertical pole of height h’.

∠BCD = θ, suppose ∠DCA = α and ∠BCA = β.
tan α = \(\frac{h / 4}{40}=\frac{h}{160}\)
tan β = \(\frac{h}{40}\)
Also β = θ + α ⇒ θ = β – α

∴ tan θ = tan(β – α) = \(\frac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}=\frac{\frac{h}{40}-\frac{h}{160}}{1+\frac{h}{40} \cdot \frac{h}{160}}=\frac{120 \mathrm{~h}}{6400} \cdot \frac{6400}{6400+\mathrm{h}^2}=\frac{120 \mathrm{~h}}{6400+\mathrm{h}^2}\)
⇒ \(\frac{3}{5}=\frac{120 h}{6400+h^2}\) ⇒ 3h² + 19200 = 600h ⇒ 3h² – 600h + 19200 = 0
⇒ h² – 200h + 6400 = 0 ⇒ h² – 160h – 40h + 6400 = 0
⇒ h(h – 160) – 40(h – 160) = 0 ⇒ (h – 40)(h – 160) = 0 ⇒ h = 40 or h = 160
Given that vertical pole is a height less than 100 m, from the ground we take h = 40 m as the height of the pole.

Question 17.
AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7 m. From D, the angle of elevation of the point A is 45°. Find the height of the pole.
Answer:
Let AB = ‘h’ be the height of the pole.

Given CD = 7
∠ACB = 60°, ∠ADB = 45° and line BC = x.
In the ΔABC, tan 60° = \(\frac{h}{x}\) ⇒ √3 = \(\frac{h}{x}\) ⇒ x = \(\frac{h}{\sqrt{3}}\)
In the ΔABC, tan 45° = \(\frac{h}{x+7}\) ⇒ x + 7 = h ⇒ \(\frac{h}{\sqrt{3}}\) + 7 = h ⇒ h\(\left(\frac{\sqrt{3}-1}{\sqrt{3}}\right)\) = 7
⇒ h = \(\frac{7 \sqrt{3}}{\sqrt{3}-1}=\frac{7 \sqrt{3}(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\frac{7 \sqrt{3}(\sqrt{3}+1)}{3-1}=\frac{21+7 \sqrt{3}}{2}\)

Question 18.
Let an object he placed at some height h cm and let P and Q be two points of observation which are at a distance of 10 cm apart on a line Inclined at angle 15° to the horizontal. If the angles of elevation of the object from P and Q are 300 and 600 respectively then find h.
Answer:
Let AB h cm be the height of the tower P and Q are points of observation.
From the geometry of the figure ∠BPA = 30° given ∠BPQ = 15°. Also ∠PQB = 135.
∴ ∠PBQ = 30°, PQ = 10 cm (given).

In the PQB, applying sine rule,
\(\frac{\mathrm{PQ}}{\sin \angle \mathrm{PBQ}}=\frac{\mathrm{BP}}{\sin \angle \mathrm{PQB}} \Rightarrow \frac{10}{\sin 30^{\circ}}=\frac{\mathrm{BP}}{\sin 135^{\circ}}\)
BP = \(\frac{\left(\sin 135^{\circ}\right)(10)}{\sin 30^{\circ}}=\frac{1}{\sqrt{2}}\) (10) × 2 = √2.(10)
Also in the ΔPAB,
sin 30° = \(\frac{A B}{P B}=\frac{h}{\sqrt{2} \cdot 10}\)
h = √2.(10)sin 30° = √2.(10)\(\frac{1}{2}\) = \(\frac{10}{\sqrt{2}}\) = 5√2 cm.

Question 19.
If A = 90°, show that 2(r + R) = b + c.
Answer:
L.H.S = 2(r + R) = 2r + 2R = 2(s – a)tan\(\frac{A}{2}\) + 2R . 1 = 2(s – a)tan 45° + 2R sin A (A = 90°)
= (2s – 2a) + a = 2s – a = a + b + c – a = b + c = R.H.S

Question 20.
Prove that \(\frac{r_1\left(r_2+r_3\right)}{\sqrt{r_1 r_2+r_2 r_3+r_3 r_1}}\) = a.
Answer:

Question 21.
If r : R: r₁ = 2 : 5 : 12, then prove that the triangle is right angled at A.
Answer:
Given r : R : r₁ = 2 : 5 : 12
∴ r₁ – r = 12k – 2k = 10k = 2(5k) = 2R
⇒ 4R sin\(\frac{A}{2}\)(cos\(\frac{B}{2}\)cos\(\frac{C}{2}\) – sin\(\frac{B}{2}\)sin\(\frac{C}{2}\)) = 2R ⇒ 2sin\(\frac{A}{2}\) cos\(\left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)\) = 1
⇒ 2sin\(\frac{A}{2}\)sin\(\frac{A}{2}\) = 1 ⇒ sin²\(\frac{A}{2}=\frac{1}{2}\) ⇒ sin\(\frac{A}{2}=\frac{1}{\sqrt{2}}\) = sin 45°
⇒ \(\frac{A}{2}\) = 45° ⇒ A = 90°
Hence the triangle is right angled at A.

Question 22.
In ΔABC, if AD, BE, CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides show that
(i) \(\frac{1}{\mathrm{AD}}+\frac{1}{\mathrm{BE}}+\frac{1}{\mathrm{CF}}=\frac{1}{\mathrm{r}}\)
(ii) \(\frac{(a b c)^2}{8 R^3}\)
Answer:
In ΔABC, if AD, BE, CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides.

Area of ΔABC is A = \(\frac{1}{2}\)BC . AD = \(\frac{1}{2}\). a . AD
∴ AD = \(\frac{2 \Delta}{a}\)

Area of ΔABC is A = \(\frac{1}{2}\) AC . BE = \(\frac{1}{2}\) b . BE
∴ BE = \(\frac{2 \Delta}{b}\)

Area of ΔABC is A = \(\frac{1}{2}\) AB . CF = \(\frac{1}{2}\). c . CF
∴ CF = \(\frac{2 \Delta}{c}\)

Question 23.
Prove that \(\left(\frac{1}{r}-\frac{1}{r_1}\right)\left(\frac{1}{r}-\frac{1}{r_2}\right)\left(\frac{1}{r}-\frac{1}{r_3}\right)=\frac{a b c}{\Delta^3}=\frac{4 R}{r^2 s^2}\)
Answer:

Since Δ = \(\frac{a b c}{4 R}\)
we have abc = 4RΔ
∴ \(\frac{\mathrm{abc}}{\Delta^3}=\frac{4 \mathrm{R} \Delta}{\Delta^3}=\frac{4 \mathrm{R}}{\Delta^2}=\frac{4 \mathrm{R}}{\mathrm{r}^2 \mathrm{~s}^2}\) (∵ Δ = RS)
∴ \(\left(\frac{1}{r}-\frac{1}{r_1}\right)\left(\frac{1}{r}-\frac{1}{r_2}\right)\left(\frac{1}{r}-\frac{1}{r_3}\right)=\frac{a b c}{\Delta^3}=\frac{4 R}{r^2 s^2}\) = R.H.S

Question 24.
Prove that r(r₁ + r₂ + r₃) = ab + bc + ca = s².
Answer:
L.H.S = r(r₁ + r₂ + r₃) = \(\frac{\Delta}{s}\left(\frac{\Delta}{s-a}+\frac{\Delta}{s-b}+\frac{\Delta}{s-c}\right)=\frac{\Delta^2}{s}\left(\frac{1}{s-a}+\frac{1}{s-b}+\frac{1}{s-c}\right)\)
= \(\frac{\Delta^2[(s-b)(s-c)+(s-a)(s-c)+(s-a)(s-b)]}{s(s-a)(s-b)(s-c)}\)
= \(\frac{\Delta^2}{\Delta^2}\)[(s² + s² + s²) – s(b + c) – s(a + c) – s(a + b) + bc + ca + ab]
= [3s² – 2s(a + b + c) + bc + ca + ab] = 3s² – 2s(2s) + ab + bc + ca
= ab + bc + ca – s² = R.H.S

Question 25.
Show that cos A + cos B + cos C = 1 + \(\frac{r}{R}s\).
Answer:
L.H.S = cos A + cos B + cos C = cos A + 2 cos \(\left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)\) cos\(\left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)\)

Question 26.
Show that sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + sin²\(\frac{C}{2}\) = 1 – \(\frac{r}{2R}\).
Answer:
L.H.S = sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + sin²\(\frac{C}{2}\) = sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + 1 – cos²\(\frac{C}{2}\)

Question 27.
Prove that r₁² + r₂² + r₃² + r² = 16R² – (a² + b² + c²).
Answer:
(r₁ + r₂ + r₃ – r)² = [(r₁ + r₂ + r₃) – r]² = (r₁ + r₂ + r₃)² – 2(r₁ + r₂ + r₃)r + r²
But using results r₁ + r₂ + r₃ – r = 4R and r₁r₂ + r₂r₃ + r₃r₁ = s²
We have 16R² = (r₁² + r₂² + r₃² + r²) – 2r(r₁ + r₂ + r₃) + 2s² ………..(1)

∴ From (1)
r₁² + r₂² + r₃² + r² = 16R² + 2(ab + bc + ca – s²) – 2s² = 16R² + 2(ab + bc + ca) – 4s²
= 16R² = [4s – 2(ab + bc + ca)] = 16R² – {(a + b + c)² – 2(ab + bc + ca)}
= 16R² – (a² + b² + c²)

Question 28.
In a ΔABC show that \(\frac{b^2-c^2}{a^2}=\frac{\sin (B-C)}{\sin (B+C)}\).
Answer:

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Short Answer Type

Question 1.
In ΔABC, show that a = b cos C + c cos B. [May ’09]
Answer:
R.H.S = b cos C + c cos B

∴ a = b cos C + c cos B

Question 2.
In a ΔABC, show that tan\(\left(\frac{B-C}{2}\right)=\frac{b-c}{b+c}\)cot\(\frac{\mathrm{A}}{2}\). [Mar ’08; B.P]
Answer:
R.H.S = \(\frac{b-c}{b+c}\)cot\(\frac{\mathrm{A}}{2}\)

∴ tan\(\left(\frac{B-C}{2}\right)=\frac{b-c}{b+c}\)cot\(\frac{\mathrm{A}}{2}\)

Question 3.
In a ΔABC, if a = 3, b = 4 and sin A = \(\frac{3}{4}\), find the angle B. [May ’99]
Answer:
Given a = 3, b = 4, sin A = \(\frac{3}{4}\)
By sine rule, \(\frac{a}{\sin A}=\frac{b}{\sin B}\) ⇒ sin B = \(\frac{\mathrm{b} \sin \mathrm{A}}{\mathrm{a}}=\frac{4 \times 3 / 4}{3}\) = 1 ⇒ sin B = 1 ⇒ B = 90°

Question 4.
If the lengths of the sides of a triangle are 3, 4, 5, find the circumradius of the triangle. [May ’98]
Answer:
Since 32 + 42 = 52 the triangle is right angled and hypotenuse = 5 = circum diameter.
∴ Circum radius = \(\frac{5}{2}\) cm.

Question 5.
If a = 6, b = 5, c = 9, then find the angle A. [May ’10]
Answer:
Given a = 6, b = 5, c = 9
Since cos A = \(\frac{b^2+c^2-a^2}{2 b c}=\frac{5^2+9^2-6^2}{2(5)(9)}=\frac{25+81-36}{90}=\frac{70}{90}=\frac{7}{9}\)
∴ A = cos^-1\(\left(\frac{7}{9}\right)\)

Question 6.
In a ΔABC, if (a + b + c) (b + c – a) = 3bc, find A. [May ’08]
Answer:
Given (a + b + c) (b + c – a) = 3bc
⇒ (2s) 2(s – a) = 3bc ⇒ \(\frac{s(s-a)}{b c}=\frac{3}{4}\) ⇒ cos²\(\frac{\mathrm{A}}{2}=\frac{3}{4}\) ⇒ cos\(\frac{\mathrm{A}}{2}=\frac{\sqrt{3}}{2}\)
⇒ \(\frac{A}{2}\) = 30° ⇒ A = 60° (∵ cos\(\frac{A}{2}=\sqrt{\frac{s(s-a)}{b c}}\))

Question 7.
If a = 4, b = 5, c = 7, find cos\(\frac{B}{2}\). [May ’12, ’09; Mar. ’90]
Answer:
Given a = 4, b = 5, c = 7
2s = a + b + c = 4 + 5 + 7 = 16 ⇒ s = 8
∴ s – b = 8 – 5 = 3 and cos\(\frac{B}{2}=\sqrt{\frac{s(s-b)}{a c}}=\sqrt{\frac{8 \times 3}{4 \times 7}}=\sqrt{\frac{6}{7}}\)

Question 8.
If tan\(\frac{A}{2}=\frac{5}{6}\) and tan \(\frac{C}{2}=\frac{2}{5}\), determine the relation between a, b, c. [May ’05]
Answer:
Given tan\(\frac{A}{2}=\frac{5}{6}\) and tan \(\frac{C}{2}=\frac{2}{5}\), tan\(\frac{A}{2}\).tan\(\frac{C}{2}\) = \(\frac{C}{2}=\left(\frac{5}{6}\right)\left(\frac{2}{5}\right)=\frac{1}{3}\)
∴ \(\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \sqrt{\frac{(s-b)(s-a)}{s(s-c)}}=\frac{1}{3}\)
⇒ \(\frac{s-b}{s}=\frac{1}{3}\) ⇒ 3s – 3b = s ⇒ 2s – 3b ⇒ a + b + c = 3b ⇒ a + c = 2b ⇒ a, b, c are in A.P

Question 9.
Show that (b – c)²cos² + (b + c)²sin² = a². [May ’08, ’90]
Answer:
L.H.S = (b – c)²cos² + (b + c)²sin² = (b² – 2bc + c²)cos²\(\frac{A}{2}\) + (b² + 2bc + c²)sin²\(\frac{A}{2}\)
= (b² + c²)(cos²\(\frac{A}{2}\) + sin²\(\frac{A}{2}\)) + 2bc(sin²\(\frac{A}{2}\) – cos²\(\frac{A}{2}\))
= (b² + c²)(1) – 2bc(cos²\(\frac{A}{2}\) – sin²\(\frac{A}{2}\))
= b² + c² – 2bc cos A = a² = R.H.S

Question 10.
Prove that a(b cos C – c cos B) = b² – c². [Mar. ’07]
Answer:
L.H.S = a(b cos C – c cos B) = ab cos C – ac cos B

Question 11.
Prove that cot A + cot B + cot C = \(\frac{a^2+b^2+c^2}{4 \Delta}\). [Mar. ’18, ’15 (TS); May ’12, ’97; Mar. ’10]
Answer:
L.H.S = cot A + cot B + cot C = \(\frac{\cos A}{\sin A}+\frac{\cos B}{\sin B}+\frac{\cos C}{\sin C}\)

Question 12.
In ΔABC, if a cos A = b cos B, prove that the triangle is either isosceles or right angled. [Mar ’93]
Answer:
Given a cos A = b cos B
2R sin A cos A = 2R sin B cos B ⇒ sin 2A = sin 2B = sin (180° – 2B)
Hence 2A = 2B or 2A = 180° – 2B
⇒ A = BorA = 90°- B ⇒ a = borA + B = 90° ⇒ a = b or C = 90°
∴ The triangle is isosceles or right angled.

Question 13.
If cot\(\frac{A}{2}\): cot\(\frac{B}{2}\) : cot\(\frac{C}{2}\) = 3 : 5 : 7, show that a : b : c = 6 : 5 :4. [Mar. ’17 (A.P); May ’03]
Answer:
Given cot\(\frac{A}{2}\): cot\(\frac{B}{2}\) : cot\(\frac{C}{2}\) = 3 : 5 : 7

s – a = 3k ……(1)
s – b = 5k …..(2)
s – c = 7k …….(3)

Now (1) + (2) + (3)
s – a + s – b + s – c = 3k + 5k + 7k ⇒ 3s – (a + b + c) = 15k ⇒ 3s – 2s = 15k ⇒ s = 15k
From (1) ⇒ 15k – a – 3k ⇒ a = 12k
From (2) ⇒ 15k – b = 5k ⇒ b = 10k
From (3) ⇒ 15k – c = 7k ⇒ c = 8k
a : b : c = 12k : 10k : 8k ⇒ a : b : c = 6 : 5 : 4

Question 14.
If p₁, p₂, p₃ are the altitudes of ΔABC, then show that
\(\frac{1}{p_1^2}+\frac{1}{p_2^2}+\frac{1}{p_3^2}=\frac{\cot A+\cot B+\cot C}{\Delta}\) [Mar. ’13]
Answer:
Since p₁, p₂, p₃ are the altitudes of ΔABC, we have Δ = \(\frac{1}{2}\)ap₁ = \(\frac{1}{2}\)bp₂ = \(\frac{1}{2}\)cp₃
∴ p₁ = \(\frac{2 \Delta}{a}\), p₂ = \(\frac{2 \Delta}{b}\), p₃ = \(\frac{2 \Delta}{c}\)

L.H.S = \(\frac{1}{p_1^2}+\frac{1}{p_2^2}+\frac{1}{p_3^2}=\frac{a^2}{4 \Delta^2}+\frac{b^2}{4 \Delta^2}+\frac{c^2}{4 \Delta^2}=\frac{1}{4 \Delta^2}\)(a² + b² + c²) ……….(1)
R.H.S = \(\frac{1}{\Delta}\)(cot A + cot B + cot C)
Since cot A + cot B + cot C = cot A = \(\sum \frac{\cos A}{\sin A}=\sum \frac{b^2+c^2-a^2}{2 b c \sin A}=\frac{1}{4 \Delta} \Sigma\left(b^2+c^2-a^2\right)\)
= \(\frac{1}{4 \Delta}\)(b² + c² – a² + c² + a² – b² + a² + b² – c²)
= \(\frac{1}{4 \Delta}\)(a² + b² + c²) ………..(2)
From (1) & (2) \(\frac{1}{\mathrm{p}_1^2}+\frac{1}{\mathrm{p}_2^2}+\frac{1}{\mathrm{p}_3^2}=\frac{\cot \mathrm{A}+\cot \mathrm{B}+\cot \mathrm{C}}{\Delta}\)

Question 15.
If a = 26 cm, b = 30 cm and cos C = \(\frac{63}{65}\) then find ‘c’. [Mar. ’11, ’98]
Answer:
Given a = 26 cm, b = 30 cm, cos C = \(\frac{63}{65}\). By the formula c² = a² + b² – 2ab cos C
c² = (26)² + (30)² – 2(26)(30)(\(\frac{63}{65}\)) = 676 + 900 – 1512 = 1576 – 1512 = 64
c = 8 cm

Question 16.
Prove that 2(bc cos A + ca cos B + ab cos C) = a² + b² + c². [Mar. ’05; May. ’97, 90]
Answer:
L.H.S. = Σ2bc cos A = Σ2bc \(\left(\frac{b^2+c^2-a^2}{2 b c}\right)\) = Σ2bc (b² + c² – a²)
= b² + c² – a² + c² + a² – b² + a² + b² – c² = a² + b² + c² = R.H.S.

Question 17.
Prove that (b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c. [Mar. ’98]
Answer:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + a cos B) + (c cos A + a cos C) + (b cos C + c cos B)
= c + b + a = a + b + c = R.H.S (Use projrction Formula)

Question 18.
Prove that (b – a cos C) sin A = a cos A sin C. [Mar. ’98]
Answer:
L.H.S. = (b – a cos C) sin A
= (a cos C + c cos A – a cos C) sin A
= c cos A sin A = 2R sin C cos A sin A
= (2R sin A) cos A sin C = a cos A sin C = R.H.S.

Question 19.
Show that b cos²\(\frac{C}{2}\) + cos²\(\frac{B}{2}\) = s. [Mar. ’12, ’10; May ’03]
Answer:
L.H.S = b cos²\(\frac{C}{2}\) + cos²\(\frac{B}{2}\) = b\(\left(\frac{s(s-c)}{a b}\right)\) + c\(\left(\frac{s(s-b)}{a c}\right)\) = \(\frac{s(s-c)}{a}+\frac{s(s-b)}{a}\)
= \(\frac{s}{a}\)(2s – b – c) = \(\frac{s}{a}\)(a) = s = R.H.S

Question 20.
If \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\), then show that ΔABC is an equilateral. [Mar. ’09]
Answer:
Given that \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C} \Rightarrow \frac{2 R \sin A}{\cos A}=\frac{2 R \sin B}{\cos B}=\frac{2 R \sin C}{\cos C}\)
⇒ \(\frac{\sin A}{\cos A}=\frac{\sin B}{\cos B}=\frac{\sin C}{\cos C}\) = tan A = tan B = tan C
⇒ A = B = C ⇒ ΔABC is an equilateral triangle

Question 21.
If C = 60°, then show that \(\frac{a}{b+c}+\frac{b}{c+a}\) = 1. [May ’93]
Answer:
C = 60° ⇒ c² = a² + b² – 2ab cos C = a² + b² – 2ab (cos 60°)
= a² + b² – 2ab(1/2) = a² + b² – ab ………….(1)
∴ \(\frac{a}{b+c}+\frac{b}{c+a}=\frac{a^2+a c+b^2+b c}{b c+c^2+a b+a c}=\frac{a^2+a c+b^2+b c}{a b+a c+b c+a^2+b^2-a b}=\frac{a^2+a c+b^2+b c}{a^2+b^2+a c+b c}\) = 1

Question 22.
If a : b : c = 7 : 8 : 9, find cos A : cos B : cos C. [May ’15 (AP); May ’13]
Answer:
Given \(\frac{a}{7}=\frac{b}{8}=\frac{c}{9}\) = k
∴ a = 7k, b = 8k, c = 9k

∴ cos A : cos B : cos C = \(\frac{2}{3}: \frac{11}{21}: \frac{2}{7}\) ⇒ 14 : 11 : 6

Question 23.
Show that \(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^2+b^2+c^2}{2 a b c}\). [May. ’10]
Answer:
L.H.S = \(\frac{\cos \mathrm{A}}{\mathrm{a}}+\frac{\cos \mathrm{B}}{\mathrm{b}}+\frac{\cos \mathrm{C}}{\mathrm{c}}=\frac{\mathrm{b}^2+\mathrm{c}^2-\mathrm{a}^2}{2 \mathrm{abc}}+\frac{\mathrm{c}^2+\mathrm{a}^2-\mathrm{b}^2}{2 \mathrm{abc}}+\frac{\mathrm{a}^2+\mathrm{b}^2-\mathrm{c}^2}{2 \mathrm{abc}}=\frac{\mathrm{a}^2+\mathrm{b}^2+\mathrm{c}^2}{2 \mathrm{abc}}\)

Question 24.
Express a sin²\(\frac{C}{2}\) + c sin²\(\frac{A}{2}\) in terms of s, a, b, c.
Answer:
We have sin\(\frac{C}{2}\) = \(\sqrt{\frac{(s-a)(s-b)}{a b}}\)
sin \(\frac{\mathrm{A}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{bc}}}\)
∴ a sin²\(\frac{C}{2}\) + c sin²\(\frac{A}{2}\)
= a\(\frac{(s-a)(s-b)}{b}+\frac{(s-b)(s-c)}{b}\) + c\(\frac{(s-b)(s-c)}{b c}\) = \(\frac{(s-a)(s-b)}{b}+\frac{(s-b)(s-c)}{b}\)
= \(\frac{1}{b}\)(s – b)[s – a -s – c] = \(\frac{1}{b}\)(s – b)[a + b + c – a – c]
= \(\frac{b}{b}\)(s – b) = (s – b)

Question 25.
In ΔABC, show that r = 4R sin\(\frac{A}{2}\) sin\(\frac{B}{2}\) sin\(\frac{C}{2}\) where ‘r’ is the incircie radius. [May ’00]
Answer:
RHS = 4R sin\(\frac{A}{2}\) sin\(\frac{B}{2}\) sin\(\frac{C}{2}\)

∴ r = 4R sin\(\frac{A}{2}\) sin\(\frac{B}{2}\) sin\(\frac{C}{2}\)

Question 26.
In ΔABC, Prove that \(\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}=\frac{1}{r}\). [Mar. ’97, ’96, ’94]
Answer:

Question 27.
Show that rr₁r₂r₃ = Δ²
Answer:
LHS = rr₁r₂r₃ = \(\frac{\Delta}{s} \cdot \frac{\Delta}{s-a} \cdot \frac{\Delta}{s-b} \cdot \frac{\Delta}{s-c}=\frac{\Delta^4}{s(s-a)(s-b)(s-c)}=\frac{\Delta^4}{\Delta^2}\) = Δ² = RHS
∴ rr₁r₂r₃ = Δ²

Question 28.
In an equilateral triangle, find the value of \(\frac{r}{R}\).
Answer:

Question 29.
The perimeter of ΔABC is 12 cm and its in radius is 1 cm. Then find the area of the triangle.
Answer:
Given that the perimeter of ΔABC = 12
2s = 12 ⇒ s = 6
In radius = 1
r = 1
∴ The area of the triangle = Δ = rs = (1)(6) = 6 sq.cm

Question 30.
Show that rr₁ cot\(\frac{A}{2}\) = Δ. [May’96; Mar. ’79]
Answer:

Question 31.
If rr₂ = r₁r₃, then find B. [May ’97]
Answer:
Given that rr₂ = r₁r₃
⇒ \(\frac{\Delta}{s} \cdot \frac{\Delta}{s-b}=\frac{\Delta}{s-a} \cdot \frac{\Delta}{s-c}\) ⇒ (s – a)(s – c) = s(s – b) ⇒ \(\frac{(s-c)(s-a)}{s(s-b)}\) = 1
⇒ tan²\(\frac{B}{2}\) = 1 ⇒ tan\(\frac{B}{2}\) = 1 ⇒ \(\frac{B}{2}\) = 45° ⇒ B = 90°

Question 32.
In a ΔABC, show that the sides a, b, c are in AP, if and only if r₁, r₂, r₃ are in HP. [Mar ’94]
Answer:
Given that rr₂ = r₁r₃
⇒ \(\frac{1}{r_1}, \frac{1}{r_2}, \frac{1}{r_3}\) are in AP ⇒ \(\frac{\mathrm{s}-\mathrm{a}}{\Delta}, \frac{\mathrm{s}-\mathrm{b}}{\Delta}, \frac{\mathrm{s}-\mathrm{c}}{\Delta}\) are in AP ⇒ s – a, s – b, s – c are in A.P
⇒ -a, -b, -c are in AP ⇒ a, b, c are in AP.

Question 33.
Show that \(\frac{1}{\mathbf{r}^2}+\frac{1}{\mathbf{r}_1^2}+\frac{1}{\mathbf{r}_2^2}+\frac{1}{\mathbf{r}_3^2}=\frac{\mathbf{a}^2+b^2+c^2}{\Delta^2}\). [Mar. ’19, ’17(TS), ’98, ’86; May ’93]
Answer:
L.H.S = \(\frac{\mathrm{s}^2}{\Delta^2}+\frac{(\mathrm{s}-\mathrm{a})^2}{\Delta^2}+\frac{(\mathrm{s}-\mathrm{b})^2}{\Delta^2}+\frac{(\mathrm{s}-\mathrm{c})^2}{\Delta^2}=\left(\frac{\left.\mathrm{s}^2+\mathrm{s}^2-2 \mathrm{as}+\mathrm{a}^2+\mathrm{s}^2-2 \mathrm{bs}+\mathrm{b}^2+\mathrm{s}^2-2 \mathrm{cs}+\mathrm{c}^2\right)}{\Delta^2}\right)\)
= \(\frac{1}{\Delta^2}\)[4s² – 2s(a + b + c) + a² + b² + c²]
= \(\frac{1}{\Delta^2}\)[4s² – 2s(2s) + a² + b² + c²] = \(\frac{1}{\Delta^2}\)(a² + b² + c²) = R.H.S

Question 34.
Show that r + r₃ + r₁ – r₂ = 4R cos B in a triangle ABC. [Mar. ’18(AP); Mar. ’13, ’97, ’00]
Answer:

∴ r + r₃ + r₁ – r₂ = 4R cos B

Question 35.
If A, A₁, A₂, A₃ are the areas of Incircie and excircles of a triangle respectively, then prove that \(\frac{1}{\sqrt{\mathrm{A}_1}}+\frac{1}{\sqrt{\mathrm{A}_2}}+\frac{1}{\sqrt{\mathrm{A}_3}}=\frac{1}{\sqrt{\mathrm{A}}}\). [Mar, ’91]
Answer:
If r, r₁, r₂, r₃ are the inradius and exradll of the circles whose areas are A, A₁, A₂, A₃ respectively, then A = πr², A₁ = πr₁², A₂ = πr₂² A₃ = πr₃²

Question 36.
Express Σr₁ cot\(\frac{A}{2}\) in terms of s. [May ’11, ’06; Mar. ’99]
Answer:
We have r₁ = s tan\(\frac{A}{2}\)
Σr₁cot\(\frac{A}{2}\) = Σs tan(\(\frac{A}{2}\))cot\(\frac{A}{2}\) = Σs = s + s + s = 3s

Question 37.
Show that Σa cot A = 2(R + r). [Mar ’98]
Answer:
L.H.S = Σa cot A = Σ2R sin A\(\frac{\cos A}{\sin A}\) = Σ2R cos A = 2R(cos A + cos B + cos C)
= 2R(1 + 4sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\))
= 2R + 2R(4 sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\)) = 2R + 2r (∵r = 4R sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\))
=2(R + r)

Question 38.
In ΔABC, Prove that r₁ + r₂ + r₃ – r = 4R. [Mar. ’06; Mar ’02, 92]
Answer:
r₁ + r₂ = \(\frac{\Delta}{s-a}+\frac{\Delta}{s-b}\) = Δ\(\left(\frac{1}{s-a}+\frac{1}{s-b}\right)\) = Δ\(\left(\frac{2 s-a-b}{(s-a)(s-b)}\right)\) = \(\frac{\Delta(a+b+c-a-b)}{(s-a)(s-b)}=\frac{\Delta c}{(s-a)(s-b)}\)

r₃ – r = \(\frac{\Delta}{s-c}-\frac{\Delta}{s}\) = Δ\(\left(\frac{s-s+c}{s(s-c)}\right)=\frac{\Delta c}{s(s-c)}\)
∴ L.H.S = r₁ + r₂ + r₃ – r
= Δc\(\left(\frac{1}{(s-a)(s-b)}+\frac{1}{s(s-c)}\right)=\frac{\Delta c}{\Delta^2}\)[s(s – c) + (s – a) (s – b)]
= \(\frac{\mathrm{c}}{\Delta}\)(s² – cs + s² – as – bs + ab) = \(\frac{\mathrm{c}}{\Delta}\)[2s² – s(a + b + c) + ab)
= \(\frac{\mathrm{c}}{\Delta}\)[2s² – s(2s) + ab] = \(\frac{\mathrm{abc}}{\Delta}\) = 4R

Question 39.
In ΔABC, prove that r₁ + r₂ + r₃ – r = 4R cos C. [Mar. ’12, May ’06]
Answer:

Question 40.
Prove that 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)². [Mar. ’97]
Answer:
r₁r₂ + r₂r₃ + r₁r₁ = \(\left(\frac{\Delta}{s-a}\right)\left(\frac{\Delta}{s-b}\right)+\left(\frac{\Delta}{s-b}\right)\left(\frac{\Delta}{s-c}\right)+\left(\frac{\Delta}{s-c}\right)\left(\frac{\Delta}{s-a}\right)\)
= \(\frac{\Delta^2}{(s-a)(s-b)}+\frac{\Delta^2}{(s-b)(s-c)}+\frac{\Delta^2}{(s-c)(s-a)}\)
= s(s – c) + s(s – a) + s(s – b) [∵ Δ² = s(s – a)(s – b)(s – c)]
= 3s² – s(a + b + c) = 3s² – 2s² = s²2 = \(\left(\frac{a+b+c}{2}\right)^2=\frac{(a+b+c)^2}{4}\)
∴ 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)²

Question 41.
If ΔABC, if \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\), show that C = 60°. [Mar. ’19, ’17 (TS)]
Answer:
Given that \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\)
= \(\frac{a+c+b+c}{(a+c)(b+c)}=\frac{3}{a+b+c}\)
⇒ (a + b + 2c)(a + b + c) = 3(a + c)(b + c)

⇒ a² + b² – c² = ab ⇒ 2ab cos C = ab ⇒ \(\frac{1}{2}\) cos C = \(\frac{1}{2}\) C = 60°

Telangana TSBIE TS Inter 1st Year Physics Study Material 4th Lesson Motion in a Plane Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 4th Lesson Motion in a Plane

Very Short Answer Type Questions

Question 1.
Write the equation for the horizontal range covered by a projectile and specify when it will be maximum. [TS May ’16]
Answer:
Range of a projectile (R) = \(\frac{u^2 \sin 2 \theta}{g}\)
When θ = 45° Range is maximum.
Maximum Range (R_max) = \(\frac{u^2}{g}\)

Question 2.
The vertical component of a vector is equal to its horizontal component. What is the angle made by the vector with x-axis? [AP Mar. ’19; TS May ’18]
Answer:
Let R be a vector.
Vertical component = R sin θ;
Horizontal component = R cos θ
∴ R sin θ = R cos θ.
So sin θ = cos θ ⇒ θ = 45°

Question 3.
A vector V makes an angle θ with the horizontal. The vector is rotated through an angle α. Does this rotation change the vector V?
Answer:
Magnitude of vector = V ;
Let initial angle with horizontal = θ
Angle rotated = α
So new angle with horizontal = θ + α
Now horizontal component,
V_α = V cos (θ + α)
Vertical component, V_y = V sin (θ + α)
Magnitude of vector, V = \(\sqrt{V^{2}_{x}+V^{2}_{y}}\) = V
So rotating the vector does not change its magnitude.

Question 4.
Two forces of magnitudes 3 units and 5 units act at 60° with each other. What is the magnitude of their resultant? [AP Mar. 17. 15; May 17, 16]
Answer:
Given \(\overline{\mathrm{P}}\) = 3 units, \(\overline{\mathrm{Q}}\) = 5 units and θ = 60°

Question 5.
A = \(\overrightarrow{\mathrm{i}}+\overrightarrow{\mathrm{j}}\) What is the angle between the vector and x-axis? [TS Mar. ’17; AP Mar. ’14; May ’13]
Answer:
Given that, \(\overrightarrow{\mathrm{A}}=\overrightarrow{\mathrm{i}}+\overrightarrow{\mathrm{j}}\)

If ‘θ’ is the angle made by the vector with x-axis then,

Question 6.
When two right angled vectors of magnitude 7 units and 24 units combine, what is the magnitude of their resultant? [AP Mar. 18, 16; May 18. 14]
Answer:
Given \(\overline{\mathrm{P}}\) = 7 units; \(\overline{\mathrm{Q}}\) = 24 units; 0 = 90°

Question 7.
If \(\overline{\mathrm{P}}\) = 2i + 4j + 14k and \(\overline{\mathrm{Q}}\) = 4i + 4j + 10k, find the magnitude of \(\overline{\mathrm{P}}+\overline{\mathrm{Q}}\). [TS Mar. ’16, ’15]
Answer:

Question 8.
Can a vector of magnitude zero have non-zero components?
Answer:
A vector with zero magnitude cannot have non-zero components. Because magnitude of given vector \(\overline{\mathrm{V}}\) = \(\sqrt{V^{2}_{x}+V^{2}_{y}}\) must be zero. This is possible only when V²_x and V²_y are zero.

Question 9.
What is the acceleration of a projectile at the top of its trajectory? [TS Mar. ’19]
Answer:
At highest point acceleration, a = g. In projectile, motion acceleration will always acts towards centre of earth. It is irrespective of its position, whether it is at highest point or somewhere.

Question 10.
Can two vectors of unequal magnitude add up to give the zero vector? Can three unequal vectors add up to give the zero vector?
Answer:
No. Two unequal vectors can never give zero vector by addition. But three unequal vectors when added may give zero vector.

Short Answer Questions

Question 1.
State parallelogram law of vectors. Derive an expression for the magnitude and direction of the resultant vector. [TS Mar. ’17, ’16, May ’17; AP Mar. ’14, ’13]
Answer:
Parallelogram Law :
If two vectors are represented by the two adjacent sides of a parallelogram then the diagonal passing through the intersection of given vectors represents their resultant both in direction and magnitude.

Proof :
Let \(\overline{\mathrm{P}}\) and \(\overline{\mathrm{Q}}\) be two adjacent vectors ‘θ’ be angle between them. Construct a parallelogram OACB as shown in figure. Extend the line OA and draw a normal D from C. The diagonal OC = the resultant \(\overline{\mathrm{R}}\) both in direction and magnitude.

In figure OCD = right angle triangle
⇒ OC = OD² + DC²

Angle of resultant with adjacent side ‘α’

Question 2.
What is relative motion? Explain it.
Answer:
Relative velocity is the velocity of a body with respect to another moving body.

Relative velocity in two dimensional motion :
Let two bodies A and B are moving with velocities \(\overrightarrow{\mathrm{V}}_A\) and \(\overrightarrow{\mathrm{V}}_B\) then relative velocity of Aw.r.t B is \(\overrightarrow{\mathrm{V}}_{AB}=\overrightarrow{\mathrm{V}}_{A}+\overrightarrow{\mathrm{V}}_{B}\)
Relative velocity of B w.r.t. A is
\(\overrightarrow{\mathrm{V}}_{BA}=\overrightarrow{\mathrm{V}}_{B}-\overrightarrow{\mathrm{V}}_{A}\)

Procedure to find resultant :
To find rela-tive velocity in two dimensional motion use vectorial subtraction of V_A or V_B. Generally to find relative velocity one vector \(\overrightarrow{\mathrm{V}}_A\) or \(\overrightarrow{\mathrm{V}}_B\) is reversed (as the case may be) and parallelogram is constructed. Now resultant of that parallelogram is equal to \(\overrightarrow{\mathrm{V}}_A-\overrightarrow{\mathrm{V}}_B\) or \(\overrightarrow{\mathrm{V}}_B-\overrightarrow{\mathrm{V}}_A\) (8° one vector is reversed V_A is taken as –\(\overrightarrow{\mathrm{V}}_A\) or \(\overrightarrow{\mathrm{V}}_B\) is taken as –\(\overrightarrow{\mathrm{V}}_B\))
In figure relative velocity of B w.r.t A is V_BA =V_R = V_B – V_A.

Question 3.
Show that a boat must move at an angle with respect to river water in order to cross the river in minimum time.
Answer:
Motion of a boat in a river :
Let a boat can travel with a speed of V_bE in still water w.r. to earth. It is used to cross a river which flows with a speed of V_WE with respect to earth. Let width of river is W.

We can cross the river in two different ways.
1) in shortest path 2) in shortest time.

To cross the river in shortest time :

To cross the river in shortest time boat must be rowed along the width of river i.e., boat must be rowed perpendicular to the bank or 90° with the flow of water. Because width of river is the shortest distance. So velocity must be taken in that direction to obtain shortest time. In this case V_bE and V_WE are perpendicular and boat will travel along AC. The distance BC is called drift. So to cross the river in shortest time angle with flow of water = 90°.

Question 4.
Define unit vector, null vector and position vector. [AP June ’15]
Answer:
Unit vector :
A vector whose magnitude is one unit is called unit vector.

Let a is \(\overline{\mathrm{a}}\) given vector then unit vector

Null vector :
A vector whose magnitude is zero is called null vector. But it has direction.

For a null vector the origin and terminal point are same.
Ex : Let \(\overline{\mathrm{A}}\times\overline{\mathrm{B}}=\overline{\mathrm{0}}\) . Here magnitude of \(\overline{\mathrm{A}}\times\overline{\mathrm{B}}=\overline{\mathrm{0}}\) . But still it has direction perpendicular to the plane of \(\overline{\mathrm{A}}\) and \(\overline{\mathrm{B}}\).

Position vector :
Any vector in space can be represented by the linear combination

Question 5.
If |\(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}\)| = |\(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}\)|, prove that the angle between \(\overrightarrow{\mathrm{a}}\) and \(\overrightarrow{\mathrm{b}}\) is 90°. [TS Mar., May ’18]
Answer:
Let \(\overrightarrow{\mathrm{a}}\), \(\overrightarrow{\mathrm{b}}\) are the two vectors.
Sum of vectors

by squaring on both sides,
a² + b² + 2ab cos θ = a² + b² – 2ab cos θ
∴ 4 ab cos θ = 0 or θ = 90°

Question 6.
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola. [AP Mar. ’18, ’17. ’16. ’15, May ’18, ’17, ’14. ’13; June ’15; TS Mar. ’18, ’15, May ’16, June ’15]
Answer:
Projectile :
A body thrown into the air same angle with the horizontal, (other tan 90°) its motion under the influence of gravity is called projectile. The path followed by it is called trajectory.

Let a body is projected from point O, with velocity ‘u’ at an angle θ with horizontal. The velocity u’ can be resolved into two rectangular components u_x and u_y along x-axis and y-axis.
u_x = u cos θ and u_y = u sin θ

After time t, Horizontal distance travelled x = u cos θ . t ……….. (1)

After a time t’ sec; vertical displacement

The above equation represents “parabola”. Hence the path of a projectile is a parabola.

Question 7.
Explain the terms the average velocity and instantaneous velocity. When are they equal ?
Answer:
Average velocity :
It is the ratio of total displacement to total time taken.

Average velocity is independent of path followed by the particle. It just deals with initial and final positions of the body.

Instantaneous velocity :
Velocity of a body at any particular instant of time is defined as instantaneous velocity.

as instantaneous velocity.
For a body moving with uniform velocity its average velocity = Instantaneous velocity.

Question 8.
Show that the maximum height and range

respectively where the terms have their regular meanings.
Answer:
Let a body is projected with an initial velocity ‘u’ and with an angle θ to the horizontal. Initial velocity along x direction, u_x = u cos θ Initial velocity along y direction, u_y = u sin θ

Horizontal Range :
It is the distance covered by projectile along the horizontal between the point of projection to the point on ground, where the projectile returns again.

It is denoted by R. The horizontal distance covered by the projectile in the to time of flight is called horizontal range. Therefore, R = u cos θ × t.

Angle of projection for maximum range:
For a given velocity of projection, the horizontal range will be maximum, when sin 2θ = 1.
∴ Angle of projection for maximum range is 2θ = 90° or θ = 45°
∴ R_max = \(\frac{u^2}{g}\)

Maximum height :
The vertical distance covered by the projectile until its vertical component becomes zero.

Question 9.
If the trajectory of a body is parabolic in one reference frame, can it be parabolic in another reference frame that moves at constant velocity with respect to the first reference frame? If the trajectory can be other than parabolic, what else can it be?
Answer:
Yes. According to Newton’s first law, a body at rest or a body moving with uniform velocity are treated as same. Both of them belong to inertial frame of reference.

If a frame (say 1) is moving with uniform velocity with respect to other, then that second frame must be at rest or it maintains a constant velocity w.r.t the first. So both frames are inertial frames. So if trajectory of a body in one frame is a parabola, then trajectory of that body in another frame is also a parabola.

Question 10.
A force 2i + j – k newton acts on a body which is initially at rest. At the end of 20 seconds the velocity of the body is 4i + 2j – 2k ms-1. What is the mass of the body? [AP May ’16]
Answer:
Force, F = 2i + j – k
time, t = 20
Initial velocity, u = 0
Final velocity, v = 4i + 2j – 2k = 2(2i + j – k)

Problems

Question 1.
Ship A is 10 km due west of ship B. Ship A is heading directly north at a speed of 30 km/h, while ship B is heading in a direction 60° west of north at a speed of 20 km/h.
(i) Determine the magnitude of the
(ii) What will be their distance of closest approach?
Answer:
Velocity of A = 30 kmph due North
∴ V_A = 30\(\hat{\mathbf{j}}\)
Velocity of B = 20 kmph 60° west of North
∴ V_B = -20sin60° + 20 cos60° = 10√3\(\hat{\mathbf{i}}\) + 10\(\hat{\mathbf{j}}\)

Shortest distance :
In ∆le ANB shortest distance, AN = AB sin θ
But distance, AB = 10 km
∴ AN = 10 × \(\frac{20}{10\sqrt{7}}=\frac{20}{\sqrt{7}}\) = 7.56 km

Question 2.
If θ is the angle of projection, R the range, h the maximum height, T the time of flight, then show that (a) tan θ = 4h/R and (b)h = gT²/8
Answer:
(a) Given angle of projection = θ,

Question 3.
A projectile is fired at an angle of 60° to the horizontal with an initial velocity of 800 m/s:
(i) Find the time of flight of the projectile before it hits the ground.
(ii) Find the distance it travels before it hits the ground (range).
(iii) Find the time of flight for the projectile to reach its maximum height.
Answer:
Angle of projection, θ = 60°.
Initial velocity, u = 800 m/s

iii) Time of flight to reach maximum height = \(\frac{T}{2}\)

Question 4.
For a particle projected slantwise from the ground, the magnitude of its position vector with respect to the point of projection, when it is at the highest point of the path is found to be √2 times the maximum height reached by it. Show that the angle of projection is tan^-1 (2).
Answer:
Position vector of h (max point) from 0, is

Question 5.
An object is launched from a cliff 20. m above the ground at an angle of 30° above the horizontal with an initial speed of 30 m/s. How far horizontally does the object travel before landing on the ground? (g = 10 m/s²)
Answer:
Height of cliff = 20m
Angle of projection, θ = 30°
Velocity of projection, u = 30 m/s
Total horizontal distance travelled = OC = OB’ + B’C

b) Distance B’C = Range of a horizontal projectile.
∴ Range = u cos θ t
u. cos θ = 30.\(\frac{\sqrt{3}}{2}\) = 15√3 .
Time taken to reach the ground, t = ?
Given S_y = 20, u_y = u sin θ = 30 sin 30° = 15 m/s
∴ S_y = 20 = 15t + \(\frac{10}{2}\)t² ⇒ 5t² + 15t – 20 = 0
or t² + 3t – 4 = 0 or (t + 4) (t – 1) = 0
∴ t = – 4 or t = 1 ∴ t is Not – ve use t = 1
∴ Range = 4 . cos θ . t = 15√3 → (2)
Total distance travelled before reaching the ground = 45√3 +15√3 = 60√3 m.

Question 6.
‘O’ is a point on the ground chosen as origin. A body first suffers a displacement of 10√2 mm North-East, next 10 m North and finally 10√2 North-West. How far it is from origin? [TS Mar. ’19]
Answer:
a) 10√2 m North-East
b) 10m North
c) 10√2 m North-West

From figure total displacement from origin ‘O’ is OC
ButOC = OA’ + A’B’ + B’C =10 + 10 + 10 = 30 m.

Question 7.
From a point on the ground a particle is projected with initial velocity u, such that its horizontal range is maximum. Find the magnitude of average velocity during its ascent.
Answer:
Velocity of projection = u.
Range is maximum ⇒ θ = 45°
During time of ascent ⇒ when h = h_max
⇒ u_x = V_x = u . cos θ

Average velocity, V_A = \(\sqrt{V^{2}_{x}+V^{2}_{y}}\)
V_x = Average velocity along x-axis

Average velocity during time of ascent

Question 8.
A particle is projected from the ground with some initial velocity making an angle of 45° with the horizontal. It reaches a height of 7.5 m above the ground while it travels a horizontal distance of 10 m from the point of projection. Find the initial speed of projection (g = 10 m/s2).
Anwser:
Angle of projection = 45°
Vertical height, h_y = 7.5 m
Horizontal distance, h_x = 10 m

Question 9.
Wind is blowing from the south at 5 ms^-1. To a cyclist it appears to be blowing from the east at 5 ms^-1. Show that the velocity of the cyclist is ms^-1 towards north-east.
Answer:
Direction of wind South to North 5 m/s.

Apparent direction is from East to West 5 m/s.

This is relative velocity.
To find velocity of cyclist reverse the direction of resultant vector OB and find resultant
∴ Velocity of cyclist = \(\sqrt{5^2+^2+0}\) = 5√2 m/s

Question 10.
A person walking at 4 m/s finds rain drops falling slantwise into his face with a speed of 4 m/s at ah angle of 30° with the vertical. Show that the actual speed of the rain drops is 4 m/s.
Answer:
Velocity of man = 4 m/sec
Apparent velocity of rain drop = 4 m/sec with θ = 30° with vertical. This is relative velocity V_B.

Additional Problems

Question 1.
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 ms-1 can go without hitting the ceiling of the hall?
Solution:
Here, u = 40 ms^-1; H = 25m, R = ?
Let θ be the angle of projection with the horizontal direction to have the maximum range, with maximum height = 25 m.

Question 2.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Solution:
Here, r = 80 cm = 0.8 m; o = 14/25 s^-1.

The centripetal acceleration,
a = ω²r = (\(\frac{88}{25}\))² × 0.80 = 9.90m/s²
The direction of centripetal acceleration is along the string directed towards the centre of circular path.

Question 3.
An aircraft executes a horizontal loop of radius 1 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.
Solution:
Here, r = 1 km = 1000 m;
v = 900 km h^-1 = 900 × (1000m) × (60 × 60s)^-1
= 250 ms^-1

Question 4.
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the air-craft positions 10.0 s apart is 30°, what is the speed of the aircraft?
Solution:
In Fig, O is the observation point at the ground. A and B are the positions of aircraft for which ∠AOB = 30°. Draw a perpendicular OC on AB. Here OC = 3400 m and ∠AOC = ∠COB = 15°. Time taken by aircraft from A to B is 10 s.

Question 5.
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.
Solution:

Since the muzzle velocity is fixed, therefore, Max. horizontal range,
R_max = \(\frac{u^2}{g}\) = 2√3 = 3.464 m.
So, the bullet cannot hit the target.

Telangana TSBIE TS Inter 1st Year Physics Study Material 3rd Lesson Motion in a Straight Line Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 3rd Lesson Motion in a Straight Line

Very Short Answer Type Questions

Question 1.
The states of motion and rest are relative. Explain.
Answer:
REST :
If the position of a body does not change with respect to surroundings, it is said to be at “rest”.

MOTION :
If the position of a body changes with respect to surroundings, it is said to be in “motion”.

By definitions rest and motion are relative with respect to surroundings.

Question 2.
How is average velocity different from instantaneous velocity? [AP Mar. 19, 13, May 17]
Answer:
Average velocity :
It is the ratio of total displacement to total time taken. It is independent of path of the body.

∴ Average velocity = \(\frac{\mathrm{s}_2-\mathrm{s}_1}{\mathrm{t}_2-\mathrm{t}_1}\)

Velocity of a particle at a particular instant of time is known as instantaneous velocity. Here time interval is very small.

Only in uniform motion, instantaneous velocity = average velocity. For all other cases instantaneous velocity may differ from average velocity.

Question 3.
Give an example where the velocity of an object is zero but its acceleration is not zero. [AP May ’17, Mar. ’13]
Answer:
In case of VPB at maximum height its velocity v = 0. But acceleration due to gravity ‘g’ is not zero.

So even though velocity v = 0 ⇒ acceleration is not zero.

Question 4.
A vehicle travels half the distance L with speed v₁ and the other half with speed v₂. What is the average speed?
Answer:
The average speed of a vehicle for the two equal parts.

Question 5.
A lift coming down is just about to reach the ground floor. Taking the ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
a) x < 0, v < 0, a > 0
b) x > 0, v < 0, a < 0
c) x > 0, v < 0, a > 0
d) x > 0, v > 0, a > 0
Answer:
As the lift is coming down, the value of x become less hence negative, i.e., x < 0.

Velocity is downwards (i.e., negative). So v < 0. Just before reaching ground floor, lift is retarded, i.e., acceleration is upwards. Hence a > 0.

We can conclude that x < 0, v < 0 and a > 0.
∴ (a) is correct.

Question 6.
A uniformly moving cricket ball is hit with a bat for a very short time and is turned back. Show the variation of its acceleration with time taking the acceleration in the backward direction as positive.
Answer:
For a ball moving with uniform velocity acceleration is zero. But during time of contact between ball and bat acceleration is applied in opposite direction. The shape of acceleration – time graph is as shown.

Question 7.
Give an example of one-dimensional motion where a particle moving along the positive x-direction comes to rest periodically and moves forward.
Answer:
When length of pendulum is high and amplitude is less then its motion is along a straight line. The pendulum will come to a stop at extreme position and moves back in forward direction (‘x’ + ve) periodically.

Question 8.
An object falling through a fluid is observed to have an acceleration given by a = g – bv, where g is the gravitational acceleration and b, is a constant. After a long time it is observed to fall with a constant velocity. What would be the value of this constant velocity?
Answer:
Acceleration, a = g – bv when moving with constant velocity, a = 0 ⇒ 0 = g – bv
∴ Constant velocity, v = \(\frac{g}{b}\) m/sec.

Question 9.
If the trajectory of a body is parabolic in one frame, can it be parabolic in another frame that moves with a constant velocity with respect to the first frame? If not, what can it be?
Answer:
If the trajectory of a body is parabolic with reference frames one and two then those two frames are of rest or moving with uniform velocity.

If they are not parabolic then for that reference frame it may be in straight line path.
Ex : When a body is dropped from a moving plane its path is parabolic for a person outside the plane. But for the pilot in the plane it is falling vertically downwards.

Question 10.
A spring with one end attached to a mass and the other to a rigid support is stretched and released. When is the magnitude of acceleration a maxium?
Answer:
Maximum restoring force setup in the spring, when stretched by a distance ’r’, is F = – kr

Potential energy of stretched spring = \(\frac{1}{2}\) kx²

As F ∝ r and this force is directed towards equilibrium position, hence if mass is left free, it will execute damped SHM due to gravity pull.

Magnitude of acceleration in the mass attached to one end of spring when just released is

a = \(\frac{F}{m}=\frac{-k}{m}\) r = (Maximum)

The magnitude of acceleration of the spring will be maximum when just released.

Question 11.
Define average velocity and average speed. When does the magnitude of average velocity become equal to the average speed?
Answer:
Average velocity :
It is defined as the ratio of total displacement to total time taken.

Average velocity

Average velocity is independent of path followed by the particle. It just deals with initial and final positions of the body. Average Speed: The ratio of total path length travelled to the total time taken is known as “average speed”.

Speed and average speed are scalar quantities so no direction for these quantities.

When the body is along with the straight line its average velocity and average speed are equal.

Short Answer Questions

Question 1.
Can the equations of kinematics be used when the acceleration varies with time? If not, what form would these equations take?
Answer:
a) The equations of motion are
1) v =u + at
2) s = ut + \(\frac{1}{2}\) at² and 3) v² – u² = 2as. All these three equations applicable body moves with uniform acceleration ‘a’.

No, the equations of are not applicable when the acceleration varies with time.

Question 2.
A particle moves in a straight line with uniform acceleration. Its velocity at time t = 0 is v₁ and at time t₂ = t is v₂. The average velocity of the particle in this time interval is (v₁ + v₁)/ 2. Is this correct? Substantiate your answer.
Answer:
t₁ = 0 ⇒ u = v₁
t₂ = t ⇒ v = v₂

Question 3.
Can the velocity of an object be in a direction other than the direction of acceleration of the object? If so, give an example.
Answer:
Yes. Velocity of a body and its acceleration may be in different directions.

Explanation:

1. Incase of vertically projected body ⇒ velocity of body is in the upward direction and acceleration is in a downward direction.
2. When brakes are applied the velocity of body before coming to rest is opposite to retarding acceleration.

Question 4.
A parachutist flying in an aeroplane jumps when it is ata height of 3 km above ground. He opens his parachute when he is about 1 km above ground. Describe his motion.
Answer:
a) Height of fall before opening, h = 2 km
= 2000 m
∴ Velocity at a height of 1 km

b) After parachute is opened it touches the ground with almost zero velocity.
∴ u = 200 m/sec, v = 0, S = h = 1000 m From v² – u² = 2as

The Motion is as shown in figure.

Question 5.
A bird holds a fruit in its beak and flies parallel to the ground. It lets go of the fruit at some height. Describe the trajectory of the fruit as it falls to the ground as seen by (a) the bird (b) a person on the ground.
Answer:
a) As the bird is flying parallel to the ground, it possesses velocity in horizontal direction. Hence the fruit also possess velocity in horizontal direction and acceleration in downward direction. Hence the path of the fruit is a straight line with respect to the bird.

b) With respect to a person on the ground, the fruit seems to be in a parabolic path.

Question 6.
A man runs across the roof of a tall building and jumps horizontally on to the (lower) roof of an adjacent building. If his speed is 9 ms^-1 and the horizontal distance between the buildings is 10 m and the height difference between the roofs is 9 m, will he be able to land on the next building? (take g = 10 ms^-2) [TS Mar. ’18]
Answer:
Given that,
initial speed, u = 9 ms^-1 ; g = 10m/s² height difference between the roofs, h = 9 m
horizontal distance between two buildings, d = 10 m

Range of the man = R = u × T = 9 × 1.341
= 12.069 m

Since R > d, the man will be able to land on the next building.

Question 7.
A ball is dropped from the roof of a tall building and simultaneously another ball is thrown horizontally with some velocity from the same roof. Which ball lands first? Explain your answer. [TS June ’15]
Answer:
Let ‘h’ be the height of the tall building.

For dropped ball:
Let ‘t₁‘ be the time taken by the dropped ball to reach the ground.

Initial velocity, u = 0 ; Acceleration, a = + g
Distance travelled, s = h; Time of travel, t = t₁

From the equation of motion, s = ut + \(\frac{1}{2}\) at²
we can write,

For horizontally projected ball:
If the ball is thrown horizontally then its initial velocity along vertical direction is zero and in this case let ‘t₂‘ be the time taken by the ball to reach the ground.
Again from the equation of motion,

From equations (1) and (2) t₁ = t₂
i.e., both the balls reach the ground in the same time.

Question 8.
A ball is dropped from a building and simultaneously another ball is projected upward with some velocity. Describe the change in relative velocities of the balls as a function of time.
Answer:
a) For a body dropped from building its velocity, v₁ = gt → (1) (∵ u₁ = 0)

b) For a body thrown up with a velocity ‘u’ its velocity, v₂ = u – gt → (2)
∵ The two balls are moving in opposite direction the relative velocity,
V_R = v₁ + v₂
∴ v_R =gt + u – gt = u

Here the relative velocity remains constant, but velocity of one body increases at a rate of g’ m/sec and velocity of another body decreases at a rate of ‘g’m/sec.

Question 9.
A typical raindrop is about 4 mm in diameter. If a raindrop falls from a cloud which is at 1 km above the ground, estimate its momentum when it hits the ground.
Answer:
Diameter, D = 4 m
⇒ radius, r = 2mm = 2 × 10^-3 m
mass of rain drop = volume × density = \(\frac{4}{3}\)πr³ × 1000 m
(∵ mass of one m³ of water = 1000 kg)

Question 10.
Show that the maximum height reached by a projectile launched at an angle of 45° is one quarter of its range. [AP May ’16, Mar. ’14]
Answer:

∴ When θ = 45° maximum height reached is one quarter of maximum range.

Question 11.
Derive the. equation of motion x = v₀t + \(\frac{1}{2}\) at² using appropriate graph. [TS Mar. ’19, May ’16]
Answer:
The velocity-time graph of a body moving with initial velocity u’ and with uniform acceleration a’ as shown. Let ‘v’ be the velocity of the body after a time t.

In v – t graph area of velocity-time graph = total displacement travelled by it. Area under velocity – time graph = area of OABCD
∴ Area of Rectangular part OACD = Area of OACD + Area of ABC.
A₁ = OA × OD = v₀.t. ……….. (1)

2) Area of triangle ABC = A₂
A₂ = \(\frac{1}{2}\)Base × height
= \(\frac{1}{2}\)AC × BC
= \(\frac{1}{2}\) t(v – v₀).
But v – v₀ = at
A₂ = \(\frac{1}{2}\)t.at = \(\frac{1}{2}\)at².
∴ Total area under graph = s = A₁ + A₂
s(n) = v₀t + \(\frac{1}{2}\)at².
∴ s = ut + \(\frac{1}{2}\)at² is graphically proved.

Problems

Question 1.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h^-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h^-1. What is the (a) magnitude of average velocity and (b) average speed of the man over the time interval 0 to 50 minutes? [AP Mar. ’19. May ’18; TS Mar. ’18]
Solution:
Time taken by man to go from his home to

Time take by man to go from market to his home, t₂ = \(\frac{2.5}{7.5}=\frac{1}{3}\)h
∴ Total time taken = t, + to = \(\frac{1}{2}+\frac{1}{3}=\frac{5}{6}h\)
= 50 min.
In time interval 0 to 50 min,
Total distance travelled = 2.5 + 2.5 = 5 km.
Total displacement = zero.

Question 2.
A stone is dropped from a height 300 in and at the same time another stone is projected vertically upwards with a velocity of 100 m/sec. Find when and where the two stones meet. [AP Mar. ’16]
Solution:
Height h = 300 m ;
Initial velocity U₀ = 100 m/s
Let the two stones will meet at a height ‘x’ above the ground.
For 1st stone h – x = \(\frac{1}{2}\) gt² …………. (1)
For 2nd stone x = u₀t – \(\frac{1}{2}\) gt²
⇒ \(\frac{1}{2}\) gt² = u₀t – x ……….. (2)

Since t is same for the two stones
From equations 1 & 2.
h – x = u₀t – x
⇒ u₀t = h or time t = \(\frac{h}{u_0}=\frac{300}{100}\) = 3 sec.
∴ The two stones will meet 3 seconds after the 1st stone is dropped or 2nd stone is thrown up.

Question 3.
A car travels the first third of a distance with a speed of 10 kmph, the second third at 20 kmph and the last third at 60 kmph. What is its mean speed over the entire distance? [TS Mar. ’16; AP May ’14, AP Mar. ’18]
Solution:
Total distance = s;
distance travelled, s₁ = \(\frac{s}{3}\) ;
velocity, v₁ = 10 kmph
distance, s₂ = \(\frac{s}{3}\)
velocity, v₂ = 20 kmph
distance, s₃ = \(\frac{s}{3}\)
velocity, v₃ = 60 kmph

Question 4.
A bullet moving with a speed of 150 m s^-1 strikes a tree and penetrates 3.5 cm before stopping. What is the magnitude of its retardation in the tree and the time taken for it to stop after striking the tree?
Solution:
Velocity of bullet, u = 150 m/s;
Final velocity, v = 0
Distance travelled, s = 3.5 cm = 3.5 × 10^-2 m,

Question 5.
A motorist drives north for 30 min at 85 km/h and then stops for 15 min. He continues travelling north and covers 130 km in 2 hours. What is his total displacement and average velocity?
Solution:
In first part:
Velocity, v₁ = 85 kmph
Time, t₁ = 30 min
Distance travelled, s₁ = v₁ t₁
= 85 × \(\frac{30}{60}\) = 42.5 km

In second part:
Distance travelled, s₂ = 0 ;
Time, t₂ = 15.0 min.

In third part:
Distance travelled, s₃ = 130 km ;
Time, t₃ = 120 min = 2 hours
a) Total distance of the motorist,
s = s₁ + s₂ + s₃ = 42.5 + 0 + 130 = 172.5 km

b) Total time travelled,
t = t₁ + t₂ + t₃ = 30 + 15 + 120
= 165 minutes
= 2 hrs 45 minutes
= 2\(\frac{3}{4}\)hrs. = \(\frac{11}{4}\) hrs.
∴ Average velocity,

Question 6.
A ball A is dropped from the top of a building and at the same time an identical ball B is thrown vertically upward from the ground. When the balls collide the speed of A is twice that of B. At what frac¬tion of the height of the building did the collison occur?
Solution:
Given at time of collision velocity of A = V_A
= 2 × V_B (velocity of B)
Let the body be dropped from a height h’.
Let the two stones collide at x from ground.
For the body dropped,
s = h – x = \(\frac{1}{2}\)gt² → (1)
For the body thrown up,
x = ut – \(\frac{1}{2}\)gt² → (2)
For the body dropped,
v = u + at ⇒ V_A = gt → (3)
For the body thrown up,
v = u – gt ⇒ V_B = u – gt → (4)
Given V_A = 2V_B
⇒ gt = 2 (u – gt) or u = \(\frac{3gt}{2}\) → (5)
Divide equation (1) with equation (2)

∴ Fraction of height of collision = \(\frac{2}{3}\)

Question 7.
Drops of water fall at regular intervals from the roof of a building of height 16 m. The first drop strikes the ground at the same moment as the fifth drop leaves the roof. Find the distances between successive drops.
Solution:
Height of building, h = 16 m

Number of drops, n = 5
∴ Number of intervals = n – 1 = 5 – 1 = 4

Time interval between drops = \(\frac{1.8}{4}\)
= 0.45 sec
Time of travel of 1st drop, t₁ = 4 × 0.45 = 1.8
∴ Distance travelled by
1st drop, S₁ = \(\frac{1}{2}\)gt²₁ = \(\frac{1}{2}\) × 9.8 × 1.8 × 1.8= 16 m

For 2nd drop, t₂ = 3 × 0.45 = 1.35 sec.,
∴ S₂ = \(\frac{1}{2}\) × 9.8 × 1.35²
= 4.9 × 1.822 ≅ 1.822 ≅ 9m

For 3rd drop, t₃ = 2 × 0.45 = 0.9 sec.
Distance, S₃ = \(\frac{1}{2}\)gt²₃ = \(\frac{1}{2}\) × 9.8 × 0.9² = 3.97≅4 m

For 4th drop, t₄ = 1 × 0.45 = 0.45 sec
Distance travelled, S₄ = \(\frac{1}{2}\)gt²₄ = \(\frac{1}{2}\) × 9.8 × (0.45)² = 1

For 5 th drop, t₅ = 0 ⇒ S₅ = 0
Distance between 1^st and 2^nd drop
S_{1, 2} = S₁ – S₂ = 16 – 9 = 7 m

Distance between 2^nd and 3^rd drop
S_{2, 3} = S₂ – S<₃ = 9 – 4 = 5m

Distance between 3^rd and 4^th drop
S_{3, 4} = S₃ – S4 = 4 – 1= 3 m

Distance between 4^th and 5^th drop
S_{4, 5} = S₄ – S₅ = 1 – 0 = 1 m

∴ Distances between successive drops are 7m, 5m, 3m and lm.

Question 8.
Rain is falling vertically with a speed of 35 ms^-1. A woman rides a bicycle with a speed of 12 ms^-1 in east to west direction. What is the direction in which she should hold her umbrella? [TS June ’15]
Solution:
Velocity of rain V_R = 35 m/s (vertically)
Velocity of women V_w = 12 m/s (towards east)
Resultant angle θ = tan^-1 \(\frac{V_W}{V_R}=\frac{12}{35}\)
∴ θ = tan^-1\(\frac{12}{35}\) = 0.343. or q = 19° (Nearly)
She should hold umbrella at an angle of 19c with east.

Question 9.
A hunter aims a gun at a monkey hanging from a tree some distance away. The monkey drops from the branch at the moment he fires the gun hoping to avoid the bullet. Explain why the monkey made a wrong move.
Solution:
Let the bullet is fired with an angle α and distance from hunter’s rifle to monkey = x
Vertical component of velocity v_xy = v sin α
when exactly aimed at monkey s_y = v sin α
t = h

But due to acceleration due to gravity
h₁ = u sin α t – \(\frac{1}{2}\)gt² = h – \(\frac{1}{2}\)gt² → (1)
So bullet passes through a height of \(\frac{1}{2}\)gt² below the monkey.
But when the monkey is falling freely height of fall during time t = \(\frac{1}{2}\)gt²
So new height is \(\frac{1}{2}\)gt² → (2)

From equations (1) & (2) h₁ is same i.e., if the monkey is dropped from the branch bullet will hit it exactly.

Question 10.
A food packet is dropped from an aero-plane, moving with a speed of 360 kmph in a horizontal direction, from a height of 500m. Find (i) its time of descent (ii) the horizontal distance between the point at which the food packet reaches the ground and the point above which it was dropped.
Solution:
Velocity of plane, V = 360 kmph
= 360 × \(\frac{5}{18}\) = 100 m/s

Height above ground, h = 500 m;
g = 10 m/s²

i) Time of descent,

ii) Horizontal distance between point o{ dropping and point where it reaches the ground = Range R

Question 11.
A ball is tossed from the window of a building with an initial velocity of 8 ms^-1 at an angle of 20° below the horizontal. It strikes the ground 3 s later. From what height was the ball thrown? How far from the base of the building does the ball strike the ground?
Solution:
Initial velocity, u = 8 m/s;
Angle of projection, θ = 20°
Time taken to reach the ground, t = 3 sec
Horizontal component of initial velocity,
u_x = u. cos θ = 8 cos 20°
= 8 × 0.94 = 7.52 m/s

Vertical component of initial velocity,
v_y = u sin θ = 8 sin 20°
= 8 × 0.342 = 2.736 m/s

a) From equation of motion, s = ut + \(\frac{1}{2}\)at²
we can write
h = (u sin θ)t + \(\frac{1}{2}\)gt²
⇒ h = (2.736)3 + \(\frac{1}{2}\)9.8 × (3)²
⇒ h = 8.208+ 4.9 × 9
⇒ h = 8.208 + 44.1 or h = 52.308 m

b) Horizontal distance travelled, s_x = v_x x t = 7.52 × 3 = 22.56 m

Question 12.
Two balls are projected from the same point in directions 30° and 60° with respect to the horizontal. What is the ratio of their initial velocities if they (a) attain the same height? (b) have the same range?
Solution:
Angle of projection of first ball, θ₁ = 30°
Angle of projection of second ball, θ₂ = 60°
Let u₁ and u₂ be the velocities of projections of the two balls.
i) Maximum height of first ball,

ii) If the balls have same range, then R₁ = R₂

Question 13.
A ball is thrown vertically upwards with a velocity of 20 ins’1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. [TS May ’17; AP & TS Mar. ’15]
(a) How high will the ball rise?
(b) How long will it be before the ball hits the ground?
Take g = 10 ms^-2 [Actual value of ‘g’ is 9.8 ms^-2]
(OR)
When a ball is thrown vertically upwards with a velocity of 20 ms^-1 from the top of a multistorey building, the height of the point from where the ball is thrown is 25.0 m from the ground. [TS Mar. ’15]
a) How high will the ball rise? and
b) How long will it be before the ball hits the ground?
Solution:
Initial velocity V₀ = 20 m/s;
height above ground h₀ = 2.50 m ;
g = 10 m/s²

a) For a body thrown up vertically height of rise

b) Time spent in air (t) is y₁ – y₀ = V₀t + \(\frac{1}{2}\)gt²
Where y₁ = Total displacement of the body from ground = 0
∴ 0 = y₀ + V₀t+ \(\frac{1}{2}\)gt² = 25 + 20t – \(\frac{1}{2}\). 10 . t²
[∵ g = – 10 m/s² while going up]
∴ 0 = – 5t² + 20t + 25 (or) t² – 4t – 5 = 0
i.e., (t – 5) (t + 1) = 0 ⇒ t = 5 (or) t = – 1
But time is not – ve.
∴ Time spent in air t = 5 sec

Question 14.
A parachutist flying in an aeroplane jumps when it is at a height of 3 km above the ground. He opens his parachute when he is about 1 km above ground. Describe his motion.
Answer:
Initially the path is a parabola as seen by an observer on the ground. It is a vertical straight line as seen by the pilot. He opens his parachute, it is moving vertically downwards with decreasing velocity and finally it reaches the ground.

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 10 Applications of Derivatives will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Applications of Derivatives Formulas

→ If y = f(x) is a differentiable function of x and Δx is a small change in ‘x’ then the

• actual change in y is Δy = f (x + Δx) – f(x)
• the differential of y is dy = f'(x) Δx

→ The approximate value of f(x) in a neighbourhood of Δx is f(x + Δx) – f (x) + f'(x) Δx.

→ If error in x of y = f(x) is Δx then

• Δy is the approximate error in y.
• \(\frac{\Delta \mathrm{y}}{\mathrm{y}}\) is called the relative error in v and
• \(\frac{\Delta \mathrm{y}}{\mathrm{y}}\) × 100 is the percentage error in y.

→ The slope of the curve y = f(x) at the point P(x₁, y₁) is \(\left(\frac{d y}{d x}\right)_{\left(x_1 \cdot y_1\right)}\) = m = f'(x₁).

→ If θ is the angle between the curves at y = f(x) and y = g(x) at the point of intersection P(x₁, y₁) then tan θ = \(\frac{m_1-m_2}{1+m_1 m_2}\) where m₁ = f'(x₁) and m₂ = g'(x)
If m₁ = m₂, then the two curves touch each other at (x₁, y₁) and if m₁m₂ = – 1, the two curves are said to be orthogonal.

→ If m = \(\left(\frac{d y}{d x}\right)_{\left.i x_1, y_1\right)}\) = f'(x,) is the slope of the curve at the point P(x₁, y₁) on y = f(x) then

• The length of the tangent to the curve at P is \(\frac{y_1 \sqrt{1+\left[f^{\prime}\left(x_1\right)\right]^2}}{f^{\prime}\left(x_1\right)}\)
• The length of the normal to the curve at P is y1\(\sqrt{1+\left[f\left(x_1\right)\right]^2}\)
• The length of the subtangent to the curve at P = \(\left|\frac{y_1}{f^{\prime}\left(x_1\right)}\right|\)
• The length of the subnormal to the curve at P is |y₁f(x₁)|.

→ The rate of change of the function y = f(x) with respect to ‘t’ is \(\frac{d y}{d x}\)

→ If s = f(t) is the functional relation between the distance ‘s’ and time ‘t’, then the velocity of the body at time ‘t’ is \(\frac{d s}{d x}\) = v and the acceleration of the body at time ‘t’ is \(\frac{d^2 s}{d t^2}=\frac{d v}{d t}\)

→ If a function ‘f’ is increasing and differentiable at a’ ⇔ f'(a) > 0.

• A differentiable function is said to be decreasing at ‘a’ ⇔ f'(a) < 0.
• A differentiable function is said to be stationary at ‘a’ ⇔ f'(a) = 0.

→ A differentiable function f(x) in the interval which has f'(x) and f”(x) at ‘a’ and if

• f’(a) = 0, f”(a) < 0, then f(a) has local maxima.
• f'(a) = 0. f”(a) > 0. then f(a) has local minima.

→ Rolle’s Mean Value Theorem : If a function ‘f defined over [a, b] is such that

• f is continuous over [a, b]
• f is differentiable on (a. b)
• f(a) = f(b). Then ∃ a point c ∈ (a, b) such that f'(c) = 0.

→ Lagrange’s Mean Value Theorem : If a function f is defined over [a, b] is such that

• f is continuous over [a, b] .
• f is differentiable over (a. b) then ∃ a point c ∈ (a, b) such that f’(c) = \(\frac{f(b)-f(a)}{b-a}\)

→ Mensuration fundamentals:
1. If r is the radius, x is the diameter, P is the perimeter and A is the area of the circle then

• A = πr or A = \(\frac{\pi x^2}{4}\).
• P = 2πr = πx.

2. If ‘r’ is the radius, l is the length of the arc and 0 is the angle then

• Area A = \(\frac{1}{2}\) lr = \(\frac{1}{2}\) r²θ
• Perimeter P = l + 2r = r (θ + 2)

3. If r is the radius, h is the height of the cylinder then

• Lateral surface area = 2πrh
• Total surface area S = 2πrh + 2πr²
• Volume V = πr²h

4. If r is the radius, l is the slant height, h is the height and α is the vertical angle of the cone, then

• l² = r² + h²
• Lateral surface area = πrl
• Total surface area S = πrl + πr²
• Volume V = \(\frac{1}{3}\)πr²H

5. If L is the length, T is the period of oscillation of a simple pendulum and g is the acceleration due to gravity then T = 2π\(\sqrt{\frac{l}{g}}\).

6. If r is the radius of sphere then

• Surface area = S = 4 πr²
• Volume V = \(\frac{4}{3}\)πr³

7. Let x be the side of a cube then surface area of the cube is 6x² and volume of the cube is x³.