TS Inter 1st Year Physics Study Material Chapter 4 Motion in a Plane

Telangana TSBIE TS Inter 1st Year Physics Study Material 4th Lesson Motion in a Plane Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 4th Lesson Motion in a Plane

Very Short Answer Type Questions

Question 1.
Write the equation for the horizontal range covered by a projectile and specify when it will be maximum. [TS May ’16]
Answer:
Range of a projectile (R) = \(\frac{u^2 \sin 2 \theta}{g}\)
When θ = 45° Range is maximum.
Maximum Range (R_max) = \(\frac{u^2}{g}\)

Question 2.
The vertical component of a vector is equal to its horizontal component. What is the angle made by the vector with x-axis? [AP Mar. ’19; TS May ’18]
Answer:
Let R be a vector.
Vertical component = R sin θ;
Horizontal component = R cos θ
∴ R sin θ = R cos θ.
So sin θ = cos θ ⇒ θ = 45°

Question 3.
A vector V makes an angle θ with the horizontal. The vector is rotated through an angle α. Does this rotation change the vector V?
Answer:
Magnitude of vector = V ;
Let initial angle with horizontal = θ
Angle rotated = α
So new angle with horizontal = θ + α
Now horizontal component,
V_α = V cos (θ + α)
Vertical component, V_y = V sin (θ + α)
Magnitude of vector, V = \(\sqrt{V^{2}_{x}+V^{2}_{y}}\) = V
So rotating the vector does not change its magnitude.

Question 4.
Two forces of magnitudes 3 units and 5 units act at 60° with each other. What is the magnitude of their resultant? [AP Mar. 17. 15; May 17, 16]
Answer:
Given \(\overline{\mathrm{P}}\) = 3 units, \(\overline{\mathrm{Q}}\) = 5 units and θ = 60°

Question 5.
A = \(\overrightarrow{\mathrm{i}}+\overrightarrow{\mathrm{j}}\) What is the angle between the vector and x-axis? [TS Mar. ’17; AP Mar. ’14; May ’13]
Answer:
Given that, \(\overrightarrow{\mathrm{A}}=\overrightarrow{\mathrm{i}}+\overrightarrow{\mathrm{j}}\)

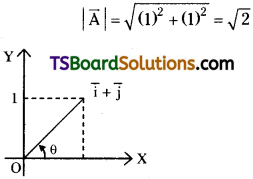
If ‘θ’ is the angle made by the vector with x-axis then,

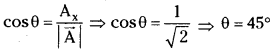
Question 6.
When two right angled vectors of magnitude 7 units and 24 units combine, what is the magnitude of their resultant? [AP Mar. 18, 16; May 18. 14]
Answer:
Given \(\overline{\mathrm{P}}\) = 7 units; \(\overline{\mathrm{Q}}\) = 24 units; 0 = 90°

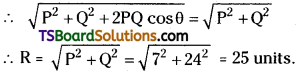
Question 7.
If \(\overline{\mathrm{P}}\) = 2i + 4j + 14k and \(\overline{\mathrm{Q}}\) = 4i + 4j + 10k, find the magnitude of \(\overline{\mathrm{P}}+\overline{\mathrm{Q}}\). [TS Mar. ’16, ’15]
Answer:

Question 8.
Can a vector of magnitude zero have non-zero components?
Answer:
A vector with zero magnitude cannot have non-zero components. Because magnitude of given vector \(\overline{\mathrm{V}}\) = \(\sqrt{V^{2}_{x}+V^{2}_{y}}\) must be zero. This is possible only when V²_x and V²_y are zero.

Question 9.
What is the acceleration of a projectile at the top of its trajectory? [TS Mar. ’19]
Answer:
At highest point acceleration, a = g. In projectile, motion acceleration will always acts towards centre of earth. It is irrespective of its position, whether it is at highest point or somewhere.

Question 10.
Can two vectors of unequal magnitude add up to give the zero vector? Can three unequal vectors add up to give the zero vector?
Answer:
No. Two unequal vectors can never give zero vector by addition. But three unequal vectors when added may give zero vector.

Short Answer Questions

Question 1.
State parallelogram law of vectors. Derive an expression for the magnitude and direction of the resultant vector. [TS Mar. ’17, ’16, May ’17; AP Mar. ’14, ’13]
Answer:
Parallelogram Law :
If two vectors are represented by the two adjacent sides of a parallelogram then the diagonal passing through the intersection of given vectors represents their resultant both in direction and magnitude.

Proof :
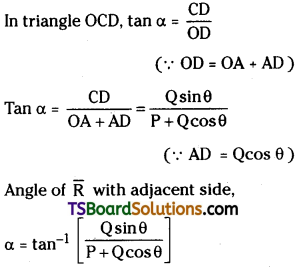
Let \(\overline{\mathrm{P}}\) and \(\overline{\mathrm{Q}}\) be two adjacent vectors ‘θ’ be angle between them. Construct a parallelogram OACB as shown in figure. Extend the line OA and draw a normal D from C. The diagonal OC = the resultant \(\overline{\mathrm{R}}\) both in direction and magnitude.

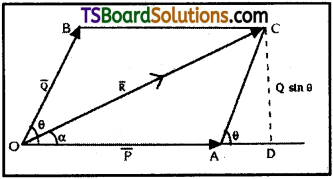
In figure OCD = right angle triangle
⇒ OC = OD² + DC²

Angle of resultant with adjacent side ‘α’

Question 2.
What is relative motion? Explain it.
Answer:
Relative velocity is the velocity of a body with respect to another moving body.

Relative velocity in two dimensional motion :
Let two bodies A and B are moving with velocities \(\overrightarrow{\mathrm{V}}_A\) and \(\overrightarrow{\mathrm{V}}_B\) then relative velocity of Aw.r.t B is \(\overrightarrow{\mathrm{V}}_{AB}=\overrightarrow{\mathrm{V}}_{A}+\overrightarrow{\mathrm{V}}_{B}\)
Relative velocity of B w.r.t. A is
\(\overrightarrow{\mathrm{V}}_{BA}=\overrightarrow{\mathrm{V}}_{B}-\overrightarrow{\mathrm{V}}_{A}\)

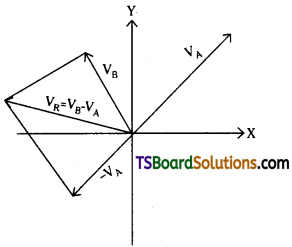
Procedure to find resultant :
To find rela-tive velocity in two dimensional motion use vectorial subtraction of V_A or V_B. Generally to find relative velocity one vector \(\overrightarrow{\mathrm{V}}_A\) or \(\overrightarrow{\mathrm{V}}_B\) is reversed (as the case may be) and parallelogram is constructed. Now resultant of that parallelogram is equal to \(\overrightarrow{\mathrm{V}}_A-\overrightarrow{\mathrm{V}}_B\) or \(\overrightarrow{\mathrm{V}}_B-\overrightarrow{\mathrm{V}}_A\) (8° one vector is reversed V_A is taken as –\(\overrightarrow{\mathrm{V}}_A\) or \(\overrightarrow{\mathrm{V}}_B\) is taken as –\(\overrightarrow{\mathrm{V}}_B\))
In figure relative velocity of B w.r.t A is V_BA =V_R = V_B – V_A.

Question 3.
Show that a boat must move at an angle with respect to river water in order to cross the river in minimum time.
Answer:
Motion of a boat in a river :
Let a boat can travel with a speed of V_bE in still water w.r. to earth. It is used to cross a river which flows with a speed of V_WE with respect to earth. Let width of river is W.

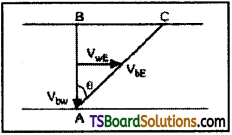
We can cross the river in two different ways.
1) in shortest path 2) in shortest time.

To cross the river in shortest time :

To cross the river in shortest time boat must be rowed along the width of river i.e., boat must be rowed perpendicular to the bank or 90° with the flow of water. Because width of river is the shortest distance. So velocity must be taken in that direction to obtain shortest time. In this case V_bE and V_WE are perpendicular and boat will travel along AC. The distance BC is called drift. So to cross the river in shortest time angle with flow of water = 90°.

Question 4.
Define unit vector, null vector and position vector. [AP June ’15]
Answer:
Unit vector :
A vector whose magnitude is one unit is called unit vector.

Let a is \(\overline{\mathrm{a}}\) given vector then unit vector

Null vector :
A vector whose magnitude is zero is called null vector. But it has direction.

For a null vector the origin and terminal point are same.
Ex : Let \(\overline{\mathrm{A}}\times\overline{\mathrm{B}}=\overline{\mathrm{0}}\) . Here magnitude of \(\overline{\mathrm{A}}\times\overline{\mathrm{B}}=\overline{\mathrm{0}}\) . But still it has direction perpendicular to the plane of \(\overline{\mathrm{A}}\) and \(\overline{\mathrm{B}}\).

Position vector :
Any vector in space can be represented by the linear combination

Question 5.
If |\(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}\)| = |\(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}\)|, prove that the angle between \(\overrightarrow{\mathrm{a}}\) and \(\overrightarrow{\mathrm{b}}\) is 90°. [TS Mar., May ’18]
Answer:
Let \(\overrightarrow{\mathrm{a}}\), \(\overrightarrow{\mathrm{b}}\) are the two vectors.
Sum of vectors

by squaring on both sides,
a² + b² + 2ab cos θ = a² + b² – 2ab cos θ
∴ 4 ab cos θ = 0 or θ = 90°

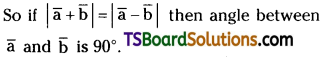
Question 6.
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola. [AP Mar. ’18, ’17. ’16. ’15, May ’18, ’17, ’14. ’13; June ’15; TS Mar. ’18, ’15, May ’16, June ’15]
Answer:
Projectile :
A body thrown into the air same angle with the horizontal, (other tan 90°) its motion under the influence of gravity is called projectile. The path followed by it is called trajectory.

Let a body is projected from point O, with velocity ‘u’ at an angle θ with horizontal. The velocity u’ can be resolved into two rectangular components u_x and u_y along x-axis and y-axis.
u_x = u cos θ and u_y = u sin θ

After time t, Horizontal distance travelled x = u cos θ . t ……….. (1)

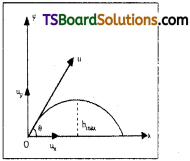
After a time t’ sec; vertical displacement

The above equation represents “parabola”. Hence the path of a projectile is a parabola.

Question 7.
Explain the terms the average velocity and instantaneous velocity. When are they equal ?
Answer:
Average velocity :
It is the ratio of total displacement to total time taken.

Average velocity is independent of path followed by the particle. It just deals with initial and final positions of the body.

Instantaneous velocity :
Velocity of a body at any particular instant of time is defined as instantaneous velocity.

as instantaneous velocity.
For a body moving with uniform velocity its average velocity = Instantaneous velocity.

Question 8.
Show that the maximum height and range

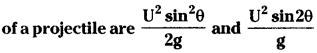
respectively where the terms have their regular meanings.
Answer:
Let a body is projected with an initial velocity ‘u’ and with an angle θ to the horizontal. Initial velocity along x direction, u_x = u cos θ Initial velocity along y direction, u_y = u sin θ

Horizontal Range :
It is the distance covered by projectile along the horizontal between the point of projection to the point on ground, where the projectile returns again.

It is denoted by R. The horizontal distance covered by the projectile in the to time of flight is called horizontal range. Therefore, R = u cos θ × t.

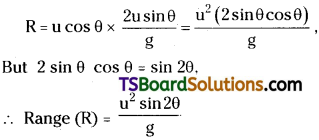
Angle of projection for maximum range:
For a given velocity of projection, the horizontal range will be maximum, when sin 2θ = 1.
∴ Angle of projection for maximum range is 2θ = 90° or θ = 45°
∴ R_max = \(\frac{u^2}{g}\)

Maximum height :
The vertical distance covered by the projectile until its vertical component becomes zero.

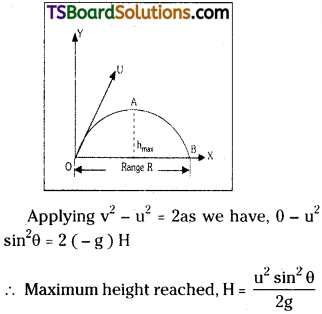
Question 9.
If the trajectory of a body is parabolic in one reference frame, can it be parabolic in another reference frame that moves at constant velocity with respect to the first reference frame? If the trajectory can be other than parabolic, what else can it be?
Answer:
Yes. According to Newton’s first law, a body at rest or a body moving with uniform velocity are treated as same. Both of them belong to inertial frame of reference.

If a frame (say 1) is moving with uniform velocity with respect to other, then that second frame must be at rest or it maintains a constant velocity w.r.t the first. So both frames are inertial frames. So if trajectory of a body in one frame is a parabola, then trajectory of that body in another frame is also a parabola.

Question 10.
A force 2i + j – k newton acts on a body which is initially at rest. At the end of 20 seconds the velocity of the body is 4i + 2j – 2k ms-1. What is the mass of the body? [AP May ’16]
Answer:
Force, F = 2i + j – k
time, t = 20
Initial velocity, u = 0
Final velocity, v = 4i + 2j – 2k = 2(2i + j – k)

Problems

Question 1.
Ship A is 10 km due west of ship B. Ship A is heading directly north at a speed of 30 km/h, while ship B is heading in a direction 60° west of north at a speed of 20 km/h.
(i) Determine the magnitude of the
(ii) What will be their distance of closest approach?
Answer:
Velocity of A = 30 kmph due North
∴ V_A = 30\(\hat{\mathbf{j}}\)
Velocity of B = 20 kmph 60° west of North
∴ V_B = -20sin60° + 20 cos60° = 10√3\(\hat{\mathbf{i}}\) + 10\(\hat{\mathbf{j}}\)

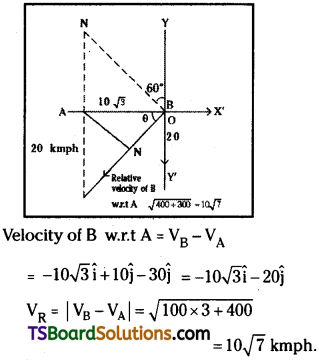
Shortest distance :
In ∆le ANB shortest distance, AN = AB sin θ
But distance, AB = 10 km
∴ AN = 10 × \(\frac{20}{10\sqrt{7}}=\frac{20}{\sqrt{7}}\) = 7.56 km

Question 2.
If θ is the angle of projection, R the range, h the maximum height, T the time of flight, then show that (a) tan θ = 4h/R and (b)h = gT²/8
Answer:
(a) Given angle of projection = θ,

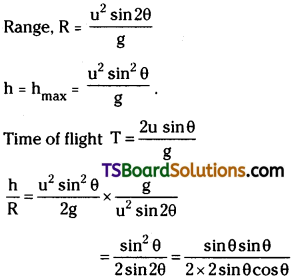
Question 3.
A projectile is fired at an angle of 60° to the horizontal with an initial velocity of 800 m/s:
(i) Find the time of flight of the projectile before it hits the ground.
(ii) Find the distance it travels before it hits the ground (range).
(iii) Find the time of flight for the projectile to reach its maximum height.
Answer:
Angle of projection, θ = 60°.
Initial velocity, u = 800 m/s

iii) Time of flight to reach maximum height = \(\frac{T}{2}\)

Question 4.
For a particle projected slantwise from the ground, the magnitude of its position vector with respect to the point of projection, when it is at the highest point of the path is found to be √2 times the maximum height reached by it. Show that the angle of projection is tan^-1 (2).
Answer:
Position vector of h (max point) from 0, is

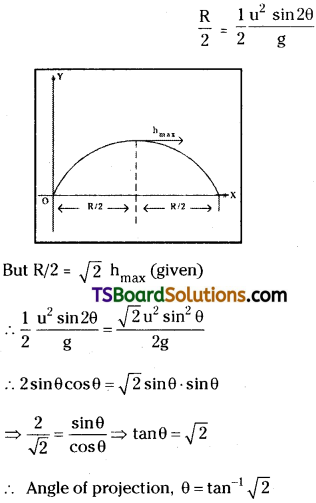
Question 5.
An object is launched from a cliff 20. m above the ground at an angle of 30° above the horizontal with an initial speed of 30 m/s. How far horizontally does the object travel before landing on the ground? (g = 10 m/s²)
Answer:
Height of cliff = 20m
Angle of projection, θ = 30°
Velocity of projection, u = 30 m/s
Total horizontal distance travelled = OC = OB’ + B’C

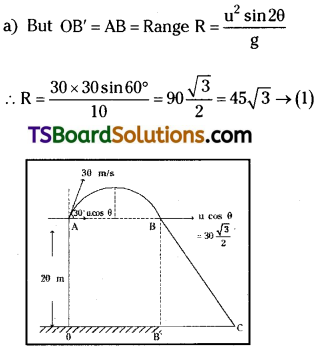
b) Distance B’C = Range of a horizontal projectile.
∴ Range = u cos θ t
u. cos θ = 30.\(\frac{\sqrt{3}}{2}\) = 15√3 .
Time taken to reach the ground, t = ?
Given S_y = 20, u_y = u sin θ = 30 sin 30° = 15 m/s
∴ S_y = 20 = 15t + \(\frac{10}{2}\)t² ⇒ 5t² + 15t – 20 = 0
or t² + 3t – 4 = 0 or (t + 4) (t – 1) = 0
∴ t = – 4 or t = 1 ∴ t is Not – ve use t = 1
∴ Range = 4 . cos θ . t = 15√3 → (2)
Total distance travelled before reaching the ground = 45√3 +15√3 = 60√3 m.

Question 6.
‘O’ is a point on the ground chosen as origin. A body first suffers a displacement of 10√2 mm North-East, next 10 m North and finally 10√2 North-West. How far it is from origin? [TS Mar. ’19]
Answer:
a) 10√2 m North-East
b) 10m North
c) 10√2 m North-West

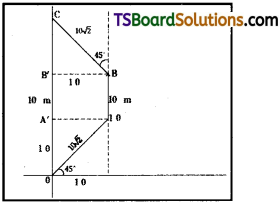
From figure total displacement from origin ‘O’ is OC
ButOC = OA’ + A’B’ + B’C =10 + 10 + 10 = 30 m.

Question 7.
From a point on the ground a particle is projected with initial velocity u, such that its horizontal range is maximum. Find the magnitude of average velocity during its ascent.
Answer:
Velocity of projection = u.
Range is maximum ⇒ θ = 45°
During time of ascent ⇒ when h = h_max
⇒ u_x = V_x = u . cos θ

Average velocity, V_A = \(\sqrt{V^{2}_{x}+V^{2}_{y}}\)
V_x = Average velocity along x-axis

Average velocity during time of ascent

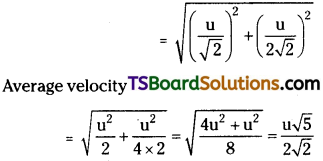
Question 8.
A particle is projected from the ground with some initial velocity making an angle of 45° with the horizontal. It reaches a height of 7.5 m above the ground while it travels a horizontal distance of 10 m from the point of projection. Find the initial speed of projection (g = 10 m/s2).
Anwser:
Angle of projection = 45°
Vertical height, h_y = 7.5 m
Horizontal distance, h_x = 10 m

Question 9.
Wind is blowing from the south at 5 ms^-1. To a cyclist it appears to be blowing from the east at 5 ms^-1. Show that the velocity of the cyclist is ms^-1 towards north-east.
Answer:
Direction of wind South to North 5 m/s.

Apparent direction is from East to West 5 m/s.

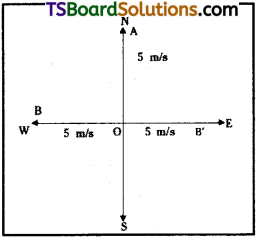
This is relative velocity.
To find velocity of cyclist reverse the direction of resultant vector OB and find resultant
∴ Velocity of cyclist = \(\sqrt{5^2+^2+0}\) = 5√2 m/s

Question 10.
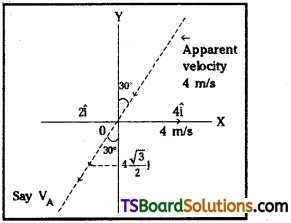
A person walking at 4 m/s finds rain drops falling slantwise into his face with a speed of 4 m/s at ah angle of 30° with the vertical. Show that the actual speed of the rain drops is 4 m/s.
Answer:
Velocity of man = 4 m/sec
Apparent velocity of rain drop = 4 m/sec with θ = 30° with vertical. This is relative velocity V_B.

Additional Problems

Question 1.
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 ms-1 can go without hitting the ceiling of the hall?
Solution:
Here, u = 40 ms^-1; H = 25m, R = ?
Let θ be the angle of projection with the horizontal direction to have the maximum range, with maximum height = 25 m.

Question 2.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Solution:
Here, r = 80 cm = 0.8 m; o = 14/25 s^-1.

The centripetal acceleration,
a = ω²r = (\(\frac{88}{25}\))² × 0.80 = 9.90m/s²
The direction of centripetal acceleration is along the string directed towards the centre of circular path.

Question 3.
An aircraft executes a horizontal loop of radius 1 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.
Solution:
Here, r = 1 km = 1000 m;
v = 900 km h^-1 = 900 × (1000m) × (60 × 60s)^-1
= 250 ms^-1

Question 4.
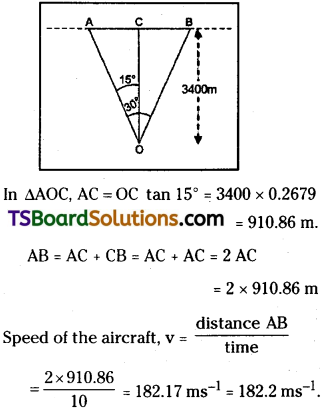
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the air-craft positions 10.0 s apart is 30°, what is the speed of the aircraft?
Solution:
In Fig, O is the observation point at the ground. A and B are the positions of aircraft for which ∠AOB = 30°. Draw a perpendicular OC on AB. Here OC = 3400 m and ∠AOC = ∠COB = 15°. Time taken by aircraft from A to B is 10 s.

Question 5.
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.
Solution:

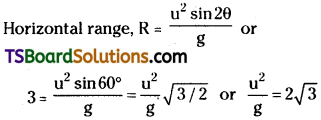
Since the muzzle velocity is fixed, therefore, Max. horizontal range,
R_max = \(\frac{u^2}{g}\) = 2√3 = 3.464 m.
So, the bullet cannot hit the target.