TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Long Answer Type

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Long Answer Type

Question 1.
In ΔABC, show that b² = c² + a² – 2ca cos B. [Mar. ’02]
Answer:
LHS = b² = (2R sin B)² = 4R² sin² B = 4R²[sin (A + C)]² = 4R² (sin A cos C + cos A sin C)²
= 4R² (sin² A cos² C + cos² A sin² C + 2 sin A sin C cos A cos C)
= 4R² [sin² A (1 – sin² C) + (1 – sin² A) sin²C + 2 sin A sin C cos A cos C]
= 4R² (sin² A – sin²A sin²C + sin²C – sin²A sin²C + 2 sin A sin C cos A cos C)
= 4R² (sin²A + sin²C – 2 sin² A sin² C + 2 sin A sin C cos A cos C)
= 4R² [sin²A + sin²C + 2 sin A sin C (cos A cos C – sin A sin C)]
= 4R² [sin² A + sin² C + 2 sin A sin C cos (A + C)]
= 4R² sin² A + 4R² sin² C – 8R² sin A sin C cos B = a² + c² – 2ac cos B = RHS.

Question 2.
In ΔABC, show that [Mar ’94]
(i) sin\(\frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{b c}}\)
Answer:

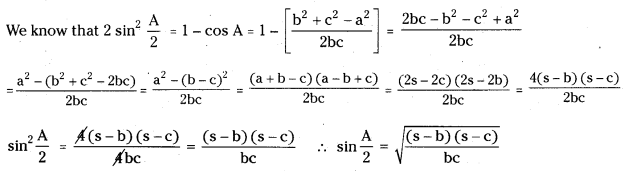
(ii) cos\(\frac{A}{2}=\sqrt{\frac{s(s-a)}{b c}}\)
Answer:

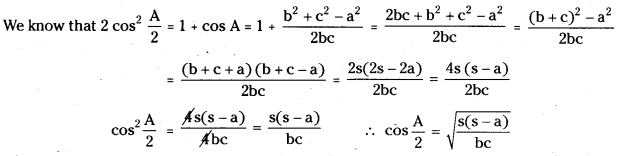
(iii) tan\(\frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}}\)
Answer:

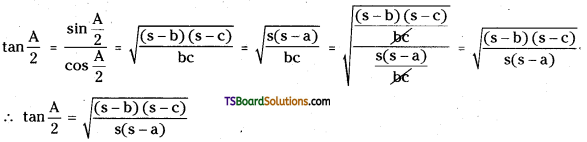
Question 3.
If a = (b – c)sec θ, prove that tan θ = \(\frac{2 \sqrt{b c}}{b-c}\)sin\(\frac{A}{2}\). [Mar; ’18(AP); Mar. ’16(TS); ’11]
Answer:
Given a = (b – c) sec θ
sec θ = \(\frac{a}{b-c}\)
tan²θ = sec²θ – 1 = \(\left(\frac{a}{b-c}\right)^2\) – 1 = \(\frac{a^2}{(b-c)^2}\) – 1 = \(\frac{a^2-(b-c)^2}{(b-c)^2}\)
= \(\frac{(a+b-c)(a-b+c)}{(b-c)^2}=\frac{(2 s-2 c)(2 s-2 b)}{(b-c)^2}=\frac{4 .(s-b)(s-c)}{(b-c)^2}\) = 4.\(\frac{(s-b)(s-c)}{(b-c)^2} \cdot \frac{b c}{b c}\)
tan²θ = 4.\(\frac{b c}{(b-c)^2}\)sin²\(\frac{A}{2}\)
tan θ = \(\frac{2 \sqrt{b c}}{b-c}\)sin\(\frac{A}{2}\)

Question 4.
Show that a cos²\(\frac{A}{2}\) + b cos²\(\frac{B}{2}\) + c cos²\(\frac{C}{2}\) = s + \(\frac{\Delta}{R}\) [May ’15(TS); Mar. ’03, ’00]
Answer:
L.H.S = a cos²\(\frac{A}{2}\) + b cos²\(\frac{B}{2}\) + c cos²\(\frac{C}{2}\)
= a\(\left[\frac{1+\cos A}{2}\right]\) + b\(\left[\frac{1+\cos B}{2}\right]\) + c\(\left[\frac{1+\cos C}{2}\right]\)
= \(\frac{\mathrm{a}}{2}+\frac{\mathrm{a}}{2}\) cos A + \(\frac{\mathrm{b}}{2}+\frac{\mathrm{b}}{2}\) cos B + \(\frac{\mathrm{c}}{2}+\frac{\mathrm{c}}{2}\) cos C
= \(\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{2}+\frac{\mathrm{c}}{2}+\frac{1}{2}\)(a cos A + b cos B + c cos C)
= \(\frac{a+b+c}{2}+\frac{1}{2}\)[2R sin A cos A + 2R sin B cos B + 2R sin C cos C]
= \(\frac{\mathrm{a}}{2}+\frac{\mathrm{b}}{2}+\frac{\mathrm{c}}{2}+\frac{1}{2}\)[sin 2A + sin 2B + sin 2C] = s + \(\frac{\mathrm{R}}{2}\)[sin 2A + sin 2B + sin 2C] …………(1)
Now sin 2A + sin2B + sin2C
= 2sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2
\mathrm{~B}}{2}\right)\) + sin2C
= 2 sin (A + B) cos (A – B) + sin 2C
= 2sin(180° – C)cos(A – B) + sin2C
= 2sin C cos (A – B) + 2sin C cos C
= 2sin C[cos(A – B) + cos C]
= 2sinC[cos(A – B) + cos[180° – (A + B)]
= 2sinC[cos(A – B) – cos(A + B)]
= 2sinC [2sin A sin B]
= 4 sin A sin B sin C
From (1) ⇒ s + \(\frac{\mathrm{R}}{2}\)[4sinA sinB sinC]
= s + 2R sin A sin B sin C
= s + \(\frac{2 \mathrm{R}^2}{\mathrm{R}}\) sin A sin B sin C = s + \(\frac{\Delta}{R}\) = R.H.S.

Question 5.
Prove that a³cos(B – C) + b³cos (C – A) + c²cos(A – B) = 3abc. [Mar. ’08; May ’00, ’98]
Answer:
L.H.S = a³ cos (B – C) + b³ cos (C – A) + c³ cos (A – B)
= Σa³ cos (B – C) = Ea². a cos (B – C) = Σa².2R sin A . cos (B – C)
= Σa² .2R sin (180° – (B + C)) cos (B – C) = Σa².2R sin(B + C) cos (B – C)
= Σa² . R[sin (B + C + B – C) + sin (B + C – B + C)] = Σa². R(sin 2B + sin 2C)
= Σa² . R (2 sin B cos B + 2 sin C cos C) = Σa² (2R sin B cos B + 2R sin C cos
= Σa² (b cos B + c cos C) = Σ(a²b cos B + a2c cos C)
= ab cos B + a c cos C + bc cos C + b a cos A + ca cos A + cb cos B
= ab(a cos B + b cos A) + bc(b cos C + c cos B) + ac (a cos C + c cos A)
= ab(c) + bc(a) + ac(b) = 3abc = RHS.

Question 6.
Prove that cot\(\frac{A}{2}\) + cot\(\frac{B}{2}\) + cot\(\frac{C}{2}\) = \(\frac{s^2}{\Delta}\). [Mar. ’09]
Answer:

Question 7.
Prove that tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\) + tan\(\frac{C}{2}\) = \(\frac{b c+c a+a b-s^2}{\Delta}\). [May ’98, ’97]
Answer:
L.H.S = tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\) + tan\(\frac{C}{2}\)

Question 8.
If sin θ = \(\frac{a}{b+c}\), then show that cos θ = \(\frac{2 \sqrt{b c}}{b+c}\)cos\(\frac{A}{2}\). [Mar. ’16(AP), ’12; May ’14]
Answer:
Given sin θ = \(\frac{a}{b+c}\)

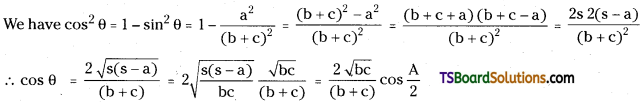
Question 9.
If a = (b + c)cos θ, then prove that sin θ = \(\frac{2 \sqrt{b c}}{b+c}\)cos\(\frac{A}{2}\). [Mar. ’19(AP); May ’11]
Answer:
Given cos θ = \(\frac{a}{b+c}\)

sin θ = \(\frac{2 \sqrt{b c}}{b+c}\)cos\(\frac{A}{2}\)

Question 10.
If a² + b² + c² = 8R², then prove that the triangle Is right angled. [Mar ’01]
Answer:
Given a² + b² + c² = 8R²
(2R sin A)² + (2R sin B)² + (2R sin C)² = 8R²
4R² sin² A + 4R² sin² B + 4R² sin²C = 8R²
sin²A + sin²B + sin²C = 2
1 – cos²A + sin²B + sin²C = 2
1 – (cos²A – sin²B) + sin²C = 2
1 – cos (A + B). cos (A – B) sin²C = 2
1 – cos(180°- C)cos(A – B) + sin2C = 2
1 + cos C cos(A – B) + 1 – cos²C = 0
cos C [cos (A – B) – cos C] = 0
cosC[cos(A – B) – cos(180° – (A + B)] = 0
cos C [cos (A – B) + cos (A + B)] = 0
cos C (2 cos A cos B) = 0
2 cos A cos B cos C = 0
cos A. cos B cos C = 0
cos A = 0 or cos B = 0 or cos C = 0
A = 90° or B = 90° or C = 900
∴ The triangle is right angled.

Question 11.
Show that \(\frac{r_1}{b c}+\frac{r_2}{c a}+\frac{r_3}{a b}=\frac{1}{r}-\frac{1}{2 R}\). [May; 14, ’09, ’07, ’01, ’99, ’95; Mar. ’99, ’95, ’93]
Answer:

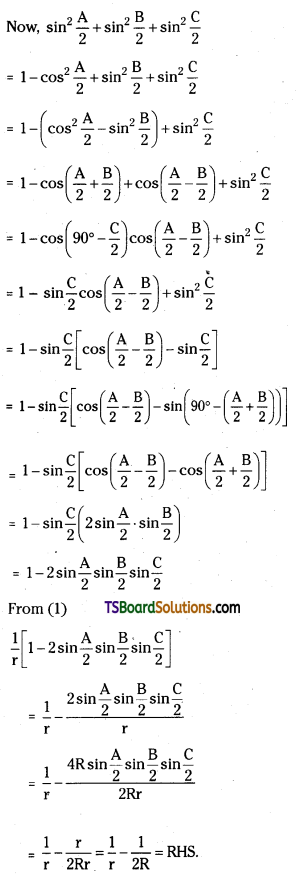
Question 12.
Show that (r₁ + r₂)sec²\(\frac{C}{2}\) = (r₂ + r₃)sec²\(\frac{A}{2}\) = (r₃ + r₁)sec²\(\frac{B}{2}\). [Mar. ’01]
Answer:

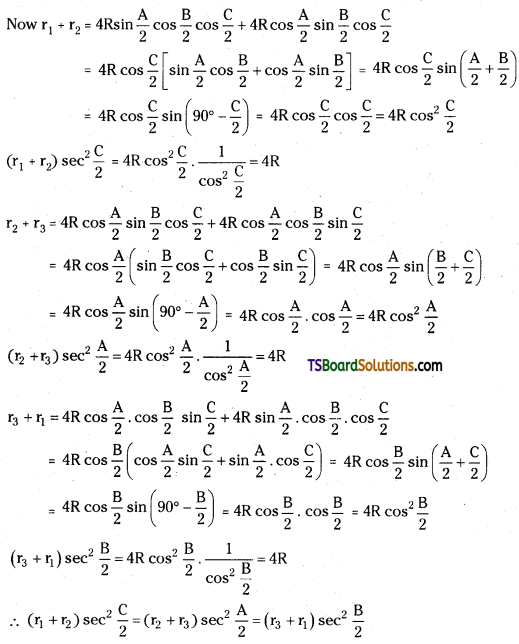
Question 13.
In ΔABC, if r₁ = 8, r₂ = 12, r₃ = 24; Find a, b and c. [Mar. ’17(AP). ’02; May ’15(AP), ’13]
Answer:
We have \(\frac{1}{\mathrm{r}}=\frac{1}{\mathrm{r}_1}+\frac{1}{\mathrm{r}_2}+\frac{1}{\mathrm{r}_3} \Rightarrow \frac{1}{\mathrm{r}}=\frac{1}{8}+\frac{1}{12}+\frac{1}{24}=\frac{3+2+1}{24}=\frac{6}{24}=\frac{1}{4}\) = r = 4
Also \(\sqrt{\mathrm{rr}_1 \mathrm{r}_2 \mathrm{r}_3}=\sqrt{4(8)(12)(24)}\) = 96
Since s = \(\frac{\Delta}{r}=\frac{96}{4}\) = 24
r₁ = \(\frac{\Delta}{s-a}\) ⇒ s – a = \(\frac{\Delta}{r_1}=\frac{96}{8}\) = 12 ⇒ a = s – 12 = 24 – 12 = 12
r₂ = \(\frac{\Delta}{s-b}\) ⇒ s – b = \(\frac{\Delta}{r_2}=\frac{96}{12}\) = 8 ⇒ b = s – 8 = 24 – 8 = 16
r₃ = \(\frac{\Delta}{s-c}\) ⇒ s – c = \(\frac{\Delta}{r_3}=\frac{96}{24}\) = 4 ⇒ b = s – 4 = 24 – 4 = 20
∴ The required values are a = 12, b = 16, c = 20

Question 14.
Show that \(\frac{a b-r_1 r_2}{r_3}=\frac{b c-r_2 r_3}{r_1}=\frac{c a-r_3 r_1}{r_2}\). [Mar. ’08]
Answer:

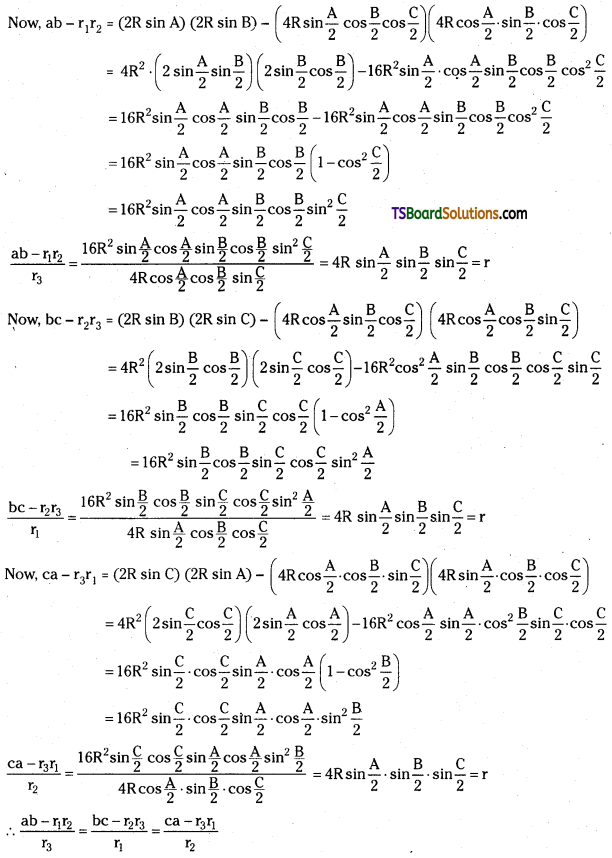
Question 15.
Prove that 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)². [Mar. ’97]
Answer:
L.H.S = 4(r₁r₂ + r₂r₃ + r₃r₁) = 4\(\left[\frac{\Delta}{s-a} \cdot \frac{\Delta}{s-b}+\frac{\Delta}{s-b} \cdot \frac{\Delta}{s-c}+\frac{\Delta}{s-c} \cdot \frac{\Delta}{s-a}\right]\)
= 4\(\left[\frac{\Delta^2}{(s-a)(s-b)}+\frac{\Delta^2}{(s-b)(s-c)}+\frac{\Delta^2}{(s-c)(s-a)}\right]\)
= 4\(\left[\frac{s(s-a)(s-b)(s-c)}{(s-a)(s-b)}+\frac{s(s-a)(s-b)(s-c)}{(s-b)(s-c)}+\frac{s(s-a)(s-b)(s-c)}{(s-c)(s-a)}\right]\)
= 4s[s – c + s – a + s – b] = 4s[3s – (a + b + c)] = 4s(3s – 2s) = 4s.s = 4s² = (2s)²
= (a + b + c)² = R.H.S

Question 16.
Show that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) + cos²\(\frac{C}{2}\) = 2 + \(\frac{r}{2R}\). [Mar ’15(TS); Mar. ’05]
Answer:

Question 17.
If P₁, P₂, P₃ are altitudes drawn from vertices A, B, C to the opposite sides of a triangle respectively, then show that
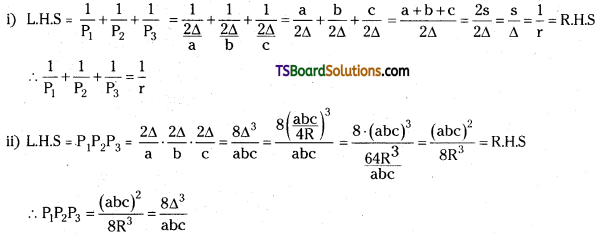
(i) \(\frac{1}{P_1}+\frac{1}{P_2}+\frac{1}{P_3}=\frac{1}{r}\) [Mar. ’18(TS); Mar. ’10]
(ii) P₁P₂P₃ = \(\frac{(a b c)^2}{8 R^3}=\frac{8 \Delta^3}{a b c}\). [Mar. ’10. ’91]
Answer:
Since P₁, P₂, P₃ are altitudes drawn from the vertices A, B, C to the opposite sides of a triangle respectively, then

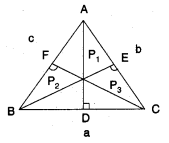
Area of triangle ABC is Δ = \(\frac{1}{2}\) BC.AD = \(\frac{1}{2}\)aP₁ ⇒ P₁ = \(\frac{2 \Delta}{a}\)
AreaoftriangleABCls Δ = \(\frac{1}{2}\)AC.BE = \(\frac{1}{2}\)bP₂ ⇒ P₂ = \(\frac{2 \Delta}{b}\)
AreaoftriangleAßCls Δ = \(\frac{1}{2}\)AB.CF = \(\frac{1}{2}\)cP₃ ⇒ P₃ = \(\frac{2 \Delta}{c}\)

Question 18.
If a = 13, b = 14, c = 15, show that R = \(\frac{65 }{8}\), r = 4, r₁ = \(\frac{21}{2}\), r₂ = 12 and r₃ = 14. [Mar. ’19, ’16(AP), ’15(AP), ’14, ’04; May ’12, ’11, ’10; B.P]
Answer:
Given a = 13, b = 14, c = 15
s = \(\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}=\frac{13+14+15}{2}=\frac{42}{2}\) = 21

Question 19.
If r₁ = 2, r₂ = 3, r₃ = 6 and r = 1, then prove that a = 3 b = 4 and c = 5
Answer:
Given r = 1, r₁ = 2, r₂ = 3, r₃ = 6
We have Δ = \(\) = 6
Δ = 6
r = 1 ⇒ \(\frac{\Delta}{\mathrm{s}}\) = 1 ⇒ \(\frac{6}{s}\) = 1 ⇒ s = 6
r₁ = 2 ⇒ \(\frac{\Delta}{\mathrm{s-a}}\) = 2 ⇒ \(\frac{6}{6-a}\) = 2 ⇒ 6 – a = 3 ⇒ a = 3
r₂ = 3 ⇒ \(\frac{\Delta}{s-b}\) = 3 ⇒ \(\frac{6}{6-b}\) = 3 ⇒ 6 – b = 2 ⇒ b = 4
r₃ = 6 ⇒ \(\frac{\Delta}{s-c}\) = 6 ⇒ \(\frac{6}{6-c}\) = 6 ⇒ 6 – c = 1 ⇒ c = 5

Some More Maths 1A Properties of Triangles Important Questions

Question 1.
In a ΔABC, prove that \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) where R is the circum radius.
Answer:
Case -I:
∠A is acute
‘s’ is the centre of the circumcircle and CD is its diameter then CS = SD = R and CD = 2R. Join BD then ∠DBC = 90° and DBC is a right angled triangle then ∠BAC = ∠BDC [ v angles in the same segment]

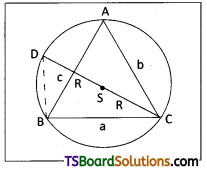
sin ∠BAC = sin ∠BDC ⇒ sin A = \(\frac{B C}{C D}=\frac{a}{2 R} \Rightarrow \frac{a}{\sin A}\) = 2R
Similarly \(\frac{b}{\sin B}\) = 2R, \(\frac{b}{\sin C}\) = 2R
∴ \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) = 2R

Case – II:
∠A is right angled then a = BC = 2R = 2R.1 = 2R sin 90° = 2R sin A

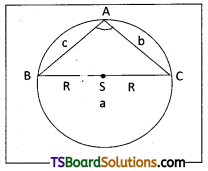
\(\frac{a}{\sin A}\) = 2R
Similarly \(\frac{b}{\sin B}\) = 2R, \(\frac{c}{\sin C}\) = 2R
∴ \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) = 2R

Case – III:
∠A is obtuse
∠DBC is right angled (∵ angle in the semi circle)

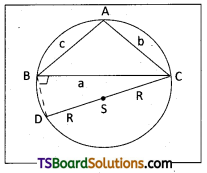
In cyclic quadrilateral BACD
∠BDC + ∠BAC = 180° ⇒ ∠BDC = 180° – ∠BAC
∠BDC = 180° – A
sin ∠BDC = sin(180° – A) ⇒ \(\frac{\mathrm{BC}}{\mathrm{CD}}\) = sin A
sin A = \(\frac{a}{2 R} \Rightarrow \frac{a}{\sin A}\) = 2R ⇒ Similarly \(\frac{b}{\sin B}\) = 2R, \(\frac{c}{\sin C}\) = 2R
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) = 2R

Question 2.
Show that a² cot A + b² cot B + c² cot C = \(\frac{abc}{R}\). [Mar. ’14]
Answer:
L.H.S. = Σ a² cot A = Σ 4R² sin²A = Σ4R²sin A cos A = 2R²Σsin 2A
= 2R² (sin 2A + sin 2B + sin 2C) = 2R² [sin 2A + 2 sin (B + C) cos (B – C]
= 2R²[2 sin A cos A + 2 sin A cos (B – C)] = 4R² sin A [cos A + cos (B – C)]
= 4R² sin A [cos (B – C) – cos (B + C)] = 4R² sin A (2 sin B sin C)
= 2R² (4 sin A sin B sin C) = 8R²\(\frac{a}{2 R} \frac{b}{2 R} \frac{c}{2 R}=\frac{a b c}{R}\) = R.H.S

Question 3.
In ΔABC, if \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\) show that C = 60°
Answer:
\(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c} \Rightarrow \frac{b+c+a+c}{(a+c)(b+c)}=\frac{3}{a+b+c}\)
⇒ 3(a + c)(b + c) = (a + b + 2c)(a + b + c)
⇒ 3(ab + ac + bc + c²) = a² + b² + 2ab + 3c(a + b) + 2c²

⇒ ab = a² + b² – c² = ab = 2ab cos C (from cosine rule)
⇒ cos c = \(\frac{1}{2}\) ⇒ C = 60

Question 4.
In ΔABC, show that (a + b + c)(tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\)) = 2c cot\(\frac{C}{2}\)
Answer:
LHS = (a + b + c)(tan\(\frac{A}{2}\) + tan\(\frac{B}{2}\)) = 2s\(\left[\frac{\Delta}{s(s-a)}+\frac{\Delta}{s(s-b)}\right]\) = 2Δ\(\left[\frac{1}{s-a}+\frac{1}{s-b}\right]\)

Question 5.
Show that b² sin 2C + c² sin 2B = 2bc sin A.
Answer:
L.H.S. = b² (2 sin C cos C) + c² (2sin B cos B)
= 2b² \(\frac{c}{2 R}\) cos C + 2c² \(\frac{b}{2 R}\) cos B = \(\frac{1}{R}\) (b²c cos C + c²b cos B)
= \(\frac{bc}{R}\) (b cos C + c cos B) = \(\frac{abc}{2}\) = 4Δ = 4 (\(\frac{1}{2}\)bc sin A) = 2bc sin A = R.H.S.

Question 6.
The angle of elevation of the top point P of the vertical tower PQ of height h from a point A is 45° and from a point B is 60°, where B is a point at a distance 30 meters from the point A measured along the line AB which makes an angle 30° with AQ. Find the height of the tower.
Answer:
Let the height of the tower PQ = h

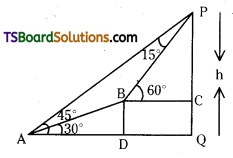
∠PAQ = 45°, ∠BAQ = 30° and ∠PBC = 60°
Given AB = 30 mts.
∴ ∠BAP = ∠APB = 15°
Hence BP = AB = 30 and h = PC + CQ
sin 60° = \(\frac{\mathrm{PC}}{\mathrm{PB}}=\frac{\mathrm{PC}}{30}\) and sin30° = \(\frac{B D}{A B}=\frac{B D}{30}\)
∴ PC = 30 sin 60° = 30.\(\left(\frac{\sqrt{3}}{2}\right)\) = 15√3 and BD = 30.sin30° = 30.\(\left(\frac{1}{2}\right)\) = 15
∴ Height of the tower h = PC + CQ = 15(√3 + 1) mts.

Question 7.
Two trees A and B are on the same side of a river. From a point C in the river the distances of the trees A and B are 250 m and 300 m respectively. If the angle C is 45°, find the distance between the trees (use √2 = 1.414).
Answer:
Given AC = 300 m and BC = 250.m and in the ΔABC, using cosine rule

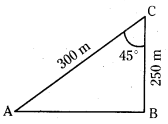
AB² = AC² + BC² – 2AC.BC.cos 45° = (300)² + (250)² – 2 (300) (250)\(\frac{1}{\sqrt{2}}\)
= 46450
∴ AB = 215.5 m (approximately)

Question 8.
Prove that \(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^2+b^2}{a^2+c^2}\)
Answer:

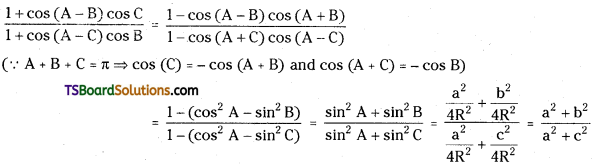
Question 9.
If C = 60°, then show that \(\frac{b}{c^2-a^2}+\frac{a}{c^2-b^2}\) = 0.
Answer:
C = 60° ⇒ c² = a² + b² – 2ab cos C = a² + b² – 2ab(cos 60°) = a² + b² – 2ab(1/2)
= a² + b² – ab …………..(1)

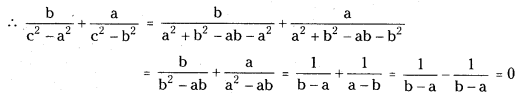
Question 10.
Prove that \(\frac{\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}}{\cot A+\cot B+\cot C}=\frac{(a+b+c)^2}{\left(a^2+b^2+c^2\right)}\).
Answer:

Question 11.
If \(\frac{a^2+b^2}{a^2-b^2}=\frac{\sin C}{\sin (A-B)}\), prove that ΔABC is either isosceles or right angled.
Answer:
Given \(\frac{a^2+b^2}{a^2-b^2}=\frac{\sin C}{\sin (A-B)} \Rightarrow \frac{a^2+b^2}{a^2-b^2}=\frac{\sin (A+B)}{\sin (A-B)}\)
By componendo and dividedo
⇒ \(\frac{a^2+b^2+a^2-b^2}{a^2+b^2-\left(a^2-b^2\right)}=\frac{\sin (A+B)+\sin (A-B)}{\sin (A+B)-\sin (A-B)} \Rightarrow \frac{2 a^2}{2 b^2}=\frac{2 \sin A \cos B}{2 \cos A \sin B}\)
⇒ \(\frac{a^2}{b^2}=\frac{2 R \sin A \cos B}{2 R \cos A \sin B}=\frac{a \cos B}{b \cos A} \Rightarrow \frac{a}{b}=\frac{\cos B}{\cos A}\)
⇒ 2R sin A cos A = 2R sin B cos B ⇒ R sin 2A = R sin 2B
⇒ sin 2A – sin 2B = 0 ⇒ A = B
∴ ΔABC is isosceles. (or) 2A = 180° – 2B ⇒ A + B = 90°
Hence A ≠ B ⇒ ΔABC is a right angled triangle.
∴ ΔABC is either isosceles or right angled.

Question 12.
If cos²A + cos²B + cos²C = 1, then show that AABC is right angled.
Answer:
Given cos²A + cos²B + cos²C = 1 …. (1)
∴ cos²A + cos²B + cos²C = cos²A + cos²B + 1 – sin²C = 1 + cos²A + cos (B + C) cos (B – C)
= 1 + cos²A – cos A cos (B – C) = 1 + cos A [cos A – cos (B – C)] = 1 – cos A [cos (B + C) + cos (B – C)] = 1 – 2cos A cos B cos C (∵ A + B + C = π, cos (B + C) = – cos A)
∴ 1 – 2 cos A cos B cos C = 1 ⇒ 2 cos A cos B cos C = 0 ⇒ A = 90° or B = 90° or C = 90°
∴ ΔABC is right angled.

Question 13.
If cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are in A.P., then prove that a, b, c are in A.P.
Answer:
cot\(\frac{A}{2}\), cot\(\frac{B}{2}\), cot\(\frac{C}{2}\) are in A.P.
⇒ \(\frac{s(s-a)}{\Delta}, \frac{s(s-b)}{\Delta}, \frac{s(s-c)}{\Delta}\) are in A.P.
⇒ (s – a), (s – b), (s – c) are in A.P ⇒ -a, -b, -c are in A.P ⇒ a, b, c are in A.P.

Question 14.
If sin²\(\frac{A}{2}\), sin²\(\frac{B}{2}\), sin²\(\frac{C}{2}\) are in H.P., then show that a, b, c are in H.P.
Answer:
Given sin²\(\frac{A}{2}\), sin²\(\frac{B}{2}\), sin²\(\frac{C}{2}\) are in H.P.

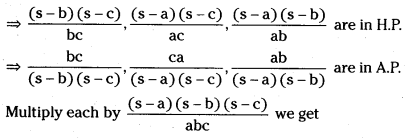
⇒ \(\frac{s-a}{a}, \frac{s-b}{b}, \frac{s-c}{c}\) are in A.P. ⇒ \(\frac{s}{a}, \frac{s}{b}, \frac{s}{c}\) are in A.P ⇒ \(\frac{1}{\mathrm{a}}, \frac{1}{\mathrm{~b}}, \frac{1}{\mathrm{c}}\) are in A.P
∴ a, b, c are in H.P.

Question 15.
Two ships leave a port at the same time. One goes 24 km per hour in the direction N 45° E and other travel 32 kms per hour in the direction S 75° E. Find the distance between the ships at the end of 3 hours.
Answer:
The first ship goes 24 km/hr.
∴ After 3 hrs. first ship goes 72 kms.

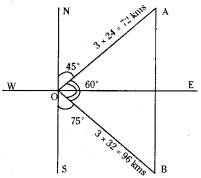
The second ship goes 32 km/hr.
∴ After 3 hrs. second ship goes 96 kms.
Let AB = x be the distance between the ships.
From the geometry of the figure ∠AOB = 60°
Using cosine rule in ΔAOB we have
cos 60° = \(\frac{(72)^2+(96)^2-x^2}{2(72)+(96)} \Rightarrow \frac{1}{2}=\frac{5184+9216-x^2}{13824}\)
⇒ 13824 = 28800 – 2x² ⇒ 2x² = 14976 ⇒ x² = 7488 ⇒ x = 86.4 (approximately)
At the end of 3 hours the difference between the ships is 86.4 kms.

Question 16.
The upper 374th portion of a vertical pole subtends an angle tan-13/5 at a point in the horizontal plane through its foot and at a distance of 40 m from the foot. Given that the vertical pole is at a height less than 100 m from the ground, find its height.
Answer:
From the figure AB is the vertical pole of height h’.

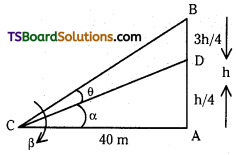
∠BCD = θ, suppose ∠DCA = α and ∠BCA = β.
tan α = \(\frac{h / 4}{40}=\frac{h}{160}\)
tan β = \(\frac{h}{40}\)
Also β = θ + α ⇒ θ = β – α

∴ tan θ = tan(β – α) = \(\frac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}=\frac{\frac{h}{40}-\frac{h}{160}}{1+\frac{h}{40} \cdot \frac{h}{160}}=\frac{120 \mathrm{~h}}{6400} \cdot \frac{6400}{6400+\mathrm{h}^2}=\frac{120 \mathrm{~h}}{6400+\mathrm{h}^2}\)
⇒ \(\frac{3}{5}=\frac{120 h}{6400+h^2}\) ⇒ 3h² + 19200 = 600h ⇒ 3h² – 600h + 19200 = 0
⇒ h² – 200h + 6400 = 0 ⇒ h² – 160h – 40h + 6400 = 0
⇒ h(h – 160) – 40(h – 160) = 0 ⇒ (h – 40)(h – 160) = 0 ⇒ h = 40 or h = 160
Given that vertical pole is a height less than 100 m, from the ground we take h = 40 m as the height of the pole.

Question 17.
AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7 m. From D, the angle of elevation of the point A is 45°. Find the height of the pole.
Answer:
Let AB = ‘h’ be the height of the pole.

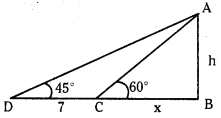
Given CD = 7
∠ACB = 60°, ∠ADB = 45° and line BC = x.
In the ΔABC, tan 60° = \(\frac{h}{x}\) ⇒ √3 = \(\frac{h}{x}\) ⇒ x = \(\frac{h}{\sqrt{3}}\)
In the ΔABC, tan 45° = \(\frac{h}{x+7}\) ⇒ x + 7 = h ⇒ \(\frac{h}{\sqrt{3}}\) + 7 = h ⇒ h\(\left(\frac{\sqrt{3}-1}{\sqrt{3}}\right)\) = 7
⇒ h = \(\frac{7 \sqrt{3}}{\sqrt{3}-1}=\frac{7 \sqrt{3}(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\frac{7 \sqrt{3}(\sqrt{3}+1)}{3-1}=\frac{21+7 \sqrt{3}}{2}\)

Question 18.
Let an object he placed at some height h cm and let P and Q be two points of observation which are at a distance of 10 cm apart on a line Inclined at angle 15° to the horizontal. If the angles of elevation of the object from P and Q are 300 and 600 respectively then find h.
Answer:
Let AB h cm be the height of the tower P and Q are points of observation.
From the geometry of the figure ∠BPA = 30° given ∠BPQ = 15°. Also ∠PQB = 135.
∴ ∠PBQ = 30°, PQ = 10 cm (given).

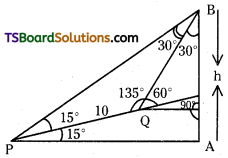
In the PQB, applying sine rule,
\(\frac{\mathrm{PQ}}{\sin \angle \mathrm{PBQ}}=\frac{\mathrm{BP}}{\sin \angle \mathrm{PQB}} \Rightarrow \frac{10}{\sin 30^{\circ}}=\frac{\mathrm{BP}}{\sin 135^{\circ}}\)
BP = \(\frac{\left(\sin 135^{\circ}\right)(10)}{\sin 30^{\circ}}=\frac{1}{\sqrt{2}}\) (10) × 2 = √2.(10)
Also in the ΔPAB,
sin 30° = \(\frac{A B}{P B}=\frac{h}{\sqrt{2} \cdot 10}\)
h = √2.(10)sin 30° = √2.(10)\(\frac{1}{2}\) = \(\frac{10}{\sqrt{2}}\) = 5√2 cm.

Question 19.
If A = 90°, show that 2(r + R) = b + c.
Answer:
L.H.S = 2(r + R) = 2r + 2R = 2(s – a)tan\(\frac{A}{2}\) + 2R . 1 = 2(s – a)tan 45° + 2R sin A (A = 90°)
= (2s – 2a) + a = 2s – a = a + b + c – a = b + c = R.H.S

Question 20.
Prove that \(\frac{r_1\left(r_2+r_3\right)}{\sqrt{r_1 r_2+r_2 r_3+r_3 r_1}}\) = a.
Answer:

Question 21.
If r : R: r₁ = 2 : 5 : 12, then prove that the triangle is right angled at A.
Answer:
Given r : R : r₁ = 2 : 5 : 12
∴ r₁ – r = 12k – 2k = 10k = 2(5k) = 2R
⇒ 4R sin\(\frac{A}{2}\)(cos\(\frac{B}{2}\)cos\(\frac{C}{2}\) – sin\(\frac{B}{2}\)sin\(\frac{C}{2}\)) = 2R ⇒ 2sin\(\frac{A}{2}\) cos\(\left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)\) = 1
⇒ 2sin\(\frac{A}{2}\)sin\(\frac{A}{2}\) = 1 ⇒ sin²\(\frac{A}{2}=\frac{1}{2}\) ⇒ sin\(\frac{A}{2}=\frac{1}{\sqrt{2}}\) = sin 45°
⇒ \(\frac{A}{2}\) = 45° ⇒ A = 90°
Hence the triangle is right angled at A.

Question 22.
In ΔABC, if AD, BE, CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides show that
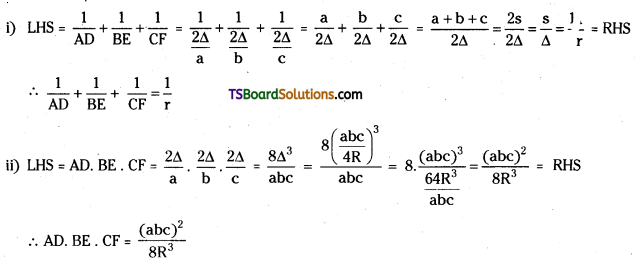
(i) \(\frac{1}{\mathrm{AD}}+\frac{1}{\mathrm{BE}}+\frac{1}{\mathrm{CF}}=\frac{1}{\mathrm{r}}\)
(ii) \(\frac{(a b c)^2}{8 R^3}\)
Answer:
In ΔABC, if AD, BE, CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides.

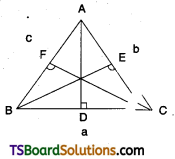
Area of ΔABC is A = \(\frac{1}{2}\)BC . AD = \(\frac{1}{2}\). a . AD
∴ AD = \(\frac{2 \Delta}{a}\)

Area of ΔABC is A = \(\frac{1}{2}\) AC . BE = \(\frac{1}{2}\) b . BE
∴ BE = \(\frac{2 \Delta}{b}\)

Area of ΔABC is A = \(\frac{1}{2}\) AB . CF = \(\frac{1}{2}\). c . CF
∴ CF = \(\frac{2 \Delta}{c}\)

Question 23.
Prove that \(\left(\frac{1}{r}-\frac{1}{r_1}\right)\left(\frac{1}{r}-\frac{1}{r_2}\right)\left(\frac{1}{r}-\frac{1}{r_3}\right)=\frac{a b c}{\Delta^3}=\frac{4 R}{r^2 s^2}\)
Answer:

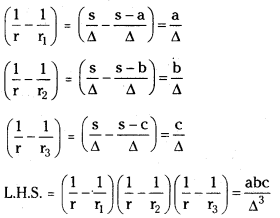
Since Δ = \(\frac{a b c}{4 R}\)
we have abc = 4RΔ
∴ \(\frac{\mathrm{abc}}{\Delta^3}=\frac{4 \mathrm{R} \Delta}{\Delta^3}=\frac{4 \mathrm{R}}{\Delta^2}=\frac{4 \mathrm{R}}{\mathrm{r}^2 \mathrm{~s}^2}\) (∵ Δ = RS)
∴ \(\left(\frac{1}{r}-\frac{1}{r_1}\right)\left(\frac{1}{r}-\frac{1}{r_2}\right)\left(\frac{1}{r}-\frac{1}{r_3}\right)=\frac{a b c}{\Delta^3}=\frac{4 R}{r^2 s^2}\) = R.H.S

Question 24.
Prove that r(r₁ + r₂ + r₃) = ab + bc + ca = s².
Answer:
L.H.S = r(r₁ + r₂ + r₃) = \(\frac{\Delta}{s}\left(\frac{\Delta}{s-a}+\frac{\Delta}{s-b}+\frac{\Delta}{s-c}\right)=\frac{\Delta^2}{s}\left(\frac{1}{s-a}+\frac{1}{s-b}+\frac{1}{s-c}\right)\)
= \(\frac{\Delta^2[(s-b)(s-c)+(s-a)(s-c)+(s-a)(s-b)]}{s(s-a)(s-b)(s-c)}\)
= \(\frac{\Delta^2}{\Delta^2}\)[(s² + s² + s²) – s(b + c) – s(a + c) – s(a + b) + bc + ca + ab]
= [3s² – 2s(a + b + c) + bc + ca + ab] = 3s² – 2s(2s) + ab + bc + ca
= ab + bc + ca – s² = R.H.S

Question 25.
Show that cos A + cos B + cos C = 1 + \(\frac{r}{R}s\).
Answer:
L.H.S = cos A + cos B + cos C = cos A + 2 cos \(\left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)\) cos\(\left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)\)

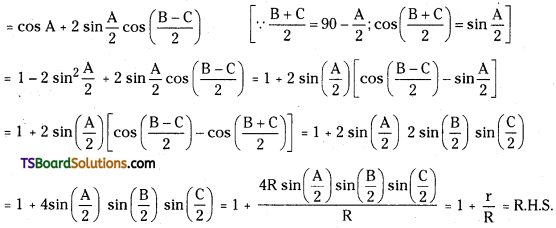
Question 26.
Show that sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + sin²\(\frac{C}{2}\) = 1 – \(\frac{r}{2R}\).
Answer:
L.H.S = sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + sin²\(\frac{C}{2}\) = sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) + 1 – cos²\(\frac{C}{2}\)

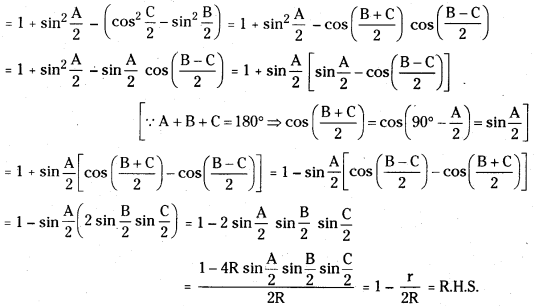
Question 27.
Prove that r₁² + r₂² + r₃² + r² = 16R² – (a² + b² + c²).
Answer:
(r₁ + r₂ + r₃ – r)² = [(r₁ + r₂ + r₃) – r]² = (r₁ + r₂ + r₃)² – 2(r₁ + r₂ + r₃)r + r²
But using results r₁ + r₂ + r₃ – r = 4R and r₁r₂ + r₂r₃ + r₃r₁ = s²
We have 16R² = (r₁² + r₂² + r₃² + r²) – 2r(r₁ + r₂ + r₃) + 2s² ………..(1)

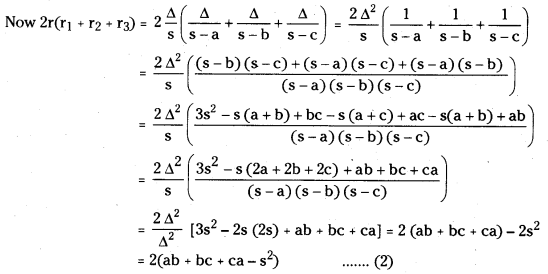
∴ From (1)
r₁² + r₂² + r₃² + r² = 16R² + 2(ab + bc + ca – s²) – 2s² = 16R² + 2(ab + bc + ca) – 4s²
= 16R² = [4s – 2(ab + bc + ca)] = 16R² – {(a + b + c)² – 2(ab + bc + ca)}
= 16R² – (a² + b² + c²)

Question 28.
In a ΔABC show that \(\frac{b^2-c^2}{a^2}=\frac{\sin (B-C)}{\sin (B+C)}\).
Answer: