TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Short Answer Type

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Properties of Triangles Important Questions Short Answer Type

Question 1.
In ΔABC, show that a = b cos C + c cos B. [May ’09]
Answer:
R.H.S = b cos C + c cos B

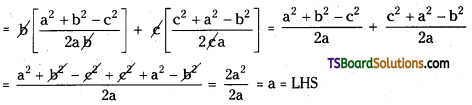
∴ a = b cos C + c cos B

Question 2.
In a ΔABC, show that tan\(\left(\frac{B-C}{2}\right)=\frac{b-c}{b+c}\)cot\(\frac{\mathrm{A}}{2}\). [Mar ’08; B.P]
Answer:
R.H.S = \(\frac{b-c}{b+c}\)cot\(\frac{\mathrm{A}}{2}\)

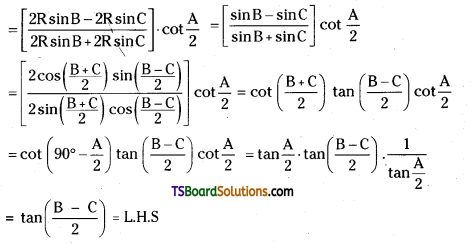
∴ tan\(\left(\frac{B-C}{2}\right)=\frac{b-c}{b+c}\)cot\(\frac{\mathrm{A}}{2}\)

Question 3.
In a ΔABC, if a = 3, b = 4 and sin A = \(\frac{3}{4}\), find the angle B. [May ’99]
Answer:
Given a = 3, b = 4, sin A = \(\frac{3}{4}\)
By sine rule, \(\frac{a}{\sin A}=\frac{b}{\sin B}\) ⇒ sin B = \(\frac{\mathrm{b} \sin \mathrm{A}}{\mathrm{a}}=\frac{4 \times 3 / 4}{3}\) = 1 ⇒ sin B = 1 ⇒ B = 90°

Question 4.
If the lengths of the sides of a triangle are 3, 4, 5, find the circumradius of the triangle. [May ’98]
Answer:
Since 32 + 42 = 52 the triangle is right angled and hypotenuse = 5 = circum diameter.
∴ Circum radius = \(\frac{5}{2}\) cm.

Question 5.
If a = 6, b = 5, c = 9, then find the angle A. [May ’10]
Answer:
Given a = 6, b = 5, c = 9
Since cos A = \(\frac{b^2+c^2-a^2}{2 b c}=\frac{5^2+9^2-6^2}{2(5)(9)}=\frac{25+81-36}{90}=\frac{70}{90}=\frac{7}{9}\)
∴ A = cos^-1\(\left(\frac{7}{9}\right)\)

Question 6.
In a ΔABC, if (a + b + c) (b + c – a) = 3bc, find A. [May ’08]
Answer:
Given (a + b + c) (b + c – a) = 3bc
⇒ (2s) 2(s – a) = 3bc ⇒ \(\frac{s(s-a)}{b c}=\frac{3}{4}\) ⇒ cos²\(\frac{\mathrm{A}}{2}=\frac{3}{4}\) ⇒ cos\(\frac{\mathrm{A}}{2}=\frac{\sqrt{3}}{2}\)
⇒ \(\frac{A}{2}\) = 30° ⇒ A = 60° (∵ cos\(\frac{A}{2}=\sqrt{\frac{s(s-a)}{b c}}\))

Question 7.
If a = 4, b = 5, c = 7, find cos\(\frac{B}{2}\). [May ’12, ’09; Mar. ’90]
Answer:
Given a = 4, b = 5, c = 7
2s = a + b + c = 4 + 5 + 7 = 16 ⇒ s = 8
∴ s – b = 8 – 5 = 3 and cos\(\frac{B}{2}=\sqrt{\frac{s(s-b)}{a c}}=\sqrt{\frac{8 \times 3}{4 \times 7}}=\sqrt{\frac{6}{7}}\)

Question 8.
If tan\(\frac{A}{2}=\frac{5}{6}\) and tan \(\frac{C}{2}=\frac{2}{5}\), determine the relation between a, b, c. [May ’05]
Answer:
Given tan\(\frac{A}{2}=\frac{5}{6}\) and tan \(\frac{C}{2}=\frac{2}{5}\), tan\(\frac{A}{2}\).tan\(\frac{C}{2}\) = \(\frac{C}{2}=\left(\frac{5}{6}\right)\left(\frac{2}{5}\right)=\frac{1}{3}\)
∴ \(\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \sqrt{\frac{(s-b)(s-a)}{s(s-c)}}=\frac{1}{3}\)
⇒ \(\frac{s-b}{s}=\frac{1}{3}\) ⇒ 3s – 3b = s ⇒ 2s – 3b ⇒ a + b + c = 3b ⇒ a + c = 2b ⇒ a, b, c are in A.P

Question 9.
Show that (b – c)²cos² + (b + c)²sin² = a². [May ’08, ’90]
Answer:
L.H.S = (b – c)²cos² + (b + c)²sin² = (b² – 2bc + c²)cos²\(\frac{A}{2}\) + (b² + 2bc + c²)sin²\(\frac{A}{2}\)
= (b² + c²)(cos²\(\frac{A}{2}\) + sin²\(\frac{A}{2}\)) + 2bc(sin²\(\frac{A}{2}\) – cos²\(\frac{A}{2}\))
= (b² + c²)(1) – 2bc(cos²\(\frac{A}{2}\) – sin²\(\frac{A}{2}\))
= b² + c² – 2bc cos A = a² = R.H.S

Question 10.
Prove that a(b cos C – c cos B) = b² – c². [Mar. ’07]
Answer:
L.H.S = a(b cos C – c cos B) = ab cos C – ac cos B

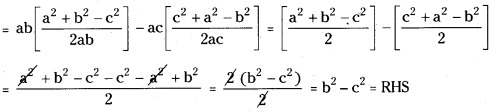
Question 11.
Prove that cot A + cot B + cot C = \(\frac{a^2+b^2+c^2}{4 \Delta}\). [Mar. ’18, ’15 (TS); May ’12, ’97; Mar. ’10]
Answer:
L.H.S = cot A + cot B + cot C = \(\frac{\cos A}{\sin A}+\frac{\cos B}{\sin B}+\frac{\cos C}{\sin C}\)

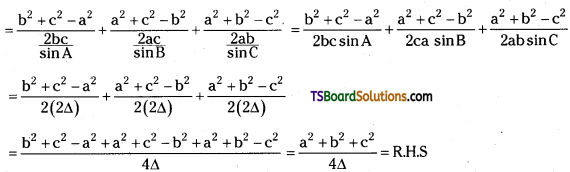
Question 12.
In ΔABC, if a cos A = b cos B, prove that the triangle is either isosceles or right angled. [Mar ’93]
Answer:
Given a cos A = b cos B
2R sin A cos A = 2R sin B cos B ⇒ sin 2A = sin 2B = sin (180° – 2B)
Hence 2A = 2B or 2A = 180° – 2B
⇒ A = BorA = 90°- B ⇒ a = borA + B = 90° ⇒ a = b or C = 90°
∴ The triangle is isosceles or right angled.

Question 13.
If cot\(\frac{A}{2}\): cot\(\frac{B}{2}\) : cot\(\frac{C}{2}\) = 3 : 5 : 7, show that a : b : c = 6 : 5 :4. [Mar. ’17 (A.P); May ’03]
Answer:
Given cot\(\frac{A}{2}\): cot\(\frac{B}{2}\) : cot\(\frac{C}{2}\) = 3 : 5 : 7

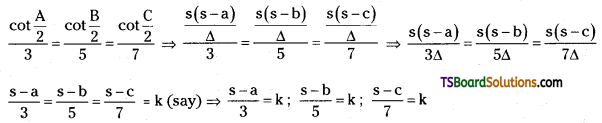
s – a = 3k ……(1)
s – b = 5k …..(2)
s – c = 7k …….(3)

Now (1) + (2) + (3)
s – a + s – b + s – c = 3k + 5k + 7k ⇒ 3s – (a + b + c) = 15k ⇒ 3s – 2s = 15k ⇒ s = 15k
From (1) ⇒ 15k – a – 3k ⇒ a = 12k
From (2) ⇒ 15k – b = 5k ⇒ b = 10k
From (3) ⇒ 15k – c = 7k ⇒ c = 8k
a : b : c = 12k : 10k : 8k ⇒ a : b : c = 6 : 5 : 4

Question 14.
If p₁, p₂, p₃ are the altitudes of ΔABC, then show that
\(\frac{1}{p_1^2}+\frac{1}{p_2^2}+\frac{1}{p_3^2}=\frac{\cot A+\cot B+\cot C}{\Delta}\) [Mar. ’13]
Answer:
Since p₁, p₂, p₃ are the altitudes of ΔABC, we have Δ = \(\frac{1}{2}\)ap₁ = \(\frac{1}{2}\)bp₂ = \(\frac{1}{2}\)cp₃
∴ p₁ = \(\frac{2 \Delta}{a}\), p₂ = \(\frac{2 \Delta}{b}\), p₃ = \(\frac{2 \Delta}{c}\)

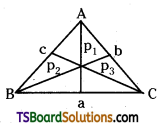
L.H.S = \(\frac{1}{p_1^2}+\frac{1}{p_2^2}+\frac{1}{p_3^2}=\frac{a^2}{4 \Delta^2}+\frac{b^2}{4 \Delta^2}+\frac{c^2}{4 \Delta^2}=\frac{1}{4 \Delta^2}\)(a² + b² + c²) ……….(1)
R.H.S = \(\frac{1}{\Delta}\)(cot A + cot B + cot C)
Since cot A + cot B + cot C = cot A = \(\sum \frac{\cos A}{\sin A}=\sum \frac{b^2+c^2-a^2}{2 b c \sin A}=\frac{1}{4 \Delta} \Sigma\left(b^2+c^2-a^2\right)\)
= \(\frac{1}{4 \Delta}\)(b² + c² – a² + c² + a² – b² + a² + b² – c²)
= \(\frac{1}{4 \Delta}\)(a² + b² + c²) ………..(2)
From (1) & (2) \(\frac{1}{\mathrm{p}_1^2}+\frac{1}{\mathrm{p}_2^2}+\frac{1}{\mathrm{p}_3^2}=\frac{\cot \mathrm{A}+\cot \mathrm{B}+\cot \mathrm{C}}{\Delta}\)

Question 15.
If a = 26 cm, b = 30 cm and cos C = \(\frac{63}{65}\) then find ‘c’. [Mar. ’11, ’98]
Answer:
Given a = 26 cm, b = 30 cm, cos C = \(\frac{63}{65}\). By the formula c² = a² + b² – 2ab cos C
c² = (26)² + (30)² – 2(26)(30)(\(\frac{63}{65}\)) = 676 + 900 – 1512 = 1576 – 1512 = 64
c = 8 cm

Question 16.
Prove that 2(bc cos A + ca cos B + ab cos C) = a² + b² + c². [Mar. ’05; May. ’97, 90]
Answer:
L.H.S. = Σ2bc cos A = Σ2bc \(\left(\frac{b^2+c^2-a^2}{2 b c}\right)\) = Σ2bc (b² + c² – a²)
= b² + c² – a² + c² + a² – b² + a² + b² – c² = a² + b² + c² = R.H.S.

Question 17.
Prove that (b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c. [Mar. ’98]
Answer:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + a cos B) + (c cos A + a cos C) + (b cos C + c cos B)
= c + b + a = a + b + c = R.H.S (Use projrction Formula)

Question 18.
Prove that (b – a cos C) sin A = a cos A sin C. [Mar. ’98]
Answer:
L.H.S. = (b – a cos C) sin A
= (a cos C + c cos A – a cos C) sin A
= c cos A sin A = 2R sin C cos A sin A
= (2R sin A) cos A sin C = a cos A sin C = R.H.S.

Question 19.
Show that b cos²\(\frac{C}{2}\) + cos²\(\frac{B}{2}\) = s. [Mar. ’12, ’10; May ’03]
Answer:
L.H.S = b cos²\(\frac{C}{2}\) + cos²\(\frac{B}{2}\) = b\(\left(\frac{s(s-c)}{a b}\right)\) + c\(\left(\frac{s(s-b)}{a c}\right)\) = \(\frac{s(s-c)}{a}+\frac{s(s-b)}{a}\)
= \(\frac{s}{a}\)(2s – b – c) = \(\frac{s}{a}\)(a) = s = R.H.S

Question 20.
If \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\), then show that ΔABC is an equilateral. [Mar. ’09]
Answer:
Given that \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C} \Rightarrow \frac{2 R \sin A}{\cos A}=\frac{2 R \sin B}{\cos B}=\frac{2 R \sin C}{\cos C}\)
⇒ \(\frac{\sin A}{\cos A}=\frac{\sin B}{\cos B}=\frac{\sin C}{\cos C}\) = tan A = tan B = tan C
⇒ A = B = C ⇒ ΔABC is an equilateral triangle

Question 21.
If C = 60°, then show that \(\frac{a}{b+c}+\frac{b}{c+a}\) = 1. [May ’93]
Answer:
C = 60° ⇒ c² = a² + b² – 2ab cos C = a² + b² – 2ab (cos 60°)
= a² + b² – 2ab(1/2) = a² + b² – ab ………….(1)
∴ \(\frac{a}{b+c}+\frac{b}{c+a}=\frac{a^2+a c+b^2+b c}{b c+c^2+a b+a c}=\frac{a^2+a c+b^2+b c}{a b+a c+b c+a^2+b^2-a b}=\frac{a^2+a c+b^2+b c}{a^2+b^2+a c+b c}\) = 1

Question 22.
If a : b : c = 7 : 8 : 9, find cos A : cos B : cos C. [May ’15 (AP); May ’13]
Answer:
Given \(\frac{a}{7}=\frac{b}{8}=\frac{c}{9}\) = k
∴ a = 7k, b = 8k, c = 9k

∴ cos A : cos B : cos C = \(\frac{2}{3}: \frac{11}{21}: \frac{2}{7}\) ⇒ 14 : 11 : 6

Question 23.
Show that \(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^2+b^2+c^2}{2 a b c}\). [May. ’10]
Answer:
L.H.S = \(\frac{\cos \mathrm{A}}{\mathrm{a}}+\frac{\cos \mathrm{B}}{\mathrm{b}}+\frac{\cos \mathrm{C}}{\mathrm{c}}=\frac{\mathrm{b}^2+\mathrm{c}^2-\mathrm{a}^2}{2 \mathrm{abc}}+\frac{\mathrm{c}^2+\mathrm{a}^2-\mathrm{b}^2}{2 \mathrm{abc}}+\frac{\mathrm{a}^2+\mathrm{b}^2-\mathrm{c}^2}{2 \mathrm{abc}}=\frac{\mathrm{a}^2+\mathrm{b}^2+\mathrm{c}^2}{2 \mathrm{abc}}\)

Question 24.
Express a sin²\(\frac{C}{2}\) + c sin²\(\frac{A}{2}\) in terms of s, a, b, c.
Answer:
We have sin\(\frac{C}{2}\) = \(\sqrt{\frac{(s-a)(s-b)}{a b}}\)
sin \(\frac{\mathrm{A}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{bc}}}\)
∴ a sin²\(\frac{C}{2}\) + c sin²\(\frac{A}{2}\)
= a\(\frac{(s-a)(s-b)}{b}+\frac{(s-b)(s-c)}{b}\) + c\(\frac{(s-b)(s-c)}{b c}\) = \(\frac{(s-a)(s-b)}{b}+\frac{(s-b)(s-c)}{b}\)
= \(\frac{1}{b}\)(s – b)[s – a -s – c] = \(\frac{1}{b}\)(s – b)[a + b + c – a – c]
= \(\frac{b}{b}\)(s – b) = (s – b)

Question 25.
In ΔABC, show that r = 4R sin\(\frac{A}{2}\) sin\(\frac{B}{2}\) sin\(\frac{C}{2}\) where ‘r’ is the incircie radius. [May ’00]
Answer:
RHS = 4R sin\(\frac{A}{2}\) sin\(\frac{B}{2}\) sin\(\frac{C}{2}\)

∴ r = 4R sin\(\frac{A}{2}\) sin\(\frac{B}{2}\) sin\(\frac{C}{2}\)

Question 26.
In ΔABC, Prove that \(\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}=\frac{1}{r}\). [Mar. ’97, ’96, ’94]
Answer:

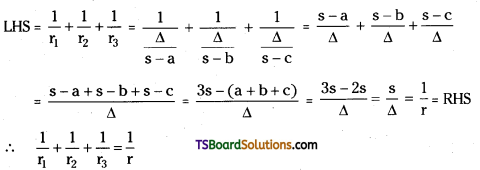
Question 27.
Show that rr₁r₂r₃ = Δ²
Answer:
LHS = rr₁r₂r₃ = \(\frac{\Delta}{s} \cdot \frac{\Delta}{s-a} \cdot \frac{\Delta}{s-b} \cdot \frac{\Delta}{s-c}=\frac{\Delta^4}{s(s-a)(s-b)(s-c)}=\frac{\Delta^4}{\Delta^2}\) = Δ² = RHS
∴ rr₁r₂r₃ = Δ²

Question 28.
In an equilateral triangle, find the value of \(\frac{r}{R}\).
Answer:

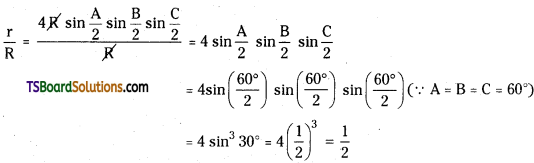
Question 29.
The perimeter of ΔABC is 12 cm and its in radius is 1 cm. Then find the area of the triangle.
Answer:
Given that the perimeter of ΔABC = 12
2s = 12 ⇒ s = 6
In radius = 1
r = 1
∴ The area of the triangle = Δ = rs = (1)(6) = 6 sq.cm

Question 30.
Show that rr₁ cot\(\frac{A}{2}\) = Δ. [May’96; Mar. ’79]
Answer:

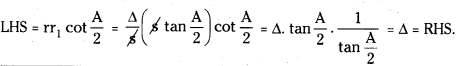
Question 31.
If rr₂ = r₁r₃, then find B. [May ’97]
Answer:
Given that rr₂ = r₁r₃
⇒ \(\frac{\Delta}{s} \cdot \frac{\Delta}{s-b}=\frac{\Delta}{s-a} \cdot \frac{\Delta}{s-c}\) ⇒ (s – a)(s – c) = s(s – b) ⇒ \(\frac{(s-c)(s-a)}{s(s-b)}\) = 1
⇒ tan²\(\frac{B}{2}\) = 1 ⇒ tan\(\frac{B}{2}\) = 1 ⇒ \(\frac{B}{2}\) = 45° ⇒ B = 90°

Question 32.
In a ΔABC, show that the sides a, b, c are in AP, if and only if r₁, r₂, r₃ are in HP. [Mar ’94]
Answer:
Given that rr₂ = r₁r₃
⇒ \(\frac{1}{r_1}, \frac{1}{r_2}, \frac{1}{r_3}\) are in AP ⇒ \(\frac{\mathrm{s}-\mathrm{a}}{\Delta}, \frac{\mathrm{s}-\mathrm{b}}{\Delta}, \frac{\mathrm{s}-\mathrm{c}}{\Delta}\) are in AP ⇒ s – a, s – b, s – c are in A.P
⇒ -a, -b, -c are in AP ⇒ a, b, c are in AP.

Question 33.
Show that \(\frac{1}{\mathbf{r}^2}+\frac{1}{\mathbf{r}_1^2}+\frac{1}{\mathbf{r}_2^2}+\frac{1}{\mathbf{r}_3^2}=\frac{\mathbf{a}^2+b^2+c^2}{\Delta^2}\). [Mar. ’19, ’17(TS), ’98, ’86; May ’93]
Answer:
L.H.S = \(\frac{\mathrm{s}^2}{\Delta^2}+\frac{(\mathrm{s}-\mathrm{a})^2}{\Delta^2}+\frac{(\mathrm{s}-\mathrm{b})^2}{\Delta^2}+\frac{(\mathrm{s}-\mathrm{c})^2}{\Delta^2}=\left(\frac{\left.\mathrm{s}^2+\mathrm{s}^2-2 \mathrm{as}+\mathrm{a}^2+\mathrm{s}^2-2 \mathrm{bs}+\mathrm{b}^2+\mathrm{s}^2-2 \mathrm{cs}+\mathrm{c}^2\right)}{\Delta^2}\right)\)
= \(\frac{1}{\Delta^2}\)[4s² – 2s(a + b + c) + a² + b² + c²]
= \(\frac{1}{\Delta^2}\)[4s² – 2s(2s) + a² + b² + c²] = \(\frac{1}{\Delta^2}\)(a² + b² + c²) = R.H.S

Question 34.
Show that r + r₃ + r₁ – r₂ = 4R cos B in a triangle ABC. [Mar. ’18(AP); Mar. ’13, ’97, ’00]
Answer:

∴ r + r₃ + r₁ – r₂ = 4R cos B

Question 35.
If A, A₁, A₂, A₃ are the areas of Incircie and excircles of a triangle respectively, then prove that \(\frac{1}{\sqrt{\mathrm{A}_1}}+\frac{1}{\sqrt{\mathrm{A}_2}}+\frac{1}{\sqrt{\mathrm{A}_3}}=\frac{1}{\sqrt{\mathrm{A}}}\). [Mar, ’91]
Answer:
If r, r₁, r₂, r₃ are the inradius and exradll of the circles whose areas are A, A₁, A₂, A₃ respectively, then A = πr², A₁ = πr₁², A₂ = πr₂² A₃ = πr₃²

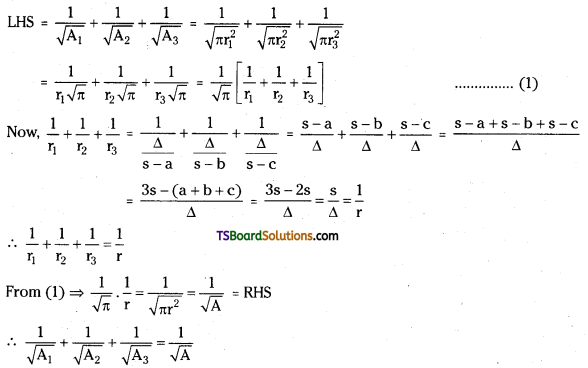
Question 36.
Express Σr₁ cot\(\frac{A}{2}\) in terms of s. [May ’11, ’06; Mar. ’99]
Answer:
We have r₁ = s tan\(\frac{A}{2}\)
Σr₁cot\(\frac{A}{2}\) = Σs tan(\(\frac{A}{2}\))cot\(\frac{A}{2}\) = Σs = s + s + s = 3s

Question 37.
Show that Σa cot A = 2(R + r). [Mar ’98]
Answer:
L.H.S = Σa cot A = Σ2R sin A\(\frac{\cos A}{\sin A}\) = Σ2R cos A = 2R(cos A + cos B + cos C)
= 2R(1 + 4sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\))
= 2R + 2R(4 sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\)) = 2R + 2r (∵r = 4R sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\))
=2(R + r)

Question 38.
In ΔABC, Prove that r₁ + r₂ + r₃ – r = 4R. [Mar. ’06; Mar ’02, 92]
Answer:
r₁ + r₂ = \(\frac{\Delta}{s-a}+\frac{\Delta}{s-b}\) = Δ\(\left(\frac{1}{s-a}+\frac{1}{s-b}\right)\) = Δ\(\left(\frac{2 s-a-b}{(s-a)(s-b)}\right)\) = \(\frac{\Delta(a+b+c-a-b)}{(s-a)(s-b)}=\frac{\Delta c}{(s-a)(s-b)}\)

r₃ – r = \(\frac{\Delta}{s-c}-\frac{\Delta}{s}\) = Δ\(\left(\frac{s-s+c}{s(s-c)}\right)=\frac{\Delta c}{s(s-c)}\)
∴ L.H.S = r₁ + r₂ + r₃ – r
= Δc\(\left(\frac{1}{(s-a)(s-b)}+\frac{1}{s(s-c)}\right)=\frac{\Delta c}{\Delta^2}\)[s(s – c) + (s – a) (s – b)]
= \(\frac{\mathrm{c}}{\Delta}\)(s² – cs + s² – as – bs + ab) = \(\frac{\mathrm{c}}{\Delta}\)[2s² – s(a + b + c) + ab)
= \(\frac{\mathrm{c}}{\Delta}\)[2s² – s(2s) + ab] = \(\frac{\mathrm{abc}}{\Delta}\) = 4R

Question 39.
In ΔABC, prove that r₁ + r₂ + r₃ – r = 4R cos C. [Mar. ’12, May ’06]
Answer:

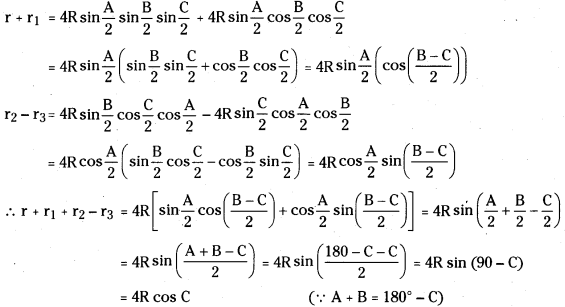
Question 40.
Prove that 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)². [Mar. ’97]
Answer:
r₁r₂ + r₂r₃ + r₁r₁ = \(\left(\frac{\Delta}{s-a}\right)\left(\frac{\Delta}{s-b}\right)+\left(\frac{\Delta}{s-b}\right)\left(\frac{\Delta}{s-c}\right)+\left(\frac{\Delta}{s-c}\right)\left(\frac{\Delta}{s-a}\right)\)
= \(\frac{\Delta^2}{(s-a)(s-b)}+\frac{\Delta^2}{(s-b)(s-c)}+\frac{\Delta^2}{(s-c)(s-a)}\)
= s(s – c) + s(s – a) + s(s – b) [∵ Δ² = s(s – a)(s – b)(s – c)]
= 3s² – s(a + b + c) = 3s² – 2s² = s²2 = \(\left(\frac{a+b+c}{2}\right)^2=\frac{(a+b+c)^2}{4}\)
∴ 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)²

Question 41.
If ΔABC, if \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\), show that C = 60°. [Mar. ’19, ’17 (TS)]
Answer:
Given that \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\)
= \(\frac{a+c+b+c}{(a+c)(b+c)}=\frac{3}{a+b+c}\)
⇒ (a + b + 2c)(a + b + c) = 3(a + c)(b + c)

⇒ a² + b² – c² = ab ⇒ 2ab cos C = ab ⇒ \(\frac{1}{2}\) cos C = \(\frac{1}{2}\) C = 60°