TS Inter 1st Year Physics Study Material Chapter 3 Motion in a Straight Line

Telangana TSBIE TS Inter 1st Year Physics Study Material 3rd Lesson Motion in a Straight Line Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 3rd Lesson Motion in a Straight Line

Very Short Answer Type Questions

Question 1.
The states of motion and rest are relative. Explain.
Answer:
REST :
If the position of a body does not change with respect to surroundings, it is said to be at “rest”.

MOTION :
If the position of a body changes with respect to surroundings, it is said to be in “motion”.

By definitions rest and motion are relative with respect to surroundings.

Question 2.
How is average velocity different from instantaneous velocity? [AP Mar. 19, 13, May 17]
Answer:
Average velocity :
It is the ratio of total displacement to total time taken. It is independent of path of the body.

∴ Average velocity = \(\frac{\mathrm{s}_2-\mathrm{s}_1}{\mathrm{t}_2-\mathrm{t}_1}\)

Velocity of a particle at a particular instant of time is known as instantaneous velocity. Here time interval is very small.

Only in uniform motion, instantaneous velocity = average velocity. For all other cases instantaneous velocity may differ from average velocity.

Question 3.
Give an example where the velocity of an object is zero but its acceleration is not zero. [AP May ’17, Mar. ’13]
Answer:
In case of VPB at maximum height its velocity v = 0. But acceleration due to gravity ‘g’ is not zero.

So even though velocity v = 0 ⇒ acceleration is not zero.

Question 4.
A vehicle travels half the distance L with speed v₁ and the other half with speed v₂. What is the average speed?
Answer:
The average speed of a vehicle for the two equal parts.

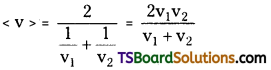
Question 5.
A lift coming down is just about to reach the ground floor. Taking the ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
a) x < 0, v < 0, a > 0
b) x > 0, v < 0, a < 0
c) x > 0, v < 0, a > 0
d) x > 0, v > 0, a > 0
Answer:
As the lift is coming down, the value of x become less hence negative, i.e., x < 0.

Velocity is downwards (i.e., negative). So v < 0. Just before reaching ground floor, lift is retarded, i.e., acceleration is upwards. Hence a > 0.

We can conclude that x < 0, v < 0 and a > 0.
∴ (a) is correct.

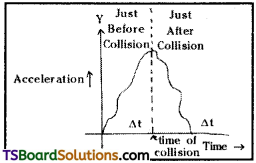
Question 6.
A uniformly moving cricket ball is hit with a bat for a very short time and is turned back. Show the variation of its acceleration with time taking the acceleration in the backward direction as positive.
Answer:
For a ball moving with uniform velocity acceleration is zero. But during time of contact between ball and bat acceleration is applied in opposite direction. The shape of acceleration – time graph is as shown.

Question 7.
Give an example of one-dimensional motion where a particle moving along the positive x-direction comes to rest periodically and moves forward.
Answer:
When length of pendulum is high and amplitude is less then its motion is along a straight line. The pendulum will come to a stop at extreme position and moves back in forward direction (‘x’ + ve) periodically.

Question 8.
An object falling through a fluid is observed to have an acceleration given by a = g – bv, where g is the gravitational acceleration and b, is a constant. After a long time it is observed to fall with a constant velocity. What would be the value of this constant velocity?
Answer:
Acceleration, a = g – bv when moving with constant velocity, a = 0 ⇒ 0 = g – bv
∴ Constant velocity, v = \(\frac{g}{b}\) m/sec.

Question 9.
If the trajectory of a body is parabolic in one frame, can it be parabolic in another frame that moves with a constant velocity with respect to the first frame? If not, what can it be?
Answer:
If the trajectory of a body is parabolic with reference frames one and two then those two frames are of rest or moving with uniform velocity.

If they are not parabolic then for that reference frame it may be in straight line path.
Ex : When a body is dropped from a moving plane its path is parabolic for a person outside the plane. But for the pilot in the plane it is falling vertically downwards.

Question 10.
A spring with one end attached to a mass and the other to a rigid support is stretched and released. When is the magnitude of acceleration a maxium?
Answer:
Maximum restoring force setup in the spring, when stretched by a distance ’r’, is F = – kr

Potential energy of stretched spring = \(\frac{1}{2}\) kx²

As F ∝ r and this force is directed towards equilibrium position, hence if mass is left free, it will execute damped SHM due to gravity pull.

Magnitude of acceleration in the mass attached to one end of spring when just released is

a = \(\frac{F}{m}=\frac{-k}{m}\) r = (Maximum)

The magnitude of acceleration of the spring will be maximum when just released.

Question 11.
Define average velocity and average speed. When does the magnitude of average velocity become equal to the average speed?
Answer:
Average velocity :
It is defined as the ratio of total displacement to total time taken.

Average velocity

Average velocity is independent of path followed by the particle. It just deals with initial and final positions of the body. Average Speed: The ratio of total path length travelled to the total time taken is known as “average speed”.

Speed and average speed are scalar quantities so no direction for these quantities.

When the body is along with the straight line its average velocity and average speed are equal.

Short Answer Questions

Question 1.
Can the equations of kinematics be used when the acceleration varies with time? If not, what form would these equations take?
Answer:
a) The equations of motion are
1) v =u + at
2) s = ut + \(\frac{1}{2}\) at² and 3) v² – u² = 2as. All these three equations applicable body moves with uniform acceleration ‘a’.

No, the equations of are not applicable when the acceleration varies with time.

Question 2.
A particle moves in a straight line with uniform acceleration. Its velocity at time t = 0 is v₁ and at time t₂ = t is v₂. The average velocity of the particle in this time interval is (v₁ + v₁)/ 2. Is this correct? Substantiate your answer.
Answer:
t₁ = 0 ⇒ u = v₁
t₂ = t ⇒ v = v₂

Question 3.
Can the velocity of an object be in a direction other than the direction of acceleration of the object? If so, give an example.
Answer:
Yes. Velocity of a body and its acceleration may be in different directions.

Explanation:

1. Incase of vertically projected body ⇒ velocity of body is in the upward direction and acceleration is in a downward direction.
2. When brakes are applied the velocity of body before coming to rest is opposite to retarding acceleration.

Question 4.
A parachutist flying in an aeroplane jumps when it is ata height of 3 km above ground. He opens his parachute when he is about 1 km above ground. Describe his motion.
Answer:
a) Height of fall before opening, h = 2 km
= 2000 m
∴ Velocity at a height of 1 km

b) After parachute is opened it touches the ground with almost zero velocity.
∴ u = 200 m/sec, v = 0, S = h = 1000 m From v² – u² = 2as

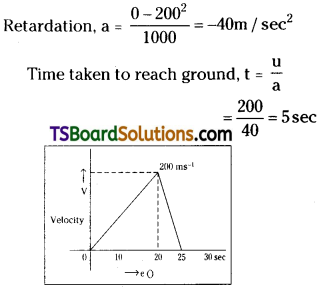
The Motion is as shown in figure.

Question 5.
A bird holds a fruit in its beak and flies parallel to the ground. It lets go of the fruit at some height. Describe the trajectory of the fruit as it falls to the ground as seen by (a) the bird (b) a person on the ground.
Answer:
a) As the bird is flying parallel to the ground, it possesses velocity in horizontal direction. Hence the fruit also possess velocity in horizontal direction and acceleration in downward direction. Hence the path of the fruit is a straight line with respect to the bird.

b) With respect to a person on the ground, the fruit seems to be in a parabolic path.

Question 6.
A man runs across the roof of a tall building and jumps horizontally on to the (lower) roof of an adjacent building. If his speed is 9 ms^-1 and the horizontal distance between the buildings is 10 m and the height difference between the roofs is 9 m, will he be able to land on the next building? (take g = 10 ms^-2) [TS Mar. ’18]
Answer:
Given that,
initial speed, u = 9 ms^-1 ; g = 10m/s² height difference between the roofs, h = 9 m
horizontal distance between two buildings, d = 10 m

Range of the man = R = u × T = 9 × 1.341
= 12.069 m

Since R > d, the man will be able to land on the next building.

Question 7.
A ball is dropped from the roof of a tall building and simultaneously another ball is thrown horizontally with some velocity from the same roof. Which ball lands first? Explain your answer. [TS June ’15]
Answer:
Let ‘h’ be the height of the tall building.

For dropped ball:
Let ‘t₁‘ be the time taken by the dropped ball to reach the ground.

Initial velocity, u = 0 ; Acceleration, a = + g
Distance travelled, s = h; Time of travel, t = t₁

From the equation of motion, s = ut + \(\frac{1}{2}\) at²
we can write,

For horizontally projected ball:
If the ball is thrown horizontally then its initial velocity along vertical direction is zero and in this case let ‘t₂‘ be the time taken by the ball to reach the ground.
Again from the equation of motion,

From equations (1) and (2) t₁ = t₂
i.e., both the balls reach the ground in the same time.

Question 8.
A ball is dropped from a building and simultaneously another ball is projected upward with some velocity. Describe the change in relative velocities of the balls as a function of time.
Answer:
a) For a body dropped from building its velocity, v₁ = gt → (1) (∵ u₁ = 0)

b) For a body thrown up with a velocity ‘u’ its velocity, v₂ = u – gt → (2)
∵ The two balls are moving in opposite direction the relative velocity,
V_R = v₁ + v₂
∴ v_R =gt + u – gt = u

Here the relative velocity remains constant, but velocity of one body increases at a rate of g’ m/sec and velocity of another body decreases at a rate of ‘g’m/sec.

Question 9.
A typical raindrop is about 4 mm in diameter. If a raindrop falls from a cloud which is at 1 km above the ground, estimate its momentum when it hits the ground.
Answer:
Diameter, D = 4 m
⇒ radius, r = 2mm = 2 × 10^-3 m
mass of rain drop = volume × density = \(\frac{4}{3}\)πr³ × 1000 m
(∵ mass of one m³ of water = 1000 kg)

Question 10.
Show that the maximum height reached by a projectile launched at an angle of 45° is one quarter of its range. [AP May ’16, Mar. ’14]
Answer:

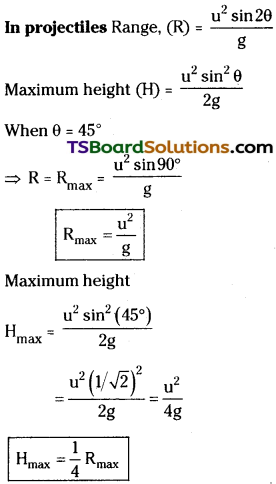
∴ When θ = 45° maximum height reached is one quarter of maximum range.

Question 11.
Derive the. equation of motion x = v₀t + \(\frac{1}{2}\) at² using appropriate graph. [TS Mar. ’19, May ’16]
Answer:
The velocity-time graph of a body moving with initial velocity u’ and with uniform acceleration a’ as shown. Let ‘v’ be the velocity of the body after a time t.

In v – t graph area of velocity-time graph = total displacement travelled by it. Area under velocity – time graph = area of OABCD
∴ Area of Rectangular part OACD = Area of OACD + Area of ABC.
A₁ = OA × OD = v₀.t. ……….. (1)

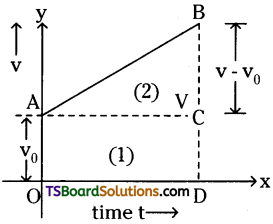
2) Area of triangle ABC = A₂
A₂ = \(\frac{1}{2}\)Base × height
= \(\frac{1}{2}\)AC × BC
= \(\frac{1}{2}\) t(v – v₀).
But v – v₀ = at
A₂ = \(\frac{1}{2}\)t.at = \(\frac{1}{2}\)at².
∴ Total area under graph = s = A₁ + A₂
s(n) = v₀t + \(\frac{1}{2}\)at².
∴ s = ut + \(\frac{1}{2}\)at² is graphically proved.

Problems

Question 1.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h^-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h^-1. What is the (a) magnitude of average velocity and (b) average speed of the man over the time interval 0 to 50 minutes? [AP Mar. ’19. May ’18; TS Mar. ’18]
Solution:
Time taken by man to go from his home to

Time take by man to go from market to his home, t₂ = \(\frac{2.5}{7.5}=\frac{1}{3}\)h
∴ Total time taken = t, + to = \(\frac{1}{2}+\frac{1}{3}=\frac{5}{6}h\)
= 50 min.
In time interval 0 to 50 min,
Total distance travelled = 2.5 + 2.5 = 5 km.
Total displacement = zero.

Question 2.
A stone is dropped from a height 300 in and at the same time another stone is projected vertically upwards with a velocity of 100 m/sec. Find when and where the two stones meet. [AP Mar. ’16]
Solution:
Height h = 300 m ;
Initial velocity U₀ = 100 m/s
Let the two stones will meet at a height ‘x’ above the ground.
For 1st stone h – x = \(\frac{1}{2}\) gt² …………. (1)
For 2nd stone x = u₀t – \(\frac{1}{2}\) gt²
⇒ \(\frac{1}{2}\) gt² = u₀t – x ……….. (2)

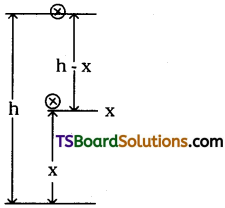
Since t is same for the two stones
From equations 1 & 2.
h – x = u₀t – x
⇒ u₀t = h or time t = \(\frac{h}{u_0}=\frac{300}{100}\) = 3 sec.
∴ The two stones will meet 3 seconds after the 1st stone is dropped or 2nd stone is thrown up.

Question 3.
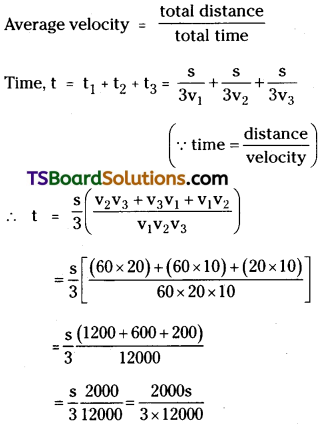
A car travels the first third of a distance with a speed of 10 kmph, the second third at 20 kmph and the last third at 60 kmph. What is its mean speed over the entire distance? [TS Mar. ’16; AP May ’14, AP Mar. ’18]
Solution:
Total distance = s;
distance travelled, s₁ = \(\frac{s}{3}\) ;
velocity, v₁ = 10 kmph
distance, s₂ = \(\frac{s}{3}\)
velocity, v₂ = 20 kmph
distance, s₃ = \(\frac{s}{3}\)
velocity, v₃ = 60 kmph

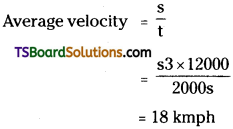
Question 4.
A bullet moving with a speed of 150 m s^-1 strikes a tree and penetrates 3.5 cm before stopping. What is the magnitude of its retardation in the tree and the time taken for it to stop after striking the tree?
Solution:
Velocity of bullet, u = 150 m/s;
Final velocity, v = 0
Distance travelled, s = 3.5 cm = 3.5 × 10^-2 m,

Question 5.
A motorist drives north for 30 min at 85 km/h and then stops for 15 min. He continues travelling north and covers 130 km in 2 hours. What is his total displacement and average velocity?
Solution:
In first part:
Velocity, v₁ = 85 kmph
Time, t₁ = 30 min
Distance travelled, s₁ = v₁ t₁
= 85 × \(\frac{30}{60}\) = 42.5 km

In second part:
Distance travelled, s₂ = 0 ;
Time, t₂ = 15.0 min.

In third part:
Distance travelled, s₃ = 130 km ;
Time, t₃ = 120 min = 2 hours
a) Total distance of the motorist,
s = s₁ + s₂ + s₃ = 42.5 + 0 + 130 = 172.5 km

b) Total time travelled,
t = t₁ + t₂ + t₃ = 30 + 15 + 120
= 165 minutes
= 2 hrs 45 minutes
= 2\(\frac{3}{4}\)hrs. = \(\frac{11}{4}\) hrs.
∴ Average velocity,

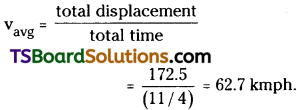
Question 6.
A ball A is dropped from the top of a building and at the same time an identical ball B is thrown vertically upward from the ground. When the balls collide the speed of A is twice that of B. At what frac¬tion of the height of the building did the collison occur?
Solution:
Given at time of collision velocity of A = V_A
= 2 × V_B (velocity of B)
Let the body be dropped from a height h’.
Let the two stones collide at x from ground.
For the body dropped,
s = h – x = \(\frac{1}{2}\)gt² → (1)
For the body thrown up,
x = ut – \(\frac{1}{2}\)gt² → (2)
For the body dropped,
v = u + at ⇒ V_A = gt → (3)
For the body thrown up,
v = u – gt ⇒ V_B = u – gt → (4)
Given V_A = 2V_B
⇒ gt = 2 (u – gt) or u = \(\frac{3gt}{2}\) → (5)
Divide equation (1) with equation (2)

∴ Fraction of height of collision = \(\frac{2}{3}\)

Question 7.
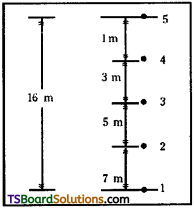
Drops of water fall at regular intervals from the roof of a building of height 16 m. The first drop strikes the ground at the same moment as the fifth drop leaves the roof. Find the distances between successive drops.
Solution:
Height of building, h = 16 m

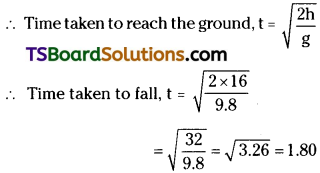
Number of drops, n = 5
∴ Number of intervals = n – 1 = 5 – 1 = 4

Time interval between drops = \(\frac{1.8}{4}\)
= 0.45 sec
Time of travel of 1st drop, t₁ = 4 × 0.45 = 1.8
∴ Distance travelled by
1st drop, S₁ = \(\frac{1}{2}\)gt²₁ = \(\frac{1}{2}\) × 9.8 × 1.8 × 1.8= 16 m

For 2nd drop, t₂ = 3 × 0.45 = 1.35 sec.,
∴ S₂ = \(\frac{1}{2}\) × 9.8 × 1.35²
= 4.9 × 1.822 ≅ 1.822 ≅ 9m

For 3rd drop, t₃ = 2 × 0.45 = 0.9 sec.
Distance, S₃ = \(\frac{1}{2}\)gt²₃ = \(\frac{1}{2}\) × 9.8 × 0.9² = 3.97≅4 m

For 4th drop, t₄ = 1 × 0.45 = 0.45 sec
Distance travelled, S₄ = \(\frac{1}{2}\)gt²₄ = \(\frac{1}{2}\) × 9.8 × (0.45)² = 1

For 5 th drop, t₅ = 0 ⇒ S₅ = 0
Distance between 1^st and 2^nd drop
S_{1, 2} = S₁ – S₂ = 16 – 9 = 7 m

Distance between 2^nd and 3^rd drop
S_{2, 3} = S₂ – S<₃ = 9 – 4 = 5m

Distance between 3^rd and 4^th drop
S_{3, 4} = S₃ – S4 = 4 – 1= 3 m

Distance between 4^th and 5^th drop
S_{4, 5} = S₄ – S₅ = 1 – 0 = 1 m

∴ Distances between successive drops are 7m, 5m, 3m and lm.

Question 8.
Rain is falling vertically with a speed of 35 ms^-1. A woman rides a bicycle with a speed of 12 ms^-1 in east to west direction. What is the direction in which she should hold her umbrella? [TS June ’15]
Solution:
Velocity of rain V_R = 35 m/s (vertically)
Velocity of women V_w = 12 m/s (towards east)
Resultant angle θ = tan^-1 \(\frac{V_W}{V_R}=\frac{12}{35}\)
∴ θ = tan^-1\(\frac{12}{35}\) = 0.343. or q = 19° (Nearly)
She should hold umbrella at an angle of 19c with east.

Question 9.
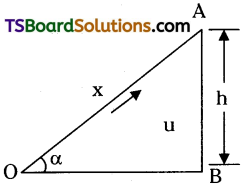
A hunter aims a gun at a monkey hanging from a tree some distance away. The monkey drops from the branch at the moment he fires the gun hoping to avoid the bullet. Explain why the monkey made a wrong move.
Solution:
Let the bullet is fired with an angle α and distance from hunter’s rifle to monkey = x
Vertical component of velocity v_xy = v sin α
when exactly aimed at monkey s_y = v sin α
t = h

But due to acceleration due to gravity
h₁ = u sin α t – \(\frac{1}{2}\)gt² = h – \(\frac{1}{2}\)gt² → (1)
So bullet passes through a height of \(\frac{1}{2}\)gt² below the monkey.
But when the monkey is falling freely height of fall during time t = \(\frac{1}{2}\)gt²
So new height is \(\frac{1}{2}\)gt² → (2)

From equations (1) & (2) h₁ is same i.e., if the monkey is dropped from the branch bullet will hit it exactly.

Question 10.
A food packet is dropped from an aero-plane, moving with a speed of 360 kmph in a horizontal direction, from a height of 500m. Find (i) its time of descent (ii) the horizontal distance between the point at which the food packet reaches the ground and the point above which it was dropped.
Solution:
Velocity of plane, V = 360 kmph
= 360 × \(\frac{5}{18}\) = 100 m/s

Height above ground, h = 500 m;
g = 10 m/s²

i) Time of descent,

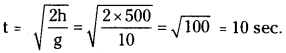
ii) Horizontal distance between point o{ dropping and point where it reaches the ground = Range R

Question 11.
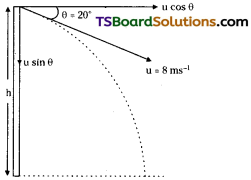
A ball is tossed from the window of a building with an initial velocity of 8 ms^-1 at an angle of 20° below the horizontal. It strikes the ground 3 s later. From what height was the ball thrown? How far from the base of the building does the ball strike the ground?
Solution:
Initial velocity, u = 8 m/s;
Angle of projection, θ = 20°
Time taken to reach the ground, t = 3 sec
Horizontal component of initial velocity,
u_x = u. cos θ = 8 cos 20°
= 8 × 0.94 = 7.52 m/s

Vertical component of initial velocity,
v_y = u sin θ = 8 sin 20°
= 8 × 0.342 = 2.736 m/s

a) From equation of motion, s = ut + \(\frac{1}{2}\)at²
we can write
h = (u sin θ)t + \(\frac{1}{2}\)gt²
⇒ h = (2.736)3 + \(\frac{1}{2}\)9.8 × (3)²
⇒ h = 8.208+ 4.9 × 9
⇒ h = 8.208 + 44.1 or h = 52.308 m

b) Horizontal distance travelled, s_x = v_x x t = 7.52 × 3 = 22.56 m

Question 12.
Two balls are projected from the same point in directions 30° and 60° with respect to the horizontal. What is the ratio of their initial velocities if they (a) attain the same height? (b) have the same range?
Solution:
Angle of projection of first ball, θ₁ = 30°
Angle of projection of second ball, θ₂ = 60°
Let u₁ and u₂ be the velocities of projections of the two balls.
i) Maximum height of first ball,

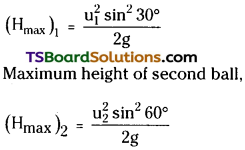
ii) If the balls have same range, then R₁ = R₂

Question 13.
A ball is thrown vertically upwards with a velocity of 20 ins’1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. [TS May ’17; AP & TS Mar. ’15]
(a) How high will the ball rise?
(b) How long will it be before the ball hits the ground?
Take g = 10 ms^-2 [Actual value of ‘g’ is 9.8 ms^-2]
(OR)
When a ball is thrown vertically upwards with a velocity of 20 ms^-1 from the top of a multistorey building, the height of the point from where the ball is thrown is 25.0 m from the ground. [TS Mar. ’15]
a) How high will the ball rise? and
b) How long will it be before the ball hits the ground?
Solution:
Initial velocity V₀ = 20 m/s;
height above ground h₀ = 2.50 m ;
g = 10 m/s²

a) For a body thrown up vertically height of rise

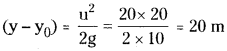
b) Time spent in air (t) is y₁ – y₀ = V₀t + \(\frac{1}{2}\)gt²
Where y₁ = Total displacement of the body from ground = 0
∴ 0 = y₀ + V₀t+ \(\frac{1}{2}\)gt² = 25 + 20t – \(\frac{1}{2}\). 10 . t²
[∵ g = – 10 m/s² while going up]
∴ 0 = – 5t² + 20t + 25 (or) t² – 4t – 5 = 0
i.e., (t – 5) (t + 1) = 0 ⇒ t = 5 (or) t = – 1
But time is not – ve.
∴ Time spent in air t = 5 sec

Question 14.
A parachutist flying in an aeroplane jumps when it is at a height of 3 km above the ground. He opens his parachute when he is about 1 km above ground. Describe his motion.
Answer:
Initially the path is a parabola as seen by an observer on the ground. It is a vertical straight line as seen by the pilot. He opens his parachute, it is moving vertically downwards with decreasing velocity and finally it reaches the ground.