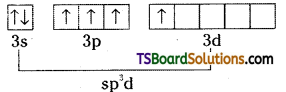
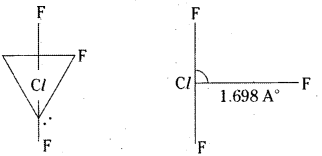
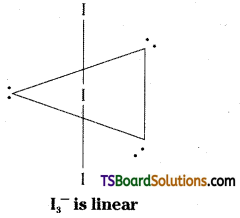
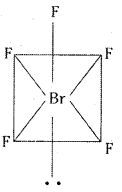
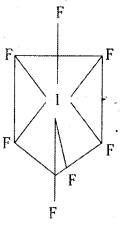
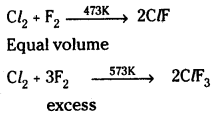
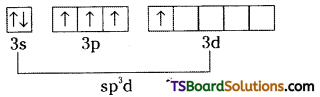
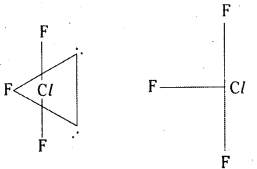
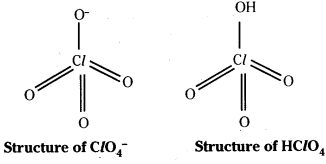
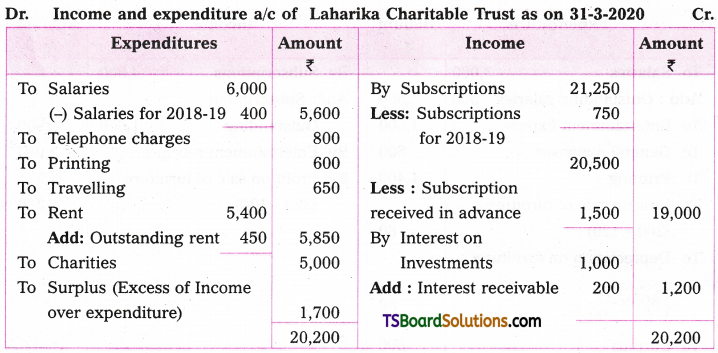
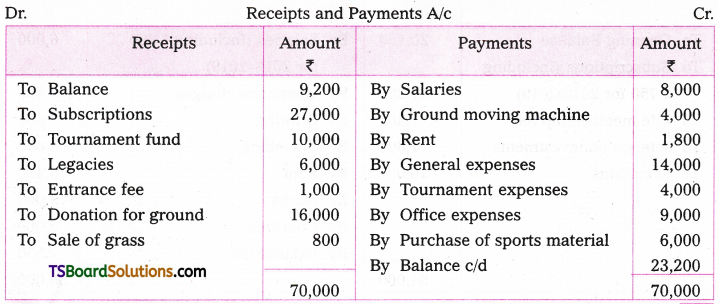
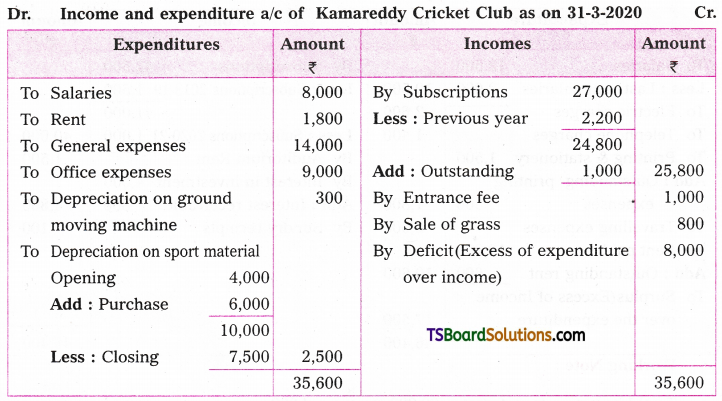
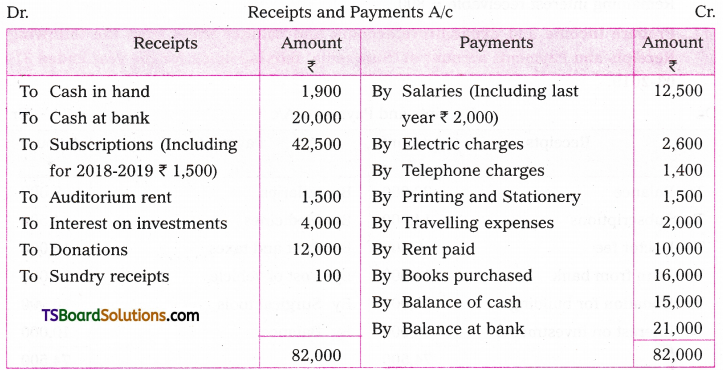
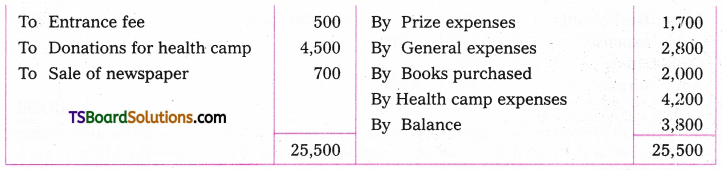
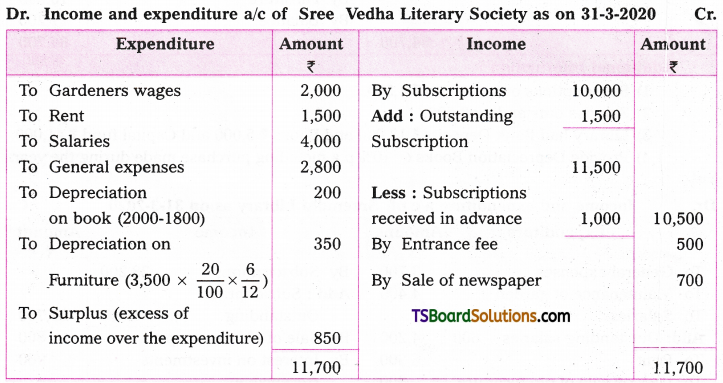
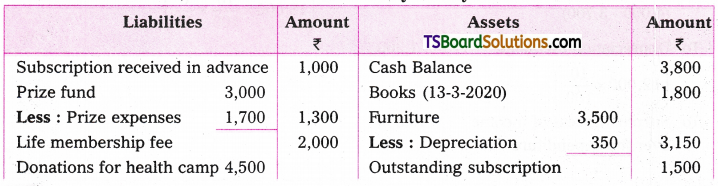
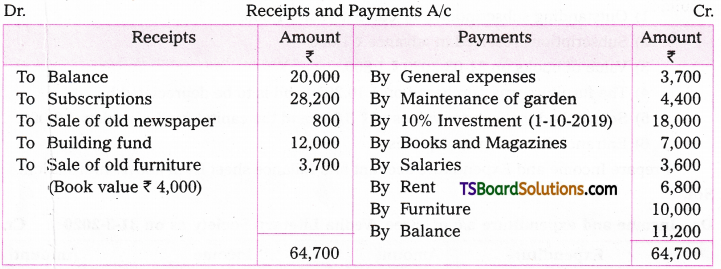
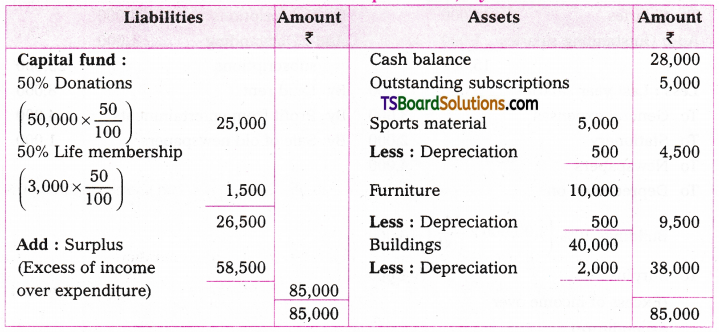
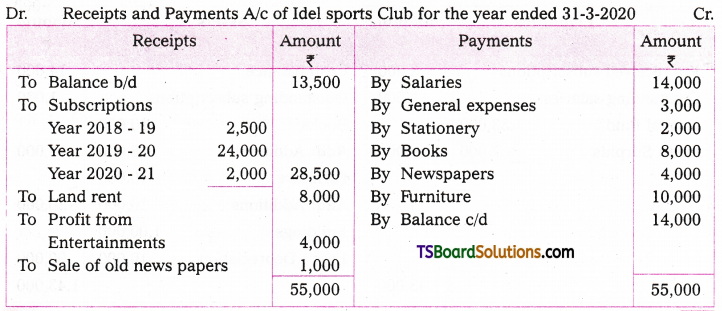
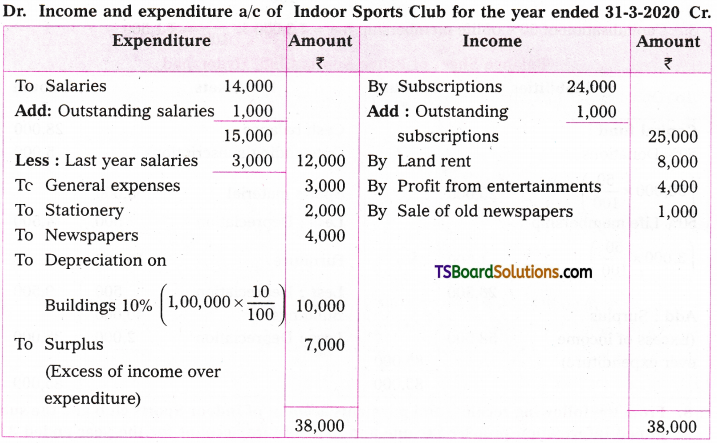
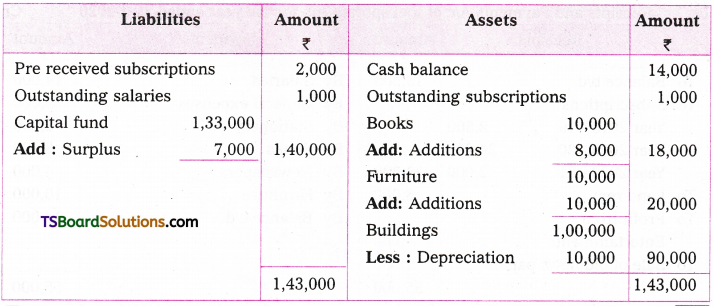
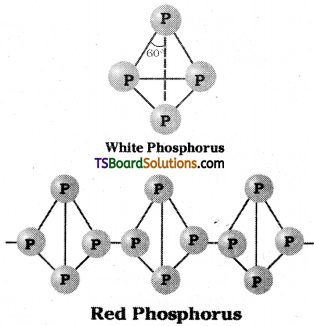
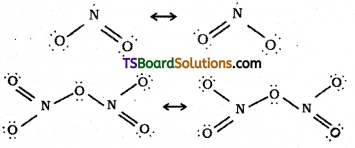
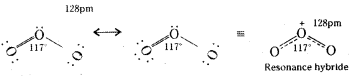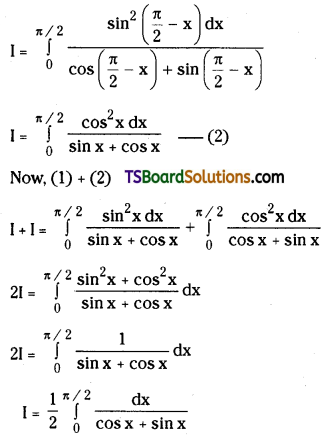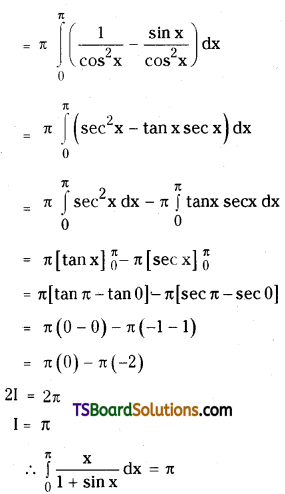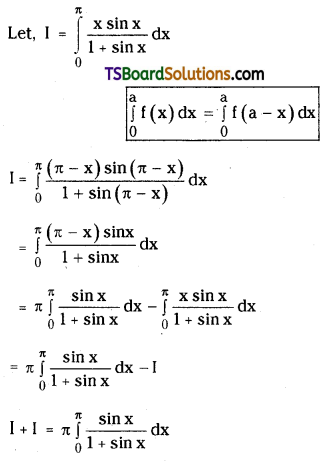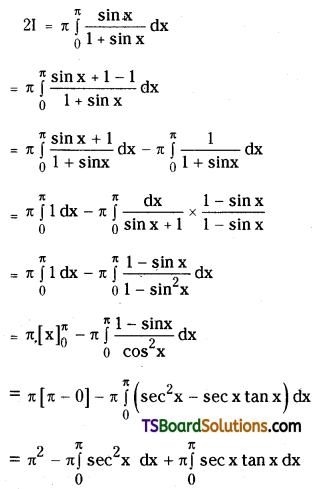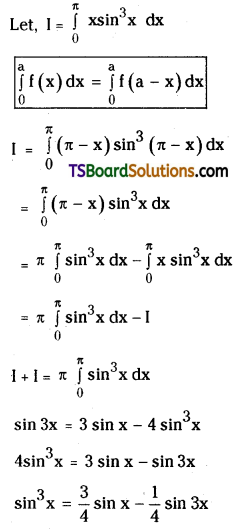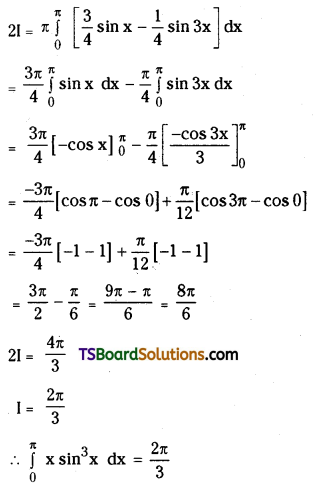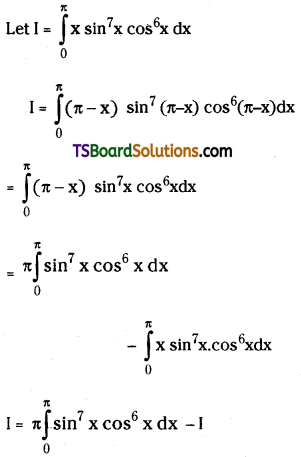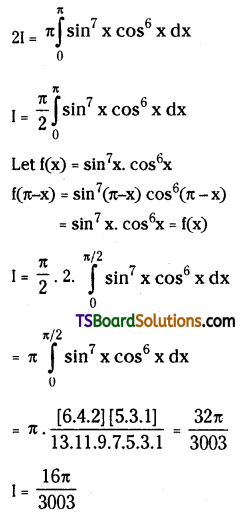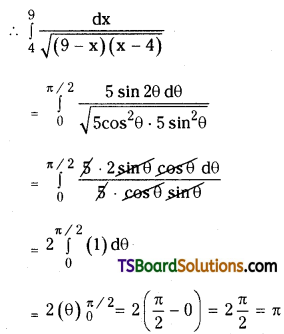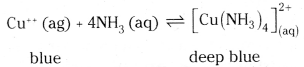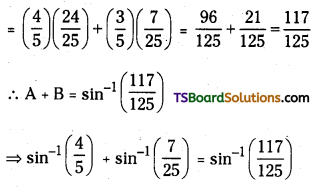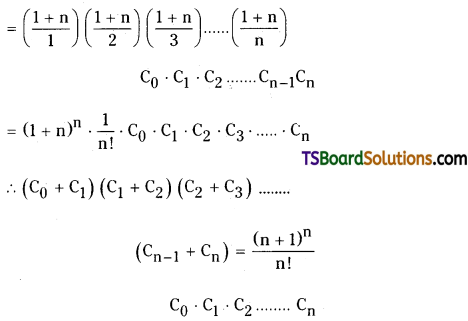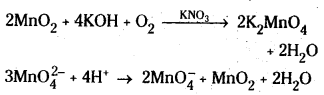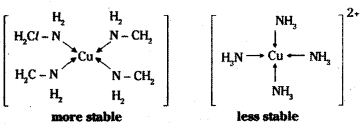Telangana TSBIE TS Inter 2nd Year Chemistry Study Material 7th Lesson d and f Block Elements & Coordination Compounds Textbook Questions and Answers.
TS Inter 2nd Year Chemistry Study Material 7th Lesson d and f Block Elements & Coordination Compounds
Very Short Answer Questions (2 Marks)
Question 1.
What are transition elements ? Give examples.
Answer:
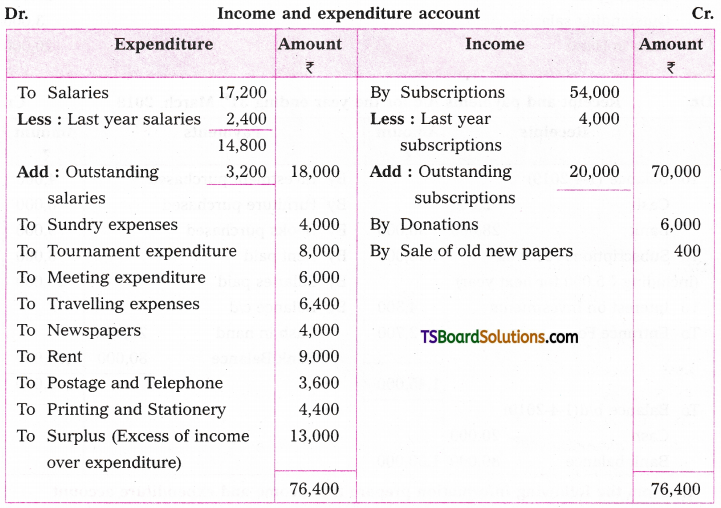
Transition elements are defined as the elements having partially filled d-orbitals in the atoms in the elemental form or in the chemically significant stable oxidation states. Examples : Fe, Mn, Cr.
Question 2.
Which elements of 3d, 4d, and 5d series are not regarded as transition elements and why ?
Answer:
The elements Zn, Cd, Hg are not regarded as transition elements. They belong to 3d, 4d and 5d series respectively. Their general electronic configuration is (n – 1) d10 ns2. The d-orbitals in these elements are completely filled. Therefore, they are not regarded as transition elements.

Question 3.
Why are d-block elements called transition elements ?
Answer:
The d-block elements are placed in between s and p-blocks in the periodic table. There is a transition in properties between the electropositive s-block elements and the electronegative p-block elements. Hence, d- block elements are named transition elements.
Question 4.
Write the general electronic configuration of transition elements.
Answer:
(n – 1) d10 ns1-2
The (n – 1) stands for the penultimate shell. The (n -1) d orbitals may have one to ten electrons and the outermost ns orbital may have one or two electrons.
Question 5.
In what way is the electronic configuration of transition elements different from non-transition elements ?
Answer:
The transition elements have incompletely filled (n – 1) d orbitals.
In transition elements, the valence shell and penultimate shell are incompletely filled. Their general electronic configuration is (n- 1) d1 – 10 ns1 – 2.
The non-transition elements i.e., the representative elements have the incompletely filled valence shell. The inner transition elements have the outer three energy levels incomplete.
Question 6.
Write the electronic configuration of chromium (Cr) and copper (Cu).
Answer:
Cr (24) – 1s2 2s2 2p6 3s2 3p6 3d 4s1 or [Ar] 4s1 3d5
Cu (29) – 1s2 2s2 2p6 3s2 3p6 3d10 4s1 or [Ar] 4s1 3d10

Question 7.
Why do transition elements exhibits characteristic properties ?
Answer:
The transition elements are characterised by specific and special properties which can be explained on the basis of their chara-cteristic electronic configuration. The partly filled (n -1) d orbital is the cause of special properties like variable oxidation states, magnetic properties etc.
Question 8.
Scandium is a transition element. But zinc is not. Why ? [IPE 14]
Answer:
The atom of Sc has one unpaired d-electron. So it is a transition element. The electronic configuration of Zn is (Z = 30) 1s2 2s2 2p6 3s2 3p6 3d10 4s2.
The common oxidation state of Zn is +2.
The electronic configuration of Zn++ is 1s2 2s2 2p6 3s2 3p6 3d10.
As neither Zn nor Zn++ have partly filled 3d orbitals, Zinc is not considered as transition element.
Question 9.
Even though silver has d10 configuration, it is regarded as transition element Why ?
Answer:
Silver (Z = 47) can exhibit +2 oxidation state where in it will have incompletely filled d- orbitals (4d), hence it is a transition element.
Question 10.
Write the electronic configuration of Co2+ and Mn2+.
Answer:
Co2+ : 1s2 2s2 2p6 3s2 3p6 3d7 Or [Ar] 3d7
Mn2+ : 1s2 2s2 2p6 3s2 3p6 3d5 Or [Ar] 3d5

Question 11.
Why are Mn2+ compounds more stable than Fe2+ towards oxidation to their +3 state ?
Answer:
Mn2+ has stable configuration because 3d orbitals are half-filled. Hence it is stable.
Fe2+ has the configuration [Ar] 3d6. As it gains half-filled electronic configuration jt! by losing an electron it is susceptible to oxidation.
Question 12.
Which metal in the first series of transition metals exhibits + 1 oxidation state most frequently and why ?
Answer:
Copper
Reason : The second ionisation enthalpy , is unusually high. Removal of second electron disrupts the stable configuration of Cu+.
Question 13.
Why do transition elements exhibit more than one oxidation state (variable oxidation states)?
Answer:
Transition elements exhibit general Oxidation state of + II by loosing the electrons in the outer “s” orbital. They also Show other oxidation states because of the participation of (n – 1) d electrons in bonding.
Both ns and (n -1) d electrons are available for bonding because there is very little difference between the energies of ns & (n – 1) d orbitals.
Question 14.
Though Sc is a transition element, it does not exhibit variable oxidation state. Why ?
Answer:
As there is only one d-electron Sc does not show vairable oxidation states. Thus Sc (II) is unknown. Further d1 configuration is unstable.

Question 15.
Why is it difficult to obtain M3+ oxidation state in Ni, Cu and Zn ?
Answer:
As the third ionisation enthalpies are quite high, it is difficult to obtain M+3 state in Ni, Cu and Zn.
Question 16.
Why is Cr2+ reducing and Mn3+ oxidizing even though both have the same d4 electronic configuration ?
Answer:
Cr2+ is reducing as its configuration changes from d4 to d3, the latter having a half- filled dxy, dyz, dzx orbitals. On the other hand, the change from Mn2+ to Mn3+ results in the half-filled d5 configuration which has extra stability.
Question 17.
Although Cr, Mo and W belong to the same group (group 6) Cr (VI) is a strong oxidizing agent while Mo (VI) and W (VI) are not. Why ?
Answer:
In Group 6, Mo(VI) and W(VI) are found to be more stable than Cr(VI). Thus Cr (VI) in the form of dichromate acidic medium is a strong oxidising agent, whereas MnO3 and WO3 are not.
Question 18.
What do you infer from the fact that M3+ / M2+ standard electrode potential of Mn is comparatively higher and that of Fe is comparitively lower ?
Answer:
The higher value for Mn shows that Mn2+ (d5) is particularly stable whereas comparatively low value for Fe shows the extra stability of Fe3+ (d5 configuration).

Question 19.
Transition elements have high melting points. Why ?
Answer:
The melting points of the metals are very high. The high values are attributed to the strong interactions present in the metals.
The involvement of greater number of electrons from (n – 1) d in addition to the ns electrons in the interatomic metallic bonding is the reason for high m.p.’s.
Question 20.
Among the first transition series (3d series) Chromium has highest melting point. Why ?
Answer:
In chromium, there is involvement of maximum number of (n -1) d electrons (d5) and one ns electron is interatomic metallic bonding. So the metallic bonding is strong. Hence the m.p is high.
Question 21.
Compared to s-block elements, the transition elements exhibit higher enthalpy of atomization. Why ?
Answer:
Because of large number of unpaired electrons in their atoms, they have stronger interatomic interaction. Hence stronger bonding between atoms resulting in higher enthalpies of atomisation.
Question 22.
Among the first transition series (3d series) zinc has lowest enthalpy of atomization. Why?
Answer:
As there are only two electrons available for metallic bond formation, the interatomic attractions are less. Hence the zinc has lowest enthalpy of atomisation.

Question 23.
How do you expect the density of transition element to vary in a given series and why ?
Answer:
Increase in density is expected from in the transition elements from Sc Z = 21 to copper Z = 29.
Reason :
- Metallic bond strength increases due to increase in (n – 1) d electrons.
- Metallic radius decreases.
- Increase in atomic mass.
As expected, the density increases from scandium to copper in the 3d series.
Question 24.
How do the atomic and ionic sizes vary among transition metals in a given series ?
Answer:
The atomic and ionic radii decrease slightly with the increase in a series of transition elements. This is because of poor screening by d-electrons.
New electron enters into a d orbital each time, nuclear charge increases by unity as we move from one element to the other in the transition series. As the shielding effect of a d-electron is not effective, the net attraction between the nuclear charge and the outermost electron increases and the ionic radius decreases.
Question 25.
Why do Mn, Ni and Zn exhibit more negative E⊖ values than expected ?
Answer:
The stability of the half-filled d-subshell in Mn2+ and completely filled d10 configuration in Zn++ are related to their more negative E⊖ values. The value is more for Ni because of its highest negative \(\Delta \mathrm{H}_{\text {hyd }}^{\ominus}\) .

Question 26.
Among the first transition series (3d series) only copper has positive E⊖ M2+/M value. Why?
Answer:
Positive E⊖ value means less ability to act as reducing agent. Thus Cu cannot liberate H2 from acids.
Reason:
- Cu has high value for enthalpy of atomisation ∆aH⊖.
- Low value for enthalpy of hydration ∆hydH⊖
- The high energy to transform Cu(s) to Cu++ (aq) is not balanced by its hydration enthalpy.
Question 27.
Cu11 forms halides like CuF2, CuCl2 and CuBr2 but not Cul2. Why ?
Answer:
Cu2+ oxidises I– to I2. Hence CuI2 is not known.
2CU2+ + 4I2+ → Cu2I2 (s) + I2
Question 28.
The highest Mil fluoride is MnF4 where as the highest oxide is Mn2O7. Why ?
Answer:
Oxygen can form multiple bonds with metals. This explains the ability of oxygen to stabilise high oxidation states. In the covalent oxide Mn2O7 each Mn is tetra-hedrally surrounded by O’s including a Mn – O – Mn bridge. The ability to stabilise higher oxidation state is less for fluorine when compared to oxygen. Hence it can form MnF4 Only.
Question 29.
In its fluoride or Oxide, in which a transition metal exhibits highest oxidation state and why ?
Answer:
Mn exhibits its highest oxidation state in Mn2O7, because of the ability of oxygen to form multiple bonds with metals. In the covalent oxide, Mn2O7 each Mn is tetrahedrally surrounded by oxygen including a Mn – O – Mn bridge.

Question 30.
Why Zn2+ is diamagnetic whereas Mn2+ is paramagnetic ? [TS 15]
Answer:
Electronic configuration of Zn++ is [Ar] 3d10.
As there are no unpaired electrons, Zn++ is diamagnetic.
Electronic configuration of Mn++ is [Ar] 3d5. As there are unpaired electrons, Mn++ is paramagnetic.
Question 31.
Write ‘spin only’ formula to calculate the magnetic moment of transition metal ions.
Answer:
Magnetic moment μ = \(\sqrt{n(n+2)}\)
n = number of unpaired electrons
m = magnetic moment in Bohr magnetons
Question 32.
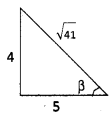
Calculate the ‘spin only’ magnetic moment of Fe2+ (aq) ion. [AP 17]
Answer:
Fe (26) Electronic configuration [Ar] 3d6.4s2 Fe2+. Electronic configuration is [Ar] 3d6
No. of unpaired electrons is 4.
Spin only formula μ = \(\sqrt{n(n+2)}\)
= \(\sqrt{4 \times 6}=\sqrt{24}\) = 4.9 BM
Question 33.
What is meant by ‘disproportionation’ ? Give an example of disproportionation reaction in aqueous solution.
Answer:
If an element undergoes both oxidation and reduction, it is called disproportionation reaction.
Ex : Many copper (I) compounds are un-stable in aqueous solution and undergo disproportionation.
2 Cu+ → Cu++ + Cu

Question 34.
Aqueous Cu2+ ions are blue in colour, where as Aqueous Zn2+ ions are colourless. [TS 16]
Answer:
Cu++ contains unpaired electron. It is coloured due to d-d transition. Zn++ does not contain unpaired electron. Hence it is colourless.
Question 35.
What are complex compounds ? Give examples.
Answer:
Complex compounds are those in which the metal ions bind a number of anions or neutral molecules.
Ex: [Fe (CN)6]3-, [Fe(CN)6]4-, [Cu (NH3)4]2+
Question 36.
Why do the transition metals form a large number of complex compounds ?
Answer:
Transition metals form a large number of complex compounds due to
- smaller sizes of the metal ions,
- high ionic charges,
- availability of d-orbitals for bond formation.
Question 37.
How do transition metals exhibit catalytic activity ?
Answer:
Transition metals possess good catalytic properties. This property is due to the the free valencies of the metals and also due to variable oxidation states.

Question 38.
Give two reactions in which transition metals or their compounds acts as catalysts.
Answer:
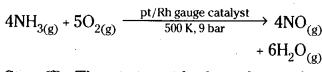
- Vanadium pentoxide is used as catalyst in the manufacture of sulphuric acid by Contact process.
- Pt is used as catalyst in Ostwald process.
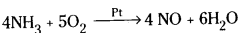
Question 39.
What is an alloy ? Give example.
Answer:
When metals are mixed and the resulting liquid is allowed to solidify, the product formed is called an alloy. It may also contain non-metals.
Ex: German silver 25 – 50% Cu,
10 – 30% Ni
25 – 35% Zn
Nichrome 60% Ni, 25% Fe, 15% Cr.
Bell metal 80% Cu, 20% Sn
Question 40.
Why do the transition metals readily form alloys ?
Answer:
As the crystal structures of the transition metals are similar, alloys are formed among them readily.
Question 41.
How does the ionic character and acidic nature vary among the oxides of first transition series?
Answer:
The oxides dissolve in acids and bases to form oxometallic salts. Potassium dichromate and potassium permanganate are common examples.

Question 42.
What is the efffect of increasing pH on a solution of potassium dichromate ?
Answer:
It is converted into chromate by alkali. Chromate is yellow in colour.
K2Cr2O7 + 2KOH → 2K2CrO4 + H2O
Question 43.
Name the oxometal anions of the first series of transition metals in which the metal exhibits the oxidation state equal to its group number.
Answer:
6th group – K2Cr2O7
Cr2O7– – – is dichromate anion in which the oxidation number of Cr is + VI which is equal to its group number.
In permanganate anion \(\mathrm{MnO}_4^{-}\), Mn shows + VII state which is equal to its group number.
Question 44.
Permanganate titrations are carried out in the presence of sulphuric acid but not in presence of hydrochloric acid. Why ?
Answer:
The oxidation reactions of potassium per- mangante are generally carried out in presence of sulphuric acid. Hydrochloric acid should not be Used as the medium since it liberates chlorine by reaction with permanganate.
2KMnO4 + 16HCl → 2MnCl2 + 2KCl + 5Cl2 ↑ + 8H2O

Question 45.
What is lanthanoid contraction ? [T.S. Mar. 19]
Answer:
Gradual decrease in atomic and ionic sizes from La to Lu is called Lanthanoid con-traction.
Reason:
- Imperfect shielding of one electron by another in the same set of orbitals (4f)
- The shielding of one 4f electron by another is less than that of one d electron by another.
- Nuclear charge increases along the series from La to Lu.
- Due to poor shielding of 4f electrons, there is fairly regular decrease in the size of the entire 4f orbitals.
Question 46.
What are the different oxidation states exhibited by the lanthanoids ?
Answer:
Lanthanides react easily with water to give solutions giving + 3 ions. The principal oxidation state is + 3 although +4 and +2 oxidation states are also exhibited.
Question 47.
What is misch metal ? Give its composition and uses. [AP 16]
Answer:
Misch metal is an alloy of Lanthanoid metal.
Composition : 95% Lanthanoid metal and 5% iron and traces of S, C, Ca and Al.
It is used in making tracer bullets.
Question 48.
What is actinoid contraction ?
Answer:
The elements from Ac to Lr (Z = 89 to 103) are called actinides. In these elements the 5f orbital is gradually filled.
There is steady decrease in the size of M3+ and M4+ cations in actinide elements. The shielding of one electron in 5f orbital by another electron present in the same orbital is very poor. Due to this poor shielding effect, the increase in the nuclear charge by one unit brings the valence shell nearer to the nucleus and the size of the cation decreases.

Question 49.
What are coordination compounds ? Give two examples.
Answer:
Coordination compounds are those in which metal ions bind a number of anions or neutral molecules giving complex species with characteristic properties.
The molecules or ions containing one pair of electrons donate the electron pair to the central metal ion to form coordinate covalent bond.
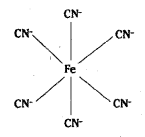
Ex: [Fe(CN)6]4-
Hexacyanoferrate (II)
Question 50.
What is a coordination polyhedron ?
Answer:
The spacial arrangement of the ligand atoms which are directly attached to the central atom/ion defines a coordination polyhedron about the central atom. Most common coordination polyhedra are octahedral, square planar and tetrahedral.
For example, [Co(NH3)6]2+ is octahedral, Ni(CO)4 is tetrahedral.
Question 51.
What is a double salt ? Give example.
Answer:
Those compounds which lose their identity in solution and break down into simple ions are called double salts. For example, an aqueous solution of potash alum K2SO4. Al2 Al2(SO4)3 . 24H2O gives the test for K+, Al3+ and \(\mathrm{SO}_4^{2-}\) ions in its solution form.

Question 52.
What is the difference between a double salt and a complex compound ?
Answer:
| Double Salts | Complex compounds |
| 1) Compounds which lose their identity in solution and break down into simple ions are called double salts. | 1) Compounds which retain their identity even when dissolved in water are called complex compounds. |
2) Metal ions exhibit their normal valency.
Ex : Carnalite KCl. MgCl2 6H2O2 | 2) Metal ion is surrounded by a number of oppositely charged ions or neutral molecules which are more in number than its normal valency.
Ex : Potassium Ferro Cyanide ku[Fe(CN)6] |
Question 53.
What is a ligand ? [Mar. 2018, TS]
Answer:
A ligand is an ion or a molecule containing lone pairs of electrons which can be donated to a transition metal ion to form metal- ligand coordinate covalent bond.
Ex: NH3, CN–
Question 54.
Give one example each for ionic and neutral ligands.
Answer:
Ionic Ligands: Cyano CN–; amino NH2–
Neutral Ligands : Carbonyl CO ; Ammine NH3

Question 55.
How many moles of AgCl is precipitated when 1 mole of CoCl3 is treated with AgNO3 solution ?
Answer:
Three moles of AgCl is precipitated when 1 mole of COCl3 is treated with AgNO3 solution.
Question 56.
What is a chelate ligand ? Give example.
Answer:
A ligand which can form ring type complex is called chelate ligand.
Ethylenediamine H2N – CH2 – CH2 – NH2 is a chelate ligand. It can form ring type complex.
Question 57.
What is an ambidentate ligand ? Give example.
Answer:
Ligands which have two or more different donor sites but only one of these is attached to a single metal atom at a given time, are called ambidentate ligand.
Ex : NCS– Thiocyanato M ← SCN isothio- cyanato M ← NSC
Question 58.
CuSO4 . 5H2O is blue in colour where as anhydrous CuSO4 is colourless. Why ?
Answer:
A) Colour of a complex is due to splitting of d-orbitals and d-d transition of the electron.
In the absence of ligand, crystal field splitting does not occur and hence the substance is colourless. Due to the absence of ligand, the water molecules, anhydrous CuSO4 is colourless. CuSO4 . 5H2O is blue in colour due to the water molecules and the splitting of d-orbitals.

Question 59.
FeSO4 solution mixed with (NH4)2SO4 solution in 1:1 molar ratio gives the test for Fe2+ ion but CuSO4 mixed with aqueous ammonia in 1:4 molar ratio does not give the test of Cu2+ ion. Why?
Answer:
FeSO4 with (NH4)2SO4 in 1 : 1 molar ratio forms a double salt FeSO4. (NH4)2 SO4 . 6H2O which gives a test for all its constituent ions. On the other hand, CuSO4 with aq. ammonia in 1 :4 molar ratio forms a coordination compound [Cu (NH3)4] SO4. Hence it does not give test for Cu++ ion.
Question 60.
How many geometrical isomers are poss-ible in the following coordination entities ?
i) [Cr(C2O4)3]3-
ii) [Co(NH3)3Cl3]
Answer:
i) No geometric isomers are possible.
ii)
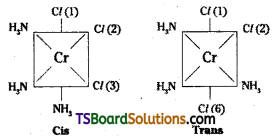
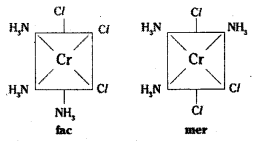
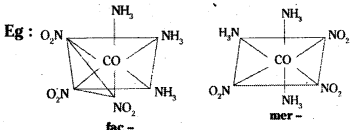
Another geometrical isomer occurs in [Ma3b3] type like [Co (NH3)3 Cl3]. If three donor atoms of the same ligands occupy adjacent positions, at the corners of octa-hedral face we have the facial isomer (fac). When the positions occupied are around the meridian of the octahedron, we get the meridonial (mer) isomer.
Question 61.
What is the coordination entity formed when excess of aqueous KCN is added to an aqueous solution copper sulphate ? Why?
Answer:
When aq KCN is added to the aq. solution of CuSO4, Octahedral complex of hexa cyan- idocuprate (10 is formed ,
CuSO4 + 6KCN → K4[CU(CN)6] + K2SO4

Question 62.
[Cr(NH3)6]3+ is paramagnetic while [Ni(CN)4]2- is diamagnetic. Why ?
Answer:
In [Cr(NH3)6]3+, NH3 is a weak field ligand and Cr has an electronic configuration of [Ar] 3d3 with three unpaired electrons. Hence [Cr(NH3)6]3 is paramagnetic. In [Ni(CN)4]2-, CN– is a strong field ligand therefore Ni2+ ion has all the d-electrons paired. Hence, [Ni(CN)4]2- is diamagnetic.
Question 63.
A solution of [Ni(H2O)6]2+ is green but a solution of [Ni(CN)2]2- is colourless. Why ?
Answer:
In [Ni(H2O)6]2+, Ni2+ ion has two unpaired electron and it shows colour.
In [Ni(CN)4]2-, there is no unpaired electron. Hence it is colourless.
A solution of [Ni (H2O)6]2+ is green but a solution of [Ni (CN)4]2- colourless.
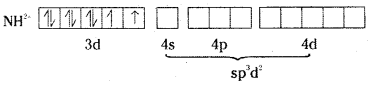
[Ni(H2O)6]2+ is an outer orbital complex.
As it contains two unpaired electrons, it is paramagnetic and coloured.
In the formation of [Ni(CN)4]2-, electron pairing takes place in Ni2+.
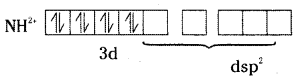
Ni2+ undergoes dsp2 hybridisation and it is square planar. As it does not contain unpaired electron, it is colourless.
Question 64.
[Fe(CN)4]2- and [Fe(H2O)6]2+ are of different colours in dilute solutions. Why ?
Answer:
- Different ligands produce different crystal field splittings.
- Different geometric fields also produce different crystal field splittings.
As d – d transitions require different energies, the colours exhibited by [Fe(CN)4]2- and [Fe(H2O)6]2+ are different.

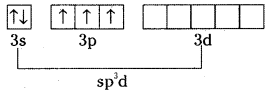
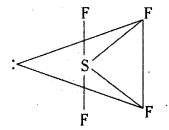
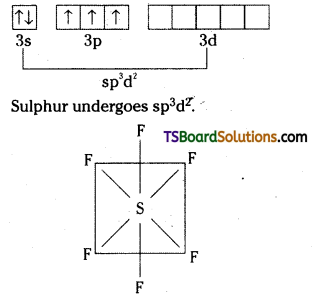
Question 65.
What is the oxdiation state of cobalt in [AP 16]
i) K3[CO(CO4)3] and
ii) [Co(NH3)6]3+
iii) K[Co(CO)4] ?
Answer:
i) Ox. number of of Co in K3 [Co(C2O4)3] is + 3.
ii) Ox. no. of Co in [Co (NH3)6]3+ is + 3.
iii) Ox. on of cobalt in K[Co(CO)4] is -1.
Short Answer Questions (4 Marks)
Question 66.
Compared to 3d series the corresponding transition metals of 4d and 5d transition series show high enthalpy of atomization. Explain.
Answer:
The melting points and boiling points of the transition elements are generally very high.
In the second and third row elements M – M bonds are much more common. The Metal – Metal (M – M) bonding occurs not only in the metals themselves but also in some compounds. M – M bonding is quite rare in the first row transition elements.
Hence because of increasing in atomic weight and also strong metallic bonding, the enthalpies of 4d and 5d series are higher than those of 3d series.
Question 67.
Compared to the changes in atomic and ionic sizes of elements of 3d and 4d series, the change in radii of elements of 4d and 5d series is virtually the same. Comment.
Answer:
When we compare the changes in ionic and atomic sizes of 3d series with those of 4d and 5d series, there is an increase from the 3d to 4d series of elements. But the radii of the third (5d) series are virtually the same as those of the corresponding members of 4d series (second series).
This is because of the filling of 4f before the 5d series of elements begin. The filling of 4f before 5d orbital results in a regular decrease in atomic radii called lanthanoid contraction. Because of lanthanide contraction, the expected increase in atomic size with increasing atomid number.

Question 68.
Account for the zero oxidation state of Ni and Fe in [Ni (CO)4] and [Fe(CO)5] respectively.
Answer:
Low oxidation are found when a complex compound has ligands capable of π-accep- tor character in addition to σ bonding. For example, Ni(CO)4 and Fe(CO)5, the oxidation of nickel and iron is zero. The metal- carbon-bond in metal carboyls possesses both σ and π character.
Question 69.
Why do the transition metal ions exhibit characteristic colours in aqueous solution. Explain giving examples.
Answer:
When an electron from a lower energy d- orbital of a metal ion in a complex is excited to a higher energy d-orbital of the same n value, the energy of excitation corresponds to the frequency of light absorbed. This frequency generally lies in the visible region. The colour absorbed corresponds to the complementary colour of the light absorbed. The frequency of light absorbed is determined by the nature of the ligand. In aqueous solutions, where water molecules are ligands
Ti3+ …………… purple
V4+ …………… blue
Cr3+ ……………. violet
Fe3+ ……………. yellow
Fe2+ ……………. green
To exhibit colour the ion should have at least unpaired (n -1) d electron. The colour is due to d – d transitions.
Question 70.
Explain the catalytic action of Iron (III) in the reaction between I– and S2O82- ions.
Answer:
Transition metals and their compounds are known for their catalytic activity. This activity is ascribed to their ability to adopt multiple oxidation states to form complexes. For example, iron (III) catalyses the reaction between iodide and persulphate ions.
2I– + S2O82- → I2 + 2SO42-
An explanation of this catalytic action can be given as :
2Fe3+ + 2I– → 2Fe2+ + I2
2Fe2+ + S2O82- → 2Fe2+ + 2SO42-

Question 71.
What are interstitial compounds ? How are they formed ? Give two examples. [AP 15]
Answer:
Interstitial compounds are those which are formed when small atoms like H, C, or N are trapped inside the crystal lattices of metals. They are usually non-stoichiometric and are neither typically ionic nor covalent.
Example: TiC, Mn4N, VH0.56 and Ti H1.7 etc.
Question 72.
Write the characteristics of interstitial compounds.
Answer:
- Interstitial compounds are non-stoichiometric.
- They are neither typically ionic nor covalent.
- They have high melting points, higher than those of pure metals.
- They are very hard.
- They retain metallic conductivity.
- They are chemically inert.
Question 73.
Write the characteristics properties of transition elements. [AP ’15]
Answer:
The transition elements are characterised by specific and special properties which are explained on the basis of their characteristic electronic configurations. They are
- They exhibit variable oxidation states.
- Most of the transition elements and their ions show paramagnetic property. This is due to presence unpaired d-electron.
- They form coloured compounds.
- They have alloy forming ability.
- Complex forming ability.

Question 74.
Write down the electronic configuration of
(i) Cr3+
(ii) Cu+
(iii) Co2+
(iv) Mn2+
Answer:
i) Electronic configuration of Cr3+ = [Ar] 3d3
ii) Electronic configuration of Cu+ = [Ar] 3d10
iii) Electronic configuration of Co2+ = [Ar] 3d7 4s3
iv) Electronic configuration of Mn2+ =[Ar] 3d5
Question 75.
What may be the stable oxidation state of the transition element with the following d electron configurations in the ground state of their atoms: 3d3 3d5 3d8 and 3d4 ?
Answer:
Electronic configuration ………… Stable state
3d3 4s2 ………….. +2, and +5
3d5 4s2 ………….. +2, +7
3d8 4s2 …………. +2, +5
3d4 4s2 ………….. +3, +6
Question 76.
What is lanthanoid contraction? What are the consequences of lanthanoid contraction ?
Answer:
There is gradual decrease in the atomic and ionic sizes of the lanthanide elements. The filling of 4f before 5d orbital results in a regular decrease in atomic radii called lanthanoid contraction. This is due to the imperfect shielding of one electron by another in the same set of orbitals. However, the shielding of one 4f electron by another is less than that of one d electron by another, and as the nuclear charge increases along the series, there is fairly regular decrease in the size of the entire 4fn orbitals.
Consequences:
- The net result of the lanthanoid contraction is that the second and the third series exhibit similar radii (e.g.: Zr 160 pm Hf 159 pm) and have very similar physical and chemical properties much more than the expected on the basis of usual family relationship.
- The decrease in metallic radius coupled with increase in atomic mass results in a general increase in the density of these elements.

Question 77.
How is the variability in oxidation states of transition metals different from that of the non transition metals ? Illustrate with examples.
Answer:
The variability of oxdiation states, a characteristic property of transition elements arises due to incomplete filling of d orbitals in such a way that their oxdiation states differ from each other by unity.
Ex: VII, VIII, VIV, VV.
But in non-transition elements the oxidation states normally differ by a unit of two.
Although in the p-block elements the lower oxidation states are favoured by the heavier members (due to inert pair effect.)
The opposite is true in the groups of d- block. For example, in group 6, Mo(VI) and W(VI) are found to be more stable than Cr (VJ). Thus Cr (VI) in the form of dichromate in acidic medium is a strong oxidising agent, whereas MoO3 and WO3 are not.
Question 78.
Describe the preparation of potassium dichromate from iron chromite ore.
Answer:
Dichromates are generally prepared from chromite. Chromites are obtained by the fusion of chromite ore. (FeCr2O4) with potassium carbonate in free access of air. The yellow solution of chromate is filtered and acidifed with sulphuric acid to give a solution from which orange coloured potassium dicromate can be crystallised.
4FeCr2O4 + 8K2CO3 + 7O2→ 8K2CrO4 + 2Fe2O3 + 8CO2
2K2CrO4 + 2H+ → K2Cr2O7 + 2K+ + H2O
Question 79.
Describe the oxidisingaction of potassium dichromate and write the ionic equations for its
With (i) iodide
(ii) iron (II) solution
(iii) H2S and
(iv) Sn (II)
Answer:
In acidic solution the oxidising action of dicromate can be represented as follows.
Cr2O72- + 14H+ + 6e– → 2Cr3+ + 7H2O
It oxidises iodide to iodine.
Cr2O72- + 14H+ + 6I– → 2Cr3+ + 3I2 + 7H2O
It oxidises H2S to sulphur.
Cr2O72- + 14H+ + 3H2S → 2Cr3+ + 6H+ + 3S + 7H2O
It oxidises Sn2+ to Sn4+
Cr2O72- + 14H+ + 3Sn2+ → 3Sn4+ + 2Cr3++ 7H2O

Question 80.
Describe the preparation of potassium permanganate.
Answer:
Potassium permanganate is prepared by the fusion of MnO2 with an alkali metal hydroxide and an oxidising agent like KNO3. This produces dark green K2MnO4 which disproportionates in a neutral or acidic solution to give permanganate.
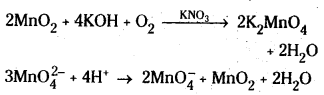
Question 81.
How does the acidified permanganate solution react with (i) iron (ii) ions (iii) SO2 and (iv) oxalic acid.
Write die ionic equations fur the reactions.
Answer:
KMnO4 oxidises FeSO4 to Fe2(SO4)3,
2KMnO4 + 8H2SO4 + 10 FeSO4 → K2SO4 + 2 MnSO4 + 5 Fe2(SO4)3 + 8H2O
(or) 5 Fe2+ + \(\mathrm{MnO}_4^{-}\) + 8H+ → Mn2+ + 4H2O + 5Fe3+
II) Sulphurous acid is oxidised to sulphate or sulphuric acid,
5 \(\mathrm{SO}_3^{2-}\) + 2 \(\mathrm{MnO}_4^{-}\) + 6H+ → 2Mn++ + 3H2O + 5SO42-
III) It oxidises oxalic acid to CO2.
2KMnO4 + 3H2 SO4 + 5H2C2O4 → K2SO4 + 2MnSO4 + 8H2O – 10 CO2
(or) 5\(\mathrm{C}_2 \mathrm{O}_4^{2-}\) + 2\(\mathrm{MnO}_4^{-}\) + 16H+ → 2Mn2+ + 8H2O + 10CO2
Question 82.
Predict which of the ions, Cu+, Sc3+, Mn2+, Fe2+ are coloured in aqueous solution ? Give reasons.
Answer:
Electronic configuration of Cu+ = [Ar ] 3d10 – colourless
Electronic configuration of Sc3+ = [Ar] colourless
Electronic configuration of Mn2+ = [Ar] 3d5 coloured
Electronic configuration of Fe2+ = [Ar] 3d5 coloured
Cu+ and Sc3+ are colourless because they do not have unpaired d-electrons.
Mn2+ and Fe2+ are coloured due to the presence of unpaired d-electron. Electronic transition takes from lower energy d-orbital to higher energy d-orbital with absorption of visible light. Complementary colour is observed.

Question 83.
Compare the stability of + 2 oxidation state of the elements of the first transition series.
Answer:
The standard values E⊖ for M2+/M indicate a decreasing tendency to form divalent cations across the series.
E⊖ values for Mn, Ni and Zn are more negative than expected from the general trend. This is due to the stability associated with half-filled d subshell (d5) in Mn2+ and completely filled d shell (d10) in Zinc.
For Nickel E⊖ value is related to the highest negative value of enthalpy of hydration.
Many copper ©compounds are unstable in aqueous solution and undergo disporportionation.
2Cu+ → Cu++ + Cu
The stability of Cu++ (aq) rather than Cu+ (aq) is due to the much more negative ∆Ehyd of Cu2+ than Cu+. It compensates for the second ionisation enthalpy of Cu.
Question 84.
Use Hund’s rule to derive the electronic configuration of Ce3+ ion, and calculate its magnetic moment on the basis of ‘spin- only’ formula.
Answer:
Electronic configuration of Ce is [Xe] 4f1 5d1 6s2.
Electronic configuration of Ce3+ is [Xe] 4f1.
Magnetic moment = \(\sqrt{n(n+2)}=\sqrt{3}\) = 1.73 B.M.

Question 85.
Write down the number of 3d electrons in each of the following ions : Ti2+, V2+, Cr3+ and Mn2+. Indicate how would you expect the five 3d orbitals to be occupied for these hydrated ions (octahedral).
Answer:
| Element | Electronic configuration of the atom | Ion/Electronic configuration | No. of d-electrons |
| Ti | [Ar] 3d2 4s2 | Ti2‘, [Ar] 3d2 | 2 |
| V | [Ar] 3d3 4s2 | V2+, [Ar] 3d3 | 3 |
| Cr | [Ar] 3d5 4s1 | Cr3+, [Ar] 3d4 | 4 |
| Mn | [Ar]3dS4s2 | Mn2+, [Ar] 3d5 | 5 |
As H2O is a weak ligand, electron pairing does not take place.

Question 86.
Explain Werner’s theory of coordination compounds with suitable examples. [AP 17; TS 15; IPE 14] [Mar. 2018, AP & TS]
Answer:
Werner proposed two types of valencies to explain the formation and the structure of these complex compounds.
i) The Primary valence:
This corresponds to the oxidation state of the central transition metal ion in the complex compounds. This primary valence is satisfied by a negative ion only in the complex compound.
ii) Secondary valence:
This is equal to the number of chemical groups bound to central metal ion. The no. of secondary valencies is called co-ordination number of the metal.
iii) These secondary valencies are directed in space which determines the shape of the complex.
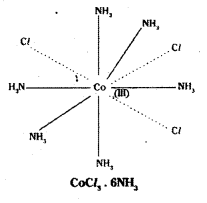
Ex: 1
Coordination no.: 6 Structure: octahedral The ligand NH3 satisfies only secondary valency.
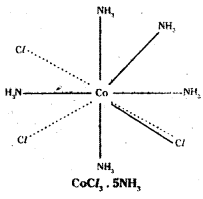
Ex: 2
Coordination no.: 6 Structure: octahedral One Cl– ion satisfies both primary and secondary valencies.
Ex:3
Co-ordination no.: 6 Structure: octahedral Two Cl– ions satisfy both primary and secondary valencies.
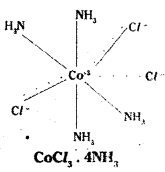
Ex: 4
Co-ordination no.: 6 Structure: octahedral Three Cl– ions satisfy both primary and secondary valencies.
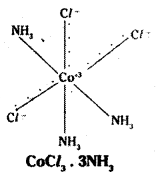
In Werner’s representation, dotted lines represent primary valency whereas thick lines represent secondary valency.
Some negative ligands, depending upon the complex, may satisfy both primary and secondary valencies. Such ligands do not ionise.
iv) Primary valencies are ionisable vale-ncies. Secondary valencies are non-ion- isable valencies.

Question 87.
Give the geometrical shapes of the following complex entities.
(i) [CO(NH3)6]3+
(ii) [Ni(CO)4]
(iii) [Pt Cl4]2- and
(iv) [Fe(CN)6]3-
Answer:
(i) [CO(NH3)6]3+ is octahedral with d2sp3 hybridisation.
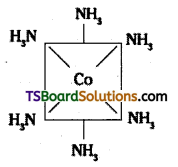
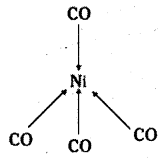
(ii) [Ni(CO)4] is tetrahedral with sp3 hybridisation.
(iii) [Pt Cl4]-2 is square planar with dsp2 hybridisation.
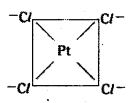
(iv) [Fe (CN)6]3- is octahedral with d2sp3 hybridisation.
Question 88.
Explain the terms
i) Ligand
ii) Coordination number
iii) Coordination entity
iv) Central metal atom / ion.
Answer:
(i) Ligands:
The ions or molecules bound to the central atom / ion in the coordination entity are called ligands. Ligands are capable of donating electron pairs.
These may be simple ions such as Cl–, small molecules such as H2O or NH3.
ii) The coordination number of a metal ion (CN–) in a complex can be defined as the number of ligand donor atoms to which the metal is directly bonded. For example, in the complex ions [Pt Cl6]2- and [Ni (NH3)4]2+, the coordination number of Pt and Ni are 6 and 4 respectively.
Coordination number of the central atom/ion is determined only by the number of sigma bonds formed by the * ligand with the central atom/ion.
iii) Coordination entity :
A coordination entity constitutes, a central metal atom or ion bonded to a fixed number of ions or molecules. For example, [CoCl3 (NH3)3] is a coordination entity in which the cobalt ion is surrounded by three ammonia molecules and three chloride ions.
iv) Central atom/ion :
In a coordination entity, the atom/ion to which a fixed number of ions/groups are bound in a definite geometrical arrangement around it, is called the central atom or ion. In [NiCl2(H2O)4] central ion is Ni2+. In [Fe(CN)6]2-, central metal ion is Fe2+.

Question 89.
Explain the terms
i) unidentate ligand
ii) bidentate ligand
iii) polydentate ligand and
iv) ambidentate ligand giving one example for each.
Answer:
i) Unidentate ligand :
When a ligand is bound to a metal ion through a single donor atom as with Cl–, H2O or NH3 the ligand is said to be unidentate.
ii) Bidentate ligand :
When a ligand is bound to a metal ion through two donor atoms as in ethylene diamine.
H2N CH2CH2NH2, the ligand is said to be bidentate.
iii) Polydentate ligand:
When several donor atoms are present in a single ligand [N(CH2CH2NH2)3] the ligand is said to be polydentate.
EDTA Ethylenediamine tetraacetate ion is an important hexadentate ligand.
iv) Ambidentate ligand:
Ligand which can ligate through two different atoms is called ambidentate ligand.
Examples are – NO2– and SCN– ions. NO2– ion can coordinate either through nitrogen or through oxygen to a central metal atom/ion.
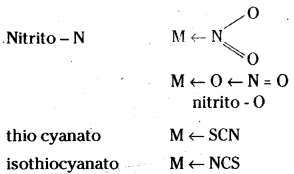
Question 90.
What is meant by chelate effect ? Give example.
Answer:
When a di- or polydentate ligand uses its two or more donor atoms to bind a single metal ion, it is said to be a chelate ligand. Such complexes are called chelate com-plexes. They are more stable than similar complexes containing unidentate ligands.
The complexes formed by chelating ligands are more stable than their mono- dentate analogs. The effect is called chelate effect. Ex: [Cu (en)4]2+ is more stable than [Cu (NH3)4]2+ ion.
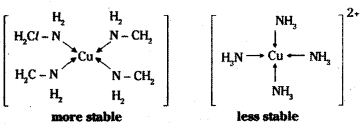

Question 91.
Give the oxidation numbers of the central metal atoms in the following complex entities.
(i) [Ni(CO)4]
(ii) [Co(NH3)6]3+
(iii) (Fe(CN)6]4- and
(iv) [Fe(C2O4)3]3-
Answer:
i) Oxidation number of Ni in Ni(CO)4 is zero.
ii) [Co(NH3)6]3+
Let the oxidation number of Co be x.
x + 0 = + 3
x = + 3
iii) [Fe(CN)6]4-
x – 6 = -4
x = 6 – 4 = +2
Ox. no. of Fe in [Fe(CN)0]4- is + 2
iv) [Fe(C2O4)3]3-
x – 6 = – 3 [C2O4 is bidenate ligand]
x = 6 – 3 = +3
Ox. no. of Fe in [Fe(C2O4)3]3- is + 3
Question 92.
Using IUPAC norms write the formulas for the following:
(i) Tetrahydroxozincate (II)
(ii) Hexaamminecobalt (III) sulphate
(iii) Potassium tetrachloropalladate (II) and
(iv) Potassium tri(oxalato) chromate (III)
Answer:
i) Tetrahydroxozincate (II) [Zn(OH)4]2-
ii) Hexammine cobalt (III) Sulphate [Co(NH3)6]2(SO4)3
iii) Potassium tetrachlorido palladate (II) K2[Pd Cl4]
iv) Potassium trioxalato chromate (III) K3 [Cr(C2O4)3]
Question 93.
Using IUPAC norms write the systematic names of the following:
(i) [C0(NH3)6]Cl3
(ii) [Pt(NH3)2Cl(NH2 CH3) Cl
(iii) [Ti(H2O)6]3+ and
(iv) [NiCl4]2-
Answer:
i) [C0(NH3)6]Cl3
Hexammine cobalt (III) chloride
ii) [Pt(NH3)2Cl(NH2 CH3) Cl diammine chloro methyl amino platinium (II) chloride.
iii) [Ti(H2O)6]3+
Hexahydro titanium (III) ion
iv) [NiCl4]2-
Tetra chloro Nickelate (II) ion

Question 94.
Explain geometrical isomerism in coordination compounds giving suitable examples. [AP ’15]
Answer:
Stereo isomers have the same chemical for-mula and chemical bonds but they have different special arrangment.
Geometrical isomerism :
This type of iso-merism arises in heteroleptic complexes due to different possible geometric arrangements of the ligands.
In square planar complexes of formula MX2L2, the two ligands X may be arranged adjacent to each other in a cis isomer or opposite to each other in a trans isomer.
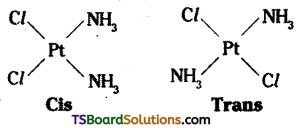
Octahedral complexes of formula [MX2L4] in which two ligands X may be oriented cis or trans to each other.
Tetrahedral complexes do not show geometrical isomerism because the rela-tive positions of the unidentate ligands attached to the central atom are the same respect to each other.
Question 95.
What are homoleptic and heteroleptic complexes ? Give one example for each.
Answer:
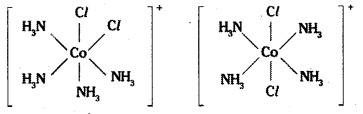
Complexes in which a metal is bound to only one kind of donor groups. Ex: [Co(NH3)6]3+, are known as homoleptic. Complexes in which a metal is bound to more than one. This type of isomerism arises in heteroleptic complexes due to different possible geometric arrangements of the ligands. Important examples of this behaviour are found with coordination numbers 4 and 6. In a square planar complex of formula [MX2L2] (X and L are unidentate), the two ligands X may be arranged adjacent to each other in a cis isomer, or opposite to each other in a trans isomer as depicted in the figure.
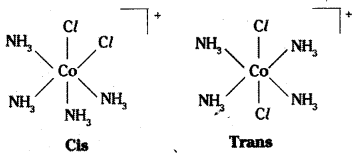
Geometrical isomers (cis and trans) of [Co (NH3)4 Cl2]+
Other square planar complex of the type MABXL (where A, B, X, L are unidentates) shows three isomers-two cis and one trans. Such isomerism is not possible for a tetrahedral geometry but similar behaviour is possible in octahedral complexes of formula [MX2L2] in which the two ligands X may be oriented cis or trans to each other.
Geometrical Isomers of (CoCl2 (en)2]
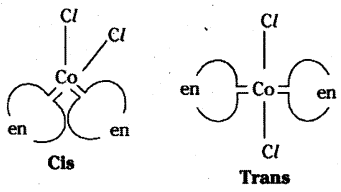
Kind of donor groups. Ex : [Co (NH3)4 Cl2]+ are known as heteroleptic.

Long Answer Questions (8 Marks)
Question 96.
Explain giving reasons :
(i) Transition metals and many of their compounds show paramagnetic behaviour.
(ii) The enthalpies of atomisation of the transition meals are high.
(iii) The transition metal generally form coloured compounds.
(iv) Transition metals and their many compounds act as good catalysts.
Answer:
i) Transition metals and many of their compounds show paramagnetic behaviour :
Diamagnetic substances are repelled by the applied magnetic field while the paramagnetic substances are attracted. Many of the transition metal ions are paramagnetic.
Paramagnetism arises from the presence of unpaired electrons. Each such electron having a magnetic moment associated with its spin angular momentum and orbital angular momentum.
The magnetic moment is determined by the number of unpaired electrons and is calculated by using the spin only formula size.
µ = \(\sqrt{n(n+2)}\)
Where n is the number of unpaired electrons and µ is the magnetic moment in units of Bohr magneton (BM). A single unpaired electron has a magnetic moment of 1.73 Bohr magnetons. (BM).
ii) The enthalpies of atomisation of the transition metals are high :
The transition metals (with the exception of Zn, Cd and Hg) are very much hard and have low volatility. Their melting and boiling points are high. They have high enthalpies of atomisation the maxima at about the middle of each transition series indicate that one unpaired electron for d- orbital is particularly favourable for strong interatomic interaction. In general greater the number of valence electrons, stronger is the resultant bonding.
Metals with very high enthalphy of atomisation are noble in their reaction. The metals of the second and third series have higher values than the corresponding elements of first series. This accounts for the occurrence of more metal-metal bonding in compounds of the heavy transition metals.
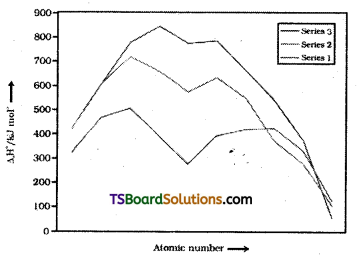
Trends in enthalpies of atomisation of transition elements
iii) The transition metals generally form coloured compounds:
The electron from a lower energy d-orbital of a metal ion in a complex is exited to a higher energy d-orbital of the same n value, the energy of excitation corresponds to the frequency of light absorbed. This frequency generally lies in the visible region. The colour observed corresponds to the com-plementary colour of the light absorbed. The frequency of the light absorbed is determined by the nature of the ligand. In aqueous solutions where water molecules are the ligands the ions exhibit different colours.
Ex: Cr3+ violet
Fe2+ green
Fe3+ yellow
iv) Transition metals and their many com-pounds act as good catalysts :
The transition metals and their compounds are known for their catalytic activity. This activity is due to their ability to adopt multiple oxidation states and to form complexes.
Eg: V2O5 in contact process.
Ni in Hydrogenation of oils.
Catalysts at a solid surface involve the formation of bonds b/w reactant molecules and atoms of the surface of the catalyst. This has the affect of increasing the con-centration of the reactants at the catalyst surface.
Eg : Iron (III) catalyses the reaction between Iodide and per sulphate ions.
2I– + S2O82- → I2 + 2SO42-
An explanation of the catalytic action can be given as
2Fe3+ + 2I → 2Fe2+ + I2
2Fe2+ + S2O82- → 2Fe3+ + 2SO42-

Question 97.
Describe the preparation of potassium permanganate. How does the acidified permanganate solution react with (I) Iron (“) Ions (II) SO2 and (iii) oxalic acid? Write
the Ionic equatIons.
Answer:
Potassium permanganate is prepared by the fusion of MnO2 with an alkali metal hydroxide and an oxidising agent like KNO3. This produces dark green K2MnO4 which disproportionates in a neutral or acidic solution to give permanganate.
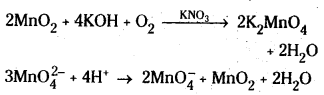
KMnO4 oxidises FeSO4 to Fe2(SO4)3,
2KMnO4 + 8H2SO4 + 10 FeSO4 → K2SO4 + 2 MnSO4 + 5 Fe2(SO4)3 + 8H2O
(or) 5 Fe2+ + \(\mathrm{MnO}_4^{-}\) + 8H+ → Mn2+ + 4H2O
+ 5Fe3+
II) Sulphurous acid is oxidised to sulphate or sulphuric acid,
5 \(\mathrm{SO}_3^{2-}\) + 2 \(\mathrm{MnO}_4^{-}\) + 6H+ → 2Mn++ + 3H2O + 5SO42-
III) It oxidises oxalic acid to CO2.
2KMnO4 + 3H2 SO4 + 5H2C2O4 → K2SO4 + 2MnSO4 + 8H2O – 10 CO2
(or) 5\(\mathrm{C}_2 \mathrm{O}_4^{2-}\) + 2\(\mathrm{MnO}_4^{-}\) + 16H+ → 2Mn2+ + 8H2O + 10CO2
Question 98.
Compare the chemistry of actinoids with that of the lanthanoids with special reference to:
(i) electronic configuration
(ii) oxidation state
(iii) atomic and ionic sizes and
(iv) chemical reactivity
Answer:
| Lanthanoids | Actinoids |
| a) Electronic configuration 4f1 – 14 5d0 – 1 6s2 | a) 5f1 – 146d0 – 1 7s2 * |
b) Oxidation states : They all show + 3 common state.
+ 2 is shown by Eu and Yb and
+ 4 by Ce and Tb. | b) They shows along with + 3, +4, + 5, +7 other oxidation states also. |
| c) Atomic size: Difference between the two successive lanthanoids sizes smaller than actinoid. | c) Difference between the two successive actinoid is larger them lanthanoids. |
| d) Decrease in size in series is called lanthanoid contraction. | d) Decrease in size in series is called actinoid contraction. |
| e) The ionisation enthalpies are high. | e) Their ionisation enthalpies are lower than lanthanoids. |
| f) Their magnetic character is explained. | f) Their magnetic characteristic cannot be explained. |
| g) They are non-radioactiVe (except promethium). | g) All are radioactive. |
| h) When reacted with water form hydroxide and H2 gas. | h) They form oxides and hydrides. |
| i) Reacts with non-metals at higher temperature. | i) Reacts with non-metal at moderate temperature. |

Question 99.
How would you account for the following:
(i) Of the d4 species, Cr2+ is strongly reducing while manganese (III) is strongly oxidising.
(ii) Cobalt (U) is stable in aqueous solution but in the presence of complexing reagents it is easily oxidised.
(iii) The d1 configuration is very unstable in ions.
Answer:
i) Cr2+ is reducing as its configuration changes from d4 to d3. In d3 the t2g level is half-filled. On the otherhand, the change from Mn2+ to Mn3+ results in the half- filled (d5) configuration which has extra stability.
ii) Cobalt (II) is stable in aqueous solution, but in the presence of complexing reagents, it is easily oxidised.
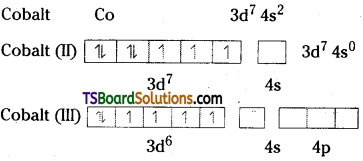
In the presence of complexing agents electron pairs takes place, and t2g orbital is completely filled.
Hence cobalt (II) is oxidised to cobalt (III).
Practically, all complexes of Co (+ III) have six ligands in an octahedral arrangements.
The metal has a d6 configuration and most of the ligands are strong enough to cause spin pairing, giving the electronic arrangement (t2g)6 (eg)0. This arrangement has a very large crystal field stabilisation energy. Such complexes are diamagnetic.
Eg: [Co (NH3)6]3+
The one exception is [C0F6]3- which is a high spin complex and is paramagnetic.
iii) The d’, configuration is very unstable in ions.
The d’, configuration has lower CFSE value. Hence very unstable.
Question 100.
Give examples and suggest reasons for the following features of the transition metals.
(i) The lowest oxide of transition metal is basic, the highest is amphoteric / acidic.
(ii) A transition metal exhibits highest oxidation state in oxides and fluorides.
(iii) The highest oxidation state is exhibited in oxoanions of a metal.
Answer:
i) The lowest oxide of transition metal is basic, the highest is amphoteric/acidic:
Lowest oxidation compounds of transition metals are basic due to their ability to get oxidised to higher states. Whereas the higher oxidation state of metal and compounds gets reduced to lower ones and hence acts as acidic in nature.
ii) A transition metal exhibits highest oxidation state in oxides and fluorides:
Due to high electronegativities of oxygen and fluorine, the oxides and fluorides of transition metals exhibits highest oxidation state.
iii) In oxo anions of metals, the metals form bonds with oxygen and hence present in their highest oxidation states. For example, Cr forms CrO42- and Cr2O72- both contain chromium in + 6 state. Permanganate ion, MnO4– contains Mn in its highest oxidation state of + 7.

Question 101.
Compare the chemistry of the actinoids with that of lanthanoids with reference to:
(i) eletronic configuration
(ii) oxidation states and
(iii) chemical reactivity
Answer:
| Lanthanoids | Actinoids |
| a) Electronic configuration 4f1 – 14 5d0 – 1 6s2 | a) 5f1 – 146d0 – 1 7s2 * |
b) Oxidation states : They all show + 3 common state.
+ 2 is shown by Eu and Yb and
+ 4 by Ce and Tb. | b) They shows along with + 3, +4, + 5, +7 other oxidation states also. |
| c) Atomic size: Difference between the two successive lanthanoids sizes smaller than actinoid. | c) Difference between the two successive actinoid is larger them lanthanoids. |
| d) Decrease in size in series is called lanthanoid contraction. | d) Decrease in size in series is called actinoid contraction. |
| e) The ionisation enthalpies are high. | e) Their ionisation enthalpies are lower than lanthanoids. |
| f) Their magnetic character is explained. | f) Their magnetic characteristic cannot be explained. |
| g) They are non-radioactiVe (except promethium). | g) All are radioactive. |
| h) When reacted with water form hydroxide and H2 gas. | h) They form oxides and hydrides. |
| i) Reacts with non-metals at higher temperature. | i) Reacts with non-metal at moderate temperature. |
Question 102.
Explain IUPAC nomenclature of coordination compounds with suitable examples.
Answer:
The rules which are to be followed while writing down the names of the coordinate compounds are –
- The cationic part of the coordinate of compound Is written first followed by the names of the anion with a small gap.
- Within a coordination sphere, ligands names are written in alphabetical order before the name of the central metal atom or ion without leaving any gap.
- To indicate thenumber of ligands in the coordination sphere two types of prefixes are used-
a) One are di-tri-tetra – etc. These are used when the ligands names are simple.
b) If the ligands names are complex and contains the prefixes, like di-tri-tetra etc. in their names, then pre-fixes-bis, tris, tetrakis, etc. are used. - The names of anionic ligands (both organic and inorganic) ends with-O-. If a ligands name is already having prefix its name is enclosed in simple brackets.
Neutral and cationic ligands names are written as such except – water (-aqua), NH3 (-ammine), -Co (-Carbonyl) and NO (Nitrosyl). - The oxidation state of the central atom or ion is indicated in Roman numerates after the name of the central metal atom in simple brackets with no gap in between.
- When coordination sphere is an anion then -ate is added as suffix to the name of the central metal atom / ion.
- Prefixes cis and trans are used to desig-nate adjacent and opposite geometrical locations of the ligands in a complex.

Question 103.
Explain different types of isomerism exhibited by coordination compounds, giving suitable examples.
Answer:
Esorners are two or more compounds that have the same chemical formula but a different arrangement of atoms. Because of the different arrangement of atoms, they differ in one or more physical or chemical properties. Two principal types of Isomerism are known among coordination compounds. Each of which can be further subdivided.
a) Stereoisomerism.
- Geometrical isomerism
- Optical isomerism
b) Structural isomerism
- Linkage isomerism
- Coordination isomerism
- Ionisation isomerism
- Solvate isomerism
Stereo isomers have the same chemical formula and chemical bonds but they have different spatial arragement. Structural isomers have different bonds. A detailed account of these isomers are given below.
Geometric isomerism:
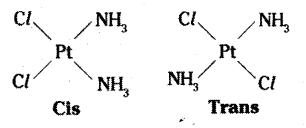
Geometrical isomers (cis and trans) of [Pt (NH3)2 Cl2]
This type of isomerism also arises when bidentate ligands L – L (eg : NH2 CH2 CH2 NH2(en)] are present in complexes of formula [MX2 (L – L)2].
Another type of isomerism occurs in octahedral coordination entities of the type [Ma3b3] like [Co (NH3)3 (NO2)3]. If three donor atoms of the same ligands occupy adjacent positions at the corner of an octachedral face, we have facial (fac) isomer.
When positions are around the meridian of octahedron, we get the meridional isomer.
Optical isomerism:
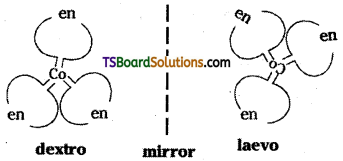
Optical isomers are the mirror images that cannot be super imposed on one another. These are called as enantiomers. The molecules (or) ions that cannot be superimposible are called chiral. The two forms are called dextro & laevo forms depending on the direction
they rotate plane polarised light in a polarimeter. {d-rotates to right & / to left}.
Optical isomers (d and l) of [Co (en)3]3+
Optical isomerism is commmon in octahedral complexes involving different ligands.
In a coordination utility of the [Pt Cl2 [en]2]2+ only cis-isomer shows optical activity.
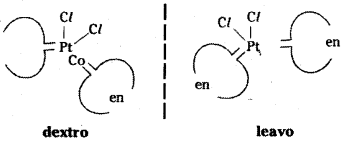
Optical isomers of [d and l] of cis [Pt Cl2 (en)2]2+
Linkage isomerism :
Linkage isomerism arise in a coordination compound containing ambidentate ligand.
A simple example is provided by complexes containing the thiocyanate ligand, NCS–, which may bind through the nitrogen to give M – NCS are through sulphur to give M-SCN.
Example : [Co(NH2)5 (NO2)] C l2
Which is obtained as the red form, in which the nitrite ligand is bond through oxygen (-ONO) and as the yellow form in which the nitrite ligand is bond through nitrogen (-NO2).
Ionisation isomerism:
This type of isomerism is shown by such compounds which have same composition but literate different ions in solution. In such isomers, the positions of groups within or outside coordination sphere differs.

Coordination isomerism: This type of isomerism arises from the interchange of ligands between cationic and anionic entities of different metal ions present in a complex.
Ex : [CoCNH3)6] [Cr(CN)6] and [Cr(NH3)6] [Co (CN)6]

Question 104.
Discuss the nature of bonding and magnetic behaviour in the following coordination entities on the basis of valence bond theory.
(i) [Fe(CN)6]4-
(ii) [FeF6]3-
(iii) [Co(C2O4)3]3- and
(iv) [CoF6]3-
Answer:
i) [Fe(CN)6]4-:
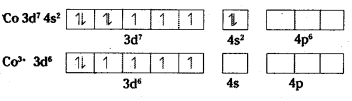
In this complex ion, iron is in +2 oxidation state. The electronic configuration of Fe [Z = 26] is 4s2 3d6.
The configuration of Fe2+ is 3d6. Thus the ion has four vacant orbitals, one s and three p. In order to make six vacant orbitals available, the electrons in 3d orbital are forced to pair up. d2 sp3 hybridisation takes place clearly, six pairs of electrons one from each CN- ion occupy six vacant hybrid orbitals.
i) [Fe(CN)6]4-
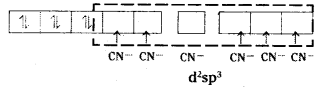
Geometry : The complex ion is octahedral. After the complex ion formation, no unpaired electron is left. Thus the given ion is diamagnetic.
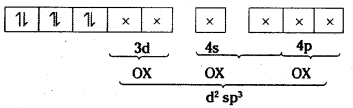
ii) [FeF6]3- : Oxidation state of Fe = + 3 Fe3+ 3d5 4s0

As six F– ion approaches, no pairing of electron occur and the sp3d2 hybridisation occurs accommodate six F– ions.

Since five unpaired electrons are available, it is paramagnetic. Geometry is octahedral.
iii) [Co(C2O4)3]3-: Oxidation state of Co is +3
As didentate oxalate ions approach, pairing takes places.
All electrons are paired. The substance is diamagnetic octahedral.
iv) [CoF6]3-: Oxidation state of Co is + 3.
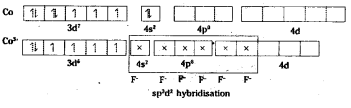
As there are four unpaired electrons, the complex is paramagnetic in nature.
Question 105.
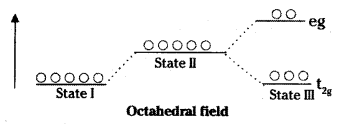
Sketch the splitting of d-orbitals in an octahedral crystal field.
Answer:
The field created by the anionic ligands or due to the polarity of neutral molecules is called crystal field. The crystal field distorts the symmetry of the central metal atom / ion and splitting of d-orbitals takes places.
It the six ligands of octahedral complex are approaching the central metal atom/ion along the cartesian axes, initially the energy of the orbitals is increased. Then the orbital lying along the axis (dx2,/sup> – y2 & dz2) gets repelled strongly by the approaching crystal fields, then dxy, dyz, dzx orbitals which lie in between the axes.
The energy of dx2,/sup> – y2 & dz2 orbitals gets increase whereas energy of the other three gets lowered relative to the average energy of the spherical crystal field.
The lower energy set of d-orbitals is called t2g and the higher energy set is called eg. The energy of separation is called crystal field stabilisation energy.

Question 106.
What is spectrochemical series ? Explain the difference between a weak field ligand and a strong field ligand.
Answer:
The magnitude of crystal field splitting ∆0, depends upon the field produced by the ligand and charge on the metal ion. Some * ligands are able to produce strong fields in which case, the splitting will be large whereas others produce weak fields and consequently result in small splitting of d orbitals.
In general, ligands can be arranged in a series in the order of increasing field strength as given below:
I– < Br– < S2- < SCN– < Cl– < N3-< F– < OH– < C2O42- < H2O < NCS– < NH3 < en < CN– < Co
Such a series is termed as spectra chemical series. It is an experimentally determined series based on the absorption of light by complexes with different ligands.
Ligands for which the crystal filed stabilisation energy is less than the pairing energy are called weak field ligands. These ligands result in the formation of high spin complexes.
∆0 < p
Ligands for which the crystal field stabilisation energy is greater than the pairing energy are called strong field ligands. These ligands results in the formation of low spin complexes.
∆0 >p
In oxoanions of metals, the metals form bonds with oxygen and hence are present in their highest oxidation states. For example, Cr form CrO42- and Cr2O72-, both contains chromium ion + 6 oxidation state.
Permanganate ion, MnO4– contains Mn in its highest oxidation state of +7.
Question 107.
Discuss the nature of bonding in metal carbonyls.
Answer:
Metal carbonyls are formed by most of the transition metals. These carbonyls have simple well defined structure, tetra carbonyl nickel (O) is tetrahedral, pentacarbonyl- iron (O) is trigonal bipyramidal while hexa- carbonyl chromium (O) is octahedral. (O) indicates zero oxidation state.
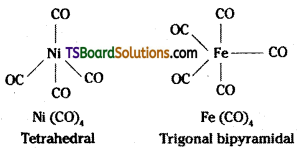
The metal carbon bond in metal carboynyls posses both σ and π character. The MC σ bond is formed by the donation of lone pair of electrons on the carbonyl carbon into a vacant orbital of the metal. The M – C π bond is formed by the donation of a pair of electrons from a filled d-orbital of metal into the vacant antibonding π orbital of carbon monoxide. The metal to ligand bonding creates a synergic effect which strengthens the bond between CO and the metal.

Question 108.
Explain the applications of coordination compounds in different fields.
Answer:
1) Coordination compounds find use in many qualitative and quantitative chemical analysis. Examples of such reagents include EDTA, DMG (dimethylglyoxime), d-nitroso-β-naphthol, cupron, etc.
2) Hardness of water is estimated- by simple titration with Na2EDTA the Ca2+ and Mg2+ ions form table complexes with EDTA.
3) Some important extraction processes of metals, like those of silver and gold, make use of complex formation. Gold, for example, combines with cyanide in the presence of oxygen and. water to form the coordination entity [Au(CN)2] in aqueous solution. Gold can be separated in metal is form from this solution by the addition of Zinc.
4) Coordination compounds are of great importance in biological systems. The pigment responsible for photosynthesis, chlorophyll, is a coordination compound of magnesium. Haemoglobin the red pigment of blood which acts as oxygen carrier is a coordination compound of iron. Vitamin B12, Cyanocobalamine, the anti- pernicious anaemia factor, is a coordination compound of cobalt.
5) Coordination compounds are used as catalysts for many industrial processes. Examples include rhodium complex, [(Ph3P)3 RhCl], a Wilkinson catalyst, is used for the hydrogenation of alkenes.
6) Articles can be electroplated with silver and gold much more smoothly and evenly from solutions of the complexes, [Ag(CN)2] and [Au(CN)2] than from a solution of simple metal ions.
7) In black and white photography, the developed film is fixed by washing with hyposolution which dissolves the undercomposed Ag Br to form a complex ion, [Ag (S2O3)2]3 EDTA is used in the treatment of lead poisoning.
![]()
![]()
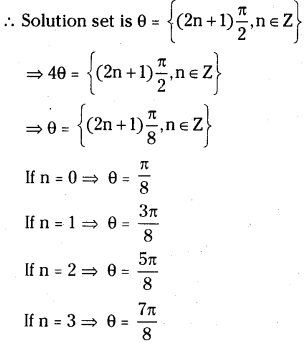
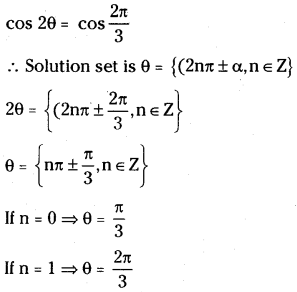
![]()

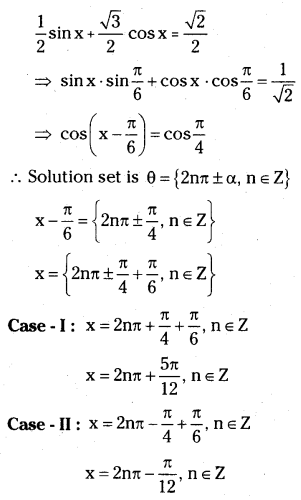
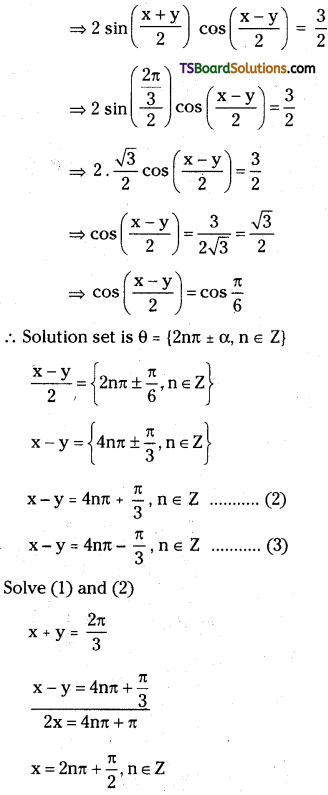
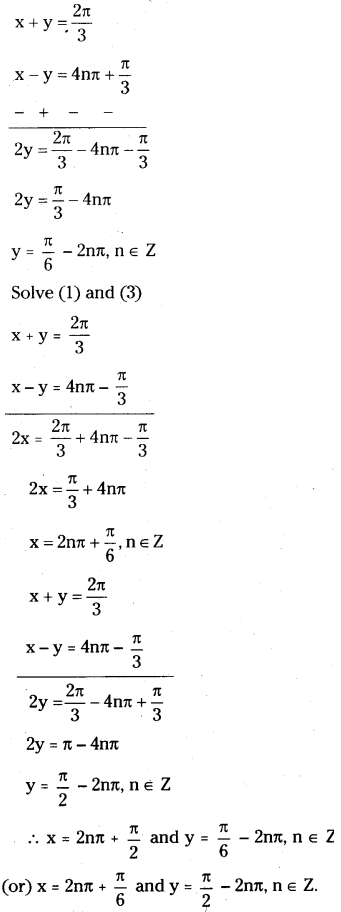
![]()
![]()
![]()