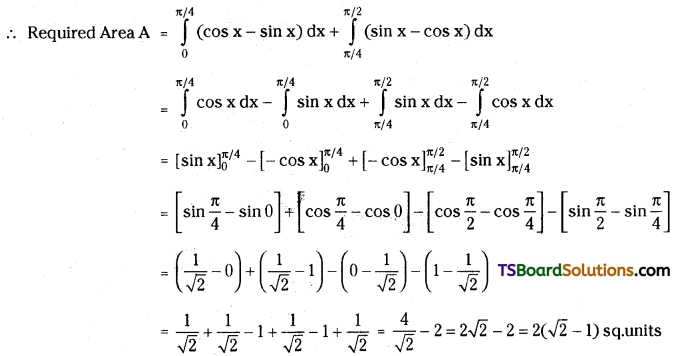TS Inter Second Year Maths 2B Definite Integrals Important Questions Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Definite Integrals Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Definite Integrals Important Questions Short Answer Type

Question 1.
Evaluate \(\int_0^{\pi / 2} \frac{a \sin x+b \cos x}{\sin x+\cos x} d x\). [(AP) May ’17]
Solution:

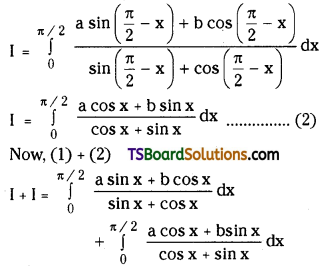
Question 2.
Evaluate \(\int_{-\pi / 2}^{\pi / 2} \frac{\cos x}{1+e^x} d x\). [(TS) May ’17]
Solution:

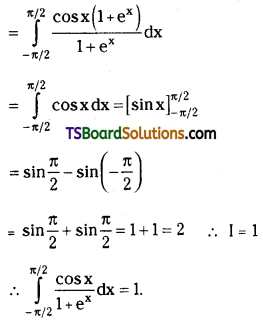
Question 3.
Evaluate \(\int_0^\pi \frac{1}{3+2 \cos x} d x\)
Solution:

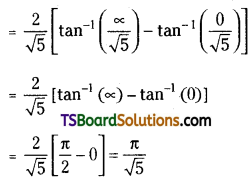
Question 4.
Evaluate \(\int_{-3}^3\left(9-x^2\right)^{3 / 2} d x\)
Solution:

Question 5.
Evaluate \(\int_{-a}^a x^2\left(a^2-x^2\right)^{3 / 2} d x\). [(TS) May ’17]
Solution:

Question 6.
Evaluate \(\int_0^4\left(16-x^2\right)^{5 / 2} d x\). [(AP) May ’19]
Solution:
Put x = 4 sin θ
dx = 4 cos θ dθ

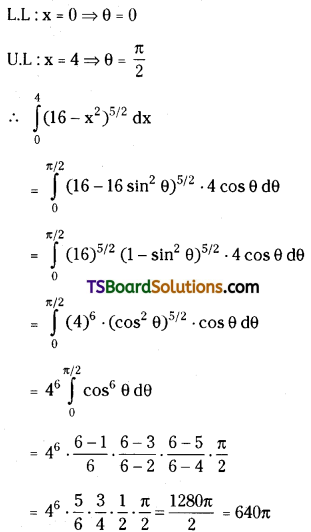
Question 7.
Evaluate \(\int_0^2\left(x^2+1\right) d x\) as the limit of a sum.
Solution:

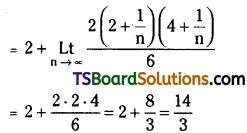
Question 8.
Evaluate \({Lt}_{n \rightarrow \infty} \sum_{i=1}^n \frac{i^3}{i^4+n^4}\)
Solution:

Question 9.
Evaluate \(\underset{n \rightarrow \infty}{L t}\left[\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right) \ldots\left(1+\frac{n}{n}\right)\right]^{1 / n}\)
Solution:

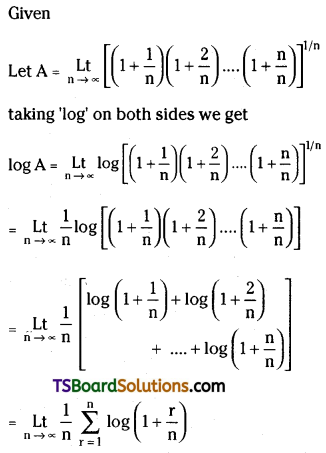
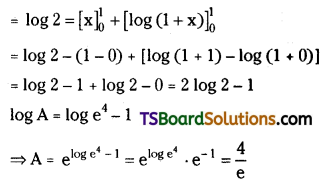
Question 10.
Evaluate \({Lt}_{n \rightarrow \infty}\left[\left(1+\frac{1}{n^2}\right)\left(1+\frac{2^2}{n^2}\right) \cdots\left(1+\frac{n^2}{n^2}\right)\right]^{1 / n}\)
Solution:

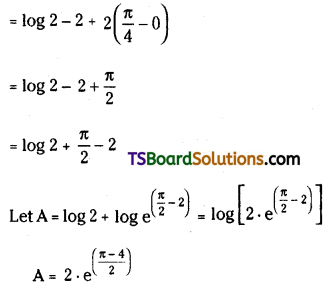
Question 11.
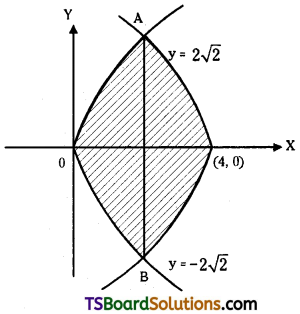
Find the area bounded between the curves y² = 4x, y² = 4(4 – x). [(TS) May ’19, ’11]
Solution:
Given curves are y² = 4x
⇒ y = 2√x ………(1)
y² = 4(4 – x) ………(2)
⇒ y = \(\sqrt{4(4-x)}\)
Solving (1) and (2)
4x = 4(4 – x)
⇒ x = 4 – x
⇒ 2x = 4
⇒ x = 2
from (1) ⇒ y = ± 2√2
Points of Intersections of (1) and (2) are A = (2, 2√2) and B = (2, -2√2)

Question 12.
Find the area enclosed between y = x² – 5x and y = 4 – 2x.
Solution:
Given curves are
y = x² – 5x ………(1)
y = 4 – 2x ………..(2)

Solving (1) and (2)
x² – 5x = 4 – 2x
⇒ x² – 3x – 4 = 0
⇒ (x – 4) (x + 1) = 0
∴ x = 4 and x = -1

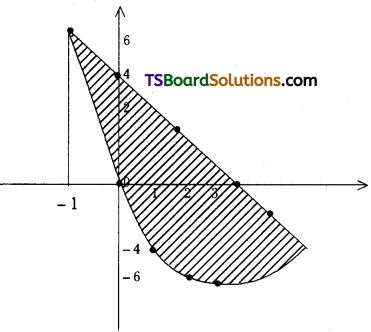
Question 13.
Find the area enclosed between the curves y = 4x – x², y = 5 – 2x. [(TS) Mar. ’16]
Solution:
Given curves are
y = 4x – x² ………(1)
y = 5 – 2x ………(2)
Solving (1) and (2)
4x – x² = 5 – 2x
⇒ x² – 6x + 5 = 0
⇒ x² – 5x – x + 5 = 0
⇒ x(x – 5) – 1(x – 5) = 0
⇒ x = 1 or 5

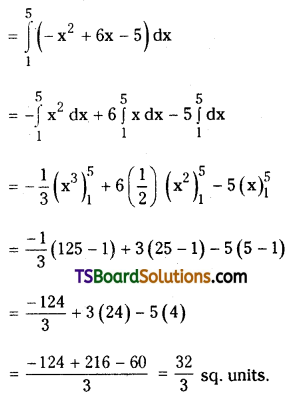
Question 14.
Find the area between the parabolas y² = 4x and x² = 4y. [(AP) Mar. ’20; (TS) ’17; May ’14]
Solution:
Given equations of curves are
y² = 4x ………(1)
and x² = 4y ……..(2)
Solving (1) and (2) the points of intersection can be obtained.
y² = 4x
⇒ y⁴ = 16x²
⇒ y⁴ = 64y
⇒ y = 4
∴ 4x = y²
⇒ 4x = 16
⇒ x = 4

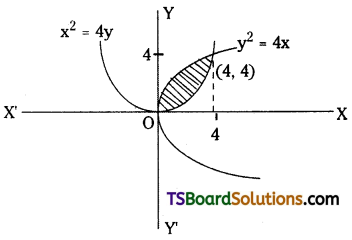
Points of intersection are (0, 0) and (4, 4).
∴ The area bounded between the parabolas

Question 15.
Evaluate \(\int_0^2 e^x d x\) as the limit of the sum.
Solution:

Question 16.
Evaluate \(\int_0^4\left(x+e^{2 x}\right) d x\) as the limit of a sum.
Solution:

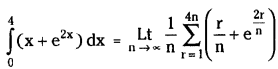
Question 17.
Evaluate \(\int_0^{16} \frac{x^{1 / 4}}{1+x^{1 / 2}} d x\)
Solution:
L.C.M of 2, 4 is 4
Put x = t⁴
⇒ dx = 4t³ dt
L.L: x = 0 ⇒ t = 0
U.L: x = 16 ⇒ t = 2

Question 18.
Evaluate \(\int_0^{\pi / 4} \log (1+\tan x) d x\). [(AP) Mar. ’19, ’16; May ’18, (TS) ’16]
Solution:

Question 19.
Evaluate \(\underset{n \rightarrow \infty}{L t} \frac{1}{n}\left[\tan \frac{\pi}{4 n}+\tan \frac{2 \pi}{4 n}+\ldots \ldots+\tan \frac{n \pi}{2 n}\right]\)
Solution:

Question 20.
Find \({Lt}_{n \rightarrow \infty}\left(\frac{n !}{n^n}\right)^{1 / n}\)
Solution:

Question 21.
Evaluate \(\int_0^5 x^3\left(25-x^2\right)^{7 / 2} d x\)
Solution:
Put x = 5 sin θ, then dx = 5 cos θ dθ
L.L: x = 0 ⇒ θ = 0
U.L: x = 5 ⇒ θ = \(\frac{\pi}{2}\)

Question 22.
Evaluate \(\int_0^2 x \sqrt{2-x} d x\)
Solution:

Question 23.
Find \(\int_0^1 x^{3 / 2} \sqrt{1-x} d x\)
Solution:
Put x = sin²θ then dx = 2 sin θ cos θ dθ
Lower limit: x = 0 ⇒ θ = 0
Upper limit: x = 1 ⇒ θ = \(\frac{\pi}{2}\)

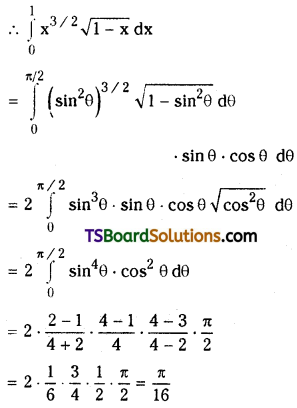
Question 24.
Evaluate \(\int_0^1 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right) d x\)
Solution:
Put x = tan θ, then θ = tan^-1x
dx = sec²θ dθ
L.L: x = 0 ⇒ θ = 0
U.L: x = 1 ⇒ θ = \(\frac{\pi}{4}\)

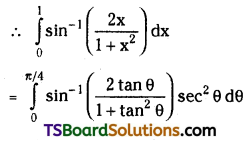
Question 25.
Evaluate \(\int_0^1 x \tan ^{-1} x d x\)
Solution:

Question 26.
Find the area enclosed by the curves y = 3x and y = 6x – x².
Solution:
Given curves are
y = 3x ……..(1)
y = 6x – x² ………(2)

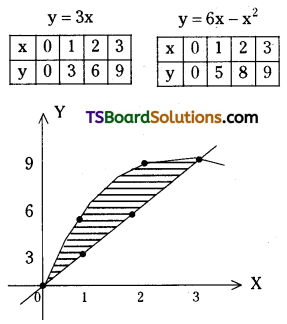
Solving (1) and (2)
3x = 6x – x²
⇒ x² = 3x
⇒ x(x – 3) = 0
⇒ x = 0 and x = 3

Question 27.
Find the area bounded between the curves y = 4x – x², y = 5 – 2x.
Solution:
Given curves are
y = 4x – x² ……..(1)
y = 5 – 2x ……..(2)

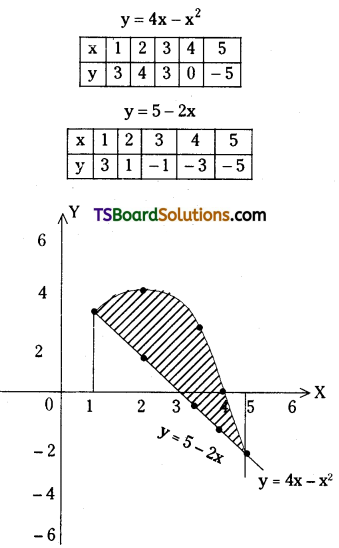
Solving (1) and (2)
4x – x² = 5 – 2x
⇒ x² – 6x + 5 = 0
⇒ (x – 1) (x – 5) = 0
⇒ x = 1, x = 5

Question 28.
Find the area bounded between the curves y = 2 – x, y = x². [Mar. ’01]
Solution:
Given curves are
y = 2 – x² ……(1)
y = x² ………(2)

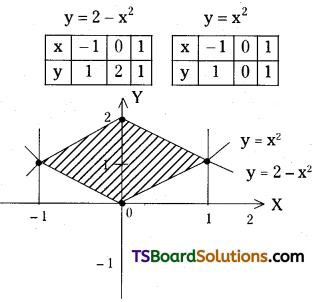
Question 29.
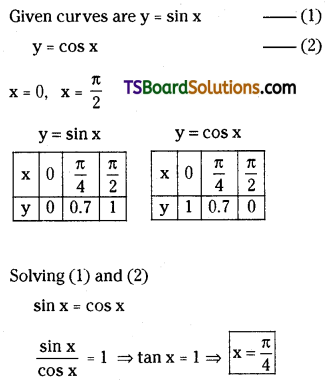
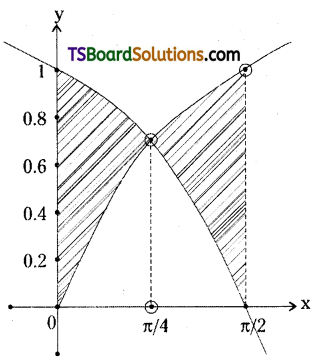
Find the area of the region enclosed by the curves y = sin x, y = cos x, x = 0, x = \(\frac{\pi}{2}\).
Solution: