TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions

Question 1.
Solve 2 cos²θ – √3 sin θ + 1 = 0. [May ’09; B.P]
Answer:
Given equation is 2 cos2 θ – √3 sin θ + 1 = 0
⇒ 2(1 – sin2 θ) – √3 sin θ + 1 = 0
⇒ 2 – 2sin2 θ – √3 sin θ + 1=0
⇒ 2 sin2 θ + √3 sin θ – 3 = 0
⇒ 2 sin2 θ + 2 √3 sin θ – √3 sin θ – 3 = 0
⇒ 2 sin θ (sin θ + √3 ) – + √3 (sin θ + √3 ) = 0
⇒ (sin θ + √3)- (2 sin θ – √3) = 0
⇒ sin θ + √3 = 0 (or) 2 sin θ – √3 = 0
⇒ sin 0θ = – J3 (or) sin θ = \(\frac{\sqrt{3}}{2}\)

Case -1: sin θ = -√3 ∉ [- 1, 1 ]
∴ There is no solution set.

Case – II : sin θ = \(\frac{\sqrt{3}}{2}\) ⇒ sin θ = sin \(\)
∴ Solution set is θ = {nπ + (-1)ⁿ α, n ∈ Z} ⇒
θ = {nπ + (-1)ⁿ\(\frac{\pi}{3}\) α, n ∈ Z}
∴ The solution of the given equation is
θ = {nπ + (-1)ⁿ\(\frac{\pi}{3}\) α, n ∈ Z}

Question 2.
Find all values of x ≠ 0 in (-π, π) satisfying the equation 8^{1+cosx+cos2x+……………..} = 4³. [Mar. ’09]
Answer:
Given 8^{1+cosx+cos2x+……………..} = 4³
8^{\(\frac{1}{1-\cos x}\)} = 4³ [∵ s_∞ = \(\frac{a}{1-r}\)]
(2³)^{\(\frac{1}{1-\cos x}\)} = 2⁶
2^{\(\frac{1}{1-\cos x}\)} = 2⁶
\(\frac{1}{1-\cos x}\) = 6
1 – cos x = \(\frac{1}{2}\)
⇒ cos x = \(\frac{1}{2}\)
⇒ x = ±\(\frac{\pi}{3}\)
∴ x = \(\frac{\pi}{3}\) (or) –\(\frac{\pi}{3}\) [∵x ∈ (-π, π)]

Question 3.
Solve tan θ + 3 cot θ = 5 sec θ. [Mar. ’02; May ’99, ’84]
Answer:
Given tan θ + 3 cot θ = 5 sec θ
⇒ \(\frac{\sin \theta}{\cos \theta}+3 \cdot \frac{\cos \theta}{\sin \theta}=\frac{5}{\cos \theta}\)
⇒ \(\frac{\sin ^2 \theta+3 \cos ^2 \theta}{\cos \theta \cdot \sin \theta}=\frac{5}{\cos \theta}\)
⇒ sin² θ + 3 cos²θ = 5 sin θ
⇒ sin² θ + 3 (1 – sin²θ) = 5 sin θ
⇒ sin² θ + 3 – 3 sin²θ = 5 sin θ
⇒ 2 sin²θ + 5 sin θ – 3 = 0
⇒ 2 sin²θ + 6 sin θ – sin θ – 3 = 0
⇒ 2 sin θ(sin θ + 3) – 1 (sin θ + 3) = 0
⇒ (sin θ + 3) (2 sin θ – 1) = 0
⇒ sin θ + 3 = 0 (or) 2 sin θ – 1 = 0
⇒ sin θ = -3 (or) sin θ = \(\frac{1}{2}\)

Case – I: sin θ = -3 ∈ [-1, 1]
There is no solution set.

Case – II: sin θ = \(\frac{1}{2}\)
⇒ sin θ = sin \(\frac{\pi}{6}\)
∴ Solution set is θ = {nπ + (-1)ⁿ α, n ∈ Z}
⇒ θ = {nπ + (-1)ⁿ \(\frac{\pi}{6}\), n ∈ Z}

∴ The solution set of the given equation is
θ = {nπ + (-1)ⁿ \(\frac{\pi}{6}\), n ∈ Z}

Question 4.
Solve 1 + sin²θ = 3sin θ. cos θ. [Mar.(AP & TS) ’17, ’11; May ’00]
Answer:
Given 1 + sin²θ = 3sin θ. cos θ
On dividing both sides with cos2θ, we get
⇒ \(\frac{1}{\cos ^2 \theta}+\frac{\sin ^2 \theta}{\cos ^2 \theta}=\frac{3 \sin \theta \cos \theta}{\cos ^2 \theta}\)
⇒ sec²θ + tan²θ = 3 tanθ
⇒ 1 + tan²θ + tan²θ = 3 tan θ
⇒ 2 tan²θ – 3 tan θ + 1 = 0
⇒ 2 tan²θ – 2 tan θ – tan θ + 1 = 0
⇒ 2 tan θ (tan θ – 1) – l(tan θ – 1) = 0
⇒ (tan θ – 1) (2 tan θ – 1) = 0
⇒ tan θ – 1=0 (or) 2 tan θ – 1 = 0
⇒ tan θ = 1 (or) 2 tan θ = \(\frac{1}{2}\)

Case – I: tan θ = 1 ⇒ tan θ = tan \(\frac{\pi}{4}\)
∴ Solution set is θ = {nπ + α, n ∈ Z}
⇒ θ = {nπ + \(\frac{\pi}{4}\), n ∈ z}

Case – II: tan θ = 1 ⇒ tan θ = 0.5
⇒ tan θ = tan 26°. 34′
Solution set is θ =
⇒ θ = {nπ + 26°.34′, n ∈ Z)
∴ The solution set of the given equation is
θ = {nπ + \(\frac{\pi}{4}\), n ∈ z} ∪ {nπ + 26°.34′, n ∈ Z}

Question 5.
Solve √2(sin x + cos x) = √3. [Mar. ’16(AP), Mar. 15(AP); May ’12, ’08]
Answer:
Given equation is √2(sin x + cos x) = √3
⇒ sin x + cos x = \(\frac{\sqrt{3}}{\sqrt{2}}\)
On dividing Both sides with \(\sqrt{a^2+b^2}\)
= \(\sqrt{1^2+1^2}\) = , we get
⇒ \(\frac{1}{\sqrt{2}}\)sin x + \(\frac{1}{\sqrt{2}}\)cos x = \(\frac{1}{\sqrt{2}}\)
⇒ cos x.cos\(\frac{\pi}{4}\) + sin x sin\(\frac{\pi}{4}=\frac{\sqrt{3}}{2}\)
⇒ cos(x – \(\frac{\pi}{4}\)) = cos\(\frac{\pi}{6}\)

∴ Solution set is θ = {2nπ ± α, n ∈ Z}
⇒ x – \(\frac{\pi}{4}\) = {2nπ + \(\frac{\pi}{6}\), n ∈ Z}

Case – I: x – \(\frac{\pi}{4}\) = 2nπ + \(\frac{\pi}{6}\), n ∈ Z
x = 2nπ + \(\frac{\pi}{6}\) + \(\frac{\pi}{4}\)
x = 2nπ + \(\frac{5\pi}{12}\)
x = {(24n + 5)\(\frac{\pi}{12}\)}, n ∈ Z

Case – II: x – \(\frac{\pi}{4}\) = 2nπ – \(\frac{\pi}{6}\), n ∈ Z
x = 2nπ – \(\frac{\pi}{6}\) + \(\frac{\pi}{4}\)
x = 2nπ + \(\frac{\pi}{12}\)
x = {(24n + 1)\(\frac{\pi}{12}\)}, n ∈ Z

∴ The solution set of the given equation is
x = {(24n + 5)\(\frac{\pi}{12}\)} ∪ {(24n + 1)\(\frac{\pi}{12}\)}, n ∈ Z

Question 6.
If θ₁, θ₂ are solutions of the equation a cos 2θ + b sin 2θ = c, tan θ₁ ≠ tan θ₂ and a + c ≠ 0, then find the values of
(i) tan θ₁ + tan θ₂
(ii) tan θ₁. tan θ₂.
Answer:
Given equation is a cos 2θ + b sin 2θ = c
⇒ a\(\left[\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right]\) + b\(\left[\frac{2 \tan \theta}{1+\tan ^2 \theta}\right]\) = c
⇒ \(\frac{\mathrm{a}-\mathrm{a} \tan ^2 \theta+2 b \tan \theta}{1+\tan ^2 \theta}\) = c
⇒ a – a tan²θ + 2b tan θ = c + c tan²θ
⇒ c + c tan²θ – a + a tan²θ – 2b tan θ = 0
⇒ (a + c) tan²θ – 2b tan θ + (c – a) = 0 ……… (1)
This is a quadratic equation in tan θ since θ₁, θ₂ are the roots of the given equation.

tan θ₁, tan θ₂ are the roots of the equation (1).
i) Sum of the roots = tan θ₁ + tan θ₂
= \(\frac{-b}{a}=\frac{-(-2 b)}{a+c}\)
tan θ₁ + tan θ₂ = \(\frac{2 b}{a+c}\)

ii) Product of the roots = tan θ₁ . tan θ₂
= \(\frac{c}{a}=\frac{c-a}{a+c}\)
tan θ₁ . tan θ₂ = \(\frac{c}{a}=\frac{c-a}{a+c}\)

Question 7.
Solve : 4 sin x. sin 2x. sin 4x = sin 3x.
Answer:
Given sin 3x = 4 sin x . sin 2x. sin 4x
= 2 sin x (2 sin 2x sin 4x)
= 2 sin x (cos 2x – cos 6x)
⇒ sin 3x = 2 cos 2x sin x – 2 cos 6x sin x
⇒ sin 3x = sin 3x – sin x – 2 cos 6x sin x
⇒ 2 cos 6x sin x + sin x = 0
⇒ sin x (2 cos 6x + 1) = 0
⇒ sin x = 0 or cos 6x = – \(\frac{1}{2}\)

Case (1): sin x = 0 ⇒ x = nπ, n ∈ Z is the general solution.

Case (2): cos 6x = –\(\frac{1}{2}\)
Principal solution is α = \(\frac{2 \pi}{3}\)
General solution is 6x = 2nπ ± \(\frac{2 \pi}{3}\)
⇒ x = \(\frac{\mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z.
∴ The solution set of the given equation is x = {nπ, n ∈ Z} ∪ {\(\frac{\mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z}

Question 8.
If θ < 0 < π, solve cos θ cos 2θ cos 3θ = \(\frac{1}{4}\).
Answer:
Given equation is cos θ cos 2θ cos 3θ = \(\frac{1}{4}\)
⇒ 4 cos θ cos 2θ cos 3θ = 1
⇒ 2 cos 2θ (2 cos 3θ cosθ) = 1
⇒ 2 cos 2θ [cos (3θ + θ) + cos(3θ – θ)] = 1
⇒ 2 cos 2θ (cos 4θ + cos 2θ) = 1
⇒ 2 cos 4θ cos 2θ + 2 cos2 2θ – 1 = 0
⇒ 2 cos 4θ cos 2θ + cos 4θ = 0
⇒ cos 4θ (2 cos 2θ + 1) = 0
⇒ cos4θ = 0 (or) ⇒ 2 cos 2θ + 1 = 0
cos 2θ = –\(\frac{1}{2}\)

Case – I: cos 4θ = 0

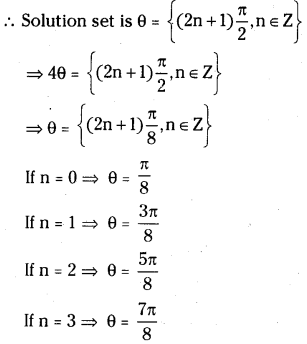
∴ The solutions of the case – I in (0, π) are \(\frac{\pi}{8}, \frac{3 \pi}{8}, \frac{5 \pi}{8}, \frac{7 \pi}{8}\)

Case – II: cos 2θ = –\(\frac{1}{2}\)

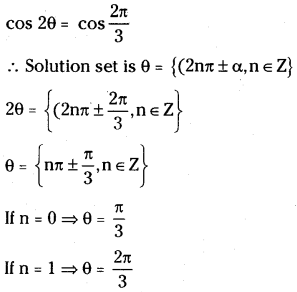
∴ The solutions of the case – II in (0, π) are \(\frac{\pi}{3}, \frac{2 \pi}{3}\)
∴ The solutions of the given equation in (0, π) are \(\frac{\pi}{8}, \frac{\pi}{3}, \frac{3 \pi}{8}, \frac{5 \pi}{8}, \frac{2 \pi}{3} \frac{7 \pi}{8}\)

Question 9.
Solve sin 2x – cos 2x = sin x – cos x [Mar. ’99]
Answer:
Given equation is
(sin 2x – sin x) – (cos 2x – cos x) = 0

Case – I: sin\(\left(\frac{x}{2}\right)\) = 0
Solution set is θ = {nπ, n ∈ Z}
\(\frac{x}{2}\) = {nπ, n ∈ Z}
x = {2nπ, n ∈ Z}

Case – II: tan\(\left(\frac{3 \mathrm{x}}{2}\right)\) = -1
tan\(\left(\frac{3 \mathrm{x}}{2}\right)\) = tan\(\left(\frac{-\pi}{4}\right)\)
∴ The solution set is θ = {nπ + α, n ∈ Z}
\(\frac{3 x}{2}\) = {n – \(\frac{\pi}{4}\), n ∈ Z}
x = {\(\frac{2 n \pi}{3}-\frac{\pi}{6}\), n ∈ Z}
∴ The solution set of the given equation is x = {2nπ, n ∈ Z} ∪ {\(\frac{2 n \pi}{3}-\frac{\pi}{6}\), n ∈ Z}

Question 10.
Solve 2 cos²θ + 11 sin θ = 7.
Answer:
Given equation is 2 cos²θ + 11 sin θ = 7
⇒ 2(1 – sin² θ) + 11 sin θ = 7
⇒ -2 sin² θ + 11 sin θ = 5
⇒ 2 sin² θ – 11 sin θ + 5 = 0
⇒ 2 sin² θ – 10 sin θ – sin θ + 5 = 0
⇒ 2 sin θ (sin θ – 5) – 1 (sin θ – 5) = 0
⇒ (2 sin θ – 1) (sin θ – 5) = 0

If sin θ – 5 = 0 then sin θ = 5 is not admissible.
If 2 sin θ – 1 = 0 ⇒ sin θ = \(\frac{1}{4}\) and the principal solution is α = \(\frac{\pi}{6}\)
∴ General solution is θ = nπ + (-1)ⁿ\(\frac{\pi}{6}\), n ∈ Z.

Question 11.
Solve sin x + √3 cos x = √2. [Mar. ’18(TS); Mar. ’10; May ’98, ’93]
Answer:
Given equation is sin x + √3 cos x = √2
On dividing both sides with \(\sqrt{a^2+b^2}\)

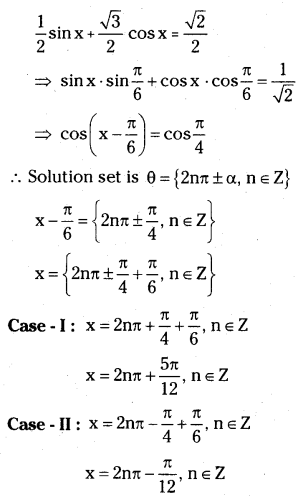
Hence the solution set of the given equation is x = {2nπ + \(\frac{5\pi}{12}\), n ∈ Z} ∪ {2nπ – \(\frac{\pi}{12}\), n ∈ Z}

Question 12.
Solve cot 2x – (√3 + 1)cot x + √3 = 0. [Mar. ’14, ’12]
Answer:
Given cot 2x – (√3 + 1)cot x + √3 = 0
⇒ cot 2x – √3 cot x – cot x + √3 = 0
⇒ cot x(cot x – √3) – 1(cot x – √3) = 0
⇒ (cot x – √3) (cot x – 1) = 0
⇒ cot x – √3=0 (or) cot x – 1 = 0
⇒ cot x = √3 (or) cot x = 1
⇒ cot x = cot 30° (or) cot x = cot 45°
⇒ x = 30° (or) x = 45°

General solutions:
x = nπ + 30°, n ∈ Z
Let n = 0 ⇒ x = 30°

General solution:
x = nπ + 45°, n ∈ Z
Let n = 0 ⇒ x = 45°
∴ Solutions set = {30°, 45°}

Question 13.
If x + y = \(\frac{2 \pi}{3}\) and sin x + sin y = \(\frac{3}{2}\), find x and y. [Mar. ’97]
Answer:
Given x + y = \(\frac{2 \pi}{3}\) …………(1)
sin x + sin y = \(\frac{3}{2}\)

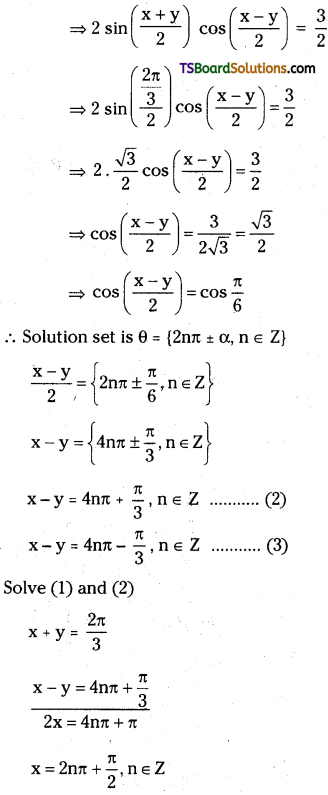
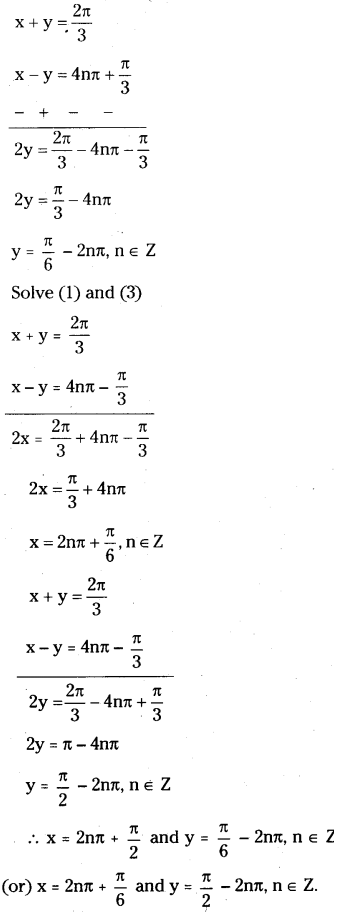
Some More Maths 1A Trigonometric Equations Important Questions

Question 1.
If x is acute and sin (x + 10°) = cos (3x – 68°) find x in degrees.
Answer:
Given sin (x + 10°) = cos (3x – 68°)
⇒ sin(x + 10°) = sin[90° + (3x – 68°)]
= sin (22° + 3x)
⇒ x + 10°= nπ + (-1)ⁿ (22° + 3x)

If n = 2k (even) k ∈ Z then
x + 10° = 2k7t + (-1)” (22° + 3x)
⇒ 2kπ + (-1)2k (22° + 3x) = 2kπ + 22° + 3x
⇒ 2x = -k(2π) – 12°
⇒ x = \(θ\) = -k(180°) – 6°

If n = 2k + 1 then
x + 10° = (2k + 1) 180° – (22° + 3x)
⇒ 4x = (2k +1) 180° – 32°
⇒ x = (2k + 1)45° – 8°
When k = 0 we get x = 37°
If we take k = 1, 2, ………… the value of x is not acute.
Hence the value of x is 37°.

Question 2.
Solve 5 cos²θ + 7 sin²θ = 6.
Answer:
Given 5 cos²θ + 7 sin²θ = 6
Dividing by cos²θ we get,
5 + 7 tan²θ = 6 sec²θ
⇒ 5 + 7 tan²θ = 6(1 + tan²θ)
⇒ tan²θ – 1 = 0 ⇒ tan²θ = 1 ⇒ tan θ = ±1
θ = nπ ± \(\frac{\pi}{4}\),n ∈ Z is the general solution.

Question 3.
Solve 2 sin²θ – 4 = 5 cos θ.
Answer:
2 sin²θ – 4 = 5 cos θ
⇒ 2(1 – cos²θ) – 5 cos θ – 4 = 0
⇒ 2cos²θ + 5cos θ + 4-2 = 0
⇒ 2cos²θ + 5cos θ + 2 = 0
⇒ 2cos²θ + 4cos θ + cos θ + 2 = 0
⇒ 2cos θ(cos θ + 2) + 1(cos θ + 2) = 0
⇒ (cos θ + 2)(2cos θ + 1) = 0
cos θ + 2 = 0 is not admissible.
Consider 2cos θ + 1 = 0 ⇒ cos θ = –\(\frac{1}{2}\), the principal solution is α = \(\frac{2 \pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{2 \pi}{3}\),n ∈ Z.

Question 4.
Solve 4cos²θ + √3 = 2(√3 + 1)cos θ.
Answer:
4cos²θ – 2(√3 + 1)cosθ + √3 = 0
⇒ 4cos²θ – 2√3cos θ – 2cos θ + √3 =0
⇒ 2cosθ(2cosθ – √3)- 1(2cos θ – √3) = 0
⇒ (2cosθ – 1)(2cosθ – √3) = 0
If cos θ = \(\frac{1}{2}\) then θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
If 2cos θ – √3 = 0 then cos θ = \(\frac{\sqrt{3}}{2}\)
Hence the general solution in this case is
θ = 2nπ ± \(\frac{\pi}{6}\) ,n ∈ Z.

Question 5.
Solve √3 sin θ – cos θ = √2. [May ’14, Mar. ’18(AP)]
Answer:
Given √3 sin θ – cos θ = √2
Divide both sides by
\(\sqrt{3+1}\) = 2, \(\frac{\sqrt{3}}{2}\)sin θ – \(\frac{1}{2}\)cos θ = \(\frac{1}{\sqrt{2}}\)

∴ The principal solution for θ – \(\frac{\pi}{6}\) is α = \(\frac{\pi}{4}\)
∴General soIutio is θ – \(\frac{\pi}{6}\) = nπ + (-1)ⁿ \(\frac{\pi}{4}\)
⇒ θ = \(\frac{\pi}{6}\) + nπ + (-1)ⁿ \(\frac{\pi}{4}\)

Question 6.
Solve cos 2θ + cos 8θ = cos 5θ.
Answer:
Given cos 2θ + cos 8θ = cos 5θ
⇒ 2 cos 5θ cos 3θ = cos 5θ
⇒ cos 5θ(2 cos 3θ – 1) = 0
Case (i): cos 5θ = 0
⇒ 5θ = (2n + 1)\(\frac{\pi}{2}\) ⇒ θ = (2n + 1)\(\frac{\pi}{10}\), n ∈ Z

Case (ii): 2cos 3θ – 1 = 0 ⇒ cos 3θ = \(\frac{1}{2}\)
Principal solution is α = \(\frac{\pi}{3}\)

∴ General Solution is
3θ = 2nπ ± \(\frac{\pi}{3}\) ⇒ θ = \(\frac{2 \mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z

∴ General Solutions are
{(2n + 1)\(\frac{\pi}{10}, \frac{2 \mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z}

Question 7.
Solve cos θ – cos 7θ = sin 4θ.
Answer:
2sin\(\left(\frac{\theta+7 \theta}{2}\right)\) sin\(\left(\frac{7 \theta-\theta}{2}\right)\) = sin 4θ
⇒ 2sin4θ sin 3θ = sin 4θ
⇒ sin 4θ(2 sin 3θ – 1) = 0

Case (i): sin 4θ = 0 ⇒ 4θ = nθ ⇒ \(\frac{\mathrm{n} \pi}{4}\), n ∈ Z

Case (ii): 2sin 3θ – 1 = 0 ⇒ sin 3θ = \(\frac{1}{2}\)
Principal solution is α = \(\frac{\pi}{6}\)

∴ General solution is 3θ = nπ + (-1)ⁿ\(\frac{\pi}{6}\)
⇒ θ = \(\frac{\mathrm{n} \pi}{3}\) + (-1)ⁿ\(\frac{\pi}{18}\), n ∈ Z

Question 8.
If tan(π cos θ) = cot (π sin θ), then prove that cos(θ – \(\frac{\pi}{4}\)) = ±\(\frac{1}{2 \sqrt{2}}\). [Mar ’15(TS)]
Answer:
Given that tan(π cos θ)
= cot(π sin θ) = tan(\(\frac{\pi}{2}\) – π cos θ)
∴ π cos θ = ±\(\frac{\pi}{2}\) – π sin θ
⇒ cos θ = ±\(\frac{1}{2}\) – sin θ ⇒ cos θ + sin θ = ±\(\frac{1}{2}\)
⇒ cos θ\(\frac{1}{\sqrt{2}}\) + sin θ\(\frac{1}{\sqrt{2}}=\pm \frac{1}{2 \sqrt{2}}\)
⇒ cos θ cos\(\frac{\pi}{4}\) + sin θ sin\(\frac{\pi}{4}\) = \(\pm \frac{1}{2 \sqrt{2}}\)

Question 9.
If α, β are the solutions of the equation a cos θ + b sin θ = c, where a, b, c ∈ R and if a² + b² > 0, cos α ≠ cos β and sin α ≠ sin β then show that
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α. cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α. sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Answer:
Given acos θ + bsin θ = c ⇒ acos θ = c – bsin θ ⇒ a²cos2θ = c² – 2bcsinθ + b²sin²θ
⇒ a² (1 – sin²θ) = c² – 2bcsinθ + b² sin²θ
⇒ (a² + b²)sin²θ – 2bcsinθ + (c² – a²) = 0
This is a quadratic equation in sin θ and let the roots be sin α and sin β. Then
sin α + sin β = \(\frac{2 b c}{a^2+b^2}\); sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Also b sin θ = c – acos θ ⇒ b²sin²θ = c² -2accos θ + a²cos²θ
⇒ b²(1 – cos²θ) = c² – 2ac cosθ + a² cos²θ
⇒ (b² + a²)cos²θ – 2ac cosθ + (c² – b²) =0
This is a quadratic equation in cos θ and let cos α, cos β be the roots. Then
cos α + cos β = \(\frac{2 a c}{a^2+b^2}\) and cos α. cos β = \(\frac{c^2-b^2}{a^2+b^2}\)

Hence from above we have
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α. cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

Question 10.
Give p ≠ ± q, show that the solutions of cos p0 + cos q0 = 0 form two series each of which is in A.P. Also find the common difference of each A.P. [Mar. ’19(AP)]
Answer:
Given equation is cos pθ + cos qθ = 0

which are two A.P.’s is with common differences