TS Inter 1st Year Maths 1A Functions Important Questions Long Answer Type

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Functions Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Functions Important Questions Long Answer Type

Question 1.
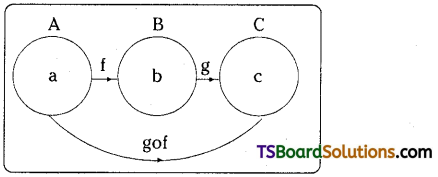
If f : A → B, g : B → C are two bijective functions, then prove that gof : A → C is also a bijective function. [Mar. 18, 16 (AP), 09 ; May 13, 12, 10, 08, 06, 04 00, 96, 92]
Answer:
Since f: A →B is a bijective function
o f: A → B is both one-one and onto functions.
Since f: A → B is a one-one function
⇔ a₁, a₂ ∈ A, f(a₁) = f(a₂) ⇒ a₁ = a₂
Since f: A → B is a onto function ⇔ ∃ one element a ∈ A such that f(a) = b, ∀ b ∈ B.
Since g: B → C is a bijective function
⇔ g: B → C is both one-one and onto functions.
Since g: B → C is a one-one function
⇔ b₁, b₂ ∈ B, g (b₁) = g (b₂) ⇒ b₁ = b₂
Since g: B → C is an onto function ⇔ ∃ one element b e B such that g(b) = c, ∀ c ∈ C.
If f: A → B, g : B → C ⇒ gof: A → C.

To prove that gof: A → C is a one-one function:
If gof: A → C is a one-one function
⇔ a₁, a₂ ∈ A, (gof) (a₁) = (gof) (a₂) ⇒ a₁ = a₂
Now (gof) (a₁) = (gof) (a₂)
g [f(a₁)] = g [ f(a₂)] [∵ g is one-one]
f(a₁) = f(a₂) [∵ f is one-one]
a₁ = a₂
Hence, gof: A → C is a one-one function.

To prove that gof: A → C is an onto function:
Let c ∈ C
If gof: A → C is an onto function ⇔ ∃ one element a ∈ A, such that
(gof) (a) = c, ∀ c ∈ C.
Now (gof) (a) = g [f(a)] = g(b) = c
Thus for any element c ∈ C, there is an element a ∈ A such that (gof) (a) = c.
∴ gof: A → C is an onto function.
Since gof: A → C is both one-one function and onto function then
gof: A → C is a bijective function.

Question 2.
If f : A → B, g : B → C are two bijective functions, then prove that (gof)^-1 = f^-1og^-1. [Mar. ’16 (TS), 14, 11, 10, 06, 04, 02, 00, 92; May 15 (AP) 14, 11, 09, 02, 98, 94 Mar. 19 (AP) ]
Answer:
Since f: A → B, g : B → C are bijections
⇒ gof: A → C is a bijection
⇒ (gof)^-1: C → A is also a bijection
Since f: A → B is a bijective function
then f^-1: B → A is also a bijective function
Since g: B → C is a bijective function
then g^-1: C → B is also a bijective function
⇒ f^-1og^-1: C → A is also a bijection
Since the two functions (gof)^-1, f^-1og^-1 are from C → A their domains are same.
Let c ∈ C
Since f : A → B is onto ⇔ ∃ one element
a ∈ A such that
f(a) = b, ∀ b ∈ B
f(a) = b ⇒ f^-1 (b) = a
Since g : B → C is onto ⇔ ∃ one element be B such that g(b) = c, ∀ c ∈ C
g(b) = c ⇒ g^-1(c) = b
Now (gof) (a) = g[f(a)] = g (b) = c ⇒ a = (gof)^-1(c)
⇒ (gof)^-1(c) = a ………………. (1)
Also (f^-1og^-1) (c) = f^-1 [g^-1(c)] = f^-1(b) = a ……………… (2)
∴ From (1) and (2)
(gof)^-1(c) = (f^-1og^-1) (c)
∴ (gof)^-1 = f^-1og^-1.

Question 3.
Let f : A → B, is a function and I_A, I_B are identity functions on A and B respectively. Then prove that foI_A = f = I_Bof. [Mar. 18 (TS); Mar. 13, 08, 05; May 92]
Answer:
If f: A → B is a function.
If I_A and I_B are identity functions on A and B respectively.
i.e., I_A : A → B, I_B : B → B

(i) I_A: A → A, f: A → B ⇒ f o I_A : A → B
Hence, functions f o I_A and f are defined on same domain A.
Let a ∈ A
(f o I_A) (a) = f[I_A (a)] = f(a)
∴ f o I_A = f

(ii) f: A → B, I_B: B → B ⇒ I_B o f: A → B
The functions (I_B o f) and f are defined on the same domain A.
Let a ∈ A
Now (I_B o f)(a) = I_B[f(a)] = f(a)
∴ I_B o f = f ………………. (2)
From (1) and (2) we get
f o I_A = I_B o f = f

Question 4.
If f: A → B is a bijection, then prove that fof^-1 = I_B and f^-1 o f = I_A. [Mar. 17, 15 (AP); Mar. 12, 07, 03, 02; May 07, 05, 01 Mar. 19 (TS)]
Answer:

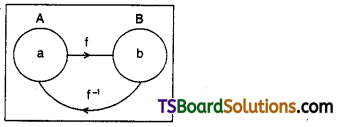
(i) Since f: A → B is a bijection ⇒ f^-1: B → A is also a bijection
I_A; f: A → B, f^-1: B → A ⇒ f^-1 o f: A → A is also bijection
Clearly I_A: A → A such that I_A(a) = a, ∀ a ∈ A
Let a ∈ A
Since f^-1: B → A is onto function ⇔ ∃ one element b ∈ B,
such that
f^-1(b) = a, ∀ a ∈ A
f^-1 (b) = a ⇒ f(a) = b
Now (f^-1of) (a) = f^-1[f(a)] = f^-1(b) = a = I_A(a)
∴ f^-1of = I_A

(ii) Since f: A → B is a bijection ⇒ f^-1: B → A is also bijection
I_B: f^-1:B → A, f: A → B = fof^-1:B → B is also a bijection
Clearly I_B: B → B such that I_B(b) = b, ∀ b ∈ B
Let b ∈ B
Since f^-1: B → A is an onto function ⇔ ∃
one element b ∈ B such that f^-1(b) = a, ∀ a ∈ A
f^-1(b) = a ⇒ f(a) = b
Now (fof^-1) (b) = f[f^-1(b)] = f(a) = b = I_B(b)
∴ fof^-1 = I_B

Question 5.
If f:A → B, g:B → A are two functions such that gof = I_A and fog = I_B, then prove that f is a bijection and g = f^-1. [May 15 (TS); Mar. 08, 01; May 03]
Answer:

(i) To prove that f is one-one
Let a₁, a₂ ∈ A and since f : A → B, f(a₁), f(a₂) ∈ B
Now f(a₁) = f(a₂ ) ⇒ g[f(a₁)] = g[f(a₂)]
⇒ (gof) (a₁) = (gof) (a₂)
⇒ I_A(a₁) = I_A(a₂)
∴ a₁ = a₂
∴ f is one-one

(ii) To prove that f is onto
Let b be an element of B
I_B (b) = (fog) (b)
⇒ b = f[g(b)] ⇒ f(g(b)) = b
i.e., there exists a pre-image g(b) ∈ A for b, under the mapping f.
∴ f is onto
Thus ‘f’ is one-one and onto hence, f^-1: B → A exists and is also one-one onto.

(iii) To prove g = f^-1
Now g:B → A and f^-1:B → A
Let a ∈ A and b be the f – image of a where b ∈ B
∴ f(a) = b ⇒ a = f^-1 (b)
Now g(b) = g[f(a)] (gof) (a) = I_AA(a) = a
⇒ a = f^-1 (b)
∴ g = f^-1

Question 6.
If f:A → B, g: B → C and h: C → D are three functions then prove that ho(gof) = (hog) of. That is composition of functions is associative. [May ‘99, ‘95]
Answer:
f:A → B, g:B → C, h:C → D be three functions.
f:A → B, and g:B → C = gof: A → C
Now gof: A → C and h:C → D ⇒ ho(gof): A → D
g:B → C and h:C → D = (hog):B → D
Now f: A → B ⇒ hog: B→D
(hog)of: A → D
Thus ho(gof) and (hog)of both exist and have the same domain A and co-domain D.
Let a ∈ A,
Hence ho(gof) = (hog) of ∈ A
Now [ho(gof)] (a) = h [(gof) (a)] = h[g(f(a))]
= (hog) [f(a)] = [(hog) of] (a)
∴ [ho(gof)] (a) = [(hog) of] (a)

Question 7.
If f: A → B, g: B → C be surjections, then show that gof: A → C is a surjection. [May 98, 97, 96, 94, 93, 91]
Answer:
Let c ∈ C
Since f: A → B is a onto ⇔ ∃ one element
a ∈ A such that f(a) = b,∀ b ∈ B
Since g: B → C is a onto ⇔ ∃ one element
b ∈ B such that g(b) = c, ∀ c ∈ C.
If f: A → B, g:B → C = gof: A → C
To prove that gof : A → C is a onto

If gof : A → C is a onto ⇔ ∃ one element a ∈ A
such that
(gof) (a) = c, ∀ c ∈ C.
Now (gof) (a) = g[f(a)] = g(b) = c
Thus for any element c € C, there is an
element a ∈ A such that (gof) (a) = c.
∴ gof: A → C is an onto function.

Question 8.
If f = ((1, a), (2, c), (4, d), (3, b)} and g^-1 = {(2, a), (4, b), (1, c), (3, d)}, then show that (gof)^-1 = f^-1og^-1. {Mar. 15 (TS); May 07, 93}
Answer:
Given
f = {(1, a), (2, c), (4, d), (3, b))
f^-1 = ((a, 1), (c, 2), (d, 4), (b, 3))
g = ((a, 2), (b, 4), (c, 1), (d, 3))
g^-1 = {(2, a), (4, b), (1, c), (3, d)}

gof:

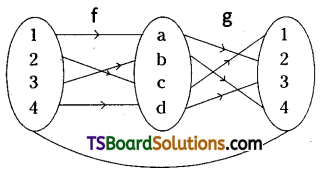
∴ gof = {(1, 2), (2, 1), (3, 4), (4, 3)}
(gof)^-1 = {(2, 1), (1, 2), (4, 3), (3, 4)}
f^-1og^-1

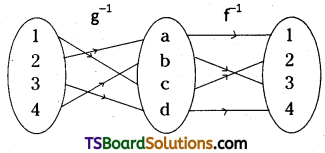
f^-1og^-1 = {(1, 2), (2, 1), (3, 4), (4, 3)}
∴ (gof)^-1 = f^-1og^-1

Question 9.
If the function f is defined by

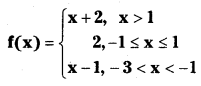
then find the values of
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(- 2)
(v) f(- 5).
Answer:
Given

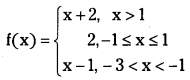
(i) For x > 1; f(x) = x + 2; f(3) = 3 + 2 = 5
(ii) For – 1 ≤ x ≤ 1; f(x) = 2, f(0) = 2
(iii) For – 3 < x < – 1; f(x) = x – 1 ∴ f(- 1.5) = – 1.5 – 1 = – 2.5 (iv) For x > 1, f(x) = x + 2
f(2) = 2 + 2 = 4
For – 3 < x < – 1, f(x) = x – 1
∴ f(- 2) = – 2 – 1 = – 3
f(2) + f(- 2) = 4 – 3 = 1
(v) f(- 5) is not defined.

Question 10.
If A = {- 2, – 1, 0, 1, 2) and f: A → B is a surjection defined by f(x) = x² + x + 1 find B.
Answer:
Given, A = {- 2, – 1, 0, 1, 2)
f(x) = x² + x + 1
Since f : A → B is a surjection then f(A) = B
f(-2) = (- 2)² – 2 + 1 = 4 – 2 + 1 = 3
f(-1) = (- 1)² – 1 + 1 = 1 – 1 + 1 = 1
f(0) = 0² + 0 + 1 = 1
f(1) = 1² + 1 + 1 = 1 + 1 + 1 = 3
f(2) = 2² + 2 + 1 = 4 + 2 + 1 = 7
∴ B = f(A) = {3. 1, 7}

Question 11.
If A = {1, 2, 3, 4} and f:A → R is a function defined by f(x) = \(\frac{x^2-x+1}{x+1}\), then find the range of f.
Answer:
Given A = {1, 2, 3, 4) and f(x) = \(\frac{x^2-x+1}{x+1}\)
Since f: A → R is a function, then

Question 12.
If f: Q → Q, is defined by f(x) = 5x + 4 for all x ∈ Q, find f^-1. [Mar. 17 (TS)]
Answer:
Let y = f(x) = 5x + 4
y = f(x) ⇒ x = f^-1(y) ……………… (1)
y = 5x + 4 ⇒ y – 4 = 5x
x = \(\frac{y-4}{5}\) ………………… (2)
From (1) and (2),
f^-1(y) = \(\frac{y-4}{5}\) ⇒ f(x) = \(\frac{x-4}{5}\), ∀ x ∈ Q

Question 13.
If f(x) = \(\frac{x+1}{x-1}\) (x ≠ ± 1), then find (fofofof) (x).
Answer:
Given f(x) = \(\frac{x+1}{x-1}\) (x ≠ ± 1)
Now (fofofof) (x) = f[f[f{f(x)}]]

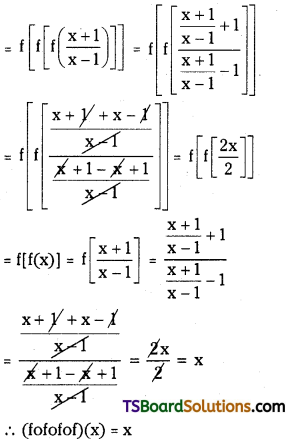
Question 14.
Find the domain of the real valued function f(x) = \(\sqrt{16-x^2}\).
Answer:
Given f(x) = \(\sqrt{16-x^2}\) ∈ R
⇒ 16 – x² ≥ 0
⇒ x² – 16 ≤ 0
⇒ (x + 4) (x – 4) ≤ 4
⇒ x ∈ [- 4, 4]
∴ Domain of ‘f’ is [- 4, 4]

Question 15.
Find the domain of the real valued function f(x) = \(\sqrt{9-x^2}\).
Answer:
Given f(x) = \(\sqrt{9-x^2}\) ∈ R
⇒ 9 – x² ≥ 0
⇒ x² – 9 ≤ 0
⇒ (x + 3) (x – 3) ≤ 0
⇒ x ∈ [- 3 ,3]
∴ Domain of f’ is [- 3, 3]

Question 16.
Find the domain of the real valued function f(x) = \(\frac{1}{6 x-x^2-5}\).
Answer:
Given f(x) = \(\frac{1}{6 x-x^2-5}\) ∈ R
⇒ 6x – x² – 5 ≠ 0
⇒ x² – 6x + 5 ≠ 0
⇒ x² – 5x – x + 5 ≠ 0
⇒ x(x – 5) – 1 (x – 5) ≠ 0
⇒ x – 1 ≠ 0 or x – 5 ≠ 0
⇒ x ≠ 1 or x ≠ 5
∴ x ≠ 1, 5
∴ Domain of ‘f’ is R – {1, 5}

Question 17.
Find the domain of the real valued function f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\).
Answer:
Given f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\) ∈ R
⇒ (x – 1) (x – 2) (x – 3) ≠ 0
⇒ x – 1 ≠ 0, x – 2 ≠ 0, x – 3 ≠ 0
⇒ x ≠ 1, x ≠ 2, x ≠ 3
∴ x ≠ 1, 2, 3
∴ Domain of ‘f’ is R – {1, 2, 3}

Question 18.
Find the domain of the real valued function f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\).
Answer:
Given f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\) ∈ R

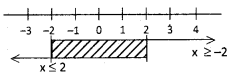
⇒ 2 + x ≥ 0, 2 – x ≥ 0 and x ≠ 0
x ≥ – 2, 2 ≥ x and x ≠ 0
x ≤ 2 and x ≠ 0
⇒ x ∈ [- 2, 0) ∪ (0, 2]
∴ Domain of ‘f’ is [- 2, 0) ∪ (0, 2]

Question 19.
If f = {(1, 2), (2, – 3), (3, – 1)}, then find
(i) 2f
(ii) 2 + f
(iii) f²
(iv) √f
Answer:
Given f = {(1, 2), (2, – 3), (3, – 2)}
Domain of ‘f’ is A = {1, 2, 3}
f(1) = 2f(2) = – 3, f(3) = – 1

(i) (2f) (x) = 2f(x)
(2f) (1) = 2f(1) = 2(2) = 4
(2f) (2) = 2f(2) = 2(- 3) = – 6
(2f) (3) = 2f(3) = 2(- 1) = – 2
∴ 2f = {(1, 4), (2, – 6),(3, – 2)}

(ii) (2 + f) (x) = 2 + f(x)
(2 + f) (1) = 2 + f(1) = 2 + 2 = 4
(2 + f) (2) = 2 + f(2) = 2 – 3 = – 1
(2 + f) (3) = 2 + f(3) = 2 – 1 = 1
∴ 2 + f = {(1, 4), (2, – 1), (3, 1)}

(iii) (f²) (x) = [f(x)]²
(f²) (1) = [f(1)]² = 2² = 4
(f²) (2) = [f(2)]² = (- 3)² = 9
(f²) (3) = (f(3)]² = (- 1)² = 1
∴ f² = {(1, 4), (2, 9), (3, 1)}

(iv) (√f)(x) = √f(x)
(√f) (1) = √f(1) = √2
(√f) (2) = √f(2) = √- 3 (not valid)
(√f) (3) = √f(3) = √- 1 (not valid)
∴ √f = {(1, √2)}

Some More Maths 1A Functions Important Questions

Question 1.
If f(x) = \(\frac{\cos ^2 x+\sin ^4 x}{\sin ^2 x+\cos ^4 x}\), ∀ x ∈ R then show that f(2012) = 1.
Answer:

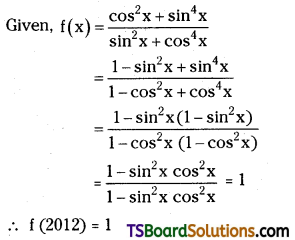
Question 2.
If f: R → R is defined by f(x) = \(\frac{1-x^2}{1+x^2}\), then show that f(tan θ) = cos 2θ.
Answer:
Given f: R → R, f(x) = \(\frac{1-x^2}{1+x^2}\)
LHS = f(tan θ)
= \(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\) = cos 2θ + RHS
∴ f(tan θ) = cos 2θ

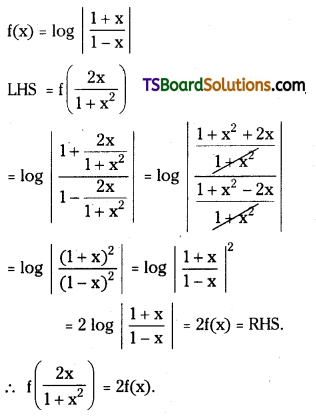
Question 3.
If f: R – {±1} → R is defined by f(x) = log \(\left|\frac{1+x}{1-x}\right|\), then show that f(\(\left(\frac{2 x}{1+x^2}\right)\)) = 2f(x)
Answer:
Given f: R – {±1} → R

Question 4.
If A = {x/ – 1 ≤ x ≤ 1}, f(x) = x², g(x) = x³ which of the following are surjections?
(i) f : A → A
(ii) g: A → A
Answer:
(i) Given A = {x/ – 1 ≤ x ≤ 1}
∴ A = {- 1, 0, 1}
f(x) = x²
f(- 1) = (- 1)² = 1
f(0) = (0)² = 0
f(1) = (1)² = 1
∴ f = (- 1, 1), (0 , 0), (1, 1))

f: A → A

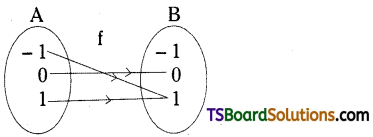
Range of f(A) = {0, 1) ≠ A (co-domain)
∴ f : A → A is not a surjection.

(ii) Given A = {x/ – 1 ≤ x ≤ 1}
∴ A = {- 1, 0, 1}
g(x) = x³
g(- 1) = (- 1)³ = – 1
g(0) = (0)³ = 0
g(1) = (1)³ = 1
∴ g = {(- 1, -1), (0, 0), (1, 1)}
g: A → A

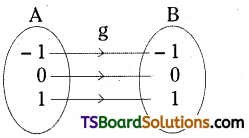
Range of g(A) = {- 1, 0, 1} = A (co-domain)
∴ g is a surjection.

Question 5.
If f(x) = cos (log x) then show that
\(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\) = 0
Answer:
Given f(x) = cos (log x)
f\(\left(\frac{1}{x}\right)\) = cos\(\left(\log \frac{1}{x}\right)\) = cos (log x^-1)
= cos (- log x) = cos (log x)
Similarly f\(\left(\frac{1}{y}\right)\) = cos (log y)
f\(\left(\frac{x}{y}\right)\) = cos \(\left(\log \left(\frac{x}{y}\right)\right)\)
= cos (log x – log y)
f(xy) = cos (log xy)
= cos (log x + log y)
L.H.S: f\(\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left(f\left(\frac{x}{y}\right)+f(x y)\right)\)
= cos (log x) . cos (log y) – \(\frac{1}{2}\) [cos (log x – log y) + cos (log x + log y)]
= cos (log x) . cos (log y)

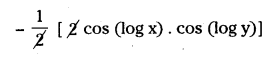
= cos (log x) . cos (log y) – cos (log x) . cos (log y) = 0
= R.H.S

Question 6.
Find the inverse function of f(x) = log₂x.
Answer:
Given f: (0, ∝) → R, f(x) = log₂x
Let y = f(x) = log₂x
y = f(x) = x = f^-1(y) ……………. (1)
y = log₂x ⇒ x = 2^y (2)
From (1) & (2)
f^-1(y) = 2y
⇒ f^-1(x) = 2x

Question 7.
If f(x) = 1 + x + x² +…….. for |x| < 1, then show that f^-1(x) = \(\frac{\mathbf{x}-1}{\mathbf{x}}\).
Answer:
Given that f(x) = 1 + x + x² + ………….
f(x) = \(\frac{1}{1-\mathrm{x}}\)

Question 8.
Find the domain of the real valued function f(x) = \(\frac{1}{\sqrt{\mathbf{x}^2-a^2}}\) (a >0). [Mar.15 (AP)]
Answer:
Given f(x) = \(\frac{1}{\sqrt{x^2-a^2}}\) ∈ R
⇒ x² – a²
⇒ (x + a) (x – a) > 0
⇒ x < – a or x > a
⇒ x ∈ (- ∝, – a) ∪ (a, ∝)
∴ Domain of f’ is (- ∝, – a) ∪ (a, ∝)

Question 9.
Find the domain of the real valued function f(x) = \(\sqrt{(\mathbf{x}-\alpha)(\beta-\mathbf{x})}\) (0 < α < β).
Answer:
Given f(x) = \(\sqrt{(\mathbf{x}-\alpha)(\beta-\mathbf{x})}\) ∈ R
⇒ (x – α) (x – β) ≥ 0
⇒ (x – α) (x – β) ≤ 0
⇒ α ≤ x ≤ β
⇒ x ∈ [α, β]
∴ Domain of ‘f’ is [α, β]

Question 10.
Find the domain of the real valued function f(x) = \(\sqrt{2-x}+\sqrt{1+x}\).
Answer:
Given f(x) = \(\sqrt{2-x}+\sqrt{1+x}\) ∈ R
⇒ 2 – x ≥ 0 and 1 + x ≥ 0
⇒ 2 ≥ x and x ≥ – 1
⇒ x ≤ 2 and x ≥ – 1
⇒ x ∈ [- 1, 2]
∴ Domain of ‘f’ is [-1, 2]

Question 11.
Find the domain of the real valued function f(x) = \(\sqrt{|\mathbf{x}|-\mathbf{x}}\)
Answer:
Given f(x) = \(\sqrt{|\mathbf{x}|-\mathbf{x}}\) ∈ R
⇒ |x| – x ≥ 0
⇒ |x| ≥ x
⇒ x ∈ R
∴ Domain of ‘f’ is ‘R.

Question 12.
Find the domain and range of the real valued function f(x) = \(\frac{2+x}{2-x}\)
Answer:
Given f(x) = \(\frac{2+x}{2-x}\) ∈ R
⇒ 2 – x ≠ 0 ⇒ x ≠ 2
Domain of T is R – { 2 }.
Let y = f(x) = \(\frac{2+x}{2-x}\)
y = \(\frac{2+x}{2-x}\)
2yx – xy = 2 + x
2y – 2 = x + xy
2y – 2 = x(1 + y)
x ∈ R – {2}, y + 1 ≠ 0
y ≠ – 1
∴ Range of ‘f’ is R – {- 1}.

Question 13.
Find the domain and range of the real valued function f(x) = \(\sqrt{9-x^2}\) [Mar. 15 (TS)]
Answer:
Given f(x) = \(\sqrt{9-x^2}\) ∈ R
⇒ 9 – x² ≥ 0
⇒ x² – 9 ≤ 0
⇒ (x + 3) (x -3) ≤ 0
⇒ x ∈ [- 3, 3]
∴ Domain of ‘f’ is [- 3, 3]
Let y = f(x) = \(\sqrt{9-x^2}\)
y = \(\sqrt{9-x^2}\)
y² = 9 – x²
x² = 9 – y²
x = \(\sqrt{9-y^2}\) ∈ R
⇒ 9 – y² ≥ 0
⇒ y² – 9 ≤ 0
⇒ (y + 3) (y – 3) ≤ 0
⇒ y ∈ [- 3, 3]
But f(x) attains only non-negative values.
∴ Range of f = [0, 3].

Question 14.
Determine whether the function f(x) = x\(\left(\frac{e^x-1}{e^x+1}\right)\) is even or odd.
Answer:

Since f(- x) = f(x) then f is an even function.

Question 15.
Determine whether the function f(x) = log(x + \(\sqrt{x^2+1}\)) is even or odd.
Answer:

Since f(- x) = – f(x) then f(x) is an odd function.

Question 16.
Find the domain of the real valued function f(x) = log [x – (x)].
Answer:
Given f(x) = log [x – (x)] ∈ R
⇒ x – (x)> 0
⇒ x > (x)
Then x is a non – integer.
∴ Domain of ‘f’ is R – Z.

Question 17.
Find the domain of the real valued function f(x) = \(\frac{1}{\log (2-x)}\).
Answer:
Given f(x) = \(\frac{1}{\log (2-x)}\) ∈ R
⇒ log (2 – x) ≠ 0 and 2 – x > 0
⇒ log (2 – x) ≠ log 1 and 2 > x
⇒ 2 – x ≠ 1 and x < 2
⇒ x ≠ 1
∴ Domain of ‘f’ is (- ∝, 1) ∪ (1, 2)

Question 18.
Find the domain of the real valued function f(x) = \(\sqrt{\mathbf{x}-[\mathbf{x}]}\).
Answer:
Given f(x) = \(\sqrt{\mathbf{x}-[\mathbf{x}]}\) ∈ R
⇒ [x] – x ≥ 0 ⇒ x ≥ [x] ⇒ x ∈ R
∴ Domain of ’f is Z.

Question 19.
Find the domain of the real valued function f(x) = \(\sqrt{[\mathbf{x}]-\mathbf{x}}\).
Answer:
Given f(x) = \(\sqrt{[\mathbf{x}]-\mathbf{x}}\) ∈ R
⇒ [x] – x ≥ 0 ⇒ [x] ≥ x ⇒ x ∈ Z
∴ Domain of ‘f’ is Z.

Question 20.
If f and g are real valued functions defined by f(x) = 2x – 1 and g(x) = x² then find
(i) (3f – 2g)(x)
(ii) (fg) (x)
(iii) \(\left(\frac{\sqrt{f}}{g}\right)\)(x)
(iv) (f + g + 2) (x)
Answer:
Given f(x) = 2x – 1 and g(x) = x²
Domain of f = domain of g R
Hence the domain of all the functions is R.
(i) (3f – 2g) (x) = 3f(x) – 2g(x)
= 3(2x – 1) – 2(x²)
= 6x – 3 – 2x²
= – 2x² + 6x – 3

(ii) (fg)(x) f(x) . g(x)
= (2x – 1)(x²) = 2x³ – x².

(iii) \(\left(\frac{\sqrt{f}}{g}\right)\) (x) = \(\frac{\sqrt{f(x)}}{g(x)}\) = \(\frac{\sqrt{2 x-1}}{x^2}\)

(iv) (f + g + 2) (x) = f(x) .g(x) + 2
= 2x – 1 + x² + 2
= x² + 2x + 1 = (x + 1)²

Question 21.
Find the domain of the real valued function f(x) = \(\sqrt{x^2-3 x+2}\).
Answer:
Given f(x)= \(\sqrt{x^2-3 x+2}\) ∈ R
⇒ x² – 3x + 2 ≥ 0
⇒ x² – 2x – x + 2 ≥ 0
⇒ x(x – 2) – 1(x – 2) ≥ 0
⇒ (x – 1) (x – 2) ≥ 0
⇒ x ≤ 1 or x ≥ 2
⇒ x ∈ (- ∝, 1] ∪ [2, ∝)
∴ Domain of ‘f’ is (- ∝, 1] ∪ [2, ∝)

Question 22.
f:R → R defined by f(x) = \(\frac{2 x+1}{3}\), then this function Is injection or not ? Justify. (Mar. 15 (TS)
Answer:
Given that f(x) = \(\frac{2 x+1}{3}\)
Let x₁, x₂ ∈ R.
Take f(x₁) = f(x₂) ⇒ \(\frac{2 x_1+1}{3}=\frac{2 x_2+1}{3}\)
⇒ 2x₁ + 1 = 2x₂ + 1 ⇒ 2x₁ = 2x₂ = x₁ = x₂
∴ f(x₁) = f(x₂) ⇒ x₁ = x₂
⇒ f is one – one.

Question 23.
If f = {(4, 5), (5, 6),(6, – 4)} and g = ((4, – 4), (6, 5), (8, 5)) then find f + g and fg. [Mar. ‘17(TS)]
Answer:
Given f = {(4, 5), (5, 6), (6, – 4)} and
g = {(4, – 4), (6, 5), (8, 5’)) then domain of f = {4, 5, 6) and Range of f = {4, 6, 8}
Domain of f + g = A ∩ B = {4, 6}
= (domain of f) ∩ (domain of g)
(i) f.g={(4, 5, – 4), (6, – 4 + 5)}
= {(4, 1), (6, 1)}

(ii) Domain of fg = (domain of f) ∩ (domain of g)
= A ∩ B = (4, 6)
= {(4, 5 × – 4).(6, – 4 × 5)}.
= {(4, – 20), (6, – 20)}

Question 24.
If f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) for all x ∈ R, are two functions, then find,
(i) (gof) (x)
(ii) (fog) (x) [Mar. 19(TS)]
Answer:
Given f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\)

(i) (gof) (x) = g[ f(x) ]
= g[2x – 1] = \(\frac{2 x-1+1}{2}\) = \(\frac{2 x}{2}\) = x

(ii) (fog) (x) = f [g(x)]
= \(f\left(\frac{x+1}{2}\right)\) = 2\(\left(\frac{\mathrm{x}+1}{2}\right)\) – 1 = x + 1 – 1 = x