TS Inter 2nd Year

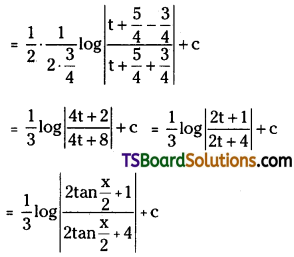
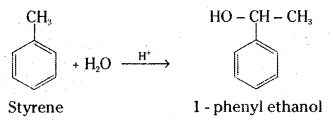
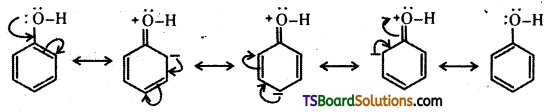
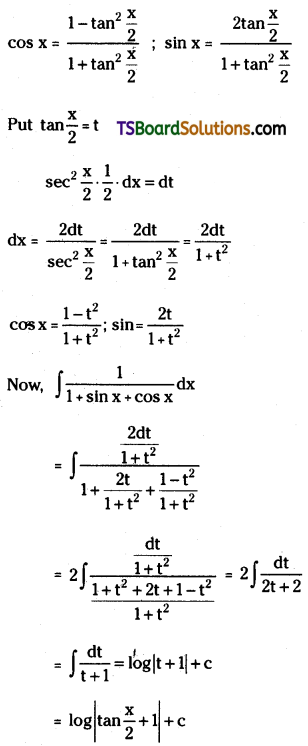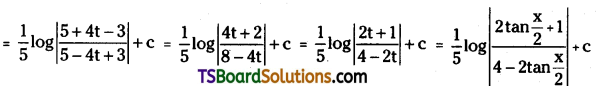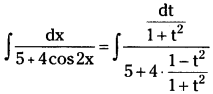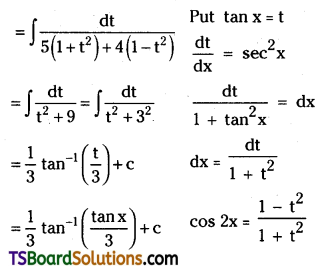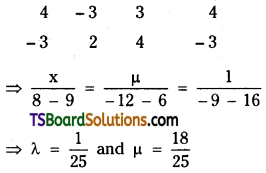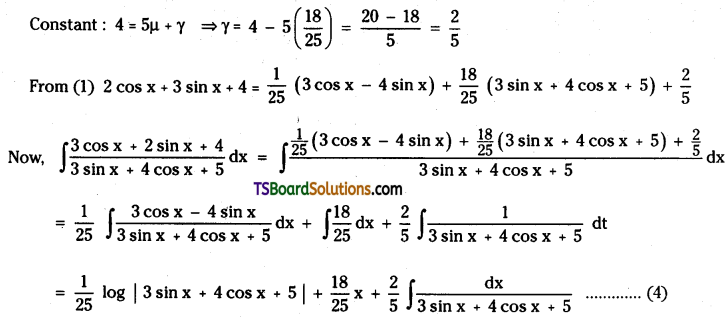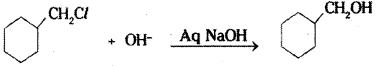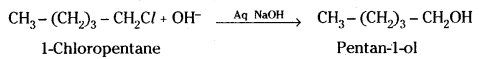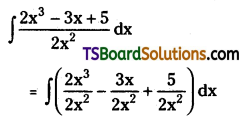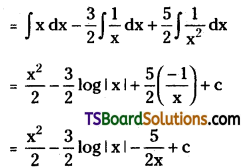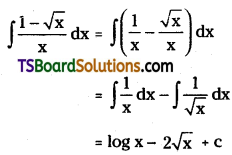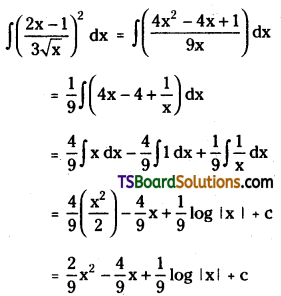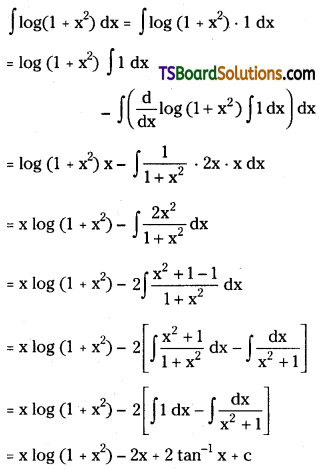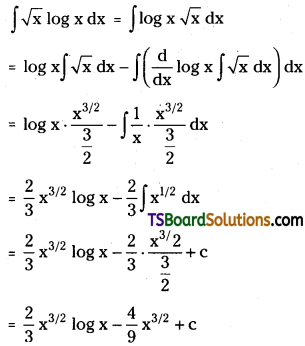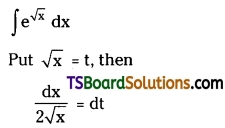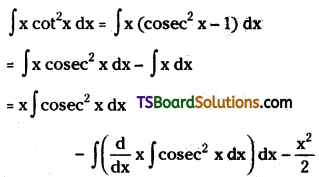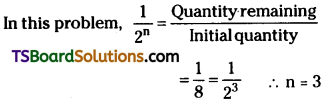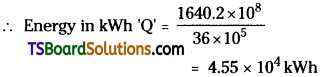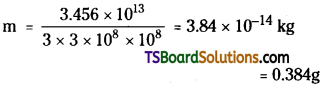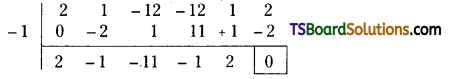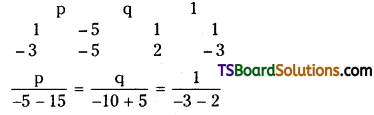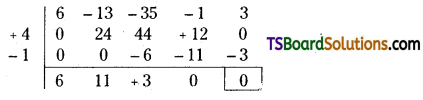Telangana TSBIE TS Inter 2nd Year Accountancy Study Material 1st Lesson Depreciation Textbook Questions and Answers.

TS Inter 2nd Year Accountancy Study Material 1st Lesson Depreciation

Short Answer Questions

Question 1.
Write the need or significance of depreciation.
Answer:
Need or significance or providing depreciation:
1. To ascertain true results of business operations: As depreciation is treated as expenditure, it must be charged to profit and loss account against income to assess the real profit/loss of the business.

2. To show the fixed asset at their original worth in the balance sheet: If depreciation is not provided, the value of the asset shown in the balance sheet is not correct. Hence, the real value of the asset must be shown in the balance sheet after deducting depre¬ciation from its book value.

Question 2.
Briefly explain different methods of providing depreciation.
Answer:
The various methods pf providing depreciation are given below:
1) Fixed Instalment method: Fixed instalment method is also called as equal instalment method or original cost method or straight-line method under this method depreciation is charged on the original cost of the asset every year. In this method annual depreciation is fixed or uniform.

2) Diminishing Balance method: Diminishing balance method is also called as written down value method (WDU) or reducing balance method under this method deprecia¬tion is calculated at a fixed percentage on the diminishing value of the asset.

3) Annuity method: This method takes into account the interest lost on the acqisition of an asset. Interest is calculated on the book value of the asset in the beginning of every year, and is debited to asset account. The amount of depreciation to be charged is uniform and is calculated on the basis of annuity tables.

4) Depreciaton fund method: This method provides funds for replacement of assets. The amount writtenoff as depreciation is kept aside and that amount is invested in certain securities. When the life of the asset expires, the securities are sold and a new asset is purchased with the help of sale proceeds. Depreciation amount is calculated with the help of Sinking Fund Tables.

5) Depletion method: Under this method total quantity of output likely to be available is estimated. Depreciation rate is calculated by dividing the cost of the asset by the esti-mated quantity of product likely to be available.
Suitability: It is used for mines and quarries.

6) Machine Hour Bate method: In this method the life of asset is estimated in hours. In order to calculate depreciation the actual number of hours in a particular year is multiplied by the hourly rate.

Suitability: This method is Used for Machines.

Question 3.
Write the merits and demerits of straight-line method.
Answer:
Merits:

1. This method is very easy to understand.
2. It is very simple to calculating depreciation & rate of depreciation.
3. Under this method, assets can be written off completely. That is upto zero, so the value of asset is equally spread out over the useful life of the asset.
4. This method is suitable for small businesses.
5. This method is useful to those assets having lower value and fixed life.

Demerits:

1. The method is illogical, because, depreciation is charged on original cost every year, but to the balance of asset is declining every year.
2. This method is not recognised by the income tax authorities.
3. This method is not useful incase any additions and expansions made to assets.
4. In put pressure on the asset in the slack years, in the end of the asset’s life, it bears more repairs and maintence charges but the depreciation charge is equal for all years.

Question 4.
What are the advantages and limitations of the diminishing balance method?
Answer:
Advantages:

1. This method is easy to calculate depreciation when there are no additions to the asset.
2. It equalises the burden on profit and loss account in respect of repairs and deprecia¬tion put together.
3. This method is accepted by income tax authorities under the income tax Act 1961.
4. This method is logical in the sence that as the asset value decreases the amount of depreciation also goes on decreasing.
5. This method can be used where obsolescence rare is high.

Limitations:

1. It is very difficult to determine the appropriate rate of depreciation.
2. In this method the value of the asset cannot be reduced to zero. Some balance will be left at the end of its useful life.
3. This method is not suitable for the assets which have shorter life.
4. It does not provide for the replacement of the asset.

Question 5.
Distinguish between stright line method and diminishing balance method.
Answer:

Very Short Answer Questions

Question 1.
Define the term Depreciation.
Answer:

1. Depreciation is a permanent, continuous and gradual shrinkage in the value of fixed asset.
2. Depreciation means a fell in the value or quality of an asset.
3. According to companies Act 2013, “Depreciation is the systematic allocation of the depreciable amount of an asset over its useful life”.

Question 2.
What is obsolescene?
Answer:

1. Obsolescene means diminution in the value of fixed asset due to new inventions, new improvements, change in fashions, change in customer’s tastes and preferences.
2. For Example: Invention of computer made typewriters becomes obsiete or out dated.

Question 3.
What are the causes of depreciation?
Answer:
Causes of depreciation are:

1. Wear and Tear,
2. Depletion,
3. Accidents,
4. Obsolescence,
5. Effluxion of time/passage of time, 6) Fluctuations.

Question 4.
What is Depletion?
Answer:

1. Depletion means loss of natural resources mineral wealth due to extraction of raw material from mines, quarries, oil wells etc.
2. It refers to the physical deterioration by the exhaustion of natural resources like oil wells, mines quarries etc.

Question 5.
What is the straight-line method?
Answer:

1. The method under which, the same amount of depreciation is charged on the original cost of the asset every year throughout the life of the asset, is called straight line method.
2. Straight line method is also known as “Fixed Instalment Method” or Equal Instalment method” or original cost method”.

Question 6.
What is diminishing Balance Method?
Answer:

1. A method under which depreciation is calculated at a fixed percentage on the original cost of the asset in the first year and on written down value in the subsequent year is called dininishing balance method.
2. It is also called reducing balance method (or) written down value method.

Question 7.
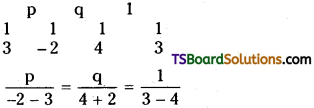
Distinguish depletion from depreciation.
Answer:

Textual Problems

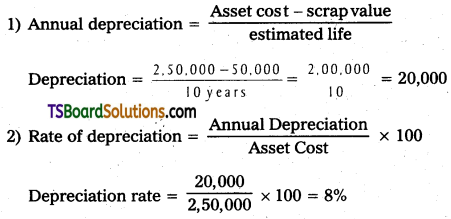
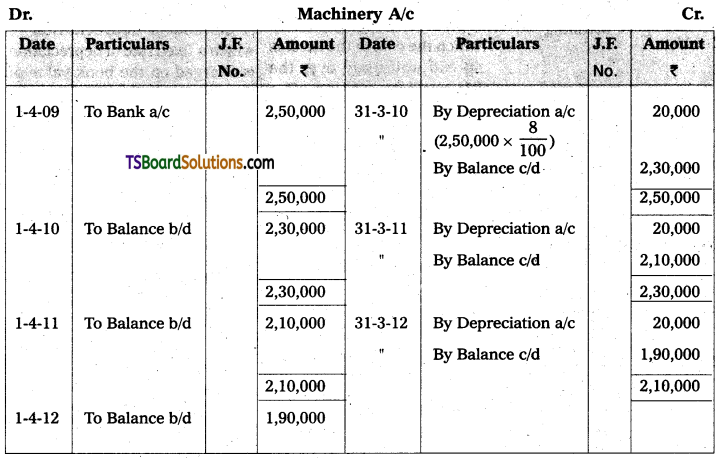
Question 1.
Straight Line Method:
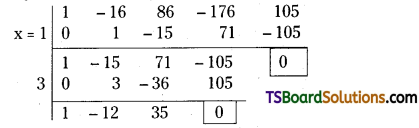
Sri sai & Co purchased a machine for Rs. 2,50,000 on 1st April 2009. Estimated life of the machine is 10 years. The scrap value at the end of its life is Rs. 50,000. Calculate the annual depreciation and rate of depreciation assuming that accounts are closed on 31st March every year. Show the machinery a/c for the first three years under fixed instalment method.
Answer:
Calculation of depreciation and rate of depreciation:

Question 2.
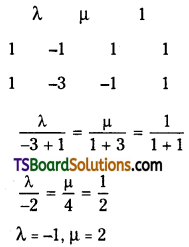
Ganesh bought a machine or Rs. 17,000 and paid for its installation Rs. 3,000 on 30th Sept. 2017. Depreciation is provided at 20% under the straight-line method. Prepare machine a/c up to 31st March, 2020.
Answer:

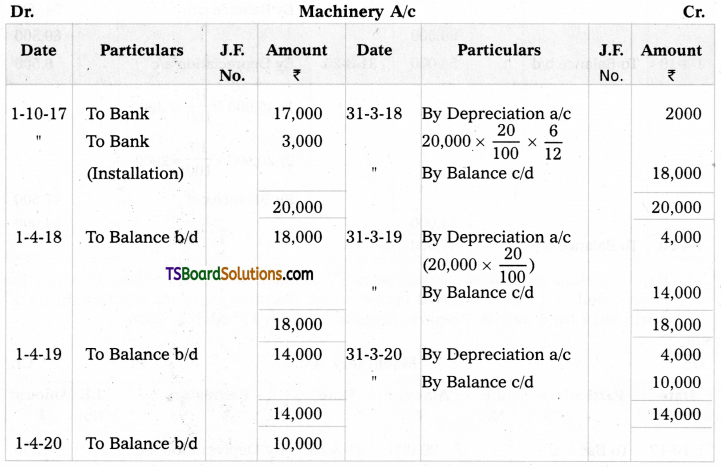
Question 3.
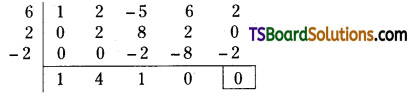
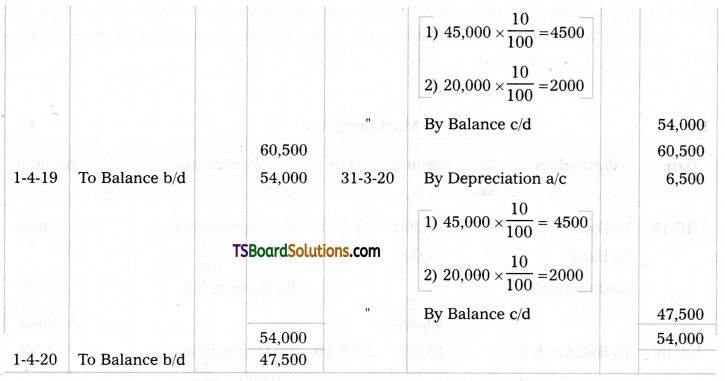
Kiran & Sons purchased a machine for 142,000 and paid Rs. 3,000 for its erection on 1st April 2017. Additions are made to the machine on 31st March 2018 for Rs. 20,000. Accounts are closed at the end of financial year. Depreciation is allowed at 10% under fixed instalment method. Prepare machine a/c for three years.
Answer:

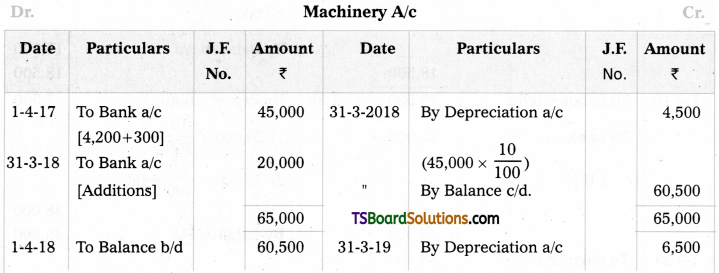
Question 4.
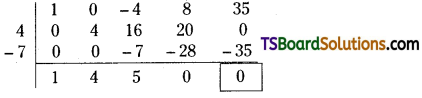
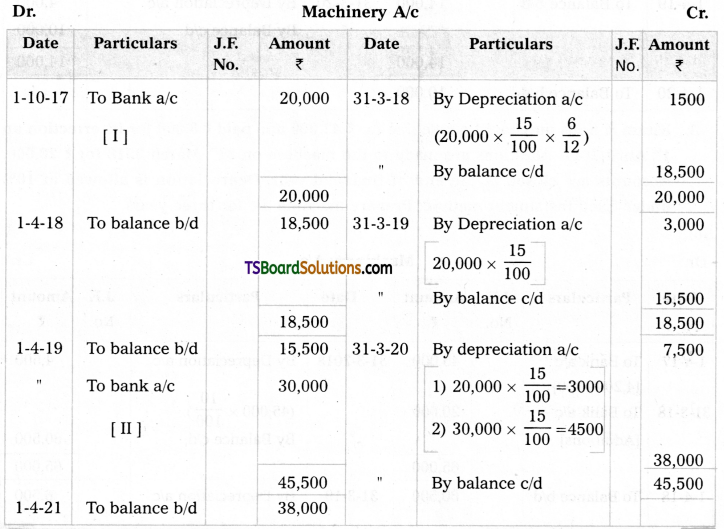
Rajesh & Sons purchased a machine on 1st October, 2017 for Rs. 20,000. Depreciation is provided at 15% on original cost method. Another machine was bought on 1st April, 2019 for Rs. 30,000. Prepare machine a/c upto 31st March, 2020.
Answer:

Question 5.
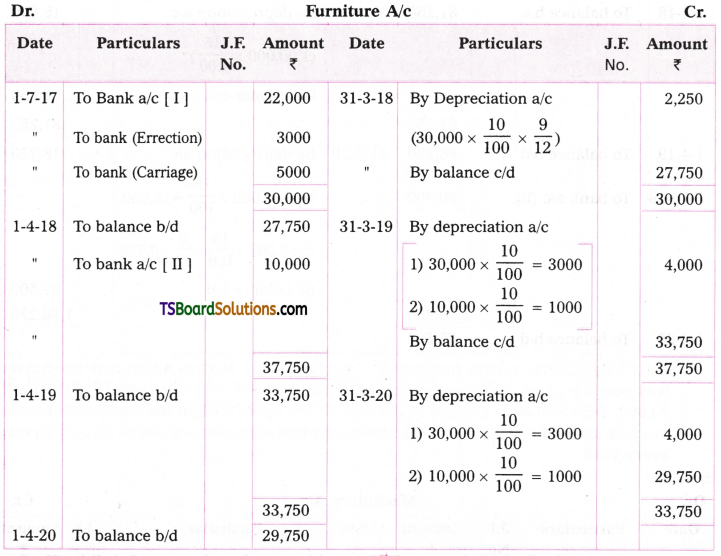
Ramana & Brothers purchased furniture for Rs. 22,000 on 1st July 2017. Errection charges paid for Rs. 3,000 and paid for carriage Rs. 5,000. Depreciation is to be charged at the rate of 10% on original cost method. Additions are made to the asset for Rs. 10,000 on 1st April 2018. Show the furniture a/c for three years assuming that accounts are closed on 31st March every year.
Answer:

Question 6.
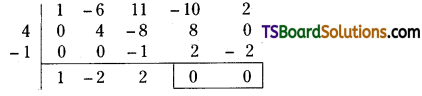
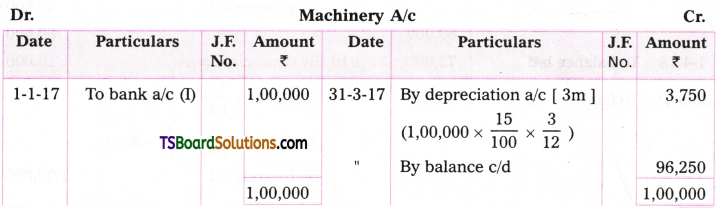
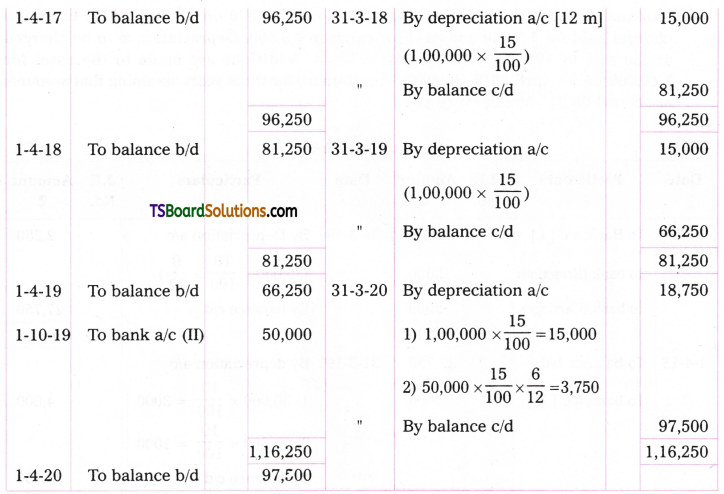
Karthik & Company bought a machine on 1st January, 2017 for Rs. 1,00,000. Depreciation is provided at 15% under straight line method. Another machine was purchased on 1st October 2019 for Rs. 50,000. Company closes its accounts every year at the end of the financial year. Prepare machine a/c for four years.
Answer:

Question 7.
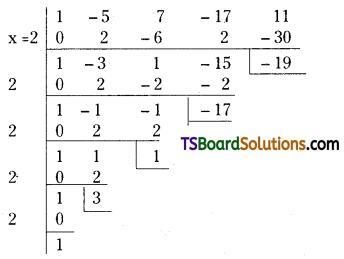
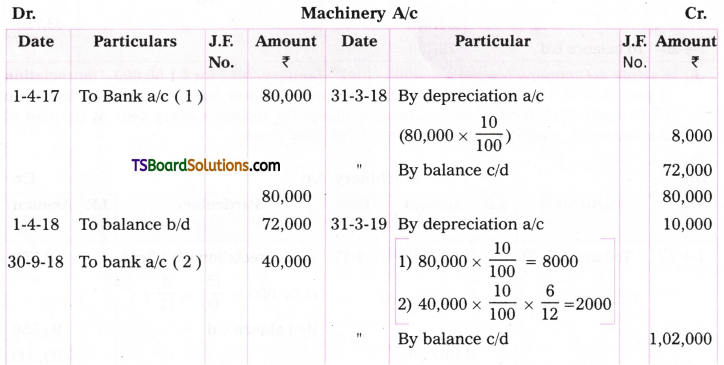
On 1st April, 2017 a firm purchased a machine for Rs. 80,000. Additional machinery was purchased on 30th September, 2018 for Rs. 40,000 and on April 1st 2019 for Rs. 20,000. Depict iation is charged at the rate of 10% under straight line method. Show the machine a/c for 2018, 2019 and 2020 assuming that accounts are closed on 31st March,
Answer:

Question 8.
Raghava bought a plant and machine on 1st April, 2017 for Rs. 23,000 and paid Rs. 2,000 for its installation. Depreciation is to be allowed at 10% under straight line method. On 31st March 2020 the plant was sold for Rs. 8,000. Assuming that the accounts are closed at the end of the financial year. Prepare plants machine a/c.
Answer:

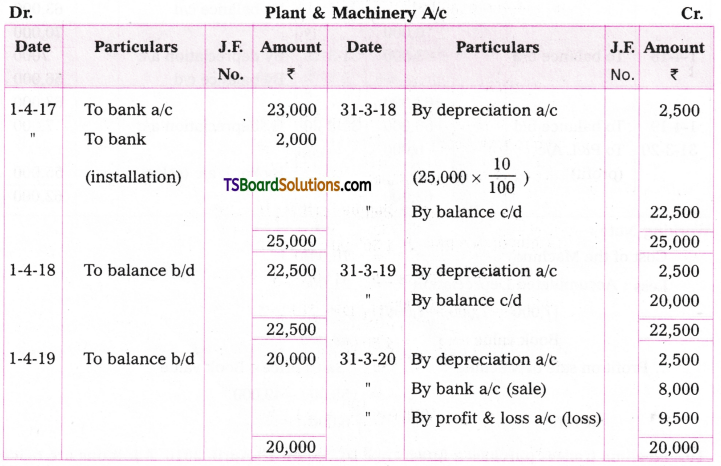
Working Note:
Cost of the plant & machine = 25,000
Loss calculation on the date of sale of machine:
Accumulated depreciaton = 7,500
(2,500 + 2,500 + 2,500)
Bank value = 17,500
Sale Price of the Machine = 8,000
Loss = 9,500

Question 9.
Vardhan purchased a machine on 31st March 2017 for Rs. 70,000. Depreciation is charged at 10% under original cost method. After three years he found that the machine was not suitable and sold for Rs. 55,000. Show the machine a/c.
Answer:

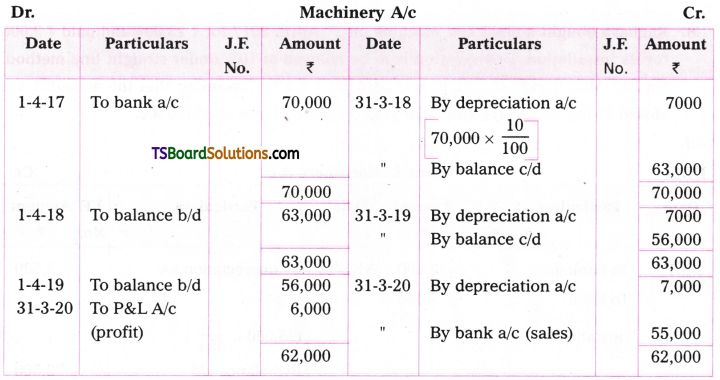
Working Note:
Cost of the Machine = 70,000
Less: Accumulated Depreciation = 21,000
[7,000 + 7,000 + 7,000]
Book value = 49,000
Profit on sale of Machine = Sales price – Book value
= 55,000 – 49,000
= 6,000

Question 10.
Neelima traders purchased furniture Rs. 20,000 on 1st April, 2016. Additions are made to the furniture on 30th September, 2017 for Rs. 10,000. On 31st December, 2019, the furniture purchased on 1st April 2016 was sold for Rs. 7,000. Depreciation is charged at 10% on fixed instalment method. The firm closes its books at the end of financial year. Prepare furniture a/c for four years.
Answer:


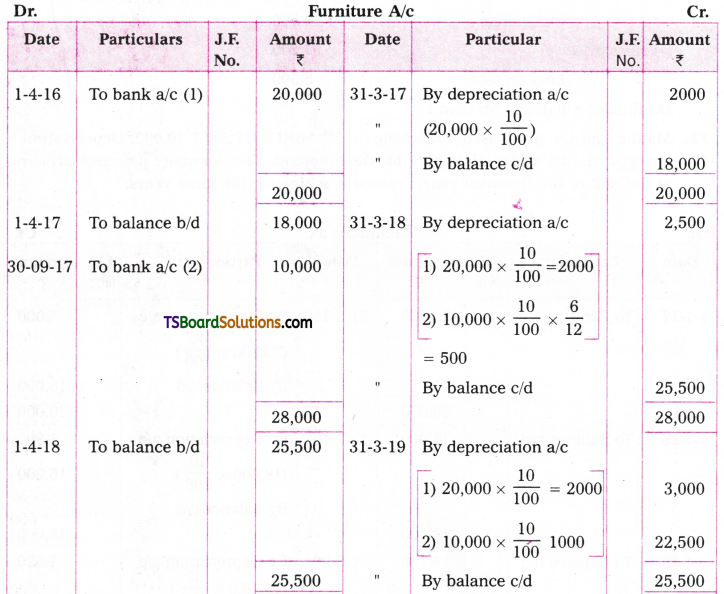
Working Note:
Calculation of profit / loss on sale of Furniture:
Cost of the furniture = 20,000

Diminishing Balance Method:

Question 11.
Madhu and Co. purchased a machine on 1st April 2017 for Rs. 20,000. Depreciation is charged at 10% under dimishing balance method. The company prepares accounts at the end of the financial year. Prepare machine a/c for three years.
Answer:

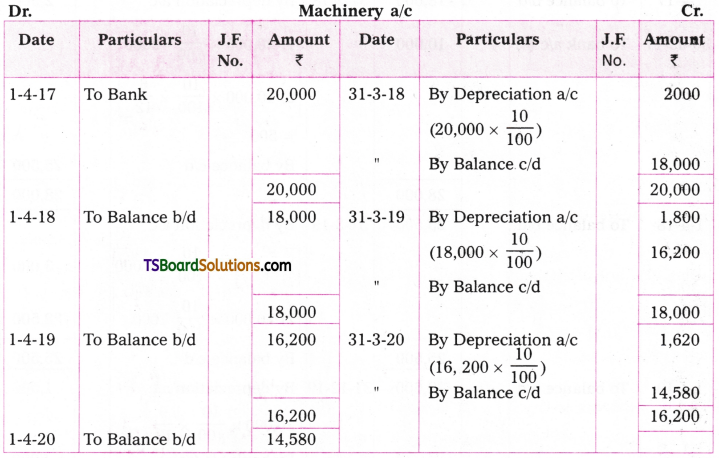
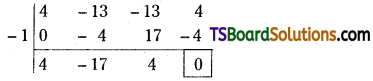
Question 12.
A firm purchased a machine on 1st April 2017 for Rs. 30,000 and paid errection charges Rs. 5,000. Depreciation is provided at 20% under diminishing balance method. Prepare machine a/c upto 31st March, 2020.
Answer:

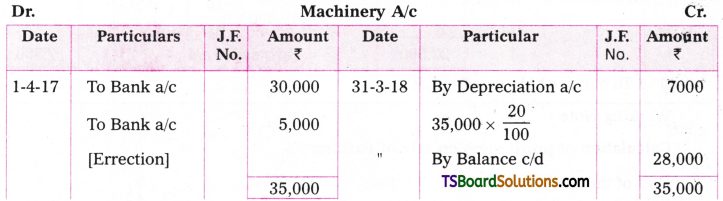
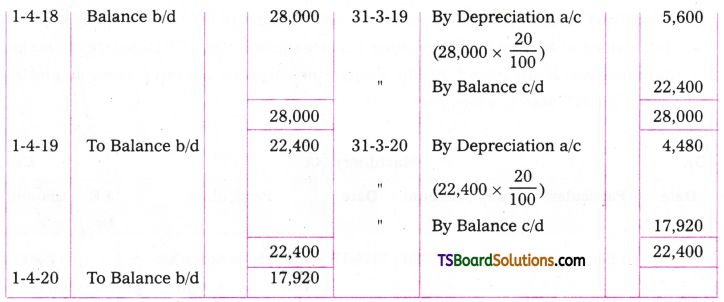
Question 13.
On 1st October 2017, Raju traders bought a machine for Rs. 15,000. Additions made to the machine on 1st April, 2019 were Rs. 10,000. Depreciation is charged at 10% under reducing balance method. Prepare machine a/c for three years assuming that accounts are closed on 31st March, every year.
Answer:

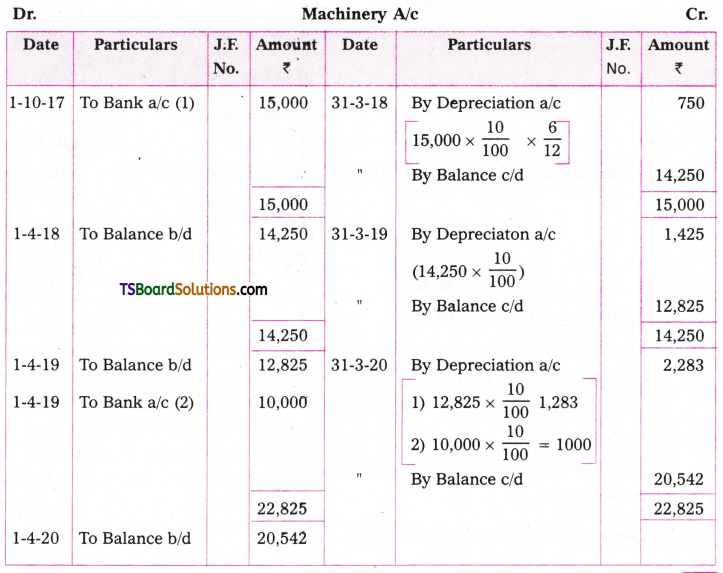
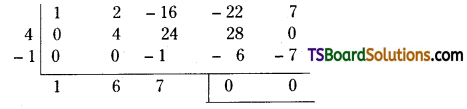
Question 14.
Dinesh & Company purchased a machine on 1st July, 2016 for Rs. 1,00,000. Depreciation is provided at 20% under diminishing balance method. On 1st October 2016 another machine was bought for Rs. 20,000. Prepare machine a/c for three years by closing books on 81st March, every year.
Answer:

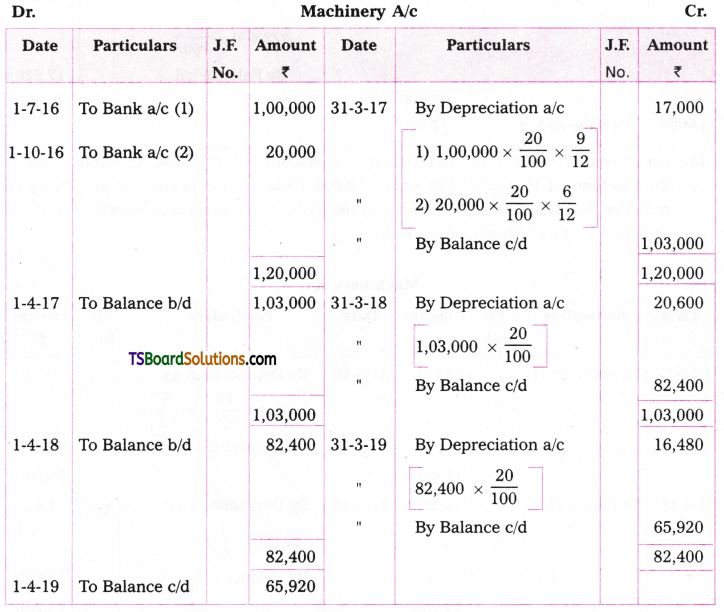
Question 15.
Siva traders bought a machine for Rs. 75,000 on 1st April, 2017. Depreciation was provided at 10% under diminishing balance method. On 31st March, 2020, the machine became obsolute and sold for t 30,000. Prepare machine a/c.
Answer:

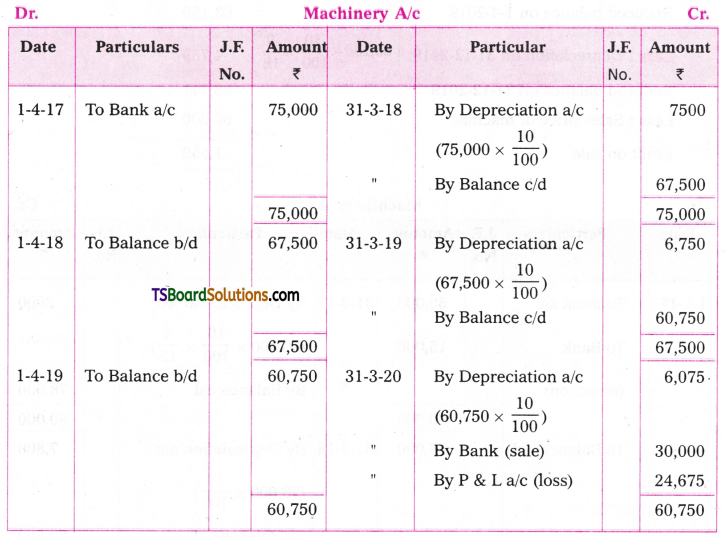
Working Note:
Calculate profit/loss on sale of machine:

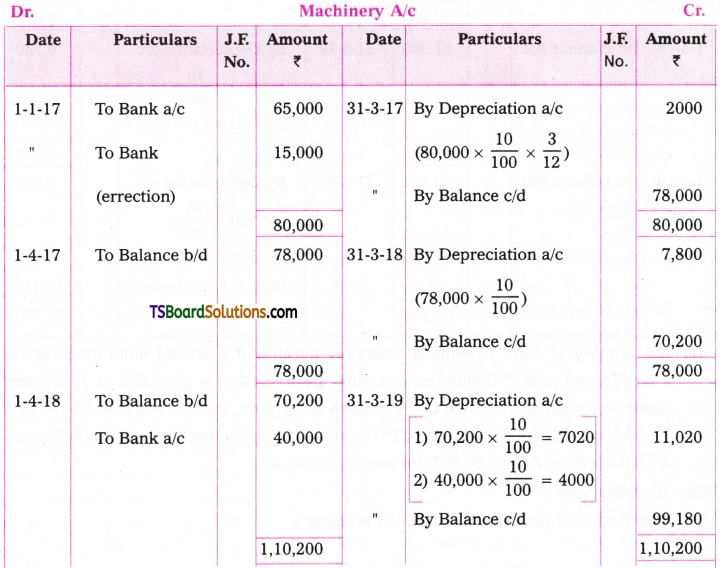
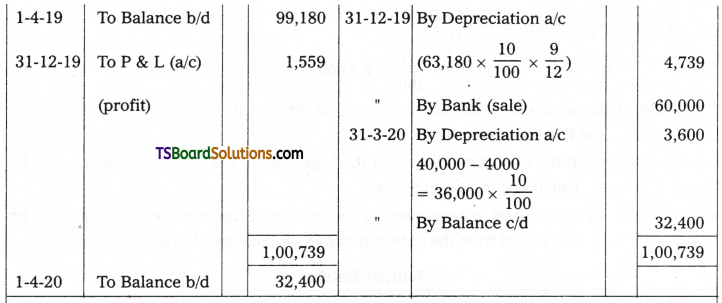
16. On January 1st 2017 Krishna & Company purchased a second hand machine for Rs. 65,000 and paid Rs. 15,000 for errection. Depreciation is provided at 10% under diminishing balance method on 31st March every year. Another machine was bought on 1st April 2018 for Rs. 40,000. On 31st December 2019, the machine bought on January 1st 2017 was sold for Rs. 60,000. Prepare machine a/c.
Answer:
Working Note:
Calculation of profit/loss on sale of I machine:

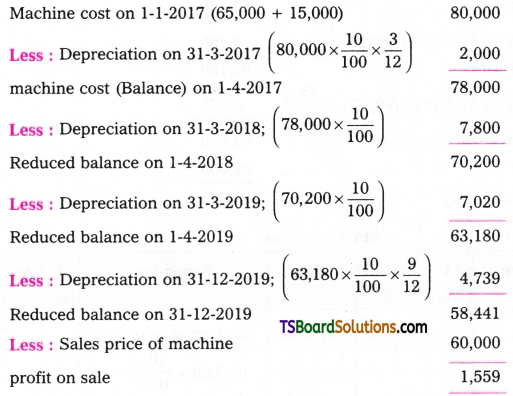
Textual Examples

Question 1.
Sri Raghavendra Traders purchased machinery costing Rs. 25,000 on 01-04-2020. Depreciation is provided annually under (equal) fixed instalment method. Estimated life of the machine is 10 years. The residual value at the end of its life is Rs. 5,000. Calculate annual depreciation and rate of depreciation assuming that accounts are closed on 31st March every year.
Answer:

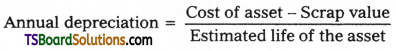
Cost of the machine = Rs. 25,000
Residual scrap value = Rs. 5,000
Life of the Asset =10 years.

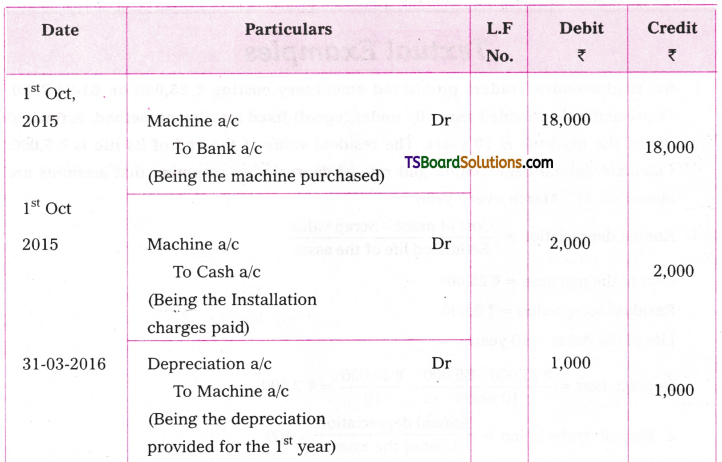
Question 2.
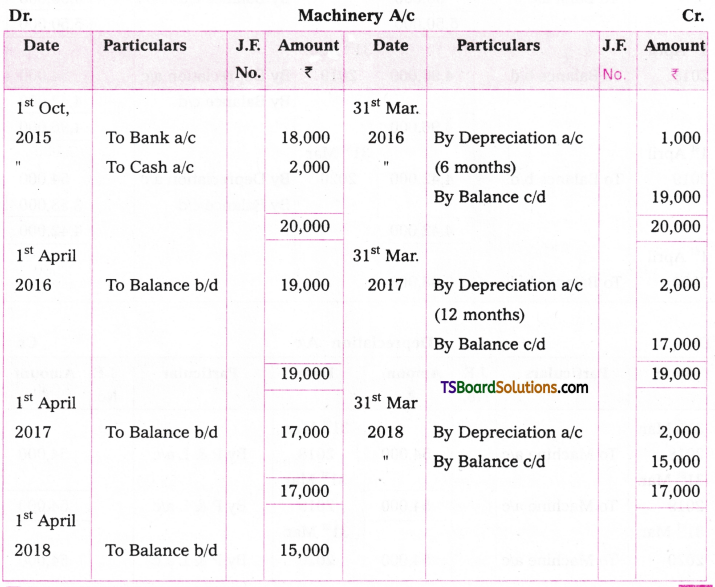
Srinivas bought a machine for Rs. 18,000 on 1st October 2015 and paid Rs. 2,000 for its installation. Depreciation is charged at 10% under original cost method. Every year accounts and closed at the end of financial year. Record necessary journal entries and also prepare Machine a/c for the first three years.
Answer:
Cost of the Asset = Rs. 18,000 + Rs. 2,000
= Rs. 20,000

Note: 1. Generally, accounts are closed only at the end of the March, that is the end of the financial year.
2. a) If the asset is purchased at the beginning of the year, depreciation is to be calculated for the full year.
b) If the asset is purchased in the middle of the year, depreciation is to be calculated from the date of purchase to the date of closing of books.

Question 3.
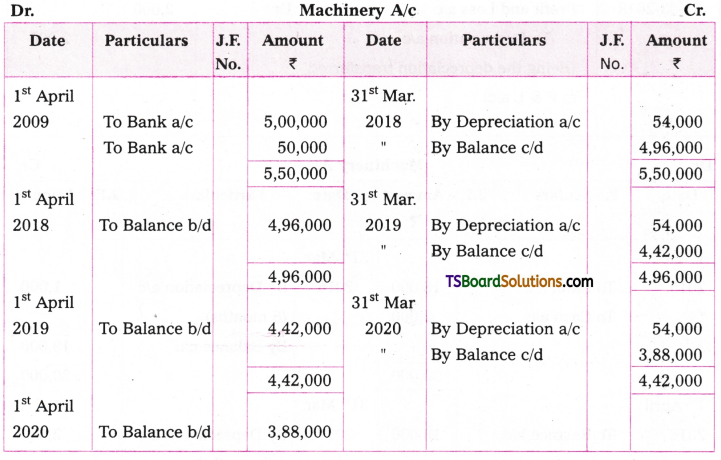
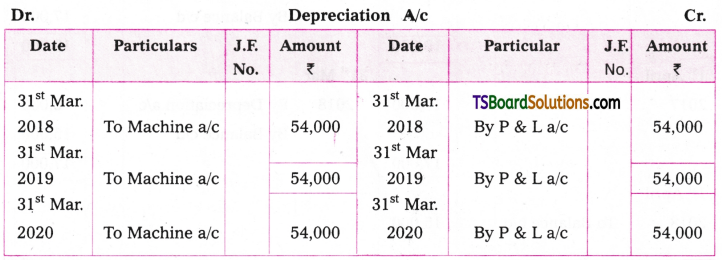
Sharada & Sons acquired a machine for Rs. 5,00,000 on 1st April, 2017 and spent 150,000 for its installation. The scrap value of the plant after is useful life of 10 years is Rs. 10,000. Prepare Machine a/c, Depreciation a/c for the first four years assuming that depreciation is provided under straight line method. Accounts are closed every year on 31st March.
Answer:
Cost = Rs. 5,00,000 + 50,000 = Rs. 5,50,000

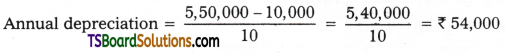
Question 4.
Rama and Company purchased machine for Rs. 60,000 on 1st April, 2017 and spent Rs.5,000 for its errection. Depreciation is charged at the rate of 10% under straight line method. Additional machinery purchased on 1st Oct. 2018 for Rs. 20,000. Prepare Machine a/c for first three years assuming that accounts are closed at the end of March 31st every year.
Answer:

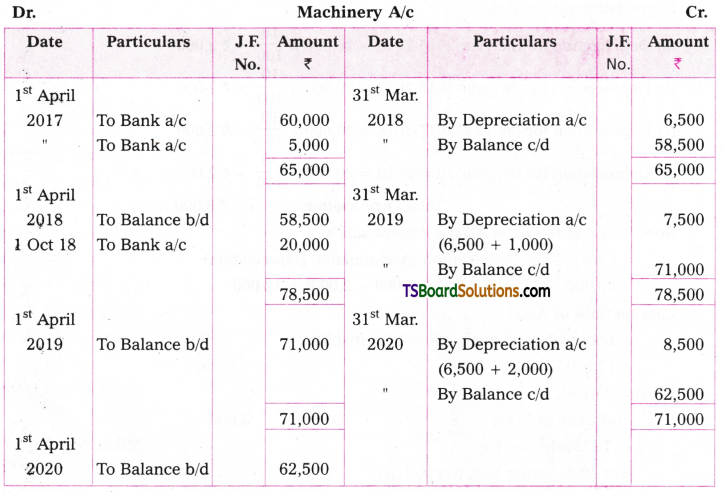
Working Notes:
Cost of the asset = Rs. 60,000 + Rs. 5,000 = Rs. 65,000
Rate of Depreciation = 10%

Note: For the calculation of depreciation, one must be careful about the following dates
(i) Date of purchase of asset,
(ii) Date of commencement of the year and
(iii) Date of closing of books.

Example: A machine is purchased on 1st April 2015 for Rs. 20,000. Depreciation is to be , provided th<; rate of 10% under straight line method. The machine was sold on 31st March 2019 for Rs. 9,000. Find out the profit or loss on sale of asset.
Cost of the Machine = 20,000
Depreciation rate = 10%

(a) Depreciation for the year 2015-2016 = 20,000 x 10/100 = Rs. 2,000
(b) Depreciation for the year 2016-2017 = 20,000 x 10/100 = Rs. 2,000
(c) Depreciation for the year 2017-2018 = 20,000 x 10/100 = t 2,000
(d) Depreciation for the year 2018-2019 = 20,000 x 10/100 = Rs. 2,000

Total Depreciation = Rs. 8,000
Book value of the asset on the date of sale:
= Cost – Total Depreciation (Accumulated Depreciation)
= 20,000 – (2,000 + 2,000 + 2,000 + 2,000) = 12,000

Loss on Sale of Asset:
= Book value – Selling price of the machine = 12,000 – 9,000 = 3,000.

Journal Entry:

5. Raghu & Company purchased furniture on 1st April, 2016 for Rs. 40,000. Depreciation is provided at the rate of 10% under straight fine method. On 31st March, 2020 the scrap of the furniture was sold for Rs. 18,000. Prepare Furniture a/c.
Answer:


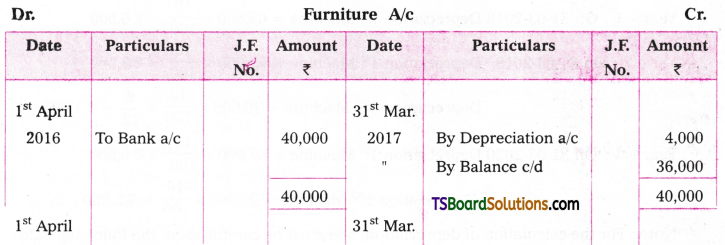
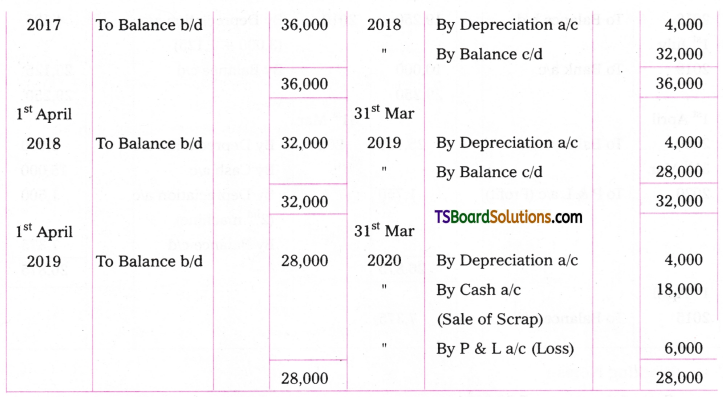
Working Notes:
Cost of the asset = Rs. 40,000
Accumulated Depreciation = 4,000 + 4,000 + 4,000 + 4,000 = 16,000
Book value of the asset = Cost – Total Depreciation
= Rs. 40,000 – Rs. 16,000 = Rs. 24,000
Loss on Sale of Asset = Book value – Selling Price of the Furniture
= Rs. 24,000 – Rs. 18,000 = Rs. 6,000.

Question 6.
Dinesh & Co. Purchased a Machine on 31-12-2017 for Rs. 20,000. Depreciation provided at the rate of 15% under straight line method. On 1st July 2018 another machine was purchased for Rs. 10,000. On 31st March 2020, the machine purchased on 31st December 2017 was sold for Rs. 15,000. Prepare Machine a/c upto 31st March 2020.
Answer:


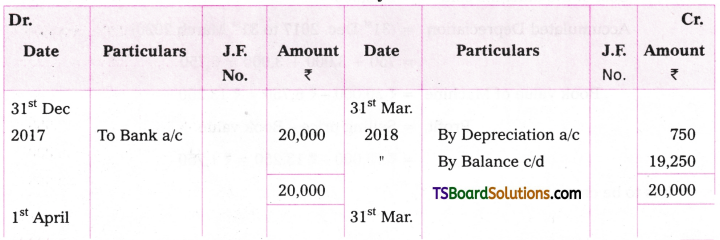
Working Notes:
Cost of the asset = Rs. 20,000
Rate of Depreciation = 15%
Depreciation (31-12-2017 to 31-03-2018) on 1st Machine = 20,000 x 15/100 x 3/12 = Rs. 750
Depreciation on 1st Machine (01-04-2018 to 31-03-2019) = 20,000 x 15/100 = Rs. 3,000
Depreciation on 2nd Machine 1st July, 2018 to 31st March 2019

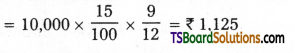
Depreciation on 2nd Machine from 1st April, 2019 to 31st March 2020
= 10,000 x 15/100 = Rs. 1,500

Profit on Sale of Machine:
Cost of the Machine sold = Rs. 20,000
Accumulated Depreciation = (31st Dec. 2017 to 31st March 2020)
= 750 + 3,000 + 3,000 = 6,750
Book value of Machine = Rs. 20,000 – Rs. 6,750 = Rs. 13,250
Profit value = Selling price – Book value
= Rs. 15,000 – Rs. 13,250 = Rs. 1,750
It is to be credited to P & L a/c

Journal Entry:

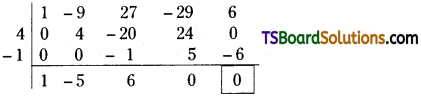
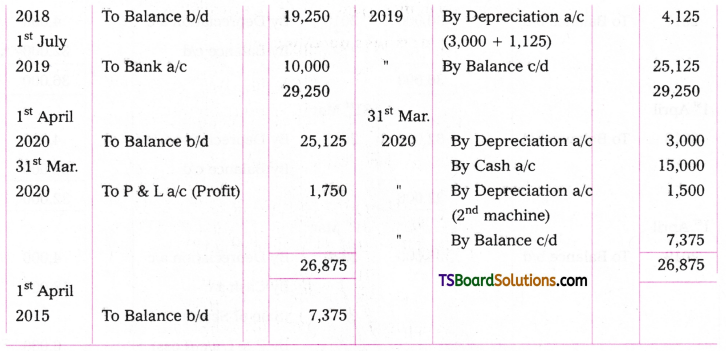
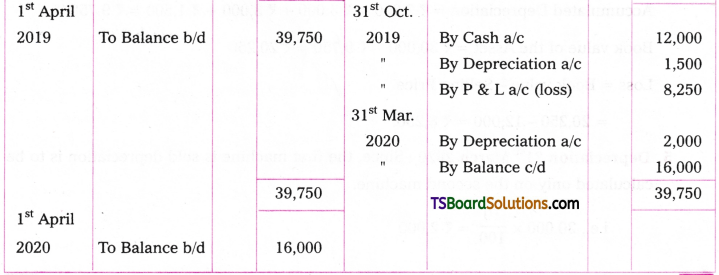
Question 7.
Kiran Traders bought machinery on 1st July 2016 for Rs. 30,000. Depreciation is to be provided at the rate of 10% under straight line method. On 1st April. 2018, additional machinery was purchased for Rs. 20,000. On 1st Oct 2019 the machinery bought on 1st July, 2016 became obsolute and sold for Rs. 12,000. Prepare machinery a/c for four years assuming that books are closed every year on 31st March.
Answer:


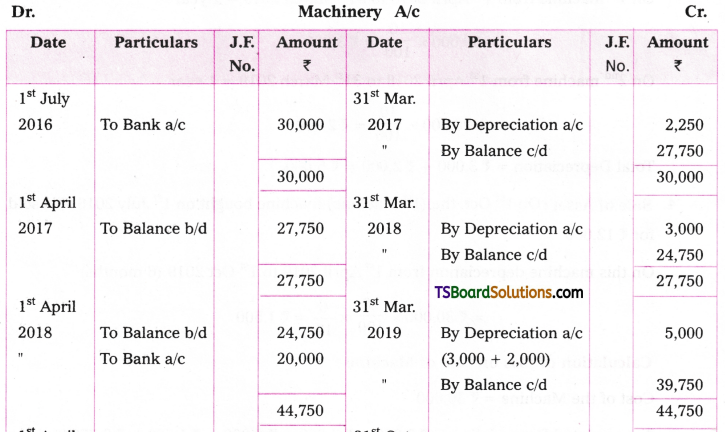
Working Notes:
Cost of the asset = Rs. 30,000 Rate of Depreciation = 10%
1. Depreciation on 31-03-2017 = (July 1st, 2016 to March 31st, 2017 = 9 months)

2. Depreciation on 31 1 March 2018 = 30,000 x 10/100 = Rs. 3,000,
(1st April 2017 to March 31st, 2018 = 1 year)

3. Depreciation on 31st March 2019.
On 1st machine from 1st April 2018 to 31st March 2019 = 1 year
= 30,000 x 10/100 = Rs. 3,000
On 2nd machine from 1st April 2018 to 31st March 2019 = 1 year
= 20,000 x 10/100 = Rs. 2,000
Total Depreciation = Rs. 3,000 + Rs. 2,000 = Rs. 5,000.

4. Sale of Asset: On 1st Oct. the (1st Machine) machine bought on 1st July 2016 was sold for Rs. 12,000
On this machine depreciation from 1st April 2019 to 1st Oct 2019 (6 months)

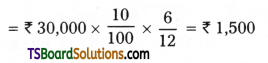
Calculation of loss on sale of Machine:
Cost of the Machine = Rs. 30,000
Accumulated Depreciation = Rs. 2,250 + Rs. 3,000 + Rs. 3,000 + Rs. 1,500 = Rs. 9,750
Book value of the Asset = Rs. 30,000 – Rs. 9,750 = Rs. 20,250
Loss = Book value – Selling Price
= 20,250 – 12,000 = Rs. 8,250.

5. Depreciation 31st March 2020 Since, the first machine is sold depreciation is to be calculated only on the second machine.
i.e., 20,000 x 10/100 = Rs. 2,000

Question 8.
The Original cost of the asset is 9,00,000 and its scrap value is 50,000, expected working life is 16 years. Then the rate of depreciation is calculated as
Answer:

Illustrations on the Diminishing Balance Method:

Question 9.
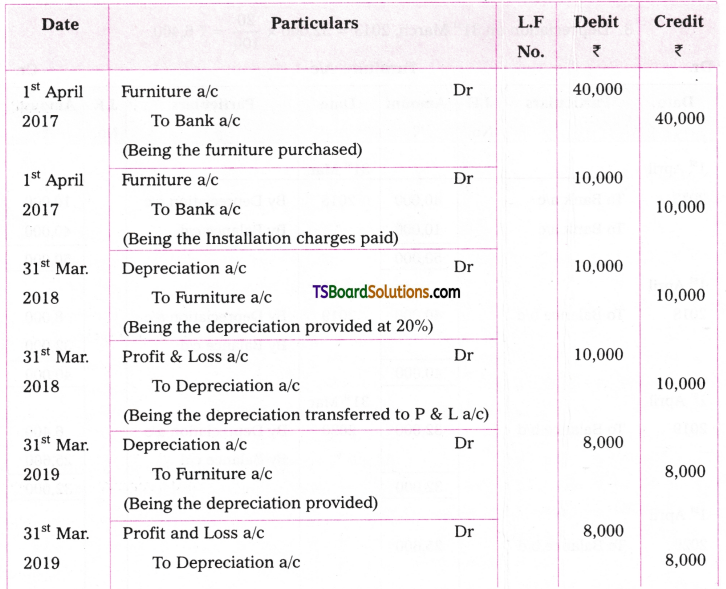
On 1st April, 2017 Santhosh Brothers purchased furniture for Rs. 40,000. Installation charges paid by them Rs. 10,000. Depreciation is provided at 20% under diminishing balance method. Pass journal entries and prepare Furniture a/c for the first three years assuming that accounts are closed on 31st March every year.
Answer:
Journal entries in the Books of Santhosh Brothers.
Journal Entries

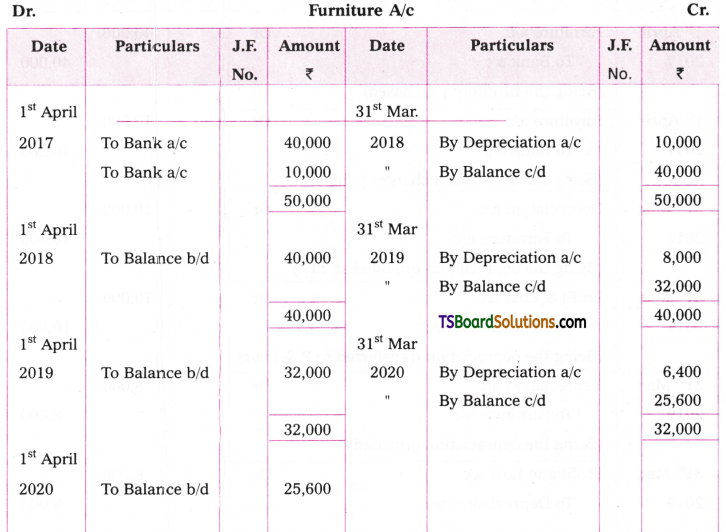
Working Notes:
Cost of the Furniture = Rs. 40,000 + Rs. 10,000 = Rs. 50,000

1. Depreciation on 31st March, 2011 = 50,000 x 20/100 = 10,000
2. Depreciation on 31st March, 2012 = 40,000 x 20/100 = Rs. 8,000
3. Depreciation on 31st March, 2013 = 32,000 x 20/100 = 6,400

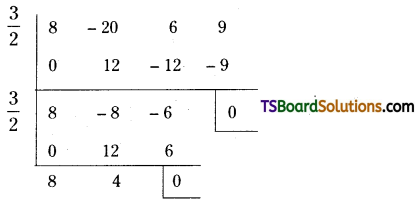
Question 10.
Jagadesh & Co. purchased a machine on 1st July 2017 for Rs. 28,000. They spent Rs. 1,000 for carriage and Rs. 1,000 for installation. The machine is depreciated by 15% every year on written down value basis. Prepare machine a/c upto March 31st, 2020.
Answer:

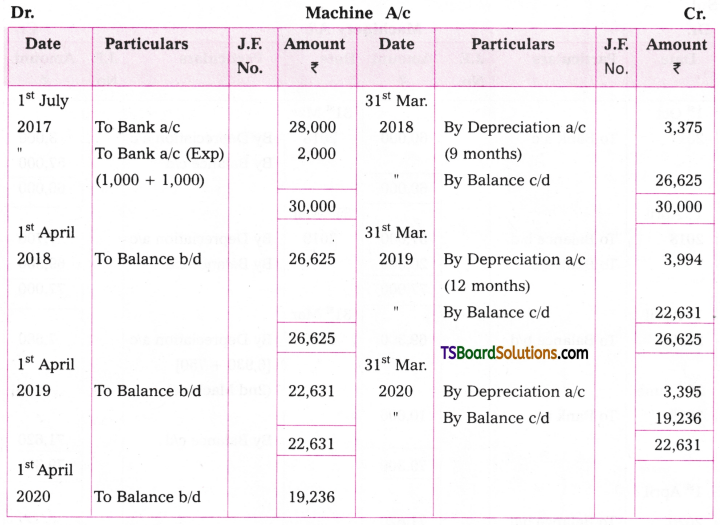
Working Note:
Cost of the asset = Purchase price 4- Carriage + Installation charges
= Rs. 28,000 + Rs. 1,000 + Rs. 1,000 = Rs. 30,000

1. Depreciation on 31st March, 2018 = 30,000 x 15/100 x 9/2 = Rs. 3,375 (July 1st 2017 to 31st March 2018 = 9 months)
Write down value on 31st March 2018 = Rs. 30,000 – Rs. 3,375 = Rs. 26,625
2. Depreciation on 31st March 2019 = 26,625 x 15/100 = Rs. 3,994
Written down value on 31st March 2019 = Rs. 26,625 – Rs. 3,394 = Rs. 22,631
3. Depreciation on 31st March 2020 = Rs. 22.631 x 15/100 = Rs. 3,395

Question 11.
Ramesh & Company purchased a machine for Rs. 60,000 on 1st October 2017. Additions are made to the machine on 1st April 2009, for Rs. 20,000 and on 30th June 2019 for Rs. 10,000. Depreciation is provided at 10% under reducing balance method. Prepare machine a/c from 1st Oct. 2017 to 31st March 2020.
Answer:

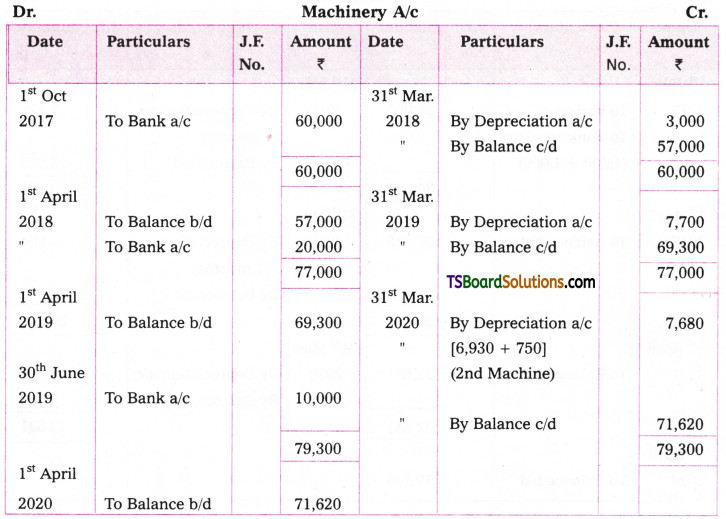
Working Notes:

Year – 1: Depreciation on 31st March, 2018 = 60,000 x 10/100 x 6/12 = Rs. 3,000
Reduced Balance = Rs. 60,000 – Rs. 3,000 = Rs. 57,000

Year – 2: Depreciation on 31st March 2019:
Depreciation on 1 Machine = 57,000 x 10/100 = Rs. 5,700
Depreciation on 2nd Machine = 20,000 x 10/100 = Rs. 2,000
Total Depreciation = Rs. 7,700
Reduced Balance = Rs. 77,000 – Rs. 7,700 = Rs. 69,300

Year – 3: Depreciation on 31st March 2020:
On the reduced Balance of 1st and 2nd Machines
Depreciation = 69,300 x 10/100 = Rs. 6,930
Depreciation on 3rd machine from 2019 June 30th to 2020 March 31st. Since, it is bought on 30th June 2019 only for 9 months depreciation is to be calculated.

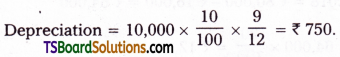
Question 12.
Sripathi traders bought a Machine on 1st April 2016 for Rs. 90,000. They paid for installation Rs. 10,000. Depreciation is to be provided at 20% on the diminishing balance method. On 31st March 2020, scrap of the Machine was sold for Rs. 50,000. Show the Machine a/c assuming that books are closed at the end of the financial year.
Answer:

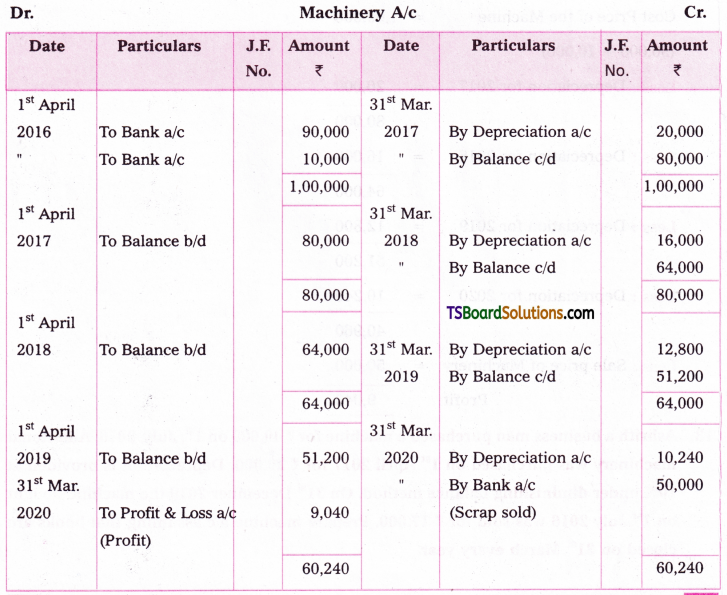
Cost of the Machine = Rs. 90,000 + Rs. 10,000 = Rs. 1,00,000
a) Depreciation on 31st March 2017 = 1,00,000 x 20/100 = Rs. 20,000
Written down value on 31st March 2017 = Rs. 1,00,000 – Rs. 20,000 = Rs. 80,000

b) Depreciation on 31 * March, 2018 = 80,000 x 20/100 = Rs. 16,000
Written down value on 31st March 2018 = Rs. 80,000 – Rs. 16,000 = Rs. 64,000

c) Depreciation on 31st March, 2019 = 64,000 x 20/100 = Rs. 12,800
Written down value on 31st March 2019 = Rs. 64,000 – Rs. 12,800 = Rs. 51,200
d) Depreciation on 31st March, 2020 = 51,200 x 20/100 = Rs. 10,240

Calculation of Profit on Sold Machine:

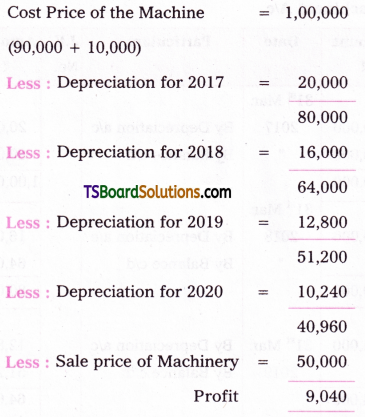
Question 13.
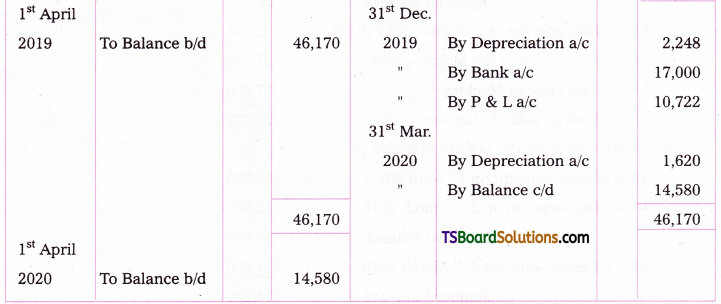
Ashrith a business man purchased a machine for Rs. 40,000 on 1st, July, 2016. Additional machinery was purchased on 1st April 2017 for Rs. 20,000. Depreciation is provided at 10% under diminishing balance method. On 31st December 2019 the machine bought on 1st July 2016 was sold for Rs. 17,000. Prepare machine a/c assuming that books are closed on 31st March every year.
Answer:


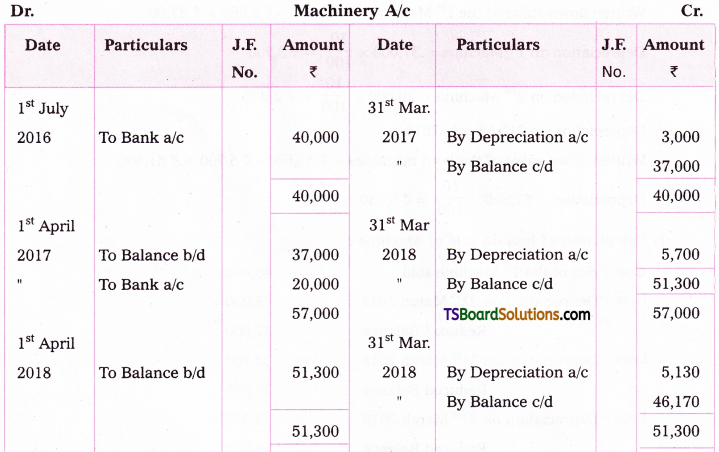
Working Notes:
a) Depreciation on 31st March, 2017
Cost = Rs. 40,000,
Rate = 10%, Machine was bought on July 1st, 2016
Depreciation period from July 1st 2016 to March 31st 2017 is 9 months

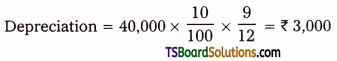
b) Depreciation on 31st March, 2018
Written down value of the 1st Machine = Rs. 40,000 – Rs. 3,000 = Rs. 37,000
Depreciation on 1st Machine = 37,000 x 10/100 = Rs. 3,700
Depreciation on 2 d Machine = 20,000 x 10/100 = Rs. 2,000

c) Depreciation on 31st March, 2019
Written down value of the both machines = Rs. 57,000 – Rs. 5,700 = Rs. 51,300
Depreciation = 51,300 x 10/100 = Rs. 5,130

d) Calculation of loss on sale of Machine:

e) Depreciation on the second machine:

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Integration Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Integration Important Questions Long Answer Type

Question 1.
Evaluate \(\int \frac{d x}{4+5 \sin x}\). [Mar. ’05]
Solution:

Question 2.
Evaluate \(\int \frac{d x}{5+4 \cos x}\). [Mar. ’12, ’11, ’10]
Solution:
Write tan \(\frac{x}{2}\) = t
Differentiating on both sides with respect to ‘x’.

Question 3.
Evaluate \(\int \frac{1}{1+\sin x+\cos x} d x\). [(AP) Mar. ’20; (TS) ’15]
Solution:

Question 4.
Evaluate \(\int \frac{d x}{4 \cos x+3 \sin x}\). [(TS) Mar. ’18]
Solution:

Question 5.
Find \(\int \frac{d x}{3 \cos x+4 \sin x+6}\). [May ’15 (AP); Mar. ’13]
Solution:
Let tan \(\frac{x}{2}\) = t
Differentiating on both sides with respect to ‘x’

Question 6.
Evaluate \(\int \frac{1}{2-3 \cos 2 x} d x\). [May ’10, ’05]
Solution:

Question 7.
Evaluate \(\int \frac{d x}{5+4 \cos 2 x}\). [May ’13, Mar. ’11]
Solution:

Question 8.
Evaluate \(\int \frac{\cos x+3 \sin x+7}{\cos x+\sin x+1} d x\). [(AP) Mar. ’19; May ’06]
Solution:
Let cos x + 3 sin x + 7 = \(\frac{d}{dx}\) (cos x + sin x + 1) + µ (cos x + sin x + 1) + γ
= λ(-sin x + cos x) + µ (cos x + sin x + 1) + γ …….(1)
= -λ sin x + λ cos x + µ cos x + µ sin x + µ + γ
Comparing the coefficients of cos x on both sides, we get
λ + µ = 1 ……..(2)
Comparing the coefficients of sinx on both sides, we get
-λ + µ = 3 ………(3)
Solving (2) and (3)

Comparing constant terms on both sides, we get
µ + γ = 7
⇒ 2 + γ = 7
⇒ γ = 5



where k is an integration constant.

Question 9.
Evaluate \(\int \frac{2 \sin x+3 \cos x+4}{3 \sin x+4 \cos x+5} d x\). [Mar. ’16 (AP & TS); Mar. ’14, ’11]
Solution:
2 sin x + 3 cos x + 4 = λ(3 sin x + 4 cos x + 5) + µ(3 sin x + 4 cos x + 5) + γ
= λ(3 cos x – 4 sin x) + µ(3 sin x + 4 cos x + 5) + γ …….(1)
Comparing,
Coeff. of cos x, 3 = 3λ + 4µ
⇒ 3λ + 4µ – 3 = 0 ……….(2)
Coeff. of sin x, 2 = -4λ + 3µ
⇒ 4λ – 3µ + 2 = 0 ……..(3)
Solving (2) and (3),

Question 10.
Evaluate \(\int \frac{9 \cos x-\sin x}{4 \sin x+5 \cos x} d x\). [Mar. ’17 (TS), Mar. ’08]
Solution:
9 cos x – sin x = λ(4 sin x + 5 cos x) + µ(4 sin x + 5 cos x) + γ
= λ(4 cos x – 5 sin x) + µ(4 sin x + 5 cos x) + γ ………(1)
Comparing,
Coeff. of cos x, 9 = 4λ + 5µ
⇒ 4λ + 5µ – 9 = 0 ……….(2)
Coeff. of sin x, -1 = -5λ + 4µ
⇒ -5λ + 4µ + 1 = 0 ………(3)
Coeff. of constant, 0 = γ
Solving (2) & (3),

Question 11.
Evaluate \(\int \frac{2 \cos x+3 \sin x}{4 \cos x+5 \sin x} d x\). [(TS) May ’19, ’16; (AP) Mar. ’18, ’15]
Solution:
Let 2 cos x + 3 sin x = λ \(\frac{d}{dx}\) (4 cos x + 5 sin x) + µ(4 cos x + 5 sin x) + γ
= λ(-4 sin x + 5 cos x) + µ(4 cos x + 5 sin x) + γ ………(1)
= -4λ sin x + 5λ cos x + 4µ cos x + 5µ sin x + γ
Comparing the coefficients of cos x on both sides, we get
5λ + 4µ = 2 ……..(2)
Comparing the coefficients of sinx on both sides, we get
-4λ + 5µ = 3 ……….(3)
Solving (2) and (3)

Comparing constant terms on both sides, we get X = 0
From (1),
2 cos x + 3 sin x = \(\frac{-2}{41}\) (-4 sin x + 5 cos x) + \(\frac{23}{41}\) (4 cos x + 5 sin x) + 0
= \(\frac{-2}{41}\) (-4 sin x + 5 cos x) + \(\frac{23}{41}\) (4 cos x + 5 sin x)
Now,

Put 4 cos x + 5 sin x = t
(-4 sin x + 5 cos x) dx = dt

Question 12.
Evaluate \(\int \frac{2 x+5}{\sqrt{x^2-2 x+10}} d x\). [(AP) May ’17; Mar. ’15 (TS)]
Solution:
Write 2x + 5 = A . \(\frac{d}{dx}\) (x2 – 2x + 10) + B
= A(2x – 2) + B ………(1)
Coeff. of x, 2 = 2A then A = 1
Constant, 5 = -2A + B then B = 5 + 2 = 7
From (1), 2x + 5 = (2x – 2) + 7

Question 13.
Evaluate \(\int \frac{x+1}{x^2+3 x+12} d x\). [(AP) Mar. ’17; May ’16]
Solution:
Write x + 1 = A \(\frac{d}{dx}\) [x2 + 3x + 12) + B
= A(2x + 3) + B ……..(1)
Coefficient of x, 1 = A(2) then A = \(\frac{1}{2}\)
Constant, 1 = 3A + B then B = 1 – \(\frac{3}{2}\) = \(\frac{-1}{2}\)
From (1), x + 1 = \(\frac{1}{2}\)(2x + 3) – \(\frac{1}{2}\)

Question 14.
Evaluate \(\int \sqrt{\frac{5-x}{x-2}} d x\). [(AP) May ’19, (TS) ’17]
Solution:

Question 15.
Evaluate \(\int(6 x+5) \sqrt{6-2 x^2+x} d x\). [(AP) & (TS) May ’18]
Solution:

Question 16.
Evaluate \(\int x \sqrt{1+x-x^2} d x\). [May ’12]
Solution:
Take x = A \(\frac{d}{dx}\) (1 + x – x²) + B
x = A(1 – 2x) + B …….(1)
= A – 2Ax + B
Comparing the coefficient of x on both sides, we get
-2A = 1
⇒ A = \(-\frac{1}{2}\)
Comparing constant terms on both sides, we get
A + B = 0
⇒ \(-\frac{1}{2}\) + B = 0
⇒ B = \(\frac{1}{2}\)
From (1), x = \(-\frac{1}{2}\)(1 – 2x) + \(\frac{1}{2}\)

Question 17.
Evaluate \(\int(3 x-2) \sqrt{2 x^2-x+1} d x\). [(TS) May ’15; May ’03]
Solution:
Take 3x – 2 = A \(\frac{d}{dx}\)(2x² – x + 1) + B
3x – 2 = A(4x – 1) + B …….(1)
3x – 2 = 4Ax – A + B
Comparing the coefficients of x on both sides, we get
4A = 3
⇒ A = \(\frac{3}{4}\)
Comparing the constant terms on both sides
-A + B = -2
⇒ \(-\frac{3}{4}\) + B = -2
⇒ B = \(\frac{-5}{4}\)
From (1), 3x – 2 = \(\frac{3}{4}\) (4x – 1) – \(\frac{5}{4}\)

Question 18.
Evaluate \(\int \frac{d x}{(1+x) \sqrt{3+2 x-x^2}}\). [(TS) Mar. ’20; May ’14, ’05]
Solution:

Question 19.
Evaluate \(\int \frac{d x}{(x+1) \sqrt{2 x^2+3 x+1}}\). [Mar. ’18 (TS)]
Solution:

Question 20.
Evaluate the Reduction formula for I_n = ∫sinⁿx dx and hence find ∫sin⁴x dx, ∫sin⁵x dx. [(TS) Mar. ’20, May 18; (AP) May ’19, 15; Mar. ’17; Mar. ’14, ’13]
Solution:

Question 21.
Obtain the Reduction formula for ∫cosⁿx dx for n ≥ 2 and deduce the value of ∫cos⁵x dx. [(AP) Mar. ’20, May ’18; (TS) May ’19, ’16; Mar. ’17]
Solution:

Question 22.
Find the Reduction formula of ∫tanⁿx dx for an integer n ≥ 2. And deduce the value of ∫tan⁶x dx. [(AP) Mar. ’18, ’15; May ’16; (TS) ’17; Mar. ’12; May ’13]
Solution:

Question 23.
Find the Reduction formula of ∫cotⁿx dx for an integer n ≥ 2. And deduce the value of ∫cot⁴x dx. [Mar. ’19 (TS); Mar. ’16 (AP); May ’11]
Solution:

Question 24.
Find the Reduction formula for ∫cosecⁿx dx for an integer n ≥ 2 and deduce the value of ∫cosec⁵x dx. [Mar. ’19 (AP); Mar. ’16 (TS); May ’14]
Solution:

Question 25.
Find the Reduction formula for ∫secⁿx dx for an integer n ≥ 2 and deduce the value of ∫sec⁵x dx. [(AP) May ’17; (TS) May ’15; Mar. ’04]
Solution:
\(I_n=\int \sec ^n x d x=\int \sec ^{n-2} x \cdot \sec ^2 x d x\)

Question 26.
Evaluate \(\int \frac{\sin 2 x}{a \cos ^2 x+b \sin ^2 x} d x\)
Solution:
Put a cos²x + b sin²x = t
then [a . 2 cos x (-sin x) + b . 2 sin x . cos x] dx = dt
⇒ [-a sin 2x + b sin 2x] dx = dt
⇒ (b – a) sin 2x dx = dt
⇒ sin 2x dx = \(\frac{1}{b-a}\) dt

Question 27.
Evaluate ∫x cos^-1x dx. [Mar. ’09]
Solution:

Question 28.
Evaluate ∫x sin^-1x dx. [Mar. ’04]
Solution:

Question 29.
Evaluate \(\int \frac{d x}{x^2+x+1}\)
Solution:

Question 30.
Evaluate \(\int \frac{d x}{\sqrt{1+x-x^2}}\)
Solution:

Question 31.
Evaluate \(\int \frac{\cos x}{\sin ^2 x+4 \sin x+5} d x\). [Mar. ’07, ’03]
Solution:
Put sin x = t then cos dx = dt

Question 32.
Evaluate \(\int \frac{\sin x \cos x}{\cos ^2 x+3 \cos x+2} d x\)
Solution:
Put cos x = t
⇒ -sin x dx = dt
⇒ sin x dx = -dt

Question 33.
Evaluate \(\int \frac{d x}{\left(x^2+a^2\right)\left(x^2+b^2\right)}\)
Solution:

Question 34.
Evaluate \(\int \frac{d x}{\left(x^2+a^2\right)^2}\)
Solution:

Question 35.
Evaluate ∫e^ax sin(bx + c) dx. [Mar. ’19 (TS)]
Solution:

Question 36.
Evaluate \(\int \sqrt{\mathbf{a}^2-x^2} d x\). [Mar. ’02]
Solution:

Question 37.
Evaluate \(\int \sqrt{1+3 x-x^2} d x\). [Mar. ’11]
Solution:

Question 38.
Evaluate \(\int \frac{d x}{\sin x+\sqrt{3} \cos x}\)
Solution:

Question 39.
Evaluate \(\int \frac{\tan ^{-1} x}{x^2} d x\). [May ’01]
Solution:
\(\int \frac{\tan ^{-1} x}{x^2} d x=\int \tan ^{-1} x \cdot x^{-2} d x\)

Question 40.
Evaluate \(\int \frac{1}{a \sin x+b \cos x} d x\). [May ’03]
Solution:
Let a = r cos θ, b = r sin θ then r = \(\sqrt{a^2+b^2}\)
Now a sin x + b cos x = r cos θ sin x + r sin θ cos x = r[sin (x + θ)]

Question 41.
Evaluate ∫e^x log(e^2x + 5e^x + 6) dx.
Solution:

Question 42.
Evaluate \(\int \frac{1}{(1+\sqrt{x}) \sqrt{x-x^2}} d x\)
Solution:
Put x = t², then dx = 2t dt

Question 43.
Evaluate \(\int \frac{1}{(x-a)(x-b)(x-c)} d x\)
Solution:

Question 44.
Evaluate \(\int \frac{d x}{x(x+1)(x+2)}\)
Solution:

Question 45.
Evaluate \(\int \frac{7 x-4}{(x-1)^2(x+2)} d x\)
Solution:
Let \(\frac{7 x-4}{(x-1)^2(x+2)}=\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+2}\)
⇒ \(\frac{7 x-4}{(x-1)^2(x+2)}=\frac{A(x-1)(x+2)+B(x+2)+C(x-1)^2}{(x-1)^2(x+2)}\)
⇒ 7x – 4 = A(x – 1) (x + 2) + B(x + 2) + C(x – 1)²
If x = 1,
1 = 7(1) – 4 = B(1 + 2)
⇒ 3 = 3B
⇒ B = 1
If x = -2,
7(-2) – 4 = C(-2 – 1)²
⇒ -14 – 4 = C(-3)²
⇒ -18 = 9C
⇒ C = -2
(1) ⇒ 7x – 4 = Ax² + Ax – 2A + Bx + 2B + Cx² – 2Cx + C
Comparing the coefficients of x² on both sides, we get
A + C = 0
⇒ A – 2 = 0
⇒ A = 2

Question 46.
Evaluate \(\int \frac{x^2}{(x+1)(x+2)^2} d x\)
Solution:
Let \(\frac{x^2}{(x+1)(x+2)^2}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\)
⇒ \(\frac{x^2}{(x+1)(x+2)^2}=\frac{A(x+2)^2+B(x+1)(x+2)+C(x+1)}{(x+1)(x+2)^2}\)
⇒ x² = A(x + 2)² + B(x + 1)(x + 2) + C(x + 1) …..(1)
If x = -1, then (-1)² = A(-1 + 2)²
⇒ 1 = A(1)²
⇒ A = 1
If x = -2, then (-2) = C(-2 + 1)
⇒ 4 = C(-1)
⇒ 4 = -C
⇒ C = -4
(1) ⇒ x² = Ax² + 4Ax + 4A + Bx² + 3Bx + 2B + Cx + C
Comparing the coefficients of x² on both sides, we get
1 = A + B
⇒ 1 + B = 1
⇒ B = 0

Question 47.
Evaluate \(\int \frac{2 x+3}{x^3+x^2-2 x} d x\)
Solution:
Given \(\int \frac{2 x+3}{x^3+x^2-2 x} d x=\int \frac{2 x+3}{x\left(x^2+x-2\right)} d x=\int \frac{2 x+3}{x(x+2)(x-1)} d x\)
Let \(\frac{2 x+3}{x(x+2)(x-1)}=\frac{A}{x}+\frac{B}{x+2}+\frac{C}{x-1}\)
⇒ \(\frac{2 x+3}{x(x+2)(x-1)}=\frac{A(x+2)(x-1)+B x(x-1)+C x(x+2)}{x(x+2)(x-1)}\)
⇒ 2x + 3 = A(x + 2)(x – 1) + B(x – 1) x + Cx(x + 2)
If x = 0, then 2(0) + 3 = A(0 + 2) (0 – 1)
⇒ 3 = A(2)(-1)
⇒ 3 = -2A
⇒ A = \(\frac{-3}{2}\)
If x = -2, then 2(-2) + 3 = B(-2 – 1) (-2)
⇒ -4 + 3 = B(-2)(-3)
⇒ -1 = 6B
⇒ B = \(\frac{-1}{6}\)
If x = 1, then 2(1) + 3 = C(1)(1 + 2)
⇒ 5 = C(1)(3)
⇒ 3C = 5
⇒ C = \(\frac{5}{3}\)

Question 48.
Evaluate \(\int \frac{x+3}{(x-1)\left(x^2+1\right)} d x\). [May ’07]
Solution:
Let \(\frac{x+3}{(x-1)\left(x^2+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+1}\)
\(\frac{x+3}{(x-1)\left(x^2+1\right)}=\frac{A\left(x^2+1\right)+(B x+C)(x-1)}{(x-1)\left(x^2+1\right)}\)
x + 3 = A(x² + 1) + (Bx + C) (x – 1) ………(1)
If x = 1 then 1 + 3 = A(1² + 1)
⇒ 4 = A(2)
⇒ A = 2
from (1), x + 3 = Ax² + A + Bx² – Bx + Cx – C
Comparing x² coefficients on both sides, we get
A + B = 0
⇒ 2 + B = 0
⇒ B = -2
Comparing coefficients of x on both sides, we get
-B + C = 1
⇒ -(-2) + C = 1
⇒ 2 + C = 1
⇒ C = 1 – 2
⇒ C = -1

Question 49.
Evaluate \(\int \frac{2 x+3}{(x+3)\left(x^2+4\right)} d x\). [May ’02]
Solution:
Let \(\frac{2 x+3}{(x+3)\left(x^3+4\right)}=\frac{A}{x+3}+\frac{B x+C}{x^2+4}\)
\(\frac{2 x+3}{(x+2)\left(x^2+4\right)}=\frac{A\left(x^2+4\right)+(B x+C)(x+3)}{(x+3)\left(x^2+4\right)}\)
2x + 3 = A(x² + 4) + (Bx + C)(x + 3) …….(1)
If x = -3 then
2(-3) + 3 = A[(-3)² + 4]
⇒ -6 + 3 = A(9 + 4)
⇒ 13A = -3
⇒ A = \(\frac{-3}{13}\)
From (1),
2x + 3 = Ax² + 4A + Bx² + 3Bx + Cx + 3C
Comparing x² coefficients on both sides, we get
A + B = 0
⇒ \(\frac{-3}{13}\) + B = 0
⇒ B = \(\frac{3}{13}\)
Comparing x coefficients on both sides, we get
3B + C = 2
⇒ 3(\(\frac{3}{13}\)) + C = 2
⇒ C = 2 – \(\frac{3}{13}\)
⇒ C = \(\frac{17}{13}\)

Question 50.
Evaluate \(\int \frac{1}{(1-x)\left(4+x^2\right)} d x\)
Solution:
\(\frac{1}{(1-x)\left(4+x^2\right)}=\frac{A}{1-x}+\frac{B x+C}{x^2+4}\)
1 = A(x² + 4) + (Bx + C)(1 – x)
Put x = 1 then A = \(\frac{1}{5}\)
Coeff. of x², 0 = A – B ⇒ B = \(\frac{1}{5}\)
Constant, 1 = C + 4A ⇒ C = \(\frac{1}{5}\)

Question 51.
Evaluate \(\int \frac{d x}{x^3+1}\). [May ’03]
Solution:
\(\frac{1}{x^3+1}=\frac{1}{(x+1)\left(x^2-x+1\right)}=\frac{A}{x+1}+\frac{B x+C}{x^2-x+1}\) ……(1)
1 = A(x² – x + 1) + (Bx + C) (x + 1)
Put x = -1, 1 = A(3) ⇒ A = \(\frac{1}{3}\)
Coeff. of x², 0 = A + B ⇒ B = \(\frac{-1}{3}\)
Constant, 1 = A + C ⇒ C = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)

Question 52.
Evaluate \(\int \tan ^{-1} \sqrt{\frac{1-x}{1+x}} d x\)
Solution:

Question 53.
Find the Reduction formula for ∫sin^mx cosⁿx dx for a +ve integer and n ≥ 2.
Solution:

Question 54.
If I_n = ∫(log x)ⁿ dx, then show that I_n = x(log x)ⁿ – nI_n – 1 and find ∫(log x)⁴ dx.
Solution:

Now I₄ = ∫(log x)⁴ dx
= x(log x)⁴ – 4I₃
= x(log x)⁴ – 4[x(log x)³ – 4I₂]
= x(log x)⁴ – 4x(log x)³ + 16I₂
= x(log x)⁴ – 4x(log x)³ + 16[x(log x)² – 2I₁]
= x(log x)⁴ – 4x(log x)³ + 16x(log x)² – 32I₁
= x(log x)⁴ – 4x(log x)³ + 16x(log x)² – 32[x(log x) – x] + c
= x(log x)⁴ – 4x(log x)³ + 16x(log x)² – 32x log x + 32x + c

Telangana TSBIE TS Inter 2nd Year Chemistry Study Material Lesson 12(a) Alcohols, Phenols, and Ethers Textbook Questions and Answers.

TS Inter 2nd Year Chemistry Study Material Lesson 12(a) Alcohols, Phenols, and Ethers

Very Short Answer Questions (2 Marks)

Question 1.
Explain why propanol has higher boiling point than that of the hydrocarbon butane.
Answer:
Propanol and butane are of comparable molecular mass. However, the boiling point of propanol is higher than that of butane, due to the presence of intermolecular hydrogen bonding.

Question 2.
Alcohols are comparatively more soluble in water than hydrocarbons of comparable molecular masses. Explain this fact.
Answer:
Alcohols are comparatively more soluble in water than hydrocarbons of comparable molecular masses, due to their ability to form hydrogen bonds with water molecules.

Question 3.
Give the structures and 1UPAC names of monohydric phenols of molecular formula, C₇H₈O.
Answer:

Common Name:
o – Cresol
m – Cresol
p – Creol

IUPAC Name:
2 – Methylphenol
3 – Methylphenol
4 – Methylphenol

Question 4.
Give the reagents used for the preparation of phenol from chlorobenzene.
Answer:

1. NaOH
2. HCl.

Question 5.
Preparation of ethers by acid dehydration of secondary or tertiary alcohols is not a suitable method. Give reason.
Answer:
This is because elimination competes over substitution and as a consequence, alkenes are easily formed.

Question 6.
Write the mechanism of the reaction of HI with methoxymethane.
Answer:

Question 7.
Name the reagents used in the following reactions.

1. Oxidation of primary alcohol to carboxylic acid.
2. Oxidation of primary alcohol to aldehyde.

Answer:

1. Acidified potassium permanganate.
2. Pyridinium chlorochromate (PCC) or CrO₃ in anhydrous medium.

Question 8.
Write the equations for the following reactions.
i) Bromination of phenol to 2, 4, 6-tribromophenoI.
ii) Benzyl alcohol to benzoic acid.
Answer:
i) A white precipitate of 2,4,6 – tribromophenol is formed when phenol is treated with bromine water.

ii) Benzyl alcohol is oxidised to benzoic acid by acidified KMn04 or acidic solution of sodium dichromate.

Question 9.
Identify the reactant needed to form t-butyl alcohol from acetone.
Answer:
Methyl magnesium halide (Grignard reagent) is needed to form t-butyl alcohol from acetone.

Question 10.
Write the structures for the following compounds.
i) Ethoxyethane
ii) Ethoxybutane
iii) Phenoxyethane
Answer:
i) C₂H₅OC₂H₅ – Ethoxyethane
ii) CH₃CH₂CH₂CH₂OCH₂CH₃ – Ethoxybutane
iii) C₂H₅OC₆H₅ – Phenoxyethane

Short Answer Questions (4 Marks)

Question 11.
Draw the structures of all isomeric alcohols of molecular formula C₅H₁₂O and give their IUPAC names and classify them as primary, secondary and tertiary alcohols.
Answer:

Question 12.
While separating a mixture of ortho and para nitrophenols by steam distillation, name the isomer which will be steam volatile. Give reason.
Answer:
O-nitrophenol will be steam volatile due to intramolecular hydrogen bonding while p-nitro- phenol will be less volatile due to intermolecular hydrogen bonding which causes association of molecules.

Question 13.
Give the equations for the preparation of phenol from Cumene.
Answer:

Question 14.
Write the mechanism of hydration of ethene to yield ethanol.
Answer:

Mechanism : The mechanism of the reaction involves three steps.
Step 1: Protonation of the alkene (ethene) to form carbonation by electrophilic attack of H₃O⁺.

Step 2 : Nucleophilic attack of water on carbocation.

Step 3 : Deprotonation to form an alcohol.

Question 15.
Explain the acidic nature of phenols and compare with that of alcohols.
Answer:
The reactions of phenol with metals (e.g. : Na, Al) and NaOH indicate its acidic nature. The hydroxyl group, in phenol is directly attached to the sp² hybridised carbon of benzene ring which acts as an electron withdrawing group. The charge distribution in phenol molecule as depicted in its resonance structures, causes the oxygen of – OH group to be positive.

The reaction of phenol with NaOH solution indicates that phenols are stronger acids than alcohols and water. Let us compare the acidic nature of phenol with that of alcohol.
The ionisation of an alcohol and a phenol takes place as shown below.

Owing to the higher electronegativity of sp² hybridised carbon of phenol to which – OH is attached, electron density decreases on oxygen. This increases the polarity of – OH bond and results in an increase in ionisation of phenols than that of alcohols.

The relative stabilities of alkoxide and phenoxide ions should be considered. In alkoxide ion, the negative charge is localised on oxygen whereas in phenoxide ion, the charge is delocalised. The delocalisation of negative charge makes phenoxide ion more stable and favours the ionisation of phenol. There is delocalisation in unionised phenol also but the resonance structures have charge separation. Hence, phenol molecule is less stable them phenoxide ion.

Question 16.
Write the products formed by the reduction and oxidation of phenol. [IPE 14]
Answer:
Reduction of phenol: Phenol is converted to benzene when heated with zinc dust.

Oxidation : Phenol gives benzoquinone on oxidation with chromic acid.

In the presence of air, phenols are slowly oxidised to dark coloured mixtures containing quinones.

Question 17.
Ethanol with H₂SO₄, at 443K forms ethane while at 413 K it forms ethoxy ethane. Explain the mechanism.
Answer:

Step 2 : Formation of carbocation.

Mechanism : The formation of ether is a nucleophilic bimolecular reaction (S_N2) involving the attack of alcohol molecule on a protonated alcohol.

Question 18.
Account for the statement: Alcohols boil at highest temperature than hydrocarbons and ethers of comparable molecular masses.
Answer:
The higher boiling points of alcohols are mainly due to the presence of inter molecular hydrogen bonding in them which is lacking in ethers and hydrocarbons.

Question 19.
Explain why in anisole electrophilic substitution takes place at ortho and para positions and not at meta position.
Answer:
In benzene derivatives the electrophile is most likely to react at the position of highest electron density. The methoxy group ih anisole is an electron releasing group. It increases the relative electron density at ortho and para positions and hence electrophilic substitution takes place at these positions and not at the meta position.

Question 20.
Write the products of the following reactions:

Answer:

Long Answer Questions (8 Marks)

Question 21.
Write the IUPAC names of the following compounds:

Answer:

Question 22.
Write structures of the compounds whose IUPAC names are as follows: [IPE 14]
i) 2- Methyl butan-1- ol
ii) 1-Phenylpropan-2-ol
iii) 3, 5-Dimethythexane- 1, 3, 5- triol
iv) 2, 3- Dlethylphenol
v) 1 – Ethoxypropane
vi) 2- Ethoxy -3- methylpentane
vii) Cyclohexylmethanol
viii) 3- Chloromethylpentan – 1 – ol
Answer:

Question 23.
Write the equations for the preparation of phenol using benzene, Cone. H₂SO₄ and NaOH.
Answer:
Benzene is sulphonated with oleum and benzene sulphonic acid so formed is converted to sodium phenoxide on heating with molten sodium hydroxide. Acidification of the sodium salt gives phenol.

Question 24.
Illustrate hydroboration-oxidation reaction with a suitable example.
Answer:
Diborane B₂H₆ [or (BH₃)₂] reacts with aikenes to give trialkyl boranes as addition product. This is oxidised to alcohol by hydrogen peroxide in the presence of aqueous sodium hydroxide.
Ex : Propene gives Propan-1-ol on hydroboration – oxidation reaction.

Question 25.
Write the IUPAC names of the following compounds.

Answer:
i) 2-methyl phenol
ii) 4 – methyl phenol
iii) 2, 5 – dimethyl phenol
iv) 2, 6 – dimethyl phenol

Question 26.
How will you synthesise :
i) 1 – Phenylethanol from a suitable alkene ?
ii) Cyclohexylmethanol using an alkyl halide by an S_N2 reaction ?
iii) Pentan-1-ol using a suitable alkyl halide ?
Answer:
i) Styrene on acid catalysed hydration gives 1-phenyl ethanol.

ii) Cyclohexyl chloromethane reacts with aqueous sodium hydroxide solution to give cyclohexyl methanol.

iii) Pentan-1-ol is obtained by the reaction of 1-chloropentane with aqueous NaOH solution.

Question 27.
Explain why –
i) Ortho nitrophenol is more acidic than ortho methoxyphenol.
ii) OH group attached to benzene ring activates it towards electrophilic substitution.
Answer:
i) Electron withdrawing groups enhance the acidic strength of phenol. This effect is more pronounced if these groups are present in ortho and para positions. It is due to the effective delocalisation of negative charge in phenoxide ion. On the other hand electron releasing
‘ groups do not favour the formation of phenoxide ion resulting in decrease in acid strength.

Nitro group is an electron withdrawing group. It increases the acidic strength of phenol. Methoxy group is an electron releasing group. It decreases the acidic strength of phenol. Hence o-nitrophenol is more acidic than orthomethoxyphenol.

ii) The – OH group attached to the benzene ring activates it towards electrophilic substitution. Further, it directs the incoming group to ortho and para positions in the ring as these positions become electron rich due to the resonance effect caused by – OH group.

Question 28.
With a suitable example write equations for the following:
i) Kolbe’s reaction.
ii) Reimer-Tiemann reaction.
iii) Willamson’s ether synthesis.
Answer:
i) Kolbe’s synthesis: When sodium salt of phenol (sodium phenoxide) is heated with carbon dioxide under pressure, a carboxylic group is introduced in the aromatic ring preferably at ortho position with respect to phenolic group. The sodium salt of o-hydroxybenzoic acid (sodium salicylate) formed, when treated with acid yields salicylic acid.

ii) Reimer-Tiemann reaction : When phenol is heated with chloroform in the presence of sodium hydroxide at 60°C, a – CHO group is introduced at the ortho position with respect to the phenolic group. This reaction is known as Reimer-Tiemann reaction.

iii) Willamson’s ether synthesis: It is an important method for the preparation of symmetrical and unsymmetrical ethers. In this method, an alkyl halide is allowed to react with sodium alkoxide.

Ethers containing substituted alkyl groups (2° or 3°) may also be prepared by this method. The reaction involves S_N2 attack of an alkoxide ion on primary alkyl halide.

In case of secondary and tertiary alkyl halides, elimination competes over substitution. If a tertiary alkyl halide is used, an alkene is the only reaction product and no ether is formed.

Question 29.
How are the following conversions carried out ?
i) Benzyl chloride to Benzyl alcohol
ii) Ethyl magnesium bromide to Propan-1-ol
iii) 2-butanone to 2-butanol
Answer:
i) Benzyl chloride is converted to benzyl alcohol by hydrolysis with aqueous sodium hydroxide.

ii) Ethyl magnesium bromide reacts with formaldehyde to form an adduct. Hydrolysis of the adduct yields an propan-1-ol.

iii) 2-butanone bn reduction with sodium borohydride (NaBH₄) gives 2-butanol.

Question 30.
Write the names of the reagents and equations for the preparation of the following ethers by Williamson’s synthesis:
i) 1-Propoxypropane
ii) Ethoxybenzene
iii) 2-Methoxy-2-methylpropane
iv) 1-Methoxyethane
Answer:
i) Sodium propoxide and propyl bromide.
CH₃CH₂CH₂ONa + CH₃CH₂CH₂ – Br → CH₃CH₂CH₂OCH₂CH₂CH₃ + NaBr

ii) Chlorobenzene and sodium ethoxide.

iii) Sodium tertiary butoxide and methylbromide.

iv) Sodium ethoxide and methyl bromide.

Question 31.
How is 1-propoxypropane synthesized from propan-1-ol ? Write mechanism of this reaction.
Answer:
1-rpropoxypropane is synthesised from propan-1-ol by dehydration in the presence of sulphuric acid.
Mechanism :
The formation of 1-propoxypropane is an S_N2 reaction involving the attack of alcohol molecule on a protonated alcohol.

Question 32.
Explain the fact that in aryl alkyl ethers the alkoxy group activates the benzene ring towards electrophilic substitution.
Answer:
Alkoxy group is an electron releasing group. When attached to benzene ring alkoxy group activates the ring towards electrophilic substitution. Further, it directs the incoming group to ortho and para positions in the benzene ring as these positions become electron rich due to the resonance effect caused by the – OR group.

Question 33.
Write equations of the below given reactions :
i) Alkylation of anisole
ii) Nitration of anisole
iii) Friedel-Crafts acylation of anisole
Answer:
i) Alkylation of anisole: Anisole undergoes Friedel-Crafts alkylation reaction with alkyl halide in the presence of anhydrous AlCl₃ as catalyst. The alkyl group is introduced in the ortho and para positions.

ii) Nitration of anisole : Anisole on nitration with a mixture of concentrated H₂SO₄ and HNO₃ yields a mixture of ortho and para nitroanisole.

iii) Friedel-Crafts acylation of anisole : Anisole undergoes Friedel-Crafts acylation with acyl halide in the presence of anhydrous AlCl₃.

The acyl group is introduced in the ortho and para positions.

Question 34.
Show how you would synthesize Hie following alcohols from appropriate aikenes ?

Answer:
By acid – catalysed hydration

Question 35.
Explain why phenol with bromine water forms 2, 4, 6-tribromophenol while on reaction with bromine in CS2 at low temperatures forms para-bromophenol as the major product.
Answer:
The hydroxyl group (- OH) is a very powerful activating substituent, and electrophilic substitution in phenols occurs faster, and under milder conditions, than in benzene.

Bromination of phenol occurs readily even in the absence of a catalyst at low temperature; Substitution occurs primarily at the para position to the hydroxyl group. When the para position is blocked, ortho substitution is observed. The reaction is carried out in a non-polar solvent CS₂ or ClCH₂CH₂Cl. In polar solvents such as water it is difficult to limit the bromination of phenols to monobromination. With bromine water all three positions that are ortho or para to the hydroxyl undergo rapid substitution.

Intext Questions – Answers

Question 1.
Classify the following as primary, secondary and teritary alcohols :

Answer:
i) Primary alcohol
ii) Primary alcohol
iii) Primary alcohol
iv) Secondary alcohol
v) Secondary alcohol
vi) Tertiary alcohol

Question 2.
Identify allylic alcohols in the above examples.
Answer:
In the examples given above (under question 1), (ii) and (vi) are allylic alcohols.

Question 3.
Name the following compounds according to IUPAC system.

Answer:

Question 4.
Show how the following alcohols are prepared by the reaction of a suitable Grignard reagent on methanal ?

Answer:

Question 5.
Write structures of the products of the following reactions.

Answer:

Question 6.
Write the structures of the major products expected from the following reactions :
a) Mononitration of 3-methylphenol
b) Dinitration of 3-methylphenol
c) Mononitration of phenyl methanoate.
Answer:

Question 7.
Give structures of the products you would expect when each of the following alcohol reacts with
a) HCl – ZnCl₂,
b) HBr and
c) SOCl₂.
i) Butan-1-ol
ii) 2-Methylbutan-2-ol
Answer:

Question 8.
Predict the major product of acid catalysed dehydration of
i) 1-methylcyclohexanol and
ii) butan-1-ol
Answer:

A mixture of but-l-ene and but-2-ene will be obtained. The 1 ° carbocation formed as intermediate will undergo rearrangement to give a more stable 2° carbocation. Loss of proton results in the mixture of but-1-ene and but-2-ene. However, but-l-ene will be the major product.

Question 9.
Ortho and para nitrophenols are more acidic titan phenol. Draw the resonance structures of the corresponding phenoxide ions.
Answer:
Electron delocalization in o-nitrophenoxide ion.

Electron delocalization in p-nitrophenoxide ion.

Question 10.
Write the equations involved in the following reactions:
i) Reimer – Tiemann reaction
ii) Kolbe’s reaction
Answer:
i) Reimer-Tiemann reaction :

ii) Kolbe’s reaction

Question 11.
Write the reactions of Williamson synthesis of 2-ethoxy-3-methylpentane starting from ethanol and 3-methylpentan-2-ol
Answer:

Question 12.
Which of the following is an appropriate set of reactants for the preparation of 1-methoxy- 4-nitrobenzene and why ?

Answer:
Set (ii) is appropriate.

Question 13.
Predict the products of the following reactions:
i) CH₃-CH₂-CH₂-O-CHS + HBr →
Answer:
CH₃ – CH₂ – CH₂ – OH + CH₃Br

ii)

Answer:

iii)

Answer:

iv)

Answer:
(CH₃)₃C – I + C₂H₅OH

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Binomial Theorem Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Binomial Theorem Important Questions Very Short Answer Type

Questions 1.
Find the 6th term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\). [May ’13, AP – Mar. 2019]
Solution:
Given \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\)
Here, x = \(\frac{2 x}{3}\); a = \(\frac{3 y}{2}\); n = 9
r + 1 = 6
⇒ r = 5
The general term in the expansion of (x + a)ⁿ is given by
T_{r + 1} = \({ }^n C_r\) . x^{n – r} . a^r
The 6th term in the expansion of \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) is
T_{5 + 1} = \({ }^9 C_5\left(\frac{2 x}{3}\right)^{9-5}\left(\frac{3 y}{2}\right)^5\)
T₆ = \({ }^9 \mathrm{C}_5 \cdot\left(\frac{2 \mathrm{x}}{3}\right)^4 \cdot\left(\frac{3 \mathrm{y}}{2}\right)^5\)
T₆ = 126 . \(\frac{2^4 \cdot x^4}{3^4} \cdot \frac{3^5 y^5}{2^5}\)
T₆ = 126 . \(\frac{3 x^4 y^5}{2}\)
T₆ = 189 . x⁴y⁵

Question 2.
Find the 3rd term from the end in the expansion of \(\left(x^{-\frac{2}{3}}-\frac{3}{x^2}\right)^8\).
Solution:
Given \(\left(x^{-\frac{2}{3}}-\frac{3}{x^2}\right)^8\)
Here, x = \(\mathrm{x}^{\frac{-2}{3}}\); a = \(\frac{-3}{x^2}\); n = 8
r + 1 = 7
⇒ r = 6
The general term th the expansion of (x + a)ⁿ is
T_{r + 1} = \({ }^n C_r\) x^{n – r} a^r.
The 7th term in the expansion of \(\left(x^{\frac{-2}{3}}-\frac{3}{x^2}\right)^8\) is
T_{6 + 1} = \({ }^8 C_6\left(x^{\frac{-2}{3}}\right)^{8-6} \cdot\left(\frac{-3}{x^2}\right)^6\)
T₇ = 28 \(\left(x^{\frac{-2}{3}}\right)^2\left(\frac{3}{x^2}\right)^6\)
= 28 . \(x^{-4} \cdot \frac{3^6}{x^{12}}\)
= 28 . 3⁶ . \(\frac{-40}{x^3}\)
The 3rd term from the end is 28 . 3⁶ . \(x^{\frac{-40}{3}}\).

Question 3.
Find the 4th term from the end ¡n the expansion of (2a + 5b)⁸.
Solution:
Given (2a + 5b)⁸
Here x = 2a, a = 5b, n = 8.
The expansion has 9 terms so that, the fourth term from the end is 6th term from the beginning, in the expansion of (2a + 5b)⁸.
r + 1 = 6
⇒ r = 5
The general term in the expansion of (x + a)ⁿ is T_{r + 1} = \({ }^n \mathrm{C}_r\) x^{n – r} a^r.
The r term in the expansion of (2a + 5b)⁸ is
T_{5 + 1} = \({ }^8 C_5\) (2a)^{8 – 5} (5b)⁵
= \({ }^8 C_5\) (2a)³ (5b)⁶
= \({ }^8 C_5\) . 2³ . a³ . 5³ . b⁵
∴ The 4th term from the end is \({ }^8 C_5\) . 2³ . 5⁵ . a³ . b⁵.

Question 4.
Find the middle term (s) in the expansion of \(\left(\frac{3 x}{7}-2 y\right)^{10}\) [March’12, May ‘10]
Solution:
Given \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
Here x = \(\frac{3 x}{7}\); a = – 2y, n = 10
Since, n = 10 is even then
Middle term = \(\frac{n}{2}\) + 1 = \(\frac{10}{2}\) + 1
= 5 + 1 = 6th term.
r + 1 = 6
⇒ r = 5
The general term in the expansion of \(\left(\frac{3 x}{7}-2 y\right)^{10}\) is
T_{r + 1} = \({ }^n C_r\) x^{n – r} a^r
= \({ }^{10} C_5\left(\frac{3 x}{7}\right)^{10-5}(-2 y)^5\)
6th term of \(\left(\frac{3 x}{7}-2 y\right)^{10}\) is
T_{5 + 1} = \({ }^{10} C_5\left(\frac{3 x}{7}\right)^5(-2 y)^5\)
= \({ }^{-10} C_5 \frac{3^5}{7^5}\) 2⁵ . x⁵ . y⁵.

Question 5.
Find the middle term(s) in \(\left(4 a+\frac{3 b}{2}\right)^{11}\).
Solution:
Given \(\left(4 a+\frac{3 b}{2}\right)^{11}\)
Here x = 4a, a = \(\frac{3}{2}\)b; n = 11
Since, n = 11 is odd,
Middle terms = \(\frac{\mathrm{n}+1}{2}, \frac{\mathrm{n}+3}{2}\) = 6, 7 terms
6th term:
r + 1 = 6
⇒ r = 5
The general term in this expansion ¡s
T_{r + 1} = \({ }^n C_r\) x^{n – r} . a^r
∴ 6th term of given expansion is
T_{5 + 1} = \({ }^{11} \mathrm{C}_5\) (4a)^{11 – 5} (\(\frac{3}{2}\)b)⁵
T₆ = \({ }^{11} \mathrm{C}_5\) (4a)⁶ (\(\frac{3}{2}\)b)⁵
= \({ }^{11} C_5 \frac{4^6 \cdot 3^5}{2^5} \cdot a^6 \cdot b^5\)
T6 = \({ }^{11} C_5 \frac{2^{12} \cdot 3^5}{2^5} \cdot a^6 b^5\)
= \({ }^{11} \mathrm{C}_5\) . 2⁷ . 3⁵ . a⁶ . b⁵

7th term:
r + 1 = 7
⇒ r = 6
The general term in this expansion is
T_{r + 1} = \({ }^n C_r\) x^{n – r} . a^r
∴ 7th term of given expansion is
T_{6 + 1} = \({ }^{11} C_5(4 a)^{11-6}\left(\frac{3}{2} b\right)^6\)
T₇ = \({ }^{11} C_6(4 a)^5\left(\frac{3}{2} b\right)^6\)
= \({ }^{11} C_6 \frac{4^5 \cdot 3^6}{2^6}\) . a⁵ . b⁶
T₇ = \({ }^{11} \mathrm{C}_6 \frac{2^{10} \cdot 3^6}{2^6}\) . a⁵ . b⁶
= \({ }^{11} \mathrm{C}_6\) 2⁴ . 3⁶ . a⁵ . b⁶.

Question 6.
Find the coefficient of x^-7 in \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\).
Solution:
Given \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\).

Question 7.
Find the coefficients of x⁹ and x¹⁰ in the expansion of (2x² – \(\frac{1}{x}\))²⁰
Solution:
Given (2x² – \(\frac{1}{x}\))²⁰
Here x = 2x²; a = \(-\frac{1}{x}\); n = 20
Now, the general term in this expansion is
T_{r + 1} = \({ }^n C_r\) x^{n – r} . a^r
= \({ }^{20} \mathrm{C}_{\mathrm{r}}\) (2x²)^20-r (\(-\frac{1}{x}\))^r
= \({ }^{20} \mathrm{C}_{\mathrm{r}}\) 2^20-r x^40-2r (- 1)^r x^{– r}
= \({ }^{20} \mathrm{C}_{\mathrm{r}}\) 2^20-r (- 1)^r x^40-3r …………(1)
I) To find the coefficient of x⁹:
put 40 – 3r = 9
⇒ 3r = 31
⇒ r = \(\frac{31}{3}\)
Since, r is a positive integer, this is not possible.
This means, that the expansion of \(\left(2 x^2-\frac{1}{x}\right)^{20}\) does not possess x⁹ term.
This means that,
The coeff. of x⁹ in the exp. of \(\left(2 x^2-\frac{1}{x}\right)^{20}\) is zero.

ii) To find the coefficient of x¹⁰:
Put 40 – 3r = 10 of substituting r = 10 in equation (1), we get
T_{10 + 1} = \({ }^{20} \mathrm{C}_{10}\) 2^20-10 (- 1)¹⁰ x^40-30
T₁₁ = \({ }^{20} \mathrm{C}_{10}\) . 1 . x¹⁰
= \({ }^{20} \mathrm{C}_{10}\) 2¹⁰ x¹⁰
The coeff. of \(\left(2 x^2-\frac{1}{x}\right)^{20}\) in the expansion of is \({ }^{20} \mathrm{C}_{10}\) 2¹⁰.

Question 8.
Find the term independent of x in the expansion of \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\).
Solution:
Given, \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
Here, x = \(\frac{3}{\sqrt[3]{x}}\), a = 5√x, n = 25
The general term in this expansion is
T_{r + 1} = \({ }^n C_r\) x^n-r a^r
= \({ }^{25} C_r\left(\frac{3}{\sqrt[3]{x}}\right)^{25-r}(5 \sqrt{x})^r\)
= \({ }^{25} \mathrm{C}_{\mathrm{r}} 3^{25-\mathrm{r}} \mathrm{x}^{\frac{-25+\mathrm{r}}{3}} \cdot 5^{\mathrm{r}} \cdot \mathrm{x}^{\mathrm{r} / 2}\)
= \({ }^{25} \mathrm{C}_{\mathrm{r}} 3^{25-\mathrm{r}} 5^{\mathrm{r}} \times \frac{-25+\mathrm{r}}{3}+\frac{\mathrm{r}}{2}\) ………………..(1)

To find the term independent of x:
i.e., the coeff. of x⁰ put \(\) = 0
⇒ – 50 + 2r + 3r = 0
⇒ 5r = 50
⇒ r = 10
Substitute r = 10 in equation (1),
T₁₀₊₁ = \({ }^{25} \mathrm{C}_{10} 3^{15} 5^{10} \mathrm{x}^{\frac{-25+10}{3}+\frac{1}{10}}\)
T₁₁ = \({ }^{25} \mathrm{C}_{10}\) . 3¹⁵ . 5¹⁰ . x⁰
∴ The term independent of x in the given expansion is
T₁₁ = \({ }^{25} \mathrm{C}_{10}\) . 3¹⁵ . 5¹⁰ . x⁰

Question 9.
Find largest binomial coefficients in the expansion of (1 + x)²⁴.
Solution:
Given (1 + x)²⁴
Here, n = 24, an even integer.
∴ The largest binomial coefficient is \({ }^{\mathrm{n}} \mathrm{C}_{\left(\frac{\mathrm{n}}{2}\right)}={ }^{24} \mathrm{C}_{12}\).

Question 10.
If \({ }^{22} \mathrm{C}_{\mathrm{r}}\) is the largest binomial coefficient in the expansion of (1 + x)²² find the value of \({ }^{13} \mathrm{C}_{\mathrm{r}}\). [TS & AP – May 2015; May ’11] [AP. Mar. 2016]
Solution:
Given, (1 + x)²²
Here n = 22 an even integer.
∴ The Largest binomial coefficient = \({ }^{\mathrm{n}} \mathrm{C}_{\left(\frac{\mathrm{n}}{2}\right)}={ }^{22} \mathrm{C}_{\left(\frac{22}{2}\right)}={ }^{22} \mathrm{C}_{11}\)
Given that the largest binomial coeff. = \({ }^{22} \mathrm{C}_{11}\)
[∵ \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s]
⇒ \({ }^{22} \mathrm{C}_{\mathrm{r}}={ }^{22} \mathrm{C}_{11}\)
⇒ r = 11
Now, \({ }^{13} C_r={ }^{13} C_{11}={ }^{13} C_2\)
= \(\frac{13 \times 12}{2 \times 1}\) = 78.

Question 11.
If n is a positive integer, then prove that \(\sum_{r=1}^n \mathbf{r} \cdot C_r\) = n . 2^{n – 1}. [May ’97]
Solution:
We know that,
(1 + x)ⁿ = C₀ + C₁x + C₂x² + C₃x³ ± …………… + C_nxⁿ ……………(1)
Now differentiating (1) on both sides with respect to ‘x’ we get
n(1 + x)^{n – 1} = 0 + C₁(1) + C₂(2x) + C₃(3x²) + …………….. + C_n (nx^n-1)
n(1 + x)^n-1 = C₁ + 2x . C₂ + 3x² . C₃ + nx^{n – 1}C_n
Now, put x = 1 we get
n(2)^{n – 1} = C₁ + 2(1) C₂ + 3(1)²C₃ + …………… + (n) (1)^{n – 1} C_n
n₂^{n – 1} = C₁ + 2C₂ + 3C₃ + …………. + nC_n
C₁ + 2C₂ + 3C₃ + …………… nC_n = n . 2^{n – 1}
\(\sum_{r=1}^n\) r . C_r = n . 2^{n – 1}

Question 12.
If the coefficients of (2r + 4)th, (3r + 4)th terms in the expansion of (1 + x)²¹ are equal, find ‘r’. [TS – Mar, 2015]
Solution:
Given (1 + x)²¹
The general term in the expansionof (x + a)ⁿ is
T_{r + 1} = nCr x^{n – r} . a^r.
(2r + 4)th term in the expansion of (1 + x)²¹ is
T_{(2r + 3) + 1} = \({ }^{21} \mathrm{C}_{2 \mathrm{r}+3}\) (1)^{21 – (r + 3)} (x)^{2r + 3}
T_{2r + 4} = \({ }^{21} \mathrm{C}_{2 \mathrm{r}+3}\) x^{2r + 3}
The coefficient of (2 + 4)th term is \({ }^{21} C_{2 r+3}\)
(3r + 4)th term in the expansion of (4 + x)²¹ is .
T_{(3r + 3) + 1} = \({ }^{21} \mathrm{C}_{3 \mathrm{r}+3}\) (1)^{21 – (3r + 3)} x^{3r + 3}
T_{3r + 4} = \({ }^{21} \mathrm{C}_{3 \mathrm{r}+3}\) x^{3r + 3}
The coeff. of (3r + 4)th term is \({ }^{21} \mathrm{C}_{3 \mathrm{r}+3}\)
Given that, two coeff. are equal.
\({ }^{21} \mathrm{C}_{2 \mathrm{r}+3}={ }^{21} \mathrm{C}_{3 \mathrm{r}+3}\)
\({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
n = r + s
21 = 21 + 3 + 3r + 3
5r = 15
⇒ r = 3

r = s
2r + 3 = 3r + 3
⇒ r = 0.

Question 13.
Prove that C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + …………. + 2_n . C_n = 3ⁿ. [AP – Mar. ’15; May ’07] [TS – Mar. ’18]
Solution:
We know that,
(1 + x)ⁿ = C₀ + C₁x + C₂x² + C₃x³ + ………….. + C_nxⁿ …………….(1)
put x = 2 in the equation (1) we get,
(1 + 2)ⁿ = C₀ + C₁(2) + C₂(2)² + C₃(2)³ + …………….. + C_n.(2)ⁿ
∴ C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + …………… + 2ⁿ C_n = 3ⁿ .

Question 14.
Prove that C₀ + 3 . C₁ + 3² . C₂ + ………….. + 3ⁿ . C_n = 4
Solution:
We know that,
(1 + x)ⁿ = C₀ + C₁x + C₂x² + C₃x³ + ………….. + C_nxⁿ …………….(1)
Put x = 3 in equation (1), we get
(1 + 3)ⁿ = C₀ + C₁ (3) + C₂ (3)² + C₃ (3)³ + ………………… + C_n . 3ⁿ
C₀ + 3 . C₁ + 3² . C₂ + 3³ . C₃ + …………… + 3ⁿ C_n = 4ⁿ.

Question 15.
Prove that \(\frac{\mathrm{C}_1}{\mathrm{C}_0}+2 \cdot \frac{\mathrm{C}_2}{\mathrm{C}_1}+3 \cdot \frac{\mathrm{C}_3}{\mathrm{C}_2}+\ldots \ldots\) + \(\mathbf{n} \cdot \frac{\mathbf{C}_{\mathbf{n}}}{\mathbf{C}_{\mathbf{n}-\mathbf{1}}}=\frac{(\mathbf{n}+\mathbf{1})}{2}\)
[March ’88]
Solution:
L.H.S:
\(\frac{\mathrm{C}_1}{\mathrm{C}_0}+2 \cdot \frac{\mathrm{C}_2}{\mathrm{C}_1}+3 \cdot \frac{\mathrm{C}_3}{\mathrm{C}_2}+\ldots \ldots+\mathrm{n} \cdot \frac{\mathrm{C}_{\mathrm{n}}}{\mathrm{C}_{\mathrm{n}-1}}\)
= \(\frac{{ }^n C_1}{{ }^n C_0}+2 \cdot \frac{{ }^n C_2}{{ }^n C_1}+3 \cdot \frac{{ }^n C_3}{{ }^n C_2}+\ldots . .+n \cdot \frac{{ }^n C_n}{{ }^n C_{n-1}}\)
= \(\frac{\mathrm{n}}{1}+2 \cdot \frac{\frac{\mathrm{n}(\mathrm{n}-1)}{1 \cdot 2}}{\frac{\mathrm{n}}{1}}+3 \cdot \frac{\frac{\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2)}{1 \cdot 2 \cdot 3}}{\frac{\mathrm{n}(\mathrm{n}-1)}{1 \cdot 2}}+\ldots \ldots+\mathrm{n} \cdot \frac{1}{5}\)

= n + (n – 1) + (n – 2) + …………… + 1
= 1 + 2 + 3 + ………….. + n
= Σn = \(\frac{n(n+1)}{2}\) = R.H.S

Question 16.
Find the number of terms in the expansion of (2x + 3y + z)⁷. [May ’14, March ’14, ’13] [TS – Mar. 2019]
Solution:
Given (2x + 3y + z)⁷
Here, n = 7
∴ Number of terms in the expansion of
(2x + 3y + z)⁷ = \(\frac{(n+1)(n+2)}{2}\)
= \(\frac{(7+1)(7+2)}{2}=\frac{8 \times 9}{2}\) = 36.

Question 17.
Find the number of terms with non-zero coefficients in (4x – 7y) + (4x + 7y) .
Solution:

Question 18.
Find the sum of last 20 coefficients in the expansion of (1 + x)³⁹.
Solution:
The last 20 coefficients in the expansion of (1 + x)³⁹ are \(\).
We know that

Question 19.
If A and B are coefficients of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^2n-1 respectively, then find the value of \(\frac{A}{B}\).
Solution:
Coefficient of xⁿ in the expansion of (1 + x)²ⁿ is \({ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{n}}\)
Coefficient of xⁿ in the expansion of (1 + x)^2n-1 is \({ }^{2 n-1} C_n\)
∴ A = \({ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{n}}\) and B = \({ }^{2 n-1} C_n\)
∴ \(\frac{A}{B}=\frac{{ }^{2 n} C_n}{2 n-1}=\frac{\frac{2 n !}{n ! n !}}{\frac{(2 n-1) !}{(n-1) ! \cdot n !}}\)
= \(\frac{2 n !}{(2 n-1) ! n !} \cdot(n-1) !=\frac{2 n}{n}\)
⇒ \(\frac{\mathrm{A}}{\mathrm{B}}\) = 2.

Question 20.
Find the set E of x for which the binomial expansion (2 + 3x)^-2/3. [March ‘11, ‘06] [TS – Mar. 2016]
Solution:
Given, (2 + 3x)^-2/3 = 2^-2/3 (1 + \(\frac{3}{2}\)x)^-2/3
The binomial expansion of (2 + 3x)^-2/3 is valid when
\(\left|\frac{3 x}{2}\right|<1 \Rightarrow|x|<\frac{2}{3}\)
⇒ x ∈ (\(\left.\frac{-2}{3}, \frac{2}{3}\right)\)).

Question 21.
Find the set E of x for which the binomial expansion of (3 – 4x)^3/4. [AP-Mar. 2017] [May ’12]
Solution:
Given (3 – 4x)^3/4 = \(3^{\frac{3}{4}}\left(1-\frac{4 x}{3}\right)^{\frac{3}{4}}\)
The binomial expansion of (3 – 4x)^3/4 is valid
when \(\left|\frac{-4 x}{3}\right|<1 \Rightarrow\left|\frac{4 x}{3}\right|<1\)
x < \(\frac{3}{4}\)
x ∈ (\(\frac{-3}{4}\), \(\frac{3}{4}\))
E = (\(\frac{-3}{4}\), \(\frac{3}{4}\))

Question 22.
Find the 7th term of \(\left(1-\frac{x^2}{3}\right)^{-4}\).
Solution:
Given \(\left(1-\frac{x^2}{3}\right)^{-4}\)
Comparing this with (1 + x)ⁿ
where x = , n = – 4,
r + 1 = 7
⇒ r = 6
The general term in the expression of (1 + x)ⁿ is
T_{r + 1} = \(\frac{n(n-1) \ldots \ldots(n-r+1)}{5 n}\) . x
= \(\frac{(-4)(-4-1)(-4-2)(-4-3)(-4-4)(-4-5)}{6 !}\) \(\left(\frac{-x^2}{3}\right)^6\)
= \(\frac{(-4)(-5)(-6)(-7)(-8)(-9)}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \cdot \frac{x^{12}}{3^6}\)
= 84 . \(\frac{28}{243}\) x¹².

Question 23.
Find the set E of the values of x for which, the binomial expansion (2 + 5x)^-1/2 is valid. [TS – Mar. 2017]
Solution:
Given (2 + 5x)^-1/2
The binomial expansion of (2 + 5x)^-1/2 is valid when
|\(\frac{5 x}{2}\)| < 1
|x| < \(\frac{2}{5}\)
x ∈ (- \(\frac{2}{5}\), \(\frac{2}{5}\)).

Question 24.
Find the 7th term in the expansion of \(\left(\frac{4}{x^3}+\frac{x^2}{2}\right)^{14}\). [AP – May 2016]
Solution:
\({ }^{14} C_6 \cdot \frac{2^{10}}{x^{12}}\)

Question 25.
Find the 5th term in the expansion of (3x – 4y)⁷.
Solution:
241920 x³ y⁴.

Question 26.
Find the middle term(s) in \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\).
Solution:
\({ }^{20} \mathrm{C}_{10}\) (15)¹⁰ (a)¹⁰.

Question 27.
Find the middle term(s) in the expansion of (4x² + 5x³)¹⁷.
Solution:
\({ }^{17} \mathrm{C}_{9}\) 4⁸ . 5⁹ . x⁴³

Question 28.
Find the coefficient of x¹¹ in (2x² + \(\frac{3}{x^3}\))¹³
Solution:
\({ }^{13} \mathrm{C}_3\) 2¹⁰ . 3³

Question 29.
Find the term independent of x in the expansion of \(\left(\sqrt{\frac{x}{3}}+\frac{3}{2 x^2}\right)^{10}\).
Solution:
\(\frac{5}{4}\)

Question 30.
Find the largst binomial coefficients in the expansion of (1 + x)¹⁹.
Solution:
\({ }^{19} \mathrm{C}_9 ;{ }^{19} \mathrm{C}_{10}\)

Question 31.
If the coefficients of (2x + 4)th, (r – 2)th terms in the expansion of (1 + x)²¹ are equal find ‘r’.
Solution:
6

Question 32.
Find the set E of x for which the binomial expansion (7 + 3x)^-5. [May ’09]
Solution:
\(\left(\frac{-7}{3}, \frac{7}{3}\right)\)

Question 33.
Find the set E of x for which the binomial expansion (7- 4x)^-5 is valid.
Solution:
\(\left(\frac{-7}{4}, \frac{7}{4}\right)\)

Question 34.
Find the 6th term of \(\left(1+\frac{x}{2}\right)^{-5}\).
Solution:
\(\frac{-63}{16}\) x⁵.

Telangana TSBIE TS Inter 2nd Year Chemistry Study Material 13th Lesson Organic Compounds Containing Nitrogen Textbook Questions and Answers.

TS Inter 2nd Year Chemistry Study Material 13th Lesson Organic Compounds Containing Nitrogen

Very Short Answer Questions (2 Marks)

Question 1.
Write the IUPAC names of the following compounds and classify them into primary, secondary and tertiary amines. [TS 15]
(i) (CH₃)₃C NH₂
(ii) CH₃(CH₂)₂ NH₂
(iii) (CH₃ CH₂)₂ NCH₃
Answer:
(i) 1,1- dimethylethanamine. It is a primary amine.
(ii) Propan -1 – amine. It is a primary amine.
(iii) N – methyl – N – ethylethanamine. It is a tertiary amine.

Question 2.
Explain why ethylamine is more soluble in water whereas aniline is not soluble.
Answer:
Ethylamine is soluble in water because it can form hydrogen bonds with water mole-cules. The phenyl group in aniline is bulky and hydrophobic. It opposes the formation of hydrogen bonds with water molecules. Hence, aniline is insoluble in water.

Question 3.
Why aniline does not undergo Friedel – Craft’s reaction ?
Answer:
Aniline does not undergo Friedel – Craft’s reaction (alkylation and acylation)’due to salt formation with AlCl₃, the Lewis acid, which is used as a catalyst. Because of this, nitrogen of aniline acquires positive charge and hence acts as a strong deactivation group for further reaction.
C₆H₅ NH₂ + AlCl₃ → [C₆H₅NH₂]⁺ [AlCl₃]^–

Question 4.
Gabriel phthalimide synthesis exclusively forms primary amines only. Explain.
Answer:
Because there is only one hydrogen bonded to the nitrogen of pathalimide, only one alkyl group can be placed on the nitrogen. This means that the gabriel synthesis can be used only for the preparation of primary amines.

Question 5.
Arrange the following bases in decreasing order of pK_b values.
C₂H₅NH₂, C₂H₅NHCH₃, (C₂H₅)₂ NH and C₆H₅NH₂.
Answer:
C₆H₅NH₂ > C₂H₅NHCH₃ > C₂H₅NH₂ > (C₂H₅)₂ NH
pK_b Values: 9.38 9.30 3.29 3.00

Question 6.
Arrange the following bases in increasing order of their basic strength. Aniline, p – nitro- aniline and p – toluidine.
Answer:
p – nitro Aniline < aniline < p – toluidine.

Question 7.
Write equations for carbylamine reaction of any one aliphatic amine. [TS Mar. 19; (IPE 14)]
Answer:
A primary amine, for example, n – butyla-mine forms foul smelling isocyanide or carbylamine when heated with chloroform and alcoholic potassium hydroxide.

Question 8.
Give structures of A, B and C in the following reaction.

Answer:
A is C₆H₅CN Phenylcyanide or Benzonitrile
B is C₆H₅COOH Benzoic acid
C is C₆H₅CONH₂ Benzamide

Question 9.
Accomplish the following conversions : [IPE 14]
i) Benzoic acid to Benzamide
ii) Aniline to p – Bromoaniline
Answer:
i) Benzoic acid reacts with ammonia to give ammonium benzoate which on fur-ther heating at temperature gives benza-mide.

ii) The amino group of aniline is protected by acetylation. Acetanilide, so obtained, is reacted with bromine in acetic acid followed by hydrolysis to get p – bromoaniline.

Question 10.
Why cannot aromatic primary amines be prepared by Gabriel phthalimide synthesis ?
Answer:
Aromatic primary amines cannot be prepared by Gabriel phthalimide synthesis because arylhalides do not undergo nucleophilic substitution with the anion formed by phthalimide.

Short Answer Questions (4 Marks)

Question 11.
Write the IUPAC names of the following compounds.
i) CH₃CH₂NH CH₂CH₂CH₃
ii) PhCH₂ CN
iii)

iv)

Answer:
i) N – Ethylpropanamine
ii) Phenylethanenitrile or Benzylcyanide
iii) 3 – Bromoaniline or 3 – Bromobenzenamine
iv) 4 – Bromophenyl methylisocyanide

Question 12.
Give one chemical test to distinguish between the following pairs of compounds.
i) Methylamine and dimethylamine
ii) Aniline and N – methylaniline
iii) Ethylamine and aniline
Answer:
i) Methylamine on heating with chloroform and alcoholic potassium hydroxide forms foul smelling isocyanide or carbylamine. Dimethylamine does not give this test.

ii) Aniline (a primary amine) gives positive carbylamine test N – methylaniline (a secondary amine) does not give this test. Thus when aniline is heated with chloroform and alcoholic KOH forms fouls melling phenylisocyanide or carbylamine.

iii) Ethylamine reacts with nitrous acid to give nitrogen gas and ethylalcohol. Aniline reacts with nitrous acid (NaNO₂ + HCl) at low temperatures (0 – 5°C) to form diazonium salt.

Question 13.
Account for the following :
i) pK_b of aniline is more than that of methylamine.
ii) Reduction of alkylcyanide forms primary amine whereas alkylisocyanide forms secondary amine.
Answer:
i) In aniline the -NH₂ group is directly attached to the benzene ring. It results in the unshared electron pair on nitrogen atom to be in conjugation with the benzene ring and thus making it less available for protonation. Such a situation is absent in methylamine. Hence PKb value of aniline is greater than that of methylamine.

ii) In, alkylcyanides, the alkylgroup is linked to the carbon of the cyanide ion while in isocyanides the alkyl group is linked to the nitrogen of cyanide.
R – C ≡ N R – N ≡ C
Hence, alkylcyanide gives primary amine whereas alkyl isocyanide gives secondary amine on reduction.

Question 14.
How do you prepare the following?
i) N, N – Dimethyipropanamine from ammonia
ii) Propanamine from chloroethane
Answer:

Question 15.
Compare the basicity of the following in gaseous and in aqueous state and arrange them in increasing order of basicity. [TS 15[
CH₃NH₂, (CH₃)₂NH, (CH₃)₃N and NH₃
Answer:
The alkyl (methyl) group has electron – releasing inductive effect. It pushes the electrons towards nitrogen and makes the electron pair more available for sharing with the proton of the acid. Hence, in the gaseous state the basicity of the amines follows the order.
(CH₃)₃N > (CH₃)₂NH > CH₃NH₂ > NH₃
In the aqueous state the basicity of the amines depends upon inductive effect, solvation effect and steric hindrance of the alkyl group. Hence, the order basic strength of the methyl substituted amine in the aqueous solution is
(CH₃)₂NH > CH₃NH₂ > (CH₃)₃N > NH₃

Question 16.
How do you carryout the following conversions ?
i) N – Ethylamine to N, N – Diethyl propanamine
ii) Aniline to p – Aminobenzene sulphonamide
Answer:
i) N – ethylamine is first reacted with propylchloride to convert it to N – ethyl propanamine. It is then reacted with ethyl chloride to convert it to N, N – Diethyl propanamine.

ii) Aniline is converted to acetanilide by reaction with acetylchloride. Acetanilide is treated with chlorosulphonic acid and the product on reaction with ammonia followed by hydrolysis gives sulphanilamide.

Question 17.
Explain with a suitable example how benzene sulphonylchloride can distinguish primary, secondary and tertiary amines.
Answer:
Benzene sulphonylchloride (Hinsberg reagent) reacts with a primary amine, ethylamine, to give N – ethylbenzene sulphonyl amide.

This compound contains hydrogen attached to nitrogen. It is acidic in nature and hence it is soluble in sodium hydroxide solution.

When benzene sulphonyl chloride reacts with a secondary amine, for example diethyl amine, to give N, N – diethyl benzene sulphonamide. It does not contain hydrogen attached to nitrogen. It is not acidic and hence it is insoluble in sodium hydroxide solution.

Tertiary amines do not react with Hinsberg reagent.

Question 18.
Write the reactions of
i) aromatic and
ii) aliphatic primary amines with nitrous acid.
Answer:
Aromatic primary amines react with nitrous acid at low temperatures (0 – 5°C) to form diazonium salts.

Aliphatic primary amines react with nitrous acid to form alcohol and nitrogen gas.

Question 19.
Explain why amines are less acidic than alcohols of comparable molecular masses.
Answer:
The acidic character of alcohols is due to the polar nature of O – H bond. The polarity of the N – H bond in amines is less than that of the O – H bond in alcohols of comparable molecular mass. Hence amines are less acidic than alcohols of comparable molecular mass.

Question 20.
How do you prepare Ethyl cyanide and Ethyl isocyanide from a common alkyl halide. [IPE 14]
Answer:
Ethyl chloride reacts with ethanolic potassium cyanide to form ethyl cyanide as the major product. However, when ethyl chloride reacts with ethanolic silver cyanide ethyl isocyanide will be the major product.

Long Answer Questions (8 Marks)

Question 21.
An aromatic compound ‘A’ on treatment with aqueous ammonia and heating forms compound ‘B’ which on heating with Br₂ and KOH forms compound ‘C’ of molecular formula C₆H₇N. Write the structures and IUPAC names of compounds A, B and C.
Answer:
The final product ‘C’ with molecular formula C₆H₇N is Aniline. The sequence of reactions can be explained as follows.

Compound A is Benzoic acid. On treatment with aqueous ammonia gives ammonium benzoate which on heating gives Benzamide (B). Benzamide on heating with bromine and potassium hydroxide (Hofmann hypobromite reaction) gives Aniline (C) with molecular formula C₆H₇N.

Question 22.
Complete the following conversations.
i) CH₃NC + HgO → ?
ii) ? + 2H₂O → CH₃NH₂ + HCOOH
iii) CH₃CN + C₂H₅ Mg Br → ?
iv) CH₃ CH₂ NH₂ + CHCl₃ + KOH ?
v)
Answer:
i) HgO is a mild oxidising agent. It converts isocyanides to isocyanates. Thus, methyl isocyanide is converted to methyl isocyanate.

ii) Isocyanides on hydrolysis give amines and formic acid.

iii) Ethyl magnesium bromide adds on to methylcyanide or acetonitrile to give an addition product which on hydrolysis forms acetone.

iv) Primary amine on heating with chloroform and alcoholic KOH gives foul smelling isocyanide or carbylamine.

v) Aniline on treatment with bromine water gives a white precipitate of 2,4,6 – tribromoaniline.

Question 23.
i) Write the structures of different isomeric amines corresponding to the molecular formula C₉H₁₃N.
ii) What reducing agents can bring about reduction of nitrobenzene ?
iii) Write the product formed when benzyl chloride is reacted with ammonia followed by treatment with methyl and ethyl chlorides.
Answer:
i)

ii) The following reagents can bring about reduction of nitrobenzene.
a) Sn / HCl (or)Fe/HCl
b)Zn/NaOH
c) Zn / NH₄Cl/ H₂O
d)H₂/Pd

iii)

Question 24.
i) Identify the amide and cyanide which on reduction with appropriate reducing agent give n – butylamine.
ii) Write the mechanism of Hoffmann bromamide reaction.
Answer:
i) Butanamide, CH₃CH₂CH₂CONH₂ on reduction with lithium aluminium hydride yields n – butylamine

n – propylcyanide on reduction LiAlH₄ or Na(Hg)/C₂H₅OH gives n – Butylamine.

ii) Hoffmann bromamide reaction mechanism :

Question 25.
How do you make the following conversions ?
i) Chlorophenylmethane to phenylacetic acid
ii) Chlorophenylmethane to 2 – phenylethanamine
Answer:
i)

Chlorophenyl methane is reacted with potassium cyanide and converted to benzylcyanide which on hydrolysis gives phenylacetic acid.

ii)

Chlorophenylmethane is reacted with KCN and converted to benzylcyanide which on reduction gives 2 – phenylethanamine.

Question 26.
Identify the starting amide which gives p – methyl aniline on reaction with bromine and sodium hydroxide and write all the steps involved in the reaction.
Answer:
p – methylbenzamide on reaction with bromine and sodium hydroxide (Hoffmann bromamide degradation reaction) gives p – methylaniline.

The following steps are involved in the reaction.
2NaOH + Br₂ → NaBr + NaOBr + H₂O

Question 27.
Explain wiy the order of basicity methylamine, N, N – dimethylamine and N, N, N – trimethylamine changes in gaseous and aqueous medium.
Answer:
In the gaseous state the basicity of the methyl substituted amines follows the order.
N, N, N – trimethylamine > N, N – dimethylamine > methylamine

It can be explained as follows. The methyl group has electron releasing nature. It pushes electrons towards nitrogen and thus makes the unshared electron pair on nitrogen more available for sharing with the proton of the acid.

Thus the methyl substituted ammonium gets stabilised due to to the dispersal of the positive charge by the +1 effect of thecilkyl group. Thus the basic nature of the methyl substituted amines increases with the increase in the number of methyl groups. This trend is followed in the gaseous phase.

In the aqueous phase, the substituted ammonium cations get stabilised not only by electron releasing effect of the methyl group but also by solvation with water molecules. Another factor that decides the basic strength of the alkylamines in aqueous state is steric hindrance of the alkyl groups:

Hence, due to the presence of two electron releasing methyl groups attached to the nitrogen atom, dimethylamine is a stronger base than methylamine. If so, trimethyl amine having three methyl groups attached to nitrogen should be expected to be more basic them dimethyl amine. But actually trimethylamine is considerably less basic than dimethyl amine.

Why so ? In methyl amine and dimethylamine the ‘electronic effect’ increases the basic strength of the amine. However, in trimethylamine the over crowding of the three methyl groups attached to nitrogen causes the ‘steric effect’ – to dominate over the ‘electronic effect’. This steric effect retards the protonation of nitrogen which results in an appreciably lower basic strength of trimethylamine. Hence the basic strength of the amines in the aqueous phase follows the order :
(CH₃)₂ NH > CH₃NH₂ > (CH₃)₃N > NH₃.

Question 28.
Write the equations involved in the reaction of Nitrous acid with ethylamine and aniline.
Answerw:
Ethyl amine reacts with nitrous acid to form ethyl diazonium salt which being unstable liberates nitrogen gas and forms ethyl alcohol.

Aniline reacts with nitrous acid at low temperatures (0 – 5°C) to form diazonium salt.

Question 29.
Explain with equations how methylamine, N, N – dimethylamine and N, N, N-trimethylamine react with benzene sulphonyl chloride and how this reaction is useful to separate these amines.
Answer:
Methylamine reacts with benzene suphonyl chloride to give N – methyl benzene sulphonamide.

The hydrogen attached to nitrogen in sulphonamide is strongly acidic due to the presence of strong electron withdrawing sulphonyl group. Hence, it is soluble in alkali, say NaOH solution. N, N – dimethylamine reacts with benzene sulphonyl chloride to give N, N – dimethylbenzene sulphonair; le. Since this compound does not contain any hydrogen atom attached to nitrogen atom it is not soluble in alkali.

N, N, N – trimethylamine does not react with benzene sulphonyl chloride. This property of these three methylamines reacting with benzene sulphonylchloride in a different manner is used for their separation from a mixture.

Question 30.
Explain why aniline in strong acidic medium gives a mixture of Nitro anilines and what steps need to be take to prepare selectively p-nitroaniline.
Answer:
In strongly acidic medium, aniline is protonated to form the anilinium ion which is meta directing. That is why besides the ortho and para derivatives, significant amount of meta derivative is also formed.

However, by protecting the -NH₂ group by acetylation reaction with acetic anhydride, the nitration reaction can be controlled and the p-nitro derivative can be obtained as the major product.

Question 31.
i) Account for the stability of aromatic diazonium ions when compared to aliphatic diazonium ions.
ii) Write the equations showing the conversion of aniline diazonium chloride to
a) Chlorobenzene, b) Iodobenzene and c) Bromobenzene.
Answer:
i) The relative stability of aromatic diazonium ions can be ascribed to the fact that its structure is a resonance hybrid of the canonical forms involving the participation of the benzene ring.

The hybrid structure shows that: a) benzene ring is deactivated to attack of electrophiles, (b) the C -N bond acquires some double bond character and becomes stronger. Alkyl diazonium ions cannot exhibit such resonance and hence C – N bond in them is weak. That is why they are unstable relative to their aromatic counterparts.

ii) a) Aqueous solution of benzene diazonium chloride when heated with cuprous chloride gives chlorobenzene.

b) Iodobenzene is formed when benzene diazonium chloride solution is treated with potassium iodide.

c) Bromobenzene is formed when benzenediazonium chloride solution is treated with hydrobromic acid in the presence of copper power.

Question 32.
Complete the following conversions:
Aniline to i) Fluorobenzene iQ Cyanobenzene iif) Benzene and iv) Phenol
Answer:

Question 33.
Explain the following name reactions : [AP 16, 15]
i) Sandmeyer reaction
ii) Gatterman reaction.
Answer:
i) Sandmeyer reaction: The diazonium group of a diazonium salt can be replaced by chlorine (-Cl) or bromine (-Br) by heating the aqueous solution of the diazonium salt with cuprous chloride or cuprous bromide. This reaction is called Sandmeyer reaction.

ii) Gatterman reaction : It is a modification of Sandmeyer reaction. The diazonium group is replaced by – Cl or – Br when the diazonium salt solution is treated with the corresponding halogen acid in the presence of copper powder.

Question 34.
Write the steps involved in the coupling of Benzene diazoniumchloride with aniline and phenol.
Answer:D
iazonium salts react with aromatic amines and phenols to give azocompounds having the general formula Ar – N = N – Ar. The reaction is known as coupling reaction. The coupling of benzene diazonium chloride with phenols is carried out in mild alkaline solution and with amines in weakly acidic medium.
Coupling with aniline :

Coupling with Phenol :

Question 35.
Write the equations involved in the conversion of acetamide and propanaldehydeoxime to methyl cyanide and ethyl cyanide respectively.
Answer:
Acetamide is converted to methyl cyanide by heating it with benzene sulphonyl chloride in pyridine at 70°C.
CH₃ CO NH₂ + C₆H₅SO₂Cl > CH₃CN + C₆H₅SO₃H + HCl
Propanaldehydeoxime is converted to ethylcyanide by dehydrating with acetic anhydride.
CH₃ – CH₂ – CH = NOH + (CH₃CO)₂O → CH₃ – CH₂ – CN + 2CH₃COOH

Intext Questions – Answers

Question 1.
Classify the following amines as primary, secondary or tertiary.

iii) (C₂H₅)₂ CHNH₂
iv) (C₂H₅)₂ NH
Answer:
i) and
iii) are primary amines
ii) is a tertiary amine
iv) is a secondary amine

Question 2.
i) Write structures of different isomeric amines to the molecular formula, C₄H₁₁N
ii) Write IUPAC names of all the isomers.
iii) What types of isomerism is exhibited by different types of amines ?.
Answer:
Molecular formula C₄H₁₁N

ii) IUPAC names ;
a) Butan-1-amine
b) 2-methyl propanamine
c) 2-methyl-propan-2-amine
d) N-methyl propan-1-amine
e) N-ethyl ethanamine
f) N-methyl-1-methylethanamine
g) N, N-Dimethylmethanamine

iii) Primary amines (a), (b) and (c) exhibit chain isomerism.
Secondary amines (a), (e) and (b) exhibit metamerism.

Question 3.
How will you convert
i) Benzene into aniline
ii) Benzene into N, N – dimethylaniline
iii) Cl – (CH₂)₄ – Cl into hexan -1, 6 – diamine ?
Answer:
i) Benzene is first converted into nitrobenzene by nitration. Nitrobenzene on reduction with tin and hydrohloric acid gives aniline.

ii) Benzene is converted into aniline by nitration followed by reduction. Aniline on heating with excess of methyliodide gives N, N – Dimethylaniline.

iii) Cl – (CH₂)₄ – Cl is converted to NC – (CH₂)₄ – CN by reacting with ethanolic potassium cyanide. NC – (CH₂)₄ – CN on reduction with LiAlH₄ or sodium and alcohol gives H₂N (CH₂)₆ NH₂.

Question 4.
Arrange the following in increasing order of their basic strength :
i) C₂H₅NH₂, C₆H₅NH₂, NH₃,C₆H₅CH₂ NH₂ and (C₂H₅)₂NH
ii) C₂H₅NH₂, (C₂H₅)₂ NH, (C₂H₅)₃N, C₆H₅NH₂
iii) CH₃NH₂, (CH₃)₂ NH, (CH₃)₃N, C₆H₅NH₂, C₆H₅CH₂NH₂
Answer:
i) C₆H₅NH₂ < NH₃ < C₆H₅CH₂NH₂ < C₂H₅NH₂ < (C₂H₅)₂ NH
ii) C₆H₅NH₂ < C₂H₅NH₂ < (C₂H₅)₃N < (C₂H₅)₂ NH
iii) C₆H₅NH₂ < C₆H₅CH₂NH₂ < (CH₃)₃ N < CH₃NH₂ < (CH₃)₂ NH

Question 5.
Complete the following acid – base reactions and name the products.
i) CH₃CH₂CH₂NH₂ + HCl →
ii) (C₂H₅)₃N + HCl →
Answer:

Question 6.
Write reactions of the final alkylation product of aniline with excess of methyl iodide in the presence Of sodium carbonate solution.
Answer:

Thus, when aniline is treated with an excess of methyl iodide in a basic medium, the final product obtained is N, N-dimethylaniline.

Question 7.
Write chemical reaction of aniline with benzoyl chloride and write the name of the product obtained.
Answer:
Aniline reacts with benzoylchloride to give benzanilide.

Question 8.
Write structures of different isomers corresponding to the molecular formula, C₃H₉N. Write IUPAC names of the isomers which will liberate nitrogen gas on treatment with nitrous acid.
Answer:

Propanamine (a) and 1- methylethenamine (b) being aliphatic primary amines liberate nitrogen gas on treatment with nitrous acid.

Question 9.
Convert
i) 3-Methylaniline into 3-nitrotoluene
ii) Aniline into 1, 3, 5 – tribromobenzene.
Answer:

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Integration Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Integration Important Questions Very Short Answer Type

Question 1.
Find ∫(1 – x)(4 – 3x)(3 + 2x) dx
Solution:

Question 2.
Evaluate \(\int \frac{2 x^3-3 x+5}{2 x^2} d x\)
Solution:

Question 3.
Evaluate \(\int \frac{x^2+3 x-1}{2 x} d x\)
Solution:

Question 4.
Evaluate \(\int \frac{(3 x+1)^2}{2 x} d x\). [(AP) May ’18, ’16]
Solution:

Question 5.
Evaluate \(\int\left(x+\frac{4}{1+x^2}\right) d x\). [(TS) May ’15]
Solution:

Question 6.
Evaluate \(\int\left[\frac{1}{\sqrt{1-x^2}}+\frac{2}{\sqrt{1+x^2}}\right] d x\). [May ’11]
Solution:

Question 7.
Evaluate \(\int\left(x+\frac{1}{x}\right)^3 d x\), x > 0. [May ’12]
Solution:

Question 8.
Evaluate \(\int \frac{x^2+1}{x^4+1} d x\) on R. [May ’14]
Solution:

Question 9.
Evaluate \(\int\left(\frac{x^6-1}{1+x^2}\right) d x\)
Solution:

Question 10.
Evaluate \(\int \frac{\left(a^x-b^x\right)^2}{a^x b^x} d x\)
Solution:

Question 11.
Evaluate \(\int \sec ^2 x cosec^2 x d x\). [(TS) May ’18; Mar. ’16; (AP) May ’17]
Solution:

Question 12.
Evaluate \(\int \frac{1+\sin ^2 x}{1+\cos 2 x} d x\). [Mar. ’06, May ’95]
Solution:

Question 13.
Evaluate \(\int \frac{1+\cos ^2 x}{1-\cos 2 x} d x\). [Mar. ’19 (TS); ’13]
Solution:

Question 14.
Find \(\int \sqrt{1+\sin 2 x} d x\)
Solution:

Question 15.
Evaluate \(\int \sqrt{1-\sin 2 x} d x\). [(TS) May ’17]
Solution:

Question 16.
Evaluate \(\int \sqrt{1-\cos 2 x} d x\). [Mar. ’09, May ’06]
Solution:

Question 17.
Evaluate \(\int \frac{d x}{\sqrt{1+5 x}}\)
Solution:

Question 18.
Find \(\int \frac{x}{1+x^2} d x\)
Solution:

Question 19.
Evaluate \(\int \frac{e^x}{e^x+1} d x\)
Solution:

Question 20.
Evaluate \(\int \frac{1}{x \log x[\log (\log x)]} d x\). [Mar. ’19 (TS); ’11]
Solution:

Question 21.
Evaluate \(\int \frac{1}{x \log x} d x\). [May ’99, ’94]
Solution:

Question 22.
Evaluate \(\int \frac{1-\tan x}{1+\tan x} d x\).
Solution:

Question 23.
Evaluate \(\int \frac{\cos \sqrt{x}}{\sqrt{x}} d x\). [May & Mar. ’98]
Solution:

Question 24.
Evaluate \(\int\left(1-\frac{1}{x^2}\right) e^{\left(x+\frac{1}{x}\right)} d x\). [Mar. ’12]
Solution:

Question 25.
Evaluate \(\int \frac{e^x(1+x)}{\cos ^2\left(x e^x\right)} d x\). [(AP) Mar. ’19; May ’17 (TS) Mar. ’17; May ’16]
Solution:

Question 26.
Evaluate \(\int \frac{\cot (\log x)}{x} d x\). [Mar. ’05]
Solution:

Question 27.
Evaluate \(\int \frac{(1+\log x)^n}{x} d x\). [(AP) May ’18]
Solution:

Question 28.
Evaluate \(\int \frac{\log (1+x)}{1+x} d x\). [(TS) Mar. ’15]
Solution:

Question 29.
Evaluate \(\int \frac{\sin ^4 x}{\cos ^6 x} d x\). [Mar. ’11]
Solution:

Question 30.
Evaluate \(\int \frac{{cosec}^2 x}{(a+b \cot x)^5} d x\)
Solution:

Question 31.
Evaluate \(\int \frac{1}{\sqrt{\sin ^{-1} x} \sqrt{1-x^2}} d x\). [(AP) May ’15]
Solution:
Put sin^-1x = t² then

Question 32.
Evaluate \(\int \frac{\sin \left(\tan ^{-1} x\right)}{1+x^2} d x\). [Mar. ’18, ’15 (AP); May ’13]
Solution:

Question 33.
Evaluate \(\int \frac{\mathrm{e}^{\tan ^{-1} x}}{1+\mathrm{x}^2} d x\)
Solution:

Question 34.
Evaluate ∫sin mx cos nx dx
Solution:

Question 35.
Evaluate ∫cos mx cos nx dx
Solution:

Question 36.
Evaluate ∫sin mx sin nx dx
Solution:

Question 37.
Evaluate ∫cos x cos 3x dx
Solution:

Question 38
Evaluate \(\int \frac{d x}{\sin x+\sqrt{3} \cos x}\). [May ’12]
Solution:

Question 39.
Evaluate \(\int \frac{\mathbf{x}^2}{\sqrt{1-x^6}} d \mathbf{x}\)
Solution:

Question 40.
Evaluate \(\int \frac{2 x^3}{1+x^8} d x\). [May ’08]
Solution:

Question 41.
Evaluate \(\int \frac{x^8}{1+x^{18}} d x\). [(TS) May ’19; (AP) Mar. ’16]
Solution:

Question 42.
Evaluate \(\int \frac{x^5}{1+x^{12}} d x\)
Solution:

Question 43.
Evaluate \(\int \frac{3 x^2}{1+x^6} d x\)
Solution:

Question 44.
Evaluate \(\int \frac{d x}{(x+5) \sqrt{x+4}}\). [May ’09, ’02]
Solution:

Question 45.
Find \(\int \frac{1}{(x+3) \sqrt{x+2}} d x\). [May ’14, ’12; Mar. ’14]
Solution:

Question 46.
Evaluate ∫sec x log(sec x + tan x) dx
Solution:

Question 47.
Evaluate \(\int \frac{\sec ^2 x}{\sqrt{16+\tan ^2 x}} d x\). [May ’08, ’07]
Solution:

Question 48.
Evaluate \(\int \frac{d x}{x^2-81}\)
Solution:

Question 49.
Evaluate \(\int \frac{3}{\sqrt{9 x^2-1}} d x\)
Solution:

Question 50.
Evaluate \(\int \frac{d x}{(x+1)(x+2)}\). [Mar. ’19(AP); Mar. ’14, ’12, May ’11]
Solution:

Question 51.
Evaluate \(\int \frac{d x}{\sqrt{x^2+2 x+10}}\). [May ’06]
Solution:

Question 52.
Evaluate ∫log x dx. [Mar. ’99, May ’10, ’99]
Solution:

Question 53.
Evaluate ∫x log x dx. [(AP) Mar. ’20; May ’94]
Solution:

Question 54.
Evaluate \(\int \sin ^{-1} x d x\). [Mar. ’00, May ’05]
Solution:

Question 55.
Evaluate \(\int x \tan ^{-1} x d x\). [Mar. ’05, May ’02]
Solution:

Question 56.
Evaluate \(\int e^x \cos x d x\). [May ’15 (AP)]
Solution:

Question 57.
Evaluate ∫e^x (sec x + sec x tan x) dx. [(AP) May ’16]
Solution:

Question 58.
Evaluate ∫(tan x + log sec x) e^x dx. [May ’18, ’15 (TS); Mar. ’08, May ’07]
Solution:

Question 59.
Evaluate \(\int e^x\left(\frac{1+x \log x}{x}\right) d x\). [(TS) May ’19; Mar. ’18, ’15 (AP); Mar. ’13]
Solution:

Question 60.
Evaluate \(\int \frac{e^x(x+1)}{(x+2)^2} d x\). [May ’09, ’98]
Solution:

Question 61.
Evaluate \(\int e^x\left[\tan ^{-1} x+\frac{1}{1+x^2}\right] d x\). [May ’94]
Solution:

Question 62.
Evaluate \(\int e^x\left(\tan x+\sec ^2 x\right) d x\). [Mar. ’06, ’00, ’92]
Solution:

Question 63.
Evaluate ∫e^x (sin x + cos x) dx. [(AP) Mar. ’17]
Solution:

Question 64.
Evaluate \(\int \frac{1}{1+\cos x} d x\). [Mar. ’15 (TS)]
Solution:

Question 65.
Evaluate \(\int \frac{1}{\cosh x+\sinh x} d x\). [(AP) May ’19, ’16 ; Mar. ’17 (TS)]
Solution:

Question 66.
Evaluate \(\int\left(1-x^2\right)^3 d x\)
Solution:

Question 67.
Evaluate \(\int\left(\frac{1}{1-x^2}+\frac{1}{1+x^2}\right) d x\). [(TS) May ’16]
Solution:

Question 68.
Evaluate \(\int \frac{1-\cos 2 x}{1+\cos 2 x} d x\). [May ’02]
Solution:

Question 69.
Evaluate \(\int \sqrt{1+\cos 2 x} d x\). [Mar. ’94]
Solution:

Question 70.
Evaluate \(\int \frac{1}{x \sqrt{x}} d \mathbf{x}\). [May ’92]
Solution:

Question 71.
Evaluate ∫2x√x dx.
Solution:

Question 72.
Evaluate ∫x³ (4 + x²)² dx. [May ’82]
Solution:

Question 73.
Evaluate \(\int \frac{1-x^4}{1-x} d x\). [Mar. ’99]
Solution:

Question 74.
Evaluate \(\int \frac{x^4}{x^2+1} d x\). [May ’98, ’99]
Solution:

Question 75.
Evaluate \(\int e^{2 \log x} d x\). [May ’99]
Solution:

Question 76.
Evaluate ∫5^x dx. [May ’93]
Solution:
\(\int 5^x d x=\frac{5^x}{\log 5}+c\)

Question 77.
Evaluate \(\int \frac{\cos ^2 x}{1-\sin x} d x\). [Mar. ’01, May ’93]
Solution:

Question 78.
Evaluate \(\int \frac{\cos x+\sin x}{\sqrt{1+\sin 2 x}} d x\). [Mar. ’98, May ’92]
Solution:

Question 79.
Find \(\int \frac{x^3}{\sqrt{x+1}} d x\). [Mar. ’00]
Solution:

Question 80.
Find \(\int \frac{x^2}{\sqrt{x+5}} d x\). [May ’99]
Solution:

Question 81.
Find \(\int \frac{2 x+3}{\sqrt{4 x+3}} d x\). [May ’99]
Solution:

Question 82.
Evaluate ∫x³ sin x⁴ dx. [Mar. ’01]
Solution:

Question 83.
Evaluate ∫e^x sin(e^x) dx. [(AP) Mar. ’17]
Solution:
Put e^x = t then e^x dx = dt
Now ∫e^x sin(e^x) dx = ∫sin t dt
= -cos t + c
= -cos(e^x) + c

Question 84.
Evaluate ∫2x sin(x² + 1) dx.
Solution:
Put x² + 1 = t then 2x dx = dt
Now ∫2x sin(x² + 1) dx = ∫sin t dt
= -cos t + c
= -cos(x² + 1) + c

Question 85.
Evaluate \(\int \frac{x}{1+x^4} d x\)
Solution:

Question 86.
Evaluate \(\int \frac{(\log x)^2}{x} d x\). [(AP) May ’18]
Solution:

Question 87.
Evaluate ∫sec(tan x) sec²x dx.
Solution:
Put tan x = t then sec²x dx = dt
Now ∫sec(tan x) sec²x dx = ∫sec t dt
= log|sec t + tan t| + c
= log|sec(tan x) + tan(tan x)| + c

Question 88.
Evaluate \(\int \frac{\sin (\log x)}{x} d x\)
Solution:

Question 89.
Evaluate \(\int \frac{\cos (\log x)}{x} d x\)
Solution:

Question 90.
Evaluate \(\int \frac{3 x+7}{3 x^2+14 x-5} d x\). [Mar. ’00]
Solution:

Question 91.
Evaluate \(\int \frac{3 \cos 3 x-2 \sin 2 x}{\cos 2 x+\sin 3 x} d x\). [May ’93]
Solution:

Question 92.
Find \(\int \frac{6 x}{3 x^2-2} d x\)
Solution:

Question 93.
Evaluate \(\int \frac{\left(\sin ^{-1} x\right)^2}{\sqrt{1-x^2}} d x\)
Solution:

Question 94.
Evaluate \(\int \frac{{cosec}^2 x}{(1+\cot x)^2} d x\). [Mar. ’01]
Solution:

Question 95.
Evaluate ∫cos³x sin x dx. [(TS) Mar. ’18]
Solution:

Question 96.
Evaluate \(\int \sqrt[3]{\sin x} \cdot \cos x d x\)
Solution:

Question 97.
Evaluate \(\int \sqrt{\sin x} \cdot \cos x d x\)
Solution:

Question 98.
Evaluate \(\int {cosec}^2 x \cdot \sqrt{\cot x} d x\)
Solution:

Question 99.
Evaluate \(\int \frac{d x}{4-9 x^2}\). [May ’98]
Solution:

Question 100.
Evaluate \(\int \frac{1}{\sqrt{1-4 x^2}} d x\)
Solution:

Question 101.
Evaluate \(\int \frac{d x}{\sqrt{25+x^2}}\)
Solution:

Question 102.
Evaluate \(\int \frac{1}{e^x+e^{-x}} d \mathbf{x}\)
Solution:

Question 103.
Evaluate \(\int \frac{1}{x^2+6 x+10} d x\). [Mar. ’98, May ’93]
Solution:

Question 104.
Evaluate \(\int \frac{1}{\sqrt{x^2-3}} d x\). [May ’92]
Solution:

Question 105.
Evaluate \(\int \frac{1}{x^2-4} d x\). [May ’94]
Solution:

Question 106.
Evaluate \(\int \sqrt{x^2+4} d x\). [May ’93]
Solution:

Question 107.
Evaluate \(\int \sqrt{4 x^2+9} d x\)
Solution:

Question 108.
Evaluate \(\int \sqrt{16-25 x^2} d x\)
Solution:

Question 109.
Evaluate ∫x e^x dx. [Mar. ’99]
Solution:

Question 110.
Evaluate ∫tan^-1x dx. [May ’98]
Solution:

Question 111.
Evaluate ∫e^x (cos x – sin x) dx. [May ’99, ’95, Mar. ’99]
Solution:

Question 112.
Evaluate \(\int \frac{x e^x}{(x+1)^2} d x\). [May ’14, ’98, ’94: Mar. ’05]
Solution:

Question 113.
Evaluate \(\int \frac{1}{\sqrt{2 x-3 x^2+1}} d x\). [May ’08]
Solution:

Question 114.
Evaluate ∫cot²x dx.
Solution:
∫cot²x dx = ∫(cosec²x – 1) dx
= ∫cosec²x dx – ∫1 dx
= -cot x – x + c

Question 115.
Evaluate \(\int e^{\log \left(1+\tan ^2 x\right)} d x\)
Solution:

Question 116.
Evaluate \(\int \frac{\sin ^2 x}{1+\cos 2 x} d x\). [(TS) Mar. ’20]
Solution:

Question 117.
Evaluate ∫sin²x dx.
Solution:

Question 118.
Evaluate \(\int \frac{x}{1+x^2} d x\)
Solution:

Question 119.
Evaluate \(\int \frac{\sin x}{\sin (a+x)} d x\)
Solution:

Question 120.
Evaluate \(\int 2 x e^{x^2} d x\)
Solution:

Question 121.
Evaluate \(\int \frac{1}{1+\sin 2 x} d x\)
Solution:

Question 122.
Evaluate ∫tan⁴x sec²x dx.
Solution:

Question 123.
Evaluate \(\int \frac{2 x+3}{\sqrt{x^2+3 x-4}} d x\)
Solution:
Put x² + 3x – 4 = t² then (2x + 3) dx = 2t dt

Question 124.
Evaluate ∫sin³x dx.
Solution:

Question 125.
Evaluate ∫cos³x dx.
Solution:

Question 126.
Evaluate \(\int \frac{d x}{1+e^x}\)
Solution:
Put 1 + e^x = t then e^x = t – 1
⇒ e^x dx = dt

Question 127.
Evaluate \(\int e^x\left[\frac{1-\sin x}{1-\cos x}\right] d x\)
Solution:

Question 128.
Evaluate ∫x sin²x dx. [Mar. ’02]
Solution:

Question 129.
Evaluate \(\int \frac{e^x(x+2)}{(x+3)^2} d x\)
Solution:

Question 130.
Evaluate \(\int \frac{e^{\mathbf{x}}}{e^x+1} d x\). [Mar. ’18 (TS)]
Solution:

Question 131.
Evaluate \(\int\left(x^3-\cos x+\frac{4}{\sqrt{x^2+1}}\right) d x\)
Solution:

Question 132.
Evaluate ∫(x³ – 2x² + 3) dx.
Solution:

Question 133.
Find ∫2x⁷ dx.
Solution:

Question 134.
Evaluate ∫(1 – 2x³) x² dx.
Solution:

Question 135.
Evaluate \(\int \sqrt[3]{2 x^2} d x\)
Solution:

Question 136.
Evaluate \(\int\left(1+\frac{2}{x}-\frac{3}{x^2}\right) d x\)
Solution:

Question 137.
Evaluate \(\int \frac{2 x^3-3 x+5}{2 x^2} d x\)
Solution:

Question 138.
Evaluate \(\int\left(\frac{3}{\sqrt{x}}-\frac{2}{x}+\frac{1}{3 x^2}\right) d x\)
Solution:

Question 139.
Evaluate \(\int \frac{1-\sqrt{x}}{x} d x\)
Solution:

Question 140.
Evaluate \(\int\left(\frac{2 x-1}{3 \sqrt{x}}\right)^2 d x\)
Solution:

Question 141.
Evaluate \(\int\left(e^x-\frac{1}{x}+\frac{2}{\sqrt{x^2-1}}\right) d x\)
Solution:

Question 142.
Evaluate \(\int\left(\frac{1}{\sqrt{x}}+\frac{2}{\sqrt{x^2-1}}-\frac{3}{2 x^2}\right) d x\)
Solution:

Question 143.
Evaluate ∫(sec²x – cos x + x²) dx.
Solution:

Question 144.
Evaluate \(\int\left(\sec x \tan x+\frac{3}{x}-4\right) d x\)
Solution:

Question 145.
Evaluate \(\int\left(\cosh x+\frac{1}{\sqrt{x^2+1}}\right) d x\)
Solution:

Question 146.
Evaluate \(\int\left(\sin h x+\frac{1}{\left(x^2-1\right)^{1 / 2}}\right) d x\)
Solution:

Question 147.
Evaluate \(\int(3 x-1)^{1 / 2} d x\)
Solution:

Question 148.
Evaluate ∫e^2x dx
Solution:
\(\int \mathrm{e}^{2 \mathrm{x}} \mathrm{dx}=\frac{\mathrm{e}^{2 \mathrm{x}}}{2}+\mathrm{c}\)

Question 149.
Evaluate \(\int \frac{e^{\log x}}{x} d x\)
Solution:

Question 150.
Evaluate ∫sin 7x dx
Solution:
∫sin 7x dx = \(\frac{-\cos 7 x}{7}+c\)

Question 151.
Evaluate ∫(3x² – 4)x dx
Solution:

Question 152.
\(\int \frac{1}{7 x+3} d x\)
Solution:

Question 153.
Evaluate \(\int \frac{1}{1+(2 x+1)} d x\)
Solution:

Question 154.
Evaluate ∫e^x cot e^x dx
Solution:
Put e^x = t ⇒ e^x dx = dt
∴ ∫e^x cot e^x dx = ∫cot t dt
= log|sin t| + c
= log|sin e^x| + c

Question 155.
Evaluate ∫cot hx dx
Solution:
∫cot hx dx = \(\int \frac{\cos h x}{\sin h x} d x\)
= log|sin hx| + c

Question 156.
Evaluate \(\int \frac{\cos x}{(1+\sin x)^2} d x\)
Solution:

Question 157.
Evaluate ∫cos⁴x dx
Solution:

Question 158.
Evaluate \(\int \frac{x}{\sqrt{1-x}} d x\)
Solution:

Question 159.
Evaluate \(\int x \sqrt{4 x+3} d x\)
Solution:

Question 160.
Evaluate \(\int \frac{x^2}{\sqrt{1-x^2}} d x\)
Solution:

Question 161.
Evaluate \(\int \frac{\sin \theta}{\sqrt{2-\cos ^2 \theta}} d \theta\)
Solution:

Question 162.
Evaluate \(\int \frac{3}{\sqrt{9 x^2-1}} d x\)
Solution:

Question 163.
Evaluate \(\int \frac{1}{1+4 x^2} d x\)
Solution:

Question 164.
Evaluate \(\int \frac{1}{8+2 x^2} d x\)
Solution:

Question 165.
Evaluate \(\int\left(\sqrt{x}-\frac{2}{1-x^2}\right) d x\)
Solution:

Question 166.
Evaluate \(\int \sqrt{9 x^2-25} d x\)
Solution:

Question 167.
Evaluate \(\int \frac{1}{e^x-1} d x\)
Solution:

Question 168.
Evaluate \(\int \frac{1}{1-\cot x} d x\)
Solution:

Question 169.
Evaluate \(\int \frac{1}{1+\tan x} d x\)
Solution:

Question 170.
Evaluate ∫e^x (1 + x²) dx
Solution:

Question 171.
Evaluate ∫cot^-1x dx
Solution:

Question 172.
Evaluate ∫sec^-1x dx
Solution:

Question 173.
Evaluate ∫cosec^-1x dx
Solution:

Question 174.
Evaluate ∫x² cos x dx
Solution:

Question 175.
Evaluate ∫x sec²x dx
Solution:

Question 176.
Evaluate \(\int \frac{\log x}{x^2} d x\)
Solution:

Question 177.
Evaluate ∫(log x)² dx
Solution:

Question 178.
Evaluate ∫xⁿ log x dx
Solution:

Question 179.
Evaluate ∫log(1 + x)² dx
Solution:

Question 180.
Evaluate ∫√x log x dx. [(TS) Mar. ’16]
Solution:

Question 181.
Evaluate \(\int \mathbf{e}^{\sqrt{\mathbf{x}}} d \mathbf{x}\). [(AP) May ’19]
Solution:

Question 182.
Evaluate ∫cos√x dx. [(TS) May ’17]
Solution:

Question 183.
Evaluate ∫x cot²x dx
Solution:

Question 184.
Evaluate ∫x² e^-3x dx
Solution:

Question 185.
Evaluate ∫x³ e^ax dx
Solution:

Question 186.
Evaluate ∫cos (log x) dx
Solution:

Question 187.
If f(x) is a differentiable function, then prove that \(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log|f(x)| + c.
Solution:
Let f(x) = t
⇒ f'(x) dx = dt
∴ \(\int \frac{f^{\prime}(x)}{f(x)} d x=\int \frac{1}{t} d t\)
= log|t| + c
= log|f(x)| + c

Question 188.
If f(x) is a differentiable function and n ≠ -1, then prove that \(\int[f(x)]_{f^{\prime}(x)}^n \cdot d x=\frac{[f(x)]^{n+1}}{n+1}+c\)
Solution:
Put f(x) = t
⇒ f'(x) dx = dt

Question 189.
Prove that ∫tan x dx = log|sec x| + c.
Solution:

Question 190.
Prove that ∫cot x dx = log|sin x| + c.
Solution:

Question 191.
Prove that ∫sec x dx = log|sec x + tan x| + c = \(\log \left|\tan \left(\frac{\pi}{4}+\frac{x}{2}\right)\right|\) + c
Solution:

Question 192.
Prove that ∫cosec x dx = log|cosec x – cot x| + c = \(\log \left|\tan \frac{x}{2}\right|\) + c
Solution:

Question 193.
Prove that ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
Solution:

Question 194.
If \(I_n=\int x^n \cdot e^{-x} d x\), then prove that \(I_n=-x^n \cdot e^{-x}+n I_{n-1}\).
Solution:

Telangana TSBIE TS Inter 2nd Year Physics Study Material 16th Lesson Communication Systems Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 16th Lesson Communication Systems

Very Short Answer Type Questions

Question 1.
What are the basic blocks of a communication system? [TS June ’15]
Answer:
The basic blocks of a communication system are

1. Transmitter
2. Communication channel
3. Receiver.

Question 2.
What is “world wide web” (www)? [IMP]
Answer:
It is an encyclopedia of knowledge accessible to everyone round the clock throughout year with the help of computer connectivity.

Question 3.
Mention the frequency range of speech signals.
Answer:
Frequency range of speech signals is 300 Hz to 3100 Hz.

Question 4.
What is sky wave propagation? (IMP)[AP May ’16; June ’15]
Answer:
In the frequency range from a few MHz upto about 30 MHz, long distance communication can be achieved by the ionospheric reflection of radio waves back towards the earth. This mode of propagation is called sky wave pro-pagation and it is used by short wave broadcast services.

Question 5.
Mention the various parts of the ionosphere? [TS May ’16]
Answer:
Parts of ionosphere are

1. D – Layer at a height of 65 to 75 km from ground.
2. E – Layer at a height of nearly 100 km.
3. F₁ – Layer at a height of 170 to 190 km.
4. F₂ – Layer at a height of 250 to 400 km.
   Note : F₁ and F₂ will merge during night.

Question 6.
Define modulation. Why is it necessary? [AP Mar. 18, 17, 16, 14; May 17, 14; TS Mar. 19, 16, 15, May 18, 17]
Answer:
Modulation :
The process of combining audio frequency signal with high frequency signal is called modulation. Modulation is necessary for the following reasons.

1. to reduce the size of antenna.
2. to increase the effective power radiated by antenna.
3. to avoid mixing up of signals from different transmitters.

Question 7.
Mention the basic methods of modulation [AP Mar. 19. 16; TS Mar.’ 18, ’17, ’15]
Answer:
The basic methods of modulation are :
a) Amplitude modulation
b) Frequency modulation and
c) Phase modulation.

Question 8.
Which type of communication is employed in mobile phones? [AP May ’18, Mar. ’15]
Answer:
Space wave communication is employed in mobile phones.

Short Answer Questions

Question 1.
Draw the block diagram of a generalized communication system and explain it briefly.
Answer:
The block diagram of a generalized communication system are as shown. It consists of the following three parts.

1. Transmitter
2. Communication channel and
3. Receiver.

In this system, the transmitter and receiver are located at two different places and the channel is the physical medium that connects them depending upon the type of communication system. A channel may be in the form of wires (or) cables connecting the transmitter and the receiver, or it may be wireless.

Using the transmitter, the original message is converted into a form so that it can be transmitted over the communication channel. Hence it is called as a-message signal.

The uses of these three parts are :
1) Transmitter :
Purpose of transmitter is to convert the message signal produced by source into a form suitable for transmission through channel.

2) Channel :
Channel is used for transmission of signals. It may consist a medium like coaxial cable, optical fibre, (or) even space is used as channel in wireless communication where E.M waves are used.

3) Receiver :
Receiver will convert the signals received through channel into a recognisable form of the original message signal.

Question 2.
What is a ground wave? When is it used for communication?
Answer:
Ground wave :
In A.M. broadcasting ground based vertical metallic towers called antennas are used for transmission. For such antennas ground has strong influence on transmission. Near transmitting antennas energy of E.M wave is high. They have strong influence on propagation of signals along the ground surface. A strong E.M. wave near antenna will induce current on surface of ground over which it passes. So E.M waves slides along surface of ground.

For ground wave propagation attenuation on surface of earth is high. The magnitude of attenuation is proportional to frequency. Due to very high energy absorption of ground.

The ground wave propagation is limited to few kilometers from transmitting antenna.

Question 3.
What are sky waves? Explain sky wave propagation, briefly.
Answer:
Sky waves :
The electromagnetic waves which suffers reflection of ionosphere and reaches earth are called sky waves.

Sky wave propagation :
Electromagnetic waves with in the range of 30 to 40 MHz are reflected by ionosphere. The degree of ioni-sation varies with height above ground. Due to ionospheric reflection long range com-munication is possible with sky waves. Because these reflected waves reach earth at a longer distance. Short wave broadcast for long distance is possible with sky waves. Generally E.M waves with in the frequency range of 3 to 30 MHz are highly suitable for sky wave propagation. E.M waves of higher frequencies i.e., frequency > 30 MHz will penetrate ionosphere. Hence sky wave propagation is not possible with high frequency electro magnetic waves.

Question 4.
What is space wave communication? Explain.
Answer:
Space wave :
A space wave will travel from transmitting antenna to receiver in the form of straight lines. Space waves will obey line of sight properties.

Space wave propagation :
This type of propagation of E.M waves is called space wave propagation.

Space wave propagation is mainly used in television transmission. Due to curvature of earth range of space wave propagation is limited to certain distance only. Range depends on height of the antenna. Let height of transmitting antenna is ‘h_T’ and radius of earth is ‘R’ the distance upto which signals will reach with LOS (hne-of-sight) properties is d_r = \(\sqrt{2Rh_T}\). If receiving antenna is at a height h_R then also distance d_r upto which signals can be reached with LOS properties will increase. In this case d_r = \(\sqrt{2Rh_T}+\sqrt{2Rh_R}\).

Question 5.
What do you understand by modulation? Explain the need for modulation.
Answer:
Modulation :
The process of super imposing a low frequency signal onto a high frequency carrier wave is known as modulation.

Modulation is necessary for long range transmission of signals.

Modulation is a very essential part of communication. Transmission of low frequency of voice signals (frequency range 20 Hz to 20,000 Hz) to longer distances is not possible because energy associated with low frequency signals is less.

So our voice signals after converting into electrical signals must be superposed on to a high frequency signal called carrier wave. Generally frequency of carrier wave is high. This will help for efficient transmis¬sion and reception. Modulation is necessary for the following reasons,

1. To reduce the size of antenna for E.M. waves to be transmitted as antenna is necessary.
2. To increase effective power radiation by transmitter.
3. To avoid mixing up of signals from different transmitters.

To obtain the above advantages we are using modulation techniques where a low frequency signal is superposed on a high requency carrier wave.

Question 6.
What should be the size of the antenna or aerial? How the power radiated is related to length of the antenna and wavelength?
Answer:
Antenna and its size :
It is a must for every transmitter to have an antenna. Without antenna, it is not possible to radiate electrical energy output of transmitter into space in the form of electromagnetic radiation.

Antenna size must be comparable to wavelength of the signal to be transmitted.

To transmit all information contained in a signal without any loss in quality the minimum size of antenna must be at least \(\frac{\lambda}{4}\).

For good transmission output power of transmitter must be high.

Relation between length of antenna ‘l’ and wavelength ‘ λ’ and power radiated is
Power radiated ∝ (\(\frac{1}{\lambda}\))²

Question 7.
Explain amplitude modulation.
Answer:
Amplitude modulation (A.M.) :
In amplitude modulation (A.M.) the amplitude of carrier wave is varied in accordance with the voice signal superimposing on it.

Theory :
Let time varying carrier wave is c(t) = A_c sin ω_ct

Time varying modulating wave is m(t) = A_m sin ω_mt

when these two waves are superposed modulated wave is given by
c_m(t) = (A_c + A_m sin ωt) sin ω_ct

Because modulating wave changes only amplitude of carrier wave but not its frequencies

is the modulated wave. Where (ω_c – ω_m) and (ω_c + ω_m) are lower and upper side frequencies. Production of amplitude modulated wave.

Question 8.
How can an amplitude modulated wave be generated?
Answer:
The block diagram to produce amplitude modulated wave is as shown. Here modulating signal A_m sin ω_mt is mixed with a carrier signal A_c sin ω_ct in a square law device.

The output of square law device y(t) = B x (t) + Cx²t

Where B and C are constants.
∴ y(t) = BA_m sin ω_mt + BA_c sin ω_ct + C (A_m sin ω_mt + A_c sin ω_ct)² …………… (1)

By using trigonometric relations (1)
sin²A = (1 – cos 2A) / 2

and (2) sin A sin B = \(\frac{1}{2}\) [cos (A – B) – cos (A + B)] equation (1) can be written as
y(t) = BA_msin ω_mt + BA_c sin ω_ct
+ C\(\frac{\mathrm{A}_{\mathrm{m}}^2}{2}\) + A²_c – \(\frac{c\mathrm{A}_{\mathrm{m}}^2}{2}\) cos 2ω_mt – cos 2ω_mt
\(\frac{C\mathrm{A}_{\mathrm{c}}^2}{2}\) cosω_ct + cA_mA_ccos(ω_c – ω_m
CA_mA_c cos(ω_c

This signal is passed through a b filter which rejects the D.C compc sinusoidal frequencies ω_m , 2ω_m a, ailows the frequencies ω_c, ω_c ω_m + ω_m at the out put side. This me signal is transmitted through ante

In this way amplitude modulat is produced.

Question 9.
How can an amplitude modulated wave be detected?
Answer:
The block diagram of amplitude modulated wave detector is as shown.

The receiving antenna will collect the amplitude modulated waves from space. These are passed through an amplifier to increase strength of signals.

These signals are passed through intermediate frequency stage (I.F. stage) to frequency of carrier.

For recovery of original massage signal m(t) with angular frequency ω_m the modulated signal is passed detector which consists (1) a rectifier where lower half (- ve half) p modulated signals is eliminated. (2) Later it was sent through envelope detector to recive the original signal.

This signal is passed through a amplifier and finally signal with sufficient strength is going to a microphone to convert electrical signals into audio signals.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits

Very Short Answer Type Questions

Question 1.
What is an n-type semiconductor? What are the majority and minority charge carriers in it?
Answer:
When intrinsic Germanium / Silicon crystal is doped with a pentavalent impurity then “n-type semiconductor” will be formed.

The majority charge carriers are electrons and minority charge carriers are holes.

Question 2.
What are intrinsic and extrinsic semiconductors? [AP May ’18, Mar, ’15; June ’15]
Answer:
Intrinsic semiconductor :
Ultra high pure semiconductor are called “intrinsic semi-conductor”.

Extrinsic semiconductor :
The doped semi-conductor is called extrinsic semiconductor.

Question 3.
What is a p-type semiconductor? What are the majority and minority charge carriers in it? [TS May ’18, Mar. ’17; AP Mar. ’17]
Answer:
When third group impurities like boron, aluminium, galium, indium etc., are added to intrinsic semiconductor then it is called “p-type semiconductor.”

In p-type semiconductor majority, charge carriers are holes and minority charge carriers are electrons.

Question 4.
Give examples of “photosensitive substances”. Why are they called so? [AP May ’16]
Answer:

1. Metals like zinc, cadmium and magnesium will respond to ultraviolet rays.
2. Alkalimetals such as sodium, potassium, caesium and rubidium will respond to visible light.

These substances are called photo sensitive surfaces because they will emit electrons when light falls on them.

Question 5.
What is p-n junction diode? Define depletion layer. [TS Mar. ’19 May ’16]
Answer:
p-n semiconductor diode :
When a semiconductor material such as silicon or germanium crystal is doped in such a way that one side of it becomes a p-type and the other side becomes n-type then a p-n semi-conductor diode is formed.

Depletion layer :
The formation of a narrow region on either side of the junction which becomes free from mobile charge carriers is called “depletion layer”.

Question 6.
How is a battery connected to a Junction diode in i) forward and ii) reverse bias?
Answer:
In Forward Bias :
In a p-n junction diode if p-side is connected to positive terminal of a battery and n – side to negative terminal it is called “forward biased”.

In Reverse Bias :
If p-side is connected to negative terminal of the battery and n-side to positive terminal of the cell it is called “reverse biased”.

Question 7.
What is die maximum percentage of rectification in half wave and full wave rectifiers?
Answer:
The maximum percentage of rectification in a half wave rectifier is 40.6% and in a full wave rectifier maximum percentage of rectification is 81.2%.

Question 8.
What is zener voltage (V_Z) and how will a zener diode be connected in circuits generally?
Answer:
When a zener diode is reverse biased at a particular voltage the current increases suddenly. The voltage at which the current increases is called “breakdown voltage” or “zener voltage”, so zener is always connected in “reverse bias”.

Question 9.
Write the expressions for the efficiency of a half wave rectifier and a full wave rectifier.
Answer:
Efficiency of half wave rectifier

Efficiency of full wave rectifier

Question 10.
What happens to the width of the depletion layer in a p – n junction diode when it is i) forward biased and ii) reverse biased? [AP Mar. ’19]
Answe:
When a p – n diode is forward biased thickness of depletion layer decreases and in reverse bias condition the thickness of depletion layer increases.

Question 11.
Draw the circuit symbols for p – n – p and n – p – n transistors. [TS & AP Mar. ’18, May ’17; AP May ’16, ’14; Mar. ’14; TS Mar. ’16]
Answer:

Question 12.
Draw the symbol of NOT gate and explain its operation. Give its truth table. [TS June ’15]
Answer:
NOT gate :
It has one input terminal and one output terminal. The output of NOT gate is the opposite of input i.e., if input is ‘0’ then output is ‘1’. If input is ‘1’ then output is ‘O’.

Implementation of NOT gate using a transistor :
NOT gate can be implemented with transistor. If A = 0 the emitter base junction is open and there is no current through the transistor. The current through the resistor. R_L = 0 and Q becomes equal to a potential of 5V i.e., Q when A = 1 then Q = 1 in the emitter base junction. So large current flows and Q approximately 0 volt i.e., Q =0. Thus output is same as that of a NOT gate.

Truth tables of NOT gate :
The truth tables of NOT gate interms of low and high (0 and 1) are as given below.

Question 13.
Define amplifier and amplification factor.
Answer:
Amplifier :
Raising the strength of a weak signal is known as amplification and the device used for this purpose is called amplifier.

Amplification factor :
It is the ratio between output voltage to the input,
Voltage, (A) = \(\frac{V_0}{V_i}\)

Question 14.
In which bias, can a zener diode be used as voltage regulator? [AP Mar. 16; TS June 15]
Answer:
In reverse bias, zener diode can be used as voltage regulator.

Question 15.
Which gates are called universal gates? [TS Mar. ’15]
Answer:
NAND and NOR gates are known as the basic building blocks of logic gates or universal gates.

Question 16.
Write the truth tables of NAND gate. How does it differ from AND gate?
Answer:

The output of NAND gate is opposite to output of AND gate.

Short Answer Questions

Question 1.
What are n-type and p-type semiconductors? How is a semiconductor junction formed?
Answer:
n-type semiconductors :
When pentavalent impurities such as phosphorous (P), arsenic (As), antimony (Sb) are added to intrinsic semiconductors then they are called n-type semiconductors.

p-type semiconductors :
When trivalent. impurities such as Boron (B), Aluminium (AI), Galium (Ga), Indium (In) etc. are added to intrinsic semiconductor then it is called p-type semiconductor.

p-n junction :
A p-n junction is formed by adding a small quantity of pentayalent impurities in a highly controlled manner to a p-type silicon/germanium wafer.

• During the formation of p-n junction diffusion and drift of charge carriers takes place.
• In a p-n junction concentration of holes is high at p – side and concentration of electrons is high at n-side.

Due to the concentration gradient between p-type and n-type region holes diffuse to n- region and electrons diffuse to p-region.

Due to diffusion of changes a chargeless region is formed near junction called depleted layer.

Question 2.
Discuss the behaviour of p-n junction. How does a potential barrier develop at the junction?
Answer:
p-n junction :
A p-n junction is formed by adding a small quantity of pentavalent impurities in a highly controlled manner to a p-type silicon/germanium wafer.

• During the formation of p-n junction diffusion and drift of charge carriers takes place.
• In a p-n junction concentration of holes is high at p – side and concentration of electrons is high at n-side.

Due to the concentration gradient between p-type and n-type region holes diffuse to n- region and electrons diffuse to p-reglon. This leads to diffusion current.

Due to diffusion of electron an ionised donor is developed at n-region and due to diffusion of holes to n- region an ionised acceptor. These ions are immobile. So some – ve charge is developed in p – region and positive charge is developed in n-region. This space charge prevents further motion of electrons and holes near junction.

Depletion layer :
Both the negative and positive space charge regions near junc-tion are called depletion region.

Question 3.
Draw and explain the current-voltage (I-V) characteristic curves of a junction diode in forward and reverse bias.
Answer:
When a graph is plotted between junction potential ‘V’ and junction current T of a p-n junction then it is called V-I characteristics.

In forward bias p-side of p-n junction is connected to + ve terminal and n – side is connected to – ve terminal of external voltage ‘V’. The external voltage ‘V’ is gradually increased and junction current T is measured.

Initially junction potential is slowly increased in steps of 0.1 V. Until junction potential reaches a minimum value called threshold potential junction current is almost zero. ;

Once applied potential crosses threshold potential then junction current increases exponentially with applied voltage. On the reverse bias side nearly a steady current of few micro amperes was observed with applied voltage. When reverse bias potential reaches a high valued suddenly the diode is thrown into conduction. This is called breakdown potential.

Question 4.
Describe how a semiconductor diode is used as a half wave rectifier. [TS May. 18. Mar. 16; AP Mar. 16, 14]
Answer:
A junction diode allows current through it in forward bias only. In a half wave rectifier an a.c. source, p-n junction and load resistance (R_L) are connected in series as shown.

For ‘+ve’ half cycle p-n junction is for-ward biased so current flows through diode and we will get output current across load resistance.

For ‘+’ ve half cycle the p-n junction is reverse biased so current does not flow through p-n junction. So we are not able to get current through load resistance.

In half wave rectifier the out put voltage changes sinusoidally. But still it is flowing in only one direction through load resistance (R_L) so input a.c. voltage is rectified.

Question 5.
What is rectification? Explain the work¬ing of a full wave rectifier. [AP Mar. ’18, ’15; May ’17, ’14; TS Mar. ’19. ’15, May ’17]
Answer:
Rectification :
The process of converting alternating current (a.c) into direct current (d.c) is called rectification. Instruments used for rectification is called rectifier.

In a full wave rectifier, two p-n diodes are connected at the output side of a center-tapped transformer through a load resistance as shown.

The centre tap will divide the output a.c. wave exactly into two equal halves say + ve half cycle and – ve half cycle.

Let diode D₁ is connected to ‘+ve’ half cycle then it is forward biased. So current flows through D₁ at the same time ‘-ve’ half cycle is applied to diode D₂ so it is reverse biased and current does not flow through it. Hence we will get output through diode D₁.

As the applied a.c. wave is progressing we will get ‘+ve’ half cycle to diode D₂ at that time diode D₂ is forward biased so current flows through D₂. But now ‘-ve’ half cycle is applied to diode D₁. So it is in reverse bias hence current does not flow through D₁.

In full wave rectifier diodes D₁ and D₂ will conduct current alternately. Even though out put current oscillates between a minimum and maximum value it always passes through same direction through load resistance (R_L). So input a.c. is rectified.

Question 6.
Distinguish between half-wave and full-wave rectifiers. [AP Mar. ’19. ’17; May. ’16; TS Mar. ’18, May, ’18]
Answer:

Question 7.
Distinguish between zener breakdown and avalanche breakdown.
Answer:
Avalanche breakdown:

1. In avalanche breakdown, the thermally generated electrons and holes acquire sufficient energy from the applied potential to produce new carries by removing valence electrons from their bonds.
2. These new carries, in turn produce additional carriers again through the process of disrupting bonds.
3. This cumulative process is referred to as avalanche multiplication. It results in the large flow of current, and the diode finds itself in avalanche breakdown.
4. This occurs in lightly doped diodes at high reverse bias voltages.

Zener breakdown:

1. If a diode is heavily doped, direct rupture of covalent bonds takes place because of strong electric field at the junction.
2. As a result of heavy doping of p and n regions, the depletion region width becomes very small and an applied voltage causes an electric field of 10⁷ V/m of the junction making condition suitable for zener breakdown. This occurs in heavily doped diodes at low reverse bias voltages.

Question 8.
Explain hole conduction in intrinsic semiconductors.
Answer:
Intrinsic semiconductors :
Semiconductors with ultra high pure state are called “intrinsic semiconductors”.

In pure germanium (Ge) or silicon(Si) crystal every germanium or Silicon atom forms four covalent bonds with neighbouring Ge/Si crystal.

At very low temperatures intrinsic semiconductors are insulators. When temperature increases electrons absorbs more thermal energy and it may become a free electron and that atom will become positive.

In intrinsic semiconductors number of free electrons (n_e) is equal to number of holes (n_h)

Due to thermal energy some of the electrons escapes from the bonds and an empty spaces left behind in the valence band. This vacancy in the valence band is called a “hole”.

Due to applied electric field the holes drift in opposite direction to the electrons with lesser speed and behave like positive charge carriers and current is produced due to the both electrons and holes.

Current contribution by electrons (l_e) and holes (I_h) is same.
∴ In an intrinsic semiconductor n_e = n_h = n_i.
Total current I = I_e + I_h

Question 9.
What is a photodiode? Explain its working with a circuit diagram and draw its I-V characteristics.
Answer:
Photodiode :
A photodiode consists of a p-n junction diode with a transparent window to allow light to fall on to the junction.

When light photons falls on this p-n junction it will produce electron – hole pair. These pairs are separated by the applied potential ‘V’ before they recombine. The magnitude of photo current depends on intensity of incident light.

i.e., current, i ∝ intensity of light I. So a photodiode can convert light intensity variations into current variations. This property is used to detect optical signals.

The I-V characteristics of photodiode can easily studied with reverse bias potential on it. The junction voltage ‘V’ and current ‘I’ characteristics are as shown in figure.

Question 10.
Explain the working of LED and what are its advantages over conventional incandescent low power lamps.
Answer:
Light emitting diode (LED) :
It is a highly doped p-n junction. Under forward biased condition it emits spontaneous radiation in visible region. This p-n junction is coated with a transparent cover so that emitted light can come out.

Working :
When LED is forward biased holes are driven to n-region and electrons are driven to p-region due to electric potential of battery. As a result charge concentration near junction region increases. The electrons and holes while recombining with them they will release the recombination energy in the form of light photons.

Generally LED breakdown voltages are very low such as 5V. For the fabrication of visible LED the energy band gap of 1.8 eV to 3 eV is necessary. The minimum energy gap must be 1.8 eV. It LED materials are selected with in this range then we can get visible light in the wavelength range of 0.7 pm to 0.4 pm or in wavelength range of 7000Å to 4000Å.

Generally LEDs are biased to emit light with maximum efficiency. Intensity of light emitted depends on strength of current. Colour of light depends on energy band width.

For gallium arsenide-phosphide energy gap is ≅ 1.9 eV, it will emit red light.

For galium Arsenide Ga, As energy gap is ≅ 1.4 eV, it will emit infrared light. These LEDs are widely used in T.V remote control and in burglar alarm systems.

Advantages of LED:

1. They require low operational voltage and consumes less power.
2. They are surged and life period is very high.
3. They will respond very quickly to current changes.

Question 11.
Explain the working of a solar cell and draw its I-V characteristics.
Answer:
Solar cells :
A solar cell is also a p-n junction which generates emf when solar radiation falls on it. A p-type silicon wafer of nearly 300 pm is taken. A n-type impurity layer of nearly 0.3 µm is developed on it through diffusion process, junction surface area Is kept large. A metallic grid is deposited on n-region and the other p- side is also coated with metal. These two will provide electrical contact.

Working :
Generally semiconductors width a band width of nearly 1.5 eV or less are selected in solar cells when solar radiation falls on p-n junction electron hole pair is produced.

Separation of electrons and holes will takes place (before they recombine) due to the electric field produced across depleted region.

Electrons on reaching n – side are collected by front metallic grill. Holes reaching p – side are collected by back contact.

V.I characteristics of solar cells are drawn in fourth quadrant of the coordinate axis. It is as shown in figure.

Solar cells are widely used to tame solar energy from which electricity is produced.

These solar cell plays an important role in supplying electrical energy to satellites and in remote forest areas.

Question 12.
Explain the different transistor configurations with diagrams.
Answer:
Transistors are connected in three ways. They are :

1. Common base configuration
   Common emitter configuration
2. Common collector configuration

1) Common base configuration :
In this configuration, base is common to both input and output. Base terminal is earthed and input is given across base emitter and output is taken across base collector.

2) Common emitter configuration :
In this configuration emitter is common to both input and output. The emitter is earthed and input is given across base emitter and output is taken across collector emitter.

3) Common collector configuration :
In this configuration, collector is common to both input and output. The collector is earthed and input is given across base collector and output is taken across emitter-collector.

Question 13.
Explain how transistor can be used as a switch?
Answer:
In a transistor D.C. input voltage V_i = I_BR_B + V_BE …….. (1)

Sum of D.C potential between emitter base i.e., and product of base current and base resistance (V_BE) / I_BR_B.

D.C. output voltage V₀ = V_CC – I_CR_C ……….. (2)

As far as V_i is less than active region minimum voltage of 0.6 V (nearly), output voltage V₀ is high because Collector current (I_C) is zero.

When input voltage V_i increases collector current I_C increases and output voltage V₀ decreases because V₀ = V_i – I_CR_C. i.e., when V_i is less V₀ is high and whenV_i is high output voltage V₀ is less. By changing the input potential a transistor can be made to move between high and low states or ON and OFF states. Hence by selecting proper input voltage V_i a transistor can be used as a switch.

Question 14.
Explain how transistor can be used as an oscillator.
Answer:
In an oscillator, we will get out put without any external input. The oscillator circuit is as shown in figure.

When switch ‘S₁‘ is closed a surge current will flow in transistor and it produces output in collector circuit. Current in coil T₂ will gradually increase from minimum value ‘x’ to maximum value ‘y’ with changing time. Current in T₂ is connected to oscillator LC in collector circuit. This induces current in coil T₁ due to inductive coupling between T₁ and T₂. Coil T₁ is connected to emitter base circuit. So a part of output is given as feedback to input.

When collector current reaches maximum value rate of change in collector current is zero. So induced current in T₁ is zero i.e., input feedback is zero. So collector current begin to decrease while decreasing again emf is induced in T₁ and feedback is given to emitter base circuit. Like this the signal is self sustained
Frequency of oscillator υ = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)

In this way a transistor can be used as an oscillator.

Question 15.
Define NAND and NOR gates. Give their truth tables. [TS Mar. ’17; AP June ’15]
Answer:
NOR Gate :
It is the combination of OR gate and NOT gate OR + NOT = NOR.

In this logic gate the output of OR gate is given to the input of NOT gate as shown in figure.

NAND gate :
It is the combination of AND gate and NOT gate.
AND + NOT = NAND.
In this logic gate the output of AND gate is given to the input of NOT gate.

The NAND and NOR gates are basic build¬ing blocks of logic gates; because any logic gates can be constructed by using only NAND or only NOR gates.

Question 16.
Explain the operation of a NOT gate and give its truth table. [TS June ’15]
Answer:
NOT gate :
It has one input terminal and one output terminal. When the input is low, the output is high and when the input is high, the output is low.

Implementation of NOT gate using a transistor :
NOT gate can be implemented with transistor. If A = 0 the emitter base junction is open and there is no current through the transistor. The current through the resistor. R_L = 0 and Q becomes equal to a potential of 5V i.e., Q when A = 1 then Q = 1 in the emitter base junction. So large current flows and Q approximately 0 volt i.e., Q =0. Thus output is same as that of a NOT gate.

Truth tables of NOT gate :
The truth tables of NOT gate interms of low and high (0 and 1) are as given below.

Long Answer Questions

Question 1.
What is a junction diode? Explain the for-mation of depletion region at the junction. Explain the variation of depletion region in forward and reverse biased condition.
Answer:
p-n junction :
A p-n junction is formed by adding a small quantity of pentavalent impurities in a highly controlled manner to a p-type silicon/germanium wafer.

During the formation of p-n junction diffusion and drift of charge, carriers takes place.

In a p-n junction concentration of holes is high at p – side and concentration of electrons is high at n-side. Due to the concentration gradient between p-type and n-type regions holes diffuse to n-region and electrons diffuse to p-region. This leads to diffusion current.

Due to diffusion of electron an ionised donor is developed at n-region and due to diffusion of holes to n- region an ionised acceptor. These ions are immobile. So some – ve charge is developed in p – region and positive charge is developed in n-region. This space charge prevents further motion of electrons and holes near junction.

Depletion layer :
Both the negative and positive space charge regions near junction are called depletion region.

Variation of depletion region :
In forward bias due to applied voltage electrons from n – region crosses junction layer and goes to p-region. Similarly holes from p-region crosses junction and goes to n-region. Since charge carriers are freely crossing the junction depleted region vanishes in forward bias condition.

In reverse bias condition electrons in n- region are attracted by + ve terminal of bat-tery connected to it. Similarly holes in p – region are attracted by ’-ve’ terminal con-nected to it. As a result charges will travel towards battery terminals. We can not find charge carriers near p-n junction.

So in reverse bias condition width of depleted region increases.

Question 2.
What is a rectifier? Explain the working of half wave and full wave rectifiers with diagrams.
Answer:
The process of converting alternating current (a.c) into direct current (d.c) is called “rectification”. Instruments used for rectification is called “rectifier”.

A junction diode allows current through it in forward bias only. In a half wave rectifier an a.c. source, p-n junction and load resistance (R_L) are connected in series as shown.

For ‘+ve’ half cycle p-n junction is forward biased so current flows through diode and we will get output current across load resistance.

For + ve half cycle the p-n junction is reverse biased so current does not flow through p-n junction. So we are not able to get current through load resistance.

In half wave rectifier the out put voltage changes sinusoidally. But still it is flowing in only one direction so input a.c. voltage rectified.

In a full wave rectifier two p-n diodes are connected at the output side of a center tapped transformer through a load resistance as shown.

The centre tap will divide the output a.c. wave exactly into two equal halves say + ve half cycle and – ve half cycle.

Let diode D₁ is connencted to ’+ve’ half cycle then it is forward biased. So current flows through D₁ at the same time ‘-ve’ half cycle is applied to diode D₂. So it is reverse biased and current does not flow through it. Hence we will get output through diode D₁.

As the applied a.c. wave is progressing we will get ‘+ve’ half cycle to diode D₂ at that time diode D₂ is forward biased so current flows through D₂. But now -ve’ half cycle is applied to diode D₁. So it is in reverse bias hence current does not flow through D₁.

In full wave rectifier diodes D₁ and D₂ will conduct current alternately. Even though out put current oscillates between a minimum and maximum value it always passes through same direction. So input a.c. is rectified.

Question 3.
What is a zener diode? Explain how it is used as a voltage regulator.
Answer:
Zener diode :
A zener diode is a highly doped p-n junction with sharp breakdown voltage. Generally zener is operated in “reverse bias condition”.

Note:
In forward bias condition zener diode will also act as ordinary p-n junction.

Zener diode as voltage regulator :
Principle :
Zener diode has sharp breakdown voltage in “reverse bias condition”.

In zener diode release of large scale of charge carriers at breakdown voltage is due to field emission of electrons from host atoms. For field ionisation nearly an electric field of 10⁶ V/m is necessary.

The speciality of zener diode is even though current through zener increases largely its potential (zener potential) remains almost constant.

Working :
Let a zener diode is connected to unregulated supply through a series resistance R_s. The value of zener voltage is selected such that zener voltage V_z is less than the minimum value of unregulated supply. A load resistance R_L is connected parallel to zener. Output is taken across load resistance R_L.

Case – I :
Let voltage of unregulated supply is at Its minimum value say V_{i min}. Zener potential V_z is constant. So V_{i min} – V_z is voltage drop across R_s. Current through R_s = I_min
= \(\frac{V_{i min}-V_z}{R_s}\)
Load current, I_L = \(\frac{V_z}{R_L}\)
∴ Current through zener I_{z min} = I_min – \(\frac{V_z}{R_L}\)

Case – II :
When applied voltage is maximum say, V_{i max} then voltage drop across
R_s = V_{i max} – V_z

Maximum current through R_s is
I_max = \(\frac{V_{i max}-V_z}{R_s}\)
Current through zener is also max.
I_{z max} = I_max = \(\frac{V_z}{R_L}\)

In zener diode voltage regulator voltage changes in unregulated supply are converted into current changes in series resistance R_s. These current changes are absorbed by zener.

As a result we will get a constant voltage and current at output. In this way zener diode acts as a voltage regulator.

Question 4.
Describe a transistor and explain its working.
Answer:
Transistor :
A transistor is a three layered electronic device. These layers are called emitter, base and collector.

Transistors are two types 1) p-n-p 2) n-p-n.

Emitter :
Emitter region is of moderate size. It is heavily doped. It supplies large number of majority charge carriers for the current flow through transistor.

Base :
Width of base region is very less. It is lightly doped nearly with 3 to 5% Impurity concentration of emitter.

Collector :
Size of collector region is larger than emitter. It is moderately doped (i.e., impurity concentration is less than emitter).

Biasing of transistor :
In a transistor for transistor action to takes place (i) Emitter base region must be forward biased, (ii) Base collector region must be reverse biased, (iii) Forward bias emitter base potential V_EB must be less than reverse bias collector base potential V_CB.

If a transistor is biased as above, then the transistor is said to be in active state.

Working principle :
Electrons/holes in emitter region are injected into base region due to forward bias potential in emitter base region.

In base region nearly 3 to 5% of electrons/ holes are recombined so a small amount of current (I_B) will flow in emitter base circuit. Due to less impurity concentration the remaining charges injected into base will cross base collector region.

The high reverse bias potential in base collector region will act as forward bias for the charges left unrecombined in base region.

So these charges are attracted by collector region. These charges will recombine at collector region and some current (I_C) will flow in base collector region.

In a transistor emitter current (I_E) = Base current (I_B) + Collector current (I_C)
∴ I_E = I_B + I_C

Hence transistor is a current controlled device.

Question 5.
What is amplification? Explain the working of a common emitter amplifier with necessary diagram.
Answer:
Amplifier :
An amplifier is an electronic device used to strengthen weak signals.

Transistor as an amplifier (C.E. configuration) :
A transistor can be used as an amplifier in its active region. In this region output voltage V₀ increases drastically even for a small change in input voltage’ V_i‘.

In transistor amplifier the mid point of active region is taken as operating point (also called input potential) on which varying signal voltage is superposed. This variation is magnified at output side by a factor equals to amplification factor p.

In a transistor output voltage of collector, V_OC = V_CE + I_LR_L

Input voltage V_BB = V_BE + I_BR_B when input signal voltage V_i ≠ 0 the,

V_BE + V_i + V_BE + I_BR_B + ∆I_B(R_B + r_i)

Where r_i is input resistance.

Input signal voltage
V_i = ∆I_B(R_B + r_i) = r∆I_B.

Current amplification factor β is defined as the ratio of change in collector current ∆I_C to change In base current ∆I_B when V_CC Is constant.

Voltage amplification factor A_v :
It is defined as the ratio of output signal voltage (V₀) to input signal voltage (V_i).

Question 6.
Draw an OR gate using two diodes and explain its operation. Write the truth table and logic symbol of OR gate.
Answer:
Implementation of OR gate using diodes :
Let ‘D₁‘ and ‘D₂‘ represent two diodes. A potential of 5V represent the logical value 1 and a potential of 0V represents the logical value zero.

When A = 0, B = 0 both the diodes are reverse biased and there is no current through the resistance. So, the potential at ‘Q’ is zero, i.e., Q = 0. When A = 0 or B = 0 and the other equal to a potential behaves like a closed switch. The output potential then becomes 5V. i.e., Q=l. When both A and B are 1, both the diodes are forward biased and the potential at Q’ is same as that at A and B which is 5V i.e., Q =1. The output is same as that of the OR gate.

Truth table of OR gate :
The truth table of OR gate interms of low, high; 0 and 1 are below.

Logical symbol of OR gate :
The logical function OR is represented by the symbol plus. So that the output, Q = A + B

Questuion 7.
Sketch a basic AND circuit with two diodes and explain its operation. Explain how doping increases the conductivity in semiconductors?
Answer:
AND gate :

1. It has two input terminals and one output terminal.
2. When both the inputs low or one of the input is low the output is low in an AND gate.
3. The output of the gate is high only when both the inputs are high.
4. The output of the gate is high only when both the inputs are high.
5. If the input of the gate are A and B and the outputs in Q than Q is logical function of A and B. The value of Q for different combinations of A and B is shown by means of a table called truth table.

Truth Table :
It is defined as the table that shows the values of the output of all possible combinations of the value of the input variables.

Implementation of AND gate using diodes:

1. Let D₁ and D2 represent two diodes. A potential of 5V represents the logical value 1 and potential of OV represents the logical value zero (0).
2. When A = 0, B = 0, both the diodes D₁ and D₂ are forward biased and they behave like open switches. There is no current through the resistance R’ making the potential of Q equal to 5V i.e., Q = 1. The output is same as that of an AND gate.

Doping – Conductivity of semiconductors:
When a p – type impurity is doped it will develop acceptor energy levels near valance band in Forbidden region. So Forbidden gap width decreases and electrons can easily sent to conduction band.

When n-type impurities are doped they will develop donor energy levels near conduction band in Forbidden gap. As a result Forbidden gap decreases and electrons in valance band will be sent to conduction band with very little energy (< 0.01 eV).

As a result due to doping conductivity of semiconductors will increase.

Problems

Question 1.
In a half wave rectifier, a p-n junction diode with internal resistance 20 ohm is used. If the load resistance of 2 ohm is used in the circuit, then find the efficiency of this half wave rectifier.
Answer:
Internal resistance of diode r_f = 20 Ω;
Load resistance R_L = 2kΩ = 2000 Ω
Efficiency of half wave rectifier =

\(\frac{812}{2020}\) = 0.4019
% of η = 0.4019 × 100 = 40.19% = 40.2%

Question 2.
A full wave p-n junction diode rectifier uses a load resistance of 1300 ohm. The internal resistance of each diode is 9 ohm. Find the efficiency of this full wave rectifier.
Answer:
Load resistance R_L = 1300 Ω;
Internal resistance of diode r_f = 9 Ω
Efficiency of full wave rectifier

% of efficiency η = 0.8064 × 100 = 80.64%

Question 3.
Calculate the current amplification factor b (beta) when change in collector current is 1 mA and change in base current is 20 mA.
Answer:
Change in collector current ∆I_C = 1mA = 1 × 10^-3 A
Change in base current ∆I_b =20µA = 20 × 10^-6 A
Current amplification

Question 4.
For a transistor amplifier, the collector load resistance R_L = 2k ohm and the input resistance R_i = 1 k ohm. If the current gain is 50, calculate voltage gain of the amplifier.
Answer:
Load resistance RL = 2 kD = 2000 Ω;
Input resistance Rj = 1 kQ = 1000 Ω
Current gain b = 50 ; Voltage gain A_v = ?

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Very Short Answer Type

Question 1.
If \({ }^{\mathrm{n}} \mathrm{P}_4\) = 1680, find n. [Mar.’14, May ’06]
Solution:
Given \({ }^{\mathrm{n}} \mathrm{P}_4\) = 1680
\({ }^{\mathrm{n}} \mathrm{P}_4\) = 8 . 7 . 6 . 5
= \({ }^8 \mathrm{P}_4\)
⇒ n = 8

Question 2.
If \({ }^{12} \mathrm{P}_{\mathrm{r}}\) = 1320, find r. [March ’09, AP – May 2015]
Solution:
Given \({ }^{12} \mathrm{P}_{\mathrm{r}}\) = 1320
\({ }^{12} \mathrm{P}_{\mathrm{r}}\) = 12 . 11 . 10
= \({ }^{12} \mathrm{P}_3\)
r = 3.

Question 3.
If \({ }^{(n+1)} P_5:{ }^n P_5\) = 3 : 2, find n.
Solution:
Given \({ }^{(n+1)} P_5:{ }^n P_5\) = 3 : 2
\(\frac{(n+1) P_5}{{ }^n P_5}=\frac{3}{2}\)

⇒ 2n + 2 = 3n – 12
⇒ n = 14.

Question 4.
If \({ }^n \mathbf{P}_7\) = 42 . \({ }^n \mathbf{P}_5\), find n. [TS – Mar. 2017, ’15; May ’12, ’11, ’09, ’07]
Solution:
Given \({ }^n \mathbf{P}_7\) = 42 . \({ }^n \mathbf{P}_5\)
n (n – 1) (n – 2) (n – 3) (n – 4) (n – 5) (n – 6) = 42 . n(n – 1) (n – 2) (n – 3) (n – 4)
(n – 5) (n – 6) = 42
⇒ n² – 11n + 30 – 42 = 0
⇒ n² – 11n – 12 = 0
⇒ n – 12n + n – 12 = 0
⇒ n (n – 12) + 1 (n – 12) = 0
⇒ (n – 12) (n + 1) = 0
⇒ n = 12; n = – 1
Since, n is a positive integer, n = 12.

Question 5.
If \({ }^{56} \mathbf{P}_{(r+6)}:^{54} P_{(r+3)}\) = 30800: 1, find ‘r’.
Solution:
Given \({ }^{56} \mathbf{P}_{(r+6)}:^{54} P_{(r+3)}\) = 30800 : 1
\(\frac{\frac{56 !}{(56-r-6) !}}{\frac{54 !}{(54-r-3) !}}=\frac{30800}{1}\)
⇒ \(\frac{\frac{56 !}{(50-r) !}}{\frac{54 !}{(51-r) !}}=\frac{30800}{1}\)
⇒ \(\frac{\frac{56 \cdot 55 \cdot 54 !}{(50-r) !}}{\frac{54 !}{(51-r)(50-r) !}}=\frac{30800}{1}\)
⇒ 56 55(51 – r) = 30800
⇒ 51 – r = 10
⇒ r = 41.

Question 6.
If \({ }^{12} \mathbf{P}_5+5 \cdot{ }^{12} \mathbf{P}_4={ }^{13} \mathbf{P}_{\mathrm{r}}\), find ‘r’. [TS – May 2015]
Solution:
Given \({ }^{12} \mathbf{P}_5+5 \cdot{ }^{12} \mathbf{P}_4={ }^{13} \mathbf{P}_{\mathrm{r}}\)
\({ }^{(13-1)} P_5+5{ }^{(13-1)} P_{(5-1)}={ }^{13} P_r\)
We know that,
\({ }^n P_r={ }^{(n-1)} P_r+r^{(n-1)} P_{r-1}\)
∴ r = 5
(or) Given \({ }^{12} \mathrm{P}_5+5 \cdot{ }^{12} \mathrm{P}_4={ }^{13} \mathrm{P}_{\mathrm{r}}\)
12 . 11 . 10 . 9 . 8 + 5 . 12 . 11 . 10 . 9 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
95040 + 59400 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
⇒ 154440 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
13 . 12 . 11 . 10 . 9 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
⇒ \({ }^{13} \mathrm{P}_5\) = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
⇒ r = 5.

Question 7.
If \({ }^{\mathrm{n}} \mathrm{C}_4\) = 210, find n. [TS – Mar.2019]
Solution:
Given \({ }^{\mathrm{n}} \mathrm{C}_4\) = 210
⇒ \(\frac{n(n-1)(n-2)(n-3)}{1 \cdot 2 \cdot 3 \cdot 4}\) = 210
⇒ n (n – 1) (n -2) (n -3) = 5040
n (n – 1) (n – 2) (n – 3) (n – 4) = 10 . 9 . 8 . 7
∴ n = 10.

Question 8.
If \({ }^{12} \mathrm{C}_{\mathrm{r}}\) = 495, find the possible values of ‘r’.
Solution:
Given \({ }^{12} \mathrm{C}_{\mathrm{r}}\) = 495 = 11 . 9 . 5
= \(\frac{11 \cdot 10 \cdot 9 \cdot 5}{10}=\frac{11 \cdot 10 \cdot 9}{1 \cdot 2}=\frac{12 \cdot 11 \cdot 10 \cdot 9}{1 \cdot 2 \cdot 12}\)
= \(\frac{12 \cdot 11 \cdot 10 \cdot 9}{1 \cdot 2 \cdot 3 \cdot 4}={ }^{12} \mathrm{C}_4 \text { (or) }{ }^{12} \mathrm{C}_8\)
∴ r = 4 (or) 8.

Question 9.
If 10. \({ }^n c_2\) = 3 . \({ }^{n+1} C_3\), find ’n’. [May ’12], [AP – Mar. 2015]
Solution:
Given 10. \({ }^n c_2\) = 3 . \({ }^{n+1} C_3\)
⇒ 10 . \(\frac{\mathrm{n}(\mathrm{n}-1)}{1 \cdot 2}\) = 3. \(\frac{(n+1) n(n-1)}{1 \cdot 2 \cdot 3}\)
⇒ n + 1 = 10
⇒ n = 9.

Question 10.
If \({ }^{{ }^n} P_{\mathbf{r}}\) = 5040 and \({ }^n C_{\mathbf{r}}\) = 210 find n and r. [AP – Mar. ‘17, ‘16; Board Paper]
Solution:
\({ }^{{ }^n} P_{\mathbf{r}}\) = 5040 ……………(1)
\({ }^n C_{\mathbf{r}}\) = 210 ……………..(2)
\(\frac{(2)}{(1)} \Rightarrow \frac{{ }^n C_r}{{ }^n P_r}=\frac{210}{5040}\)
\(\frac{\frac{n !}{(n-r) ! r !}}{\frac{n !}{(n-r) !}}=\frac{1}{24} \Rightarrow \frac{1}{r !}=\frac{1}{4 !}\)
r = 4
Now, substituting r = 4 in equation (1)
\({ }^n \mathrm{p}_4\) = 5040
\({ }^n \mathrm{p}_4\) = 10 . 9 . 8 . 7
\({ }^n \mathrm{p}_4={ }^{10} \mathrm{P}_4\)
n = 10.

Question 11.
If \({ }^n C_4={ }^n C_6\), find ‘n’.
Solution:
Given \({ }^n C_4={ }^n C_6\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
Now, n = r + s
⇒ n = 4 + 6
⇒ n = 10.

Question 12.
If \({ }^{15} \mathrm{C}_{2 \mathrm{r}-1}={ }^{15} \mathrm{C}_{2 \mathrm{r}+4}\) find ’r’. [Mar. ’14, ’05]
Solution:
Given \({ }^{15} \mathrm{C}_{2 \mathrm{r}-1}={ }^{15} \mathrm{C}_{2 \mathrm{r}+4}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ 2r – 1 = 2r + 4
⇒ – 1 ≠ 4
It is not possible.
n = r + s
⇒ 15 = 2r – 1 + 2r + 4
⇒ 15 = 4r + 3
⇒ 4r = 12
⇒ r = 3.

Question 13.
If \({ }^{12} \mathrm{C}_{\mathrm{r}+1}={ }^{12} \mathrm{C}_{3 \mathrm{r}-5}\), find ‘r’. [TS- Mar. 2016; March ’08]
Solution:
Given \({ }^{12} \mathrm{C}_{\mathrm{r}+1}={ }^{12} \mathrm{C}_{3 \mathrm{r}-5}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ r + 1 = 3r – 5
⇒ 2r = 6
⇒ r = 3
(or)
n = r + s
⇒ 12 = r – 1 + 3r – 5
⇒ 12 = 4r – 4
⇒ 4r = 16
⇒ r = 4.
∴ r = 3 (or) 4.

Question 14.
If \({ }^9 C_3+{ }^9 C_5={ }^{10} C_{r^{\prime}}\) then find ‘r’.
Solution:
Given \({ }^9 C_3+{ }^9 C_5={ }^{10} C_{r^{\prime}}\)

Question 15.
Find the number of ways of forming a committee of 5 members from 6 men and 3 ladies.
Solution:
Number of ways of forming a committee of 5 members from 6 men and 3 ladies is
\({ }^9 \mathrm{C}_5=\frac{9 \cdot 8 \cdot 7 \cdot 6 \cdot 5}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}\) = 126.

Question 16.
If \({ }^n C_5={ }^n C_6\) then find \({ }^{13} \mathrm{C}_{\mathrm{n}}\). [AP – Mar.2019] [TS-Mar. ‘18; May’14, ‘10, March ’13].
Solution:
Given \({ }^n C_5={ }^n C_6\)
If \({ }^{13} \mathrm{C}_{\mathrm{n}}\)
r = s (or) n = r + s
n = r + s = 5 + 6 =11
Now,
\({ }^{13} C_n={ }^{13} C_2\)
= \({ }^{13} \mathrm{C}_2=\frac{13 \cdot 12}{2 \cdot 1}\)
= 13 . 6 = 78.

Question 17.
Prove that \({ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_6={ }^{11} \mathrm{C}_4\).
Solution:
Given \({ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_6={ }^{11} \mathrm{C}_4\)
L.H.S: \({ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_6={ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_4\)
[∵ \({ }^n C_r={ }^n C_{n-r}\)]
= \(={ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_{4-1}={ }^{(10+1)} \mathrm{C}_4\)
[∵ \({ }^n C_r+{ }^n C_{n-r}={ }^{(n+1)} C_r\)]
= \({ }^{11} \mathrm{C}_4\)
= R.H.S

Question 18.
If \({ }^{12} C_{s+1}={ }^{12} C_{2 s-5}\) find ‘s’. [Mar. ’11]
Solution:
Given \({ }^{12} C_{s+1}={ }^{12} C_{2 s-5}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ r = s
⇒ s + 1 = 2s – 5
⇒ s = 6 (or)
n = r + s
12 = s + 1 + 2s – 5
12 = 3s – 4 = 3s = 16
s = \(\frac{16}{3}\)
Since s is integer, s = 6.

Question 19.
If \({ }^n C_{21}={ }^n C_{27}\) find \({ }^{50} \mathrm{C}_{\mathrm{n}}\).
Solution:
Given \({ }^n C_{21}={ }^n C_{27}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ n = r + s
⇒ n = 21 + 27
⇒ n = 48
Now, \({ }^{50} \mathrm{C}_{\mathrm{n}}={ }^{50} \mathrm{C}_{48}\)
= \({ }^{50} \mathrm{C}_2=\frac{50 \cdot 49}{2 \cdot 1}\)
= 25 . 49 = 1225.

Question 20.
Find the number of positive divisors of 1080. [AP – May, Mar. 2016; May ‘13]
Solution:
1080 = 2³ × 3³ × 5¹
The number of positive divisors of 1080 = (3 + 1) (3 + 1) (1 + 1)
= 4 . 4 . 2 = 32.

Question 21.
Find the value of \({ }^{10} \mathrm{C}_5+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_3\). [AP – Mar. ‘18; TS- Mar. 2017; March ‘10]
Solution:
Given \({ }^{10} \mathrm{C}_5+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_3\)
= \(\left({ }^{10} \mathrm{C}_5+{ }^{10} \mathrm{C}_4\right)+\left({ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_3\right)\)
= \({ }^{11} C_5+{ }^{11} C_4\)
= \({ }^{12} \mathrm{C}_5=\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}\)
= 792

Question 22.
Find the number of injections ofaset A with 5 elements to a set B with 7 elements.
Solution:
If a set A has m elements and the set B has n elements, then the number of injections from A into B is \(\mathrm{n}_{\mathrm{m}}\) if m ≤ n and 0 if m > n.
Given n = 7, m = 5
∴ The number of injections from A to B is \({ }^7 \mathrm{P}_5\) = 7. 6 . 5 . 4 . 3 = 2520.

Question 23.
Find the number of ways in which 4 letters can be put in 4 addressed envelopes so that no letter goes into the envelope meant for it. [TS -May 2016]
Solution:
The number of derangements of n distinct things is
\(\mathrm{n} !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}-\frac{1}{5 !}+\ldots \ldots+(-1)^{\mathrm{n}} \frac{1}{\mathrm{n} !}\right)\)
Required number of ways is \(4 !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)\) = 12 – 4 + 1 = 9.

Question 24.
A man has 4 sons and there are 5 schools within his reach. In how many ways can he admit his sons in the schools so that no two of them will be in the saine school?
Solution:
The number of ways of admitting four sons into five schools if no two of them will be in the same school.
\({ }^n P_r={ }^5 P_4\) = 5 . 4 . 3 . 2 = 120.

Question 25.
If there are 25 railway stations on a railway line, how many types of single second class tickets must be printed, so as to enable a passenger to travel from one station to another?
Solution:
Number of stations on a railway line = 25
Num ber of single different second class tickets must be printed so as to enable a passenger to travel from one station to another = Number of ways of arranging two station names out of 25 station names = \({ }^{25} \mathrm{P}_2\)
= 25 . 24 = 600.

Question 26.
In a class, there are 30 students on the new year day, every student posts a greeting card to all his/her classmates. Find the total number of greeting cards posted by them.
Solution:
Total number of students in a class = 30.
Total number of greeting cards posted by all the students to their classmates = number of ways of arranging names of two students from 30 names of students
= \({ }^n P_r={ }^{30} P_2\)
= 30 × 29 = 870.

Question 27.
Find the number of 4 letter words that can be formed using the letters of the word PISTON in which atleast one letter is repeated. [AP – Mar. 2015]
Solution:
The given word has six letters.
When repetition is allowed:
The number of four letter words that can be formed using these six letters when repetition is allowed is \(n^r=6^4\) = 6 . 6 . 6 . 6 = 1296.

When repetition is not allowed:
The number of four letter words that can be formed using these letters of the six letters when repitition is not allowed is
\({ }^n \mathrm{P}_{\mathrm{r}}={ }^6 \mathrm{P}_4\) = 360

The number of four letter words in which atleast one letter repeated is \(n^r-{ }^n P_r=6^4-{ }^6 P_4\) = 1296 – 360 = 936.

Question 28.
A number lock has 3 rings and each ring has 9 digits 1, 2, 3, ……………, 9. Find the maximum number of unsuccessful attempts that can be made by a persoti who tries to open the lock without knowing the key code.
Solution:

Each ring can be rotated in 9 different ways.
The total no. of different ways in which three kings can be rotated is = 9³ = 9 . 9 . 9 = 729
Out of these attempts, only one attempt is successful attempt.
Therefore, the maximum no. of unsuccessful attempts is 729 – 1 = 728.

Question 29.
Find the number of functions from a set A containing 5 elements into a set B containing 4 elements.
Solution:
Given number of A = n(A) = m = 5
number of B = n(B) = n = 4
Set A contains 5 elements and set B contains 4 elements.
The total number of functions from set A containing m elements to set B containing n elements is \(n^m=4^5\) = 1024.

Question 30.
Find the number of bijections from a set A contaIning 7 elements onto itself.
Solution:
Given n(A) = n = 7.
∴ The number of bijections from set A with n elements to set B with same number of elements ‘n’, A is n!.
The number of bijections from set A with 7 elements onto itself = 7!
= 7. 6 . 5 . 4 . 3 . 2 . 1 = 5040.

Question 31.
Find the number of ways of arranging 7 persons around a circle.
Solution:
Given number of persons, n = 7.
∴ The number of ways of arranging 7 persons around a circle is
(n – 1)! = (7 – 1)! = 6!
= 6 . 5 . 4 . 3 . 2 . 1 = 720.

Question 32.
Find the number of ways of preparing a chain with 6 different coloured beads. [TS – Mar. ‘19, 16; March ‘08]
Solution:
Neglecting the directions of beads in the chain.
Number of ways of preparing a chain with 6 different coloured beads = \(\frac{(n-1) !}{2}\)
= \(\frac{(6-1) !}{2}=\frac{5 !}{2}=\frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2}\) = 60.

Question 33.
Find the number of ways of arranging the Chief Minister and 10 Cabinet Ministers at a circular table so that the Chief Minister always sits in a particular seat.
Solution:
Total number of persons = 11
Chief Minister can sit in a particular seat in one way.
Now, remaining positions are well defined relative to Chief Minister.
Hence, the remaining can sit in 10 places in 10! ways.
∴ The number of required arrangements = 10! × 1
= 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3628800.

Question 34.
Find the number of ways of arranging the letters of the word a⁴ b³ c⁵ in its expanded form.
Solution:
The expanded form of a⁴ b³ c⁵ is a . a . a . a . b . b . b . c . c . c . c . c.
This word has 12 letters in which there are 4a’s, 3b’s, 5c’s.
∴ They can be arranged in \(\frac{12 !}{4 ! 3 ! 5 !}\) ways.

Question 35.
There are 4 copies (alike) each of 3 different books. Find the number of ways of arranging these 12 books in a shelf in a single row.
Solution:
We have 12 books in which 4 books are alike of 1 kind. 4 books are alike of 2nd kind and 4 books are alike of 3rd kind.
Hence, they can be arranged in a shelf in a row in \(\frac{12 !}{4 ! 4 ! 4 !}\) ways = \(\frac{12 !}{(4 !)^3}\) ways.

Question 36.
Find the number of ways of arranging the letters of the word INDEPENDENCE. [TS – May 2016; March ’09, May ’13].
Solution:
Given word is INDEPENDENCE
There are 12 letters in INDEPENDENCE, in which there are 3 Ns are alike. 2 D’s are alike, 4 E’s are alike, and rest are different.
∴ The no. of required arrangements = \(\frac{12 !}{3 ! \cdot 2 ! \cdot 4 !}\)

Question 37.
Find the number of ways of arranging the letters of the word MATHEMATICS. [AP & TS – Mar. ’18; May ’97, ’10, March ’11, ’06]
Solution:
Given word is MATHEMATICS.
The word MATHEMATICS contains 11 letters in which there are , 2 M’s are alike, 2 A’s are alike, 2 T’s are alii ice and rest are different.
∴ The no. of required arran igements 11! = \(\frac{11 !}{2 ! \cdot 2 ! \cdot 2 !}\).

Question 38.
Find the number of ways of arranging the letters of the word INTERMEDIATE. [AP -Mar. ’19; May 2016; May ’14, Board Paper]
Solution:
Given word is INTERMEDIATE.
The word INTERMEDIATE contains 121 letters in which there are 2 I’s are alike, 2 T’s are alike, 3 E’s are alike and rest are different.
∴ The no. of required arrangements = \(\frac{12 !}{2 ! \cdot 2 ! \cdot 3 !}\).

Question 39.
Find the number of 7 digit numbers that can be fonned using 2, 2, 2, 3, 3, 4 4.
Solution:
In the given seven digits, there are three 2’s, two 3’s, two 4’s.
∴ The number of seven digited numbers that can be formed using th given digits = \(\frac{7 !}{3 ! \cdot 2 ! \cdot 2 !}\).

Question 40.
Find the number of ways of selecting 7 members from a continent of 10 soldiers.
Solution:
The number of ways of selecting 7 members out of 10 soldiers is \({ }^{10} \mathrm{C}_7\) = 120.

Question 41.
A set A has 8 elements, find the number of subsets of A, containing atleaist 6 elements.
Solution:
The no. of subsets of A containing atlast 6 elements then the number of subsets of A containing 6 or 7 or 8 elements.
Number of subsets of A containing exactly 6 elements = \({ }^8 \mathrm{C}_6\)
Number cf subsets of A containing exactly 7 elements = \({ }^8 \mathrm{C}_7\)
Number of :ubsets of A containing exactly 8 elements = \({ }^8 \mathrm{C}_8\)
The nurrber of subsets of A containing at least 6 elements = \({ }^8 \mathrm{C}_6+{ }^8 \mathrm{C}_7+{ }^8 \mathrm{C}_8\)
= \({ }^8 \mathrm{C}_2+{ }^8 \mathrm{C}_1+{ }^8 \mathrm{C}_0\)
= \(\frac{8 \cdot 7}{2 \cdot 1}\) + 8 + 1
= 28 + 8 – 1 = 37.

Question 42.
Find the number of ways of selecting 4 boys and 3 girls from a group of 8 boys and 5 girls. [TS – Mar. 2015]
Solution:
4 boys can be selected from the given boys in \({ }^8 \mathrm{C}_4\) ways.
3 girls can be seleted from the given 5 girls in \({ }^5 \mathrm{C}_3\) ways.
∴ The required number of selections is \({ }^8 \mathrm{C}_4 \cdot{ }^{! 5} \mathrm{C}_3\) = \(\frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1} \frac{5 \cdot 4}{2 \cdot 1}\) = 700.

Question 43.
If there are 5 alIke pens, 6 alike pencils and 7 alike erasers, find the number of ways of selecting any number of (one or
more ) things out of them.
Solution:
The required number of ways is (p + 1) (q + 1) (r + 1) – 1
= (5 + 1) (6 + 1) (7 + 1) – 1
= 6 . 7 . 8 – 1
= 336 – 1 = 335.

Question 44.
To pass an examination a student has to pass in each of the three papers. In how many ways can a student fail in the exaimination? [TS- May 2015]
Solution:
For each of the three papers there are two choices P or F.
There are 2³ = 8 choices.
But a student passes only il he/she passes in all papers.
∴ Required number of ways = 2³ – 1 = 7.

Question 45.
In a class, there are 30 students. If each student plays a chess game with each of the other student, then find the total number of chess games played by them.
Solution:
Number of students in a class is 30.
Since each student plays a chess game with each of the student the total number of games played by them = \({ }^{30} \mathrm{C}_2\)
= \(\frac{30 \cdot 29}{2}\) = 435.

Question 46.
Find the number of diagonals of a polygon with 12 sides. [AP – May 2015]
Solution:
Number of sides of a polygon = 12
Number of diagonals of a n – sided polygon = \({ }^n C_2\) – n
∴ Number of diagonals of 12 sided polygon = \({ }^{12} \mathrm{C}_2\) – 12 = 54.

Question 47.
If \({ }^{\mathrm{n}} \mathrm{P}_3\) = 1320, find n. [May ‘08, March ‘05]
Solution:
12

Question 48.
If \({ }^{(n+1)} P_5:{ }^n P_6\) = 2 : 7, find n. [March ‘10, ‘07]
Solution:
11

Question 49.
If \({ }^{18} P_{(r-1)}:^{17} P_{(r-1)}\) = 9 : 7, find ‘r’.
Solution:
5

Question 50.
FInd the number of different chains that can be prepared using 7 different coloured beads. [AP – Mar. 2017]
Solution:
360

Telangana TSBIE TS Inter 2nd Year Physics Study Material 14th Lesson Nuclei Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 14th Lesson Nuclei

Very Short Answer Type Questions

Question 1.
What are isotopes and isobars?
Answer:
Isotopes :
The nuclei having the same atomic number (Z) but different mass number (A) are called isotopes.
Ex: ₈O¹⁶ , ₈O¹⁷, ₈O¹⁸.

Isobars :
The nuclei having the same mass number (A) but different atomic numbers (Z) are called isobars.
Ex: 14 ¹⁴₆C, ¹⁴₇N.

Question 2.
What are isotones and isomers?
Answer:
Isotones :
The nuclei having same neutron number (N) but different atomic number (Z) are called isotones.
Ex: ₈₀Hg¹⁹⁸, ¹⁹⁷₇₉Au.

Isomers :
Nuclei having the same atomic number (Z) and mass number (A) but different nuclear properties such as radioactive decay and magnetic moments are called isomers.
Ex: ⁸⁰₃₅Br^m, ⁸⁰₃₅Br^g. Here’m’ denotes metastable state and ‘g’ denotes ground state.

Question 3.
What is a.m.u.,? What is its equivalent energy?
Answer:
Atomic mass unit (lu) :
1/12th mass of ¹²₆C atom is taken as atomic mass unit.

Energy equivalent of 1 u = 931.5 MeV.

Question 4.
What will be the ratio of the radii of two nuclei of mass numbers A₁ and A₂?
Answer:
We know the radius of the nucleus
R = R₀ A^1/3

Question 5.
Natural radioactive nuclei are mostly nuclei of high mass number, why?
Answer:
As the atomic number increases coulombian repulsive force increases in the nucleus and hence the stability of the nucleus decreases.

That is why the nuclei after lead are unstable and they exhibit natural radioactivity.

Question 6.
Does the ratio of neutrons to protons in a nucleus increase, decrease or remain the same after the emission of an a – particle?
Answer:
α – particle means Helium nucleus (₂He⁴).

If the nucleus emits α -particle, it loses 2 protons and 2 neutrons. But in the nuclei of radio active elements number of neutrons is greater than the number of protons.

When neutrons number and protons number decreases equally, their ratio increases.

Question 7.
A nucleus contains no electrons but can emit them. How?
Answer:
Natural radioactive elements undergo β – decay. Then a neutron loses one electron and converts into proton.

This electron is ejected out with high velocity called β – ray. The proton remains inside the nucleus.

Question 8.
What are the units and dimensions of the disintegration constant?
Answer:
Since \(\frac{N}{N_0}\) = e^λt . λt has no unit and no
dimensions. So unit of λ = s^-1
Dimensional formula λ = T^-1

Question 9.
Why do all electrons emitted during β^– – decay not have the same energy?
Answer:
In negative beta decay (β^–) emission of electron is accompanied by a neutrino. These neutrinos have very small mass cempared to electron and some kinetic energy. Due to this neutrino energy of electrons liberated in β^– decay is not constant.

Question 10.
Neutrons are the best projectiles to produce nuclear reactions. Why?
Answer:
Neutron is an uncharged particle so it is not deflected by electric and magnetic fields and has high penetrating power. So the neutron required lesser energy than a positive charged particle for producing nuclear reactions. Hence neutron is the best projectile for producing nuclear reactions.

Question 11.
Neutrons cannot produce ionization. Why?
Answer:
Since neutron does not posses any charge, its ionising power is very less when compared to α and β rays.

Question 12.
What are delayed neutrons?
Answer:
The neutrons which are liberated over a period of time after the fission process has taken place are called delayed neutrons.

They play an important role in the nuclear reactor.

Question 13.
What are thermal neutrons? What is their importance?
Answer:
Slow neutrons are called thermal neutrons. Their energy is 0.025 eV. They produce nuclear fission.

Question 14.
What is the value of neutron multiplication factor in a controlled reaction and in an uncontrolled chain reaction?
Answer:
In controlled chain reaction K = 1.
In uncontrolled chain reaction K > 1.

Question 15.
What is the role of controlling rods in a nuclear reactor?
Answer:
They can control chain reaction by absorbing neutrons in nuclear reactor.

Question 16.
Why are nuclear fusion reactions called thermo nuclear reactions?
Answer:
As nuclear fusion reactions occur at very high temperature of the order of 10⁷K, the fusion reactions are known as thermonuclear reactions.

Question 17.
Define Becquerel and Curie.
Answer:
Becquerel (Bq) :
It is a unit to measure radioactivity of a substance. If a radioactive substance undergoes one disintegration or decay per second then it is called Becquerel.

Curie :
It is a unit to measure radioactivity of a substance. If a radioactive substance undergoes 3.7 × 10¹⁰ decays per second the radioactivity of that substance is called curie.
1 Curie = 3.7 × 10¹⁰ Bq (Becquerel)

Question 18.
What is a chain reaction?
Answer:

1. Chain reaction : If a fission reaction is self-maintained due to the neutrons released in that reaction then it is called chain reaction.
2. For chain reaction to takes place (1) At- least one external neutron is necessary 2) neutron multiplication factor K ≥ 1.
3. Initial mass of uranium must be greater than critical mass.

Question 19.
What is the function of moderator in a nuclear reactor?
Answer:
The function of moderator in a nuclear reactor is, to slow down the neutrons, thus neutrons will participate actively in fission reaction. It decreases the speed of neutrons from 2 MeV to 0.025 eV in the nuclear reactor. A good moderator does not absorb the neutrons.

Question 20.
What is the energy released in the fusion of four protons to form a helium nucleus?
Answer:
Energy released due to fusion of four protons is 26.7 MeV.

Short Answer Questions

Question 1.
Why is the density of the nucleus more than that of the atom? Show that the density of nuclear matter is same for all nuclei.
Answer:
a) In an atom nearly 99.9% of mass is concentrated in a very small volume called nucleus. Volume of nucleus is 10^-12 times less than volume of atom. From above explanation density of nucleus is clearly more than density of atom.

b) Density = ρ = mass / volume. But mass of nucleus m = A.m_p.

The above equation is independent of mass number of nucleus A. So density of nuclear matter is same for all nuclei.

Question 2.
Write a short note on the discovery of neutron.
Answer:
Chadwick observed emission of neutral radiation when beryllium nuclei were bombarded with alpha particles.

This neutral radiation when passed through lighter elements like helium, CO₂ and nitrogen knock out a proton.

If the particle is a photon, then its energy must be for higher than the α – particle participating in the reaction.

The energy of neutral particle and also that of a proton released when that neutral particle passes through the lighter element gave some energy discrepancy.

To explain this energy discrepancy Chadwick proposed that the neutral particle is not photon. But a new particle with its mass equal to that of proton and he called it neutron.

Mass of neutron is m_n = 1.00866 u.

In this way Chadwick discovered Neutron.

Question 3.
What are the properties of a neutron?
Answer:
Properties of a neutron :

1. Neutron is a chargeless particle and its mass is almost equal to mass of proton.
2. A free neutron is unstable when it is out side the nucleus. Its mean life period is 1000 sec.
3. Inside nucleus neutron is stable.
4. Number of neutrons in an atom is (A – Z) where A is mass number and Z is atomic number.

Question 4.
What are nuclear forces? Write their pro-perties. .
Answer:
Nuclear forces :
Forces between nucleons present inside the nucleus are called nuclear forces. Properties of nuclear forces are

1. A nuclear force is mych stronger than the coulomb force and the gravitational force.
2. Nuclear force between two nucleons are distance dependent.
3. From potential energy graph of a pair of nucleons these forces are found to be attractive forces when separation between nucleons is 0.8 Fermi or more. These forces are found to be repulsive forces when separation between nucleons is less than 0.8 Fermi.
4. Nuclear forces are saturated forces.
5. Nuclear forces are independent on charge. So nuclear force between proton-proton, proton – neutron and neutron – neutron are equal.

Question 5.
For greater stability, a nucleus should have greater value of binding energy per nucleon. Why?
Answer:
When a graph is plotted between binding energy per nucleon (E_bn) and mass number (A) for different elements it is called
E_bn – A graPh

Salient features of the graphs :
i) The binding energy per nucleon (E_bn) is constant in mass number range of 30 to 170 these elements are found to be more stable. E_bn value is maximum at 8.75 MeV / nucleon for Iron A = 56 which is highly stable.

ii) For heavy nuclei (A > 170) Binding energy per nucleon gradually decreases with increasing mass number.
Ex : Uranium has low binding energy per nucleon of 7.6 MeV. To obtain greater stability under suitable conditions it always tries to break up into two intermediate masses.

For E_bn Vs mass number A graph for region A > 30 to A < 170 is almost same we cannot break easily in two separate nuclei.

Hence atoms with high E_bn are more stable.

Question 6.
Explain α – decay.
Answer:
Alpha decay :
In α – decay ⁴₂He nuclie is emitted from given radioactive substance. Mass number of product nucleons (called daughter nucleus) is decreased by Four units and Atomic number is decreased by two units. Equation of α – decay is

Disintegration energy (OR) Q – value :
The Q – value of a nuclear reaction is the difference between the initial mass energy and total mass-energy of decay products. For α – decay Q value is given by Q = (m_x – m_y – m_He)c².

Question 7.
Explain β – decay.
Answer:
Beta decay (β) :
In Beta decay an electron (or) a positron is liberated from given radioactive substance.

Positive beta decay (β⁺) : In this decay a positron (e⁺) and a neutrino (v) are liberated from radioactive substance.
Ex: ²²₁₁Na → ²²₁₀Ne + e⁺ + v

In + Ve beta decay a proton looses positron and converts into neutron.
⇒ p → n + e⁺ + ν

Negative beta decay (β^–) :
In this decay an electron (e^–) and an antineutrino (\(\overline{\mathrm{ν}}\))are liberated.

In – Ve beta decay a neutron loses electron and converted into proton i.e.,
n → p + e“ + \(\overline{\mathrm{ν}}\)

Question 8.
Explain γ – decay.
Answer:
Nucleus also has discrete energy levels like that of an atom. The energy difference bet-ween these energy levels is in the order of MeV. They are called ground state and exi-ted states.

When a nucleon is in an excited state it will spontaneously return ground state.

While returning to ground state the nucleons will emit energy photons whose energy is equal to difference of those two energy levels.

Since energy difference is in the order of MeV. The photons emitted are highly energetic. This highly energetic radiation is called gamma(γ) radiation.

Question 9.
Define balf-life period and decay constant for a radioactive substance. Deduce the relation between them.
Answer:
Half-life period (T_½) : It is the time taken for the number of nuclei (N) to become half of initial nuclei (N₀) i.e., N = \(\frac{N_0}{2}\).

Decay constant (λ) :
Let N is the number of nuclie in a sample. The number of nuclei (∆N) undergoing radioactive decay during the time ‘∆t’ is given by \(\frac{\triangle N}{\triangle t}\) ∝ N or \(\frac{\triangle N}{\triangle T}\) = λN.

where λ = disintegration constant (or) decay constant.

Relation between half-life peirod T_½ and decay constant λ :
From definition of halflife period N = \(\frac{N_0}{2}\) ; dt = T_½ …………… (1)
But N (t) = N₀ e^-λt ………….. (2) i:e., Number of nuclei after a time ‘t’
From above equation
T_(½) = \(\frac{log 2}{\lambda}=\frac{0.693}{\lambda}\)

Question 10.
Define average life of a radioactive substance. Obtain the relation between decay constant and average life.
Answer:
Average life time :
In a radioactive substance, some nuclei may live for a long time and some nuclei may live for a short time. So we are using average life time τ.

Relation between decay constant and average life time:

When integrated with in the limits o to ∞
⇒ τ = \(\frac{1}{\lambda}\).

Question 11.
Deduce the relation between half-life and average life of a radioactive substance.
Answer:
1) Half-life period (T_½) :
The half-life period of a radioactive nuclide is the time taken for the number of nuclei (N) to become half of initial nuclei (N₀) i.e., N = \(\frac{N_0}{2}\).

2) Average life time :
In a radioactive substance, some nuclei may live for a long time and some nuclei may live for a short time. So we are using average life time τ.

Relation between half-life period and Average life period :
half-life period τ_½ =\(\frac{log 2}{\lambda}\) …………. (1)
But from average life period τ = \(\frac{1}{\lambda}\) ….. (2)
From equations (1) & (2)
∴ τ_½ = t log²_e

Question 12.
What is nuclear fission? Give an example to illustrate it.
Answer:
Nuclear fission:
It is a nuclear reaction in which a heavy nucleus is divided into smaller nuclei along with some energy.

Explanation:
When uranium isotope ²³⁵₉₂U is bombarded with a neutron it will break up into two intermediate mass nuclei.

The atomic number of products is not constant it may vary from 35 to 57.

The fragments produced are radioactive nuclei. They will emit β – particles to achieve stable end products.

Energy liberated in this process is in the form of kinetic energy of fragments and neutrons. Later it is transferred into surroundings in the form of heat energy.

Question 13.
What is nuclear fusion? Write the Conditions for nuclear fusion to occur.
Answer:
Fusion :
The process of combining lighter nuclei to form a heavy nucleus is called “fusion reaction” (or) “nuclear fission”.

Conditions for fusion to occur :

1. For fusion to take place the two nuclie must come close enough so that nuclear attractive short range force is able to effect them.
2. Since protons have positive charge on them coulomb repulsive forces will come into account. These forces will develop nearly a potential barrier of 400 keV.
3. Fusion will be achieved if temperature is raised to nearly 108 K. So that protons will overcome coulomb repulsive forces. At this temperature the particles have enough kinetic energy to overcome coulomb repulsive force.

Question 14.
Distinguish between nuclear fission and nuclear fusion. [TS June ’15]
Answer:

Question 15.
Explain the terms ‘chain reaction’ and ‘multiplication factor’. How is a chain reaction sustained?
Answer:
1) Chain reaction :
If a fission reaction is self maintained due to the neutrons released in that reaction, then it is called “chain reaction”.

2) Multiplication factor K :
The ratio of number of fissions produced by neutrons of present generation to the number of fissions produced in preceding generation is called “multiplication factor”.

3) Condition to sustain chain reaction :
For chain reaction to takes place

1. Atleast one external neutron is necessary.
2. Neutron multiplication factor K ≥ 1.
3. Initial mass of uranium must be greater than critical mass.

Long Answer Questions

Question 1.
Define mass defect and binding energy. How does binding energy per nucleon vary with mass number? What is its significance?
Answer:
Mass defect :
The difference in mass of nucleus and its constituents is known as mass defect. In every nucleus the theoretical mass (Mt) is always less than practical mass (M).

Mass defect ∆m = [Zm_p + (A – Z) m_n] – M

Binding energy :
The energy released while forming a nucleus is called Binding energy E_b. Binding energy E_b = ∆mc².

When a certain number of protons and neutrons are brought together to form a nucleus then certain amount of energy E_b is released.

To divide a nucleus into its constituents, we have to supply an amount of energy equals to E_b from outside.

Binding energy per nucleon :
The ratio of Binding energy E_b to mass number ‘A’ of nucleus is cated’Binding energy per nucleon”.

Binding energy per nucleon E_bn = \(\frac{E_b}{A}\).

Binding energy per nucleon (E_bn) – Mass number (A) graphs :
When a graph is plotted between binding energy per nucleon (E_bn) and mass number (A) for different elements it is called “E_bn -A graph”.

Salient features of the graphs:

1. The binding energy per nucleon (E_bn) is almost constant within mass number range of 30 to 170.
2. For mass number A < 30 Binding energy per nucleon is less it gradually increases with increasing of mass number.
   This region suggested that when lighter nuclei are fused to form large nucleus then they release energy (Fusion process).
3. For heavy nuclei(where A > 170) Binding energy per nucleon gradually decreases with increasing mass number (A).

This region suggested that when larger nuclei are divided into small nuclei then energy is released (Fission process).

Question 2.
What is radioactivity? State the law of radioactive decay. Show that radioactive decay is exponential in nature. [TS May 18. 16; Mar. 16]
Answer:
Radioactive decay :
The spontaneous disintegration of unstable nucleus is referred as “radioactivity or radioactive decay”.

When a nucleus undergoes radioactive decay three types of radioactive decay takes place.

1. α – decay : In this process ⁴₂He nuclei are emitted.
2. β – deay : In this process electrons or positrons are emitted.
3. γ – decay : In this process high energy photons (E.M. Waves) are liberated.

Law of radioactive decay :
Let N is the number of nuclie in a sample. The number of nuclie (∆N) undergoing radioactive decay during the time ‘∆t’ is given by
\(\frac{\triangle N}{\triangle t}\) ∝ N or \(\frac{\triangle N}{\triangle t}\) = λN

Where λ is disintegration constant or decay constant.

Decay rate (R) (OR) activity :
The total decay rate of a sample is the number of nuclei disintegrating per unit time.
∴ Total decay rate R = – \(\frac{dN}{dt}\) (OR)
R = R₀ e^-λt (or) R = λN (activity)

Total decay rate is also called activity. Radioactive decay is exponential because the total decay rate R = R₀ e^-λt Where R0 is a constant.
∴ R ∝ e^-λt Here e-W is exponential function whose value decreases with time.

Hence total radioactive decay of a substance decreases exponentially.

Question 3.
Explain the principle and working of a nuclear reactor with the help of a labelled diagram. [TS Mar. 17, 15, AP Mar. ’17, ’16, ’15, ’14; May 18, 16, 14; AP & TS Mar. 19, 18; May 17; AP June 15]
Answer:
Principle :
A nuclear reactor works on the principle of “sustained and controlled chain reaction”.

The labelled diagram of nuclear reactor is as shown. The important parts of nuclear reactor are

1) Core :
The core of the reactor is the site of nuclear fission. Generally it is made with graphite bricks. Core contains fuel elements in suitably fabricated form.

2) Fuel :
Generally used fuel is enriched uranium which contain ²³⁵₉₂U at high conentration than in natural uranium. Fuel is responsible for fission reaction in reactor.

3) Reflector :
Generally inner part of core is provided with some reflecting material which prevents leakage of neutrons from core.

4) Coolant :
The purpose of coolant is to remove heat energy produced in reactor, generally water is used as a coolant.

5) Moderator :
Core is filled with Heavy water. It is a good moderator. Purpose of moderator is to slow down the neutrons. Slow neutrons will effectively participate in fission reaction.

6) Control rods :
Purpose of control rods is to reduce number of neutrons inside the core. Generally control rods are made with neutron absorbing material like boron or cadmium.

Radiation shield :
The whole assembly of core is shielded with suitable material which prevents leakage of radioactive radiation from core.

Working :
Due to fission reaction energy is released in the core. It is transferred to an outside tank by means of coolant. As a result water in the tank is heated and steam is produced. This steam is used to run a turbine and power is produced. Power produced in this method is called atomic power.

Question 4.
Explain the source of stellar energy. Explain the carbon-nitrogen cycle, proton-proton cycle occurring in stars. [TS June ’15]
Answer:
The source of stellar energy is nuclear fusion reaction, for which hydrogen is the fuel.

Energy from Sun and Stars :
Sun and Stars have been radiating huge amounts of energy by nuclear fusion reactions taking place in their core, where the temperature is of the order 10⁷ K. More scientists proposed two types of cyclic processes for the source of energy in the Sun & Stars. They are :

Carbon – Nitrogen Cycle :
Carbon – Nitrogen cycle is one of the most important nuclear reactions for the production of solar energy by fusion.

The entire cycle can be summed up as,
4₁H¹ → ₂He⁴ + 2 _{+ 1}e⁰ + 3γ + 2υ + 26.70MeV

The energy released during this process is 26.70 MeV.

Proton-Proton Cycle : [TS June ’15]
At higher temperature, the thermal energy of the protons is sufficient to form a deuteron and a positron. The deuteron then combines with another proton to form higher nuclei of helium ³₂He. Two such helium nuclei combine with another proton releasing a total amount of energy 25.71 MeV. The nuclear fusion reactions are given below.
₁H¹ + ₁H¹ → ₁H² + ₊₁e⁰ + υ + 0.42MeV ………. (1)
e⁺ + e^– → γ + γ + 1.02MeV …………. (2)
₁H² + ₁H² → ₂He³ + γ + 5.49MeV ………. (3)
₂He³ + ₂He³ → ₂He⁴ + 2 ₁H¹ + energy 12.86 MeV ………….. (4)

For this equation to takes place first three equations must occur twice.

The nef result of the above reactions is 4 ₁H¹ → ₂He⁴ + 2 ₊₁e⁰ + 2γ + 2υ + 26.70 MeV

The energy released during this process is 26.70 MeV.

Problems

Question 1.
Show that the density of a nucleus does not depend upon its mass number (density is independent of mass).
Answer:
Volume of nucleus

But volume V ac A (mass number )
Density of nucleus matter

The above expression is independent of mass number ‘A’. Hence density of nuclear matter is independent of mass number of nucleus.

Question 2.
Compare the radii of the nuclei of mass numbers 27 and 64.
Answer:
Ratio of radii of nuclie is

Question 3.
The radius of the oxygen nucleus ¹⁶₈O is 2.8 × 10^-15m. Find the radius of lead nucleus ²⁰⁵₈₂Pb.
Answer:
Given, Radius of the oxygen nucleus R_o = 2.8 × 10^-15 m ;
Mass number of oxygen, A₀ = 16 ;
Mass number of lead = A_pb = 205 ; Radius of the lead nucleus R_pb = ?
Radius of nucleus

Question 4.
Find the binding energy of ⁵⁶₂₆Fe. Atomic mass of Fe is 55.9349 u and that of Hydrogen is 1.00783u and mass of neutrons is 1.00876 u.
Answer:
Mass of Hydrogen atom M_H = 1.00783u;
Mass of neutron m_n = 1.00867u
Mass of Iron atom M₁ = 55.9349u
Atomic number Z = 26;
Mass number A = 56;
Mass defect ∆m = [Zm_H + (A – Z)m_n – M_I]
∆m = [26 × 1.00783 + (56 – 26) 1.00867] – 55.9349 u
∆m = 0.52878 u
Binding energy = ∆mc² = 0.52878 × (3 × 10⁸)²
∴ B.E. = 0.52878 × 9 × 10¹⁶ or 0.52878 × 931.5 MeV
∵ [lu × C²] = 931.5 MeV energy
∴ B.E. =492.55
Binding energy per nucleon BE/ n = \(\frac{492.55}{56}\)
= 8:79 MeV

Question 5.
How much energy is required to separate the typical middle mass nucleus ¹²⁰₅₀Sn k its constituent nucleons? (Mass of ¹²⁰₅₀Sn = 119.902199 u, mass of proton = 1.007825 u and mass of neutron = 1.008665 u)
Answer:
Mass of proton m_p = 1.007825 amu ;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of Sn, Z = 50 ;
Mass number of Sn, A = 120 ;
Mass of nucleus of Sn atom = 119.902199 amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z) m_n – M_N]
= [ (50) (1.007825) + (120 – 50) (1.008665) – 119.902199]
= (50 × 1.007825 + 70 × 1.008665 -119.902199)
= (50.39125 + 70.60655 – 119.902199)
∆m = [120.9978 – 119.902199] = 1.095601 amu

(ii) Energy required to separate the nucleons = Binding energy of the nucleus
B.E = ∆mc² (∵ lamu × c² = 931.5MeV)
= ∆m × 931.5MeV = 1.095601 × 931.5 MeV
= 1021 MeV

Question 6.
Calculate the binding energy of an α – particle. Given that mass of proton – 1.0073u, mass of neutron = 1.0087u, and mass of α – particle = 4.0015u.
Answer:
An α – particle is nothing but helium nucleus ⁴₂He.
It contains 2 protons, 2 neutrons with a mass number A = 4.
Mass of proton m_p = 1.0073 amu ;
Mass of neutron m_n = 1.0087 amu ;
Atomic number of helium Z = 2 ;
Mass number of helium A = 4 ;
Mass of helium atom M_N = 4.0015 amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z)m_n – M_N]
= [(2) (1.0073) + (4 – 2) (1.0087) – 4.00260]
= (2 × 1.0073 + 2 × 1.0087-4.00260)
= (2.0146 + 2.0174)-4.0015 Am = [4.032 – 4.0015] = 0.0305 amu

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ lamu × c² = 931.5MeV)
= ∆m × 931.5 MeV = 0.0305 × 931.5 MeV
= 28.41 MeV

Question 7.
Find the energy required to split ¹⁶₈O nucleus into four α – particles. The mass of an α – particle is 4.002603u and that of oxygen is 15.994915u.
Answer:
The energy required to split
Q = [ Total mass of the products
– Total mass of the reactants] c²
= [Mass of four ⁴₂He – Mass of ¹⁶₈O] × c²
= [(4 × 4.002603) -15.994915] amu × c²
= [16.010412 – 15.994915] amu × c²
= (0.015497) 931.5 MeV = 14.44 MeV.

Question 8.
Calculate the binding energy per nucleon of ³⁵₁₇Cl nucleus. Given that mass of ³⁵₁₇Cl nucleus = 34.9800u, mass of proton = 1.007825u, mass of neutron = 1.008665 u and lu is equivalent to 931 MeV.
Answer:
Given, Mass of proton m_p = 1.007825 amu;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of ³⁵₁₇Cl, Z = 17 ;
Mass number of ³⁵₁₇Cl, A = 35 ;
Mass of nucleus of ³⁵₁₇Cl atom =34.98 amu.

(i) Mass defect ∆m = [Zm_p + (A – Z)m_n – M_N]
= [(17) (1.007825) + (35 – 17) (1.008665) – 34.98]
= (17 × 1.007825 + 18 × 1.008665 – 34.98)
= (17.13303 + 18.15597 -34.98)
∆m = [35.289 – 34.98] = 0.3089

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ 1amu × c² = 931.5 MeV)
B.E = ∆m × 931.5 MeV = 0.3089×931.5 MeV
= 287.83 MeV

(iii) Binding energy per nucleon of Cl = \(\frac{B.E}{A}\)
= \(\frac{287.83}{35}\) = 8.22 MeV

Question 9.
Calculate the binding energy per nucleon of ⁴⁰₂₀Ca. Given that mass of ⁴⁰₂₀Ca nucleus = 39.962589 u, mass of a proton = 1.007825 u ; mass of neutron = 1.008665 u and 1 u is equivalent to 931 MeV.
Answer:
Given, Mass of proton m_p = 1.007825 amu;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of ⁴⁰₂₀Ca Z = 20 ;
Mass number of ⁴⁰₂₀Ca A = 40 ;
Mass of nucleus of ⁴⁰₂₀Ca atom = 39.962589 amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z)m_n – M_N]
= [ (20) (1.007825) + (40 – 20) (1.008665) – 39.962589]
= (20 × 1.007825 + 20 × 1.008665 – 39.962589)
= (20.1565 + 20.1733 – 39.962589)
∆m = [ 40.3298 – 39.962589 ] = 0.3672 amu

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ lamu × c² = 931.5 MeV)
∴ B E = ∆m × 931.5MeV
= 0.3672 × 931.5 MeV = 342.06 MeV

(iii) Binding energy per nucleon of Ca = \(\frac{B.E}{A}\)
= \(\frac{342.06}{40}\) = 8.55 MeV

Question 10.
Calculate(i) maw defect, (ii) binding energy and (iii) the binding energy per nucleon of ¹²₆C nucleus. Nuclear mass of ¹²₆C 12.000000 u; maw of proton = 1.007825 u and maw of neutron = 1.008665 u.
Answer:
Given, Mass of proton m_p = 1.007825 amu;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of ¹²₆C, Z = 6 ;
Mass number of ¹²₆C, A = 12;
Mass of nucleus of ¹²₆C atom = 12.00amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z)m_n – M_N]
= [6(1.007825) + (12 – 6) (1.008665) – 12.00]
= (6 × 1.007825 + 6 × 1.008665 – 12.00)
= (6.04695 + 6.05199 – 12.00)
∆m = [12.09894 – 12.00] = 0.09894 amu

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ lamu × c² = 931.5 MeV)
∴ B.E = ∆m × 931.5 MeV
= 0.09895 × 931.5 MeV = 92.16 MeV

(iii) Binding energy per nucleon of carbon =
\(\frac{B.E}{A}=\frac{92.16}{12}\) = 7.86 MeV

Question 11.
The binding energies per nucleon for deuterium and helium are 1.1 MeV and 7.0 MeV respectively. What energy in joules will be liberated when 10v deuterons take part in the reaction.
Answer:
Given, Binding energies per nucleon for deuterium (\(\frac{B.E}{A}\))_D = 1.1 MeV
Mass number of deuterium A = 2
Binding energy of deuterium
B.E = (\(\frac{B.E}{A}\))_D × A = 1.1 × 2 = 2.2 MeV
Binding energies per nucleon for helium (\(\frac{B.E}{A}\))_He = 7.0 MeV
Mass number of helium A = 4
Binding energy of helium
B.E = (\(\frac{B.E}{A}\))_D × A = 7 × 4 = 28MeV
We know, ₁H² + ₁H² → ₂He⁴
Energy released = B.E. of 10⁶ deuterons
– B.E. of \(\frac{1}{2}\) × 10⁶ Helium atoms
Binding energy = 2.2 × 10⁶ – \(\frac{1}{2}\) × 10⁶ × 28
= 10⁶ (2.2 – 14) = – 11.8 × 10⁶ MeV
= -11.8 × 10⁶ × 1.6 × 10^-31J
= -18.88 × 10^-7J
(- ve sign indicates that energy is released)
∴ Energy released = 18.88 × 10^-7J

Question 12.
Bombardment of lithium with protons gives rise to the following reaction :

Find the Q – value of the reaction. The atomic masses of lithium, proton, and helium are 7.016u, 1.008u, and 4.004u respectively.
Answer:
Given, Mass of Lithium = 7.016 amu ;
Mass of Proton = 1.008 amu ;
Mass of Helium = 4.004 amu ;
1 a.m.u = 931.5 MeV energy
Q = [Total mass of the reactants – total mass of the products] c²
= [mass of Lithium + mass of Proton – ( 2 × mass of Helium)] 931.5 MeV
= [ 7.016 + 1.008 – 2 ( 4.004 ) ] 931.5 MeV
= [8.024 – 8.008] 931.5. MeV
∴ Energy Q. = 0.016 × 931.5 = 14.904 MeV

Question 13.
The half-life of radium is 1600 years. How much time does 1 g of radium take to reduce to 0.125 g. [TS May, ’18, ’16, Mar. ’16]
Answer:
1g become \(\frac{1}{2}\) g after one half-life period and it become \(\frac{1}{4}\) g after 2 half-life periods and \(\frac{1}{8}\) after 3 half-life periods.
But \(\frac{1}{8}\) g = 0.125g.
So number of half-life periods, n = 3.
Time taken = n x half-life period
= 3 × 1600 = 4800 years.

Question 14.
Plutonium decays with a half-life of 24.000 years. If plutonium is stored for 72,000 years, what fraction of it remains?
Answer:
Given, Half-life of Plutonium = 24,000 years;
The duration of the time = 72,000 years
Initial mass = x g ; Final mass = mx g

Fraction of Plutonium that remains

Question 15.
A certain substance decays to 1/232 of its initial activity in 25 days. Calculate its half-life.
Answer:
Given, Fraction of substance decays

Question 16.
The half-life period of a radioactive sub¬stance is 20 days. What is the time taken for 7 / 8th of its original mass to disintegrate?
Answer:
Given, Half-life period = 20 days

∴ Time taken to disintegrate
= n × Half-life time = 3 × 20 = 60 days

Question 17.
How many disintegration per second will occur in one gram of ²³⁸₉₂U if its half – life against ∝ – decay is 1.42 × 10¹⁷ s?
Answer:
Given, Half-life period T = 1.42 × 10¹⁷s.;
mass of uranium m = 238

Number of disintegrations / sec = nλ

Question 18.
The half – life of a radioactive substance is 100 years. Calculate in how many years die activity will decay to 1/10th of its initial value.
Answer:
Given, Half – life period = 100 years

∴ Time taken to disintegrate
= n × Half-life time = 3 × 20 = 60 days

Question 19.
One gram of a radium is reduced by 2 milligram in 5 years by β – decay. Calculate the half-life of radium.
Answer:
Initial Mass of radium M₀ = 1 gram ;
∴ Mass reduced = 2mg
Final mass of radium M = 1 – 0.002
= 0.998 mg;
Time taken to reduce the mass t = 5 years
But number of atoms N α mass of the sample

Question 20.
The half-life of a radioactive substance is 5000 years. In how many years, its activity will decay to 0.2 times of its initial value? Give log₁₀ 5 = 0.6990.
Answer:
Half-life period T = 5000 years ;
Activity A = Nλ = 0.2 times initial value
Initial activity A₀ = N₀λ
In radioactivity N = N₀e^-λt

Question 21.
An explosion of atomic bomb releases an energy of 7.6 x 1013 J. If 200 MeV energy is released on fission of one atom calculate CD the number of uranium atoms undergoing fission. 00 the mass of uranium used in the bomb.
Answer:
i) Energy released E = 7.6 × 10¹³J
Energy released per fission = 200 MeV
= 200 × 10⁶ × 1.6 × 10^-19J
= 200 × 1.6 × 10^-13J = 3.2 × 10^-11 J

ii) Number of Uranium atoms participated

Question 22.
If one microgram of ²³⁸₉₂U is completely destroyed in an atom bomb, how much energy will be released? [AP Mar. ’19]
Answer:
Given, Mass of Uranium destroyed = 1
Micro gram = 1 × 10^-6 gr = 10^-9 Kg.
According to Einstein mass energy relation Energy released E = me² = 10^-9 × [ 3 × 10⁸]² (∵ Velocity of light c = 3 x 108 m/s)
∴ Energy released = 9 × 10^-9 × 10¹⁶ = 9 × 10⁷J

Question 23.
Calculate the energy released by fission from 2g of ²³⁸₉₂U in kWh. Given that the energy released per fission is 200 MeV.
Answer:
Given, Mass of Uranium (m) = 2g ;
Energy per fission = 200 MeV
Number of atoms in 2 grams of Uranium

Energy released per fission = 200 MeV
= 200 × 10⁶ × 1.6 × 10^-19J
= 200 × 1.6 × 10^-13 J = 3.2 × 10^-11J

Total Energy released ’Q’ = 5.1256 × 3.2 × 10^-11 = 1640.2 × 10⁸J
But, 1 kWh = 1000 × 60 × 60 = 36 × 10⁵J

Question 24.
200 MeV energy is released when one nucleus of ²³⁸U undergoes fission. Find the number of fissions per second required for producing a power of 1 megawatt.
Answer:
Given, Total power produced = 1 Mega Watt = 10⁶ Watt
Energy per fission = 200 MeV
= 200 × 1.6 × 10^-13 J = 3.2 × 10^-11 J
∴ Number of fissions per second

Question 25.
How much ²³⁸U is consumed in a day in an atomic power house operating at 400 MW, provided the whole of mass ²³⁸U is converted into energy?
Answer:
Power P = 400 MW = 400 × 10⁶ watt;
Time T = 1 day = 86,400 sec.
∴ Energy produced per day
= 400 × 10⁶ × 86400 = 3.456 × 10¹³J
But Energy E = me² × m = E/c²
Mass of uranium consumed

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 6 Integration will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Integration Formulas

→ A function F(x) Is called an anti derivative or indefinite Integral of a function f(x) If \(\frac{d}{d x}\)[F (x)] = f(x).

→ Indefinite Integrals:
Let f(x) be a function. Then the collection of all its anti derivatives is called the indefinite integral of f(x) and it is denoted by ∫f(x) dx.
Thus \(\frac{d}{d x}\) [F(x) + c] = f(x) ⇔ ∫f(x)dx = F(x) + c
where F(x) is the anti derivative and c is the arbitrary constant known as the constant of integration.

→ Standard forms:
∫K dx = Kx + c, K is constant

→ ∫1 dx = x + c

→ ∫xⁿ dx = \(\frac{x^{n+1}}{n+1}\) + c, n ≠ -1

→ ∫x dx = \(\frac{x^2}{2}\) + c

→ ∫√x dx = \(\frac{2}{3}\)x√x + c

→ ∫\(\frac{1}{\sqrt{x}}\)dx = 2√x + c

→ ∫\(\frac{1}{x^2}\)dx = \(\frac{-1}{x}\) + c

→ ∫\(\frac{1}{x}\)dx = log |x| + c

→ ∫e^xdx = e^x + c

→ ∫a^xdx = \(\frac{a^x}{\log a}\) + c

→ ∫sin x dx = – cos x + c

→ ∫cos x dx = sin x + c

→ ∫tan x dx = log|sec x| + c = -log |cos x| + c

→ ∫cot x dx = log|sin x| + c = -log|cosec x| + c

→ ∫sec x dx = log|sec x + tan x| + c = log|tan\(\left(\frac{\pi}{4}+\frac{x}{2}\right)\)| + c

→ ∫cosec x dx = log|cosec x – cot x| + c = log|tan\(\frac{x}{2}\)| + c

→ ∫sec²x dx = tan x + c

→ ∫cosec²x dx = -cot x + c

→ ∫sec x tan x dx = sec x + c

→ ∫cosec x cot x dx = -cosec x + c

→ ∫sin hx dx = cos hx + c

→ ∫cos hx dx = sin hx + c

→ ∫tan hx dx = log|cos hx| + c

→ ∫cot hx dx = log |sin hx| + c

→ ∫sech²x dx = tan hx + c

→ ∫cosech²x dx = -cot hx + c

→ ∫sec hx tan hx dx = -sec hx + c

→ ∫cosec hx cot hx dx = – cosec hx + c

→ ∫\(\frac{1}{\sqrt{1-x^2}}\) dx = sin^-1x + c

→ ∫\(\frac{1}{\sqrt{x^2-1}}\) dx = cosh^-1x + c = log(x + \(\sqrt{x^2-1}\)) + c

→ ∫\(\frac{1}{\sqrt{x^2+1}}\) dx = sin h^-1x + c = log(x + \(\sqrt{x^2+1}\)) + c

→ ∫\(\frac{1}{1+x^2}\)dx = tan^-1 x + c

→ ∫\(\frac{1}{1-x^2}\)dx = \(\frac{1}{2}\)log\(\left|\frac{1+x}{1-x}\right|\) + c

→ ∫\(\frac{1}{x^2-1}\)dx = \(\frac{1}{2}\)log\(\left|\frac{x-1}{x+1}\right|\) + c

→ ∫\(\frac{1}{x \sqrt{x^2-1}}\)dx = sec^-1x + c

→ ∫\(\frac{1}{\sqrt{a^2-x^2}}\)dx = sin^-1\(\left(\frac{x}{a}\right)\) + c

→ \(\frac{1}{a^2+x^2}\)dx = \(\frac{1}{a}\)tan^-1\(\left(\frac{x}{a}\right)\) + c = \(\frac{-1}{a}\)cot^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\frac{1}{\sqrt{a^2+x^2}}\)dx = sinh^-1\(\left(\frac{x}{a}\right)\) + c = log(x + \(\sqrt{a^2+x^2}\)) + c

→ ∫\(\frac{1}{\sqrt{x^2-a^2}}\)dx = cosh^-1\(\left(\frac{x}{a}\right)\) + c = log(x + \(\sqrt{x^2-a^2}\)) + c

→ ∫\(\frac{1}{a^2-x^2}\)dx = \(\frac{1}{2 a}\)log \(\left|\frac{a+x}{a-x}\right|\) + c

→ ∫\(\frac{1}{x^2-a^2}\)dx = \(\frac{1}{2 a}\)log \(\left|\frac{x-a}{x+a}\right|\) + c

→ ∫\(\sqrt{a^2-x^2}\)dx = \(\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2}\)sin^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\sqrt{a^2+x^2}\)dx = \(\frac{x}{2} \sqrt{a^2+x^2}+\frac{a^2}{2}\)sinh^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\sqrt{x^2-a^2}\)dx = \(\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2}\)cosh^-1\(\left(\frac{x}{a}\right)\) + c

→ \(\frac{d}{d x}\)[∫f(x)dx] = f(x)

→ ∫kf(x) dx = k.∫f(x)dx

→ ∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g(x)dx

→ ∫\(\frac{f^{\prime}(x)}{f(x)}\)dx = log|f(x)| + c

→ ∫\(\frac{f^{\prime}(x)}{\sqrt{f(x)}}\)dx = 2\(\sqrt{f(x)}\) + c

→ ∫[f(x)]ⁿ.f'(x)dx = \(\frac{f^{n+1}(x)}{n+1}\) + c, n ≠ -1

→ ∫\(\frac{f^{\prime}(x)}{1+[f(x)]^2}\)dx = tan^-1f(x) + c

→ Evaluation of Integral of various types by using standard results:

→ IntegratIon by parts: If U and V are two functions of x, then
∫UV dx = U∫V dx – ∫[\(\frac{dU}{d x}\)∫Vdx]dx

Extension Rule: ∫UVdx = UV₁ – U’V₂ + U”V₃ – U”’V₄ + ……….. + U where U’, U”, U”’ etc., are the successive derivatives of U and V₁, V₂, V₃ etc., are successive integrals of V.
Note : This rule is very useful if one of the Integrand Is an algebraic function.

→ Formulae:

• ∫e^ax sinbx dx = \(\frac{e^{a x}}{a^2+b^2}\)[a sin bx – b cos bx] + c
• ∫e^ax cos bx dx = \(\frac{e^{a x}}{a^2+b^2}\)[a cos bx – b sin bx] + c
• ∫e^x[f(x) + f'(x)]dx = e^xf(x) + c
• ∫e^-x[f(x) + f'(x)]dx = -e^-xf(x) + c
• ∫e^ax[af(x) + f'(x)]dx = e^axf(x) + c

→ Reduction Formulae:

• If I_n = ∫xⁿe^ax dx then I_n = \(\frac{x^n e^{a x}}{a}-\frac{n}{a}\)I_n-1
• If I_n = ∫sinⁿx dx then I_n = \(\frac{-\sin ^{n-1} x \cos x}{n}+\frac{n-1}{n}\)I_n-2
• If I_n = ∫cosⁿxdx then I_n = \(\frac{\cos ^{n-1} x \sin x}{n}+\frac{n-1}{n}\)I_n-2
• If I_n = ∫tanⁿx dx then I_n = \(\frac{\tan ^{n-1} x}{n-1}\) – I_n-2
• If I_n = ∫cotⁿx dx then I_n = \(\frac{-\cot ^{n-1} x}{n-1}\)I_n-2
• If I_n = ∫secⁿx dx then I_n = \(\frac{\sec ^{n-2} x \tan x}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = ∫cosecⁿx dx then I_n = \(\frac{-{cosec}^{n-2} x \cot x}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = ∫(log x)ⁿ dx then I_n = x(log x)ⁿ – nI_n-1

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Theory of Equations Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Theory of Equations Important Questions Long Answer Type

Question 1.
If the roots of the equation x³ + 3px² + 3qx + r = 0 are in AP then show that 2p³ – 3pq + r = 0. [May ’08]
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
Since the roots are in A.P then they must be of the form a – d, a, a + d.
Now, s₁ = a – d + a + a + d = \(\frac{-3 p}{1}\)
3a = – 3p
a = – p
Since a is a root of x³ + 3px² + 3qx + r = 0 then
(- p)³ + 3p (- p)² + 3q(- p) + r = 0
⇒ – p³ + 3p³ – 3pq + r = 0
⇒ 2p³ – 3pq + r = 0.

Question 2.
If the roots of the equation x³ + 3px² + 3qx + r = 0 are in G.P then show that p³r = q³. [March ‘03]
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
Since the roots are in G.P then they must be of the form \(\frac{a}{r}\), a, ar
Now, s₃ = \(\frac{a}{r}\) . a . ar
= \(\frac{-\mathrm{r}}{1}\) = – r
⇒ a³ = – r
⇒ a = (- r)^1/3
Since a is a root of x³ + 3px² + 3qx + r = 0 then
\(\left((-r)^{1 / 3}\right)^3+3 p\left((-r)^{1 / 3}\right)^2+3 q\left((-r)^{1 / 3}\right)\) + r = 0
⇒ – r + 3p (- r)^2/3 + 3q(- r)^1/3 + r = 0
⇒ 3p(- r)^2/3 = – 3q(- r)^1/3
Cubing on both sides,
⇒ p³ (- r)² = – q³(- r)
⇒ p³ r² = q³r
⇒ p³r = q³

Question 3.
If the roots of the equation x³ + 3px² + 3q + r = 0 are in H.P then show that 2q³ = r (3pq – r).
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
The roots of x³ + 3px² + 3qx + r = 0 are in H.P.
The roots of \(\left(\frac{1}{x}\right)^3+3 p\left(\frac{1}{x}\right)^2+3 q\left(\frac{1}{x}\right)\) + r = 0 are in A.p.
\(\frac{1}{x^3}+\frac{3 p}{x^2}+\frac{3 q}{x}\) + r = 0 are in A.P
⇒ 1 + 3px + 3qx² + rx³ = o
⇒ rx³ + 3qx² + 3px + 1 = 0 ……………..(1)
Let the roots of (1) be a – d, a, a + d
s₁ = a – d + a + a + d = \(\frac{-3 q}{r}\)
⇒ 3a = \(\frac{-3 q}{r}\)
a = \(\frac{-q}{r}\)
Since a is a root of (1)
⇒ \(r \cdot \frac{-q^3}{r^3}+3 q \cdot \frac{q^2}{r^2}+3 p \cdot \frac{-q}{r}+1\) = 0
⇒ \(\frac{-q^3}{r^2}+\frac{3 q^3}{r^2}-\frac{3 p q}{r}\) + 1 = 0
⇒ 2q³ = r (3pq – r). +
Hence proved.

Question 4.
Solve 4x³ – 24x² + 23x + 18 = 0, given that the roots of this equation are in arithmetic
progression. [Mar. ’14, May ’06, ’01]
Solution:
Given equation is 4x³ – 24x² + 23x + 18 = 0
Given that the roots of this equation are in A.P.
Since the roots are in A.P, they must be of the form, a – d, a, a + d.
Now, a – d + a + a + d = \(-\frac{-24}{4}\) = 6
⇒ 3a = 6
⇒ a = 2
(a – d) a (a + d) = \(\frac{-18}{4}\)
(a² – d²)a = \(\frac{-9}{2}\)
(4 – d²)2 = \(\frac{-9}{2}\)
4 – d² = \(\frac{-9}{4}\)
d² = 4 + \(\frac{9}{4}\) = \(\frac{25}{4}\)
d = ± \(\frac{5}{2}\)

Case – I:
If a = 2, d = \(\frac{5}{2}\)
The roots of given equation are – \(\frac{-1}{2}\), 2, \(\frac{9}{2}\).

Case-2:
If a = 2, d = \(\frac{-5}{2}\)
The roots of given equation are \(\frac{9}{2}\), 2, \(\frac{-1}{2}\).

Question 5.
Solve x³ – 3x² – 6x + 8 = 0, given that the : roots are in A.P. [March ’07]
Solution:
Given equation is x³ – 3x² – 6x + 8 = 0
Since, the roots are in A.P., thus they must; be of the form a – d, a, a + d.
Now, a – d + a + a + d = \(\frac{-(-3)}{1}\) = 3
⇒ 3a = 3
⇒ a = 1
⇒ (a – d) a (a + d) = \(\frac{-8}{1}\)
a² – d² = – 8
1 – d² = – 8
d = 9
⇒ d = ±3
Case – 1 : If d = 3; a = 1
The roots of the given equation are; a – d, a, a + d = – 2, 1, 4.

Case – 2: If d = – 3; – a = 1;
The roots of the given equation are (a – d) a, (a + d) = 4, 1, – 2 .

Question 6.
Solve x³ – 7x² + 14x – 8 = 0, given that the roots are in geometric progression. [May ’07]
Solution:
Given equation is x³ – 7x² + 14x – 8 = 0
Given that the roots are in G.P then they may be of the form \(\frac{a}{r}\), a, ar
\(\frac{a}{r}\) + a + ar = a [\(\frac{1}{r}\) + 1 + r] = \(\frac{-(-7)}{1}\)
⇒ a[\(\frac{1}{r}\) + 1 + r] = 7 …………..(1)
\(\frac{a}{r}\) . a . ar = 1
⇒ a³ = 8
⇒ a = 2
(1) ⇒ 2\(\left(\frac{r^2+r+1}{r}\right)\) = 7
⇒ 2r² – 5r + 2 = 0
⇒ 2r² – 4r – r + 2 = 0
⇒ 2r (r – 2) – 1 (r – 2) = 0
⇒ (2r – 1) (r – 2) = 0
⇒ r = \(\frac{1}{2}\) (or) r = 2
Case – 1:
If a = 2, r = \(\frac{1}{2}\)
The roots of given equation are \(\frac{a}{r}\), a, ar = 4, 2, 1
Case – 2 :
If a = 2, r = 2
The roots of given equation are \(\frac{a}{r}\), a, ar = 1, 2, 4.

Question 7.
Solve the equation 15x³ – 23x² + 9x – 1 = 0, the roots being in H.P. [May ’02]
Solution:
Giveti equation is 15x³ – 23x² + 9x – 1 = 0
The roots of 15x³ – 23x² + 9x – 1 = 0 are in H.P
The roots of
\(15 \cdot \frac{1}{x^3}-23 \cdot \frac{1}{x^2}+9 \cdot \frac{1}{x}-1\) = 0 are in A.P.
15 – 23x + 9x² – x³ = 0
⇒ x³ – 9x² + 23x – 15 = 0
Let the roots be a – d, a, a + d
a – d + a + a + d = \(\frac{-(-9)}{1}\) = 9
⇒ 3a = 9
⇒ a = 3
(a – d) a (a + d) = \(\frac{-(-15)}{1}\) = 15
⇒ a(a² – d²) = 15
⇒ 3(9 – d²) = 15
9 – d² = 5
d² = 4
d = 21
The roots of x³ – 9x² + 23x – 15 = 0 are a – d, a, a + d =3 – 2, 3, 3 + 2 = 1, 3, 5
The roots of 15x³ – 23x² + 9x – 1 = 0 are \(\frac{1}{1}, \frac{1}{3}, \frac{1}{5}\) = 1, \(\frac{1}{3}, \frac{1}{5}\).

Question 8.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots. [May ’11, March ‘05] [AP – Mar.2019]
Solution:
Given that one root is equal to half of the sum of the remaining roots.
Given equation is 18x³ + 81x² + 121x + 60 = 0
i.e., the roots are in A.P.
Let a – d, a, a + d be the roots of the given equation.
∴ a – d + a + a + d = \(\frac{-81}{18}\)
3a = \(\frac{-81}{18}\)
a = \(\frac{-3}{2}\)
(a – d) a (a + d) = \(\frac{-60}{18}\)
a(a – d) = \(\frac{-81}{18}\)
\(\frac{-3}{2}\left(\frac{9}{4}-d^2\right)=\frac{-60}{18}\)
d² = \(\frac{9}{4}-\frac{20}{9}=\frac{81-80}{36}=\frac{1}{36}\)
d = \(\frac{1}{6}\)
∴ The roots of the given equation are a – d, a, a + d = \(\frac{-3}{2}-\frac{1}{6}, \frac{-3}{2}, \frac{-3}{2}+\frac{1}{6}\)
= \(\frac{-5}{3}, \frac{-3}{2}, \frac{-4}{3}\)

Question 9.
Given that one root of 2x³ + 3x² – 8x + 3 = 0 is double the other root, find the roots of the equation. [May ’03]
Solution:
Given equation is 2x³ + 3x² – 8x + 3 = 0
Now, α + β + γ = \(\frac{-3}{2}\) …………..(1)
αβ + βγ + γα = \(\frac{-8}{2}\) = – 4 ……………(2)
αβγ = \(\frac{-3}{2}\) ……………..(3)
Given one root is double the other then
α = 2β
(1) ⇒ 2β + β + γ = \(\frac{-3}{2}\)
⇒ 3β + γ = \(\frac{-3}{2}\)
⇒ γ = \(\frac{-3}{2}\) – 3β …………….(4)
(2) ⇒ 2β . β + βγ + γ . 2β = – 4
2β² + βγ + 2βγ = – 4
2β² + 3βγ = – 4 ……………..(5)
From (4) & (5)
2β² + 3β(\(\frac{-3}{2}\) – 3β) = – 4
2β² – \(\frac{9 \beta}{2}\) – 9β²=
⇒ \(\frac{4 \beta^2-9 \beta-18 \beta^2}{2}\) = – 4
⇒ – 14β² – 9β = – 8
⇒ 14β² + 9β – 8 = 0
⇒ 14β² + 16β – 7β – 8 = 0
⇒ (2β – 1) (7β + 8) = 0
⇒ β = \(\frac{-8}{7}\) (or) β = \(\frac{1}{2}\)
β = \(\frac{-8}{7}\) does not satisfy the given equation.
β = \(\frac{1}{2}\)
⇒ α = 2 . \(\frac{1}{2}\) = 1
Substitute the value of β in equation (4)
⇒ γ = \(\frac{-3}{2}\) – 3 . \(\frac{1}{2}\)
= \(\frac{-3-3}{2}=\frac{-6}{2}\) = – 3.
∴ The roots of the given equation are 1, \(\frac{1}{2}\), – 3.

Question 10.
Solve x⁴ + x³ – 16x² – 4x + 48 = 0, given that the product of two of the roots is 6. [TS – Mar. 2019; May ’12. ’09]
Solution:
Given equation is x⁴ + x³ – 16x² – 4x + 48 = 0
Let α, β, γ, δ are the roots of the given equation.
Then αβγδ = \(\frac{48}{1}\) = 48
Given that the product of the two roots of the given equation is 6.
Suppose that αβ = 6
Now, 6γδ = 48
γδ = 8
Let α + β = p, γ + δ = q
The quadratic equation whose roots are α, β is
x² – x(α + β) + αβ = 0
x² – px + 6 = 0 ………….(1)
The quadratic equation whose roots are γ, δ is
x² – x (γ + δ) + γδ = 0
⇒ x² – qx + 8 = 0 ……………(2)
∴ x⁴ + x³ – 16x² – 4x + 48
= (x² – px + 6) (x² – qx + 8)
= x⁴ – qx³ + 8x² – px³ + pqx² – 8px + 6x² – 6qx + 48
= x⁴ + (- p – q)x³ + (pq+ 14)x² + (- 8p – 6q) x + 48
Now comparing coefficients of x³ on both sides, we get
⇒ – p – q = 1
⇒ p + q = – 1 ………………(3)
Now comparing coefficients of x on both sides, we get
– 8p – 6q = – 4
⇒ 4p + 3q = 2 ……………….(4)
Solve (3) and (4);

⇒ p = \(\frac{-5}{-1}\)
⇒ q = \(\frac{6}{-1}\)
⇒ p = 5, q = – 6
Substitute ‘p’ value in (1),
x² – 5x + 6 = 0
⇒ x² – 3x – 2x + 6 = 0
⇒ x (x – 3) – 2 (x – 3) = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, x = 3
Substitute ‘q’ value in (2),
(2) ⇒ x² + 6x + 8 = 0
⇒ x² + 4x . 2x + 8 = 0
⇒ (x + 2) (x +4) = 0
⇒ x = – 4, x = – 2
∴ The roots of given equation are 3, 2, – 4, – 2.

Question 11.
Given that two roots of 4×3+20×2-23x+6=O are equal, find all the roots of the given equation.
Solution:
Given equation is 4x³ + 20x² – 23x + 6 = 0
Let α, β, γ be the roots of given equation.
Then s₁ = α + β + γ = \(\frac{-(20)}{4}\)
⇒ α + β + γ = – 5 …………….(1)
⇒ αβ + βγ + γα = \(\frac{-23}{4}\) ……………(2)
⇒ αβγ = \(\frac{-6}{4}=\frac{-3}{2}\) ………….(3)
Given that two roots are equal
⇒ β = α
(1) ⇒ 2α + γ = – 5
⇒ γ = – 5 – 2α
(2) ⇒ α² + αy + αy = \(\frac{-23}{4}\)
⇒ α² + 2αγ = \(\frac{-23}{4}\)
⇒ α² + α (- 5 – 2α) = \(\frac{-23}{4}\)
⇒ 4 (α² – 10α – 4α²) = – 23
⇒ 4 (- 3α² – 10α) = – 23
⇒ 12α² + 40α – 23 = 0
⇒ 12α² + 46α – 6α – 23 = 0
⇒ 2α (6α + 23) – 1(6α + 23) = 0
⇒ (6α + 23) (2α – 1) = 0
∴ α = \(\frac{-23}{6}\) does not satisfy given equation.
∴ α = \(\frac{1}{2}\)
⇒ β = \(\frac{1}{2}\)
γ = – 5 – 2 . \(\frac{1}{2}\) = – 6
γ = – 6
∴ The roots of the given equation are \(\frac{1}{2}\), \(\frac{1}{2}\), – 6.

Question 12.
Solve x⁴ + 4x³ – 2x² – 12x + 9 = 0, given that it has two pairs of equal roots. [March ’11, ’03]
Solution:
Given equation is x⁴ + 4x³ – 2x² – 12x + 9 = 0
Given that it has two pairs of equal roots then let the roots of the given equation be
α + α + β + β = \(\frac{-4}{1}\)
⇒ 2 (α + β) = – 4
⇒ α + β = – 2
αα + αβ + βα + βα + αβ + β² = \(\frac{-2}{1}\)
α² + 4αβ + β²
(α + β)² + 2αβ = – 2
4 + 2αβ = – 2
2αβ = – 6
αβ = – 3
We know that,
(α – β)² = (α + β)² – 4αβ
= 4 – 4 (- 3)
= 4 + 12 = 16

α – β = 4
α + β = – 2
⇒ 2α = 2
⇒ α = 1

α + β = – 2
1 + β = – 2
β = – 3
∴ The roots of the given equation are 1, 1, – 3, – 3.

Question 13.
Find the roots of x⁴ – 16x³ + 86x² – 176x + 105 = 0. [March ’08, ’02]
Solution:
Let f(x) = x⁴ – 16x³ + 86x² – 176x + 105 = 0
If x = 1 then f(1)= 1 – 16 + 86 – 176 + 105 = 0
= 192 – 192 = 0
Hence, 1 is a root of f(x) = 0
If x = 3 then
f(3) = 81 – 16 (27) + 86(9) – 176(3) + 105
= 81 – 432+ 774 – 528 + 105
= 960 – 960 = 0
Hence 3 is a root of f(x) = 0.
By the method of synthetic division we have

∴ The quotient is x² – 12x + 35 and remainder is zero.
∴ f(x) = x⁴ – 16x³ + 86x² – 176x + 105
= (x – 1)(x – 3) (x² – 12x + 35)
= (x – 1) (x – 3) (x – 5) (x – 7)
Hence the roots of the given equation are 1, 3, 5, 7.

Question 14.
Solve x⁴ – 10x³ + 26x² – 10x + 1 = 0. [TS – Mar. ‘18; Mar. ‘12, ’10, Board Paper]
Solution:
Given equation is x – 10x³ + 26x² – 10x + 1 = O
This is standard form of reciprocal equation.
The given equation is a reciprocal degree of class – 1 on dividing with x²
⇒ x² – 10x + 26 – \(\frac{10}{x}+\frac{1}{x^2}\) = 0
\(\left(x^2+\frac{1}{x^2}\right)-10\left(x+\frac{1}{x}\right)\) + 26 = 0
If x + \(\frac{1}{x}\) = a
⇒ x² + \(\frac{1}{x^2}\) = a² – 2
⇒ (a² – 2) – 10a + 26 = 0
⇒ a² – 10a + 24 = 0
⇒ a² – 6a – 4a + 24 = 0
⇒ a (a – 6) – 4 (a – 6) = 0
If (a – 4) (a – 6) = 0
⇒ a = 4, a = 6
If a = 4
⇒ x + \(\frac{1}{x}\) = 4
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{-(-4) \pm \sqrt{16-4(1)}}{2(1)}\)
= \(\frac{4 \pm \sqrt{12}}{2}\)
= 2 ± √3
If a = 6 x + \(\frac{1}{x}\) = 4
⇒ x² – 6x + 1 = 0
x = \(\frac{-(-6) \pm \sqrt{36-4(1)(1)}}{2(1)}=\frac{6 \pm \sqrt{32}}{2}\)
= 3 ± 2√2
Hence ti roots of the given equation are 2 ± √3, 3 ± 2√2.

Question 15.
Solve the quation 6x⁴ – 35x³ + 62x² – 35x + 6 = 0. [May ’13, ’10]
Solution:
Given equation is 6x⁴ – 35x³ + 62x² – 35x + 6 = 0
This is a standard form of reciprocal equation.
The given equation is an even degree reciprocal equation of class – 1
On dividing both sides of given equation by x², we get
6x² – 35x + 62 – \(\frac{35}{x}+\frac{6}{x^2}\) = 0
\(6\left(x^2+\frac{1}{x^2}\right)-35\left(x+\frac{1}{x}\right)\) + 62 = 0
Let x + \(\frac{1}{x}\) = a
⇒ \(\mathrm{x}^2+\frac{1}{\mathrm{x}^2}\) = a² – 2
⇒ 6(a² – 2) – 35a + 62 = 0
⇒ 6a² – 12 – 35a + 62 = 0
⇒ 6a² – 35a + 50 = 0
⇒ 6a² – 15a – 20a + 50 = 0
⇒ 3a (2a – 5) – 10 (2a – 5) = 0
⇒ (2a – 5)(3a – 10) = 0
⇒ 2a = 5; 3a = 10
a = \(\frac{5}{2}\) a = \(\frac{10}{3}\)
If a = \(\frac{5}{2}\)
⇒ x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0
⇒ 2x² – 4x – x + 2 = 0
⇒ 2x (x – 2) – 1 (x – 2) = 0
⇒ x = \(\frac{1}{2}\) (or) x = 2
If a = \(\frac{10}{3}\)
⇒ x + \(\frac{1}{x}\) = \(\frac{10}{3}\)
⇒ 3x² + 3 = 10x
⇒ 3x² – 10x + 3 = 0
⇒ 3x² – 9x – x + 3 = 0
⇒ 3x (x – 3) – 1 (x – 3) = 0
x = \(\frac{1}{3}\) (or) x = 3
∴ The roots are 2, 3, \(\frac{1}{2}\), \(\frac{1}{3}\).

Question 16.
Solve 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0. [TS – May ‘15: AP-Mar. ’17, ‘16; March ‘08, ‘07]
Solution:
Given equation is 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
Let f(x) = 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
If x = – 1
⇒ (- 1) = 2 (- 1) + 1 – 12 (- 1) – 12(1) + (- 1) + 2
= – 2 + 1 + 12 – 12 – 1 + 2 = 0
∴ (x + 1) is a factor of f(x).
On dividing f(x) by (x + 1) we get,

∴ 2x⁴ – x³ – 11x² – x + 2 = 0
On dividing with x² on both sides, we get
⇒ 2x² – x – 11 – \(\frac{1}{x}+\frac{2}{x^2}\) = 0
⇒ \(2\left(x^2+\frac{1}{x^2}\right)-1\left(x+\frac{1}{x}\right)\) – 11 = 0
Let x + \(\frac{1}{x}\) = a
⇒ x² + \(\frac{1}{x^2}\) + 2 = a²
⇒ x² + \(\frac{1}{x^2}\) = a² – 2
⇒ 2(a² – 2) – 1 (a) – 11 = 0
⇒ 2a² – 4 – a – 11 = 0
⇒ 2a² – a – 15 = 0
⇒ 2a² – 6a + 5a – 15 = 0
⇒ 2a (a – 3) + 5 (a – 3) = 0
⇒ (a – 3) (2a + 5) = 0
a = 3; a = – \(\frac{5}{2}\)
If a = 3;
x + \(\frac{1}{x}\) = 3
x² – 3x + 1 = 0
x = \(\frac{-(-3) \pm \sqrt{9-4}}{2(1)}=\frac{3 \pm \sqrt{5}}{2}\)
If a = – \(\frac{5}{2}\)
x + \(\frac{1}{x}\) = – \(\frac{5}{2}\)
⇒ 2x² + 5x + 2 = 0
⇒ 2x² + 4x + x + 2 = 0
⇒ 2x (x + 2) + 1 (x + 2) = 0
⇒ (2x + 1) (x + 2) = 0
∴ x = – \(\frac{1}{2}\), x = – 2
∴ The roots are – 1, – \(\frac{1}{2}\), – 2, \(\frac{3 \pm \sqrt{5}}{2}\).

Question 17.
Solve the equation x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0. [AP – May 2016; March ‘13]
Solution:
Given equation is x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0
Let f(x) = x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1
If x = 1
f(1)= 1⁵ – 5(1)⁴ + 9(1)³ – 9(1)² + 5(1) – 1
= 1 – 5 + 9 – 9 + 5 – 1 = 0
∴ (x – 1) is a factor of 1(x).
On dividing x⁵ – 5x³ + 9x³ – 9x² + 5x – 1 by x – 1

∴ x⁴ – 4x³ + 5x² – 4x + 1 = 0
This is a standard form of reciprocal equation.
Now, on dividing with x² on both sides, we get
x² – 4x + 5 – \(\frac{4}{x}+\frac{1}{x^2}\) = 0
\(\left(x^2+\frac{1}{x^2}\right)\) – 4 \(\left(x+\frac{1}{x}\right)\) + 5 = 0
Let x + \(\frac{1}{x}\) = a
⇒ [x + \(\frac{1}{x}\)]² = a²
⇒ x² + \(\frac{1}{x^2}\) + 2 = a²
⇒ x² + \(\frac{1}{x^2}\) = a² – 2
⇒ a² – 2 – 4a + 5 = 0
⇒ a² – 4a + 3 = 0
⇒ a² – 3a – a + 3 = 0
⇒ a (a – 3) – 1 (a – 3) = 0
⇒ (a – 1) (a – 3) = 0
⇒ a = 1 (or) a = 3
If a = 1
⇒ x + \(\frac{1}{x}\) = 1
⇒ x² – x + 1 = 0
⇒ x = \(\frac{-(-1) \pm \sqrt{1-4}}{2(1)}=\frac{1 \pm \mathrm{i} \sqrt{3}}{2}\)
If a = 3
⇒ x + \(\frac{1}{x}\) = 3
⇒ x² – 3x + 1 = 0
⇒ x = \(\frac{-(-3) \pm \sqrt{9-4}}{2(1)}=\frac{3 \pm \sqrt{5}}{2}\)
∴ The roots are 1, \(\frac{1 \pm \mathrm{i} \sqrt{3}}{2}\), \(\frac{3 \pm \sqrt{5}}{2}\).

Question 18.
Solve the equation 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0. [AP – Mar. ‘18. May 2015]
Solution:
Given equation is 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0
The given equation is an even degree reciprocal equation of class – 2.
Let f(x) = 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0
If x = 1 then f(1) = 6 – 25 + 31 – 31 + 25 – 6 = 0
∴ (x – 1) is a factor of f(x).
If x = – 1 then
f(- 1) = 6 + 25 + 31 – 31 – 25 – 6 = 0
∴ (x + 1) is a factor of f(x).
On dividing 1(x) by x + 1 and x – 1 we get,

∴ Quotient is 6x⁴ – 25x³ + 37x² – 25x + 6
6x⁴ – 25x³ + 37x² – 25x + 6 = 0
This is standard form of reciprocal equation.
This is an even degree reciprocal equation of class – 1.
On dividing both sides with x².
6x² – 25x + 37 – \(\frac{25}{x}+\frac{6}{x^2}\) = 0
\(6\left(x^2+\frac{1}{x^2}\right)-25\left(x+\frac{1}{x}\right)\) + 37 = 0
Let x + \(\frac{1}{x}\) = a
\(x^2+\frac{1}{x^2}\) = a² – 2
⇒ 6(a² – 2) – 25a + 37 = 0
⇒ 6a² – 25a + 25 = 0
⇒ 6a² – 15a – 10a + 25 = 0
⇒ 3a(2a – 5) – 5 (2a – 5) = 0
⇒ (3a -5) (2a – 5) = 0
⇒ a = \(\frac{5}{2}\), a = \(\frac{5}{3}\)
If a = \(\frac{5{2}\)
⇒ x + \(\frac{1}{x}\) = a
⇒ x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ 2x² – 5x + 2 = 0
⇒ 2x² – 4x – x + 2 = 0
⇒ 2x (x – 2) – 1 (x – 2) = 0
⇒ x = \(\frac{1}{2}\); x = 2
If a = \(\frac{5}{3}\)
⇒ x + \(\frac{1}{x}\) = \(\frac{5}{3}\)
⇒ 3x² – 5x + 3 = 0
x = \(\frac{-(-5) \pm \sqrt{25-4(3)(3)}}{2(3)}\)
= \(\frac{5 \pm \sqrt{25-36}}{6}=\frac{5 \pm \mathrm{i} \sqrt{11}}{6}\)
∴ The roots are ± 1, 2, \(\frac{1}{2}\), \(\frac{5 \pm \mathrm{i} \sqrt{11}}{6}\).

Question 19.
Find the polynomial equation of degree 5 whose roots are the translates of the roots of x₅ + 4x₃ – x₂ + 11 = 0 by – 3. [March ’06]
Solution:
Let f(x) = x⁵ + 4x³ – x² + 11 = 0
∴ The required equation is f(x + 3) = 0
∴ f(x + 3) = A₀x⁵ + A₁x⁴ + A₂x³ + A₃x² + A₄x + A₅
The coefficients A₀, A₁, A₂, A₃, A₄, A₅ can be obtained as follows

∴ Required equation is f(x + 3) = 0
x₅ + 15x₄ + 94x³ + 305x₂ + 507x + 353 = 0

Question 20.
Solve the equation x⁴ – 9x³ + 27x² – 29x + 6 = 0 given that one root is 2 – √3. [May ’03]
Solution:
Given equation is x⁴ – 9x³ + 27x² – 29x + 6 = 0
2 – √3 is a root of it then 2 + √3 is also root.
The quadratic factor of these two roots is (x – (2 + √3)) (x – (2 – √3))
= (x – (2 – √3)) (x – (2 + √3))
= ((x – 2) – √3) ((x – 2) + √3)
= (x – 2)² – (√3)²
= x² – 4x + 4 – 3
= x² – 4x + 1
On dividing x⁴ – 9x³ + 27x² – 29x + 6 with x² – 4x + 1