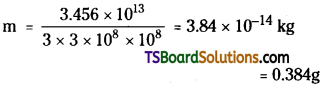TS Inter 2nd Year Physics Study Material Chapter 14 Nuclei

Telangana TSBIE TS Inter 2nd Year Physics Study Material 14th Lesson Nuclei Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 14th Lesson Nuclei

Very Short Answer Type Questions

Question 1.
What are isotopes and isobars?
Answer:
Isotopes :
The nuclei having the same atomic number (Z) but different mass number (A) are called isotopes.
Ex: ₈O¹⁶ , ₈O¹⁷, ₈O¹⁸.

Isobars :
The nuclei having the same mass number (A) but different atomic numbers (Z) are called isobars.
Ex: 14 ¹⁴₆C, ¹⁴₇N.

Question 2.
What are isotones and isomers?
Answer:
Isotones :
The nuclei having same neutron number (N) but different atomic number (Z) are called isotones.
Ex: ₈₀Hg¹⁹⁸, ¹⁹⁷₇₉Au.

Isomers :
Nuclei having the same atomic number (Z) and mass number (A) but different nuclear properties such as radioactive decay and magnetic moments are called isomers.
Ex: ⁸⁰₃₅Br^m, ⁸⁰₃₅Br^g. Here’m’ denotes metastable state and ‘g’ denotes ground state.

Question 3.
What is a.m.u.,? What is its equivalent energy?
Answer:
Atomic mass unit (lu) :
1/12th mass of ¹²₆C atom is taken as atomic mass unit.

Energy equivalent of 1 u = 931.5 MeV.

Question 4.
What will be the ratio of the radii of two nuclei of mass numbers A₁ and A₂?
Answer:
We know the radius of the nucleus
R = R₀ A^1/3

Question 5.
Natural radioactive nuclei are mostly nuclei of high mass number, why?
Answer:
As the atomic number increases coulombian repulsive force increases in the nucleus and hence the stability of the nucleus decreases.

That is why the nuclei after lead are unstable and they exhibit natural radioactivity.

Question 6.
Does the ratio of neutrons to protons in a nucleus increase, decrease or remain the same after the emission of an a – particle?
Answer:
α – particle means Helium nucleus (₂He⁴).

If the nucleus emits α -particle, it loses 2 protons and 2 neutrons. But in the nuclei of radio active elements number of neutrons is greater than the number of protons.

When neutrons number and protons number decreases equally, their ratio increases.

Question 7.
A nucleus contains no electrons but can emit them. How?
Answer:
Natural radioactive elements undergo β – decay. Then a neutron loses one electron and converts into proton.

This electron is ejected out with high velocity called β – ray. The proton remains inside the nucleus.

Question 8.
What are the units and dimensions of the disintegration constant?
Answer:
Since \(\frac{N}{N_0}\) = e^λt . λt has no unit and no
dimensions. So unit of λ = s^-1
Dimensional formula λ = T^-1

Question 9.
Why do all electrons emitted during β^– – decay not have the same energy?
Answer:
In negative beta decay (β^–) emission of electron is accompanied by a neutrino. These neutrinos have very small mass cempared to electron and some kinetic energy. Due to this neutrino energy of electrons liberated in β^– decay is not constant.

Question 10.
Neutrons are the best projectiles to produce nuclear reactions. Why?
Answer:
Neutron is an uncharged particle so it is not deflected by electric and magnetic fields and has high penetrating power. So the neutron required lesser energy than a positive charged particle for producing nuclear reactions. Hence neutron is the best projectile for producing nuclear reactions.

Question 11.
Neutrons cannot produce ionization. Why?
Answer:
Since neutron does not posses any charge, its ionising power is very less when compared to α and β rays.

Question 12.
What are delayed neutrons?
Answer:
The neutrons which are liberated over a period of time after the fission process has taken place are called delayed neutrons.

They play an important role in the nuclear reactor.

Question 13.
What are thermal neutrons? What is their importance?
Answer:
Slow neutrons are called thermal neutrons. Their energy is 0.025 eV. They produce nuclear fission.

Question 14.
What is the value of neutron multiplication factor in a controlled reaction and in an uncontrolled chain reaction?
Answer:
In controlled chain reaction K = 1.
In uncontrolled chain reaction K > 1.

Question 15.
What is the role of controlling rods in a nuclear reactor?
Answer:
They can control chain reaction by absorbing neutrons in nuclear reactor.

Question 16.
Why are nuclear fusion reactions called thermo nuclear reactions?
Answer:
As nuclear fusion reactions occur at very high temperature of the order of 10⁷K, the fusion reactions are known as thermonuclear reactions.

Question 17.
Define Becquerel and Curie.
Answer:
Becquerel (Bq) :
It is a unit to measure radioactivity of a substance. If a radioactive substance undergoes one disintegration or decay per second then it is called Becquerel.

Curie :
It is a unit to measure radioactivity of a substance. If a radioactive substance undergoes 3.7 × 10¹⁰ decays per second the radioactivity of that substance is called curie.
1 Curie = 3.7 × 10¹⁰ Bq (Becquerel)

Question 18.
What is a chain reaction?
Answer:

1. Chain reaction : If a fission reaction is self-maintained due to the neutrons released in that reaction then it is called chain reaction.
2. For chain reaction to takes place (1) At- least one external neutron is necessary 2) neutron multiplication factor K ≥ 1.
3. Initial mass of uranium must be greater than critical mass.

Question 19.
What is the function of moderator in a nuclear reactor?
Answer:
The function of moderator in a nuclear reactor is, to slow down the neutrons, thus neutrons will participate actively in fission reaction. It decreases the speed of neutrons from 2 MeV to 0.025 eV in the nuclear reactor. A good moderator does not absorb the neutrons.

Question 20.
What is the energy released in the fusion of four protons to form a helium nucleus?
Answer:
Energy released due to fusion of four protons is 26.7 MeV.

Short Answer Questions

Question 1.
Why is the density of the nucleus more than that of the atom? Show that the density of nuclear matter is same for all nuclei.
Answer:
a) In an atom nearly 99.9% of mass is concentrated in a very small volume called nucleus. Volume of nucleus is 10^-12 times less than volume of atom. From above explanation density of nucleus is clearly more than density of atom.

b) Density = ρ = mass / volume. But mass of nucleus m = A.m_p.

The above equation is independent of mass number of nucleus A. So density of nuclear matter is same for all nuclei.

Question 2.
Write a short note on the discovery of neutron.
Answer:
Chadwick observed emission of neutral radiation when beryllium nuclei were bombarded with alpha particles.

This neutral radiation when passed through lighter elements like helium, CO₂ and nitrogen knock out a proton.

If the particle is a photon, then its energy must be for higher than the α – particle participating in the reaction.

The energy of neutral particle and also that of a proton released when that neutral particle passes through the lighter element gave some energy discrepancy.

To explain this energy discrepancy Chadwick proposed that the neutral particle is not photon. But a new particle with its mass equal to that of proton and he called it neutron.

Mass of neutron is m_n = 1.00866 u.

In this way Chadwick discovered Neutron.

Question 3.
What are the properties of a neutron?
Answer:
Properties of a neutron :

1. Neutron is a chargeless particle and its mass is almost equal to mass of proton.
2. A free neutron is unstable when it is out side the nucleus. Its mean life period is 1000 sec.
3. Inside nucleus neutron is stable.
4. Number of neutrons in an atom is (A – Z) where A is mass number and Z is atomic number.

Question 4.
What are nuclear forces? Write their pro-perties. .
Answer:
Nuclear forces :
Forces between nucleons present inside the nucleus are called nuclear forces. Properties of nuclear forces are

1. A nuclear force is mych stronger than the coulomb force and the gravitational force.
2. Nuclear force between two nucleons are distance dependent.
3. From potential energy graph of a pair of nucleons these forces are found to be attractive forces when separation between nucleons is 0.8 Fermi or more. These forces are found to be repulsive forces when separation between nucleons is less than 0.8 Fermi.
4. Nuclear forces are saturated forces.
5. Nuclear forces are independent on charge. So nuclear force between proton-proton, proton – neutron and neutron – neutron are equal.

Question 5.
For greater stability, a nucleus should have greater value of binding energy per nucleon. Why?
Answer:
When a graph is plotted between binding energy per nucleon (E_bn) and mass number (A) for different elements it is called
E_bn – A graPh

Salient features of the graphs :
i) The binding energy per nucleon (E_bn) is constant in mass number range of 30 to 170 these elements are found to be more stable. E_bn value is maximum at 8.75 MeV / nucleon for Iron A = 56 which is highly stable.

ii) For heavy nuclei (A > 170) Binding energy per nucleon gradually decreases with increasing mass number.
Ex : Uranium has low binding energy per nucleon of 7.6 MeV. To obtain greater stability under suitable conditions it always tries to break up into two intermediate masses.

For E_bn Vs mass number A graph for region A > 30 to A < 170 is almost same we cannot break easily in two separate nuclei.

Hence atoms with high E_bn are more stable.

Question 6.
Explain α – decay.
Answer:
Alpha decay :
In α – decay ⁴₂He nuclie is emitted from given radioactive substance. Mass number of product nucleons (called daughter nucleus) is decreased by Four units and Atomic number is decreased by two units. Equation of α – decay is

Disintegration energy (OR) Q – value :
The Q – value of a nuclear reaction is the difference between the initial mass energy and total mass-energy of decay products. For α – decay Q value is given by Q = (m_x – m_y – m_He)c².

Question 7.
Explain β – decay.
Answer:
Beta decay (β) :
In Beta decay an electron (or) a positron is liberated from given radioactive substance.

Positive beta decay (β⁺) : In this decay a positron (e⁺) and a neutrino (v) are liberated from radioactive substance.
Ex: ²²₁₁Na → ²²₁₀Ne + e⁺ + v

In + Ve beta decay a proton looses positron and converts into neutron.
⇒ p → n + e⁺ + ν

Negative beta decay (β^–) :
In this decay an electron (e^–) and an antineutrino (\(\overline{\mathrm{ν}}\))are liberated.

In – Ve beta decay a neutron loses electron and converted into proton i.e.,
n → p + e“ + \(\overline{\mathrm{ν}}\)

Question 8.
Explain γ – decay.
Answer:
Nucleus also has discrete energy levels like that of an atom. The energy difference bet-ween these energy levels is in the order of MeV. They are called ground state and exi-ted states.

When a nucleon is in an excited state it will spontaneously return ground state.

While returning to ground state the nucleons will emit energy photons whose energy is equal to difference of those two energy levels.

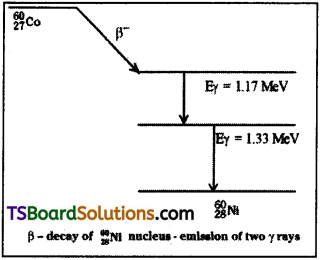
Since energy difference is in the order of MeV. The photons emitted are highly energetic. This highly energetic radiation is called gamma(γ) radiation.

Question 9.
Define balf-life period and decay constant for a radioactive substance. Deduce the relation between them.
Answer:
Half-life period (T_½) : It is the time taken for the number of nuclei (N) to become half of initial nuclei (N₀) i.e., N = \(\frac{N_0}{2}\).

Decay constant (λ) :
Let N is the number of nuclie in a sample. The number of nuclei (∆N) undergoing radioactive decay during the time ‘∆t’ is given by \(\frac{\triangle N}{\triangle t}\) ∝ N or \(\frac{\triangle N}{\triangle T}\) = λN.

where λ = disintegration constant (or) decay constant.

Relation between half-life peirod T_½ and decay constant λ :
From definition of halflife period N = \(\frac{N_0}{2}\) ; dt = T_½ …………… (1)
But N (t) = N₀ e^-λt ………….. (2) i:e., Number of nuclei after a time ‘t’
From above equation
T_(½) = \(\frac{log 2}{\lambda}=\frac{0.693}{\lambda}\)

Question 10.
Define average life of a radioactive substance. Obtain the relation between decay constant and average life.
Answer:
Average life time :
In a radioactive substance, some nuclei may live for a long time and some nuclei may live for a short time. So we are using average life time τ.

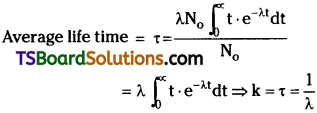
Relation between decay constant and average life time:

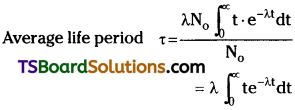
When integrated with in the limits o to ∞
⇒ τ = \(\frac{1}{\lambda}\).

Question 11.
Deduce the relation between half-life and average life of a radioactive substance.
Answer:
1) Half-life period (T_½) :
The half-life period of a radioactive nuclide is the time taken for the number of nuclei (N) to become half of initial nuclei (N₀) i.e., N = \(\frac{N_0}{2}\).

2) Average life time :
In a radioactive substance, some nuclei may live for a long time and some nuclei may live for a short time. So we are using average life time τ.

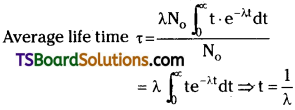
Relation between half-life period and Average life period :
half-life period τ_½ =\(\frac{log 2}{\lambda}\) …………. (1)
But from average life period τ = \(\frac{1}{\lambda}\) ….. (2)
From equations (1) & (2)
∴ τ_½ = t log²_e

Question 12.
What is nuclear fission? Give an example to illustrate it.
Answer:
Nuclear fission:
It is a nuclear reaction in which a heavy nucleus is divided into smaller nuclei along with some energy.

Explanation:
When uranium isotope ²³⁵₉₂U is bombarded with a neutron it will break up into two intermediate mass nuclei.

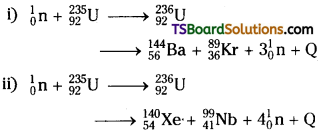
The atomic number of products is not constant it may vary from 35 to 57.

The fragments produced are radioactive nuclei. They will emit β – particles to achieve stable end products.

Energy liberated in this process is in the form of kinetic energy of fragments and neutrons. Later it is transferred into surroundings in the form of heat energy.

Question 13.
What is nuclear fusion? Write the Conditions for nuclear fusion to occur.
Answer:
Fusion :
The process of combining lighter nuclei to form a heavy nucleus is called “fusion reaction” (or) “nuclear fission”.

Conditions for fusion to occur :

1. For fusion to take place the two nuclie must come close enough so that nuclear attractive short range force is able to effect them.
2. Since protons have positive charge on them coulomb repulsive forces will come into account. These forces will develop nearly a potential barrier of 400 keV.
3. Fusion will be achieved if temperature is raised to nearly 108 K. So that protons will overcome coulomb repulsive forces. At this temperature the particles have enough kinetic energy to overcome coulomb repulsive force.

Question 14.
Distinguish between nuclear fission and nuclear fusion. [TS June ’15]
Answer:

NUCLEAR FISSION	NUCLEAR FUSION
1) When a heavy nucleus like U-235 splits up into nearly two equal parts by the bombardment of slow moving energy is released.	1) When two or more lighter atoms of hydrogen or protons are fused into heavier neutrons considerable amount of atom, large amount of energy is released.
2) The principle behind atom bomb is Nuclear fission.	2) The principle behind hydrogen bomb is nuclear fusion.
3) In this reaction 200 MeV of energy is released per fission.	3) In this reaction 26.70 MeV of energy is released.
4) Energy released per nucleon is less.	4) Energy released per nucleon is more.
5) Particles involved are neutrons.	5) Particles involved are protons.
6) Fission takes place at room temperature.	6) Fusion takes place only at very high temperature and high pressure.
7) Fission produces radioactive elements like Barium and Krypton which are harmful (radioactive).	7) The products of fusion are harmless (not radioactive).

Question 15.
Explain the terms ‘chain reaction’ and ‘multiplication factor’. How is a chain reaction sustained?
Answer:
1) Chain reaction :
If a fission reaction is self maintained due to the neutrons released in that reaction, then it is called “chain reaction”.

2) Multiplication factor K :
The ratio of number of fissions produced by neutrons of present generation to the number of fissions produced in preceding generation is called “multiplication factor”.

3) Condition to sustain chain reaction :
For chain reaction to takes place

1. Atleast one external neutron is necessary.
2. Neutron multiplication factor K ≥ 1.
3. Initial mass of uranium must be greater than critical mass.

Long Answer Questions

Question 1.
Define mass defect and binding energy. How does binding energy per nucleon vary with mass number? What is its significance?
Answer:
Mass defect :
The difference in mass of nucleus and its constituents is known as mass defect. In every nucleus the theoretical mass (Mt) is always less than practical mass (M).

Mass defect ∆m = [Zm_p + (A – Z) m_n] – M

Binding energy :
The energy released while forming a nucleus is called Binding energy E_b. Binding energy E_b = ∆mc².

When a certain number of protons and neutrons are brought together to form a nucleus then certain amount of energy E_b is released.

To divide a nucleus into its constituents, we have to supply an amount of energy equals to E_b from outside.

Binding energy per nucleon :
The ratio of Binding energy E_b to mass number ‘A’ of nucleus is cated’Binding energy per nucleon”.

Binding energy per nucleon E_bn = \(\frac{E_b}{A}\).

Binding energy per nucleon (E_bn) – Mass number (A) graphs :
When a graph is plotted between binding energy per nucleon (E_bn) and mass number (A) for different elements it is called “E_bn -A graph”.

Salient features of the graphs:

1. The binding energy per nucleon (E_bn) is almost constant within mass number range of 30 to 170.
2. For mass number A < 30 Binding energy per nucleon is less it gradually increases with increasing of mass number.
   This region suggested that when lighter nuclei are fused to form large nucleus then they release energy (Fusion process).
3. For heavy nuclei(where A > 170) Binding energy per nucleon gradually decreases with increasing mass number (A).

This region suggested that when larger nuclei are divided into small nuclei then energy is released (Fission process).

Question 2.
What is radioactivity? State the law of radioactive decay. Show that radioactive decay is exponential in nature. [TS May 18. 16; Mar. 16]
Answer:
Radioactive decay :
The spontaneous disintegration of unstable nucleus is referred as “radioactivity or radioactive decay”.

When a nucleus undergoes radioactive decay three types of radioactive decay takes place.

1. α – decay : In this process ⁴₂He nuclei are emitted.
2. β – deay : In this process electrons or positrons are emitted.
3. γ – decay : In this process high energy photons (E.M. Waves) are liberated.

Law of radioactive decay :
Let N is the number of nuclie in a sample. The number of nuclie (∆N) undergoing radioactive decay during the time ‘∆t’ is given by
\(\frac{\triangle N}{\triangle t}\) ∝ N or \(\frac{\triangle N}{\triangle t}\) = λN

Where λ is disintegration constant or decay constant.

Decay rate (R) (OR) activity :
The total decay rate of a sample is the number of nuclei disintegrating per unit time.
∴ Total decay rate R = – \(\frac{dN}{dt}\) (OR)
R = R₀ e^-λt (or) R = λN (activity)

Total decay rate is also called activity. Radioactive decay is exponential because the total decay rate R = R₀ e^-λt Where R0 is a constant.
∴ R ∝ e^-λt Here e-W is exponential function whose value decreases with time.

Hence total radioactive decay of a substance decreases exponentially.

Question 3.
Explain the principle and working of a nuclear reactor with the help of a labelled diagram. [TS Mar. 17, 15, AP Mar. ’17, ’16, ’15, ’14; May 18, 16, 14; AP & TS Mar. 19, 18; May 17; AP June 15]
Answer:
Principle :
A nuclear reactor works on the principle of “sustained and controlled chain reaction”.

The labelled diagram of nuclear reactor is as shown. The important parts of nuclear reactor are

1) Core :
The core of the reactor is the site of nuclear fission. Generally it is made with graphite bricks. Core contains fuel elements in suitably fabricated form.

2) Fuel :
Generally used fuel is enriched uranium which contain ²³⁵₉₂U at high conentration than in natural uranium. Fuel is responsible for fission reaction in reactor.

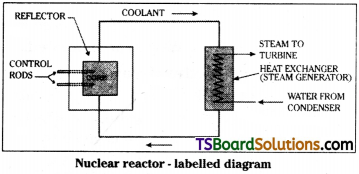
3) Reflector :
Generally inner part of core is provided with some reflecting material which prevents leakage of neutrons from core.

4) Coolant :
The purpose of coolant is to remove heat energy produced in reactor, generally water is used as a coolant.

5) Moderator :
Core is filled with Heavy water. It is a good moderator. Purpose of moderator is to slow down the neutrons. Slow neutrons will effectively participate in fission reaction.

6) Control rods :
Purpose of control rods is to reduce number of neutrons inside the core. Generally control rods are made with neutron absorbing material like boron or cadmium.

Radiation shield :
The whole assembly of core is shielded with suitable material which prevents leakage of radioactive radiation from core.

Working :
Due to fission reaction energy is released in the core. It is transferred to an outside tank by means of coolant. As a result water in the tank is heated and steam is produced. This steam is used to run a turbine and power is produced. Power produced in this method is called atomic power.

Question 4.
Explain the source of stellar energy. Explain the carbon-nitrogen cycle, proton-proton cycle occurring in stars. [TS June ’15]
Answer:
The source of stellar energy is nuclear fusion reaction, for which hydrogen is the fuel.

Energy from Sun and Stars :
Sun and Stars have been radiating huge amounts of energy by nuclear fusion reactions taking place in their core, where the temperature is of the order 10⁷ K. More scientists proposed two types of cyclic processes for the source of energy in the Sun & Stars. They are :

Carbon – Nitrogen Cycle :
Carbon – Nitrogen cycle is one of the most important nuclear reactions for the production of solar energy by fusion.

The entire cycle can be summed up as,
4₁H¹ → ₂He⁴ + 2 _{+ 1}e⁰ + 3γ + 2υ + 26.70MeV

The energy released during this process is 26.70 MeV.

Proton-Proton Cycle : [TS June ’15]
At higher temperature, the thermal energy of the protons is sufficient to form a deuteron and a positron. The deuteron then combines with another proton to form higher nuclei of helium ³₂He. Two such helium nuclei combine with another proton releasing a total amount of energy 25.71 MeV. The nuclear fusion reactions are given below.
₁H¹ + ₁H¹ → ₁H² + ₊₁e⁰ + υ + 0.42MeV ………. (1)
e⁺ + e^– → γ + γ + 1.02MeV …………. (2)
₁H² + ₁H² → ₂He³ + γ + 5.49MeV ………. (3)
₂He³ + ₂He³ → ₂He⁴ + 2 ₁H¹ + energy 12.86 MeV ………….. (4)

For this equation to takes place first three equations must occur twice.

The nef result of the above reactions is 4 ₁H¹ → ₂He⁴ + 2 ₊₁e⁰ + 2γ + 2υ + 26.70 MeV

The energy released during this process is 26.70 MeV.

Problems

Question 1.
Show that the density of a nucleus does not depend upon its mass number (density is independent of mass).
Answer:
Volume of nucleus

But volume V ac A (mass number )
Density of nucleus matter

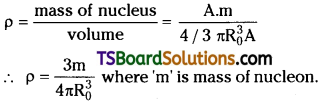
The above expression is independent of mass number ‘A’. Hence density of nuclear matter is independent of mass number of nucleus.

Question 2.
Compare the radii of the nuclei of mass numbers 27 and 64.
Answer:
Ratio of radii of nuclie is

Question 3.
The radius of the oxygen nucleus ¹⁶₈O is 2.8 × 10^-15m. Find the radius of lead nucleus ²⁰⁵₈₂Pb.
Answer:
Given, Radius of the oxygen nucleus R_o = 2.8 × 10^-15 m ;
Mass number of oxygen, A₀ = 16 ;
Mass number of lead = A_pb = 205 ; Radius of the lead nucleus R_pb = ?
Radius of nucleus

Question 4.
Find the binding energy of ⁵⁶₂₆Fe. Atomic mass of Fe is 55.9349 u and that of Hydrogen is 1.00783u and mass of neutrons is 1.00876 u.
Answer:
Mass of Hydrogen atom M_H = 1.00783u;
Mass of neutron m_n = 1.00867u
Mass of Iron atom M₁ = 55.9349u
Atomic number Z = 26;
Mass number A = 56;
Mass defect ∆m = [Zm_H + (A – Z)m_n – M_I]
∆m = [26 × 1.00783 + (56 – 26) 1.00867] – 55.9349 u
∆m = 0.52878 u
Binding energy = ∆mc² = 0.52878 × (3 × 10⁸)²
∴ B.E. = 0.52878 × 9 × 10¹⁶ or 0.52878 × 931.5 MeV
∵ [lu × C²] = 931.5 MeV energy
∴ B.E. =492.55
Binding energy per nucleon BE/ n = \(\frac{492.55}{56}\)
= 8:79 MeV

Question 5.
How much energy is required to separate the typical middle mass nucleus ¹²⁰₅₀Sn k its constituent nucleons? (Mass of ¹²⁰₅₀Sn = 119.902199 u, mass of proton = 1.007825 u and mass of neutron = 1.008665 u)
Answer:
Mass of proton m_p = 1.007825 amu ;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of Sn, Z = 50 ;
Mass number of Sn, A = 120 ;
Mass of nucleus of Sn atom = 119.902199 amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z) m_n – M_N]
= [ (50) (1.007825) + (120 – 50) (1.008665) – 119.902199]
= (50 × 1.007825 + 70 × 1.008665 -119.902199)
= (50.39125 + 70.60655 – 119.902199)
∆m = [120.9978 – 119.902199] = 1.095601 amu

(ii) Energy required to separate the nucleons = Binding energy of the nucleus
B.E = ∆mc² (∵ lamu × c² = 931.5MeV)
= ∆m × 931.5MeV = 1.095601 × 931.5 MeV
= 1021 MeV

Question 6.
Calculate the binding energy of an α – particle. Given that mass of proton – 1.0073u, mass of neutron = 1.0087u, and mass of α – particle = 4.0015u.
Answer:
An α – particle is nothing but helium nucleus ⁴₂He.
It contains 2 protons, 2 neutrons with a mass number A = 4.
Mass of proton m_p = 1.0073 amu ;
Mass of neutron m_n = 1.0087 amu ;
Atomic number of helium Z = 2 ;
Mass number of helium A = 4 ;
Mass of helium atom M_N = 4.0015 amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z)m_n – M_N]
= [(2) (1.0073) + (4 – 2) (1.0087) – 4.00260]
= (2 × 1.0073 + 2 × 1.0087-4.00260)
= (2.0146 + 2.0174)-4.0015 Am = [4.032 – 4.0015] = 0.0305 amu

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ lamu × c² = 931.5MeV)
= ∆m × 931.5 MeV = 0.0305 × 931.5 MeV
= 28.41 MeV

Question 7.
Find the energy required to split ¹⁶₈O nucleus into four α – particles. The mass of an α – particle is 4.002603u and that of oxygen is 15.994915u.
Answer:
The energy required to split
Q = [ Total mass of the products
– Total mass of the reactants] c²
= [Mass of four ⁴₂He – Mass of ¹⁶₈O] × c²
= [(4 × 4.002603) -15.994915] amu × c²
= [16.010412 – 15.994915] amu × c²
= (0.015497) 931.5 MeV = 14.44 MeV.

Question 8.
Calculate the binding energy per nucleon of ³⁵₁₇Cl nucleus. Given that mass of ³⁵₁₇Cl nucleus = 34.9800u, mass of proton = 1.007825u, mass of neutron = 1.008665 u and lu is equivalent to 931 MeV.
Answer:
Given, Mass of proton m_p = 1.007825 amu;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of ³⁵₁₇Cl, Z = 17 ;
Mass number of ³⁵₁₇Cl, A = 35 ;
Mass of nucleus of ³⁵₁₇Cl atom =34.98 amu.

(i) Mass defect ∆m = [Zm_p + (A – Z)m_n – M_N]
= [(17) (1.007825) + (35 – 17) (1.008665) – 34.98]
= (17 × 1.007825 + 18 × 1.008665 – 34.98)
= (17.13303 + 18.15597 -34.98)
∆m = [35.289 – 34.98] = 0.3089

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ 1amu × c² = 931.5 MeV)
B.E = ∆m × 931.5 MeV = 0.3089×931.5 MeV
= 287.83 MeV

(iii) Binding energy per nucleon of Cl = \(\frac{B.E}{A}\)
= \(\frac{287.83}{35}\) = 8.22 MeV

Question 9.
Calculate the binding energy per nucleon of ⁴⁰₂₀Ca. Given that mass of ⁴⁰₂₀Ca nucleus = 39.962589 u, mass of a proton = 1.007825 u ; mass of neutron = 1.008665 u and 1 u is equivalent to 931 MeV.
Answer:
Given, Mass of proton m_p = 1.007825 amu;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of ⁴⁰₂₀Ca Z = 20 ;
Mass number of ⁴⁰₂₀Ca A = 40 ;
Mass of nucleus of ⁴⁰₂₀Ca atom = 39.962589 amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z)m_n – M_N]
= [ (20) (1.007825) + (40 – 20) (1.008665) – 39.962589]
= (20 × 1.007825 + 20 × 1.008665 – 39.962589)
= (20.1565 + 20.1733 – 39.962589)
∆m = [ 40.3298 – 39.962589 ] = 0.3672 amu

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ lamu × c² = 931.5 MeV)
∴ B E = ∆m × 931.5MeV
= 0.3672 × 931.5 MeV = 342.06 MeV

(iii) Binding energy per nucleon of Ca = \(\frac{B.E}{A}\)
= \(\frac{342.06}{40}\) = 8.55 MeV

Question 10.
Calculate(i) maw defect, (ii) binding energy and (iii) the binding energy per nucleon of ¹²₆C nucleus. Nuclear mass of ¹²₆C 12.000000 u; maw of proton = 1.007825 u and maw of neutron = 1.008665 u.
Answer:
Given, Mass of proton m_p = 1.007825 amu;
Mass of neutron m_n = 1.008665 amu ;
Atomic number of ¹²₆C, Z = 6 ;
Mass number of ¹²₆C, A = 12;
Mass of nucleus of ¹²₆C atom = 12.00amu.

(i) Mass defect, ∆m = [Zm_p + (A – Z)m_n – M_N]
= [6(1.007825) + (12 – 6) (1.008665) – 12.00]
= (6 × 1.007825 + 6 × 1.008665 – 12.00)
= (6.04695 + 6.05199 – 12.00)
∆m = [12.09894 – 12.00] = 0.09894 amu

(ii) Binding energy of the nucleus B.E = ∆mc²
(∵ lamu × c² = 931.5 MeV)
∴ B.E = ∆m × 931.5 MeV
= 0.09895 × 931.5 MeV = 92.16 MeV

(iii) Binding energy per nucleon of carbon =
\(\frac{B.E}{A}=\frac{92.16}{12}\) = 7.86 MeV

Question 11.
The binding energies per nucleon for deuterium and helium are 1.1 MeV and 7.0 MeV respectively. What energy in joules will be liberated when 10v deuterons take part in the reaction.
Answer:
Given, Binding energies per nucleon for deuterium (\(\frac{B.E}{A}\))_D = 1.1 MeV
Mass number of deuterium A = 2
Binding energy of deuterium
B.E = (\(\frac{B.E}{A}\))_D × A = 1.1 × 2 = 2.2 MeV
Binding energies per nucleon for helium (\(\frac{B.E}{A}\))_He = 7.0 MeV
Mass number of helium A = 4
Binding energy of helium
B.E = (\(\frac{B.E}{A}\))_D × A = 7 × 4 = 28MeV
We know, ₁H² + ₁H² → ₂He⁴
Energy released = B.E. of 10⁶ deuterons
– B.E. of \(\frac{1}{2}\) × 10⁶ Helium atoms
Binding energy = 2.2 × 10⁶ – \(\frac{1}{2}\) × 10⁶ × 28
= 10⁶ (2.2 – 14) = – 11.8 × 10⁶ MeV
= -11.8 × 10⁶ × 1.6 × 10^-31J
= -18.88 × 10^-7J
(- ve sign indicates that energy is released)
∴ Energy released = 18.88 × 10^-7J

Question 12.
Bombardment of lithium with protons gives rise to the following reaction :

Find the Q – value of the reaction. The atomic masses of lithium, proton, and helium are 7.016u, 1.008u, and 4.004u respectively.
Answer:
Given, Mass of Lithium = 7.016 amu ;
Mass of Proton = 1.008 amu ;
Mass of Helium = 4.004 amu ;
1 a.m.u = 931.5 MeV energy
Q = [Total mass of the reactants – total mass of the products] c²
= [mass of Lithium + mass of Proton – ( 2 × mass of Helium)] 931.5 MeV
= [ 7.016 + 1.008 – 2 ( 4.004 ) ] 931.5 MeV
= [8.024 – 8.008] 931.5. MeV
∴ Energy Q. = 0.016 × 931.5 = 14.904 MeV

Question 13.
The half-life of radium is 1600 years. How much time does 1 g of radium take to reduce to 0.125 g. [TS May, ’18, ’16, Mar. ’16]
Answer:
1g become \(\frac{1}{2}\) g after one half-life period and it become \(\frac{1}{4}\) g after 2 half-life periods and \(\frac{1}{8}\) after 3 half-life periods.
But \(\frac{1}{8}\) g = 0.125g.
So number of half-life periods, n = 3.
Time taken = n x half-life period
= 3 × 1600 = 4800 years.

Question 14.
Plutonium decays with a half-life of 24.000 years. If plutonium is stored for 72,000 years, what fraction of it remains?
Answer:
Given, Half-life of Plutonium = 24,000 years;
The duration of the time = 72,000 years
Initial mass = x g ; Final mass = mx g

Fraction of Plutonium that remains

Question 15.
A certain substance decays to 1/232 of its initial activity in 25 days. Calculate its half-life.
Answer:
Given, Fraction of substance decays

Question 16.
The half-life period of a radioactive sub¬stance is 20 days. What is the time taken for 7 / 8th of its original mass to disintegrate?
Answer:
Given, Half-life period = 20 days

∴ Time taken to disintegrate
= n × Half-life time = 3 × 20 = 60 days

Question 17.
How many disintegration per second will occur in one gram of ²³⁸₉₂U if its half – life against ∝ – decay is 1.42 × 10¹⁷ s?
Answer:
Given, Half-life period T = 1.42 × 10¹⁷s.;
mass of uranium m = 238

Number of disintegrations / sec = nλ

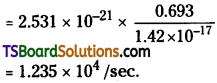
Question 18.
The half – life of a radioactive substance is 100 years. Calculate in how many years die activity will decay to 1/10th of its initial value.
Answer:
Given, Half – life period = 100 years

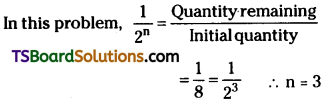
∴ Time taken to disintegrate
= n × Half-life time = 3 × 20 = 60 days

Question 19.
One gram of a radium is reduced by 2 milligram in 5 years by β – decay. Calculate the half-life of radium.
Answer:
Initial Mass of radium M₀ = 1 gram ;
∴ Mass reduced = 2mg
Final mass of radium M = 1 – 0.002
= 0.998 mg;
Time taken to reduce the mass t = 5 years
But number of atoms N α mass of the sample

Question 20.
The half-life of a radioactive substance is 5000 years. In how many years, its activity will decay to 0.2 times of its initial value? Give log₁₀ 5 = 0.6990.
Answer:
Half-life period T = 5000 years ;
Activity A = Nλ = 0.2 times initial value
Initial activity A₀ = N₀λ
In radioactivity N = N₀e^-λt

Question 21.
An explosion of atomic bomb releases an energy of 7.6 x 1013 J. If 200 MeV energy is released on fission of one atom calculate CD the number of uranium atoms undergoing fission. 00 the mass of uranium used in the bomb.
Answer:
i) Energy released E = 7.6 × 10¹³J
Energy released per fission = 200 MeV
= 200 × 10⁶ × 1.6 × 10^-19J
= 200 × 1.6 × 10^-13J = 3.2 × 10^-11 J

ii) Number of Uranium atoms participated

Question 22.
If one microgram of ²³⁸₉₂U is completely destroyed in an atom bomb, how much energy will be released? [AP Mar. ’19]
Answer:
Given, Mass of Uranium destroyed = 1
Micro gram = 1 × 10^-6 gr = 10^-9 Kg.
According to Einstein mass energy relation Energy released E = me² = 10^-9 × [ 3 × 10⁸]² (∵ Velocity of light c = 3 x 108 m/s)
∴ Energy released = 9 × 10^-9 × 10¹⁶ = 9 × 10⁷J

Question 23.
Calculate the energy released by fission from 2g of ²³⁸₉₂U in kWh. Given that the energy released per fission is 200 MeV.
Answer:
Given, Mass of Uranium (m) = 2g ;
Energy per fission = 200 MeV
Number of atoms in 2 grams of Uranium

Energy released per fission = 200 MeV
= 200 × 10⁶ × 1.6 × 10^-19J
= 200 × 1.6 × 10^-13 J = 3.2 × 10^-11J

Total Energy released ’Q’ = 5.1256 × 3.2 × 10^-11 = 1640.2 × 10⁸J
But, 1 kWh = 1000 × 60 × 60 = 36 × 10⁵J

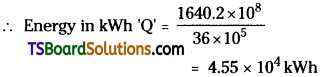
Question 24.
200 MeV energy is released when one nucleus of ²³⁸U undergoes fission. Find the number of fissions per second required for producing a power of 1 megawatt.
Answer:
Given, Total power produced = 1 Mega Watt = 10⁶ Watt
Energy per fission = 200 MeV
= 200 × 1.6 × 10^-13 J = 3.2 × 10^-11 J
∴ Number of fissions per second

Question 25.
How much ²³⁸U is consumed in a day in an atomic power house operating at 400 MW, provided the whole of mass ²³⁸U is converted into energy?
Answer:
Power P = 400 MW = 400 × 10⁶ watt;
Time T = 1 day = 86,400 sec.
∴ Energy produced per day
= 400 × 10⁶ × 86400 = 3.456 × 10¹³J
But Energy E = me² × m = E/c²
Mass of uranium consumed