TS Inter Second Year Maths 2B Integration Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Integration Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Integration Important Questions Very Short Answer Type

Question 1.
Find ∫(1 – x)(4 – 3x)(3 + 2x) dx
Solution:

Question 2.
Evaluate \(\int \frac{2 x^3-3 x+5}{2 x^2} d x\)
Solution:

Question 3.
Evaluate \(\int \frac{x^2+3 x-1}{2 x} d x\)
Solution:

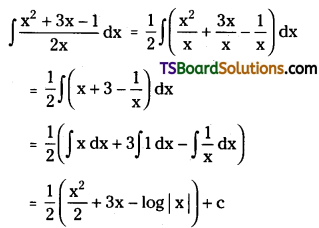
Question 4.
Evaluate \(\int \frac{(3 x+1)^2}{2 x} d x\). [(AP) May ’18, ’16]
Solution:

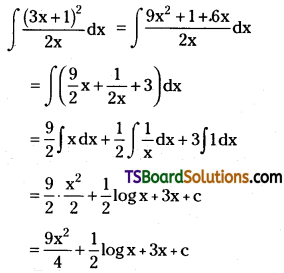
Question 5.
Evaluate \(\int\left(x+\frac{4}{1+x^2}\right) d x\). [(TS) May ’15]
Solution:

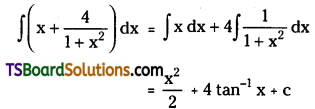
Question 6.
Evaluate \(\int\left[\frac{1}{\sqrt{1-x^2}}+\frac{2}{\sqrt{1+x^2}}\right] d x\). [May ’11]
Solution:

Question 7.
Evaluate \(\int\left(x+\frac{1}{x}\right)^3 d x\), x > 0. [May ’12]
Solution:

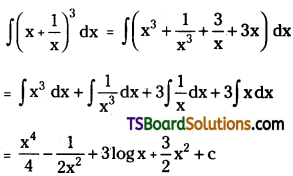
Question 8.
Evaluate \(\int \frac{x^2+1}{x^4+1} d x\) on R. [May ’14]
Solution:

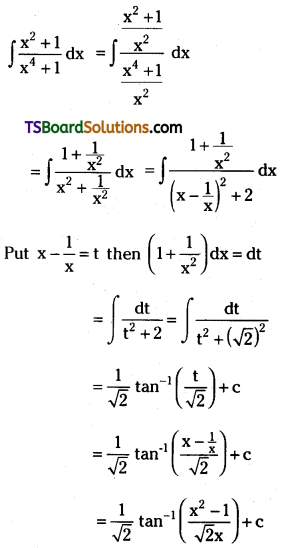
Question 9.
Evaluate \(\int\left(\frac{x^6-1}{1+x^2}\right) d x\)
Solution:

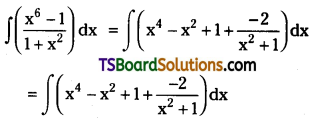
Question 10.
Evaluate \(\int \frac{\left(a^x-b^x\right)^2}{a^x b^x} d x\)
Solution:

Question 11.
Evaluate \(\int \sec ^2 x cosec^2 x d x\). [(TS) May ’18; Mar. ’16; (AP) May ’17]
Solution:

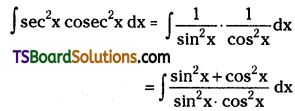
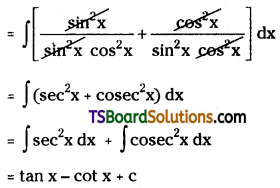
Question 12.
Evaluate \(\int \frac{1+\sin ^2 x}{1+\cos 2 x} d x\). [Mar. ’06, May ’95]
Solution:

Question 13.
Evaluate \(\int \frac{1+\cos ^2 x}{1-\cos 2 x} d x\). [Mar. ’19 (TS); ’13]
Solution:

Question 14.
Find \(\int \sqrt{1+\sin 2 x} d x\)
Solution:

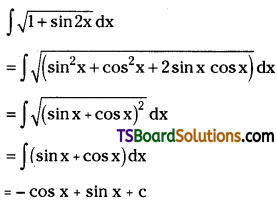
Question 15.
Evaluate \(\int \sqrt{1-\sin 2 x} d x\). [(TS) May ’17]
Solution:

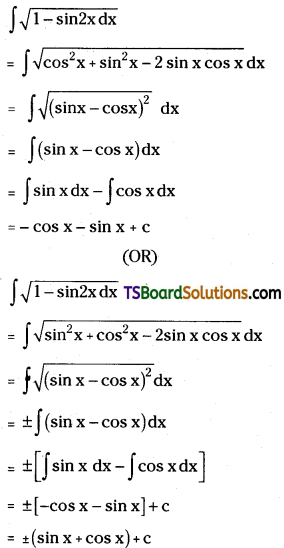
Question 16.
Evaluate \(\int \sqrt{1-\cos 2 x} d x\). [Mar. ’09, May ’06]
Solution:

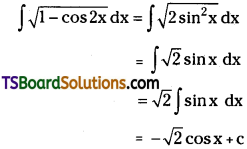
Question 17.
Evaluate \(\int \frac{d x}{\sqrt{1+5 x}}\)
Solution:

Question 18.
Find \(\int \frac{x}{1+x^2} d x\)
Solution:

Question 19.
Evaluate \(\int \frac{e^x}{e^x+1} d x\)
Solution:

Question 20.
Evaluate \(\int \frac{1}{x \log x[\log (\log x)]} d x\). [Mar. ’19 (TS); ’11]
Solution:

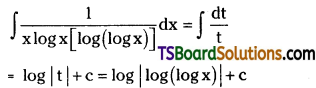
Question 21.
Evaluate \(\int \frac{1}{x \log x} d x\). [May ’99, ’94]
Solution:

Question 22.
Evaluate \(\int \frac{1-\tan x}{1+\tan x} d x\).
Solution:

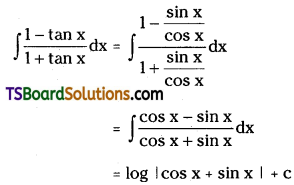
Question 23.
Evaluate \(\int \frac{\cos \sqrt{x}}{\sqrt{x}} d x\). [May & Mar. ’98]
Solution:

Question 24.
Evaluate \(\int\left(1-\frac{1}{x^2}\right) e^{\left(x+\frac{1}{x}\right)} d x\). [Mar. ’12]
Solution:

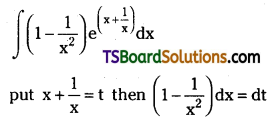
Question 25.
Evaluate \(\int \frac{e^x(1+x)}{\cos ^2\left(x e^x\right)} d x\). [(AP) Mar. ’19; May ’17 (TS) Mar. ’17; May ’16]
Solution:

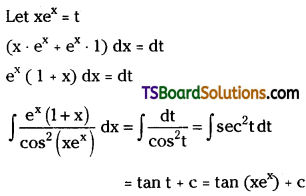
Question 26.
Evaluate \(\int \frac{\cot (\log x)}{x} d x\). [Mar. ’05]
Solution:

Question 27.
Evaluate \(\int \frac{(1+\log x)^n}{x} d x\). [(AP) May ’18]
Solution:

Question 28.
Evaluate \(\int \frac{\log (1+x)}{1+x} d x\). [(TS) Mar. ’15]
Solution:

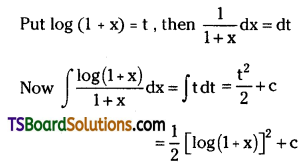
Question 29.
Evaluate \(\int \frac{\sin ^4 x}{\cos ^6 x} d x\). [Mar. ’11]
Solution:

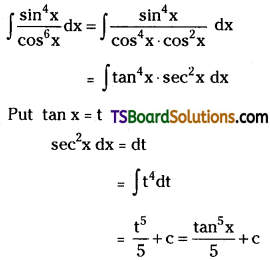
Question 30.
Evaluate \(\int \frac{{cosec}^2 x}{(a+b \cot x)^5} d x\)
Solution:

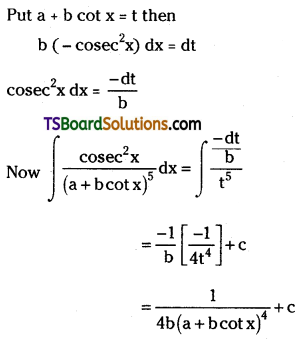
Question 31.
Evaluate \(\int \frac{1}{\sqrt{\sin ^{-1} x} \sqrt{1-x^2}} d x\). [(AP) May ’15]
Solution:
Put sin^-1x = t² then

Question 32.
Evaluate \(\int \frac{\sin \left(\tan ^{-1} x\right)}{1+x^2} d x\). [Mar. ’18, ’15 (AP); May ’13]
Solution:

Question 33.
Evaluate \(\int \frac{\mathrm{e}^{\tan ^{-1} x}}{1+\mathrm{x}^2} d x\)
Solution:

Question 34.
Evaluate ∫sin mx cos nx dx
Solution:

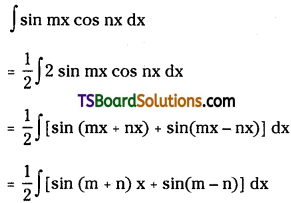
Question 35.
Evaluate ∫cos mx cos nx dx
Solution:

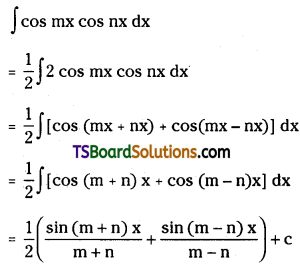
Question 36.
Evaluate ∫sin mx sin nx dx
Solution:

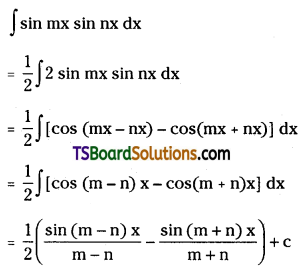
Question 37.
Evaluate ∫cos x cos 3x dx
Solution:

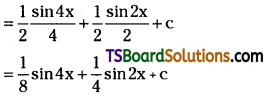
Question 38
Evaluate \(\int \frac{d x}{\sin x+\sqrt{3} \cos x}\). [May ’12]
Solution:

Question 39.
Evaluate \(\int \frac{\mathbf{x}^2}{\sqrt{1-x^6}} d \mathbf{x}\)
Solution:

Question 40.
Evaluate \(\int \frac{2 x^3}{1+x^8} d x\). [May ’08]
Solution:

Question 41.
Evaluate \(\int \frac{x^8}{1+x^{18}} d x\). [(TS) May ’19; (AP) Mar. ’16]
Solution:

Question 42.
Evaluate \(\int \frac{x^5}{1+x^{12}} d x\)
Solution:

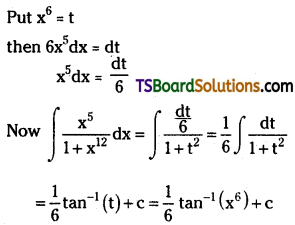
Question 43.
Evaluate \(\int \frac{3 x^2}{1+x^6} d x\)
Solution:

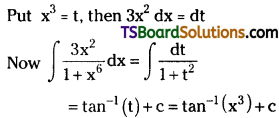
Question 44.
Evaluate \(\int \frac{d x}{(x+5) \sqrt{x+4}}\). [May ’09, ’02]
Solution:

Question 45.
Find \(\int \frac{1}{(x+3) \sqrt{x+2}} d x\). [May ’14, ’12; Mar. ’14]
Solution:

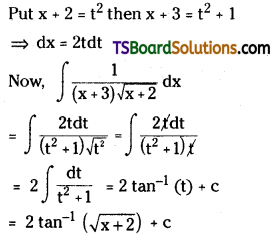
Question 46.
Evaluate ∫sec x log(sec x + tan x) dx
Solution:

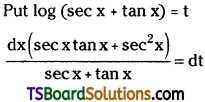
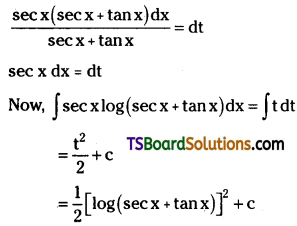
Question 47.
Evaluate \(\int \frac{\sec ^2 x}{\sqrt{16+\tan ^2 x}} d x\). [May ’08, ’07]
Solution:

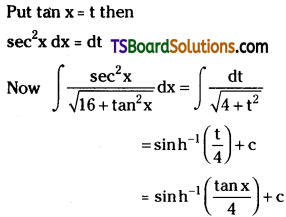
Question 48.
Evaluate \(\int \frac{d x}{x^2-81}\)
Solution:

Question 49.
Evaluate \(\int \frac{3}{\sqrt{9 x^2-1}} d x\)
Solution:

Question 50.
Evaluate \(\int \frac{d x}{(x+1)(x+2)}\). [Mar. ’19(AP); Mar. ’14, ’12, May ’11]
Solution:

Question 51.
Evaluate \(\int \frac{d x}{\sqrt{x^2+2 x+10}}\). [May ’06]
Solution:

Question 52.
Evaluate ∫log x dx. [Mar. ’99, May ’10, ’99]
Solution:

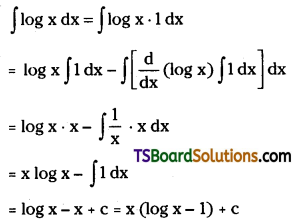
Question 53.
Evaluate ∫x log x dx. [(AP) Mar. ’20; May ’94]
Solution:

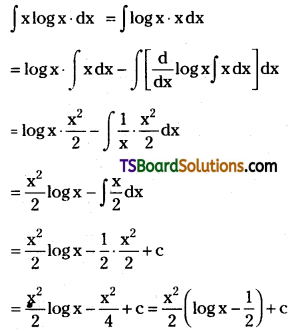
Question 54.
Evaluate \(\int \sin ^{-1} x d x\). [Mar. ’00, May ’05]
Solution:

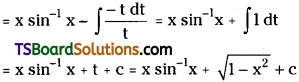
Question 55.
Evaluate \(\int x \tan ^{-1} x d x\). [Mar. ’05, May ’02]
Solution:

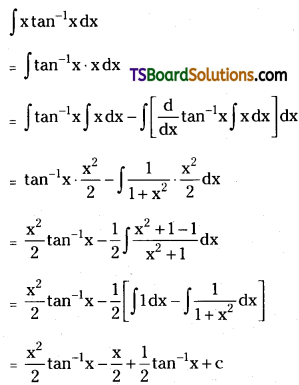
Question 56.
Evaluate \(\int e^x \cos x d x\). [May ’15 (AP)]
Solution:

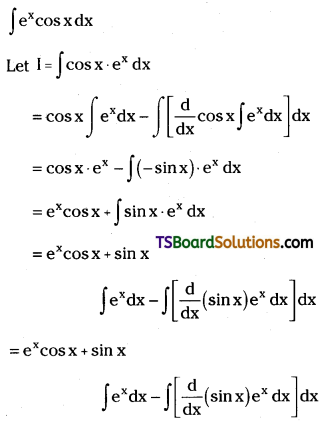
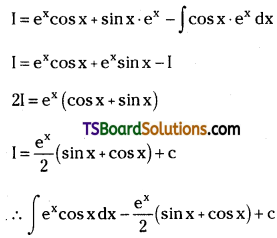
Question 57.
Evaluate ∫e^x (sec x + sec x tan x) dx. [(AP) May ’16]
Solution:

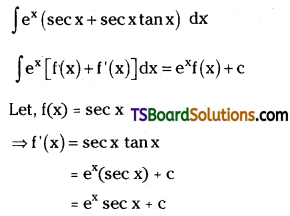
Question 58.
Evaluate ∫(tan x + log sec x) e^x dx. [May ’18, ’15 (TS); Mar. ’08, May ’07]
Solution:

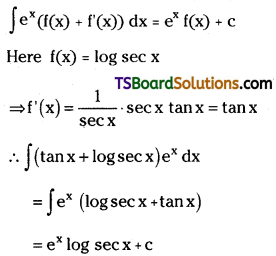
Question 59.
Evaluate \(\int e^x\left(\frac{1+x \log x}{x}\right) d x\). [(TS) May ’19; Mar. ’18, ’15 (AP); Mar. ’13]
Solution:

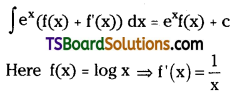
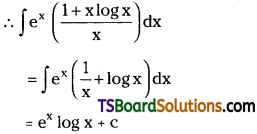
Question 60.
Evaluate \(\int \frac{e^x(x+1)}{(x+2)^2} d x\). [May ’09, ’98]
Solution:

Question 61.
Evaluate \(\int e^x\left[\tan ^{-1} x+\frac{1}{1+x^2}\right] d x\). [May ’94]
Solution:

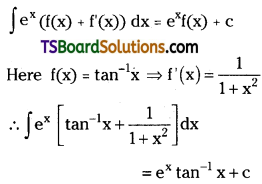
Question 62.
Evaluate \(\int e^x\left(\tan x+\sec ^2 x\right) d x\). [Mar. ’06, ’00, ’92]
Solution:

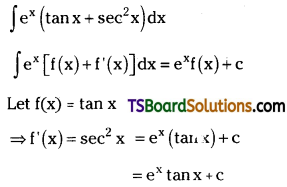
Question 63.
Evaluate ∫e^x (sin x + cos x) dx. [(AP) Mar. ’17]
Solution:

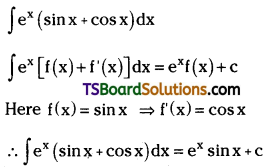
Question 64.
Evaluate \(\int \frac{1}{1+\cos x} d x\). [Mar. ’15 (TS)]
Solution:

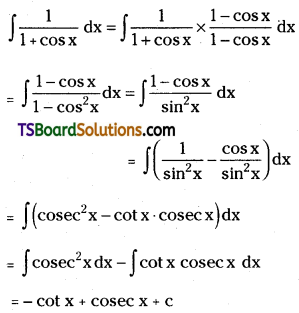
Question 65.
Evaluate \(\int \frac{1}{\cosh x+\sinh x} d x\). [(AP) May ’19, ’16 ; Mar. ’17 (TS)]
Solution:

Question 66.
Evaluate \(\int\left(1-x^2\right)^3 d x\)
Solution:

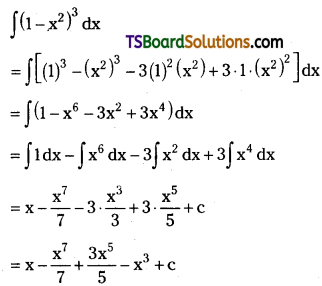
Question 67.
Evaluate \(\int\left(\frac{1}{1-x^2}+\frac{1}{1+x^2}\right) d x\). [(TS) May ’16]
Solution:

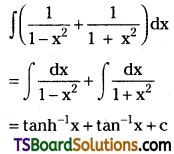
Question 68.
Evaluate \(\int \frac{1-\cos 2 x}{1+\cos 2 x} d x\). [May ’02]
Solution:

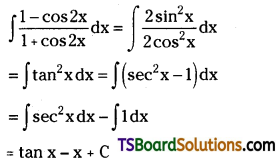
Question 69.
Evaluate \(\int \sqrt{1+\cos 2 x} d x\). [Mar. ’94]
Solution:

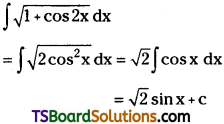
Question 70.
Evaluate \(\int \frac{1}{x \sqrt{x}} d \mathbf{x}\). [May ’92]
Solution:

Question 71.
Evaluate ∫2x√x dx.
Solution:

Question 72.
Evaluate ∫x³ (4 + x²)² dx. [May ’82]
Solution:

Question 73.
Evaluate \(\int \frac{1-x^4}{1-x} d x\). [Mar. ’99]
Solution:

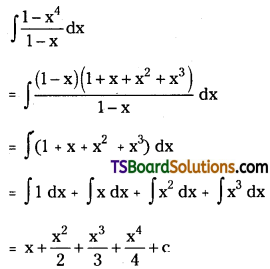
Question 74.
Evaluate \(\int \frac{x^4}{x^2+1} d x\). [May ’98, ’99]
Solution:

Question 75.
Evaluate \(\int e^{2 \log x} d x\). [May ’99]
Solution:

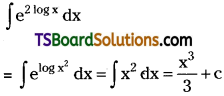
Question 76.
Evaluate ∫5^x dx. [May ’93]
Solution:
\(\int 5^x d x=\frac{5^x}{\log 5}+c\)

Question 77.
Evaluate \(\int \frac{\cos ^2 x}{1-\sin x} d x\). [Mar. ’01, May ’93]
Solution:

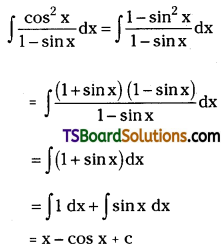
Question 78.
Evaluate \(\int \frac{\cos x+\sin x}{\sqrt{1+\sin 2 x}} d x\). [Mar. ’98, May ’92]
Solution:

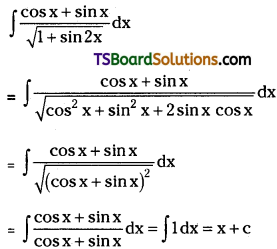
Question 79.
Find \(\int \frac{x^3}{\sqrt{x+1}} d x\). [Mar. ’00]
Solution:

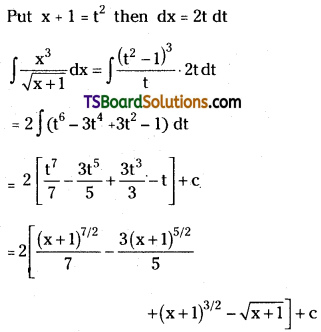
Question 80.
Find \(\int \frac{x^2}{\sqrt{x+5}} d x\). [May ’99]
Solution:

Question 81.
Find \(\int \frac{2 x+3}{\sqrt{4 x+3}} d x\). [May ’99]
Solution:

Question 82.
Evaluate ∫x³ sin x⁴ dx. [Mar. ’01]
Solution:

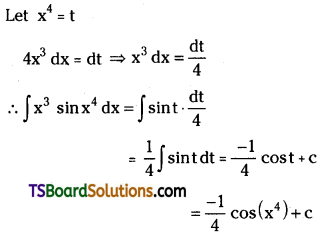
Question 83.
Evaluate ∫e^x sin(e^x) dx. [(AP) Mar. ’17]
Solution:
Put e^x = t then e^x dx = dt
Now ∫e^x sin(e^x) dx = ∫sin t dt
= -cos t + c
= -cos(e^x) + c

Question 84.
Evaluate ∫2x sin(x² + 1) dx.
Solution:
Put x² + 1 = t then 2x dx = dt
Now ∫2x sin(x² + 1) dx = ∫sin t dt
= -cos t + c
= -cos(x² + 1) + c

Question 85.
Evaluate \(\int \frac{x}{1+x^4} d x\)
Solution:

Question 86.
Evaluate \(\int \frac{(\log x)^2}{x} d x\). [(AP) May ’18]
Solution:

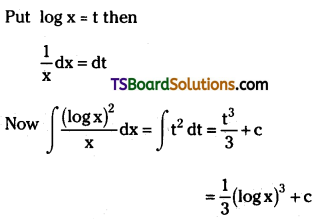
Question 87.
Evaluate ∫sec(tan x) sec²x dx.
Solution:
Put tan x = t then sec²x dx = dt
Now ∫sec(tan x) sec²x dx = ∫sec t dt
= log|sec t + tan t| + c
= log|sec(tan x) + tan(tan x)| + c

Question 88.
Evaluate \(\int \frac{\sin (\log x)}{x} d x\)
Solution:

Question 89.
Evaluate \(\int \frac{\cos (\log x)}{x} d x\)
Solution:

Question 90.
Evaluate \(\int \frac{3 x+7}{3 x^2+14 x-5} d x\). [Mar. ’00]
Solution:

Question 91.
Evaluate \(\int \frac{3 \cos 3 x-2 \sin 2 x}{\cos 2 x+\sin 3 x} d x\). [May ’93]
Solution:

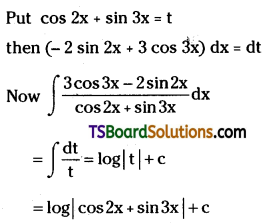
Question 92.
Find \(\int \frac{6 x}{3 x^2-2} d x\)
Solution:

Question 93.
Evaluate \(\int \frac{\left(\sin ^{-1} x\right)^2}{\sqrt{1-x^2}} d x\)
Solution:

Question 94.
Evaluate \(\int \frac{{cosec}^2 x}{(1+\cot x)^2} d x\). [Mar. ’01]
Solution:

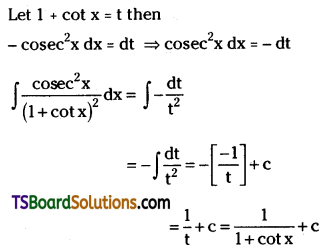
Question 95.
Evaluate ∫cos³x sin x dx. [(TS) Mar. ’18]
Solution:

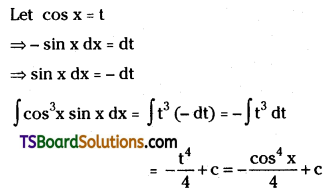
Question 96.
Evaluate \(\int \sqrt[3]{\sin x} \cdot \cos x d x\)
Solution:

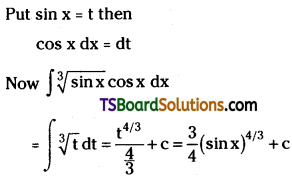
Question 97.
Evaluate \(\int \sqrt{\sin x} \cdot \cos x d x\)
Solution:

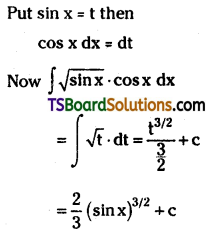
Question 98.
Evaluate \(\int {cosec}^2 x \cdot \sqrt{\cot x} d x\)
Solution:

Question 99.
Evaluate \(\int \frac{d x}{4-9 x^2}\). [May ’98]
Solution:

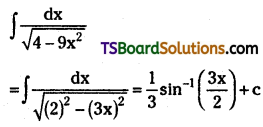
Question 100.
Evaluate \(\int \frac{1}{\sqrt{1-4 x^2}} d x\)
Solution:

Question 101.
Evaluate \(\int \frac{d x}{\sqrt{25+x^2}}\)
Solution:

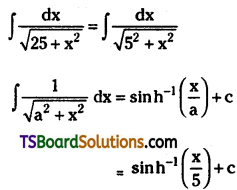
Question 102.
Evaluate \(\int \frac{1}{e^x+e^{-x}} d \mathbf{x}\)
Solution:

Question 103.
Evaluate \(\int \frac{1}{x^2+6 x+10} d x\). [Mar. ’98, May ’93]
Solution:

Question 104.
Evaluate \(\int \frac{1}{\sqrt{x^2-3}} d x\). [May ’92]
Solution:

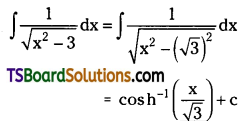
Question 105.
Evaluate \(\int \frac{1}{x^2-4} d x\). [May ’94]
Solution:

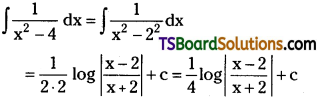
Question 106.
Evaluate \(\int \sqrt{x^2+4} d x\). [May ’93]
Solution:

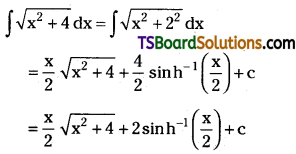
Question 107.
Evaluate \(\int \sqrt{4 x^2+9} d x\)
Solution:

Question 108.
Evaluate \(\int \sqrt{16-25 x^2} d x\)
Solution:

Question 109.
Evaluate ∫x e^x dx. [Mar. ’99]
Solution:

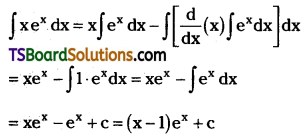
Question 110.
Evaluate ∫tan^-1x dx. [May ’98]
Solution:

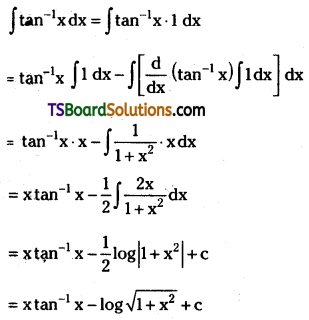
Question 111.
Evaluate ∫e^x (cos x – sin x) dx. [May ’99, ’95, Mar. ’99]
Solution:

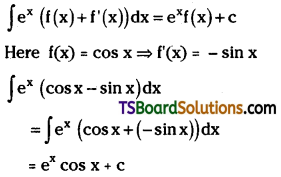
Question 112.
Evaluate \(\int \frac{x e^x}{(x+1)^2} d x\). [May ’14, ’98, ’94: Mar. ’05]
Solution:

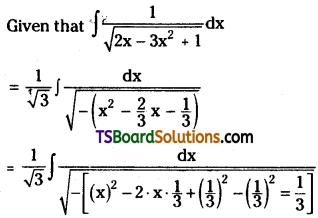
Question 113.
Evaluate \(\int \frac{1}{\sqrt{2 x-3 x^2+1}} d x\). [May ’08]
Solution:

Question 114.
Evaluate ∫cot²x dx.
Solution:
∫cot²x dx = ∫(cosec²x – 1) dx
= ∫cosec²x dx – ∫1 dx
= -cot x – x + c

Question 115.
Evaluate \(\int e^{\log \left(1+\tan ^2 x\right)} d x\)
Solution:

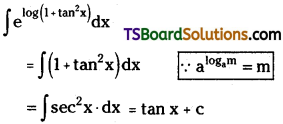
Question 116.
Evaluate \(\int \frac{\sin ^2 x}{1+\cos 2 x} d x\). [(TS) Mar. ’20]
Solution:

Question 117.
Evaluate ∫sin²x dx.
Solution:

Question 118.
Evaluate \(\int \frac{x}{1+x^2} d x\)
Solution:

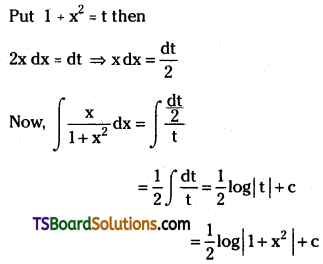
Question 119.
Evaluate \(\int \frac{\sin x}{\sin (a+x)} d x\)
Solution:

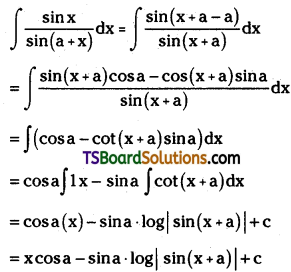
Question 120.
Evaluate \(\int 2 x e^{x^2} d x\)
Solution:

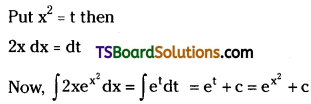
Question 121.
Evaluate \(\int \frac{1}{1+\sin 2 x} d x\)
Solution:

Question 122.
Evaluate ∫tan⁴x sec²x dx.
Solution:

Question 123.
Evaluate \(\int \frac{2 x+3}{\sqrt{x^2+3 x-4}} d x\)
Solution:
Put x² + 3x – 4 = t² then (2x + 3) dx = 2t dt

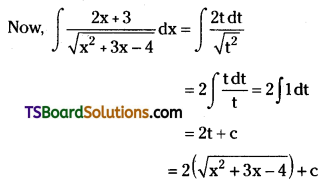
Question 124.
Evaluate ∫sin³x dx.
Solution:

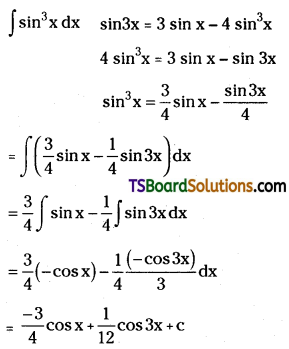
Question 125.
Evaluate ∫cos³x dx.
Solution:

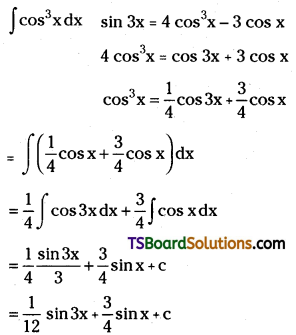
Question 126.
Evaluate \(\int \frac{d x}{1+e^x}\)
Solution:
Put 1 + e^x = t then e^x = t – 1
⇒ e^x dx = dt

Question 127.
Evaluate \(\int e^x\left[\frac{1-\sin x}{1-\cos x}\right] d x\)
Solution:

Question 128.
Evaluate ∫x sin²x dx. [Mar. ’02]
Solution:

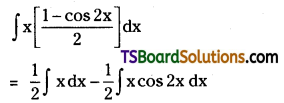
Question 129.
Evaluate \(\int \frac{e^x(x+2)}{(x+3)^2} d x\)
Solution:

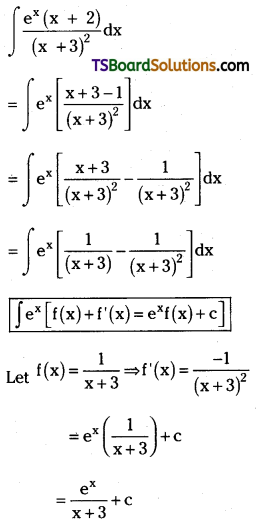
Question 130.
Evaluate \(\int \frac{e^{\mathbf{x}}}{e^x+1} d x\). [Mar. ’18 (TS)]
Solution:

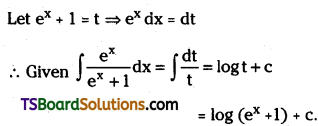
Question 131.
Evaluate \(\int\left(x^3-\cos x+\frac{4}{\sqrt{x^2+1}}\right) d x\)
Solution:

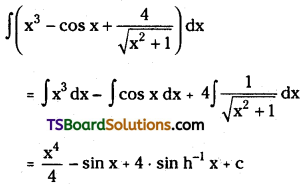
Question 132.
Evaluate ∫(x³ – 2x² + 3) dx.
Solution:

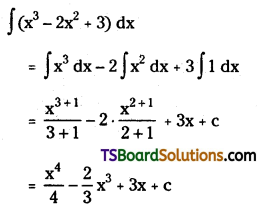
Question 133.
Find ∫2x⁷ dx.
Solution:

Question 134.
Evaluate ∫(1 – 2x³) x² dx.
Solution:

Question 135.
Evaluate \(\int \sqrt[3]{2 x^2} d x\)
Solution:

Question 136.
Evaluate \(\int\left(1+\frac{2}{x}-\frac{3}{x^2}\right) d x\)
Solution:

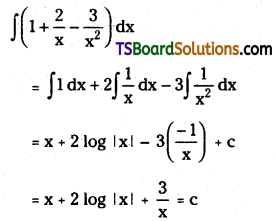
Question 137.
Evaluate \(\int \frac{2 x^3-3 x+5}{2 x^2} d x\)
Solution:

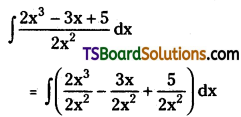
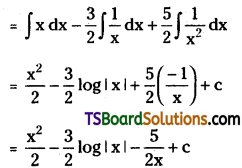
Question 138.
Evaluate \(\int\left(\frac{3}{\sqrt{x}}-\frac{2}{x}+\frac{1}{3 x^2}\right) d x\)
Solution:

Question 139.
Evaluate \(\int \frac{1-\sqrt{x}}{x} d x\)
Solution:

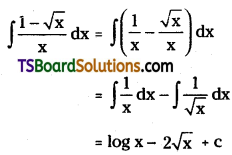
Question 140.
Evaluate \(\int\left(\frac{2 x-1}{3 \sqrt{x}}\right)^2 d x\)
Solution:

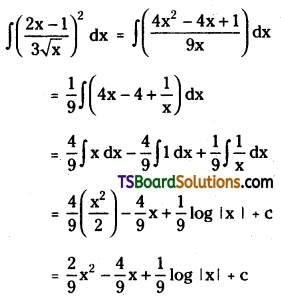
Question 141.
Evaluate \(\int\left(e^x-\frac{1}{x}+\frac{2}{\sqrt{x^2-1}}\right) d x\)
Solution:

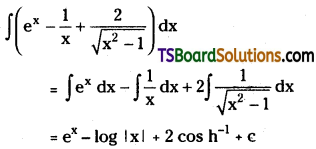
Question 142.
Evaluate \(\int\left(\frac{1}{\sqrt{x}}+\frac{2}{\sqrt{x^2-1}}-\frac{3}{2 x^2}\right) d x\)
Solution:

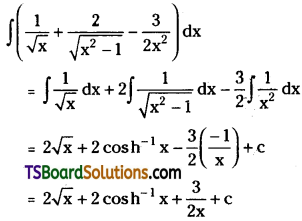
Question 143.
Evaluate ∫(sec²x – cos x + x²) dx.
Solution:

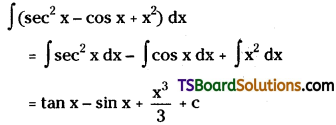
Question 144.
Evaluate \(\int\left(\sec x \tan x+\frac{3}{x}-4\right) d x\)
Solution:

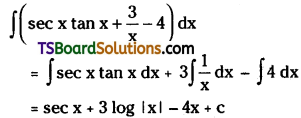
Question 145.
Evaluate \(\int\left(\cosh x+\frac{1}{\sqrt{x^2+1}}\right) d x\)
Solution:

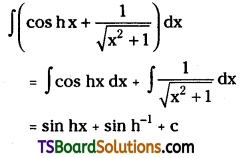
Question 146.
Evaluate \(\int\left(\sin h x+\frac{1}{\left(x^2-1\right)^{1 / 2}}\right) d x\)
Solution:

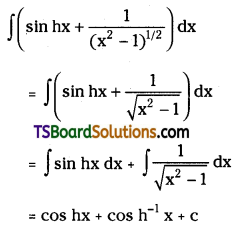
Question 147.
Evaluate \(\int(3 x-1)^{1 / 2} d x\)
Solution:

Question 148.
Evaluate ∫e^2x dx
Solution:
\(\int \mathrm{e}^{2 \mathrm{x}} \mathrm{dx}=\frac{\mathrm{e}^{2 \mathrm{x}}}{2}+\mathrm{c}\)

Question 149.
Evaluate \(\int \frac{e^{\log x}}{x} d x\)
Solution:

Question 150.
Evaluate ∫sin 7x dx
Solution:
∫sin 7x dx = \(\frac{-\cos 7 x}{7}+c\)

Question 151.
Evaluate ∫(3x² – 4)x dx
Solution:

Question 152.
\(\int \frac{1}{7 x+3} d x\)
Solution:

Question 153.
Evaluate \(\int \frac{1}{1+(2 x+1)} d x\)
Solution:

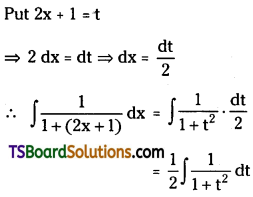
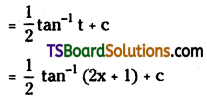
Question 154.
Evaluate ∫e^x cot e^x dx
Solution:
Put e^x = t ⇒ e^x dx = dt
∴ ∫e^x cot e^x dx = ∫cot t dt
= log|sin t| + c
= log|sin e^x| + c

Question 155.
Evaluate ∫cot hx dx
Solution:
∫cot hx dx = \(\int \frac{\cos h x}{\sin h x} d x\)
= log|sin hx| + c

Question 156.
Evaluate \(\int \frac{\cos x}{(1+\sin x)^2} d x\)
Solution:

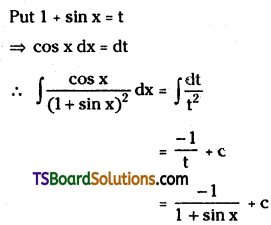
Question 157.
Evaluate ∫cos⁴x dx
Solution:

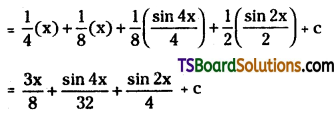
Question 158.
Evaluate \(\int \frac{x}{\sqrt{1-x}} d x\)
Solution:

Question 159.
Evaluate \(\int x \sqrt{4 x+3} d x\)
Solution:

Question 160.
Evaluate \(\int \frac{x^2}{\sqrt{1-x^2}} d x\)
Solution:

Question 161.
Evaluate \(\int \frac{\sin \theta}{\sqrt{2-\cos ^2 \theta}} d \theta\)
Solution:

Question 162.
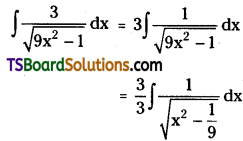
Evaluate \(\int \frac{3}{\sqrt{9 x^2-1}} d x\)
Solution:

Question 163.
Evaluate \(\int \frac{1}{1+4 x^2} d x\)
Solution:

Question 164.
Evaluate \(\int \frac{1}{8+2 x^2} d x\)
Solution:

Question 165.
Evaluate \(\int\left(\sqrt{x}-\frac{2}{1-x^2}\right) d x\)
Solution:

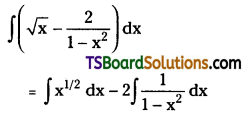
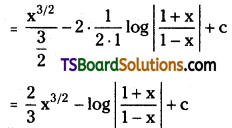
Question 166.
Evaluate \(\int \sqrt{9 x^2-25} d x\)
Solution:

Question 167.
Evaluate \(\int \frac{1}{e^x-1} d x\)
Solution:

Question 168.
Evaluate \(\int \frac{1}{1-\cot x} d x\)
Solution:

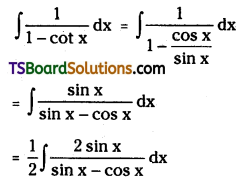
Question 169.
Evaluate \(\int \frac{1}{1+\tan x} d x\)
Solution:

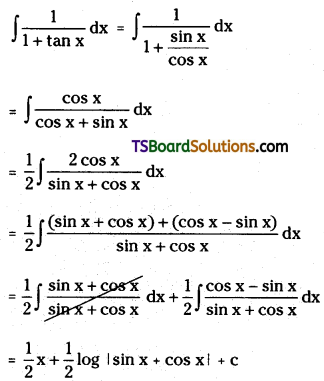
Question 170.
Evaluate ∫e^x (1 + x²) dx
Solution:

Question 171.
Evaluate ∫cot^-1x dx
Solution:

Question 172.
Evaluate ∫sec^-1x dx
Solution:

Question 173.
Evaluate ∫cosec^-1x dx
Solution:

Question 174.
Evaluate ∫x² cos x dx
Solution:

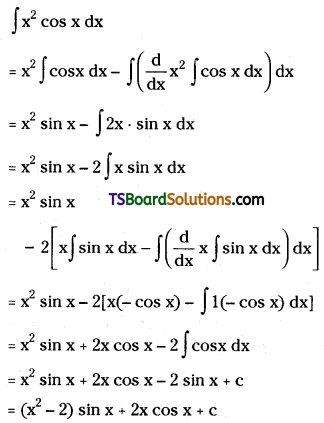
Question 175.
Evaluate ∫x sec²x dx
Solution:

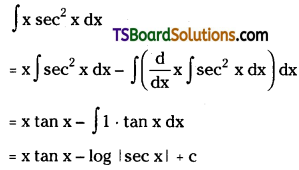
Question 176.
Evaluate \(\int \frac{\log x}{x^2} d x\)
Solution:

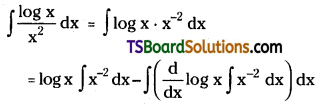
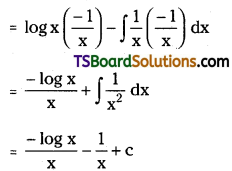
Question 177.
Evaluate ∫(log x)² dx
Solution:

Question 178.
Evaluate ∫xⁿ log x dx
Solution:

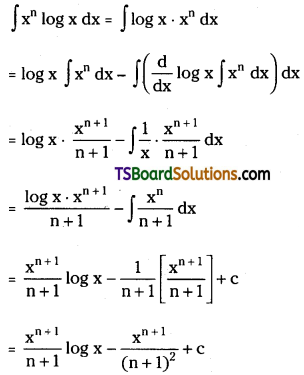
Question 179.
Evaluate ∫log(1 + x)² dx
Solution:

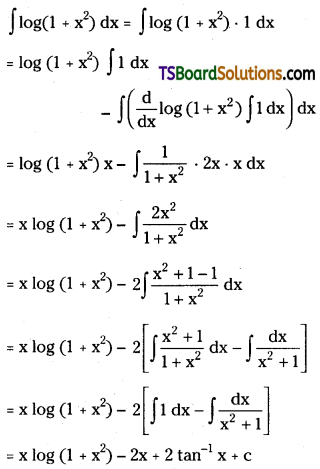
Question 180.
Evaluate ∫√x log x dx. [(TS) Mar. ’16]
Solution:

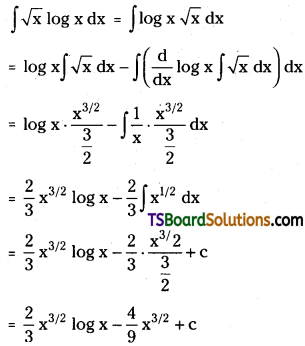
Question 181.
Evaluate \(\int \mathbf{e}^{\sqrt{\mathbf{x}}} d \mathbf{x}\). [(AP) May ’19]
Solution:

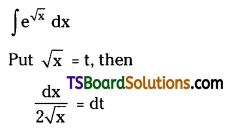
Question 182.
Evaluate ∫cos√x dx. [(TS) May ’17]
Solution:

Question 183.
Evaluate ∫x cot²x dx
Solution:

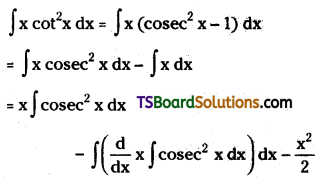
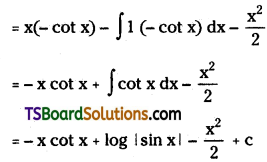
Question 184.
Evaluate ∫x² e^-3x dx
Solution:

Question 185.
Evaluate ∫x³ e^ax dx
Solution:

Question 186.
Evaluate ∫cos (log x) dx
Solution:

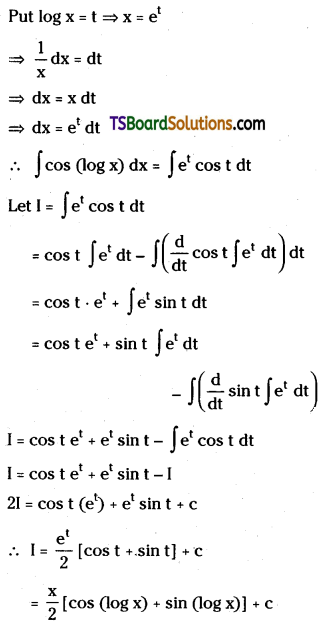
Question 187.
If f(x) is a differentiable function, then prove that \(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log|f(x)| + c.
Solution:
Let f(x) = t
⇒ f'(x) dx = dt
∴ \(\int \frac{f^{\prime}(x)}{f(x)} d x=\int \frac{1}{t} d t\)
= log|t| + c
= log|f(x)| + c

Question 188.
If f(x) is a differentiable function and n ≠ -1, then prove that \(\int[f(x)]_{f^{\prime}(x)}^n \cdot d x=\frac{[f(x)]^{n+1}}{n+1}+c\)
Solution:
Put f(x) = t
⇒ f'(x) dx = dt

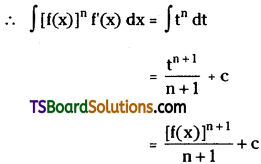
Question 189.
Prove that ∫tan x dx = log|sec x| + c.
Solution:

Question 190.
Prove that ∫cot x dx = log|sin x| + c.
Solution:

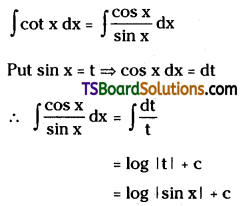
Question 191.
Prove that ∫sec x dx = log|sec x + tan x| + c = \(\log \left|\tan \left(\frac{\pi}{4}+\frac{x}{2}\right)\right|\) + c
Solution:

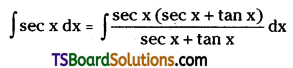
Question 192.
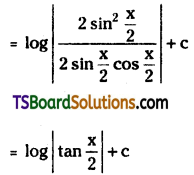
Prove that ∫cosec x dx = log|cosec x – cot x| + c = \(\log \left|\tan \frac{x}{2}\right|\) + c
Solution:

Question 193.
Prove that ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
Solution:

Question 194.
If \(I_n=\int x^n \cdot e^{-x} d x\), then prove that \(I_n=-x^n \cdot e^{-x}+n I_{n-1}\).
Solution: