TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Very Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Very Short Answer Type

Question 1.
If \({ }^{\mathrm{n}} \mathrm{P}_4\) = 1680, find n. [Mar.’14, May ’06]
Solution:
Given \({ }^{\mathrm{n}} \mathrm{P}_4\) = 1680
\({ }^{\mathrm{n}} \mathrm{P}_4\) = 8 . 7 . 6 . 5
= \({ }^8 \mathrm{P}_4\)
⇒ n = 8

Question 2.
If \({ }^{12} \mathrm{P}_{\mathrm{r}}\) = 1320, find r. [March ’09, AP – May 2015]
Solution:
Given \({ }^{12} \mathrm{P}_{\mathrm{r}}\) = 1320
\({ }^{12} \mathrm{P}_{\mathrm{r}}\) = 12 . 11 . 10
= \({ }^{12} \mathrm{P}_3\)
r = 3.

Question 3.
If \({ }^{(n+1)} P_5:{ }^n P_5\) = 3 : 2, find n.
Solution:
Given \({ }^{(n+1)} P_5:{ }^n P_5\) = 3 : 2
\(\frac{(n+1) P_5}{{ }^n P_5}=\frac{3}{2}\)

⇒ 2n + 2 = 3n – 12
⇒ n = 14.

Question 4.
If \({ }^n \mathbf{P}_7\) = 42 . \({ }^n \mathbf{P}_5\), find n. [TS – Mar. 2017, ’15; May ’12, ’11, ’09, ’07]
Solution:
Given \({ }^n \mathbf{P}_7\) = 42 . \({ }^n \mathbf{P}_5\)
n (n – 1) (n – 2) (n – 3) (n – 4) (n – 5) (n – 6) = 42 . n(n – 1) (n – 2) (n – 3) (n – 4)
(n – 5) (n – 6) = 42
⇒ n² – 11n + 30 – 42 = 0
⇒ n² – 11n – 12 = 0
⇒ n – 12n + n – 12 = 0
⇒ n (n – 12) + 1 (n – 12) = 0
⇒ (n – 12) (n + 1) = 0
⇒ n = 12; n = – 1
Since, n is a positive integer, n = 12.

Question 5.
If \({ }^{56} \mathbf{P}_{(r+6)}:^{54} P_{(r+3)}\) = 30800: 1, find ‘r’.
Solution:
Given \({ }^{56} \mathbf{P}_{(r+6)}:^{54} P_{(r+3)}\) = 30800 : 1
\(\frac{\frac{56 !}{(56-r-6) !}}{\frac{54 !}{(54-r-3) !}}=\frac{30800}{1}\)
⇒ \(\frac{\frac{56 !}{(50-r) !}}{\frac{54 !}{(51-r) !}}=\frac{30800}{1}\)
⇒ \(\frac{\frac{56 \cdot 55 \cdot 54 !}{(50-r) !}}{\frac{54 !}{(51-r)(50-r) !}}=\frac{30800}{1}\)
⇒ 56 55(51 – r) = 30800
⇒ 51 – r = 10
⇒ r = 41.

Question 6.
If \({ }^{12} \mathbf{P}_5+5 \cdot{ }^{12} \mathbf{P}_4={ }^{13} \mathbf{P}_{\mathrm{r}}\), find ‘r’. [TS – May 2015]
Solution:
Given \({ }^{12} \mathbf{P}_5+5 \cdot{ }^{12} \mathbf{P}_4={ }^{13} \mathbf{P}_{\mathrm{r}}\)
\({ }^{(13-1)} P_5+5{ }^{(13-1)} P_{(5-1)}={ }^{13} P_r\)
We know that,
\({ }^n P_r={ }^{(n-1)} P_r+r^{(n-1)} P_{r-1}\)
∴ r = 5
(or) Given \({ }^{12} \mathrm{P}_5+5 \cdot{ }^{12} \mathrm{P}_4={ }^{13} \mathrm{P}_{\mathrm{r}}\)
12 . 11 . 10 . 9 . 8 + 5 . 12 . 11 . 10 . 9 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
95040 + 59400 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
⇒ 154440 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
13 . 12 . 11 . 10 . 9 = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
⇒ \({ }^{13} \mathrm{P}_5\) = \({ }^13 \mathrm{P}_{\mathrm{r}}\)
⇒ r = 5.

Question 7.
If \({ }^{\mathrm{n}} \mathrm{C}_4\) = 210, find n. [TS – Mar.2019]
Solution:
Given \({ }^{\mathrm{n}} \mathrm{C}_4\) = 210
⇒ \(\frac{n(n-1)(n-2)(n-3)}{1 \cdot 2 \cdot 3 \cdot 4}\) = 210
⇒ n (n – 1) (n -2) (n -3) = 5040
n (n – 1) (n – 2) (n – 3) (n – 4) = 10 . 9 . 8 . 7
∴ n = 10.

Question 8.
If \({ }^{12} \mathrm{C}_{\mathrm{r}}\) = 495, find the possible values of ‘r’.
Solution:
Given \({ }^{12} \mathrm{C}_{\mathrm{r}}\) = 495 = 11 . 9 . 5
= \(\frac{11 \cdot 10 \cdot 9 \cdot 5}{10}=\frac{11 \cdot 10 \cdot 9}{1 \cdot 2}=\frac{12 \cdot 11 \cdot 10 \cdot 9}{1 \cdot 2 \cdot 12}\)
= \(\frac{12 \cdot 11 \cdot 10 \cdot 9}{1 \cdot 2 \cdot 3 \cdot 4}={ }^{12} \mathrm{C}_4 \text { (or) }{ }^{12} \mathrm{C}_8\)
∴ r = 4 (or) 8.

Question 9.
If 10. \({ }^n c_2\) = 3 . \({ }^{n+1} C_3\), find ’n’. [May ’12], [AP – Mar. 2015]
Solution:
Given 10. \({ }^n c_2\) = 3 . \({ }^{n+1} C_3\)
⇒ 10 . \(\frac{\mathrm{n}(\mathrm{n}-1)}{1 \cdot 2}\) = 3. \(\frac{(n+1) n(n-1)}{1 \cdot 2 \cdot 3}\)
⇒ n + 1 = 10
⇒ n = 9.

Question 10.
If \({ }^{{ }^n} P_{\mathbf{r}}\) = 5040 and \({ }^n C_{\mathbf{r}}\) = 210 find n and r. [AP – Mar. ‘17, ‘16; Board Paper]
Solution:
\({ }^{{ }^n} P_{\mathbf{r}}\) = 5040 ……………(1)
\({ }^n C_{\mathbf{r}}\) = 210 ……………..(2)
\(\frac{(2)}{(1)} \Rightarrow \frac{{ }^n C_r}{{ }^n P_r}=\frac{210}{5040}\)
\(\frac{\frac{n !}{(n-r) ! r !}}{\frac{n !}{(n-r) !}}=\frac{1}{24} \Rightarrow \frac{1}{r !}=\frac{1}{4 !}\)
r = 4
Now, substituting r = 4 in equation (1)
\({ }^n \mathrm{p}_4\) = 5040
\({ }^n \mathrm{p}_4\) = 10 . 9 . 8 . 7
\({ }^n \mathrm{p}_4={ }^{10} \mathrm{P}_4\)
n = 10.

Question 11.
If \({ }^n C_4={ }^n C_6\), find ‘n’.
Solution:
Given \({ }^n C_4={ }^n C_6\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
Now, n = r + s
⇒ n = 4 + 6
⇒ n = 10.

Question 12.
If \({ }^{15} \mathrm{C}_{2 \mathrm{r}-1}={ }^{15} \mathrm{C}_{2 \mathrm{r}+4}\) find ’r’. [Mar. ’14, ’05]
Solution:
Given \({ }^{15} \mathrm{C}_{2 \mathrm{r}-1}={ }^{15} \mathrm{C}_{2 \mathrm{r}+4}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ 2r – 1 = 2r + 4
⇒ – 1 ≠ 4
It is not possible.
n = r + s
⇒ 15 = 2r – 1 + 2r + 4
⇒ 15 = 4r + 3
⇒ 4r = 12
⇒ r = 3.

Question 13.
If \({ }^{12} \mathrm{C}_{\mathrm{r}+1}={ }^{12} \mathrm{C}_{3 \mathrm{r}-5}\), find ‘r’. [TS- Mar. 2016; March ’08]
Solution:
Given \({ }^{12} \mathrm{C}_{\mathrm{r}+1}={ }^{12} \mathrm{C}_{3 \mathrm{r}-5}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ r + 1 = 3r – 5
⇒ 2r = 6
⇒ r = 3
(or)
n = r + s
⇒ 12 = r – 1 + 3r – 5
⇒ 12 = 4r – 4
⇒ 4r = 16
⇒ r = 4.
∴ r = 3 (or) 4.

Question 14.
If \({ }^9 C_3+{ }^9 C_5={ }^{10} C_{r^{\prime}}\) then find ‘r’.
Solution:
Given \({ }^9 C_3+{ }^9 C_5={ }^{10} C_{r^{\prime}}\)

Question 15.
Find the number of ways of forming a committee of 5 members from 6 men and 3 ladies.
Solution:
Number of ways of forming a committee of 5 members from 6 men and 3 ladies is
\({ }^9 \mathrm{C}_5=\frac{9 \cdot 8 \cdot 7 \cdot 6 \cdot 5}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}\) = 126.

Question 16.
If \({ }^n C_5={ }^n C_6\) then find \({ }^{13} \mathrm{C}_{\mathrm{n}}\). [AP – Mar.2019] [TS-Mar. ‘18; May’14, ‘10, March ’13].
Solution:
Given \({ }^n C_5={ }^n C_6\)
If \({ }^{13} \mathrm{C}_{\mathrm{n}}\)
r = s (or) n = r + s
n = r + s = 5 + 6 =11
Now,
\({ }^{13} C_n={ }^{13} C_2\)
= \({ }^{13} \mathrm{C}_2=\frac{13 \cdot 12}{2 \cdot 1}\)
= 13 . 6 = 78.

Question 17.
Prove that \({ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_6={ }^{11} \mathrm{C}_4\).
Solution:
Given \({ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_6={ }^{11} \mathrm{C}_4\)
L.H.S: \({ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_6={ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_4\)
[∵ \({ }^n C_r={ }^n C_{n-r}\)]
= \(={ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_{4-1}={ }^{(10+1)} \mathrm{C}_4\)
[∵ \({ }^n C_r+{ }^n C_{n-r}={ }^{(n+1)} C_r\)]
= \({ }^{11} \mathrm{C}_4\)
= R.H.S

Question 18.
If \({ }^{12} C_{s+1}={ }^{12} C_{2 s-5}\) find ‘s’. [Mar. ’11]
Solution:
Given \({ }^{12} C_{s+1}={ }^{12} C_{2 s-5}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ r = s
⇒ s + 1 = 2s – 5
⇒ s = 6 (or)
n = r + s
12 = s + 1 + 2s – 5
12 = 3s – 4 = 3s = 16
s = \(\frac{16}{3}\)
Since s is integer, s = 6.

Question 19.
If \({ }^n C_{21}={ }^n C_{27}\) find \({ }^{50} \mathrm{C}_{\mathrm{n}}\).
Solution:
Given \({ }^n C_{21}={ }^n C_{27}\)
If \({ }^n C_r={ }^n C_s\)
⇒ n = r + s (or) r = s
⇒ n = r + s
⇒ n = 21 + 27
⇒ n = 48
Now, \({ }^{50} \mathrm{C}_{\mathrm{n}}={ }^{50} \mathrm{C}_{48}\)
= \({ }^{50} \mathrm{C}_2=\frac{50 \cdot 49}{2 \cdot 1}\)
= 25 . 49 = 1225.

Question 20.
Find the number of positive divisors of 1080. [AP – May, Mar. 2016; May ‘13]
Solution:
1080 = 2³ × 3³ × 5¹
The number of positive divisors of 1080 = (3 + 1) (3 + 1) (1 + 1)
= 4 . 4 . 2 = 32.

Question 21.
Find the value of \({ }^{10} \mathrm{C}_5+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_3\). [AP – Mar. ‘18; TS- Mar. 2017; March ‘10]
Solution:
Given \({ }^{10} \mathrm{C}_5+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_3\)
= \(\left({ }^{10} \mathrm{C}_5+{ }^{10} \mathrm{C}_4\right)+\left({ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_3\right)\)
= \({ }^{11} C_5+{ }^{11} C_4\)
= \({ }^{12} \mathrm{C}_5=\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}\)
= 792

Question 22.
Find the number of injections ofaset A with 5 elements to a set B with 7 elements.
Solution:
If a set A has m elements and the set B has n elements, then the number of injections from A into B is \(\mathrm{n}_{\mathrm{m}}\) if m ≤ n and 0 if m > n.
Given n = 7, m = 5
∴ The number of injections from A to B is \({ }^7 \mathrm{P}_5\) = 7. 6 . 5 . 4 . 3 = 2520.

Question 23.
Find the number of ways in which 4 letters can be put in 4 addressed envelopes so that no letter goes into the envelope meant for it. [TS -May 2016]
Solution:
The number of derangements of n distinct things is
\(\mathrm{n} !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}-\frac{1}{5 !}+\ldots \ldots+(-1)^{\mathrm{n}} \frac{1}{\mathrm{n} !}\right)\)
Required number of ways is \(4 !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)\) = 12 – 4 + 1 = 9.

Question 24.
A man has 4 sons and there are 5 schools within his reach. In how many ways can he admit his sons in the schools so that no two of them will be in the saine school?
Solution:
The number of ways of admitting four sons into five schools if no two of them will be in the same school.
\({ }^n P_r={ }^5 P_4\) = 5 . 4 . 3 . 2 = 120.

Question 25.
If there are 25 railway stations on a railway line, how many types of single second class tickets must be printed, so as to enable a passenger to travel from one station to another?
Solution:
Number of stations on a railway line = 25
Num ber of single different second class tickets must be printed so as to enable a passenger to travel from one station to another = Number of ways of arranging two station names out of 25 station names = \({ }^{25} \mathrm{P}_2\)
= 25 . 24 = 600.

Question 26.
In a class, there are 30 students on the new year day, every student posts a greeting card to all his/her classmates. Find the total number of greeting cards posted by them.
Solution:
Total number of students in a class = 30.
Total number of greeting cards posted by all the students to their classmates = number of ways of arranging names of two students from 30 names of students
= \({ }^n P_r={ }^{30} P_2\)
= 30 × 29 = 870.

Question 27.
Find the number of 4 letter words that can be formed using the letters of the word PISTON in which atleast one letter is repeated. [AP – Mar. 2015]
Solution:
The given word has six letters.
When repetition is allowed:
The number of four letter words that can be formed using these six letters when repetition is allowed is \(n^r=6^4\) = 6 . 6 . 6 . 6 = 1296.

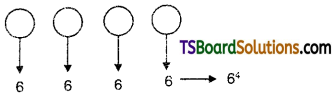
When repetition is not allowed:
The number of four letter words that can be formed using these letters of the six letters when repitition is not allowed is
\({ }^n \mathrm{P}_{\mathrm{r}}={ }^6 \mathrm{P}_4\) = 360

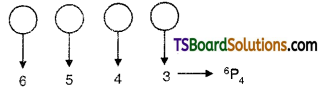
The number of four letter words in which atleast one letter repeated is \(n^r-{ }^n P_r=6^4-{ }^6 P_4\) = 1296 – 360 = 936.

Question 28.
A number lock has 3 rings and each ring has 9 digits 1, 2, 3, ……………, 9. Find the maximum number of unsuccessful attempts that can be made by a persoti who tries to open the lock without knowing the key code.
Solution:

Each ring can be rotated in 9 different ways.
The total no. of different ways in which three kings can be rotated is = 9³ = 9 . 9 . 9 = 729
Out of these attempts, only one attempt is successful attempt.
Therefore, the maximum no. of unsuccessful attempts is 729 – 1 = 728.

Question 29.
Find the number of functions from a set A containing 5 elements into a set B containing 4 elements.
Solution:
Given number of A = n(A) = m = 5
number of B = n(B) = n = 4
Set A contains 5 elements and set B contains 4 elements.
The total number of functions from set A containing m elements to set B containing n elements is \(n^m=4^5\) = 1024.

Question 30.
Find the number of bijections from a set A contaIning 7 elements onto itself.
Solution:
Given n(A) = n = 7.
∴ The number of bijections from set A with n elements to set B with same number of elements ‘n’, A is n!.
The number of bijections from set A with 7 elements onto itself = 7!
= 7. 6 . 5 . 4 . 3 . 2 . 1 = 5040.

Question 31.
Find the number of ways of arranging 7 persons around a circle.
Solution:
Given number of persons, n = 7.
∴ The number of ways of arranging 7 persons around a circle is
(n – 1)! = (7 – 1)! = 6!
= 6 . 5 . 4 . 3 . 2 . 1 = 720.

Question 32.
Find the number of ways of preparing a chain with 6 different coloured beads. [TS – Mar. ‘19, 16; March ‘08]
Solution:
Neglecting the directions of beads in the chain.
Number of ways of preparing a chain with 6 different coloured beads = \(\frac{(n-1) !}{2}\)
= \(\frac{(6-1) !}{2}=\frac{5 !}{2}=\frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2}\) = 60.

Question 33.
Find the number of ways of arranging the Chief Minister and 10 Cabinet Ministers at a circular table so that the Chief Minister always sits in a particular seat.
Solution:
Total number of persons = 11
Chief Minister can sit in a particular seat in one way.
Now, remaining positions are well defined relative to Chief Minister.
Hence, the remaining can sit in 10 places in 10! ways.
∴ The number of required arrangements = 10! × 1
= 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3628800.

Question 34.
Find the number of ways of arranging the letters of the word a⁴ b³ c⁵ in its expanded form.
Solution:
The expanded form of a⁴ b³ c⁵ is a . a . a . a . b . b . b . c . c . c . c . c.
This word has 12 letters in which there are 4a’s, 3b’s, 5c’s.
∴ They can be arranged in \(\frac{12 !}{4 ! 3 ! 5 !}\) ways.

Question 35.
There are 4 copies (alike) each of 3 different books. Find the number of ways of arranging these 12 books in a shelf in a single row.
Solution:
We have 12 books in which 4 books are alike of 1 kind. 4 books are alike of 2nd kind and 4 books are alike of 3rd kind.
Hence, they can be arranged in a shelf in a row in \(\frac{12 !}{4 ! 4 ! 4 !}\) ways = \(\frac{12 !}{(4 !)^3}\) ways.

Question 36.
Find the number of ways of arranging the letters of the word INDEPENDENCE. [TS – May 2016; March ’09, May ’13].
Solution:
Given word is INDEPENDENCE
There are 12 letters in INDEPENDENCE, in which there are 3 Ns are alike. 2 D’s are alike, 4 E’s are alike, and rest are different.
∴ The no. of required arrangements = \(\frac{12 !}{3 ! \cdot 2 ! \cdot 4 !}\)

Question 37.
Find the number of ways of arranging the letters of the word MATHEMATICS. [AP & TS – Mar. ’18; May ’97, ’10, March ’11, ’06]
Solution:
Given word is MATHEMATICS.
The word MATHEMATICS contains 11 letters in which there are , 2 M’s are alike, 2 A’s are alike, 2 T’s are alii ice and rest are different.
∴ The no. of required arran igements 11! = \(\frac{11 !}{2 ! \cdot 2 ! \cdot 2 !}\).

Question 38.
Find the number of ways of arranging the letters of the word INTERMEDIATE. [AP -Mar. ’19; May 2016; May ’14, Board Paper]
Solution:
Given word is INTERMEDIATE.
The word INTERMEDIATE contains 121 letters in which there are 2 I’s are alike, 2 T’s are alike, 3 E’s are alike and rest are different.
∴ The no. of required arrangements = \(\frac{12 !}{2 ! \cdot 2 ! \cdot 3 !}\).

Question 39.
Find the number of 7 digit numbers that can be fonned using 2, 2, 2, 3, 3, 4 4.
Solution:
In the given seven digits, there are three 2’s, two 3’s, two 4’s.
∴ The number of seven digited numbers that can be formed using th given digits = \(\frac{7 !}{3 ! \cdot 2 ! \cdot 2 !}\).

Question 40.
Find the number of ways of selecting 7 members from a continent of 10 soldiers.
Solution:
The number of ways of selecting 7 members out of 10 soldiers is \({ }^{10} \mathrm{C}_7\) = 120.

Question 41.
A set A has 8 elements, find the number of subsets of A, containing atleaist 6 elements.
Solution:
The no. of subsets of A containing atlast 6 elements then the number of subsets of A containing 6 or 7 or 8 elements.
Number of subsets of A containing exactly 6 elements = \({ }^8 \mathrm{C}_6\)
Number cf subsets of A containing exactly 7 elements = \({ }^8 \mathrm{C}_7\)
Number of :ubsets of A containing exactly 8 elements = \({ }^8 \mathrm{C}_8\)
The nurrber of subsets of A containing at least 6 elements = \({ }^8 \mathrm{C}_6+{ }^8 \mathrm{C}_7+{ }^8 \mathrm{C}_8\)
= \({ }^8 \mathrm{C}_2+{ }^8 \mathrm{C}_1+{ }^8 \mathrm{C}_0\)
= \(\frac{8 \cdot 7}{2 \cdot 1}\) + 8 + 1
= 28 + 8 – 1 = 37.

Question 42.
Find the number of ways of selecting 4 boys and 3 girls from a group of 8 boys and 5 girls. [TS – Mar. 2015]
Solution:
4 boys can be selected from the given boys in \({ }^8 \mathrm{C}_4\) ways.
3 girls can be seleted from the given 5 girls in \({ }^5 \mathrm{C}_3\) ways.
∴ The required number of selections is \({ }^8 \mathrm{C}_4 \cdot{ }^{! 5} \mathrm{C}_3\) = \(\frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1} \frac{5 \cdot 4}{2 \cdot 1}\) = 700.

Question 43.
If there are 5 alIke pens, 6 alike pencils and 7 alike erasers, find the number of ways of selecting any number of (one or
more ) things out of them.
Solution:
The required number of ways is (p + 1) (q + 1) (r + 1) – 1
= (5 + 1) (6 + 1) (7 + 1) – 1
= 6 . 7 . 8 – 1
= 336 – 1 = 335.

Question 44.
To pass an examination a student has to pass in each of the three papers. In how many ways can a student fail in the exaimination? [TS- May 2015]
Solution:
For each of the three papers there are two choices P or F.
There are 2³ = 8 choices.
But a student passes only il he/she passes in all papers.
∴ Required number of ways = 2³ – 1 = 7.

Question 45.
In a class, there are 30 students. If each student plays a chess game with each of the other student, then find the total number of chess games played by them.
Solution:
Number of students in a class is 30.
Since each student plays a chess game with each of the student the total number of games played by them = \({ }^{30} \mathrm{C}_2\)
= \(\frac{30 \cdot 29}{2}\) = 435.

Question 46.
Find the number of diagonals of a polygon with 12 sides. [AP – May 2015]
Solution:
Number of sides of a polygon = 12
Number of diagonals of a n – sided polygon = \({ }^n C_2\) – n
∴ Number of diagonals of 12 sided polygon = \({ }^{12} \mathrm{C}_2\) – 12 = 54.

Question 47.
If \({ }^{\mathrm{n}} \mathrm{P}_3\) = 1320, find n. [May ‘08, March ‘05]
Solution:
12

Question 48.
If \({ }^{(n+1)} P_5:{ }^n P_6\) = 2 : 7, find n. [March ‘10, ‘07]
Solution:
11

Question 49.
If \({ }^{18} P_{(r-1)}:^{17} P_{(r-1)}\) = 9 : 7, find ‘r’.
Solution:
5

Question 50.
FInd the number of different chains that can be prepared using 7 different coloured beads. [AP – Mar. 2017]
Solution:
360