TS Inter 1st Year Maths 1A Matrices Formulas

Learning these TS Inter 1st Year Maths 1A Formulas Chapter 3 Matrices will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1A Matrices Formulas

→ Matrix: If the real or complex numbers are arranged in the form of a rectangular or square array consisting the complex numbers in horizontal and vertical lines, then that arrangement is called a matrix.
Ex: A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 0 & -6
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
4 & -3
\end{array}\right]\)

→ Order of a matrix: A matrix ‘A1 is said to be of type (or) order (or) size m × n (read as m by n), if the matrix A’ has m rows and n’ columns.

→ Square matrix: A matrix ‘A’ is said to be a square matrix if the number of rows in A is equal to the number of columns in A.
Ex: \(\left[\begin{array}{cc}
1 & -1 \\
0 & 4
\end{array}\right]\)_2×2
\(\left[\begin{array}{ccc}
2 & 0 & 1 \\
4 & -1 & 2 \\
7 & 6 & 9
\end{array}\right]\)_2×2

→ Trace of a matrix : If ‘A’ is a square matrix then the sum of elements in the principle diagonal of A’ is called trace of A’. It is denoted by tra A .
Ex: A = \(\left[\begin{array}{ccc}
2 & 0 & 1 \\
4 & -1 & 2 \\
7 & 6 & 9
\end{array}\right]\)
The elements of the principle diagonal = 2, – 1, 9
Tra (A) = 2 + (- 1) + 9 = 10.

→ Null matrix : A matrix ‘A’ is said to be a zero matrix or null matrix of every element of A is equal to zero.
Ex: O₂ = \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
O_3×2 = \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0 \\
0 & 0
\end{array}\right]\)

→ Upper triangular matrix: A square matrix A = [a_ij]_n×n is said to be an upper triangular matrix if a_ij, = 0, whenever i > i.
Ex: \(\left[\begin{array}{ccc}
2 & -1 & 5 \\
0 & 3 & 6 \\
0 & 0 & 1
\end{array}\right]_{3 \times 3}\)

→ Lower triangular matrix :
A square matrix A = [a_ij]_n×n is said to he a lower triangular matrix if a_ij, = 0 whenever i < j .
Ex: \(\left[\begin{array}{ccc}
2 & 0 & 0 \\
1 & 3 & 0 \\
5 & 4 & 6
\end{array}\right]_{3 \times 3}\)

→ Triangular matrix : A square matrix. A is said to be a triangular matrix ifA is either an upper triangular matrix or a lower triangular matrix.
Ex: \(\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 3 & 0 \\
7 & 5 & 2
\end{array}\right]_{3 \times 3}\)

→ Diagonal matrIx : A square matrix, A is said to be a diagonal matrix if A is both upper triangnlar and lower triangular matrix. (or) A square matrix in which every element is equal to zero except those of principle diagonal of the matrix Is a diagonal matrix.
Ex: \(\left[\begin{array}{ccc}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & -1
\end{array}\right]_{3 \times 3}\)

→ Scalar matrix : A diagonal matrix, A is said to be a scalar matrix if all elements in the principle diagonal are equal.
Ex: \(\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]_{2 \times 2}\)
\(\left[\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right]_{3 \times 3}\)

→ Unit matrix : A diagonal matrix is said to be a unit matrix if every element in the principle diagonal is equal to unity. It is denoted by 1.
Ex: I₂ = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
I₃ = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

→ Transpose of a matrix: The matrix obtained by changing the rows of a given matrix, A into columns is called transpose of ‘A’. It is denoted by A^T or A’.
Ex: A = \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & 2 & 3
\end{array}\right]\) then A^T = \(\left[\begin{array}{cc}
2 & 1 \\
3 & 2 \\
-1 & 3
\end{array}\right]\)

→ Symmetric matrix : A square matrix, A is said to be a symmetric matrix, if A^T = A.
Ex: If A = \(\left[\begin{array}{lll}
2 & 3 & 1 \\
3 & 4 & 5 \\
1 & 5 & 7
\end{array}\right]\), then A^T = \(\left[\begin{array}{lll}
2 & 3 & 1 \\
3 & 4 & 5 \\
1 & 5 & 7
\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{lll}
2 & 3 & 1 \\
3 & 4 & 5 \\
1 & 5 & 7
\end{array}\right]\) = A
A is a symmetric matrix.

→ Skew symmetric matrix : A square matrix A’ is said to be a skew symmetric matrix, if A^T = – A.
Ex: A = \(\left[\begin{array}{ccc}
0 & 1 & -2 \\
-1 & 0 & 3 \\
2 & -3 & 0
\end{array}\right]\), then AT = \(\left[\begin{array}{ccc}
0 & 1 & -2 \\
-1 & 0 & 3 \\
2 & -3 & 0
\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ccc}
0 & -1 & 2 \\
1 & 0 & -3 \\
-2 & 3 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & 1 & -2 \\
-1 & 0 & 3 \\
2 & -3 & 0
\end{array}\right]\) = -A
A is a skew symmetric matrix.

→ Adjoint of a matrix : The transpose of the matrix obtained by replacing the elements of a square matrix. A by the corresponding cofactors is called the adjoint matrix of A. It is denoted by Adi A or adj A.

→ Inverse of a square matrix : A sqiictre matrix A is said to be an invertible matrix, if there exists a square matrix, B such that AB = BA = I. The matrix B is called inverse of A’.
If A is a non-singular matrix, then A is invertible and A^-1 = \(\frac{{adj} A}{{det} A}\)

→ Sub matrix : A matrix obtained by deleting some rows or columns or both of a matrix is called a sub matrix of the given matrix.
Ex: If A = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 2
\end{array}\right] \cdot\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right] \cdot\left[\begin{array}{ll}
2 & 3 \\
3 & 1 \\
2 & 0
\end{array}\right]\) then some matrices of A are \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 2
\end{array}\right] \cdot\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right] \cdot\left[\begin{array}{ll}
2 & 3 \\
3 & 1 \\
2 & 0
\end{array}\right]\), [0]

→ Rank of a matrix : Let ‘A’ be a non zero matrix. The rank of A is defined as the maximum of the orders of the non singular square sub-matrices of A. The rank of a null matrix is defined ^ as zero. The rank of a matrix A is denoted by rank [A].

→ Rank of 3 × 3 matrix : Suppose A is a non-zero 3 × 3 matrix, then

• If A is a non – singular then its rank is 3.
• If A is a singular matrix and if at least one of its 2 × 2 sub matrix is non-singular, then the rank of A is 2.
• If A is a singular matrix and every 2×2, sub matrix is also singular, then the rank of ’A’ is 1.

→ Properties of matrices :

• If A and B are two matrices of same type, then A + B = B + A.
• If A, B and C are three matrices of same type then (A + B) + C = A + (B + C).
• If confirmability is assured for the matrices A, B and C then A(BC) = (AB)C.
• If confirmability is assured for the matrices A, B and C then
  (a) A(B + C) = AB + AC
  (b) (B + C) A = BA + CA.
• If A is any matrix then (A^T)^T = A.
• If A and B are two matrices of same type then (A + B)^T = A^T + B^T.
• If A and B are two matrices for which confirmability for multiplication is assured then (AB)^T = B^T. A^T.
• If I is the identity matrix of order n then for every square matrix A of order n. AI = IA = A.
• If A is an invertible matrix then A^-1 is also invertible and (A^-1)^-1 = A.
• If A and B are two invertible matrices of same type then AB is also invertible and (AB)^-1 = B^-1. A^-1.
• If A is an invertible matrix then A is also invertible and (A^T)^-1 = (A^-1)^T

→ Methods of solving linear equations :
1. Cramer’s rule : Let a₁x + b₁y + c₁z = d₁
a₂x + b₂y + c₂z = d₂
a₃x + b₃y + c₃z = d₃
be a system of linear equations

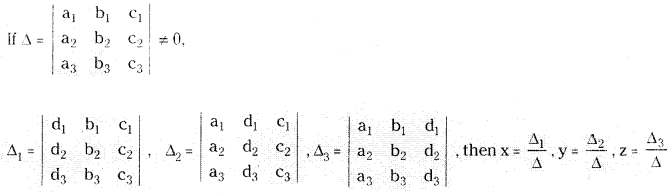
2. Matrix inversion method : If ‘A’ is a non-singular matrix then the solution of AX’ = B is X = A^-1 B.

3. Gauss Jordan method : Let a₁x + b₁y + c₁z = d₁
a₂x + b₂y + c₂z = d₂
a₃x + b₃y + c₃z = d₃
be a system of linear equations. If the augmented matrix \(\left[\begin{array}{llll}
\mathrm{a}_1 & \mathrm{~b}_1 & \mathrm{c}_1 & \mathrm{~d}_1 \\
\mathrm{a}_2 & \mathrm{~b}_2 & \mathrm{c}_2 & \mathrm{~d}_2 \\
\mathrm{a}_3 & \mathrm{~b}_3 & \mathrm{c}_3 & \mathrm{~d}_3
\end{array}\right]\) can be reduced to the form \(\left[\begin{array}{llll}
1 & 0 & 0 & \alpha \\
0 & 1 & 0 & \beta \\
0 & 0 & 1 & \gamma
\end{array}\right]\) by using elementary row transformations then x = α, y = β, z = γ, i.e., unique solution is the solution.

i) In the above matrix \(\left[\begin{array}{llll}
1 & 0 & 0 & \alpha \\
0 & 1 & 0 & \beta \\
0 & 0 & 1 & \gamma
\end{array}\right]\) is called final matrix of the system of equations.

ii) In the final matrix, if ‘O’ is obtained in place of 1 and in the same rows last element α or β or γ is
a) ‘O’ then the system has infinite number of solutions.
b) non-zero then the system of equations has no solution.

→ The system of non-homogeneous equations AX = D has

• a unique solution if rank [A] = rank [AD] = 3
• Infinitely many solutions if rank [A] = rank [AD] < 3
• No solution if rank [A] * rank [AD],

→ The system of homogeneous equations AX = O has

• The trivial solution only if Rank [A] = 3 = The number of unknowns (variables)
• An infinite number of solutions (non-trivial solution), if Rank of A less than the number of unknowns (variables) < 3.