TS Inter 2nd Year

Students can go through TS Inter 2nd Year Chemistry Notes 1st Lesson Solid State will help students in revising the entire concepts quickly.

TS Inter 2nd Year Chemistry Notes 1st Lesson Solid State

→ Solids are of two types. They are crystal-line solids and amorphous solids.

→ Crystalline solids are of four types. They are :

• Covalent solid
• Ionic solid
• Molecular solid and
• Metallic solid.

→ Depending on the type of attractive forces between molecules the molecular solids are again categorised into three types :

• Non – polar molecular solids: In which atoms such as Ar, Kr, Xe etc., or molecules of covalent compounds are held together by weak van der Waal’s forces. These solids have low m.pts and the particles are widely separated than in close packed ionic or metallic lattices.
• Polar molecular solids: In which molecules are held together by relatively stronger dipole-dipole interactions. These solids are soft and non – conductors of electricity. Their m.pts are higher than those of non – polar molecular solids e.g., solid CO₂.
• Hydrogen bonded molecular solids : are those in which molecules participate in hydrogen bonding. In crystals of benzoic acid, hydrogen bonds cause the association into dimers which are then held together van der Waal’s forces. These are also non – conductor of electricity.

→ The smallest repetitive unit of a crystal lattice which is used to describe the lattice is called the unit cell. Crystals possess the same symmery as their constituent unit cells.

→ In a simple or primitive cubic lattice the lattice points are located at the corners of each unit cell and can contribute only 1/8 of each particle at the corner to the unitj cell shared by unit cells in space lattice, So a simple cubic unit cell has particle per unit cell.

→ In a body centred cubic unit cell particles are located at the centre of the ceil as well as at the corners.
8 (at corners) × \(\frac{1}{8}\) + 1 (at body centre) × 1
= 2 particles.

→ In a face centred cubic unit cell atoms are found at the centre of the six faces of the cell as well as at each of the eight corners. The number of particles per unit cell in fee is
6 (at centre of each face) × \(\frac{1}{2}\) + 8 (at corners) × \(\frac{1}{8}\) (at comers) = 4 particles.

→ In hep and ccp structures the coordination number i.e., the number of surrounding atoms in contact with atom is 12.

→ The void created when six spherical particles are contact with each other is called octahedral void or octahedral hole.

→ The void created when four spherical particles are in contact with each other called tetrahedral void or tetrahedral hole.

→ In a close packed structure of N atoms there are 2N tetrahedral voids and N octahedral voids because the octahedral voids are larger than tetrahedral voids.

→ When X – rays are incident on a crystal face, they are reflected by the atoms in different planes.

→ Bragg’s equation is useful to calculate the distance between the repeating planes of particles in crystals from the reflected x – rays. It is, nλ = 2d sin θ where n is an integer like 1, 2, 3 and represents order of reflection, λ is the wavelength of the x – rays used and d is the distance between the repeating places.

→ A Schottky defect consists of a pair of holes in the crystalline lattice due to the absence of one positive ion and one negative ion.

→ Frenkel defect is created when an ion occupies an interstitial site instead occupying its correct lattice site.

→ The metal excess defect is due to the absence of a negative ion from its lattice site leaving a hole which is occupied by an electron, there by maintaining the electrical balance.

→ The solids having F – centres have colour and the intensity of the colour increases with increase in the number of F – centres.

→ Metal excess defects also occurs when an extra positive ion occupies an interstitial position in the lattice and to maintain ele-ctrical neutrality one electron is included in an interstitial position e.g. ZnO, CaO, Cr₂O₃ and Fe₂O₃.

→ The solids with metal excess defect contain free electrons and behave as n – type semi-conductor.

→ Metal deficiency defect is due to the absence of a positive ion from its lattice point and the charge can be balanced by an adjacent metal ion having an extra positive charge e.g. FeO, NiO, FeS and Cul.

→ Crystals with metal deficiency defects are p – type semiconductors.

→ Doping is a process of mixing pure silicon or germanium with an impurity.

→ n-type semiconductors (n – stands for negative) are obtained due to metal excess defect or by adding trace amounts of V or 15th group elements (P, As) to pure silicon or germanium.

→ p-type semiconductors (p – stands for positive) are obtained due to metal defi-ciency defect or by doping with impurity atoms containing less electrons (i.e., atoms of III or 13th group).

→ Diamagnetic solids contain paired electrons (↑↓) and repel the external magnetic field.

→ Paramagnetic solids contain unpaired electrons and are attracted into the applied magnetic field.

→ In ferromagnetic solids there occurs mag-netic interaction between the neighbouring centres (domains) and the electrons in these centres interact in parallel direction (↑↑↑↑↑). This interaction leads to an increase in magnetic moment. Iron, cobalt and nickel are ferromagnetic substances.

→ In antiferromagnetic solids there occurs magnetic interaction between the neigh-bouring centres and the electrons in these centres interact in antiparallel (↑↓ ↑↓ ↑↓) direction which leads to a decrease in magnetic moment e.g., [Cu(CH₃COO)^– H₂O]₂;
VO (CH₃COO)₂, MnO, MnO₂, Mn₂O₃.

→ In ferrimagnetic solids there occurs mag-netic interactions between the neighbou-ring centres and the electrons in these cen-tres interact in such a way which leads to the presence of uncompensated spins (↑↑↓↑↑↓) in the opposite direction resulting some magnetic moment e.g. magnetite (Fe₃O₄); ferrite M FeO₄ (where M = Mg²⁺, Cu , Zn²⁺ etc.)

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B System of Circles Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B System of Circles Important Questions Very Short Answer Type

Question 1.
Show that the circles given by the equations x² + y² + 4x – 2y – 11 = 0, x² + y² – 4x – 8y + 11 = 0 intersect each other orthogonally.
Solution:
Given equations of the circles are
x² + y² + 4x – 2y – 11 = 0 ……(1)
x² + y² – 4x – 8y + 11 = 0 ………(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 2, f = -1, c = -11
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = -2, f = -4, c’ = 11
Now, 2gg’ + 2ff’ = 2(2)(-2) + 2(-1)(-4)
= -8 + 8
= 0
c + c’ = -11 + 11 = 0
∴ 2gg’ + 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 2.
Show that the circles given by the equations x² + y² – 2lx + g = 0, x² + y² + 2my – g = 0 intersect each other orthogonally.
Solution:
Given equations of the circles are
x² + y² – 2lx + g = 0 ……..(1)
x² + y² + 2my – g = 0 …………(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -l, f = 0, c = g
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 0, f’ = m, c’ = -g
Now, 2gg’+ 2ff’ = 2(-l)(0) + 2(m)(0)
= 0 + 0
= 0
c + c’ = g – g = 0
∴ 2gg’+ 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 3.
Show that the circles given by the equations x² + y² – 2x – 2y – 7 = 0, 3x² + 3y² – 8x + 29y = 0, intersect each other orthogonally. [May ’15 (AP)]
Solution:
Given equations of the circles are
x² + y² – 2x – 2y – 7 = 0 ……….(1)
3x² + 3y² – 8x + 29y = 0
\(x^2+y^2-\frac{8}{3} x+\frac{29}{3} y=0\) ………(2)
Comparing (1) with
x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = -1, c = -7
Comparing (2) with
x² + y² + 2g’x + 2f’y + c’ = 0, we get

c + c’ = -7 + 0 = -7
∴ 2gg’ + 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 4.
Find ‘k’ if the pair of circles x² + y² + 4x + 8 = 0, x² + y² – 16y + k = 0 are orthogonal. [Mar.’16 (AP)]
Solution:
Given equations of the circles are
x² + y² + 4x + 8 = 0 ………(1)
x² + y² – 16y + k = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 2, f = 0, c = 8
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 0, f = -8, c’ = k
Since the given circles are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(2)(0) + 2(0)(-8) = 8 + k
⇒ 0 + 0 = 8 + k
⇒ k = -8

Question 5.
Find ‘k’ if the pair of circles x² + y² + 2by – k = 0, x² + y² + 2ax + 8 = 0 are orthogonal.
Solution:
Given equations of the circles are
x² + y² + 2by – k = 0 ……….(1)
x² + y² + 2ax + 8 = 0 ……..(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 0, f = b, c = -k
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = a, f’ = 0, c’ = 8
Since the given circles are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(0)(a) + 2(b)(0) = -k + 8
⇒ 0 + 0 = -k + 8
⇒ k = 8

Question 6.
Find ‘k’ if the pair of circles x² + y² – 6x – 8y + 12 = 0, x² + y² – 4x + 6y + k = 0 are orthogonal.
Solution:
Given equations of the circles are
x² + y² – 6x – 8y + 12 = 0 ……….(1)
x² + y² – 4x + 6y + k = 0 ………(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -3, f = -4, c = 12
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = -2, f’ = 3, c’ = k
Since the given circles are orthogonal then
2gg’+ 2ff’ = c + c’
⇒ 2(-3)(-2) + 2(-4)(3) = 12 + k
⇒ 12 – 24 = 12 + k
⇒ k = -24

Question 7.
Find the angle between the circles x² + y² – 12x – 6y + 41 = 0, x² + y² + 4x + 6y – 59 = 0. [(AP) May ’19, ’18; (TS) ’15, Mar. ’17, ’15]
Solution:
Given equations of the circles are
x² + y² – 12x – 6y + 41 = 0 ……….(1)
x² + y² + 4x + 6y – 59 = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -6, f = -3, c = 41
∴ C₁ = (-g, -f) = (6, 3)

Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 2, f = 3, c’ = -59
∴ C₂ = (-g’, -f’) = (-2, -3)

Question 8.
Find the angle between the circles x² + y² + 4x – 14y + 28 = 0, x² + y² + 4x – 5 = 0. [(AP) May ’17]
Solution:
Given equations of the circles are
x² + y² + 4x – 14y + 28 = 0 ………(1)
x² + y² + 4x – 5 = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0, we get
g = 2, f = -7, c = 28
∴ C₁ = (-g, -f) = (-2, 7)

Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 2, f’ = 0, c’ = -5
∴ C₂ = (-g’, -f’) = (-2, 0)

If ‘θ’ is the angle between the circles then

Question 9.
Find the angle between the circles x² + y² + 6x – 10y – 135 = 0, x² + y² – 4x + 14y – 116 = 0.
Solution:
Given equations of the circles are
x² + y² + 6x – 10y – 135 = 0 ………(1)
x² + y² -4x + 14y – 116 = 0 ………..(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 3, f = -5, c = -135
∴ C₁ = (-g, -f) = (-3, 5)

Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = -2, f’ = 7, c’ = -116
∴ C₂ = (-g’, -f’) = (2, -7)

Question 10.
Show that the angle between the circles x² + y² = a² , x² + y² = ax + ay is \(\frac{3 \pi}{4}\). [(TS) Mar. ’20, ’16, May ’16 (TS) Mar. ’14]
Solution:
Given equations of the circles are
x² + y² – a² = 0 ………..(1)
x² + y² – ax – ay = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 0, f = 0, c = -a²
C₁ = (-g, -f) = (0, 0)

Question 11.
Find the equation of the radical axis of the circles x² + y² – 2x – 4y – 1 = 0, x² + y² – 4x – 6y + 5 = 0. [(AP) May ’16]
Solution:
Given equations of the circles are
S = x² + y² – 2x – 4y – 1 = 0
S’ = x² + y² – 4x – 6y + 5 = 0
∴ The equation of the radical axis of the given circle is S – S’ = 0
⇒ (x² + y² – 2x – 4y – 1) – (x² + y² – 4x – 6y + 5) = 0
⇒ x² + y² – 2x – 4y – 1 – x² – y² + 4x + 6y – 5 = 0
⇒ -2x – 4y – 1 + 4x + 6y – 5 = 0
⇒ 2x + 2y – 6 = 0
⇒ x + y – 3 = 0

Question 12.
Find the equation of the radial axis of the circles x² + y² – 5x + 6y + 12 = 0 and x² + y² + 6x – 4y – 14 = 0.
Solution:
Given equations of the circles are
S = x² + y² – 5x + 6y + 12 = 0
S’ = x² + y² + 6x – 4y – 14 = 0
The equation of the radical axis of the circles S’ = 0 and S = 0 is S – S’ = 0
⇒ x² + y² – 5x + 6y + 12 – (x² + y² + 6x – 4y – 14) = 0
⇒ x² + y² – 5x + 6y + 12 – x² – y² – 6x + 4y + 14 = 0
⇒ -11x + 10y + 26 = 0
⇒ 11x – 10y – 26 = 0

Question 13.
Find the equation of the radical axis of the circles 2x² + 2y² + 3x + 6y – 5 = 0 and 3x² + 3y² – 7x + 8y – 11 = 0. [(AP) Mar. ’17]
Solution:
Given equations of the circles are
S = 2x² + 2y² + 3x + 6y – 5 = 0

Question 14.
Find the equation of the common chord of x² + y² – 4x – 4y + 3 = 0, x² + y² – 5x – 6y + 4 = 0. [(TS) Mar. ’20]
Solution:
Given equations of the circles are
S = x² + y² – 4x – 4y + 3 = 0
S’ = x² + y² – 5x – 6y + 4 = 0
The equation of the common chord (radical axis) of the given circles is S – S’ = 0
⇒ (x² + y² – 4x – 4y + 3) – (x² + y² – 5x – 6y + 4) = 0
⇒ x² + y² – 4x – 4y + 3 – x² – y² + 5x + 6y – 4 = 0
⇒ x + 2y – 1 = 0

Question 15.
Find the equation of the common chord of (x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b).
Solution:
Given equations of the circles are
S = (x – a)² + (y – b)² = c²
⇒ x² + a² – 2ax + y² + b² – 2by – c² = 0
⇒ x² + y² – 2ax – 2by + a² + b² – c² = 0
S’ = (x – b)² + (y – a)² = c²
⇒ x² + b² – 2bx + y² + a² – 2ay – c² = 0
⇒ x² + y² – 2bx – 2ay + a² + b² – c² = 0
The equation of the common chord (radical axis) of the given circles is S – S’ = 0
⇒ x² + y² – 2ax – 2by + a² + b² – c² – (x² + y² – 2bx – 2ay + a² + b² – c²) = 0
⇒ x² + y² – 2ax – 2by + a² + b² – c² – x² – y² + 2bx + 2ay – a² – b² + c² = 0
⇒ -2ax – 2by + 2bx + 2ay = 0
⇒ 2x(b – a) – 2y(b – a) = 0
⇒ x – y = 0

Question 16.
Find the equation of the common tangent of x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0.
Solution:
Given equations of the circles are
S = x² + y² + 10x – 2y + 22 = 0
S’ = x² + y² + 2x – 8y + 8 = 0
The equation of the common tangent at the point of contact (radical axis) of the circles S = 0, S’ = 0 is S – S’ = 0
⇒ x² + y² + 10x – 2y + 22 – (x² + y² + 2x – 8y + 8) = 0
⇒ x² + y² + 10x – 2y + 22 – x² – y² – 2x + 8y – 8 = 0
⇒ 8x + 6y + 14 = 0
⇒ 4x + 3y + 7 = 0

Question 17.
If the angle between the circles x² + y² – 12x – 6y + 41 = 0 and x² + y² + kx + 6y – 59 = 0 is 45°, find k. [(TS) Mar. ’18]
Solution:
Given equations of the circles are
x² + y² – 12x – 6y + 41 = 0 ………(1)
x² + y² + kx + 6y – 59 = 0 ………..(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -6, f = -3, c = 41
C₁ = (-g, -f) = (6, 3)

Given that, θ = 45°
If ‘θ’ is the angle between the circles, then

Question 18.
Show that the circles given by the equations x² + y² – 2x + 4y + 4 = 0, x² + y² + 3x + 4y + 1 = 0 intersect each other orthogonally.
Solution:
Given equations of the circles are
x² + y² – 2x + 4y + 4 = 0 ……..(1)
x² + y² + 3x + 4y + 1 = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = 2, c = 4
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = \(\frac{3}{2}\), f’ = 2, c’ = 1
Now, 2gg’+ 2ff’ = 2(-1)(\(\frac{3}{2}\)) + 2(2)(2)
= -3 + 8
= 5
c + c’ = 4 + 1 = 5
∴ 2gg’+ 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 19.
Find the equation of the radical axis of the circles x² + y² – 3x – 4y + 5 = 0, 3(x² + y²) – 7x + 8y – 11 = 0. [(TS) May ’17]
Solution:
Given equations of the circles are
S = x² + y² – 3x – 4y + 5 = 0
S’ = 3[x² + y²] – 7x + 8y – 11 = 0
\(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}=0\)
∴ The equation of the radical axis of the given circles is S – S’ = 0

Question 20.
Find the equation of the radical axis of the circles x² + y² + 4x + 6y – 7 = 0, 4(x² + y²) + 8x + 12y – 9 = 0. [(TS) May ’19. Mar. ’19. (AP) ’19]
Solution:
Given equations of the circles are
S = x² + y² + 4x + 6y – 7 = 0
S’ = 4(x² + y²) + 8x + 12y – 9 = 0
⇒ x² + y² + 2x + 3y – \(\frac{9}{4}\) = 0
The equation of the radical axis of the given circles is S – S’ = 0
⇒ x² + y² + 4x + 6y – 7 – (x² + y² + 2x + 3y – \(\frac{9}{4}\)) = 0
⇒ x² + y² + 4x + 6y – 7 – x² – y² – 2x – 3y + \(\frac{9}{4}\) = 0
⇒ 2x + 3y – 7 + \(\frac{9}{4}\) = 0
⇒ 8x + 12y – 28 + 9 = 0
⇒ 8x + 12y – 19 = 0

Question 21.
Find the equation of the common chord of the pair of circles x² + y² + 2x + 3y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
Solution:
Given equations of the circles are
S = x² + y² + 2x + 3y + 1 = 0
S’ = x² + y² + 4x + 3y + 2 = 0
The equation of the common chord (radical axis) of the given circles is S – S’ = 0
⇒ x² + y² + 2x + 3y + 1 – x² – y² – 4x – 3y – 2 = 0
⇒ -2x – 1 = 0
⇒ 2x + 1 = 0

Telangana TSBIE TS Inter 2nd Year Physics Study Material 5th Lesson Electrostatic Potential and Capacitance Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 5th Lesson Electrostatic Potential and Capacitance

Very Short Answer Type Questions

Question 1.
Can there be electric potential at a point with zero electric intensity? Give an example.
Answer:
Yes. At the mid point of line joining two similar charges, electric field is zero but potential will exist. Ex : Inside a charged hallow spherical shell field is zero but potential is not zero.

Question 2.
Can there be electric intensity at a point with zero electric potential? Give an example.
Answer:
Yes. At the midpoint or on the equatorial line of an electric dipole potential is zero but eletric field is not zero.

Question 3.
What are meant by equipotential surfaces?
Answer:
An equipotential surface is a surface with constant value of potential at all points on the surface.

Question 4.
Why is the electric field always at right angles to the equipotential surface? Explain.
Answer:
If the electric field is not normal to the equipotential surface, then the work done in moving a charge from one point to the other will not be zero, which is a contradiction, thus the field is normal to equipotential surface.

Question 5.
Three capacitors of capacitances 1 µF, 2 µF, and 3 µF are Connected in parallel.
a) What is the ratio of charges?
b) What is the ratio of potential differences?
Answer:
Charge q = CV
a) ⇒ q ∝ C ⇒ q₁ : q₂ : q₃ = C₁ : C₂ : C₃ = 1 : 2 : 3
b) In parallel combination potential across combination is
Constant : V₁ : V₂ : V₃ = 1 : 1 : 1

Question 6.
Three capacitors of capacitances 1 µF, 2 µF, and 3 µF are connected in series
a) What is the ratio of charges?
b) What is the ratio of potential differences?
Answer:
q = CV, in series combination charge q’ is constant on each capacitor.
a) ⇒ q₁ : q₂ : q₃ = 1 : 1 : 1
b) V ∝ \(\frac{1}{C}\) ⇒ V₁ : V₂ : V₃ : \(\frac{1}{1}: \frac{1}{2} : \frac{1}{3}\) = 6 : 3 : 2

Question 7.
What happens to the capacitance of a parallel plate capacitor if the area of its plates is doubled?
Answer:
The capacity of a parallel plate capacitor

when area is doubled (A’ = 2A) then capacity is also doubled.

Question 8.
The dielectric strength of air is 3 × 10⁶ Vm^-1 at certain pressure. A parallel plate capacitor with air in between the plates has a plate separation of 1 cm. Can you charge the capacitor to 3 × 10⁶ V?
Answer:
No ; The dielectric strength of air means the max. electric field that the medium will with-stand. Given E_max = 3 × 10⁶Vm^-1,

Short Answer Questions

Question 1.
Derive an expression for the electric potential due to a point charge. [Mar. ’16; TS Mar. ’16]
Answer:
Consider a point charge Q at ‘O’ and a unit positive charge is placed at ‘P’, distance r’. The force acting on it is

Let dW be the work done in moving this test charge through dr’ towards ‘O’.

The total work done in bringing this test charge from r’ = ∞ to r’ = r is

By the definition of potential this work- done is the electrostatic potential at that point.
∴ V = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r}\)

Question 2.
Derive an expression for the electrostatic potential energy of a system of two point charges and find its relation with electric potential of a charge.
Answer:
Consider a system of two charges q₁ and q₂ with position vectors \(\overline{\mathrm{r_1}}\) and \(\overline{\mathrm{r_2}}\) relative to origin at points A & B respectively. The electrostatic potential due to q₁ at B is V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1}{\mathrm{r}_2}\)
The work done in bringing q2 from infinity to the
point B is W = q₂ V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1\mathrm{q}_2}{\mathrm{r}_{12}}\)

As the electrostatic force is a conservative force, this work done will be stored as energy in the system.

Hence this work done is called electrostatic potential energy ‘U’ of the system of the charges q₁ and q₂.

Question 3.
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field.
Answer:
Consider a dipole with charges + q and – q placed in a uniform electric field E as shown.

Forces are F₁ = qE and F₂ = – qE but dipole experiences torque given by

Let ‘dW’ be the small amount of work done in rotating the dipole through d0 without any angular acceleration.
dW = τdθ
The toal work done to deflect from θ₁ to θ₂ is

W = pE [cos θ₁ – cos θ₂]
This work done is stored as potential energy in the dipole.
If the dipole is intially parallel to \(\overline{\mathrm{E}}\) and now turned through an angle θ, the work- done is
W = pE [cosθ – cosθ] = pE [ 1 – cosθ]
Then the potential energy of the dipole in this displaced position is U = U₀ + W = – pE + pE [ 1 – cos θ] = – pE cos θ = – \(\overline{\mathrm{E}}.\overline{\mathrm{E}}\)

Question 4.
Derive an expression for the capacitance of a parallel plate capacitor. [AP Mar. 18, 16, May 17. 16; TS Mar. 18. May 18. 16]
Answer:
A parallel plate capacitor consists of two plane conducting plates of area A separated by a small distance d’. Let the medium between the plates is vacuum.
Let the surface charge densities of the plates (1) and (2) be + σ and – σ.
The electric fields in regions I and III will be

In the inner region i.e., II the fields due to these plates will add up and given by

as ‘d’ is the separation between the plates, the potential difference between the plates given by

Question 5.
Explain the behaviour of dielectrics in an external field. [AP Mar. ’19]
Answer:
All dielectrics are two types 1) Non-polar dielectrics 2) Polar dielectrics.
a) For Non-polar dielectrics the centre of all positive and negative charges will coincide. Ex: O₂ molecule. So net dipole moment of these molecules is zero.

When these molecules are placed in an external electric field the positive and negative charges will be displaced in opposite directions. So they will develop induced dipolemoment. Total dipolemoment of these substances is the sum of all such dipolements and dielectrics are said to be polarised.

b) In case of polarised dielectrics in a molecule the centres of all positive charges and negative charges are separate. So they will develop some resultant dipolemoment. Under the absence of external electric field these dipole moments are random and resultant dipolemoment is zero.

When they are placed in external electric field these dipoles are arranged in an order and the dipolemoments are polarised.
The dipole moment per unit volume (\(\overline{\mathrm{p}}\)) is called polarisation.
\(\overline{\mathrm{p}}\) = χ\(\overline{\mathrm{E}}\)
where χ is called electric susceptibility.

Long Answer Questions

Question 1.
Define electric potential. Derive an expression for the electric potential due to an electric dipole and hence the electric potential at a point (a) the axial line of electric dipole (b) on the equatorial line of electric dipole.
Answer:
Electric potential :
Work done to bring the unit positive charge from infinity to the point in the electric field is called potential.
Potential due to point charge q at a distance r (V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)

Electric dipole :
Two equal and opposite charges (q, -q) separated by a distance (say 2a) is called electric dipole.

Potential due to an electric dipole :
Consider an electric dipole with charge q, – q.

Let separation between them is 2a. Let P is a point at a distance r’ from centre of dipole.

Join qp, -qp and OP. Let the line OP makes an angle ‘θ’ with the dipole axis (q, – q).
Total potential at P is V =\(\frac{1}{4 \pi \varepsilon_0}\) \(\frac{q}{r_1}-\frac{q}{r_2}\)

From geometry r²₁ = r² + a² – 2a r cos θ and
r²₂ = r² + a² + 2a r cos θ
These equations are rearranged as

But 2aq = p. dipole moment

Potential at any point on axis of dipole :
Consider a dipole of charges q, – q with separation ‘2a’. At point p potential V is given by V = V₁ + V₂

Potential at any point on equatorial line of dipole :
Let P is any point on equatorial line of a dipole at a distance r.

∴ Potential on equatorial line of dipole is zero.

Question 2.
Explain series and parallel combination of capacitors. Derive the formula for equivalent capacitance in each combination. [TS Mar. 19, 17, 15; AP May 16, June 15, Mar. 15]
Answer:
Capacitors in series :
If number of capacitors are connected in such a way that the charge on the plates of every one of them is same, then the capacitors are said to be
“connected in series”.

Explanation :
Let three capacitors C₁, C₂ and C₃ are connected in series as shown.

The charge q on the plates of the capacitors is same, let, V₁, V₂ and V₃ be the potential differences across C₁, C₂ and C₃ respectively. Let V be the p.d across the combination
then V = V₁ + V₂ + V₃

The reciprocal of equivalent capacity = the sum of reciprocal values of individual capacities of the combination.

Capacitors in parallel :
If a number of capacitors connected in such a way that the p. d between the plates of every one of them is same, then the capacitors are said to be “connected in parallel”.

Explanation :
Let the capacitors of capacities C₁, C₂ and C₃ connected in parallel as shown.

The potential difference across each condenser is same and is equal to V. Let q₁ and q₂ and q₃ be the charges on the plates of the capacitors.
∴ q = q₁ + q₂ + q₃. here q₁ = C₁V, q₂ = C₂V, q₃ = C₃V
If C is equivalent capacity of the combination, the C = \(\frac{p}{V}\) ⇒ q = CV
∴ CV = C₁V + C₂V + C₃V
∴ C = C₁ + C₂ + C₃
The equivalent capacity of the parallel combination = the sum of the capacities of the capacitors.

Question 3.
Derive an expression for the energy stored in a capacitor. What is the energy stored when the space between the plates is filled with a dielectric.
a) With charging battery disconnected?
b) With charging battery connected in the circuit?
Answer:
Let ‘q’ be the charge on the plates of a capacitor and V be the potential difference between plates. The work done dW in charging the capacitor with an additional charge dq.
dW = Vdq
⇒ dW = \(\frac{q}{C}\)dq (∵ q = CV)
The total work done in charging the plates it to a charge Q = W

This work done in charging the capacitor stored as electrostatic potential energy.

Effect of dielectric :
a) When charging battery is disconnected:
The charge on the plates remain constant, but capacity increases.

∴ The energy stored will get reduced to \(\frac{1}{K}\) th of initial value.

b) When charging battery remain connected the p.d across the capacitor remains same, but the capacity and the charge increases.

∴ The energy stored will increases by K times initial value.

Problems

Question 1.
An elementary particle of mass in’ and charge + e initially at a very large distance is projected with velocity ‘v’ at a much more massive particle of charge + Ze at rest. The closest possible distance of approach of the incident particle is
Answer:
At closest approach kinetic energy of charged particle = electrostatic potential between them.

Given : Mass of particle = m; velocity = V
∴ KE = 1/2 mv² → (1)
Charge of particle q₁ = e ; Charge on massive particle q₂ = Ze
∴ Electrostatic potential

Question 2.
In a hydrogen atom the electron and proton are at a distance of 0.5 Å. The dipole moment of the system is
Answer:
Distance between electron and proton = 0.5Å = 0.5 × 10^–10 m
Charge on proton = Charge on electron = 1.6 × 10^-19 C
Dipole moment = charge × separation between charges
∴ Dipolemoment p = 1.6 × 10^-19 × 0.5 × 10^-10 = 0.8 × 10^-29 = 8 × 10^-30 Cm

Question 3.
There is a uniform electric field in the XOY plane represented by (\(\mathbf{40} \hat{\mathbf{i}}+\mathbf{30} \hat{\mathbf{j}}\)) Vm^-1. If the electric potential at the origin is 200 V, the electric potential at the point with co-ordinates (2m, lm) is
Answer:
Intensity of electric field E = \(\mathbf{40} \hat{\mathbf{i}}+\mathbf{30} \hat{\mathbf{j}}\)
Position of the given point = 2 m, 1 m
i.e., 2m along \(\hat{\mathbf{i}}\) and lm along \(\hat{\mathbf{j}}\). Potential
= \(\overline{\mathrm{E}}.\overline{\mathrm{r}}\) =40 × 2 + 30 × 1 = 80 + 30 = 110V
Potential at origin = 200V.
Potential difference at point p = 200 – 110 = 90V.

Question 4.
An equilateral triangle has a side length L. A charge + q is kept at the centroid of the triangle. P is a point on the perimeter of the triangle. The ratio of the minimum and maximum possible electric potentials for the point P is
Answer:
Length of side = L. Charge at centroid = + q
Let ‘O’ be the centroid.
Centroid will divide the angle bisector in the ratio 2 : 1.
∴ Maximum distance from centroid is say ‘2a’ then minimum distance from centroid is ‘a’.

Ratio of minimum potential to maximum potential is 1 : 2.

Question 5.
ABC is an equilateral triangle of side 2m. There is a uniform electric field of intensity 100 V/m in the plane of the triangle and parallel to BC as shown. If the electric potential at A is 200 V, then the electric potentials at B and C are respectively
Answer:
Side of triangle L = 2m
Intensity of electric field = 100 V/m
(parallel to BC)

Potential at A = 200V.
Let D is the mid point of BC.
Now AD is an equipotential line with a potential of 200V.
Potential at B = 200 + E. r where r₁ = BD = 1m.
∴ Potential at B = 200 + 100 × 1 = 300 V
∴ Potential at C = Pot. at D – E. r₂ where
r₂ = 1m
V_D = 200 – 100 × 1 = 100v
Note : By definition potential is the work done against the field.

Question 6.
An electric dipole of moment p is called in a uniform electric field E, with p parallel to E. It is then rotated by an angle q. The work done is
Answer:
Electric dipolemoment = p;
Intensity of electric field = E
p and E are parallel ⇒ θ = 0;
Angle rotated = q
Work done by external force to rotate the dipole without acceleration
W = PE (cos θ₁ – cos θ₂)
Here θ₁ = 0 and θ₂ = q
∴ Work done = PE (cos 0 – cos q) = pE (1 – cos q)

Question 7.
Three identical metal plates each of area ‘A’ are arranged parallel to each other, ‘d’ is the distance between the plates as shown. A battery of V volts is connected as shown. The charge stored in the system of plates is

Answer:
Area of plates = A, Separation between the plates = d.
Potential supplied by battery = V.
From given arrangement it is a parallel combination of two identical capacitors.

Question 8.
Four identical metal plates each of area A are separated mutually by a distance d and are connected as shown. Find the capacity of the system between the terminals A and B.

Answer:
Area of each plate = A
Total separation between the plates = d
Separation between two adjacent plates = d₁ = d/3
Capacity of each capacitor \(C_1=\frac{\varepsilon_0 A}{d_1}=\frac{\varepsilon_0 A}{d / 3}=\frac{3 \varepsilon_0 A}{d}\)
For two similar capacitors in series the resultant

Question 9.
In the circuit shown the battery of’V’ volts has no internal resistance. All three con-densers are equal in capacity. Find the condenser that carries more charge.

Answer:
In the diagram the battery polarities are as show.

So all capacitors are connected in parallel. Since capacity ‘C’ is same and potential of battery V is same charge will exist on all the three capacitors.

Question 10.
Two capacitors A and B of capacities C and 2C are connected in parallel and the combination is connected to a battery of volts. After the charging is over, the bat-tery is removed. Now a dielectric slab of K = 2 is inserted between the plates of A so as to fill file space completely. The energy lost by the system during the sharing of charges is
Answer:
Capacity C₁ = C; Capacity C₂ = 2C
Let the capacitors are charged to the potential V.
Charge on capacitor Q₁ = CV
Charge on capacitor Q₂ = 2CV
Total charge Q = Q₁ + Q₂ = 3CV → (1)
Energy stored U₁ = \(\frac{1}{2}\)CV² +\(\frac{1}{2}\)(2C) V²
\(\frac{CV^2}{2}\) + CV² = \(\frac{3}{2}\)CV² → (2)
Now dielectric is introduced in C₁
New capacity = KC₁
Where K₁ = 2 and C₁ = C ∴ C_N = 2C.
Cherge is not changed because battery is disconnected from circuit.

Question 11.
A condenser of certain capacity is charged to a potential V and stores some energy. A second condenser of twice the capacity is to stored half the energy of the first, find to what potential one must be charged?
Answer:
For 1st capacitor
Let capacity of capacitor = x; Potential = V
Energy stored U₁ = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × V²₁ → (1)
For 2nd capacitor capacity C₂ = 2x
Energy stored = \(\frac{1}{2}\)U₁ = \(\frac{1}{2}.\frac{1}{2}\) × V²₁ → (2)
But for 2nd capacitor energy stored

Intext Question and Answers

Question 1.
Two charges 5 × 10^-8 C and -3 × 10^-8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Answer:
There are two charges,
q₁ = 5 × 10^-8C, q₂ = -3 × 10^-8C
Distance between the two charges, d = 16 cm = 0.16 m
Consider a point P on the line joining the two charges, as shown in the given figure.

Let the electric potential (V) at point P be zero. It is at a distance r from q₁
Potential at point P is the sum of potentials caused by charges q₁ and q₂ respectively.

Therefore, the potential is zero at a distance of 10 cm from the positive charge between the charges.

Suppose point P is outside the system of two charges at a distance s from the negative charge, where potential is zero, as shown in the following figure.

Therefore, the potential is zero at a distance of 40 cm from the positive charge outside the system of charges.

Question 2.
A regular hexagon of side 10 cm has a charge 5 µC at each of its vertices. Calculate the potential at the centre of the hexagon.
Answer:
The given figure shows six equal amount of charges, q, at the vertices of a regular hexagon.

Charge, q = 5 µC = 5 × 10^-6C
Side of the hexagon, l = AB = BC = CD = DE
= EF = FA = 10 cm
Distance of each vertex from centre O, d = 10 cm

Therefore, the potential at the centre of the hexagon is 2.7 × 10⁶ V.

Question 3.
Two charges 2 µC and -2 µC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Answer:
(a) The situation is represented in the given figure.

An equipotential surface is the plane on which total potential is zero everywhere. This plane is normal to line AB.

The plane is located at the mid-point of line AB because the magnitude of charges is the same.

(b) The direction of the electric field at every point on this surface is normal to the plane in the direction of AB.

Question 4.
A spherical conductor of radius 12 cm has a charge of 1.6 × 10^-7C distributed uniformly on its surface. What is the electric field
(a) Inside the sphere?
(b) Just outside the sphere?
(c) At a point 18 cm from the centre of the sphere?
Answer:
(a) Radius of the spherical conductor, r = 12 cm = 0.12 m
Charge is uniformly distributed over the conductor, q = 1.6 × 10^-7 C
Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.

(b) Electric field E just outside the conductor is given by the relation,

Therefore, the electric field just outside the sphere is 10⁵ NC^-1.

(c) Electric field at a point 18 m from the centre of the sphere = E₁
Distance of the point from the centre, d = 18 cm = 0.18 m

Therefore, the electric field at a point 18 cm from the centre of the sphere is 4.4 × 10⁴ N/C.

Question 5.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (lpF = 10^-12 F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Answer:
Capacitance between the parallel plates of the capacitor, C = 8 pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k = 1
Capacitance, C, is given by the formula,
C = \(\frac{k\varepsilon_{0}A}{d}=\frac{\varepsilon_{0}A}{d}\) ………….. (i)
Where, A = Area of each plate; ∈₀ = permittivity of free space
If distance between the plates is reduced to half, then new distance, d’ = \(\frac{d}{2}\).
Dielectric constant of the substance filled in between the plates, k’ = 6
Hence, capacitance of the capacitor
becomes C’ = = \(\frac{k\varepsilon_{0}A}{d}=\frac{6\varepsilon_{0}A}{d_2}\) ………… (ii)
From eqn (i) & (ii)
C’ = 2 × 6C = 12 C = 12 × 8 = 96 pF
Therefore, the capacitance between the plates is 96 pF.

Question 6.
Three capacitors each of capacitance 9 pF are connected in series. [AP Mar ’14]
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Answer:
(a) Capacitance of each of the three capacitors, C = 9 pF
Equivalent capacitance (C’) of the combination of the capacitors is given by the relation,

Therefore, total capacitance of the combination is 3µF.

(b) Supply voltage, V = 100 V
Potential difference (V’) across each capacitor is equal to one-third of the supply voltage.
∴ V’ = \(\frac{V}{3}=\frac{120}{3}\) = 40V
Therefore, the potential difference across each capacitor is 40 V.

Therefore, total capacitance of the combination is pµF.
(b) Supply voltage, V = 100 V

Question 7.
Three capacitors of capacitances 2µF, 3µF and 4µF are connected in parallel.
(i) What is the total capacitance of the combination?
(ii) Determine the charge on each capacitor, if the combination is connected to a 200V supply. [AP Mar. 1 7; TS May 1 7, June 15]
Answer:
(a) Capacitances of the given capacitors are
C₁ = 2µF ; C₂ = 3µF ; C₃ = 4µF
For the parallel combination of the capacitors, equivalent capacitor C’ is given by the algebraic sum, C’ = 2 + 3 + 4 = 9
Therefore, total capacitance of the combination is pµF.

(b) Supply voltage, V = 100 V
The voltage through all the three capacitors is same = V = 100V
Charge on a capacitor of C and potential difference V is given by the relation,
q = CV … (i)
For C = 2µF, Charge = VC = 100 × 2 = 200µC = 2 × 10^-4 C
For C = 3µF,
Charge = VC = 100 × 3 = 300 µC = 3 × 10^-4 C
For C = 4µF,
Charge = VC = 100 × 4 = 200µC = 4 × 10^-4 C

Question 8.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel.
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
(a) Capacitances of the given capacitors are
C₁ = 2 pF ; C₂ = 3 pF ; C₃ = 4 pF
For the parallel combination of the capacitors, equivalent capacitor C’ is given by the algebraic sum, C’ = 2 + 3 + 4 = 9
Therefore, total capacitance of the combination is 9 pF.

(b) Supply voltage, V = 100 V
The voltage through all the three capacitors is same = V = 100 V
Charge on a capacitor of capacitance C and potential difference V is given by the relation,
q = VC … (i)
For C = 2 pF, Charge = VC = 100 × 2 = 200 pC = 2 × 10“10 C
For C = 3 pF,
Charge = VC = 100 × 3 = 300 pC = 3 × 10^-10 C
For C = 4 pF,
Charge = VC = 100 × 4 = 200 pC = 4 × 10^-10 C

Question 9.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10^-3 m² and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Answer:
Area of each plate of the parallel plate capacitor, A = 6 × 10^-3 m²
Distance between the plates, d = 3 mm
= 3× 10^-3 m; Supply voltage, V = 100 V
Capacitance C of a parallel plate capacitor is given by, C = \(\frac{\varepsilon_{0}A}{d}\)
Where, ε₀ = Permittivity of free space

Potential V is related with the charge q and capacitance C as V = \(\frac{q}{C}\)
∴ q = VC = 100 × 17.71 × 10^-12 = 1.771 × 10^-9C.
Therefore, capacitance of the capacitor is 17.71 pF and charge on each plate is 1.771 × 10^-9C.

Question 10.
Expalin what would happen if in the capacitor given in Exercise 8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Answer:
(a) Dielectric constant of the mica sheet, k = 6;
Initial capacitance, C = 1.771 × 10^-11 F
New capacitance,
C’ = kc = 6 × 1.771 × 10^-11 = 106 pF;
Supply voltage, V = 100 V
New charge,
q’ C’V = 6 × 1.771 × 10^-9 = 1.06 × 10^-8C
Potential across the plates remains 100 V.

(b) Dielectric constant, k = 6 ;
Initial capacitance, C = 1.771 × 10^-11 F
New capacitance,
C’ = kC = 6 × 1.771 × 10^-11 = 106 pF

If supply voltage is removed, then there will be no effect on the amount of charge in the plates.
∴ Charge = 1.771 × 10^-9 C
Potential across the plates is gives by,

Question 11.
A 12 pF capacitor is connected to a 50V battery. How much electrostatic energy is stored in the capacitor?
Answer:
Capacitor of the capacitance, C = 12 pF = 12 × 10^-12 F ; Potential difference, V = 50 V
Electrostatic energy stored in the capacitor is given by the relation,
E = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × 12 × 10^-12 × (50)² = 1.5 × 10^-8 J
Therefore, the electrostatic energy stored in the capacitor is 1.5 × 10^-8 J.

Question 12.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Answer:
Capacitance of the capacitor, C = 600 pF ; Potential difference, V = 200 V Electrostatic energy stored in the capacitor is given by,
E = \(\frac{1}{2}\)cV² = \(\frac{1}{2}\) × (600 × 10^-12) × (200)² = 1.2 × 10⁵ J
If supply is disconnected from the capacitor and another capacitor of capacitance C = 600 pF is connected to it, then equivalent capacitance (C’) of the combination is given by,

New electrostatic energy can be calculated as
E’ = \(\frac{1}{2}\) × C’ × V² = \(\frac{1}{2}\) × 300 × (200)² = 0.6 × 10^-6J
Loss in electrostatic energy = E – E’
= 1.2 × 10^-5 -0.6 × 10^-5 = 0.6 × 10^-5 = 6 × 10^-6 J
Therefore, the electrostatic energy lost in the process is 6 × 10^-6 J.

Question 13.
In a Van de Graaff type generator, a spherical metal shell is to be a 15 × 10⁶ V electrode. The dielectric strength of the gas surrounding the electrode is 5 × 10⁷ Vm^-1. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)
Answer:
Potential difference, V = 15× 10⁶V ;
Dielectric strength of the surrounding gas = 5 × 10⁷ V/m
Electric field intensity, E = Dielectric strength = 5 × 10⁷ V/m
Minimum radius of the spherical shell required for the purpose is given by,

Hence, the minimum radius of the spherical shell required is 30 cm.

Question 14.
A small sphere of radius r₁ and charge q₁ is enclosed by a spherical shell of radius r₂ and charge q₂. Show that if q₁ is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q₂ on the shell is.
Answer:
According to Gauss’s law, the electric field between a sphere and a shell is determined by the charge q₁ on a small sphere. Hence, the potential difference, V, between the sphere and the shell is independent of charge q₂. For positive charge q₁, potential difference V is always positive.

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Very Short Answer Type

Question 1.
Simplify \(\frac{(\cos \alpha+i \sin \alpha)^4}{(\sin \beta+i \cos \beta)^8}\)
Solution:

Question 2.
Find the value of (1 – i)⁸. [March ’07]
Solution:

Let 1 – i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = – 1
Hence,
√2 cos θ = 1, √2 sin θ = – 1
cos θ = \(\frac{1}{\sqrt{2}}\), sin θ = – \(\frac{1}{\sqrt{2}}\)
∴ θ lies in the Q₄
∴ θ = – \(\frac{\pi}{4}\)
1 – i = √2 [cos (- \(\frac{\pi}{4}\)) + i sin (\(\frac{\pi}{4}\))]
= √2 (cos \(\frac{\pi}{4}\) – i sin \(\frac{\pi}{4}\))
Now,
(1 – i)⁸ = [√2 (cos (\(\frac{\pi}{4}\)) – i sin (\(\frac{\pi}{4}\)))]⁸
= 16 (cos 2π – i sin 2π)
= 16 (1 – i . 0) = 16.

Question 3.
Find the value of (1 + i)¹⁶. [Board Paper]
Solution:

Let (1 – i) = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = 1, √2 sin θ = 1
cos θ = \(\frac{1}{\sqrt{2}}\), sin θ = \(\frac{1}{\sqrt{2}}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{4}\)
∴ 1 + i = √2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))
Now,
(1 + i)¹⁶ = [√2 (cos(\(\frac{\pi}{4}\)) + i sin (\(\frac{\pi}{4}\))]¹⁶
= (√2)¹⁶ (cos 4π + i sin 4π)
= 256 (1 + i (0)) = 256

Question 4.
Find the value of \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5\). [May 2004]
Solution:

Question 5.
If A, B, C are angles of a triangle such that x = cis A, y = cis B, z = cis C, then find the value of xyz.
[Mar. ’98, ’94 AP – Mar. ’18, ’16, ’15, May ’16; TS – May ’15]
Solution:
Since, A, B, C are angles of a triangle then A+ B + C = π
Given that,
x = cis A, y= cis B, z = cis C
Now, xyz = cis A . cis B . cis C
= cis (A + B + C)
= cos (A + B + C) + i sin (A + B + C)
= cos π + i sin π
= – 1 + i (0) = – 1.

Question 6.
If x = cis θ then find the value of \(\left(x^6+\frac{1}{x^6}\right)\).
[TS – Mar. 2018, May 2016, May ’14, ’07, March ’14, ’04, ’91]
Solution:
Given, x = cis θ
= cos θ + i sin θ
Now, x⁶ = (cos θ + i sin θ)⁶
= cos 6θ + i sin 6θ
\(\frac{1}{x^6}\) = cos 6θ – i sin 6θ
Now,
x⁶ + \(\frac{1}{x^6}\) = cos 6θ + i sin 6θ + cos 6θ – i sin 6θ = 2 cos 6θ.

Question 7.
Find the cube roots of 8.
Solution:
Let, x = \(\sqrt[3]{8}=(8)^{1 / 3}=8^{1 / 3} 1^{1 / 3}\)
= \(\left(2^3\right)^{1 / 3}\) [cos 0° + i sin 0°]^1/3
= 2[cos(2kπ + 0°) + isin(2kπ + 0°)]^1/3
k = 0, 1, 2
= 2[cos 2kπ + isin2kπ]^1/3
= 2 \(\left[\cos \frac{2 \mathrm{k} \pi}{3}+\mathrm{i} \sin \frac{2 \mathrm{k} \pi}{3}\right]\)
= 2 cis \(\frac{2 \mathrm{k} \pi}{3}\), k = 0, 1, 2
If k = 0
⇒ x = 2 cis 0° = 2 (cos 0 + i sin 0)
= 2 (1 + i . 0) = 2

If k = 1
⇒ x = 2 cis \(\frac{2 \pi}{3}\)
= 2 (cos \(\frac{2 \pi}{3}\) + i sin \(\frac{2 \pi}{3}\))
= \(2\left[\frac{-1}{2}+\frac{\mathrm{i} \sqrt{3}}{2}\right]=2\left[\frac{-1+\mathrm{i} \sqrt{3}}{2}\right]\) = 2ω

If k = 2
⇒ x = 2 cis \(\frac{4 \pi}{3}\)
= 2 (cos \(\frac{4 \pi}{3}\) + i sin \(\frac{4 \pi}{3}\))
= \(2\left(\frac{-1}{2}-\mathrm{i} \frac{\sqrt{3}}{2}\right)=2\left[\frac{-1-\mathrm{i} \sqrt{3}}{2}\right]\)
= 2ω²
∴ The cube roots of 8 are 2, 2ω, 2ω².

Question 8.
Prove that – ω and – ω² are roots of z² – z + i = 0, where ω and ω² are the complex cube roots of unity.
Solution:
Since ω, ω² are the cube roots of unity then
ω = \(\frac{-1+i \sqrt{3}}{2}\)
⇒ – ω = \(\frac{1-i \sqrt{3}}{2}\)

ω² = \(\frac{-1-i \sqrt{3}}{2}\)
⇒ – ω² = \(\frac{1+i \sqrt{3}}{2}\)

Given quadratic equation is z² – z + 1 = 0
Comparing with ax² + bx + c = 0
a = 1, b = – 1, c = 1
∴ The roots of the quadratic equation z² – z + 1 = 0 then
z = \(\frac{-\mathrm{b} \pm \sqrt{\mathrm{b}^2-4 \mathrm{ac}}}{2 \mathrm{a}}\)
= \(\frac{-(-1) \pm \sqrt{(-1)^2-4 \cdot 1 \cdot 1}}{2(1)}\)
= \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm i \sqrt{3}}{2}\)
∴ – ω and – ω² are the roots of z² – z + 1 = 0.

Question 9.
If 1, ω, ω² are the cube roots of unity, prove that [TS – Mar. 2016]
(1 – ω + ω²)⁶ + (1 – ω² + ω)⁶ = 128 = (1 – ω + ω²)⁷ + (1 + ω – ω²)⁷
Solution:
Given that 1, ω, ω² are the cube roots of unity then
1 + ω + ω² = 0 and ω³ = 1
(1 – ω + ω²)⁶ + (1 – ω² + ω)⁶ = (- ω – ω)⁶ + (- ω² – ω²)⁶
= (2ω)⁶ + (- 2ω²)⁶
= (- 2)⁶ ω⁶ + (- 2)⁶ ω⁶
= 64 . 1 + 64 . 1
= 64 + 64 = 128
∴ (1 – ω + ω²) + (1 – ω² + ω) = 128
and (1 – ω + ω²)⁷ + (1 + ω – ω²)⁷
= (- ω – ω)⁷ + (- ω – ω)⁷
= (- 2ω)⁷ + (- 2ω²)⁷
= (- 2)⁷ ω⁷ + (- 2)⁷ ω¹⁴
= – 128 . ω + (- 128) ω²
= – 128 (ω + ω²)
= – 128 (- 1) = 128
(1 – ω + ω²)⁷ + (1 + ω – ω²)⁷ = 128.

Question 10.
If 1, ω, ω are the cube roots of unity, prove that (a + b) (aω + bω²) (aω² + bω) = a³ + b³ (AP – Mar. 2017)
Solution:
L.H.S:
(a + b) (aω + bω²) (aω² + bω)
= (a + b) (a²ω³ + abω² + abω⁴ + b²ω³)
= (a + b) [a² . 1 + abω² + abω + b²2 . 1]
= (a + b) [a² + ab(ω² + ω) + b²]
= (a + b) (a² + ab(- 1) + b²)
= (a + b) (a² – ab + b²)
= (a³ + b³) = R.H.S.
∴ (a + b) (aω + bω²) (aω² + bω) = a³ + b³.

Question 11.
If 1, ω, ω² are the cube roots of unity, prove that x² + 4x + 7 = 0, where x = ω – ω² – 2.
Solution:
Given,
x = ω – ω² – 2
x + 2 = ω – ω²
Squaring on both sides
(x + 2)² = (ω – ω²)²
x² + 4x + 4 = ω² + ω⁴ – 2ω³
x² + 4x + 4 = ω² + ω – 2 . 1
x² + 4x + 4 = – 1 – 2
x² + 4x + 4 + 1 + 2 = 0
x² + 4x + 7 = 0.

Question 12.
If α, β are the roots of the equation x² + x + 1 = 0 then prove that α⁴ + β⁴ + α^-1 β^-1 = 0. [AP – May 2015]
Solution:
Since, α, β are the roots of the equation x² + x + 1 = 0 then
α = ω, β = ω²

L.H.S:
α⁴ + β⁴ + α^-1 β^-1 = α⁴ + β⁴ + \(\frac{1}{\alpha} \frac{1}{\beta}\)
= ω⁴ + (ω²)⁴ + \(\frac{1}{\omega \cdot \omega^2}\)
= ω⁴ + ω⁸ + \(\frac{1}{\omega^3}\)
= ω + ω² + 1 = 0 =R.H.S.

Question 13.
If 1, ω, ω² are cube roots of unity, then prove that \(\frac{1}{2+\omega}+\frac{1}{1+2 \omega}=\frac{1}{1+\omega}\). [TS – Mar.2015] [May ’01, Mar. ’87]
Solution:
Given 1, ω, ω² are the cube roots of unity then 1 + ω + ω² = 0, ω³ = 1

L.H.S:

Question 14.
If 1, ω, ω² are cube roots of unity, then prove that (2 – ω) (2 – ω) (2 – ω) (2 – ω) = 49. [TS – Mar.2017]
Solution:
LHS:
= (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω11)
= (2 – ω) (2 – ω²) (2 – ω) (2 – ω²)
= [(2 – ω) (2 – (ω²)]²
= [4 – 2ω² – 2ω + ω³]²
= [4 – 2(ω² + ω) + 1]²
= (5 – 2(- 1))²
= 7² = 49 = R.H.S
∴ (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω¹¹) = 49

Question 15.
If 1, ω, ω² are cube roots of unity, then prove that (x + y + z) (x + yω + zω²) (x + yω² + zω) = x³ + y³ + z³ – 3xyz
Solution:
L.H.S:
= (x + y + z) (x + yω + zω²) (x + yω² + zω)
= (x + y + z) (x² + xyω² + xzω + xyω + y²ω³ + yzω² + yxω² + zyω⁴ + z²ω³)
= (x + y + z) [x² + xyω² + xzω + xyω + y² + yzω² + zxω² + zyω + z²]
= (x + y + z) [x² + y² + z² + xy(ω + ω²) + yz (ω + ω²) + zx (ω + ω²)]
= (x + y + z) [x² + y² + z² + xy (- 1) + yz (- 1) + zx (- 1)]
= (x + y + z) [x² + y² + z² – xy – yz – zx]
= x³ + y³ + z³ – 3xyz
= R.H.S
(x + y + z) (x + yω + zω²) (x + yω² + zω) = x³ + y³ + z³ – 3xyz.

Question 16.
If 1, ω, ω² are the cube roots of unity, then find the value of (a + b)³ + (aω + bω²)³ + (aω² + bω)³.
Solution:
Given that. 1, ω, ω² are the cube roots of unity, then 1 + ω + ω² = 0 and ω³ = 1.
(a + b)³ + (aω + bω²)³ + (aω² + bω)³
= a³ + b³ + 3a²b + 3ab² + a³ω³ + b³ω⁶ + 3a²bω⁴ + 3ab²ω⁵ + a³ω⁶ + b³ω³ + 3a²bω⁵ + 3ab²ω⁴
= a³ + b³ + 3a²b + 3ab² + a³ . 1 + b³ . 1 + 3a²bω + 3ab²ω² + a³ . 1 + b³ . 1 + 3a²bω^{2/sup> + 3ab2ω
= 3a3 + 3b3 + 3a2b(1 + ω + ω2) + 3ab2(1 + ω + ω2)
= 3a3 + 3b3 + 3a2b(0) + 3ab2(0)
= 3a3 + 3b3 = 3(a3 + b3)}

Question 17.
If 1, ω, ω² are the cube roots of unity, then find the value of (a + 2b)² + (aω² + 2bω)² + (aω +2bω²)²
Solution:
Given,
(a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)²
a² + 4b² + 4ab + a²ω + 4b²ω² + 4abω³ + a²ω² + 4b²ω⁴ + 4abω³
= a² + 4b² + 4ab + a²ω + 4b²ω² + 4abω³ + 4ab . 1 + a²ω² + 4b²ω + 4ab – 1
= a² (1 + ω + ω²) + 4b²(1 + ω + ω²) + 4ab + 4ab + 4ab
= a²(0) + 4b²(0) + 12ab
= 12ab

Question 18.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω + ω²)³. [TS- Mar. 2019]
Solution:
Given, (1 – ω² + ω²)³
= (- ω – ω)³
= (- 2ω)³
= – 8ω³
= – 8 – 1 = – 8.

Question 19.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸).
Solution:
Given, (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
= (1 – ω) (1 – ω²) (1 – ω) (1 – ω²)
= [(1 – ω) (1 – ω²)]²
= [1 – ω² – ω + ω³]²
= [1 – ω² – ω + 1]²
= [2 – ω – ω²]²
= (2 + 1)² = 3² = 9.

Question 20.
If 1, ω, ω² are the cube roots of unity, then find the value of \(\left(\frac{a+b \omega+c \omega^2}{c+a \omega+b \omega^2}\right)+\left(\frac{a+b \omega+c \omega^2}{b+c \omega+a \omega^2}\right)\).
Solution:

Question 21.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 + ω)³ + (1 + ω²)³.
Solution:
Given, (1 + ω)³ + (1 + ω²)³
= (- ω²)³ + (- ω)³
= – ω⁶ – ω³
= – 1 – 1 = – 2.

Question 22.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω + ω²)⁵ + (1 + ω – ω²)⁵. [AP – Mar. 2019]
Solution:
Given,
(1 – ω + ω²)⁵ + (1 + ω – ω²)⁵
= (- ω – ω)⁵ + (- ω² – ω²)⁵
= (- 2ω)⁵ + (- 2ω²)⁵
= (- 2)⁵ ω + (- 2)⁵ ω¹⁰
= – 32 ω² + (- 32)ω
= – 32 (ω² + ω)
= – 32 (- 1) = 32.

Question 23.
1f the cube roots of unity are 1, ω, ω², then find the roots of the equation (x – 1)³ + 8 = 0.
Solution:
Since, 1, ω, ω² are the cube roots of unity then 1 + ω + ω² = 0 and ω³ = 1.
Given equation is (x – 1)³ + 8 = 0
(x – 1)³ = – 8
x – 1 = \(\sqrt[3]{-8}\)
= \(\sqrt[3]{(-8) \cdot 1}\)
= – 2 (1)^1/3
= – 2 (1, ω, ω²)
= – 2, – 2ω, – 2ω²
x – 1 = – 2, – 2ω, – 2ω²
x = – 2 + 1, – 2ω + 1, – 2ω² + 1
= – 1, – 2ω + 1, – 2ω² + 1
∴ The roots of the given equation are = – 1, 1 – 2ω, 1 – 2ω².

Question 26.
Find all the roots of (1 – i√3)^1/3.
Solution:

Let 1 – i√3 = r(cos θ + i sin θ)
then r cos θ = 1, r sin θ = – √3
r = \(\sqrt{x^2+y^2}=\sqrt{(1)^2+(-\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence,
2 cos θ = 1
cos θ = \(\frac{1}{2}\)

2 sin θ = – √3
sin θ = \(-\frac{\sqrt{3}}{2}\)

∴ θ lies in the Q₄.
∴ θ = \(\frac{-\pi}{3}\)

Question 25.
Find the values of (1 + i)^2/3.
Solution:

Let. 1 + i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = 1
cos θ = \(\frac{1}{\sqrt{2}}\)

√2 sin θ = 1
sin θ = \(\frac{1}{\sqrt{2}}\)

∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{4}\).

Question 26.
Find all the values of (√3 + 1)^1/4.
Solution:

Let, √3 + 1 = r(cos θ + i sin θ)
then r cos θ = r sin θ = 1
∴ r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{(\sqrt{3})^2+1^2}\)
= \(\sqrt{3+1}=\sqrt{4}\) = 2
Hence,
2 cos θ = √3, 2 sin θ = 1
cos θ = \(\frac{\sqrt{3}}{2}\), sin θ = \(\frac{1}{2}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{6}\)
∴ √3 + i = 2 (cos \(\frac{\pi}{6}\) + i sin \(\frac{\pi}{6}\))
Now,

Question 27.
Find all the values of (- i)^1/6.
Solution:

Question 28.
Find all the values of (- 16)^1/4.
Solution:
Let, (- 16)^1/4 = (16)^1/4 . (- 1)^1/4
= (2⁴)^1/4 (- 1)^1/4
= 2 [cos π + i sin π]^1/4
= 2 [cos(2kπ + π) + isin(2kπ + π)]^1/4, k = 0, 1, 2, 3
= 2 [cos(2k + 1)π + isin(2k + 1)π]^1/4
= 2 [cos(2k + 1)\(\frac{\pi}{4}\) + i sin (2k + 1)\(\frac{\pi}{4}\)]
= 2 cis(2k + 1)\(\frac{\pi}{4}\), k = 0, 1, 2, 3
If k = 0
⇒ x = 2 cis \(\frac{\pi}{4}\)
If k = 1
⇒ x = 2 cis \(\frac{3 \pi}{4}\)
If k = 2
⇒ x = 2 cis \(\frac{5 \pi}{4}\)
If k = 3
⇒ x = 2 cis \(\frac{7 \pi}{4}\)
∴ All the values of (- 16)^1/4 are 2 cis \(\frac{\pi}{4}\), 2 cis \(\frac{3 \pi}{4}\), 2 cis \(\frac{5 \pi}{4}\), 2 cis \(\frac{7 \pi}{4}\)

Question 29.
Find all the values of (- 32)^1/5.
Solution:
Let, x = (- 32)^1/5
= (32)^1/5 (- 1)^1/5
= (2⁵)^1/5 [cos π + i sin π]^1/5
= 2 [cos π + i sin π]^1/5
= 2 [cos (2kπ + π) + i sin (2kπ + π)]^1/5
k = 0, 1, 2, 3, 4
= 2 [cos (2k + 1)π + i sin (2k + 1)π]^1/5
= 2 [cos (2k + 1)\(\frac{\pi}{5}\), i sin(2k + 1)\(\frac{\pi}{2}\)]
= 2 cis(2k + 1)\(\frac{\pi}{2}\), k = 0,1 , 2, 3, 4
If k = 0
⇒ x = 2 cis \(\frac{\pi}{5}\)
If k = 1
⇒ x = 2 cis \(\frac{3 \pi}{5}\)
If k = 2
⇒ x = 2 cis π
If k = 3
⇒ x = 2 cis \(\frac{7 \pi}{5}\)
If k = 4
⇒ x = 2 cis \(\frac{9 \pi}{5}\)
∴ All the values of (- 32)^1/5 are 2 cis \(\frac{\pi}{5}\), 2 cis \(\frac{3 \pi}{5}\), 2 cis π, 2 cis \(\frac{7 \pi}{5}\), 2 cis \(\frac{9 \pi}{5}\).

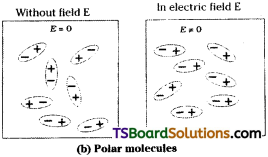
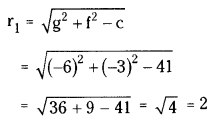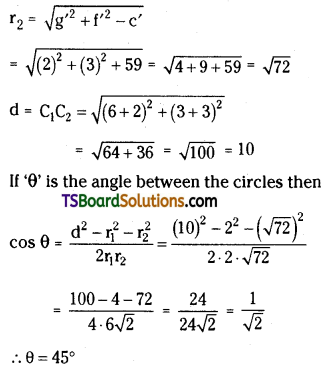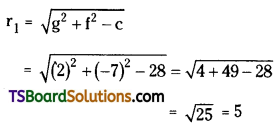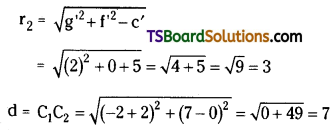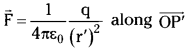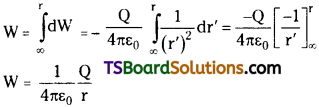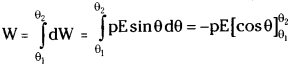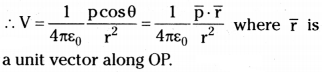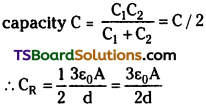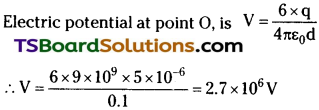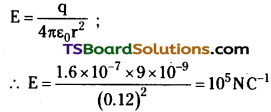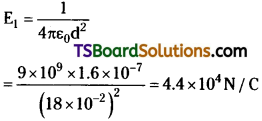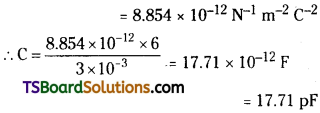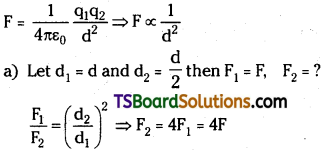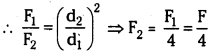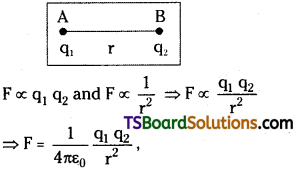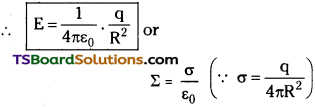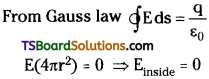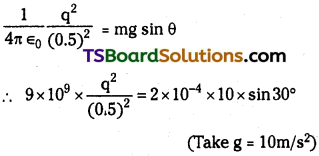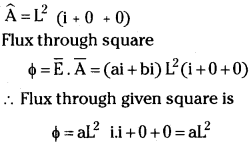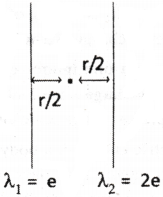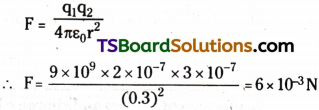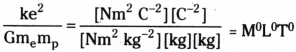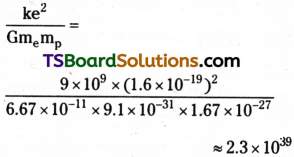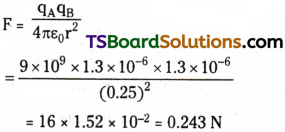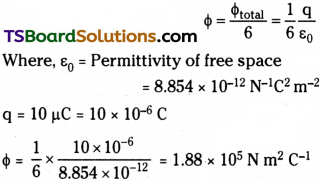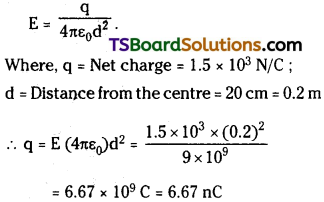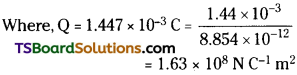Telangana TSBIE TS Inter 2nd Year Physics Study Material 4th Lesson Electric Charges and Fields Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 4th Lesson Electric Charges and Fields

Very Short Answer Type Questions

Question 1.
What is meant by the statement ‘charge is quantized’?
Answer:
The minimum charge that can be transferred from one body to another is equal to the charge of an electron ‘e’.

So charge always exists as an integral multiple of charge of electron i.e., Q = ne. (1 e = 1.6 × 10^-19 C). Therefore charge in quantized.

Question 2.
Repulsion is the sure test of charging than attraction. Why?
Answer:
A charged body can attract opposite charged body and also a neutral body. But repu¬lsion is only between two charged bodies of same polarity. Hence repulsion is sure test for charging than attraction.

Question 3.
How many electrons constitute 1 C of charge?
Answer:
Chargeq = ne; q = 1 C; e- 1.6 × 10^-19 C.

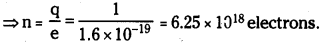
Question 4.
What happens to the weight of a body when it is charged positively?
Answer:
When a body is positively charged it looses electrons, hence its weight decreases (or) it looses weight.

Question 5.
What happens to the force between two charges if the distance between them is a) halved b) doubled?
Answer:

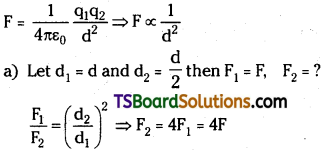
‘F’ increases four times its initial value

b) Let d₁ = d and d₂ = 2d and F₁ = F, F₂ = ?

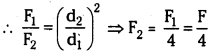
Force between them reduces to 1/4 of initial value.

Question 6.
The electric lines of force do not intersect. Why?
Answer:
The tangent drawn at a point to the line of force gives direction of electric field. If two lines intersect at point of intersection field will be in two different directions, which is not possible. Therefore electric lines of force do not intersect.

Question 7.
Consider two charges + q and – q placed at B and C of an equilateral triangle ABC. For this system, the total charge is zero. But the electric field (intensity) at A which is equidistant from B and C is not zero. Why?
Answer:
Charge is a scalar so total charge Q = q + (- q) = 0. But electric field intensity is a vector and they must be add up vectorially at any given point. So at the point A of equilateral triangle

Question 8.
Electrostatic field lines of force do not form closed loops. If they form closed loops then the work done in moving a charge along a closed path will not be zero. From the above two statements can you guess the nature of electrostatic force?
Answer:
The electrostatic force is conservative force.

Question 9.
State Gauss’s law in electrostatics. Explain its importance. [AP June 15; TS Mar. 15, May 15]
Answer:
Def :
The total electrical flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the charge enclosed by the surface.

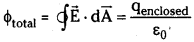
ε₀ = permittivity of free space.

Importance :
It is used to find the electric intensity due to various bodies due to charge distributions.

Question 10.
When is the electric flux negative and when is it positive?
Answer:
Electric flux, Φ = \(\overline{\mathrm{E}}.\overline{\mathrm{A}}\) = EA cos θ.
where θ = angle between \(\overline{\mathrm{E}}\) and \(\overline{\mathrm{A}}\).
If 0° < θ ≤ 90°. ⇒ Φ is positive.
When 90° < θ ≤ 180°. ⇒ Φ is negative.

Question 11.
Write the expression for electric intensity due to an infinite long charged wire at a distance radial distance r from the wire.
Answer:
The electric intensity at a point due to an infinitely long charged wire (E) = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\), λ = the linear charge density of the wire.
r = the radial distance of the point from the axis of the wire.

Question 12.
Write the expression for electric intensity due to an infinite plane sheet of charge.
Answer:
The electric intensity due to an infinite plane sheet of charge is, E = \(\frac{\sigma}{2 \varepsilon_0}\), σ – is surface charge density of the sheet.

Question 13.
Write the expression for electric intensity due to a charged conducting spherical shell at points outside and inside the shell.
Answer:
Electric field intensity due to a charged conducting spherical shell
a) At a point outside the shell intensity of electric field E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}=\frac{\sigma}{\varepsilon_0} \frac{\mathrm{R}^2}{\mathrm{r}^2}\)
q = σA = σ 4πR²

b) At a point inside the shell intensity of electric field E = 0.
Because potential inside a conducting shell is zero.

Short Answer Questions

Question 1.
State and explain Coulomb’s inverse square law in electricity. [AP May 18, 17; TS Mar. 17, ’14]
Answer:
Coulomb’s Law :
The force of attraction or repulsion between two charges is directly proportional to the product of the two charges and is inversely proportional to square of the distance between them. This force acts along the line joining the two charges.
Explanation:

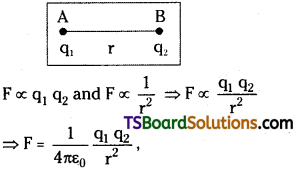
ε₀ = permittivity of free space.
ε₀ = 8.85 × 10^-12Nm²/C²

This electrostatic force between the charges depends on the nature of the medium between them.
In any medium F = \(\frac{1}{4 \pi \varepsilon} \frac{\mathrm{q_1q_2}}{\mathrm{r}^2}\)
ε = permittivity of that medium.
\(\frac{\mathrm{F_{vacuum}}}{\mathrm{F_{med}}}= \frac{\varepsilon}{\varepsilon_0} \) = ε_r = k

where ε_r (or) k is called relative permittivity or dielectric constant.

Note :- This force is an action and reaction pair i.e., \(\overline{\mathrm{F}}_{21}=-\overline{\mathrm{F}}_{21}\)
In vector form of Coulomb’s law is

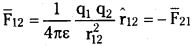
Question 2.
Define intensity of electric field at a point. Derive an expression for the intensity due to a point charge. [AP Mar. ’16]
Answer:
Intensity of electric field: It is defined as the force on a unit positive charge when placed in the electric field.

Proof :-
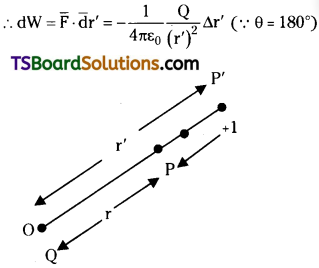
Consider a point charge ‘Q’ at O’, electric field will exist around that charge.
P = point at a distance r from the charge Q,
q₀ = Test charge placed at that point.

Due to a negative charge field is towards it.
Note : The electric field due to a point charge is non-uniform.

Question 3.
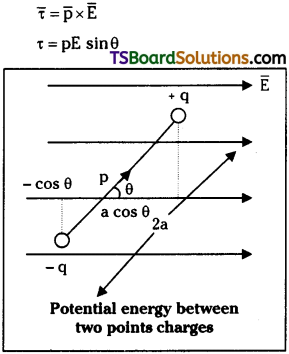
Derive the equation for the couple acting on an electric dipole in a uniform electric field. [TS Mar. ’19, May ’18; AP May ’16, ’14]
Answer:
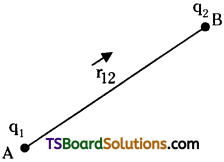
Consider electric dipole of moment ‘p’ in an uniform electric field ‘E’, situated at an angle θ with the field.

The positive charge experiences force “qE” in the direction of field and negative charge experiences as a force – qE opposite to the direction of field. Net force on the dipole is zero. But these two forces will constitute a couple, they will produce torque on the dipole.

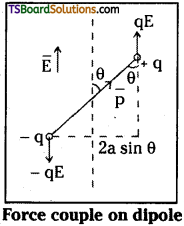
Magnitude of torque (τ) = force × perpendicular distance
= qE (AC) = qE (2a sin θ) = q(2a) E sin θ = pE sin θ
\(\bar{\tau}=\overline{\mathrm{p}} \times \overline{\mathrm{E}}\)
When \(\overline{\mathrm{p}}\) and \(\overline{\mathrm{E}}\) are in the plane of the paper then direction of torque is normal to the plane of paper.
If θ = 90° ⇒ τ_max = pE.
The electric dipole moment of a dipole is equal to the torque acting on it when placed in a uniform electric field.

Question 4.
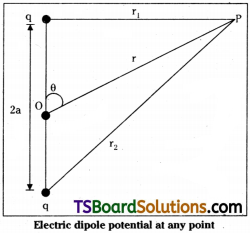
Derive an expression for the intensity of the electric field at a point on the axial line of an electric dipole. [AP Mar. 19, 18, 17, 16, May 16; TS Mar. May 16]
Answer:
Consider an electric dipole with charges q, – q with separation ‘2a’ between them.
Let p = a point on its axial line at a distance r from the mid point of the dipole
E_axial = intensity of electric field at p
E_axial = E_+q + E_-q.
The electric field at p due to the charge + q

Question 5.
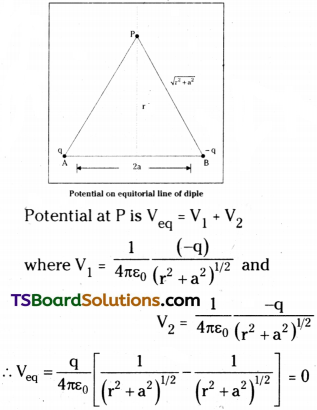
Derive an expression for the intensity of the electric field at a point on the equatorial plane of an electric dipole.
Answer:
Consider an electric dipole with charges q, -q with a separation ‘2a’ between them. Consider a point p’ on the equatorial of the dipole at a distance r from the centre of the dipole. Electric field at p is the resultant of E_+q and E_-q.
The electric field due to the charge +q at p

These are equal in magnitude. The components of E_+q and E_-q normal to the axis of the dipole cancel each other, the components along the axis will add up.

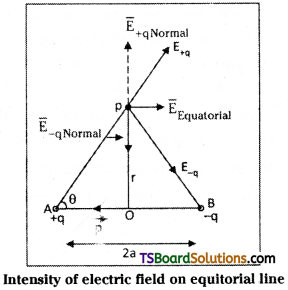
Question 6.
State Gauss’s law in electrostatics and explain its importance. [TS Mar. ’ 18,’ 15, May ‘ 17; AF June 15, Mar. 15]
Answer:
Gauss’s Law :
The total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface.

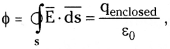
where ε₀ = permittivity of free space,
q = total cherge enclosed by the surface.

Importance:

1. Using Gauss law we can find field due to a distribution of charge.
2. Gauss’s law is often useful towards a much easier calculation of the electrostatic field when the system has symmetry.

Long Answer Questions

Question 1.
Define electric flux. Applying Gauss’s law and derive the expression for electric intensity due to an infinite long straight charged wire. (Assume that the electric field is everywhere radial and depends only on the radial distance r of the point from the wire.)
Answer:
Electric flux :
The number of electric lines of force passing normally through a given surface is called “electric flux” (Φ).

Expression for electric intensity :
Let us consider an infinitely long thin straight wire having linear charge density λ. (∵ λ= Q/L)

Consider a cylindrical Gaussian surface ABCD of length ‘l’ and radial distance r. The electric field \(\overline{\mathrm{E}}\) is radial and which perpendicular to the length of the wire.

The flux through the flat surfaces AB and CD are zero. (∵ \(\overrightarrow{E}\) ⊥ \(\overrightarrow{A}\))

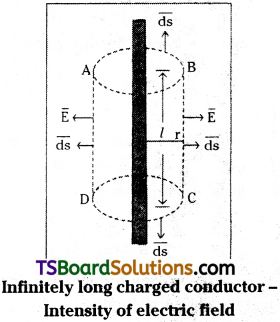
The flux through the curved surface ABCD is given by

λ is positive ⇒ direction will be radially outwards
λ is negative ⇒ direction will be radially inwards 2

Question 2.
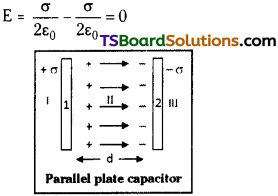
State Gauss’s law in electrostatics. Applying Gauss’s law derive the expression for electric intensity due to an infinite plane sheet of charge.
Answer:
Gauss’s law :
The total electrical flux through any closed surface is equal to 1/ε₀ times the net charge enclosed by that surface.

Expression for electric intensity:

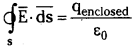
Consider an infinite plane sheet ABCD of uniform surface charge density ‘σ’.
Surface charge density

Take a Gaussian surface in the form of a rectangular parallelopiped.

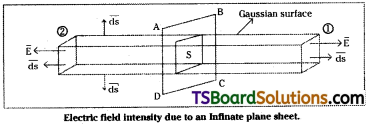
Assume the area of cross section of the two surfaces (1) and (2) be ‘S’. These two surfaces only will contribute to electric flux, since \(\overrightarrow{E}\) and area vector \(\overrightarrow{ds}\) are parallel. The remaining surfaces will give rise to zero flux as \(\overrightarrow{E}\) and \(\overrightarrow{ds}\) are perpendicular.
The total flux through the surface

This field is independent of distance of the point, this field is a uniform field.

Question 3.
Applying Gauss’s law derive the expression for electric intensity due to a charged conducting spherical shell at (i) a point outside the shell (ii) a point on the surface of the shell and (iu) a point inside the shell.
Answer:
Consider a charged spherical shell of radius R and of uniform surface charge density σ.

1) Field out side the shell:
Consider a point P outside the shell with a radius vector \(\overrightarrow{r}\). (\(\overrightarrow{r}\) > \(\overrightarrow{R}\))
Now consider a Gaussian surface which is spherical of radius r.
As all the points on this surface are at same distance.
The flux through the Gaussian surface

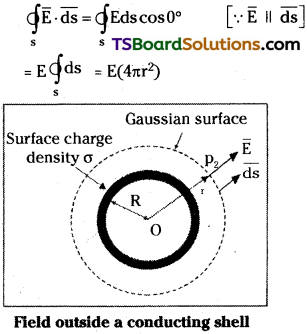
The charge enclosed by the
Gaussian surface is q = σ.(4πr²)

2) Field at a point on the shell:
If the point lies on the surface of the shell
⇒ r = R.

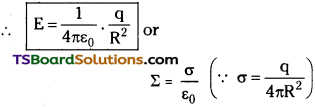
3) Field at a point inside the shell:
Consider a spherical Gaussian surface passing through P inside the shell with centre as ’O’.

The flux through this surface is

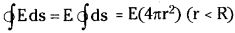
But the there is no charge enclosed by the surface i.e., q = 0.

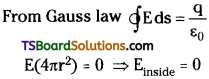
∴ The field inside a uniformly charged thin shell at all points inside is zero.

Intext Question and Answer

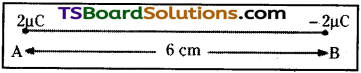
Question 1.
Two small identical balls, each of mass 0.20 g, carry identical charges and are suspended by two threads of equal lengths. The balls position themselves at equilibrium such that the angle between the threads is 60°. If the distance between the balls is 0.5m, find the charge on each ball.
Answer:
Mass of each ball = 0.20g = 20 × 10^-4kg
Angle between them θ = 60°
Separation between balls = 0.5m

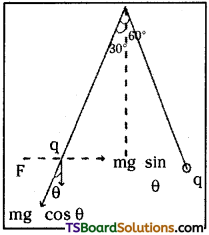
At equilibrium
Electrostatic force F is
balanced by component of weight mg sin θ.

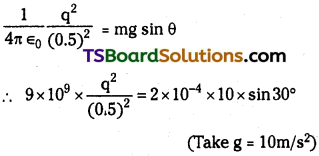
Question 2.
An infinite number of charges each of magnitude q are placed on x – axis at distances of 1, 2, 4,8, …………. meter from the origin respectively. Find intensity of the electric field at origin.
Answer:
The charges are as shown.

Question 3.
A clock face has negative charges-q, -2q, -3q, …….. – 12q fixed at the position of the corresponding numberals on the dial. The clock hands do not disturb the net field due to the point charges. At what time does the hour, hand point in the direction of the electric field at the centre of the dial?
Answer:
Negative charges are arranged on the clock as shown.

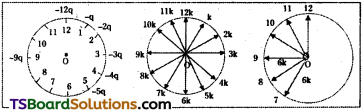
Charge arrangement
Electric field due to – q = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}\) = say k

Where r is distance from centre ‘O’ to the numbers on dial
Field due to- 2q = 2k; due to -3q = 3k ……….. Field due to -12q = 12k
Electric field is directed as shown in figure.

They are as shown in figure.
Consider E₇ and E₉ magnitude of each = 6k angle between them is 60°.
∴ Resultant of E₇ & E₉ is along E₈.
Magnitude is
\(\sqrt{6 \mathrm{k}^2+6 \mathrm{k}^2+2 \times 6 \mathrm{k} \times 6 \mathrm{k} \times \cos \theta}\) say x.
Field along E₈ = 6k + x …………. (1)
Consider E₁₀ and E₁₂ their magnitudes are 6k and 6k angle between them is 60°.
Resultant of E₁₀, E₁₂ is along E₁₁.
Resultant field along
E₁₁ = \(\sqrt{6 \mathrm{k}^2+6 \mathrm{k}^2+2 \times 6 \mathrm{k} \times 6 \mathrm{k} \cdot \cos 60^{\circ}}\) say y.
Now x, y are equal.
Total field along E₁₁ = 6k + y ……….. (2)
From eq 1, 2 magnitudes of E₈, E₁₁ are equal and angle between them is 90°.
∴ Angle of resultant θ = 45° with E₈.
In clock Anglb between each digit say 8 & 9 = 30°
9 & 10 = 30° i.e., 1 hour corresponds to 30° angle so angle 45° ⇒ 1\(\frac{1}{2}\) hour
Direction of resultant field = 8 + 1\(\frac{1}{2}\) = 9\(\frac{1}{2}\) hours = 9 hours 30 minutes.

Question 4.
Consider a uniform electric field E = 3 × 10³ N/C. (a) What is the flux of this field through a square of 10 cm on aside whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x – axis?
Answer:
Intensity of electric field E = 3 × 10³ N/C along x-axis.
Area of Square = 1² = 10 × 10 = 100 cm²
= 100 × 10^-4 m² = 10^-2m²

(a) When plane of square is parallel to y – z plane it is perpendicular to x-axis
⇒ 0 = 90°
∴ Flux through square Φ = \(\overline{\mathrm{E}}.\overline{\mathrm{A}}\) (or)
Φ = EA cos θ
Φ = 3 × 10³ × 10^-2 = 3 × 10 = 30 vm

(b) When square makes an angle θ = 60°
with x- axis, θ =60°.

Question 5.
There are four charges, each with a magnitude Q. Two are positive and two are negative. The charges are fixed to the corners of a square of side ‘L’, one to each corner, in such a way that the force on any charge is directed toward the center of the square. Find the magnitude of the net electric force experienced by any charge?
Answer:
Given two charges are +ve and two charges are -ve.

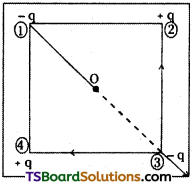
Force on any charge is directed towards centre.
Side of square = L at point 3
Consider charge 3 total forces on it are

Question 6.
The electric field in a region is given by \(\overrightarrow{\mathbf{E}}=\mathbf{a} \hat{\mathbf{i}}+\mathbf{b} \hat{\mathbf{j}}\). Here a and b are constants. Find the net flux passing through a square area of side L parallel to y – z plane.
Answer:
Electric field \(\overrightarrow{\mathbf{E}}=\mathbf{a} \hat{\mathbf{i}}+\mathbf{b} \hat{\mathbf{j}}\)
Side of square = L
∴ Area of square = L²
Give square is parallel to y – z plane ⇒ it is perpendicular x – axis ⇒ Area vector

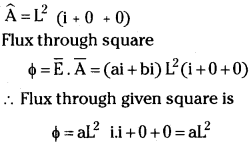
Question 7.
A hollow spherical shell of radius r has a uniform charge density σ. It is kept in a cube of edge 3r such that the center of the cube coincides with the center of the shell. Calculate the electric flux that comes out of a face of the cube.
Answer:
(Charge density on sphere = σ. But σ = \(\frac{Q}{A}\)
Area of spere A = 4πr²
⇒ Charge Q = 4πr²σ
For a point out side the sphere it seems to be concentrated at centre.
∴ Charge at centre of cube Q = 4πr²σ)
From gauss’s law total flux comming out of

Question 8.
An electric dipole consists of two equal and opposite point charges + Q and – Q, separated by a distance 2l. P is a point collinear with the charges such that is distance from the positive charge is half of its distance from the negative charge.
Answer:
Each charge on dipole = q, -q
Separation between charges = 2l

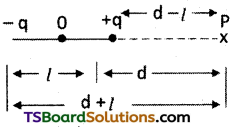
P is on the line joining the charges ⇒ it is on axial line.
Given : distance from +ve’ charge = \(\frac{1}{2}\) distance from -ve’ charge.
From given data d – l = \(\frac{1}{2}\) ( d + l) ⇒ 2d – 2l = d + l (or) d = 3l
Intensity of electric field at any point on

Question 9.
Two infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart. The intensity of the electric field at a point midway between them is
Answer:
Charge densities of infinitely long conductors = λ and 2λ
Distance between conductors = r
Intensity of electric field of mid point = ?
For mid point distance d = r/2
Intensity of electric field due to a long conductor.

Question 10.
Two infinitely long thin straight wires having uniform linear charge densities \(\ddot{\mathrm{e}}\) and 2\(\ddot{\mathrm{e}}\) are arranged parallel to each other at a distance r apart. The intensity of the electric field at a point midway between them is
Answer:
Linear charge densities σ₁ = σ₂ and σ₂ = 2e.
Separation between two parallel conductors d = r
For mid-way between them d = r/2

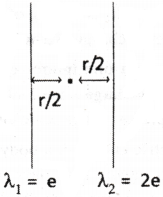
At midpoint intensities are in oppisite direction so resultant intensity E_R = E₁ ~ E₂
Intensity of electric field from an infinitely long charged conductor E = \(\frac{\lambda}{2 \pi \varepsilon_0r}\)

Intensity of electric field at mid point E = \(\frac{e}{\pi \varepsilon_0r}\)

Question 11.
An electron of mass m and chargee is fired perpendicular to a uniform electric field of intensity E with an initial velocity u. If the electron traverses a distance x in the field in the direction of firing. Find the transverse displacement y it suffers.
Answer:
Mass of electron = m ;
Charge on electron = e
Intensity of electric field = E
∴ Force F = E . e
Initial velocity of electron = u; acceleration of electron a = F/m = E.e/m

Distance travelled S = x. along x-axis
⇒ time t = \(\frac{x}{4}\) …………. (1)
Distance travelled along y-axis = ?
Initial velocity along y-axis = u = 0
Vertical displacement y = ut + \(\frac{1}{2}\) at² = \(\frac{1}{2}\)at²
⇒ y = \(\frac{1}{2}\frac{Ee}{m}.\frac{x}{u^2}\)
∴ Vertical displacement after travelling a eEx2 distance x is y = \(\frac{eEx^2}{2mu^2}\)

Additional Exercises

Question 1.
What is the force between two small charged spheres having charges of 2 × 10^-7 C and 3 × 10^-7 C placed 30 cm apart in air?
Answer:
Repulsive force of magnitude 6 × 10^-3 N ;
Charge on the first sphere, q: = 2 × 10^-7
C Charge on the second sphere, q² = 3 × 10^-7 C ;
Distance between the spheres, r = 30 cm = 0.3 m
Electrostatic force between the spheres is given by the relation,

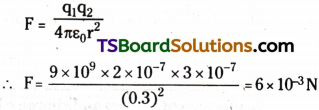
Hence, force between the two small charged spheres is 6 × 10^-3 N. The charges are of same nature. Hence, force between them will be repulsive.

Question 2.
The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge – 0.8 µC in air is 0.2 N. (a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
Answer:
a) Electrostatic force on the first sphere, F = 0.2 N
Charge on this sphere, = 0.4 µC
= 0.4 × 10^-6 C
Charge on the second sphere,
q₂ = -0.8 µC = -0.8 × 10^-6

Electrostatic force between the spheres

The distance between the two spheres is 0.12 m.

b) Both the spheres attract each other with the same force. Therefore, the force on the second sphere due to the first is 0.2 N.

Question 3.
Check that the ratio ke²/G m_em_p is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Answer:
1) The given ratio is \(\frac{\mathrm{ke^2}}{\mathrm{Gm_em_p}}\)
Where, G = Gravitational constant
m_e and m_p = Masses of electron and proton.; e = Electric charge is C.
k = A constant. = \(\frac{1}{4 \pi \varepsilon_0}\),
Where ε₀ = Permittivity of free space
Therefore, unit of the given ratio

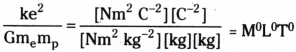
Hence, the given ratio is dimensionless,

ii) e = 1.6 × 10^-19C; G = 6.67 × 10^-11 N m²kg^-2; m_e = 9.1 × 10^-31 kg ; m_p = 1.66 × 10^-27kg
Hence, the numerical value of the given ratio is

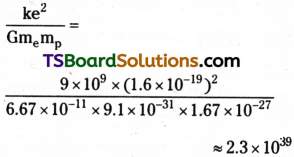
This is the ratio of electric force to the gravitational force between a proton and an electron, keeping distance between them constant.

Question 4.
a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges?
Answer:
a) Electric charge of a body is quantized. This means that only integral (1, 2, …………, n) number of electrons can be transferred from one body to the other. Charges are not transferred in fraction. Hence, a body possesses total charge only in integral multiples of electric charge.

b) In macroscopic or large scale charges, the charges used are huge as compared to the magnitude of electric charge. Hence, quantization of electric charge is of no use on macroscopic scale. Therefore, it is ignored and it is considered that electric charge is continuous.

Question 5.
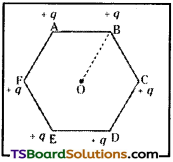
Four point charges q_A = 2 µC, q_B = – 5µC, q_C = 2 µC, and q_D = – 5 µC are located at thecomereofasquare ABCD of side 10cm. What is the force on a charge of 1 µC placed at the centre of the square?
Answer:
The given figure shows a square of side 10 cm with four charges placed at its corners. O is the centre of the square.

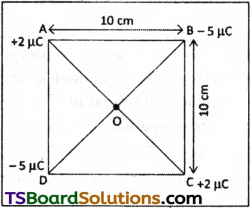
Where, (Sides) AB = BC = CD = AD = 10 cm
(Diagonals) AC = BD = 10√2 cm
AO = OC = DO = OB = 5√2 cm
A charge of amount 1 µC is placed at point O.

Force of repulsion between charges placed at corner A and centre O is equal in magnitude but opposite in direction relative to the force of repulsion between the charges placed at corner C and centre O. Hence, they will cancel each other. Similarly, force of attraction between charges placed at corner B and centre O is equal in magnitude but opposite in direction relative to the force of attraction between the charges placed at corner D and centre O. Hence, they will also cancel each other. Therefore, net force caused by the four charges placed at the corner of the square on 1 µC charge at centre O is zero.

Question6.
a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
b) Explain why two field lines never cross each other at any point?
Answer:
a) An electrostatic field line is a continuous curve because a charge experiences a continuous force when traced in an electrostatic field. The field line cannot have sudden breaks because the charge moves continuously and does not jump from one point to the other.

b) If two field lines cross each other at a point, then electric field intensity will show two directions at that point. This is not possible. Hence, two field lines never crosr. each other.

Question 7.
An electric dipole with dipole moment 4 × 10^-9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 × 10⁴ N C^-1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Electric dipole moment, p = 4 × 10^-9 C m ;
Electric field, E = 5 × 10⁴ N C^-1
Angle made by p with a uniform electric field, θ = 30°

Torque acting on the dipole is given by the relation, τ = pE sin θ
= 4 × 10^-9 × 5 × 10⁴ × sin 30
= 20 × 10^-5 × 1/2 = 10^-4 Nm

Therefore, the magnitude of the torque acting on the dipole is 10^-4 N m.

Question 8.
a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 × 10^-7 C? The radii of A and B are negligible compared to the distance of separation.
b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Answer:
a) Charge on sphere A, q_A = Charge on sphere B, q_B = 6.5 × 10^-7 C
Distance between the spheres,
r = 50 cm = 0.5 m

Force of repulsion between the two

Therefore, the force between the two spheres is 1.52 × 10^-2 N.

b) After doubling the charge, charge on sphere A, q_A = Charge on sphere B,
q_B = 2 x 6.5 × 10^-7C = 1.3 × 10^-6C
The distance between the spheres is halved.
∴ r = \(\frac{0.5}{2}\) = 0.25 m
Force of repulsion between the two spheres,

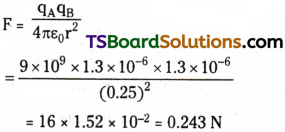
Therefore, the force between the two spheres is 0.243 N.

Question 9.
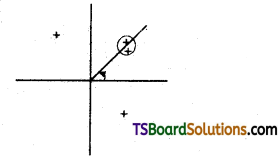
Figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

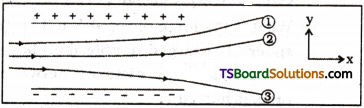
Answer:
Opposite charges attract each other and same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively chargee plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged.

The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.

Question 10.
What is the net flux of the uniform electric field of Exercise 15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Answer:
All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.

Question 11.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 10³ N m²/C.
a) What is the net charge inside the box?
b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Answer:
a) Net outward flux through the surface of the box, Φ = 8.0 × 10³ N m²/C
For a body containing net charge q, flux is given by the relation, Φ = \(\frac{q}{\varepsilon_0}\)
ε₀ = Permittivity of free space = 8.854 × 10^-12 N^-1C²m^-2
q = ε₀Φ = 8.854 × 10^-12 × 8.0 × 10³
= 7.08 × 10^-8 = 0.07 µC
Therefore, the net charge inside the box is 0.07 µC.

b) No
Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that net charge inside the body is zero. The body may have equal amount of positive and negative charges.

Question 12.
A point charge + 10 µC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)

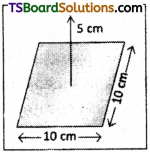
Answer:
The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed. According to Gauss’s theorem for a cube, total electric flux is through all its six faces.
Hence, electric flux through one face of the cube
Φ_total = \(\frac{q}{\varepsilon_0}\)
Hence, electric flux through one fact of the cube i.e., through the square,

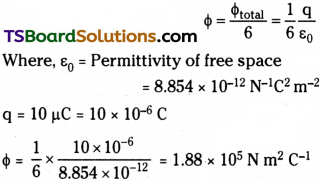
Therefore, electric flux through the square is 1.88 × 10⁵ Nm²C^-1

Question 13.
A point charge of 2.0 µC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Answer:
Net electric flux (Φ_net) through the cubic surface is given by, Φ_net = \(\frac{q}{\varepsilon_0}\)
Where, ε₀ = Permittivity of free space = 8.854 × 10^-12N^-1C²m^-2
q = Net charge contained inside the cube = 2.0 µC = 2 × 10^-6 C

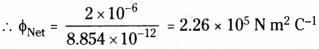
The net electric flux through the surface is 2.26 × 10⁵ Nm²C^-1.

Question 14.
A point charge causes an electric flux of -1.0 × 10³ Nm²/C to pass through a sphe¬rical Gaussian surface of 10.0 cm radius centered on the charge.
a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
b) What is the value of the point charge?
Answer:
a) Electric flux, Φ = -1.0 × 10³ Nm²/C ;
Radius of the Gaussian surface, r = 10.0 cm
Electric flux piercing out through a surface depends on the net charge enclosed inside a body. It does not depend on the size of the body. If the radius of the Gaussian surface is doubled, then the flux passing through the surface remains the same i.e., – 10³ N m²/C.

b) Electric flux is given by the relation, Φ = \(\frac{q}{\varepsilon_0}\)
Where, q = Net charge enclosed by the spherical surface
ε₀ = Permittivity of free space
= 8.854 × 10^-12 N^-1C²m^-2
∴ q = Φε₀ = – 1.0 × 10³ × 8.854 × 10^-12
= – 8.854 × 10^-9 C = – 8.854 nC

Therefore, the value of the point charge is-8.854 nC.

Question 15.
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 10³ N/C and points radially inward, what is the net charge on the sphere?
Answer:
Electric field intensity (E) at a distance (d) from the centre of a sphere containing net charge q is given by the relation,

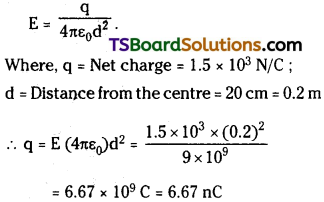
Therefore, the net charge on the sphere is 6.67 nC.

Question 16.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 µC/m².
a) Find the charge on the sphere.
b) What is the total electric flux leaving the surface of the sphere?
Answer:
a) Diameter of the sphere, d = 2.4 m ;
Radius of the sphere, r = 1.2 m
Surface charge density σ = 80.0 µC/m²
= 80 × 10^-6C/m²

Total charge on the surface of the sphere,
Q = Charge density × Surface area
Q = σ × 4πr² = 80 × 10^-6 × 4 × 3.14 × (1.2)²
= 1.447 × 10^-3C
Therefore, the charge on the sphere is 1.447 × 10^-3 C.

b) Total electric flux (Φ_total) leaving out the surface of a sphere containing net charge
Q is given by the relation, Φ_total = \(\frac{Q}{\varepsilon_0}\)

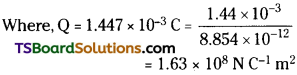
Therefore, the total electric flux leaving the surface of the sphere is 1.63 × 10^-8NC^-1m²

Question 17.
An infinite line charge produces a field of 9 × 10⁴ N/C at a distance of 2 cm. Calculate the linear charge density.
Answer:
Electric field produced by the infinite line charges at a distance d having linear charge density λ is given by the relation,

Therefore, the linear charge density is 10 µC/m

Here students can locate TS Inter 2nd Year Zoology Notes 8th Lesson Applied Biology to prepare for their exam.

TS Inter 2nd Year Zoology Notes 8th Lesson Applied Biology

→ Biology has applications in Animal husbandry, Agriculture, Aquaculture, Pollution Management, Synthetic preparation of Hormonal analogues, Manufacture of vaccines, Molecular Diagnosis of various human ailments etc.

→ Applied Biology also deals with Medical Biotechnology tools and Testing Methodologies.

→ The Green revolution, Blue revolution and White revolution etc., are applied branches of Biology.

→ Breeding Technologies to improve high milk, egg and meat yielding animals improved with the acquisition of in depth knowledge in the fields of Genetics.

→ Molecular Biology and related sciences such as Biochemistry paved the way to developing Biomedical technology ‘kits’ in the field of testing certain human body functions, in easy and quick ways.

→ Providing certain scientific inputs into rearing fish, poultry birds, honey bees silkworm moths proved very useful.

→ An insight in Cancer biology, Gene Therapy and Bio-safety issues also comes under applied biology.

→ Animal husbandry is the agricultural practice of breeding and raising livestock.

→ Padmasri Dr. B.V. Rao is the “Father of Modern Poultry in India”.

→ Bee keeping or apiculture is the maintenance of hives of honey bees for the production of honey and wax. Bee keeping is an age old cottage industry.

→ Recombinant DNA technology involves manipulation of genes or micro¬organisms to produce certain products useful to mankind.

→ J. Michael Bishop:
John Michael Bishop (born February 22, 1936) is an American immunologist and microbiologist who shared the 1989 Nobel Prize in Physiology or Medicine with Harold E. Varmus and was co – winner of 1984 Alfred P. Sloan Prize. He currently serves as an active faculty member at the University of California, San Francisco.
Bishop is best known for his Nobel – winning work on retroviral oncogenes. Working with Harold E. Varmus in the 1980s, he discovered the first human oncogene, c – Src. Their findings allowed the understanding of how malignant tumors are formed from changes to the normal genes of a cell These changes can be produced by viruses, by radiation, or by exposure to some chemicals.

→ Jonas Salk
Jonas Edward Salk (October 28,1914 – June 23,1995) was an American medical researcher and virologist, best known for his discovery and development of the first successful polio vaccine. He was born in New York City to Jewish parents.

Here students can locate TS Inter 2nd Year Zoology Notes 7th Lesson Organic Evolution to prepare for their exam.

TS Inter 2nd Year Zoology Notes 7th Lesson Organic Evolution

→ The term ‘Organic Evolution’ was coined by Herbert Spencer.

→ Lamarck theory of Use and Disuse and Inheritance of acquired characters is the first organised theory to explain evolutionary process.

→ Theory of Natural Selection was put forward by Charles Darwin.

→ Book written by Darwin “Origin of Species”.

→ Theory on mutations put forward by ‘Hugo de Vries’.

→ Anon evolving population is in a state of equilibrium called “Hardy-Weinberg Equilibrium”.

→ Evolution is the branch of biology that deals with the origin, of life and the diversity of organisms on earth through ages.

→ Theory of special creation is purely a mythological belief.

→ Aristotle, Thales, Plato and Von Helmont believed in the idea of a biogenesis. Louis Pasteur confirmed the theory of Biogenesis by his swan-neck flask experiment. Theory of Origin of life or Coacervate theory was proposed by A.I. Oparin and supported by JBS Haldane.

→ The origin of life is a phenomenon of “Chemical evolution” that led to biological evolution.

→ Charles Darwin:
Charles Darwin, FRS (1809 -1882) was an English naturalist. Wj He established that all species of life have descended over time I from common ancestors and proposed the scientific theory that this branching pattern of evolution resulted from a process that he called natural selection, in which the struggle for existence has a similar effect to the artificial selection inv’olved in selective breeding.

Darwin published his theory of evolution with compelling evidence in his 1859 book on the Origin of Species, overcoming scientific rejection of earlier concepts of transmutation of species. By the 1870s the scientific community and much of the general public had accepted evolution as a fact.
His five-year voyage on HMS Beagle established him as an eminent geologist whose observations and theories supported Charles Lyell’s uniformitarian ideas, and publication of his journal of the voyage made him famous as a popular author.

→ Hugo de Vries
Hugo Marie de Vries (Dutch 1848 – 1935) was a Dutch botanist and one of the first geneticists. He is known chiefly for suggesting the concept of genes, rediscovering the laws of heredity in the 1890s while unaware of Gregor Mendel’s work, II for introducing the term “mutation” and for developing a mutation theory of evolution.

Here students can locate TS Inter 2nd Year Zoology Notes 6th Lesson Genetics to prepare for their exam.

TS Inter 2nd Year Zoology Notes 6th Lesson Genetics

→ Genetics, a discipline of biology, is the science of heredity and hereditary variations in living organisms.

→ The word ‘Genetics’ is derived from the Greek word genesis which means origin of anything or a beginning.

→ The term Genetics was coined by W. Bateson.

→ T.H. Morgan, contributed to the glory of the science of ‘Genetics’ with his experiments on Drosophila melanogaster the fruit fly.

→ Heredity is the study of transmission of characters from one generation to the next.

→ Variations are defined as the difference in characteristics shown by the individuals of a species and also by the progeny of the same parents.

→ Modern science of genetics only began with the work of Gregor Mendel in the Mid 19th Century.

→ After the rediscovery of Mendel’s work by de Vries, Correns and Tschermak, scientists tried to determine which molecules in the cell were responsible for inheritance.

→ Theory of inheritance or Sutton – Boveri Theory is a fundamental unifying theory of genetics.

→ Experimental verification of the ‘Chromosomal theory of inheritance’ by T.H. Morgan and his colleagues, led to discovering the basis for the variation that sexual reproduction produced.

→ The phenomenon of multiple effects of a single gene is called Pleiotropy.

→ When more than two alleles exist in a population of specific organism, the phenomenon is called multiple allelism.

→ Gregor Mendel
Gregor Johann Mendel (1822 – 1884) was a German – speaking It Silesian scientist and Augustinian friar who gained posthumous fame I as the founder of the new science of genetics. Mendel demonstrated | that the inheritance of certain traits in pea plants follows particular patterns, now referred to as the laws of Mendelian ^inheritance. The profound significance of Mendel’s work was not recognized until the turn of the 20th century, when the independent rediscovery of these laws initiated the modern science of genetics.

→ Francis Galton
Sir Francis Galton, (1822 -1911), cousin of Douglas Strutt Galton, cousin of Charles Darwin, was an Hnglish Victorian polymath: anthropologist, eugenicist, tropical explorer, geographer, inventor, meteorologist, proto – geneticist,psychometrician, and statistician. He was knighted in 1909. Galton produced over 340 papers and books. He also created the statistical concept of correlation and widely promoted regression toward the mean. He was the first to apply statistical methods to the study of human differences and inheritance of intelligence, and introduced the use of questionnaires and surveys for collecting data on human communities, which he needed for genealogical and biographical works and for his anthropometric studies. He was a pioneer in eugenics, coining the term itself and the phrase “nature versus nurture”. His book Hereditary Genius (1869) was the first social scientific attempt to study genius and greatness.

Here students can locate TS Inter 2nd Year Zoology Notes 5th Lesson Human Reproduction to prepare for their exam.

TS Inter 2nd Year Zoology Notes 5th Lesson Human Reproduction

→ A sexual reproduction is the process adopted by many lower organisms, which have a high degree of regenerative capacity.

→ Sexual reproduction creates another organism (s) showing variation from the parent

→ Variations are raw materials for evolution.

→ Formation of gametes taking part in sexual reproduction involves meiosis.

→ Among the sexually reproducing organisms viviparity is of a higher degree of evolution, where the mother supplies nourishment and ‘oxygen through placenta.

→ The wealth of a Nation is the health of its people. As many people are under educated, atleast regarding reproductive health, it is necessary to educate adolescents on reproductive health.

→ The reproductive events in humans include formation of gametes i.e., sperms in males and ova in females.

→ Union of male and female gametes is called Fertilisation leading to the formation of zygote.

→ Embryonic development in the mother’s uterus is called Gestation. Delivery of the baby is called Parturition.

→ In simple terms, the term reproductive health refers to having healthy reproductive organs with normal functioning.

→ Reproductive health in a broader point of view, it includes the emotional and social aspects of reproduction also.

→ According to the World Health Organization (WHO) reproductive health is a state of complete well being of individual in physical functional emotional, behavioral and social aspects of reproductive system.

→ A society will be considered ‘reproductively healthy’ when the people have physically and functionally normal reproductive processes and normal emotional and behavioral interactions among themselves, in all sex related aspects.

→ In India maternal mortality rate and infant mortality rate are high.

→ Spread of sexually transmitted diseases (STDs) is still a major problem.

→ Approximately 2 million people in India live with HIV/AIDS.

→ Improved programmes covering wider reproductive and child health care (RCH) programmes are Janani Suraksha Yojana etc.

→ Introduction of sex education in schools will provide right information to the young on sex and other related issues.

→ Awareness should be created in the society on problems caused by uncontrolled population growth and social evils like sex abuse and sex related crimes etc.

→ Karl Ernst von Baer
Karl Ernst Ritter von Baer (1792-1876), from the Governorate of Estonia, was a naturalist, biologist, geologist, meteorologist, geographer, a founding father of embryology, explorer of European Russia and Scandinavia, a member of the Russian Academy of Sciences, a co – founder of the Russian Geographical Society and the first President of the Russian Entomological Society.
von Baer studied the embryonic development of animals, discovering the blastula stage of development and the notochord Together with Heinz Christian Pander and based on the work by Caspar Friedrich Wolff he described the germ layer theory of development (ectoderm, mesoderm, and endoderm) as a principle in a variety of species, laying the foundation for comparative embryology in the book Uber Entwickelungsgeschichte der Thiere (1828). In 1826 Baer discovered the mammalian ovum. The first human ovum was described by Allen in 1928. In 1827 he completed research Ovi Mammalium’et- Hominis genesi for Saint – Petersburg’s Academy of Science (published at Leipzig) and established that mammals develop from eggs. He formulated what would later be called Baer’s laws of embryology.

→ Hans Spemann
Hans Spemann (1869 -1941) was a German embryologist who was awarded a Nobel Prize in Physiology or Medicine in 1935 for his discovery of the effect now known as embryonic induction, an influence, exercised by various parts of the embryo, that directs the development of groups of cells into particular tissues and organs.

→ Gonorrhea
Gonorrhea (colloquially known as the clap) is a common human sexually transmitted infection caused by the bacterium Neisseria gonorrhoeae. The usual symptoms in men are burning with urination and penile discharge. Women, on the other hand, are asymptomatic half the time or have vaginal discharge and pelvic pain. In both men and women if gonorrhea is left untreated, it may spread locally causing epididymitis or pelvic inflammatory disease or throughout the body, affecting joints and heart valves.

Treatment is commonly with ceftriaxone as antibiotic resistance has developed to many previously used medications. This is typically given in combination with either azithromycin or doxycycline, because gonorrhea infections typically occur along with chlamydia, an infection which ceftriaxone does not cover. However, some strains of gonorrhea have begun showing resistance to treatment. In April 2013, it was reported that H041, a new strain, is incurable, can cause death within days, and might be worse than AIDS.

→ Gonorrhea:
Classification and external resources during World War II, the U.S government used posters to warn military personnel about the dangers of gonorrhea and other sexually transmitted infections.

→ Syphilis:
Syphilis is a sexually transmitted infection caused by the spirochete bacterium Treponema pallidum subspecies pallidum. The primary route of transmission is through sexual contact; it may also be transmitted from mother to fetus during pregnancy or at birth, resulting in congenital syphilis. Other human diseases caused by related Treponema pallidum include yaws (subspecies pertenue), pinta (subspecies carateum), and bejel (subspecies endemicum).

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Circles Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Circles Important Questions Long Answer Type

Question 1.
Find the equation of the circle passing through the points (5, 7), (8, 1), (1, 3). (May ’10)
Solution:
Let the equation of the required circle
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since equation (1) passes through (5, 7), then
(5)² + (7)² + 2g(5) + 2f(7) + c = 0
⇒ 25 + 49 + 10g + 14f + c = 0
⇒ 10g + 14f + c = -74 …….(2)
Since equation (1) passes through (8, 1) then
(8)² + (1)² + 2g(8) + 2f(1) + c = 0
⇒ 64 + 1 + 16g + 2f + c = 0
⇒ 16g + 2f + c = -65 ……..(3)
Since equation (1) passes through (1, 3)
(1)² + (3)² + 2g(1) + 2f(3) + c = 0
⇒ 1 + 9 + 2g + 6f + c = 0
⇒ 2g + 6f + c = -10 ………(4)

Question 2.
Find the equation of the circle passing through (-2, 3), (2, -1), and (4, 0).
Solution:
Let, the required equation of the circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through (-2, 3), then
(-2)² + (3)² + 2g(-2) + 2f(3) + c = 0
⇒ 4 + 9 – 4g + 6f + c = 0
⇒ -4g + 6f + c = -13 ……….(2)
Since (1) passes through (2, -1), then
(2)² + (-1)² + 2g(2) + 2f(-1) + c = 0
⇒ 4 + 1 + 4g – 2f + c = 0
⇒ 4g – 2f + c = -5 ……..(3)
Since (1) passes through (4, 0) then
(4)² + (0)² + 2g(4) + 2f(0) + c = 0
⇒ 16 + 8g + c = 0
⇒ 8g + c = -16 ………(4)
From (2) and (3)


Substitute the value of ‘g’ in (4)
8(\(\frac{-3}{2}\)) + c = -16
⇒ -12 + c = -16
⇒ c = -4
Now substitute the values of g, f, c in (1)
∴ The required equation of the circle is
x² + y² + 2(\(\frac{-3}{2}\)) x + 2(\(\frac{-5}{2}\)) y – 4 = 0
⇒ x² + y² – 3x – 5y – 4 = 0

Question 3.
Find the equation of the circle passing through the points (3, 4), (3, 2), (1, 4). [(AP) Mar. ’18, May ’16; (TS) ’16]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point (3, 4), then
(3)² + (4)² + 2g(3) + 2f(4) + c = 0
⇒ 9 + 16 + 6g + 8f + c = 0
⇒ 6g + 8f + c = -25 ……..(2)
Since, (1) passes through the point (3, 2)
(3)² + (2)² + 2g(3) + 2f(2) + c = 0
⇒ 9 + 4 + 6g + 4f + c = 0
⇒ 6g + 4f + c = -13 ……(3)
Since, (1) passes through the point (1, 4)
(1)² + (4)² + 2g + 2f(4) + c = 0
⇒ 1 + 16 +2g + 8f + c = 0
⇒ 2g + 8f + c = -17 ……….(4)
From (2) and (3)

Substitute the value of g, f in (2)
6(-2) + 8(-3) + c = -25
⇒ -12 – 24 + c = – 25
⇒ c = -25 + 36
⇒ c = 11
Substitute the values of g, f, c in (1)
x² + y² + 2(-2)x + 2(-3)y + 11 = 0
⇒ x² + y² – 4x – 6y + 11 = 0
∴ The equation of the required circle is x² + y² – 4x – 6y + 11 = 0.

Question 4.
Find the equation of the circle passing through (2, 1), (5, 5), (-6, 7).
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since (1) passes through the point (2, 1), then
(2)² + (1)² + 2g(2) + 2f(1) + c = 0
⇒ 4 + 1 + 4g + 2f + c = 0
⇒ 4g + 2f + c = -5 …….(2)
Since (1) passes through point (5, 5), then
(5)² + (5)² + 2g(5) + 2f(5) + c = 0
⇒ 25 + 25 + 10g + 10f + c = 0
⇒ 10g + 10f + c = -50 ………(3)
Since (1) passes through the point (-6, 7) then
(-6)² + (7)² + 2g(-6) + 2f(7) + c = 0
⇒ 36 + 49 – 12g + 14f + c = 0
⇒ -12g + 14f + c = -85 …….(4)
From (2) and (3)

Substitute the value of g, f in (2)
4(\(\frac{1}{2}\)) + 2(-6) + c = -5
2 – 12 + c = -5
⇒ c = -5 + 10
⇒ c = 5
Now, substitute the values of g, f, c in (1)
∴ The required equation of the circle is x² + y² + 2(\(\frac{1}{2}\))x + 2(-6)y + 5 = 0
⇒ x² + y² + x – 12y + 5 = 0

Question 5.
Show that the points (1, 2), (3, -4), (5, -6), (19, 8) are concyclic and find the equation of the circle on which they lie. [(TS) Mar. ’16, May ’15]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since the eq.(1) passes through the point (1, 2) then
(1)² + (2)² + 2g(1) + 2f(2) + c = 0
⇒ 2g + 4f + c = -5 ……….(2)
Since the eq.(1) passes through the point (3, -4) then
(3)² + (-4)² + 2g(3) + 2f(-4) + c = 0
⇒ 9 + 16 + 6g – 8f + c = 0
⇒ 6g – 8f + c = -25 …………. (3)
Since the eq.(1) passes through the point (5, -6) then
(5)² + (-6)² + 2g(5) + 2f(-6) + c = 0
⇒ 25 + 36 + 10g – 12f + c = 0
⇒ 10g – 12f + c = -61 ………(4)
From (2) & (3)


Substitute the values of g, f in eq. (2)
2(-11) + 4(-2) + c = -5
⇒ -22 – 8 + c = -5
⇒ c = 25
Substitute the values of g, f, c in eq. (1)
x² + y² + 2(-11)x + 2(-2)y + 25 = 0
⇒ x² + y² – 22x – 4y + 25 = 0 ………(7)
Now, substitute the point (19, 8) in eq. (7)
(19)² + (8)² – 22(19) – 4(8) + 25 = 0
⇒ 361 + 64 – 418 – 32 + 25 = 0
⇒ 0 = 0
∴ Given points are concyclic.
∴ The equation of the circle is x² + y² – 22x – 4y + 25 = 0.

Question 6.
Show that the points (9, 1), (7, 9) (-2, 12), (6, 10) are concyclic and find the equation of the circle on which they lie. [(TS) Mar. ’19]
Solution:
Let, the equation of the required circle is x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through point (9, 1), then
(9)² + (1)² + 2g(9) + 2f(1) + c = 0
⇒ 81 + 1 + 18g + 2f + c = 0
⇒ 18g + 2f + c = -82 ………(2)
Since (1) passes through the point (7, 9), then
(7)² + (9)² + 2g(7) + 2f(9) + c = 0
⇒ 49 + 81 + 14g + 18f + c = 0
⇒ 14g + 18f + c = -130 ……..(3)
Since (1) passes through the point (-2, 12) then
(-2)² + (12)² + 2g(-2) + 2f(12) + c = 0
⇒ 4 + 144 – 4g + 24f + c = 0
⇒ -4g + 24f + c = -148 ……..(4)

Substitute the value of g, f in (2)
18(0) + 2(-3) + c = -82
⇒ 6 + c = -82
⇒ c = -82 + 6
⇒ c = -76
Substitute the values of g, f, c in (1)
∴ The equation of the required circle is x² + y² + 2(0)x + 2(-3)y – 76 = 0
⇒ x² + y² – 6y – 76 = 0 ………(7)
Substitute the point (6, 10) in (7)
(6)² + (10)² – 6(10) – 76 = 0
⇒ 36 + 100 – 60 – 76 = 0
⇒ 136 – 136 = 0
⇒ 0 = 0
∴ The given points are concyclic.
∴ The equation of the required circle is x² + y² – 6y – 76 = 0

Question 7.
If (2, 0), (0, 1), (4, 5), and (0, c) are concyclic then find ‘c’. [(AP) May ’19. ’15, Mar. ’17, ’15) (TS) Mar. ’17, ’15, May ’14]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since eq. (1) passes through the point (2, 0) then
(2)² + (0)² + 2g(2) + 2f(0) + c = 0
⇒ 4 + 4g + c = 0
⇒ 4g + c = -4 ……(2)
Since eq. (1) passes through the point (0, 1) then
(0)² + (1)² + 2g(0) + 2f(1) + c = 0
⇒ 2f + c = -1 ……..(3)
Since eq. (1) passes through the point (4, 5) then
(4)² + (5)² + 2g(4) + 2f(5) + c = 0
⇒ 16 + 25 + 8g + 10f + c = 0
⇒ 8g + 10f + c = -41 ……(4)
From (2) & (3)


3x² + 3y² – 13x – 17y + 14 = 0 ……..(7)
Since the given points are concyclic, then the point (0, c) lies on (7).
3(0)² + 3(c)² – 13(0) – 17(c) + 14 = 0
⇒ 3c² – 17c + 14 = 0
⇒ 3c² – 14c – 3c + 14 = 0
⇒ 3c(c – 1) – 14(c – 1) = 0
⇒ (c – 1) (3c – 14) = 0
⇒ c = 1, c = \(\frac{14}{3}\)

Question 8.
If (1, 2), (3, -4), (5, -6), and (c, 8) are concyclic, then find ‘c’.
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since (1) passes through the point (1, 2), then
(1)² + (2)² + 2g(1) + 2f(2) + c = 0
⇒ 1 + 4 + 2g + 4f + c = 0
⇒ 2g + 4f + c = -5 …….(2)
Since (1) passes through point (3, -4), then
(3)² + (-4)² + 2g(3) + 2f(-4) + c = 0
⇒ 9 + 16 + 6g – 8f + c = 0
⇒ 6g – 8f + c = -25 …….(3)
Since (1) passes through point (5, -6) then
(5)² + (-6)² + 2g(5) + 2f(-6) + c = 0
⇒ 25 + 36 + 10g – 12f + c = 0
⇒ 10g – 12f + c = -61 ……(4)
From (2) and (3)


Substitute the value of g, f in (2)
2(-11) + 4(-2) + c = -5
⇒ -22 – 8 + c = -5
⇒ -30 + c = -5
⇒ c = 25
Substitute the values of g, f, c in (1)
The equation of the required circle is x² + y² + 2(-11)x + 2(-2)y + 25 = 0
⇒ x² + y² – 22x – 4y + 25 = 0 ……..(7)
Substitute point (c, 8) in (7)
(c)² + (8)² – 22c – 4(8) + 25 = 0
⇒ c² + 64 – 22c – 32 + 25 = 0
⇒ c² – 22c + 57 = 0
⇒ c² – 19c – 3c + 57 = 0
⇒ c(c – 19) – 3(c – 19) = 0
⇒ (c – 19)(c – 3) = 0
⇒ c = 19, 3

Question 9.
Find the equation of the circle whose centre lies on the X-axis and passes through (-2, 3) and (4, 5). [Mar. ’15 (AP&TS)]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Centre of (1) is (-g, -f) lies on the X-axis then -f = 0
⇒ f = 0
Since eq. (1) passes through the point (-2, 3) then
(-2)² + 3² + 2g(-2) + 2f(3) + c = 0
⇒ 4 + 9 – 4g + 6f + c = 0
⇒ -4g + 6f + c = -13
If f = 0 then
-4g + c = -13 ………(2)
Since eq. (1) passes through the point (4, 5) then
(4)² + (5)² + 2g(4) + 2f(5) + c = 0
⇒ 16 + 25 + 8g + 10f + c = 0
⇒ 8g + 10f + c = -41 ………(3)
If f = 0 then 8g + c = -41
Solving (2) & (3)

Now, substituting the values of g, f, c in equation (1)
x² + y² + 2(\(\frac{-7}{3}\))x + 2(0)y + \(\frac{-67}{3}\) = 0
⇒ 3x² + 3y² – 14x – 67 = 0

Question 10.
Find the equation of the circle which passes through (4, 1) (6, 5) and has the centre of 4x + 3y – 24 = 0.
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through point (4, 1) then
(4)² + (1)² + 2(4)g + 2f(1) + c = 0
⇒ 16 + 1 + 8g + 2f + c = 0
⇒ 8g + 2f + c = -17 ………(2)
Since, (1) passes through the point (6, 5) then
(6)² + (5)² + 2g(6) + 2f(5) + c = 0
⇒ 36 + 25 + 12g + 10f + c = 0
⇒ 12g + 10f + c = – 61 …….(3)
Centre of (1) is C = (-g, -f) lies on the line 4x + 3y – 24 = 0 then
4(-g) + 3(-f) – 24 = 0
⇒ -4g – 3f – 24 = 0
⇒ -4g – 3f = 24 ……..(4)
From (2) and (3)

Now, substitute the values of g and f in (2)
8(-3) + 2(-4) + c = -17
⇒ -24 – 8 + c = 17
⇒ c = -17 + 32
⇒ c = 15
Substitute the values of g, f, c in (1)
x² + y² + 2(-3)x + 2(-4)y + 15 = 0
⇒ x² + y² – 6x – 8y + 15 = 0

Question 11.
Find the equation of a circle which passes through (4, 1) and (6, 5) and has the centre on 4x + 3y – 24 = 0. [(AP) Mar. ’20, ’16. (TS) Mar. ’18; Mar. ’11]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since equation (1) passes through point (4, 1) then
(4)² + (1)² + 2g(4) + 2f(1) + c = 0
⇒ 16 + 1 + 8g + 2f + c = 0
⇒ 8g + 2f + c = -17 ………..(2)
Since equation (1) passes through the point (6, 5) then
(6)² + (5)² + 2g(6) + 2f(5) + c = 0
⇒ 36 + 25 + 12g + 10f + c = 0
⇒ 12g + 10f + c = -61 ……….(3)
Centre of (1) is C = (-g, -f) lies on the line 4x + 3y – 24 = 0 then
4(-g) + 3(-f) – 24 = 0
⇒ -4g – 3f – 24 = 0
⇒ 4g + 3f + 24 = 0 ………(4)
Now (2) – (3)

Substitute the values of g, f in eq. (2) we get
8(-3) + 2(-4) + c = -17
⇒ -24 – 8 + c = -17
⇒ c = -17 + 32
⇒ c = 15
Substitute the values of g, f, c in eq. (1)
x² + y² + 2(-3)x + 2(-4)y + 15 = 0
⇒ x² + y² – 6x – 8y + 15 = 0 which is the required equation of the circle.

Question 12.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 touch each other. Also, find the point of contact and common tangent at this point of contact. [(AP) Mar. ’17]
Solution:
Given equations of the circles are
x² + y² – 4x – 6y – 12 = 0 ……..(1)
x² + y² + 6x + 18y + 26 = 0 ………(2)
For circle (1),
Centre, C₁ = (2, 3)

Now, r₁ + r₂ = 8 + 5 = 13
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch each other externally.
Let, P be the point of contact.
Now, the point of contact divides C₁C₂ in the ratio r₁ : r₂ = 5 : 8 internally.
∴ Point of contact,

⇒ x – 21y – 26x – 2 – 39y + 63 – 156 = 0
⇒ -25x – 60y – 95 = 0
⇒ 5x + 12y + 19 = 0

Question 13.
Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. [(TS) Mar. ’20, ’18; (AP & TS) May ’18]
Solution:
Given equations of the circles are
x² + y² – 6x – 9y + 13 = 0 …….(1)
x² + y² – 2x – 16y = 0 ………(2)
Centre of (1) is C₁ = (3, \(\frac{9}{2}\))

Question 14.
Show that the circles x² + y² – 6x – 2y + 1 = 0, x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. [(AP) May ’19, ’17, ’16; Mar. ’16]
Solution:
Given equations of the circles are
x² + y² – 6x – 2y + 1 = 0 ……..(1)
x² + y² + 2x – 8y + 13 = 0 ………(2)
Centre of (1) is C₁ = (3, 1)
Radius of (1) is r₁ = \(\sqrt{9+1-1}\) = 3
Centre of (2) is C₂ = (-1, 4)
Radius of (2) is r₂ = \(\sqrt{1+16-13}\) = 2
C₁C₂ = \(\sqrt{(3+1)^2+(1-4)^2}\)
= \(\sqrt{16+9}\)
= 5
r₁ + r₂ = 3 + 2 = 5
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch each other externally.
Let ‘P’ is the point of contact.
Now, ‘P’ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r1 : r2 (3 : 2) internally.
∴ Point of contact

Question 15.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and 5(x² + y²) – 8x – 14y – 32 = 0 touch each other and find their point of contact. [(TS) May ’17]
Solution:
Given equations of the circles are
x² + y² – 4x – 6y – 12 = 0 ……….(1)
5(x² + y²) – 8x – 14y – 32 = 0
⇒ \(x^2+y^2-\frac{8}{5} x-\frac{14}{5} y-\frac{32}{5}=0\) ………(2)
For circle (1),
Centre, C₁ = (2, 3)

Now, |r₁ – r₂| = |5 – 3| = 2
∴ C₁C₂ = |r₁ – r₂|
∴ The given circles touch each other internally.
Let, ‘P’ be the point of contact.
Now, P divides C₁C₂ in the ratio r₁ : r₂ (5 : 3) externally.

Question 16.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x – 6y + 4 = 0. [(TS) May ’19, Mar. ’17; (AP) Mar. ’19, ’15, ’14]
Solution:
Given equations of the circles are
x² + y² – 4x – 10y + 28 = 0 ……..(1)
x² + y² + 4x – 6y + 4 = 0 ………(2)
Centre of (1) = (2, 5)
Centre of (2) = (-2, 3)
r₁ = \(\sqrt{4+25-28}\) = 1
r₂ = \(\sqrt{4+9-4}\) = 3
Distance between \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) = √20
r₁ + r₂ = 4 = √16
C₁C₂ > r₁ + r₂
Given circles completely lie outside each other.
Let A be the internal centre of similitude.

Now, A₁ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ (1 : 3) internally.
∴ Internal centre of similitude

∴ The equation of the pair of transverse common tangents is S . S₁₁ = \(S_1{ }^2\)

⇒ (x² + y² + 4x – 6y + 4) (9) = 9(2x + y – 5)²
⇒ x² + y² + 4x – 6y + 4 = 4x² + y² + 25 + 4xy – 10y – 20x
⇒ 3x² + 4xy – 24x – 4y + 21 = 0
Now, 3x² + 4xy = 0
⇒ x(3x + 4y) = 0
⇒ x = 0, 3x + 4y = 0
3x² + 4xy – 24x – 4y + 21 = (x + l) (3x + 4y + k)
Comparing ‘x’ coefficients on both sides
k + 3l = -24 ……….(1)
4l = -4 ………(2)
⇒ l = -1
Substitute l = -1 in eq. (1)
k – 3 = – 24
⇒ k = -24 + 3
⇒ k = -21
∴ The transerve common tangents are x – 1 = 0, 3x + 4y – 21 = 0

Question 17.
Find the direct common tangents of the circles x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0. [Mar. ’18 (AP); May&Mar. ’15 (TS)]
Solution:
Given the equation of the circles are
x² + y² + 22x – 4y – 100 = 0 ……..(1)
x² + y² – 22x + 4y + 100 = 0 ……….(2)
Centre of (1) is C₁ = (-11, 2)
r₁ = \(\sqrt{121+4+100}\) = 15
C₂ = (11, -2)
r₂ = \(\sqrt{121+4-100}\) = 5
C₁C₂ = \(\sqrt{(-11-11)^2+(2+2)^2}\)
= \(\sqrt{(-22)^2+(4)^2}\)
= √500
r₁ + r₂ = 20
C₁C₂ > r₁ + r₂
∴ The given circles completely lie outside the circle.
Let A₂ be the external centre of similitude.

Now, A₂ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ (3 : 1) externally.
External of similitude

The equation to the pair of direct common tangents is S . S₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + y² + 22x – 4y – 100) ((22)² + (-4)² + 2(11) (22) + 2(-2) (-4) – 100) = ((22)x + y(-4) + 2(11) (22) + 11(x) – 2(y) + 1(-2) (-4) – 100)²
⇒ (x² + y² + 22x – 4y – 100) (484 + 16 + 484 + 16 – 100) = (22x – 4y + 242 + 11x – 2y + 8 – 100)²
⇒ (x² + y² + 22x – 4y – 100) (900) = (33x – 6y + 150)²
⇒ 100(x² + y² + 22x – 4y – 100) = (11x – 2y + 50)²
⇒ 100x² + 100y² + 2200x – 400y – 10000 = 121x² + 4y² + 2500 – 44xy – 200xy + 1100x
⇒ 21x² – 96y² – 44xy – 1100x + 200y + 12500 = 0
Now, 21x² – 44xy – 96y² = 0
⇒ 21x² – 72xy + 28xy – 96y² = 0
⇒ 3x(7x – 24y) + 4y(7x – 24y) = 0
⇒ (7x – 24y) (3x + 4y) = 0
⇒ 7x – 24y = 0, 3x + 4y = 0
∴ 21x² – 44xy – 96y² – 1100x + 200y + 12500 = (7x – 24y + l) (3x + 4y + k)
Comparing ‘x’ coeff. on both sides
7k + 3l = -1100 …….(1)
Comparing ‘y’ coeff. on both sides
-24k + 4l = 200 ………(2)
Solve (1) & (2)

∴ The direct common tangent are 7x – 24y – 250 = 0, 3x + 4y – 50 = 0

Question 18.
Find all common tangents to the circles x² + y² + 4x + 2y – 4 = 0 and x² + y² – 4x – 2y + 4 = 0.
Solution:
Given equations of the circles are
x² + y² + 4x + 2y – 4 = 0 ………(1)
x² + y² – 4x – 2y + 4 = 0 ……….(2)
for the circle (1)
Centre C₁ = (-2, -1)

Now, r₁ + r₂ = 3 + 1 = 4 = √16
∴ C₁C₂ > r₁ + r₂
∴ In the two given circles, each circle lies completely outside the other.
To find the external centre of similitude (A₂):
Let A₂ be the external centre of similitude.
The external centre of similitude, A₂ divides C₁C₂ in the ratio r₁ : r₂ (3 : 1) externally.

The equation of pair of direct common tangent is SS₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + y² + 2gx + 2fy + c) \(\left(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{fy}_1+\mathrm{c}\right)\) = (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c)²
⇒ (x² + y² + 4x + 2y – 4) [(4)² + (2)² + 2(2)(4) + 2(1)(2) – 4] = [x(4) + y(2) + 2(x + 4) + 1(y + 2) – 4]²
⇒ (x² + y² + 4x + 2y – 4) (16 + 4 + 16 + 4 – 4) = (4x + 2y + 2x + 8 + y + 2 – 4)²
⇒ (x² + y² + 4x + 2y – 4) (36) = (6x + 3y + 6)²
⇒ (x² +y² + 4x + 2y – 4) (36) = 9(2x + 4 + 2)²
⇒ (x² + y² + 4x + 2y – 4) (4) = (2x + y + 2)²
⇒ (x² + y² + 4x + 2y – 4) (4) = 4x² + y² + 4 + 4xy + 4y + 8x
⇒ 4x² + 4y² + 16x + 8y – 16 = 4x² + y² + 4xy + 4y + 8x + 4
⇒ 4xy – 3y² – 8x – 4y + 20 = 0
Consider 4xy – 3y² = 0
⇒ y(4x – 3y) = 0
⇒ y = 0 (or) 4x – 3y = 0
∴ 4xy – 3y2 – 8x – 4y + 20 = (y + l)(4x – 3y + k)
Comparing the coefficient of x on both sides
4l = -8
⇒ l = -2
Comparing the coefficient of y on both sides.
-3l + k = – 4
⇒ -3(-2) + k = -4
⇒ 6 + k = -4
⇒ k = -10
∴ The equations to the direct common tangents are y – 2 = 0, 4x – 3y – 10 = 0
To find the internal centre of similitude (A₁):
Let A₁ be the internal centre of similitude.
The internal centre of similitude, A₁ divides C₁C₂ in the ratio r₁ : r₂ (3 : 1) internally.


⇒ (x² + y² + 4x + 2y – 4) (9) = (9) (2x + y – 1)²
⇒ x² + y² + 4x + 2y – 4 = 4x² + y² + 1 + 4xy – 2y – 4x
⇒ 3x² + 4xy – 8x – 4y + 5 = 0
Consider 3x² + 4xy = 0
⇒ x(3x + 4y) = 0
⇒ x = 0 (or) 3x + 4y = 0
∴ 3×2 + 4xy – 8x – 4y + 5 = (x + l) (3x + 4y + k)
Comparing the coefficient of x on. both sides
3l + k = -8 ………(3)
Comparing the coefficient of y on both sides.
4l = -4 ⇒ l = -1
(3) ⇒ 3(-1) + k = -8
⇒ -3 + k = -8
⇒ k = -5
∴ The equations of the transverse common tangents are x – 1 = 0, 3x + 4y – 5 = 0
∴ The common tangents are x – 1 = 0, 3x + 4y – 5 = 0, y – 2 = 0, 4x – 3y – 10 = 0

Question 19.
Find the equations of circles that touch 2x – 3y + 1 = 0 at (1, 1) and have a radius √13.
Solution:
Let, the equation of the required circle is x² + y² + 2gx + 2fy + c = 0

The equation of the tangent at P(1, 1) to the given circle is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(1) + g(x + 1) + f(y + 1) + c = 0
⇒ x + y + gx + g + fy + f + c = 0
⇒ x(1 + g) + (1 + f)y + g + f + c = o ………(1)
Given the equation of the tangent is
2x – 3y + 1 = 0 ……….(2)
Now, (1) and (2) represent the same line we get

2k – 1 – 3k – 1 + c = k
⇒ -k – 2 + c = k
⇒ c = 2k + 2
Given that, radius, r = √13
\(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{13}\)
Squaring on both sides
g² + f² – c = 13
⇒ (2k – 1)² + (-3k – 1)² – (2k + 2) = 13
⇒ 4k² + 1 – 4k + 9k² + 1 + 6k – 2k – 2 = 13
⇒ 13k² = 13
⇒ k² = 1
⇒ k = ±1
Case 1: If k = 1 then
g = 2(1) – 1 = 2 – 1 = 1
f = -3(1) – 1 = -3 – 1 = -4
c = 2(1) + 2 = 2 + 2 = 4
∴ The equation of the required circle is x² + y² + 2(1)x + 2(-4)y + 4 = 0
⇒ x² + y² + 2x – 8y + 4 = 0
Case 2: If k = -1 then
g = 2(-1) – 1 = -2 – 1 = -3
f = -3(-1) – 1 = 3 – 1 = 2
c = 2(-1) + 2 = -2 + 2 = 0
∴ The equation of the required circle is x² + y² + 2(-3)x + 2(2)y + 0 = 0
⇒ x² + y² – 6x + 4y = 0
∴ The required circles are x² + y² + 2x – 8y + 4 = 0, x² + y² – 6x + 4y = 0

Question 20.
If ABCD is a square, then show that the points A, B, C, and D are concyclic.
Solution:
ABCD is a square
Let AB = a, then AD = a
∴ A = (0, 0), B = (a, 0), C = (a, a), D = (0, a)

Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since, (1) passes through point A(0, 0)
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Since (1) passes through point B(a, 0)
(a)² + (0)² + 2g(a) + 2f(0) + c = 0
⇒ a² + 2ga + c = 0
⇒ a² + 2ga = 0
⇒ a + 2g = 0
⇒ g = \(\frac{-a}{2}\)
Since, (1) passes through the point D(0, a)
(0)² + a² + 2g(0) + 2f(a) + c = 0
⇒ 0 + a² + 2af = 0
⇒ a + 2f = 0
⇒ f = \(\frac{-a}{2}\)
Now, substitute the values of g, f, c in (1), and we get
x² + y² + 2(\(\frac{-a}{2}\))x + 2(\(\frac{-a}{2}\))y + 0 = 0
x² + y² – ax – ay = 0 ……(2)
Now, substitute the point c(a, a) in (2)
(a)² + (a)² – a(a) – a(a) = 0
⇒ a² + a² – a² – a² = 0
⇒ 0 = 0
∴ Points A, B, C, and D are concyclic.

Question 21.
Find the equation of the circumcircle of the triangle formed by the line ax + by + c = 0 (abc ≠ 0) and the coordinate axes.
Solution:
Let the line ax + by + c = 0, and cut the x, y axes at A and B respectively.

Let the equation of the required circle is
x² + y² + 2gx + 2fy + k = 0 ……..(1)
Since, (1) passes through the point O(0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + k = 0
⇒ k = 0
Since, (1) passes through the point A(\(\frac{-c}{a}\), 0), then

Now, substitute the values of g, f, k in (1)
∴ The equation of the required circle is
x² + y² + 2(\(\frac{c}{2a}\))x + 2(\(\frac{c}{2b}\))y + 0 = 0
⇒ abx² + aby² + bcx + acy = 0
⇒ ab(x² + y²) + (bx + ay)c = 0

Question 22.
Find the equation of the circumcircle of the triangle formed by the straight lines x + 3y – 1 = 0, x + y + 1 = 0, 2x + 3y + 4 = 0.
Solution:
Given lines are x + 3y – 1 = 0, x + y + 1 = 0, 2x + 3y + 4 = 0
Consider a curve through vertices of the triangle formed by the given lines whose equation is
a(x + 3y – 1) (x + y + 1) + b(x + y + 1) (2x + 3y + 4) + c(2x + 3y + 4) (x + 3y – 1) = 0
⇒ a(x² + xy + x + 3xy + 3y² + 3y – x – y – 1) + b(2x² + 3xy + 4x + 2xy + 3y² + 4y + 2x + 3y + 4) + c(2x² + 6xy – 2x + 3xy + 9y² – 3y + 4x + 12y – 4) = 0
⇒ a(x² + 3y² + 4xy + 2y – 1) + b(2x² + 5xy + 3y² + 6x + 7y + 4) + c(2x² + 9xy + 9y² + 2x + 9y – 4) = 0 ……..(1)
Coefficient of x² = a + 2b + 2c
Coefficient of y² = 3a + 3b + 9c
Coefficient of xy = 4a + 5b + 9c
(1) represents a circle, then
(i) Coefficient of x² = Coefficient of y²
⇒ a + 2b + 2c = 3a + 3b + 9c
⇒ 3a + 3b + 9c – a – 2b – 2c = 0
⇒ 2a + b + 7c = 0 …….(2)
(ii) Coefficient of xy = 0
⇒ 4a + 5b + 9c = 0 …….(3)
Solve (2) and (3)

\(\frac{a}{9-35}=\frac{b}{28-18}=\frac{c}{10-4}\)
\(\frac{a}{-26}=\frac{b}{10}=\frac{c}{6}\)
∴ a = -26, b = 10, c = 6
Substitute the value of a, b, c in (1)
-26(x² + 4xy + 3y² + 2y – 1) + 10(2x² + 5xy + 3y² + 6x + 7y + 4) + 6(2x² + 9xy + 9y² + 2x + 9y – 4) = 0
⇒ -26x² – 104xy – 78y² – 52y + 26 + 20x² + 50xy + 30y² + 60x + 10y + 40 + 12x² + 54xy + 54y² + 12x + 54y – 24 = 0
⇒ 6x² + 6y² + 72x + 72y + 42 = 0
⇒ x² + y² + 12x + 12y + 7 = 0
∴ The equation of the required circle is x² + y² + 12x + 12y + 7 = 0

Question 23.
Find the equation of the circle passing through (-1, 0) and touching x + y – 7 = 0 at (3, 4).
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)

Since (1) passes through point A(-1, 0), then
(-1)² + (0)² + 2g(-1) + 2f(0) + c = 0
⇒ 1 – 2g + c = 0
⇒ c = 2g – 1 ……..(2)
Since, the line x + y – 7 = 0 touches the circle (1), then the given equation of a tangent is
x + y – 7 = 0 ………(3)
Now, the equation of tangent at P(3, 4) is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(4) + g(x + 3) + f(y + 4) + 2g – 1 = 0
⇒ 3x + 4y + gx + 3g + fy + 4f + 2g – 1 = 0
⇒ 3x + 4y + gx + fy + 4f + 5g – 1 = 0
⇒ (3 + g)x + (4 + f)y + 5g + 4f – 1 = 0 ……….(4)
(3) and (4) represent the same line

Substitute the value of g in (2)
c = 2(-1) – 1
⇒ c = -2 – 1
⇒ c = -3
Substitute the values of g, f, c in (1)
∴ The required equation of the circle is x² + y² + 2(-1)x + 2(-2) y – 3 = 0
⇒ x² + y² – 2x – 4y – 3 = 0

Question 24.
Find the equation of the circle which touches the circle x² + y² – 2x – 4y – 20 = 0 externally at (5, 5) with radius 5. [(AP) Mar. ’20; (TS) May ’16]
Solution:
Given equation of the circle is x² + y² – 2x – 4y – 20 = 0

Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = -2, c = -20
Centre C₁ = (-g, -f) = (1, 2)
Radius r₁ = \(\sqrt{1+4+20}=\sqrt{25}\) = 5
Let centre of the required circle is C₂ = (h, k)
Radius r₂ = 5
Given point of contact P = (5, 5)
Now, the point of contact ‘P’ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ (5 : 5 = 1 : 1) internally.

Hence, centre C₂ = (9, 8)
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 9)² + (y – 8)² = 5²
⇒ x² + 81 – 18x + y² + 64 – 16y = 25
⇒ x² + y² – 18x – 16y + 120 = 0

Question 25.
If θ₁, θ₂ are the angles of inclination of tangents through a point P to the circle x² + y² = a², then find the locus of P when cot θ₁ + cot θ₂ = k.
Solution:
Given the equation of the circle is x² + y² = a²

Let P(x₁, y₁) be a point on the locus.
The equation of the tangent to x² + y² = a² having slope m is
y = mx ± \(a \sqrt{1+m^2}\) ……..(1)
If the tangent (1) passes through P, then

Let the roots of (2) be m₁, m₂
Since, the tangents make angles θ₁, θ₂ with x-axis then their slopes m₁ = tan θ₁ and m₂ = tan θ₂
∴ m₁ + m₂ = tan θ₁ + tan θ₂

∴ The locus of P is k(y² – a²) = 2xy.

Question 26.
Show that the poles of the tangents to the circle x² + y² = a² w.r.t the circle (x + a)² + y² = 2a² lie on y² + 4ax = 0.
Solution:
Given the equation of the circle
(x + a)² + y² = 2a²
⇒ x² + a² + 2ax + y² – 2a² = 0
⇒ x² + y² + 2ax – a² = 0 …….(1)

Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
g = a, f = 0, c = -a²
Let P(x₁, y₁) be the pole
Now, the polar of P(x₁, y₁) w.r.t the circle (1) is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ xx₁ + yy₁ + a(x + x₁) + 0(y + y₁) – a² = 0
⇒ xx₁ + yy₁ + ax + ax₁ – a² = 0
⇒ (x₁ + a)x + y₁y + (ax₁ – a²) = 0 ………(2)
Given equation of the circle is x² + y² = a² ……..(3)
Centre C = (0, 0), Radius r = a
Since (2) is a tangent to the circle (3), then r = d

∴ The poles of the tangents to the circle (2) w.r.t the circle (1) lie on the curve y² + 4ax = 0.

Question 27.
If the chord of contact of a point P w.r.t the circle x² + y² = a² cut the circle at A and B such that ∠AOB = 90°, then show that P lies on the circle x² + y² = 2a².
Solution:
Given the equation of the circle is
x² + y² = a² ……(1)
Let P(x₁, y₁) be a point.

The equation of the chord of contact of P(x₁, y₁) w.r.t the circle x² + y² = a² is S₁ = 0
xx₁ + yy₁ = a²
\(\frac{xx_1+y y_1}{a^2}=1\) ……..(2)
Now homogenizing (1) with help of (2)
∴ The combined equation of \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OB}}\) is x² + y² = a² (1)²

Hence, the point P(x₁, y₁) lies on the circle x² + y² = 2a².

Question 28.
Show that the equation to the pair of tangents to the circle S = 0 from P(x₁, y₁) is \(S_1^2\) = SS₁₁. [May ’14; Mar. ’03]
Solution:
Let the equation of the circle be S = x² + y² + 2gx + 2fy + c = 0

Let a line l = 0 through P(x₁, y₁) meet the circle in A and B.
Let Q(x, y) be any point on the line.
Let k : 1 be the ratio in which A divides \(\overline{\mathrm{PQ}}\)


If L = 0 is a tangent to S = 0 then A & B coincide and the roots of (1) are equal.
∴ b² – 4ac = 0
⇒ (2S₁)² – 4(S) (S₁₁) = 0
⇒ 4\(S_1^2\) – 4SS₁₁ = 0
⇒ \(S_1^2\) – SS₁₁ = 0
⇒ \(S_1^2\) = SS₁₁
∴ The locus of ‘Q’ is \(S_1^2\) = SS₁₁
∴ The equation to the pair of tangents from P(x₁, y₁) is \(S_1^2\) = SS₁₁.

Question 29.
Find the condition that the tangents drawn from the exterior point (g, f) to S = x² + y² + 2gx + 2fy + c = 0 are perpendicular to each other.
Solution:
Given the equation of the circle is
S = x² + y² + 2gx + 2fy + c = 0
Centre C = (-g, -f)
Radius r = \(\sqrt{g^2+f^2-c}\)
Let the given point P(x₁, y₁) = (g, f)
The angle between the tangents θ = 90°
Length of the tangents = \(\sqrt{S_{11}}\)

squaring on both sides
3g² + 3f² + c = g² + f² – c
⇒ 2g² + 2f² + 2c = 0
⇒ g² + f² + c = 0

Question 30.
Find the equation of the circle passing through P(1, 1), Q(2, -1) and R(3, 2).
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point P(1, 1), then
(1)² + (1)² + 2g(1) + 2f(1) + c = 0
⇒ 1 + 1 + 2g + 2f + c = 0
⇒ 2g + 2f + c = -2 ……..(2)
Since, (1) passes through the point Q(2, -1), then
(2)² + (-1)² + 2g(2) + 2f(-1) + c = 0
⇒ 4 + 1 + 4g – 2f + c = 0
⇒ 4g – 2f + c = -5 …….(3)
Since, (1) passes through the point R(3, 2), then
(3)² + (2)² + 2g(3) + 2f(2) + c = 0
⇒ 9 + 4 + 6g + 4f + c = 0
⇒ 6g + 4f + c = -13 ………(4)
from (2) and (3)

Question 31.
From a point on the circle x² + y² + 2gx + 2fy + c = 0, two tangents are drawn to the circle x² + y² + 2gx + 2fy + c sin² α + (g² + f²) cos² α = 0. Prove that the angle between them is 2α.
Solution:
Given equations of the circles are
x² + y² + 2gx + 2fy + c = 0 ……..(1)
x² + y² + 2gx + 2fy + c sin² α + (g² + f²) cos² α = 0 …….(2)

Let P(x₁, y₁) be a point on the circle (1), then
\(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}=0\) ……..(3)
The radius of the circle (2) is

Length of the tangent of the circle (2)

If θ is the angle between the tangents then

∴ The angle between the tangents θ = 2α.

Question 32.
Find the pair of tangents from the origin to the circle x² + y² + 2gx + 2fy + c = 0 and hence deduce a condition for these tangents to be perpendicular. (Mar. ’81)
Solution:
Given equation of the circle is x² + y² + 2gx + 2fy + c = 0
Here g = g, f = f, c = c
Let the given point P(x₁, y₁) = (0, 0)
The equation of the pair of tangents drawn from (0, 0) to the given circle is \(\mathrm{S}_1^2\) = SS₁₁
⇒ [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]² = (x² + y² + 2gx + 2fy + c) \(\left(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\right)\)
⇒ [x(0) + y(0) + g(x + 0) + f(y + 0) + c]² = (x² + y² + 2gx + 2fy + c) (0 + 0 + 0 + 0 + c)
⇒ (gx + fy + c)² = (x² + y² + 2gx + 2fy + c) (c)
⇒ g² x² + f² y² + c² + 2gf xy + 2fcy + 2gcx = cx² + cy² + 2gcx + 2fcy + c²
⇒ (g² – c) x² + 2gf xy + (f² – c) y² = 0
Given that these tangents are perpendicular then
coefficient of x² + coefficient of y² = 0
⇒ g² – c + f² – c = 0
⇒ g² + f² = 2c

Question 33.
Find the locus of the midpoint of the chords of contact of x² + y² = a² from the points lying on the line lx + my + n = 0. [May ’03; Mar. ’90]
Solution:
Given the equation of the circle is
x² + y² = a² …….(1)
Given the equation of the line is
lx + my + n = 0 ……..(2)

Let P(x₁, y₁) be a point on the locus then the point P(x₁, y₁) is the midpoint of the chord of the circle x² + y² = a².
∴ The equation of the chord having P(x₁, y₁) as the midpoint of the circle (1) is S₁ = S₁₁.
⇒ xx₁ + yy₁ – a² = \(\mathrm{x}_1{ }^2+\mathrm{y}_1^2\) – a²
⇒ xx₁ + yy₁ – (\(\mathrm{x}_1{ }^2+\mathrm{y}_1^2\)) = 0 ……….(3)
Now, the pole of (3) with respect to the circle is

Hence the locus of P(x₁, y₁) is a²(lx + my) + n(x² + y²) = 0.

Here students can locate TS Inter 2nd Year Zoology Notes 4th Lesson Human Anatomy and Physiology – IV to prepare for their exam.

TS Inter 2nd Year Zoology Notes 4th Lesson Human Anatomy and Physiology – IV

→ Hormones are mostly the body’s long distance signaling substances.

→ Hormones are released by the endocrine glands.

→ Many animals like insects are known to produce regulatory molecules called pheromones which are released to the exterior.

→ Certain hormones which stimulate the production of other hormones in other parts of the body are called Tropic hormones’, (eg : ACTH)

→ Endocrine glands are otherwise called ductless glands.

→ As per current scientific definition “hormones are non-nutrient chemicals which act as intercellular messengers and are produced in trace amounts”.

→ The term hormone was coined by starling.

→ Secretin was the first harmone to be detected.

→ Hormones are biomolecules of small size and are effective in very low concentrations.

→ Chemically hormones fall into 3 classes, namely

• Amine hormones
• Peptide and protein hormones
• Steroid hormones.

→ Immune system is the 24hrs / 7 days body guard system.

→ The 3 lines of defence in human beings is
(a) Skin
(b) Neutrophils
(c) Antibodies produced by lymphocytes.

→ The basic requirement of the immune system is to differentiate between self and non self and to protect the body from harmful foreign substances, toxins etc.

→ The branch of biology that deals with immunity or the study of immune system is called immunology.

→ Edward Jenner is acknowledged as the father of immunology.

→ Cells of immune system are mainly 3 types

• Lymphocytes
• Phagocytes
• Auxiliary cells.

→ Based on the size, the lymphocytes can be divided into small lymphocytes and large lymphocytes.

→ Small lymphocytes include p – cells and T – cells.

→ Large lymphocytes include large granular lymphocytes that consist of Natural Killer cells (NK cells).

→ The basic requirement of the immune system is to differentiate between self and non self and to protect the body from harmful microorganisms.

→ Frederick G. Banting
Frederick Grant Banting was born on November 14,1891, at Alliston, Ont., Canada. He was the youngest of five children of William Thompson Banting and Margaret Grant. Educated at the Public and High Schools at ‘/ Alliston, he later went to the University of Toronto to study divinity, but soon transferred to the study of medicine. In 1916 he took his M.B. degree and at once joined the Canadian Army Medical Corps, and served, during the First World War, in France. In 1918 he was wounded at the battle of Cambrai and in 1919 he was awarded the Military Cross for heroism under fire.

When the war ended in 1919. Banting returned to Canada and was for a short time a medical practitioner at London, Ontario. He studied orthopaedic medicine and was, during the year 1919 -1920, Resident Surgeon at the Hospital for Sick Children, Toronto. From 1920 until 1921 he did part – time teaching in orthopaedics at the University of Western Ontario at London Canada, besides his general practice, and from 1921 until 1922 he was Lecturer in Pharmacology at the University of Toronto, in 1922 he was awarded his M.D. degree, together with a gold medaL

Earlier, however, Banting had become deeply interested in diabetes. The work of Naunyn, Minkowski, Opie, Schafer, and others had indicated that diabetes was caused by lack of a protein hormone secreted by the islands of Langerhans in the pancreas. To this hormone Schafer had given the name insulin, and it was supposed that insulin controls the metabolism of sugar, so that lack of it results in the accumulation of sugar in the blood and the excretion of the excess of sugar in the urine. Attempts to supply the missing insulin by feeding patients with fresh pancreas or extracts of it; had failed, presumably because the protein insulin in these had been destroyed by the proteolytic enzyme of the pancreas. The problem therefore, was how to extract insulin from the pancreas before it had been thus destroyed.

While he was considering this problem, Banting read in a medical journal an article by Moses Baron, which pointed out that; when the pancreatic duct was experimentally closed by ligatures, the cells of the pancreas which secrete trypsin degenerate, but that the islands of Langerhans remain intact. This suggested to Banting the idea that ligation of the pancreatic duct would, by destroying the cells which secrete trypsin, avoid the destruction of the insulin, so that; after sufficient time had been allowed for the degeneration of the trypsin – secreting cells, insulin might be extracted from the intact islands of Langerhans.

→ Charles Herbert Best
Charles Herbert Best, CC, CH, CBE, MD, FRS, FRSC, FRCP (1899 -1978) was an American – Canadian medical scientist and one of the co-discoverers of insulin.

→ Niels Kaj Jerne
Niels Kaj Jerne, FRS (1911 – 1994) was a Danish immunologist. He shared the Nobel Prize in Physiology or Medicine in 1984 with Georges J.F. Kohler and Cesar Milstein “[f] or theories concerning the specificity in development and control of the immune system and the discovery of the principle for production of monoclonal antibodies”.

→ Cesar Milstein „
Cesar Milstein, FRS 1927 was an Argentine biochemist in the field of antibody research. Milstein shared the Nobel Prize in Physiology or Medicine in 1984 with Niels Kaj Jerne and Georges J.F. Kohler.

→ Georges J.F. Kohler
German biologist.
Together with Cesar Milstein and Niels Kaj Jerne, Kohler won the Nobel Prize in Physiology or Medicine in 1984, “for work on the immune system and the production of monoclonal antibodies”. A portion of this research was performed at the Basel Institute for Immunology.

Here students can locate TS Inter 2nd Year Zoology Notes 3rd Lesson Human Anatomy and Physiology – III to prepare for their exam.

TS Inter 2nd Year Zoology Notes 3rd Lesson Human Anatomy and Physiology – III

→ Human body has two important systems to give it the right posture and movement of body parts
(a) Muscular system
(b) Skeletal system.

→ Human body has hundreds of muscles, about 640 in total.

→ Skeletal muscles constitute the bulk of our body.

→ Skeletal muscles are controlled by the somatic nervous system and the cardiac and visceral muscles are controlled by the autonomous system.

→ Skeletal system has two major components, the axial skeleton (skull, vertebral column, ribs and sternum) and appendicular system (the limb skeletons, girdles etc.).

→ We use limbs for changing body postures and locomotion too.

→ In animals locomotion is performed generally to search for food, shelter, , mate suitable breeding grounds, and favourable climatic conditions or to escape from enemies/ predators.

→ In adult human beings skeletal system is made up of 206 bones and a few cartilages. It is grouped into two principal divisions. The axial skeleton and the appendicular skeleton.

→ Axial skeleton comprises of 80 bones.

→ Appendicular skeleton comprises of 126 bones.

→ Nervous system evolved from the basic non-polarised nerve cells forming a diffuse nerve net as seen in the diploblastic organisms to a highly organized integrating system with the brain.

→ Man came to know more about brain with the help of “Functional Magnetic Resonance Imaging” (FMRI) technique.

→ Nervous tissue has connecting cells called neurons and supporting cells called glial cells.

→ The system mainly controls the body activities by receiving stimuli, processing them and reacting to them by sending motor signals.

→ Hippocampus of the brain is responsible for the formation and recall of memory.

→ Research is going on why people develop dementia, involving memory loss as seen in Alzheimers.

→ Co- ordination is the process through which two or more organs interact and complement the functions of one another.

→ The neural system provides an organized network of point to point connections for a quick co-ordination.

→ Human neural system is divided into two parts

• Central Neural System (CNS)
• Peripheral Neural System (PNS).

→ CNS includes the brain and the spinal cord.

→ Archibald Hill:
A.V. Hill christened Archibald Vivian, CH OBE FRS (26 September 1886 – 3 June 1977), was an English physiologist one of the founders of the diverse disciplines of biophysics and operations research. He shared the 1922 Nobel Prize in Physiology or Medicine for his elucidation of the production of heart and mechanical work in muscles.

→ Otto Fritz Meyerhof:
Biography; Meyerhof was born in Hildesheim. He spent most of his childhood in Berlin, where he started his study of medicine.
In 1912, he moved to the University of Kiel, where he became professor in 1918. In 1922, he was awarded the Nobel Prize in Medicine, with Archibald Vivian Hill, for his work on muscle metabolism, including glycolysis.

→ Camillo Golgi:
Camillo Golgi : (1843-1926) was an Italian physician, pathologist, scientist; and Nobel laureate. Camillo Golgi was born in July 1843 in the village of Corteno, Lombardy, then part of the Austrian Empire. The village is now named Corteno Golgi in his honour. His father was a physician and district medical officer. Golgi studied at the University of Pavia, where he worked in the experimental pathology laboratory under Giulio Bizzozero, who elucidated the properties of bone marrow. He graduated in 1865. He spent much of his career studying the central nervous system. Tissue staining techniques in the later half of the 19th century were inadequate for studying nervous tissue. While working as chief medical officer in a psychiatric hospital he experimented with metal impregnation of nervous tissue, using mainly silver (silver staining). He discovered a method of staining nervous tissue which would stain a limited number of cells at random, in their entirety. This enabled him to view the paths of nerve cells in the brain for the first time. He called his discovery the “black reaction” (in Italian, reazine nera), which later received his name (Golgi’s method) or Golgi stain.

→ Santiago Ramon y Cajal:
Santiago Ramon y Cajal For MemRS (Spanish 1852-1934) was a Spanish pathologist, histologist, neuroscientist, and Nobel laureate. His pioneering investigations of the microscopic structure of the brain were original: he is considered by many to be the father of modern neuroscience. He was skilled at drawing, and hundreds of his illustrations of brain cells are still used for educational purposes today.