TS Inter 2nd Year Physics Study Material Chapter 5 Electrostatic Potential and Capacitance

Telangana TSBIE TS Inter 2nd Year Physics Study Material 5th Lesson Electrostatic Potential and Capacitance Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 5th Lesson Electrostatic Potential and Capacitance

Very Short Answer Type Questions

Question 1.
Can there be electric potential at a point with zero electric intensity? Give an example.
Answer:
Yes. At the mid point of line joining two similar charges, electric field is zero but potential will exist. Ex : Inside a charged hallow spherical shell field is zero but potential is not zero.

Question 2.
Can there be electric intensity at a point with zero electric potential? Give an example.
Answer:
Yes. At the midpoint or on the equatorial line of an electric dipole potential is zero but eletric field is not zero.

Question 3.
What are meant by equipotential surfaces?
Answer:
An equipotential surface is a surface with constant value of potential at all points on the surface.

Question 4.
Why is the electric field always at right angles to the equipotential surface? Explain.
Answer:
If the electric field is not normal to the equipotential surface, then the work done in moving a charge from one point to the other will not be zero, which is a contradiction, thus the field is normal to equipotential surface.

Question 5.
Three capacitors of capacitances 1 µF, 2 µF, and 3 µF are Connected in parallel.
a) What is the ratio of charges?
b) What is the ratio of potential differences?
Answer:
Charge q = CV
a) ⇒ q ∝ C ⇒ q₁ : q₂ : q₃ = C₁ : C₂ : C₃ = 1 : 2 : 3
b) In parallel combination potential across combination is
Constant : V₁ : V₂ : V₃ = 1 : 1 : 1

Question 6.
Three capacitors of capacitances 1 µF, 2 µF, and 3 µF are connected in series
a) What is the ratio of charges?
b) What is the ratio of potential differences?
Answer:
q = CV, in series combination charge q’ is constant on each capacitor.
a) ⇒ q₁ : q₂ : q₃ = 1 : 1 : 1
b) V ∝ \(\frac{1}{C}\) ⇒ V₁ : V₂ : V₃ : \(\frac{1}{1}: \frac{1}{2} : \frac{1}{3}\) = 6 : 3 : 2

Question 7.
What happens to the capacitance of a parallel plate capacitor if the area of its plates is doubled?
Answer:
The capacity of a parallel plate capacitor

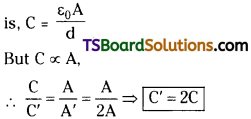
when area is doubled (A’ = 2A) then capacity is also doubled.

Question 8.
The dielectric strength of air is 3 × 10⁶ Vm^-1 at certain pressure. A parallel plate capacitor with air in between the plates has a plate separation of 1 cm. Can you charge the capacitor to 3 × 10⁶ V?
Answer:
No ; The dielectric strength of air means the max. electric field that the medium will with-stand. Given E_max = 3 × 10⁶Vm^-1,

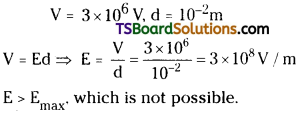
Short Answer Questions

Question 1.
Derive an expression for the electric potential due to a point charge. [Mar. ’16; TS Mar. ’16]
Answer:
Consider a point charge Q at ‘O’ and a unit positive charge is placed at ‘P’, distance r’. The force acting on it is

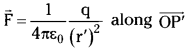
Let dW be the work done in moving this test charge through dr’ towards ‘O’.

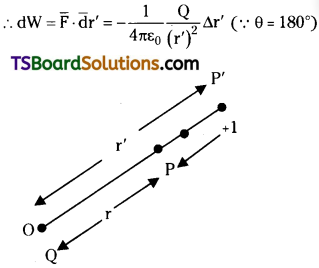
The total work done in bringing this test charge from r’ = ∞ to r’ = r is

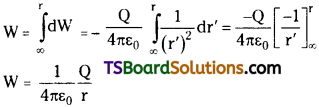
By the definition of potential this work- done is the electrostatic potential at that point.
∴ V = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r}\)

Question 2.
Derive an expression for the electrostatic potential energy of a system of two point charges and find its relation with electric potential of a charge.
Answer:
Consider a system of two charges q₁ and q₂ with position vectors \(\overline{\mathrm{r_1}}\) and \(\overline{\mathrm{r_2}}\) relative to origin at points A & B respectively. The electrostatic potential due to q₁ at B is V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1}{\mathrm{r}_2}\)
The work done in bringing q2 from infinity to the
point B is W = q₂ V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1\mathrm{q}_2}{\mathrm{r}_{12}}\)

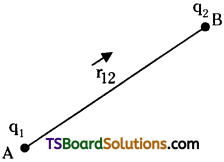
As the electrostatic force is a conservative force, this work done will be stored as energy in the system.

Hence this work done is called electrostatic potential energy ‘U’ of the system of the charges q₁ and q₂.

Question 3.
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field.
Answer:
Consider a dipole with charges + q and – q placed in a uniform electric field E as shown.

Forces are F₁ = qE and F₂ = – qE but dipole experiences torque given by

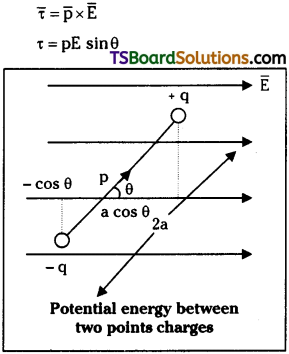
Let ‘dW’ be the small amount of work done in rotating the dipole through d0 without any angular acceleration.
dW = τdθ
The toal work done to deflect from θ₁ to θ₂ is

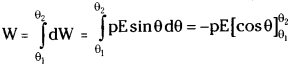
W = pE [cos θ₁ – cos θ₂]
This work done is stored as potential energy in the dipole.
If the dipole is intially parallel to \(\overline{\mathrm{E}}\) and now turned through an angle θ, the work- done is
W = pE [cosθ – cosθ] = pE [ 1 – cosθ]
Then the potential energy of the dipole in this displaced position is U = U₀ + W = – pE + pE [ 1 – cos θ] = – pE cos θ = – \(\overline{\mathrm{E}}.\overline{\mathrm{E}}\)

Question 4.
Derive an expression for the capacitance of a parallel plate capacitor. [AP Mar. 18, 16, May 17. 16; TS Mar. 18. May 18. 16]
Answer:
A parallel plate capacitor consists of two plane conducting plates of area A separated by a small distance d’. Let the medium between the plates is vacuum.
Let the surface charge densities of the plates (1) and (2) be + σ and – σ.
The electric fields in regions I and III will be

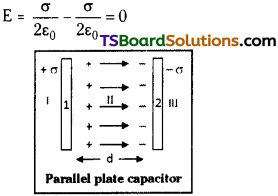
In the inner region i.e., II the fields due to these plates will add up and given by

as ‘d’ is the separation between the plates, the potential difference between the plates given by

Question 5.
Explain the behaviour of dielectrics in an external field. [AP Mar. ’19]
Answer:
All dielectrics are two types 1) Non-polar dielectrics 2) Polar dielectrics.
a) For Non-polar dielectrics the centre of all positive and negative charges will coincide. Ex: O₂ molecule. So net dipole moment of these molecules is zero.

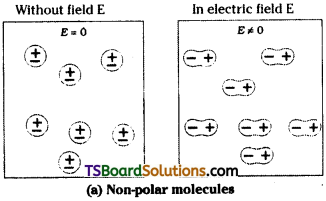
When these molecules are placed in an external electric field the positive and negative charges will be displaced in opposite directions. So they will develop induced dipolemoment. Total dipolemoment of these substances is the sum of all such dipolements and dielectrics are said to be polarised.

b) In case of polarised dielectrics in a molecule the centres of all positive charges and negative charges are separate. So they will develop some resultant dipolemoment. Under the absence of external electric field these dipole moments are random and resultant dipolemoment is zero.

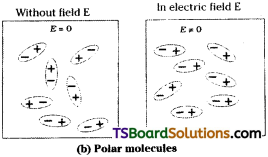
When they are placed in external electric field these dipoles are arranged in an order and the dipolemoments are polarised.
The dipole moment per unit volume (\(\overline{\mathrm{p}}\)) is called polarisation.
\(\overline{\mathrm{p}}\) = χ\(\overline{\mathrm{E}}\)
where χ is called electric susceptibility.

Long Answer Questions

Question 1.
Define electric potential. Derive an expression for the electric potential due to an electric dipole and hence the electric potential at a point (a) the axial line of electric dipole (b) on the equatorial line of electric dipole.
Answer:
Electric potential :
Work done to bring the unit positive charge from infinity to the point in the electric field is called potential.
Potential due to point charge q at a distance r (V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)

Electric dipole :
Two equal and opposite charges (q, -q) separated by a distance (say 2a) is called electric dipole.

Potential due to an electric dipole :
Consider an electric dipole with charge q, – q.

Let separation between them is 2a. Let P is a point at a distance r’ from centre of dipole.

Join qp, -qp and OP. Let the line OP makes an angle ‘θ’ with the dipole axis (q, – q).
Total potential at P is V =\(\frac{1}{4 \pi \varepsilon_0}\) \(\frac{q}{r_1}-\frac{q}{r_2}\)

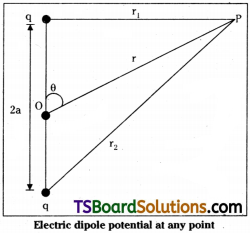
From geometry r²₁ = r² + a² – 2a r cos θ and
r²₂ = r² + a² + 2a r cos θ
These equations are rearranged as

But 2aq = p. dipole moment

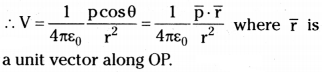
Potential at any point on axis of dipole :
Consider a dipole of charges q, – q with separation ‘2a’. At point p potential V is given by V = V₁ + V₂

Potential at any point on equatorial line of dipole :
Let P is any point on equatorial line of a dipole at a distance r.

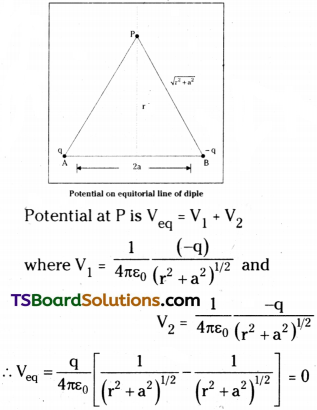
∴ Potential on equatorial line of dipole is zero.

Question 2.
Explain series and parallel combination of capacitors. Derive the formula for equivalent capacitance in each combination. [TS Mar. 19, 17, 15; AP May 16, June 15, Mar. 15]
Answer:
Capacitors in series :
If number of capacitors are connected in such a way that the charge on the plates of every one of them is same, then the capacitors are said to be
“connected in series”.

Explanation :
Let three capacitors C₁, C₂ and C₃ are connected in series as shown.

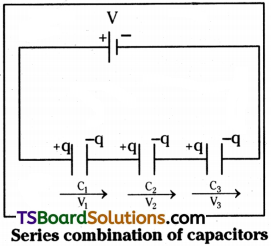
The charge q on the plates of the capacitors is same, let, V₁, V₂ and V₃ be the potential differences across C₁, C₂ and C₃ respectively. Let V be the p.d across the combination
then V = V₁ + V₂ + V₃

The reciprocal of equivalent capacity = the sum of reciprocal values of individual capacities of the combination.

Capacitors in parallel :
If a number of capacitors connected in such a way that the p. d between the plates of every one of them is same, then the capacitors are said to be “connected in parallel”.

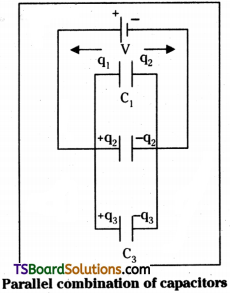
Explanation :
Let the capacitors of capacities C₁, C₂ and C₃ connected in parallel as shown.

The potential difference across each condenser is same and is equal to V. Let q₁ and q₂ and q₃ be the charges on the plates of the capacitors.
∴ q = q₁ + q₂ + q₃. here q₁ = C₁V, q₂ = C₂V, q₃ = C₃V
If C is equivalent capacity of the combination, the C = \(\frac{p}{V}\) ⇒ q = CV
∴ CV = C₁V + C₂V + C₃V
∴ C = C₁ + C₂ + C₃
The equivalent capacity of the parallel combination = the sum of the capacities of the capacitors.

Question 3.
Derive an expression for the energy stored in a capacitor. What is the energy stored when the space between the plates is filled with a dielectric.
a) With charging battery disconnected?
b) With charging battery connected in the circuit?
Answer:
Let ‘q’ be the charge on the plates of a capacitor and V be the potential difference between plates. The work done dW in charging the capacitor with an additional charge dq.
dW = Vdq
⇒ dW = \(\frac{q}{C}\)dq (∵ q = CV)
The total work done in charging the plates it to a charge Q = W

This work done in charging the capacitor stored as electrostatic potential energy.

Effect of dielectric :
a) When charging battery is disconnected:
The charge on the plates remain constant, but capacity increases.

∴ The energy stored will get reduced to \(\frac{1}{K}\) th of initial value.

b) When charging battery remain connected the p.d across the capacitor remains same, but the capacity and the charge increases.

∴ The energy stored will increases by K times initial value.

Problems

Question 1.
An elementary particle of mass in’ and charge + e initially at a very large distance is projected with velocity ‘v’ at a much more massive particle of charge + Ze at rest. The closest possible distance of approach of the incident particle is
Answer:
At closest approach kinetic energy of charged particle = electrostatic potential between them.

Given : Mass of particle = m; velocity = V
∴ KE = 1/2 mv² → (1)
Charge of particle q₁ = e ; Charge on massive particle q₂ = Ze
∴ Electrostatic potential

Question 2.
In a hydrogen atom the electron and proton are at a distance of 0.5 Å. The dipole moment of the system is
Answer:
Distance between electron and proton = 0.5Å = 0.5 × 10^–10 m
Charge on proton = Charge on electron = 1.6 × 10^-19 C
Dipole moment = charge × separation between charges
∴ Dipolemoment p = 1.6 × 10^-19 × 0.5 × 10^-10 = 0.8 × 10^-29 = 8 × 10^-30 Cm

Question 3.
There is a uniform electric field in the XOY plane represented by (\(\mathbf{40} \hat{\mathbf{i}}+\mathbf{30} \hat{\mathbf{j}}\)) Vm^-1. If the electric potential at the origin is 200 V, the electric potential at the point with co-ordinates (2m, lm) is
Answer:
Intensity of electric field E = \(\mathbf{40} \hat{\mathbf{i}}+\mathbf{30} \hat{\mathbf{j}}\)
Position of the given point = 2 m, 1 m
i.e., 2m along \(\hat{\mathbf{i}}\) and lm along \(\hat{\mathbf{j}}\). Potential
= \(\overline{\mathrm{E}}.\overline{\mathrm{r}}\) =40 × 2 + 30 × 1 = 80 + 30 = 110V
Potential at origin = 200V.
Potential difference at point p = 200 – 110 = 90V.

Question 4.
An equilateral triangle has a side length L. A charge + q is kept at the centroid of the triangle. P is a point on the perimeter of the triangle. The ratio of the minimum and maximum possible electric potentials for the point P is
Answer:
Length of side = L. Charge at centroid = + q
Let ‘O’ be the centroid.
Centroid will divide the angle bisector in the ratio 2 : 1.
∴ Maximum distance from centroid is say ‘2a’ then minimum distance from centroid is ‘a’.

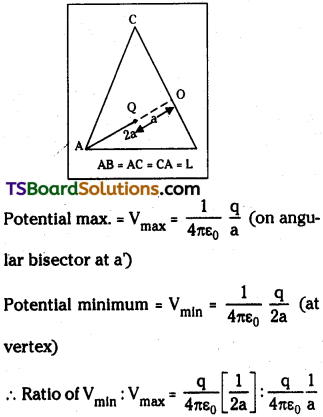
Ratio of minimum potential to maximum potential is 1 : 2.

Question 5.
ABC is an equilateral triangle of side 2m. There is a uniform electric field of intensity 100 V/m in the plane of the triangle and parallel to BC as shown. If the electric potential at A is 200 V, then the electric potentials at B and C are respectively
Answer:
Side of triangle L = 2m
Intensity of electric field = 100 V/m
(parallel to BC)

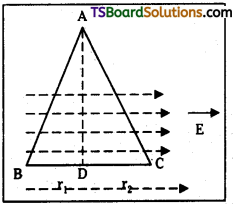
Potential at A = 200V.
Let D is the mid point of BC.
Now AD is an equipotential line with a potential of 200V.
Potential at B = 200 + E. r where r₁ = BD = 1m.
∴ Potential at B = 200 + 100 × 1 = 300 V
∴ Potential at C = Pot. at D – E. r₂ where
r₂ = 1m
V_D = 200 – 100 × 1 = 100v
Note : By definition potential is the work done against the field.

Question 6.
An electric dipole of moment p is called in a uniform electric field E, with p parallel to E. It is then rotated by an angle q. The work done is
Answer:
Electric dipolemoment = p;
Intensity of electric field = E
p and E are parallel ⇒ θ = 0;
Angle rotated = q
Work done by external force to rotate the dipole without acceleration
W = PE (cos θ₁ – cos θ₂)
Here θ₁ = 0 and θ₂ = q
∴ Work done = PE (cos 0 – cos q) = pE (1 – cos q)

Question 7.
Three identical metal plates each of area ‘A’ are arranged parallel to each other, ‘d’ is the distance between the plates as shown. A battery of V volts is connected as shown. The charge stored in the system of plates is

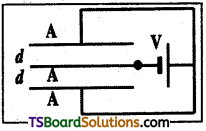
Answer:
Area of plates = A, Separation between the plates = d.
Potential supplied by battery = V.
From given arrangement it is a parallel combination of two identical capacitors.

Question 8.
Four identical metal plates each of area A are separated mutually by a distance d and are connected as shown. Find the capacity of the system between the terminals A and B.

Answer:
Area of each plate = A
Total separation between the plates = d
Separation between two adjacent plates = d₁ = d/3
Capacity of each capacitor \(C_1=\frac{\varepsilon_0 A}{d_1}=\frac{\varepsilon_0 A}{d / 3}=\frac{3 \varepsilon_0 A}{d}\)
For two similar capacitors in series the resultant

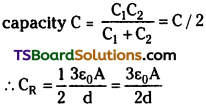
Question 9.
In the circuit shown the battery of’V’ volts has no internal resistance. All three con-densers are equal in capacity. Find the condenser that carries more charge.

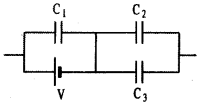
Answer:
In the diagram the battery polarities are as show.

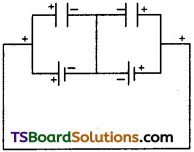
So all capacitors are connected in parallel. Since capacity ‘C’ is same and potential of battery V is same charge will exist on all the three capacitors.

Question 10.
Two capacitors A and B of capacities C and 2C are connected in parallel and the combination is connected to a battery of volts. After the charging is over, the bat-tery is removed. Now a dielectric slab of K = 2 is inserted between the plates of A so as to fill file space completely. The energy lost by the system during the sharing of charges is
Answer:
Capacity C₁ = C; Capacity C₂ = 2C
Let the capacitors are charged to the potential V.
Charge on capacitor Q₁ = CV
Charge on capacitor Q₂ = 2CV
Total charge Q = Q₁ + Q₂ = 3CV → (1)
Energy stored U₁ = \(\frac{1}{2}\)CV² +\(\frac{1}{2}\)(2C) V²
\(\frac{CV^2}{2}\) + CV² = \(\frac{3}{2}\)CV² → (2)
Now dielectric is introduced in C₁
New capacity = KC₁
Where K₁ = 2 and C₁ = C ∴ C_N = 2C.
Cherge is not changed because battery is disconnected from circuit.

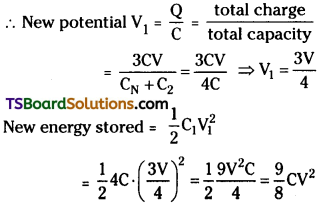
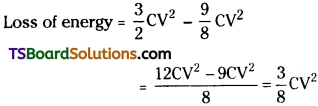
Question 11.
A condenser of certain capacity is charged to a potential V and stores some energy. A second condenser of twice the capacity is to stored half the energy of the first, find to what potential one must be charged?
Answer:
For 1st capacitor
Let capacity of capacitor = x; Potential = V
Energy stored U₁ = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × V²₁ → (1)
For 2nd capacitor capacity C₂ = 2x
Energy stored = \(\frac{1}{2}\)U₁ = \(\frac{1}{2}.\frac{1}{2}\) × V²₁ → (2)
But for 2nd capacitor energy stored

Intext Question and Answers

Question 1.
Two charges 5 × 10^-8 C and -3 × 10^-8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Answer:
There are two charges,
q₁ = 5 × 10^-8C, q₂ = -3 × 10^-8C
Distance between the two charges, d = 16 cm = 0.16 m
Consider a point P on the line joining the two charges, as shown in the given figure.

Let the electric potential (V) at point P be zero. It is at a distance r from q₁
Potential at point P is the sum of potentials caused by charges q₁ and q₂ respectively.

Therefore, the potential is zero at a distance of 10 cm from the positive charge between the charges.

Suppose point P is outside the system of two charges at a distance s from the negative charge, where potential is zero, as shown in the following figure.

Therefore, the potential is zero at a distance of 40 cm from the positive charge outside the system of charges.

Question 2.
A regular hexagon of side 10 cm has a charge 5 µC at each of its vertices. Calculate the potential at the centre of the hexagon.
Answer:
The given figure shows six equal amount of charges, q, at the vertices of a regular hexagon.

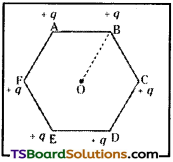
Charge, q = 5 µC = 5 × 10^-6C
Side of the hexagon, l = AB = BC = CD = DE
= EF = FA = 10 cm
Distance of each vertex from centre O, d = 10 cm

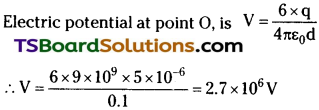
Therefore, the potential at the centre of the hexagon is 2.7 × 10⁶ V.

Question 3.
Two charges 2 µC and -2 µC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Answer:
(a) The situation is represented in the given figure.

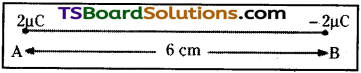
An equipotential surface is the plane on which total potential is zero everywhere. This plane is normal to line AB.

The plane is located at the mid-point of line AB because the magnitude of charges is the same.

(b) The direction of the electric field at every point on this surface is normal to the plane in the direction of AB.

Question 4.
A spherical conductor of radius 12 cm has a charge of 1.6 × 10^-7C distributed uniformly on its surface. What is the electric field
(a) Inside the sphere?
(b) Just outside the sphere?
(c) At a point 18 cm from the centre of the sphere?
Answer:
(a) Radius of the spherical conductor, r = 12 cm = 0.12 m
Charge is uniformly distributed over the conductor, q = 1.6 × 10^-7 C
Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.

(b) Electric field E just outside the conductor is given by the relation,

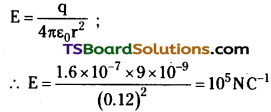
Therefore, the electric field just outside the sphere is 10⁵ NC^-1.

(c) Electric field at a point 18 m from the centre of the sphere = E₁
Distance of the point from the centre, d = 18 cm = 0.18 m

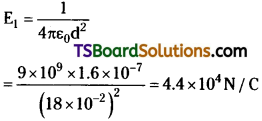
Therefore, the electric field at a point 18 cm from the centre of the sphere is 4.4 × 10⁴ N/C.

Question 5.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (lpF = 10^-12 F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Answer:
Capacitance between the parallel plates of the capacitor, C = 8 pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k = 1
Capacitance, C, is given by the formula,
C = \(\frac{k\varepsilon_{0}A}{d}=\frac{\varepsilon_{0}A}{d}\) ………….. (i)
Where, A = Area of each plate; ∈₀ = permittivity of free space
If distance between the plates is reduced to half, then new distance, d’ = \(\frac{d}{2}\).
Dielectric constant of the substance filled in between the plates, k’ = 6
Hence, capacitance of the capacitor
becomes C’ = = \(\frac{k\varepsilon_{0}A}{d}=\frac{6\varepsilon_{0}A}{d_2}\) ………… (ii)
From eqn (i) & (ii)
C’ = 2 × 6C = 12 C = 12 × 8 = 96 pF
Therefore, the capacitance between the plates is 96 pF.

Question 6.
Three capacitors each of capacitance 9 pF are connected in series. [AP Mar ’14]
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Answer:
(a) Capacitance of each of the three capacitors, C = 9 pF
Equivalent capacitance (C’) of the combination of the capacitors is given by the relation,

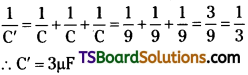
Therefore, total capacitance of the combination is 3µF.

(b) Supply voltage, V = 100 V
Potential difference (V’) across each capacitor is equal to one-third of the supply voltage.
∴ V’ = \(\frac{V}{3}=\frac{120}{3}\) = 40V
Therefore, the potential difference across each capacitor is 40 V.

Therefore, total capacitance of the combination is pµF.
(b) Supply voltage, V = 100 V

Question 7.
Three capacitors of capacitances 2µF, 3µF and 4µF are connected in parallel.
(i) What is the total capacitance of the combination?
(ii) Determine the charge on each capacitor, if the combination is connected to a 200V supply. [AP Mar. 1 7; TS May 1 7, June 15]
Answer:
(a) Capacitances of the given capacitors are
C₁ = 2µF ; C₂ = 3µF ; C₃ = 4µF
For the parallel combination of the capacitors, equivalent capacitor C’ is given by the algebraic sum, C’ = 2 + 3 + 4 = 9
Therefore, total capacitance of the combination is pµF.

(b) Supply voltage, V = 100 V
The voltage through all the three capacitors is same = V = 100V
Charge on a capacitor of C and potential difference V is given by the relation,
q = CV … (i)
For C = 2µF, Charge = VC = 100 × 2 = 200µC = 2 × 10^-4 C
For C = 3µF,
Charge = VC = 100 × 3 = 300 µC = 3 × 10^-4 C
For C = 4µF,
Charge = VC = 100 × 4 = 200µC = 4 × 10^-4 C

Question 8.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel.
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
(a) Capacitances of the given capacitors are
C₁ = 2 pF ; C₂ = 3 pF ; C₃ = 4 pF
For the parallel combination of the capacitors, equivalent capacitor C’ is given by the algebraic sum, C’ = 2 + 3 + 4 = 9
Therefore, total capacitance of the combination is 9 pF.

(b) Supply voltage, V = 100 V
The voltage through all the three capacitors is same = V = 100 V
Charge on a capacitor of capacitance C and potential difference V is given by the relation,
q = VC … (i)
For C = 2 pF, Charge = VC = 100 × 2 = 200 pC = 2 × 10“10 C
For C = 3 pF,
Charge = VC = 100 × 3 = 300 pC = 3 × 10^-10 C
For C = 4 pF,
Charge = VC = 100 × 4 = 200 pC = 4 × 10^-10 C

Question 9.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10^-3 m² and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Answer:
Area of each plate of the parallel plate capacitor, A = 6 × 10^-3 m²
Distance between the plates, d = 3 mm
= 3× 10^-3 m; Supply voltage, V = 100 V
Capacitance C of a parallel plate capacitor is given by, C = \(\frac{\varepsilon_{0}A}{d}\)
Where, ε₀ = Permittivity of free space

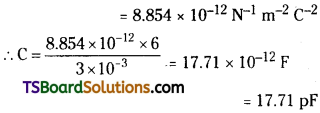
Potential V is related with the charge q and capacitance C as V = \(\frac{q}{C}\)
∴ q = VC = 100 × 17.71 × 10^-12 = 1.771 × 10^-9C.
Therefore, capacitance of the capacitor is 17.71 pF and charge on each plate is 1.771 × 10^-9C.

Question 10.
Expalin what would happen if in the capacitor given in Exercise 8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Answer:
(a) Dielectric constant of the mica sheet, k = 6;
Initial capacitance, C = 1.771 × 10^-11 F
New capacitance,
C’ = kc = 6 × 1.771 × 10^-11 = 106 pF;
Supply voltage, V = 100 V
New charge,
q’ C’V = 6 × 1.771 × 10^-9 = 1.06 × 10^-8C
Potential across the plates remains 100 V.

(b) Dielectric constant, k = 6 ;
Initial capacitance, C = 1.771 × 10^-11 F
New capacitance,
C’ = kC = 6 × 1.771 × 10^-11 = 106 pF

If supply voltage is removed, then there will be no effect on the amount of charge in the plates.
∴ Charge = 1.771 × 10^-9 C
Potential across the plates is gives by,

Question 11.
A 12 pF capacitor is connected to a 50V battery. How much electrostatic energy is stored in the capacitor?
Answer:
Capacitor of the capacitance, C = 12 pF = 12 × 10^-12 F ; Potential difference, V = 50 V
Electrostatic energy stored in the capacitor is given by the relation,
E = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × 12 × 10^-12 × (50)² = 1.5 × 10^-8 J
Therefore, the electrostatic energy stored in the capacitor is 1.5 × 10^-8 J.

Question 12.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Answer:
Capacitance of the capacitor, C = 600 pF ; Potential difference, V = 200 V Electrostatic energy stored in the capacitor is given by,
E = \(\frac{1}{2}\)cV² = \(\frac{1}{2}\) × (600 × 10^-12) × (200)² = 1.2 × 10⁵ J
If supply is disconnected from the capacitor and another capacitor of capacitance C = 600 pF is connected to it, then equivalent capacitance (C’) of the combination is given by,

New electrostatic energy can be calculated as
E’ = \(\frac{1}{2}\) × C’ × V² = \(\frac{1}{2}\) × 300 × (200)² = 0.6 × 10^-6J
Loss in electrostatic energy = E – E’
= 1.2 × 10^-5 -0.6 × 10^-5 = 0.6 × 10^-5 = 6 × 10^-6 J
Therefore, the electrostatic energy lost in the process is 6 × 10^-6 J.

Question 13.
In a Van de Graaff type generator, a spherical metal shell is to be a 15 × 10⁶ V electrode. The dielectric strength of the gas surrounding the electrode is 5 × 10⁷ Vm^-1. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)
Answer:
Potential difference, V = 15× 10⁶V ;
Dielectric strength of the surrounding gas = 5 × 10⁷ V/m
Electric field intensity, E = Dielectric strength = 5 × 10⁷ V/m
Minimum radius of the spherical shell required for the purpose is given by,

Hence, the minimum radius of the spherical shell required is 30 cm.

Question 14.
A small sphere of radius r₁ and charge q₁ is enclosed by a spherical shell of radius r₂ and charge q₂. Show that if q₁ is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q₂ on the shell is.
Answer:
According to Gauss’s law, the electric field between a sphere and a shell is determined by the charge q₁ on a small sphere. Hence, the potential difference, V, between the sphere and the shell is independent of charge q₂. For positive charge q₁, potential difference V is always positive.