TS Inter Second Year Maths 2B System of Circles Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B System of Circles Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B System of Circles Important Questions Very Short Answer Type

Question 1.
Show that the circles given by the equations x² + y² + 4x – 2y – 11 = 0, x² + y² – 4x – 8y + 11 = 0 intersect each other orthogonally.
Solution:
Given equations of the circles are
x² + y² + 4x – 2y – 11 = 0 ……(1)
x² + y² – 4x – 8y + 11 = 0 ………(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 2, f = -1, c = -11
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = -2, f = -4, c’ = 11
Now, 2gg’ + 2ff’ = 2(2)(-2) + 2(-1)(-4)
= -8 + 8
= 0
c + c’ = -11 + 11 = 0
∴ 2gg’ + 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 2.
Show that the circles given by the equations x² + y² – 2lx + g = 0, x² + y² + 2my – g = 0 intersect each other orthogonally.
Solution:
Given equations of the circles are
x² + y² – 2lx + g = 0 ……..(1)
x² + y² + 2my – g = 0 …………(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -l, f = 0, c = g
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 0, f’ = m, c’ = -g
Now, 2gg’+ 2ff’ = 2(-l)(0) + 2(m)(0)
= 0 + 0
= 0
c + c’ = g – g = 0
∴ 2gg’+ 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 3.
Show that the circles given by the equations x² + y² – 2x – 2y – 7 = 0, 3x² + 3y² – 8x + 29y = 0, intersect each other orthogonally. [May ’15 (AP)]
Solution:
Given equations of the circles are
x² + y² – 2x – 2y – 7 = 0 ……….(1)
3x² + 3y² – 8x + 29y = 0
\(x^2+y^2-\frac{8}{3} x+\frac{29}{3} y=0\) ………(2)
Comparing (1) with
x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = -1, c = -7
Comparing (2) with
x² + y² + 2g’x + 2f’y + c’ = 0, we get

c + c’ = -7 + 0 = -7
∴ 2gg’ + 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 4.
Find ‘k’ if the pair of circles x² + y² + 4x + 8 = 0, x² + y² – 16y + k = 0 are orthogonal. [Mar.’16 (AP)]
Solution:
Given equations of the circles are
x² + y² + 4x + 8 = 0 ………(1)
x² + y² – 16y + k = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 2, f = 0, c = 8
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 0, f = -8, c’ = k
Since the given circles are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(2)(0) + 2(0)(-8) = 8 + k
⇒ 0 + 0 = 8 + k
⇒ k = -8

Question 5.
Find ‘k’ if the pair of circles x² + y² + 2by – k = 0, x² + y² + 2ax + 8 = 0 are orthogonal.
Solution:
Given equations of the circles are
x² + y² + 2by – k = 0 ……….(1)
x² + y² + 2ax + 8 = 0 ……..(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 0, f = b, c = -k
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = a, f’ = 0, c’ = 8
Since the given circles are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(0)(a) + 2(b)(0) = -k + 8
⇒ 0 + 0 = -k + 8
⇒ k = 8

Question 6.
Find ‘k’ if the pair of circles x² + y² – 6x – 8y + 12 = 0, x² + y² – 4x + 6y + k = 0 are orthogonal.
Solution:
Given equations of the circles are
x² + y² – 6x – 8y + 12 = 0 ……….(1)
x² + y² – 4x + 6y + k = 0 ………(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -3, f = -4, c = 12
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = -2, f’ = 3, c’ = k
Since the given circles are orthogonal then
2gg’+ 2ff’ = c + c’
⇒ 2(-3)(-2) + 2(-4)(3) = 12 + k
⇒ 12 – 24 = 12 + k
⇒ k = -24

Question 7.
Find the angle between the circles x² + y² – 12x – 6y + 41 = 0, x² + y² + 4x + 6y – 59 = 0. [(AP) May ’19, ’18; (TS) ’15, Mar. ’17, ’15]
Solution:
Given equations of the circles are
x² + y² – 12x – 6y + 41 = 0 ……….(1)
x² + y² + 4x + 6y – 59 = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -6, f = -3, c = 41
∴ C₁ = (-g, -f) = (6, 3)

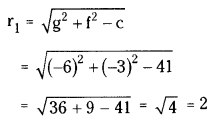
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 2, f = 3, c’ = -59
∴ C₂ = (-g’, -f’) = (-2, -3)

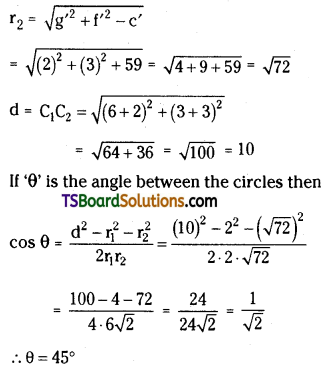
Question 8.
Find the angle between the circles x² + y² + 4x – 14y + 28 = 0, x² + y² + 4x – 5 = 0. [(AP) May ’17]
Solution:
Given equations of the circles are
x² + y² + 4x – 14y + 28 = 0 ………(1)
x² + y² + 4x – 5 = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0, we get
g = 2, f = -7, c = 28
∴ C₁ = (-g, -f) = (-2, 7)

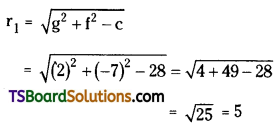
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = 2, f’ = 0, c’ = -5
∴ C₂ = (-g’, -f’) = (-2, 0)

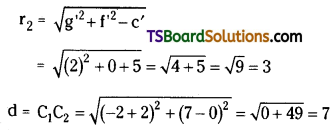
If ‘θ’ is the angle between the circles then

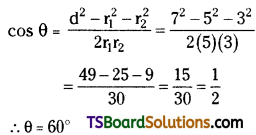
Question 9.
Find the angle between the circles x² + y² + 6x – 10y – 135 = 0, x² + y² – 4x + 14y – 116 = 0.
Solution:
Given equations of the circles are
x² + y² + 6x – 10y – 135 = 0 ………(1)
x² + y² -4x + 14y – 116 = 0 ………..(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 3, f = -5, c = -135
∴ C₁ = (-g, -f) = (-3, 5)

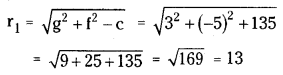
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = -2, f’ = 7, c’ = -116
∴ C₂ = (-g’, -f’) = (2, -7)

Question 10.
Show that the angle between the circles x² + y² = a² , x² + y² = ax + ay is \(\frac{3 \pi}{4}\). [(TS) Mar. ’20, ’16, May ’16 (TS) Mar. ’14]
Solution:
Given equations of the circles are
x² + y² – a² = 0 ………..(1)
x² + y² – ax – ay = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = 0, f = 0, c = -a²
C₁ = (-g, -f) = (0, 0)

Question 11.
Find the equation of the radical axis of the circles x² + y² – 2x – 4y – 1 = 0, x² + y² – 4x – 6y + 5 = 0. [(AP) May ’16]
Solution:
Given equations of the circles are
S = x² + y² – 2x – 4y – 1 = 0
S’ = x² + y² – 4x – 6y + 5 = 0
∴ The equation of the radical axis of the given circle is S – S’ = 0
⇒ (x² + y² – 2x – 4y – 1) – (x² + y² – 4x – 6y + 5) = 0
⇒ x² + y² – 2x – 4y – 1 – x² – y² + 4x + 6y – 5 = 0
⇒ -2x – 4y – 1 + 4x + 6y – 5 = 0
⇒ 2x + 2y – 6 = 0
⇒ x + y – 3 = 0

Question 12.
Find the equation of the radial axis of the circles x² + y² – 5x + 6y + 12 = 0 and x² + y² + 6x – 4y – 14 = 0.
Solution:
Given equations of the circles are
S = x² + y² – 5x + 6y + 12 = 0
S’ = x² + y² + 6x – 4y – 14 = 0
The equation of the radical axis of the circles S’ = 0 and S = 0 is S – S’ = 0
⇒ x² + y² – 5x + 6y + 12 – (x² + y² + 6x – 4y – 14) = 0
⇒ x² + y² – 5x + 6y + 12 – x² – y² – 6x + 4y + 14 = 0
⇒ -11x + 10y + 26 = 0
⇒ 11x – 10y – 26 = 0

Question 13.
Find the equation of the radical axis of the circles 2x² + 2y² + 3x + 6y – 5 = 0 and 3x² + 3y² – 7x + 8y – 11 = 0. [(AP) Mar. ’17]
Solution:
Given equations of the circles are
S = 2x² + 2y² + 3x + 6y – 5 = 0

Question 14.
Find the equation of the common chord of x² + y² – 4x – 4y + 3 = 0, x² + y² – 5x – 6y + 4 = 0. [(TS) Mar. ’20]
Solution:
Given equations of the circles are
S = x² + y² – 4x – 4y + 3 = 0
S’ = x² + y² – 5x – 6y + 4 = 0
The equation of the common chord (radical axis) of the given circles is S – S’ = 0
⇒ (x² + y² – 4x – 4y + 3) – (x² + y² – 5x – 6y + 4) = 0
⇒ x² + y² – 4x – 4y + 3 – x² – y² + 5x + 6y – 4 = 0
⇒ x + 2y – 1 = 0

Question 15.
Find the equation of the common chord of (x – a)² + (y – b)² = c², (x – b)² + (y – a)² = c² (a ≠ b).
Solution:
Given equations of the circles are
S = (x – a)² + (y – b)² = c²
⇒ x² + a² – 2ax + y² + b² – 2by – c² = 0
⇒ x² + y² – 2ax – 2by + a² + b² – c² = 0
S’ = (x – b)² + (y – a)² = c²
⇒ x² + b² – 2bx + y² + a² – 2ay – c² = 0
⇒ x² + y² – 2bx – 2ay + a² + b² – c² = 0
The equation of the common chord (radical axis) of the given circles is S – S’ = 0
⇒ x² + y² – 2ax – 2by + a² + b² – c² – (x² + y² – 2bx – 2ay + a² + b² – c²) = 0
⇒ x² + y² – 2ax – 2by + a² + b² – c² – x² – y² + 2bx + 2ay – a² – b² + c² = 0
⇒ -2ax – 2by + 2bx + 2ay = 0
⇒ 2x(b – a) – 2y(b – a) = 0
⇒ x – y = 0

Question 16.
Find the equation of the common tangent of x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0.
Solution:
Given equations of the circles are
S = x² + y² + 10x – 2y + 22 = 0
S’ = x² + y² + 2x – 8y + 8 = 0
The equation of the common tangent at the point of contact (radical axis) of the circles S = 0, S’ = 0 is S – S’ = 0
⇒ x² + y² + 10x – 2y + 22 – (x² + y² + 2x – 8y + 8) = 0
⇒ x² + y² + 10x – 2y + 22 – x² – y² – 2x + 8y – 8 = 0
⇒ 8x + 6y + 14 = 0
⇒ 4x + 3y + 7 = 0

Question 17.
If the angle between the circles x² + y² – 12x – 6y + 41 = 0 and x² + y² + kx + 6y – 59 = 0 is 45°, find k. [(TS) Mar. ’18]
Solution:
Given equations of the circles are
x² + y² – 12x – 6y + 41 = 0 ………(1)
x² + y² + kx + 6y – 59 = 0 ………..(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -6, f = -3, c = 41
C₁ = (-g, -f) = (6, 3)

Given that, θ = 45°
If ‘θ’ is the angle between the circles, then

Question 18.
Show that the circles given by the equations x² + y² – 2x + 4y + 4 = 0, x² + y² + 3x + 4y + 1 = 0 intersect each other orthogonally.
Solution:
Given equations of the circles are
x² + y² – 2x + 4y + 4 = 0 ……..(1)
x² + y² + 3x + 4y + 1 = 0 ……….(2)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = 2, c = 4
Comparing (2) with x² + y² + 2g’x + 2f’y + c’ = 0,
we get g’ = \(\frac{3}{2}\), f’ = 2, c’ = 1
Now, 2gg’+ 2ff’ = 2(-1)(\(\frac{3}{2}\)) + 2(2)(2)
= -3 + 8
= 5
c + c’ = 4 + 1 = 5
∴ 2gg’+ 2ff’ = c + c’
∴ The two circles cut each other orthogonally.

Question 19.
Find the equation of the radical axis of the circles x² + y² – 3x – 4y + 5 = 0, 3(x² + y²) – 7x + 8y – 11 = 0. [(TS) May ’17]
Solution:
Given equations of the circles are
S = x² + y² – 3x – 4y + 5 = 0
S’ = 3[x² + y²] – 7x + 8y – 11 = 0
\(x^2+y^2-\frac{7}{3} x+\frac{8}{3} y-\frac{11}{3}=0\)
∴ The equation of the radical axis of the given circles is S – S’ = 0

Question 20.
Find the equation of the radical axis of the circles x² + y² + 4x + 6y – 7 = 0, 4(x² + y²) + 8x + 12y – 9 = 0. [(TS) May ’19. Mar. ’19. (AP) ’19]
Solution:
Given equations of the circles are
S = x² + y² + 4x + 6y – 7 = 0
S’ = 4(x² + y²) + 8x + 12y – 9 = 0
⇒ x² + y² + 2x + 3y – \(\frac{9}{4}\) = 0
The equation of the radical axis of the given circles is S – S’ = 0
⇒ x² + y² + 4x + 6y – 7 – (x² + y² + 2x + 3y – \(\frac{9}{4}\)) = 0
⇒ x² + y² + 4x + 6y – 7 – x² – y² – 2x – 3y + \(\frac{9}{4}\) = 0
⇒ 2x + 3y – 7 + \(\frac{9}{4}\) = 0
⇒ 8x + 12y – 28 + 9 = 0
⇒ 8x + 12y – 19 = 0

Question 21.
Find the equation of the common chord of the pair of circles x² + y² + 2x + 3y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
Solution:
Given equations of the circles are
S = x² + y² + 2x + 3y + 1 = 0
S’ = x² + y² + 4x + 3y + 2 = 0
The equation of the common chord (radical axis) of the given circles is S – S’ = 0
⇒ x² + y² + 2x + 3y + 1 – x² – y² – 4x – 3y – 2 = 0
⇒ -2x – 1 = 0
⇒ 2x + 1 = 0