TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Very Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Very Short Answer Type

Question 1.
Simplify \(\frac{(\cos \alpha+i \sin \alpha)^4}{(\sin \beta+i \cos \beta)^8}\)
Solution:

Question 2.
Find the value of (1 – i)⁸. [March ’07]
Solution:

Let 1 – i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = – 1
Hence,
√2 cos θ = 1, √2 sin θ = – 1
cos θ = \(\frac{1}{\sqrt{2}}\), sin θ = – \(\frac{1}{\sqrt{2}}\)
∴ θ lies in the Q₄
∴ θ = – \(\frac{\pi}{4}\)
1 – i = √2 [cos (- \(\frac{\pi}{4}\)) + i sin (\(\frac{\pi}{4}\))]
= √2 (cos \(\frac{\pi}{4}\) – i sin \(\frac{\pi}{4}\))
Now,
(1 – i)⁸ = [√2 (cos (\(\frac{\pi}{4}\)) – i sin (\(\frac{\pi}{4}\)))]⁸
= 16 (cos 2π – i sin 2π)
= 16 (1 – i . 0) = 16.

Question 3.
Find the value of (1 + i)¹⁶. [Board Paper]
Solution:

Let (1 – i) = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = 1, √2 sin θ = 1
cos θ = \(\frac{1}{\sqrt{2}}\), sin θ = \(\frac{1}{\sqrt{2}}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{4}\)
∴ 1 + i = √2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))
Now,
(1 + i)¹⁶ = [√2 (cos(\(\frac{\pi}{4}\)) + i sin (\(\frac{\pi}{4}\))]¹⁶
= (√2)¹⁶ (cos 4π + i sin 4π)
= 256 (1 + i (0)) = 256

Question 4.
Find the value of \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5\). [May 2004]
Solution:

Question 5.
If A, B, C are angles of a triangle such that x = cis A, y = cis B, z = cis C, then find the value of xyz.
[Mar. ’98, ’94 AP – Mar. ’18, ’16, ’15, May ’16; TS – May ’15]
Solution:
Since, A, B, C are angles of a triangle then A+ B + C = π
Given that,
x = cis A, y= cis B, z = cis C
Now, xyz = cis A . cis B . cis C
= cis (A + B + C)
= cos (A + B + C) + i sin (A + B + C)
= cos π + i sin π
= – 1 + i (0) = – 1.

Question 6.
If x = cis θ then find the value of \(\left(x^6+\frac{1}{x^6}\right)\).
[TS – Mar. 2018, May 2016, May ’14, ’07, March ’14, ’04, ’91]
Solution:
Given, x = cis θ
= cos θ + i sin θ
Now, x⁶ = (cos θ + i sin θ)⁶
= cos 6θ + i sin 6θ
\(\frac{1}{x^6}\) = cos 6θ – i sin 6θ
Now,
x⁶ + \(\frac{1}{x^6}\) = cos 6θ + i sin 6θ + cos 6θ – i sin 6θ = 2 cos 6θ.

Question 7.
Find the cube roots of 8.
Solution:
Let, x = \(\sqrt[3]{8}=(8)^{1 / 3}=8^{1 / 3} 1^{1 / 3}\)
= \(\left(2^3\right)^{1 / 3}\) [cos 0° + i sin 0°]^1/3
= 2[cos(2kπ + 0°) + isin(2kπ + 0°)]^1/3
k = 0, 1, 2
= 2[cos 2kπ + isin2kπ]^1/3
= 2 \(\left[\cos \frac{2 \mathrm{k} \pi}{3}+\mathrm{i} \sin \frac{2 \mathrm{k} \pi}{3}\right]\)
= 2 cis \(\frac{2 \mathrm{k} \pi}{3}\), k = 0, 1, 2
If k = 0
⇒ x = 2 cis 0° = 2 (cos 0 + i sin 0)
= 2 (1 + i . 0) = 2

If k = 1
⇒ x = 2 cis \(\frac{2 \pi}{3}\)
= 2 (cos \(\frac{2 \pi}{3}\) + i sin \(\frac{2 \pi}{3}\))
= \(2\left[\frac{-1}{2}+\frac{\mathrm{i} \sqrt{3}}{2}\right]=2\left[\frac{-1+\mathrm{i} \sqrt{3}}{2}\right]\) = 2ω

If k = 2
⇒ x = 2 cis \(\frac{4 \pi}{3}\)
= 2 (cos \(\frac{4 \pi}{3}\) + i sin \(\frac{4 \pi}{3}\))
= \(2\left(\frac{-1}{2}-\mathrm{i} \frac{\sqrt{3}}{2}\right)=2\left[\frac{-1-\mathrm{i} \sqrt{3}}{2}\right]\)
= 2ω²
∴ The cube roots of 8 are 2, 2ω, 2ω².

Question 8.
Prove that – ω and – ω² are roots of z² – z + i = 0, where ω and ω² are the complex cube roots of unity.
Solution:
Since ω, ω² are the cube roots of unity then
ω = \(\frac{-1+i \sqrt{3}}{2}\)
⇒ – ω = \(\frac{1-i \sqrt{3}}{2}\)

ω² = \(\frac{-1-i \sqrt{3}}{2}\)
⇒ – ω² = \(\frac{1+i \sqrt{3}}{2}\)

Given quadratic equation is z² – z + 1 = 0
Comparing with ax² + bx + c = 0
a = 1, b = – 1, c = 1
∴ The roots of the quadratic equation z² – z + 1 = 0 then
z = \(\frac{-\mathrm{b} \pm \sqrt{\mathrm{b}^2-4 \mathrm{ac}}}{2 \mathrm{a}}\)
= \(\frac{-(-1) \pm \sqrt{(-1)^2-4 \cdot 1 \cdot 1}}{2(1)}\)
= \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm i \sqrt{3}}{2}\)
∴ – ω and – ω² are the roots of z² – z + 1 = 0.

Question 9.
If 1, ω, ω² are the cube roots of unity, prove that [TS – Mar. 2016]
(1 – ω + ω²)⁶ + (1 – ω² + ω)⁶ = 128 = (1 – ω + ω²)⁷ + (1 + ω – ω²)⁷
Solution:
Given that 1, ω, ω² are the cube roots of unity then
1 + ω + ω² = 0 and ω³ = 1
(1 – ω + ω²)⁶ + (1 – ω² + ω)⁶ = (- ω – ω)⁶ + (- ω² – ω²)⁶
= (2ω)⁶ + (- 2ω²)⁶
= (- 2)⁶ ω⁶ + (- 2)⁶ ω⁶
= 64 . 1 + 64 . 1
= 64 + 64 = 128
∴ (1 – ω + ω²) + (1 – ω² + ω) = 128
and (1 – ω + ω²)⁷ + (1 + ω – ω²)⁷
= (- ω – ω)⁷ + (- ω – ω)⁷
= (- 2ω)⁷ + (- 2ω²)⁷
= (- 2)⁷ ω⁷ + (- 2)⁷ ω¹⁴
= – 128 . ω + (- 128) ω²
= – 128 (ω + ω²)
= – 128 (- 1) = 128
(1 – ω + ω²)⁷ + (1 + ω – ω²)⁷ = 128.

Question 10.
If 1, ω, ω are the cube roots of unity, prove that (a + b) (aω + bω²) (aω² + bω) = a³ + b³ (AP – Mar. 2017)
Solution:
L.H.S:
(a + b) (aω + bω²) (aω² + bω)
= (a + b) (a²ω³ + abω² + abω⁴ + b²ω³)
= (a + b) [a² . 1 + abω² + abω + b²2 . 1]
= (a + b) [a² + ab(ω² + ω) + b²]
= (a + b) (a² + ab(- 1) + b²)
= (a + b) (a² – ab + b²)
= (a³ + b³) = R.H.S.
∴ (a + b) (aω + bω²) (aω² + bω) = a³ + b³.

Question 11.
If 1, ω, ω² are the cube roots of unity, prove that x² + 4x + 7 = 0, where x = ω – ω² – 2.
Solution:
Given,
x = ω – ω² – 2
x + 2 = ω – ω²
Squaring on both sides
(x + 2)² = (ω – ω²)²
x² + 4x + 4 = ω² + ω⁴ – 2ω³
x² + 4x + 4 = ω² + ω – 2 . 1
x² + 4x + 4 = – 1 – 2
x² + 4x + 4 + 1 + 2 = 0
x² + 4x + 7 = 0.

Question 12.
If α, β are the roots of the equation x² + x + 1 = 0 then prove that α⁴ + β⁴ + α^-1 β^-1 = 0. [AP – May 2015]
Solution:
Since, α, β are the roots of the equation x² + x + 1 = 0 then
α = ω, β = ω²

L.H.S:
α⁴ + β⁴ + α^-1 β^-1 = α⁴ + β⁴ + \(\frac{1}{\alpha} \frac{1}{\beta}\)
= ω⁴ + (ω²)⁴ + \(\frac{1}{\omega \cdot \omega^2}\)
= ω⁴ + ω⁸ + \(\frac{1}{\omega^3}\)
= ω + ω² + 1 = 0 =R.H.S.

Question 13.
If 1, ω, ω² are cube roots of unity, then prove that \(\frac{1}{2+\omega}+\frac{1}{1+2 \omega}=\frac{1}{1+\omega}\). [TS – Mar.2015] [May ’01, Mar. ’87]
Solution:
Given 1, ω, ω² are the cube roots of unity then 1 + ω + ω² = 0, ω³ = 1

L.H.S:

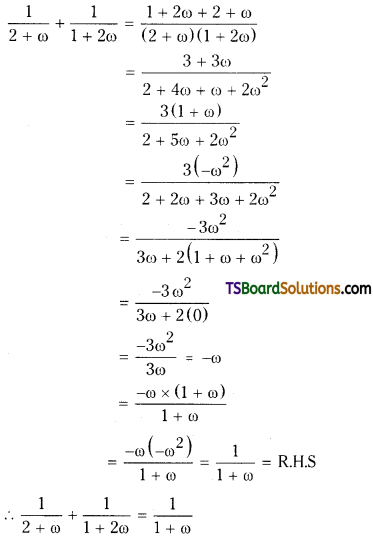
Question 14.
If 1, ω, ω² are cube roots of unity, then prove that (2 – ω) (2 – ω) (2 – ω) (2 – ω) = 49. [TS – Mar.2017]
Solution:
LHS:
= (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω11)
= (2 – ω) (2 – ω²) (2 – ω) (2 – ω²)
= [(2 – ω) (2 – (ω²)]²
= [4 – 2ω² – 2ω + ω³]²
= [4 – 2(ω² + ω) + 1]²
= (5 – 2(- 1))²
= 7² = 49 = R.H.S
∴ (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω¹¹) = 49

Question 15.
If 1, ω, ω² are cube roots of unity, then prove that (x + y + z) (x + yω + zω²) (x + yω² + zω) = x³ + y³ + z³ – 3xyz
Solution:
L.H.S:
= (x + y + z) (x + yω + zω²) (x + yω² + zω)
= (x + y + z) (x² + xyω² + xzω + xyω + y²ω³ + yzω² + yxω² + zyω⁴ + z²ω³)
= (x + y + z) [x² + xyω² + xzω + xyω + y² + yzω² + zxω² + zyω + z²]
= (x + y + z) [x² + y² + z² + xy(ω + ω²) + yz (ω + ω²) + zx (ω + ω²)]
= (x + y + z) [x² + y² + z² + xy (- 1) + yz (- 1) + zx (- 1)]
= (x + y + z) [x² + y² + z² – xy – yz – zx]
= x³ + y³ + z³ – 3xyz
= R.H.S
(x + y + z) (x + yω + zω²) (x + yω² + zω) = x³ + y³ + z³ – 3xyz.

Question 16.
If 1, ω, ω² are the cube roots of unity, then find the value of (a + b)³ + (aω + bω²)³ + (aω² + bω)³.
Solution:
Given that. 1, ω, ω² are the cube roots of unity, then 1 + ω + ω² = 0 and ω³ = 1.
(a + b)³ + (aω + bω²)³ + (aω² + bω)³
= a³ + b³ + 3a²b + 3ab² + a³ω³ + b³ω⁶ + 3a²bω⁴ + 3ab²ω⁵ + a³ω⁶ + b³ω³ + 3a²bω⁵ + 3ab²ω⁴
= a³ + b³ + 3a²b + 3ab² + a³ . 1 + b³ . 1 + 3a²bω + 3ab²ω² + a³ . 1 + b³ . 1 + 3a²bω^{2/sup> + 3ab2ω
= 3a3 + 3b3 + 3a2b(1 + ω + ω2) + 3ab2(1 + ω + ω2)
= 3a3 + 3b3 + 3a2b(0) + 3ab2(0)
= 3a3 + 3b3 = 3(a3 + b3)}

Question 17.
If 1, ω, ω² are the cube roots of unity, then find the value of (a + 2b)² + (aω² + 2bω)² + (aω +2bω²)²
Solution:
Given,
(a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)²
a² + 4b² + 4ab + a²ω + 4b²ω² + 4abω³ + a²ω² + 4b²ω⁴ + 4abω³
= a² + 4b² + 4ab + a²ω + 4b²ω² + 4abω³ + 4ab . 1 + a²ω² + 4b²ω + 4ab – 1
= a² (1 + ω + ω²) + 4b²(1 + ω + ω²) + 4ab + 4ab + 4ab
= a²(0) + 4b²(0) + 12ab
= 12ab

Question 18.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω + ω²)³. [TS- Mar. 2019]
Solution:
Given, (1 – ω² + ω²)³
= (- ω – ω)³
= (- 2ω)³
= – 8ω³
= – 8 – 1 = – 8.

Question 19.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸).
Solution:
Given, (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
= (1 – ω) (1 – ω²) (1 – ω) (1 – ω²)
= [(1 – ω) (1 – ω²)]²
= [1 – ω² – ω + ω³]²
= [1 – ω² – ω + 1]²
= [2 – ω – ω²]²
= (2 + 1)² = 3² = 9.

Question 20.
If 1, ω, ω² are the cube roots of unity, then find the value of \(\left(\frac{a+b \omega+c \omega^2}{c+a \omega+b \omega^2}\right)+\left(\frac{a+b \omega+c \omega^2}{b+c \omega+a \omega^2}\right)\).
Solution:

Question 21.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 + ω)³ + (1 + ω²)³.
Solution:
Given, (1 + ω)³ + (1 + ω²)³
= (- ω²)³ + (- ω)³
= – ω⁶ – ω³
= – 1 – 1 = – 2.

Question 22.
If 1, ω, ω² are the cube roots of unity, then find the value of (1 – ω + ω²)⁵ + (1 + ω – ω²)⁵. [AP – Mar. 2019]
Solution:
Given,
(1 – ω + ω²)⁵ + (1 + ω – ω²)⁵
= (- ω – ω)⁵ + (- ω² – ω²)⁵
= (- 2ω)⁵ + (- 2ω²)⁵
= (- 2)⁵ ω + (- 2)⁵ ω¹⁰
= – 32 ω² + (- 32)ω
= – 32 (ω² + ω)
= – 32 (- 1) = 32.

Question 23.
1f the cube roots of unity are 1, ω, ω², then find the roots of the equation (x – 1)³ + 8 = 0.
Solution:
Since, 1, ω, ω² are the cube roots of unity then 1 + ω + ω² = 0 and ω³ = 1.
Given equation is (x – 1)³ + 8 = 0
(x – 1)³ = – 8
x – 1 = \(\sqrt[3]{-8}\)
= \(\sqrt[3]{(-8) \cdot 1}\)
= – 2 (1)^1/3
= – 2 (1, ω, ω²)
= – 2, – 2ω, – 2ω²
x – 1 = – 2, – 2ω, – 2ω²
x = – 2 + 1, – 2ω + 1, – 2ω² + 1
= – 1, – 2ω + 1, – 2ω² + 1
∴ The roots of the given equation are = – 1, 1 – 2ω, 1 – 2ω².

Question 26.
Find all the roots of (1 – i√3)^1/3.
Solution:

Let 1 – i√3 = r(cos θ + i sin θ)
then r cos θ = 1, r sin θ = – √3
r = \(\sqrt{x^2+y^2}=\sqrt{(1)^2+(-\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence,
2 cos θ = 1
cos θ = \(\frac{1}{2}\)

2 sin θ = – √3
sin θ = \(-\frac{\sqrt{3}}{2}\)

∴ θ lies in the Q₄.
∴ θ = \(\frac{-\pi}{3}\)

Question 25.
Find the values of (1 + i)^2/3.
Solution:

Let. 1 + i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = 1
cos θ = \(\frac{1}{\sqrt{2}}\)

√2 sin θ = 1
sin θ = \(\frac{1}{\sqrt{2}}\)

∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{4}\).

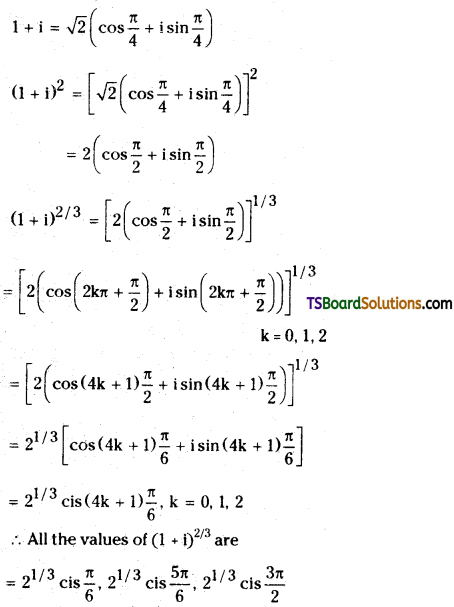
Question 26.
Find all the values of (√3 + 1)^1/4.
Solution:

Let, √3 + 1 = r(cos θ + i sin θ)
then r cos θ = r sin θ = 1
∴ r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{(\sqrt{3})^2+1^2}\)
= \(\sqrt{3+1}=\sqrt{4}\) = 2
Hence,
2 cos θ = √3, 2 sin θ = 1
cos θ = \(\frac{\sqrt{3}}{2}\), sin θ = \(\frac{1}{2}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{6}\)
∴ √3 + i = 2 (cos \(\frac{\pi}{6}\) + i sin \(\frac{\pi}{6}\))
Now,

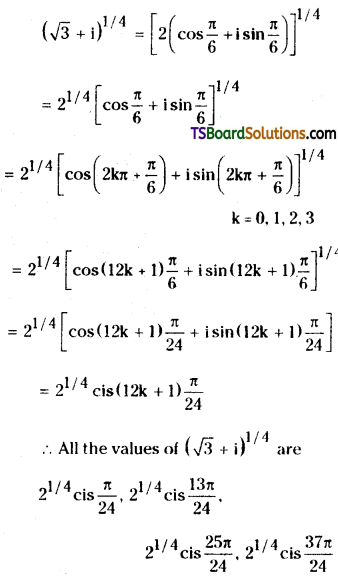
Question 27.
Find all the values of (- i)^1/6.
Solution:

Question 28.
Find all the values of (- 16)^1/4.
Solution:
Let, (- 16)^1/4 = (16)^1/4 . (- 1)^1/4
= (2⁴)^1/4 (- 1)^1/4
= 2 [cos π + i sin π]^1/4
= 2 [cos(2kπ + π) + isin(2kπ + π)]^1/4, k = 0, 1, 2, 3
= 2 [cos(2k + 1)π + isin(2k + 1)π]^1/4
= 2 [cos(2k + 1)\(\frac{\pi}{4}\) + i sin (2k + 1)\(\frac{\pi}{4}\)]
= 2 cis(2k + 1)\(\frac{\pi}{4}\), k = 0, 1, 2, 3
If k = 0
⇒ x = 2 cis \(\frac{\pi}{4}\)
If k = 1
⇒ x = 2 cis \(\frac{3 \pi}{4}\)
If k = 2
⇒ x = 2 cis \(\frac{5 \pi}{4}\)
If k = 3
⇒ x = 2 cis \(\frac{7 \pi}{4}\)
∴ All the values of (- 16)^1/4 are 2 cis \(\frac{\pi}{4}\), 2 cis \(\frac{3 \pi}{4}\), 2 cis \(\frac{5 \pi}{4}\), 2 cis \(\frac{7 \pi}{4}\)

Question 29.
Find all the values of (- 32)^1/5.
Solution:
Let, x = (- 32)^1/5
= (32)^1/5 (- 1)^1/5
= (2⁵)^1/5 [cos π + i sin π]^1/5
= 2 [cos π + i sin π]^1/5
= 2 [cos (2kπ + π) + i sin (2kπ + π)]^1/5
k = 0, 1, 2, 3, 4
= 2 [cos (2k + 1)π + i sin (2k + 1)π]^1/5
= 2 [cos (2k + 1)\(\frac{\pi}{5}\), i sin(2k + 1)\(\frac{\pi}{2}\)]
= 2 cis(2k + 1)\(\frac{\pi}{2}\), k = 0,1 , 2, 3, 4
If k = 0
⇒ x = 2 cis \(\frac{\pi}{5}\)
If k = 1
⇒ x = 2 cis \(\frac{3 \pi}{5}\)
If k = 2
⇒ x = 2 cis π
If k = 3
⇒ x = 2 cis \(\frac{7 \pi}{5}\)
If k = 4
⇒ x = 2 cis \(\frac{9 \pi}{5}\)
∴ All the values of (- 32)^1/5 are 2 cis \(\frac{\pi}{5}\), 2 cis \(\frac{3 \pi}{5}\), 2 cis π, 2 cis \(\frac{7 \pi}{5}\), 2 cis \(\frac{9 \pi}{5}\).