TS Inter Second Year Maths 2B Circles Important Questions Long Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Circles Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Circles Important Questions Long Answer Type

Question 1.
Find the equation of the circle passing through the points (5, 7), (8, 1), (1, 3). (May ’10)
Solution:
Let the equation of the required circle
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since equation (1) passes through (5, 7), then
(5)² + (7)² + 2g(5) + 2f(7) + c = 0
⇒ 25 + 49 + 10g + 14f + c = 0
⇒ 10g + 14f + c = -74 …….(2)
Since equation (1) passes through (8, 1) then
(8)² + (1)² + 2g(8) + 2f(1) + c = 0
⇒ 64 + 1 + 16g + 2f + c = 0
⇒ 16g + 2f + c = -65 ……..(3)
Since equation (1) passes through (1, 3)
(1)² + (3)² + 2g(1) + 2f(3) + c = 0
⇒ 1 + 9 + 2g + 6f + c = 0
⇒ 2g + 6f + c = -10 ………(4)

Question 2.
Find the equation of the circle passing through (-2, 3), (2, -1), and (4, 0).
Solution:
Let, the required equation of the circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through (-2, 3), then
(-2)² + (3)² + 2g(-2) + 2f(3) + c = 0
⇒ 4 + 9 – 4g + 6f + c = 0
⇒ -4g + 6f + c = -13 ……….(2)
Since (1) passes through (2, -1), then
(2)² + (-1)² + 2g(2) + 2f(-1) + c = 0
⇒ 4 + 1 + 4g – 2f + c = 0
⇒ 4g – 2f + c = -5 ……..(3)
Since (1) passes through (4, 0) then
(4)² + (0)² + 2g(4) + 2f(0) + c = 0
⇒ 16 + 8g + c = 0
⇒ 8g + c = -16 ………(4)
From (2) and (3)


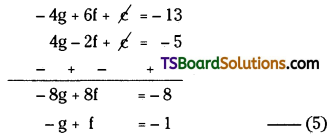
Substitute the value of ‘g’ in (4)
8(\(\frac{-3}{2}\)) + c = -16
⇒ -12 + c = -16
⇒ c = -4
Now substitute the values of g, f, c in (1)
∴ The required equation of the circle is
x² + y² + 2(\(\frac{-3}{2}\)) x + 2(\(\frac{-5}{2}\)) y – 4 = 0
⇒ x² + y² – 3x – 5y – 4 = 0

Question 3.
Find the equation of the circle passing through the points (3, 4), (3, 2), (1, 4). [(AP) Mar. ’18, May ’16; (TS) ’16]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point (3, 4), then
(3)² + (4)² + 2g(3) + 2f(4) + c = 0
⇒ 9 + 16 + 6g + 8f + c = 0
⇒ 6g + 8f + c = -25 ……..(2)
Since, (1) passes through the point (3, 2)
(3)² + (2)² + 2g(3) + 2f(2) + c = 0
⇒ 9 + 4 + 6g + 4f + c = 0
⇒ 6g + 4f + c = -13 ……(3)
Since, (1) passes through the point (1, 4)
(1)² + (4)² + 2g + 2f(4) + c = 0
⇒ 1 + 16 +2g + 8f + c = 0
⇒ 2g + 8f + c = -17 ……….(4)
From (2) and (3)

Substitute the value of g, f in (2)
6(-2) + 8(-3) + c = -25
⇒ -12 – 24 + c = – 25
⇒ c = -25 + 36
⇒ c = 11
Substitute the values of g, f, c in (1)
x² + y² + 2(-2)x + 2(-3)y + 11 = 0
⇒ x² + y² – 4x – 6y + 11 = 0
∴ The equation of the required circle is x² + y² – 4x – 6y + 11 = 0.

Question 4.
Find the equation of the circle passing through (2, 1), (5, 5), (-6, 7).
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since (1) passes through the point (2, 1), then
(2)² + (1)² + 2g(2) + 2f(1) + c = 0
⇒ 4 + 1 + 4g + 2f + c = 0
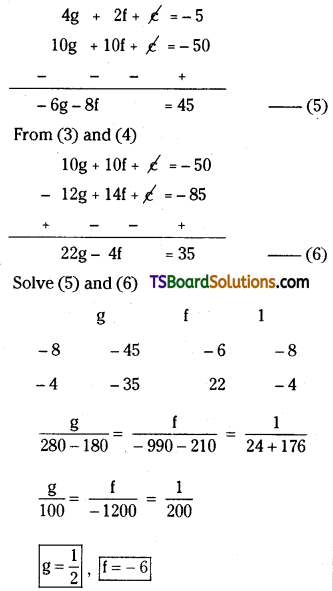
⇒ 4g + 2f + c = -5 …….(2)
Since (1) passes through point (5, 5), then
(5)² + (5)² + 2g(5) + 2f(5) + c = 0
⇒ 25 + 25 + 10g + 10f + c = 0
⇒ 10g + 10f + c = -50 ………(3)
Since (1) passes through the point (-6, 7) then
(-6)² + (7)² + 2g(-6) + 2f(7) + c = 0
⇒ 36 + 49 – 12g + 14f + c = 0
⇒ -12g + 14f + c = -85 …….(4)
From (2) and (3)

Substitute the value of g, f in (2)
4(\(\frac{1}{2}\)) + 2(-6) + c = -5
2 – 12 + c = -5
⇒ c = -5 + 10
⇒ c = 5
Now, substitute the values of g, f, c in (1)
∴ The required equation of the circle is x² + y² + 2(\(\frac{1}{2}\))x + 2(-6)y + 5 = 0
⇒ x² + y² + x – 12y + 5 = 0

Question 5.
Show that the points (1, 2), (3, -4), (5, -6), (19, 8) are concyclic and find the equation of the circle on which they lie. [(TS) Mar. ’16, May ’15]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since the eq.(1) passes through the point (1, 2) then
(1)² + (2)² + 2g(1) + 2f(2) + c = 0
⇒ 2g + 4f + c = -5 ……….(2)
Since the eq.(1) passes through the point (3, -4) then
(3)² + (-4)² + 2g(3) + 2f(-4) + c = 0
⇒ 9 + 16 + 6g – 8f + c = 0
⇒ 6g – 8f + c = -25 …………. (3)
Since the eq.(1) passes through the point (5, -6) then
(5)² + (-6)² + 2g(5) + 2f(-6) + c = 0
⇒ 25 + 36 + 10g – 12f + c = 0
⇒ 10g – 12f + c = -61 ………(4)
From (2) & (3)


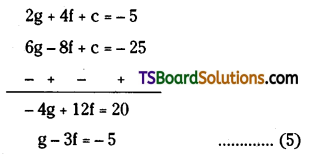
Substitute the values of g, f in eq. (2)
2(-11) + 4(-2) + c = -5
⇒ -22 – 8 + c = -5
⇒ c = 25
Substitute the values of g, f, c in eq. (1)
x² + y² + 2(-11)x + 2(-2)y + 25 = 0
⇒ x² + y² – 22x – 4y + 25 = 0 ………(7)
Now, substitute the point (19, 8) in eq. (7)
(19)² + (8)² – 22(19) – 4(8) + 25 = 0
⇒ 361 + 64 – 418 – 32 + 25 = 0
⇒ 0 = 0
∴ Given points are concyclic.
∴ The equation of the circle is x² + y² – 22x – 4y + 25 = 0.

Question 6.
Show that the points (9, 1), (7, 9) (-2, 12), (6, 10) are concyclic and find the equation of the circle on which they lie. [(TS) Mar. ’19]
Solution:
Let, the equation of the required circle is x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through point (9, 1), then
(9)² + (1)² + 2g(9) + 2f(1) + c = 0
⇒ 81 + 1 + 18g + 2f + c = 0
⇒ 18g + 2f + c = -82 ………(2)
Since (1) passes through the point (7, 9), then
(7)² + (9)² + 2g(7) + 2f(9) + c = 0
⇒ 49 + 81 + 14g + 18f + c = 0
⇒ 14g + 18f + c = -130 ……..(3)
Since (1) passes through the point (-2, 12) then
(-2)² + (12)² + 2g(-2) + 2f(12) + c = 0
⇒ 4 + 144 – 4g + 24f + c = 0
⇒ -4g + 24f + c = -148 ……..(4)

Substitute the value of g, f in (2)
18(0) + 2(-3) + c = -82
⇒ 6 + c = -82
⇒ c = -82 + 6
⇒ c = -76
Substitute the values of g, f, c in (1)
∴ The equation of the required circle is x² + y² + 2(0)x + 2(-3)y – 76 = 0
⇒ x² + y² – 6y – 76 = 0 ………(7)
Substitute the point (6, 10) in (7)
(6)² + (10)² – 6(10) – 76 = 0
⇒ 36 + 100 – 60 – 76 = 0
⇒ 136 – 136 = 0
⇒ 0 = 0
∴ The given points are concyclic.
∴ The equation of the required circle is x² + y² – 6y – 76 = 0

Question 7.
If (2, 0), (0, 1), (4, 5), and (0, c) are concyclic then find ‘c’. [(AP) May ’19. ’15, Mar. ’17, ’15) (TS) Mar. ’17, ’15, May ’14]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since eq. (1) passes through the point (2, 0) then
(2)² + (0)² + 2g(2) + 2f(0) + c = 0
⇒ 4 + 4g + c = 0
⇒ 4g + c = -4 ……(2)
Since eq. (1) passes through the point (0, 1) then
(0)² + (1)² + 2g(0) + 2f(1) + c = 0
⇒ 2f + c = -1 ……..(3)
Since eq. (1) passes through the point (4, 5) then
(4)² + (5)² + 2g(4) + 2f(5) + c = 0
⇒ 16 + 25 + 8g + 10f + c = 0
⇒ 8g + 10f + c = -41 ……(4)
From (2) & (3)


3x² + 3y² – 13x – 17y + 14 = 0 ……..(7)
Since the given points are concyclic, then the point (0, c) lies on (7).
3(0)² + 3(c)² – 13(0) – 17(c) + 14 = 0
⇒ 3c² – 17c + 14 = 0
⇒ 3c² – 14c – 3c + 14 = 0
⇒ 3c(c – 1) – 14(c – 1) = 0
⇒ (c – 1) (3c – 14) = 0
⇒ c = 1, c = \(\frac{14}{3}\)

Question 8.
If (1, 2), (3, -4), (5, -6), and (c, 8) are concyclic, then find ‘c’.
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since (1) passes through the point (1, 2), then
(1)² + (2)² + 2g(1) + 2f(2) + c = 0
⇒ 1 + 4 + 2g + 4f + c = 0
⇒ 2g + 4f + c = -5 …….(2)
Since (1) passes through point (3, -4), then
(3)² + (-4)² + 2g(3) + 2f(-4) + c = 0
⇒ 9 + 16 + 6g – 8f + c = 0
⇒ 6g – 8f + c = -25 …….(3)
Since (1) passes through point (5, -6) then
(5)² + (-6)² + 2g(5) + 2f(-6) + c = 0
⇒ 25 + 36 + 10g – 12f + c = 0
⇒ 10g – 12f + c = -61 ……(4)
From (2) and (3)


Substitute the value of g, f in (2)
2(-11) + 4(-2) + c = -5
⇒ -22 – 8 + c = -5
⇒ -30 + c = -5
⇒ c = 25
Substitute the values of g, f, c in (1)
The equation of the required circle is x² + y² + 2(-11)x + 2(-2)y + 25 = 0
⇒ x² + y² – 22x – 4y + 25 = 0 ……..(7)
Substitute point (c, 8) in (7)
(c)² + (8)² – 22c – 4(8) + 25 = 0
⇒ c² + 64 – 22c – 32 + 25 = 0
⇒ c² – 22c + 57 = 0
⇒ c² – 19c – 3c + 57 = 0
⇒ c(c – 19) – 3(c – 19) = 0
⇒ (c – 19)(c – 3) = 0
⇒ c = 19, 3

Question 9.
Find the equation of the circle whose centre lies on the X-axis and passes through (-2, 3) and (4, 5). [Mar. ’15 (AP&TS)]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Centre of (1) is (-g, -f) lies on the X-axis then -f = 0
⇒ f = 0
Since eq. (1) passes through the point (-2, 3) then
(-2)² + 3² + 2g(-2) + 2f(3) + c = 0
⇒ 4 + 9 – 4g + 6f + c = 0
⇒ -4g + 6f + c = -13
If f = 0 then
-4g + c = -13 ………(2)
Since eq. (1) passes through the point (4, 5) then
(4)² + (5)² + 2g(4) + 2f(5) + c = 0
⇒ 16 + 25 + 8g + 10f + c = 0
⇒ 8g + 10f + c = -41 ………(3)
If f = 0 then 8g + c = -41
Solving (2) & (3)

Now, substituting the values of g, f, c in equation (1)
x² + y² + 2(\(\frac{-7}{3}\))x + 2(0)y + \(\frac{-67}{3}\) = 0
⇒ 3x² + 3y² – 14x – 67 = 0

Question 10.
Find the equation of the circle which passes through (4, 1) (6, 5) and has the centre of 4x + 3y – 24 = 0.
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through point (4, 1) then
(4)² + (1)² + 2(4)g + 2f(1) + c = 0
⇒ 16 + 1 + 8g + 2f + c = 0
⇒ 8g + 2f + c = -17 ………(2)
Since, (1) passes through the point (6, 5) then
(6)² + (5)² + 2g(6) + 2f(5) + c = 0
⇒ 36 + 25 + 12g + 10f + c = 0
⇒ 12g + 10f + c = – 61 …….(3)
Centre of (1) is C = (-g, -f) lies on the line 4x + 3y – 24 = 0 then
4(-g) + 3(-f) – 24 = 0
⇒ -4g – 3f – 24 = 0
⇒ -4g – 3f = 24 ……..(4)
From (2) and (3)

Now, substitute the values of g and f in (2)
8(-3) + 2(-4) + c = -17
⇒ -24 – 8 + c = 17
⇒ c = -17 + 32
⇒ c = 15
Substitute the values of g, f, c in (1)
x² + y² + 2(-3)x + 2(-4)y + 15 = 0
⇒ x² + y² – 6x – 8y + 15 = 0

Question 11.
Find the equation of a circle which passes through (4, 1) and (6, 5) and has the centre on 4x + 3y – 24 = 0. [(AP) Mar. ’20, ’16. (TS) Mar. ’18; Mar. ’11]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since equation (1) passes through point (4, 1) then
(4)² + (1)² + 2g(4) + 2f(1) + c = 0
⇒ 16 + 1 + 8g + 2f + c = 0
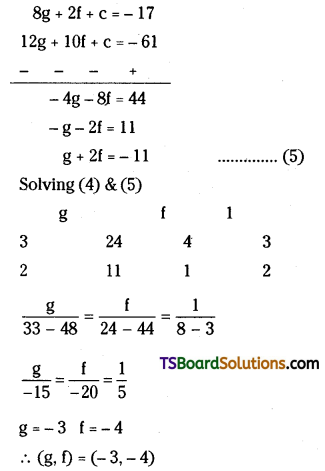
⇒ 8g + 2f + c = -17 ………..(2)
Since equation (1) passes through the point (6, 5) then
(6)² + (5)² + 2g(6) + 2f(5) + c = 0
⇒ 36 + 25 + 12g + 10f + c = 0
⇒ 12g + 10f + c = -61 ……….(3)
Centre of (1) is C = (-g, -f) lies on the line 4x + 3y – 24 = 0 then
4(-g) + 3(-f) – 24 = 0
⇒ -4g – 3f – 24 = 0
⇒ 4g + 3f + 24 = 0 ………(4)
Now (2) – (3)

Substitute the values of g, f in eq. (2) we get
8(-3) + 2(-4) + c = -17
⇒ -24 – 8 + c = -17
⇒ c = -17 + 32
⇒ c = 15
Substitute the values of g, f, c in eq. (1)
x² + y² + 2(-3)x + 2(-4)y + 15 = 0
⇒ x² + y² – 6x – 8y + 15 = 0 which is the required equation of the circle.

Question 12.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 touch each other. Also, find the point of contact and common tangent at this point of contact. [(AP) Mar. ’17]
Solution:
Given equations of the circles are
x² + y² – 4x – 6y – 12 = 0 ……..(1)
x² + y² + 6x + 18y + 26 = 0 ………(2)
For circle (1),
Centre, C₁ = (2, 3)

Now, r₁ + r₂ = 8 + 5 = 13
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch each other externally.
Let, P be the point of contact.
Now, the point of contact divides C₁C₂ in the ratio r₁ : r₂ = 5 : 8 internally.
∴ Point of contact,

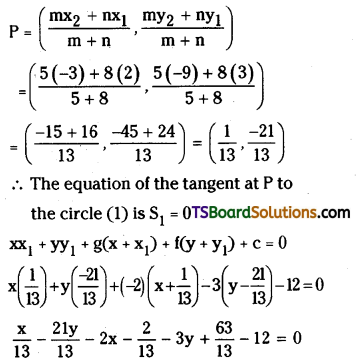
⇒ x – 21y – 26x – 2 – 39y + 63 – 156 = 0
⇒ -25x – 60y – 95 = 0
⇒ 5x + 12y + 19 = 0

Question 13.
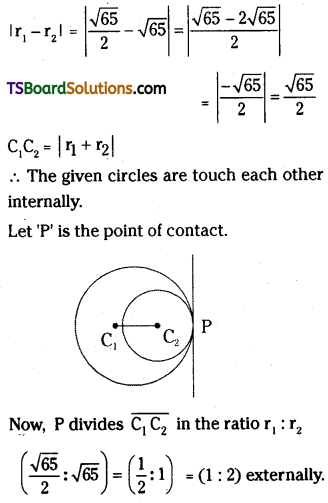
Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. [(TS) Mar. ’20, ’18; (AP & TS) May ’18]
Solution:
Given equations of the circles are
x² + y² – 6x – 9y + 13 = 0 …….(1)
x² + y² – 2x – 16y = 0 ………(2)
Centre of (1) is C₁ = (3, \(\frac{9}{2}\))

Question 14.
Show that the circles x² + y² – 6x – 2y + 1 = 0, x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. [(AP) May ’19, ’17, ’16; Mar. ’16]
Solution:
Given equations of the circles are
x² + y² – 6x – 2y + 1 = 0 ……..(1)
x² + y² + 2x – 8y + 13 = 0 ………(2)
Centre of (1) is C₁ = (3, 1)
Radius of (1) is r₁ = \(\sqrt{9+1-1}\) = 3
Centre of (2) is C₂ = (-1, 4)
Radius of (2) is r₂ = \(\sqrt{1+16-13}\) = 2
C₁C₂ = \(\sqrt{(3+1)^2+(1-4)^2}\)
= \(\sqrt{16+9}\)
= 5
r₁ + r₂ = 3 + 2 = 5
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch each other externally.
Let ‘P’ is the point of contact.
Now, ‘P’ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r1 : r2 (3 : 2) internally.
∴ Point of contact

Question 15.
Show that the circles x² + y² – 4x – 6y – 12 = 0 and 5(x² + y²) – 8x – 14y – 32 = 0 touch each other and find their point of contact. [(TS) May ’17]
Solution:
Given equations of the circles are
x² + y² – 4x – 6y – 12 = 0 ……….(1)
5(x² + y²) – 8x – 14y – 32 = 0
⇒ \(x^2+y^2-\frac{8}{5} x-\frac{14}{5} y-\frac{32}{5}=0\) ………(2)
For circle (1),
Centre, C₁ = (2, 3)

Now, |r₁ – r₂| = |5 – 3| = 2
∴ C₁C₂ = |r₁ – r₂|
∴ The given circles touch each other internally.
Let, ‘P’ be the point of contact.
Now, P divides C₁C₂ in the ratio r₁ : r₂ (5 : 3) externally.

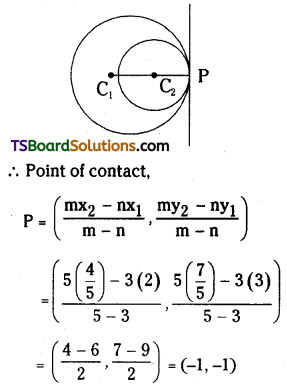
Question 16.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x – 6y + 4 = 0. [(TS) May ’19, Mar. ’17; (AP) Mar. ’19, ’15, ’14]
Solution:
Given equations of the circles are
x² + y² – 4x – 10y + 28 = 0 ……..(1)
x² + y² + 4x – 6y + 4 = 0 ………(2)
Centre of (1) = (2, 5)
Centre of (2) = (-2, 3)
r₁ = \(\sqrt{4+25-28}\) = 1
r₂ = \(\sqrt{4+9-4}\) = 3
Distance between \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) = √20
r₁ + r₂ = 4 = √16
C₁C₂ > r₁ + r₂
Given circles completely lie outside each other.
Let A be the internal centre of similitude.

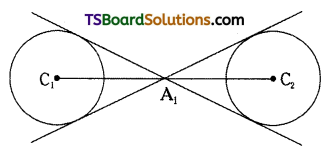
Now, A₁ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ (1 : 3) internally.
∴ Internal centre of similitude

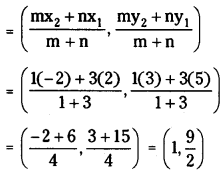
∴ The equation of the pair of transverse common tangents is S . S₁₁ = \(S_1{ }^2\)

⇒ (x² + y² + 4x – 6y + 4) (9) = 9(2x + y – 5)²
⇒ x² + y² + 4x – 6y + 4 = 4x² + y² + 25 + 4xy – 10y – 20x
⇒ 3x² + 4xy – 24x – 4y + 21 = 0
Now, 3x² + 4xy = 0
⇒ x(3x + 4y) = 0
⇒ x = 0, 3x + 4y = 0
3x² + 4xy – 24x – 4y + 21 = (x + l) (3x + 4y + k)
Comparing ‘x’ coefficients on both sides
k + 3l = -24 ……….(1)
4l = -4 ………(2)
⇒ l = -1
Substitute l = -1 in eq. (1)
k – 3 = – 24
⇒ k = -24 + 3
⇒ k = -21
∴ The transerve common tangents are x – 1 = 0, 3x + 4y – 21 = 0

Question 17.
Find the direct common tangents of the circles x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0. [Mar. ’18 (AP); May&Mar. ’15 (TS)]
Solution:
Given the equation of the circles are
x² + y² + 22x – 4y – 100 = 0 ……..(1)
x² + y² – 22x + 4y + 100 = 0 ……….(2)
Centre of (1) is C₁ = (-11, 2)
r₁ = \(\sqrt{121+4+100}\) = 15
C₂ = (11, -2)
r₂ = \(\sqrt{121+4-100}\) = 5
C₁C₂ = \(\sqrt{(-11-11)^2+(2+2)^2}\)
= \(\sqrt{(-22)^2+(4)^2}\)
= √500
r₁ + r₂ = 20
C₁C₂ > r₁ + r₂
∴ The given circles completely lie outside the circle.
Let A₂ be the external centre of similitude.

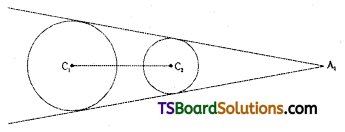
Now, A₂ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ (3 : 1) externally.
External of similitude

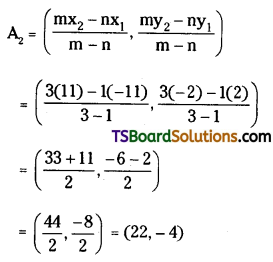
The equation to the pair of direct common tangents is S . S₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + y² + 22x – 4y – 100) ((22)² + (-4)² + 2(11) (22) + 2(-2) (-4) – 100) = ((22)x + y(-4) + 2(11) (22) + 11(x) – 2(y) + 1(-2) (-4) – 100)²
⇒ (x² + y² + 22x – 4y – 100) (484 + 16 + 484 + 16 – 100) = (22x – 4y + 242 + 11x – 2y + 8 – 100)²
⇒ (x² + y² + 22x – 4y – 100) (900) = (33x – 6y + 150)²
⇒ 100(x² + y² + 22x – 4y – 100) = (11x – 2y + 50)²
⇒ 100x² + 100y² + 2200x – 400y – 10000 = 121x² + 4y² + 2500 – 44xy – 200xy + 1100x
⇒ 21x² – 96y² – 44xy – 1100x + 200y + 12500 = 0
Now, 21x² – 44xy – 96y² = 0
⇒ 21x² – 72xy + 28xy – 96y² = 0
⇒ 3x(7x – 24y) + 4y(7x – 24y) = 0
⇒ (7x – 24y) (3x + 4y) = 0
⇒ 7x – 24y = 0, 3x + 4y = 0
∴ 21x² – 44xy – 96y² – 1100x + 200y + 12500 = (7x – 24y + l) (3x + 4y + k)
Comparing ‘x’ coeff. on both sides
7k + 3l = -1100 …….(1)
Comparing ‘y’ coeff. on both sides
-24k + 4l = 200 ………(2)
Solve (1) & (2)

∴ The direct common tangent are 7x – 24y – 250 = 0, 3x + 4y – 50 = 0

Question 18.
Find all common tangents to the circles x² + y² + 4x + 2y – 4 = 0 and x² + y² – 4x – 2y + 4 = 0.
Solution:
Given equations of the circles are
x² + y² + 4x + 2y – 4 = 0 ………(1)
x² + y² – 4x – 2y + 4 = 0 ……….(2)
for the circle (1)
Centre C₁ = (-2, -1)

Now, r₁ + r₂ = 3 + 1 = 4 = √16
∴ C₁C₂ > r₁ + r₂
∴ In the two given circles, each circle lies completely outside the other.
To find the external centre of similitude (A₂):
Let A₂ be the external centre of similitude.
The external centre of similitude, A₂ divides C₁C₂ in the ratio r₁ : r₂ (3 : 1) externally.

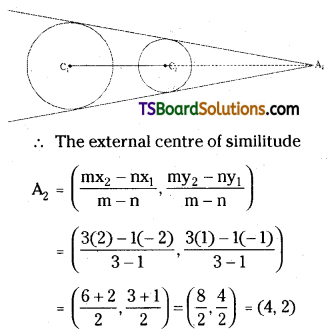
The equation of pair of direct common tangent is SS₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + y² + 2gx + 2fy + c) \(\left(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{fy}_1+\mathrm{c}\right)\) = (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c)²
⇒ (x² + y² + 4x + 2y – 4) [(4)² + (2)² + 2(2)(4) + 2(1)(2) – 4] = [x(4) + y(2) + 2(x + 4) + 1(y + 2) – 4]²
⇒ (x² + y² + 4x + 2y – 4) (16 + 4 + 16 + 4 – 4) = (4x + 2y + 2x + 8 + y + 2 – 4)²
⇒ (x² + y² + 4x + 2y – 4) (36) = (6x + 3y + 6)²
⇒ (x² +y² + 4x + 2y – 4) (36) = 9(2x + 4 + 2)²
⇒ (x² + y² + 4x + 2y – 4) (4) = (2x + y + 2)²
⇒ (x² + y² + 4x + 2y – 4) (4) = 4x² + y² + 4 + 4xy + 4y + 8x
⇒ 4x² + 4y² + 16x + 8y – 16 = 4x² + y² + 4xy + 4y + 8x + 4
⇒ 4xy – 3y² – 8x – 4y + 20 = 0
Consider 4xy – 3y² = 0
⇒ y(4x – 3y) = 0
⇒ y = 0 (or) 4x – 3y = 0
∴ 4xy – 3y2 – 8x – 4y + 20 = (y + l)(4x – 3y + k)
Comparing the coefficient of x on both sides
4l = -8
⇒ l = -2
Comparing the coefficient of y on both sides.
-3l + k = – 4
⇒ -3(-2) + k = -4
⇒ 6 + k = -4
⇒ k = -10
∴ The equations to the direct common tangents are y – 2 = 0, 4x – 3y – 10 = 0
To find the internal centre of similitude (A₁):
Let A₁ be the internal centre of similitude.
The internal centre of similitude, A₁ divides C₁C₂ in the ratio r₁ : r₂ (3 : 1) internally.


⇒ (x² + y² + 4x + 2y – 4) (9) = (9) (2x + y – 1)²
⇒ x² + y² + 4x + 2y – 4 = 4x² + y² + 1 + 4xy – 2y – 4x
⇒ 3x² + 4xy – 8x – 4y + 5 = 0
Consider 3x² + 4xy = 0
⇒ x(3x + 4y) = 0
⇒ x = 0 (or) 3x + 4y = 0
∴ 3×2 + 4xy – 8x – 4y + 5 = (x + l) (3x + 4y + k)
Comparing the coefficient of x on. both sides
3l + k = -8 ………(3)
Comparing the coefficient of y on both sides.
4l = -4 ⇒ l = -1
(3) ⇒ 3(-1) + k = -8
⇒ -3 + k = -8
⇒ k = -5
∴ The equations of the transverse common tangents are x – 1 = 0, 3x + 4y – 5 = 0
∴ The common tangents are x – 1 = 0, 3x + 4y – 5 = 0, y – 2 = 0, 4x – 3y – 10 = 0

Question 19.
Find the equations of circles that touch 2x – 3y + 1 = 0 at (1, 1) and have a radius √13.
Solution:
Let, the equation of the required circle is x² + y² + 2gx + 2fy + c = 0

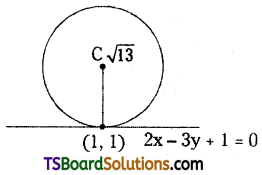
The equation of the tangent at P(1, 1) to the given circle is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(1) + g(x + 1) + f(y + 1) + c = 0
⇒ x + y + gx + g + fy + f + c = 0
⇒ x(1 + g) + (1 + f)y + g + f + c = o ………(1)
Given the equation of the tangent is
2x – 3y + 1 = 0 ……….(2)
Now, (1) and (2) represent the same line we get

2k – 1 – 3k – 1 + c = k
⇒ -k – 2 + c = k
⇒ c = 2k + 2
Given that, radius, r = √13
\(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{13}\)
Squaring on both sides
g² + f² – c = 13
⇒ (2k – 1)² + (-3k – 1)² – (2k + 2) = 13
⇒ 4k² + 1 – 4k + 9k² + 1 + 6k – 2k – 2 = 13
⇒ 13k² = 13
⇒ k² = 1
⇒ k = ±1
Case 1: If k = 1 then
g = 2(1) – 1 = 2 – 1 = 1
f = -3(1) – 1 = -3 – 1 = -4
c = 2(1) + 2 = 2 + 2 = 4
∴ The equation of the required circle is x² + y² + 2(1)x + 2(-4)y + 4 = 0
⇒ x² + y² + 2x – 8y + 4 = 0
Case 2: If k = -1 then
g = 2(-1) – 1 = -2 – 1 = -3
f = -3(-1) – 1 = 3 – 1 = 2
c = 2(-1) + 2 = -2 + 2 = 0
∴ The equation of the required circle is x² + y² + 2(-3)x + 2(2)y + 0 = 0
⇒ x² + y² – 6x + 4y = 0
∴ The required circles are x² + y² + 2x – 8y + 4 = 0, x² + y² – 6x + 4y = 0

Question 20.
If ABCD is a square, then show that the points A, B, C, and D are concyclic.
Solution:
ABCD is a square
Let AB = a, then AD = a
∴ A = (0, 0), B = (a, 0), C = (a, a), D = (0, a)

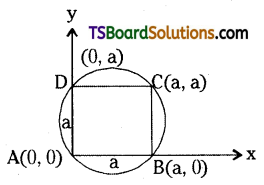
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since, (1) passes through point A(0, 0)
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Since (1) passes through point B(a, 0)
(a)² + (0)² + 2g(a) + 2f(0) + c = 0
⇒ a² + 2ga + c = 0
⇒ a² + 2ga = 0
⇒ a + 2g = 0
⇒ g = \(\frac{-a}{2}\)
Since, (1) passes through the point D(0, a)
(0)² + a² + 2g(0) + 2f(a) + c = 0
⇒ 0 + a² + 2af = 0
⇒ a + 2f = 0
⇒ f = \(\frac{-a}{2}\)
Now, substitute the values of g, f, c in (1), and we get
x² + y² + 2(\(\frac{-a}{2}\))x + 2(\(\frac{-a}{2}\))y + 0 = 0
x² + y² – ax – ay = 0 ……(2)
Now, substitute the point c(a, a) in (2)
(a)² + (a)² – a(a) – a(a) = 0
⇒ a² + a² – a² – a² = 0
⇒ 0 = 0
∴ Points A, B, C, and D are concyclic.

Question 21.
Find the equation of the circumcircle of the triangle formed by the line ax + by + c = 0 (abc ≠ 0) and the coordinate axes.
Solution:
Let the line ax + by + c = 0, and cut the x, y axes at A and B respectively.

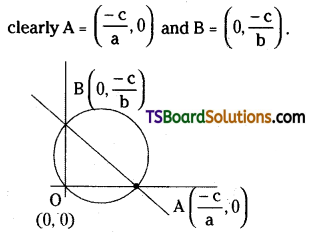
Let the equation of the required circle is
x² + y² + 2gx + 2fy + k = 0 ……..(1)
Since, (1) passes through the point O(0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + k = 0
⇒ k = 0
Since, (1) passes through the point A(\(\frac{-c}{a}\), 0), then

Now, substitute the values of g, f, k in (1)
∴ The equation of the required circle is
x² + y² + 2(\(\frac{c}{2a}\))x + 2(\(\frac{c}{2b}\))y + 0 = 0
⇒ abx² + aby² + bcx + acy = 0
⇒ ab(x² + y²) + (bx + ay)c = 0

Question 22.
Find the equation of the circumcircle of the triangle formed by the straight lines x + 3y – 1 = 0, x + y + 1 = 0, 2x + 3y + 4 = 0.
Solution:
Given lines are x + 3y – 1 = 0, x + y + 1 = 0, 2x + 3y + 4 = 0
Consider a curve through vertices of the triangle formed by the given lines whose equation is
a(x + 3y – 1) (x + y + 1) + b(x + y + 1) (2x + 3y + 4) + c(2x + 3y + 4) (x + 3y – 1) = 0
⇒ a(x² + xy + x + 3xy + 3y² + 3y – x – y – 1) + b(2x² + 3xy + 4x + 2xy + 3y² + 4y + 2x + 3y + 4) + c(2x² + 6xy – 2x + 3xy + 9y² – 3y + 4x + 12y – 4) = 0
⇒ a(x² + 3y² + 4xy + 2y – 1) + b(2x² + 5xy + 3y² + 6x + 7y + 4) + c(2x² + 9xy + 9y² + 2x + 9y – 4) = 0 ……..(1)
Coefficient of x² = a + 2b + 2c
Coefficient of y² = 3a + 3b + 9c
Coefficient of xy = 4a + 5b + 9c
(1) represents a circle, then
(i) Coefficient of x² = Coefficient of y²
⇒ a + 2b + 2c = 3a + 3b + 9c
⇒ 3a + 3b + 9c – a – 2b – 2c = 0
⇒ 2a + b + 7c = 0 …….(2)
(ii) Coefficient of xy = 0
⇒ 4a + 5b + 9c = 0 …….(3)
Solve (2) and (3)

\(\frac{a}{9-35}=\frac{b}{28-18}=\frac{c}{10-4}\)
\(\frac{a}{-26}=\frac{b}{10}=\frac{c}{6}\)
∴ a = -26, b = 10, c = 6
Substitute the value of a, b, c in (1)
-26(x² + 4xy + 3y² + 2y – 1) + 10(2x² + 5xy + 3y² + 6x + 7y + 4) + 6(2x² + 9xy + 9y² + 2x + 9y – 4) = 0
⇒ -26x² – 104xy – 78y² – 52y + 26 + 20x² + 50xy + 30y² + 60x + 10y + 40 + 12x² + 54xy + 54y² + 12x + 54y – 24 = 0
⇒ 6x² + 6y² + 72x + 72y + 42 = 0
⇒ x² + y² + 12x + 12y + 7 = 0
∴ The equation of the required circle is x² + y² + 12x + 12y + 7 = 0

Question 23.
Find the equation of the circle passing through (-1, 0) and touching x + y – 7 = 0 at (3, 4).
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)

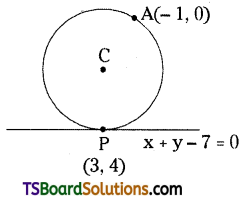
Since (1) passes through point A(-1, 0), then
(-1)² + (0)² + 2g(-1) + 2f(0) + c = 0
⇒ 1 – 2g + c = 0
⇒ c = 2g – 1 ……..(2)
Since, the line x + y – 7 = 0 touches the circle (1), then the given equation of a tangent is
x + y – 7 = 0 ………(3)
Now, the equation of tangent at P(3, 4) is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(4) + g(x + 3) + f(y + 4) + 2g – 1 = 0
⇒ 3x + 4y + gx + 3g + fy + 4f + 2g – 1 = 0
⇒ 3x + 4y + gx + fy + 4f + 5g – 1 = 0
⇒ (3 + g)x + (4 + f)y + 5g + 4f – 1 = 0 ……….(4)
(3) and (4) represent the same line

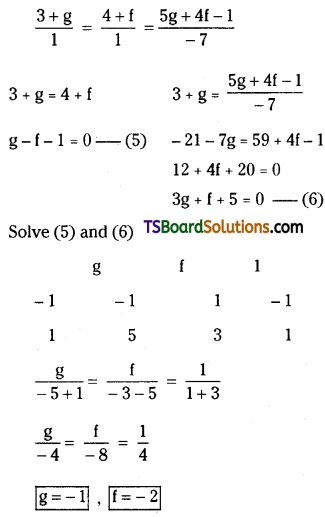
Substitute the value of g in (2)
c = 2(-1) – 1
⇒ c = -2 – 1
⇒ c = -3
Substitute the values of g, f, c in (1)
∴ The required equation of the circle is x² + y² + 2(-1)x + 2(-2) y – 3 = 0
⇒ x² + y² – 2x – 4y – 3 = 0

Question 24.
Find the equation of the circle which touches the circle x² + y² – 2x – 4y – 20 = 0 externally at (5, 5) with radius 5. [(AP) Mar. ’20; (TS) May ’16]
Solution:
Given equation of the circle is x² + y² – 2x – 4y – 20 = 0

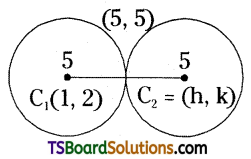
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = -2, c = -20
Centre C₁ = (-g, -f) = (1, 2)
Radius r₁ = \(\sqrt{1+4+20}=\sqrt{25}\) = 5
Let centre of the required circle is C₂ = (h, k)
Radius r₂ = 5
Given point of contact P = (5, 5)
Now, the point of contact ‘P’ divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ (5 : 5 = 1 : 1) internally.

Hence, centre C₂ = (9, 8)
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 9)² + (y – 8)² = 5²
⇒ x² + 81 – 18x + y² + 64 – 16y = 25
⇒ x² + y² – 18x – 16y + 120 = 0

Question 25.
If θ₁, θ₂ are the angles of inclination of tangents through a point P to the circle x² + y² = a², then find the locus of P when cot θ₁ + cot θ₂ = k.
Solution:
Given the equation of the circle is x² + y² = a²

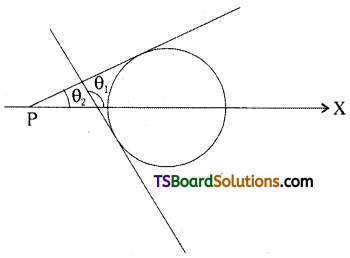
Let P(x₁, y₁) be a point on the locus.
The equation of the tangent to x² + y² = a² having slope m is
y = mx ± \(a \sqrt{1+m^2}\) ……..(1)
If the tangent (1) passes through P, then

Let the roots of (2) be m₁, m₂
Since, the tangents make angles θ₁, θ₂ with x-axis then their slopes m₁ = tan θ₁ and m₂ = tan θ₂
∴ m₁ + m₂ = tan θ₁ + tan θ₂

∴ The locus of P is k(y² – a²) = 2xy.

Question 26.
Show that the poles of the tangents to the circle x² + y² = a² w.r.t the circle (x + a)² + y² = 2a² lie on y² + 4ax = 0.
Solution:
Given the equation of the circle
(x + a)² + y² = 2a²
⇒ x² + a² + 2ax + y² – 2a² = 0
⇒ x² + y² + 2ax – a² = 0 …….(1)

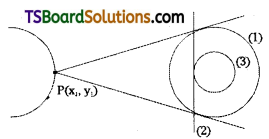
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
g = a, f = 0, c = -a²
Let P(x₁, y₁) be the pole
Now, the polar of P(x₁, y₁) w.r.t the circle (1) is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ xx₁ + yy₁ + a(x + x₁) + 0(y + y₁) – a² = 0
⇒ xx₁ + yy₁ + ax + ax₁ – a² = 0
⇒ (x₁ + a)x + y₁y + (ax₁ – a²) = 0 ………(2)
Given equation of the circle is x² + y² = a² ……..(3)
Centre C = (0, 0), Radius r = a
Since (2) is a tangent to the circle (3), then r = d

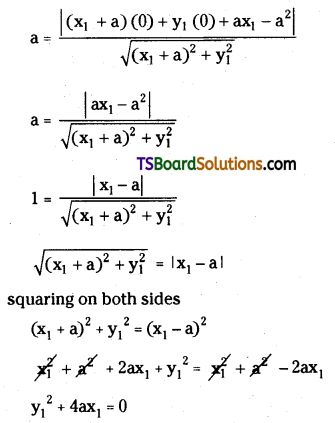
∴ The poles of the tangents to the circle (2) w.r.t the circle (1) lie on the curve y² + 4ax = 0.

Question 27.
If the chord of contact of a point P w.r.t the circle x² + y² = a² cut the circle at A and B such that ∠AOB = 90°, then show that P lies on the circle x² + y² = 2a².
Solution:
Given the equation of the circle is
x² + y² = a² ……(1)
Let P(x₁, y₁) be a point.

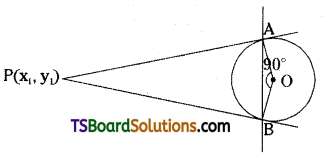
The equation of the chord of contact of P(x₁, y₁) w.r.t the circle x² + y² = a² is S₁ = 0
xx₁ + yy₁ = a²
\(\frac{xx_1+y y_1}{a^2}=1\) ……..(2)
Now homogenizing (1) with help of (2)
∴ The combined equation of \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OB}}\) is x² + y² = a² (1)²

Hence, the point P(x₁, y₁) lies on the circle x² + y² = 2a².

Question 28.
Show that the equation to the pair of tangents to the circle S = 0 from P(x₁, y₁) is \(S_1^2\) = SS₁₁. [May ’14; Mar. ’03]
Solution:
Let the equation of the circle be S = x² + y² + 2gx + 2fy + c = 0

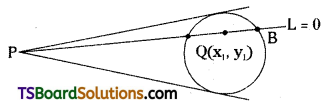
Let a line l = 0 through P(x₁, y₁) meet the circle in A and B.
Let Q(x, y) be any point on the line.
Let k : 1 be the ratio in which A divides \(\overline{\mathrm{PQ}}\)


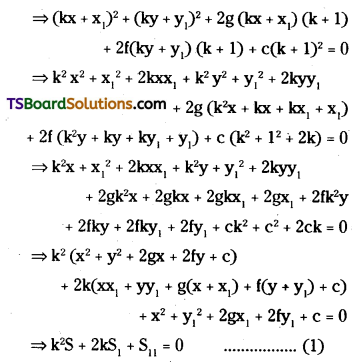
If L = 0 is a tangent to S = 0 then A & B coincide and the roots of (1) are equal.
∴ b² – 4ac = 0
⇒ (2S₁)² – 4(S) (S₁₁) = 0
⇒ 4\(S_1^2\) – 4SS₁₁ = 0
⇒ \(S_1^2\) – SS₁₁ = 0
⇒ \(S_1^2\) = SS₁₁
∴ The locus of ‘Q’ is \(S_1^2\) = SS₁₁
∴ The equation to the pair of tangents from P(x₁, y₁) is \(S_1^2\) = SS₁₁.

Question 29.
Find the condition that the tangents drawn from the exterior point (g, f) to S = x² + y² + 2gx + 2fy + c = 0 are perpendicular to each other.
Solution:
Given the equation of the circle is
S = x² + y² + 2gx + 2fy + c = 0
Centre C = (-g, -f)
Radius r = \(\sqrt{g^2+f^2-c}\)
Let the given point P(x₁, y₁) = (g, f)
The angle between the tangents θ = 90°
Length of the tangents = \(\sqrt{S_{11}}\)

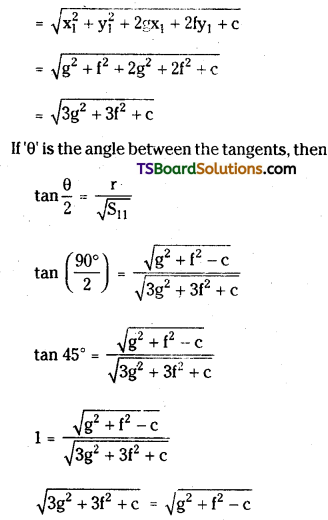
squaring on both sides
3g² + 3f² + c = g² + f² – c
⇒ 2g² + 2f² + 2c = 0
⇒ g² + f² + c = 0

Question 30.
Find the equation of the circle passing through P(1, 1), Q(2, -1) and R(3, 2).
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point P(1, 1), then
(1)² + (1)² + 2g(1) + 2f(1) + c = 0
⇒ 1 + 1 + 2g + 2f + c = 0
⇒ 2g + 2f + c = -2 ……..(2)
Since, (1) passes through the point Q(2, -1), then
(2)² + (-1)² + 2g(2) + 2f(-1) + c = 0
⇒ 4 + 1 + 4g – 2f + c = 0
⇒ 4g – 2f + c = -5 …….(3)
Since, (1) passes through the point R(3, 2), then
(3)² + (2)² + 2g(3) + 2f(2) + c = 0
⇒ 9 + 4 + 6g + 4f + c = 0
⇒ 6g + 4f + c = -13 ………(4)
from (2) and (3)

Question 31.
From a point on the circle x² + y² + 2gx + 2fy + c = 0, two tangents are drawn to the circle x² + y² + 2gx + 2fy + c sin² α + (g² + f²) cos² α = 0. Prove that the angle between them is 2α.
Solution:
Given equations of the circles are
x² + y² + 2gx + 2fy + c = 0 ……..(1)
x² + y² + 2gx + 2fy + c sin² α + (g² + f²) cos² α = 0 …….(2)

Let P(x₁, y₁) be a point on the circle (1), then
\(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}=0\) ……..(3)
The radius of the circle (2) is

Length of the tangent of the circle (2)

If θ is the angle between the tangents then

∴ The angle between the tangents θ = 2α.

Question 32.
Find the pair of tangents from the origin to the circle x² + y² + 2gx + 2fy + c = 0 and hence deduce a condition for these tangents to be perpendicular. (Mar. ’81)
Solution:
Given equation of the circle is x² + y² + 2gx + 2fy + c = 0
Here g = g, f = f, c = c
Let the given point P(x₁, y₁) = (0, 0)
The equation of the pair of tangents drawn from (0, 0) to the given circle is \(\mathrm{S}_1^2\) = SS₁₁
⇒ [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]² = (x² + y² + 2gx + 2fy + c) \(\left(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\right)\)
⇒ [x(0) + y(0) + g(x + 0) + f(y + 0) + c]² = (x² + y² + 2gx + 2fy + c) (0 + 0 + 0 + 0 + c)
⇒ (gx + fy + c)² = (x² + y² + 2gx + 2fy + c) (c)
⇒ g² x² + f² y² + c² + 2gf xy + 2fcy + 2gcx = cx² + cy² + 2gcx + 2fcy + c²
⇒ (g² – c) x² + 2gf xy + (f² – c) y² = 0
Given that these tangents are perpendicular then
coefficient of x² + coefficient of y² = 0
⇒ g² – c + f² – c = 0
⇒ g² + f² = 2c

Question 33.
Find the locus of the midpoint of the chords of contact of x² + y² = a² from the points lying on the line lx + my + n = 0. [May ’03; Mar. ’90]
Solution:
Given the equation of the circle is
x² + y² = a² …….(1)
Given the equation of the line is
lx + my + n = 0 ……..(2)

Let P(x₁, y₁) be a point on the locus then the point P(x₁, y₁) is the midpoint of the chord of the circle x² + y² = a².
∴ The equation of the chord having P(x₁, y₁) as the midpoint of the circle (1) is S₁ = S₁₁.
⇒ xx₁ + yy₁ – a² = \(\mathrm{x}_1{ }^2+\mathrm{y}_1^2\) – a²
⇒ xx₁ + yy₁ – (\(\mathrm{x}_1{ }^2+\mathrm{y}_1^2\)) = 0 ……….(3)
Now, the pole of (3) with respect to the circle is

Hence the locus of P(x₁, y₁) is a²(lx + my) + n(x² + y²) = 0.