TS Inter 2nd Year

Telangana TSBIE TS Inter 2nd Year Physics Study Material 9th Lesson Electromagnetic Induction Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 9th Lesson Electromagnetic Induction

Very Short Answer Type Questions

Question 1.
What did the experiments of Faraday and Henry show?
Answer:

1. Faraday and Henry experiments showed that the relative motion between the magnet and a coil is responsible for generation of electric current in the coil.
2. The relative motion is not an absolute requirement to induce the current in a coil. If the current in a coil changes then also emf is induced in the nearby coil.

Question 2.
Define magnetic flux.
Answer:
Magnetic flux :
The number of magnetic field lines crossing unit area when placed perpendicular to the field is defined as “Magnetic flux”.
Magnetic flux, Φ = \(\overline{\mathrm{B}}.\overline{\mathrm{A}}\) = B A cos θ

Question 3.
State Faraday’s law of electromagnetic induction.
Answer:
Faraday’s law of Induction :
The rate of change of magnetic flux through a circular coil induces emf in it.

Question 4.
State Lenz’s law. [TS Mar. 19, June 15]
Answer:
Lenz’s Law :
The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produces current in that coil.

Question 5.
What happens to the mechanical energy (of motion) when a conductor is moved in a uniform magnetic field?
Answer:
When a condutor is moved in a magnetic field
Power of this motion, P = Fv F = Bil

The work done is in the form of mechanical energy.
This is dissipated into the form of joule heat.
∴ Joule heat = Power P_j = I²r = \(\frac{B^2l^2v^2}{r}\)

Question 6.
What are Eddy currents? [TS Mar. ’19; AP June ’15]
Answer:
Eddy currents :
When large pieces of conductors are subjected to changing magnetic flux then current is induced in them. These induced currents are called ”Eddy currents”.

Eddy currents will oppose the motion of the coil (or) they oppose the change in magnetic flux.

Question 7.
Define ‘inductance’.
Answer:
Inductance :
The process of producing emf in a coil due to changing current in that coil or in a coil nearby it is called “Inductance”.

Flux associated with a coil Φ_B is proportional to current i.e., Φ_B ∝ I

This constant of proportionality is called Inductance.

Question 8.
What do you understand by ‘self induetance’? [AP & TS June ’15]
Answer:
Self inductance :
If emf is induced in a single isolated coil due to change of flux in that coil by means of changing current through that coil then that phenomenon is called “Self Inductance L”.
In Self inductance, ε = -L\(\frac{dI}{dt}\)

Short Answer Questions

Question 1.
Obtain an expression for the emf induced across a conductor which is moved in a uniform magnetic field which is perpendicular to the plane of motion. [TS May ’16]
Answer:
Let a conductor of length T is moving with a velocity “v” in a uniform and time independent magnetic field B.

Consider a rectangular metallic frame PQRS in which the side PQ is free to move without friction.

Let PQ move with a velocity ‘v’ in a perpendicular magnetic field B.

Magnetic flux in the loop Φ_B = Bl . x, where x = RQ a time changing quantity.

Here \(\frac{dx}{dt}\) = -v = Velocity of the rod.
Induced emf, ε = Blv is called Motional emf.

Question 2.
Describe the ways in which Eddy currents are used to advantage. [AP Mar. ’19, ’18, ’17, ’16, ’15, May ’18, ’17, ’16; TS Mar. ’18, ’15. May ’17]
Answer:
Advantages of Eddy currents:

1. Electromagnetic breaking : In some electrically powered trains strong electromagnets are placed above rails. When these electromagnets are activated eddy currents induced in rails will oppose motion of train. These breaks are smooth.
2. In galvanometers, a fixed core is made with non-magnetic material. When coil oscillates eddy currents induced in core will oppose the motion. As a result, the coil will come to rest quickly.
3. In induction furnaces high frequency oscillating currents are passed through a coil which surrounds the metal to be melted. These currents will produce eddy currents in the metal and it is heated sufficiently to melt it.
4. In electric power meters a metal disc is made to rotate due to eddy currents with some arrangement. Rotation of this disc is made to measure power consumed.

Question 3.
Obtain an expression for the mutual inductance of two long co-axial solenoids.
Answer:
Consider two long solenoids S₁ and S₂ each of length ‘l’, radius r₁ and r₂ and number of turns n₁ and n₂ respectively. When a current I₂ is sent through S₂ it will set up a magnetic flux Φ₁ through S₁.

Flux linkage with S₁ is N₁ Φ₁ = M₁₂I₂ where
M₁₂ is mutual inductance between the coils.
But Φ₁ = N₁A₁B where N₁ = n₁l ; A = πr²₁ and B = µ₀n₂I₂.
∴ N₁Φ₁ =(n₁l)(πr²₁ )(µ₀n₂I₂) = µ₀n₁n₂r²₁ …………. (1)

This approximation is highly valid when l > > r₂.

If current I₁ is passed through S₁ then
N₂Φ₂ = M₂₁I₁ where Φ₂ = N₂A₂B and
B = µ₀n₁I₁ and N₂ = n₂l.
∴ N₂Φ₂ =(n₂l)(πr²₁ )(µ₀n₁I₁) = µ₀n₁n₂πr²₁l …………. (2)

From eq. (1) & (2) Mutual inductance bet-ween co-axial solenoids M₁₂ = M₂₁. If the solenoid is on a core of permeability µ_r then
[M₁₂ = M₂₁ = µ₀µ_rn₁n₂πr²₁l]
Mutual inductance of a pair of coils or solenoids etc., depends on seperation between them and also on their orientaton.

Question 4.
Obtain an expression for the magnetic energy stored in a solenoid in terms of the magnetic field, area and length of the solenoid.
Answer:
When current is passed through a single isolated coil or solenoid changing magnetic flux can be developed by changing current through it. This changing flux will induce emf in that coil.
This phenomenon is called self induction (L).
Flux linkage NΦ_B ∝ I or NΦ_B = L . I
Induced emf, ε = \(\frac{d}{dt}\)(NΦ_B) = -L\(\frac{dI}{dt}\) ………. (1)

– ve sign indicates that induced emf will always oppose the flux changes in that coil (or) solenoid.

Let length of solenoid is ‘l’, area of cross section = A
then NΦ_B = (nl)(µ₀nI) (I) (∵ Φ_B =nµ₀I) ……….. (2)
and total number of turns N = n × l.
i.e., turns per unit length ‘n’ × length of solenoid ‘l’.
∴ L = \(\frac{\mathrm{N} \phi_{\mathrm{B}}}{\mathrm{I}}\) = µ₀n²Al …………. (3)

This self induced emf also called back emf will oppose any change in current in the coil. So to drive current in the circuit we must do some work.
Rate of work done = \(\frac{dW}{dt}\) = |ε|I = LI.\(\frac{dI}{dt}\) …………. (4)
∴ Energy required to send the currrent or Energy stored in inductor

Long Answer Questions

Question 1.
Outline the path-breaking experiments of Faraday and Henry and highlight the contributions of these experiments to our understanding of electromagnetism.
Answer:
Faraday and Henry conducted a series of experiments to understand electromagnetic inductioin.

First Experiment:
In this experiment, a galvanometer is connected to a coil. A magnet is moved towards the coil. They observed that current is flowing in the coil when magnet is in motion.

The direction of induced current is in opposite direction when the direction of motion of magnet is changed.

So they concluded that relative motion between magnet and coil is responsible for generation of electric current in the coil.

Second Experiment:
In this experiment a steady current is passed through one coil with the help of a battery and the second coil is connected to a galvanometer. When one of the coil is moved then current is induced in the coil. This current losts as far as there is relative motion between them.

Again they concluded that relative motion between the coils is responsible for induced electric current.

Third Experiment:
In this experiment, they connected one coil to a battery and a tapping key to make and break electric contact in that coil. The second coil is placed near the first coil. When electric contact is established current is induced in the second coil and momentary deflection is observed in galvanometer.

When electric contact is breaked again they got deflection in galvanometer in opposite direction.

So they concluded that it is not the relative motion between the coil and magnet or relative motion between the coils that induces the current. The changing magnetic flux is responsible for induced emf or current in the coil.

Finally Faraday proposed that induced emf ε = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) ⇒ ε = N.\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
But from Lenz’s explanation he corrected this equation as ε = –\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) ⇒ ε = -N\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)

Question 2.
Describe the working of a AC generator with the aid of a simple diagram and necessary expressions.
Answer:
AC generator consists of a coil of N turns placed in a magnetic field B produced by magnetic poles when the coil is rotated its effective area changes so flux linked with the coil changes. This changing flux will induce emf in the coil.

Electric generator converts mechanical energy into electrical energy.

Flux associated with the coil,
Φ_B = (\(\overline{\mathrm{B}}\) • \(\overline{\mathrm{A}}\)) = BA cos θ, where θ = ωt
Induced emf, ε = -N\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = -NBA\(\frac{d}{dt}\)cos ωt
∴ Induced emf, ε = -NBAω sin ωt
The term NBAω is called maximum emf produced (ε_m).
∴ ε_m = NBAω
ε = ε_m sin ωt
Induced emf at any time E = ε_m sin ωt
When θ = 0, Induced emf is zero i.e., ε = 0.
The induced emf is maximum when θ = 90°
i.e., the plane of the coil is perpendicular
to magnetic field.
When θ = 90° ⇒ emf ε = ε_m
When θ = 180° ⇒ induced emf ε = 0.
When θ = 270° ⇒ induced emf ε = – ε_m.
again for θ = 360° ⇒ emf ε = 0.
∴ The induced emf varies sinusoidally in AC generator.

The coil is mounted on a rotor shaft. The axis of rotation of coil is perpendicular to magnetic field. The coil is connected to external circuit by means of slip rings and brushes.

Induced emf at any time is given by ε = ε_m sin ωt = ε_m sin 2πυt.

Depending on the method of supplying mechanical energy to rotate shaft these AC generators are classified as 1) Hydroelectric generators, 2) Thermal generators and 3) Nuclear generators.

Exercises

Question 1.
Obtain an expression for the emf induced across a conductor which is moved in a uniform magnetic field which is perpendicular to the plane of motion. [AP May ’14]
Answer:
Let a conductor of length ‘l’ is moving with a velocity “v” in a uniform and time independent magnetic field B.

Consider a rectangular metallic frame PQRS in which the side PQ is free to move without friction.

Let the wire PQ is moved with a velocity ‘v’ in a perpendicular magnetic field B.

Magnetic flux in the loop Φ_B = Bl . x, where x = RQ a time changing quantity.

Here \(\frac{dx}{dt}\) = -v = Velocity of the rod.
Induced emf, ε = Blv is called Motional emf.

Question 2.
Current in a circuit falls from 5.0 A to 0.0 A in 0.1 s. If an average emf of 200 V induced, give an estimate of the self inductance of the circuit. [AP Mar. 14; TS Mar. 16]
Answer:
Initial current, I₁ = 5.0 A ;
Final current, I₂ = 0.0 A ;
Change in current, dl = I₁ – I₂ = 5 A
Time taken for the change, t = 0.1 s;
Average emf, ε = 200 V
For self-inductance (L) of the coil, we have the relation for average emf as

Hence, the self induction of the coil is 4H.

Question 3.
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil? [TS May ’18, Mar. ’17]
Answer:
Mutual inductance of a pair of coils, µ = 1.5 H;
Initial current, I₁ = 0 A
Final current I₂ = 20 A ;
Change in current, dl – I₂ – I₁ = 20 – 0 = 20 A
Time taken for the change, t = 0.5 s

Where dΦ is the change in the flux linkage with the coil.
Equating equations (1) and (2), we get
\(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = µ\(\frac{dI}{dt}\) ; dΦ = 1.5 × (20) = 30 Wb
Hence, the change in the flux linkage is 30 Wb.

Question 4.
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10^-4 T and the dip angle is 30°.
Answer:
Speed of the jet plane, v = 1800 km/h = 500 m/s ;
Wing span of jet plane, l = 25 m
Earth’s magnetic field strength,
B = 5.0 × 10^-4 T ; Angle of dip, δ = 30°

Vertical component of Earth’s magnetic field,
B_v = B sin δ = 5 × 10^-4 sin 30° = 2.5 × 10^-4T

Voltage difference between the ends of the wing can be calculated as
ε = (B_v) × l × v = 2.5 × 10^-4 × 25 × 500 = 3.125 V

Hence, the voltage difference developed between the ends of the wings is 3.125 V.

Here students can locate TS Inter 1st Year Chemistry Notes 7th Lesson Chemical Equilibrium and Acids-Bases to prepare for their exam.

TS Inter 1st Year Chemistry Notes 7th Lesson Chemical Equilibrium and Acids-Bases

→ The mixture of reactants and products in the equilibrium state is called an equilibrium mixture.

→ Reactions which proceed in one direction only are called irreversible reactions.

→ Reactions which proceed from reactants to products and also from products to reactants, simultaneously are called reversible reactions.

→ The state of a reversible reaction at which the rate of forward reaction is equal to the rate of backward reaction is called Equilibrium.

→ Chemical equilibrium is dynamic.

→ Increased concentration of reactants shifts the equilibrium position to products side and increased concentration of products shifts the equilibrium position to reactants side.

→ High temperature favours Exothermic reaction and low temperature favours Endothermic reaction.

→ A catalyst has no influence on the position of equilibrium. The catalyst is used to establish the equilibrium quickly.

→ For a general reaction aA + bB ⇌ cC + dD
K_c = \(\frac{[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}}}{[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}}\); K_p = \(\frac{P_C^c P_D^d}{P_A^a P_B^b}\)
K_p = K_c(RT)^Δn; Δn = (c + d) – (a + b)

→ For, H₂ + I₂ ⇌ 2HI; K_p = K_c
For, N₂ + 3H₂ ⇌ 2NH₃; K_p < K_c (∵ Δn = -2)
For, PCl₅ ⇌ PCl₃ + Cl₂; K_p > K_c (∵ Δn = 1)

→ Le Chatelier principle states that When a system at equilibrium was subjected to stress, the system shifts in such a way so as to undo the effect of the change.

→ According to Le Chatelier principle, High pressure and low temperature are favourable in Haber’s process and in Con-tact process.

→ Substances are classified into acids, bases and salts depending on their chemical behaviour and properties.

→ According to Bronsted theory proton donor is an acid and proton acceptor is a base.

→ An acid and a base which differ by a single proton are called conjugate acid-base pairs.

→ Leveling by water of all strong acids to the strength of H₃O⁺ and all strong bases to the strength of OH^– ions is called leveling effect of water.

→ According to Lewis electron pair acceptor is an acid and electron pair donor is a base.

→ The product of hydrogen ion (H⁺) and hydroxyl ion (OH^–) in pure water or in any aqueous solution is called ionic product of water.

→ The negative value of the logarithm of the hydrogen ion concentration is called pH.
A solution which resists the change in its pH value on dilution or on addition of small amounts of acid or base is called buffer solution.

→ The number of moles of acid or base requi-red to be added to the one litre of a buffer solution to register a change of one unit in the pH is called buffer capacity (Φ).

→ The substance which exhibits one colour in acidic medium and another colour in alkaline medium is known as acid-base indicator.

→ The interaction of anion or cation or both of a salt with water to form basic or acidic or neutral solution is known as salt hydrolysis.

→ The aqueous solutions of salts of weak acid and strong base are basic. The aqueous solutions of salts of weak base and strong acid are acidic.

→ The product of the concentrations of the cation and the anion in a saturated solution of a salt at room temperature is called solubility product (K_sp)
K_sp = [Mⁿ⁺][A^n-]

→ Relation between solubility product (K_sp) and solubility (s) is, S = \(\left[\frac{K_{S p}}{x^x y^y}\right]^{y_{x+y}}\)

→ The solubility of an electrolyte in water decreases on addition of an electrolyte which has one ion common with the electrolyte, is called common ion effect.

→ Common ion effect principle is used in the systematic qualitative analysis of cations.

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Theory of Equations Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Theory of Equations Important Questions Very Short Answer Type

Question 1.
Form the polynomial equation of the lowest degree whose roots are 1, – 1, 3. [May ’06]
Solution:
Let α = 1; β = – 1, γ = 3
The equation having roots α, β, γ is
(x – α) (x – β) (x – γ) = 0
⇒ (x – 1) (x + 1) ( x – 3) = 0
⇒ (x² – 1) (x – 3) = 0
⇒ x³ – 3x² – x + 3 = 0.

Question 2.
Form the polynomial equation of the lowest degree whose roots are 2 ± √3, 1 ± 2i. [May ’02, ’01]
Solution:
Let
α = 2 + √3, β = 2 – √3, γ = 1 + 2i, δ = 1 – 2i
The equation having α, β, γ, δ is
(x – α) (x – β) (x – γ) (x – δ) = 0
⇒ (x – 2 – √3) (x – 2 + √3) ((x – 1) – 2i) ((x – 1) + 2i) = 0
⇒ ((x – 2) – √3) ((x – 2) + √3) ((x – 1) – 2i) ((x – 1) + 2i) = 0
⇒ (x² + 4 – 4x – 3) (x² + 1 – 2x + 4) = 0
⇒ (x² – 4x + 1) (x² – 2x + 5) = 0
⇒ x⁴ + 5x² – 2x³ – 4x³ + 8x² – 20x + x² – 2x + 5 = 0
⇒ x⁴ – 6x³ + 14x² – 22x + 5 = 0

Question 3.
If 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0. then find α. [AP – Mar. ’18; TS – May 2016; May ’11]
Solution:
Given equation is x³ – 6x² + 9x – 4 = 0
Comparing this equation with ax³ + bx² + cx + d = 0
we get, a = 1; b = – 6; c = 9; d = – 4
Since 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0
then sum of the roots = s₁ = \(\frac{-b}{a}\)
⇒ 1 + 1 + α = \(\frac{-(-6)}{1}\) = 6
⇒ 2 + α = 6
⇒ α = 4.

Question 4.
If – 1, 2 and α are the roots of 2x³ + x² – 7x – 6 = 0, then find α.
[AP-Mar. 18; Mar. ’14, ’13, ’10, ’06, May’ 12, ’10]
Solution:
Given equation is 2x³ + x² – 7x – 6 = 0
Comparing this with ax³ + bx² + cx + d = 0 we get,
a = 2; b = 1; c = – 7; d = – 6
Since – 1, 2, α are the roots of 2x³ + x² – 7x – 6 = 0
The sum of the roots = s₁ = \(\frac{-b}{a}\)
– 1 + 2 + α = – \(\frac{1}{2}\)
1 + α = – \(\frac{1}{2}\)
⇒ α = – 1 – \(\frac{1}{2}\)
α = – \(\frac{3}{2}\)

Question 5.
If 1, – 2 and 3 are the roots of x³ – 2x² + ax + 6 = 0, then find ‘a’. [TS – May 2015; March ‘04]
Solution:
Given equation is x³ – 2x² + ax + 6 = 0
Since 1, – 2, 3 are the roots of x³ – 2x² + ax + 6
Now 1 is a root of given equation then
1³ – 2(1)² + a(1) + 6 = 0
⇒ 1 – 2 + a + 6 = 0
a + 5 = 0
a = – 5

Question 6.
If the product of the roots of 4x³ + 16x² – 9x – a = 0, is 9, then find ‘a’. [AP – Mar. 19, 17; TS – Mar. 16; May 13, 12, 08]
Solution:
Given equation is 4x³ + 16x² – 9x – a = 0
Comparing this equation with ax³ + bx² + cx + d = 0
we get, a = 4, b = 16, c = – 9, d = – a
Given that, the product of the roots = 9
s₃ = 9
⇒ \(\frac{-\mathrm{d}}{\mathrm{a}}\) = 9
⇒ \(\frac{-(-a)}{4}\) = 9
⇒ a = 36.

Question 7.
If α, β and 1 are the roots of x³ – 2x² – 5x + 6 = 0, then find α and β. [AP – May, Mar. 2016; May 09, March 08]
Solution:
Given equation is x³ – 2x² – 5x + 6 = 0
Comparing this equation with ax³ + bx² + cx + d = 0
we get a = 1, b = – 2, c = – 5, d = 6
Since α, β and 1 are the roots of x³ – 2x² – 5x + 6 = 0
then s₁ = α + β + 1
= \(\frac{-b}{a}=\frac{-(-2)}{1}\) = 2
⇒ α + β = 1 …………(i)
s₃ = αβ . 1 = \(\frac{-d}{a}\)
⇒ αβ = \(\frac{-6}{1}\) =
⇒ αβ = – 6
(α – β)² = (α + β)² – 4αβ
= 1 – 4 ( -6)
= 1 + 24 = 25
⇒ α – β = 5 ……………(2)
Solve (1) and (2);

Question 8.
If α, β and γ are the roots of x³ + 2x² + 3x – 4 = 0, then find α²β². [May ’07]
Solution:
Given equation is x³ + 2x² + 3x – 4 = 0
Since α, β and γ are the roots of x³ + 2x² + 3x – 4 = 0 then
α + β + γ = \(\frac{-(-2)}{1}\) = 2
αβ + βγ + γα = \(\frac{3}{1}\) = 3
αβγ = \(\frac{-(-4)}{1}\) = 4
Σα²β² = α²β² + β²γ² + γ²α²
= (αβ + βγ + γα)² – 2αβγ (α + β + γ)
= 3² – 2 . 4(2)
= 9 – 16 = – 7.

Question 9.
If α, β and γ are the roots of 4x³ – 6x² + 7x + 3 = 0, then find the value of αβ + βγ + γα. [TS – Mar. 2019]
Solution:
Given equation is 4x³ – 6x² + 7x + 3 = 0
Comparing this equation with ax³ + bx² + cx + d = 0
where a = 4; b = – 6; c = 7; d = 3
Since α, β, γ are the roots of 4x³ – 6x² + 7x + 3 = 0 then
αβ + βγ + γα = S₂ = \(\frac{c}{a}=\frac{7}{4}\).

Question 10.
Find the relations between the roots and the coefficients of the cubic equation 3x³ – 10x² + 7x + 10 = 0.
Solution:
Given cubic equation is 3x³ – 10x² + 7x + 10 = 0
Comparing this equation with
ax³ + bx² + cx + d = 0, we get
a = 3, b = – 10, c = 7, d = 10
Let α, β, γ be the roots of given equation
s₁ = \(\frac{-b}{a}\)
α + β + γ = \(\frac{-(-10)}{3}=\frac{10}{3}\)
s₂ = αβ + βγ + γα
= \(\frac{c}{a}=\frac{7}{3}\)
s₃ = αβγ
= \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-10}{3}\).

Question 11.
Write down the relations between the roots and the coefficients of the biquadratic equation x⁴ – 2x³ + 4x² + 6x – 21 = 0.
Solution:
Given biquadratic equation is
x⁴ – 2x³ + 4x² + 6x – 21 = 0 ……………… (1)
Comparing this equation with
ax⁴ + bx³ + cx² + dx + e = 0,
we get a = 1, b = – 2; c = 4; d = 6; e = – 21
Let α, β, γ, δ are the roots of equation (1) then
i) s₁ = α + β + γ + δ
= Σα = \(\frac{-b}{a}=\frac{-(-2)}{1}\) = 2
ii) s₂ = Σαβ
= \(\frac{c}{a}=\frac{4}{1}\) = 4
iii) s3 = Σαβγ
= \(\frac{-d}{a}=\frac{-6}{1}\) = – 6
iv) s = Σαβγδ
= \(\frac{\mathrm{e}}{\mathrm{a}}=\frac{-21}{1}\) = – 21

Question 12.
If 1, 2, 3 and 4 are the roots of x⁴ + ax³+ bx² + cx + d = 0, then find the values of a, b, c and d. [AP – May 2015]
Solution:
Given that the roots of the polynomial equation are 1, 2, 3 and 4.
Then(x – 1) (x – 2) (x – 3) (x – 4) = 0
(x² – 3x + 2) (x² – 7x + 12) = 0
x⁴ – 7x³ + 12x² – 3x³ + 21x² – 36x + 2x² – 14x + 24 = 0
x⁴ – 10x³ + 35x² – 50x + 24 = 0
Now, comparing this equation with
x⁴ + ax³ + bx² + cx + d = 0
we get a = – 10; b = 35; c = – 50; d = 24.

Question 13.
If a, b, c are the roots of x³ – px² + qx – r = 0 and r ≠ 0, then find \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\) in terms of p, q, r.
Solution:
Given equation is x³ – px² + qx – r = 0
Since a, b and c are the roots of the equation x³ – px² + qx – r = 0 then
s₁ = a + b + c
= \(\frac{-(-p)}{1}\) = p;
s₂ = ab + bc + ca
= \(\frac{q}{1}\) = q;
s₃ = abc
= \(\frac{-(-r)}{1}\) = r
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=\frac{b^2 c^2+a^2 c^2+a^2 b^2}{a^2 b^2 c^2}\)
= \(\frac{(a b+b c+c a)^2-2 a b c(a+b+c)}{(a b c)^2}\)
= \(\frac{q^2-2 p \cdot r}{r^2}=\frac{q^2-2 p r}{r^2}\).

Question 14.
Find the sum of the squares and the sum of the cubes of the roots of the equation x³ – px² + qx – r = o in terms of p, q, r.
Solution:
Given equation is x³ – px² + qx – r = 0
Let α, β, γ are the roots of the equation x³ – px² + qx – r = 0 then
s₁ = α + β + γ
= \(\frac{-\mathrm{b}}{\mathrm{a}}=\frac{-(-\dot{\mathrm{p}})}{1}\) = p;
s₂ = αβ + βγ + γα
= \(\frac{q}{1}\) = q;
s₃ = αβγ
= \(\frac{-(-r)}{1}\) = r
i) The sum of the squares of the roots of the equation = α² + β² + γ²
= (α + β + γ)² – 2(αβ + βγ + γα)
= p² – 2q
ii) The sum of the cubes of the roots is α³ + β³ + γ³ = (α + β + γ)
(α² + β² + γ² – αβ – βγ – γα) + 3αβγ
= p(p² – 2q – q) + 3r
= p³ – 3pq + 3r.

Question 15.
Let α, β, γ be the roots of x³ + px² + qx + r = 0. Then find Σα³. [March ’03]
Solution:
Given equation is x³ + px² + qx + r = 0
Since α, β, γ are the roots of the equation x³ + px² + qx + r = 0 then
s₁ = α + β + γ
= \(\frac{-\mathrm{p}}{1}\) = – p;
s₂ = αβ + βγ + γα
= \(\frac{q}{1}\) = q;
s₃ = αβγ
= \(\frac{-r}{1}\) = – r
Σα³ = α³ + β³ + γ³
= (α + β + γ) (α² + β² + γ² – αβ – βγ – γα) + 3αβγ
= (- p) ((p² – 2q) – (q)) + 3 (- r)
= – p (p² – 3q) – 3r
= – p³ + 3pq – 3r

Question 16.
Find s₁, s₂, s₃ and s₄ for the equation x⁴ – 16x³ + 86x² – 176x + 105 = 0.
Solution:
Given equation is x⁴ – 16x³ + 86x² – 176x + 105 = 0
Comparing this equation with ax⁴ + bx³ + cx² + dx + e = 0
we get a = 1; b = – 16; c = 86; d = – 176; e = 105
Now, s₁ = \(=\frac{-b}{a}=\frac{-(-16)}{1}\) = 16;
s₂ = \(\frac{c}{\mathrm{a}}=\frac{86}{1}\) = 86;
s₃ = \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-(-176)}{1}\) = 176;
s₄ = \(\frac{\mathrm{e}}{\mathrm{a}}=\frac{105}{1}\) = 105

Question 17.
Find the algebraic equation whose roots are 2 times the roots of x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0. [Board Paper]
Solution:
Let f(x) = x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0
∴ Required equation is f(\(\frac{x}{2}\)) = 0
⇒ \(\frac{x^5}{32}-\frac{2 x^4}{16}+\frac{3 x^3}{8}-\frac{2 x^2}{4}+\frac{4 x}{2}+3\) = 0
⇒ x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0

Question 18.
Find the transformed equation whose roots are the negatives of the roots of x⁷ + 3x⁵ + x³ – x² + 7x + 2 = 0.
Solution:
Let f(x) = x⁷ + 3x⁵ + x³ – x² + 7x + 2 = 0
Required equation is f(- x) = 0
(- x)⁷ + 3(- x)⁵ + (- x)³ – (- x)² + 7(- x) + 2 = 0
x⁷ + 3x⁵ + x³ + x² + 7x – 2 = 0

Question 19.
Find the polynomial equation whose roots are the reciprocals of the roots of x⁴ – 3x³ + 7x² + 5x – 2 = 0. [March ’11] [TS – Mar. 2015]
Solution:
Let f(x) = x⁴ – 3x³ + 7x² + 5x – 2 = 0
The required equation is f(\(\frac{1}{x}\)) = 0
⇒ \(\frac{1}{x^4}-\frac{3}{x^3}+\frac{7}{x^2}+\frac{5}{x}-2\) = 0
⇒ 1 – 3x + 7x² + 5x³ – 2x⁴ = 0
⇒ 2x⁴ – 5x³ – 7x² + 3x – 1 = 0

Question 20.
Form the polynomial equation whose roots are the squares of the roots of x³ + 3x² – 7x + 6 = 0. [May ’02]
Solution:
Let f(x) = x³ + 3x² – 7x + 6 = 0
The required equation is f(√x) = 0
(√x)³ + 3 (√x)² – 7√x +6 = 0
⇒ x√x + 3x – 7√x + 6 = 0
⇒ 3x + 6 = – √x (x – 7)
Squaring on both sides
9x² + 36 + 36x = x (x² + 49 – 14x)
= x³ + 49x – 14x²
x³ – 23x² + 13x – 36 = 0.

Question 21.
Form the polynomial equation whose roots are the cubes of the roots of x³ + 3x² + 2 = 0.
Solution:
Let f(x) = x³ + 3x² + 2 = 0
The required equation is f(\(\sqrt[3]{x}\))= 0
\((\sqrt[3]{x})^3+3(\sqrt[3]{x})^2\) + 2 = 0
⇒ x + 3 . x^2/3 + 2 = 0
x + 2 = – 3x^2/3
Cubing on both sides (x + 2)³ = – 27x²
⇒ x³ + 8 + 6x² + 12x + 8 = – 27x²
x³ + 33x² + 12x + 8 = 0

Question 22.
If α, β, γ are the roots of x³ + px² + qx + r = 0 then find
i) Σα²
ii) Σα³
iii) Σ \(\frac{1}{\alpha}\)
Solution:
Given equation is x³ + px² + qx + r = 0
Since α, β, γ are the roots of the equation x³ + px² + qx + r = 0 then
s₁ = α + β + γ = \(\frac{-\mathrm{p}}{1}\) = – p;
s₂ = αβ + βγ + γα = \(\frac{q}{1}\) = q;
s₃ = αβγ = \(\frac{-r}{1}\) = – r.

i) Σα² = α² + β² + γ²
= (α + β + γ)² – 2(αβ + βγ + γα)
= (- p)² – 2(q)
= p² – 2q

ii) Σα³ = α³ + β³ + γ³
= (α + β + γ) (α² + β² + γ² – αβ – βγ – γα) + 3αβγ
= (- p) ((p² – 2q) – (+ q)) + 3(- r)
= – p (p² – 2q – q) – 3r
= – p³ + 3pq – 3r

iii) \(\Sigma \frac{1}{\alpha}=\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}\)
= \(\frac{\beta \gamma+\alpha \gamma+\alpha \beta}{\alpha \beta \gamma}=\frac{q}{-r}=\frac{-q}{r}\)

Question 23.
Form the polynomial equation of the lowest degree with roots as 0, 0, 2, 2, – 2, – 2.
Solution:
The polynomial equation whose roots are 0, 0, 2, 2, – 2, – 2 is
(x – 0) (x – 0) (x – 2) (x – 2) (x + 2) (x + 2) = 0
⇒ x² (x – 2)² (x + 2)² = 0
⇒ x² (x² + 4 – 4x) (x² + 4 + 4x) = 0
⇒ x² [(x² + 4)² – (4x)²] = 0
⇒ x² (x⁴ + 16 + 8x² – 16x²) = 0
⇒ x² (x⁴ – 8x² + 16) = 0
⇒ x⁶ – 8x⁴ + 16x² = 0.

Question 24.
Form the monic polynomial equation of degree 3 whose roots are 2, 3 and 6. [May ’14, March ’02]
Solution:
x³ – 11x² + 36x – 36 = 0

Question 25.
Form the monic polynomial equation of degree 4 whose roots are 4 + √3, 4 – √3, 2 + i and 2 – i.
Solution:
x⁴ – 12x³ + 50x² – 92x + 65 = 0

Question 26.
Find s₁, s₂, s₃ and s₄ for the equation 8x⁴ – 2x³ – 27x² – 6x + 9 = 0.
Solution:
s₁ = \(\frac{1}{4}\),
s₂ = \(\frac{-27}{8}\),
s₃ = \(\frac{3}{4}\),
s₄ = \(\frac{9}{8}\)

Question 27.
Find the algebraic equation whose roots are 3 times the roots of x³ + 2x² – 4x + 1 = 0.
Solution:
x³ + 6x² – 36x + 27 = 0

Question 28.
Find an algebraic equation of degree 4 whose roots are 3 times the roots of the equation 6x⁴ – 7x³ + 8x² – 7x + 2 = 0. [March ’09]
Solution:
6x⁴ – 21x³ + 72x² – 189x + 162 = 0.

Question 29.
Find the transformed equation whose roots are the negatives of the roots of x⁴ + 5x³ + 11x + 3 = 0. [AP – Mar. 2015]
Solution:
x⁴ – 5x³ – 11x + 3 = 0

Question 30.
Find the polynomial equation of degree 4 whose roots are the negatives of the roots of x⁴ – 6x³ + 7x² – 2x + 1 = 0.
Solution:
x⁴ + 6x³ + 7x² + 2x + 1 = 0

Question 31.
Find the polynomial equation whose roots are the reciprocals of the roots of x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0.
Solution:
6x⁵ – 13x⁴ + 4x³ + x² + 11x + 1 = 0

Question 32.
Find the polynomial equation whose roots are the reciprocals of the roots of the equation x⁴ + 3x³ – 6x² + 2x – 4 = 0.
Solution:
4x⁴ – 2x³ + 6x² – 3x – 1 = 0

Question 33.
Find the polynomial equation whose roots are the squares of the roots of x⁴ + x³ + 2x² + x + 1 = 0.
Solution:
x⁴ + 3x³ + 4x² + 3x + 1 = 0

Question 34.
Find the polynomial equation whose roots are the squares of the roots of x³ – x² + 8x – 6 = 0.
Solution:
x³ + 15x² + 52x – 36 = 0

Telangana TSBIE TS Inter 2nd Year Physics Study Material 8th Lesson Magnetism and Matter Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 8th Lesson Magnetism and Matter

Very Short Answer Type Questions

Question 1.
A magnetic dipole placed in a magnetic field experiences a net force. What can you say about the nature of the magnetic field?
Answer:
For a magnetic dipole placed in a magnetic field, some net force is experienced It implies that force on the two poles of dipole is not equal.

This will happen only when magnetic dipole is in non-uniform magnetic field.

Question 2.
There is no question in text book. [TS Mar. 19, 17, May 14]
Question 3.
What happens to compass needles at the Earth’s poles? [TS Mar. 19, 17, May 14]
Answer:
When a compass is taken to earth poles say north pole then south pole of compass will adhere to north pole. It will align it self along magnetic meridian line.

Similarly when it is taken to south pole then north pole of compass is attracted by south pole and it will align itself along magnetic meridian line.

Question 4.
What do you understand by the ‘magnetisation’ of a sample?
Answer:
Magnetisation (T) :
It is the ratio of magnetic moment per unit volume.

I = (\(\frac{M}{V}\)) where M = the magnetic moments and V = volume of the given material.

Magnetic intensity is a vector, dimensions L^-1 A.
Unit : Ampere/metre : Am^-1

Question 5.
What is the magnetic moment associated with a solenoid?
Answer:
Magnetic moment associated with a solenoid (M) = nIA. Where
n = Number of turns in solenoid;
I = Current through it;
A = Area vector

Question 6.
What are the units of magnetic moment, magnetic induction and magnetic field? [AP Mar. 16. May 17, 16; TS Mar. 16]
Answer:
1. Magnetic moment m is a vector. Unit A-m², dimensions L^-2 A.
2. Magnetic induction (B) and magnetic field (B) are used with same meaning. Magnetic induction B is a vector.
Unit: Tesla (T), Dimension : MT^-2A^-1.

Question 7.
Magnetic lines form continuous closed loops. Why? [AP Mar. ’19, ’16, May ’18; TS May ’18, Mar. ’17]
Answer:
In magnetism magnetic monopole (single pole) is not existing. The simple possible way is to take a magnetic dipole. So the path a free magnetic needle or compass starts from north pole and terminates at south pole forms a loop.

Hence magnetic field lines are always closed loops.

Question 8.
Define magnetic declination. [TS Mar. 18, May 18, 17, 16; AP Mar. 18, 14, May 17, 16]
Answer:
Magnetic declination (D) :
The magnetic meridian at a place makes some angle (D) with true geographic north and south direction.

The angle between true geographic north to the north shown by magnetic compass is called “magnetic declination or simply declinations (D).”

Question 9.
Define magnetic inclination or angle of dip. [AP Mar. ’17, ’15; TS Mar. ’15]
Answer:
Magnetic inclination or angle of dip (I) :
It is the angle of total magnetic field BE at a given place with the surface of earth.
(OR)
The angle between horizontal to earth’s surface and net magnetic field of earth BE at that point.

Question 10.
Classify the following materials with regard to magnetism: Manganese, Cobalt, Nickel, Bismuth, Oxygen, Copper. [AP Mar. 19. 18. 17, 16, 15; TS Mar. 16. 15]
Answer:
Manganese : Paramagnetic substance
Cobalt : Ferromagnetic substance
Nickel : Ferromagnetic substance
Bismuth : Diamagnetic substance
Oxygen : Paramagnetic substance
Copper : Diamagnetic substance

Question 11.
In the magnetic meridian of a certain place, the horizontal component of the earth’s magnetic field is 0.26 G and the dip angle is 60°. What Is the magnetic field of the earth at this location?
Answer:
Given HE = 0.26 G; Dip angle = 60
But Dip angle = \(\frac{H_E}{B_E}\) = cos θ ⇒ B_E = H_E cos θ
∴ Magnetic field of earth = 0.26 × cos 60° = 2 × 0.26 = 0.52 G

Question 12.
Define Magnetisation of a sample. What is its SI unit?
Answer:
Magnetisation (I) : It is the ratio of net magnetic moment per unit volume.
I = \(\frac{m_{net}}{V}\) where m_net = the vectorial sum of magnetic moments of atoms in bulk material and V is volume of the given material.
Magnetic intensity is a vector, dimensions L^-1 A.
Unit: Ampere/metre : A m^-1.

Question 13.
Define Magnetic susceptibility. Mention its unit. [AP Mar. ’15]
Answer:
Magnetic susceptibility (χ) :
It is a measure for the response of magnetic materials to an external field.

It is a dimensionless quantity.

Short Answer Questions

Question 1.
What are Ferromagnetic materials? Give examples. What happens to a ferromagnetic material at Curie temperature?
Answer:
Ferromagnetism:

1. These substances are strongly attracted by magnets.
2. The susceptibility (χ) is +ve and very large.
3. Individual atoms of these substances will spontaneously align in a common direction over a small volume called domain.
4. Size of domain is nearly 1 mm³ or a domain may contain nearly 10¹¹ atoms.
5. In these substances, magnetic field lines are very crowded.
6. Every ferromagnetic substance will transform into paramagnetic substance at a temperature called Curie Temperature (T_c).
   Ex: Manganese, Iron, Cobalt, Nickel etc.

Effect of temperature on Ferromagnetic substances :
When ferromagnetic substances are heated upto Curie temperature, they will be converted into paramagnetic substances.

Question 2.
Derive an expression for the axial field of a solenoid of radius “r”, containing “n” turns per unit length and carrying current “I”.
Answer:
The behaviour of a magnetic dipole and a current carrying solenoid are similar.

Let a solenoid of radius ‘a’ and length 2l contains n turns and a current ‘I’ is passed through it.

Magnetic moment of solenoid (M) = nlA.

Consider a circular element of thickness dx of solenoid at a distance x from its centre. Choose any point ‘P’ on the axis of solenoid at a distance ‘r’ from centre of the axis.

Magnetic field at point P

This is similar to magnetic field at any point on the axial line of magnetic dipole.

Question 3.
The force between two magnet poles separated by a distance ‘d’ in air is ‘F. At what distance between them does the force become doubled?
Answer:
Force between two magnetic poles F = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m_1m_2}}{\mathrm{d^2}}\)


When separation between the poles is reduced by √2 times their force between them is doubled.

Question 4.
Compare the properties of para, dia and ferromagnetic substances. [TS & AP June ’15]
Answer:

Question 5.
Explain the elements of the Earth’s magnetic field and draw a sketch showing the relationship between the vertical component, horizontal component and angle of dip.
Answer:
Earth’s magnetism :
The magnetic field of earth is believed to arise due to electrical currents produced by convective motion of metallic fluids in outer core of earth. This effect is also known as the “dynamo effect”.

• The magnetic north pole of earth is at a latitude of 79.74° N and at a longitude of 71.8° W. It is some where in North Canada.
• The magnetic south pole of earth is at 79.74° S and 108.22° E in the Antarctica.

Magnetic declination (D) :
The angle between true geographic north to the mag-netic north shown by magnetic compass is called “magnetic declination or simply declination (D).”

Angle of dip or inclination (I):
The angle of dip is the angle of total magnetic field BE at a given place with the surface of earth.

At a given place horizontal component of earth’s magnetic field H_E = B_E cos I.

Vertical component of earth’s magnetic field Z_E = B_E sin I.

Tangent of dip tan I = \(\frac{Z_E}{H_E}\)

Question 6.
Define retentivity and coercivity. Draw the hysteresis curve for soft iron and steel. What do you infer from these curves?
Answer:
Hysteresis loop :
Magnetic hysteresis loop a graph between magnetic field (B) and magnetic intensity (H) of a ferromagnetic substance. It is as shown in figure.

i) When applied magnetic field B is gradually increased then magnetic intensity in the material will also gradually increases and reaches a saturation point a’. It indicates that all atomic magnets of the sample are parallel to applied field.

ii) When applied magnetic field is gradually decreased to zero still then some magnetic intensity will remain in the material.

Retentivity or Remanence :
The magnetic intensity (H) of a material at applied magnetic field B – 0 is called “retentivity”. In hysteresis loop value of H on +ve Y-axis i.e., at B = 0 gives retentivity.

iii) When applied magnetic field (B) is reversed then magnetic intensity of the sample gradually decreases and finally it is magnetised in opposite direction upto saturation say point’d’.

Coercivity :
The -ve value of magnetic field (B^applied (i.e., in opposite direction of mag netisation) at which the magnetic intensity (H) inside the sample is zero is called “coer-civity”.

In hysteresis diagram the-value of B on -ve X-axis gives coercivity.

iv) When direction of magnetic field is reversed and gradually increased again we can reach the point of saturation a’.

Area of hysteresis loop is large for ferromagnetic substances with high permeability value.

Question 7.
If B is the magnetic field produced at the centre of adrcular coil of one turn of length L carrying current I then what is the manetic field at the centre of the same coil which is made into 10 turns?
Answer:
One turn coil means it is a circular loop.

For 1^st Case:
Magnetic field at the centre of a loop B₁ = \(\frac{\mu_0}{2} \frac{\mathrm{I}}{\mathrm{r_1}}\)
Given that length of the wire = L.

For 2^nd Case :
Given wire is made into a coil of 10 turns ⇒ n = 10
∴ 2πr₂10 = L ⇒ r₂ = \(\frac{L}{2 \pi}.\frac{1}{10}\)
For a coil of n turns magnetic field at its centre B₂ = \(\frac{\mu_0}{2} \frac{\mathrm{nI}}{\mathrm{r_2}}\)


When same length of wire is made into a coil of n turns then B₂ at centre = n² times previous value B₁.
⇒ B₂ = n² B₁ for given current T.

Question 8.
If the number of turns of a solenoid is doubled, keeping the other factors constant, how does the magnetic held at the axis of the solenoid change?
Answer:
A solenoid will produce almost uniform magnetic field (B) along its axis.

Magnetic field along the axis of a solenoid B = µ₀nI.

Where n is number of turns per unit length.
In our case number of turns of a solenoid is doubled keeping others as constant i.e., length of solenoid L is not changed and permeability p0, and current T not changed. So new number of turns n₂ = 2n₁.
∴ New magnetic field at the same given point B₂ = µ₀n₂I.
But n₂ = 2n₁; ∴ B₂ = µ₀2n₁I = 2B₁

When number of turns of a solenoid is doubled then magnetic field at the given point on the axis of solenoid will also double.

Long Answer Questions

Question 1.
Derive an expression for the magnetic field at a point on the axis of a current carrying circular loop.
Answer:
Consider a circular loop of radius R’ carrying a steady current i. Consider any point P’ on the axis of the coil (say X – axis).

From Biot – Savart’s law magnetic field at

The magnetic field at ‘P’ makes some angle ‘θ’ with X – axis. So resolve \(\mathrm{d} \bar{B}\) into components \(\mathrm{d} \bar{B}_x\) and \(\mathrm{d} \bar{B}\)⊥. Sum of \(\mathrm{d} \bar{B}\)⊥ is zero. Because \(\mathrm{d} \bar{B}\)⊥ component by an element d/ is cancelled by another diametrically opposite component. From fig \(\mathrm{d} \bar{B}_x\) = dB. cos θ. Where

Total magnetic field due to all elements on the circular loop

Question 2.
Prove that a bar magnet and a solenoid produce similar fields. (IMP)
Answer:
Magnetic field lines suggest that the behaviour of a current-carrying solenoid and a bar magnet are similar.

When a bar magnet is cut into two parts it will behave like two weak bar magnets. Similarly when a solenoid is cut into two parts and current is circulated through them they will also act as two solenoids of weak magnetic properties. Analogy between solenoid and bar magnet.

Let a solenoid of radius ‘a’ and length 2l contains n turns and a current ‘I’ is passed through it.

Magnetic moment of solenoid M = nlA.
Consider a circular element of thickness dx of solenoid at a distance x from its centre. Choose any point ‘P’ on the axis of solenoid at a distance r from centre of the axis.

∴ Total magnetic field B is obtained by integrating dB with in the limits -1 to 1.

This value is similar to magnetic field at any point on the axial line of magnetic dipole. Thus, a bar magnet and a solenoid produce ! similar magnetic fields.

Question 3.
A small magnetic needle is set into oscillations in a magnetic field B. Obtain an expression for the time period of oscillation.
Answer:
Let a small compass of magnetic moment m and moment of inertia ‘I’ is placed in a uniform magnetic field ’B’.
Let the compass is set into oscillation in a horizontal plane.
Torque on the needle is τ = MB sin θ.
Where 0 angle between M and B.
At equilibrium the magnitude of deflecting torque and restoring torque are equal.
∴ Restoring torque τ = I\(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) = – MB sin θ.
– ve sign indicates that restoring torque is in opposite direction of deflecting torque.
θ is small; sin θ = θ.

Magnetic needle in a uniform field

From principles of angular.
Simple harmonic motion \(\frac{MB}{I}\) = ω²
⇒ ω = \(\sqrt{\frac{MB}{I}}\)

∴ Time period of oscillation of a magnetic needle placed in a magnetic field T = 2π\(\sqrt{\frac{I}{MB}}\)
and magnetic field at that point B = 4π²\(\frac{I}{MT^2}\).

Question 4.
A bar magnet, held horizontally, is set into angular oscillations in the Earth’s magnetic field. It has time periods T₁ and T₂ at two places, where the angles of dip are θ₁ and θ₂ respectively. Deduce an expression for the ratio of the resultant magnetic fields at the two places.
Answer:
Let a bar magnet is held horizontally at a given place where earth’s magnetic field is B_B. When it is set into vibration in a horizontal plane it will oscillate with a time period T = 2π\(\sqrt{\frac{I}{MH_E}}\) ……….. (1)

Where H_E is horizontal component of earth’s magnetic field.

The relation between resultant magnetic field B_E, horizontal magnetic field H_E and angle of dip or inclination ‘I’ of earth’s magnetic field is H_E = B_E cos I. — (2)
Given at place ‘1’ angle of dip = θ₁
Given at place ‘2’ angle of dip = θ₂.

Question 5.
Define magnetic susceptibility of a material. Name two elements one having positive susceptibility and other having negative susceptibility. [AP Mar. ’15]
Answer:
Susceptibility χ :
The ratio of magnetisation of a sample (I) to the magnetic intensity (H) is called “susceptibility”.
Susceptibility χ = \(\frac{I}{H}\)
It is a dimensionless quantity.
It is a measure of how a magnetic material responds to external magnetic field.

For ferromagnetic materials susceptibility is +ve and χ >> 1 and χ is nearly in the order of 1000.
Ex: Iron, Cobalt, Nickel.
For paramagnetic substances χ is positive and nearly equals to one (χ ≅ 1).
Ex : Calcium, Aluminium, Platinum.

For diamagnetic substances χ is small and negative, magnetisation M and magnetic intensity H are in opposite direction.
Ex : Bismuth, Copper, Mercury, Gold.

Question 6.
Obtain Gauss’ Law for magnetism and explain it.
Answer:
Gauss Law in magnetism: Gauss law states that the net magnetic flux through any closed loop is zero.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{ds}}=0\)
Explanation :
Consider Gaussian surface I & II as shown in figure. In both cases the number of magnetic field lines entering the surface is equal to number of magnetic field lines leaving the surface.

The net magnetic flux is zero for both surfaces. This law is true for any surface of any shape. Consider an irregular Gaussian surface as shown in figure. Consider a smdl vector area element ∆S of closed surface ‘S’ placed in a Φ magnetic field B. Flux through ∆s is say ∆Φ.

When applied magnetic field B is gradually increased then magnetic intensity in the material will also gradually increases and reaches a saturation point ‘a’. It indicates that all atomic magnets of the sample are parallel to applied field.

Now flux (i.e., Number of magnetic field lines through unit area) through the element ∆S is given by ∆Φ_B = B . ∆S.

Let us divided the total Gaussian surface ‘S’ into number of small areas ∆S₁, ∆S₂, ∆S₃, ………… ∆S_n.

The total flux through the Gaussian surface

Where all’ term includes surface area of all surface elements ∆S₁, ∆S₂, ………… ∆S_n.

Magnetic monopole is not existing so there is no source or sinks of B’ in Gaussian surface. The simplest possible source is magnetic dipole i.e., bar magnet. Magnetic field lines of a bar magnet are closed curves of loops. So all the lines entering the Gaussian surface must leave from it.

Hence net magnetic flux through a closed surface is zero.

Question 7.
What do you understand by “hysteresis”? How does this property influence the choice of materials used in different appliances where electromagnets are used?
Answer:
Hysteresis loop :
Magnetic hysteresis loop is a graph between magnetic field (B) and magnetic intensity (H) of a ferromagnetic substance. It is as shown in figure.
i) When applied magnetic field B is gradually increased then magnetic intensity in the material will also gradually increases and reaches a saturation point ‘a’. It indicates that all atomic magnets of the sample are parallel to applied field.

ii) When applied magnetic field is gradually decreased to zero still then some magnetic intensity will remain in the material.

Retentivity or Remanence :
The magnetic intensity (H) of a material at applied magnetic field B = 0 is called “retentivity”. In hysteresis loop value of H on +ve Y-axis i.e., at B = 0 gives retentivity.

iii) When applied magnetic field (B) is reversed then magnetic intensity of the sample gradually decreases and finally it is magnetised in opposite direction upto saturation say point d’.

Coercivity :
The -ve value of magnetic field (B) applied (i.e., in opposite direction of magnetisation) at which the magnetic inten-sity (H) inside the sample is zero is called “coercivity”.

In hysteresis diagram the value of B on -ve X-axis gives coercivity.

iv) When direction of magnetic field is reversed and gradually increased again we can reach the point of saturation a’. Area of hysteresis loop is large for ferromagnetic substances with high permeability value.

Application of hysteresis in electromagnets. Hysteresis curve allows us to select suitable materials for permanent magnets and for electromagnets.

For materials to use as permanent magnets they must have high retentivity and high coercivity.

For electromagnets ferromagnetic substances of high permeability and low retentivity are used because when current is switched off it must loose magnetic properties quickly.

In case of transformers and telephone diaphragms they are subjected to prolonged AC cycles. For these applications the hysteresis curve of ferromagnetic materials must be narrow.

In this way hysteresis loop helps us to select magnetic materials for various applications.

Problems

Question 1.
What is the torque acting on a plane coil of “n” turns carrying a current “i” and having an area A, when placed in a constant magnetic field B?
Solution:
Number of turns = n ; Current = i;
Area of coil = A; Magnetic field = B.
Torque on a current carrying coil in a magnetic field τ = ni (\(\overline{\mathrm{A}}\times\overline{\mathrm{B}}\)) = niAB sin θ.

Question 2.
Acoilof 20 turns has an area of 800 mm² and carries a current of 0.5 A. If it is placed in a magnetic field of intensity 0.3 T with its plane parallel to the field, what is the torque that it experiences?
Solution:
Number of turns n = 200; Current i = 0.5 A;
Area A = 800 mm² = 800 × 10^-6 m² (∵ 1 mm² = 10^-6 m²) ;
Magnetic field B = 0.3 T.
Area of coil parallel to the field ⇒ Angle between area vector \(\overline{\mathrm{A}}\) and magnetic filed \(\overline{\mathrm{B}}\) =90°. Since area vector \(\overline{\mathrm{A}}\) is perpendicular to area of the coil.
∴ τ = niBA = 200 × 0.5 × 0.3 × 800 × 10^-6
= 3 × 800 × 10^-6 = 2.4 × 10^-3 N-m.

Question 3.
In the Bohr atom model the electrons move around the nucleus in circular orbits. Obtain an expression for the magnetic moment (µ) of the electron in a Hydrogen atom in terms of its angular momentum L.
Solution:
Charge of electron = e ;
Angular momentum = L;
Mass of electron = m_e;
Magnetic moment of electron = µ = ?
When electron revolves in orbit current i = \(\frac{e}{T}\) ; Where time period T = 2π \(\frac{r}{υ}\)
∴ Current i = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}}\)
Magnetic moment of electron in orbit µ = iA

But m_e υr = L
∴ Magnetic moment of electron in orbit
µ = \(\frac{e}{2m_e}\)L

Question 4.
A solenoid of length 22.5 cm has a total of 900 turns and carries a current of 0.8 A. What is the magnetising field H near the centre and far away from the ends of the solenoid?
Solution:
Length of solenoid l = 22.5 cm = 22.5 × 10^-2m
Number of turns N = 900; Current I = 0.8 A.
a) Magnetising field near the centre H = ?
The behaviour of a solenoid is equal to that of a bar magnet.
Magnetic field due to a solenoid B = µ₀nI.
Magnetising field H = \(\frac{B}{\mu_0}\) = nI.
Where n = Nil.
∴ H = \(\frac{900}{22.5 \times 10^-2}\) × 0.8 = 3200 Am^-1.
A solenoid will give a uniform magnetic field along its axis.
Magnetising field far away from ends = 3200 Am^-1.

Question 5.
A bar magnet of length 0.1 m and with a magnetic moment of 5 Am² is placed in a uniform magnetic field of intensity 0.4 T, with its axis making an angle of 60° with the field. What is the torque on the magnet? [Mar. ’14]
Solution:
Length of bar magnet l = 0.1 m.;
Magnetic moment m = 5 Am².
Magnetic field B = 0.4 T ;
Angle with field θ = 60°.
Torque on the magnet τ = mB sin θ.
= 5 × 0.4 × sin 60°
= 5 × 0.4 × 0.8660 = 1.732 N-m.

Question 6.
If the Earth’s magnetic field at the equator is about 4 × 10^-5 T, what is its approximate magnetic dipole moment? (radius ofi Earth = 6.4 × 10⁶ m)
Solution:
Radius of earth r = 6.4 × 10⁶ m ; Magnetic field near equator B = 4 × 10^-5 T
Magnetic dipolemoment of earth = M.

Question 7.
The horizontal component of the earth’s magnetic field at a certain place is 2.6 × 10^-5 T and the angle of dip is 60°. What is the magnetic field of the earth at this location?
Solution:
Horizontal component of earth’s magnetic field HE = 2.6 × 10^-5 T

Angle of dip ‘I’ = 60°.
Earth’s magnetic field B_E = ?
Angle between B_E and H_E is called dip angle ‘I’.
H_E = B_E = cos θ ⇒ B_E = H_E/cos θ = 2.6 × 10^-5/ cos 60°
∴ B_E = 2.6 × 10^-5/ (0.5) = 5.2 × 10^-5T.

Question 8.
A solenoid, of insulated wire, is wound on a core with relative permeability 400. If the number of turns per metre is 1000 and the solenoid carries a current of 2A, calculate H, B and the magnetisation M.
Solution:
Relative permeability µ_r = 400 ;
Current I = 2A;
Number of turns / metre = n = 1000.
Magnetising force H = nl = 1000 × 2 = 2000 Am^-1.
Magnetic field along axis of solenoid B = ?
When solenoid is on a magnetic material B
= µ_r nl = 400 × 1000 × 2 = 8 × 10⁵ Am^-1

Intext Questions and Answer

Question 1.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 × 10^-2 J. What is the magnitude of magnetic moment of the magnet?
Solution:
Magnetic field strength, B = 0.25 T; Torque on the bar magnet, τ = 4.5 × 10^-2 J
Angle between the bar magnet and the external magnetic field, θ = 30°
Torque is related to magnetic moment (M) as : τ = MB sin θ

Hence, the magnetic moment of the magnet is 0.36 J T^-1.

Question 2.
A short bar magnet of magnetic moment m = 0.32 J T^-1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Solution:
Moment of the bar magnet, M = 0.32 J T^-1 ;
External magnetic field, B = 0.15 T
a) The bar magnet is aligned along the magnetic field. This system is considered as being instable equilibrium. Hence, the angle 0, between the bar magnet and the magnetic field is 0°.
Potential energy of the system
= -MB cos θ
= – 0.32 × 0.15 cos 0° = – 4.8 × 10^-2 J

b) The bar magnet is oriented 180° to the magnetic field. Hence, it is in unstable equilibrium.
Potential energy = – MB cos θ ;
where θ = 180°
= -0.32 × 0.15 cos 180° = 4.8 × 10^-2 J.

Question 3.
A closely wound solenoid of800 turns and area of cross-section 2.5 × 10^-4 m² carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
Solution:
Number of turns in the solenoid, n = 800 ;
Area of cross-section, A = 2.5 × 10^-4 m²
Current in the solenoid, I = 3.0 A
A current-carrying solenoid behaves as a bar magnet because a magnetic field develops along its axis, i.e., along its length. The magnetic moment associated with the given current-carrying solenoid is calculated as :
M = nIA = 800 × 3 × 2.5 × 10^-4 = 0.6 J T^-1.

Question 4.
If the solenoid in exercise 8.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30° with the direction of applied field?
Solution:
Magnetic field strength, B = 0.25 T ;
Magnetic moment, M = 0.6 T^-1
The angle θ, between the axis of the solenoid and the direction of the applied field is 30°.
Therefore, the torque acting on the solenoid is given as : τ = MB sin θ
τ = 0.6 × 0.25 sin 30° = 7.5 × 10^-2 J.

Question 5.
A bar magnet of magnetic moment 1.5 JT^-1 lies aligned with the direction of a uniform magnetic field of 0.22 T.
a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment : (i) normal to die field direction, (ii) opposite to the field direction?
b) What is the torque on the magnet in cases (i) and (ii)?
Solution:
a) Magnetic moment, M = 1.5 J T^-1 ;
Magnetic field strength, B = 0.22 T

i) Initial angle between the axis and the magnetic field, θ₁ = 0°.
Final angle between the axis and the magnetic field, θ₂ = 90°.
The work required to make the magnetic moment normal to the direction of magnetic field is given as :
W = -MB (cos θ₂ – cos θ₁)
∴ B = -1.5 × 0.22 (cos 90° – cos 0°)
= -0.33 (0 – 1) = 0.33 J.

ii) Initial angle between the axis and the magnetic field, θ₁ = 0°.
Final angle between the axis and the magnetic field, θ₂ = 180°.
The work required to make the magnetic moment opposite to the direction of magnetic field is given as :
W = – MB (cos θ₂ – cos θ₁)
∴ W = – 1.5 × 0.22 (cos 180° – cos 0°)
= -0.33 (-1 – 1) = 0.66 J.

b) For case CD : θ = θ₂ = 90° then
Torque, τ = MB sin θ τ = 1.5 × 0.22 sin 90°
= 0.33 J

For case (ii): θ = θ₂ = 180° then
Torque, τ = MB sin θ τ = MB sin 180° = 0 J

Question 6.
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10^-4 m², carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
a) What is the magnetic moment associated with the solenoid?
b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10^-2 T is set up at an angle of 30° with the axis of the solenoid?
Solution:
Number of turns on the solenoid, n = 2000,
Area of cross-section of the solenoid, A = 1.6 × 10^-4 m²;
Current in the solenoid, I = 4 A

a) The magnetic moment along the axis of the solenoid is calculated as :
M = nAI = 2000 × 1.6 × 10^-4 × 4 = 1.28 Am²

b) Magnetic field, B = 7.5 × 10^-2 T
Angle between the magnetic field and the axis of the solenoid, 0 = 30°
Torque, τ = MB sin θ
∴ τ = 1.28 × 7.5 × 10^-2 sin 30°
= 4.8 × 10^-2 Nm.

Since the magnetic field is uniform, the force on the solenoid is zero. The torque on the solenoid is 4.8 × 10^-2 Nm.

Question 7.
A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 8.0 × 10^-2T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s^-1. What is the moment of inertia of the coil about its axis of rotation?
Solution:
Number of turns in the circular coil, N = 16;
Radius of the coil, r = 10 cm = 0.1 m
Cross-section of the coil, A = πr² = π × (0.1)² m² ;
Current in the coil, I = 0.75 A
Magnetic field strength, B = 5.0 × 10^-2 T ;
Frequency of oscillations of the coil, v = 2.0 s^-1
∴ Magnetic moment, M = NIA = Nlπr²
= 16 × 0.75 × π × (0.1)²
∴ M = 0.377 J T^-1

Hence, the moment of inertia of the coil about its axis of rotation is 1.19 × 10^-4 kg m².

Question 8.
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 22° with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Solution:
Horizontal component of earth’s magnetic field, B_H = 0.35 G
Angle made by the needle with the horizontal plane = Angle of dip = δ = 22°
Relation between B and B_H is B_H = B cos δ

Hence, the strength of earth’s magnetic field at the given location is 0.377 G.

Question 9.
At a certain location in Africa, a compass points 12° west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points 60° above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Solution:
Angle of declination, θ = 12°;
Angle of dip, δ = 60°
Horizontal component of earth’s magnetic field, B_H = 0.16 G
Earth’s magnetic field at the given location = B
Relation between B and BH is B_H = B cos θ

Earth’s magnetic field lies in the vertical plane, 12° West of the geographic meridian, making an angle of 60° (upward) with the horizontal direction. Its magnitude is 0.32 G.

Question 10.
A short bar magnet has a magnetic moment of 0.48 J T^-1. Give the direction and mag-nitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equatorial lines (normal bisector) of the magnet.
Solution:
Magnetic moment of the bar magnet,
M = 0.48 J T^-1.
a) Distance, d = 10 cm = 0.1 m
The magnetic field at distance d, from the centre of the magnet on the axis is

The magnetic field is along the S – N direction.

b) The magnetic field at a distance of 10 cm (i.e., d = 0.1 m) on the equatorial line of the magnet is

The magnetic field is along the N – S direction.

Question 11.
A short bar magnet of magnetic moment 5.25 × 10^-2 J T^-1 is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45° with earth’s field on
a) its normal bisector and
b) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Solution:
Magnetic moment of the bar magnet,
M = 5.25 × 10^-2 J T^-1
Magnitude of earth’s magnetic field at a place, H = 0.42 G = 0.42 × 10^-4 T
a) The magnetic field at a distance R from the centre of the magnet on the normal bisector is given by the relation :
B = \(\frac{\mu_0M}{4\pi R^3}\) ; When the resultant field is inclined at 45° with earth’s field, B = H

(OR) R = 0.05 m = 5 cm

b) The magnetic field at a distance R’ from the centre of the magnet on its axis is given as:
\(\frac{\mu_02M}{4\pi R^3}\)
B = The resultant field is inclined at 45° with earth’s field. ∴ B’ = H.

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Parabola Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Parabola Important Questions Long Answer Type

Question 1.
Show that the equation of a parabola in the standard form is y² = 4ax. [(TS) Mar. ’20, ’18, ’17, ’16; May ’18; (AP) May ’19, ’15; Mar. ’17, ’15]
Solution:

Let S be the focus and l = 0 be the directrix of the parabola.
Let ‘P’ be a point on the parabola.
Let M, Z be the projection (foot of the perpendiculars) of P, S on the directrix L = 0 respectively.
Let ‘N’ be the projection of P on ‘SZ’.
Let ‘A’ be the midpoint of SZ.
Since SA = AZ
‘A’ lies on the parabola let AS = a.
Take AS, the principal axis of the parabola as X-axis and AY ⊥r to SZ as Y-axis.
Then S = (a, 0) and the parabola is in the standard form.
Let P(x₁, y₁)
Now PM = NZ = AN + AZ = x₁ + a
‘P’ lies on the parabola then
\(\frac{\mathrm{SP}}{\mathrm{PM}}\) = 1
SP = PM
\(\sqrt{\left(x_1-a\right)^2+\left(y_1-0\right)^2}=x_1+a\)
Squaring on both sides,
(x₁ – a)² + (y₁ – 0)² = (x₁ + a)²
⇒ \(\mathrm{y}_1^2\) = (x₁ + a)² – (x₁ – a)²
⇒ \(\mathrm{y}_1^2\) = 4ax₁
The locus of ‘P’ is y² = 4ax
∴ The equation to the parabola is y² = 4ax

Question 2.
Find the coordinates of the vertex and focus and the equation of the directrix and axes of the parabola y² – x + 4y + 5 = 0. (Mar. ’05)
Solution:
Given the equation of the parabola is
y² – x + 4y + 5 = 0
⇒ y² + 4y = x – 5
⇒ (y)² + 2 . 2 . y + (2)² – (2)² = x – 5
⇒ (y + 2)² – 4 = x – 5
⇒ (y + 2)² = x – 1
⇒ (y + 2)² = 1(x – 1)
Comparing with (y – k)² = 4a(x – h), we get
h = 1, k = -2, a = \(\frac{1}{4}\)
(i) Vertex = (h, k) = (1, -2)
(ii) Focus = (h + a, k) = (1 + \(\frac{1}{4}\), -2) = (\(\frac{5}{4}\), -2)
(iii) Equation of the directrix is x = h – a
⇒ x = 1 – \(\frac{1}{4}\)
⇒ x = \(\frac{3}{4}\)
⇒ 4x – 3 = 0
(iv) Equation of the axis is y = k
⇒ y = -2
⇒ y + 2 = 0

Question 3.
Find the vertex and focus of 4y² + 12x – 20y + 67 = 0.
Solution:
Given equation of the parabola is 4y² + 12x – 20y + 67 = 0
4y² – 20y = -12x – 67
4(y² – 5y) = -12x – 67

Question 4.
Find the coordinates of the vertex and focus, the equation of the directrix, and the axis of the parabola y² + 4x + 4y – 3 = 0.
Solution:
Given the equation of the parabola is
y² + 4x + 4y – 3 = 0
⇒ y² + 4y = -4x + 3
⇒ (y)² + 2 . y(2) + (2)² – (2)² = -4x + 3
⇒ (y + 2)² – 4 = -4x + 3
⇒ (y + 2)² = -4x + 7
⇒ (y + 2)² = -4(x – \(\frac{7}{4}\))
[y-(-2)]² = -4(x – \(\frac{7}{4}\))
Comparing with (y – k)² = -4a(x – h), we get
h = \(\frac{7}{4}\), k = -2, 4a = 4 ⇒ a = 1
(i) Vertex = (h, k) = (\(\frac{7}{4}\), -2)
(ii) Focus = (h – a, k) = (\(\frac{7}{4}\) – 1, -2) = (\(\frac{3}{4}\), -2)
(iii) Equation of the directrix is x = h + a
⇒ x = \(\frac{7}{4}\) + 1
⇒ x = \(\frac{11}{4}\)
⇒ x = 4x – 11 = 0
(iv) Equation of the axis is y = k
⇒ y = -2
⇒ y + 2 = 0

Question 5.
Find the equations of the axis and directrix of the parabola 4x² + 12x – 20y + 67 = 0.
Solution:
Given equation of the parabola is 4x² + 12x – 20y + 67 = 0
⇒ 4x² + 12x = 20y – 67
⇒ 4(x² + 3x) = 20y – 67

Comparing with (x – h)² = 4a(y – k) we get
h = \(-\frac{3}{2}\), k = \(\frac{29}{10}\),
4a = 5 ⇒ a = \(\frac{5}{4}\)
(i) Equation of the axis is x = h
⇒ x = \(-\frac{3}{2}\)
⇒ 2x + 3 = 0
(ii) Equation of the directrix is y = k – a
⇒ y = \(\frac{29}{10}-\frac{5}{4}\)
⇒ y = \(\frac{33}{20}\)
⇒ 20y – 33 = 0

Question 6.
Find the coordinates of the vertex and focus and the equations of the directrix and axes of the parabola 3x² – 9x + 5y – 2 = 0.
Solution:
Given equation of the parabola
3x² – 9x + 5y – 2 = 0
⇒ 3x² – 9x = -5y + 2
⇒ 3(x² – 3x) = -5y + 2

Question 7.
Find the equation of the parabola whose axis is parallel to the X-axis and which passes through die points (-2, 1), (1, 2), and (-1, 3). [(AP) May ’18, ’16, (TS) ’17]
Solution:
Let, the given points are A(-2, 1), B(1, 2), C(-1, 3)
The equation of the parabola whose axis is parallel to the X-axis is
x = ly² + my + n ……….(1)
Since, eq. (1) passes through point A(-2, 1) then
(-2) = l(1)² + m(1) + n
⇒ -2 = l + m + n
⇒ l + m + n = -2
Since, (1) passes through point B(1, 2) then
(1)² = l(2)² + m(2) + n
⇒ 1 = 4l + 2m + n
⇒ 4l + 2m + n = 1 …….(3)
Since, (1) passes through point C(-1, 3), then
-1 = l(3)² + m(3) + n
9l + 3m + n = -1 ………(4)
From (2) and (3)

Substitute the values of l, m in (2)
\(\frac{-5}{2}+\frac{21}{2}\) + n = -2
⇒ -5 + 21 + 2n = -4
⇒ 16 + 2n = -4
⇒ 2n = -20
⇒ n = -10
Substitute the values of l, m, n in (1),
The required equation of the parabola is
\(\mathbf{x}=\frac{-5}{2} \mathbf{y}^2+\frac{21}{2} \mathbf{y}-10\)
⇒ -5y² + 21y – 20 = 2x
⇒ 5y² + 2x – 21y + 20 = 0

Question 8.
Find the equation of the parabola passing through the points (-1, 2), (1, -1), and (2, 1) and having its axis parallel to the X-axis.
Solution:
Let, the given points are A(-1, 2), B(1, -1), C(2, 1)
The equation of the parabola whose axis is parallel to the X-axis is
x = ly² + my + n …….(1)
Since, (1) passes through point A(-1, 2) then
(-1) = l(2)² + m(2) + n
⇒ -1 = 4l + 2m + n
⇒ 4l + 2m + n = -1 ……..(2)
Since, (1) passes through point B(1, -1) then
(1) = l(-1)² + m(-1) + n
⇒ l – m + n = 1 ……..(3)
Since (1) passes through point C(2, 1) then
2 = l(1)² + m(1) + n
⇒ l + m + n = 2 ……(4)
From (2) and (3)

Question 9.
Find the equation of the parabola whose X-axis is parallel to the Y-axis and which passes through the point (4, 5), (-2, 11), (-4, 21). (May ’12)
Solution:
The equation of the parabola whose axis is parallel to the Y-axis then
y = lx² + mx + n ……..(1)
Since eq. (1) passes through the point (4, 5) then
5 = l(4)² + m(4) + n
⇒ 16l + 4m + n = 5 ………(2)
Since eq. (1) passes through the point (-2, 11) then
11 = l(-2)² + m(-2) + n
⇒ 4l – 2m + n = 11 ………(3)
Since eq. (1) passes through the point (-4, 21) then
21 = l(-4)² + m(-4) + n
⇒ 16l + 4m + n = 21 ……….(4)

Question 10.
Find the equation of the parabola whose focus is (-2, 3) and whose directrix is the line 2x + 3y – 4 = 0. Also, find the length of the latus rectum and the equation of the axis of the parabola.
Solution:
2x + 3y – 4 = 0
Given that, focus, S = (-2, 3)

The equation of the directrix is 2x + 3y – 4 = 0
Let, P(x, y) be a point on the parabola.
Now, SP = \(\sqrt{(\mathrm{x}+2)^2+(\mathrm{y}-3)^2}\)
PM = the ⊥r distance from P(x, y) to the directrix 2x + 3y – 4 = 0

Squaring on both sides
(x + 2)² + (y – 3)² = \(\frac{(2 x+3 y-4)^2}{13}\)
13x² + 52x + 52 + 13y² + 117 – 78y = 4x² + 9y² + 12xy – 24y – 16x + 16
9x² – 12xy + 4y² + 68x – 54y + 153 = 0
∴ The equation to the parabola is 9x² – 12xy + 4y² + 68x – 54y + 153 = 0
Now, the length of the latus rectum = 4a
= 2(2a)
= 2(the ⊥r distance from focus S(-2, 3) to the directrix 2x + 3y – 4 = 0)

The equation of the axis of the parabola is b(x – x₁) – a(y – y₁) = 0
⇒ 3(x + 2) – 2(y – 3) = 0
⇒ 3x + 6 + 2y – 6 = 0
⇒ 3x + 2y = 0

Question 11.
Find the locus of the point of trisection of the double ordinate of a parabola y² = 4ax (a > 0).
Solution:
The given equation of a parabola is y² = 4ax (a > 0)

Let, the ends double-ordinate the parabola
y² = 4ax are P(at², 2at), Q(at², -2at)
Let R(x₁, y₁) be any point on the locus trisection ratio = 1 : 2
R(x₁, y₁) is the trisection point, then

Question 12.
Show that the equation of a common tangent to the circle x² + y² = 2a² and the parabola y² = 8ax are y = ±(x + 2a). [(TS) May ’19, ’16 (AP) ’17]
Solution:
Given the equation of the parabola is y² = 8ax
The equation of the tangent to the parabola
y² = 4ax is y = mx + \(\frac{a}{m}\)
The equation of the tangent to the parabola
y² = 8ax is y = mx + \(\frac{2a}{m}\) (∵ a = 2a)
Given the equation of the circle is x² + y² = 2a²
Centre C = (0, 0)
Radius r = √2a
Since eq. (1) is a tangent to the circle x² + y² = 2a² then r = d

Squaring on both sides we get
2(1 + m²) = \(\frac{4}{\mathrm{~m}^2}\)
⇒ m²(1 + m²) = 2
⇒ m² + m⁴ – 2 = 0
⇒ m⁴ + m² – 2 = 0
⇒ m⁴ + 2m² – m² – 2 = 0
⇒ m²(m² + 2) – 1(m² + 2) = 0
⇒ (m² + 2) (m² – 1) = 0
⇒ m² + 2 = 0 or m² – 1 = 0
⇒ m² = -2 or m² = 1
⇒ m = ±√-2 ∉ R or m = ± 1
Substitute the value of ‘m’ in eq. (1)
∴ The equation of the common tangents is
y = \(\pm x+\frac{2 a}{\pm 1}\)
⇒ y = ±(x + 2a)

Question 13.
Show that the common tangent to the parabola y² = 4ax and x² = 4by is \(x a^{1 / 3}+y b^{1 / 3}+a^{2 / 3} \cdot b^{2 / 3}=0\). [(AP) Mar. ’16]
Solution:
Given equations of the parabola are
y² = 4ax …….(1) and x² = 4by …..(2)

Equation of any tangent to (1) is of the form
y = mx + \(\frac{a}{m}\) ……..(3)
If line (3) is a tangent to (2) also.
The points of intersection of (2) and (3) coincide.
Substituting the value of y from (3) in (2), we get
⇒ x² = \(4 b\left(m x+\frac{a}{m}\right)\)
⇒ x² = 4bmx + \(\frac{4ab}{m}\)
⇒ mx² = 4bm²x + 4ab
⇒ mx² – 4bm²x – 4ab = 0
This equation has equal roots, then it’s discriminant = 0
b² – 4ac = 0
⇒ (-4bm²)² – 4(m) (-4ab) = 0
⇒ 16b²m⁴ + 16abm = 0
⇒ b²m⁴ + abm = 0
⇒ bm⁴ + am = 0
⇒ m(bm³ + a) = 0
⇒ m = 0 (or) bm³ + a = 0

Question 14.
The normal at a point ‘t₁’ on y² = 4ax meets the parabola again in the point ‘t₂’ then prove that t₁t₂ + \(t_1^2\) + 2 = 0. (May ’13)
Solution:

Given the equation of the parabola is y² = 4ax
The equation of the normal at P(\(\mathrm{at}_1{ }^2\), 2at₁) is
y + xt₁ = 2at₁ + \(\mathrm{at}_1{ }^3\) …….(1)
Since eq. (1) meets the parabola again in the Q(\(\mathrm{at}_2{ }^2\), 2at₂) then

Question 15.
If lx + my + n = 0 is a normal to the parabola y² = 4ax, then show that al³ + 2alm² + nm² = 0.
Solution:

Given the equation of the parabola is y² = 4ax
Given the equation of the normal is
lx + my + n = 0 ……..(1)
Now, the equation of the normal at P(at², 2at) is
y + xt = 2at + at³ ……..(2)
Now, (1) and (2) represent the same line then

Which is the required condition.

Question 16.
If a normal chord at a point t on the parabola y² = 4ax subtends a right angle at the vertex then show that t = ±√2. (May ’14)
Solution:
Given the equation of the parabola is y² = 4ax

Question 17.
Show that the locus of the point of intersection of perpendicular tangents to the parabola y² = 4ax is the directrix x + a = 0.
Solution:
Given, the equation of the parabola is y² = 4ax.
Let P(x₁, y₁) be the point of intersection of perpendicular tangents of y² = 4ax.
The equation to the pair of tangents drawn from P(x₁, y₁) is \(\mathrm{S}_1{ }^2\) = S.S₁₁
⇒ [yy₁ – 2a(x + x₁)]² = (y² – 4ax) (\(\mathbf{y}_1{ }^2\) – 4ax₁)
Since the tangents are at right angles, then
coefficient of x² + coefficient of y² = 0
4a² + \(\mathbf{y}_1{ }^2\) – (\(\mathbf{y}_1{ }^2\) – 4ax₁) = 0
⇒ 4a² + \(\mathbf{y}_1{ }^2\) – \(\mathbf{y}_1{ }^2\) + 4ax₁ = 0
⇒ 4a² + 4ax₁ = 0
⇒ a + x₁ = 0
⇒ x₁ + a = 0
∴ The equation to the locus of P(x₁, y₁) is x + a = 0.

Question 18.
Show that the feet of the perpendicular from focus to the tangent of the parabola y² = 4ax lie on the tangent at the vertex.
Solution:
Given equation of the parabola is y² = 4ax.

Equation of a tangent to the parabola y² = 4ax is
y = mx + \(\frac{a}{m}\)
⇒ y = \(\frac{m^2 x+a}{m}\)
⇒ m²x – my + a = 0 ……..(1)
Equation of a line passing through the focus S(a, 0) and perpendicular to the line (1) is
y – y₁ = \(\frac{-1}{m}\)(x – x₁)
⇒ y – 0 = \(\frac{-1}{m}\)(x – a)
⇒ y = \(\frac{-1}{m}\)(x – a)
⇒ my = -x + a
⇒ x + my – a = 0 …….(2)
Solve (1) and (2)
(1) + (2) ⇒ m²x – my + a + x + my – a = 0
⇒ x(m² + 1) = 0
⇒ x = 0 (∵ m² ≠ 1)
∴ The point of intersections of lines (1) and (2) lies on x = 0.
Which is the tangent at the vertex.

Question 19.
From an external point, P tangents are drawn to the parabola y² = 4ax and these tangents make angles θ₁, θ₂ with its axis, such that cot θ₁ + cot θ₂ is a constant ‘d’. Then show that all such P lie on a horizontal line. [Mar. ’19 (TS)]
Solution:
Given the equation of the parabola is y² = 4ax

Let P(x₁, y₁) be any point on the required locus.
∴ The equation of any tangent to the parabola y² = 4ax is y = mx + \(\frac{a}{m}\)
If this line passes through P then
y₁ = mx₁ + \(\frac{a}{m}\)
⇒ y₁ = \(\frac{m^2 x_1+a}{m}\)
⇒ my₁ = m²x₁ + a
⇒ x₁m² – y₁m + a = 0 ………(1)
Which is a quadratic equation in m.
If m₁, m₂ are the slopes of the tangents drawn from P to the parabola then m₁, m₂ are the roots of (1)
Sum of the slopes = \(\frac{-b}{a}\)
m₁ + m₂ = \(\frac{-\left(-y_1\right)}{x_1}=\frac{y_1}{x_1}\)
tan θ₁ + tan θ₂ = \(\frac{\mathrm{y}_1}{\mathrm{x}_1}\)
product of the slopes = \(\frac{c}{a}\)
m₁m₂ = \(\frac{\mathrm{a}}{\mathrm{x}_1}\)
tan θ₁ tan θ₂ = \(\frac{\mathrm{a}}{\mathrm{x}_1}\)
(∵ The tangents made angles θ₁, θ₂ with its axis (X -axis) then their slopes m₁ = tan θ₁ and m₂ = tan θ₂)
Given that cot θ₁ + cot θ₂ = d

∴ P lies on a horizontal line y = ad.

Question 20.
From an external point, P tangents are drawn to the parabola y² = 4ax and these tangents make angles θ₁, θ₂ with its axis such that tan θ₁ + tan θ₂ is a constant, b. Then show that P lies on the line y = bx. [(AP) Mar. ’20]
Solution:
Given the equation of the parabola is y² = 4ax

Let, P(x₁, y₁) be any point on the required locus.
∴ The equation of any tangent to the parabola y² = 4ax is y = mx + \(\frac{a}{m}\)
If this line passes through P then
y₁ = mx₁ + \(\frac{a}{m}\)
⇒ y₁ = \(\frac{m^2 x_1+a}{m}\)
⇒ my₁ = m²x₁ + a
⇒ x₁m² – y₁m + a = 0 ……(1)
which is a quadratic equation in m.
If m₁, m₂ are the slopes of the tangents drawn from P to the parabola then m₁, m₂ are the roots of (1).
Sum of the slopes = \(\frac{-b}{a}\)
m₁ + m₂ = \(\frac{-\left(-y_1\right)}{x_1}=\frac{y_1}{x_1}\)
tan θ₁ + tan θ₂ = \(\frac{y_1}{x_1}\)
[∵ The tangents made angles θ₁, θ₂ with its axis (X-axis) then their slopes m₁ = tan θ₁ and m₂ = tan θ₂]
Given that, tan θ₁ + tan θ₂ = b
⇒ \(\frac{y_1}{x_1}\) = b
⇒ y₁ = bx₁
∴ P(x₁, y₁) lies on the line y = bx.

Question 21.
Prove that the two parabolas y² = 4ax and x² = 4by intersect (other than the origin) at an angle of \(\tan ^{-1}\left[\frac{3 a^{\frac{1}{3}} b^{\frac{1}{3}}}{2\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)}\right]\). (Mar. ’14)
Solution:
Without loss of generality, we can assume that a > 0 and b > 0

Let, P(x, y) be the point of intersection of the parabolas other than the origin.
Given equations of the parabolas are y² = 4ax, x² = b4y
⇒ y² = 4ax
Squaring on both sides
y⁴ = 16a²x²
⇒ y⁴ = 16a²(4by)
⇒ y⁴ = 64a²by
⇒ y⁴ – 64a²by = 0
⇒ y(y³ – 64a²b) = 0
⇒ y = 0 or y³ – 64a²b = 0
⇒ y³ = 64a²b
⇒ y = \(4 \mathrm{a}^{2 / 3} \mathrm{~b}^{1 / 3}\)
From y² = 4ax, we get

Question 22.
Show that the straight line 7x + 6y = 13 is a tangent to the parabola y² – 7x – 8y + 14 = 0 and find the point of contact.
Solution:
Given the equation of the parabola is
y² – 7x – 8y + 14 = 0 ………(1)
Given the equation of the straight line is
7x + 6y = 13
⇒ 7x = 13 – 6y
⇒ x = \(\frac{13-6 y}{7}\) ………(2)
From (1) and (2) by eliminating x we get the ordinates of the points of intersection of the line and parabola.
y² – 7(\(\frac{13-6 y}{7}\)) – 8y + 14 = 0
⇒ y² – 13 + 6y – 8y + 14 = 0
⇒ y² – 2y + 1 = 0
⇒ (y – 1)² = 0
⇒ y = 1, 1
∴ The given line is tangent to the given parabola substitute the value of y = 1 in (2)
x = \(\frac{13-6}{7}=\frac{7}{7}=1\)
∴ Point of contact = (1, 1)

Question 23.
Show that the common tangents to the circle 2x² + 2y² = a² and the parabola y² = 4ax intersect at the focus of the parabola y² = -4ax.
Solution:
Given the equation of the parabola is y² = 4ax
The equation of the tangent to the parabola y² = 4ax is
y = mx + \(\frac{a}{m}\) ……..(1)
Given the equation of the circle is
2x² + 2y² = a²
⇒ x² + y² = \(\frac{\mathrm{a}^2}{2}\)
∴ Centre, C = (0, 0)
Radius = \(\frac{a}{\sqrt{2}}\)
Since (1) is a tangent to the circle 2x² + 2y² = a² then r = d

⇒ m² + m⁴ = 2
⇒ m⁴ + m² – 2 = 0
⇒ m⁴ + 2m² – m² – 2 = 0
⇒ m²(m² + 2) – 1(m² + ²) = 0
⇒ (m² + 2)(m² – 1) = 0
⇒ m² + 2 = 0 or m² – 1 = 0
⇒ m² = -2 or m² = 1
⇒ m = ±√-2 ∉ R or m = ±1
Substitute the values of m in (1)
∴ The equations of the common tangents are
y = \(\pm 1 \cdot x+\frac{a}{\pm 1}\)
⇒ y = ±x ± a
⇒ y = ±(x ± a) …….(2)
The focus of the parabola y² = -4ax is S = (-a, 0)
Now, (2) intersects at the focus of the parabola y² = -4ax then
(2) passes through focus, S(-a, 0)
0 = ±(-a + a)
∴ 0 = 0
∴ The common tangents to the circle 2x² + 2y² = a² and the parabola y² = 4ax intersect at the focus of the parabola y² = -4ax.

Question 24.
Show that the condition that the line y = mx + c may be a tangent to the parabola y² = 4ax is c = \(\frac{a}{m}\). (Mar. ’99, ’94; May ’98)
Solution:
Suppose y = mx + c ………(1)
is a tangent to the parabola y² = 4ax
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at ‘P’ is S₁ = 0
⇒ yy₁ – 2a(x + x₁) = 0
⇒ yy₁ – 2ax – 2ax₁ = 0
⇒ 2ax – yy₁ + 2ax₁ = 0 ………(2)
Now, (1) & (2) represent the same line

Since ‘P’ lies on the line

Question 25.
Find the condition for the line y = mx + c to be a tangent to the parabola x² = 4ay. (Mar. ’12; May ’03)
Solution:
Given the equation of the parabola is x² = 4ay
Let the line y = mx + c ………(1)
be a tangent to the parabola x² = 4ay.

The equation of the tangent at P(x₁, y₁) is S₁ = 0
xx₁ – 2a(y + y₁) = 0
⇒ xx₁ – 2ay – 2ay₁ = 0 ……….(2)
Now equations (1) & (2) represent the same line then

Since P(x₁, y₁) lies on the line y = mx + c then y₁ = mx₁ + c
⇒ -c = m(2am) + c
⇒ 2am² + 2c = 0
⇒ am² + c = 0
Which is the required condition.

Question 26.
Prove that the tangents at the extremities of a focal chord of a parabola intersect at right angles on the directrix.
Solution:
Let the equation of the parabola is y² = 4ax.
Let P(\(\mathrm{at}_1^2\), 2at₁), Q(\(\mathrm{at}_2^2\), 2at₂) are two points on the parabola.


∴ The tangents are drawn at P, Q are perpendicular
The coordinates of R = [-a, a(t₁ + t₂)]
The equation of the directrix of a parabola y = 4ax is x + a = 0
Now, substitute the point R in the directrix x + a = 0
⇒ -a + a = 0
⇒ 0 = 0
∴ The tangents at the extremities of a focal chord of a parabola intersect at right angles on the directrix.

Question 27.
Find the equation of the parabola whose focus is S(3, 5) and the vertex is A(1, 3).
Solution:

Question 28.
Find the equations of the tangents to the parabola y² = 16x, which are parallel and perpendicular respectively to the line 2x – y + 5 = 0. Find the coordinates of their points of contact also.
Solution:
Given parabola is y² = 16x
Comparing with y² = 4ax
we get 4a = 16 ⇒ a = 4
Given line is 2x – y + 5 = 0
⇒ y = 2x + 5
Comparing with y = mx + c we get
m = 2, c = 5
(i) Equation of the tangent with slope ‘m’ is

(ii) Slope of the perpendicular given line is m = \(\frac{-1}{2}\)
equation of tangent with slope ‘m’ is

Question 29.
If L and L’ are the ends of the latus rectum of the parabola x² = 6y. Find the equations of OL and OL’ where ‘O’ is the origin. Also, find the angle between them.
Solution:

Question 30.
Two parabolas have the same vertex and equal length of latus rectum such that their axes are at right angles. Prove that the common tangent touches each at the end of the latus rectum.
Solution:
Equations of the parabolas can be taken as y² = 4ax and x² = 4ay

Equation of the tangent at P(2at, at²) to the parabola x² = 4ay is S₁ = 0
⇒ xx₁ – 2a(y + y₁) = 0
⇒ x(2at) – 2a(y + at²) = 0
⇒ xt – y – at² = 0
⇒ tx – y – at² = 0 ………(1)
⇒ y = tx – at²
This is a tangent to y² = 4ax, then
c = \(\frac{a}{m}\)
⇒ -at² = \(\frac{a}{t}\)
⇒ -t³ = 1
⇒ t³ = -1
⇒ t = -1
Substitute the value of t = -1 in (1)
-x – y – a(1) = 0
⇒ x + y + a = 0
Equation of the tangent at L'(a, -2a) to the parabola y² = 4ax is S₁ = 0
⇒ yy₁ – 2a(x + x₁) = 0
⇒ y(-2a) – 2a(x + a) = 0
⇒ y + x + a = 0
⇒ x + y + a = 0
Common tangent to the parabolas touches the parabola y² = 4ax at L'(a, -2a).
Equation of the tangent at L'(-2a, a) to the parabola x² = 4ay is S₁ = 0
⇒ xx₁ – 2a(y + y₁) = 0
⇒ x(-2a) – 2a(y + a) = 0
⇒ x + y + a = 0
∴ Common tangent to the parabolas touches the parabola x² = 4ay at L'(-2a, a).

Question 31.
Show that the tangent at one extremity of a focal chord of a parabola is parallel to the normal at the other extremity.
Solution:
Let, the equation of the parabola is y² = 4ax

Let P(\(\mathrm{at}_1^2\), 2at₁), Q(\(\mathrm{at}_2^2\), 2at₂) be the two ends of a focal chord of the parabola y² = 4ax, then
t₁t₂ = -1
⇒ -t₂ = \(\frac{1}{t_1}\)
Let \(\frac{1}{t_1}\) = m₁
Slope of the normal at Q(\(\mathrm{at}_2^2\), 2at₂) is
m₂ = -t₂ = \(\frac{1}{t_1}\) = m₁
∴ m₁ = m₂, then the tangent at P and the normal at Q are parallel.

Question 32.
Prove that the normal chord at the point other than the origin whose ordinate is equal to its abscissa subtends a right angle at the focus.
Solution:
Let, the equation of the parabola is y² = 4ax ……..(1)

Let P(at², 2at) be any point on the parabola given that, whose ordinate is equal to its abscissa, then
2at = at²
⇒ t² = 2t
⇒ t² – 2t = 0
⇒ t(t – 2) = 0
⇒ t = 0, t = 2
But t ≠ 0, then P(4a, 4a)
The equation of the normal at P(4a, 4a) is
y + xt = 2at + at³
⇒ y + x(2) = 2a(2) + a(2)³
⇒ y + 2x = 4a + 8a
⇒ y + 2x = 12a
⇒ y = 12a – 2x …….(2)
Substituting the value of y = 12a – 2x in (1) we get
(12a – 2x)² = 4ax
⇒ 4(6a – x)² = 4ax
⇒ (6a – x)² = ax
⇒ 36a² + x² – 12ax – ax = 0
⇒ 36a² + x² – 13ax = 0
⇒ x² – 9ax – 4ax + 36a² = 0
⇒ x(x – 9a) – 4a(x – 9a) = 0
⇒ (x – 9a) (x – 4a) = 0
⇒ x – 9a = 0 (or) x – 4a = 0
⇒ x = 9a (or) x = 4a
⇒ x = 4a, 9a
If x = 4a, then y = 12a – 8a = 4a
∴ P = (4a, 4a)
If x = 9a, then y = 12a – 18a = -6a
∴ Q = (9a, -6a)
∴ P = (4a, 4a), Q = (9a, -6a)
Focus S = (a, 0)

Since m₁m₂ = -1, then
\(\overline{\mathrm{SP}}\) is perpendicular to \(\overline{\mathrm{SQ}}\)
∴ The normal chord subtends a right angle at the focus.

Question 33.
(i) If the coordinates of the ends of a focal chord of the parabola y² = 4ax are (x₁, y₁) and (x₂, y₂) then prove that x₁x₂ = a², y₁y₂ = -4a².
(ii) For a focal chord PQ of the parabola y² = 4ax, if SP = l and SQ = l’ then prove that \(\frac{1}{l}+\frac{1}{l^{\prime}}=\frac{1}{a}\).
Solution:
Given the equation of the parabola is y² = 4ax
Let P(x₁, y₁) = (\(a \mathrm{t}_1^2\), 2at₁) and Q(x₂, y₂) = (\(a \mathrm{t}_2^2\), 2at₂) be two endpoints of a focal chord.

Question 34.
Prove that the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂)(y₂ – y₃)(y₃ – y₁)| sq. units where y₁, y₂, y₃ are the ordinates of its vertices. [(TS) May. ’15]
Solution:

Question 35.
Prove that the area of the triangle formed by the tangents at (x₁, y₁), (x₂, y₂), and (x₃, y₃) to the parabola y² = 4ax (a > 0) is \(\frac{1}{16a}\) |(y₁ – y₂)(y₂ – y₃)(y₃ – y₁)| sq.units. [(AP) Mar. ’18, (TS) ’15]
Solution:
Given parabola y² = 4ax

Question 36.
Prove that the orthocentre of the triangle formed by any three tangents to a parabola lies on the directrix of the parabola.
Solution:
Let the equation of the parabola is y² = 4ax
Let A, B, C be the triangle formed by the tangents to the parabola at P(\(\mathrm{at}_1^2\), 2at₁), Q(\(\mathrm{at}_2^2\), 2at₂) and R(\(\mathrm{at}_3^2\), 2at₃) as shown in the figure.

A = Point of intersection of the tangents at P, Q = [at₁t₂, a(t₁ + t₂)]
B = Point of intersection of the tangents at P, R = [at₁t₃, a(t₁ + t₃)]
C = Point of Intersection of the tangents at Q, R = [at₂t₃, a(t₂ + t₃)]
Let, AD and CE be the two altitudes of ∆ABC.
\(\overline{\mathrm{BC}}\) is the tangent at R, then the equation of \(\overline{\mathrm{BC}}\) is yt₃ = x + \(\mathrm{at}_3^2\).


(1) ⇒ t₃(-a) + y – at₁ – at₂ – at₁t₂t₃ = 0
y = a(t₁ + t₂ + t₃ + t₁t₂t₃)
∴ Orthocentre H = [-a, a(t₁ + t₂ + t₃ + t₁t₂t₃)]
The equation of the directrix of the parabola y² = 4ax is x + a = 0
Now substitute H in the directrix
-a + a = 0
⇒ 0 = 0
∴ H lies on the directrix x + a = 0.

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type

Question 1.
Find the range of \(\frac{x^2+x+1}{x^2-x+1}\). [Mar.’10. ’04, May ’10]
Solution:
Let y = \(\frac{x^2+x+1}{x^2-x+1}\)
⇒ y(x² – x + 1) = x² + x + 1
⇒ yx² – yx + y – x² – x – 1 = 0
⇒ (y – 1)x² + (- y – 1) x + y – 1 = 0
x is real;
⇒ discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (- y – 1)² – 4 (y – 1) (y – 1) ≥ 0
⇒ y² + 1 + 2y – 4 (y² – y – y + 1) ≥ 0
⇒ y² + 1 + 2y – 4y² + 8y – 4 ≥ 0
⇒ – 3y² + 10y – 3 ≥ 0
⇒ 3y² – 10y + 3 ≤ 0
⇒ 3y² – 9y – y + 3 ≤ 0
⇒ 3y (y – 3) – 1 (y – 3) ≤ 0
⇒ \(\frac{1}{3}\) ≤ y ≤ 3
∴ y lies between \(\frac{1}{3}\) and 3.
∴ Range = [\(\frac{1}{3}\), 3]

Question 2.
Find the range of \(\frac{x+2}{2 x^2+3 x+6}\). [AP – May ’16; Mar ’13, ’08, Mar. 2000, B.P]
Solution:
Let y = \(\frac{x+2}{2 x^2+3 x+6}\)
⇒ 2x²y + 3xy + 6y = x + 2
⇒ (2y)x² + (3y – 1)x + (6y – 2) = 0
x is real;
⇒ Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (3y – 1)² – 4(2y) (6y – 2) ≥ 0
⇒ 9y² + 1 – 6y – 48y² + 16y ≥ 0
⇒ – 39y² + 10y + 1 ≥ 0
⇒ 39y² – 10y – 1 ≤ 0
⇒ 39y2 – 13y + 3y – 1 ≤ 0
⇒ 13y (3y – 1) + (3y – 1) ≤ 0
⇒ (13y + 1) (3y – 1) ≤ 0
⇒ \(\frac{-1}{13} \leq y \leq \frac{1}{3}\)
y lies between \(\frac{-1}{13}\) and \(\frac{1}{3}\).
∴ Range = [\(\frac{-1}{13}\), \(\frac{1}{3}\)].

Question 3.
Find the range of \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\). [Mar. ’09, ’98].
Solution:
Let y = \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\)
⇒ x²y – 3xy + 2y = 2x² – 6x + 5
⇒ x²y – 3xy + 2y – 2x² + 6x – 5 = 0
⇒ (y – 2)x² +(- 3y+ 6)x + 2y – 5 = 0
x is real ;
⇒ Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (- 3y + 6)² – 4(y – 2) (2y – 5) ≥ 0
⇒ 9y² + 36 – 36y – 4(2y² – 5y – 4y + 10) ≥ 0
⇒ 9y² + 36 – 36y – 8y² + 20y + 16y – 40 ≥ 0
⇒ y² – 4 ≥ 0
⇒ (y – 2) (y + 2) ≥ 0
⇒ y ≤ – 2 (or) y ≥ 2 y ≤ – 2 y ≥ 2
∴ y does not lies between – 2, 2.

∴ Range = (- ∞, – 2] u [2, ∞).

Question 4.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real. [TS – Mar. ’18, ’16, May ’12, March ’11, ’05; AP – Mar. ’17, ’16, ’15].
Solution:
Let y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
(3x + 1) (x + 1) y = x + 1 + 3x + 1 – 1
⇒ y[3x² + 4x + 1] = 4x + 1
⇒ 3x²y + 4xy . y – 4x – 1 = 0
⇒ (3y)x² + (4y – 4) x + (y – 1) = 0
If x is real ;
⇒ Discriminant ≥ 0
b2 – 4ac ≥ 0
⇒ (4y – 4)² – 4 (3y) (y – 1) ≥ 0
⇒ 16y² + 16 – 32y – 12y² + 12y ≥ 0
⇒ 4y² – 20y + 16 ≥ 0
⇒ 4 (y² – 5y + 4) ≥ 0
⇒ y² – 4y – y + 4 ≥ 0
⇒ (y -4) – 1 (y – 4) ≥ 0
⇒ =(y – 1) (y – 4) ≥ 0
⇒ y ≤ 1 (or) y ≥ 4

∴ y does not lies between 1 and 4.
∴ Range is (- ∞, 1] [4, ∞)

Question 5.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between and 1. [TS – May 2016] [May ‘11, ‘07, March ‘14, ’13, ‘08, ‘02] [AP – Mar. 2019]
Solution:
Let y = \(\frac{x}{x^2-5 x+9}\)
⇒ x² – 5xy + 9y = x
⇒ y . x² + (- 5y – 1) x + 9y = 0
If x is real
⇒ Discriminant, b2 – 4ac ≥ 0
⇒ (- 5y – 1)² – 4 . y . 9y ≥ 0
⇒ 25y² + 1 + 10y – 36y² ≥ 0
⇒ – 11y² + 10y + 1 ≥ 0
⇒ 11y² – 10y – 1 ≤ 0
⇒ 11y (y – 1) + 1 (y – 1) ≤ 0
⇒ (11y + 1) (y – 1) ≤ 0
⇒ \(\frac{-1}{11}\) ≤ y ≤ 1
∴ y lies between \(\frac{-1}{11}\) and 1.

Question 6.
If the expression \(\frac{x-p}{x^2-3 x+2}\) takes all real values for x ∈ R, then find the bounds for p. [May ‘09, ‘06. March ‘06] [TS & AP – May 2015].
Solution:
Let y = \(\frac{x-p}{x^2-3 x+2}\)
⇒ yx² – 3xy + 2y = x – p
⇒ y . x² + (- 3y – 1) x + (2y + p) = 0
x is real
⇒ Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (- 3y – 1)² – 4y (2y + p) ≥ 0
⇒ 9y² + 1 + 6y – 8y² – 4py ≥ 0
⇒ y² + (6 – 4p) y + 1 ≥ 0
⇒ y is real then, y² + (6 – 4p) y + 1 ≥ 0
The roots of y² + (6 – 4p) y + 1 = 0 are real and equal or lmaginary.
Then discriminant ≤ 0
⇒ b² – 4ac ≤ 0
⇒ (6 – 4p)² – 4(1)(1) ≤ 0
⇒ 36 + 16p² – 48p – 4 ≤ 0
⇒ 16p² – 48p + 32 ≤ 0
⇒ p² – 3p + 2 ≤ 0
⇒ p² – 2p – p + 2 ≤ 0
⇒ p(p – 2) – 1(p – 2) ≤ 0
⇒ (p – 1) (p – 2) ≤ 0
⇒ 1 ≤ p ≤ 2
If p = 1 (or) p = 2 then \(\frac{x-p}{x^2-3 x+2}\) is not defined.
∴ 1 < p < 2.

Question 7.
Show that none of the values of the function \(\frac{x^2+34 x-71}{x^2+2 x-7}\) over R lies between 5 and 9. [March ‘12. ‘07]
Solution:
Let y = \(\frac{x^2+34 x-71}{x^2+2 x-7}\)
⇒ y(x² + 2x – 7) = x² + 34x – 71 = 0
⇒ yx² + 2xy – 7y – x² – 34x + 71 = o
⇒ (y – 1)x² + (2y – 34) x – 7y + 71 = 0
If x is real ;
= Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (2y – 34)² -4 (y – 1) (- 7y + 71) ≥ 0
⇒ 4y² + 1156 – 136y – 4 (- 7y² + 71y + 7y – 71) ≥ 0
⇒ 4y² + 1156 – 136y + 28y² – 284y – 28y + 284 ≥ 0
⇒ 32y² – 448y + 1440 ≥ 0
⇒ y² – 14y + 45 ≥ 0
⇒ y² – 9y – 5y + 45 ≥ 0
⇒ y (y – 9) – 5(y – 9) ≥ 0
⇒ (y – 5) (y – 9) ≥ 0
⇒ y ≤ 5 (or) y ≥ 9
∴ y does not Lies between 5 and 9.
Hence, none of the values of given function over R lies between 5 and 9.

Question 8.
Find the maximum and minimum values of the function \(\frac{x^2+14 x+9}{x^2+2 x+3}\) over R. [AP – March 2018; May ’14, ‘05].
Solution:
Let y = \(\frac{x^2+14 x+9}{x^2+2 x+3}\)
⇒ yx² + 2xy + 3y – x – 14x – 9 = 0
⇒ (y – 1)x² + (2y – 14)x + 3y – 9 = 0
If x is real
⇒ Discriminant, b2 – 4ac ≥ O
⇒ (2y – 14)² – 4(y – 1)(3y – 9) ≥ 0
⇒ 24y² + 196 – 56y – 4[3y² – 9y – 3y + 9]≥ 0
⇒ 4y² + 196 – 56y – 12y² + 36y. 12y – 36 ≥ 0
⇒ – 8y² – 8y + 160 ≥ 0
⇒ y² + y – 20 ≤ 0
⇒ y² + 5y – 4y – 20 ≤ 0
⇒ y(y + 5) – + 5) ≤ 0
⇒ (y + 5) (y – 4) ≤ 0
⇒ – 5 ≤ y ≤ 4
⇒ y lies between – 5 and 4.
Minimum value = – 5, Maximum value = 4
Range = [- 5, 4].

Question 9.
If c² ≠ ab and the roots of (c² – ab) x² – 2 (a² – bc) x + (b² – ac) = 0 are equal, then show that a³ + b³ + c³ = 3abc or a = 0. [May ’01] [TS – Mar. ’19].
Solution:
Given quadratic equation is (c² – ab) x² – 2 (a² – bc)x + b² – ac = 0 ……………(1)
Comparing this equation with
ax² + bx +c = 0, we have
⇒ a = c² – ab, b = – 2 (a² – bc), c = b² – ac
Since (1) has equal roots.
⇒ b² – 4ac = 0
⇒ [- 2 (a² – bc)]² – 4 (c² – ab) (b² – ac)= 0
⇒ 4 [a⁴ + b²c² – 2a²bc] – 4[b²c² – ⇒ ac³ – ab³ – a²bc] = 0
⇒ 4a⁴ + 4b²c² – 8a²bc – 4b²c² + ⇒ 4ac³ + 4ab³ – 4a²bc = 0
⇒ 4a[a³ – 3abc + c³ + b³] = 0
⇒ a = 0 (or)a³ + b³ + c³ = 3abc.

Question 10.
Let a, b, c ∈ R and a ≠ 0 then the roots of ax² + bx + c = 0 are non-real complex numbers If and only If ax² + bx + c and a have the same sign for all x ∈ R. [May ’98. ‘93. Mar.’99]
Solution:
The roots of the quadratic equation ax² + bx + c = 0 are imaginary then
b² – 4ac < 0
4ac – b² > 0.
Now, ax² + bx + c = a [x² + \(\frac{b}{a} x+\frac{c}{a}\)]
\(\frac{a x^2+b x+c}{a}\) = x² + \(\frac{b}{a} x+\frac{c}{a}\)
= x² + 2 . x . \(\frac{b}{2 a}\) + \(\left(\frac{b}{2 a}\right)^2-\left(\frac{b}{2 a}\right)^2+\frac{c}{a}\)
= \(\left(x+\frac{b}{2 a}\right)^2+\frac{c}{a}-\frac{b^2}{4 a^2}\)
= \(\left(x+\frac{b}{2 a}\right)^2+\frac{4 a c-b^2}{4 a^2}\) > 0
∴ \(\frac{a x^2+b x+c}{a}\) > 0
∴ For x ∈ R, ax² + bx + c and a have the same sign.

Question 11.
Let a, b, c ∈ R and a 0 such that the equation ax² + bx + c = 0 has real roots α and β with α < β, then
i) for α < x <, ax² + bx + c and a have opposite signs.
ii) for x < α or x > β, ax² + bx + c and a have the same sign.
Solution:
α, β are the roots of ax² + bx + c = 0.
Then ax² + bx + c = a (x – α) (x – β)
\(\frac{a x^2+b x+c}{a}\) = (x – α) (x – β) ……………(1)

i) Suppose x ∈ R, α < x < β x > α, x – β < 0 (x – α) > 0
(x – α) (x – β) < 0
From (1),
⇒ \(\frac{a x^2+b x+c}{a}\) < 0
∴ ax² + bx + c, a have opposite sign.

ii) Suppose x ∈ R, x < α Suppose x ∈ R, x > β
x < α < β.
x< α x < β
x – α < 0 x – β < 0 x- β > 0 x – α > 0
(x – α) (x – β) >0
from (1)
\(\frac{a x^2+b x+c}{a}\) > 0
ax² + bx + c, a have same sign.

x > β > α
x > β x > α
x – β > 0 x – α > 0
(x – α) (x – β) > 0
from (1)
\(\frac{a x^2+b x+c}{a}\) > 0
ax² + bx + c, a have same sign.
∴ x ∈ R, x < α (or) x > β then ax² + bx + c and a have the same sign.

Question 12.
Suppose that a, b, c ∈ R, a ≠ 0 and f(x) = ax² + bx + c
i) If a > 0, then f(x) has absolute minimum at x = \(\frac{-b}{2 a}\) and the minimum value is \(\frac{4 a c-b^2}{4 a}\).
ii) If a < 0, then f(x) has absolute maximum at x = \(\frac{-b}{2 a}\) and the maximum value is \(\frac{4 a c-b^2}{4 a}\).
Solution:
f(x) = ax² + bx + c
f’(x) =2ax + b
⇒ For f(x) has max. or min.
then f’(x) = 0
⇒ 2ax + b = 0
⇒ x = \(\frac{-b}{2 a}\)
Now, f”(x) = 2a
i) If a >0 then f”(x) > 0 and hence f has min. value at x = \(\frac{-b}{2 a}\)
Minimum of f = f(\(\frac{-b}{2 a}\))
= \(a\left(\frac{-b}{2 a}\right)^2+b\left(\frac{-b}{2 a}\right)+c\)
= \(a \frac{b^2}{4 a^2}-\frac{b^2}{2 a}+c\)
= \(\frac{b^2-2 b^2+4 a c}{4 a}=\frac{4 a c-b^2}{4 a}\)

ii) If a < 0 then f”(x) < 0 and hence f has max. value at x = \(\frac{-b}{2 a}\)
Maximum of f = f(\(\frac{-b}{2 a}\))
= \(a\left(\frac{-b}{2 a}\right)^2+b\left(\frac{-b}{2 a}\right)+c\)
= \(a \cdot \frac{b^2}{4 a^2}-\frac{b^2}{2 a}+c\)
= \(\frac{b^2-2 b^2+4 a c}{4 a}=\frac{4 a c-b^2}{4 a}\).

Question 13.
If x₁, x₂ are the roots of the quadratic equation ax² + bx + c = 0 and c ≠ 0, find
the value of (ax₁ + b) + (ax₂ + b) in terms of a, b, c. [TS – Mar. 2017]
Solution:
Given that x₁, x₂ are the roots of ax² + bx + c = 0
⇒ x₁ + x₂ = – b/a, x₁x₂ = c/a
also ax₁² + bx₁ + c = 0,
ax₂² + bx₂ + c = 0
⇒ x₁ (ax₁ + b) = – c,
x₂(ax₂ + b) = – c
⇒ (ax₁ + b) = – c/x₁,
(ax₂ + b) = – c/x₂
Now (ax₁ + b)^-2 + (ax₂ + b)^-2 = \(\left(\frac{-c}{x_1}\right)^{-2}+\left(\frac{-c}{x_2}\right)^{-2}=\frac{x_1^2}{c^2}+\frac{x_2^2}{c^2}=\frac{x_1^2+x_2^2}{c^2}\)
= \(\frac{\left(x_1+x_2\right)^2-2 x_1 x_2}{c^2}\)
= \(\frac{\left(\frac{-b}{a}\right)^2-2 \cdot \frac{c}{a}}{c^2}=\frac{b^2-2 a c}{c^2 a^2}\).

Some More Maths 2A Quadratic Expressions Important Questions

Question 1.
Find the roots of the equation 6√5 x² – 9x – 3√5 = 0.
Solution:
Given quadratic equation is
6√5x² – 9x – 3√5 = 0
Comparing this with ax² + bx + c = 0, we have
a = 6√5, b = – 9, c = – 3√5
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
are the roots of quadratic equation.
x = \(\frac{9 \pm \sqrt{81+360}}{12 \sqrt{5}}=\frac{9 \pm \sqrt{441}}{12 \sqrt{5}}=\frac{9 \pm 21}{12 \sqrt{5}}\)
= \(\frac{9+21}{12 \sqrt{5}} \text { (or) } \frac{9-21}{12 \sqrt{5}}\)
= \(\frac{30}{12 \sqrt{5}} \text { (or) } \frac{-12}{12 \sqrt{5}}=\frac{\sqrt{5}}{2} \text { (or) } \frac{-1}{\sqrt{5}}\)
∴ The roots of the quadratic equation are \(\frac{\sqrt{5}}{2} \text { (or) } \frac{-1}{\sqrt{5}}\).

Question 2.
Form a quadratic equation whose roots are 2√3 – 5 and – 2√3 – 5.
Solution:
Let a = 2√3 – 5, p = – 2√3 – 5
Now, a+ = 2√3 – 5 – 2√3 – 5 = – 10
= (2√3 – 5) (- 2√3 – 5) = – (12 – 25) = 13
The quadratic equation whose roots are α, β is x² – (α + β) + αβ = 0
⇒ x² + 10x + 13 = 0

Question 3.
Form a quadratic equation whose roots are \(\frac{\mathbf{m}}{\mathbf{n}}, \frac{-\mathbf{n}}{\mathbf{m}}\), (m ≠ 0, n ≠ 0).
Solution:
Let α = \(\frac{m}{n}\), β = \(\frac{-\mathrm{n}}{\mathrm{m}}\)
Now, α + β = \(\frac{m}{n}-\frac{n}{m}=\frac{m^2-n^2}{m n}\)
αβ = \(\frac{m}{n} \cdot \frac{-n}{m}\) = – 1
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
x² – \(\frac{\left(m^2-n^2\right)}{m n}\)x – 1 = 0
mnx² – (m² – n²)x – mn = 0.

Question 4.
If α, β are the roots of ax² + bx + c = 0 then find α³ + β³.
Solution:
Since a, are the roots of ax² + bx + c = 0
α + β = – \(\frac{b}{a}\), αβ = \(\frac{c}{a}\)
α³ + β³ = (α + β)³ – 3αβ(α + β)
= \(\left(\frac{-b}{a}\right)^3-3 \cdot \frac{c}{a}\left(\frac{-b}{a}\right)\)
= \(\frac{-b^3}{a^3}+\frac{3 b c}{a^2}\)
⇒ \(\frac{3 a b c-b^3}{a^3}\).

Question 5.
For what values of m, x² + (m + 3) x + (m + 6) = 0 will have equa roots?
Solution:
Given quadratic equation is x² + (m + 3) x + (m + 6) = 0 ……………(1)
Comparing this with ax² + bx c = 0 we get
a = 1, b = m + 3, c = m + 6
Since (1) have equal roots
⇒ b² – 4ac = 0
⇒ [m + 3]² – 4(1)(m + 6) = 0
⇒ m² + 9 + 6m – 4m – 24 = 0
⇒ m² + 2m – 15 = 0
⇒ m² + 5m – 3m – 15 = 0
⇒ m (m + 5) – 3 (m + 5) = 0
⇒ (m – 3) (m + 5) = 0
⇒ m = 3 (or) m = – 5
The values of m are 3, – 5.

Question 6.
For what values of m, x² – 2 (1 + 3m) x + 7(3 + 2m) = 0 will have equal roots?
Solution:
Given quadratic equation is
x² – 2 (1 + 3m) x + 7 (3 + 2m) = 0 …………….(1)
Comparing this with ax² + bx + c = 0,
we get a = 1, b = – 2 (1 + 3m), c = 7 (3 + 2m)
Since (1) have equal roots
⇒ b² – 4ac = 0
⇒ [- 2 (1 + 3m)]² – 4(1) . 7 . (3 + 2m) = 0
⇒ 4 (1 + 9m² + 6m) – 28 (3 + 2m) = 0
⇒ 9m² + 6m + 1 – 21 – 14m = 0
⇒ 9m² – 8m – 20 = 0
⇒ 9m² – 18m + 10m – 20 = 0
⇒ 9m (m – 2) + 10(m – 2) = 0
⇒ (9m + 10) (m – 2) = 0
m = \(\frac{-10}{9}\) (or) m = 2
The values of m are \(\frac{-10}{9}\), 2.

Question 7.
For what values of m, (2m + 1) x² + 2(m + 3) x + (m + 5) = 0 will have equal roots?
Solution:
Given quadratic equation is (2m + 1) x² + 2(m + 3) x + (m + 5) = 0
Comparing this with ax² + bx + c = 0,
we get a = 2m + 1, b = 2 (m + 3), c = m + 5
SInce (1) have equal roots
⇒ b² – 4ac = 0
⇒ (2 (m + 3))² – 4(2m + 1) (m + 5) = 0
⇒ 4(m² + 9 + 6m) – 4[2m² + 10m + m + 5] = 0
⇒ m² + 9 + 6m – 2m² – 11m + 5 = 0
⇒ – m² – 5m + 4 = 0
⇒ m² + 5m -4 = 0
m = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-5 \pm \sqrt{25-4(1)(-4)}}{2(1)}\)
= \(\frac{-5 \pm \sqrt{25+16}}{2}=\frac{-5 \pm \sqrt{41}}{2}\)

Question 8.
Show that the roots of the equation x² – 2px + p² – q² + 2qr – r² = 0 are rational, where p, q, r are rational.
sol.
Given that, p, q, r are rational.
Given quadratic equation is
x² – 2px + p² – q² + 2qr – r² = 0
Comparing this with ax² + bx + c = 0 we get
a = 1, b = – 2p, c = p² – q² + 2qr – r²
b² – 4ac = 4p² – 4(1) (p² – q² + 2qr – r²)
= 4p² – 4p² + 4q² – 8qr + 4r²
= 4q² – 8qr + 4r²
= 4 (q² – 2qr + r²) = 4 (q – r)² = [2 (q – r)]² ≥ 0
Since b² – 4ac ≥ 0 then the roots of the given equation are rational.

Question 9.
Find the quadratic equation, the sum of whose roots is 7 and sum of the squares of the roots is 25.
Solution:
Let α and β be the roots of a required equation.
Given that the sum of roots = 7
α + β = 7
The sum of squares of the roots = 25
αβ = 25
We know that, (α + β)² = α² + β² + 2αβ
7² = 25 + 2αβ
2αβ = 49 – 25 = 24
αβ = 12
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
x² – 7x + 12 = 0.

Question 10.
Solve the equation 3^{1 + x} + 3^{1 – x} = 10.
Solution:
Given equation is 3 . 3^x + \(\frac{3}{3^x}\) = 10
Let 3^x = a
⇒ 3a + \(\frac{3}{a}\) = 10
⇒ 3a² – 10a + 3 = 0
⇒ a² – 9a – a + 3 = 3 = 0
⇒ 3a (a – 3) – 1 (a – 3) = 0
⇒ (a – 3) (3a – 1) = 0
⇒ a = 3 (or) a = \(\frac{1}{3}\)

Case-1 :
If a = 3
⇒ 3 = 3^x
⇒ x = 1

Case – 2 :
If a = \(\frac{1}{3}\)
⇒ \(\frac{1}{3}\) = 3^x
⇒ 3^x = 3^{– 1}
⇒ x = – 1.

∴ The solution set of the given equation is {- 1, 1}.

Question 11.
Solve 7^1+x + 7^1-x = 50 for real x.
Solution:
Given equation is 7^1+x + 7^1-x = 50
7 . 7^x + \(\frac{7}{a}\) = 50 ……………..(1)
Let 7^x = a
⇒ 7a + \(\frac{7}{a}\) = 50
⇒ 7a² – 50a + 7 = 0
⇒ 7a² – 49a – a + 7 = 0
⇒ 7a (a – 7) – 1(a – 7) = 0
⇒ (a – 7) (7a – 1) = 0
⇒ a = 7 (or) \(\frac{1}{7}\)
Case – 1:
If a = 7
⇒ 7^x = 7
⇒ x = 1

Case – 2:
If a = \(\frac{1}{7}\)
⇒ 7^x = 7^-1
x = – 1
Hence the solution set of the given equation is {- 1, 1}.

Question 12.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
Given quadratic equations are x² – 6x + 5 = 0
Comparing with a₁x² + b₁x + c₁ = 0, we get
a₁ = 1, b₁ = – 6, c₁ = 5
Now, x² – 3ax + 35 = 0
Comparing with a₂x² + b₂x + c₂ = 0
we get, a₂ = 1, b₂ = – 3a c₂ = 35
The condition for two quadratic equation. to have a common root is
(c₁a₂ – c₂a₁1)2 = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁)
⇒ (5(1) – 35(1))² = (1 – 3a) – (1) – 6) (- 6(35) – (- 3a) 5)
⇒ (5 – 35)² = (- 3a + 6) (- 210 + 15a)
⇒ 900 = 3(- a + 2) 5 (- 42 + 3a)
⇒ 900 = 15(- a + 2) (- 42 + 3a)
⇒ 42a – 3a² – 84 + 6a = 60
⇒ 3a² – 48a+ 144 = 0
⇒ a² – 16a + 48 = 0
⇒ a – 12a – 4a + 48 = 0
⇒ a(a – 12) – 4(a – 12) = 0
⇒ (a – 4) (a – 12) = 0
⇒ a = 4 (or) a = 12.

Question 13.
For what values of x, the expression x² – 5x + 14 is positive?
Solution:
Given expression is x² – 5x + 14
The roots of x² – 5x + 14 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{5 \pm \sqrt{25-4 \cdot 1(14)}}{2(1)}\)
= \(\frac{5 \pm \sqrt{25-56}}{2}=\frac{5 \pm \mathrm{i} \sqrt{31}}{2}\)
which are not real.
∴ For all x ∈ R, the expression x² – 5x + 14 is + ve.

Question 14.
For what values of x, the expression 3x² + 4x + 4 is positive?
Solution:
The given quadratic expression is 3x² + 4x + 4
The roots of 3x² + 4x + 4 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{-4 \pm \sqrt{16-48}}{2(3)}\)
= \(\frac{-4 \pm \sqrt{-32}}{6}\)
= \(\frac{-2 \pm i \sqrt{8}}{3}=\frac{-2 \pm 2 \mathrm{i} \sqrt{2}}{3}\)
which are complex numbers (non real).
∴ For all x ∈ R, the expression 3x² + 4x + 4 is + ve.

Question 15.
For what values of x, the expression x² – 7x + 10 is negative?
Solution:
Given expression is x² – 7x + 10
= x² – 5x – 2x + 10
= x (x – 5) – 2 (x – 5)
= (x – 2) (x – 5)
i) If 2 < x < 5, then the expression x² – 7x + 10 is ‘- ve’.
ii) If x < 2 (or) x > 5, then the expression x² – 7x + 10 is ’+ve’.
iii) If x = 2 (or) x = 5, then the expression : x² – 7x + 10 = 0.

Question 16.
For what values of x, the expression 15 + 4x – 3x² is negative?
Solution:
Given expression is 15 + 4x – 3x²
= – 3x² + 9x – 5x + 15 = 3x (- x + 3) + 5(- x + 3)
= (3x + 5) (- x + 3)
i) If \(\frac{-5}{3}\) < x < 3, then the expression is 15 + 4x – 3×2 is ‘+ ve’.
ii) If x < \(\frac{-5}{3}\) (or) x > 3, then the expression is 15 + 4x – 3x² is ‘- ve’.
iii) If x = \(\frac{-5}{3}\) (or) x = 3,then the expression 15 + 4x – 3x² = 0.

Question 17.
Find the changes in the sign of 4x – 5x² + 2 for x ∈ R.
Solution:
Given quadratic expression is 4x – 5x² + 2
The roots of given expression are

Questi0n 18.
Find the roots of the equation 4x² – 4x + 17 = 3x² – 10x – 17.
Solution:
Given equation can be rewritten as x² + 6x + 34 = 0.
The roots of the quadratic equation, ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
Here a = 1, b = 6 and c = 34.
Therefore the roots of the given equation are \(\frac{-6 \pm \sqrt{(6)^2-4(1)(34)}}{2(1)}\)
= \(\frac{-6 \pm \sqrt{-100}}{2}\)
= \(\frac{-6 \pm 10 \mathrm{i}}{2}\) (since i² = – 1)
= – 3 + 5i, – 3 – 5i
Hence the roots of the given equation are – 3 + 5i and – 3 – 5i.

Questi0n 19.
Solve, \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\).
Solution:
Given equation is \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\)
Let \(\sqrt{\frac{x}{1-x}}\) = a
\(\sqrt{\frac{1-x}{x}}=\frac{1}{a}\)
a + \(\frac{1}{a}=\frac{13}{6}\)
⇒ 6a² + 6 = 13a
⇒ 6a² – 13a + 6 = 0
⇒ 6a² – 9a – 4a + 6 = 0
⇒ 3a (2a – 3) – 2 (2a – 3) = 0
⇒ 2a – 3 = 0, 3a – 2 = 0
⇒ 3a = 2
⇒ a = \(\frac{2}{3}\)
⇒ a = \(\frac{2}{3}\)
Case – 1:
If a = \(\frac{2}{3}\)
⇒ \(\sqrt{\frac{x}{1-x}}=\frac{2}{3}\)
⇒ \(\frac{x}{1-x}=\frac{4}{9}\)
9x = 4 – 4x
13x = 4
x = \(\frac{4}{13}\)

Case-2: .
If a = \(\frac{2}{3}\)
⇒ \(\sqrt{\frac{x}{1-x}}=\frac{3}{2}\)
⇒ \(\frac{x}{1-x}=\frac{9}{4}\)
⇒ 4x = 9 – 9x
⇒ 13x = 9
⇒ x = \(\frac{9}{13}\)
∴ The solution set of given equation is {\(\frac{9}{13}\), \(\frac{4}{13}\)}

Question 20.
Find the numbers which exceed their square root by 12.
Solution:
Let ‘x’ be any number.
Given that, x = √x + 12 ………….(1)
x – 12 = √x
⇒ squaring on both sides
⇒ x² + 144 – 24x = x
⇒ x² + 144 – 25x = 0
⇒ x² – 16x – 9x + 144= 0
⇒ x (x – 16) – 9 (x – 16) = 0
⇒ (x – 9) (x – 16) = 0
⇒ x = 9 (or) x = 16.
But x = 9 does not satisfy (1) whilex = 16 satisfy.
∴ The required number is 16.

Question 21.
Prove that there is a unique pair of con-secutive positive odd Integers such that the sum of their squares is 290 and find it.
Solution:
Since two consecutive odd integers differ by 2.
Let a pair of consecutive .ve odd integers are x, x + 2.
Given that, the sum of their squares is 290
⇒ x² + (x + 2)² = 290 ………………..(1)
⇒ x² + x² + 4 + 4x = 290
⇒ 2x² + 4x – 286 = 0
⇒ x² + 2x- 143 = 0
⇒ x² + 13x – 11x – 143 = 0
⇒ x (x + 13) – 11 (x + 13) = 0
⇒ (x – 11) (x + 13) = 0
⇒ x = 11 (or) x = – 13
Since x is positive, x = 11
Hence 11 is the only +ve odd integer satisfying equation (1).
∴ A pair of consecutive +ve odd integers are x, x + 2 = 11, 13.
∴ (11, 13) is the unique pair of integers which satisfy the given condition.

Question 22.
If α, β are the roots of the equation ax² + bx + c = 0, find the values of the following expressions in terms of a, b, c.
i) α⁴ β⁷ + α⁷ β⁴
ii) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\)
iii) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\)
Solution:
Since α, β are the roots of the equation ax² + bx + c = 0 then
α + β = \(\frac{-b}{a}\); αβ = \(\frac{c}{a}\)
i) α⁴ β⁷ + α⁷ β⁴ = α⁴β⁴ (β³ + α³)
= α⁴β⁴ (α³ + β³)
= α⁴β⁴ [(α + β)³ – 3αβ(α + β)]
= \(\left(\frac{c}{a}\right)^4\left[\left(\frac{-b}{a}\right)^3-3 \cdot \frac{c}{a} \cdot \frac{-b}{a}\right]\)
= \(\frac{c^4}{a^4}\left(\frac{-b^3}{a^3}+\frac{3 b c}{a^2}\right)\)
= \(\frac{c^4}{a^4} \frac{\left(-b^3+3 a b c\right)}{a^3}=\frac{c^4\left(3 a b c-b^3\right)}{a^7}\)

ii) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\), if c ≠ 0.

iii) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\) if c ≠ 0.
= \(\frac{\alpha^2+\beta^2}{\frac{1}{\alpha^2}+\frac{1}{\beta^2}}=\frac{\alpha^2+\beta^2}{\frac{\alpha^2+\beta^2}{\left(\alpha^2 \beta^2\right)}}\)
= (αβ)² = \(\frac{c^2}{a^2}\).

Question 23.
If x² + 4ax + 3 = 0 and 2x² + 3ax – 9 = 0 have a common root, then find the values of ‘a’ and the common roots.
Solution:
Given quadratic equations are x² + 4ax + 3 = 0
Comparing this equation with
a₁x² + b₁x + c₁ = 0
a₁ = 1, b₁ = 4a, c₁ = 3
Now 2x² + 3ax – 9 = 0
Comparing this equation with
a₂x² + b₂x + c₂ = 0
a₂ = 2, b₂ = 3a, c₂ = 9
The condition for two quadratic equations
a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0
to have a common root is
(c₁a₂ – c₂a₁)² = (a₁b₂ – b₁a₂) (b₁c₂ – c₁b₂)
⇒(3 . 2 – (- 9)(1))² = (1 . 3a – 2 . 4a) (4a (- 9) – 3a (3))
⇒ (6 + 9)² = (3a – 8a)(- 36a – 9a)
⇒ 15² = (- 5a) (- 45a)
⇒ 225 = 225a²
⇒ a² = 1
⇒ a = ± 1

Case – I:
If a = 1 then the given equation reduces to
x² + 4x + 3 = 0
x² + 3x + x + 3 = 0
x (x + 3) + 1 (x + 3) = 0
(x + 3) (x + 1) = 0
x = – 1, x = – 3

2x² + 3x – 9 = 0
2x² + 6x – 3x – 9 = 0
2x (x + 3) – 3 (x + 3) = 0
(x + 3) (2x – 3) = 0
2x = 3, x = – 3
x = \(\frac{3}{2}\)
∴ The roots of the given equation are respectively – 1, – 3 and \(\frac{3}{2}\), – 3.
In this case the common root of the given equation is – 3.

Case – II:
If a = – 1 then the given equation reduces to
x² – 4x + 3 = 0,
x²-3x-x.3 = 0
x (x – 3) – 1(x – 3) = 0
(x – 3) (x – 1) = 0
x = 3, x = 1

2x² – 3x – 9 = 0
2x² – 6x + 3x – 9 = 0
2x (x – 3) + 3 (x – 3) = 0
(x – 3)(2x + 3)=0
x = 3, 2x = – 3
x = \(\frac{-3}{2}\)
∴ The roots of the given equation are respectively 3, 1 and 3
In this case the common root of the given equation is 3.

Question 24.
Discuss the signs of the expression x² + x + 1 for x ∈ R.
Solution:
Given quadratic expression is x² + x + 1
The roots of x² + x + 1 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{-1 \pm \sqrt{1-4}}{2(1)}\)
= \(\frac{-1 \pm i \sqrt{3}}{2}\)
which are complex roots (non real)
for all x ∈ R, the expression x² + x + 1 is positive.

Question 25.
For what values of x the expression x² – 5x + 14 is positive?
Solution:
Given expression is x² – 5x + 14 = 0
The roots of x² – 5x + 14 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{5 \pm \sqrt{25-4 \cdot 1(14)}}{2(1)}\)
= \(\frac{5 \pm \sqrt{25-56}}{2}\)
= \(\frac{5 \pm i \sqrt{31}}{2}\)
which are non real.
∴ For all x ∈ R, the expression x² – 5x + 1 is +ve.

Question 26.
For what values of x the expression – 6x² + 2x – 3 is negative?
Solution:
Given quadratic expression is – 6x² + 2x -3
The roots of – 6x² + 2x – 3 = 0 is

which are non real.
Here the coefficient of x² is – ve’.
∴ x ∈ R, the expression – 6x² + 2x – 3 is ‘-ve’.

Question 26.
Find the value of x at which the following expressions have maximum or minimum?
i) x² + 5x + 6
ii) 2x – x² + 7
Solution:
i) x² – 5x – 6
Given quadratic expression is x² + 5x + 6
Comparing this expression with ax² + bx + c
We have a = 1, b = 5, c = 6
Here a = 1 > 0. x² + 5x + 6 has minimum at
x = \(\frac{-\mathrm{b}}{2 \mathrm{a}}\)
x = \(\frac{-5}{2(1)}=\frac{-5}{2}\)

ii) 2x – x² + 7
Given quadratic expression is – x² + 2x + 7
Comparint. this expression with ax² + bx + c
we get. a = – 1, b = 2, c = 7
Here, a = – 1 < 0 – x² + 2x + 7 has absolute maximum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(-1)}\) = 1.

Question 27.
Solve 2x⁴ + x³ – 11x² + x + 2 = 0. [TS – Mar. 2015]
Solution:
Given equation is 2x⁴ + x³ – 11x² + x + 2 = 0

Let x + \(\frac{1}{x}\) = t
⇒ 2t² + t – 15 = 0
⇒ 2t² + 6t – 5t – 15 = 0
⇒ 2t (t + 3) – 5 (t + 3) = 0
⇒ (t + 3) (2t – 5) = 0
⇒ t + 3 = 0
⇒ x + \(\frac{1}{x}\) + 3 = 0
⇒ \(\frac{x^2+1+3 x}{x}\) = 0
⇒ x² + 3x + 1 = 0
⇒ x = \(\frac{-3 \pm \sqrt{9-4}}{2}\)
∴ x = \(\frac{-3 \pm \sqrt{5}}{2}\)
⇒ 2t – 5 = 0
⇒ 2 (\(\left(x+\frac{1}{x}\right)\)) – 5 = 0
⇒ \(\frac{2 x^2+2-5 x}{x}\) = 0
= 2x² – 5x + 2 = 0
2x² – 4x – x + 2 = 0
2x (x – 2) – 1 (x – 2) = 0
(x – 2) (2x – 1) = 0
∴ x = 2, ½
∴ Solution set = \(\left\{\frac{-3 \pm \sqrt{5}}{2}, 2 . \frac{1}{2}\right\}\).

Question 28.
For what values of x the expression x² – 5x – 14 is positive. [AP-Mar. 2018]
Solution:
x² – 5x – 14 = (x + 2) (x – 7)
The roots of x² – 5x – 14 = 0 are – 2, 7.
Here coeff. x² is 1. This is positive.
So x < – 2 or x > 7 then x² – 5x – 14 is positive.

Question 29.
Find the set of solutions of x² + x – 12 ≤ 0 by algebraic method. [TS – Mar. 2019]
Solution:
Algebraic method:
x² + x – 12 = 0
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4) (x -3) = 0
⇒ x = – 4 or 3
⇒ x² + x – 12 ≤ 0
⇒ – 4 ≤ x ≤ 13

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Parabola Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Parabola Important Questions Very Short Answer Type

Question 1.
Find the vertex and focus, and the equations of the directrix and axis of the parabola y² = 16x.
Solution:
Given parabola is y² = 16x
Compare with y² = 4ax
we get 4a = 16 ⇒ a = 4
Vertex A = (0, 0)
Focus S = (a, 0) = (4, 0)
The equation of the directrix is x + a = 0
⇒ x + 4 = 0
The equation of the axis is y = 0

Question 2.
Find the equations of the axis and directrix of the parabola y² + 6y – 2x + 5 = 0.
Solution:
Given equation of the parabola is y² + 6y – 2x + 5 = 0
⇒ y² + 6y = 2x – 5
⇒ (y)² + 2 . y . 3 + (3)² – (3)² = 2x – 5
⇒ (y + 3)² – 9 = 2x – 5
⇒ (y + 3)² = 2x + 4
⇒ (y + 3)² = 2(x + 2)
⇒ [y – (-3)]² = 2[x – (-2)]
Comparing with (y – k)² = 4a(x – h), we get
h = -2, k = -3,
4a = 2 ⇒ a = \(\frac{1}{2}\)
(i) Equation of the axis is y = k
⇒ y = -3
⇒ y + 3 = 0
(ii) Equation of the directrix is x = h – a
⇒ x = -2 – \(\frac{1}{2}\)
⇒ x = \(\frac{-5}{2}\)
⇒ 2x + 5 = 0

Question 3.
Find the coordinates of the vertex and focus, the equation of the directrix, and the axis of the parabola x² – 2x + 4y – 3 = 0.
Solution:
Given the equation of the parabola is
x² – 2x + 4y – 3 = 0
⇒ x² – 2x = -4y + 3
⇒ (x)² – 2 . x . (1) + (1)² – (1)² = -4y + 3
⇒ (x – 1)² – 1 = -4y + 3
⇒ (x – 1)² + 0 = -4y + 4
⇒ (x – 1)² = -4(y – 1)
Comparing with (x – h)² = -4a(y – k), we get
h = 1, k = 1, 4a = 4 ⇒ a = 1
(i) Vertex = (h, k) = (1, 1)
(ii) Focus = (h, k – a) = (1, 1 – 1) = (1, 0)
(iii) Equation of the directrix is y = k + a
⇒ y = 1 + 1
⇒ y = 2
⇒ y – 2 = 0
(iv) Equation of the axis is x = h
⇒ x = 1
⇒ x – 1 = 0

Question 4.
Find the vertex and focus of x² – 6x – 6y + 6 = 0.
Solution:
Given the equation of the parabola is
x² – 6x – 6y + 6 = 0
⇒ x² – 6x = 6y – 6
⇒ (x)² – 2 . (x) . (3) + (3)² – (3)² = 6y – 6
⇒ (x – 3)² – 9 = 6y – 6
⇒ (x – 3)² = 6y + 3
⇒ (x – 3)² = 6(y + \(\frac{1}{2}\))
⇒ (x – 3)² = 6(y – (\(-\frac{1}{2}\)))
Comparing with (x – h)² = 4a(y – k), we get
h = 3, k = \(\frac{-1}{2}\), 4a = 6 ⇒ a = \(\frac{3}{2}\)
(i) Vertex = (h, k) = (3, \(\frac{-1}{2}\))
(ii) Focus = (h, k + a) = (3, \(\frac{-1}{2}+\frac{3}{2}\)) = (3, 1)

Question 5.
Find the coordinates of the vertex and focus and the equations of the directrix and axis of the parabola x² = -4y.
Solution:
Given parabola is x² = -4y
Comparing with x² = -4ay
we get 4a = 4 ⇒ a = -1
Vertex A = (0, 0)
Focus S = (0, -a) = (0, -1)
The equation of the directrix is y – a = 0
⇒ y – 1 = 0
The equation of the axis is x = 0.

Question 6.
Find the equation of the parabola whose vertex is (3, -2) and focus is (3, 1). [(AP) Mar. ’20, May ’17; (TS) May ’19, Mar. ’18]
Solution:
Given that Vertex = (3, -2)
Focus = (3, 1)
In abscissae of the vertex and focus are equal to 3.
Hence the axis of the parabola is x = 3, a line parallel to Y-axis.
a = distance between focus and vertex
= \(\sqrt{(3-3)^2+(-2-1)^2}\)
= 3
Since in vertex y-coordinate is less than the y-coordinate of focus.
∴ The equation of the parabola is (x – h)² = 4a(y – k)
⇒ (x – 3)² = 4(3) (y + 2)
⇒ (x – 3)² = 12(y + 2)

Question 7.
Find the equations of the parabola whose focus is S(1, -7) and vertex is A(1, -2). [(TS) May & Mar. ’15]
Solution:
Given that,
Focus, S = (1, -7)
Vertex, A(h, k) = (1, -2)
In vertex and focus, x-coordinates are equal to 1.
Hence, the axis of the parabola is x = 1, a line parallel to Y-axis,
a = distance between focus and vertex.
= \(\sqrt{(1-1)^2+(-7+2)^2}\)
= \(\sqrt{0+(-5)^2}\)
= √25
= 5
The y-coordinates of the vertex are greater than the y-coordinate of focus.
Focus is below the vertex.
∴ Equation of the parabola is (x – h)² = -4a(y – k)
⇒ (x – 1)² = -4(5) (y + 2)
⇒ (x – 1)² = -20(y + 2)

Question 8.
Find the coordinates of the points on the parabola y² = 2x whose focal distance is \(\frac{5}{2}\). [(AP) May & Mar. ’15]
Solution:

Given the equation of the parabola is y² = 2x
Comparing with y² = 4ax, we get
4a = 2 ⇒ a = \(\frac{1}{2}\)
Let, P(x₁, y₁) be a point on the parabola y² = 2x
Given that, focal distance = \(\frac{5}{2}\)
⇒ x₁ + a = \(\frac{5}{2}\)
⇒ x₁ + \(\frac{1}{2}\) = \(\frac{5}{2}\)
⇒ x₁ = 2
Since P(x₁, y₁) lies on the parabola y² = 2x then
⇒ \(\mathrm{y}_1^2\) = 2x₁
⇒ \(\mathrm{y}_1^2\) = 2(2)
⇒ \(\mathrm{y}_1^2\) = 4
⇒ \(\mathrm{y}_1^2\) = ±2
∴ The required points are (2, 2), (2, -2).

Question 9.
Find the coordinates of the point on the parabola y² = 8x whose focal distance is 10. [(AP) May ’19, Mar. ’17, ’16; (TS) May & Mar. ’17; 14]
Solution:

Given the equation of the parabola is y² = 8x
Comparing with y² = 4ax, we get
4a = 8 ⇒ a = 2
Let P(x1, y1) be a point on the parabola y² = 8x
Given that focal distance = 10
⇒ x₁ + a = 10
⇒ x₁ + 2 = 10
⇒ x₁ = 8
Since P(x₁, y₁) lies on the parabola then \(\mathrm{y}_1^2\) = 8x₁
⇒ \(\mathrm{y}_1^2\) = 8(8)
⇒ \(\mathrm{y}_1^2\) = 64
⇒ \(\mathrm{y}_1^2\) = ±8
∴ The required points are (8, 8), (8, -8).

Question 10.
If (\(\frac{1}{2}\), 2) is one extremity of a focal chord of the parabola y² = 8x. Find the coordinates of the other extremity. [(AP) May ’18, (TS) ’16; ’14]
Solution:

Given the equation of the parabola is y² = 8x
Comparing with y² = 4ax, we get
4a = 8 ⇒ a = 2
Given that one end of the focal chord is P = (\(\frac{1}{2}\), 2)
Let other end of the focal chord is Q(x, y) = \((\frac{1}{2}\), 2)
‘PSQ’ is a focal chord.
Since P, S, Q are collinear then
slope of \(\overline{\mathrm{SP}}\) = slope of \(\overline{\mathrm{SQ}}\)
⇒ \(\frac{2-0}{\frac{1}{2}-2}=\frac{y-0}{\frac{y^2}{8}-2}\)
⇒ \(\frac{2}{\frac{-3}{2}}=\frac{y}{\frac{y^2-16}{8}}\)
⇒ \(\frac{4}{-3}=\frac{8 y}{y^2-16}\)
⇒ y² – 16 = -6y
⇒ y² + 6y – 16 = 0
⇒ y² + 8y – 2y – 16 = 0
⇒ y(y + 8) – 2(y + 8) = 0
⇒ (y + 8)(y – 2) = 0
⇒ y + 8 = 0 or y – 2 = 0
⇒ y = -8 or y = 2
If y = -8 then Q = (8, -8)
If y = 2 then Q = (\(\frac{1}{2}\), 2)
∴ Other end of the focal chord Q = (8, -8)

Question 11.
Prove that the point on the parabola y² = 4ax (a > 0) nearest to the focus is its vertex.
Solution:
Given equation of the parabola is y² = 4ax (a > 0)

Let P(at², 2at) be a point on the parabola y² = 4ax
Which is nearest to the focus, S(a, 0), then
SP = \(\sqrt{\left(a t^2-a\right)^2+(2 a t-0)^2}\)
⇒ SP = \(\sqrt{\left(a t^2-a\right)^2+4 a^2 t^2}\)
⇒ SP² = (at² – a)² + 4a²t²
⇒ SP² = a²(t² – 1)² + 4a²t²
Let f(t) = a²(t² – 1)² + 4a²t²
f'(t) = a² . 2(t² – 1) . 2t + 4a² . 2t
= 4a²t(t² – 1) + 8a²t
= 4a²t(t² – 1 + 2)
= 4a²t (t² + 1)
= 4a²(t³ + 1)
for minimum value of f(t), then f'(t) = 0
4a²t(t² + 1) = 0 ⇒ t = 0
f”(t) = 4a²(3t² + 1)
If t = 0, then f”(0) = 4a² > 0
∴ At t = 0, f(t) is minimum
Then P = [a(0)², 2a(0)] = (0, 0)
∴ The point on the parabola y² = 4ax, which is nearest to the focus is its vertex A(0, 0).

Question 12.
Find the equation of the parabola whose vertex and focus are on the positive X-axis at a distance ‘a’ and a’ from the origin respectively.
Solution:

Since the vertex and focus are on the positive X-axis
∴ The equation of the parabola is
(y – k)² = 4a(x – h) ………..(1)
Now, given that OA = a
vertex, A(h, k) = (a, 0)
a = SA = a’ – a
∴ The equation of the parabola is
(y – 0)² = 4(a’ – a) (x – a)
⇒ y² = 4(a’ – a) (x – a)

Question 13.
Find the value of k if the line 2y = 5x + k is a tangent to the parabola y² = 6x. [(TS) May ’18, Mar. ’16, (AP) ’18]
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax, we get
4a = 6 ⇒ a = \(\frac{3}{2}\)
Given the equation of the straight line is
2y = 5x + k
⇒ y = \(\frac{5}{2} x+\frac{k}{2}\)
Comparing with y = mx + c, we get
m = \(\frac{5}{2}\), c = \(\frac{k}{2}\)
Given that the line y = \(\frac{5}{2} x+\frac{k}{2}\) is tangent to the parabola y² = 6x then c = \(\frac{a}{m}\)
⇒ \(\frac{k}{2}=\frac{3 / 2}{5 / 2}\)
⇒ \(\frac{k}{2}=\frac{3}{5}\)
⇒ k = \(\frac{6}{5}\)

Question 14.
Find the equation of a tangent to the parabola y² = 16x inclined at an angle of 60° with its axis and the point of contact. [(AP) May ’16]
Solution:

Given the equation of the parabola is y² = 16x
Comparing with y² = 4ax we get a = 4
Given that inclination of a tangent θ = 60°
The slope of the tangent, m = tan θ
= tan 60°
= √3
∴ The equation of the tangent

Question 15.
Find the condition for the straight line lx + my + n = 0 to be a tangent to the parabola y² = 4ax and find the coordinates of the point of contact. (Mar. ’99, ’93)
Solution:

Suppose lx + my + n = 0 …….(1)
be a tangent to the parabola y² = 4ax
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at ‘P’ is S₁ = 0
yy₁ – 2a(x + x₁) = 0
yy₁ – 2ax – 2ax₁ = 0
2ax – y₁y + 2ax₁ = 0 ……….(2)
Now (1) & (2) represent the same line

∴ Point of contact P(x₁, y₁) = \(\left(\frac{\mathbf{n}}{l}, \frac{-2 \mathrm{am}}{l}\right)\)
Suppose ‘P’ lies on the lx + my + n = 0, lx₁ + my₁ + n = 0
⇒ \(l\left(\frac{\mathrm{n}}{l}\right)+\mathrm{m}\left(\frac{-2 \mathrm{am}}{l}\right)+\mathrm{n}=0\)
⇒ ln – 2am² + ln = 0
⇒ 2ln – 2am² = 0
⇒ ln – am² = 0
⇒ am² = ln

Question 16.
Find the equation of the tangent and normal to the parabola x² – 4x – 8y + 12 = 0 at (4, \(\frac{3}{2}\)).
Solution:
Given equation of the parabola is x² – 4x – 8y + 12 = 0
given point P(x₁, y₁) = (4, \(\frac{3}{2}\))
∴ The equation of the tangent is S₁ = 0
⇒ xx₁ – 2(x + x₁) – 4(y + y₁) + 12 = 0
⇒ x(4) – 2(x + 4) – 4(y + \(\frac{3}{2}\)) + 12 = 0
⇒ 4x – 2x – 8 – 4y – 6 + 12 = 0
⇒ 2x – 4y – 2 = 0
⇒ x – 2y – 1 = 0
Slope of x – 2y – 1 = 0 is m = \(\frac{-1}{-2}=\frac{1}{2}\)
Slope of normal is \(\frac{-1}{m}=\frac{-1}{\frac{1}{2}}\) = -2
∴ Equation of normal at (4, \(\frac{3}{2}\)) is
⇒ y – \(\frac{3}{2}\) = -2(x – 4)
⇒ \(\frac{2 y-3}{2}\) = -2x + 8
⇒ 2y – 3 = -4x + 16
⇒ 4x + 2y – 19 = 0

Question 17.
Find the equation of the normal to the parabola y² = 4x which is parallel to y- 2x + 5 = 0. [(TS) Mar. ’19]
Solution:
Given the equation of the parabola is y² = 4x
∴ a = 1
Given the equation of the straight line is y – 2x + 5 = 0
slope m = \(\frac{-(-2)}{1}\) = 2
slope of normal = 2
equation of the normal at ‘t’ is y + xt = 2at + at³
∴ slope = -t = 2
⇒ t = -2
equation of the normal is
y – 2x = 2 . 1(-2) + 1(-2)
⇒ y – 2x = -4 – 8
⇒ y – 2x = -12
⇒ 2x – y – 12 = 0

Question 18.
Show that the equation of the tangent to the parabola y² = 4ax at the point ‘t’ is yt = x + at².
Solution:
Given the equation of the parabola is y2 = 4ax
Given a point on the parabola is P(at², 2at)
The equation of the tangent at P(at², 2at) is S₁ = 0
⇒ yy₁ – 2a(x + x₁) = 0
⇒ y(2at) – 2a(x + at²) = 0
⇒ yt – (x + at²) = 0
⇒ yt = x + at²

Question 19.
Find the equations of the tangent and normal to the parabola y² = 6x at the positive end of the latus rectum. [(TS) Mar. ’20]
Solution:

Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax we get
4a = 6 ⇒ a = \(\frac{3}{2}\)
The positive end of the latus rectum,
L = (a, 2a) = (\(\frac{3}{2}\), 3)
The equation of the tangent at L(\(\frac{3}{2}\), 3) to the parabola y² = 6x is S₁ = 0
⇒ yy₁ – 2a(x + x₁) = 0
⇒ \(y(3)-2\left(\frac{3}{2}\right)\left(x+\frac{3}{2}\right)=0\)
⇒ \(3 y-3\left(x+\frac{3}{2}\right)=0\)
⇒ 3y – 3x – \(\frac{9}{2}\) = 0
⇒ 6y – 6x – 9 = 0
⇒ 2x – 2y + 3 = 0
The equation of the normal at L(\(\frac{3}{2}\), 3) to the parabola y² = 6x is
y – y₁ = \(\frac{-y_1}{2 a}\) (x – x₁)
⇒ y – 3 = \(\frac{-3}{2\left(\frac{3}{2}\right)}\left(x-\frac{3}{2}\right)\)
⇒ y – 3 = \(-1\left(x-\frac{3}{2}\right)\)
⇒ y – 3 = \(\frac{-2 x+3}{2}\)
⇒ 2y – 6 = -2x + 3
⇒ 2x + 2y – 9 = 0

Question 20.
Show that the line 2x – y + 2 = 0 is a tangent to the parabola y² = 16x. Find the point of contact also.
Solution:
Given the equation of the parabola is y² = 16x
Comparing with 4ax = y² we get
4a = 16 ⇒ a = 4
Given the equation of the straight line is 2x – y + 2 = 0
⇒ y = 2x + 2
Comparing with y = mx + c we get
m = 2, c = 2
Now, c = 2
\(\frac{\mathrm{a}}{\mathrm{m}}=\frac{4}{2}\) = 2
⇒ c = \(\frac{\mathrm{a}}{\mathrm{m}}\)
∴ The line 2x – y + 2 = 0 is a tangent to the parabola y² = 16x
∴ Point of contact, P = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)
= \(\left(\frac{4}{(2)^2}, \frac{2 \cdot 4}{2}\right)\)
= (1, 4)

Question 21.
Find the position of the point (6, -6) with respect to the parabola y² = 6x.
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax,
we get 4a = 6 ⇒ a = \(\frac{3}{2}\)
Let the given point A(x₁, y₁) = (6, -6)
Now \(S_{11}=y_1{ }^2-4 a x_1\)
= (-6)² – 4(\(\frac{3}{2}\))(6)
= 36 – 36
= 0
Since S₁₁ = 0, then the point A(6, -6) lies on the parabola y² = 6x.

Question 22.
Find the position of the point (0, 1) with respect to the parabola y² = 6x.
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax,
we get 4a = 6 ⇒ a = \(\frac{3}{2}\)
Let the given point A(x₁, y₁) = (0, 1)
Now \(S_{11}=y_1{ }^2-4 a x_1\)
= (1)² – 4(\(\frac{3}{2}\))(0)
= 1 > 0
Since S₁₁ > 0, then the point A(0, 1) lies outside the parabola y² = 6x.

Question 23.
Find the position of the point (2, 3) with respect to the parabola y² = 6x.
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax,
we get 4a = 6 ⇒ a = \(\frac{3}{2}\)
Let the given point A(x₁, y₁) = (2, 3)
Now \(S_{11}=y_1{ }^2-4 a x_1\)
= (3)² – 4(\(\frac{3}{2}\))(2)
= 9 – 12
= -3 > 0
Since S₁₁ < 0, then the point A(2, 3) lies inside the parabola y² = 6x.

Question 24.
A comet moves in a parabolic orbit with the sun in a focus. When the comet is 2 × 10⁷ km from the sun, the line from the sun to it makes an angle π/2 with the axis of the orbit Find how near the comet comes to the sun.
Solution:
Suppose, the equation of the parabolic orbit of the comet is y² = 4ax.

P is the position of the comet,
given ∠XSP = π/2
SP is perpendicular to the axis of the parabola
SP is the semi latus rectum
2a = 2 × 10⁷
⇒ a = 10⁷ km
∴ The nearest point on the parabola is 10⁷ km from the sun.

Question 25.
A double ordinate of the curve y² = 4ax is of length 8a. Prove that the line from the vertex to it is at right angles.
Solution:
Given equation of the parabola is y² = 4ax.

Let P = (at², 2at) and P’ = (at², -2at) be the ends of double ordinate PP’
given that, the length of the double ordinate = 8a

Question 26.
Find the length of the latus rectum of the parabola y² = 4ax.
Solution:
The equation of the parabola is y² = 4ax …….(1)

Let LSL’ be the latus rectum of the parabola.
Let LL’ be the length of the latus rectum of the parabola y² = 4ax.
If SL = l, then L = (a, l)
Since L lies on the parabola, y² = 4ax, then
l² = 4a × a
⇒ l² = 4a²
⇒ l = 2a
∴ SL = 2a
Now LL’ = 2SL = 2(2a) = 4a
∴ Length of the latus rectum = 4a.

Question 27.
Prove that the equation of the normal to the parabola y² = 4ax at P(x₁, y₁) is y – y₁ = \(\frac{-\mathbf{y}_1}{2 a}\)(x – x₁).
Solution:
Let S = y² – 4ax = 0 be the given parabola.

The slope of the tangent at P is
m = \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\mathrm{P}}=\frac{2 \mathrm{a}}{\mathrm{y}_1}\)
The slope of the normal at
P = \(\frac{-1}{m}=\frac{-1}{\frac{2 a}{y_1}}=\frac{-y_1}{2 a}\)
∴ The equation of the normal at P is
y – y₁ = \(\frac{-1}{m}\)(x – x₁)
y – y₁ = \(\frac{-y_1}{2 a}\)(x – x₁)

Telangana TSBIE TS Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism

Very Short Answer Type Questions

Question 1.
What is the importance of Oersted’s experiment? [AP May ’18; TS Mar. ’17, May ’14]
Answer:
Oersted concluded that moving charges (or) currents produces a magnetic field in the surrounding space.

Question 2.
State Ampere’s law and Biot – Savart law.
Answer:
Ampere’s circuital law :-
The total magnetic flux coming out of a current carrying conductors enclosed in a perpendicular plane is p0 times greater than the alzebraic sum of currents (I_encl) enclosed by all the conductors in that plane.
\(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{I_{encl}}\)

Biot – Savart’s Law :
The magnetic field (dB) due to a current carrying element (dl) at any point r from the conductor is given by

Question 3.
Write the expression for the magnetic induction at any point on the axis of a circular current – carrying coil. Hence, obtain an expression for the magnetic induction at the centre of the circular coil.
Answer:
(i) Magnetic induction of any point x on the axis of a coil of radius (R) is

(ii) At centre of the coil (x = 0);

Question 4.
A circular coil of radius ‘r’ having N turns carries a current “i”. What is its magnetic moment?
Answer:
Magnetic induction at the centre of the coil
B = \(\frac{\mu_0}{2} \frac{\mathrm{i}}{\mathrm{R}}\)
For n turns the total magnetic field = (n times more)
∴ B = \(\frac{\mu_0}{2} \frac{\mathrm{ni}}{\mathrm{R}}\)

Question 5.
What is the force on a conductor of length L carrying a current “i” placed in a magnetic field of induction B? When does it become maximum?
Answer:
Let a conductor of length L’ and current i through it is placed in a magnetic field B then force on it F = i (\(\overline{\mathrm{L}}\times\overline{\mathrm{B}}\)) = i LB sin θ where θ = the angle between the length of conductor (L) and magnetic field direction \(\overline{\mathrm{B}}\). Force on current carrying conductor is maximum when tlie conductor makes an angle θ = 90° with magnetic field (F_man) = iLB.

Question 6.
What is the force on a charged particle of charge “q” moving with a velocity “v” in a uniform mangnetic field of induction B? When does it become maximum?
Answer:
Let a charge q is moving with a velocity v in a magnetic field B then force on the charged particle F = q(\(\overline{\mathrm{v}}\times\overline{\mathrm{B}}\)) =q\(\overline{\mathrm{v}}\)B sin θ. Where ‘θ’ is the angle between the direction of velocity (\(\overline{\mathrm{v}}\)) and direction of magnetic field (\(\overline{\mathrm{B}}\)).

Force on charged particle is maximum when it moves perpendicular to the magnetic field.
i. e., when θ = 90° ⇒ F_max = qvB

Question 7.
Distinguish between ammeter and voltmeter. [AP Mar. 18, 17, 15; May 17, 16; TS June 15]
Answer:

Question 8.
What is the principle of a moving coil galvanometer? [TS May ’16]
Answer:
Principle of moving coil galvanometer :
When a current carrying coil placed in a radial magnetic field is free to rotate then torque acting on it is τ = NIAB.

In M. C. G deflection torque (τ = NIBA) is produced by the current in the coil. Restoring torque is produced by torsional constant (K) of the spring. At equilibrium deflection θ = (\(\frac{NAB}{k}\))I

Question 9.
What is the smallest value of current that can be measured with a moving coil galvanometer?
Answer:
The smallest value of current that can be measured with moving coil galvanometer is in the order of 10^-6 to 10^-12 amperes.

Generally galvanometers will give full scale deflections for few micro amperes (µA)

Question 10.
How do you convert a moving coil galva-nometer into an ammeter? [AP Mar. 19, May 18, June 15; TS May 18, Mar. 18]
Answer:
A M.C.G is converted into an ammeter by connecting a low resistance (shunt) in parallel to it.
Shunt S = \(\frac{R_G}{n-1}\) where R_G = Resistance of galvanometer.
n = Ratio of currents \(\frac{i}{i_g}\)

Question 11.
How do you convert a moving coil galvanometer into a voltmeter? [AP May. 18. Mar. 16, 15; TS Mar. 16. 15]
Answer:
A M.C.G can be converted into a voltmeter by connecting a high resistance in series with it.
Series resistance R_s = (V/i_g – R_G)
V = Potential to be measured; i = maximum current through M.C.G
R_g = Resistance of M.C.G

Question 12.
What is the relation between the permittivity of free space ε₀, the permeability of free space µ₀, and the speed of light in vacuum?
Answer:
Relation between permittivity of free space ε₀ and permeability of free space µ₀is

Question 13.
A current carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic field be set up in such a manner that the loop turns about the vertical axis?
Answer:
No.

Question 14.
A current carrying circular loop is placed in a uniform external magnetic field. If the loop is free to turn, what is its orientation when it is achieves stable equilibrium?
Answer:
When a current carrying loop is placed in a uniform magnetic field the most stable state of equilibrium is magnetic moment of the loop (\(\overline{\mathrm{m}}\) = iA) and magnetic field \(\overline{\mathrm{B}}\) are parallel to each other, (i.e., θ = 0 between \(\overline{\mathrm{m}}\) and \(\overline{\mathrm{B}}\))

Question 15.
A wire loop of irregular shape carrying current is placed in an external magnetic field. If the wire is flexible, what shape will the loop change to? Why?
Answer:
If a flexible wire loop carrying current is placed in an external magnetic field it will attain circular shape.

Due to flow of charges (i.e., current) in the loop a force F = Bqv is acting at every point of flexible loop. So it attains circular shape.

Short Answer Questions

Question 1.
State and explain Biot – Savart’s law. [AP Mar. 18. 17, 16, May 14; TS Mar. 17, 16]
Answer:
According to Biot – Savart’s Law,

1. The magnitude of magnetic field dB is proportional to the current [dB α I]
2. Magnetic field dB is proportional to length of current carrying element [dB α dl]
3. Since of the angle between the current carrying element and the line joining the midpoint of the element and the given point and
4. Magnetic field dB is inversely proportional to the square of the distance ‘r’ of given point from the current carrying element dB α \(\frac{1}{r^2}\).

2) θ = the angle between the current carrying element d/ and the line joining the conductor and the given point.

Question 2.
State and explain Ampere’s law. [TS Mar. ’18]
Answer:
Ampere’s law :
The magnetic field lines emerging out of a long straight current carrying conductor are in the form of anti clock wise concentric circles with the wire at their centre.

The magnetic field emerging out through a small element dl is given by \(\overline{\mathrm{B}} \cdot \mathrm{d} \bar{l}=\overline{\mathrm{B}} \cdot \mathrm{d} \bar{l} \cos \theta\)

Here B and d/ are parallel to each other, so cos θ = 1.
Total magnetic field due to the entire loop \(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{i}\)

Ampere’s circuital Law :
Total magnetic field coming out of a current carrying conductor in a perpendicular plane is times greater than the current flowing through it.

1. If there are number of conductors ‘n’ in an enclosure then i is the alzebraic sum of currents in that enclosure and total magnetic field \(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{I_{encl}}\)
2. Ampere’s circuital law is valid to a closed loop of any shape.

Question 3.
Find the magnetic induction due to a long current carrying conductor. [AP June ’15]
Answer:
Consider a long straight conductor perpendicular to plane of paper, carrying a current I. Then the magnetic field lines emerging out of the conductor are in the plane of the paper. These magnetic field lines will form concentric circles with the conductor at the centre.

Take a small element d/ on the circle which is at a distance ‘r’ from the wire \(\overline{\mathrm{B}} \cdot \mathrm{d} \bar{l}\)
= B dl cos θ where (\(\overline{\mathrm{B}}\)) and d\(\overline{\mathrm{l}}\) are in same direction. (θ = 0°)

Total magnetic field due to a straight current carrying conductor B = \(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{I}\)
From Ampere’s law total magnetic field = µ₀ I

∴ Magnetic field of any point due to a straight current carrying conductor B = \(\frac{\mu_0}{2 \pi} \frac{I}{r}\)

Question 4.
Derive an expression for the magnetic induction at the centre of a current carry-ing circular coil using Biot – Savart’s law. [TS May ’16]
Answer:
Consider a circular loop of radius ‘R’ carrying a current i. P is a point on the axis of the coil (say X – axis).
From Biot – Savart’s law magnetic field at any point can be written as

Element d/ is on Y axis and point P is in XY – plane.
∴ \(|\mathrm{d} \bar{l} \times \overline{\mathbf{r}}|\) = rdl

The magnetic field at ‘P’ makes some angle ‘θ’ with X – axis. So resolve d \(\overline{\mathrm{B}}\) into two perpendicular components say d\(\overline{\mathrm{B}}_{x}\) and d \(\overline{\mathrm{B}}\)⊥. Sum of d\(\overline{\mathrm{B}}\)⊥ is zero. Because d\(\overline{\mathrm{B}}\)⊥ component by an element d/ is cancelled by another diametrically opposite component.

Question 5.
Derive an expression for the magnetic induction (B) at a point on the axis of a current carrying circular coil using Biot – Savart’s law. [TS May ’16]
Answer:
Consider a circular loop of radius ‘R’ carrying a current i and P is a point on the axis of the coil (say X – axis).
From Biot – Savart’s law magnetic field at

The magnetic field at ‘P’ makes some angle ‘0’ with X – axis. So resolve d\(\overline{\mathrm{B}}\) into two perpendicular components say d\(\overline{\mathrm{B}}_{x}\) and d\(\overline{\mathrm{B}}\)⊥. Sum of d\(\overline{\mathrm{B}}\)⊥ is zero. Because d\(\overline{\mathrm{B}}\)⊥ component by an element dl is cancelled by another diametrically opposite component. From fig d\(\overline{\mathrm{B}}_{x}\) = dB. cos θ. Where

Question 6.
Obtain an expression for the magnetic dipole moment of a current loop.
Answer:
Let a rectangular loop of length ‘l’, breadth ‘b’ is placed in a uniform magnetic field B. Let a current I is passed through the loop. Now force on each side F₁ = F₂ = I b. B

Current passes through the loop in opposite direction, so F₁ and F₂ are opposite. So F₁ and F₂ forms a couple.

Let the coil is rotated by an angle θ then the perpendicular distance between F and B is a/2 cos θ.
∴ Total torque
τ = IbB.\(\frac{a}{2}\)sin θ + IbB.\(\frac{a}{2}\)sinθ = I(ab)B sinθ = IAB sinθ
Torque τ = moment of force couple = Force x ⊥^lr distance
Here we are defining a new term called a magnetic dipole moment of the loop \(\overline{\mathrm{m}}\) = IA.
∴ Torque τ = \(\overline{\mathrm{mB}}\)sinθ = \(\overline{\mathrm{m}}\times\overline{\mathrm{B}}\)
This is similar to torque τ = \(\overline{\mathrm{r}}\times\overline{\mathrm{F}}\)
∴ Magnetic dipole moment \(\overline{\mathrm{m}}\) = IA for a loop of one turn.
\(\overline{\mathrm{m}}\) = nIA for a coil of n turns.

Question 7.
Derive an expression for the magnetic dipole moment of a revolving electron. [AP Mar. ’16]
Answer:
Let an electron (e) be revolving around the nucleus in a circular path of radius r’. Current I = number of electrons flowing per second.

Dipolement ot electron
Let time period of revolution of electron = T
Then current I = \(\frac{e}{T}\) But T = \(\frac{2\pi r}{υ}\)
∴ I = eν/2πr
Magnetic moment is associated with a circulating current in a loop or closed path. Magnetic moment (M) = IA.
Here magnetic moment is represented by µ_r.

The direction of this magnetic moment is into the plane of the paper.

Question 8.
Explain how crossed E and B fields serve as a velocity selector.
Answer:
Let a charge ‘q’ is moving with a velocity in the presence of both electric field E and magnetic field B. Let these two fields are perpendicular to each other and also perpendicular to the velocity of the particle.
Force due to electric field F_E = qE
Force due to magnetic field F_B = qvB
Let the two fields are adjusted such that force applied by the two fields are equal and opposite. Then total force on the charged particle is zero.

Now qE = qvB (or) v = \(\frac{E}{B}\)

∴ Velocity of charged particle (v) is the ratio of strength of electric field E and magnetic field B.

So crossed electric field E and magnetic field B will serve as a velocity selector because only particles with a velocity v = \(\frac{E}{B}\) will pass undeflected through crossed electric and magnetic fields.

Question 9.
What are the basic components of a cyclotron? Mention its uses? [AP May ’16]
Answer:
Cyclotron is used to accelerate the charged particles.

The main parts of cyclotron are

1. ‘D’ shaped metal boxes called dees
2. Variable electric field
3. Variable magnetic field and
4. A Radio frequency oscillator.

1) Dees : Two ‘D’ shaped metal boxes are placed side by side with a small gap between them. An exit port is provided to one of the Dee’.

2) Electric field E is useful to accelerate the charged particles in the gap between the dees, electric field is shield by the metallic dees. Inside D’ there is no effect of electric field.

3) Magnetic field B is used to rotate the charged particle. In magnetic field B time

m = mass of charged particle ;
q = charge on particle
Time period T is independent of velocity of the particle.

4) Radio frequency oscillator is used to obtain resonance condition. When frequency of applied voltage (V_a) is equal to frequency of cyclotron υ_c then cyclotron is said to be in resonance condition. By adjusting phase difference between dees the charged particles can be accelerated upto required energy. Kinetic energy of charged particle depends on its velocity ‘v’.

Long Answer Questions

Question 1.
Deduce an expression for the force on a current carrying conductor placed in a magnetic field. Derive an expression for the force per unit length between two parallel current carrying conductors.
Answer:
Consider a rod of uniform cross section A and length ‘l’. Let the density of the mobile charge carriers per unit volume is ‘n’.

For a steady current i the total number of mobile charge carriers in it nAl.

Let average drift velocity of each charge = v_d

When this conductor is placed in a magnetic field B. Force on it F = total charge

Force between two long parallel conductors :
If two long conductors ‘a’ and ‘b’ are carrying the currents I_a and I_b. Separated by the distance ‘d’. Conductor ‘A’ produces a magnetic field B_a at all points along conductor ‘B’ due to the current flowing through it.
Magnetic field due to ‘A’ = B_a = \(\frac{\mu_0}{2\pi } \frac{\mathrm{I_a}}{\mathrm{d}}\) …………… (1)

Conductor ‘B’ carrying a current Ib is in the magnetic field produced by ‘A’. Force acting on conductor ‘B’ due to ‘A’ is F_ba = I_b L B_a = \(\frac{\mu_0}{2\pi } \frac{\mathrm{I_aI_b}}{\mathrm{d}}\).L

Where L is length of conductor ‘B’.

Now conductor ‘A’ is in the magnetic field produced by ‘B’.
Force due to ‘B’ on ‘A’ = F_ab.
From Newton’s 3^rd law F_ab = – F_ba
∴ Force between two parallel conductors F_ab = F_ba = \(\frac{\mu_0}{2\pi } \frac{\mathrm{I_aI_b}}{\mathrm{d}}\).L
∴ Force between parallel conductors per unit lenght = \(\frac{F_{ab}}{L }=\frac{\mu_0}{2\pi } \frac{\mathrm{I_aI_b}}{\mathrm{d}}\) ……….. (2)

Question 2.
Obtain an expression for the torque on a current carrying loop placed in a uniform magnetic field. Describe the construction and working of a moving coil galvanometer.
Answer:
Let a rectangular loop of length b’, breadth a’ is placed in a uniform magnetic field B. Let a current I is passed through the loop. Now force on each side F₁ = F₂ = I b. B
Current passes through the loop in opposite direction so F₁ and F₂ are opposite. So F₁ and F₂ forms a force couple.

Where A = ab = Area of coil
Let the coil is rotated by an angle 0 then the perpendicular distance between F and B is a/2 sinG.
∴ Total torque τ = IbB\(\frac{a}{2}\) sinθ + IbB.\(\frac{a}{2}\) sinθ = I(ab)B sinθ = IAB sinθ
∴ Torque on a coil placed in a magnetic field τ = IAB sinθ

Construction and working of a moving coil galvanometer :
A moving coil galvanometer consists of a rectangular coil of n’ turns. It is placed in a uniform radial magnetic field. So \(\overline{\mathrm{B}}\) is perpendicular to area vector \(\overline{\mathrm{A}}\).

Hence torque is maximum.
Torque on coil τ = NiAB
This torque tends to rotate the coil. So it is called deflecting torque. A spring attached to the coil will provide the restoring torque. At equilibrium deflection (say Φ) is given by kΦ = NIAB (or) Φ = \(\frac{(NAB)}{k}\)I
Where k is torsional constant of spring. NAB
The term \(\frac{(NAB)}{k}\)is called constant of galvanometer.

Current sensitivity of Galvanometer is defined as deflection for unit current
\(\frac{\phi}{I}=\frac{(NAB)}{k}\) = constant of galvanometer.

In this galvanometer the coil is moving so it is called moving coil galvanometer. Its sensitivity is high for few microamperes (µA) of current it gives full deflection.

Question 3.
How can a galvanometer be converted to an ammeter? Why is the parallel resistance smaller that the galvanometer resistance? [Mar. ’14]
Answer:
A galvanometer can be converted into an ammeter by connecting a low resistance called shunt resistance in parallel to the galvanometer.

Every galvanometer has two important properties.

1. Resistance of galvanometer R_G,
2. Maximum current tolerable by it say I_G.

Ammeter :
The block diagram of ammeter is as shown. Let I is the current to be measured. When ammeter is connected in a circuit current I_G will flow through galvanometer and current I_s will flow through shunt.

Let ‘r’ is the total resistance of ammeter, G is resistance of galvanometer and R_s is shunt connected in parallel combination of

ammeter is equals to resistance of shunt.

Necessity of small shunt resistance :
Ammeter is used to measure current in a circuit. In a circuit current is constant for series combination only. So ammeter must be connected in series in a circuit. To measure the value of current exactly our ammeter must have zero resistance because in series combination (R = R₁ + R₂ + ………… etc) if resistance of shunt Rs is small effective resistance of ammeter is nearly equals to resistance of shunt and error in the value of current measured is also less.

Question 4.
How can a galvanometer be converted to a voltmeter? Why is the series resistance greater than the galvanometer resistance?
Answer:
A galvanometer can be converted into voltmeter by connecting a high resistance in series with galvanometer.

Conversion of galvanometer into voltmeter :
Every galvanometer has two important properties

1. Resistance of galvanometer R_G
2. Maximum current tolerable by it say I_G.

The block diagram of a voltmeter is as shown in figure.

Let voltage to be measured is ‘V’.
Total resistance of voltmeter R = \(\frac{V}{I_G}\)

But from block diagram R = R_G + R_s because they are in series. If R_s > > R_G then resistance of voltmeter R ≅ R_s

Necessity of high series resistance :
A voltmeter is used to measure potential difference between two given points. So it must always be connected parallelly in a circuit. In parallel combination, high current will flow through low resistance. To measure potential difference exactly the voltmeter should not draw any current from circuit. Theoritically resistance of ideal voltmeter is infinity. Practically it is kept as high as possible when series resistance of volt-meter is high it draws very little current from the circuit and measurement of voltage with it is more accurate.

Question 5.
Derive an expression for the force acting between two very long parallel current-carrying conductors and hence define the ampere.
Answer:
Let two long conductors say ‘a’ and ‘b’ are carrying the currents I_a and I_b. Separation between them is say ‘d’. Conductor ‘a’ produces a magnetic field B_a at all points a long conductor b’ due to the current flowing through it.

Magnetic field due to ‘a” = B_a = \(\frac{\mu_0}{2 \pi} \frac{I_a}{d}\) ……(1)
Conductor ‘b’ carrying a current I_b is in the magnetic field produced by ‘a’. Force acting on conductor ‘b‘ due to ‘a’ is F_ba = I_bLB_a = \(\frac{\mu_0}{2 \pi} \frac{I_aI_b}{a}\).L

Where L is length of conductor ‘b’.
Now conductor ‘a’ is in the magnetic field produced by ‘b’. Force due to ‘b’ on ‘a’ is F_ab From Newton’s 3^rd law F_ab = – F_ba
∴ Force between two parallel conductors

Force between parallel conductors per unit

If the currents in the two wires are parallel then force between them is attractive force because at the point of intersection of the two fields their directions are opposite so polarity is opposite.

Hence if currents are in same direction the conductors will attract. If currents are in opposite direction then the conductors will repel.

Definition of ampere :
From the force between two parallel conductors ampere is defined as follows.

Ampere is that value of steady current which when maintained through each conductor separated by a distance of 1 metre a part in vacuum produces a force of 2 × 10^-7 newton per metre between them.

Problems

Question 1.
A current of 10A passes through two very long wires held parallel to each other and separated by a distance of lm. What is the force per unit length between them? [TS Mar. 19. 15; AF Mar. 15]
Solution:
Current i₁ = i₂ = 10A
Separation d = lm
Force per unit length L = lm
Force between two parallel conductors

Question 2.
A moving coil galvanometer can measure a current of 10^-6A. What is the resistance of the shunt required if it is to measure 1A?
Solution:
Old range i.e., maximum current to be measured i₁ = 10^-6 A
New range i.e., maximum current to be measured i₂ = 1A
Ratio of ranges or currents to be measured,

Where G is resistance of galvanometer.

Question 3.
A circular wire loop of radius 30cm carries a current of 3.5 A. Find the magnetic field at a point on its axis 40 cm away from the centre.
Solution:
Radius of loop r = 30cm = 0.3m = 3 × 10^-1m.
Current i = 3.5A ; Distance of point on the axis r = 40cm = 0.4m = 4 × 10^-1m.
Magnetic induction field on the axis of a

Intext Question and Answer

Question 1.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil? [TS May ’18]
Answer:
Number of turns on the circular coil,
n = 100 ; Radius of each turn,
r = 8.0 cm = 0.08 m ; Current I = 0.4 A
Magnitude of the magnetic field at the centre of the coil is given by the relation,

∴ Magnitude of the magnetic field
B = 3.14 × 10^-4T.

Question 2.
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire? [TS June ’15]
Answer:
Current in the wire, 1 = 35 A ; Distance of a point from the wire, r = 20 cm = 0.2 m ; Magnitude of the magnetic field at this point is given as:

∴ Magnitude of the magnetic field at 20 cm from the wire B = 3.5 × 10^-5T.

Question 3.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of Bat a point 2.5m east of the wire.
Answer:
Current in the wire, I = 50A ; ∴ Distance of the point from the wire, r = 2.5 m.
Given point is 2.5 m away from the east of the wire.


∴ Direction of magnetic field B is vertically upwards.
Note : The point is located normal to the . wire length at a distance of 2.5 m. The direction of the current in the wire is vertically downward. Hence, according to the Maxwell’s right hand thumb rule, the direction of the magnetic field at the given point is vertically upward.

Question 4.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
Answer:
Current I = 90 A; Distance of point r = 1 .5 m

Note : The current is flowing from East to West. The point is below the power line. Hence, according to Maxwell’s right hand thumb rule, the direction of the magnetic field is towards the South.

Question 5.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of 30° with the direction of a uniform magnetic field of 0.15 T?
Answer:
Current in the wire, I = 8 A ; uniform magnetic field, B = 0.15 T
Angle between the wire and magnetic field, θ = 30°;
Magnetic force per unit length f = BI sinθ
∴ f = 0.15 × 8 × 1 × sin30° = 0.6 N m^-1

Question 6.
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Answer:
Length of the wire, l = 3 cm = 0.03 m;
Current flowing in the wire, I = 10 A
Magnetic field, B = 0.27 T ; Angle between the current and magnetic field, θ = 90°
From F = BIl sinθ; F = 0.27 × 10 × 0.03 sin90°
= 8.1 × 10^-2 N
∴ Magnetic force on the wire is 8.1 × 10^-2 N.

Question 7.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Answer:
Current flowing in wire A, I_A = 8.0 A ;
Current flowing in wire B, l_B = 5.0 A
Distance between the two wires, r = 4.0 cm = 0.04 m;
Length of wire A, l = 10 cm = 0.1 m

The magnitude of force is 2 × 10^-5 N. This is an attractive force normal to A towards B because the direction of the currents in the wires is the same.

Question 8.
A closely wound solenoid 80 cm long has 5 layers of windings of400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Answer:
Length of the solenbid, l = 80 cm = 0.8 m
There are five layers of windings of 400 turns each on the solenoid.
∴ Total number of turns on the solenoid, N = 5 × 400 = 2000
Diameter of the solenoid, D = 1.8 cm = 0.018 m ; Current in the solenoid, I = 8.0 A
Magnetic field inside the solenoid near its

∴ Magnetic field inside the solenoid near its centre is 2.512 × 10^-2 T.

Question 9.
A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?
Answer:
Length of a side of the square coil, 1 = 10 cm = 0.1 m; Current in the coil, l = 12 A

Number of turns n = 20 ; Angle between plane of the coil and magnetic field, θ = 30°
Strength of magnetic field, B = 0.80 T ; But τ = n BI A sin θ
Where, A = Area of the square coil = l × l = 0.1 × 0.1 = 0.01 m²
∴ τ = 20 × 0.8 × 12 × 0.01 × sin 30° = 0.96 N m

Question 10.
Two moving coil meters, Mj and M2 have the following particulars:
R₁ = 10 Ω, N₁ = 30, A₁ = 3.6 × 10^-3 m², B₁ = 0.25 T
R₂ = 14 n, N₂ = 42, A₂ = 1.8 × 10^-3 m² , B₂ = 0.50 T
(The spring constants are identical for the two meters).
Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M₂ and M₁.
Answer:
a) Current sensitivity of M.C.G is given as:
I = NBA/k

Hence, the ratio of current sensitivity of M₂ to M₁ is 1.4.

b) Voltage sensitivity for M.C.G is given as:
Vs₂ = \(\frac{N_2B_2A_2}{k_2R_2}\)

Hence, the ratio of voltage sensitivity of M₂ to M₁ is 1.

Question 11.
In a chamber, a uniform magnetic field of 6.5 G (1 G = 10^-4 T) is maintained. An electron is shot into the field with a speed of 4.8 × 10⁶ m s^-1 normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.
(e = 1.6 × 10^-19 C,m_e = 9.1 × 10^-31 kg)
Answer:
Magnetic field strength, B = 6.5 G = 6.5 × 10^-4 ;
Speed of the electron, v = 4.8 × 10⁶ m/s
Charge on the electron, e = 1.6 × 10^-19 C ;
Mass of the electron, mg = 9.1 × 10^-31 kg
Angle between the shot electron and magnetic field, θ = 90°;
Force on electron, F = evB sin θ
This force will make the electron in circular path.
∴ Centripetal force exerted on the electron, F_c = \(\frac{mυ^2}{r}\) at equilibrium F_c = F

Hence, the radius of the circular orbit of the electron is 4.2 cm.

Question 12.
In exercise 11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain.
Answer:
Magnetic field strength, B = 6.5 × 10^-4 T ;
Charge of the electron, e = 1.6 × 10^-19 C
Mass of the electron, m_e = 9.1 × 10^-31 kg ;
Velocity of the electron, v = 4.8 × 10⁶ m/s
Radius of the orbit, r = 4.2 cm = 0.042 m ;
Frequency of revolution of the electron = υ
Angular frequency of the electron = co = 2πν
But v = rω

Hence, the frequency of the electron is around 18 MHz and is independent of the speed of the electron.

Question 13.
(a) A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is sus-pended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of die counter torque that must be applied to prevent the coil from turning.
(b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)
Answer:
(a) Number of turns, n = 30 ; Radius of the coil, r = 8.0 cm = 0.08 m
Area, A = πr² = π(0.08)² = 0.0201 m² ;
Current, I = 6.0 A
Magnetic field B = 1 T
Angle between the field lines and normal with the coil, θ = 60°
∴ Torque τ = n IBA sinθ …
∴ τ = 30 × 6 × 1 × 0.0201 × sin 60° = 3.133 N m

(b) Magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. So if the circular coil is replaced by a planar coil of some irregular shape of same area still then torque does not change.

Question 14.
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid.
Answer:
Inner radius of the toroid, r₁ = 25 cm = 0.25 m ;
Outer radius of the toroid, r² = 26 cm = 0.26 m
Number of turns , N = 3500 ; Current in the coil, I = 11 A
(a) Magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.
(b) Magnetic field inside the core of a toroid

(c) Magnetic field in the empty space surrounded by the toroid is zero.

Question 15.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Answer:
Current in both wires, I = 300 A ;
Distance between the wires, r = 1.5 cm = 0.015 m
Length of the two wires, / = 70 cm = 0.7 m

Since the direction of the current in the wires is opposite, a repulsive force exists between them.

Question 16.
A galvanometer coil has a resistance of 12 Ω and the metre shows full scale deflection for a current of 3 mA. How will you convert the metre into a voltmeter of range 0 to 18 V?
Answer:
Resistance of the galvanometer coil, G = 12 Ω
Current for which there is full scale deflection, I_g = 3 mA = 3 × 10^-3 A
Range of the voltmeter is 0, which needs to be converted to 18 V. ∴ V = 18 V
Let a resistor of resistance R be connected in series with the galvanometer to convert it into a voltmeter. This resistance is given as:

Hence, a resistor of resistance 5988Ω is to be connected in series with the galvanometer.

Question 17.
A galvanometer coil has a resistance of 15Ω and the metre shows full scale deflection for a current of 4 mA. How will you convert the metre into an ammeter of range 0 to 6 A?
Answer:
Resistance of the galvanometer coil, G = 15 Ω Current for which the galvanometer shows full scale deflection,
I_g = 4 mA = 4 × 10^-3 A
Range of the ammeter is 0, which needs to be converted to 6 A.; ∴ Current, I = 6 A

A shunt resistor of resistance S is to be connected in parallel with the galvanometer to convert it into an ammeter.

But shunt resistance is given by,

Hance, 10 mΩ shunt resistor is to be connected in parallel with the galvanometer.

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Very Short Answer Type

Question 1.
Find the roots of the quadratic equation ax² + bx + c = 0. [March ’02]
Solution:
Given quadratic equation is ax² + bx + c = 0
Now, multiplying with ‘4a’ on both sides
4a (ax² + bx – c) = 0
= 4ax²x² + 4abx + 4ac = 0
(2ax)² + 2 . 2ax . b + b² + b² – b² + 4ac = 0
(2ax + b)² = b² – 4ac
2ax + b = ± \(\sqrt{b^2-4 a c}\)
2ax = – b ± \(\sqrt{b^2-4 a c}\)
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ The roots of the quadratic equation, ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\).

Question 2.
Fmd the roots of the following equation √3x² + 10x – 8√3 = 0.
Solution:
Given quadratic equation is √3x² + 10x – 8√3 = 0
Comparing this with ax² + bx + c = 0,
we have a = √3, b = 10 c = – 8√3
The roots of quadratic equation are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-10 \pm \sqrt{100+96}}{2 \sqrt{3}}=\frac{-10 \pm \sqrt{196}}{2 \sqrt{3}}\)
= \(\frac{-10 \pm 14}{2 \sqrt{3}}=\frac{-10+14}{2 \sqrt{3}} \text { (or) } \frac{-10-14}{2 \sqrt{3}}\)
= \(\frac{4}{2 \sqrt{3}} \text { (or) } \frac{-24}{2 \sqrt{3}}=\frac{2}{\sqrt{3}} \text { (or) } \frac{-12}{\sqrt{3}}\)
= \(\frac{2}{\sqrt{3}}\) (or) – 4√3
∴ The roots of the quadratic equation are \(\frac{2}{\sqrt{3}}\) (or) – 4√3

Question 3.
Form a quadratic equation whose roots are 7 ± 2√5. [TS – May ’16; March ’11, ’05, AP – March 2018]
Solution:
Let α = 7 + 2√5, β = 7 – 2√5
Now, α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – 20 = 29
The quadratic equation whose roots are α, β is
x² – (α + β)x + αβ = 0
x² – 14x + 29 = 0.

Question 4.
Form a quadratic equation whose roots are – 3 ± 5i.
Solution:
Let α = – 3 + 5i, β = – 3 – 5i
Now, α + β = – 3 + 5i – 3 – 5i = – 6
αβ = (- 3 + 5i) (- 3 – 5i)
= 9 – 25i² = 34
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
⇒ x² + 6x + 34 = 0

Question 5.
Form a quadratic equation whose roots are \(\frac{p-q}{p+q}\), – \(\frac{p+q}{p-q}\) (p ≠ q).
Solution:

The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
x² + \(\frac{4 p q}{p^2-q^2}\) . x – 1 = 0
⇒ (p² – q²)x² + 4pqx – (p² – q²) = 0

Question 6.
Find the nature of the roots of 4x² – 20x + 25 = 0.
Solution:
Given quadratic equation is 4x² – 20x + 25 = 0.
Comparing this with ax² + bx + c = 0, we get
a = 4; b = – 20; c = 25
b² – 4ac = 400 – 4 . 4 . 25 = 400 – 400 = 0
Since ² – 4ac = 0 then the roots of the given equation are real and equal.

Question 7.
Find the nature of the roots of 2x² – 8x + 3 = 0.
Solution:
Given quadratic equation is 2x² – 8x + 3 = 0
Comparing this with ax² + bx + c = 0, we get
a = 2, b = – 8, c = 3
Now, b² – 4ac = 64 – 4 . 2 . 3
Since, b² – 4ac > 0 then the roots of the given equation are real and distinct.

Question 8.
Find the nature of the roots of 2x² – 7x + 10 = 0.
Solution:
Given quadratic equation is 2x² – 7x + 10 = 0
Comparing this with ax² + bx + c = 0, we get a = 2, b = – 7, c = 10
Now, b² – 4ac = 49 – 80 = – 31 < 0
Since, b² – 4ac < 0 then the roots of the given equation are conjugate complex numbers.

Question 9.
Find the nature of the roots of 3x² + 7x + 2 = 0.
Solution:
Given quadratic equation is 3x² + 7x + 2 = 0
Comparing this with ax² + bx + c = 0, we get a = 3, b = 7, c = 2
Now, b² – 4ac = 49 – 4 . 3 . 2
= 49 – 24 = 25 = 52 > 0
Since, b² – 4ac > 0 then the roots of the given equation are rational and unequal.

Question 10.
If α, β are the roots of ax² + bx + c = 0 then find \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}\).
Solution:
If α, β are the roots of ax² + bx + c = 0 then
α + β = \(\frac{-b}{a}\)
αβ = \(\frac{c}{a}\)
Now, \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}=\frac{\beta^2+\alpha^2}{\alpha^2 \beta^2}=\frac{(\alpha+\beta)^2-2 \alpha \beta}{(\alpha \beta)^2}\)
= \(\frac{\left(\frac{-b}{a}\right)^2-2 \cdot \frac{c}{a}}{\left(\frac{c}{a}\right)^2}=\frac{b^2-2 c a}{c^2}\)

Question 11.
If α, β are the roots of ax² + bx + c = 0 then find \(\frac{1}{\alpha}+\frac{1}{\beta}\). [March ’10]
Solution:
If α, β are the roots of ax² + bx + c = 0
then α + β = \(\frac{-b}{a}\)
αβ = \(\frac{c}{a}\)
Now \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{\frac{-b}{a}}{\frac{c}{a}}=\frac{-b}{c}\)

Question 12.
If α, β are the roots of ax² + bx + c = 0 then find α² + β². [May ’13]
Solution:
If α, β are the roots of ax² + bx + c = 0
then α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)
Now α² + β² = (α + β)² – 2αβ
= \(\left(\frac{-b}{a}\right)^2-\frac{2 c}{a}=\frac{b^2}{a^2}-\frac{2 c}{a}=\frac{b^2-2 a c}{a^2}\).

Question 13.
For what values of m, the equation x² – 15 – m (2x – 8) = 0 will have equal roots ?
[March ’13 ’04, May ’08, TS – Mar. 2015; AP – Mar. ’19,’17]
Solution:
Given equation is x² – 15 – m (2x – 8) = 0
x² – 15 – 2mx + 8m = 0
⇒ x² – 2mx + 8m- 15 = 0 ……………(1)
Comparing this equation with
ax² + bx + c = 0, we get
a = 1, b = – 2m, c = 8m – 15
Since (1) have equal roots
⇒ b² – 4ac = 0
⇒ 4m² – 4 (1) (8m – 15) = 0
⇒ 4m² – 32m + 60 = 0
⇒ m² – 8m + 15 = 0
⇒ m² – 5m – 3m+ 15 = 0
⇒ m (m – 5) – 3 (m – 5) = 0
⇒ (m – 3) (m – 5) = 0
⇒ m = 3 (or) m = 5
∴ The values of m are 3, 5.

Question 14.
For what values of in, (m + 1) x² + 2(m + 3) x + (m + 8) = 0 has equal roots? [March ‘03]
Solution:
Given quadratic equation is (m + 1) x² + 2 (m + 3) x +(m + 8) = 0 …………..(1)
Comparing this with ax² + bx + c = 0, we get
a = m + 1, b = 2 (m + 3), c = m + 8
Since (1) have equal roots then b² – 4ac =0
⇒ [2 (m + 3)]² – 4 (m + 1) (m + 8) = 0
⇒ 4 (m + 3)² – 4(m + 1) (m + 8) = 0
⇒ m² + 6m + 9 – m² – 8m – m – 8 = 0
⇒ – 3m – 1 = 0 m = \(\frac{1}{3}\)

Question 15.
For what values of m, (3m + 1) x² + 2(m + 1) x + m = 0 will have equal roots?
Solution:
Given quadratic equation is (3m + 1)x² + 2(m + 1)x +m = 0 ………….(1)
Comparing this with ax² + bx + c = 0, we get
a = 3m + 1, b = 2(m + 1), c = m
since (1) have equal roots then b² – 4ac = 0
4 (m + 1)² – 4m (3m + 1) = 0
m² + 2m + 1 – 3m² – m = 0
– 2m² + m + 1 = 0
2m² – m – 1 = 0
2m² – 2m + m – 1 = 0
2m (m – 1) + 1 (m – 1) = 0
(m – 1) (2m + 1) = 0
m = 1, m = – \(\frac{1}{2}\)

Question 16.
Prove that the roots of (x – a) (x – b) = h² are always real. [AP – May 2013, May ’09]
Solution:
Given quadratic equation is
(x – a) (x – b) = h²
⇒ x² – ax – bx + ab – h² = 0
⇒ x² + (- a – b)x + ab – h² = 0
Comparing this with ax² + bx + c =0, we get
⇒ a = 1, b = – a – b, c = ab – h²
Now,
b² – 4ac = (- a – b)² – 4 (1) (ab – h²)
= a² + b² + 2ab – 4ab + 4h²
=(a² + b² – 2ab) + 4h²
= (a – b)² + (2h)² > 0
Since b² – 4ac > 0 then the roots of the given equation are always real.

Question 17.
Find the quadratic equation, the sum of whose roots is 1 and sum of the sqares of the roots is 13. [May ’07]
Solution:
Let α, β be the roots of required equation.
Given that, the sum of roots, α + β = 1
Sum of squares of the roots, α² + β² = 13
We know that, (α + β)² = α² + β² + 2αβ
⇒ 1 = 13 + 2αβ
⇒ 2αβ = – 12
⇒ αβ = – 6
∴ The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
⇒ x² – x – 6 = 0

Question 18.
Solve the equation 4^{x – 1} – 3 . 2^{x – 1} + 2 = 0. [March ’04]
Solution:
Given equation is 4^{x – 1} – 3 . 2^{x – 1} + 2 = 0
\(\frac{4^x}{4}-3 \cdot \frac{2^x}{2}+2\) = 0
\(\frac{\left(2^2\right)^x}{4}-3 \cdot \frac{2^x}{2}+2\) = 0
\(\frac{\left(2^x\right)^2}{4}-3 \cdot \frac{2^x}{2}+2\) = 0
Let 2^x = a
⇒ \(\frac{\mathrm{a}^2}{4}-\frac{3 \mathrm{a}}{2}\) + 2 = 0
⇒ a² – 6a + 8 = 0
⇒ a² – 4a – 2a + 8 = 0
⇒ (a – 4) (a – 2) = 0
⇒ a = 4 (or) 2.

Case – I:
lf a = 4
⇒ 2^x = 4
⇒ 2^x = 2²
⇒ x = 2.

Case – 2:
If a = 2
⇒ 2^x = 2
⇒ x = 1
∴ The solution set of the given equation is {2, 1}.

Question 19.
Find the maximum or minimum of the expression 12x – x² – 32 x varies over R.
Solution:
Given quadratic expression is – x + 12x – 32
Comparing this expression with ax + bx + c, we have a = – 1, b = 12, c = – 32
Here a = – 1 < 0.
Then – x² + 12x – 32 has absolute maximum at x = \(\frac{-b}{2 a}=\frac{-12}{2(-1)}\) = 6
∴ The maximum value = \(\frac{4 a c-b^2}{4 a}\)
= \(\frac{4(-1)(-32)-144}{4(-1)}\)
= \(\frac{128-144}{-4}=\frac{-16}{-4}\) = 4.

Question 20.
If the quadratic equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0, (b ≠ c) have a common root then show that a + 4b + 4c = 0.
Solution:
Given quadratic equations are ax² + 2bx + c = 0
Comparing this equation with a₁x² + b₁x + c₁ = 0, we get
a₁ = a, b₁ = 2b, c₁ = c
Now, a₂x + 2cx + b = 0
Comparing this with a₂x² + b₂x + c₂ = 0
we get a₂ = a, b₂ = 2c, c₂ = b
The condition for two quadratic equations
a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0 to have a common root is
(c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁)
⇒ (ca – ba)² = (a₂c – a₂b) (2bb – 2cc)
⇒ a² (c – b)² = 2a (c – b) 2 (b² – c²)
⇒ a² (c – b)² = 4a (c – b) (b – c) (c – b)
⇒ a = – 4 (c + b) a = – 4c – 4b
a + 4b + 4c = 0.

Question 21.
If x² – 6x + 5 = 0 and x² – 12x + p = 0 have a common root, then find p. [TS – May 2015, Mar. 2017]
Solution:
Given quadratic equations are x² – 6x + 5 = 0
Comparing this equation with
a₁x² + b₁x + c₁ = 0, we get
a₁ = 1, b₁ = – 6, c₁ = 5
Now, x² – 12x + p = 0,
Corn paring with a₂x² + b₂x + c₂ = 0
we get a₂ = 1, b₂ = – 12, c₂ = p
The condition for two quadratic equations
a₁x² + b₁x + c₁ = 0 and a₂x2 + b₂x + c₂ = 0 to have a common root is
(c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁)
(5 (1) – p(1))² = (1 (- 12) – 1 (- 6)) ((- 6)p – (- 12) 5)
⇒ (5 – p)² = – 6 (- 6p + 60)
⇒ p² + 25 – 10p = 36p – 360
⇒ p² – 16p + 385 = 0
⇒ p² – 35p – 11p + 385 = 0
⇒ p (p – 35) – 11 (p – 35) = 0
⇒ (p – 11) (p – 35) = 0
⇒ p = 11 (or) p = 35
∴ p = 11 (or) 35.

Question 22.
For what values of x, the expression x² – 5x + 6 is positive?
Solution:
The given quadratic expression is x² – 5x + 6
⇒ x² – 3x – 2x + 6 = x (x – 3) – 2 (x – 3) = (x – 2)(x – 3)
i) If 2 < x < 3 then the expression x² – 5x + 6 is ‘- ve’.
ii) If x < 2 (or) x> 3 then the expression x² – 5x + 6 is ‘+ ve’.
iii) If x = 2 (or) x = 3 then the expression x² – 5x + 6 = 0

Question 23.
For what values of x, the expression x² – 5x – 6 is negative? [March ‘95]
Solution:
Given quadratic expression is x² – 5x – 6
= x² – 6x + x – 6
= x (x – 6) + 1 (x – 6)
= (x + 1)(x – 6)
i) If – 1 < x < 6 then the expression x² – 5x – 6 is ‘-ve’.
ii) If x < – 1 or x > 6 then the expression x² – 5x – 6 is ‘+ ve’.
iii) If x = – 1 (or) x = 6 then the expression x² – 5x – 6 = 0.

Question 24.
Discuss the signs of the expression x² – 5x + 4 for x ∈ R. [May ’95].
Solution:
Given quadratic expression is x² – 5x + 4
= x² – 4x – x + 4
= x (x – 4) + 1 (x – 4)
= (x – 1) (x – 4)
i) If 1 < x < 4 then the expression x² – 5x + 4 is ’-ve’.
ii) If x < 1 (or) x > 4 then the expression x² – 5x + 4 is ’+ve’.
iii) If x = 1 (or) x = 4 then the expression x² – 5x + 4 = 0.

Question 25.
Find the maximum or minimum value of the expression 12x – x² – 32. [May ’06]
Solution:
Given quadratic expression is – x² + 12x – 32 = 0
Comparing this expression with ax² + bx + c, we have a = – 1, b = 12, c = – 32
Here, a = – 1 < 0.
Then – x² + 12x – 32 has absolute maximum at x = \(\frac{-b}{2 a}=\frac{-12}{2(-1)}\) = 6
The maximum value = \(\frac{4 a c-b^2}{4 a}\)
= \(\frac{4(-1)(-32)-144}{4(-1)}=\frac{128-144}{-4}\)
= \(\frac{-16}{-4}\) = 4.

Question 26.
Find the maximum or minimum value of the expression 2x – 7 – 5x². [May ’10. March ’14, ’12].
Solution:
Given quadratic expression is – 5x² + 2x – 7
Comparing this expression with ax² + bx + c,
we have a = – 5, b = 2, c = – 7
Here, a = – 5 < 0, – 5x² + 2x – 7 has absolute maximum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(-5)}=\frac{1}{5}\)
∴ Maximum value is \(\frac{4 a c-b^2}{4 a}=\frac{4(-5)(-7)-4}{4(-5)}\)
= \(\frac{140-4}{-20}=\frac{136}{-20}=\frac{-34}{5}\)

Question 27.
Find the maximum or minimum value of the expression 3x² + 2x + 11. [May ’92]
Solution:
Given quadratic expression is 3x² + 2x + 11
Comparing this expression with ax² + bx + c, we have a = 3, b = 2, c = 11
Here, a = 3 >0, 3x² + 2x + 11 has absolute minimum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(3)}=\frac{-1}{3}\)
∴ The minimum value = \(\frac{4 a c-b^2}{4 a}=\frac{4(3)(11)-4}{4(3)}\)
= \(\frac{132-4}{12}=\frac{128}{12}=\frac{32}{3}\).

Question 28.
Find the maximum or minimum value of the expression x² – x + 7 as x varies over R. [May ’14]
Solution:
Given quadratic expression is x² – x + 7
Comparing this expression with ax² + bx + c, we have a = 1, b = – 1, c = 7
Here, a = 1 > 0, x² – x + 7 has absolute minimum at x = \(\frac{-b}{2 a}=\frac{-(-1)}{2 \cdot 1}=\frac{1}{2}\)
∴ The minimum value = \(\frac{4 a c-b^2}{4 a}=\frac{4(1)(7)-(-1)^2}{4(1)}\)
= \(\frac{28-1}{4}=\frac{27}{4}\)

Question 29.
Find the roots of the equation 6√5 x² – 9x – 3√5 = 0.
Solution:
\(\frac{\sqrt{5}}{2}, \frac{-1}{\sqrt{5}}\)

Question 30.
Form a quadratic equation whose roots are 2√3 – 5 and – 2√3 – 5.
Solution:
x² + 10x + 13 = 0.

Question 31.
Form a quadratic equation whose roots are \(\frac{\mathbf{m}}{\mathbf{n}}, \frac{-\mathbf{n}}{\mathbf{m}}\), (m ≠ 0, n ≠ 0)
Solution:
mnx² – (m² – n²)x – mn = 0

Question 32.
If α, β are the roots of ax² + bx + c = 0 then find α³ + β³.
Solution:
\(\frac{3 a b c-b^3}{a^3}\)

Question 33.
For what values of m, x² + (m + 3) x + (m + 6) = 0 will have equal roots?
Solution:
m = 3, – 5.

Question 34.
For what values of m, z² – 2 (1 + 3m) x + 7 (3 + 2m) = 0 will have equal roots?
Solution:
m = 2, \(\frac{-10}{9}\).

Question 35.
For what vaIueof m, (2m+ 1)x² + 2(m + 3)x + (m + 5) = 0 will have equal rooti?
Solution:
m = \(\frac{-5 \pm \sqrt{41}}{2}\)

Question 36.
Find the quadratic equation, the sum of whose roots is 7 and sum of the squares of the roots is 25.
Solution:
x² – 7x + 12 = 0

Question 37.
So1ve the equation 3^{1 + x} + 3^{1 – x} = 10.
Solution:
{- 1, 1}

Question 38.
Solve 7^{1 + x} + 7^{1 – x} = 50 for real x.
Solution:
{- 1, 1}

Question 39.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
4 (or) 2.

Question 40.
For what values of x, the expression x² – 5x + 14 is positive?
Solution:
∀ x ∈ R

Question 41.
For what values of x, the expression 3x² + 4x + 4 is positive?
Solution:
∀ x ∈ R

Question 42.
For what values of x, the expression x² – 7x + 10 is negative?
Solution:
2 < x < 5

Question 43.
For what values of x, the expression 15 + 4x – 3x² is negative? [AP – Mar. 2015]
Solution:
x < – \(\frac{5}{3}\) (or) x > 3.

Question 44.
Find the changes in the sign of 4x – 5x² + 2 for x ∈ R.
Solution:
Positive for \(\frac{2-\sqrt{14}}{5}<x<\frac{2+\sqrt{14}}{5}\)
negative for x < \(\frac{2-\sqrt{14}}{5}\) (or) x > \(\frac{2+\sqrt{14}}{5}\)

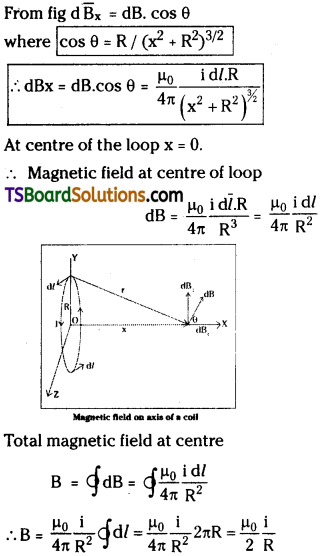
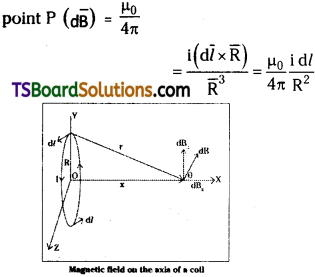
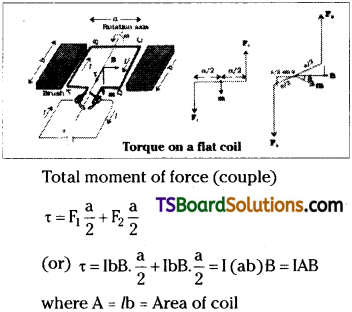
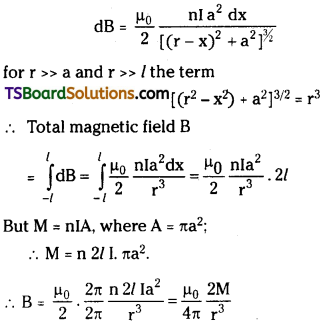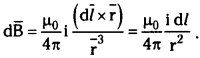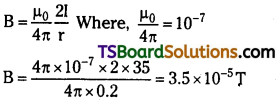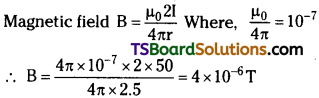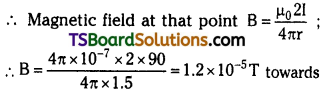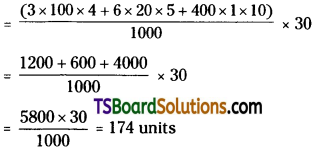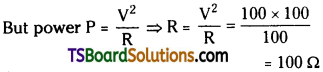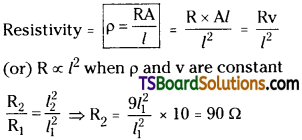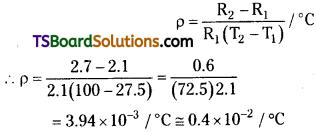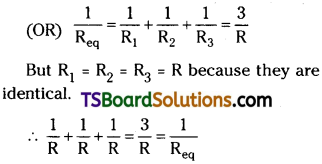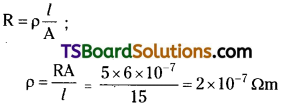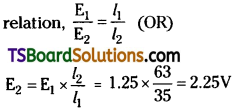Telangana TSBIE TS Inter 2nd Year Physics Study Material 6th Lesson Current Electricity Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 6th Lesson Current Electricity

Very Short Answer Type Questions

Question 1.
Define mean free path of electron in a conductor.
Answer:
Mean free path :
It is defined as the average distance that an electron can travel between two successive collisions.

Question 2.
State Ohm’s law and write its mathematical form.
Answer:
Ohm’s law :
At constant temperature current (I) flowing through a conductor is proportional to the potential difference between the ends of that conductor.
V ∝ I ⇒ V = RI where R = constant called resistance. Unit: Ohm (Ω).

Question 3.
Define resistivity (or) specific resistance.
Answer:
Resistivity :
Resistivity of a substance ρ = \(\frac{RA}{l}\)

It is defined as the resistance of a unit cube between its opposite parallel surfaces.

It depends on the nature of substance but not on its dimensions.
Unit: Ohm – metre (Ωm).

Question 4.
Define temperature coefficient of resistance.
Answer:
Temperature coefficient of resistivity :
The resistivity of a substance changes with temperature. ρ_τ = ρ₀ [1 + ∝ (T – T₀)]. Where a is temperature coefficient of resistivity.

Question 5.
Under what conditions is the current through the mixed grouping of cells maximum?
(Note: Mixed grouping of cells not given in New Syllabus.)
Answer:
Let m cells are in series and there are n such rows this arrangement is called mixed grouping.
In mixed grouping current (i) = \(\frac{mnE}{mr + nR}\)
Current will be maximum when mr = nR
∴ i_max = \(\frac{nE}{2r}\)

Question 6.
If a wire is stretched to double its original length without loss of mass, how will the resistivity of the wire be influenced?
Answer:
Resistivity (ρ) is independent of dimensions of the material. It depends only on nature of material.
So even though the wire is stretched its resistivity does not change.

Question 7.
Why is manganin used for making standard resistors?
Answer:
Temperature coefficient of resistance of manganin is very less. So its resistance is almost constant over a wide range of temperature.

Due to this reason manganin is used to prepare standard resistances.

Question 8.
The sequence of bands marked on a carbon resistor are : Red, Red, Red, Silver. What is its resistance and tolerance?
Answer:
Given sequence of colour band Red Red Red Silver
Colour code for Red = 2
1st band red = 2 ; ‘
2nd band Red = 2
3rd band = No. of zeros = 2 (∵ Red) :
∴ Resistance R = 2200 Ω
tolerance band (4th band) Silver = 10%
∴ For silver resistor R = 2200 Ω with 10% tolerance.

Question 9.
Write the colour code of a carbon resistor of resistance 23 kilo ohms.
Answer:
Reistance 23 kilo ohms = 23000
∴ 1st band = 2 ⇒ Red ;
2nd band = 3 ⇒ orange
3rd band = No. of zeroes = 3 ⇒ orange
∴ Colour code for 23 kΩ = Red Orange, Orange.

Question 10.
If the voltage V applied across a conductor is increased to 2V, how will the drift velocity of the electrons change?
Answer:
Drift velocity will also double.
Drift velocity vd = \(\frac{-p}{m}\)Eτ
Where E = intensity of electric field. It depends on applied potential. When applied potential is doubled (V to 2V). Intensity of electric field E is also doubled.

(∵ E = \(\frac{V}{d}\) , where d is not charged). So drift d velocity is doubled.

Question 11.
Two wires of equal length, of copper and manganin, have the same resistance. Which wire is thicker?
Answer:
Manganin wire is thicker.
Resistance R = ρ\(\frac{l}{A}\) given l is same.
For copper specific resistance ρ is less than manganin.
∵ R is constant material with high ‘ρ’ must have larger area A.
Hence manganin wire is thicker.

Question 12.
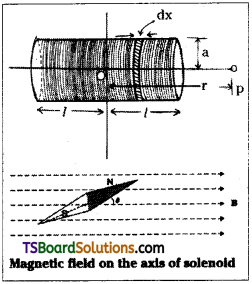
What is the magnetic moment associated with a solenoid of ‘N’ turns having radius of cross-section ‘r’ carrying a current I?
Answer:
Magnetic moment of solenoid (N) = πr² In × 2l where ‘2l’ = length of solenoid, r = radius, I = current
n = number of turns.

Question 13.
Why are household appliances connected in parallel?
Answer:
In parallel combination potential drop is constant. Different amounts of current is allowed through each component separately. i.e., we may switch off unwanted connections without disturbing other.

Hence parallel connection of appliances is prefered in household connections.

Question 14.
The electron drift speed in metals is small (~ m^-1) and the charge of the electron is also very small (~ 10^-19) Q, but we can still obtain a large amount of current in a metal. Why?
Answer:
Eventhough charge of electron ‘e’, drift velocity v_d are less number of electrons n is very high, current i = ne v_d. (i.e., charges flowing per second)
∵ n is extremely high we are getting large current.

Short Answer Questions

Question 1.
A battery of emf 10 V and internal resistance 3Ω is connected to a resistor R.
(i) If the current in the circuit is 0.5 A. Calculate the value of R.
(ii) What is the terminal voltage of the battery when the circuit is closed? [TS Mar. ’15]
Answer:
emf E = 10V, Internal resistance r = 3Ω

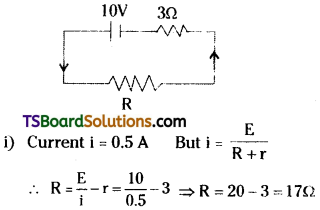
ii) Terminal voltage V = E – ir
∴ V = 10 – 0.5 × 3 = 10 – 1.5 = 8.5V

Question 2.
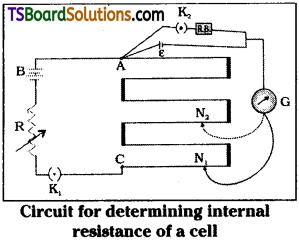
Draw a circuit diagram showing how a, potentiometer may be used to find internal resistance of a cell and establish a formula for it.
Answer:
Circuit diagram to find internal resistance; of a cell is

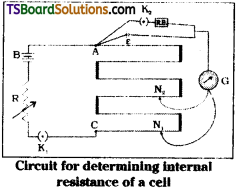
Theory :
i) In circuit key ‘k₂’ is open and potentiometer jockey is adjusted to zero deflection.
Balancing length l₁ is measured.
Now ε = Φl₁ → (1)

ii) Key ‘k₂‘ is closed. Balancing length l₁ is measured.
Now V = Φl₁ → (2)
But ε = I (R + r) and V = IR so from eq (1) & (2)

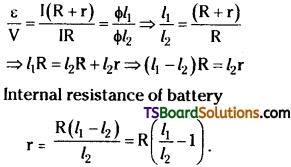
Question 3.
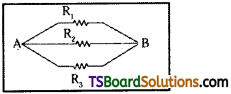
Derive an expression for the effective resistance when three resistors are connected i) series ii) parallel.
Answer:
i) Series combination :
Let three resistors R₁, R2 and R₃ be connected in series as shown in figure.

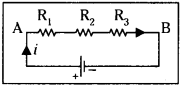
Same current i flows through all resistors.
Potential drop across R₁ ⇒ (V₁) = iR₁
Similarly V₂ = iR₂ and V₃ = iR₃ are P.D across R₂ + R₃
Total potential across AB (V) = V₁ + V₂ + V₃
∴ V = iR₁ + iR₂ + iR₃ = i (R₁ + R₂ + R₃), But V = i R
∴ V = i R_eq = i(R₁ + R₂ + R₃)
In series combination R_eq = R₁ + R₂ + R₃
∴ Equivalent resistance is the sum of individual resistors.

ii) Parallel combination of resistors :
Let three resistors R₁, R₂ and R₃ be connected in parallel as shown in figure.

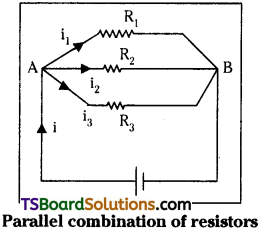
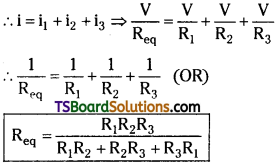
In this combination potential drop across AB is constant. But different values of current flows though each resistor. Total current i = i₁ + i₂+ i₃

Current through R₁ ⇒ (i₁) = \(\frac{V}{R_1}\) Similarly,
⇒ i₂ = \(\frac{V}{R_2}\) and i₃ = \(\frac{V}{R_3}\).

Question 4.
‘m’ cells each of emf E and internal resistance ‘r’ are connected in parallel. What is the total emf and internal resistance? Under what conditions is the current drawn from the mixed grouping of cells a maximum?
Answer:
i) Let m’ identical cells each of emf E’ and internal resistance V be connected in parallel as shown in the figure.
ii) Applying Kirchoffs voltage law to the circuit, we have for the first cell,

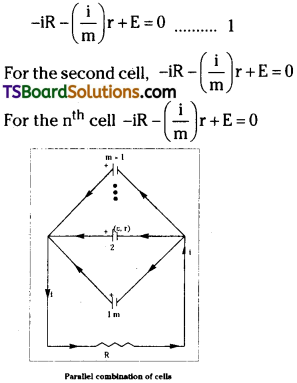
iii) Adding the above m’ equations, we get, – m(iR) – m(\(\frac{i}{m}\))r + mE = 0
(mR + r)i = mE
∴ I = \(\frac{mE}{mR+r}\)

iv) The above expression can be written as

Mixed grouping of cells :
Note : Mixed grouping of cells not given in New Syllabus.
Answer:
Let m cells are in series and there are n such rows this arrangement is called mixed grouping.
In mixed grouping current i = \(\frac{mnE}{mr+nR}\)
Current will be maximum when mr = nR
∴ i_max = \(\frac{nE}{2r}\)

Question 5.
Define electric resistance and write it’s SI unit. How does the resistance of a conductor vary if
a) Conductor is stretched to 4 times of it’s length.
b) Temperature of conductor is increased?
Answer:
Resistance :
The obstruction created by a conductor for the mobility of charges through it is known as resistance.
i) The resistance of a conductor (R) is proportional to length R ∝ l → (1)
ii) and inversely proportional to area of cross-section of the conductor.

where “ρ” = resistivity of the conductor.

a) When conductor is stretched by four times its new length l₂ = 4l₁ or \(\frac{l_1}{l_2}\) = 4
When a wire is stretched by keeping its mass
constant then Rg = R₁[latex]\frac{l_2}{l_1}[/latex]²
∴ R₂ = R₁ . (4)² = 16R₁
So when a wire is stretched by 4 time its resistance is increased by 16 times.

b) When temperature of conductor is increased its resistance will increase.
Resistance at t°C is R_t = R₀ (1 + αt)
where α’ = temperature coefficient of resistance of that conductor.

Question 6.
When the resistance connected in series with a cell is havled, the current is equal to or slightly less or slightly greater than double. Why?
Answer:
Let a cell of emf ‘E’ and internal resistance ‘r’ is connected with external resistance R as shown in figure.

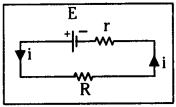
Total resistance in circuit R_T = R + r → (1)
Current in circuit i₁ = \(\frac{E}{R+r}\) → (2)

a) Now external resistance R is reduced to \(\frac{R}{2}\).
Total resistance in circuit R_T1 = \(\frac{R}{2}\) + r
\(\frac{R+2r}{2}\) → (2)
From eq (1) and (3)
\(\frac{R+2r}{2}\) is not equals to \(\frac{R+r}{2}\).
i.e., when R is reduced to \(\frac{R}{2}\) total resistance R_T1 is not equals to \(\frac{R_T}{2}\).
So current in the circuit i₂ ≠ 2i₁. But i₂ is slightly less than 2i₁ it depends on the value of internal resistance ‘r’.

b) In case of ideal battery where r = 0 then R_T2 = \(\frac{R}{2}\) in this case R_T2 = \(\frac{R_{T_1}}{2}\)and
current i₂ = 2i₁.

So when reistance R in the circuit is reduced to half of its value current in circuit is doubled or slightly less than double.

Question 7.
Two cells of emfs 4.5V and 6.0V and internal resistance 6Ω and 3Ω respectively have their negative terminals joined by a wire of 18Ω and positive terminals by a wire of 12Ω resistance. A third resistance wire of 24Ω connects middle points of these wires. Using Kirchhoff s laws, find the potential difference at the ends of this third wire.
Answer:
The circuit diagram as per given data is as shown

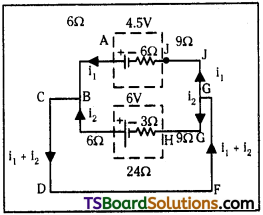
From fig for loop ABCDFGJA
6i₁ + 24 (i₁ + i₂) + 9i₁ – 6i₁ = 4.5
33i₁ + 24i₂ = 4.5 → (1)

For loop IBCDFGHI
6i₂ + 24(i₁ + i₂) + 9i₂ – 3i₂ = 4.5
24i₁ + 36i₂ = 6.0 → (2)

Question 8.
Three resistors each of resistance 10 ohm are connected, in turn, to obtain (i) minimum resistance (ii) maximum resistance. Compute (a) The effective resistance in each case (b) The ratio of minimum to maximum resistance so obtained.
Answer:
Resistance of each resistor R = 10Ω ;
Number of Resistors n = 3
a) In parallel combination resistance is minimum.

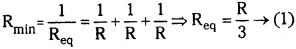
b) In series combination resultant resistance is maximum.

Question 9.
State Kirchhoff s law for an electrical network. Using these laws deduce the condition for balance in a Wheatstone bridge. [AP Mar. ’19. ’18. ’14. May ’16. ’14; TS May ’18. Mar. ’18, ’16, June ’15]
Answer:
Kirchhoffs Laws:
i) Junction rule :
At any junction, the sum of currents towards the junction is equal ‘ to sum of currents away from the junction.
(OR)
Alzebraic sum of currents around a junction is zero.

ii) Loop rule :
Alzebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.

Applying Kirchoff’s Law to Wheatstones bridge:
Wheatstones bridge consists of four resistances P, Q, R, S connected as shown in the figure and are referred as arms of the bridge.

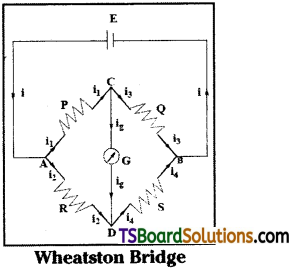
A battery of emf ‘E’ is connected between two junctions A and B and a galvanometer of resistance ‘G’ is connected between ‘C’ and ‘D’.

Applying Kirchoff’s first law,
at the junction C; i₁ = i_g + i₃ — (1)
at the junction D; i₂ + i_g = i₄ — (2)
Applying Kirchoff’s second law for the loop ACDA
– i₁ P – i_g G + i₂ R = 0 — (3)
For the loop CBDC,
– i₃ Q + i₄ S + i_g G = 0 — (4)

If no current passes through the galvanometer then the bridge is said to be balanced.
So, i_g = 0, then (1), (2), (3) and (4) becomes
i₁ = i₃, i₂ = i₄, i₁P = i₂R and i₃ Q = i₄ S.
By adjusting the above equations we get \(\frac{P}{Q}=\frac{R}{S}\).
This is the balancing conditions of a Wheatstones bridge.

Question 10.
State the working principle of potentiometer explain with the help of circuit diagram how the emf of two primary cells are compared by using the potentiometer. [AP Mar. 17,16, May ‘ 17; June ’15; TS Mar. 19, May 16]
Answer:
Potentiometer working principle :
Potentiometer consists of 10 meters length of wire with uniform internal resistance. Let total length of wire is L and its total resistance is R_p.

where Φ = Potential drop per unit length i.e., potential gradient.

Comparison of e.m.f. of two cells :
The circuit diagram used to compare emf of two cells is as shown in figure.
Circuit connection were given as per diagram.

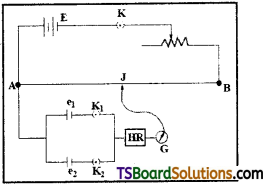
The potentiometer contains two circuits, primary and secondary.

The primary circuit consists of a cell of emf ‘E’ that a plug key (K) and a rheostat (Rh). These are connected in series with potentiometer wire AB.

The secondary circuit consists of two cells of emf e₁ and e₂, two plug keys K₁ and K₂, a galvanometer (G) and a Jockey (J) as shown in the figure.

The positive terminals of the two cells in primary and secondary are connected to terminal A’.

Procedure:
i) The plug keys K and K₁ are closed and by adjusting Jockey on the wire, the balancing length ‘l₁‘ is determined.
e₁ ∝ l₁ ——- (1)

ii) Now plug key K₁ is opened and K₂ is closed. Again the Jockey is adjusted and balancing length ‘l₂‘ is determined.
e₂ ∝ l₂ ——- (2)
from (1) and (2 ) \(\frac{e_1}{e_2}=\frac{l_1}{l_2}\) Ratio of emf of two cells.

Question 11.
State the working principle of potentiometer explain with the help of circuit diagram how the potentiometer is used to determine the internal resistance of the given primary cell. I [AP May 18, Mar. 15; TS Mar. 17. 15, May 17]
Answer:
Potentiometer working principle :
Potentiometer consists of 10 meters length of wire with uniform internal resistance. Let total length of wire is L and its total resistance is R_p.

Current through potentiometer wire i

where Φ = Potential drop per unit length i.e., potential gradient.

Determination of internal resistance (r) :
Circuit diagram used to find internal resistance of battery is as shown in figure.

Battery E is connected in primary circuit through plus key k₁.

Another battery E₁ is connected in secondary circuit. A low resistance R’ is connected in parallel to Battery E₁ along with key k₂.

Plug k₂ is open. Jockey J is moved on potentiometer until zero deflection is obtained. Balancing length l₁ is measured.

Plug key k₂ is closed so resistance R will come into operatioin. Again Jockey J is moved on potentiometer wire to find balancing point. When zero deflection is obtained balancing length l₂ is measured.

Question 12.
Show the variation of current versus voltage graph for GaAs and mark the (i) Nonlinear region (ii) Negative resistance region.
Answer:
The voltage-current characteristic graph of galium arsinide (GaAs) is as shown in figure.

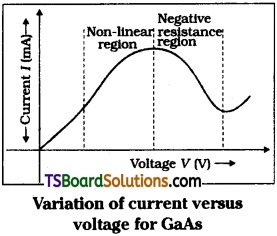
GaAs is a semiconducting substance. Its V-I characteristics are non-ohmic. So V-I graph is not linear.
The region OA is linear. In which Ohm’s Law is obeyed.
The region AB is a curve (i). Here voltage V is not linear with currrent (i). So It is a non-linear region.

(ii) In the region BC current I decreases even though voltage ‘V’ increases.
Resistance R = \(\frac{V}{I}\)
∵ I decreases resistance in the region BC is negative.
The regions (1) and (2) are shown in figure.

Question 13.
A student has two wires of iron and copper of equal length and diameter. He first joins two wires in series and passes an electric current through the combination which increases gradually. After that, he joins two wires in parallel and repeats the process of passing current. Which wire will glow first in each case?
Answer:
Iron and copper wires of equal length and diameter are taken. For Iron, resistivity is ρ_i high. For copper resistivity, ρ_c is less.
∴ Resistance of Iron wire R_i is high and Resistance of copper wire R_c is less.

a) When connected in series same current flows through Iron and Copper wires. Heat produced Q = I²R. So heat produced in copper wire is less and that of Iron wire is high.

In series combination when current increases gradually than Iron wire will glow first.

b) When the two wires are connected in parallel and current is increased gradually.

In parallel combination high current flows through low resistance and low current through high resistance. They follow the relation I_c/I_i = R_i/R_c.

So current through copper wire is high. Heat produced Q = i²R ⇒ Q_c > Q_t
Heat produced in copper wire is more than that in iron wire.
So in parallel combination copper wire will glow first.

Question 14.
Three identical resistors are connected in parallel and total resistance of the circuit is R/3. Find the value of each resistance.
Answer:
In parallel combination when ‘n’ identical wires are connected parallelly equivalent resistance is given by R_eq = R/n.

Given three identical wires ⇒ n = 3.
∴ R_eq = R/3 where R is resistance of each wire.
∴ Resistance of each wire used in parallel combination is R.

Hence resistance of each wire used in parallel combination is R.

Long Answer Questions

Question 1.
Under what condition is the heat produced in an electric circuit (a) directly pro-portional (b) inversely proportional to the resistance of the circuit? Compute the ratio of the total quantity of heat produced in the two cases.
Answer:
Let a current I is flowing through a conductor between its ends say A and B. Let potential at A is V(A) and potential at B is V(B).

Potential difference across AB is say V = V(A) – V(B)

Let charge flowing in time ∆t is ∆Q = I∆T
Change in potential energy ∆V = Final P.E – Initial P.E
= ∆Q[V(B) – V(A)] = -∆QV = -TV∆t < 0 → (1)
Let charges are moving without collision with atoms.
Then kinetic energy of charges will also increase.
∆K = -∆U_Pot or ∆K = IV ∆t > 0 → (2)
Work done in this process ∆W = IV ∆t → (3)
But power

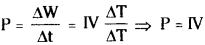
From Ohm’s Law V = IR
∴ Power P = I.I.R = I²R
In this case power p ∝ R.

In this case energy of charge carriers is useful to heat the conductor. Amount of energy dissipated in conductor per second is power.

Where priority is given to current through conductor, at ordinary voltages we will say that p ∝ R.

i) In case of transmission lines the primary purpose is to transmit electrical energy from one place to another place. While doing so a part of energy is wasted in conductor in the form of heat. Let total power to be transmitted = P. Resistance of conductor = R_c,
Line voltage = V

Power wasted in transmission or transmission losses P_c = \(\frac{P^2R_c}{V^2}\). Due to this reason to reduce transmission losses we are transmitting electric power at very high voltages.

When voltage is given priority power P = \(\frac{V^2}{R}\)

In this case power P is said to be inversely proportional to resistance ‘R’.
Ratio of heats produced in the two cases is I²R: V²/R
But V = IR
∴ Ratio is I²R = \(\frac{I^2R^2}{R}\) = 1 : 1

Question 2.
Two metallic wires A and B are connected in parallel. Wire A has length L and radius r wire B has a length 2Land radius 2r. Compute the ratio of the total resistance of the parallel combination and resistance of wire A.
Answer:
Let resistivity of metallic wire A is ρ_A and that of B is ρ_B.

For wire A :
Length = L, radius = r, resistivity = ρ_R
Resistance of wire A is R_A = \(\frac{\rho_{\mathrm{A}} \mathrm{L}}{\mathrm{A}}=\frac{\rho_{\mathrm{A}} \cdot \mathrm{L}}{\pi r^2}\) → (1)

For wire B :
Length = 2L; radius = 2r ; resistivity = ρ_B.
Resistance of wire B is

a) Ratio of resistance of the wires = R_A : R_B

b) When resistors RA and Rg are connected in parallel effective resistance

Question 3.
In a house three bulbs of 100 W each are lighted for 4 hours daily and six tube lights of 20W each are lighted for 5 hours daily and a refrigerator of 400 W is worked for 10 hours daily for a month of 30 days. Calculate the electricity bill if the cost of one unit is Rs. 4.00.
Answer:
Electric consumption in KWH per one month

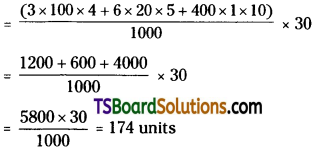
Electricity bill = No. of units × cost of unit = 174 × 4 = Rs. 696/-.
∴ Current bill, for that month is Rs. 696/-

Question 4.
Three resistors of 4 ohms, 6 ohms and 12 ohms are connected in parallel. The combination of above resistors is connected in series to a resistance of 2 ohms and then to a battery of 6 volts. Draw a circuit diagram and calculate
a) Cureent in main circuit
b) Current flowing through each of the resistors in parallel
c) P.D and the power used by the 2 ohm resistor.
Answer:
Given R₁ = 4Ω, R₂ = 6Ω and R₃ = 12Ω
i) When R₁, R₂ and R₃ are connected in parallel effective resistance

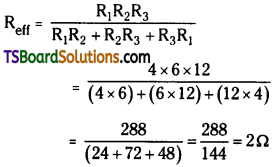
ii) R_eq is connected to a 2Ω resistor in series and then to a battery of 6V. The circuit diagram is as shown.

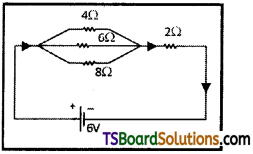
Total Resistance in circuit = R_eq + 2 = 2 + 2 = 4Ω
a) Current in main circuit I = \(\frac{V}{R}=\frac{6}{4}\) = 1.5 amp
b) Current through

c) RD across 2Ω Resistor
i = 1.5A, R = 2Ω ∴ P.D = iR= 1.5 × 2 = 3V
Power used P = i²R = 1.5 × 1.5 × 2 = 4.5 watt.

Question 5.
Two lamps, one rated 100 W at 220 V and the other 60 W at 220 V are connected in parallel to a 220 volt supply. What current is drawn from the supply line?
Answer:
For 1st Lamp power P = 100 W at potential V = 220 V
Supply voltage V = 220 V ; Power P = VI

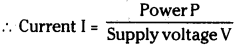
∴ I₁ = \(\frac{100}{200}\)
For 2nd lamp power P = 60 W at 220 V.
Supply voltage = 220 V
Current i₂ = \(\frac{P^2}{V}=\frac{60}{200}\)
Total current drawn by parallel combination
I = I₁ + I₂⇒ I = 0.4545 + 2727 = 0.7272 A

Question 6.
A light bulb is rated at 100W for a 220V supply. Find the resistance of the bulb. [IMP]
Answer:
Power P = 100 W; Potential V = 100 V

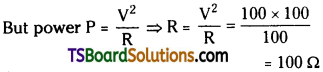
Question 7.
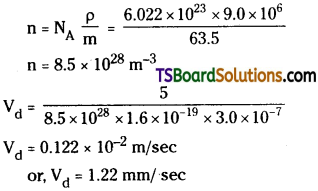
Estimate the average drift speed of conduction electrons in a copper wire of crosssectional area 3.0 × 10^-7 m² carrying a current of 5 A. Assume that each copper atom contributes roughly one conduction electron. The density of copper is 9.0 × 10³ kg/m³ and its atomic mass is 63.5 u.
Answer:
Area A = 3.0 × 10^-7m² ;
Current i = 5A
Density ρ = 9.0 × 10³ kgm^-3 = 9.0 × 10⁶gm^-3
Atomic mass m = 63.5 U
Avagadro number NA = 6.022 × 10²³;
Charge on electron e = 1.6 × 10^-19 C
Drift velocity v_d = i/neA. Where n = total number of electrons / unit volume

Question 8.
Compare the drift speed obtained above with
i) Thermal speed of copper atoms at ordinary temperatures.
ii) Speed of propagation of electric field along the conductor which causes the drift motion.
Answer:
Drift velocity of electrons in copper = 1.22 m.m/s
i) Thermal speed of copper atoms V_T = \(\sqrt{k_{B}T/m}\).
Where k_B is Boltzman’s constant.
k_B = 1.381 × 10^-25
Let T = 300 K average temperature or ordinary temperature
m = mass of copper atom, By subtituting the above values V_T = 200 m/ sec
V_d < < V_rms

Thermal speed of copper atom is 10⁵ times more than drift velocity of electrons.

ii) An electric field travels with velocity of light along the conductor is velocity of electromagnetic wave 3 × 10⁸m/s.

Speed of electric field travelling along a conductor is 10¹¹ times more than drift velocity of electrons.

Problems

Question 1.
A 10Ω thick wire is stretched so that its length becomes three times. Assuming that there is no change in its density on stretching, calculate the resistance of the stretched wire.
Solution:
Resistance R = 10Ω ; Final length l₂ = 3l₁
When a wire is stretched its total volume is constant.

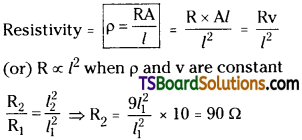
Question 2.
A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter? [AP Mar. 19,14. May 16; TS Mar. 16]
Solution:
Resistance = 4R
The wire is bent in the form of a circle and Resistance is to be calculated along its diameter.

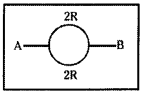
Between the point AB the wire is a parallel
combination of 2R and 2R.
∴ Resultant resistance \(\frac{1}{R_R}=\frac{1}{2R}+\frac{1}{2R}=\frac{1}{R}\)
∴ Effective resistance between A & B = R.

Question 3.
Find the resistivity of a conductor which carries a current of density of 2.5 × 10⁶ A m^-2 when an electric field of 15 Vm^-1 is applied across it.
Solution:
Current density j = 2.5 × 10⁶ A
Electric field E = 15 V m^-1
Resistivity ρ = ? Resistivity p = E/j

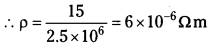
Question 4.
What is the color code for a resistor of resistance 3500Ω with 5% tolerance?
Solution:
Resistance R = 3500 Ω. Tolerance = 5%
R = 3500 First digit 4 ⇒ Orange
2nd digit 5 ⇒ Green
Last two digits represent number of zeros = 2 ⇒ Silver
Tolerance = 5% ⇒ gold colour So colour code of that resistor is orange, green, silver and gold bands.

Question 5.
You are given 8Ω resistor. What length of wire of resistivity 120 ftm should be joined in parallel with it to get a value of 6Ω?
Solution:
Resistance Rj = 8Ω, Resistivity ρ = 12Ω m
Resistance across parallel combination R_p = 6Ω
Let parallel resistance to be connected
x = 120 / metres

Question 6.
Three resistors 3Ω, 6Ω and 9Ω are connected to a battery. In which of them will the power dissipation be maximum if: (a) they all are connected in parallel (b) they all are connected in series? Give reasons.
Solution:
Values of resistors R₁ = 3 Ω ; R₂ = 6 Ω ; R₃ = 9 Ω
a) When in series R_eff = R₁</sub. + R₂ + R₃ = 3 + 6 + 9 = 18
Power consumed P = \(\frac{V^2}{R}=\frac{V^2}{18}\) → (1)

b) When connected in parallel total power consumed is the sum of powers in each resistor.

From eq 1 & 2 power dissipation is maximum when they are connected in parallel.

Question 7.
A silver wire has a resistance of 2.1Ω at 27.5°C and a resistance of 2.7Ω at 100°C. Determine the temperature coefficient of resistivity of silver.
Solution:
Temperature t₁ = 27.5°C ;
Resistance R₁ = 2.1 Ω
Temperature t₂ = 100°C ;
Resistance R₂ = 2.7 Ω
Temperature coefficient of resistivity

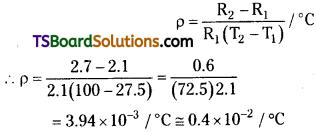
Question 8.
If the length of a wire conductor is doubled by stretching it while keeping the potential difference constant, by what factor will the drift speed of the electrons change?
Solution:
Length of wire is doubled ⇒ l₂ = 2l₁
Potential V = constant ; Same material is used ⇒ electron density per unit volume is same.
Drift velocity v_d = \(\frac{i}{neA}\) here i, n and e are constants.

∴ Drift velocity is doubled.

Question 9.
Two 120V light bulbs, one of 25W and another of 200W are connected in series. One bulb burnt out almost instantaneously. Which one was burnt and why?
Solution:
For 1st bulb, Power P₁ = 25 W; For 2nd bulb P₂ = 200 W
When they are connected to mains supply of 240 V in series

In series combination voltage drop is high on high resistance and less on low resistance.

Since voltage on 25W bulb is more than rated voltage it blows off instantly.

Question 10.
A cylindrical metallic wire is stretched to increase its length by 5%. Calculate the percentage change in resistance.
Solution:
% Increase in length = 5%

∴ Percentage change in resistance = 2 × 5 = 10%

Question 11.
Three identical resistors are connected in parallel and total resistance of the circuit is R/3. Find the value of each resistance.
Solution:
In parallel combination when ‘n’ identical wires are connected parallelly, equivalent resistance is given by R_eq = R/n.

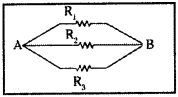
Given three identical wires ⇒ n = 3.
∴ R^eq = R/3 where R is resistance of each wire.
∴ Resistance of each wire used in parallel combination is R.

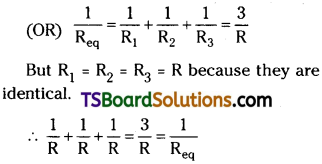
Hence resistance of each wire used in parallel combination is R.

Question 12.
Two wires A and B of same length and same material, have their cross sectional areas in the ratio 1 : 4. What would be the ratio of heat produced in these wires when the voltage across each is constant?
Solution:
Given lengths of wire are same ⇒ l₁ = l₂
Same material is used ⇒ ρ₁ = ρ₂
Ratio of area of cross sections A₁ : A₂ = 1 : 4 ⇒ A₂ = 4A₁
Potentail V is same.

∴ Ratio of Heat produced = 1 : 4

Question 13.
Two bulbs whose resistances are in the ratio of 1 : 2 are connected in parallel to a source of constant voltage. What will be the ratio of power dissipation in these?
Solution:
Ratio of resistances ⇒ R₁ : R₂ = 1 : 2
⇒ R₂ = 2R₁
When in parallel P.D is same on each bulb.

Question 14.
A potentiometer wire is 5 m long and a potential difference of 6 V is maintained between its ends. Find the emf of a cell which balances against a length of 180 cm of the potentiometer wire. [AP Mar. 17, 16. June 15; TS May 16]
Solution:
Total length of potentiometer wire L = 5 m
= 500 cm
Balancing length l₁ = 180 cm
P.D across the terminals = 6V
In potentiometer e.m.f at balancing point
V = \(\frac{El}{L}\frac{6\times180}{500}\)
∴ E.m.f of cell in secondary E₁ = 2.16 V

Question 15.
In a potentiometer arrangement, a cell of emf 1.25V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell?
Solution:
Emf of the cell, E₁ = 1.25 V
Balance point of the potentiometer, l₁ = 35 cm
The cell is replaced by another cell of emf E₂.
New balance point of the potentiometer, l₂ = 63 cm.
The balance condition is given by the

Therefore, emf of the second cell is 2.25V.

Question 16.
If the balancing point in a meter-bridge from the left is 60 cm, compare the resistances in left and right gaps of meter-bridge.
Solution:
Balancing point distance l₁ = 60 cm
∴ l₂ = 100 – 60 = 40 cm
Ratio of resistance \(\frac{R_1}{R_2}=\frac{l_1}{l_2}=\frac{60}{40}=\frac{3}{2}\)
(or) R₁ : R₂ = 3 : 2

Question 17.
A battery of emf 2.5V and internal resistance r is connected in series with a resistor of 45 ohm through an ammeter of resistance 1 ohm. The ammeter reads a current of 50 mA. Draw the circuit diagram and calculate the value of r. (Internal resistance)
Solution:
E.m.f. of battery E₁ = 2.5 V ;
Internal resistance = r
Series Resistance R = 45 Ω;
Ammeter Resistance = 1Ω
Reading in ammeter = 50 mA = 50 × 10^-3 Amp

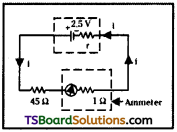
From Kirchhoff’s mesh rule
E = iR + iR₁ – ir
2.5 = i 45 + i × 1 – ir
⇒ ir = 45 i + i – ir ⇒ E – 46i = – ir
∴ 2.5 – 46 × 50 × 10^-3 = -50 × 10^-3 r ⇒ 2.5 – 2.3 = -ir
∴ r = \(\frac{-0.2}{50\times10_{-3}}\) -ve sign indicates current in opposite direction.
∴ Internal resistance of battery
r = \(\frac{200}{50}\) = 4Ω

Question 18.
Amount of charge passing through the cross section of a wire is q(t) = at² + bt + c. Write the dimensional formula for a, b and c. If the values of a, b and c in SI unit are 6, 4, 2 respectively, find the value of current at t = 6 seconds.
Solution:
Given q (t) = at² + bt + c
But current i = \(\frac{d}{dt}\) q(t) = \(\frac{d}{dt}\) (at² + bt + c) = 2at + b → (1)
Put a = 6, b = 4, c = 2 and t = 6 in eq – (1)
∴ Current i = 2x6x6 + 4 = 72 + 4 = 76 Amp

Intext Question and Answer

Question 1.
The storage battery of a car has an emf of 12V. If the internal resistance of the battery is 0.4Ω, what is the maximum current that can be drawn from the battery?
A. Emf of the battery, E = 12 V ;
Internal resistance of the battery, r = 0.4Ω
Maximum current drawn from the battery = I ; According to Ohm’s law,
E = Ir
I = \(\frac{E}{r}=\frac{12}{0.4}\) = 30 A
The maximum current drawn from the given battery is 30 A.

Question 2.
A potentiometer wire is 5 m long and a potential difference of 6V is maintained between its ends. Find the emf of a cell which balances against a length of 180 cm of the potentiometer wire. [TS May ’16]
Answer:
Total length of potentiometer wire L = 5 m = 500 cm
Balancing length l₁ = 180 cm
P.D across the terminals = 6V
In potentiometer e.m.f at balancing point
El 6×180
V = \(\frac{El}{L}=\frac{6\times180}{500}\)
∴ E.m.f of cell in secondary E₁ = 2.16 V

Question 3.
A battery of emf 10 V and internal resistance 3Ω is connected to a resistor (R). If the current in the circuit is 0.5 A, what is the resistance (K) of the resistor? What is the terminal voltage of the battery when the circuit is closed? [(IMP) TS Mar, ’15]
Answer:
Emf of the battery, E = 10 V ;
Internal resistance of the battery, r = 3 Ω
Current in the circuit, 1 = 0.5 A ;Resistance of the resistor = R
The relation for current using Ohm s law is,
I = \(\frac{E}{R+r}\) ⇒ R + r = \(\frac{E}{I}\) = \(\frac{10}{0.5}\) = 20 Ω;
∴ R = 20 – 3 = 17 Ω
Terminal voltage of the resistor = V
According to Ohm’s law,
V = IR = 0.5 × 17 = 8.5 V
Therefore, the resistance of the resistor is 17 Ω and the terminal voltage is 8.5 V.

Question 6.
A negligibly small current is passed through a wire of length 15 m and uniform crosssection 6.0 × 10^-7m², and its resistance is measured to be 5.0 Ω. What is the resistivity of the material at the temperature of the experiment?
Answer:
Length of the wire, l = 15 m
Area of cross-section of the wire, a = 6.0 × 10^-7m²
Resistance of the material of the wire.
R = 5.0 Ω
Resistivity of the material of the wire = ρ
Resistance is related with the resistivity as

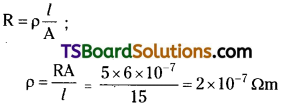
Therefore, the resistivity of the material is 2 × 10^-7 Ω m.

Question 5.
A silver wire has a resistance of 2.1 Ω at 27.5 °C, and a resistance of 2.7 Ω at 100 °C. Determine the temperature coefficient of resistivity of silver.
Answer:
Temperature, T₁ = 27.5°C ;
Resistance of the silver wire at T₁, R₁ = 2.1 Ω
Temperature, T₂ = 100°C ;
Resistance of the silver wire at T₂, R₂ = 2.7 Ω
Temperature coefficient of silver = α
It is related with temperature and resistance as

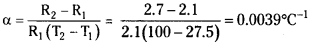
Therefore, the temperature coefficient of silver is 0.0039°C^-1.

Question 6.
Determine the current in each branch of the network shown in fig:

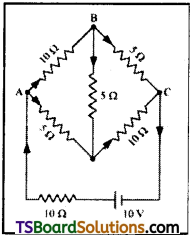
Answer:
Current flowing through various branches of the circuit is represented in the given figure.
I₁ = Current flowing through the outer circuit
I₂ = Current flowing through branch AB
I₃ = Current flowing through branch AD
I₂ – I₄ = Current flowing through branch BC
I₃ – I₄ = Current flowing through branch CD
I₄ = Current flowing through branch BD

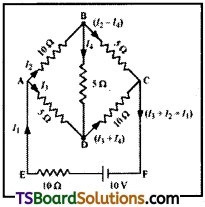
For the closed circuit ABDA, potential is zero i.e.,
10I₂ + 5I₄ – 5I₃ = 0 (OR) ⇒ 2I₂ + I₄ – I₃ = 0
I₃ = 2I₂ + I₄ …… (1)
For the closed circuit BCDB, potential is zero i.e.,
5(I₂ – I₄) – 10(I₃ + I₄) – 5I₄ = 0 (OR)
5I₂ + 5I₄ – 10I₃ – 10I₄ – 5I₄ = 0
5I₂ – 10I₃ – 20I₄ = 0 ; I₂ = 2I₃ + 4I₄ ….. (2)
For the closed circuit ABCFEA, potential is zero i.e.,
– 10 + 10(I₁) + 10(I₂) + 5(I₂ – I₄) = 0
10 = 15I₂ + 10I₂ – 5I₄ ⇒ 3I₂ + 2I₁ – I₄ = 2 ….. (3)
From equations (1) and (2), we obtain
I₃ = 2(2I₃ + 4I₄) + I₄; I₃ = 4I₃ + 8I₄ + I₄ – 3I₃ = 9I₄ ⇒ -3I₄ = + I₃ ….. (4)
Putting equation (4) in equation (1), we obtain
I₃ = 2I₂ + I₄ (OR) ⇒ -4I₄ = 2I₂ ; I₂ = – 2I₄ …… (5)
It is evident from the given figure that,
I₁ = I₃ + I₂ ……. (6)
Putting equation (6) in equation (1), we obtain
3I₂ +2(I₃ + I₂) – I₄ = 2
5I₂ + 2I₃ – I₄ = 2 ….. (7)
Putting equations (4) and (5) in equation (7), we obtain 5(-2I₄) + 2(-3I₄) – I₄ = 2 – 10I₄ – 6I₄ – I₄ = 2 (OR) 17I₄ = – 2
⇒ I₄ = \(\frac{-2}{17}\) A
Equation (4) reduces to I₃ = – 3(I₄) = -3\(\frac{-2}{17}=\frac{6}{17}\)A

Question 7.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell? [(IMP) AP Mar. ’15]
Answer:
Emf of the cell, E₁ = 1.25 V
Balance point of the potentiometer, l₁ = 35 cm
The cells is replaced by another cell of emf E₂.
New balance point of the potentiometer, l₂ = 63 cm
The balance condition is given by the

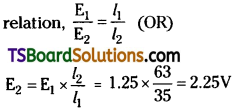
Therefore, emf of the second cell is 2.25V.

Question 8.
The number density of free electrons in a copper conductor estimated in Example 6.1 is 8.5 × 10²⁸ m^-3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10^-6 m² and it is carrying a current of 3.0 A.
Answer:
Number density of free electrons in a copper conductor, n = 8.5 × 10²⁸ m^-3,
Length of the copper wire, l = 3.0 m
Area of cross-section of the wire, A = 2.0 × 10^-6 m²
Current carried by the wire, I = 3.0 A, which is given by the relation,
I = nAeV_d
Where, e = Electric charge =1.6 × 10^-19 C
v_d = Drift velocit

Therefore, the time taken by an electron to drift from one end of the wire to the other is 2.7 × 10⁴ s.

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type

Question 1.
Find the equation of the circle which passes through the origin and intersects the circles x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0 orthogonally.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …………(1)
Since (1) passes through the point (0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Given equations of the circles are
x² + y² – 4x – 6y – 3 = 0 ……..(2)
x² + y² – 8y + 12 = 0 ……….(3)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-3) = 0 – 3
⇒ -4g – 6f = -3
⇒ 4g + 6f – 3 = 0 …….(4)
Since (1) and (3) are orthogonal, then
2gg’ + 2ff’ = c + c’
⇒ 2g(0) + 2f(-4) = 0 + 12
⇒ -8f = 12
⇒ f = \(\frac{-3}{2}\)
Substituting the value of ‘f’ in (4)
4g + 6(\(\frac{-3}{2}\)) – 3 = 0
⇒ 4g – 9 – 3 = 0
⇒ 4g = 12
⇒ g = 3
∴ The equation of the required circle is
x² + y² + 2(3)x + 2(\(\frac{-3}{2}\))y + 0 = 0
x² + y² + 6x – 3y = 0

Question 2.
Find the equation of the circle which passes through the origin and intersects the circles x² + y² – 4x + 6y + 10 = 0, x² + y² + 12y + 6 = 0 orthogonally. [(AP) May ’18]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since, (1) passes through the point (0, 0) then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Given equations of the circles are
x² + y² – 4x + 6y + 10 = 0 ……..(2)
x² + y² + 12y + 6 = 0 …….(3)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(g)(-2) + 2f(3) = c + 10
⇒ -4g + 6f = 0 + 10
⇒ -4g + 6f = 10
⇒ 2g – 3f = -5
⇒ 2g – 3f + 5 = 0 ……..(4)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(0) + 2f(6) = 0 + 6
⇒ 12f = 6
⇒ f = \(\frac{1}{2}\)
Substituting the value of f in (4)
2g – 3(\(\frac{1}{2}\)) + 5 = 0
⇒ 2g + \(\frac{7}{2}\) = 0
⇒ g = \(\frac{-7}{4}\)
∴ The equation of the required circle is from (1)
x² + y² + 2(\(\frac{-7}{4}\))x + 2(\(\frac{1}{2}\))y + 0 = 0
⇒ x² + y² – \(\frac{7}{2}\)x + y = 0
⇒ 2x² + 2y² – 7x + 2y = 0

Question 3.
Find the equation of the circle which passes through (1, 1) and cuts orthogonally each of the circles x² + y² – 8x – 2y + 16 = 0 and x² + y² – 4x – 4y – 1 = 0.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through point (1, 1) then
(1)² + (1)² – 2g(1) – 2f(1) + c = 0
⇒ 2 + 2g + 2f + c = 0
⇒ 2g + 2f + c = -2 …….(2)
Given equations of the circles are
x² + y² – 8x – 2y + 16 = 0 ……..(3)
x² + y² – 4x – 4y – 1 = 0 ………(4)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-4) + 2f(-1) = c + 16
⇒ -8g – 2f – c = 16 ………(5)
Since (1) and (4) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-2) = c – 1
⇒ -4g – 4f – c = -1
From (2) and (5)
2g + 2f + c = -2
⇒ -8g – 2f – c = 16
⇒ -6g = 14
⇒ g = \(\frac{-7}{3}\)
From (5) and (6)

Substituting the values of g, f in (2)

∴ The equation of the required circle is from (1),
x² + y² + 2(\(\frac{-7}{3}\))x + 2(\(\frac{23}{6}\))y – 5 = 0
⇒ 3x² + 3y² – 14x + 23y – 15 = 0

Question 4.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally. [May ’15 (TS) May ’13]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since eq (1) passes through the point (0, -3) then
9 + 2f(-3) + c = 0
⇒ 9 – 6f + c = 0
⇒ -6f + c = -9 ……..(2)
Given equations of the circles are
x² + y² – 6x + 3y + 5 = 0 ………(3)
x² + y² – x – 7y = 0 ………(4)
Since the circles (1) & (3) are orthogonal then 2gg’ + 2ff’ = c + c’
⇒ 2g(-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f – c = 5 …….(5)
Since the circles (1) & (4) are orthogonal then 2gg’ + 2ff’ = c + c’

Question 5.
Find the equation of the circle passing through the origin having its centre on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since eq. (1) passes through the point (0, 0) then c = 0
Centre of (1), C = (-g, -f) lies on the line
x + y = 4 then -g – f = 4 ……..(2)
Given the equation of the circle is
x² + y² – 4x + 2y + 4 = 0 ……….(3)
Since the circles (1) & (3) are orthogonal then 2gg’ + 2ff’ = c + c’
2g(-2) + 2f(1) = c + 4
⇒ -4g + 2f = 4
⇒ -2g + f = 2 ……….(4)
Solve (2) & (4)


∴ The equation of the required circle is x² + y² + 2(-2)x + 2(-2)y + 0 = 0
⇒ x² + y² – 4x – 4y = 0

Question 6.
Find the equation of the circle passing through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0. [(TS) May ’19]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point (2, 0), then
(2)² + (0)² + 2g(2) + 2f(0) + c = 0
⇒ 4 + 4g + c = 0
⇒ 4g + c = -4 ………(2)
Since (1) passes through the point (0, 2), then
(0)² + (2)² + 2g(0) + 2f(0) + c = 0
⇒ 4 + 4f + c = 0
⇒ 4f + c = -4 …….(3)
Given the equation of the circle is
2x² + 2y² + 5x – 6y + 4 = 0
⇒ x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 ………(4)
Since (1) and (4) are orthogonal, then 2gg’ + 2ff’ = c + c’
2g(\(\frac{5}{4}\)) + 2f(\(\frac{-3}{2}\)) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = c + 2
⇒ 5g – 6f = 2c + 4
⇒ 5g – 6f – 2c = 4 ………(5)

Question 7.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having the centre at (2, 3). [Mar. ’19 (TS)]
Solution:
Given the equation of the circle is
x² + y² – 4x + 2y – 7 = 0 ……….(1)
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(2)
centre (-g, -f) = (2, 3)
∴ g = -2, f = -3
since (1) &(2) are orthogonal then 2gg’ + 2ff’ = c + c’
⇒ 2(-2)(-2) + 2(-3)(1) = -7 + c
⇒ 8 – 6 = -7 + c
⇒ 2 = -7 + c
⇒ c = 7 + 2
⇒ c = 9
∴ The equation of the required circle is x² + y² – 4x – 6y + 9 = 0

Question 8.
Find the equation of the circle which is orthogonal to each of the following three circles x² + y² + 2x + 17y + 4 = 0, x² + y² + 7x + 6y + 11 = 0, and x² + y² – x + 22y + 3 = 0. [May ’08; Mar. ’03]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Given equations of the circles are
x² + y² + 2x + 17y + 4 = 0 ……..(2)
x² + y² + 7x + 6y + 11 = 0 ……..(3)
x² + y² – x + 22y + 3 = 0 ……….(4)
Since the circles (1) & (2) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(1) + 2f(\(\frac{17}{2}\)) = c + 4
⇒ 2g + 17f = c + 4 ……….(5)
Since the circles (1) & (3) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(\(\frac{7}{2}\)) + 2f(3) = c + 11
⇒ 7g + 6f – c = 11 ………(6)
Since the circles (1) & (4) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(\(\frac{-1}{2}\)) + 2f(11) = c + 3
⇒ -g + 22f – c = 3 ………(7)
From (5) & (6)

Substitute g, f values in eq. (5)
2(-3) + 17(-2) – c = 4
⇒ -6 – 34 – c = 4
⇒ c = -44
∴ The equation of the required circle is x² + y² + 2(-3)x + 2(-2)y – 44 = 0
⇒ x² + y² – 6x – 4y – 44 = 0

Question 9.
Find the equation of the circle which cuts the circles x² + y² + 2x + 4y + 1 = 0, 2x² + 2y² + 6x + 8y – 3 = 0, x² + y² – 2x + 6y – 3 = 0 orthogonally.
Solution:
Given equations of the circles are
S = x² + y² + 2x + 4y + 1 = 0
S’ = 2x² + 2y² + 6x + 8y – 3 = 0
S’ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
S” = x² + y² – 2x + 6y – 3 = 0
The equation of the radical axis of the circles S = 0 and S’ = 0 are S – S’ = 0
⇒ x² + y² + 2x + 4y + 1 – (x² + y² + 3x + 4y – \(\frac{3}{2}\)) = 0
⇒ x² + y² + 2x + 4y + 1 – x² – y² – 3x – 4y + \(\frac{3}{2}\) = 0
⇒ -x + 1 + \(\frac{3}{2}\) = 0
⇒ -2x + 2 + 3 = 0
⇒ 2x – 5 = 0 ……..(1)
The equation of the radical axis of the circles S’ = 0 and S” = 0 is S’ – S” = 0
⇒ x² + y² + 3x + 4y – \(\frac{3}{2}\) – (x² + y² – 2x + 6y – 3) = 0
⇒ x² + y² + 3x + 4y – \(\frac{3}{2}\) – x² – y² + 2x – 6y + 3 = 0
⇒ 5x – 2y – \(\frac{3}{2}\) + 3 = 0
⇒ 10x – 4y – 3 + 6 = 0
⇒ 10x – 4y + 3 = 0 ……..(2)
Solving (1) and (2)

∴ Radical centre, C = (\(\frac{5}{2}\), 7) = centre of the required circle.
Radius of the required circle, r = the length of tangent from the radical centre, C = (\(\frac{5}{2}\), 7) of the circle is \(\sqrt{\mathrm{S}_{11}}\)

4x² + 25 – 20x + 4y² – 56y + 196 = 357
x² + y² – 5x – 14y – 34 = 0