Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Theory of Equations Important Questions Very Short Answer Type to help strengthen their preparations for exams.
TS Inter Second Year Maths 2A Theory of Equations Important Questions Very Short Answer Type
Question 1.
Form the polynomial equation of the lowest degree whose roots are 1, – 1, 3. [May ’06]
Solution:
Let α = 1; β = – 1, γ = 3
The equation having roots α, β, γ is
(x – α) (x – β) (x – γ) = 0
⇒ (x – 1) (x + 1) ( x – 3) = 0
⇒ (x2 – 1) (x – 3) = 0
⇒ x3 – 3x2 – x + 3 = 0.
Question 2.
Form the polynomial equation of the lowest degree whose roots are 2 ± √3, 1 ± 2i. [May ’02, ’01]
Solution:
Let
α = 2 + √3, β = 2 – √3, γ = 1 + 2i, δ = 1 – 2i
The equation having α, β, γ, δ is
(x – α) (x – β) (x – γ) (x – δ) = 0
⇒ (x – 2 – √3) (x – 2 + √3) ((x – 1) – 2i) ((x – 1) + 2i) = 0
⇒ ((x – 2) – √3) ((x – 2) + √3) ((x – 1) – 2i) ((x – 1) + 2i) = 0
⇒ (x2 + 4 – 4x – 3) (x2 + 1 – 2x + 4) = 0
⇒ (x2 – 4x + 1) (x2 – 2x + 5) = 0
⇒ x4 + 5x2 – 2x3 – 4x3 + 8x2 – 20x + x2 – 2x + 5 = 0
⇒ x4 – 6x3 + 14x2 – 22x + 5 = 0
Question 3.
If 1, 1, α are the roots of x3 – 6x2 + 9x – 4 = 0. then find α. [AP – Mar. ’18; TS – May 2016; May ’11]
Solution:
Given equation is x3 – 6x2 + 9x – 4 = 0
Comparing this equation with ax3 + bx2 + cx + d = 0
we get, a = 1; b = – 6; c = 9; d = – 4
Since 1, 1, α are the roots of x3 – 6x2 + 9x – 4 = 0
then sum of the roots = s1 = \(\frac{-b}{a}\)
⇒ 1 + 1 + α = \(\frac{-(-6)}{1}\) = 6
⇒ 2 + α = 6
⇒ α = 4.
![]()
Question 4.
If – 1, 2 and α are the roots of 2x3 + x2 – 7x – 6 = 0, then find α.
[AP-Mar. 18; Mar. ’14, ’13, ’10, ’06, May’ 12, ’10]
Solution:
Given equation is 2x3 + x2 – 7x – 6 = 0
Comparing this with ax3 + bx2 + cx + d = 0 we get,
a = 2; b = 1; c = – 7; d = – 6
Since – 1, 2, α are the roots of 2x3 + x2 – 7x – 6 = 0
The sum of the roots = s1 = \(\frac{-b}{a}\)
– 1 + 2 + α = – \(\frac{1}{2}\)
1 + α = – \(\frac{1}{2}\)
⇒ α = – 1 – \(\frac{1}{2}\)
α = – \(\frac{3}{2}\)
Question 5.
If 1, – 2 and 3 are the roots of x3 – 2x2 + ax + 6 = 0, then find ‘a’. [TS – May 2015; March ‘04]
Solution:
Given equation is x3 – 2x2 + ax + 6 = 0
Since 1, – 2, 3 are the roots of x3 – 2x2 + ax + 6
Now 1 is a root of given equation then
13 – 2(1)2 + a(1) + 6 = 0
⇒ 1 – 2 + a + 6 = 0
a + 5 = 0
a = – 5
Question 6.
If the product of the roots of 4x3 + 16x2 – 9x – a = 0, is 9, then find ‘a’. [AP – Mar. 19, 17; TS – Mar. 16; May 13, 12, 08]
Solution:
Given equation is 4x3 + 16x2 – 9x – a = 0
Comparing this equation with ax3 + bx2 + cx + d = 0
we get, a = 4, b = 16, c = – 9, d = – a
Given that, the product of the roots = 9
s3 = 9
⇒ \(\frac{-\mathrm{d}}{\mathrm{a}}\) = 9
⇒ \(\frac{-(-a)}{4}\) = 9
⇒ a = 36.
![]()
Question 7.
If α, β and 1 are the roots of x3 – 2x2 – 5x + 6 = 0, then find α and β. [AP – May, Mar. 2016; May 09, March 08]
Solution:
Given equation is x3 – 2x2 – 5x + 6 = 0
Comparing this equation with ax3 + bx2 + cx + d = 0
we get a = 1, b = – 2, c = – 5, d = 6
Since α, β and 1 are the roots of x3 – 2x2 – 5x + 6 = 0
then s1 = α + β + 1
= \(\frac{-b}{a}=\frac{-(-2)}{1}\) = 2
⇒ α + β = 1 …………(i)
s3 = αβ . 1 = \(\frac{-d}{a}\)
⇒ αβ = \(\frac{-6}{1}\) =
⇒ αβ = – 6
(α – β)2 = (α + β)2 – 4αβ
= 1 – 4 ( -6)
= 1 + 24 = 25
⇒ α – β = 5 ……………(2)
Solve (1) and (2);
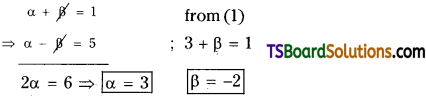
Question 8.
If α, β and γ are the roots of x3 + 2x2 + 3x – 4 = 0, then find α2β2. [May ’07]
Solution:
Given equation is x3 + 2x2 + 3x – 4 = 0
Since α, β and γ are the roots of x3 + 2x2 + 3x – 4 = 0 then
α + β + γ = \(\frac{-(-2)}{1}\) = 2
αβ + βγ + γα = \(\frac{3}{1}\) = 3
αβγ = \(\frac{-(-4)}{1}\) = 4
Σα2β2 = α2β2 + β2γ2 + γ2α2
= (αβ + βγ + γα)2 – 2αβγ (α + β + γ)
= 32 – 2 . 4(2)
= 9 – 16 = – 7.
Question 9.
If α, β and γ are the roots of 4x3 – 6x2 + 7x + 3 = 0, then find the value of αβ + βγ + γα. [TS – Mar. 2019]
Solution:
Given equation is 4x3 – 6x2 + 7x + 3 = 0
Comparing this equation with ax3 + bx2 + cx + d = 0
where a = 4; b = – 6; c = 7; d = 3
Since α, β, γ are the roots of 4x3 – 6x2 + 7x + 3 = 0 then
αβ + βγ + γα = S2 = \(\frac{c}{a}=\frac{7}{4}\).
Question 10.
Find the relations between the roots and the coefficients of the cubic equation 3x3 – 10x2 + 7x + 10 = 0.
Solution:
Given cubic equation is 3x3 – 10x2 + 7x + 10 = 0
Comparing this equation with
ax3 + bx2 + cx + d = 0, we get
a = 3, b = – 10, c = 7, d = 10
Let α, β, γ be the roots of given equation
s1 = \(\frac{-b}{a}\)
α + β + γ = \(\frac{-(-10)}{3}=\frac{10}{3}\)
s2 = αβ + βγ + γα
= \(\frac{c}{a}=\frac{7}{3}\)
s3 = αβγ
= \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-10}{3}\).
![]()
Question 11.
Write down the relations between the roots and the coefficients of the biquadratic equation x4 – 2x3 + 4x2 + 6x – 21 = 0.
Solution:
Given biquadratic equation is
x4 – 2x3 + 4x2 + 6x – 21 = 0 ……………… (1)
Comparing this equation with
ax4 + bx3 + cx2 + dx + e = 0,
we get a = 1, b = – 2; c = 4; d = 6; e = – 21
Let α, β, γ, δ are the roots of equation (1) then
i) s1 = α + β + γ + δ
= Σα = \(\frac{-b}{a}=\frac{-(-2)}{1}\) = 2
ii) s2 = Σαβ
= \(\frac{c}{a}=\frac{4}{1}\) = 4
iii) s3 = Σαβγ
= \(\frac{-d}{a}=\frac{-6}{1}\) = – 6
iv) s = Σαβγδ
= \(\frac{\mathrm{e}}{\mathrm{a}}=\frac{-21}{1}\) = – 21
Question 12.
If 1, 2, 3 and 4 are the roots of x4 + ax3+ bx2 + cx + d = 0, then find the values of a, b, c and d. [AP – May 2015]
Solution:
Given that the roots of the polynomial equation are 1, 2, 3 and 4.
Then(x – 1) (x – 2) (x – 3) (x – 4) = 0
(x2 – 3x + 2) (x2 – 7x + 12) = 0
x4 – 7x3 + 12x2 – 3x3 + 21x2 – 36x + 2x2 – 14x + 24 = 0
x4 – 10x3 + 35x2 – 50x + 24 = 0
Now, comparing this equation with
x4 + ax3 + bx2 + cx + d = 0
we get a = – 10; b = 35; c = – 50; d = 24.
Question 13.
If a, b, c are the roots of x3 – px2 + qx – r = 0 and r ≠ 0, then find \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\) in terms of p, q, r.
Solution:
Given equation is x3 – px2 + qx – r = 0
Since a, b and c are the roots of the equation x3 – px2 + qx – r = 0 then
s1 = a + b + c
= \(\frac{-(-p)}{1}\) = p;
s2 = ab + bc + ca
= \(\frac{q}{1}\) = q;
s3 = abc
= \(\frac{-(-r)}{1}\) = r
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=\frac{b^2 c^2+a^2 c^2+a^2 b^2}{a^2 b^2 c^2}\)
= \(\frac{(a b+b c+c a)^2-2 a b c(a+b+c)}{(a b c)^2}\)
= \(\frac{q^2-2 p \cdot r}{r^2}=\frac{q^2-2 p r}{r^2}\).
![]()
Question 14.
Find the sum of the squares and the sum of the cubes of the roots of the equation x3 – px2 + qx – r = o in terms of p, q, r.
Solution:
Given equation is x3 – px2 + qx – r = 0
Let α, β, γ are the roots of the equation x3 – px2 + qx – r = 0 then
s1 = α + β + γ
= \(\frac{-\mathrm{b}}{\mathrm{a}}=\frac{-(-\dot{\mathrm{p}})}{1}\) = p;
s2 = αβ + βγ + γα
= \(\frac{q}{1}\) = q;
s3 = αβγ
= \(\frac{-(-r)}{1}\) = r
i) The sum of the squares of the roots of the equation = α2 + β2 + γ2
= (α + β + γ)2 – 2(αβ + βγ + γα)
= p2 – 2q
ii) The sum of the cubes of the roots is α3 + β3 + γ3 = (α + β + γ)
(α2 + β2 + γ2 – αβ – βγ – γα) + 3αβγ
= p(p2 – 2q – q) + 3r
= p3 – 3pq + 3r.
Question 15.
Let α, β, γ be the roots of x3 + px2 + qx + r = 0. Then find Σα3. [March ’03]
Solution:
Given equation is x3 + px2 + qx + r = 0
Since α, β, γ are the roots of the equation x3 + px2 + qx + r = 0 then
s1 = α + β + γ
= \(\frac{-\mathrm{p}}{1}\) = – p;
s2 = αβ + βγ + γα
= \(\frac{q}{1}\) = q;
s3 = αβγ
= \(\frac{-r}{1}\) = – r
Σα3 = α3 + β3 + γ3
= (α + β + γ) (α2 + β2 + γ2 – αβ – βγ – γα) + 3αβγ
= (- p) ((p2 – 2q) – (q)) + 3 (- r)
= – p (p2 – 3q) – 3r
= – p3 + 3pq – 3r
Question 16.
Find s1, s2, s3 and s4 for the equation x4 – 16x3 + 86x2 – 176x + 105 = 0.
Solution:
Given equation is x4 – 16x3 + 86x2 – 176x + 105 = 0
Comparing this equation with ax4 + bx3 + cx2 + dx + e = 0
we get a = 1; b = – 16; c = 86; d = – 176; e = 105
Now, s1 = \(=\frac{-b}{a}=\frac{-(-16)}{1}\) = 16;
s2 = \(\frac{c}{\mathrm{a}}=\frac{86}{1}\) = 86;
s3 = \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-(-176)}{1}\) = 176;
s4 = \(\frac{\mathrm{e}}{\mathrm{a}}=\frac{105}{1}\) = 105
![]()
Question 17.
Find the algebraic equation whose roots are 2 times the roots of x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0. [Board Paper]
Solution:
Let f(x) = x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0
∴ Required equation is f(\(\frac{x}{2}\)) = 0
⇒ \(\frac{x^5}{32}-\frac{2 x^4}{16}+\frac{3 x^3}{8}-\frac{2 x^2}{4}+\frac{4 x}{2}+3\) = 0
⇒ x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0
Question 18.
Find the transformed equation whose roots are the negatives of the roots of x7 + 3x5 + x3 – x2 + 7x + 2 = 0.
Solution:
Let f(x) = x7 + 3x5 + x3 – x2 + 7x + 2 = 0
Required equation is f(- x) = 0
(- x)7 + 3(- x)5 + (- x)3 – (- x)2 + 7(- x) + 2 = 0
x7 + 3x5 + x3 + x2 + 7x – 2 = 0
Question 19.
Find the polynomial equation whose roots are the reciprocals of the roots of x4 – 3x3 + 7x2 + 5x – 2 = 0. [March ’11] [TS – Mar. 2015]
Solution:
Let f(x) = x4 – 3x3 + 7x2 + 5x – 2 = 0
The required equation is f(\(\frac{1}{x}\)) = 0
⇒ \(\frac{1}{x^4}-\frac{3}{x^3}+\frac{7}{x^2}+\frac{5}{x}-2\) = 0
⇒ 1 – 3x + 7x2 + 5x3 – 2x4 = 0
⇒ 2x4 – 5x3 – 7x2 + 3x – 1 = 0
Question 20.
Form the polynomial equation whose roots are the squares of the roots of x3 + 3x2 – 7x + 6 = 0. [May ’02]
Solution:
Let f(x) = x3 + 3x2 – 7x + 6 = 0
The required equation is f(√x) = 0
(√x)3 + 3 (√x)2 – 7√x +6 = 0
⇒ x√x + 3x – 7√x + 6 = 0
⇒ 3x + 6 = – √x (x – 7)
Squaring on both sides
9x2 + 36 + 36x = x (x2 + 49 – 14x)
= x3 + 49x – 14x2
x3 – 23x2 + 13x – 36 = 0.
![]()
Question 21.
Form the polynomial equation whose roots are the cubes of the roots of x3 + 3x2 + 2 = 0.
Solution:
Let f(x) = x3 + 3x2 + 2 = 0
The required equation is f(\(\sqrt[3]{x}\))= 0
\((\sqrt[3]{x})^3+3(\sqrt[3]{x})^2\) + 2 = 0
⇒ x + 3 . x2/3 + 2 = 0
x + 2 = – 3x2/3
Cubing on both sides (x + 2)3 = – 27x2
⇒ x3 + 8 + 6x2 + 12x + 8 = – 27x2
x3 + 33x2 + 12x + 8 = 0
Question 22.
If α, β, γ are the roots of x3 + px2 + qx + r = 0 then find
i) Σα2
ii) Σα3
iii) Σ \(\frac{1}{\alpha}\)
Solution:
Given equation is x3 + px2 + qx + r = 0
Since α, β, γ are the roots of the equation x3 + px2 + qx + r = 0 then
s1 = α + β + γ = \(\frac{-\mathrm{p}}{1}\) = – p;
s2 = αβ + βγ + γα = \(\frac{q}{1}\) = q;
s3 = αβγ = \(\frac{-r}{1}\) = – r.
i) Σα2 = α2 + β2 + γ2
= (α + β + γ)2 – 2(αβ + βγ + γα)
= (- p)2 – 2(q)
= p2 – 2q
ii) Σα3 = α3 + β3 + γ3
= (α + β + γ) (α2 + β2 + γ2 – αβ – βγ – γα) + 3αβγ
= (- p) ((p2 – 2q) – (+ q)) + 3(- r)
= – p (p2 – 2q – q) – 3r
= – p3 + 3pq – 3r
iii) \(\Sigma \frac{1}{\alpha}=\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}\)
= \(\frac{\beta \gamma+\alpha \gamma+\alpha \beta}{\alpha \beta \gamma}=\frac{q}{-r}=\frac{-q}{r}\)
Question 23.
Form the polynomial equation of the lowest degree with roots as 0, 0, 2, 2, – 2, – 2.
Solution:
The polynomial equation whose roots are 0, 0, 2, 2, – 2, – 2 is
(x – 0) (x – 0) (x – 2) (x – 2) (x + 2) (x + 2) = 0
⇒ x2 (x – 2)2 (x + 2)2 = 0
⇒ x2 (x2 + 4 – 4x) (x2 + 4 + 4x) = 0
⇒ x2 [(x2 + 4)2 – (4x)2] = 0
⇒ x2 (x4 + 16 + 8x2 – 16x2) = 0
⇒ x2 (x4 – 8x2 + 16) = 0
⇒ x6 – 8x4 + 16x2 = 0.
![]()
Question 24.
Form the monic polynomial equation of degree 3 whose roots are 2, 3 and 6. [May ’14, March ’02]
Solution:
x3 – 11x2 + 36x – 36 = 0
Question 25.
Form the monic polynomial equation of degree 4 whose roots are 4 + √3, 4 – √3, 2 + i and 2 – i.
Solution:
x4 – 12x3 + 50x2 – 92x + 65 = 0
Question 26.
Find s1, s2, s3 and s4 for the equation 8x4 – 2x3 – 27x2 – 6x + 9 = 0.
Solution:
s1 = \(\frac{1}{4}\),
s2 = \(\frac{-27}{8}\),
s3 = \(\frac{3}{4}\),
s4 = \(\frac{9}{8}\)
Question 27.
Find the algebraic equation whose roots are 3 times the roots of x3 + 2x2 – 4x + 1 = 0.
Solution:
x3 + 6x2 – 36x + 27 = 0
Question 28.
Find an algebraic equation of degree 4 whose roots are 3 times the roots of the equation 6x4 – 7x3 + 8x2 – 7x + 2 = 0. [March ’09]
Solution:
6x4 – 21x3 + 72x2 – 189x + 162 = 0.
![]()
Question 29.
Find the transformed equation whose roots are the negatives of the roots of x4 + 5x3 + 11x + 3 = 0. [AP – Mar. 2015]
Solution:
x4 – 5x3 – 11x + 3 = 0
Question 30.
Find the polynomial equation of degree 4 whose roots are the negatives of the roots of x4 – 6x3 + 7x2 – 2x + 1 = 0.
Solution:
x4 + 6x3 + 7x2 + 2x + 1 = 0
Question 31.
Find the polynomial equation whose roots are the reciprocals of the roots of x5 + 11x4 + x3 + 4x2 – 13x + 6 = 0.
Solution:
6x5 – 13x4 + 4x3 + x2 + 11x + 1 = 0
Question 32.
Find the polynomial equation whose roots are the reciprocals of the roots of the equation x4 + 3x3 – 6x2 + 2x – 4 = 0.
Solution:
4x4 – 2x3 + 6x2 – 3x – 1 = 0
![]()
Question 33.
Find the polynomial equation whose roots are the squares of the roots of x4 + x3 + 2x2 + x + 1 = 0.
Solution:
x4 + 3x3 + 4x2 + 3x + 1 = 0
Question 34.
Find the polynomial equation whose roots are the squares of the roots of x3 – x2 + 8x – 6 = 0.
Solution:
x3 + 15x2 + 52x – 36 = 0