TS Inter Second Year Maths 2B Parabola Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Parabola Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Parabola Important Questions Very Short Answer Type

Question 1.
Find the vertex and focus, and the equations of the directrix and axis of the parabola y² = 16x.
Solution:
Given parabola is y² = 16x
Compare with y² = 4ax
we get 4a = 16 ⇒ a = 4
Vertex A = (0, 0)
Focus S = (a, 0) = (4, 0)
The equation of the directrix is x + a = 0
⇒ x + 4 = 0
The equation of the axis is y = 0

Question 2.
Find the equations of the axis and directrix of the parabola y² + 6y – 2x + 5 = 0.
Solution:
Given equation of the parabola is y² + 6y – 2x + 5 = 0
⇒ y² + 6y = 2x – 5
⇒ (y)² + 2 . y . 3 + (3)² – (3)² = 2x – 5
⇒ (y + 3)² – 9 = 2x – 5
⇒ (y + 3)² = 2x + 4
⇒ (y + 3)² = 2(x + 2)
⇒ [y – (-3)]² = 2[x – (-2)]
Comparing with (y – k)² = 4a(x – h), we get
h = -2, k = -3,
4a = 2 ⇒ a = \(\frac{1}{2}\)
(i) Equation of the axis is y = k
⇒ y = -3
⇒ y + 3 = 0
(ii) Equation of the directrix is x = h – a
⇒ x = -2 – \(\frac{1}{2}\)
⇒ x = \(\frac{-5}{2}\)
⇒ 2x + 5 = 0

Question 3.
Find the coordinates of the vertex and focus, the equation of the directrix, and the axis of the parabola x² – 2x + 4y – 3 = 0.
Solution:
Given the equation of the parabola is
x² – 2x + 4y – 3 = 0
⇒ x² – 2x = -4y + 3
⇒ (x)² – 2 . x . (1) + (1)² – (1)² = -4y + 3
⇒ (x – 1)² – 1 = -4y + 3
⇒ (x – 1)² + 0 = -4y + 4
⇒ (x – 1)² = -4(y – 1)
Comparing with (x – h)² = -4a(y – k), we get
h = 1, k = 1, 4a = 4 ⇒ a = 1
(i) Vertex = (h, k) = (1, 1)
(ii) Focus = (h, k – a) = (1, 1 – 1) = (1, 0)
(iii) Equation of the directrix is y = k + a
⇒ y = 1 + 1
⇒ y = 2
⇒ y – 2 = 0
(iv) Equation of the axis is x = h
⇒ x = 1
⇒ x – 1 = 0

Question 4.
Find the vertex and focus of x² – 6x – 6y + 6 = 0.
Solution:
Given the equation of the parabola is
x² – 6x – 6y + 6 = 0
⇒ x² – 6x = 6y – 6
⇒ (x)² – 2 . (x) . (3) + (3)² – (3)² = 6y – 6
⇒ (x – 3)² – 9 = 6y – 6
⇒ (x – 3)² = 6y + 3
⇒ (x – 3)² = 6(y + \(\frac{1}{2}\))
⇒ (x – 3)² = 6(y – (\(-\frac{1}{2}\)))
Comparing with (x – h)² = 4a(y – k), we get
h = 3, k = \(\frac{-1}{2}\), 4a = 6 ⇒ a = \(\frac{3}{2}\)
(i) Vertex = (h, k) = (3, \(\frac{-1}{2}\))
(ii) Focus = (h, k + a) = (3, \(\frac{-1}{2}+\frac{3}{2}\)) = (3, 1)

Question 5.
Find the coordinates of the vertex and focus and the equations of the directrix and axis of the parabola x² = -4y.
Solution:
Given parabola is x² = -4y
Comparing with x² = -4ay
we get 4a = 4 ⇒ a = -1
Vertex A = (0, 0)
Focus S = (0, -a) = (0, -1)
The equation of the directrix is y – a = 0
⇒ y – 1 = 0
The equation of the axis is x = 0.

Question 6.
Find the equation of the parabola whose vertex is (3, -2) and focus is (3, 1). [(AP) Mar. ’20, May ’17; (TS) May ’19, Mar. ’18]
Solution:
Given that Vertex = (3, -2)
Focus = (3, 1)
In abscissae of the vertex and focus are equal to 3.
Hence the axis of the parabola is x = 3, a line parallel to Y-axis.
a = distance between focus and vertex
= \(\sqrt{(3-3)^2+(-2-1)^2}\)
= 3
Since in vertex y-coordinate is less than the y-coordinate of focus.
∴ The equation of the parabola is (x – h)² = 4a(y – k)
⇒ (x – 3)² = 4(3) (y + 2)
⇒ (x – 3)² = 12(y + 2)

Question 7.
Find the equations of the parabola whose focus is S(1, -7) and vertex is A(1, -2). [(TS) May & Mar. ’15]
Solution:
Given that,
Focus, S = (1, -7)
Vertex, A(h, k) = (1, -2)
In vertex and focus, x-coordinates are equal to 1.
Hence, the axis of the parabola is x = 1, a line parallel to Y-axis,
a = distance between focus and vertex.
= \(\sqrt{(1-1)^2+(-7+2)^2}\)
= \(\sqrt{0+(-5)^2}\)
= √25
= 5
The y-coordinates of the vertex are greater than the y-coordinate of focus.
Focus is below the vertex.
∴ Equation of the parabola is (x – h)² = -4a(y – k)
⇒ (x – 1)² = -4(5) (y + 2)
⇒ (x – 1)² = -20(y + 2)

Question 8.
Find the coordinates of the points on the parabola y² = 2x whose focal distance is \(\frac{5}{2}\). [(AP) May & Mar. ’15]
Solution:

Given the equation of the parabola is y² = 2x
Comparing with y² = 4ax, we get
4a = 2 ⇒ a = \(\frac{1}{2}\)
Let, P(x₁, y₁) be a point on the parabola y² = 2x
Given that, focal distance = \(\frac{5}{2}\)
⇒ x₁ + a = \(\frac{5}{2}\)
⇒ x₁ + \(\frac{1}{2}\) = \(\frac{5}{2}\)
⇒ x₁ = 2
Since P(x₁, y₁) lies on the parabola y² = 2x then
⇒ \(\mathrm{y}_1^2\) = 2x₁
⇒ \(\mathrm{y}_1^2\) = 2(2)
⇒ \(\mathrm{y}_1^2\) = 4
⇒ \(\mathrm{y}_1^2\) = ±2
∴ The required points are (2, 2), (2, -2).

Question 9.
Find the coordinates of the point on the parabola y² = 8x whose focal distance is 10. [(AP) May ’19, Mar. ’17, ’16; (TS) May & Mar. ’17; 14]
Solution:

Given the equation of the parabola is y² = 8x
Comparing with y² = 4ax, we get
4a = 8 ⇒ a = 2
Let P(x1, y1) be a point on the parabola y² = 8x
Given that focal distance = 10
⇒ x₁ + a = 10
⇒ x₁ + 2 = 10
⇒ x₁ = 8
Since P(x₁, y₁) lies on the parabola then \(\mathrm{y}_1^2\) = 8x₁
⇒ \(\mathrm{y}_1^2\) = 8(8)
⇒ \(\mathrm{y}_1^2\) = 64
⇒ \(\mathrm{y}_1^2\) = ±8
∴ The required points are (8, 8), (8, -8).

Question 10.
If (\(\frac{1}{2}\), 2) is one extremity of a focal chord of the parabola y² = 8x. Find the coordinates of the other extremity. [(AP) May ’18, (TS) ’16; ’14]
Solution:

Given the equation of the parabola is y² = 8x
Comparing with y² = 4ax, we get
4a = 8 ⇒ a = 2
Given that one end of the focal chord is P = (\(\frac{1}{2}\), 2)
Let other end of the focal chord is Q(x, y) = \((\frac{1}{2}\), 2)
‘PSQ’ is a focal chord.
Since P, S, Q are collinear then
slope of \(\overline{\mathrm{SP}}\) = slope of \(\overline{\mathrm{SQ}}\)
⇒ \(\frac{2-0}{\frac{1}{2}-2}=\frac{y-0}{\frac{y^2}{8}-2}\)
⇒ \(\frac{2}{\frac{-3}{2}}=\frac{y}{\frac{y^2-16}{8}}\)
⇒ \(\frac{4}{-3}=\frac{8 y}{y^2-16}\)
⇒ y² – 16 = -6y
⇒ y² + 6y – 16 = 0
⇒ y² + 8y – 2y – 16 = 0
⇒ y(y + 8) – 2(y + 8) = 0
⇒ (y + 8)(y – 2) = 0
⇒ y + 8 = 0 or y – 2 = 0
⇒ y = -8 or y = 2
If y = -8 then Q = (8, -8)
If y = 2 then Q = (\(\frac{1}{2}\), 2)
∴ Other end of the focal chord Q = (8, -8)

Question 11.
Prove that the point on the parabola y² = 4ax (a > 0) nearest to the focus is its vertex.
Solution:
Given equation of the parabola is y² = 4ax (a > 0)

Let P(at², 2at) be a point on the parabola y² = 4ax
Which is nearest to the focus, S(a, 0), then
SP = \(\sqrt{\left(a t^2-a\right)^2+(2 a t-0)^2}\)
⇒ SP = \(\sqrt{\left(a t^2-a\right)^2+4 a^2 t^2}\)
⇒ SP² = (at² – a)² + 4a²t²
⇒ SP² = a²(t² – 1)² + 4a²t²
Let f(t) = a²(t² – 1)² + 4a²t²
f'(t) = a² . 2(t² – 1) . 2t + 4a² . 2t
= 4a²t(t² – 1) + 8a²t
= 4a²t(t² – 1 + 2)
= 4a²t (t² + 1)
= 4a²(t³ + 1)
for minimum value of f(t), then f'(t) = 0
4a²t(t² + 1) = 0 ⇒ t = 0
f”(t) = 4a²(3t² + 1)
If t = 0, then f”(0) = 4a² > 0
∴ At t = 0, f(t) is minimum
Then P = [a(0)², 2a(0)] = (0, 0)
∴ The point on the parabola y² = 4ax, which is nearest to the focus is its vertex A(0, 0).

Question 12.
Find the equation of the parabola whose vertex and focus are on the positive X-axis at a distance ‘a’ and a’ from the origin respectively.
Solution:

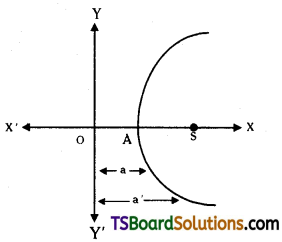
Since the vertex and focus are on the positive X-axis
∴ The equation of the parabola is
(y – k)² = 4a(x – h) ………..(1)
Now, given that OA = a
vertex, A(h, k) = (a, 0)
a = SA = a’ – a
∴ The equation of the parabola is
(y – 0)² = 4(a’ – a) (x – a)
⇒ y² = 4(a’ – a) (x – a)

Question 13.
Find the value of k if the line 2y = 5x + k is a tangent to the parabola y² = 6x. [(TS) May ’18, Mar. ’16, (AP) ’18]
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax, we get
4a = 6 ⇒ a = \(\frac{3}{2}\)
Given the equation of the straight line is
2y = 5x + k
⇒ y = \(\frac{5}{2} x+\frac{k}{2}\)
Comparing with y = mx + c, we get
m = \(\frac{5}{2}\), c = \(\frac{k}{2}\)
Given that the line y = \(\frac{5}{2} x+\frac{k}{2}\) is tangent to the parabola y² = 6x then c = \(\frac{a}{m}\)
⇒ \(\frac{k}{2}=\frac{3 / 2}{5 / 2}\)
⇒ \(\frac{k}{2}=\frac{3}{5}\)
⇒ k = \(\frac{6}{5}\)

Question 14.
Find the equation of a tangent to the parabola y² = 16x inclined at an angle of 60° with its axis and the point of contact. [(AP) May ’16]
Solution:

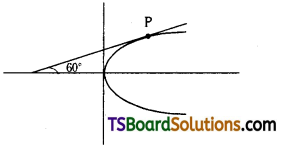
Given the equation of the parabola is y² = 16x
Comparing with y² = 4ax we get a = 4
Given that inclination of a tangent θ = 60°
The slope of the tangent, m = tan θ
= tan 60°
= √3
∴ The equation of the tangent

Question 15.
Find the condition for the straight line lx + my + n = 0 to be a tangent to the parabola y² = 4ax and find the coordinates of the point of contact. (Mar. ’99, ’93)
Solution:

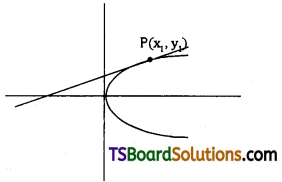
Suppose lx + my + n = 0 …….(1)
be a tangent to the parabola y² = 4ax
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at ‘P’ is S₁ = 0
yy₁ – 2a(x + x₁) = 0
yy₁ – 2ax – 2ax₁ = 0
2ax – y₁y + 2ax₁ = 0 ……….(2)
Now (1) & (2) represent the same line

∴ Point of contact P(x₁, y₁) = \(\left(\frac{\mathbf{n}}{l}, \frac{-2 \mathrm{am}}{l}\right)\)
Suppose ‘P’ lies on the lx + my + n = 0, lx₁ + my₁ + n = 0
⇒ \(l\left(\frac{\mathrm{n}}{l}\right)+\mathrm{m}\left(\frac{-2 \mathrm{am}}{l}\right)+\mathrm{n}=0\)
⇒ ln – 2am² + ln = 0
⇒ 2ln – 2am² = 0
⇒ ln – am² = 0
⇒ am² = ln

Question 16.
Find the equation of the tangent and normal to the parabola x² – 4x – 8y + 12 = 0 at (4, \(\frac{3}{2}\)).
Solution:
Given equation of the parabola is x² – 4x – 8y + 12 = 0
given point P(x₁, y₁) = (4, \(\frac{3}{2}\))
∴ The equation of the tangent is S₁ = 0
⇒ xx₁ – 2(x + x₁) – 4(y + y₁) + 12 = 0
⇒ x(4) – 2(x + 4) – 4(y + \(\frac{3}{2}\)) + 12 = 0
⇒ 4x – 2x – 8 – 4y – 6 + 12 = 0
⇒ 2x – 4y – 2 = 0
⇒ x – 2y – 1 = 0
Slope of x – 2y – 1 = 0 is m = \(\frac{-1}{-2}=\frac{1}{2}\)
Slope of normal is \(\frac{-1}{m}=\frac{-1}{\frac{1}{2}}\) = -2
∴ Equation of normal at (4, \(\frac{3}{2}\)) is
⇒ y – \(\frac{3}{2}\) = -2(x – 4)
⇒ \(\frac{2 y-3}{2}\) = -2x + 8
⇒ 2y – 3 = -4x + 16
⇒ 4x + 2y – 19 = 0

Question 17.
Find the equation of the normal to the parabola y² = 4x which is parallel to y- 2x + 5 = 0. [(TS) Mar. ’19]
Solution:
Given the equation of the parabola is y² = 4x
∴ a = 1
Given the equation of the straight line is y – 2x + 5 = 0
slope m = \(\frac{-(-2)}{1}\) = 2
slope of normal = 2
equation of the normal at ‘t’ is y + xt = 2at + at³
∴ slope = -t = 2
⇒ t = -2
equation of the normal is
y – 2x = 2 . 1(-2) + 1(-2)
⇒ y – 2x = -4 – 8
⇒ y – 2x = -12
⇒ 2x – y – 12 = 0

Question 18.
Show that the equation of the tangent to the parabola y² = 4ax at the point ‘t’ is yt = x + at².
Solution:
Given the equation of the parabola is y2 = 4ax
Given a point on the parabola is P(at², 2at)
The equation of the tangent at P(at², 2at) is S₁ = 0
⇒ yy₁ – 2a(x + x₁) = 0
⇒ y(2at) – 2a(x + at²) = 0
⇒ yt – (x + at²) = 0
⇒ yt = x + at²

Question 19.
Find the equations of the tangent and normal to the parabola y² = 6x at the positive end of the latus rectum. [(TS) Mar. ’20]
Solution:

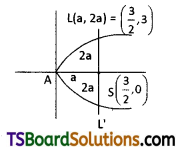
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax we get
4a = 6 ⇒ a = \(\frac{3}{2}\)
The positive end of the latus rectum,
L = (a, 2a) = (\(\frac{3}{2}\), 3)
The equation of the tangent at L(\(\frac{3}{2}\), 3) to the parabola y² = 6x is S₁ = 0
⇒ yy₁ – 2a(x + x₁) = 0
⇒ \(y(3)-2\left(\frac{3}{2}\right)\left(x+\frac{3}{2}\right)=0\)
⇒ \(3 y-3\left(x+\frac{3}{2}\right)=0\)
⇒ 3y – 3x – \(\frac{9}{2}\) = 0
⇒ 6y – 6x – 9 = 0
⇒ 2x – 2y + 3 = 0
The equation of the normal at L(\(\frac{3}{2}\), 3) to the parabola y² = 6x is
y – y₁ = \(\frac{-y_1}{2 a}\) (x – x₁)
⇒ y – 3 = \(\frac{-3}{2\left(\frac{3}{2}\right)}\left(x-\frac{3}{2}\right)\)
⇒ y – 3 = \(-1\left(x-\frac{3}{2}\right)\)
⇒ y – 3 = \(\frac{-2 x+3}{2}\)
⇒ 2y – 6 = -2x + 3
⇒ 2x + 2y – 9 = 0

Question 20.
Show that the line 2x – y + 2 = 0 is a tangent to the parabola y² = 16x. Find the point of contact also.
Solution:
Given the equation of the parabola is y² = 16x
Comparing with 4ax = y² we get
4a = 16 ⇒ a = 4
Given the equation of the straight line is 2x – y + 2 = 0
⇒ y = 2x + 2
Comparing with y = mx + c we get
m = 2, c = 2
Now, c = 2
\(\frac{\mathrm{a}}{\mathrm{m}}=\frac{4}{2}\) = 2
⇒ c = \(\frac{\mathrm{a}}{\mathrm{m}}\)
∴ The line 2x – y + 2 = 0 is a tangent to the parabola y² = 16x
∴ Point of contact, P = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)
= \(\left(\frac{4}{(2)^2}, \frac{2 \cdot 4}{2}\right)\)
= (1, 4)

Question 21.
Find the position of the point (6, -6) with respect to the parabola y² = 6x.
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax,
we get 4a = 6 ⇒ a = \(\frac{3}{2}\)
Let the given point A(x₁, y₁) = (6, -6)
Now \(S_{11}=y_1{ }^2-4 a x_1\)
= (-6)² – 4(\(\frac{3}{2}\))(6)
= 36 – 36
= 0
Since S₁₁ = 0, then the point A(6, -6) lies on the parabola y² = 6x.

Question 22.
Find the position of the point (0, 1) with respect to the parabola y² = 6x.
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax,
we get 4a = 6 ⇒ a = \(\frac{3}{2}\)
Let the given point A(x₁, y₁) = (0, 1)
Now \(S_{11}=y_1{ }^2-4 a x_1\)
= (1)² – 4(\(\frac{3}{2}\))(0)
= 1 > 0
Since S₁₁ > 0, then the point A(0, 1) lies outside the parabola y² = 6x.

Question 23.
Find the position of the point (2, 3) with respect to the parabola y² = 6x.
Solution:
Given the equation of the parabola is y² = 6x
Comparing with y² = 4ax,
we get 4a = 6 ⇒ a = \(\frac{3}{2}\)
Let the given point A(x₁, y₁) = (2, 3)
Now \(S_{11}=y_1{ }^2-4 a x_1\)
= (3)² – 4(\(\frac{3}{2}\))(2)
= 9 – 12
= -3 > 0
Since S₁₁ < 0, then the point A(2, 3) lies inside the parabola y² = 6x.

Question 24.
A comet moves in a parabolic orbit with the sun in a focus. When the comet is 2 × 10⁷ km from the sun, the line from the sun to it makes an angle π/2 with the axis of the orbit Find how near the comet comes to the sun.
Solution:
Suppose, the equation of the parabolic orbit of the comet is y² = 4ax.

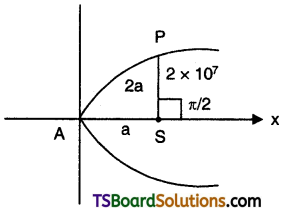
P is the position of the comet,
given ∠XSP = π/2
SP is perpendicular to the axis of the parabola
SP is the semi latus rectum
2a = 2 × 10⁷
⇒ a = 10⁷ km
∴ The nearest point on the parabola is 10⁷ km from the sun.

Question 25.
A double ordinate of the curve y² = 4ax is of length 8a. Prove that the line from the vertex to it is at right angles.
Solution:
Given equation of the parabola is y² = 4ax.

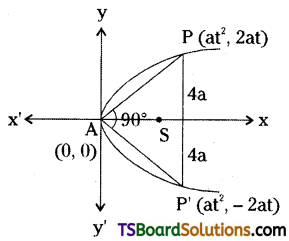
Let P = (at², 2at) and P’ = (at², -2at) be the ends of double ordinate PP’
given that, the length of the double ordinate = 8a

Question 26.
Find the length of the latus rectum of the parabola y² = 4ax.
Solution:
The equation of the parabola is y² = 4ax …….(1)

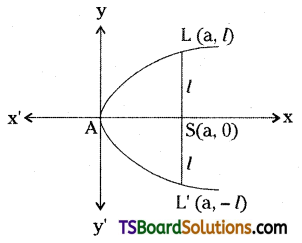
Let LSL’ be the latus rectum of the parabola.
Let LL’ be the length of the latus rectum of the parabola y² = 4ax.
If SL = l, then L = (a, l)
Since L lies on the parabola, y² = 4ax, then
l² = 4a × a
⇒ l² = 4a²
⇒ l = 2a
∴ SL = 2a
Now LL’ = 2SL = 2(2a) = 4a
∴ Length of the latus rectum = 4a.

Question 27.
Prove that the equation of the normal to the parabola y² = 4ax at P(x₁, y₁) is y – y₁ = \(\frac{-\mathbf{y}_1}{2 a}\)(x – x₁).
Solution:
Let S = y² – 4ax = 0 be the given parabola.

The slope of the tangent at P is
m = \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\mathrm{P}}=\frac{2 \mathrm{a}}{\mathrm{y}_1}\)
The slope of the normal at
P = \(\frac{-1}{m}=\frac{-1}{\frac{2 a}{y_1}}=\frac{-y_1}{2 a}\)
∴ The equation of the normal at P is
y – y₁ = \(\frac{-1}{m}\)(x – x₁)
y – y₁ = \(\frac{-y_1}{2 a}\)(x – x₁)