TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type

Question 1.
Find the equation of the circle which passes through the origin and intersects the circles x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0 orthogonally.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …………(1)
Since (1) passes through the point (0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Given equations of the circles are
x² + y² – 4x – 6y – 3 = 0 ……..(2)
x² + y² – 8y + 12 = 0 ……….(3)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-3) = 0 – 3
⇒ -4g – 6f = -3
⇒ 4g + 6f – 3 = 0 …….(4)
Since (1) and (3) are orthogonal, then
2gg’ + 2ff’ = c + c’
⇒ 2g(0) + 2f(-4) = 0 + 12
⇒ -8f = 12
⇒ f = \(\frac{-3}{2}\)
Substituting the value of ‘f’ in (4)
4g + 6(\(\frac{-3}{2}\)) – 3 = 0
⇒ 4g – 9 – 3 = 0
⇒ 4g = 12
⇒ g = 3
∴ The equation of the required circle is
x² + y² + 2(3)x + 2(\(\frac{-3}{2}\))y + 0 = 0
x² + y² + 6x – 3y = 0

Question 2.
Find the equation of the circle which passes through the origin and intersects the circles x² + y² – 4x + 6y + 10 = 0, x² + y² + 12y + 6 = 0 orthogonally. [(AP) May ’18]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since, (1) passes through the point (0, 0) then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Given equations of the circles are
x² + y² – 4x + 6y + 10 = 0 ……..(2)
x² + y² + 12y + 6 = 0 …….(3)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(g)(-2) + 2f(3) = c + 10
⇒ -4g + 6f = 0 + 10
⇒ -4g + 6f = 10
⇒ 2g – 3f = -5
⇒ 2g – 3f + 5 = 0 ……..(4)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(0) + 2f(6) = 0 + 6
⇒ 12f = 6
⇒ f = \(\frac{1}{2}\)
Substituting the value of f in (4)
2g – 3(\(\frac{1}{2}\)) + 5 = 0
⇒ 2g + \(\frac{7}{2}\) = 0
⇒ g = \(\frac{-7}{4}\)
∴ The equation of the required circle is from (1)
x² + y² + 2(\(\frac{-7}{4}\))x + 2(\(\frac{1}{2}\))y + 0 = 0
⇒ x² + y² – \(\frac{7}{2}\)x + y = 0
⇒ 2x² + 2y² – 7x + 2y = 0

Question 3.
Find the equation of the circle which passes through (1, 1) and cuts orthogonally each of the circles x² + y² – 8x – 2y + 16 = 0 and x² + y² – 4x – 4y – 1 = 0.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through point (1, 1) then
(1)² + (1)² – 2g(1) – 2f(1) + c = 0
⇒ 2 + 2g + 2f + c = 0
⇒ 2g + 2f + c = -2 …….(2)
Given equations of the circles are
x² + y² – 8x – 2y + 16 = 0 ……..(3)
x² + y² – 4x – 4y – 1 = 0 ………(4)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-4) + 2f(-1) = c + 16
⇒ -8g – 2f – c = 16 ………(5)
Since (1) and (4) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-2) = c – 1
⇒ -4g – 4f – c = -1
From (2) and (5)
2g + 2f + c = -2
⇒ -8g – 2f – c = 16
⇒ -6g = 14
⇒ g = \(\frac{-7}{3}\)
From (5) and (6)

Substituting the values of g, f in (2)

∴ The equation of the required circle is from (1),
x² + y² + 2(\(\frac{-7}{3}\))x + 2(\(\frac{23}{6}\))y – 5 = 0
⇒ 3x² + 3y² – 14x + 23y – 15 = 0

Question 4.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally. [May ’15 (TS) May ’13]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since eq (1) passes through the point (0, -3) then
9 + 2f(-3) + c = 0
⇒ 9 – 6f + c = 0
⇒ -6f + c = -9 ……..(2)
Given equations of the circles are
x² + y² – 6x + 3y + 5 = 0 ………(3)
x² + y² – x – 7y = 0 ………(4)
Since the circles (1) & (3) are orthogonal then 2gg’ + 2ff’ = c + c’
⇒ 2g(-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f – c = 5 …….(5)
Since the circles (1) & (4) are orthogonal then 2gg’ + 2ff’ = c + c’

Question 5.
Find the equation of the circle passing through the origin having its centre on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since eq. (1) passes through the point (0, 0) then c = 0
Centre of (1), C = (-g, -f) lies on the line
x + y = 4 then -g – f = 4 ……..(2)
Given the equation of the circle is
x² + y² – 4x + 2y + 4 = 0 ……….(3)
Since the circles (1) & (3) are orthogonal then 2gg’ + 2ff’ = c + c’
2g(-2) + 2f(1) = c + 4
⇒ -4g + 2f = 4
⇒ -2g + f = 2 ……….(4)
Solve (2) & (4)


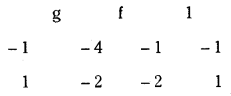
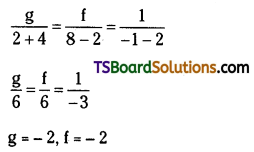
∴ The equation of the required circle is x² + y² + 2(-2)x + 2(-2)y + 0 = 0
⇒ x² + y² – 4x – 4y = 0

Question 6.
Find the equation of the circle passing through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0. [(TS) May ’19]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point (2, 0), then
(2)² + (0)² + 2g(2) + 2f(0) + c = 0
⇒ 4 + 4g + c = 0
⇒ 4g + c = -4 ………(2)
Since (1) passes through the point (0, 2), then
(0)² + (2)² + 2g(0) + 2f(0) + c = 0
⇒ 4 + 4f + c = 0
⇒ 4f + c = -4 …….(3)
Given the equation of the circle is
2x² + 2y² + 5x – 6y + 4 = 0
⇒ x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 ………(4)
Since (1) and (4) are orthogonal, then 2gg’ + 2ff’ = c + c’
2g(\(\frac{5}{4}\)) + 2f(\(\frac{-3}{2}\)) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = c + 2
⇒ 5g – 6f = 2c + 4
⇒ 5g – 6f – 2c = 4 ………(5)

Question 7.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having the centre at (2, 3). [Mar. ’19 (TS)]
Solution:
Given the equation of the circle is
x² + y² – 4x + 2y – 7 = 0 ……….(1)
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(2)
centre (-g, -f) = (2, 3)
∴ g = -2, f = -3
since (1) &(2) are orthogonal then 2gg’ + 2ff’ = c + c’
⇒ 2(-2)(-2) + 2(-3)(1) = -7 + c
⇒ 8 – 6 = -7 + c
⇒ 2 = -7 + c
⇒ c = 7 + 2
⇒ c = 9
∴ The equation of the required circle is x² + y² – 4x – 6y + 9 = 0

Question 8.
Find the equation of the circle which is orthogonal to each of the following three circles x² + y² + 2x + 17y + 4 = 0, x² + y² + 7x + 6y + 11 = 0, and x² + y² – x + 22y + 3 = 0. [May ’08; Mar. ’03]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Given equations of the circles are
x² + y² + 2x + 17y + 4 = 0 ……..(2)
x² + y² + 7x + 6y + 11 = 0 ……..(3)
x² + y² – x + 22y + 3 = 0 ……….(4)
Since the circles (1) & (2) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(1) + 2f(\(\frac{17}{2}\)) = c + 4
⇒ 2g + 17f = c + 4 ……….(5)
Since the circles (1) & (3) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(\(\frac{7}{2}\)) + 2f(3) = c + 11
⇒ 7g + 6f – c = 11 ………(6)
Since the circles (1) & (4) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(\(\frac{-1}{2}\)) + 2f(11) = c + 3
⇒ -g + 22f – c = 3 ………(7)
From (5) & (6)

Substitute g, f values in eq. (5)
2(-3) + 17(-2) – c = 4
⇒ -6 – 34 – c = 4
⇒ c = -44
∴ The equation of the required circle is x² + y² + 2(-3)x + 2(-2)y – 44 = 0
⇒ x² + y² – 6x – 4y – 44 = 0

Question 9.
Find the equation of the circle which cuts the circles x² + y² + 2x + 4y + 1 = 0, 2x² + 2y² + 6x + 8y – 3 = 0, x² + y² – 2x + 6y – 3 = 0 orthogonally.
Solution:
Given equations of the circles are
S = x² + y² + 2x + 4y + 1 = 0
S’ = 2x² + 2y² + 6x + 8y – 3 = 0
S’ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
S” = x² + y² – 2x + 6y – 3 = 0
The equation of the radical axis of the circles S = 0 and S’ = 0 are S – S’ = 0
⇒ x² + y² + 2x + 4y + 1 – (x² + y² + 3x + 4y – \(\frac{3}{2}\)) = 0
⇒ x² + y² + 2x + 4y + 1 – x² – y² – 3x – 4y + \(\frac{3}{2}\) = 0
⇒ -x + 1 + \(\frac{3}{2}\) = 0
⇒ -2x + 2 + 3 = 0
⇒ 2x – 5 = 0 ……..(1)
The equation of the radical axis of the circles S’ = 0 and S” = 0 is S’ – S” = 0
⇒ x² + y² + 3x + 4y – \(\frac{3}{2}\) – (x² + y² – 2x + 6y – 3) = 0
⇒ x² + y² + 3x + 4y – \(\frac{3}{2}\) – x² – y² + 2x – 6y + 3 = 0
⇒ 5x – 2y – \(\frac{3}{2}\) + 3 = 0
⇒ 10x – 4y – 3 + 6 = 0
⇒ 10x – 4y + 3 = 0 ……..(2)
Solving (1) and (2)

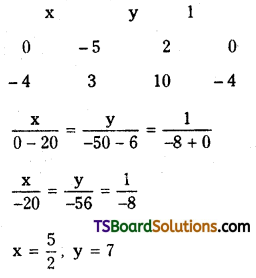
∴ Radical centre, C = (\(\frac{5}{2}\), 7) = centre of the required circle.
Radius of the required circle, r = the length of tangent from the radical centre, C = (\(\frac{5}{2}\), 7) of the circle is \(\sqrt{\mathrm{S}_{11}}\)

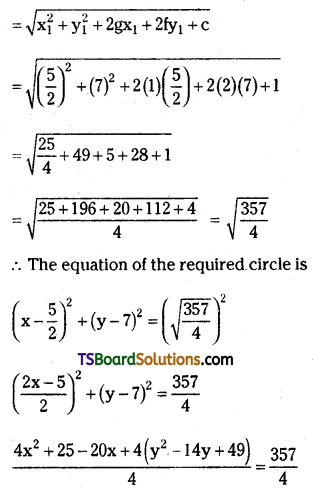
4x² + 25 – 20x + 4y² – 56y + 196 = 357
x² + y² – 5x – 14y – 34 = 0

Question 10.
Find the equation of the circle which intersects each of the following circles orthogonally.
x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……(1)
Given equations of the circles are
x² + y² + 4x + 2y + 1 = 0 …….(2)
2(x² + y²) + 8x + 6y – 3 = 0
x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ………(3)
x² + y² + 6x – 2y – 3 = 0 ……..(4)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(2) + 2f(1) = c + 1
⇒ 4g + 2f = c + 1
⇒ 4g + 2f – c = 1 ………(5)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(2) + 2f(\(\frac{3}{2}\)) = c – \(\frac{3}{2}\)
⇒ 4g + 3f = c – \(\frac{3}{2}\)
⇒ 4g + 3f – c = \(-\frac{3}{2}\) ………(6)
Since (1) and (4) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(3) + 2f(-1) = c – 3
⇒ 6g- 2f = c – 3
⇒ 6g – 2f – c = -3 ………(7)
From (5) and (6)


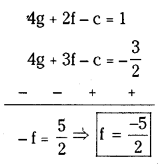
∴ The equation of the required circle is from (1)
x² + y² + 2(-7)x + 2(\(\frac{-5}{2}\))y – 34 = 0
⇒ x² + y² – 14x – 5y – 34 = 0

Question 11.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 = 0 and x² + y² – 10x – 4y + 21 = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7. [Mar. ’16 (AP); May ’07]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Given equations of the circles are
x² + y² – 4x – 6y + 11 = 0 ……..(2)
x² + y² – 10x – 4y + 21 = 0 ……..(3)
Since the circles (1) & (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-3) = c + 11
⇒ -4g – 6f – c = 11 ……..(4)
Since the circles (1) & (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-5) + 2f(-2) = c + 21
⇒ -10g – 4f – c = 21 ……..(5)
Centre of (1) is C = (-g, -f) lies on the line 2x + 3y = 7 then
2(-g) + 3(-f) = 7
⇒ -2g – 3f = 7 ……..(6)
From (4) & (5)

Substitute the values of g, f in eq. (4)
-4(-2) – 6(-1) – c = 11
⇒ 8 + 6 – c = 11
⇒ 14 – c = 11
⇒ c = 3
∴ The equation of the required circle is x² + y² + 2(-2)x + 2(-1)y + 3 = 0
⇒ x² + y² – 4x – 2y + 3 = 0

Question 12.
Find the equation of the circle passing through the points of intersection of the circles x² + y² – 8x – 6y + 21 = 0, x² + y² – 2x – 15 = 0, and (1, 2). [Mar. ’19 (AP); (TS) May ’17]
Solution:

Given equations of the circles are
S = x² + y² – 8x – 6y + 21 = 0
S’ = x² + y² – 2x – 15 = 0
Let, the given point A = (1, 2)
The equation of the circle passing through A, B is S + λS’ = 0
(x² + y² – 8x – 6y + 21) + λ(x² + y² – 2x – 15) = 0 ……….(1)
Since, (1) passes through the point (1, 2) then
((1)² + (2)² – 8(1) – 6(2) + 21) + λ[(1)² + (2)² – 2(1) – 15] = 0
⇒ 1 + 4 – 8 – 12 + 21 + λ(1 + 4 – 2 – 15) = 0
⇒ 6 + λ(-12) = 0
⇒ -12λ = -6
⇒ λ = \(\frac{1}{2}\)
∴ The equation of the required circle is
From (1)
⇒ x² + y² – 8x – 6y + 21 + \(\frac{1}{2}\)(x² + y² – 2x – 15) = 0
⇒ 2x² + 2y² – 16x – 12y + 42 + x² + y² – 2x – 15 = 0
⇒ 3x² + 3y² – 18x – 12y + 27 = 0
⇒ x² + y² – 6x – 4y + 9 = 0

Question 13.
Find the equation of the circle passing through the intersection of the circles x² + y² = 2ax and x² + y² = 2by and having its centre on the line \(\frac{x}{a}-\frac{\mathbf{y}}{b}\) = 2.
Solution:
Given equations of the circles are
S = x² + y² – 2ax = 0
S’ = x² + y² – 2by = 0

Given the equation of the straight line is
L = \(\frac{x}{a}-\frac{\mathbf{y}}{b}\) – 2 = 0
The equation of the circle passing through A, B is S + λS’ = 0
(x² + y² – 2ax) + λ(x² + y² – 2by) = 0 ……(1)
x² + y² – 2ax + λx² + λy² – 2λby = 0
(1 + λ) x² + (1 + λ) y² – 2ax – 2λby = 0

∴ The equation of the circle on \(\overline{\mathrm{AB}}\) as a diameter is from (1),
(x² + y² – 2ax) – \(\frac{1}{3}\) (x² + y² – 2by) = 0
⇒ 3x² + 3y² – 6ax – x² – y² + 2by = 0
⇒ 2x² + 2y² – 6ax + 2by = 0
⇒ x² + y² – 3ax + by = 0

Question 14.
If the straight line 2x + 3y = 1 intersects the circle x² + y² = 4 at points A and B then find the equation of the circle having \(\overline{\mathrm{AB}}\) as a diameter.
Solution:

Given equation of the circle is S = x² + y² – 4 = 0
Given the equation of the straight line is 2x + 3y – 1 = 0
The equation of the circle passing through A, B is S + λL = 0
x² + y² – 4 + λ(2x + 3y – 1) = 0 ………(1)
x² + y² – 4 + 2λx + 3λy – λ = 0
Here g = λ, f = \(\frac{3 \lambda}{2}\), c = -λ
Centre of the circle (1) is
C = (-g, -f) = (-λ, \(-\frac{3 \lambda}{2}\))
If \(\overline{\mathrm{AB}}\) is a diameter of a circle (1) then ‘C’ lies on 2x + 3y – 1 = 0
⇒ 2(-λ) + 3(\(-\frac{3 \lambda}{2}\)) – 1 = 0
⇒ -4λ – 9λ – 2 = 0
⇒ -13λ – 2 = 0
⇒ -13λ = 2
⇒ λ = \(\frac{-2}{13}\)
∴ The equation of the circle on \(\overline{\mathrm{AB}}\) as a diameter is, from (1)
⇒ x² + y² – \(\frac{2}{13}\) (2x + 3y – 1) = 0
⇒ 13x² + 13y² – 52 – 4x – 6y + 2 = 0
⇒ 13x² + 13y² – 4x – 6y – 50 = 0

Question 15.
If x + y = 3 is the equation of the chord AB of the circle x² + y² – 2x + 4y – 8 = 0. Find the equation of the circle having AB as the diameter. [(AP) May ’17, ’16, Mar. ’15]
Solution:
Given the equation of the circle is
S = x² + y² – 2x + 4y – 8 = 0

Given the equation of the straight line is
L = x + y – 3 = 0
The equation of the circle passing through A, B is S + λL = 0
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0 ……….(1)
x² + y² – 2x + 4y – 8 + λx + λy – 3λ = 0
x² + y² + (-2 + λ)x + (4 + λ)y – 8 – 3λ = 0
Here g = \(\frac{-2+\lambda}{2}\), f = \(\frac{4+\lambda}{2}\), c = -8 – 3λ
Centre of the circle (1) is
c = (-g, -f) = \(\left(\frac{2-\lambda}{2}, \frac{-4-\lambda}{2}\right)\)
If \(\overline{\mathrm{AB}}\) is diameter of circle (1), then ‘c’ lies on x + y – 3 = 0
⇒ \(\frac{2-\lambda}{2}+\frac{-4-\lambda}{2}-3=0\)
⇒ \(\frac{2-\lambda-4-\lambda-6}{2}=0\)
⇒ -8 – 2λ = 0
⇒ 2λ = -8
⇒ λ = -4
∴ The equation of the circle on \(\overline{\mathrm{AB}}\) as a diameter is from (1),
x² + y² – 2x + 4y – 8 – 4(x + y – 3) = 0
⇒ x² + y² – 2x + 4y – 8 – 4x – 4y + 12 = 0
⇒ x² + y² – 6x + 4 = 0

Question 16.
Find the radical centre of the three circles x² + y² – 4x – 6y + 5 = 0, x² + y² – 2x – 4y – 1 = 0, x² + y² – 6x – 2y = 0. [(AP) May ’19, Mar. ’18; (TS) May ’18]
Solution:
Given circles are
x² + y² – 4x – 6y + 5 = 0 …….(1)
x² + y² – 2x – 4y – 1 = 0 ……….(2)
x² + y² – 6x – 2y = 0 ……….(3)
The radical axis of (1) & (2) is
x² + y² – 4x – 6y + 5 – (x² + y² – 2x – 4y – 1) = 0
⇒ -2x – 2y + 6 = 0
⇒ x + y – 3 = 0 ……..(4)
The radical axis of (2) & (3) is
x² + y² – 2x – 4y – 1 – (x² + y² – 6x – 2y) = 0
⇒ 4x – 2y – 1 = 0 ……….(5)
Solving (4) & (5) we get

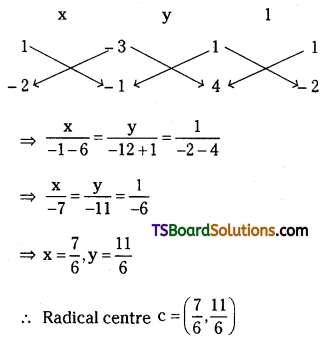
Question 17.
Find the radical centre of the circles x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0. [May ’16 (TS) May ’14]
Solution:
Given equations of the circles are
S = x² + y² + 4x – 7 = 0
S’ = 2x² + 2y² + 3x + 5y – 9 = 0
S’ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
S” = x² + y² + y = 0
The equation of the radical axis of the circles S = 0 and S’ = 0 is S – S’ = 0
⇒ (x² + y² + 4x – 7) – (\(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}\)) = 0
⇒ x² + y² + 4x – 7 – x² – y² – \(\frac{3}{2} x-\frac{5}{2} y+\frac{9}{2}\) = 0
⇒ \(4 x-\frac{3}{2} x-7-\frac{5}{2} y+\frac{9}{2}=0\)
⇒ 8x – 3x – 14 – 5y + 9 = 0
⇒ 5x – 5y – 5 = 0
⇒ x – y – 1 = 0 ……..(1)
The equation of the radical axis of the circles S = 0 and S” = 0 is S – S” = 0
⇒ x² + y² + 4x – 7 – (x² + y² + y) = 0
⇒ x² + y² + 4x – 7 – x² – y² – y = 0
⇒ 4x – y – 7 = 0 ……….(2)
Solving (1) and (2)

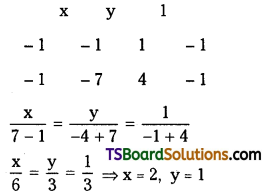
∴ Radical centre = (2, 1)

Question 18.
Find the equation and length of the common chord of the two circles x² + y² + 3x + 5y + 4 = 0 and x² + y² + 5x + 3y + 4 = 0. [Mar. ’18 (TS)]

Solution:
Given circles are
x² + y² + 3x + 5y + 4 = 0 ………(1)
x² + y² + 5x + 3y + 4 = 0 ……….(2)
Equation of common chord of (1) & (2) as
x² + y² + 3x + 5y + 4 – (x² + y² + 5x + 3y + 4) = 0
⇒ -2x + 2y = 0
⇒ x – y = 0
The centre of 1st circle is c\(\left(\frac{-3}{2}, \frac{-5}{2}\right)\) and

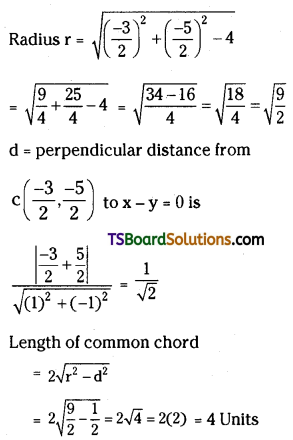
Question 19.
Find the equation and length of the common chord of the circles x² + y² + 2x + 2y + 1 = 0, x² + y² + 4x + 3y + 2 = 0. [Mar. ’17 (AP & TS); May ’15 (AP)]
Solution:
Given circles are x² + y² + 2x + 2y + 1 = 0 …….(1)
and x² + y² + 4x + 3y + 2 = 0 ……..(2)
The common chord of (1) & (2) is
x² + y² + 2x + 2y + 1 – [x² + y² + 4x + 3y + 2] = 0
⇒ -2x – y – 1 = 0
⇒ 2x + y + 1 = 0
For the 1st circle x² + y² + 2x + 2y + 1 = 0
centre C = (-1, -1) and
radius r = \(\sqrt{1+1-1}\) = 1
d = perpendicular distance from (-1, -1) to the chord 2x + y + 1 = 0

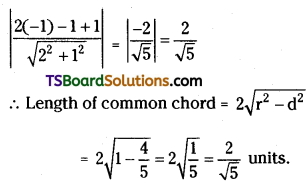
Question 20.
Find the equation of the circle whose diameter is the common chord of the circles S = x² + y² + 2x + 3y + 1 = 0 and S’ = x² + y² + 4x + 3y + 2 = 0. (Apr. ’91)
Solution:
Given equations of the circles are,
S = x² + y² + 2x + 3y + 1 = 0
S’ = x² + y² + 4x + 3y + 2 = 0

The equation of the common chord of the circles S = 0 and S’ = 0 is S – S’ = 0
x² + y² + 2x + 3y + 1 – x² – y² – 4x – 3y – 2 = 0
2x + 1 = 0
L = 2x + 1 = 0
The equation of any circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0
(x² + y² + 2x + 3y + 1) + λ(2x + 1) = 0 ……..(1)
x² + y² + 2x + 3y + 1 + 2λx + λ = 0
x² + y² + 2(1 + λ)x + 3y + 1 + λ = 0
g = (1 + λ), f = \(\frac{3}{2}\)
Centre C = (-g, -f) = \(\left(-(1+\lambda), \frac{-3}{2}\right)\)
Since \(\overline{\mathrm{AB}}\) is a diameter of circle (1) then centre C(-1 – λ, \(\frac{-3}{2}\)) lies on the L = 0
2(-1 – λ) + 1 = 0
⇒ -2 – 2λ + 1 = 0
⇒ 2λ = -1
⇒ λ = \(\frac{-1}{2}\)
∴ The equation of the required circle is, from (1)
x² + y² + 2x + 3y + 1 – \(\frac{1}{2}\)(2x + 1) = 0
⇒ 2x² + 2y² + 4x + 6y + 2 – 2x – 1 = 0
⇒ 2x² + 2y² + 2x + 6y + 1 = 0

Question 21.
Show that the common chord of the circles x² + y² – 6x – 4y + 9 = 0, x² + y² – 8x – 6y + 23 = 0 is the diameter of the second circle, and also find its length.
Solution:
Given equations of the circles are
S = x² + y² – 6x – 4y + 9 = 0 ………(1)
S’ = x² + y² – 8x – 6y + 23 = 0 ………..(2)

The equation of the common chord of the circles S = 0 and S’ = 0 is S – S’ = 0
⇒ (x² + y² – 6x – 4y + 9) – (x² + y² – 8x – 6y + 23) = 0
⇒ x² + y² – 6x – 4y + 9 – x² – y² + 8x + 6y – 23 = 0
⇒ 2x + 2y – 14 = 0
⇒ x + y – 7 = 0 ……….(1)
Centre of the circle S’ = 0 is c = (-g, -f) = (4, 3)
The radius of the circle S’ = 0 is
r = \(\sqrt{(-4)^2+(-3)^2-23}\)
= \(\sqrt{16+9-23}\)
= √2
Now substituting the centre of the circle S’ = 0, c = (4, 3) in (1)
4 + 3 – 7 = 0
⇒ 7 – 7 = 0
⇒ 0 = 0
∴ (1) is the diameter of the second circle S’ = 0
Now, the length of the common chord = diameter of the second circle
= 2 × radius of the second circle
= 2r
= 2√2

Question 22.
Show that the circles x² + y² – 2x – 4y – 20 = 0 and x² + y² + 6x + 2y – 90 = 0 touch each other internally. Find the point of contact and the equation of common tangent. [(TS) Mar. ’15)]
Solution:
Given equations of the circles are
S = x² + y² – 2x – 4y – 20 = 0 …….(1)
S’ = x² + y² + 6x + 2y – 90 = 0 …….(2)
for the circle (1)
Centre C₁ = (1, 2)

|r₁ – r₂| = |5 – 10| = |-5| = 5
∴ c₁c₂ = |r₁ – r₂|
∴ Given circles touch each other internally.
Let ‘P’ be the point of contact.

Now ‘P’ divides C₁C₂ in the ratio r₁ : r₂ (5 : 10 = 1 : 2) externally.
∴ Point of contact

In this case, the common tangent is nothing but the radical axis.
∴ The equation of the common tangent (radical axis) of the circles S = 0 and S’ = 0 is S – S’ = 0
(x² + y² – 2x – 4y – 20) – (x² + y² + 6x + 2y – 90) = 0
⇒ x² + y² – 2x – 4y – 20 – x² – y² – 6x – 2y + 90 = 0
⇒ -8x – 6y + 70 = 0
⇒ 4x + 3y – 35 = 0

Question 23.
Show that the circles x² + y² – 8x – 2y + 8 = 0 and x² + y² – 2x + 6y + 6 = 0 touch each other and find the point of contact. (Mar. ’14)

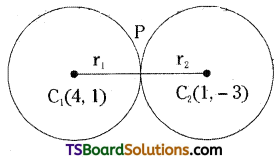
Solution:
Given equations of the circles are
S = x² + y² – 8x – 2y + 8 = 0 ………(1)
S’ = x² + y² – 2x + 6y + 6 = 0 ……..(2)
For circle (1),
centre C₁ = (-g, -f) = (4, 1)


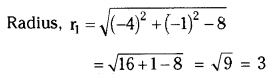
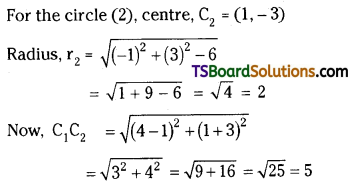
r₁ + r₂ = 3 + 2 = 5
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch other externally.
The point of contact, P divides C₁C₂ internally in the ratio (r₁ : r₂ = 3 : 2)

Question 24.
Show that the circles x² + y² – 2x = 0 and x² + y² + 6x – 6y + 2 = 0 touch each other. Find the coordinates of the point of contact. Is the point of contact external or internal?
Solution:

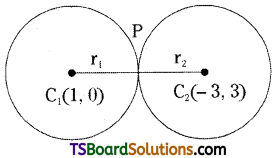
Given equations of the circles are
x² + y² – 2x = 0 ………(1)
x² + y² + 6x – 6y + 2 = 0 ……….(2)
For circle (1), centre, C₁ = (1, 0)


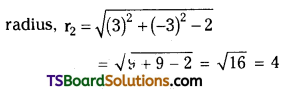
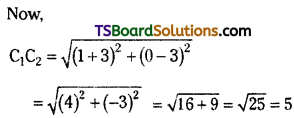
r₁ + r₂ = 1 + 4 = 5
∴ C₁C₂ = r₁ + r₂
∴ Given circles touch each other externally.
Let ‘P’ be the point of contact.
Now, the point of contact, ‘P’ divides C₁C₂ in the ratio r₁ : r₂ (1 : 4) internally.

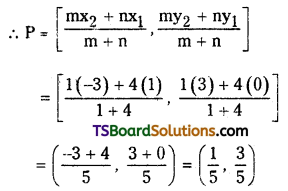
∴ The point of contact is internal.

Question 25.
Show that the circles x² + y² + 2ax + c = 0 and x² + y² + 2by + c = 0 touch each other if \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c}\).
Solution:
Given equations of the circles are
x² + y² + 2ax + c = 0 ………(1)
x² + y² + 2by + c = 0 ………(2)
Centre of (1) is C₁ = (-a, 0)
Radius of (1) is r₁ = \(\sqrt{a^2-c}\)
Centre of (2) is C₂ = (0, -b)
Radius of (2) is r₂ = \(\sqrt{b^2-c}\)
C₁C₂ = \(\sqrt{(-a+0)^2+(0+b)^2}=\sqrt{a^2+b^2}\)
Since the given two circles touch each other then
C₁C₂ = |r1 ± r2|
\(\sqrt{a^2+b^2}=\left|\sqrt{a^2-c} \pm \sqrt{b^2-c}\right|\)
Squaring on both sides

Question 26.
If the straight line represented by x cos α + y sin α = p intersects the circle x² + y² = a² at the points A and B then show that the equation of the circle with \(\overline{\mathbf{A B}}\) as the diameter is x² + y² – a² – 2p(x cos α + y sin α – p) = 0.
Solution:

Given the equation of the circle is
S = x² + y² – a² = 0
Given the equation of the straight line is
L = x cos α + y sin α – p = 0
The equation of the circle passing through A, B is S + λL = 0
(x² + y² – a²) + λ(x cos α + y sin α – p) = 0 ……(1)
x² + y² – a² + λx cos α + λy sin α – λp = 0
x² + y² + λ cos αx + λ sin αy – a² – λp = 0
Here,

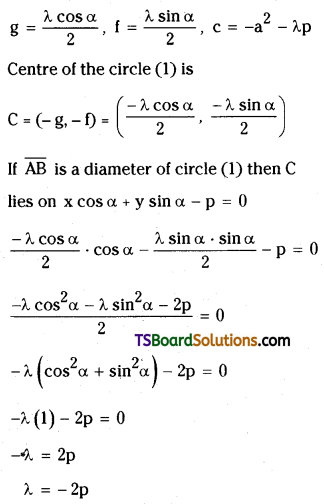
The equation of the circle on \(\overline{\mathbf{A B}}\) as diameter is from (1)
(x² + y² – a²) – 2p(x cos α + y sin α – p) = 0

Question 27.
If the two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other, then show that f’g = fg’. [(AP) Mar. ’20, (TS) ’16]
Solution:
Given equations of the circles are
x² + y² + 2gx + 2fy = 0 ……….(1)
x² + y² + 2g’x + 2f’y = 0 ……..(2)
For circle (1),
Center, C₁ = (-g, -f)
Radius, r₁ = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2}\)
For circle (2),
Center, C₂ = (-g’, -f’)
radius, r₂ = \(\sqrt{g^{\prime 2}+f^{\prime 2}}\)
Now, C₁C₂ = \(\sqrt{\left(-\mathrm{g}+\mathrm{g}^{\prime}\right)^2+\left(-\mathrm{f}+\mathrm{f}^{\prime}\right)^2}\)
Since the given circles touch each other then

Question 28.
Find the equation of a circle that cuts each of the following circles orthogonally. (Mar. ’07)
S’ = x² + y² + 3x + 2y + 1 = 0,
S” = x² + y² – x + 6y + 5 = 0,
S'” = x² + y² + 5x – 8y + 15 = 0
Solution:
Given equations of the circles are
S’ = x² + y² + 3x + 2y + 1 = 0
S” = x² + y² – x + 6y + 5 = 0
S'” = x² + y² + 5x – 8y + 15 = 0
The equation of the radical axis of S’ = 0 and S” = 0 is S’ – S” = 0
⇒ x² + y² + 3x + 2y + 1 – x² – y² + x – 6y – 5 = 0
⇒ 4x – 4y – 4 = 0
⇒ x – y – 1 = 0 ……….(1)
The equation of the radical axis of S” = 0 and S'” = 0 is S” – S'” = 0
⇒ x² + y² – x + 6y + 5 – x² – y² – 5x + 8y – 15 = 0
⇒ -6x + 14y – 10 = 0
⇒ -3x + 7y – 5 = 0
⇒ 3x – 7y + 5 = 0 ……….(2)
Solving (1) & (2)

∴ Radical centre = (3, 2) centre of the required circle
Radius = The length of the tangent from (3, 2) to the circle (1) is \(\sqrt{\mathrm{S}_{11}}\)

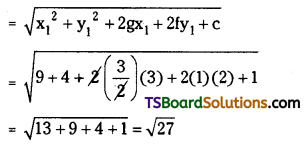
The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 3)² + (y – 2)² = 27
⇒ x² + 9 – 6x + y² + 4 – 4y – 27 = 0
⇒ x² + y² – 6x – 4y – 14 = 0

Question 29.
Prove that the radical axis of any two circles is perpendicular to the line joining their centres.
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0
S’ = x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.

The equation of the radical axis is S – S’ = 0
(x² + y² + 2gx + 2fy + c) – (x² + y² + 2g’x + 2f’y + c’) = 0
⇒ x² + y² + 2gx + 2fy + c – x² – y² – 2g’x – 2f’y – c’ = 0
⇒ 2(g – g’)x + 2(f – f’)y + c – c’ = 0
The slope of the radical axis is

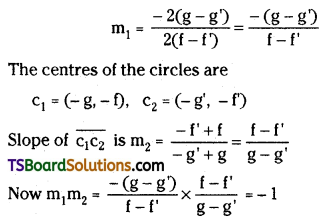
∴ The radical axis is perpendicular to the line of centres.

Question 30.
Prove that the radical axis of the circle x² + y² + 2gx + 2fy + c = 0 and x² + y² + 2g’x + 2f’y + c’ = 0 is the diameter of the latter circle (or the former bisects the circumference of the latter) if 2g'(g – g’) + 2f'(f – f’) = c – c’.
Solution:
Given equations of the circles are
S = x² + y² + 2gx + 2fy + c = 0
S’ = x² + y² + 2g’x + 2f’y + c = 0

The equation of the radical axis of the circles S = 0 and S’ = 0 is S – S’ = 0
(x² + y² + 2gx – 2fy + c) – (x² + y² + 2g’x + 2f’y + c’) = 0
⇒ x² + y² + 2gx – 2fy + c – x² – y² – 2g’x – 2f’y – c’ = 0
⇒ 2(g – g’)x+2(f – f’)y + c – c’ = 0 ……(1)
Centre of the second circle S’ = 0 is c = (-g’, -f’)
Since (1) is the diameter of the second circle S’ = 0, then
substitute the centre of the second circle S’ = 0 is c = (-g’, -f’) in (1)
⇒ 2(g – g’)(-g’) + 2(f – f’)(-f’) + c – c’ = 0
⇒ 2g'(g – g’) + 2f(f – f’) = c – c’

Question 31.
If P and Q are conjugate with respect to a circle S = x² + y² + 2gx + 2fy + c = 0, then prove that the circle on PQ as diameter cuts the circle S = 0 orthogonally.
Solution:
Let P = (x₁, y₁) and Q = (x₂, y₂),
S = x² + y² + 2gx + 2fy + c = 0 ……….(1)
Given that, the two points P, Q are conjugate w.r.t a circle S = 0, then S₁₂ = 0
⇒ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0 ………(2)
The equation of the circle having \(\overline{\mathrm{PQ}}\) as diameter is
S’ = (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ x² – x₁x₂ – xx₁ + x₁x₂ + y² – yy₂ – yy₁ + y₁y₂ = 0
⇒ x² + y² – x(x₁ + x₂) – y(y₁ + y₂) + x₁x₂ + y₁y₂ = 0 ………(3)
Now, applying orthogonally condition S = 0 and S’ = 0
2gg’ + 2ff’ = \(2 \mathrm{~g}\left(\frac{-\left(\mathrm{x}_1+\mathrm{x}_2\right)}{2}\right)+2 \mathrm{f}\left(\frac{-\left(\mathrm{y}_1+\mathrm{y}_2\right)}{2}\right)\)
= -g(x₁ + x₂) – f(y₁ + y₂)
= x₁x₂ + y₁y₂ + c (∵ from(2))
c + c’ = c + x₁x₂ + y₁y₂
= x₁x₂ + y₁y₂ + c
∴ 2gg’ + 2ff’ = c + c’
∴ The circles S = 0 and S’ = 0 are cut orthogonally.