TS Inter 1st Year Physics Notes Chapter 3 Motion in a Straight Line

Here students can locate TS Inter 1st Year Physics Notes 3rd Lesson Motion in a Straight Line to prepare for their exam.

TS Inter 1st Year Physics Notes 3rd Lesson Motion in a Straight Line

→ Motion: A body is said to be in motion if the position changes with respect to time.

→ Kinematics : It is a branch of physics dealing with the laws of motion of a body without referring to reasons of motion.

→ Motion in a straight line (or) linear motion : If the motion of a body is restricted to a straight line then it is said to be in linear motion.

→ Displacement (X) :
Change in the position of a body in particular direction is called displacement. It is a vector.
Displacement consists of magnitude and direction.

→ Path length: The total distance travelled by a body during its journey is called “path length”.
It is a scalar.
Note : The displacement of a body may or may not equal to path length. In some cases even though displacement is zero its path length is not equal to zero.

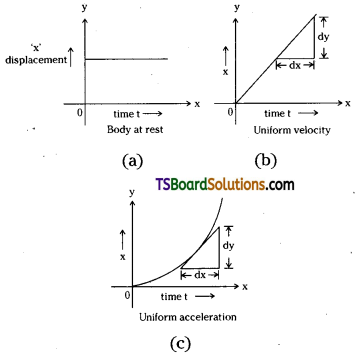
→ Displacement – time curves (x -1 graphs or x -1 curves) : When a graph is plotted with time ’t’on x- axis and displacement ‘x’ on y – axis then it is known as displacement – time graph.

→ Various types of displacement time graphs:
(a) For a body at rest ⇒ x – t graph is a straight line parallel to x – axis.
(b) For a body starting from rest and moving with uniform velocity ⇒ x -1 graph is a straight line passing through origin.
Slope of the line \(\frac{d y}{d x}\) will give uniform velocity of the body.
(c) For a body moving with uniform acceleration x – t graph is an upshooting curve. Slope of the curve \(\frac{d y}{d x}\) at any point gives velocity of the body at that point.

→ Velocity (v): The rate of change in displacement is known as velocity. Unit m/s. It is a vector.

→ Average Velocity: The ratio of total displacement of a body to the total time taken is called as average velocity. Unit: m/s, it is a vector.
Average velocity v̅ = \(\frac{x_2-x_1}{t_2-t_1}=\frac{\Delta x}{\Delta t}\)
Where x₁ and x₂ are initial and final positions of the body.

→ Average Speed: The ratio of total path length travelled to the total time taken is known as average speed.
Speed and average speed are scalar quantities so no direction for these quantities.
Average speed = \(\frac{\text { Total path length }}{\text { Total time interval }}\)

→ Instantaneous Velocity (v): The velocity of a body at a given instant of time is known as instantaneous velocity.
Mathematically v = \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}\)
When time interval is extremely small then \(\frac{d x}{d t}\) is velocity at that instant.
Note : Instantaneous velocity may be or may not be equal to average velocity of the body.

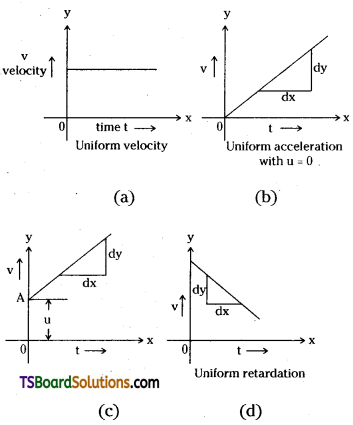
→ Velocity – time graphs (v – t graphs): When a graph is plotted with time ‘t’ on x- axis and velocity ‘v’ on y – axis then that graph is known as velocity – time graph.

→ Different types of velocity – time graphs
(a) For uniform velocity ⇒ v – t graph is a straight line parallel to x – axis.
(b) Starting from rest and moving with uniform acceleration ⇒ v-1 graph is a straight line passing through origin. It has positive slope with t – axis.
(c) For a body moves with some initial velocity ‘u’ and with some uniform acceleration ⇒ v – t graph is a straight line with some is a positive quantity).
(d) For a body moving with uniform retardation ⇒ graph is a straight line with some negative slope (i.e., \(\frac{d y}{d x}\) is a negative quantity).

→ Uses of velocity – time graphs :

• Slope (dy/dx) of velocity – time graph gives acceleration of the body.
• Area under velocity – time graph gives total displacement of the body.
• Basic equations of motion v = u0 + at,
  x = u₀t + \(\frac{1}{2}\)at² and v² – u² = 2 ax can be de-rived from v – t graphs.

→ Acceleration : Rate of change in velocity is defined as “acceleration”. It is a vector. Unit: m/s²

→ Instantaneous acceleration : It is defined as the acceleration of the body at any given instant of time.
When time interval Δt is extremely small then \(\frac{d v}{d x}\) is called instantaneous acceleration,

→ Freely falling body: When a body drops from certain height it is called freely felling body.
For a freely falling body u = 0, accelera-tion a = g

→ Relative velocity : Let two bodies A and B are in motion. The velocity of B with respect to A or velocity of A with respect to (w. r. t) B’ is called relative velocity.
Ex: Let velocity of A is v_A and that of B is v_B. When both are moving in
(a) same direction
Velocity of A w.r.t B is v_AB = v_A – v_B
Velocity of B w.r.t A is v_BA = v_B – v_A

(b) opposite direction
Velocity of A w.r.t B is v_AB = v_A + v_B
Velocity of B w.r.t A is v_BA = v_B + v_A

→ For a body moving with uniform velocity, x = vt

→ Average Speed, V = \(\frac{\text { total distance }}{\text { total time }}\)

→ Instantaneous velocity, V = \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{\mathrm{dx}}{\mathrm{dt}}\)

→ Slope of displacement (x), time (t) graph gives velocity.

→ Average acceleration,
a = \(\frac{\text { change in velocity }}{\text { change in time }}=\frac{v_2-v_1}{t_2-t_1}\)

→ Instantaneous acceleration,
a = \(\mathrm{Lt}_{\Delta t \rightarrow 0} \frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}=\frac{\mathrm{dv}}{\mathrm{dt}}\)

→ Slope of velocity (v), time (t) graph gives acceleration.

→ Area under velocity (v), time (t) graph gives total displacement.

→ For a body moving with uniform velocity (v) its v – t graph is a straight line parallel to x – axis.

→ For a body moving with some acceleration (a) its v – t graph is a straight line inclined to x-axis.

→ Equations of motion

• v = u + at
• s = ut + \(\frac{1}{2}\) at²
• v² – u² = 2as

→ Distance travelled by a body during nth second, S_n = u + a (n – \(\frac{1}{2}\))

→ Equations of a freely falling body are

• v = gt
• s = h = \(\frac{1}{2}\)gt²
• v² = 2gh

→ For a body thrown up vertically use

• v = u – gt
• s = h = ut – \(\frac{1}{2}\)gt²
• v² – u² = -2gh
• time of ascent, t = \(\frac{u}{g}\), time of descent t = \(\frac{u}{g}\)
• time spent in air, T = 2t = \(\frac{2u}{g}\)
• Maximum height reached h_max = \(\frac{\mathrm{u}^2}{2 \mathrm{~g}}\)