TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type

Question 1.
Find the range of \(\frac{x^2+x+1}{x^2-x+1}\). [Mar.’10. ’04, May ’10]
Solution:
Let y = \(\frac{x^2+x+1}{x^2-x+1}\)
⇒ y(x² – x + 1) = x² + x + 1
⇒ yx² – yx + y – x² – x – 1 = 0
⇒ (y – 1)x² + (- y – 1) x + y – 1 = 0
x is real;
⇒ discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (- y – 1)² – 4 (y – 1) (y – 1) ≥ 0
⇒ y² + 1 + 2y – 4 (y² – y – y + 1) ≥ 0
⇒ y² + 1 + 2y – 4y² + 8y – 4 ≥ 0
⇒ – 3y² + 10y – 3 ≥ 0
⇒ 3y² – 10y + 3 ≤ 0
⇒ 3y² – 9y – y + 3 ≤ 0
⇒ 3y (y – 3) – 1 (y – 3) ≤ 0
⇒ \(\frac{1}{3}\) ≤ y ≤ 3
∴ y lies between \(\frac{1}{3}\) and 3.
∴ Range = [\(\frac{1}{3}\), 3]

Question 2.
Find the range of \(\frac{x+2}{2 x^2+3 x+6}\). [AP – May ’16; Mar ’13, ’08, Mar. 2000, B.P]
Solution:
Let y = \(\frac{x+2}{2 x^2+3 x+6}\)
⇒ 2x²y + 3xy + 6y = x + 2
⇒ (2y)x² + (3y – 1)x + (6y – 2) = 0
x is real;
⇒ Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (3y – 1)² – 4(2y) (6y – 2) ≥ 0
⇒ 9y² + 1 – 6y – 48y² + 16y ≥ 0
⇒ – 39y² + 10y + 1 ≥ 0
⇒ 39y² – 10y – 1 ≤ 0
⇒ 39y2 – 13y + 3y – 1 ≤ 0
⇒ 13y (3y – 1) + (3y – 1) ≤ 0
⇒ (13y + 1) (3y – 1) ≤ 0
⇒ \(\frac{-1}{13} \leq y \leq \frac{1}{3}\)
y lies between \(\frac{-1}{13}\) and \(\frac{1}{3}\).
∴ Range = [\(\frac{-1}{13}\), \(\frac{1}{3}\)].

Question 3.
Find the range of \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\). [Mar. ’09, ’98].
Solution:
Let y = \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\)
⇒ x²y – 3xy + 2y = 2x² – 6x + 5
⇒ x²y – 3xy + 2y – 2x² + 6x – 5 = 0
⇒ (y – 2)x² +(- 3y+ 6)x + 2y – 5 = 0
x is real ;
⇒ Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (- 3y + 6)² – 4(y – 2) (2y – 5) ≥ 0
⇒ 9y² + 36 – 36y – 4(2y² – 5y – 4y + 10) ≥ 0
⇒ 9y² + 36 – 36y – 8y² + 20y + 16y – 40 ≥ 0
⇒ y² – 4 ≥ 0
⇒ (y – 2) (y + 2) ≥ 0
⇒ y ≤ – 2 (or) y ≥ 2 y ≤ – 2 y ≥ 2
∴ y does not lies between – 2, 2.

∴ Range = (- ∞, – 2] u [2, ∞).

Question 4.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real. [TS – Mar. ’18, ’16, May ’12, March ’11, ’05; AP – Mar. ’17, ’16, ’15].
Solution:
Let y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
(3x + 1) (x + 1) y = x + 1 + 3x + 1 – 1
⇒ y[3x² + 4x + 1] = 4x + 1
⇒ 3x²y + 4xy . y – 4x – 1 = 0
⇒ (3y)x² + (4y – 4) x + (y – 1) = 0
If x is real ;
⇒ Discriminant ≥ 0
b2 – 4ac ≥ 0
⇒ (4y – 4)² – 4 (3y) (y – 1) ≥ 0
⇒ 16y² + 16 – 32y – 12y² + 12y ≥ 0
⇒ 4y² – 20y + 16 ≥ 0
⇒ 4 (y² – 5y + 4) ≥ 0
⇒ y² – 4y – y + 4 ≥ 0
⇒ (y -4) – 1 (y – 4) ≥ 0
⇒ =(y – 1) (y – 4) ≥ 0
⇒ y ≤ 1 (or) y ≥ 4

∴ y does not lies between 1 and 4.
∴ Range is (- ∞, 1] [4, ∞)

Question 5.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between and 1. [TS – May 2016] [May ‘11, ‘07, March ‘14, ’13, ‘08, ‘02] [AP – Mar. 2019]
Solution:
Let y = \(\frac{x}{x^2-5 x+9}\)
⇒ x² – 5xy + 9y = x
⇒ y . x² + (- 5y – 1) x + 9y = 0
If x is real
⇒ Discriminant, b2 – 4ac ≥ 0
⇒ (- 5y – 1)² – 4 . y . 9y ≥ 0
⇒ 25y² + 1 + 10y – 36y² ≥ 0
⇒ – 11y² + 10y + 1 ≥ 0
⇒ 11y² – 10y – 1 ≤ 0
⇒ 11y (y – 1) + 1 (y – 1) ≤ 0
⇒ (11y + 1) (y – 1) ≤ 0
⇒ \(\frac{-1}{11}\) ≤ y ≤ 1
∴ y lies between \(\frac{-1}{11}\) and 1.

Question 6.
If the expression \(\frac{x-p}{x^2-3 x+2}\) takes all real values for x ∈ R, then find the bounds for p. [May ‘09, ‘06. March ‘06] [TS & AP – May 2015].
Solution:
Let y = \(\frac{x-p}{x^2-3 x+2}\)
⇒ yx² – 3xy + 2y = x – p
⇒ y . x² + (- 3y – 1) x + (2y + p) = 0
x is real
⇒ Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (- 3y – 1)² – 4y (2y + p) ≥ 0
⇒ 9y² + 1 + 6y – 8y² – 4py ≥ 0
⇒ y² + (6 – 4p) y + 1 ≥ 0
⇒ y is real then, y² + (6 – 4p) y + 1 ≥ 0
The roots of y² + (6 – 4p) y + 1 = 0 are real and equal or lmaginary.
Then discriminant ≤ 0
⇒ b² – 4ac ≤ 0
⇒ (6 – 4p)² – 4(1)(1) ≤ 0
⇒ 36 + 16p² – 48p – 4 ≤ 0
⇒ 16p² – 48p + 32 ≤ 0
⇒ p² – 3p + 2 ≤ 0
⇒ p² – 2p – p + 2 ≤ 0
⇒ p(p – 2) – 1(p – 2) ≤ 0
⇒ (p – 1) (p – 2) ≤ 0
⇒ 1 ≤ p ≤ 2
If p = 1 (or) p = 2 then \(\frac{x-p}{x^2-3 x+2}\) is not defined.
∴ 1 < p < 2.

Question 7.
Show that none of the values of the function \(\frac{x^2+34 x-71}{x^2+2 x-7}\) over R lies between 5 and 9. [March ‘12. ‘07]
Solution:
Let y = \(\frac{x^2+34 x-71}{x^2+2 x-7}\)
⇒ y(x² + 2x – 7) = x² + 34x – 71 = 0
⇒ yx² + 2xy – 7y – x² – 34x + 71 = o
⇒ (y – 1)x² + (2y – 34) x – 7y + 71 = 0
If x is real ;
= Discriminant ≥ 0
⇒ b² – 4ac ≥ 0
⇒ (2y – 34)² -4 (y – 1) (- 7y + 71) ≥ 0
⇒ 4y² + 1156 – 136y – 4 (- 7y² + 71y + 7y – 71) ≥ 0
⇒ 4y² + 1156 – 136y + 28y² – 284y – 28y + 284 ≥ 0
⇒ 32y² – 448y + 1440 ≥ 0
⇒ y² – 14y + 45 ≥ 0
⇒ y² – 9y – 5y + 45 ≥ 0
⇒ y (y – 9) – 5(y – 9) ≥ 0
⇒ (y – 5) (y – 9) ≥ 0
⇒ y ≤ 5 (or) y ≥ 9
∴ y does not Lies between 5 and 9.
Hence, none of the values of given function over R lies between 5 and 9.

Question 8.
Find the maximum and minimum values of the function \(\frac{x^2+14 x+9}{x^2+2 x+3}\) over R. [AP – March 2018; May ’14, ‘05].
Solution:
Let y = \(\frac{x^2+14 x+9}{x^2+2 x+3}\)
⇒ yx² + 2xy + 3y – x – 14x – 9 = 0
⇒ (y – 1)x² + (2y – 14)x + 3y – 9 = 0
If x is real
⇒ Discriminant, b2 – 4ac ≥ O
⇒ (2y – 14)² – 4(y – 1)(3y – 9) ≥ 0
⇒ 24y² + 196 – 56y – 4[3y² – 9y – 3y + 9]≥ 0
⇒ 4y² + 196 – 56y – 12y² + 36y. 12y – 36 ≥ 0
⇒ – 8y² – 8y + 160 ≥ 0
⇒ y² + y – 20 ≤ 0
⇒ y² + 5y – 4y – 20 ≤ 0
⇒ y(y + 5) – + 5) ≤ 0
⇒ (y + 5) (y – 4) ≤ 0
⇒ – 5 ≤ y ≤ 4
⇒ y lies between – 5 and 4.
Minimum value = – 5, Maximum value = 4
Range = [- 5, 4].

Question 9.
If c² ≠ ab and the roots of (c² – ab) x² – 2 (a² – bc) x + (b² – ac) = 0 are equal, then show that a³ + b³ + c³ = 3abc or a = 0. [May ’01] [TS – Mar. ’19].
Solution:
Given quadratic equation is (c² – ab) x² – 2 (a² – bc)x + b² – ac = 0 ……………(1)
Comparing this equation with
ax² + bx +c = 0, we have
⇒ a = c² – ab, b = – 2 (a² – bc), c = b² – ac
Since (1) has equal roots.
⇒ b² – 4ac = 0
⇒ [- 2 (a² – bc)]² – 4 (c² – ab) (b² – ac)= 0
⇒ 4 [a⁴ + b²c² – 2a²bc] – 4[b²c² – ⇒ ac³ – ab³ – a²bc] = 0
⇒ 4a⁴ + 4b²c² – 8a²bc – 4b²c² + ⇒ 4ac³ + 4ab³ – 4a²bc = 0
⇒ 4a[a³ – 3abc + c³ + b³] = 0
⇒ a = 0 (or)a³ + b³ + c³ = 3abc.

Question 10.
Let a, b, c ∈ R and a ≠ 0 then the roots of ax² + bx + c = 0 are non-real complex numbers If and only If ax² + bx + c and a have the same sign for all x ∈ R. [May ’98. ‘93. Mar.’99]
Solution:
The roots of the quadratic equation ax² + bx + c = 0 are imaginary then
b² – 4ac < 0
4ac – b² > 0.
Now, ax² + bx + c = a [x² + \(\frac{b}{a} x+\frac{c}{a}\)]
\(\frac{a x^2+b x+c}{a}\) = x² + \(\frac{b}{a} x+\frac{c}{a}\)
= x² + 2 . x . \(\frac{b}{2 a}\) + \(\left(\frac{b}{2 a}\right)^2-\left(\frac{b}{2 a}\right)^2+\frac{c}{a}\)
= \(\left(x+\frac{b}{2 a}\right)^2+\frac{c}{a}-\frac{b^2}{4 a^2}\)
= \(\left(x+\frac{b}{2 a}\right)^2+\frac{4 a c-b^2}{4 a^2}\) > 0
∴ \(\frac{a x^2+b x+c}{a}\) > 0
∴ For x ∈ R, ax² + bx + c and a have the same sign.

Question 11.
Let a, b, c ∈ R and a 0 such that the equation ax² + bx + c = 0 has real roots α and β with α < β, then
i) for α < x <, ax² + bx + c and a have opposite signs.
ii) for x < α or x > β, ax² + bx + c and a have the same sign.
Solution:
α, β are the roots of ax² + bx + c = 0.
Then ax² + bx + c = a (x – α) (x – β)
\(\frac{a x^2+b x+c}{a}\) = (x – α) (x – β) ……………(1)

i) Suppose x ∈ R, α < x < β x > α, x – β < 0 (x – α) > 0
(x – α) (x – β) < 0
From (1),
⇒ \(\frac{a x^2+b x+c}{a}\) < 0
∴ ax² + bx + c, a have opposite sign.

ii) Suppose x ∈ R, x < α Suppose x ∈ R, x > β
x < α < β.
x< α x < β
x – α < 0 x – β < 0 x- β > 0 x – α > 0
(x – α) (x – β) >0
from (1)
\(\frac{a x^2+b x+c}{a}\) > 0
ax² + bx + c, a have same sign.

x > β > α
x > β x > α
x – β > 0 x – α > 0
(x – α) (x – β) > 0
from (1)
\(\frac{a x^2+b x+c}{a}\) > 0
ax² + bx + c, a have same sign.
∴ x ∈ R, x < α (or) x > β then ax² + bx + c and a have the same sign.

Question 12.
Suppose that a, b, c ∈ R, a ≠ 0 and f(x) = ax² + bx + c
i) If a > 0, then f(x) has absolute minimum at x = \(\frac{-b}{2 a}\) and the minimum value is \(\frac{4 a c-b^2}{4 a}\).
ii) If a < 0, then f(x) has absolute maximum at x = \(\frac{-b}{2 a}\) and the maximum value is \(\frac{4 a c-b^2}{4 a}\).
Solution:
f(x) = ax² + bx + c
f’(x) =2ax + b
⇒ For f(x) has max. or min.
then f’(x) = 0
⇒ 2ax + b = 0
⇒ x = \(\frac{-b}{2 a}\)
Now, f”(x) = 2a
i) If a >0 then f”(x) > 0 and hence f has min. value at x = \(\frac{-b}{2 a}\)
Minimum of f = f(\(\frac{-b}{2 a}\))
= \(a\left(\frac{-b}{2 a}\right)^2+b\left(\frac{-b}{2 a}\right)+c\)
= \(a \frac{b^2}{4 a^2}-\frac{b^2}{2 a}+c\)
= \(\frac{b^2-2 b^2+4 a c}{4 a}=\frac{4 a c-b^2}{4 a}\)

ii) If a < 0 then f”(x) < 0 and hence f has max. value at x = \(\frac{-b}{2 a}\)
Maximum of f = f(\(\frac{-b}{2 a}\))
= \(a\left(\frac{-b}{2 a}\right)^2+b\left(\frac{-b}{2 a}\right)+c\)
= \(a \cdot \frac{b^2}{4 a^2}-\frac{b^2}{2 a}+c\)
= \(\frac{b^2-2 b^2+4 a c}{4 a}=\frac{4 a c-b^2}{4 a}\).

Question 13.
If x₁, x₂ are the roots of the quadratic equation ax² + bx + c = 0 and c ≠ 0, find
the value of (ax₁ + b) + (ax₂ + b) in terms of a, b, c. [TS – Mar. 2017]
Solution:
Given that x₁, x₂ are the roots of ax² + bx + c = 0
⇒ x₁ + x₂ = – b/a, x₁x₂ = c/a
also ax₁² + bx₁ + c = 0,
ax₂² + bx₂ + c = 0
⇒ x₁ (ax₁ + b) = – c,
x₂(ax₂ + b) = – c
⇒ (ax₁ + b) = – c/x₁,
(ax₂ + b) = – c/x₂
Now (ax₁ + b)^-2 + (ax₂ + b)^-2 = \(\left(\frac{-c}{x_1}\right)^{-2}+\left(\frac{-c}{x_2}\right)^{-2}=\frac{x_1^2}{c^2}+\frac{x_2^2}{c^2}=\frac{x_1^2+x_2^2}{c^2}\)
= \(\frac{\left(x_1+x_2\right)^2-2 x_1 x_2}{c^2}\)
= \(\frac{\left(\frac{-b}{a}\right)^2-2 \cdot \frac{c}{a}}{c^2}=\frac{b^2-2 a c}{c^2 a^2}\).

Some More Maths 2A Quadratic Expressions Important Questions

Question 1.
Find the roots of the equation 6√5 x² – 9x – 3√5 = 0.
Solution:
Given quadratic equation is
6√5x² – 9x – 3√5 = 0
Comparing this with ax² + bx + c = 0, we have
a = 6√5, b = – 9, c = – 3√5
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
are the roots of quadratic equation.
x = \(\frac{9 \pm \sqrt{81+360}}{12 \sqrt{5}}=\frac{9 \pm \sqrt{441}}{12 \sqrt{5}}=\frac{9 \pm 21}{12 \sqrt{5}}\)
= \(\frac{9+21}{12 \sqrt{5}} \text { (or) } \frac{9-21}{12 \sqrt{5}}\)
= \(\frac{30}{12 \sqrt{5}} \text { (or) } \frac{-12}{12 \sqrt{5}}=\frac{\sqrt{5}}{2} \text { (or) } \frac{-1}{\sqrt{5}}\)
∴ The roots of the quadratic equation are \(\frac{\sqrt{5}}{2} \text { (or) } \frac{-1}{\sqrt{5}}\).

Question 2.
Form a quadratic equation whose roots are 2√3 – 5 and – 2√3 – 5.
Solution:
Let a = 2√3 – 5, p = – 2√3 – 5
Now, a+ = 2√3 – 5 – 2√3 – 5 = – 10
= (2√3 – 5) (- 2√3 – 5) = – (12 – 25) = 13
The quadratic equation whose roots are α, β is x² – (α + β) + αβ = 0
⇒ x² + 10x + 13 = 0

Question 3.
Form a quadratic equation whose roots are \(\frac{\mathbf{m}}{\mathbf{n}}, \frac{-\mathbf{n}}{\mathbf{m}}\), (m ≠ 0, n ≠ 0).
Solution:
Let α = \(\frac{m}{n}\), β = \(\frac{-\mathrm{n}}{\mathrm{m}}\)
Now, α + β = \(\frac{m}{n}-\frac{n}{m}=\frac{m^2-n^2}{m n}\)
αβ = \(\frac{m}{n} \cdot \frac{-n}{m}\) = – 1
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
x² – \(\frac{\left(m^2-n^2\right)}{m n}\)x – 1 = 0
mnx² – (m² – n²)x – mn = 0.

Question 4.
If α, β are the roots of ax² + bx + c = 0 then find α³ + β³.
Solution:
Since a, are the roots of ax² + bx + c = 0
α + β = – \(\frac{b}{a}\), αβ = \(\frac{c}{a}\)
α³ + β³ = (α + β)³ – 3αβ(α + β)
= \(\left(\frac{-b}{a}\right)^3-3 \cdot \frac{c}{a}\left(\frac{-b}{a}\right)\)
= \(\frac{-b^3}{a^3}+\frac{3 b c}{a^2}\)
⇒ \(\frac{3 a b c-b^3}{a^3}\).

Question 5.
For what values of m, x² + (m + 3) x + (m + 6) = 0 will have equa roots?
Solution:
Given quadratic equation is x² + (m + 3) x + (m + 6) = 0 ……………(1)
Comparing this with ax² + bx c = 0 we get
a = 1, b = m + 3, c = m + 6
Since (1) have equal roots
⇒ b² – 4ac = 0
⇒ [m + 3]² – 4(1)(m + 6) = 0
⇒ m² + 9 + 6m – 4m – 24 = 0
⇒ m² + 2m – 15 = 0
⇒ m² + 5m – 3m – 15 = 0
⇒ m (m + 5) – 3 (m + 5) = 0
⇒ (m – 3) (m + 5) = 0
⇒ m = 3 (or) m = – 5
The values of m are 3, – 5.

Question 6.
For what values of m, x² – 2 (1 + 3m) x + 7(3 + 2m) = 0 will have equal roots?
Solution:
Given quadratic equation is
x² – 2 (1 + 3m) x + 7 (3 + 2m) = 0 …………….(1)
Comparing this with ax² + bx + c = 0,
we get a = 1, b = – 2 (1 + 3m), c = 7 (3 + 2m)
Since (1) have equal roots
⇒ b² – 4ac = 0
⇒ [- 2 (1 + 3m)]² – 4(1) . 7 . (3 + 2m) = 0
⇒ 4 (1 + 9m² + 6m) – 28 (3 + 2m) = 0
⇒ 9m² + 6m + 1 – 21 – 14m = 0
⇒ 9m² – 8m – 20 = 0
⇒ 9m² – 18m + 10m – 20 = 0
⇒ 9m (m – 2) + 10(m – 2) = 0
⇒ (9m + 10) (m – 2) = 0
m = \(\frac{-10}{9}\) (or) m = 2
The values of m are \(\frac{-10}{9}\), 2.

Question 7.
For what values of m, (2m + 1) x² + 2(m + 3) x + (m + 5) = 0 will have equal roots?
Solution:
Given quadratic equation is (2m + 1) x² + 2(m + 3) x + (m + 5) = 0
Comparing this with ax² + bx + c = 0,
we get a = 2m + 1, b = 2 (m + 3), c = m + 5
SInce (1) have equal roots
⇒ b² – 4ac = 0
⇒ (2 (m + 3))² – 4(2m + 1) (m + 5) = 0
⇒ 4(m² + 9 + 6m) – 4[2m² + 10m + m + 5] = 0
⇒ m² + 9 + 6m – 2m² – 11m + 5 = 0
⇒ – m² – 5m + 4 = 0
⇒ m² + 5m -4 = 0
m = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-5 \pm \sqrt{25-4(1)(-4)}}{2(1)}\)
= \(\frac{-5 \pm \sqrt{25+16}}{2}=\frac{-5 \pm \sqrt{41}}{2}\)

Question 8.
Show that the roots of the equation x² – 2px + p² – q² + 2qr – r² = 0 are rational, where p, q, r are rational.
sol.
Given that, p, q, r are rational.
Given quadratic equation is
x² – 2px + p² – q² + 2qr – r² = 0
Comparing this with ax² + bx + c = 0 we get
a = 1, b = – 2p, c = p² – q² + 2qr – r²
b² – 4ac = 4p² – 4(1) (p² – q² + 2qr – r²)
= 4p² – 4p² + 4q² – 8qr + 4r²
= 4q² – 8qr + 4r²
= 4 (q² – 2qr + r²) = 4 (q – r)² = [2 (q – r)]² ≥ 0
Since b² – 4ac ≥ 0 then the roots of the given equation are rational.

Question 9.
Find the quadratic equation, the sum of whose roots is 7 and sum of the squares of the roots is 25.
Solution:
Let α and β be the roots of a required equation.
Given that the sum of roots = 7
α + β = 7
The sum of squares of the roots = 25
αβ = 25
We know that, (α + β)² = α² + β² + 2αβ
7² = 25 + 2αβ
2αβ = 49 – 25 = 24
αβ = 12
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
x² – 7x + 12 = 0.

Question 10.
Solve the equation 3^{1 + x} + 3^{1 – x} = 10.
Solution:
Given equation is 3 . 3^x + \(\frac{3}{3^x}\) = 10
Let 3^x = a
⇒ 3a + \(\frac{3}{a}\) = 10
⇒ 3a² – 10a + 3 = 0
⇒ a² – 9a – a + 3 = 3 = 0
⇒ 3a (a – 3) – 1 (a – 3) = 0
⇒ (a – 3) (3a – 1) = 0
⇒ a = 3 (or) a = \(\frac{1}{3}\)

Case-1 :
If a = 3
⇒ 3 = 3^x
⇒ x = 1

Case – 2 :
If a = \(\frac{1}{3}\)
⇒ \(\frac{1}{3}\) = 3^x
⇒ 3^x = 3^{– 1}
⇒ x = – 1.

∴ The solution set of the given equation is {- 1, 1}.

Question 11.
Solve 7^1+x + 7^1-x = 50 for real x.
Solution:
Given equation is 7^1+x + 7^1-x = 50
7 . 7^x + \(\frac{7}{a}\) = 50 ……………..(1)
Let 7^x = a
⇒ 7a + \(\frac{7}{a}\) = 50
⇒ 7a² – 50a + 7 = 0
⇒ 7a² – 49a – a + 7 = 0
⇒ 7a (a – 7) – 1(a – 7) = 0
⇒ (a – 7) (7a – 1) = 0
⇒ a = 7 (or) \(\frac{1}{7}\)
Case – 1:
If a = 7
⇒ 7^x = 7
⇒ x = 1

Case – 2:
If a = \(\frac{1}{7}\)
⇒ 7^x = 7^-1
x = – 1
Hence the solution set of the given equation is {- 1, 1}.

Question 12.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
Given quadratic equations are x² – 6x + 5 = 0
Comparing with a₁x² + b₁x + c₁ = 0, we get
a₁ = 1, b₁ = – 6, c₁ = 5
Now, x² – 3ax + 35 = 0
Comparing with a₂x² + b₂x + c₂ = 0
we get, a₂ = 1, b₂ = – 3a c₂ = 35
The condition for two quadratic equation. to have a common root is
(c₁a₂ – c₂a₁1)2 = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁)
⇒ (5(1) – 35(1))² = (1 – 3a) – (1) – 6) (- 6(35) – (- 3a) 5)
⇒ (5 – 35)² = (- 3a + 6) (- 210 + 15a)
⇒ 900 = 3(- a + 2) 5 (- 42 + 3a)
⇒ 900 = 15(- a + 2) (- 42 + 3a)
⇒ 42a – 3a² – 84 + 6a = 60
⇒ 3a² – 48a+ 144 = 0
⇒ a² – 16a + 48 = 0
⇒ a – 12a – 4a + 48 = 0
⇒ a(a – 12) – 4(a – 12) = 0
⇒ (a – 4) (a – 12) = 0
⇒ a = 4 (or) a = 12.

Question 13.
For what values of x, the expression x² – 5x + 14 is positive?
Solution:
Given expression is x² – 5x + 14
The roots of x² – 5x + 14 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{5 \pm \sqrt{25-4 \cdot 1(14)}}{2(1)}\)
= \(\frac{5 \pm \sqrt{25-56}}{2}=\frac{5 \pm \mathrm{i} \sqrt{31}}{2}\)
which are not real.
∴ For all x ∈ R, the expression x² – 5x + 14 is + ve.

Question 14.
For what values of x, the expression 3x² + 4x + 4 is positive?
Solution:
The given quadratic expression is 3x² + 4x + 4
The roots of 3x² + 4x + 4 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{-4 \pm \sqrt{16-48}}{2(3)}\)
= \(\frac{-4 \pm \sqrt{-32}}{6}\)
= \(\frac{-2 \pm i \sqrt{8}}{3}=\frac{-2 \pm 2 \mathrm{i} \sqrt{2}}{3}\)
which are complex numbers (non real).
∴ For all x ∈ R, the expression 3x² + 4x + 4 is + ve.

Question 15.
For what values of x, the expression x² – 7x + 10 is negative?
Solution:
Given expression is x² – 7x + 10
= x² – 5x – 2x + 10
= x (x – 5) – 2 (x – 5)
= (x – 2) (x – 5)
i) If 2 < x < 5, then the expression x² – 7x + 10 is ‘- ve’.
ii) If x < 2 (or) x > 5, then the expression x² – 7x + 10 is ’+ve’.
iii) If x = 2 (or) x = 5, then the expression : x² – 7x + 10 = 0.

Question 16.
For what values of x, the expression 15 + 4x – 3x² is negative?
Solution:
Given expression is 15 + 4x – 3x²
= – 3x² + 9x – 5x + 15 = 3x (- x + 3) + 5(- x + 3)
= (3x + 5) (- x + 3)
i) If \(\frac{-5}{3}\) < x < 3, then the expression is 15 + 4x – 3×2 is ‘+ ve’.
ii) If x < \(\frac{-5}{3}\) (or) x > 3, then the expression is 15 + 4x – 3x² is ‘- ve’.
iii) If x = \(\frac{-5}{3}\) (or) x = 3,then the expression 15 + 4x – 3x² = 0.

Question 17.
Find the changes in the sign of 4x – 5x² + 2 for x ∈ R.
Solution:
Given quadratic expression is 4x – 5x² + 2
The roots of given expression are

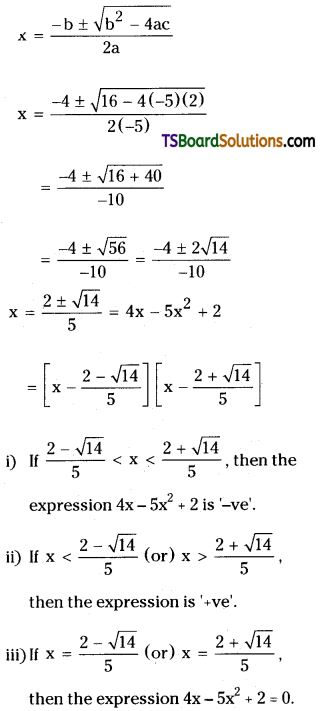
Questi0n 18.
Find the roots of the equation 4x² – 4x + 17 = 3x² – 10x – 17.
Solution:
Given equation can be rewritten as x² + 6x + 34 = 0.
The roots of the quadratic equation, ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
Here a = 1, b = 6 and c = 34.
Therefore the roots of the given equation are \(\frac{-6 \pm \sqrt{(6)^2-4(1)(34)}}{2(1)}\)
= \(\frac{-6 \pm \sqrt{-100}}{2}\)
= \(\frac{-6 \pm 10 \mathrm{i}}{2}\) (since i² = – 1)
= – 3 + 5i, – 3 – 5i
Hence the roots of the given equation are – 3 + 5i and – 3 – 5i.

Questi0n 19.
Solve, \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\).
Solution:
Given equation is \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\)
Let \(\sqrt{\frac{x}{1-x}}\) = a
\(\sqrt{\frac{1-x}{x}}=\frac{1}{a}\)
a + \(\frac{1}{a}=\frac{13}{6}\)
⇒ 6a² + 6 = 13a
⇒ 6a² – 13a + 6 = 0
⇒ 6a² – 9a – 4a + 6 = 0
⇒ 3a (2a – 3) – 2 (2a – 3) = 0
⇒ 2a – 3 = 0, 3a – 2 = 0
⇒ 3a = 2
⇒ a = \(\frac{2}{3}\)
⇒ a = \(\frac{2}{3}\)
Case – 1:
If a = \(\frac{2}{3}\)
⇒ \(\sqrt{\frac{x}{1-x}}=\frac{2}{3}\)
⇒ \(\frac{x}{1-x}=\frac{4}{9}\)
9x = 4 – 4x
13x = 4
x = \(\frac{4}{13}\)

Case-2: .
If a = \(\frac{2}{3}\)
⇒ \(\sqrt{\frac{x}{1-x}}=\frac{3}{2}\)
⇒ \(\frac{x}{1-x}=\frac{9}{4}\)
⇒ 4x = 9 – 9x
⇒ 13x = 9
⇒ x = \(\frac{9}{13}\)
∴ The solution set of given equation is {\(\frac{9}{13}\), \(\frac{4}{13}\)}

Question 20.
Find the numbers which exceed their square root by 12.
Solution:
Let ‘x’ be any number.
Given that, x = √x + 12 ………….(1)
x – 12 = √x
⇒ squaring on both sides
⇒ x² + 144 – 24x = x
⇒ x² + 144 – 25x = 0
⇒ x² – 16x – 9x + 144= 0
⇒ x (x – 16) – 9 (x – 16) = 0
⇒ (x – 9) (x – 16) = 0
⇒ x = 9 (or) x = 16.
But x = 9 does not satisfy (1) whilex = 16 satisfy.
∴ The required number is 16.

Question 21.
Prove that there is a unique pair of con-secutive positive odd Integers such that the sum of their squares is 290 and find it.
Solution:
Since two consecutive odd integers differ by 2.
Let a pair of consecutive .ve odd integers are x, x + 2.
Given that, the sum of their squares is 290
⇒ x² + (x + 2)² = 290 ………………..(1)
⇒ x² + x² + 4 + 4x = 290
⇒ 2x² + 4x – 286 = 0
⇒ x² + 2x- 143 = 0
⇒ x² + 13x – 11x – 143 = 0
⇒ x (x + 13) – 11 (x + 13) = 0
⇒ (x – 11) (x + 13) = 0
⇒ x = 11 (or) x = – 13
Since x is positive, x = 11
Hence 11 is the only +ve odd integer satisfying equation (1).
∴ A pair of consecutive +ve odd integers are x, x + 2 = 11, 13.
∴ (11, 13) is the unique pair of integers which satisfy the given condition.

Question 22.
If α, β are the roots of the equation ax² + bx + c = 0, find the values of the following expressions in terms of a, b, c.
i) α⁴ β⁷ + α⁷ β⁴
ii) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\)
iii) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\)
Solution:
Since α, β are the roots of the equation ax² + bx + c = 0 then
α + β = \(\frac{-b}{a}\); αβ = \(\frac{c}{a}\)
i) α⁴ β⁷ + α⁷ β⁴ = α⁴β⁴ (β³ + α³)
= α⁴β⁴ (α³ + β³)
= α⁴β⁴ [(α + β)³ – 3αβ(α + β)]
= \(\left(\frac{c}{a}\right)^4\left[\left(\frac{-b}{a}\right)^3-3 \cdot \frac{c}{a} \cdot \frac{-b}{a}\right]\)
= \(\frac{c^4}{a^4}\left(\frac{-b^3}{a^3}+\frac{3 b c}{a^2}\right)\)
= \(\frac{c^4}{a^4} \frac{\left(-b^3+3 a b c\right)}{a^3}=\frac{c^4\left(3 a b c-b^3\right)}{a^7}\)

ii) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\), if c ≠ 0.

iii) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\) if c ≠ 0.
= \(\frac{\alpha^2+\beta^2}{\frac{1}{\alpha^2}+\frac{1}{\beta^2}}=\frac{\alpha^2+\beta^2}{\frac{\alpha^2+\beta^2}{\left(\alpha^2 \beta^2\right)}}\)
= (αβ)² = \(\frac{c^2}{a^2}\).

Question 23.
If x² + 4ax + 3 = 0 and 2x² + 3ax – 9 = 0 have a common root, then find the values of ‘a’ and the common roots.
Solution:
Given quadratic equations are x² + 4ax + 3 = 0
Comparing this equation with
a₁x² + b₁x + c₁ = 0
a₁ = 1, b₁ = 4a, c₁ = 3
Now 2x² + 3ax – 9 = 0
Comparing this equation with
a₂x² + b₂x + c₂ = 0
a₂ = 2, b₂ = 3a, c₂ = 9
The condition for two quadratic equations
a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0
to have a common root is
(c₁a₂ – c₂a₁)² = (a₁b₂ – b₁a₂) (b₁c₂ – c₁b₂)
⇒(3 . 2 – (- 9)(1))² = (1 . 3a – 2 . 4a) (4a (- 9) – 3a (3))
⇒ (6 + 9)² = (3a – 8a)(- 36a – 9a)
⇒ 15² = (- 5a) (- 45a)
⇒ 225 = 225a²
⇒ a² = 1
⇒ a = ± 1

Case – I:
If a = 1 then the given equation reduces to
x² + 4x + 3 = 0
x² + 3x + x + 3 = 0
x (x + 3) + 1 (x + 3) = 0
(x + 3) (x + 1) = 0
x = – 1, x = – 3

2x² + 3x – 9 = 0
2x² + 6x – 3x – 9 = 0
2x (x + 3) – 3 (x + 3) = 0
(x + 3) (2x – 3) = 0
2x = 3, x = – 3
x = \(\frac{3}{2}\)
∴ The roots of the given equation are respectively – 1, – 3 and \(\frac{3}{2}\), – 3.
In this case the common root of the given equation is – 3.

Case – II:
If a = – 1 then the given equation reduces to
x² – 4x + 3 = 0,
x²-3x-x.3 = 0
x (x – 3) – 1(x – 3) = 0
(x – 3) (x – 1) = 0
x = 3, x = 1

2x² – 3x – 9 = 0
2x² – 6x + 3x – 9 = 0
2x (x – 3) + 3 (x – 3) = 0
(x – 3)(2x + 3)=0
x = 3, 2x = – 3
x = \(\frac{-3}{2}\)
∴ The roots of the given equation are respectively 3, 1 and 3
In this case the common root of the given equation is 3.

Question 24.
Discuss the signs of the expression x² + x + 1 for x ∈ R.
Solution:
Given quadratic expression is x² + x + 1
The roots of x² + x + 1 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{-1 \pm \sqrt{1-4}}{2(1)}\)
= \(\frac{-1 \pm i \sqrt{3}}{2}\)
which are complex roots (non real)
for all x ∈ R, the expression x² + x + 1 is positive.

Question 25.
For what values of x the expression x² – 5x + 14 is positive?
Solution:
Given expression is x² – 5x + 14 = 0
The roots of x² – 5x + 14 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{5 \pm \sqrt{25-4 \cdot 1(14)}}{2(1)}\)
= \(\frac{5 \pm \sqrt{25-56}}{2}\)
= \(\frac{5 \pm i \sqrt{31}}{2}\)
which are non real.
∴ For all x ∈ R, the expression x² – 5x + 1 is +ve.

Question 26.
For what values of x the expression – 6x² + 2x – 3 is negative?
Solution:
Given quadratic expression is – 6x² + 2x -3
The roots of – 6x² + 2x – 3 = 0 is

which are non real.
Here the coefficient of x² is – ve’.
∴ x ∈ R, the expression – 6x² + 2x – 3 is ‘-ve’.

Question 26.
Find the value of x at which the following expressions have maximum or minimum?
i) x² + 5x + 6
ii) 2x – x² + 7
Solution:
i) x² – 5x – 6
Given quadratic expression is x² + 5x + 6
Comparing this expression with ax² + bx + c
We have a = 1, b = 5, c = 6
Here a = 1 > 0. x² + 5x + 6 has minimum at
x = \(\frac{-\mathrm{b}}{2 \mathrm{a}}\)
x = \(\frac{-5}{2(1)}=\frac{-5}{2}\)

ii) 2x – x² + 7
Given quadratic expression is – x² + 2x + 7
Comparint. this expression with ax² + bx + c
we get. a = – 1, b = 2, c = 7
Here, a = – 1 < 0 – x² + 2x + 7 has absolute maximum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(-1)}\) = 1.

Question 27.
Solve 2x⁴ + x³ – 11x² + x + 2 = 0. [TS – Mar. 2015]
Solution:
Given equation is 2x⁴ + x³ – 11x² + x + 2 = 0

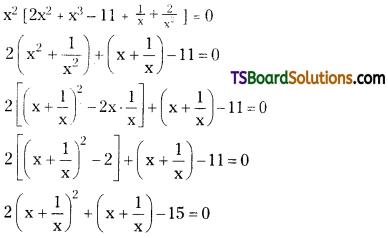
Let x + \(\frac{1}{x}\) = t
⇒ 2t² + t – 15 = 0
⇒ 2t² + 6t – 5t – 15 = 0
⇒ 2t (t + 3) – 5 (t + 3) = 0
⇒ (t + 3) (2t – 5) = 0
⇒ t + 3 = 0
⇒ x + \(\frac{1}{x}\) + 3 = 0
⇒ \(\frac{x^2+1+3 x}{x}\) = 0
⇒ x² + 3x + 1 = 0
⇒ x = \(\frac{-3 \pm \sqrt{9-4}}{2}\)
∴ x = \(\frac{-3 \pm \sqrt{5}}{2}\)
⇒ 2t – 5 = 0
⇒ 2 (\(\left(x+\frac{1}{x}\right)\)) – 5 = 0
⇒ \(\frac{2 x^2+2-5 x}{x}\) = 0
= 2x² – 5x + 2 = 0
2x² – 4x – x + 2 = 0
2x (x – 2) – 1 (x – 2) = 0
(x – 2) (2x – 1) = 0
∴ x = 2, ½
∴ Solution set = \(\left\{\frac{-3 \pm \sqrt{5}}{2}, 2 . \frac{1}{2}\right\}\).

Question 28.
For what values of x the expression x² – 5x – 14 is positive. [AP-Mar. 2018]
Solution:
x² – 5x – 14 = (x + 2) (x – 7)
The roots of x² – 5x – 14 = 0 are – 2, 7.
Here coeff. x² is 1. This is positive.
So x < – 2 or x > 7 then x² – 5x – 14 is positive.

Question 29.
Find the set of solutions of x² + x – 12 ≤ 0 by algebraic method. [TS – Mar. 2019]
Solution:
Algebraic method:
x² + x – 12 = 0
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4) (x -3) = 0
⇒ x = – 4 or 3
⇒ x² + x – 12 ≤ 0
⇒ – 4 ≤ x ≤ 13