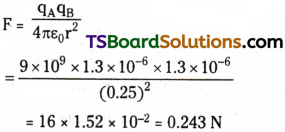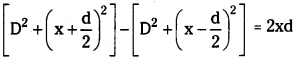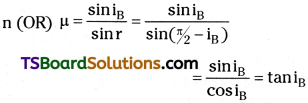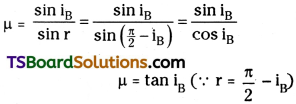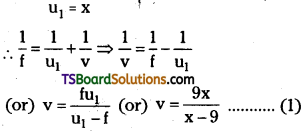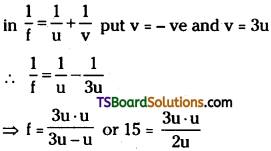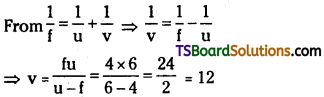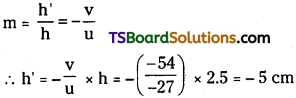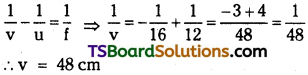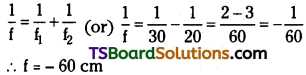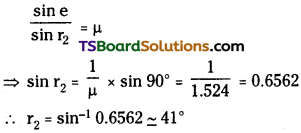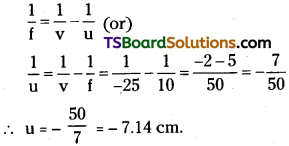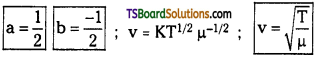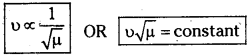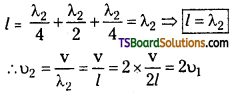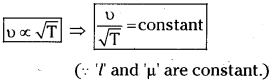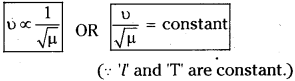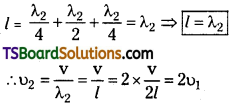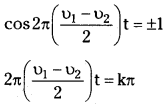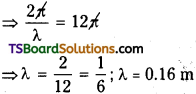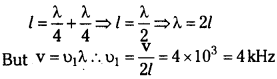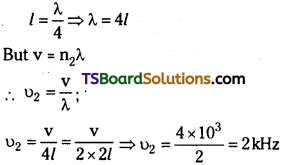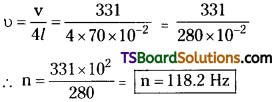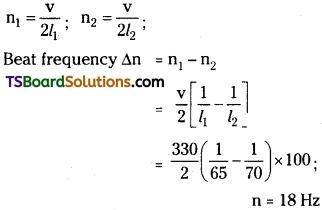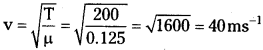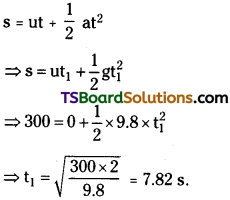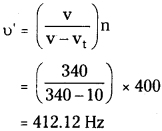Srinivas

Telangana TSBIE TS Inter 2nd Year Physics Study Material 10th Lesson Alternating Current Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 10th Lesson Alternating Current

Very Short Answer Type Questions

Question 1.
A transformer converts 200 V ac into 2000 V ac. Calculate the number of turns in the secondary if the primary has 10 turns. [TS Mar. ’16; AP Mar. 19, ’18] [IMP]
Answer:
Primary voltage V_p = 200 V ;
Secondary voltage V_s = 2000 V
Number of turns in Primary N_p = 10 ;
Number of turns in Secondary = N_s = ?

Question 2.
What type of transformer is used in a 6V bed lamp? [AP Mar. ’17]
Answer:
6V Bed lamp ⇒ V_s = 6V. But our mains supply is 220V (called primary voltage V_p).
So V_s < V_p.
Hence transformer used in bed lamp is step down transformer.

Question 3.
What is the phenomenon involved in the working of a transformer? [AP May ’18, ’17, ’16; Mar. ’16, ’14; June ’15]
Answer:
A transformer uses the principle of “mutual Induction”.
It also obeys law of conservation of energy.
In a transformer V_pI_p = V_sI_s.

Question 4.
What is transformer ratio? [TS May ’18]
Answer:
The ratio of number of turns in secondary (N_s) to number of turns in primary (N_p) is called “transformer turns ratio”.
Transformer turns ratio = \(\frac{N_s}{N_p}\)

Question 5.
What is the phase difference between A.C. emf and current in the following? Pure resistor and pure inductor. [TS Mar. ’15]
Answer:

1. In pure resistor AC emf and current are in same phase.
   ∴ Phase difference f = 0.
2. In pure inductor current lags behind emf by a phase angle Φ = 90° or \(\frac{\pi}{2}\) radians.
3. In pure capacitor current leads emf by a phase angle f = 90° or \(\frac{\pi}{2}\) radians.

Question 6.
What is Step-up transformer? How it differs from Step-down transformer?
Answer:
A Step-up transformer will convert low voltage input into high voltage output.

A Step-down transformer will convert high voltage input into low voltage output.

Question 7.
Write the expression for the reactance of (I) an inductor and (ii) a capacitor.
Answer:

1. Reactance of an Inductor X_L = ωL
2. Reactance of Capacitor X_c = \(\frac{1}{\omega C}\)

Where ω = 2πυ is the angular frequency of applied voltage.

Question 8.
What is the phase difference between AC emf and current in the following : Pure resistor, pure inductor and pure capacitor. [TS Mar. ’15]
Answer:

1. In pure resistor AC emf and current are in same phase.
   ∴ Phase difference Φ = 0.
2. In pure inductor current lags behind emf by a phase angle Φ = 90° or \(\frac{\pi}{2}\) radians.
3. In pure capacitor current leads emf by a phase angle Φ = 90° or \(\frac{\pi}{2}\) radians.

Question 9.
Define power factor. On which factors does power factor depend?
Answer:
Power of AC circuit and power factor :
Power of AC circuit P = I²Z cos Φ. It indicates that power depends not only on current I and Impedance Z of circuit, but also cosine of phase angle between I and Z.

The term cos Φ is called power factor.

Question 10.
What is meant by wattless component of current? [TS Mar. ’17]
Answer:
Wattless current :
In a circuit with pure inductance or pure capacitance the phase angle between voltage and currents are Φ= \(\frac{\pi}{2}\) , so cos Φ = 0. Hence no power is dissipated through then even though current passes through them. This current is referred as wattless current.

Question 11.
When does a LCR series circuit have minimum impedance?
Answer:
Impedance of series LCR circuit

In series LCR circuit Impedance is minimum at Resonance condition.

Question 12.
What is the phase difference between voltage and current when the power factor in LCR series circuit is unity?
Answer:
Power in a circuit P = VI cos Φ
Power factor is unity cos Φ = 1 ⇒ Φ = 0°
∴ Phase difference between voltage and current Φ = 0.

Short Answer Questions

Question 1.
Obtain an expression for the current through an inductor when an AC emf is applied.
Answer:
Let an inductor (L) of negligible resistance is connected in an AC circuit. This is treated as purely inductive circuit.

Voltage applied V = V_m sin ωt
From Kirchhoff’s loop rule
V – L \(\frac{di}{dt}\) = 0 → (1) Because induced emf
ε = – L\(\frac{di}{dt}\) is in opposite direction.
∴ \(\frac{di}{dt}=\frac{V}{L}=\frac{v_m}{L}\) sin ωt → (2)
Total current through inductor

ωL is the reactance offered by inductor for the flow of current in circuit.
Reactance of Inductor X_L = ωL, similar to Resistance.
In a pure inductor current, I lags behind applied voltage V by an angle Φ = 90° or \(\frac{\pi}{2}\) radians.

Question 2.
Obtain an expression for the current in a capacitor when an AC emf is applied.
Answer:
Let an ac voltage V = Vm sin cot is applied across the plates of a capacitor. Then charge begin to accumulate on the capacitor plates then gradually its voltage increases.

By using ac voltage the capacitor will be charged and discharged alternately due to reversal of current in each half cycle.
Potential on capacitor V = \(\frac{q}{C}\) → (1)
But V = V_m sin ωt

In a capacitor current in circuit leads the applied voltage by an angle Φ = 90° or \(\frac{\pi}{2}\) radians.

Question 3.
State the principle on which a transformer works. Describe the working of a transformer with necessary theory.
Answer:
Principle :
A transformer works on the principle of Mutual induction.

A transformer consists of two coils wound on a core made with soft iron.

The coil which is connected to mains supply is called primary coil. Let number of turns in primary are say N_p. The coil through which output is taken is called secondary coil. Let number of turns in secondary are say N_s.

Induced emf in secondary

Ratio of turns in secondary to primary \(\frac{N_s}{N_p}\) is called transformer turns ratio.

In a transformer output voltage V_s (\(\frac{N_s}{N_p}\))V_p → (4)
If V_s > V_p it is called step up transformer.
V_s < V_p it is called step down transformer.

The equation V_s = \(\frac{N_s}{N_p}\)V_p is applicable for Ideal transformers. But in real case a small amount of energy (less than 5%) is wasted due to 1) Flux leakage 2) Resistance of windings 3) Eddy currents and 4) Hysteresis,

Long Answer Questions

Question 1.
Obtain an expression for impedance and current in series LCR circuit. Deduce an expression for the resonating frequency of an LCR series resonating circuit.
Answer:
In series LCR circuit an inductance ‘L’, capacitance ‘C’ and a resistance ‘R’ are connected in series with an ac source.
Let voltage applied, V = V_m sin ωt → (1)
In series combination, total voltage in circuit is sum of voltage drops on each component

Here V_L and V_c are always in same phase but in opposite direction.

The term R² + (X_C – X_L)² is called impedance Z’. Its behaviour is like Resistance R in DC circuit.

The phasor diagram of V_R, V_c and VL are as shown.

Resonating frequency :
Resonance is a physical phenomenon at which a system tends to oscillate freely. This particular frequency is called Resonating frequency.
The reactance of Inductance X_L = ωL and
Reactance of capacitance X_c = \(\frac{1}{\omega C}\) opposite in nature.

When X_C = X_L then impedance Z = R has lowest value and current in LCR circuit is

(At resonating frequency potential across ‘L’ and potential across ‘C’ will cancell each other.

At resonance current in series LCR circuit is maximum i_m = \(\frac{V_m}{Z}=\frac{V_m}{R}\).)

Problems

Question 1.
A transformer converts 200 Vac into 2000 V ac. Calculate the number of turns in the secondaryif the primary has 10 turns.
Solution:
V₁ = 200 V, V₂ = 2000 V, n₁ = 10, n₂ = ?

∴ Number of turns on secondary n₂ = 100.

Question 2.
An ideal inductor (no internal resistance for the coil) of 20 mH is connected in series with an AC ammeter to an AC source whose emf is given by e = 20√2 sin(200t + π/3) V, where t is in seconds. Find the reading of the ammeter.
Solution:
Inductance L = 20 mH = 20 × 10^-3H
emf. e = 20√2 sin (200t + \(\frac{\pi}{3}\))V.
From standard equation e = e_m sin (ωt + Φ)
Maximum voltage em = 20√2 V
Average voltage = \(\frac{e_{\mathrm{m}}}{\sqrt{2}}=\frac{20 \sqrt{2}}{\sqrt{2}} \) = 20 V.
Impedance, Z_L = ωL. But ω = 200
∴ Z_L = 200 × 2 × 10^-3 = 4
Instantaneous current 1 = \(\frac{e}{Z}=\frac{20}{4}\) = 5A.

Question 3.
The instantaneous current and instantaneous ( voltage across a series circuit containing resistance and inductance are given by i = √2 sin (100t – π/4) A and V = 40 sin (100t) V. Calculate the resistance.
Solution:
Instantaneous current I = √2 sin(100t + \(\frac{\pi}{4}\))A
Instantaneous voltage V = 40 sin (100t) V

Question 4.
In an AC circuit, a condenser, a resistor and a pure inductor are connected in series across an alternator (AC generator). If the voltages across them are 20 V, 35 V and 20 V respectively, find the voltage supplied by the alternator.
Solution:
Voltage across Condenser V_C = 20 V
Voltage across Resistor V_R = 35 V
Voltage across Inductor V_L = 20V
In LCR circuit total potential difference =

Question 5.
An AC circuit contains a resistance R, an inductance L and a capacitance C connected in series across an alternator of constant voltage and variable frequency. At resonant frequency, it is found that the inductive reactance, the capacitive reactance and the resistance are equal and the current in the circuit is ifl. Find die current in the circuit at a frequency twice that of the resonant frequency.
Solution:
In LCR circuit at resonance Impedance Z = R
Current at resonance i₀ = \(\frac{V_0}{Z}=\frac{V_0}{R}\)
Reactance of inductor X_L = ωL and
Reactance of condenser X_C = – \(\frac{1}{\omega C}\)
When frequency is doubled (say ω₁ = 2ω)
X_L = 2 . ωL and X_C = \(\frac{1}{2\omega C}\)

Question 6.
A series resonant circuit contains L₁, R₁ and C₁. The resonant frequency is f. Another series resonant circuit contains L₂, R₂ and C₂. The resonant frequency is also f. If these two circuits are connected in series, calculate the resonant frequency.
Solution:
For first series LCR circuit
C = C₁, L = L₁ and R = R₁ and resonant
frequency f = \(\frac{1}{\sqrt{L_1 C_1}}\)

For second series LCR circuit
L = C₂, C = C₂ and R = R₂ resonant frequency f = \(\frac{1}{\sqrt{L_2 C_2}}\)

Given that f₁ = f₂ and two circuits are again in series with source.

In series combination same AC current will flow with same frequency through all the parts.

Circuits 1 and 2 are at resonance with the applied frequency f.

So when the two LCR circuits of same resonant frequency are connected in series still then there is no change in resonant frequency.

Question 7.
In a series, LCR circuit R = 200 Ω and the voltage and the frequency of the mains supply is 200 V and 50 Hz respectively. On taking out the capacitance from the circuit the current lags behind the voltage by 45°. On taking out the inductor from the circuit the current leads the voltage by 45°. Calculate the power dissipated in the LCR circuit.
Solution:
Given Resistance R = 200 Ω,
Voltage V = 200 V, Frequency u = 50 Hz.
When capacitor is removed current lags behind voltage by 45°
When Inductance is removed current leads voltage by 45°.
From above statements, the circuit is at resonance.
At resonance power dissipated P = \(\frac{V^2}{R}=\frac{200\times200}{200}\) = 200 W

Question 8.
The primary of a transformer with primary to secondary turns ratio of 1 : 2, is connected to an alternator of voltage 200 V. A current of 4 A is flowing though the primary coil: Assuming that the transformer has no losses, find the secondary voltage and current are respectively.
Solution:
Turns ratio of primary to secondary n_p : n_s = 1 : 2
Input voltage V₁ = 200 V, Input current I_i = 4A
Output voltage V₀ = V_i \(\frac{Ns}{np}\) = 200 × 2 = 400 V
In transformer V I = constant i.e., V_i.I_i = V₀I₀
∴ Output current I₀ = \(\frac{V_iI_i}{V_0}=\frac{200\times4}{400}\) = 2A

Exercises

Question 1.
A 100 Ω resistor is connected to a 220 V, 50 Hz ac supply.
a) What is therms value of current in the circuit?
b) What is the net power consumed over a full cycle?
Answer:
Resistance R = 100 Ω ; Voltage, V = 220 V; Frequency, υ = 50 Hz.
a) The rms value of current in the circuit is given as:
I = \(\frac{V}{R}=\frac{220}{100}\) = 2.20A

b)The net power consumed over a full cycle is given as:
P = VI ⇒ p = 220 × 2.2 = 484 W

Question 2.
a) The peak voltage of an ac supply is 300 V. What is the rms voltage?
b) The rms value of current in an ac circuit is 10 A. What is the peak current?
Answer:
a) Peak voltage of the ac supply, V₀ = 300 V
Rmsvoltage V = \(\frac{V_0}{\sqrt{2}}=\frac{300}{\sqrt{2}}\) = 212.1 V

b) The rms value of current I = 10 A Now, peak current
I₀ = √2I = 10√2 = 14.1 A

Question 3.
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. Determine the rms value of the current in the circuit
Answer:
Inductance of inductor, L = 44 mH = 44 × 10^-3 H ;
Supply voltage, V = 220 V
Frequency, υ = 50 Hz ;
Angular frequency, ω = 2πυ
Inductive reactance, X_L = ωL = 2πυL
= 2π × 50 × 44 × 10^-3Ω

Hence, the rms value of current in the circuit is 15.92 A.

Question 4.
A 60 µF capacitor is connected to a 110V, 60Hz ac supply. Determine the rms value of the current in the circuit.
Answer:
Capacitance of capacitor, C = 60 µF
= 60 × 10^-3 F;
Supply voltage, V = 110 V
Frequency, υ = 60 Hz;
Angular frequency, ω = 2πυ

Hence, the rms value of current is 2.49 A.

Question 5.
Obtain the resonant frequency ω_r of a series LCR circuit with L = 2.0 H, C = 32 µF, and R = 10Ω. What is the Q-value of this circuit?
Answer:
Inductance, L = 2.0 H;
Capacitance, C = 32 µF = 32 × 10^-6 F
Resistance, R = 10 W ; Resonant frequency

Hence, the Q-Value of this circuit is 25.

Question 6.
A transformer converts 200 Vac into 2000 V ac. Calculate the number of turns in the secondary coil if the primary coil has 10 turns.
Answer:
Primary voltage V_p = 200 V
Secondary voltage V_g = 2000 V
Number of turns in Primary N_p = 10
Number of turns in Secondary = N_s = ?

Question 7.
A charged 30 pF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit?
Answer:
Capacitance, C = 30µF = 30 × 10^-6 F;
Inductance, L = 27 mH = 27 × 10^-3H

Hence, the angular frequency of free oscillations of the circuit is 1.11 x 103 rad/s.

Question 8.
Suppose the initial charge on the capacitor in Exercise 7 is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
Answer:
Capacitance of the capacitor, C = 30 µF
= 30 × 10^-6F ;

Inductance of the inductor, L = 27 mH
= 27 × 10^-3 H ;

Charge on the capacitor, Q = 6 mC = 6 × 10^-3 C
Total energy stored in the capacitor E = \(\frac{1}{2}\frac{Q^2}{C}\)

Total energy at a later time will remain the same because energy is shared between the capacitor and the inductor.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 9th Lesson Electromagnetic Induction Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 9th Lesson Electromagnetic Induction

Very Short Answer Type Questions

Question 1.
What did the experiments of Faraday and Henry show?
Answer:

1. Faraday and Henry experiments showed that the relative motion between the magnet and a coil is responsible for generation of electric current in the coil.
2. The relative motion is not an absolute requirement to induce the current in a coil. If the current in a coil changes then also emf is induced in the nearby coil.

Question 2.
Define magnetic flux.
Answer:
Magnetic flux :
The number of magnetic field lines crossing unit area when placed perpendicular to the field is defined as “Magnetic flux”.
Magnetic flux, Φ = \(\overline{\mathrm{B}}.\overline{\mathrm{A}}\) = B A cos θ

Question 3.
State Faraday’s law of electromagnetic induction.
Answer:
Faraday’s law of Induction :
The rate of change of magnetic flux through a circular coil induces emf in it.

Question 4.
State Lenz’s law. [TS Mar. 19, June 15]
Answer:
Lenz’s Law :
The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produces current in that coil.

Question 5.
What happens to the mechanical energy (of motion) when a conductor is moved in a uniform magnetic field?
Answer:
When a condutor is moved in a magnetic field
Power of this motion, P = Fv F = Bil

The work done is in the form of mechanical energy.
This is dissipated into the form of joule heat.
∴ Joule heat = Power P_j = I²r = \(\frac{B^2l^2v^2}{r}\)

Question 6.
What are Eddy currents? [TS Mar. ’19; AP June ’15]
Answer:
Eddy currents :
When large pieces of conductors are subjected to changing magnetic flux then current is induced in them. These induced currents are called ”Eddy currents”.

Eddy currents will oppose the motion of the coil (or) they oppose the change in magnetic flux.

Question 7.
Define ‘inductance’.
Answer:
Inductance :
The process of producing emf in a coil due to changing current in that coil or in a coil nearby it is called “Inductance”.

Flux associated with a coil Φ_B is proportional to current i.e., Φ_B ∝ I

This constant of proportionality is called Inductance.

Question 8.
What do you understand by ‘self induetance’? [AP & TS June ’15]
Answer:
Self inductance :
If emf is induced in a single isolated coil due to change of flux in that coil by means of changing current through that coil then that phenomenon is called “Self Inductance L”.
In Self inductance, ε = -L\(\frac{dI}{dt}\)

Short Answer Questions

Question 1.
Obtain an expression for the emf induced across a conductor which is moved in a uniform magnetic field which is perpendicular to the plane of motion. [TS May ’16]
Answer:
Let a conductor of length T is moving with a velocity “v” in a uniform and time independent magnetic field B.

Consider a rectangular metallic frame PQRS in which the side PQ is free to move without friction.

Let PQ move with a velocity ‘v’ in a perpendicular magnetic field B.

Magnetic flux in the loop Φ_B = Bl . x, where x = RQ a time changing quantity.

Here \(\frac{dx}{dt}\) = -v = Velocity of the rod.
Induced emf, ε = Blv is called Motional emf.

Question 2.
Describe the ways in which Eddy currents are used to advantage. [AP Mar. ’19, ’18, ’17, ’16, ’15, May ’18, ’17, ’16; TS Mar. ’18, ’15. May ’17]
Answer:
Advantages of Eddy currents:

1. Electromagnetic breaking : In some electrically powered trains strong electromagnets are placed above rails. When these electromagnets are activated eddy currents induced in rails will oppose motion of train. These breaks are smooth.
2. In galvanometers, a fixed core is made with non-magnetic material. When coil oscillates eddy currents induced in core will oppose the motion. As a result, the coil will come to rest quickly.
3. In induction furnaces high frequency oscillating currents are passed through a coil which surrounds the metal to be melted. These currents will produce eddy currents in the metal and it is heated sufficiently to melt it.
4. In electric power meters a metal disc is made to rotate due to eddy currents with some arrangement. Rotation of this disc is made to measure power consumed.

Question 3.
Obtain an expression for the mutual inductance of two long co-axial solenoids.
Answer:
Consider two long solenoids S₁ and S₂ each of length ‘l’, radius r₁ and r₂ and number of turns n₁ and n₂ respectively. When a current I₂ is sent through S₂ it will set up a magnetic flux Φ₁ through S₁.

Flux linkage with S₁ is N₁ Φ₁ = M₁₂I₂ where
M₁₂ is mutual inductance between the coils.
But Φ₁ = N₁A₁B where N₁ = n₁l ; A = πr²₁ and B = µ₀n₂I₂.
∴ N₁Φ₁ =(n₁l)(πr²₁ )(µ₀n₂I₂) = µ₀n₁n₂r²₁ …………. (1)

This approximation is highly valid when l > > r₂.

If current I₁ is passed through S₁ then
N₂Φ₂ = M₂₁I₁ where Φ₂ = N₂A₂B and
B = µ₀n₁I₁ and N₂ = n₂l.
∴ N₂Φ₂ =(n₂l)(πr²₁ )(µ₀n₁I₁) = µ₀n₁n₂πr²₁l …………. (2)

From eq. (1) & (2) Mutual inductance bet-ween co-axial solenoids M₁₂ = M₂₁. If the solenoid is on a core of permeability µ_r then
[M₁₂ = M₂₁ = µ₀µ_rn₁n₂πr²₁l]
Mutual inductance of a pair of coils or solenoids etc., depends on seperation between them and also on their orientaton.

Question 4.
Obtain an expression for the magnetic energy stored in a solenoid in terms of the magnetic field, area and length of the solenoid.
Answer:
When current is passed through a single isolated coil or solenoid changing magnetic flux can be developed by changing current through it. This changing flux will induce emf in that coil.
This phenomenon is called self induction (L).
Flux linkage NΦ_B ∝ I or NΦ_B = L . I
Induced emf, ε = \(\frac{d}{dt}\)(NΦ_B) = -L\(\frac{dI}{dt}\) ………. (1)

– ve sign indicates that induced emf will always oppose the flux changes in that coil (or) solenoid.

Let length of solenoid is ‘l’, area of cross section = A
then NΦ_B = (nl)(µ₀nI) (I) (∵ Φ_B =nµ₀I) ……….. (2)
and total number of turns N = n × l.
i.e., turns per unit length ‘n’ × length of solenoid ‘l’.
∴ L = \(\frac{\mathrm{N} \phi_{\mathrm{B}}}{\mathrm{I}}\) = µ₀n²Al …………. (3)

This self induced emf also called back emf will oppose any change in current in the coil. So to drive current in the circuit we must do some work.
Rate of work done = \(\frac{dW}{dt}\) = |ε|I = LI.\(\frac{dI}{dt}\) …………. (4)
∴ Energy required to send the currrent or Energy stored in inductor

Long Answer Questions

Question 1.
Outline the path-breaking experiments of Faraday and Henry and highlight the contributions of these experiments to our understanding of electromagnetism.
Answer:
Faraday and Henry conducted a series of experiments to understand electromagnetic inductioin.

First Experiment:
In this experiment, a galvanometer is connected to a coil. A magnet is moved towards the coil. They observed that current is flowing in the coil when magnet is in motion.

The direction of induced current is in opposite direction when the direction of motion of magnet is changed.

So they concluded that relative motion between magnet and coil is responsible for generation of electric current in the coil.

Second Experiment:
In this experiment a steady current is passed through one coil with the help of a battery and the second coil is connected to a galvanometer. When one of the coil is moved then current is induced in the coil. This current losts as far as there is relative motion between them.

Again they concluded that relative motion between the coils is responsible for induced electric current.

Third Experiment:
In this experiment, they connected one coil to a battery and a tapping key to make and break electric contact in that coil. The second coil is placed near the first coil. When electric contact is established current is induced in the second coil and momentary deflection is observed in galvanometer.

When electric contact is breaked again they got deflection in galvanometer in opposite direction.

So they concluded that it is not the relative motion between the coil and magnet or relative motion between the coils that induces the current. The changing magnetic flux is responsible for induced emf or current in the coil.

Finally Faraday proposed that induced emf ε = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) ⇒ ε = N.\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
But from Lenz’s explanation he corrected this equation as ε = –\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) ⇒ ε = -N\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)

Question 2.
Describe the working of a AC generator with the aid of a simple diagram and necessary expressions.
Answer:
AC generator consists of a coil of N turns placed in a magnetic field B produced by magnetic poles when the coil is rotated its effective area changes so flux linked with the coil changes. This changing flux will induce emf in the coil.

Electric generator converts mechanical energy into electrical energy.

Flux associated with the coil,
Φ_B = (\(\overline{\mathrm{B}}\) • \(\overline{\mathrm{A}}\)) = BA cos θ, where θ = ωt
Induced emf, ε = -N\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = -NBA\(\frac{d}{dt}\)cos ωt
∴ Induced emf, ε = -NBAω sin ωt
The term NBAω is called maximum emf produced (ε_m).
∴ ε_m = NBAω
ε = ε_m sin ωt
Induced emf at any time E = ε_m sin ωt
When θ = 0, Induced emf is zero i.e., ε = 0.
The induced emf is maximum when θ = 90°
i.e., the plane of the coil is perpendicular
to magnetic field.
When θ = 90° ⇒ emf ε = ε_m
When θ = 180° ⇒ induced emf ε = 0.
When θ = 270° ⇒ induced emf ε = – ε_m.
again for θ = 360° ⇒ emf ε = 0.
∴ The induced emf varies sinusoidally in AC generator.

The coil is mounted on a rotor shaft. The axis of rotation of coil is perpendicular to magnetic field. The coil is connected to external circuit by means of slip rings and brushes.

Induced emf at any time is given by ε = ε_m sin ωt = ε_m sin 2πυt.

Depending on the method of supplying mechanical energy to rotate shaft these AC generators are classified as 1) Hydroelectric generators, 2) Thermal generators and 3) Nuclear generators.

Exercises

Question 1.
Obtain an expression for the emf induced across a conductor which is moved in a uniform magnetic field which is perpendicular to the plane of motion. [AP May ’14]
Answer:
Let a conductor of length ‘l’ is moving with a velocity “v” in a uniform and time independent magnetic field B.

Consider a rectangular metallic frame PQRS in which the side PQ is free to move without friction.

Let the wire PQ is moved with a velocity ‘v’ in a perpendicular magnetic field B.

Magnetic flux in the loop Φ_B = Bl . x, where x = RQ a time changing quantity.

Here \(\frac{dx}{dt}\) = -v = Velocity of the rod.
Induced emf, ε = Blv is called Motional emf.

Question 2.
Current in a circuit falls from 5.0 A to 0.0 A in 0.1 s. If an average emf of 200 V induced, give an estimate of the self inductance of the circuit. [AP Mar. 14; TS Mar. 16]
Answer:
Initial current, I₁ = 5.0 A ;
Final current, I₂ = 0.0 A ;
Change in current, dl = I₁ – I₂ = 5 A
Time taken for the change, t = 0.1 s;
Average emf, ε = 200 V
For self-inductance (L) of the coil, we have the relation for average emf as

Hence, the self induction of the coil is 4H.

Question 3.
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil? [TS May ’18, Mar. ’17]
Answer:
Mutual inductance of a pair of coils, µ = 1.5 H;
Initial current, I₁ = 0 A
Final current I₂ = 20 A ;
Change in current, dl – I₂ – I₁ = 20 – 0 = 20 A
Time taken for the change, t = 0.5 s

Where dΦ is the change in the flux linkage with the coil.
Equating equations (1) and (2), we get
\(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = µ\(\frac{dI}{dt}\) ; dΦ = 1.5 × (20) = 30 Wb
Hence, the change in the flux linkage is 30 Wb.

Question 4.
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10^-4 T and the dip angle is 30°.
Answer:
Speed of the jet plane, v = 1800 km/h = 500 m/s ;
Wing span of jet plane, l = 25 m
Earth’s magnetic field strength,
B = 5.0 × 10^-4 T ; Angle of dip, δ = 30°

Vertical component of Earth’s magnetic field,
B_v = B sin δ = 5 × 10^-4 sin 30° = 2.5 × 10^-4T

Voltage difference between the ends of the wing can be calculated as
ε = (B_v) × l × v = 2.5 × 10^-4 × 25 × 500 = 3.125 V

Hence, the voltage difference developed between the ends of the wings is 3.125 V.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 8th Lesson Magnetism and Matter Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 8th Lesson Magnetism and Matter

Very Short Answer Type Questions

Question 1.
A magnetic dipole placed in a magnetic field experiences a net force. What can you say about the nature of the magnetic field?
Answer:
For a magnetic dipole placed in a magnetic field, some net force is experienced It implies that force on the two poles of dipole is not equal.

This will happen only when magnetic dipole is in non-uniform magnetic field.

Question 2.
There is no question in text book. [TS Mar. 19, 17, May 14]
Question 3.
What happens to compass needles at the Earth’s poles? [TS Mar. 19, 17, May 14]
Answer:
When a compass is taken to earth poles say north pole then south pole of compass will adhere to north pole. It will align it self along magnetic meridian line.

Similarly when it is taken to south pole then north pole of compass is attracted by south pole and it will align itself along magnetic meridian line.

Question 4.
What do you understand by the ‘magnetisation’ of a sample?
Answer:
Magnetisation (T) :
It is the ratio of magnetic moment per unit volume.

I = (\(\frac{M}{V}\)) where M = the magnetic moments and V = volume of the given material.

Magnetic intensity is a vector, dimensions L^-1 A.
Unit : Ampere/metre : Am^-1

Question 5.
What is the magnetic moment associated with a solenoid?
Answer:
Magnetic moment associated with a solenoid (M) = nIA. Where
n = Number of turns in solenoid;
I = Current through it;
A = Area vector

Question 6.
What are the units of magnetic moment, magnetic induction and magnetic field? [AP Mar. 16. May 17, 16; TS Mar. 16]
Answer:
1. Magnetic moment m is a vector. Unit A-m², dimensions L^-2 A.
2. Magnetic induction (B) and magnetic field (B) are used with same meaning. Magnetic induction B is a vector.
Unit: Tesla (T), Dimension : MT^-2A^-1.

Question 7.
Magnetic lines form continuous closed loops. Why? [AP Mar. ’19, ’16, May ’18; TS May ’18, Mar. ’17]
Answer:
In magnetism magnetic monopole (single pole) is not existing. The simple possible way is to take a magnetic dipole. So the path a free magnetic needle or compass starts from north pole and terminates at south pole forms a loop.

Hence magnetic field lines are always closed loops.

Question 8.
Define magnetic declination. [TS Mar. 18, May 18, 17, 16; AP Mar. 18, 14, May 17, 16]
Answer:
Magnetic declination (D) :
The magnetic meridian at a place makes some angle (D) with true geographic north and south direction.

The angle between true geographic north to the north shown by magnetic compass is called “magnetic declination or simply declinations (D).”

Question 9.
Define magnetic inclination or angle of dip. [AP Mar. ’17, ’15; TS Mar. ’15]
Answer:
Magnetic inclination or angle of dip (I) :
It is the angle of total magnetic field BE at a given place with the surface of earth.
(OR)
The angle between horizontal to earth’s surface and net magnetic field of earth BE at that point.

Question 10.
Classify the following materials with regard to magnetism: Manganese, Cobalt, Nickel, Bismuth, Oxygen, Copper. [AP Mar. 19. 18. 17, 16, 15; TS Mar. 16. 15]
Answer:
Manganese : Paramagnetic substance
Cobalt : Ferromagnetic substance
Nickel : Ferromagnetic substance
Bismuth : Diamagnetic substance
Oxygen : Paramagnetic substance
Copper : Diamagnetic substance

Question 11.
In the magnetic meridian of a certain place, the horizontal component of the earth’s magnetic field is 0.26 G and the dip angle is 60°. What Is the magnetic field of the earth at this location?
Answer:
Given HE = 0.26 G; Dip angle = 60
But Dip angle = \(\frac{H_E}{B_E}\) = cos θ ⇒ B_E = H_E cos θ
∴ Magnetic field of earth = 0.26 × cos 60° = 2 × 0.26 = 0.52 G

Question 12.
Define Magnetisation of a sample. What is its SI unit?
Answer:
Magnetisation (I) : It is the ratio of net magnetic moment per unit volume.
I = \(\frac{m_{net}}{V}\) where m_net = the vectorial sum of magnetic moments of atoms in bulk material and V is volume of the given material.
Magnetic intensity is a vector, dimensions L^-1 A.
Unit: Ampere/metre : A m^-1.

Question 13.
Define Magnetic susceptibility. Mention its unit. [AP Mar. ’15]
Answer:
Magnetic susceptibility (χ) :
It is a measure for the response of magnetic materials to an external field.

It is a dimensionless quantity.

Short Answer Questions

Question 1.
What are Ferromagnetic materials? Give examples. What happens to a ferromagnetic material at Curie temperature?
Answer:
Ferromagnetism:

1. These substances are strongly attracted by magnets.
2. The susceptibility (χ) is +ve and very large.
3. Individual atoms of these substances will spontaneously align in a common direction over a small volume called domain.
4. Size of domain is nearly 1 mm³ or a domain may contain nearly 10¹¹ atoms.
5. In these substances, magnetic field lines are very crowded.
6. Every ferromagnetic substance will transform into paramagnetic substance at a temperature called Curie Temperature (T_c).
   Ex: Manganese, Iron, Cobalt, Nickel etc.

Effect of temperature on Ferromagnetic substances :
When ferromagnetic substances are heated upto Curie temperature, they will be converted into paramagnetic substances.

Question 2.
Derive an expression for the axial field of a solenoid of radius “r”, containing “n” turns per unit length and carrying current “I”.
Answer:
The behaviour of a magnetic dipole and a current carrying solenoid are similar.

Let a solenoid of radius ‘a’ and length 2l contains n turns and a current ‘I’ is passed through it.

Magnetic moment of solenoid (M) = nlA.

Consider a circular element of thickness dx of solenoid at a distance x from its centre. Choose any point ‘P’ on the axis of solenoid at a distance ‘r’ from centre of the axis.

Magnetic field at point P

This is similar to magnetic field at any point on the axial line of magnetic dipole.

Question 3.
The force between two magnet poles separated by a distance ‘d’ in air is ‘F. At what distance between them does the force become doubled?
Answer:
Force between two magnetic poles F = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m_1m_2}}{\mathrm{d^2}}\)


When separation between the poles is reduced by √2 times their force between them is doubled.

Question 4.
Compare the properties of para, dia and ferromagnetic substances. [TS & AP June ’15]
Answer:

Question 5.
Explain the elements of the Earth’s magnetic field and draw a sketch showing the relationship between the vertical component, horizontal component and angle of dip.
Answer:
Earth’s magnetism :
The magnetic field of earth is believed to arise due to electrical currents produced by convective motion of metallic fluids in outer core of earth. This effect is also known as the “dynamo effect”.

• The magnetic north pole of earth is at a latitude of 79.74° N and at a longitude of 71.8° W. It is some where in North Canada.
• The magnetic south pole of earth is at 79.74° S and 108.22° E in the Antarctica.

Magnetic declination (D) :
The angle between true geographic north to the mag-netic north shown by magnetic compass is called “magnetic declination or simply declination (D).”

Angle of dip or inclination (I):
The angle of dip is the angle of total magnetic field BE at a given place with the surface of earth.

At a given place horizontal component of earth’s magnetic field H_E = B_E cos I.

Vertical component of earth’s magnetic field Z_E = B_E sin I.

Tangent of dip tan I = \(\frac{Z_E}{H_E}\)

Question 6.
Define retentivity and coercivity. Draw the hysteresis curve for soft iron and steel. What do you infer from these curves?
Answer:
Hysteresis loop :
Magnetic hysteresis loop a graph between magnetic field (B) and magnetic intensity (H) of a ferromagnetic substance. It is as shown in figure.

i) When applied magnetic field B is gradually increased then magnetic intensity in the material will also gradually increases and reaches a saturation point a’. It indicates that all atomic magnets of the sample are parallel to applied field.

ii) When applied magnetic field is gradually decreased to zero still then some magnetic intensity will remain in the material.

Retentivity or Remanence :
The magnetic intensity (H) of a material at applied magnetic field B – 0 is called “retentivity”. In hysteresis loop value of H on +ve Y-axis i.e., at B = 0 gives retentivity.

iii) When applied magnetic field (B) is reversed then magnetic intensity of the sample gradually decreases and finally it is magnetised in opposite direction upto saturation say point’d’.

Coercivity :
The -ve value of magnetic field (B^applied (i.e., in opposite direction of mag netisation) at which the magnetic intensity (H) inside the sample is zero is called “coer-civity”.

In hysteresis diagram the-value of B on -ve X-axis gives coercivity.

iv) When direction of magnetic field is reversed and gradually increased again we can reach the point of saturation a’.

Area of hysteresis loop is large for ferromagnetic substances with high permeability value.

Question 7.
If B is the magnetic field produced at the centre of adrcular coil of one turn of length L carrying current I then what is the manetic field at the centre of the same coil which is made into 10 turns?
Answer:
One turn coil means it is a circular loop.

For 1^st Case:
Magnetic field at the centre of a loop B₁ = \(\frac{\mu_0}{2} \frac{\mathrm{I}}{\mathrm{r_1}}\)
Given that length of the wire = L.

For 2^nd Case :
Given wire is made into a coil of 10 turns ⇒ n = 10
∴ 2πr₂10 = L ⇒ r₂ = \(\frac{L}{2 \pi}.\frac{1}{10}\)
For a coil of n turns magnetic field at its centre B₂ = \(\frac{\mu_0}{2} \frac{\mathrm{nI}}{\mathrm{r_2}}\)


When same length of wire is made into a coil of n turns then B₂ at centre = n² times previous value B₁.
⇒ B₂ = n² B₁ for given current T.

Question 8.
If the number of turns of a solenoid is doubled, keeping the other factors constant, how does the magnetic held at the axis of the solenoid change?
Answer:
A solenoid will produce almost uniform magnetic field (B) along its axis.

Magnetic field along the axis of a solenoid B = µ₀nI.

Where n is number of turns per unit length.
In our case number of turns of a solenoid is doubled keeping others as constant i.e., length of solenoid L is not changed and permeability p0, and current T not changed. So new number of turns n₂ = 2n₁.
∴ New magnetic field at the same given point B₂ = µ₀n₂I.
But n₂ = 2n₁; ∴ B₂ = µ₀2n₁I = 2B₁

When number of turns of a solenoid is doubled then magnetic field at the given point on the axis of solenoid will also double.

Long Answer Questions

Question 1.
Derive an expression for the magnetic field at a point on the axis of a current carrying circular loop.
Answer:
Consider a circular loop of radius R’ carrying a steady current i. Consider any point P’ on the axis of the coil (say X – axis).

From Biot – Savart’s law magnetic field at

The magnetic field at ‘P’ makes some angle ‘θ’ with X – axis. So resolve \(\mathrm{d} \bar{B}\) into components \(\mathrm{d} \bar{B}_x\) and \(\mathrm{d} \bar{B}\)⊥. Sum of \(\mathrm{d} \bar{B}\)⊥ is zero. Because \(\mathrm{d} \bar{B}\)⊥ component by an element d/ is cancelled by another diametrically opposite component. From fig \(\mathrm{d} \bar{B}_x\) = dB. cos θ. Where

Total magnetic field due to all elements on the circular loop

Question 2.
Prove that a bar magnet and a solenoid produce similar fields. (IMP)
Answer:
Magnetic field lines suggest that the behaviour of a current-carrying solenoid and a bar magnet are similar.

When a bar magnet is cut into two parts it will behave like two weak bar magnets. Similarly when a solenoid is cut into two parts and current is circulated through them they will also act as two solenoids of weak magnetic properties. Analogy between solenoid and bar magnet.

Let a solenoid of radius ‘a’ and length 2l contains n turns and a current ‘I’ is passed through it.

Magnetic moment of solenoid M = nlA.
Consider a circular element of thickness dx of solenoid at a distance x from its centre. Choose any point ‘P’ on the axis of solenoid at a distance r from centre of the axis.

∴ Total magnetic field B is obtained by integrating dB with in the limits -1 to 1.

This value is similar to magnetic field at any point on the axial line of magnetic dipole. Thus, a bar magnet and a solenoid produce ! similar magnetic fields.

Question 3.
A small magnetic needle is set into oscillations in a magnetic field B. Obtain an expression for the time period of oscillation.
Answer:
Let a small compass of magnetic moment m and moment of inertia ‘I’ is placed in a uniform magnetic field ’B’.
Let the compass is set into oscillation in a horizontal plane.
Torque on the needle is τ = MB sin θ.
Where 0 angle between M and B.
At equilibrium the magnitude of deflecting torque and restoring torque are equal.
∴ Restoring torque τ = I\(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) = – MB sin θ.
– ve sign indicates that restoring torque is in opposite direction of deflecting torque.
θ is small; sin θ = θ.

Magnetic needle in a uniform field

From principles of angular.
Simple harmonic motion \(\frac{MB}{I}\) = ω²
⇒ ω = \(\sqrt{\frac{MB}{I}}\)

∴ Time period of oscillation of a magnetic needle placed in a magnetic field T = 2π\(\sqrt{\frac{I}{MB}}\)
and magnetic field at that point B = 4π²\(\frac{I}{MT^2}\).

Question 4.
A bar magnet, held horizontally, is set into angular oscillations in the Earth’s magnetic field. It has time periods T₁ and T₂ at two places, where the angles of dip are θ₁ and θ₂ respectively. Deduce an expression for the ratio of the resultant magnetic fields at the two places.
Answer:
Let a bar magnet is held horizontally at a given place where earth’s magnetic field is B_B. When it is set into vibration in a horizontal plane it will oscillate with a time period T = 2π\(\sqrt{\frac{I}{MH_E}}\) ……….. (1)

Where H_E is horizontal component of earth’s magnetic field.

The relation between resultant magnetic field B_E, horizontal magnetic field H_E and angle of dip or inclination ‘I’ of earth’s magnetic field is H_E = B_E cos I. — (2)
Given at place ‘1’ angle of dip = θ₁
Given at place ‘2’ angle of dip = θ₂.

Question 5.
Define magnetic susceptibility of a material. Name two elements one having positive susceptibility and other having negative susceptibility. [AP Mar. ’15]
Answer:
Susceptibility χ :
The ratio of magnetisation of a sample (I) to the magnetic intensity (H) is called “susceptibility”.
Susceptibility χ = \(\frac{I}{H}\)
It is a dimensionless quantity.
It is a measure of how a magnetic material responds to external magnetic field.

For ferromagnetic materials susceptibility is +ve and χ >> 1 and χ is nearly in the order of 1000.
Ex: Iron, Cobalt, Nickel.
For paramagnetic substances χ is positive and nearly equals to one (χ ≅ 1).
Ex : Calcium, Aluminium, Platinum.

For diamagnetic substances χ is small and negative, magnetisation M and magnetic intensity H are in opposite direction.
Ex : Bismuth, Copper, Mercury, Gold.

Question 6.
Obtain Gauss’ Law for magnetism and explain it.
Answer:
Gauss Law in magnetism: Gauss law states that the net magnetic flux through any closed loop is zero.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{ds}}=0\)
Explanation :
Consider Gaussian surface I & II as shown in figure. In both cases the number of magnetic field lines entering the surface is equal to number of magnetic field lines leaving the surface.

The net magnetic flux is zero for both surfaces. This law is true for any surface of any shape. Consider an irregular Gaussian surface as shown in figure. Consider a smdl vector area element ∆S of closed surface ‘S’ placed in a Φ magnetic field B. Flux through ∆s is say ∆Φ.

When applied magnetic field B is gradually increased then magnetic intensity in the material will also gradually increases and reaches a saturation point ‘a’. It indicates that all atomic magnets of the sample are parallel to applied field.

Now flux (i.e., Number of magnetic field lines through unit area) through the element ∆S is given by ∆Φ_B = B . ∆S.

Let us divided the total Gaussian surface ‘S’ into number of small areas ∆S₁, ∆S₂, ∆S₃, ………… ∆S_n.

The total flux through the Gaussian surface

Where all’ term includes surface area of all surface elements ∆S₁, ∆S₂, ………… ∆S_n.

Magnetic monopole is not existing so there is no source or sinks of B’ in Gaussian surface. The simplest possible source is magnetic dipole i.e., bar magnet. Magnetic field lines of a bar magnet are closed curves of loops. So all the lines entering the Gaussian surface must leave from it.

Hence net magnetic flux through a closed surface is zero.

Question 7.
What do you understand by “hysteresis”? How does this property influence the choice of materials used in different appliances where electromagnets are used?
Answer:
Hysteresis loop :
Magnetic hysteresis loop is a graph between magnetic field (B) and magnetic intensity (H) of a ferromagnetic substance. It is as shown in figure.
i) When applied magnetic field B is gradually increased then magnetic intensity in the material will also gradually increases and reaches a saturation point ‘a’. It indicates that all atomic magnets of the sample are parallel to applied field.

ii) When applied magnetic field is gradually decreased to zero still then some magnetic intensity will remain in the material.

Retentivity or Remanence :
The magnetic intensity (H) of a material at applied magnetic field B = 0 is called “retentivity”. In hysteresis loop value of H on +ve Y-axis i.e., at B = 0 gives retentivity.

iii) When applied magnetic field (B) is reversed then magnetic intensity of the sample gradually decreases and finally it is magnetised in opposite direction upto saturation say point d’.

Coercivity :
The -ve value of magnetic field (B) applied (i.e., in opposite direction of magnetisation) at which the magnetic inten-sity (H) inside the sample is zero is called “coercivity”.

In hysteresis diagram the value of B on -ve X-axis gives coercivity.

iv) When direction of magnetic field is reversed and gradually increased again we can reach the point of saturation a’. Area of hysteresis loop is large for ferromagnetic substances with high permeability value.

Application of hysteresis in electromagnets. Hysteresis curve allows us to select suitable materials for permanent magnets and for electromagnets.

For materials to use as permanent magnets they must have high retentivity and high coercivity.

For electromagnets ferromagnetic substances of high permeability and low retentivity are used because when current is switched off it must loose magnetic properties quickly.

In case of transformers and telephone diaphragms they are subjected to prolonged AC cycles. For these applications the hysteresis curve of ferromagnetic materials must be narrow.

In this way hysteresis loop helps us to select magnetic materials for various applications.

Problems

Question 1.
What is the torque acting on a plane coil of “n” turns carrying a current “i” and having an area A, when placed in a constant magnetic field B?
Solution:
Number of turns = n ; Current = i;
Area of coil = A; Magnetic field = B.
Torque on a current carrying coil in a magnetic field τ = ni (\(\overline{\mathrm{A}}\times\overline{\mathrm{B}}\)) = niAB sin θ.

Question 2.
Acoilof 20 turns has an area of 800 mm² and carries a current of 0.5 A. If it is placed in a magnetic field of intensity 0.3 T with its plane parallel to the field, what is the torque that it experiences?
Solution:
Number of turns n = 200; Current i = 0.5 A;
Area A = 800 mm² = 800 × 10^-6 m² (∵ 1 mm² = 10^-6 m²) ;
Magnetic field B = 0.3 T.
Area of coil parallel to the field ⇒ Angle between area vector \(\overline{\mathrm{A}}\) and magnetic filed \(\overline{\mathrm{B}}\) =90°. Since area vector \(\overline{\mathrm{A}}\) is perpendicular to area of the coil.
∴ τ = niBA = 200 × 0.5 × 0.3 × 800 × 10^-6
= 3 × 800 × 10^-6 = 2.4 × 10^-3 N-m.

Question 3.
In the Bohr atom model the electrons move around the nucleus in circular orbits. Obtain an expression for the magnetic moment (µ) of the electron in a Hydrogen atom in terms of its angular momentum L.
Solution:
Charge of electron = e ;
Angular momentum = L;
Mass of electron = m_e;
Magnetic moment of electron = µ = ?
When electron revolves in orbit current i = \(\frac{e}{T}\) ; Where time period T = 2π \(\frac{r}{υ}\)
∴ Current i = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}}\)
Magnetic moment of electron in orbit µ = iA

But m_e υr = L
∴ Magnetic moment of electron in orbit
µ = \(\frac{e}{2m_e}\)L

Question 4.
A solenoid of length 22.5 cm has a total of 900 turns and carries a current of 0.8 A. What is the magnetising field H near the centre and far away from the ends of the solenoid?
Solution:
Length of solenoid l = 22.5 cm = 22.5 × 10^-2m
Number of turns N = 900; Current I = 0.8 A.
a) Magnetising field near the centre H = ?
The behaviour of a solenoid is equal to that of a bar magnet.
Magnetic field due to a solenoid B = µ₀nI.
Magnetising field H = \(\frac{B}{\mu_0}\) = nI.
Where n = Nil.
∴ H = \(\frac{900}{22.5 \times 10^-2}\) × 0.8 = 3200 Am^-1.
A solenoid will give a uniform magnetic field along its axis.
Magnetising field far away from ends = 3200 Am^-1.

Question 5.
A bar magnet of length 0.1 m and with a magnetic moment of 5 Am² is placed in a uniform magnetic field of intensity 0.4 T, with its axis making an angle of 60° with the field. What is the torque on the magnet? [Mar. ’14]
Solution:
Length of bar magnet l = 0.1 m.;
Magnetic moment m = 5 Am².
Magnetic field B = 0.4 T ;
Angle with field θ = 60°.
Torque on the magnet τ = mB sin θ.
= 5 × 0.4 × sin 60°
= 5 × 0.4 × 0.8660 = 1.732 N-m.

Question 6.
If the Earth’s magnetic field at the equator is about 4 × 10^-5 T, what is its approximate magnetic dipole moment? (radius ofi Earth = 6.4 × 10⁶ m)
Solution:
Radius of earth r = 6.4 × 10⁶ m ; Magnetic field near equator B = 4 × 10^-5 T
Magnetic dipolemoment of earth = M.

Question 7.
The horizontal component of the earth’s magnetic field at a certain place is 2.6 × 10^-5 T and the angle of dip is 60°. What is the magnetic field of the earth at this location?
Solution:
Horizontal component of earth’s magnetic field HE = 2.6 × 10^-5 T

Angle of dip ‘I’ = 60°.
Earth’s magnetic field B_E = ?
Angle between B_E and H_E is called dip angle ‘I’.
H_E = B_E = cos θ ⇒ B_E = H_E/cos θ = 2.6 × 10^-5/ cos 60°
∴ B_E = 2.6 × 10^-5/ (0.5) = 5.2 × 10^-5T.

Question 8.
A solenoid, of insulated wire, is wound on a core with relative permeability 400. If the number of turns per metre is 1000 and the solenoid carries a current of 2A, calculate H, B and the magnetisation M.
Solution:
Relative permeability µ_r = 400 ;
Current I = 2A;
Number of turns / metre = n = 1000.
Magnetising force H = nl = 1000 × 2 = 2000 Am^-1.
Magnetic field along axis of solenoid B = ?
When solenoid is on a magnetic material B
= µ_r nl = 400 × 1000 × 2 = 8 × 10⁵ Am^-1

Intext Questions and Answer

Question 1.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 × 10^-2 J. What is the magnitude of magnetic moment of the magnet?
Solution:
Magnetic field strength, B = 0.25 T; Torque on the bar magnet, τ = 4.5 × 10^-2 J
Angle between the bar magnet and the external magnetic field, θ = 30°
Torque is related to magnetic moment (M) as : τ = MB sin θ

Hence, the magnetic moment of the magnet is 0.36 J T^-1.

Question 2.
A short bar magnet of magnetic moment m = 0.32 J T^-1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Solution:
Moment of the bar magnet, M = 0.32 J T^-1 ;
External magnetic field, B = 0.15 T
a) The bar magnet is aligned along the magnetic field. This system is considered as being instable equilibrium. Hence, the angle 0, between the bar magnet and the magnetic field is 0°.
Potential energy of the system
= -MB cos θ
= – 0.32 × 0.15 cos 0° = – 4.8 × 10^-2 J

b) The bar magnet is oriented 180° to the magnetic field. Hence, it is in unstable equilibrium.
Potential energy = – MB cos θ ;
where θ = 180°
= -0.32 × 0.15 cos 180° = 4.8 × 10^-2 J.

Question 3.
A closely wound solenoid of800 turns and area of cross-section 2.5 × 10^-4 m² carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
Solution:
Number of turns in the solenoid, n = 800 ;
Area of cross-section, A = 2.5 × 10^-4 m²
Current in the solenoid, I = 3.0 A
A current-carrying solenoid behaves as a bar magnet because a magnetic field develops along its axis, i.e., along its length. The magnetic moment associated with the given current-carrying solenoid is calculated as :
M = nIA = 800 × 3 × 2.5 × 10^-4 = 0.6 J T^-1.

Question 4.
If the solenoid in exercise 8.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30° with the direction of applied field?
Solution:
Magnetic field strength, B = 0.25 T ;
Magnetic moment, M = 0.6 T^-1
The angle θ, between the axis of the solenoid and the direction of the applied field is 30°.
Therefore, the torque acting on the solenoid is given as : τ = MB sin θ
τ = 0.6 × 0.25 sin 30° = 7.5 × 10^-2 J.

Question 5.
A bar magnet of magnetic moment 1.5 JT^-1 lies aligned with the direction of a uniform magnetic field of 0.22 T.
a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment : (i) normal to die field direction, (ii) opposite to the field direction?
b) What is the torque on the magnet in cases (i) and (ii)?
Solution:
a) Magnetic moment, M = 1.5 J T^-1 ;
Magnetic field strength, B = 0.22 T

i) Initial angle between the axis and the magnetic field, θ₁ = 0°.
Final angle between the axis and the magnetic field, θ₂ = 90°.
The work required to make the magnetic moment normal to the direction of magnetic field is given as :
W = -MB (cos θ₂ – cos θ₁)
∴ B = -1.5 × 0.22 (cos 90° – cos 0°)
= -0.33 (0 – 1) = 0.33 J.

ii) Initial angle between the axis and the magnetic field, θ₁ = 0°.
Final angle between the axis and the magnetic field, θ₂ = 180°.
The work required to make the magnetic moment opposite to the direction of magnetic field is given as :
W = – MB (cos θ₂ – cos θ₁)
∴ W = – 1.5 × 0.22 (cos 180° – cos 0°)
= -0.33 (-1 – 1) = 0.66 J.

b) For case CD : θ = θ₂ = 90° then
Torque, τ = MB sin θ τ = 1.5 × 0.22 sin 90°
= 0.33 J

For case (ii): θ = θ₂ = 180° then
Torque, τ = MB sin θ τ = MB sin 180° = 0 J

Question 6.
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10^-4 m², carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
a) What is the magnetic moment associated with the solenoid?
b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10^-2 T is set up at an angle of 30° with the axis of the solenoid?
Solution:
Number of turns on the solenoid, n = 2000,
Area of cross-section of the solenoid, A = 1.6 × 10^-4 m²;
Current in the solenoid, I = 4 A

a) The magnetic moment along the axis of the solenoid is calculated as :
M = nAI = 2000 × 1.6 × 10^-4 × 4 = 1.28 Am²

b) Magnetic field, B = 7.5 × 10^-2 T
Angle between the magnetic field and the axis of the solenoid, 0 = 30°
Torque, τ = MB sin θ
∴ τ = 1.28 × 7.5 × 10^-2 sin 30°
= 4.8 × 10^-2 Nm.

Since the magnetic field is uniform, the force on the solenoid is zero. The torque on the solenoid is 4.8 × 10^-2 Nm.

Question 7.
A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 8.0 × 10^-2T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s^-1. What is the moment of inertia of the coil about its axis of rotation?
Solution:
Number of turns in the circular coil, N = 16;
Radius of the coil, r = 10 cm = 0.1 m
Cross-section of the coil, A = πr² = π × (0.1)² m² ;
Current in the coil, I = 0.75 A
Magnetic field strength, B = 5.0 × 10^-2 T ;
Frequency of oscillations of the coil, v = 2.0 s^-1
∴ Magnetic moment, M = NIA = Nlπr²
= 16 × 0.75 × π × (0.1)²
∴ M = 0.377 J T^-1

Hence, the moment of inertia of the coil about its axis of rotation is 1.19 × 10^-4 kg m².

Question 8.
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 22° with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Solution:
Horizontal component of earth’s magnetic field, B_H = 0.35 G
Angle made by the needle with the horizontal plane = Angle of dip = δ = 22°
Relation between B and B_H is B_H = B cos δ

Hence, the strength of earth’s magnetic field at the given location is 0.377 G.

Question 9.
At a certain location in Africa, a compass points 12° west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points 60° above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Solution:
Angle of declination, θ = 12°;
Angle of dip, δ = 60°
Horizontal component of earth’s magnetic field, B_H = 0.16 G
Earth’s magnetic field at the given location = B
Relation between B and BH is B_H = B cos θ

Earth’s magnetic field lies in the vertical plane, 12° West of the geographic meridian, making an angle of 60° (upward) with the horizontal direction. Its magnitude is 0.32 G.

Question 10.
A short bar magnet has a magnetic moment of 0.48 J T^-1. Give the direction and mag-nitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equatorial lines (normal bisector) of the magnet.
Solution:
Magnetic moment of the bar magnet,
M = 0.48 J T^-1.
a) Distance, d = 10 cm = 0.1 m
The magnetic field at distance d, from the centre of the magnet on the axis is

The magnetic field is along the S – N direction.

b) The magnetic field at a distance of 10 cm (i.e., d = 0.1 m) on the equatorial line of the magnet is

The magnetic field is along the N – S direction.

Question 11.
A short bar magnet of magnetic moment 5.25 × 10^-2 J T^-1 is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45° with earth’s field on
a) its normal bisector and
b) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Solution:
Magnetic moment of the bar magnet,
M = 5.25 × 10^-2 J T^-1
Magnitude of earth’s magnetic field at a place, H = 0.42 G = 0.42 × 10^-4 T
a) The magnetic field at a distance R from the centre of the magnet on the normal bisector is given by the relation :
B = \(\frac{\mu_0M}{4\pi R^3}\) ; When the resultant field is inclined at 45° with earth’s field, B = H

(OR) R = 0.05 m = 5 cm

b) The magnetic field at a distance R’ from the centre of the magnet on its axis is given as:
\(\frac{\mu_02M}{4\pi R^3}\)
B = The resultant field is inclined at 45° with earth’s field. ∴ B’ = H.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism

Very Short Answer Type Questions

Question 1.
What is the importance of Oersted’s experiment? [AP May ’18; TS Mar. ’17, May ’14]
Answer:
Oersted concluded that moving charges (or) currents produces a magnetic field in the surrounding space.

Question 2.
State Ampere’s law and Biot – Savart law.
Answer:
Ampere’s circuital law :-
The total magnetic flux coming out of a current carrying conductors enclosed in a perpendicular plane is p0 times greater than the alzebraic sum of currents (I_encl) enclosed by all the conductors in that plane.
\(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{I_{encl}}\)

Biot – Savart’s Law :
The magnetic field (dB) due to a current carrying element (dl) at any point r from the conductor is given by

Question 3.
Write the expression for the magnetic induction at any point on the axis of a circular current – carrying coil. Hence, obtain an expression for the magnetic induction at the centre of the circular coil.
Answer:
(i) Magnetic induction of any point x on the axis of a coil of radius (R) is

(ii) At centre of the coil (x = 0);

Question 4.
A circular coil of radius ‘r’ having N turns carries a current “i”. What is its magnetic moment?
Answer:
Magnetic induction at the centre of the coil
B = \(\frac{\mu_0}{2} \frac{\mathrm{i}}{\mathrm{R}}\)
For n turns the total magnetic field = (n times more)
∴ B = \(\frac{\mu_0}{2} \frac{\mathrm{ni}}{\mathrm{R}}\)

Question 5.
What is the force on a conductor of length L carrying a current “i” placed in a magnetic field of induction B? When does it become maximum?
Answer:
Let a conductor of length L’ and current i through it is placed in a magnetic field B then force on it F = i (\(\overline{\mathrm{L}}\times\overline{\mathrm{B}}\)) = i LB sin θ where θ = the angle between the length of conductor (L) and magnetic field direction \(\overline{\mathrm{B}}\). Force on current carrying conductor is maximum when tlie conductor makes an angle θ = 90° with magnetic field (F_man) = iLB.

Question 6.
What is the force on a charged particle of charge “q” moving with a velocity “v” in a uniform mangnetic field of induction B? When does it become maximum?
Answer:
Let a charge q is moving with a velocity v in a magnetic field B then force on the charged particle F = q(\(\overline{\mathrm{v}}\times\overline{\mathrm{B}}\)) =q\(\overline{\mathrm{v}}\)B sin θ. Where ‘θ’ is the angle between the direction of velocity (\(\overline{\mathrm{v}}\)) and direction of magnetic field (\(\overline{\mathrm{B}}\)).

Force on charged particle is maximum when it moves perpendicular to the magnetic field.
i. e., when θ = 90° ⇒ F_max = qvB

Question 7.
Distinguish between ammeter and voltmeter. [AP Mar. 18, 17, 15; May 17, 16; TS June 15]
Answer:

Question 8.
What is the principle of a moving coil galvanometer? [TS May ’16]
Answer:
Principle of moving coil galvanometer :
When a current carrying coil placed in a radial magnetic field is free to rotate then torque acting on it is τ = NIAB.

In M. C. G deflection torque (τ = NIBA) is produced by the current in the coil. Restoring torque is produced by torsional constant (K) of the spring. At equilibrium deflection θ = (\(\frac{NAB}{k}\))I

Question 9.
What is the smallest value of current that can be measured with a moving coil galvanometer?
Answer:
The smallest value of current that can be measured with moving coil galvanometer is in the order of 10^-6 to 10^-12 amperes.

Generally galvanometers will give full scale deflections for few micro amperes (µA)

Question 10.
How do you convert a moving coil galva-nometer into an ammeter? [AP Mar. 19, May 18, June 15; TS May 18, Mar. 18]
Answer:
A M.C.G is converted into an ammeter by connecting a low resistance (shunt) in parallel to it.
Shunt S = \(\frac{R_G}{n-1}\) where R_G = Resistance of galvanometer.
n = Ratio of currents \(\frac{i}{i_g}\)

Question 11.
How do you convert a moving coil galvanometer into a voltmeter? [AP May. 18. Mar. 16, 15; TS Mar. 16. 15]
Answer:
A M.C.G can be converted into a voltmeter by connecting a high resistance in series with it.
Series resistance R_s = (V/i_g – R_G)
V = Potential to be measured; i = maximum current through M.C.G
R_g = Resistance of M.C.G

Question 12.
What is the relation between the permittivity of free space ε₀, the permeability of free space µ₀, and the speed of light in vacuum?
Answer:
Relation between permittivity of free space ε₀ and permeability of free space µ₀is

Question 13.
A current carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic field be set up in such a manner that the loop turns about the vertical axis?
Answer:
No.

Question 14.
A current carrying circular loop is placed in a uniform external magnetic field. If the loop is free to turn, what is its orientation when it is achieves stable equilibrium?
Answer:
When a current carrying loop is placed in a uniform magnetic field the most stable state of equilibrium is magnetic moment of the loop (\(\overline{\mathrm{m}}\) = iA) and magnetic field \(\overline{\mathrm{B}}\) are parallel to each other, (i.e., θ = 0 between \(\overline{\mathrm{m}}\) and \(\overline{\mathrm{B}}\))

Question 15.
A wire loop of irregular shape carrying current is placed in an external magnetic field. If the wire is flexible, what shape will the loop change to? Why?
Answer:
If a flexible wire loop carrying current is placed in an external magnetic field it will attain circular shape.

Due to flow of charges (i.e., current) in the loop a force F = Bqv is acting at every point of flexible loop. So it attains circular shape.

Short Answer Questions

Question 1.
State and explain Biot – Savart’s law. [AP Mar. 18. 17, 16, May 14; TS Mar. 17, 16]
Answer:
According to Biot – Savart’s Law,

1. The magnitude of magnetic field dB is proportional to the current [dB α I]
2. Magnetic field dB is proportional to length of current carrying element [dB α dl]
3. Since of the angle between the current carrying element and the line joining the midpoint of the element and the given point and
4. Magnetic field dB is inversely proportional to the square of the distance ‘r’ of given point from the current carrying element dB α \(\frac{1}{r^2}\).

2) θ = the angle between the current carrying element d/ and the line joining the conductor and the given point.

Question 2.
State and explain Ampere’s law. [TS Mar. ’18]
Answer:
Ampere’s law :
The magnetic field lines emerging out of a long straight current carrying conductor are in the form of anti clock wise concentric circles with the wire at their centre.

The magnetic field emerging out through a small element dl is given by \(\overline{\mathrm{B}} \cdot \mathrm{d} \bar{l}=\overline{\mathrm{B}} \cdot \mathrm{d} \bar{l} \cos \theta\)

Here B and d/ are parallel to each other, so cos θ = 1.
Total magnetic field due to the entire loop \(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{i}\)

Ampere’s circuital Law :
Total magnetic field coming out of a current carrying conductor in a perpendicular plane is times greater than the current flowing through it.

1. If there are number of conductors ‘n’ in an enclosure then i is the alzebraic sum of currents in that enclosure and total magnetic field \(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{I_{encl}}\)
2. Ampere’s circuital law is valid to a closed loop of any shape.

Question 3.
Find the magnetic induction due to a long current carrying conductor. [AP June ’15]
Answer:
Consider a long straight conductor perpendicular to plane of paper, carrying a current I. Then the magnetic field lines emerging out of the conductor are in the plane of the paper. These magnetic field lines will form concentric circles with the conductor at the centre.

Take a small element d/ on the circle which is at a distance ‘r’ from the wire \(\overline{\mathrm{B}} \cdot \mathrm{d} \bar{l}\)
= B dl cos θ where (\(\overline{\mathrm{B}}\)) and d\(\overline{\mathrm{l}}\) are in same direction. (θ = 0°)

Total magnetic field due to a straight current carrying conductor B = \(\oint \mathrm{B} . \mathrm{d} l=\mu_0 \mathrm{I}\)
From Ampere’s law total magnetic field = µ₀ I

∴ Magnetic field of any point due to a straight current carrying conductor B = \(\frac{\mu_0}{2 \pi} \frac{I}{r}\)

Question 4.
Derive an expression for the magnetic induction at the centre of a current carry-ing circular coil using Biot – Savart’s law. [TS May ’16]
Answer:
Consider a circular loop of radius ‘R’ carrying a current i. P is a point on the axis of the coil (say X – axis).
From Biot – Savart’s law magnetic field at any point can be written as

Element d/ is on Y axis and point P is in XY – plane.
∴ \(|\mathrm{d} \bar{l} \times \overline{\mathbf{r}}|\) = rdl

The magnetic field at ‘P’ makes some angle ‘θ’ with X – axis. So resolve d \(\overline{\mathrm{B}}\) into two perpendicular components say d\(\overline{\mathrm{B}}_{x}\) and d \(\overline{\mathrm{B}}\)⊥. Sum of d\(\overline{\mathrm{B}}\)⊥ is zero. Because d\(\overline{\mathrm{B}}\)⊥ component by an element d/ is cancelled by another diametrically opposite component.

Question 5.
Derive an expression for the magnetic induction (B) at a point on the axis of a current carrying circular coil using Biot – Savart’s law. [TS May ’16]
Answer:
Consider a circular loop of radius ‘R’ carrying a current i and P is a point on the axis of the coil (say X – axis).
From Biot – Savart’s law magnetic field at

The magnetic field at ‘P’ makes some angle ‘0’ with X – axis. So resolve d\(\overline{\mathrm{B}}\) into two perpendicular components say d\(\overline{\mathrm{B}}_{x}\) and d\(\overline{\mathrm{B}}\)⊥. Sum of d\(\overline{\mathrm{B}}\)⊥ is zero. Because d\(\overline{\mathrm{B}}\)⊥ component by an element dl is cancelled by another diametrically opposite component. From fig d\(\overline{\mathrm{B}}_{x}\) = dB. cos θ. Where

Question 6.
Obtain an expression for the magnetic dipole moment of a current loop.
Answer:
Let a rectangular loop of length ‘l’, breadth ‘b’ is placed in a uniform magnetic field B. Let a current I is passed through the loop. Now force on each side F₁ = F₂ = I b. B

Current passes through the loop in opposite direction, so F₁ and F₂ are opposite. So F₁ and F₂ forms a couple.

Let the coil is rotated by an angle θ then the perpendicular distance between F and B is a/2 cos θ.
∴ Total torque
τ = IbB.\(\frac{a}{2}\)sin θ + IbB.\(\frac{a}{2}\)sinθ = I(ab)B sinθ = IAB sinθ
Torque τ = moment of force couple = Force x ⊥^lr distance
Here we are defining a new term called a magnetic dipole moment of the loop \(\overline{\mathrm{m}}\) = IA.
∴ Torque τ = \(\overline{\mathrm{mB}}\)sinθ = \(\overline{\mathrm{m}}\times\overline{\mathrm{B}}\)
This is similar to torque τ = \(\overline{\mathrm{r}}\times\overline{\mathrm{F}}\)
∴ Magnetic dipole moment \(\overline{\mathrm{m}}\) = IA for a loop of one turn.
\(\overline{\mathrm{m}}\) = nIA for a coil of n turns.

Question 7.
Derive an expression for the magnetic dipole moment of a revolving electron. [AP Mar. ’16]
Answer:
Let an electron (e) be revolving around the nucleus in a circular path of radius r’. Current I = number of electrons flowing per second.

Dipolement ot electron
Let time period of revolution of electron = T
Then current I = \(\frac{e}{T}\) But T = \(\frac{2\pi r}{υ}\)
∴ I = eν/2πr
Magnetic moment is associated with a circulating current in a loop or closed path. Magnetic moment (M) = IA.
Here magnetic moment is represented by µ_r.

The direction of this magnetic moment is into the plane of the paper.

Question 8.
Explain how crossed E and B fields serve as a velocity selector.
Answer:
Let a charge ‘q’ is moving with a velocity in the presence of both electric field E and magnetic field B. Let these two fields are perpendicular to each other and also perpendicular to the velocity of the particle.
Force due to electric field F_E = qE
Force due to magnetic field F_B = qvB
Let the two fields are adjusted such that force applied by the two fields are equal and opposite. Then total force on the charged particle is zero.

Now qE = qvB (or) v = \(\frac{E}{B}\)

∴ Velocity of charged particle (v) is the ratio of strength of electric field E and magnetic field B.

So crossed electric field E and magnetic field B will serve as a velocity selector because only particles with a velocity v = \(\frac{E}{B}\) will pass undeflected through crossed electric and magnetic fields.

Question 9.
What are the basic components of a cyclotron? Mention its uses? [AP May ’16]
Answer:
Cyclotron is used to accelerate the charged particles.

The main parts of cyclotron are

1. ‘D’ shaped metal boxes called dees
2. Variable electric field
3. Variable magnetic field and
4. A Radio frequency oscillator.

1) Dees : Two ‘D’ shaped metal boxes are placed side by side with a small gap between them. An exit port is provided to one of the Dee’.

2) Electric field E is useful to accelerate the charged particles in the gap between the dees, electric field is shield by the metallic dees. Inside D’ there is no effect of electric field.

3) Magnetic field B is used to rotate the charged particle. In magnetic field B time

m = mass of charged particle ;
q = charge on particle
Time period T is independent of velocity of the particle.

4) Radio frequency oscillator is used to obtain resonance condition. When frequency of applied voltage (V_a) is equal to frequency of cyclotron υ_c then cyclotron is said to be in resonance condition. By adjusting phase difference between dees the charged particles can be accelerated upto required energy. Kinetic energy of charged particle depends on its velocity ‘v’.

Long Answer Questions

Question 1.
Deduce an expression for the force on a current carrying conductor placed in a magnetic field. Derive an expression for the force per unit length between two parallel current carrying conductors.
Answer:
Consider a rod of uniform cross section A and length ‘l’. Let the density of the mobile charge carriers per unit volume is ‘n’.

For a steady current i the total number of mobile charge carriers in it nAl.

Let average drift velocity of each charge = v_d

When this conductor is placed in a magnetic field B. Force on it F = total charge

Force between two long parallel conductors :
If two long conductors ‘a’ and ‘b’ are carrying the currents I_a and I_b. Separated by the distance ‘d’. Conductor ‘A’ produces a magnetic field B_a at all points along conductor ‘B’ due to the current flowing through it.
Magnetic field due to ‘A’ = B_a = \(\frac{\mu_0}{2\pi } \frac{\mathrm{I_a}}{\mathrm{d}}\) …………… (1)

Conductor ‘B’ carrying a current Ib is in the magnetic field produced by ‘A’. Force acting on conductor ‘B’ due to ‘A’ is F_ba = I_b L B_a = \(\frac{\mu_0}{2\pi } \frac{\mathrm{I_aI_b}}{\mathrm{d}}\).L

Where L is length of conductor ‘B’.

Now conductor ‘A’ is in the magnetic field produced by ‘B’.
Force due to ‘B’ on ‘A’ = F_ab.
From Newton’s 3^rd law F_ab = – F_ba
∴ Force between two parallel conductors F_ab = F_ba = \(\frac{\mu_0}{2\pi } \frac{\mathrm{I_aI_b}}{\mathrm{d}}\).L
∴ Force between parallel conductors per unit lenght = \(\frac{F_{ab}}{L }=\frac{\mu_0}{2\pi } \frac{\mathrm{I_aI_b}}{\mathrm{d}}\) ……….. (2)

Question 2.
Obtain an expression for the torque on a current carrying loop placed in a uniform magnetic field. Describe the construction and working of a moving coil galvanometer.
Answer:
Let a rectangular loop of length b’, breadth a’ is placed in a uniform magnetic field B. Let a current I is passed through the loop. Now force on each side F₁ = F₂ = I b. B
Current passes through the loop in opposite direction so F₁ and F₂ are opposite. So F₁ and F₂ forms a force couple.

Where A = ab = Area of coil
Let the coil is rotated by an angle 0 then the perpendicular distance between F and B is a/2 sinG.
∴ Total torque τ = IbB\(\frac{a}{2}\) sinθ + IbB.\(\frac{a}{2}\) sinθ = I(ab)B sinθ = IAB sinθ
∴ Torque on a coil placed in a magnetic field τ = IAB sinθ

Construction and working of a moving coil galvanometer :
A moving coil galvanometer consists of a rectangular coil of n’ turns. It is placed in a uniform radial magnetic field. So \(\overline{\mathrm{B}}\) is perpendicular to area vector \(\overline{\mathrm{A}}\).

Hence torque is maximum.
Torque on coil τ = NiAB
This torque tends to rotate the coil. So it is called deflecting torque. A spring attached to the coil will provide the restoring torque. At equilibrium deflection (say Φ) is given by kΦ = NIAB (or) Φ = \(\frac{(NAB)}{k}\)I
Where k is torsional constant of spring. NAB
The term \(\frac{(NAB)}{k}\)is called constant of galvanometer.

Current sensitivity of Galvanometer is defined as deflection for unit current
\(\frac{\phi}{I}=\frac{(NAB)}{k}\) = constant of galvanometer.

In this galvanometer the coil is moving so it is called moving coil galvanometer. Its sensitivity is high for few microamperes (µA) of current it gives full deflection.

Question 3.
How can a galvanometer be converted to an ammeter? Why is the parallel resistance smaller that the galvanometer resistance? [Mar. ’14]
Answer:
A galvanometer can be converted into an ammeter by connecting a low resistance called shunt resistance in parallel to the galvanometer.

Every galvanometer has two important properties.

1. Resistance of galvanometer R_G,
2. Maximum current tolerable by it say I_G.

Ammeter :
The block diagram of ammeter is as shown. Let I is the current to be measured. When ammeter is connected in a circuit current I_G will flow through galvanometer and current I_s will flow through shunt.

Let ‘r’ is the total resistance of ammeter, G is resistance of galvanometer and R_s is shunt connected in parallel combination of

ammeter is equals to resistance of shunt.

Necessity of small shunt resistance :
Ammeter is used to measure current in a circuit. In a circuit current is constant for series combination only. So ammeter must be connected in series in a circuit. To measure the value of current exactly our ammeter must have zero resistance because in series combination (R = R₁ + R₂ + ………… etc) if resistance of shunt Rs is small effective resistance of ammeter is nearly equals to resistance of shunt and error in the value of current measured is also less.

Question 4.
How can a galvanometer be converted to a voltmeter? Why is the series resistance greater than the galvanometer resistance?
Answer:
A galvanometer can be converted into voltmeter by connecting a high resistance in series with galvanometer.

Conversion of galvanometer into voltmeter :
Every galvanometer has two important properties

1. Resistance of galvanometer R_G
2. Maximum current tolerable by it say I_G.

The block diagram of a voltmeter is as shown in figure.

Let voltage to be measured is ‘V’.
Total resistance of voltmeter R = \(\frac{V}{I_G}\)

But from block diagram R = R_G + R_s because they are in series. If R_s > > R_G then resistance of voltmeter R ≅ R_s

Necessity of high series resistance :
A voltmeter is used to measure potential difference between two given points. So it must always be connected parallelly in a circuit. In parallel combination, high current will flow through low resistance. To measure potential difference exactly the voltmeter should not draw any current from circuit. Theoritically resistance of ideal voltmeter is infinity. Practically it is kept as high as possible when series resistance of volt-meter is high it draws very little current from the circuit and measurement of voltage with it is more accurate.

Question 5.
Derive an expression for the force acting between two very long parallel current-carrying conductors and hence define the ampere.
Answer:
Let two long conductors say ‘a’ and ‘b’ are carrying the currents I_a and I_b. Separation between them is say ‘d’. Conductor ‘a’ produces a magnetic field B_a at all points a long conductor b’ due to the current flowing through it.

Magnetic field due to ‘a” = B_a = \(\frac{\mu_0}{2 \pi} \frac{I_a}{d}\) ……(1)
Conductor ‘b’ carrying a current I_b is in the magnetic field produced by ‘a’. Force acting on conductor ‘b‘ due to ‘a’ is F_ba = I_bLB_a = \(\frac{\mu_0}{2 \pi} \frac{I_aI_b}{a}\).L

Where L is length of conductor ‘b’.
Now conductor ‘a’ is in the magnetic field produced by ‘b’. Force due to ‘b’ on ‘a’ is F_ab From Newton’s 3^rd law F_ab = – F_ba
∴ Force between two parallel conductors

Force between parallel conductors per unit

If the currents in the two wires are parallel then force between them is attractive force because at the point of intersection of the two fields their directions are opposite so polarity is opposite.

Hence if currents are in same direction the conductors will attract. If currents are in opposite direction then the conductors will repel.

Definition of ampere :
From the force between two parallel conductors ampere is defined as follows.

Ampere is that value of steady current which when maintained through each conductor separated by a distance of 1 metre a part in vacuum produces a force of 2 × 10^-7 newton per metre between them.

Problems

Question 1.
A current of 10A passes through two very long wires held parallel to each other and separated by a distance of lm. What is the force per unit length between them? [TS Mar. 19. 15; AF Mar. 15]
Solution:
Current i₁ = i₂ = 10A
Separation d = lm
Force per unit length L = lm
Force between two parallel conductors

Question 2.
A moving coil galvanometer can measure a current of 10^-6A. What is the resistance of the shunt required if it is to measure 1A?
Solution:
Old range i.e., maximum current to be measured i₁ = 10^-6 A
New range i.e., maximum current to be measured i₂ = 1A
Ratio of ranges or currents to be measured,

Where G is resistance of galvanometer.

Question 3.
A circular wire loop of radius 30cm carries a current of 3.5 A. Find the magnetic field at a point on its axis 40 cm away from the centre.
Solution:
Radius of loop r = 30cm = 0.3m = 3 × 10^-1m.
Current i = 3.5A ; Distance of point on the axis r = 40cm = 0.4m = 4 × 10^-1m.
Magnetic induction field on the axis of a

Intext Question and Answer

Question 1.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil? [TS May ’18]
Answer:
Number of turns on the circular coil,
n = 100 ; Radius of each turn,
r = 8.0 cm = 0.08 m ; Current I = 0.4 A
Magnitude of the magnetic field at the centre of the coil is given by the relation,

∴ Magnitude of the magnetic field
B = 3.14 × 10^-4T.

Question 2.
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire? [TS June ’15]
Answer:
Current in the wire, 1 = 35 A ; Distance of a point from the wire, r = 20 cm = 0.2 m ; Magnitude of the magnetic field at this point is given as:

∴ Magnitude of the magnetic field at 20 cm from the wire B = 3.5 × 10^-5T.

Question 3.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of Bat a point 2.5m east of the wire.
Answer:
Current in the wire, I = 50A ; ∴ Distance of the point from the wire, r = 2.5 m.
Given point is 2.5 m away from the east of the wire.


∴ Direction of magnetic field B is vertically upwards.
Note : The point is located normal to the . wire length at a distance of 2.5 m. The direction of the current in the wire is vertically downward. Hence, according to the Maxwell’s right hand thumb rule, the direction of the magnetic field at the given point is vertically upward.

Question 4.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
Answer:
Current I = 90 A; Distance of point r = 1 .5 m

Note : The current is flowing from East to West. The point is below the power line. Hence, according to Maxwell’s right hand thumb rule, the direction of the magnetic field is towards the South.

Question 5.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of 30° with the direction of a uniform magnetic field of 0.15 T?
Answer:
Current in the wire, I = 8 A ; uniform magnetic field, B = 0.15 T
Angle between the wire and magnetic field, θ = 30°;
Magnetic force per unit length f = BI sinθ
∴ f = 0.15 × 8 × 1 × sin30° = 0.6 N m^-1

Question 6.
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Answer:
Length of the wire, l = 3 cm = 0.03 m;
Current flowing in the wire, I = 10 A
Magnetic field, B = 0.27 T ; Angle between the current and magnetic field, θ = 90°
From F = BIl sinθ; F = 0.27 × 10 × 0.03 sin90°
= 8.1 × 10^-2 N
∴ Magnetic force on the wire is 8.1 × 10^-2 N.

Question 7.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Answer:
Current flowing in wire A, I_A = 8.0 A ;
Current flowing in wire B, l_B = 5.0 A
Distance between the two wires, r = 4.0 cm = 0.04 m;
Length of wire A, l = 10 cm = 0.1 m

The magnitude of force is 2 × 10^-5 N. This is an attractive force normal to A towards B because the direction of the currents in the wires is the same.

Question 8.
A closely wound solenoid 80 cm long has 5 layers of windings of400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Answer:
Length of the solenbid, l = 80 cm = 0.8 m
There are five layers of windings of 400 turns each on the solenoid.
∴ Total number of turns on the solenoid, N = 5 × 400 = 2000
Diameter of the solenoid, D = 1.8 cm = 0.018 m ; Current in the solenoid, I = 8.0 A
Magnetic field inside the solenoid near its

∴ Magnetic field inside the solenoid near its centre is 2.512 × 10^-2 T.

Question 9.
A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?
Answer:
Length of a side of the square coil, 1 = 10 cm = 0.1 m; Current in the coil, l = 12 A

Number of turns n = 20 ; Angle between plane of the coil and magnetic field, θ = 30°
Strength of magnetic field, B = 0.80 T ; But τ = n BI A sin θ
Where, A = Area of the square coil = l × l = 0.1 × 0.1 = 0.01 m²
∴ τ = 20 × 0.8 × 12 × 0.01 × sin 30° = 0.96 N m

Question 10.
Two moving coil meters, Mj and M2 have the following particulars:
R₁ = 10 Ω, N₁ = 30, A₁ = 3.6 × 10^-3 m², B₁ = 0.25 T
R₂ = 14 n, N₂ = 42, A₂ = 1.8 × 10^-3 m² , B₂ = 0.50 T
(The spring constants are identical for the two meters).
Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M₂ and M₁.
Answer:
a) Current sensitivity of M.C.G is given as:
I = NBA/k

Hence, the ratio of current sensitivity of M₂ to M₁ is 1.4.

b) Voltage sensitivity for M.C.G is given as:
Vs₂ = \(\frac{N_2B_2A_2}{k_2R_2}\)

Hence, the ratio of voltage sensitivity of M₂ to M₁ is 1.

Question 11.
In a chamber, a uniform magnetic field of 6.5 G (1 G = 10^-4 T) is maintained. An electron is shot into the field with a speed of 4.8 × 10⁶ m s^-1 normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.
(e = 1.6 × 10^-19 C,m_e = 9.1 × 10^-31 kg)
Answer:
Magnetic field strength, B = 6.5 G = 6.5 × 10^-4 ;
Speed of the electron, v = 4.8 × 10⁶ m/s
Charge on the electron, e = 1.6 × 10^-19 C ;
Mass of the electron, mg = 9.1 × 10^-31 kg
Angle between the shot electron and magnetic field, θ = 90°;
Force on electron, F = evB sin θ
This force will make the electron in circular path.
∴ Centripetal force exerted on the electron, F_c = \(\frac{mυ^2}{r}\) at equilibrium F_c = F

Hence, the radius of the circular orbit of the electron is 4.2 cm.

Question 12.
In exercise 11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain.
Answer:
Magnetic field strength, B = 6.5 × 10^-4 T ;
Charge of the electron, e = 1.6 × 10^-19 C
Mass of the electron, m_e = 9.1 × 10^-31 kg ;
Velocity of the electron, v = 4.8 × 10⁶ m/s
Radius of the orbit, r = 4.2 cm = 0.042 m ;
Frequency of revolution of the electron = υ
Angular frequency of the electron = co = 2πν
But v = rω

Hence, the frequency of the electron is around 18 MHz and is independent of the speed of the electron.

Question 13.
(a) A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is sus-pended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of die counter torque that must be applied to prevent the coil from turning.
(b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)
Answer:
(a) Number of turns, n = 30 ; Radius of the coil, r = 8.0 cm = 0.08 m
Area, A = πr² = π(0.08)² = 0.0201 m² ;
Current, I = 6.0 A
Magnetic field B = 1 T
Angle between the field lines and normal with the coil, θ = 60°
∴ Torque τ = n IBA sinθ …
∴ τ = 30 × 6 × 1 × 0.0201 × sin 60° = 3.133 N m

(b) Magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. So if the circular coil is replaced by a planar coil of some irregular shape of same area still then torque does not change.

Question 14.
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid.
Answer:
Inner radius of the toroid, r₁ = 25 cm = 0.25 m ;
Outer radius of the toroid, r² = 26 cm = 0.26 m
Number of turns , N = 3500 ; Current in the coil, I = 11 A
(a) Magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.
(b) Magnetic field inside the core of a toroid

(c) Magnetic field in the empty space surrounded by the toroid is zero.

Question 15.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Answer:
Current in both wires, I = 300 A ;
Distance between the wires, r = 1.5 cm = 0.015 m
Length of the two wires, / = 70 cm = 0.7 m

Since the direction of the current in the wires is opposite, a repulsive force exists between them.

Question 16.
A galvanometer coil has a resistance of 12 Ω and the metre shows full scale deflection for a current of 3 mA. How will you convert the metre into a voltmeter of range 0 to 18 V?
Answer:
Resistance of the galvanometer coil, G = 12 Ω
Current for which there is full scale deflection, I_g = 3 mA = 3 × 10^-3 A
Range of the voltmeter is 0, which needs to be converted to 18 V. ∴ V = 18 V
Let a resistor of resistance R be connected in series with the galvanometer to convert it into a voltmeter. This resistance is given as:

Hence, a resistor of resistance 5988Ω is to be connected in series with the galvanometer.

Question 17.
A galvanometer coil has a resistance of 15Ω and the metre shows full scale deflection for a current of 4 mA. How will you convert the metre into an ammeter of range 0 to 6 A?
Answer:
Resistance of the galvanometer coil, G = 15 Ω Current for which the galvanometer shows full scale deflection,
I_g = 4 mA = 4 × 10^-3 A
Range of the ammeter is 0, which needs to be converted to 6 A.; ∴ Current, I = 6 A

A shunt resistor of resistance S is to be connected in parallel with the galvanometer to convert it into an ammeter.

But shunt resistance is given by,

Hance, 10 mΩ shunt resistor is to be connected in parallel with the galvanometer.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 6th Lesson Current Electricity Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 6th Lesson Current Electricity

Very Short Answer Type Questions

Question 1.
Define mean free path of electron in a conductor.
Answer:
Mean free path :
It is defined as the average distance that an electron can travel between two successive collisions.

Question 2.
State Ohm’s law and write its mathematical form.
Answer:
Ohm’s law :
At constant temperature current (I) flowing through a conductor is proportional to the potential difference between the ends of that conductor.
V ∝ I ⇒ V = RI where R = constant called resistance. Unit: Ohm (Ω).

Question 3.
Define resistivity (or) specific resistance.
Answer:
Resistivity :
Resistivity of a substance ρ = \(\frac{RA}{l}\)

It is defined as the resistance of a unit cube between its opposite parallel surfaces.

It depends on the nature of substance but not on its dimensions.
Unit: Ohm – metre (Ωm).

Question 4.
Define temperature coefficient of resistance.
Answer:
Temperature coefficient of resistivity :
The resistivity of a substance changes with temperature. ρ_τ = ρ₀ [1 + ∝ (T – T₀)]. Where a is temperature coefficient of resistivity.

Question 5.
Under what conditions is the current through the mixed grouping of cells maximum?
(Note: Mixed grouping of cells not given in New Syllabus.)
Answer:
Let m cells are in series and there are n such rows this arrangement is called mixed grouping.
In mixed grouping current (i) = \(\frac{mnE}{mr + nR}\)
Current will be maximum when mr = nR
∴ i_max = \(\frac{nE}{2r}\)

Question 6.
If a wire is stretched to double its original length without loss of mass, how will the resistivity of the wire be influenced?
Answer:
Resistivity (ρ) is independent of dimensions of the material. It depends only on nature of material.
So even though the wire is stretched its resistivity does not change.

Question 7.
Why is manganin used for making standard resistors?
Answer:
Temperature coefficient of resistance of manganin is very less. So its resistance is almost constant over a wide range of temperature.

Due to this reason manganin is used to prepare standard resistances.

Question 8.
The sequence of bands marked on a carbon resistor are : Red, Red, Red, Silver. What is its resistance and tolerance?
Answer:
Given sequence of colour band Red Red Red Silver
Colour code for Red = 2
1st band red = 2 ; ‘
2nd band Red = 2
3rd band = No. of zeros = 2 (∵ Red) :
∴ Resistance R = 2200 Ω
tolerance band (4th band) Silver = 10%
∴ For silver resistor R = 2200 Ω with 10% tolerance.

Question 9.
Write the colour code of a carbon resistor of resistance 23 kilo ohms.
Answer:
Reistance 23 kilo ohms = 23000
∴ 1st band = 2 ⇒ Red ;
2nd band = 3 ⇒ orange
3rd band = No. of zeroes = 3 ⇒ orange
∴ Colour code for 23 kΩ = Red Orange, Orange.

Question 10.
If the voltage V applied across a conductor is increased to 2V, how will the drift velocity of the electrons change?
Answer:
Drift velocity will also double.
Drift velocity vd = \(\frac{-p}{m}\)Eτ
Where E = intensity of electric field. It depends on applied potential. When applied potential is doubled (V to 2V). Intensity of electric field E is also doubled.

(∵ E = \(\frac{V}{d}\) , where d is not charged). So drift d velocity is doubled.

Question 11.
Two wires of equal length, of copper and manganin, have the same resistance. Which wire is thicker?
Answer:
Manganin wire is thicker.
Resistance R = ρ\(\frac{l}{A}\) given l is same.
For copper specific resistance ρ is less than manganin.
∵ R is constant material with high ‘ρ’ must have larger area A.
Hence manganin wire is thicker.

Question 12.
What is the magnetic moment associated with a solenoid of ‘N’ turns having radius of cross-section ‘r’ carrying a current I?
Answer:
Magnetic moment of solenoid (N) = πr² In × 2l where ‘2l’ = length of solenoid, r = radius, I = current
n = number of turns.

Question 13.
Why are household appliances connected in parallel?
Answer:
In parallel combination potential drop is constant. Different amounts of current is allowed through each component separately. i.e., we may switch off unwanted connections without disturbing other.

Hence parallel connection of appliances is prefered in household connections.

Question 14.
The electron drift speed in metals is small (~ m^-1) and the charge of the electron is also very small (~ 10^-19) Q, but we can still obtain a large amount of current in a metal. Why?
Answer:
Eventhough charge of electron ‘e’, drift velocity v_d are less number of electrons n is very high, current i = ne v_d. (i.e., charges flowing per second)
∵ n is extremely high we are getting large current.

Short Answer Questions

Question 1.
A battery of emf 10 V and internal resistance 3Ω is connected to a resistor R.
(i) If the current in the circuit is 0.5 A. Calculate the value of R.
(ii) What is the terminal voltage of the battery when the circuit is closed? [TS Mar. ’15]
Answer:
emf E = 10V, Internal resistance r = 3Ω

ii) Terminal voltage V = E – ir
∴ V = 10 – 0.5 × 3 = 10 – 1.5 = 8.5V

Question 2.
Draw a circuit diagram showing how a, potentiometer may be used to find internal resistance of a cell and establish a formula for it.
Answer:
Circuit diagram to find internal resistance; of a cell is

Theory :
i) In circuit key ‘k₂’ is open and potentiometer jockey is adjusted to zero deflection.
Balancing length l₁ is measured.
Now ε = Φl₁ → (1)

ii) Key ‘k₂‘ is closed. Balancing length l₁ is measured.
Now V = Φl₁ → (2)
But ε = I (R + r) and V = IR so from eq (1) & (2)

Question 3.
Derive an expression for the effective resistance when three resistors are connected i) series ii) parallel.
Answer:
i) Series combination :
Let three resistors R₁, R2 and R₃ be connected in series as shown in figure.

Same current i flows through all resistors.
Potential drop across R₁ ⇒ (V₁) = iR₁
Similarly V₂ = iR₂ and V₃ = iR₃ are P.D across R₂ + R₃
Total potential across AB (V) = V₁ + V₂ + V₃
∴ V = iR₁ + iR₂ + iR₃ = i (R₁ + R₂ + R₃), But V = i R
∴ V = i R_eq = i(R₁ + R₂ + R₃)
In series combination R_eq = R₁ + R₂ + R₃
∴ Equivalent resistance is the sum of individual resistors.

ii) Parallel combination of resistors :
Let three resistors R₁, R₂ and R₃ be connected in parallel as shown in figure.

In this combination potential drop across AB is constant. But different values of current flows though each resistor. Total current i = i₁ + i₂+ i₃

Current through R₁ ⇒ (i₁) = \(\frac{V}{R_1}\) Similarly,
⇒ i₂ = \(\frac{V}{R_2}\) and i₃ = \(\frac{V}{R_3}\).

Question 4.
‘m’ cells each of emf E and internal resistance ‘r’ are connected in parallel. What is the total emf and internal resistance? Under what conditions is the current drawn from the mixed grouping of cells a maximum?
Answer:
i) Let m’ identical cells each of emf E’ and internal resistance V be connected in parallel as shown in the figure.
ii) Applying Kirchoffs voltage law to the circuit, we have for the first cell,

iii) Adding the above m’ equations, we get, – m(iR) – m(\(\frac{i}{m}\))r + mE = 0
(mR + r)i = mE
∴ I = \(\frac{mE}{mR+r}\)

iv) The above expression can be written as

Mixed grouping of cells :
Note : Mixed grouping of cells not given in New Syllabus.
Answer:
Let m cells are in series and there are n such rows this arrangement is called mixed grouping.
In mixed grouping current i = \(\frac{mnE}{mr+nR}\)
Current will be maximum when mr = nR
∴ i_max = \(\frac{nE}{2r}\)

Question 5.
Define electric resistance and write it’s SI unit. How does the resistance of a conductor vary if
a) Conductor is stretched to 4 times of it’s length.
b) Temperature of conductor is increased?
Answer:
Resistance :
The obstruction created by a conductor for the mobility of charges through it is known as resistance.
i) The resistance of a conductor (R) is proportional to length R ∝ l → (1)
ii) and inversely proportional to area of cross-section of the conductor.

where “ρ” = resistivity of the conductor.

a) When conductor is stretched by four times its new length l₂ = 4l₁ or \(\frac{l_1}{l_2}\) = 4
When a wire is stretched by keeping its mass
constant then Rg = R₁[latex]\frac{l_2}{l_1}[/latex]²
∴ R₂ = R₁ . (4)² = 16R₁
So when a wire is stretched by 4 time its resistance is increased by 16 times.

b) When temperature of conductor is increased its resistance will increase.
Resistance at t°C is R_t = R₀ (1 + αt)
where α’ = temperature coefficient of resistance of that conductor.

Question 6.
When the resistance connected in series with a cell is havled, the current is equal to or slightly less or slightly greater than double. Why?
Answer:
Let a cell of emf ‘E’ and internal resistance ‘r’ is connected with external resistance R as shown in figure.

Total resistance in circuit R_T = R + r → (1)
Current in circuit i₁ = \(\frac{E}{R+r}\) → (2)

a) Now external resistance R is reduced to \(\frac{R}{2}\).
Total resistance in circuit R_T1 = \(\frac{R}{2}\) + r
\(\frac{R+2r}{2}\) → (2)
From eq (1) and (3)
\(\frac{R+2r}{2}\) is not equals to \(\frac{R+r}{2}\).
i.e., when R is reduced to \(\frac{R}{2}\) total resistance R_T1 is not equals to \(\frac{R_T}{2}\).
So current in the circuit i₂ ≠ 2i₁. But i₂ is slightly less than 2i₁ it depends on the value of internal resistance ‘r’.

b) In case of ideal battery where r = 0 then R_T2 = \(\frac{R}{2}\) in this case R_T2 = \(\frac{R_{T_1}}{2}\)and
current i₂ = 2i₁.

So when reistance R in the circuit is reduced to half of its value current in circuit is doubled or slightly less than double.

Question 7.
Two cells of emfs 4.5V and 6.0V and internal resistance 6Ω and 3Ω respectively have their negative terminals joined by a wire of 18Ω and positive terminals by a wire of 12Ω resistance. A third resistance wire of 24Ω connects middle points of these wires. Using Kirchhoff s laws, find the potential difference at the ends of this third wire.
Answer:
The circuit diagram as per given data is as shown

From fig for loop ABCDFGJA
6i₁ + 24 (i₁ + i₂) + 9i₁ – 6i₁ = 4.5
33i₁ + 24i₂ = 4.5 → (1)

For loop IBCDFGHI
6i₂ + 24(i₁ + i₂) + 9i₂ – 3i₂ = 4.5
24i₁ + 36i₂ = 6.0 → (2)

Question 8.
Three resistors each of resistance 10 ohm are connected, in turn, to obtain (i) minimum resistance (ii) maximum resistance. Compute (a) The effective resistance in each case (b) The ratio of minimum to maximum resistance so obtained.
Answer:
Resistance of each resistor R = 10Ω ;
Number of Resistors n = 3
a) In parallel combination resistance is minimum.

b) In series combination resultant resistance is maximum.

Question 9.
State Kirchhoff s law for an electrical network. Using these laws deduce the condition for balance in a Wheatstone bridge. [AP Mar. ’19. ’18. ’14. May ’16. ’14; TS May ’18. Mar. ’18, ’16, June ’15]
Answer:
Kirchhoffs Laws:
i) Junction rule :
At any junction, the sum of currents towards the junction is equal ‘ to sum of currents away from the junction.
(OR)
Alzebraic sum of currents around a junction is zero.

ii) Loop rule :
Alzebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.

Applying Kirchoff’s Law to Wheatstones bridge:
Wheatstones bridge consists of four resistances P, Q, R, S connected as shown in the figure and are referred as arms of the bridge.

A battery of emf ‘E’ is connected between two junctions A and B and a galvanometer of resistance ‘G’ is connected between ‘C’ and ‘D’.

Applying Kirchoff’s first law,
at the junction C; i₁ = i_g + i₃ — (1)
at the junction D; i₂ + i_g = i₄ — (2)
Applying Kirchoff’s second law for the loop ACDA
– i₁ P – i_g G + i₂ R = 0 — (3)
For the loop CBDC,
– i₃ Q + i₄ S + i_g G = 0 — (4)

If no current passes through the galvanometer then the bridge is said to be balanced.
So, i_g = 0, then (1), (2), (3) and (4) becomes
i₁ = i₃, i₂ = i₄, i₁P = i₂R and i₃ Q = i₄ S.
By adjusting the above equations we get \(\frac{P}{Q}=\frac{R}{S}\).
This is the balancing conditions of a Wheatstones bridge.

Question 10.
State the working principle of potentiometer explain with the help of circuit diagram how the emf of two primary cells are compared by using the potentiometer. [AP Mar. 17,16, May ‘ 17; June ’15; TS Mar. 19, May 16]
Answer:
Potentiometer working principle :
Potentiometer consists of 10 meters length of wire with uniform internal resistance. Let total length of wire is L and its total resistance is R_p.

where Φ = Potential drop per unit length i.e., potential gradient.

Comparison of e.m.f. of two cells :
The circuit diagram used to compare emf of two cells is as shown in figure.
Circuit connection were given as per diagram.

The potentiometer contains two circuits, primary and secondary.

The primary circuit consists of a cell of emf ‘E’ that a plug key (K) and a rheostat (Rh). These are connected in series with potentiometer wire AB.

The secondary circuit consists of two cells of emf e₁ and e₂, two plug keys K₁ and K₂, a galvanometer (G) and a Jockey (J) as shown in the figure.

The positive terminals of the two cells in primary and secondary are connected to terminal A’.

Procedure:
i) The plug keys K and K₁ are closed and by adjusting Jockey on the wire, the balancing length ‘l₁‘ is determined.
e₁ ∝ l₁ ——- (1)

ii) Now plug key K₁ is opened and K₂ is closed. Again the Jockey is adjusted and balancing length ‘l₂‘ is determined.
e₂ ∝ l₂ ——- (2)
from (1) and (2 ) \(\frac{e_1}{e_2}=\frac{l_1}{l_2}\) Ratio of emf of two cells.

Question 11.
State the working principle of potentiometer explain with the help of circuit diagram how the potentiometer is used to determine the internal resistance of the given primary cell. I [AP May 18, Mar. 15; TS Mar. 17. 15, May 17]
Answer:
Potentiometer working principle :
Potentiometer consists of 10 meters length of wire with uniform internal resistance. Let total length of wire is L and its total resistance is R_p.

Current through potentiometer wire i

where Φ = Potential drop per unit length i.e., potential gradient.

Determination of internal resistance (r) :
Circuit diagram used to find internal resistance of battery is as shown in figure.

Battery E is connected in primary circuit through plus key k₁.

Another battery E₁ is connected in secondary circuit. A low resistance R’ is connected in parallel to Battery E₁ along with key k₂.

Plug k₂ is open. Jockey J is moved on potentiometer until zero deflection is obtained. Balancing length l₁ is measured.

Plug key k₂ is closed so resistance R will come into operatioin. Again Jockey J is moved on potentiometer wire to find balancing point. When zero deflection is obtained balancing length l₂ is measured.

Question 12.
Show the variation of current versus voltage graph for GaAs and mark the (i) Nonlinear region (ii) Negative resistance region.
Answer:
The voltage-current characteristic graph of galium arsinide (GaAs) is as shown in figure.

GaAs is a semiconducting substance. Its V-I characteristics are non-ohmic. So V-I graph is not linear.
The region OA is linear. In which Ohm’s Law is obeyed.
The region AB is a curve (i). Here voltage V is not linear with currrent (i). So It is a non-linear region.

(ii) In the region BC current I decreases even though voltage ‘V’ increases.
Resistance R = \(\frac{V}{I}\)
∵ I decreases resistance in the region BC is negative.
The regions (1) and (2) are shown in figure.

Question 13.
A student has two wires of iron and copper of equal length and diameter. He first joins two wires in series and passes an electric current through the combination which increases gradually. After that, he joins two wires in parallel and repeats the process of passing current. Which wire will glow first in each case?
Answer:
Iron and copper wires of equal length and diameter are taken. For Iron, resistivity is ρ_i high. For copper resistivity, ρ_c is less.
∴ Resistance of Iron wire R_i is high and Resistance of copper wire R_c is less.

a) When connected in series same current flows through Iron and Copper wires. Heat produced Q = I²R. So heat produced in copper wire is less and that of Iron wire is high.

In series combination when current increases gradually than Iron wire will glow first.

b) When the two wires are connected in parallel and current is increased gradually.

In parallel combination high current flows through low resistance and low current through high resistance. They follow the relation I_c/I_i = R_i/R_c.

So current through copper wire is high. Heat produced Q = i²R ⇒ Q_c > Q_t
Heat produced in copper wire is more than that in iron wire.
So in parallel combination copper wire will glow first.

Question 14.
Three identical resistors are connected in parallel and total resistance of the circuit is R/3. Find the value of each resistance.
Answer:
In parallel combination when ‘n’ identical wires are connected parallelly equivalent resistance is given by R_eq = R/n.

Given three identical wires ⇒ n = 3.
∴ R_eq = R/3 where R is resistance of each wire.
∴ Resistance of each wire used in parallel combination is R.

Hence resistance of each wire used in parallel combination is R.

Long Answer Questions

Question 1.
Under what condition is the heat produced in an electric circuit (a) directly pro-portional (b) inversely proportional to the resistance of the circuit? Compute the ratio of the total quantity of heat produced in the two cases.
Answer:
Let a current I is flowing through a conductor between its ends say A and B. Let potential at A is V(A) and potential at B is V(B).

Potential difference across AB is say V = V(A) – V(B)

Let charge flowing in time ∆t is ∆Q = I∆T
Change in potential energy ∆V = Final P.E – Initial P.E
= ∆Q[V(B) – V(A)] = -∆QV = -TV∆t < 0 → (1)
Let charges are moving without collision with atoms.
Then kinetic energy of charges will also increase.
∆K = -∆U_Pot or ∆K = IV ∆t > 0 → (2)
Work done in this process ∆W = IV ∆t → (3)
But power

From Ohm’s Law V = IR
∴ Power P = I.I.R = I²R
In this case power p ∝ R.

In this case energy of charge carriers is useful to heat the conductor. Amount of energy dissipated in conductor per second is power.

Where priority is given to current through conductor, at ordinary voltages we will say that p ∝ R.

i) In case of transmission lines the primary purpose is to transmit electrical energy from one place to another place. While doing so a part of energy is wasted in conductor in the form of heat. Let total power to be transmitted = P. Resistance of conductor = R_c,
Line voltage = V

Power wasted in transmission or transmission losses P_c = \(\frac{P^2R_c}{V^2}\). Due to this reason to reduce transmission losses we are transmitting electric power at very high voltages.

When voltage is given priority power P = \(\frac{V^2}{R}\)

In this case power P is said to be inversely proportional to resistance ‘R’.
Ratio of heats produced in the two cases is I²R: V²/R
But V = IR
∴ Ratio is I²R = \(\frac{I^2R^2}{R}\) = 1 : 1

Question 2.
Two metallic wires A and B are connected in parallel. Wire A has length L and radius r wire B has a length 2Land radius 2r. Compute the ratio of the total resistance of the parallel combination and resistance of wire A.
Answer:
Let resistivity of metallic wire A is ρ_A and that of B is ρ_B.

For wire A :
Length = L, radius = r, resistivity = ρ_R
Resistance of wire A is R_A = \(\frac{\rho_{\mathrm{A}} \mathrm{L}}{\mathrm{A}}=\frac{\rho_{\mathrm{A}} \cdot \mathrm{L}}{\pi r^2}\) → (1)

For wire B :
Length = 2L; radius = 2r ; resistivity = ρ_B.
Resistance of wire B is

a) Ratio of resistance of the wires = R_A : R_B

b) When resistors RA and Rg are connected in parallel effective resistance

Question 3.
In a house three bulbs of 100 W each are lighted for 4 hours daily and six tube lights of 20W each are lighted for 5 hours daily and a refrigerator of 400 W is worked for 10 hours daily for a month of 30 days. Calculate the electricity bill if the cost of one unit is Rs. 4.00.
Answer:
Electric consumption in KWH per one month

Electricity bill = No. of units × cost of unit = 174 × 4 = Rs. 696/-.
∴ Current bill, for that month is Rs. 696/-

Question 4.
Three resistors of 4 ohms, 6 ohms and 12 ohms are connected in parallel. The combination of above resistors is connected in series to a resistance of 2 ohms and then to a battery of 6 volts. Draw a circuit diagram and calculate
a) Cureent in main circuit
b) Current flowing through each of the resistors in parallel
c) P.D and the power used by the 2 ohm resistor.
Answer:
Given R₁ = 4Ω, R₂ = 6Ω and R₃ = 12Ω
i) When R₁, R₂ and R₃ are connected in parallel effective resistance

ii) R_eq is connected to a 2Ω resistor in series and then to a battery of 6V. The circuit diagram is as shown.

Total Resistance in circuit = R_eq + 2 = 2 + 2 = 4Ω
a) Current in main circuit I = \(\frac{V}{R}=\frac{6}{4}\) = 1.5 amp
b) Current through

c) RD across 2Ω Resistor
i = 1.5A, R = 2Ω ∴ P.D = iR= 1.5 × 2 = 3V
Power used P = i²R = 1.5 × 1.5 × 2 = 4.5 watt.

Question 5.
Two lamps, one rated 100 W at 220 V and the other 60 W at 220 V are connected in parallel to a 220 volt supply. What current is drawn from the supply line?
Answer:
For 1st Lamp power P = 100 W at potential V = 220 V
Supply voltage V = 220 V ; Power P = VI

∴ I₁ = \(\frac{100}{200}\)
For 2nd lamp power P = 60 W at 220 V.
Supply voltage = 220 V
Current i₂ = \(\frac{P^2}{V}=\frac{60}{200}\)
Total current drawn by parallel combination
I = I₁ + I₂⇒ I = 0.4545 + 2727 = 0.7272 A

Question 6.
A light bulb is rated at 100W for a 220V supply. Find the resistance of the bulb. [IMP]
Answer:
Power P = 100 W; Potential V = 100 V

Question 7.
Estimate the average drift speed of conduction electrons in a copper wire of crosssectional area 3.0 × 10^-7 m² carrying a current of 5 A. Assume that each copper atom contributes roughly one conduction electron. The density of copper is 9.0 × 10³ kg/m³ and its atomic mass is 63.5 u.
Answer:
Area A = 3.0 × 10^-7m² ;
Current i = 5A
Density ρ = 9.0 × 10³ kgm^-3 = 9.0 × 10⁶gm^-3
Atomic mass m = 63.5 U
Avagadro number NA = 6.022 × 10²³;
Charge on electron e = 1.6 × 10^-19 C
Drift velocity v_d = i/neA. Where n = total number of electrons / unit volume

Question 8.
Compare the drift speed obtained above with
i) Thermal speed of copper atoms at ordinary temperatures.
ii) Speed of propagation of electric field along the conductor which causes the drift motion.
Answer:
Drift velocity of electrons in copper = 1.22 m.m/s
i) Thermal speed of copper atoms V_T = \(\sqrt{k_{B}T/m}\).
Where k_B is Boltzman’s constant.
k_B = 1.381 × 10^-25
Let T = 300 K average temperature or ordinary temperature
m = mass of copper atom, By subtituting the above values V_T = 200 m/ sec
V_d < < V_rms

Thermal speed of copper atom is 10⁵ times more than drift velocity of electrons.

ii) An electric field travels with velocity of light along the conductor is velocity of electromagnetic wave 3 × 10⁸m/s.

Speed of electric field travelling along a conductor is 10¹¹ times more than drift velocity of electrons.

Problems

Question 1.
A 10Ω thick wire is stretched so that its length becomes three times. Assuming that there is no change in its density on stretching, calculate the resistance of the stretched wire.
Solution:
Resistance R = 10Ω ; Final length l₂ = 3l₁
When a wire is stretched its total volume is constant.

Question 2.
A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter? [AP Mar. 19,14. May 16; TS Mar. 16]
Solution:
Resistance = 4R
The wire is bent in the form of a circle and Resistance is to be calculated along its diameter.

Between the point AB the wire is a parallel
combination of 2R and 2R.
∴ Resultant resistance \(\frac{1}{R_R}=\frac{1}{2R}+\frac{1}{2R}=\frac{1}{R}\)
∴ Effective resistance between A & B = R.

Question 3.
Find the resistivity of a conductor which carries a current of density of 2.5 × 10⁶ A m^-2 when an electric field of 15 Vm^-1 is applied across it.
Solution:
Current density j = 2.5 × 10⁶ A
Electric field E = 15 V m^-1
Resistivity ρ = ? Resistivity p = E/j

Question 4.
What is the color code for a resistor of resistance 3500Ω with 5% tolerance?
Solution:
Resistance R = 3500 Ω. Tolerance = 5%
R = 3500 First digit 4 ⇒ Orange
2nd digit 5 ⇒ Green
Last two digits represent number of zeros = 2 ⇒ Silver
Tolerance = 5% ⇒ gold colour So colour code of that resistor is orange, green, silver and gold bands.

Question 5.
You are given 8Ω resistor. What length of wire of resistivity 120 ftm should be joined in parallel with it to get a value of 6Ω?
Solution:
Resistance Rj = 8Ω, Resistivity ρ = 12Ω m
Resistance across parallel combination R_p = 6Ω
Let parallel resistance to be connected
x = 120 / metres

Question 6.
Three resistors 3Ω, 6Ω and 9Ω are connected to a battery. In which of them will the power dissipation be maximum if: (a) they all are connected in parallel (b) they all are connected in series? Give reasons.
Solution:
Values of resistors R₁ = 3 Ω ; R₂ = 6 Ω ; R₃ = 9 Ω
a) When in series R_eff = R₁</sub. + R₂ + R₃ = 3 + 6 + 9 = 18
Power consumed P = \(\frac{V^2}{R}=\frac{V^2}{18}\) → (1)

b) When connected in parallel total power consumed is the sum of powers in each resistor.

From eq 1 & 2 power dissipation is maximum when they are connected in parallel.

Question 7.
A silver wire has a resistance of 2.1Ω at 27.5°C and a resistance of 2.7Ω at 100°C. Determine the temperature coefficient of resistivity of silver.
Solution:
Temperature t₁ = 27.5°C ;
Resistance R₁ = 2.1 Ω
Temperature t₂ = 100°C ;
Resistance R₂ = 2.7 Ω
Temperature coefficient of resistivity

Question 8.
If the length of a wire conductor is doubled by stretching it while keeping the potential difference constant, by what factor will the drift speed of the electrons change?
Solution:
Length of wire is doubled ⇒ l₂ = 2l₁
Potential V = constant ; Same material is used ⇒ electron density per unit volume is same.
Drift velocity v_d = \(\frac{i}{neA}\) here i, n and e are constants.

∴ Drift velocity is doubled.

Question 9.
Two 120V light bulbs, one of 25W and another of 200W are connected in series. One bulb burnt out almost instantaneously. Which one was burnt and why?
Solution:
For 1st bulb, Power P₁ = 25 W; For 2nd bulb P₂ = 200 W
When they are connected to mains supply of 240 V in series

In series combination voltage drop is high on high resistance and less on low resistance.

Since voltage on 25W bulb is more than rated voltage it blows off instantly.

Question 10.
A cylindrical metallic wire is stretched to increase its length by 5%. Calculate the percentage change in resistance.
Solution:
% Increase in length = 5%

∴ Percentage change in resistance = 2 × 5 = 10%

Question 11.
Three identical resistors are connected in parallel and total resistance of the circuit is R/3. Find the value of each resistance.
Solution:
In parallel combination when ‘n’ identical wires are connected parallelly, equivalent resistance is given by R_eq = R/n.

Given three identical wires ⇒ n = 3.
∴ R^eq = R/3 where R is resistance of each wire.
∴ Resistance of each wire used in parallel combination is R.

Hence resistance of each wire used in parallel combination is R.

Question 12.
Two wires A and B of same length and same material, have their cross sectional areas in the ratio 1 : 4. What would be the ratio of heat produced in these wires when the voltage across each is constant?
Solution:
Given lengths of wire are same ⇒ l₁ = l₂
Same material is used ⇒ ρ₁ = ρ₂
Ratio of area of cross sections A₁ : A₂ = 1 : 4 ⇒ A₂ = 4A₁
Potentail V is same.

∴ Ratio of Heat produced = 1 : 4

Question 13.
Two bulbs whose resistances are in the ratio of 1 : 2 are connected in parallel to a source of constant voltage. What will be the ratio of power dissipation in these?
Solution:
Ratio of resistances ⇒ R₁ : R₂ = 1 : 2
⇒ R₂ = 2R₁
When in parallel P.D is same on each bulb.

Question 14.
A potentiometer wire is 5 m long and a potential difference of 6 V is maintained between its ends. Find the emf of a cell which balances against a length of 180 cm of the potentiometer wire. [AP Mar. 17, 16. June 15; TS May 16]
Solution:
Total length of potentiometer wire L = 5 m
= 500 cm
Balancing length l₁ = 180 cm
P.D across the terminals = 6V
In potentiometer e.m.f at balancing point
V = \(\frac{El}{L}\frac{6\times180}{500}\)
∴ E.m.f of cell in secondary E₁ = 2.16 V

Question 15.
In a potentiometer arrangement, a cell of emf 1.25V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell?
Solution:
Emf of the cell, E₁ = 1.25 V
Balance point of the potentiometer, l₁ = 35 cm
The cell is replaced by another cell of emf E₂.
New balance point of the potentiometer, l₂ = 63 cm.
The balance condition is given by the

Therefore, emf of the second cell is 2.25V.

Question 16.
If the balancing point in a meter-bridge from the left is 60 cm, compare the resistances in left and right gaps of meter-bridge.
Solution:
Balancing point distance l₁ = 60 cm
∴ l₂ = 100 – 60 = 40 cm
Ratio of resistance \(\frac{R_1}{R_2}=\frac{l_1}{l_2}=\frac{60}{40}=\frac{3}{2}\)
(or) R₁ : R₂ = 3 : 2

Question 17.
A battery of emf 2.5V and internal resistance r is connected in series with a resistor of 45 ohm through an ammeter of resistance 1 ohm. The ammeter reads a current of 50 mA. Draw the circuit diagram and calculate the value of r. (Internal resistance)
Solution:
E.m.f. of battery E₁ = 2.5 V ;
Internal resistance = r
Series Resistance R = 45 Ω;
Ammeter Resistance = 1Ω
Reading in ammeter = 50 mA = 50 × 10^-3 Amp

From Kirchhoff’s mesh rule
E = iR + iR₁ – ir
2.5 = i 45 + i × 1 – ir
⇒ ir = 45 i + i – ir ⇒ E – 46i = – ir
∴ 2.5 – 46 × 50 × 10^-3 = -50 × 10^-3 r ⇒ 2.5 – 2.3 = -ir
∴ r = \(\frac{-0.2}{50\times10_{-3}}\) -ve sign indicates current in opposite direction.
∴ Internal resistance of battery
r = \(\frac{200}{50}\) = 4Ω

Question 18.
Amount of charge passing through the cross section of a wire is q(t) = at² + bt + c. Write the dimensional formula for a, b and c. If the values of a, b and c in SI unit are 6, 4, 2 respectively, find the value of current at t = 6 seconds.
Solution:
Given q (t) = at² + bt + c
But current i = \(\frac{d}{dt}\) q(t) = \(\frac{d}{dt}\) (at² + bt + c) = 2at + b → (1)
Put a = 6, b = 4, c = 2 and t = 6 in eq – (1)
∴ Current i = 2x6x6 + 4 = 72 + 4 = 76 Amp

Intext Question and Answer

Question 1.
The storage battery of a car has an emf of 12V. If the internal resistance of the battery is 0.4Ω, what is the maximum current that can be drawn from the battery?
A. Emf of the battery, E = 12 V ;
Internal resistance of the battery, r = 0.4Ω
Maximum current drawn from the battery = I ; According to Ohm’s law,
E = Ir
I = \(\frac{E}{r}=\frac{12}{0.4}\) = 30 A
The maximum current drawn from the given battery is 30 A.

Question 2.
A potentiometer wire is 5 m long and a potential difference of 6V is maintained between its ends. Find the emf of a cell which balances against a length of 180 cm of the potentiometer wire. [TS May ’16]
Answer:
Total length of potentiometer wire L = 5 m = 500 cm
Balancing length l₁ = 180 cm
P.D across the terminals = 6V
In potentiometer e.m.f at balancing point
El 6×180
V = \(\frac{El}{L}=\frac{6\times180}{500}\)
∴ E.m.f of cell in secondary E₁ = 2.16 V

Question 3.
A battery of emf 10 V and internal resistance 3Ω is connected to a resistor (R). If the current in the circuit is 0.5 A, what is the resistance (K) of the resistor? What is the terminal voltage of the battery when the circuit is closed? [(IMP) TS Mar, ’15]
Answer:
Emf of the battery, E = 10 V ;
Internal resistance of the battery, r = 3 Ω
Current in the circuit, 1 = 0.5 A ;Resistance of the resistor = R
The relation for current using Ohm s law is,
I = \(\frac{E}{R+r}\) ⇒ R + r = \(\frac{E}{I}\) = \(\frac{10}{0.5}\) = 20 Ω;
∴ R = 20 – 3 = 17 Ω
Terminal voltage of the resistor = V
According to Ohm’s law,
V = IR = 0.5 × 17 = 8.5 V
Therefore, the resistance of the resistor is 17 Ω and the terminal voltage is 8.5 V.

Question 6.
A negligibly small current is passed through a wire of length 15 m and uniform crosssection 6.0 × 10^-7m², and its resistance is measured to be 5.0 Ω. What is the resistivity of the material at the temperature of the experiment?
Answer:
Length of the wire, l = 15 m
Area of cross-section of the wire, a = 6.0 × 10^-7m²
Resistance of the material of the wire.
R = 5.0 Ω
Resistivity of the material of the wire = ρ
Resistance is related with the resistivity as

Therefore, the resistivity of the material is 2 × 10^-7 Ω m.

Question 5.
A silver wire has a resistance of 2.1 Ω at 27.5 °C, and a resistance of 2.7 Ω at 100 °C. Determine the temperature coefficient of resistivity of silver.
Answer:
Temperature, T₁ = 27.5°C ;
Resistance of the silver wire at T₁, R₁ = 2.1 Ω
Temperature, T₂ = 100°C ;
Resistance of the silver wire at T₂, R₂ = 2.7 Ω
Temperature coefficient of silver = α
It is related with temperature and resistance as

Therefore, the temperature coefficient of silver is 0.0039°C^-1.

Question 6.
Determine the current in each branch of the network shown in fig:

Answer:
Current flowing through various branches of the circuit is represented in the given figure.
I₁ = Current flowing through the outer circuit
I₂ = Current flowing through branch AB
I₃ = Current flowing through branch AD
I₂ – I₄ = Current flowing through branch BC
I₃ – I₄ = Current flowing through branch CD
I₄ = Current flowing through branch BD

For the closed circuit ABDA, potential is zero i.e.,
10I₂ + 5I₄ – 5I₃ = 0 (OR) ⇒ 2I₂ + I₄ – I₃ = 0
I₃ = 2I₂ + I₄ …… (1)
For the closed circuit BCDB, potential is zero i.e.,
5(I₂ – I₄) – 10(I₃ + I₄) – 5I₄ = 0 (OR)
5I₂ + 5I₄ – 10I₃ – 10I₄ – 5I₄ = 0
5I₂ – 10I₃ – 20I₄ = 0 ; I₂ = 2I₃ + 4I₄ ….. (2)
For the closed circuit ABCFEA, potential is zero i.e.,
– 10 + 10(I₁) + 10(I₂) + 5(I₂ – I₄) = 0
10 = 15I₂ + 10I₂ – 5I₄ ⇒ 3I₂ + 2I₁ – I₄ = 2 ….. (3)
From equations (1) and (2), we obtain
I₃ = 2(2I₃ + 4I₄) + I₄; I₃ = 4I₃ + 8I₄ + I₄ – 3I₃ = 9I₄ ⇒ -3I₄ = + I₃ ….. (4)
Putting equation (4) in equation (1), we obtain
I₃ = 2I₂ + I₄ (OR) ⇒ -4I₄ = 2I₂ ; I₂ = – 2I₄ …… (5)
It is evident from the given figure that,
I₁ = I₃ + I₂ ……. (6)
Putting equation (6) in equation (1), we obtain
3I₂ +2(I₃ + I₂) – I₄ = 2
5I₂ + 2I₃ – I₄ = 2 ….. (7)
Putting equations (4) and (5) in equation (7), we obtain 5(-2I₄) + 2(-3I₄) – I₄ = 2 – 10I₄ – 6I₄ – I₄ = 2 (OR) 17I₄ = – 2
⇒ I₄ = \(\frac{-2}{17}\) A
Equation (4) reduces to I₃ = – 3(I₄) = -3\(\frac{-2}{17}=\frac{6}{17}\)A

Question 7.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell? [(IMP) AP Mar. ’15]
Answer:
Emf of the cell, E₁ = 1.25 V
Balance point of the potentiometer, l₁ = 35 cm
The cells is replaced by another cell of emf E₂.
New balance point of the potentiometer, l₂ = 63 cm
The balance condition is given by the

Therefore, emf of the second cell is 2.25V.

Question 8.
The number density of free electrons in a copper conductor estimated in Example 6.1 is 8.5 × 10²⁸ m^-3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10^-6 m² and it is carrying a current of 3.0 A.
Answer:
Number density of free electrons in a copper conductor, n = 8.5 × 10²⁸ m^-3,
Length of the copper wire, l = 3.0 m
Area of cross-section of the wire, A = 2.0 × 10^-6 m²
Current carried by the wire, I = 3.0 A, which is given by the relation,
I = nAeV_d
Where, e = Electric charge =1.6 × 10^-19 C
v_d = Drift velocit

Therefore, the time taken by an electron to drift from one end of the wire to the other is 2.7 × 10⁴ s.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 5th Lesson Electrostatic Potential and Capacitance Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 5th Lesson Electrostatic Potential and Capacitance

Very Short Answer Type Questions

Question 1.
Can there be electric potential at a point with zero electric intensity? Give an example.
Answer:
Yes. At the mid point of line joining two similar charges, electric field is zero but potential will exist. Ex : Inside a charged hallow spherical shell field is zero but potential is not zero.

Question 2.
Can there be electric intensity at a point with zero electric potential? Give an example.
Answer:
Yes. At the midpoint or on the equatorial line of an electric dipole potential is zero but eletric field is not zero.

Question 3.
What are meant by equipotential surfaces?
Answer:
An equipotential surface is a surface with constant value of potential at all points on the surface.

Question 4.
Why is the electric field always at right angles to the equipotential surface? Explain.
Answer:
If the electric field is not normal to the equipotential surface, then the work done in moving a charge from one point to the other will not be zero, which is a contradiction, thus the field is normal to equipotential surface.

Question 5.
Three capacitors of capacitances 1 µF, 2 µF, and 3 µF are Connected in parallel.
a) What is the ratio of charges?
b) What is the ratio of potential differences?
Answer:
Charge q = CV
a) ⇒ q ∝ C ⇒ q₁ : q₂ : q₃ = C₁ : C₂ : C₃ = 1 : 2 : 3
b) In parallel combination potential across combination is
Constant : V₁ : V₂ : V₃ = 1 : 1 : 1

Question 6.
Three capacitors of capacitances 1 µF, 2 µF, and 3 µF are connected in series
a) What is the ratio of charges?
b) What is the ratio of potential differences?
Answer:
q = CV, in series combination charge q’ is constant on each capacitor.
a) ⇒ q₁ : q₂ : q₃ = 1 : 1 : 1
b) V ∝ \(\frac{1}{C}\) ⇒ V₁ : V₂ : V₃ : \(\frac{1}{1}: \frac{1}{2} : \frac{1}{3}\) = 6 : 3 : 2

Question 7.
What happens to the capacitance of a parallel plate capacitor if the area of its plates is doubled?
Answer:
The capacity of a parallel plate capacitor

when area is doubled (A’ = 2A) then capacity is also doubled.

Question 8.
The dielectric strength of air is 3 × 10⁶ Vm^-1 at certain pressure. A parallel plate capacitor with air in between the plates has a plate separation of 1 cm. Can you charge the capacitor to 3 × 10⁶ V?
Answer:
No ; The dielectric strength of air means the max. electric field that the medium will with-stand. Given E_max = 3 × 10⁶Vm^-1,

Short Answer Questions

Question 1.
Derive an expression for the electric potential due to a point charge. [Mar. ’16; TS Mar. ’16]
Answer:
Consider a point charge Q at ‘O’ and a unit positive charge is placed at ‘P’, distance r’. The force acting on it is

Let dW be the work done in moving this test charge through dr’ towards ‘O’.

The total work done in bringing this test charge from r’ = ∞ to r’ = r is

By the definition of potential this work- done is the electrostatic potential at that point.
∴ V = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r}\)

Question 2.
Derive an expression for the electrostatic potential energy of a system of two point charges and find its relation with electric potential of a charge.
Answer:
Consider a system of two charges q₁ and q₂ with position vectors \(\overline{\mathrm{r_1}}\) and \(\overline{\mathrm{r_2}}\) relative to origin at points A & B respectively. The electrostatic potential due to q₁ at B is V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1}{\mathrm{r}_2}\)
The work done in bringing q2 from infinity to the
point B is W = q₂ V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1\mathrm{q}_2}{\mathrm{r}_{12}}\)

As the electrostatic force is a conservative force, this work done will be stored as energy in the system.

Hence this work done is called electrostatic potential energy ‘U’ of the system of the charges q₁ and q₂.

Question 3.
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field.
Answer:
Consider a dipole with charges + q and – q placed in a uniform electric field E as shown.

Forces are F₁ = qE and F₂ = – qE but dipole experiences torque given by

Let ‘dW’ be the small amount of work done in rotating the dipole through d0 without any angular acceleration.
dW = τdθ
The toal work done to deflect from θ₁ to θ₂ is

W = pE [cos θ₁ – cos θ₂]
This work done is stored as potential energy in the dipole.
If the dipole is intially parallel to \(\overline{\mathrm{E}}\) and now turned through an angle θ, the work- done is
W = pE [cosθ – cosθ] = pE [ 1 – cosθ]
Then the potential energy of the dipole in this displaced position is U = U₀ + W = – pE + pE [ 1 – cos θ] = – pE cos θ = – \(\overline{\mathrm{E}}.\overline{\mathrm{E}}\)

Question 4.
Derive an expression for the capacitance of a parallel plate capacitor. [AP Mar. 18, 16, May 17. 16; TS Mar. 18. May 18. 16]
Answer:
A parallel plate capacitor consists of two plane conducting plates of area A separated by a small distance d’. Let the medium between the plates is vacuum.
Let the surface charge densities of the plates (1) and (2) be + σ and – σ.
The electric fields in regions I and III will be

In the inner region i.e., II the fields due to these plates will add up and given by

as ‘d’ is the separation between the plates, the potential difference between the plates given by

Question 5.
Explain the behaviour of dielectrics in an external field. [AP Mar. ’19]
Answer:
All dielectrics are two types 1) Non-polar dielectrics 2) Polar dielectrics.
a) For Non-polar dielectrics the centre of all positive and negative charges will coincide. Ex: O₂ molecule. So net dipole moment of these molecules is zero.

When these molecules are placed in an external electric field the positive and negative charges will be displaced in opposite directions. So they will develop induced dipolemoment. Total dipolemoment of these substances is the sum of all such dipolements and dielectrics are said to be polarised.

b) In case of polarised dielectrics in a molecule the centres of all positive charges and negative charges are separate. So they will develop some resultant dipolemoment. Under the absence of external electric field these dipole moments are random and resultant dipolemoment is zero.

When they are placed in external electric field these dipoles are arranged in an order and the dipolemoments are polarised.
The dipole moment per unit volume (\(\overline{\mathrm{p}}\)) is called polarisation.
\(\overline{\mathrm{p}}\) = χ\(\overline{\mathrm{E}}\)
where χ is called electric susceptibility.

Long Answer Questions

Question 1.
Define electric potential. Derive an expression for the electric potential due to an electric dipole and hence the electric potential at a point (a) the axial line of electric dipole (b) on the equatorial line of electric dipole.
Answer:
Electric potential :
Work done to bring the unit positive charge from infinity to the point in the electric field is called potential.
Potential due to point charge q at a distance r (V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)

Electric dipole :
Two equal and opposite charges (q, -q) separated by a distance (say 2a) is called electric dipole.

Potential due to an electric dipole :
Consider an electric dipole with charge q, – q.

Let separation between them is 2a. Let P is a point at a distance r’ from centre of dipole.

Join qp, -qp and OP. Let the line OP makes an angle ‘θ’ with the dipole axis (q, – q).
Total potential at P is V =\(\frac{1}{4 \pi \varepsilon_0}\) \(\frac{q}{r_1}-\frac{q}{r_2}\)

From geometry r²₁ = r² + a² – 2a r cos θ and
r²₂ = r² + a² + 2a r cos θ
These equations are rearranged as

But 2aq = p. dipole moment

Potential at any point on axis of dipole :
Consider a dipole of charges q, – q with separation ‘2a’. At point p potential V is given by V = V₁ + V₂

Potential at any point on equatorial line of dipole :
Let P is any point on equatorial line of a dipole at a distance r.

∴ Potential on equatorial line of dipole is zero.

Question 2.
Explain series and parallel combination of capacitors. Derive the formula for equivalent capacitance in each combination. [TS Mar. 19, 17, 15; AP May 16, June 15, Mar. 15]
Answer:
Capacitors in series :
If number of capacitors are connected in such a way that the charge on the plates of every one of them is same, then the capacitors are said to be
“connected in series”.

Explanation :
Let three capacitors C₁, C₂ and C₃ are connected in series as shown.

The charge q on the plates of the capacitors is same, let, V₁, V₂ and V₃ be the potential differences across C₁, C₂ and C₃ respectively. Let V be the p.d across the combination
then V = V₁ + V₂ + V₃

The reciprocal of equivalent capacity = the sum of reciprocal values of individual capacities of the combination.

Capacitors in parallel :
If a number of capacitors connected in such a way that the p. d between the plates of every one of them is same, then the capacitors are said to be “connected in parallel”.

Explanation :
Let the capacitors of capacities C₁, C₂ and C₃ connected in parallel as shown.

The potential difference across each condenser is same and is equal to V. Let q₁ and q₂ and q₃ be the charges on the plates of the capacitors.
∴ q = q₁ + q₂ + q₃. here q₁ = C₁V, q₂ = C₂V, q₃ = C₃V
If C is equivalent capacity of the combination, the C = \(\frac{p}{V}\) ⇒ q = CV
∴ CV = C₁V + C₂V + C₃V
∴ C = C₁ + C₂ + C₃
The equivalent capacity of the parallel combination = the sum of the capacities of the capacitors.

Question 3.
Derive an expression for the energy stored in a capacitor. What is the energy stored when the space between the plates is filled with a dielectric.
a) With charging battery disconnected?
b) With charging battery connected in the circuit?
Answer:
Let ‘q’ be the charge on the plates of a capacitor and V be the potential difference between plates. The work done dW in charging the capacitor with an additional charge dq.
dW = Vdq
⇒ dW = \(\frac{q}{C}\)dq (∵ q = CV)
The total work done in charging the plates it to a charge Q = W

This work done in charging the capacitor stored as electrostatic potential energy.

Effect of dielectric :
a) When charging battery is disconnected:
The charge on the plates remain constant, but capacity increases.

∴ The energy stored will get reduced to \(\frac{1}{K}\) th of initial value.

b) When charging battery remain connected the p.d across the capacitor remains same, but the capacity and the charge increases.

∴ The energy stored will increases by K times initial value.

Problems

Question 1.
An elementary particle of mass in’ and charge + e initially at a very large distance is projected with velocity ‘v’ at a much more massive particle of charge + Ze at rest. The closest possible distance of approach of the incident particle is
Answer:
At closest approach kinetic energy of charged particle = electrostatic potential between them.

Given : Mass of particle = m; velocity = V
∴ KE = 1/2 mv² → (1)
Charge of particle q₁ = e ; Charge on massive particle q₂ = Ze
∴ Electrostatic potential

Question 2.
In a hydrogen atom the electron and proton are at a distance of 0.5 Å. The dipole moment of the system is
Answer:
Distance between electron and proton = 0.5Å = 0.5 × 10^–10 m
Charge on proton = Charge on electron = 1.6 × 10^-19 C
Dipole moment = charge × separation between charges
∴ Dipolemoment p = 1.6 × 10^-19 × 0.5 × 10^-10 = 0.8 × 10^-29 = 8 × 10^-30 Cm

Question 3.
There is a uniform electric field in the XOY plane represented by (\(\mathbf{40} \hat{\mathbf{i}}+\mathbf{30} \hat{\mathbf{j}}\)) Vm^-1. If the electric potential at the origin is 200 V, the electric potential at the point with co-ordinates (2m, lm) is
Answer:
Intensity of electric field E = \(\mathbf{40} \hat{\mathbf{i}}+\mathbf{30} \hat{\mathbf{j}}\)
Position of the given point = 2 m, 1 m
i.e., 2m along \(\hat{\mathbf{i}}\) and lm along \(\hat{\mathbf{j}}\). Potential
= \(\overline{\mathrm{E}}.\overline{\mathrm{r}}\) =40 × 2 + 30 × 1 = 80 + 30 = 110V
Potential at origin = 200V.
Potential difference at point p = 200 – 110 = 90V.

Question 4.
An equilateral triangle has a side length L. A charge + q is kept at the centroid of the triangle. P is a point on the perimeter of the triangle. The ratio of the minimum and maximum possible electric potentials for the point P is
Answer:
Length of side = L. Charge at centroid = + q
Let ‘O’ be the centroid.
Centroid will divide the angle bisector in the ratio 2 : 1.
∴ Maximum distance from centroid is say ‘2a’ then minimum distance from centroid is ‘a’.

Ratio of minimum potential to maximum potential is 1 : 2.

Question 5.
ABC is an equilateral triangle of side 2m. There is a uniform electric field of intensity 100 V/m in the plane of the triangle and parallel to BC as shown. If the electric potential at A is 200 V, then the electric potentials at B and C are respectively
Answer:
Side of triangle L = 2m
Intensity of electric field = 100 V/m
(parallel to BC)

Potential at A = 200V.
Let D is the mid point of BC.
Now AD is an equipotential line with a potential of 200V.
Potential at B = 200 + E. r where r₁ = BD = 1m.
∴ Potential at B = 200 + 100 × 1 = 300 V
∴ Potential at C = Pot. at D – E. r₂ where
r₂ = 1m
V_D = 200 – 100 × 1 = 100v
Note : By definition potential is the work done against the field.

Question 6.
An electric dipole of moment p is called in a uniform electric field E, with p parallel to E. It is then rotated by an angle q. The work done is
Answer:
Electric dipolemoment = p;
Intensity of electric field = E
p and E are parallel ⇒ θ = 0;
Angle rotated = q
Work done by external force to rotate the dipole without acceleration
W = PE (cos θ₁ – cos θ₂)
Here θ₁ = 0 and θ₂ = q
∴ Work done = PE (cos 0 – cos q) = pE (1 – cos q)

Question 7.
Three identical metal plates each of area ‘A’ are arranged parallel to each other, ‘d’ is the distance between the plates as shown. A battery of V volts is connected as shown. The charge stored in the system of plates is

Answer:
Area of plates = A, Separation between the plates = d.
Potential supplied by battery = V.
From given arrangement it is a parallel combination of two identical capacitors.

Question 8.
Four identical metal plates each of area A are separated mutually by a distance d and are connected as shown. Find the capacity of the system between the terminals A and B.

Answer:
Area of each plate = A
Total separation between the plates = d
Separation between two adjacent plates = d₁ = d/3
Capacity of each capacitor \(C_1=\frac{\varepsilon_0 A}{d_1}=\frac{\varepsilon_0 A}{d / 3}=\frac{3 \varepsilon_0 A}{d}\)
For two similar capacitors in series the resultant

Question 9.
In the circuit shown the battery of’V’ volts has no internal resistance. All three con-densers are equal in capacity. Find the condenser that carries more charge.

Answer:
In the diagram the battery polarities are as show.

So all capacitors are connected in parallel. Since capacity ‘C’ is same and potential of battery V is same charge will exist on all the three capacitors.

Question 10.
Two capacitors A and B of capacities C and 2C are connected in parallel and the combination is connected to a battery of volts. After the charging is over, the bat-tery is removed. Now a dielectric slab of K = 2 is inserted between the plates of A so as to fill file space completely. The energy lost by the system during the sharing of charges is
Answer:
Capacity C₁ = C; Capacity C₂ = 2C
Let the capacitors are charged to the potential V.
Charge on capacitor Q₁ = CV
Charge on capacitor Q₂ = 2CV
Total charge Q = Q₁ + Q₂ = 3CV → (1)
Energy stored U₁ = \(\frac{1}{2}\)CV² +\(\frac{1}{2}\)(2C) V²
\(\frac{CV^2}{2}\) + CV² = \(\frac{3}{2}\)CV² → (2)
Now dielectric is introduced in C₁
New capacity = KC₁
Where K₁ = 2 and C₁ = C ∴ C_N = 2C.
Cherge is not changed because battery is disconnected from circuit.

Question 11.
A condenser of certain capacity is charged to a potential V and stores some energy. A second condenser of twice the capacity is to stored half the energy of the first, find to what potential one must be charged?
Answer:
For 1st capacitor
Let capacity of capacitor = x; Potential = V
Energy stored U₁ = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × V²₁ → (1)
For 2nd capacitor capacity C₂ = 2x
Energy stored = \(\frac{1}{2}\)U₁ = \(\frac{1}{2}.\frac{1}{2}\) × V²₁ → (2)
But for 2nd capacitor energy stored

Intext Question and Answers

Question 1.
Two charges 5 × 10^-8 C and -3 × 10^-8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Answer:
There are two charges,
q₁ = 5 × 10^-8C, q₂ = -3 × 10^-8C
Distance between the two charges, d = 16 cm = 0.16 m
Consider a point P on the line joining the two charges, as shown in the given figure.

Let the electric potential (V) at point P be zero. It is at a distance r from q₁
Potential at point P is the sum of potentials caused by charges q₁ and q₂ respectively.

Therefore, the potential is zero at a distance of 10 cm from the positive charge between the charges.

Suppose point P is outside the system of two charges at a distance s from the negative charge, where potential is zero, as shown in the following figure.

Therefore, the potential is zero at a distance of 40 cm from the positive charge outside the system of charges.

Question 2.
A regular hexagon of side 10 cm has a charge 5 µC at each of its vertices. Calculate the potential at the centre of the hexagon.
Answer:
The given figure shows six equal amount of charges, q, at the vertices of a regular hexagon.

Charge, q = 5 µC = 5 × 10^-6C
Side of the hexagon, l = AB = BC = CD = DE
= EF = FA = 10 cm
Distance of each vertex from centre O, d = 10 cm

Therefore, the potential at the centre of the hexagon is 2.7 × 10⁶ V.

Question 3.
Two charges 2 µC and -2 µC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Answer:
(a) The situation is represented in the given figure.

An equipotential surface is the plane on which total potential is zero everywhere. This plane is normal to line AB.

The plane is located at the mid-point of line AB because the magnitude of charges is the same.

(b) The direction of the electric field at every point on this surface is normal to the plane in the direction of AB.

Question 4.
A spherical conductor of radius 12 cm has a charge of 1.6 × 10^-7C distributed uniformly on its surface. What is the electric field
(a) Inside the sphere?
(b) Just outside the sphere?
(c) At a point 18 cm from the centre of the sphere?
Answer:
(a) Radius of the spherical conductor, r = 12 cm = 0.12 m
Charge is uniformly distributed over the conductor, q = 1.6 × 10^-7 C
Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.

(b) Electric field E just outside the conductor is given by the relation,

Therefore, the electric field just outside the sphere is 10⁵ NC^-1.

(c) Electric field at a point 18 m from the centre of the sphere = E₁
Distance of the point from the centre, d = 18 cm = 0.18 m

Therefore, the electric field at a point 18 cm from the centre of the sphere is 4.4 × 10⁴ N/C.

Question 5.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (lpF = 10^-12 F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Answer:
Capacitance between the parallel plates of the capacitor, C = 8 pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k = 1
Capacitance, C, is given by the formula,
C = \(\frac{k\varepsilon_{0}A}{d}=\frac{\varepsilon_{0}A}{d}\) ………….. (i)
Where, A = Area of each plate; ∈₀ = permittivity of free space
If distance between the plates is reduced to half, then new distance, d’ = \(\frac{d}{2}\).
Dielectric constant of the substance filled in between the plates, k’ = 6
Hence, capacitance of the capacitor
becomes C’ = = \(\frac{k\varepsilon_{0}A}{d}=\frac{6\varepsilon_{0}A}{d_2}\) ………… (ii)
From eqn (i) & (ii)
C’ = 2 × 6C = 12 C = 12 × 8 = 96 pF
Therefore, the capacitance between the plates is 96 pF.

Question 6.
Three capacitors each of capacitance 9 pF are connected in series. [AP Mar ’14]
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Answer:
(a) Capacitance of each of the three capacitors, C = 9 pF
Equivalent capacitance (C’) of the combination of the capacitors is given by the relation,

Therefore, total capacitance of the combination is 3µF.

(b) Supply voltage, V = 100 V
Potential difference (V’) across each capacitor is equal to one-third of the supply voltage.
∴ V’ = \(\frac{V}{3}=\frac{120}{3}\) = 40V
Therefore, the potential difference across each capacitor is 40 V.

Therefore, total capacitance of the combination is pµF.
(b) Supply voltage, V = 100 V

Question 7.
Three capacitors of capacitances 2µF, 3µF and 4µF are connected in parallel.
(i) What is the total capacitance of the combination?
(ii) Determine the charge on each capacitor, if the combination is connected to a 200V supply. [AP Mar. 1 7; TS May 1 7, June 15]
Answer:
(a) Capacitances of the given capacitors are
C₁ = 2µF ; C₂ = 3µF ; C₃ = 4µF
For the parallel combination of the capacitors, equivalent capacitor C’ is given by the algebraic sum, C’ = 2 + 3 + 4 = 9
Therefore, total capacitance of the combination is pµF.

(b) Supply voltage, V = 100 V
The voltage through all the three capacitors is same = V = 100V
Charge on a capacitor of C and potential difference V is given by the relation,
q = CV … (i)
For C = 2µF, Charge = VC = 100 × 2 = 200µC = 2 × 10^-4 C
For C = 3µF,
Charge = VC = 100 × 3 = 300 µC = 3 × 10^-4 C
For C = 4µF,
Charge = VC = 100 × 4 = 200µC = 4 × 10^-4 C

Question 8.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel.
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
(a) Capacitances of the given capacitors are
C₁ = 2 pF ; C₂ = 3 pF ; C₃ = 4 pF
For the parallel combination of the capacitors, equivalent capacitor C’ is given by the algebraic sum, C’ = 2 + 3 + 4 = 9
Therefore, total capacitance of the combination is 9 pF.

(b) Supply voltage, V = 100 V
The voltage through all the three capacitors is same = V = 100 V
Charge on a capacitor of capacitance C and potential difference V is given by the relation,
q = VC … (i)
For C = 2 pF, Charge = VC = 100 × 2 = 200 pC = 2 × 10“10 C
For C = 3 pF,
Charge = VC = 100 × 3 = 300 pC = 3 × 10^-10 C
For C = 4 pF,
Charge = VC = 100 × 4 = 200 pC = 4 × 10^-10 C

Question 9.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10^-3 m² and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Answer:
Area of each plate of the parallel plate capacitor, A = 6 × 10^-3 m²
Distance between the plates, d = 3 mm
= 3× 10^-3 m; Supply voltage, V = 100 V
Capacitance C of a parallel plate capacitor is given by, C = \(\frac{\varepsilon_{0}A}{d}\)
Where, ε₀ = Permittivity of free space

Potential V is related with the charge q and capacitance C as V = \(\frac{q}{C}\)
∴ q = VC = 100 × 17.71 × 10^-12 = 1.771 × 10^-9C.
Therefore, capacitance of the capacitor is 17.71 pF and charge on each plate is 1.771 × 10^-9C.

Question 10.
Expalin what would happen if in the capacitor given in Exercise 8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Answer:
(a) Dielectric constant of the mica sheet, k = 6;
Initial capacitance, C = 1.771 × 10^-11 F
New capacitance,
C’ = kc = 6 × 1.771 × 10^-11 = 106 pF;
Supply voltage, V = 100 V
New charge,
q’ C’V = 6 × 1.771 × 10^-9 = 1.06 × 10^-8C
Potential across the plates remains 100 V.

(b) Dielectric constant, k = 6 ;
Initial capacitance, C = 1.771 × 10^-11 F
New capacitance,
C’ = kC = 6 × 1.771 × 10^-11 = 106 pF

If supply voltage is removed, then there will be no effect on the amount of charge in the plates.
∴ Charge = 1.771 × 10^-9 C
Potential across the plates is gives by,

Question 11.
A 12 pF capacitor is connected to a 50V battery. How much electrostatic energy is stored in the capacitor?
Answer:
Capacitor of the capacitance, C = 12 pF = 12 × 10^-12 F ; Potential difference, V = 50 V
Electrostatic energy stored in the capacitor is given by the relation,
E = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × 12 × 10^-12 × (50)² = 1.5 × 10^-8 J
Therefore, the electrostatic energy stored in the capacitor is 1.5 × 10^-8 J.

Question 12.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Answer:
Capacitance of the capacitor, C = 600 pF ; Potential difference, V = 200 V Electrostatic energy stored in the capacitor is given by,
E = \(\frac{1}{2}\)cV² = \(\frac{1}{2}\) × (600 × 10^-12) × (200)² = 1.2 × 10⁵ J
If supply is disconnected from the capacitor and another capacitor of capacitance C = 600 pF is connected to it, then equivalent capacitance (C’) of the combination is given by,

New electrostatic energy can be calculated as
E’ = \(\frac{1}{2}\) × C’ × V² = \(\frac{1}{2}\) × 300 × (200)² = 0.6 × 10^-6J
Loss in electrostatic energy = E – E’
= 1.2 × 10^-5 -0.6 × 10^-5 = 0.6 × 10^-5 = 6 × 10^-6 J
Therefore, the electrostatic energy lost in the process is 6 × 10^-6 J.

Question 13.
In a Van de Graaff type generator, a spherical metal shell is to be a 15 × 10⁶ V electrode. The dielectric strength of the gas surrounding the electrode is 5 × 10⁷ Vm^-1. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)
Answer:
Potential difference, V = 15× 10⁶V ;
Dielectric strength of the surrounding gas = 5 × 10⁷ V/m
Electric field intensity, E = Dielectric strength = 5 × 10⁷ V/m
Minimum radius of the spherical shell required for the purpose is given by,

Hence, the minimum radius of the spherical shell required is 30 cm.

Question 14.
A small sphere of radius r₁ and charge q₁ is enclosed by a spherical shell of radius r₂ and charge q₂. Show that if q₁ is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q₂ on the shell is.
Answer:
According to Gauss’s law, the electric field between a sphere and a shell is determined by the charge q₁ on a small sphere. Hence, the potential difference, V, between the sphere and the shell is independent of charge q₂. For positive charge q₁, potential difference V is always positive.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 4th Lesson Electric Charges and Fields Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 4th Lesson Electric Charges and Fields

Very Short Answer Type Questions

Question 1.
What is meant by the statement ‘charge is quantized’?
Answer:
The minimum charge that can be transferred from one body to another is equal to the charge of an electron ‘e’.

So charge always exists as an integral multiple of charge of electron i.e., Q = ne. (1 e = 1.6 × 10^-19 C). Therefore charge in quantized.

Question 2.
Repulsion is the sure test of charging than attraction. Why?
Answer:
A charged body can attract opposite charged body and also a neutral body. But repu¬lsion is only between two charged bodies of same polarity. Hence repulsion is sure test for charging than attraction.

Question 3.
How many electrons constitute 1 C of charge?
Answer:
Chargeq = ne; q = 1 C; e- 1.6 × 10^-19 C.

Question 4.
What happens to the weight of a body when it is charged positively?
Answer:
When a body is positively charged it looses electrons, hence its weight decreases (or) it looses weight.

Question 5.
What happens to the force between two charges if the distance between them is a) halved b) doubled?
Answer:

‘F’ increases four times its initial value

b) Let d₁ = d and d₂ = 2d and F₁ = F, F₂ = ?

Force between them reduces to 1/4 of initial value.

Question 6.
The electric lines of force do not intersect. Why?
Answer:
The tangent drawn at a point to the line of force gives direction of electric field. If two lines intersect at point of intersection field will be in two different directions, which is not possible. Therefore electric lines of force do not intersect.

Question 7.
Consider two charges + q and – q placed at B and C of an equilateral triangle ABC. For this system, the total charge is zero. But the electric field (intensity) at A which is equidistant from B and C is not zero. Why?
Answer:
Charge is a scalar so total charge Q = q + (- q) = 0. But electric field intensity is a vector and they must be add up vectorially at any given point. So at the point A of equilateral triangle

Question 8.
Electrostatic field lines of force do not form closed loops. If they form closed loops then the work done in moving a charge along a closed path will not be zero. From the above two statements can you guess the nature of electrostatic force?
Answer:
The electrostatic force is conservative force.

Question 9.
State Gauss’s law in electrostatics. Explain its importance. [AP June 15; TS Mar. 15, May 15]
Answer:
Def :
The total electrical flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the charge enclosed by the surface.

ε₀ = permittivity of free space.

Importance :
It is used to find the electric intensity due to various bodies due to charge distributions.

Question 10.
When is the electric flux negative and when is it positive?
Answer:
Electric flux, Φ = \(\overline{\mathrm{E}}.\overline{\mathrm{A}}\) = EA cos θ.
where θ = angle between \(\overline{\mathrm{E}}\) and \(\overline{\mathrm{A}}\).
If 0° < θ ≤ 90°. ⇒ Φ is positive.
When 90° < θ ≤ 180°. ⇒ Φ is negative.

Question 11.
Write the expression for electric intensity due to an infinite long charged wire at a distance radial distance r from the wire.
Answer:
The electric intensity at a point due to an infinitely long charged wire (E) = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\), λ = the linear charge density of the wire.
r = the radial distance of the point from the axis of the wire.

Question 12.
Write the expression for electric intensity due to an infinite plane sheet of charge.
Answer:
The electric intensity due to an infinite plane sheet of charge is, E = \(\frac{\sigma}{2 \varepsilon_0}\), σ – is surface charge density of the sheet.

Question 13.
Write the expression for electric intensity due to a charged conducting spherical shell at points outside and inside the shell.
Answer:
Electric field intensity due to a charged conducting spherical shell
a) At a point outside the shell intensity of electric field E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}=\frac{\sigma}{\varepsilon_0} \frac{\mathrm{R}^2}{\mathrm{r}^2}\)
q = σA = σ 4πR²

b) At a point inside the shell intensity of electric field E = 0.
Because potential inside a conducting shell is zero.

Short Answer Questions

Question 1.
State and explain Coulomb’s inverse square law in electricity. [AP May 18, 17; TS Mar. 17, ’14]
Answer:
Coulomb’s Law :
The force of attraction or repulsion between two charges is directly proportional to the product of the two charges and is inversely proportional to square of the distance between them. This force acts along the line joining the two charges.
Explanation:

ε₀ = permittivity of free space.
ε₀ = 8.85 × 10^-12Nm²/C²

This electrostatic force between the charges depends on the nature of the medium between them.
In any medium F = \(\frac{1}{4 \pi \varepsilon} \frac{\mathrm{q_1q_2}}{\mathrm{r}^2}\)
ε = permittivity of that medium.
\(\frac{\mathrm{F_{vacuum}}}{\mathrm{F_{med}}}= \frac{\varepsilon}{\varepsilon_0} \) = ε_r = k

where ε_r (or) k is called relative permittivity or dielectric constant.

Note :- This force is an action and reaction pair i.e., \(\overline{\mathrm{F}}_{21}=-\overline{\mathrm{F}}_{21}\)
In vector form of Coulomb’s law is

Question 2.
Define intensity of electric field at a point. Derive an expression for the intensity due to a point charge. [AP Mar. ’16]
Answer:
Intensity of electric field: It is defined as the force on a unit positive charge when placed in the electric field.

Proof :-
Consider a point charge ‘Q’ at O’, electric field will exist around that charge.
P = point at a distance r from the charge Q,
q₀ = Test charge placed at that point.

Due to a negative charge field is towards it.
Note : The electric field due to a point charge is non-uniform.

Question 3.
Derive the equation for the couple acting on an electric dipole in a uniform electric field. [TS Mar. ’19, May ’18; AP May ’16, ’14]
Answer:
Consider electric dipole of moment ‘p’ in an uniform electric field ‘E’, situated at an angle θ with the field.

The positive charge experiences force “qE” in the direction of field and negative charge experiences as a force – qE opposite to the direction of field. Net force on the dipole is zero. But these two forces will constitute a couple, they will produce torque on the dipole.

Magnitude of torque (τ) = force × perpendicular distance
= qE (AC) = qE (2a sin θ) = q(2a) E sin θ = pE sin θ
\(\bar{\tau}=\overline{\mathrm{p}} \times \overline{\mathrm{E}}\)
When \(\overline{\mathrm{p}}\) and \(\overline{\mathrm{E}}\) are in the plane of the paper then direction of torque is normal to the plane of paper.
If θ = 90° ⇒ τ_max = pE.
The electric dipole moment of a dipole is equal to the torque acting on it when placed in a uniform electric field.

Question 4.
Derive an expression for the intensity of the electric field at a point on the axial line of an electric dipole. [AP Mar. 19, 18, 17, 16, May 16; TS Mar. May 16]
Answer:
Consider an electric dipole with charges q, – q with separation ‘2a’ between them.
Let p = a point on its axial line at a distance r from the mid point of the dipole
E_axial = intensity of electric field at p
E_axial = E_+q + E_-q.
The electric field at p due to the charge + q

Question 5.
Derive an expression for the intensity of the electric field at a point on the equatorial plane of an electric dipole.
Answer:
Consider an electric dipole with charges q, -q with a separation ‘2a’ between them. Consider a point p’ on the equatorial of the dipole at a distance r from the centre of the dipole. Electric field at p is the resultant of E_+q and E_-q.
The electric field due to the charge +q at p

These are equal in magnitude. The components of E_+q and E_-q normal to the axis of the dipole cancel each other, the components along the axis will add up.

Question 6.
State Gauss’s law in electrostatics and explain its importance. [TS Mar. ’ 18,’ 15, May ‘ 17; AF June 15, Mar. 15]
Answer:
Gauss’s Law :
The total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface.

where ε₀ = permittivity of free space,
q = total cherge enclosed by the surface.

Importance:

1. Using Gauss law we can find field due to a distribution of charge.
2. Gauss’s law is often useful towards a much easier calculation of the electrostatic field when the system has symmetry.

Long Answer Questions

Question 1.
Define electric flux. Applying Gauss’s law and derive the expression for electric intensity due to an infinite long straight charged wire. (Assume that the electric field is everywhere radial and depends only on the radial distance r of the point from the wire.)
Answer:
Electric flux :
The number of electric lines of force passing normally through a given surface is called “electric flux” (Φ).

Expression for electric intensity :
Let us consider an infinitely long thin straight wire having linear charge density λ. (∵ λ= Q/L)

Consider a cylindrical Gaussian surface ABCD of length ‘l’ and radial distance r. The electric field \(\overline{\mathrm{E}}\) is radial and which perpendicular to the length of the wire.

The flux through the flat surfaces AB and CD are zero. (∵ \(\overrightarrow{E}\) ⊥ \(\overrightarrow{A}\))

The flux through the curved surface ABCD is given by

λ is positive ⇒ direction will be radially outwards
λ is negative ⇒ direction will be radially inwards 2

Question 2.
State Gauss’s law in electrostatics. Applying Gauss’s law derive the expression for electric intensity due to an infinite plane sheet of charge.
Answer:
Gauss’s law :
The total electrical flux through any closed surface is equal to 1/ε₀ times the net charge enclosed by that surface.

Expression for electric intensity:

Consider an infinite plane sheet ABCD of uniform surface charge density ‘σ’.
Surface charge density

Take a Gaussian surface in the form of a rectangular parallelopiped.

Assume the area of cross section of the two surfaces (1) and (2) be ‘S’. These two surfaces only will contribute to electric flux, since \(\overrightarrow{E}\) and area vector \(\overrightarrow{ds}\) are parallel. The remaining surfaces will give rise to zero flux as \(\overrightarrow{E}\) and \(\overrightarrow{ds}\) are perpendicular.
The total flux through the surface

This field is independent of distance of the point, this field is a uniform field.

Question 3.
Applying Gauss’s law derive the expression for electric intensity due to a charged conducting spherical shell at (i) a point outside the shell (ii) a point on the surface of the shell and (iu) a point inside the shell.
Answer:
Consider a charged spherical shell of radius R and of uniform surface charge density σ.

1) Field out side the shell:
Consider a point P outside the shell with a radius vector \(\overrightarrow{r}\). (\(\overrightarrow{r}\) > \(\overrightarrow{R}\))
Now consider a Gaussian surface which is spherical of radius r.
As all the points on this surface are at same distance.
The flux through the Gaussian surface

The charge enclosed by the
Gaussian surface is q = σ.(4πr²)

2) Field at a point on the shell:
If the point lies on the surface of the shell
⇒ r = R.

3) Field at a point inside the shell:
Consider a spherical Gaussian surface passing through P inside the shell with centre as ’O’.

The flux through this surface is

But the there is no charge enclosed by the surface i.e., q = 0.

∴ The field inside a uniformly charged thin shell at all points inside is zero.

Intext Question and Answer

Question 1.
Two small identical balls, each of mass 0.20 g, carry identical charges and are suspended by two threads of equal lengths. The balls position themselves at equilibrium such that the angle between the threads is 60°. If the distance between the balls is 0.5m, find the charge on each ball.
Answer:
Mass of each ball = 0.20g = 20 × 10^-4kg
Angle between them θ = 60°
Separation between balls = 0.5m

At equilibrium
Electrostatic force F is
balanced by component of weight mg sin θ.

Question 2.
An infinite number of charges each of magnitude q are placed on x – axis at distances of 1, 2, 4,8, …………. meter from the origin respectively. Find intensity of the electric field at origin.
Answer:
The charges are as shown.

Question 3.
A clock face has negative charges-q, -2q, -3q, …….. – 12q fixed at the position of the corresponding numberals on the dial. The clock hands do not disturb the net field due to the point charges. At what time does the hour, hand point in the direction of the electric field at the centre of the dial?
Answer:
Negative charges are arranged on the clock as shown.

Charge arrangement
Electric field due to – q = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}\) = say k

Where r is distance from centre ‘O’ to the numbers on dial
Field due to- 2q = 2k; due to -3q = 3k ……….. Field due to -12q = 12k
Electric field is directed as shown in figure.

They are as shown in figure.
Consider E₇ and E₉ magnitude of each = 6k angle between them is 60°.
∴ Resultant of E₇ & E₉ is along E₈.
Magnitude is
\(\sqrt{6 \mathrm{k}^2+6 \mathrm{k}^2+2 \times 6 \mathrm{k} \times 6 \mathrm{k} \times \cos \theta}\) say x.
Field along E₈ = 6k + x …………. (1)
Consider E₁₀ and E₁₂ their magnitudes are 6k and 6k angle between them is 60°.
Resultant of E₁₀, E₁₂ is along E₁₁.
Resultant field along
E₁₁ = \(\sqrt{6 \mathrm{k}^2+6 \mathrm{k}^2+2 \times 6 \mathrm{k} \times 6 \mathrm{k} \cdot \cos 60^{\circ}}\) say y.
Now x, y are equal.
Total field along E₁₁ = 6k + y ……….. (2)
From eq 1, 2 magnitudes of E₈, E₁₁ are equal and angle between them is 90°.
∴ Angle of resultant θ = 45° with E₈.
In clock Anglb between each digit say 8 & 9 = 30°
9 & 10 = 30° i.e., 1 hour corresponds to 30° angle so angle 45° ⇒ 1\(\frac{1}{2}\) hour
Direction of resultant field = 8 + 1\(\frac{1}{2}\) = 9\(\frac{1}{2}\) hours = 9 hours 30 minutes.

Question 4.
Consider a uniform electric field E = 3 × 10³ N/C. (a) What is the flux of this field through a square of 10 cm on aside whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x – axis?
Answer:
Intensity of electric field E = 3 × 10³ N/C along x-axis.
Area of Square = 1² = 10 × 10 = 100 cm²
= 100 × 10^-4 m² = 10^-2m²

(a) When plane of square is parallel to y – z plane it is perpendicular to x-axis
⇒ 0 = 90°
∴ Flux through square Φ = \(\overline{\mathrm{E}}.\overline{\mathrm{A}}\) (or)
Φ = EA cos θ
Φ = 3 × 10³ × 10^-2 = 3 × 10 = 30 vm

(b) When square makes an angle θ = 60°
with x- axis, θ =60°.

Question 5.
There are four charges, each with a magnitude Q. Two are positive and two are negative. The charges are fixed to the corners of a square of side ‘L’, one to each corner, in such a way that the force on any charge is directed toward the center of the square. Find the magnitude of the net electric force experienced by any charge?
Answer:
Given two charges are +ve and two charges are -ve.

Force on any charge is directed towards centre.
Side of square = L at point 3
Consider charge 3 total forces on it are

Question 6.
The electric field in a region is given by \(\overrightarrow{\mathbf{E}}=\mathbf{a} \hat{\mathbf{i}}+\mathbf{b} \hat{\mathbf{j}}\). Here a and b are constants. Find the net flux passing through a square area of side L parallel to y – z plane.
Answer:
Electric field \(\overrightarrow{\mathbf{E}}=\mathbf{a} \hat{\mathbf{i}}+\mathbf{b} \hat{\mathbf{j}}\)
Side of square = L
∴ Area of square = L²
Give square is parallel to y – z plane ⇒ it is perpendicular x – axis ⇒ Area vector

Question 7.
A hollow spherical shell of radius r has a uniform charge density σ. It is kept in a cube of edge 3r such that the center of the cube coincides with the center of the shell. Calculate the electric flux that comes out of a face of the cube.
Answer:
(Charge density on sphere = σ. But σ = \(\frac{Q}{A}\)
Area of spere A = 4πr²
⇒ Charge Q = 4πr²σ
For a point out side the sphere it seems to be concentrated at centre.
∴ Charge at centre of cube Q = 4πr²σ)
From gauss’s law total flux comming out of

Question 8.
An electric dipole consists of two equal and opposite point charges + Q and – Q, separated by a distance 2l. P is a point collinear with the charges such that is distance from the positive charge is half of its distance from the negative charge.
Answer:
Each charge on dipole = q, -q
Separation between charges = 2l

P is on the line joining the charges ⇒ it is on axial line.
Given : distance from +ve’ charge = \(\frac{1}{2}\) distance from -ve’ charge.
From given data d – l = \(\frac{1}{2}\) ( d + l) ⇒ 2d – 2l = d + l (or) d = 3l
Intensity of electric field at any point on

Question 9.
Two infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart. The intensity of the electric field at a point midway between them is
Answer:
Charge densities of infinitely long conductors = λ and 2λ
Distance between conductors = r
Intensity of electric field of mid point = ?
For mid point distance d = r/2
Intensity of electric field due to a long conductor.

Question 10.
Two infinitely long thin straight wires having uniform linear charge densities \(\ddot{\mathrm{e}}\) and 2\(\ddot{\mathrm{e}}\) are arranged parallel to each other at a distance r apart. The intensity of the electric field at a point midway between them is
Answer:
Linear charge densities σ₁ = σ₂ and σ₂ = 2e.
Separation between two parallel conductors d = r
For mid-way between them d = r/2

At midpoint intensities are in oppisite direction so resultant intensity E_R = E₁ ~ E₂
Intensity of electric field from an infinitely long charged conductor E = \(\frac{\lambda}{2 \pi \varepsilon_0r}\)

Intensity of electric field at mid point E = \(\frac{e}{\pi \varepsilon_0r}\)

Question 11.
An electron of mass m and chargee is fired perpendicular to a uniform electric field of intensity E with an initial velocity u. If the electron traverses a distance x in the field in the direction of firing. Find the transverse displacement y it suffers.
Answer:
Mass of electron = m ;
Charge on electron = e
Intensity of electric field = E
∴ Force F = E . e
Initial velocity of electron = u; acceleration of electron a = F/m = E.e/m

Distance travelled S = x. along x-axis
⇒ time t = \(\frac{x}{4}\) …………. (1)
Distance travelled along y-axis = ?
Initial velocity along y-axis = u = 0
Vertical displacement y = ut + \(\frac{1}{2}\) at² = \(\frac{1}{2}\)at²
⇒ y = \(\frac{1}{2}\frac{Ee}{m}.\frac{x}{u^2}\)
∴ Vertical displacement after travelling a eEx2 distance x is y = \(\frac{eEx^2}{2mu^2}\)

Additional Exercises

Question 1.
What is the force between two small charged spheres having charges of 2 × 10^-7 C and 3 × 10^-7 C placed 30 cm apart in air?
Answer:
Repulsive force of magnitude 6 × 10^-3 N ;
Charge on the first sphere, q: = 2 × 10^-7
C Charge on the second sphere, q² = 3 × 10^-7 C ;
Distance between the spheres, r = 30 cm = 0.3 m
Electrostatic force between the spheres is given by the relation,

Hence, force between the two small charged spheres is 6 × 10^-3 N. The charges are of same nature. Hence, force between them will be repulsive.

Question 2.
The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge – 0.8 µC in air is 0.2 N. (a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
Answer:
a) Electrostatic force on the first sphere, F = 0.2 N
Charge on this sphere, = 0.4 µC
= 0.4 × 10^-6 C
Charge on the second sphere,
q₂ = -0.8 µC = -0.8 × 10^-6

Electrostatic force between the spheres

The distance between the two spheres is 0.12 m.

b) Both the spheres attract each other with the same force. Therefore, the force on the second sphere due to the first is 0.2 N.

Question 3.
Check that the ratio ke²/G m_em_p is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Answer:
1) The given ratio is \(\frac{\mathrm{ke^2}}{\mathrm{Gm_em_p}}\)
Where, G = Gravitational constant
m_e and m_p = Masses of electron and proton.; e = Electric charge is C.
k = A constant. = \(\frac{1}{4 \pi \varepsilon_0}\),
Where ε₀ = Permittivity of free space
Therefore, unit of the given ratio

Hence, the given ratio is dimensionless,

ii) e = 1.6 × 10^-19C; G = 6.67 × 10^-11 N m²kg^-2; m_e = 9.1 × 10^-31 kg ; m_p = 1.66 × 10^-27kg
Hence, the numerical value of the given ratio is

This is the ratio of electric force to the gravitational force between a proton and an electron, keeping distance between them constant.

Question 4.
a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges?
Answer:
a) Electric charge of a body is quantized. This means that only integral (1, 2, …………, n) number of electrons can be transferred from one body to the other. Charges are not transferred in fraction. Hence, a body possesses total charge only in integral multiples of electric charge.

b) In macroscopic or large scale charges, the charges used are huge as compared to the magnitude of electric charge. Hence, quantization of electric charge is of no use on macroscopic scale. Therefore, it is ignored and it is considered that electric charge is continuous.

Question 5.
Four point charges q_A = 2 µC, q_B = – 5µC, q_C = 2 µC, and q_D = – 5 µC are located at thecomereofasquare ABCD of side 10cm. What is the force on a charge of 1 µC placed at the centre of the square?
Answer:
The given figure shows a square of side 10 cm with four charges placed at its corners. O is the centre of the square.

Where, (Sides) AB = BC = CD = AD = 10 cm
(Diagonals) AC = BD = 10√2 cm
AO = OC = DO = OB = 5√2 cm
A charge of amount 1 µC is placed at point O.

Force of repulsion between charges placed at corner A and centre O is equal in magnitude but opposite in direction relative to the force of repulsion between the charges placed at corner C and centre O. Hence, they will cancel each other. Similarly, force of attraction between charges placed at corner B and centre O is equal in magnitude but opposite in direction relative to the force of attraction between the charges placed at corner D and centre O. Hence, they will also cancel each other. Therefore, net force caused by the four charges placed at the corner of the square on 1 µC charge at centre O is zero.

Question6.
a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
b) Explain why two field lines never cross each other at any point?
Answer:
a) An electrostatic field line is a continuous curve because a charge experiences a continuous force when traced in an electrostatic field. The field line cannot have sudden breaks because the charge moves continuously and does not jump from one point to the other.

b) If two field lines cross each other at a point, then electric field intensity will show two directions at that point. This is not possible. Hence, two field lines never crosr. each other.

Question 7.
An electric dipole with dipole moment 4 × 10^-9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 × 10⁴ N C^-1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Electric dipole moment, p = 4 × 10^-9 C m ;
Electric field, E = 5 × 10⁴ N C^-1
Angle made by p with a uniform electric field, θ = 30°

Torque acting on the dipole is given by the relation, τ = pE sin θ
= 4 × 10^-9 × 5 × 10⁴ × sin 30
= 20 × 10^-5 × 1/2 = 10^-4 Nm

Therefore, the magnitude of the torque acting on the dipole is 10^-4 N m.

Question 8.
a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 × 10^-7 C? The radii of A and B are negligible compared to the distance of separation.
b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Answer:
a) Charge on sphere A, q_A = Charge on sphere B, q_B = 6.5 × 10^-7 C
Distance between the spheres,
r = 50 cm = 0.5 m

Force of repulsion between the two

Therefore, the force between the two spheres is 1.52 × 10^-2 N.

b) After doubling the charge, charge on sphere A, q_A = Charge on sphere B,
q_B = 2 x 6.5 × 10^-7C = 1.3 × 10^-6C
The distance between the spheres is halved.
∴ r = \(\frac{0.5}{2}\) = 0.25 m
Force of repulsion between the two spheres,

Therefore, the force between the two spheres is 0.243 N.

Question 9.
Figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

Answer:
Opposite charges attract each other and same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively chargee plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged.

The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.

Question 10.
What is the net flux of the uniform electric field of Exercise 15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Answer:
All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.

Question 11.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 10³ N m²/C.
a) What is the net charge inside the box?
b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Answer:
a) Net outward flux through the surface of the box, Φ = 8.0 × 10³ N m²/C
For a body containing net charge q, flux is given by the relation, Φ = \(\frac{q}{\varepsilon_0}\)
ε₀ = Permittivity of free space = 8.854 × 10^-12 N^-1C²m^-2
q = ε₀Φ = 8.854 × 10^-12 × 8.0 × 10³
= 7.08 × 10^-8 = 0.07 µC
Therefore, the net charge inside the box is 0.07 µC.

b) No
Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that net charge inside the body is zero. The body may have equal amount of positive and negative charges.

Question 12.
A point charge + 10 µC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)

Answer:
The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed. According to Gauss’s theorem for a cube, total electric flux is through all its six faces.
Hence, electric flux through one face of the cube
Φ_total = \(\frac{q}{\varepsilon_0}\)
Hence, electric flux through one fact of the cube i.e., through the square,

Therefore, electric flux through the square is 1.88 × 10⁵ Nm²C^-1

Question 13.
A point charge of 2.0 µC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Answer:
Net electric flux (Φ_net) through the cubic surface is given by, Φ_net = \(\frac{q}{\varepsilon_0}\)
Where, ε₀ = Permittivity of free space = 8.854 × 10^-12N^-1C²m^-2
q = Net charge contained inside the cube = 2.0 µC = 2 × 10^-6 C

The net electric flux through the surface is 2.26 × 10⁵ Nm²C^-1.

Question 14.
A point charge causes an electric flux of -1.0 × 10³ Nm²/C to pass through a sphe¬rical Gaussian surface of 10.0 cm radius centered on the charge.
a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
b) What is the value of the point charge?
Answer:
a) Electric flux, Φ = -1.0 × 10³ Nm²/C ;
Radius of the Gaussian surface, r = 10.0 cm
Electric flux piercing out through a surface depends on the net charge enclosed inside a body. It does not depend on the size of the body. If the radius of the Gaussian surface is doubled, then the flux passing through the surface remains the same i.e., – 10³ N m²/C.

b) Electric flux is given by the relation, Φ = \(\frac{q}{\varepsilon_0}\)
Where, q = Net charge enclosed by the spherical surface
ε₀ = Permittivity of free space
= 8.854 × 10^-12 N^-1C²m^-2
∴ q = Φε₀ = – 1.0 × 10³ × 8.854 × 10^-12
= – 8.854 × 10^-9 C = – 8.854 nC

Therefore, the value of the point charge is-8.854 nC.

Question 15.
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 10³ N/C and points radially inward, what is the net charge on the sphere?
Answer:
Electric field intensity (E) at a distance (d) from the centre of a sphere containing net charge q is given by the relation,

Therefore, the net charge on the sphere is 6.67 nC.

Question 16.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 µC/m².
a) Find the charge on the sphere.
b) What is the total electric flux leaving the surface of the sphere?
Answer:
a) Diameter of the sphere, d = 2.4 m ;
Radius of the sphere, r = 1.2 m
Surface charge density σ = 80.0 µC/m²
= 80 × 10^-6C/m²

Total charge on the surface of the sphere,
Q = Charge density × Surface area
Q = σ × 4πr² = 80 × 10^-6 × 4 × 3.14 × (1.2)²
= 1.447 × 10^-3C
Therefore, the charge on the sphere is 1.447 × 10^-3 C.

b) Total electric flux (Φ_total) leaving out the surface of a sphere containing net charge
Q is given by the relation, Φ_total = \(\frac{Q}{\varepsilon_0}\)

Therefore, the total electric flux leaving the surface of the sphere is 1.63 × 10^-8NC^-1m²

Question 17.
An infinite line charge produces a field of 9 × 10⁴ N/C at a distance of 2 cm. Calculate the linear charge density.
Answer:
Electric field produced by the infinite line charges at a distance d having linear charge density λ is given by the relation,

Therefore, the linear charge density is 10 µC/m

Telangana TSBIE TS Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics

Very Short Answer Type Questions

Question 1.
What is Fresnel distance?
Answer:
Fresnel distance :
The term z = a²/λ is called “Fresnel distance”.

In explaining the spreading of beam due to diffraction we will use the equation z = a²/λ.

Where after travelling a distance zλ/a size of beam is comparable to size of slit (or) hole a’.

Question 2.
Give the justification for validity of ray optics.
Answer:
The wavelength of light is very small. For larger distances and objects of large size we will completely neglect the wave nature of light. In this case, we believe that light will travel in straight lines. Principles of geometry are used to explain various phenomena like reflection and refraction.

Fresnel distance z = a²/λ suggested that for distances far greater than ‘z’ ray optics is valid in the limit wavelength tends to zero.

Question 3.
What is polarisation of light?
Answer:
Polarisation :
It is a process in which vibrations of electric vectors of light are made to oscillate in a single direction.
Ex : Let a light wave is represented by y (x, t) = a sin (kx – ωt)
Here the displacement is in y – direction. So it is referred as y – polarised wave.

Question 4.
What is Malus’law? [TS May ’17]
Answer:
Mains’ Law :
Let two polaroids say P₁ and P₂ are arranged with some angle ‘0’ between their axes. Then intensity of light coming out of them is I = I₀ cos² θ

Where I₀ is intensity of polarised light after passing through 1^st polaroid P₁. This is known as Malus’ Law.

Question 5.
Explain Brewster’s law. [AP June 15; TS May 16]
Answer:
The angle of incidence i_B for which the reflected ray is plane polarised is called Brewster angle.

Explanation:
At Brewster angle i_B + r = \(\frac{\pi}{2}\)

∴ The tangent of Brewster’s angle tan (i_B) is equals to refractive index. This is called “Brewster’s Law” i.e, µ = tan i_B.

Question 6.
When does a monochromatic beam of light incident on a reflective surface get completely transmitted?
Answer:
Laser beam is a monochromatic light. Let a laser beam is passed through a polariser and made to fall on a prism with Brewster’s angle. Now rotate the polariser carefully, for a particular angle of incidence we can not get reflected ray from prism. Which implies that the total light is transmitted through prism.

Short Answer Questions

Question 1.
Explain Doppler effect in light. Distinguish between red shift and blue shift. [TS Mar. 19, 16; May 15; AP Mar. 16, June 15, May 18]
Answer:
Doppler’s effect in light :
When there is relative motion between source and observer then there is a change in frequency of light received by the observer.

Red shift :
If the source moves away from the observer then frequency measured by observer is less i.e., wavelength increases As a result wave length of received light moves towards red colour. This is known as “red shift”.

Blue shift :
When source of light is approaching the observer frequency of light received decreases, i.e., wavelength of light decreases. As a result wavelength of received light will move towards blue colour. This is known as “blue shift”.

Question 2.
What is total internal reflection? Explain the phenomenon using Huygens principle.
Answer:
Total internal reflection :
When light travels from denser medium to rarer medium then for angle of incidence i > i_c i.e., (critical angle) light rays are not able to cross boundary layer between the media and simply come back into the same medium. This phenomena is known as “total internal reflection”.

Explanation :
From Huygens wave theory velocity of light in medium is high. So refracted ray will bend towards normal.

When light rays are travelling from denser medium to rarer medium they will bend away from normal.

As angle of incidence ‘i’ increases then angle of refraction ‘r’ will also increase.

For a particular value of i angle of refraction r will become 90° this angle of incidence in denser medium is called critical angle.

When angle of incidence i > i_c (critical angle) the ‘r’ is more than 90° we cannot have any refracted ray. The incident ray will simply come back into the same medium. This is called total internal reflection.

Question 3.
Derive the expression for the intensity at a point where interference of light occurs. Arrive at the conditions for maximum and zero intensity. [AP Mar. 18, 16. 15; TS May 18, Mar. 15]
Answer:
In young’s experiment two pinholes (S₁, S₂) are made on a black card board with a separation’d’ between them. Light coming from a pinhole ‘S’ will fall on these two pinholes (S₁, S₂) and spherical waves are produced. A screen (G, G₁) is placed at a distance D from the slits. This is as shown in fig.

From theory of interference when the two light waves are superposed at ‘P’. We will get bright band when path difference is nλ we will get dark band when path difference is (n + \(\frac{1}{2}\))λ.

Condition for maximum intensity :
For maximum intensity path difference S₂P – S₁P = nλ
From fig . [S₂P]² – [S₁P]² =

or S₂P – S₁P = 2xd /(S₂P + S₁P) …………. (1)
When D >> and D >> d then S₂P + S₁P ≅ 2D
∴ S₂P – S₁P = \(\frac{2xd}{2D}\)nλ (or) x = nλ\(\frac{D}{d}\) ………….. (2)
For dark band or zero intensity
S₂P – S₁P = (n + \(\frac{1}{2}\))λ
From eq. (1)
∴ S₂P – S₁P = 2xd/S₂P + S₁P use S₂P + S₁P = 2D
For zero intensity
S₂P – S₁P = \(\frac{2xd}{2D}\) = (n + \(\frac{1}{2}\))λ
∴ x = (n + \(\frac{1}{2}\))λ \(\frac{D}{d}\) For dark band.
Where x is distance from centre of screen and n is a ‘+Ve’ integer.

Question 4.
Does the principle of conservation of energy hold for interference and diffraction phenomena? Explain briefly. [AP May 16 ; Mar. 17. 14]
Answer:
In case of interference and diffraction we are getting a series of dark and bright bands. While forming these bands with maximum and minimum intensity law of conservation of energy holds good.

In interference and diffraction pattern energy is redistributed, i.e,, energy is reduced in one region (dark band). This energy is superposed on another region. Where it appears bright.

So in interference and diffraction pattern redistribution of energy in the regions of dark and bright bands takes place. But there is no loss of energy or creation of energy. Hence these two phenomena will obey Law of conservation of energy.

Question 5.
How do you determine the resolving power of your eye? [AP Mar. 19, 17, May 14; TS Mar. 18]
Answer:
To find resolving power of eye draw black bands of equal width say 5mm with a separation of 0.5mm between them. Gradually increase the width of gap (white strip) between to black bands form 0.5 to 1mm and 1 mm to 1.5 mm etc. after every two white bands.

Paste that paper on a wall. Wnen your distance from wall is very high – you will see only a dark band, i.e., all dark bands merged into a single band. When you are approaching the wall the bands seems to be separated into two groups with one white band between them. Now measure distance ‘D’ from wall and also spacing between black bands, (d) (i.e., width of white band)

Resolving power of eye = d/D
In this way we can find resolving power of our eye.

Question 6.
Explain polarisation of light by reflection and arrive at Brewster’s law from it. [Mar. ’15]
Answer:
Polarisation by reflection :
When unpolarised light falls on the boundary layer separating two transparent media the reflected light is found to be partially polarised. The amount of polarisation depends on angle of incidence i.

When reflected ray and refracted ray are perpendicular the reflected ray is found to be totally plane polarised. The angle of incidence at this stage is known as Brewster angle.

Brewster’s Law :
The particular angle of incidence (i_B) for which the reflected ray is plane polarised is called “Brewster angle”.

Explanation :
At Brewster angle i_B + r = \(\frac{\pi}{2}\)

The tangent of Brewster’s angle tan (i_B) is equals to refractive index of the reflection medium. This is called “Breswter’s law”, i.e,

Question 7.
Explain polarisation by reflection with diagram and state Brewster’s law. [May ’16]
Answer:
When unpolarised light falls on the boundary of two transparent media then reflected light is found to be plane polarised. The electric vectors are vibrating perpendicular to plane of incidence.

The percentage of polarised light gradually increases with angle of incidence. For a particular angle of incidence the reflected light is totally plane polarised. This particular angle of incidence is called Brewester angle (i_B).

Brewster angle :
The angle of incidence for which the reflected light is totally plane polarised is called Brewster angle (i_B).
At Brewster angle
Refractive index n (or)

So the tangent of Brewster angle is numerically equals to refractive index of the medium on which light rays are falling. This is called “Brewster’s law”.

Question 8.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids.
Answer:
Let two polaroids say P₁ and P₂ are arranged one at the back of other. Allow unpolarised light to fall on PF first. The transmitted light through P₁ is made to fall on P₂.

When polaroid P₁ is rotated there is no change in the intensity of transmitted light. Intensity of unpolarised light after passing through P₁ is reduced to half of initial value.

Let the pass axis of polaroid P₂ makes on angle ‘θ’ with pass axis of polariod P₁. When θ = 0 i.e., the two pass axes coincides the ail the light entered P₂ will come out.

If polaroid P₂ is gradually rotated the intensity of light coming out of P₂ gradually decreases. It becomes zero when θ = \(\frac{\pi}{2}\) i.e., the two pass axes are perpendicular to each other.

Intensity of output light through polaroid P₂ will fallow the equation I = I₀ cos² θ.

Where I₀ is intensity of light coming from P₁

This equation I = I₀ cos² θ is called Malus’Law.

Long Answer Questions

Question 1.
What is Huygens Principle? Explain the optical phenomenon of refraction using Huygens principle.
Answer:
Huygens principle :
Each point of the wave front is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave. These wavelets emanating from the wavefront are usually referred to as secondary wavelets.

From Huygens principle, every wave is a secondary wave to the preceding wave.

Wavefront :
The locus of points which oscillate in phase is called “wavefront”. (OR)
A wave front is defined as a surface of constant phase.

Refraction of a plane wave :
Let PP’ is the boundary layer between the medium 1 and 2. Let AB is a plane wave falling on the boundary layer. Draw a normal at A to the boundary. Angle between A’ A and normal angle of incidence ‘i’. Draw normal to wave-front from A. It will touch at B. Let time taken by BC to reach boundary is t. Then BC = v₁t. Now draw a circle with radius R = v₂t from A.

Draw a tangent from C on to this arc. Now CE represents the wavefront of refracted ray in the medium 2.

If r < i, then velocity v₂ in the medium is less and refracted ray will bend towards normal.

Let c’ is velocity of light in vacuum then n₁ = \(\frac{c}{v_1}\) and n₂ = \(\frac{c}{v_2}\). Then n₁ sin i = n₂ sin r. This is known as Snell’s Law.

If λ₁ and λ₂ represent the wavelengths, then

Hence in refraction wavelength λ and velocity v will decrease. But frequency ‘v’ is constant.

Question 2.
Distinguish between Coherent and Incoherent addition of waves. Develop the theory of constructive and destructive interferences.
Answer:
Coherent waves :
In coherent waves at a particular point in the medium, the phase difference between the displacements produced by each wave is constant.

In case of Incoherent waves the phase difference between the two waves reaching a given point in medium changes with time.

Let two waves say y₁ = a cos ωt and y₂ = a cos ωt reaches a point ‘P’ in a medium.
Then resultant displacement y = y₁ + y₂ = 2a cos ωt

Intensity I = 4I₀ (Intensity α amplitude)

Constructive interference :
For constructive interference the two waves reaching the point P must be in same phase i.e., Φ = 0 or phase difference Φ must be 2π, 4π, …………. 2πn (or) path difference must be
λ, 2λ ……….. nλ.

Let the distance travelled by the two waves in reaching a point Q is S₁Q and S₂Q
Now S₂Q – S₁Q = λ
Then y₁ = a cos ωt and y₂ = a cos (ωt – π)
= a cos ωt.
∴ Due to super position of waves y= y₁ + y₂ = a cos ωt + a cos ωt = 2 a cos ωt
Intensity I = 4a² = 4I₀
But Intensity I₀ = a² and intensity I ∝ amplitude² (a²)

Destructive interference :
For destructive interference the two waves must reach the given point with a phase of π. i.e., a path difference of λ/2.
At point Q, Path difference of the two waves is S₂Q – S₁Q = λ/2.
∴ y₁ = a cos ωt and y₂ = a cos (ωt – π)

Now the two waves will suffer destructive interference and resultant amplitude is zero.
∴ Intensity I = 0

Theory :
Let two coherent waves have a constant phase difference Φ between them.
Then y₁ = a cos cot and y₂ = a cos (ωt + Φ)
Due to super position y = y₁ + y₂ = a cos ωt + a cos (ωt + Φ)
= a [cos ωt + cos (ωt + Φ)] = 2a cos (Φ/2) cos (ωt + Φ/2)
Amplitude of new wave is 2a cos (Φ/2)

Intensity I = (2 a cos Φ/2)² = 4a² cos² (Φ/2)
When Φ = 0, 2π, 4π even multiples of π we will get I = 4a².
This is called bright band.
When Φ = π, 3π ………. odd multiples of π i.e., (2n + 1) π then I = 0
This is called dark band.
When Incoherent waves are used their phase difference changes with time i.e., Φ is not constant. So we will use average values = 4I₀ < cos² Φ/2 >
cos Φ/2 oscillates between 0 to 1. So average value is 1/2
∴ Average value of intensity = 4I₀ × \(\frac{1}{2}\) = 2I₀
So intensities will just add up.

Question 3.
Describe Young’s experiment for observing interference and hence arrive at the expression for ‘fringe width’.
Answer:
In Young’s experiment light coming from a source is allowed to pass through a pin hole s’. The light coming form is made to fall on slits S₁ and S₂ made on a black card board. Separation between the slits is d’. Since S₁ and S₂ are illuminated from the same source light waves coming from S₁ and S₂ are coherent waves with some fixed phase difference.

Let a screen GG is placed at a distance ‘D’ from the black card board to observe interference pattern.

The spherical waves coming from S₁ and S₂ will interfere at a point ‘P’ on the screen. Let distance of ‘P’ from centre of screen is ‘x’.

Expression for fringe width :
To produce maximum intensity (bright band) the two light waves arriving at point P must be in phase, i.e., phase difference between them is ‘0’ or 2π, 4π ……….. This corresponds to a path difference of 0, λ, 2λ …………. nλ.
∴ Path difference = S₂P – S₁P = nλ ………… (1)
But from figure (S₂P)² – (S₁P)²

But x and d are very small when compared to distance between slit and screen D.

This is the condition for Bright Band.

Formation of dark band :
For formation of dark band the two light waves reaching the point ‘P’ must be out of phase i.e., Φ = π, 3π, 5π …………..
This corresponds to a path difference of λ/2, 3λ/2, 5λ/2 ………….
∴ For destructive interference path difference (\(\frac{n+1}{2}\))λ

Fringe width β :
It is defined as the separation between two consecutive dark or bright bands.

Question 4.
What is diffraction? Discuss diffraction pattern obtainable from a single slit.
Answer:
Diffraction :
Bending of light rays of sharp edges (say edge of a blade) is called “diffraction”.

Diffraction at single slit :
In young’s double slit experiment the double slit is replaced by a single narrow slit. Then on the screen a central maximum with alternate dark and bright bands of decreasing intensity are seen. These are called diffraction pattern.

Explantion :
Let LM is‘a narrow slit and a screen is placed at suitable distance. Draw a straight line through M on to the screen. It will touch the screen at C’.

The intensity of light at any point P on screen is due to the contributions from large number of coherent sources on the slit.

Let light waves reaches the point P’ from Land N
Path difference = NP – LP = NQ = a sin θ = aθ …………… (1)
(θ is very small sin θ = θ)
At central point ‘C’ on screen θ = 0. So path difference is zero. Hence all parts of slit will contribute in phase. As a result maximum intensity is produced.

Consider the first minima :
Minimum intensity is produced when a θ = λ or θ = λ/a.

Now divide the slit into two equal parts say LM and MN. For every point M₁ in the region LM there is a point M₂ in MN region. The phase difference between M₁M₂ is 180° or π radians. So light waves reaching the point P are out of phase and we will get minimum intensity.

Consider 1^st maxima :
Maxima will occur when θ = (n + \(\frac{1}{2}\)) λ/2 For 1^st maxima
n = 1
⇒ 0 = 3 λ/2 a. Let us imagine the space between MN is divided into three equal parts. Consider first two thirds of the slit. Path difference for the two ends of this region is
\(\frac{2}{3}\)a.θ = \(\frac{2}{3}\)a × \(\frac{3\lambda}{2a}\) = λ

Now divide this \(\frac{2}{3}\)^rd region into two equal points. For ever wave coming form 1^st \(\frac{1}{3}\)^rd region on there is a wave coming from 2nd \(\frac{1}{3}\)^rd region with a phase difference of 180°. So on reaching point P their vector sum of displacements is zero. Here intensity is zero. The only light received is from 3rd \(\frac{1}{3}\)^rd part for intensity between two minima. So we will get weak bright region.

In this way we are able to explain maxima and minima formed in diffraction pattern.

Question 5.
What is resolving power of Optical Instruments? Derive the condition under which images are resolved.
Answer:
Resolving power of optical instruments :
From principles of geometrical optics, a light beam will get focussed to a point. But due to diffraction effects we are getting a spot of finite size instead of a point.

In diffraction radius of central bright region

This small value of r₀ plays a vital role in fixing the resolving power of telescopes and microscopes.

Telescopes :
In telescopes if two stars are to be resolved clearly then

Where ‘λ’ is wavelength of light used and ‘a’ is the aperture or diameter of lens used. Due to this reason we are using object lens of large diameter for better resolution.

Microscopes :
In microscopes near point magnification m = D/f = 2 tan β
For two object points to be viewed clearly their image size must be v θ = v \(\frac{1.22\lambda}{D}\)

Objects with image size less than this can not be viewed clearly. So corresponding distances between them at object size

∴ Resolving power of microscope

Intext Question and Answer

Question 1.
Two slits are made 1 mm apart and the screen is placed 1 m away. What is the fringe separation when blue-green light of wavelength 500 nm is used?
Answer:
Fringe width β = \(\frac{D\lambda}{d}\). But distance of screen D = 1 m
Wave length λ = 500 nm = 5 × 10^-7 m ;
Separation between slits d = 1 mm = 1 × 10^-3 m

Question 2.
(a) The refractive index of glass is 1.5. What is the speed of light in glass? Speed of light in vacuum is 3.0 × 10⁸ m s^-1)
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Refractive index of glass, p = 1.5; Speed of light, c = 3 × 10⁸ m/s
Speed of light’in glass is given by the relation.

Hence, the speed of light in glass is 2 × 10⁸ m/s.

(b) The speed of light in glass is not independent of the colour of light.
The refractive index of a violet component of white light is greater than the refractive index of a red component. Hence, the speed of violet light is less than the speed of red light in glass. Hence, violet light travels slower than red light in a glass prism.

Question 3.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is λ/3?
Answer:
Let I₁ and I₂ be the intensity of the two light waves. Their resultant intensities can be obtained as:
∴ I’ = I₁ + I₂ + 2 \(\sqrt I_1I_2\) cos Φ
Where, Φ = Phase difference between the two waves
For monochromatic light waves ; Ii = I2
I’ = I₁ + I₂ + 2\(\sqrt I_1I_2\) cos Φ = 2I₁ + 2I₁ cos Φ
Phase difference = \(\frac{2 \pi}{\lambda}\) × Path difference
Since path difference = λ,; phase difference Φ = 2π
∴ I’ = 2I₁ + 2I₁ = 4I₁
Given, I = k ; ∴ I₁ = \(\frac{k}{4}\)

Question 4.
What is the Brewster angle for air to glass transition? (Refractive index of glass = 1.5.)
Answer:
Refractive index of glass µ= 1.5 ; Brewster angle = θ
Brewster angle is related to refractive index as: tan θ = µ
∴ θ = tan^-1(1.5) = 56.31°
Therefore, the Brewster angle for air to glass transition is 56.31°.

Question 5.
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
Answer:
Fresnel’s distance (z_F) is the distance for which the ray optics is a good approximation. It is given by the relation,

\(\mathrm{z}_{\mathrm{F}}=\frac{\mathrm{a}^2}{\lambda}\) ; Where, aperture width,
a = 4 mm = 4 × 10^-3 m
Wavelength’ of light, λ = 400 nm = 400 × 10^-9 m

Therefore, the distance for which the ray optics is a good approximation is 40 m.

Question 6.
In double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits?
Answer:
Wavelength of light used, 1 = 6000 nm = 600 × 10^-9 m
Angular width of a fringe θ = 0.1°
= 0.1 × \(\frac{\pi}{180}=\frac{3.14}{1800}\) rad
Angular width of a fringe is related to slit spacing (d) as:

Therefore, the spacing between the slits is 3.44 × 10^-4 m.

Question 7.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of nλ/a. Justify this by suitably dividing the slit to bring out the cancellation.
Answer:
Consider that a single slit of width d is divided into n smaller slits.
Width of each slit, d’ = \(\frac{d}{n}\)
Angle of diffraction is given by the relation,

Now, each of these infinitesimally small slit sends zero intensity in direction θ. Hence, the combination of these slits will give zero intensity.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 2nd Lesson Ray Optics and Optical Instruments Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 2nd Lesson Ray Optics and Optical Instruments

Very Short Answer Type Questions

Question 1.
Define focal length and radius of curvature of a concave lens.
Answer:
Focal length (f) :
The distance between centre of lens and principle focus is called “focal length (f)”

Radius of curvature :
The distance between centre of lens to centre of curvature is called “Radius of curvature” (R).

Question 2.
What do you understand by the terms ‘focus’ and ‘principal focus’ in the context of lenses?
Answer:
Principal focus :
When a paraxial beam of light making small angle with principal axis falls on a lens, after refraction the refracted rays will converge at a point or they appear to diverge from a point on principal axis. This point is called “principal focus”.

Focus :
When parallel rays making some angle with principal axis passes through a lens then after refraction they will converge at a point in a plane passing through F and perpendicular to principal axis called focal plane.

This point of convergence or divergence in a focal plane is called focus. If the focus is on principal axis it is called principal focus.

Question 3.
What is optical density and how is it different from mass density?
Answer:
An optically denser medium is one in which velocity of light is less.

An optically rarer medium may have less mass density.
Ex: Mass density of turpentine is less than water but optical density of turpentine is more than water.

Question 4.
What are the laws of reflection through curved mirrors?
Answer:
Laws of reflection :

1. Angle of reflection is equais to angle of incidence (∠r = ∠i).
2. The incident ray, the reflected ray and normal to the reflecting surface lie in the same plane.

Question 5.
Define ‘power’ of a convex lens. What is [TS Mar., May 16; AP Mar. ’17, May 16]
Answer:
Power of a lens (P) :
Power of a lens is defined as the tangent of the angle by which it converges or diverges a beam of light falling at unit distance from the optical centre, i.e.
tan δ = \(\frac{h}{f}\), h = 1, δ = \(\frac{h}{f}\)
Power P = \(\frac{1}{f}\) unit: dioptre. Here f is in metre.

Question 6.
A concave mirror of focal length 10 cm is placed at a distance 35 cm from a wall. How far from the wall should an object be placed so that its real image is formed on the wall? [TS May ’19]
Answer:
Focal length (f) = 10 cm.
Image distance (v) = 35 cm
Position of object (u) = ?

Object distance is from pole of mirror.
From wall the distance of the object
d = 35 – 14 = 21 cm.

Question 7.
A concave mirror produces an image of a long vertical pin, placed 40 cm from the mirror at the position of the object. Find the focal length of the mirror.
Answer:
Given the object and image are at a distance of 40 cm i.e., v = u = 40 cm
In concave mirror when object is at 2f then image is also at 2f ⇒ 2f = 40 cm
∴ Focal length of concave mirror = 20 cm.

Question 8.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism. [AP Mar. 19, 18, June 15]
Answer:
Angle of prism A = 4°.
Angle of deviation, d = 2.48°
Refractive index, n = 1 for small angled prism d = (n – 1) A
∴ 2.48 = (n – 1) 4
⇒ n – 1 = \(\frac{2.48}{4}\) n = \(\frac{2.48}{4}\) + 1 = 0.62 + 1 = 1.62
∴ n = 1.62.

Question 9.
What is ‘dispersion’? Which colour gets relatively more dispersed? [Mar., May ’14]
Answer:
Dispersion :
The phenomenon of splitting of light into its component colours is known as dispersion.

Dispersion takes place due to change in refractive index of medium for different wave lengths.

Bending of violet component of white light is maximum due to its short wavelength.

Question 10.
The focal length of a concave lens is 30 cm. Where should an object be placed so that its image is 1/10 of its size?
Answer:
Here f = – 30 cm, u = ? (For a concave lens)
m = \(\frac{v}{u}=\frac{1}{10}\)
v is – ve because virtual image is formed

∴ u = 9 × 30 = 270 cm

Question 11.
What is myopia? How can it be corrected? [TS May 17, Mar. 17, 15, June 15; AP Mar., June ’15]
Answer:
Hypermyopia :
It is an eye defect. Where light rays coming from distant object are converged at a point infront of retina. This defect is called “short sightendness or Hyper myopia”, This defect can be compensated by using a concave lens.

Question 12.
What is hypermetropia? How can it be corrected? [AP May 17, Mar.’ 16; TS Mar. 18]
Answer:
Hypermetropia :
It is an eye defect. In this defect, eye lens focuses the incoming light at a point behind the retina. This is called “far sightedness or Hypermetropia”. This defect can be compensated by using a convex lens.

Short Answer Questions

Question 1.
A light ray passes through a prism of angle A in a position of minimum deviation. Obtain an expression for (a) the angle of incidence in terms of the angle of the prism and the angle of minimum devia¬tion (b) the angle of refraction in terms of the refractive index of the prism.
Answer:
a) Let a light ray PQ enters the prism with angle of incidence i and emerges out with an angle ‘e’. When it is at minimum deviation position.
from quadrilateral AQNR
∠A + ∠QNR = 180° …………… (1)
In triangle QNR,
r₁ + r₂ + ∠QNR = 180° …………… (2)
From equation (1) and (2);
r₁ + r₂ = A ……………. (3)

Deviation δ = (i₁ – r₁) + (i₂ – r₂)
= (i₁ + i₂) – r₁ + r₂
At minimum deviation position
i₁ = i₂ = p and r₁ = r₂ = r
∴ δ = i₁ + i₂ – A ⇒ 2i = A + δ
∴ i = \(\frac{A+\delta}{2}\) ……….. (4)

b) From equation (3) r₁ + r₂ = A.
∴ r₁ + r₂ = 2r = A ⇒ r = \(\frac{A}{2}\)

Question 2.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length. [AP Mar. ’19, ’17. May ’18, ’16]
Answer:
Focal length (f) :
The distance between principal focus and pole of mirror is called “focal length” (f).

R = 2f proof:
Let ‘C’ be the centre of curvature of a concave mirror, ‘P’ be its pole and F be the principal focus. Line passing through P and F is called principal axis. Consider a ray parallel to principal axis falls on the mirror at ‘M’. After reflection, it passes through principal focus ‘F’. Join CM. It is perpendicular to mirror at M. Let angle of incidence is 0 and MD is the perpendicular at M. From principles of geometry

∠MCP = θ and ∠MFP = 2θ
Now tan θ = \(\frac{MD}{CD}\) = θ ………….. (1)
(∵ when θ is small tan θ = θ)
and tan 2θ = \(\frac{MD}{FD}\) = 2θ ………… (2)
From equation (1) and (2); FD = CD/2 ………….. (3)
But when D is very close to ‘P’
FD = FP & and CD = CP
∴ f = \(\frac{R}{2}\) ⇒ R = 2f
⇒ Radius of curvature R = 2 × focal length.

Question 3.
A mobile phone lies along the principal axis of a concave mirror longitudinally. Explain why the magnification is not uniform.
Answer:
Let a mobile phone is placed along the principal axis of a concave mirror longitudinally then magnification is not uniform.
Explanation :
Let the mobile phone is placed on principal axis as shown.

Let the points 1 and 2 will represent the two ends of mobile phone. For the end 1 object distance is PO₁ = u₁. For the end ‘2’ object distance is PO₂ = u₂. Light rays coming from nearer end will form more magnified image I₁ and light rays coming from remote point will form less magnified image I₂.

Because in mirrors \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Since f is same. When u increases v will decrease. So v₁ > v₂.

But linear magnification m = \(\frac{v}{u}\)
In first case m₁ = \(\frac{v_1}{u_1}\) and
in second casern m<₂ = \(\frac{v_2}{u_2}\)
Here v₁ > v₂ and u₁ < u₂ as a result m₁ > m₂.
So magnification of mobile phone placed longitudinally is not uniform.

Question 4.
Explain the Cartesian sign convention for mirrors.
Answer:
Cartesian sign convention :

1. All distances must be measured from the pole of the mirror (centre of Jens).
2. The distances measured along the direction of the incident ray are taken as positive and against the direction of incident ray are taken as negative.
3. Distances (heights) above the principal axis of mirror or lens are taken as positive and below are taken as ve’.

Question 5.
Define critical angle. Explain total internal reflection using a neat diagram. [AP Mar. 15. May 14; TS Mar. ’18. ’15, May 17]
Answer:
Critical Angle :
When the light travels from denser to rarer medium, for which angle of incidence, the angle of refraction is 90° is called critical angle of denser medium.

Explanation :
Consider two transparent media say 1 and 2. Where medium 1 is denser medium and medium 2 is a rarer medium.

Let light rays are starting from point A in denser medium. For angle of incidence i₁ they will strike the boundary layer say at ‘O₁‘. Draw normal at ‘O₁‘ when light rays are travelling from denser medium to they will bend away from normal so angle of refraction (r₁) greater than i₁.

When angle of incidence is gradually increased then angle of refraction r₂ will also increase. For a particular angle of incidence ic angle of refraction r = 90° it is called critical angle.

For angle of incidence i > i_c there is no refracted ray in medium two. At this stage light rays are not able to penetrate the boundary layer so they will come back into 1st medium. This is called total internal reflection.

Question 6.
Explain the formation of a mirage. [TS Mar. 19, May 18; AP Mar. 16]
Answer:
Mirage are formed on hot summer days. On a hot summer day earth is heated due to heat radiation from sun. So air near the earth is heated its density will decrease and hot air goes up density. In this process, we will get a special atmosphere where low density air is near earth and its density gradually increases while going up.

Now light rays coming from sun will travel from denser air layers to less dense region (rarer medium). So they will continuously bend away from normal and undergoes total internal reflection.

As a result we will get inverted images of tall objects and an illusion as if there are ponds on high ways even though there is no wet surface. This type of illusion is called mirages.

Question 7.
Explain the formation of a rainbow.
Answer:
Rainbow :
Rainbow is due to dispersion of white light through water drops.

Condition to set Rainbow are 1) Sun should be shining at one side and rain should be at the other side of sky. Formation of rainbow is at least a three step process i.e., refraction – reflection and refraction i.e., light rays entering the water drop should suffer total internal reflection and comes out of the drop through refraction.

Explanation :
Sun lightis first refracted as it enters a rain drop. This causes the different wave lengths of white light to separate. Longer wavelengths (red colour) will bend less and shorter wavelengths (blue and violet colours) will bend more. These component rays will suffer total internal reflection inside the water drop at water – air boundary and again they will travel in water drop and finally they will come out of water drop after refraction.

In this way we will get rainbow on a rainy day when sun is shining at other end.

Question 8.
Why does the setting sun appear red? [AP Mar.’ 14, June ‘ 15; TS Mar.’ 17; May 15]
Answer:
Setting sun appears red due to scattering.

The amount of scattering is inversely proportional to fourth power of the wavelength. i.e, Amount of scattering αλ⁴. This is called Rayleigh’s formula.

Light of shorter wavelengths will scatter much more than light of longer wavelength. Due to this reason, blue light will scatter more than red light.

Rayleigh formula will hold good when size of the particles << λ. For particles of large size i.e., at water droplets, large dust particles etc., visible light of all wavelengths will scatter equally.

At sun set or at sun rise light rays will pass through a longer distances through atmosphere. In this process light of shorter wavelength is removed and light of longer wave length (Red) will suffer less scattering reaches our eye. As a result at sunrise and of sunset sun will appear red.

Question 9.
With a neat labelled diagram explain the formation of image in a simple microscope. [AP Mar. 18, 16, 15. May ’16. June 15; TS Mar., May 16]
Answer:
A single convex lens is used in a simple microscope. Here object distance is adjusted to be less than focal length of the convex lens used i.e., u < f. By proper adjustment of object distance final virtual image is made to form either at near point or at infinity.

Angular magnification (m) = tan θ₀ = \(\frac{h}{d}\)
Where h’ is say height of image and ‘d’ is ‘d’ near point distance.
For maximum clarity eye will form image of parallel rays at near point.

When image is at near point:
Linear magnification m = \(\frac{v}{u}\) = 1 + \(\frac{D}{f}\) because final image is at near point D.

Question 10.
What is the position of the object for a simple microscope? What is the maximum magnification of a simple micro-scope for a realistic focal length?
Answer:
In simple microscope, object is placed in between centre of lens (C) and its principal focus (f). As a result a magnified virtual image is made to form either at near point or at infinity with suitable object distance ‘u’.

In simple microscope near point magnification m = (1 + D/f) when image is at infinity magnification m = D/f.

Magnification – Limits :
Theoretically, we can achieve very high magnification m’ for simple microscope. But due to practical consideration, we can not increase magnification beyond a limit.
Ex : For a magnification of 5 at for point focal length of convex lens
f = \(\frac{D}{m}=\frac{25}{5}\) = 5 cm
with this focal length thickness of lens is high, so dispersion takes place and chromatic aberration will come into account.

Even with a very careful design of convex lens we can not get a magnification of more than ten with simple microscope. Magnification of m = 5 to 10 is the possible limit.

Long Answer Questions

Question 1.
a) What is the cartesian sign convention? Applying this convention and using a neat diagram, derive an expression for finding the image distance using the mirror equation.
b) An object of 5 cm height is placed at a distance of 15 cm from a concave mirror of radius of curvature 20 cm. Find the size of the image.
Answer:
a) Cartesian sign convention :

1. All distances must be measured from the pole of the mirror (or) the optical centre of lens.
2. The distances measured along the direction of the incident ray are taken as positive and against the direction of incident ray are taken as negative.
3. The distances (heights) measured above the principal axis of mirror or lens are taken as positive and below are taken as ve’.

Mirror equation :
The relation \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\) is known as “mirror equation”.

Derivation of equation for image distance :

Let an object is placed infront of a con-cave mirror beyond centre of curvature then a real image is formed between f and c as shown in figure.

As per sign convention all distances must be measured from pole of mirror P.

∴ Focal length f = PF it is against to direction of incident ray so f is – ve.

Image distance from pole of mirror is v = PB’. It is measured against direction of incident ray so image distance v is – ve.

By applying sign convention to mirror equation \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\) becomes

b) Height of object (h) = 5 cm;
Object distance (u) = 15 cm
Radius of curvature (R) = 2f = 20 cm ⇒ f = 10 cm

Question 2.
a) Using a neat labelled diagram derive the mirror equation Define linear magnification.
b) An object is placed at 5 cm from a con¬vex is the position and nature of the image?
Answer:
a) Let an object AB is placed in front of a concave mirror beyond radius of curvature C’, The parallel ray comming from object after reflection at mirror (M) will pass through principal focus (F). The ray passing through centre of curvature falls normally on mirror at N. Intersection of these two rays will give position of image A’B’. This is as shown in figure.

In figure Triangle A’B’ P and MPF are similar triangles by comparing ratio of sides

But triangles A ‘ B’ P and BAP are also similar.

In this equation
B’P Image distance B’P = v, FP = Focal length and BP = object distance = u.
∵ These distances measured from pole ‘P’ are against to direction of incident ray v is – ve, f is – ve and u is – ve.
By using these values in equation (3),

This is known as “mirror equation”.

Linear magnification :
The ratio of height of image (h’) to height of object (h) is called “linear magnification”.

Linear magnification, m = \(\frac{h’}{h}=\frac{-v}{u}\).

b) Object distance u = 5 cm; Focal length of convex lens f = 15 cm
Image distance v = ?

– ve sign indicates image is virtual image.
∴ Position of image is 7.5 cm infront of the lens.

3. a) Derive an expression for a thin double convex lens. Can you apply the same to a double concave lens too?
b) An object is placed at a distance of 20 cm from a thin double convex iens of focal length 15 cm, Find the position and magnification of the image.
Answer:
a) Refraction through double convex lens :
Refraction through double convex lens is studied in two steps.

1st step :
Let the first surface will form the image of object ‘O’ at I₁ for this case
\(\frac{\mathrm{n}_1}{\mathrm{OB}}+\frac{\mathrm{n}_2}{\mathrm{BI}_1}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{BC}_1}\) ………. (1)
In 2nd step the second surface will form image at I where 1st image Ij will act as virtual object for 2nd surface,
∴ \(-\frac{\mathrm{n}_2}{\mathrm{DI_1}}+\frac{\mathrm{n}_1}{\mathrm{DI}}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{DC_2}}\) ………. (2)
For thin lens thickness, BD is small
so BI = D₁
By adding equaion (1) and (2)
\(\frac{n_1}{OB}+\frac{n_1}{DI}\) = (n₂ – n₁ [latex]\frac{1}{BC_1}+\frac{1}{DC_2}[/latex] …………… (3)
If point object is at infinity then OB = ∞ and DI = focal length f.

The distance BC₁ = + R₁ and DC₂ = – R₂ by using these values in equation (3)
\(\frac{n_1}{f}\) = (n₂ – n₁) (\(\frac{1}{R_1}-\frac{1}{R_2}\))

Here refraction is from air to glass so n₁ = 1 and n₂ = n₂₁
∴ \(\frac{1}{f}\) = (n₂₁ – 1) (\(\frac{1}{R_1}-\frac{1}{R_2}\))

This equation is known as lens makers formula.
The above equation is valid even for concave lens. In that case, R₁ is – ve and R₂ is positive and f is – ve.
So \(\frac{1}{f}\) = (n₂₁ – 1) (\(\frac{1}{R_1}-\frac{1}{R_2}\)) is vaild even for concave lens.

b) Object distance u = 20 cm; focal length f = 15 cm. Image distance v = ?

∴ Image distance v = 60 cm.
Magnification m = \(\frac{v}{u}=-\frac{60}{20}\) = 3

Question 4.
Obtain an expression for the combined focal length for two thin convex lenses kept in contact and hence obtain an expression for the combined power of the combination of the lenses.
Answer:
Let two thin lenses A, B with focal lengths f₁ and f₂ are in contact. Let ‘O’ is a point object on the principal axis. The first lens will form the image I₁ of the object

This first image I₁ will act as an object to second lens and final image I is produced.
∴ \(\frac{1}{v}-\frac{1}{v_1}=\frac{1}{f_2}\) ………….. (2)
by adding equation (1) and (2)
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_1}+\frac{1}{f_2}\).
But \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
Here the lens system is regarded as equivalent to a single lens of focal length ‘f’.
∴ \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
If there are n lenses in contact then equivalent focal length is given by

So interms of power,
P = P₁ + P₂ + P₃ + …………. + P_n
Equivalent focal length of lenses in contact is \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}+\frac{1}{f_3}+………….+\frac{1}{f_n}\)

Equivalent power of lens combination is
P = P₁ + P₂ + …………. + P_n.

Question 5.
a) Define Snell’s Law. Using a neat la¬belled diagram derive an expression for the refractive index of the material of an equilateral prism.
b) A ray of light, after passing through a medium, meets the surface separating the medium from air to an angle of 45° and is just not refracted. What is the refractive index of the medium?
Answer:
a) Snell’s Law :
The ratio of sine of angle of incidence to sine of angle of refraction is constant for a given pair of media. i.e., sin i / sin r = n₂₁.
where n₂₁ is refractive index of 2nd medium w.r.to 1st medium.

Derivation of refractive index of prism :
Let ABC is the cross-section of a prism. AB and AC are refracting surfaces. ∠A is angle of prism. Let a light ray PQ falls on AB with angle of incidence i₁. After refraction path of light ray QR is parallel to prism base. RS is emergent ray with angle of emergence ‘e’. When PQ and RS are extended they will meet at M. Angle of deviation is δ. They are as show in figure.

In figure, ∠A + ∠QNR = 180° …………. (1)
In triangle QNR,
r₁ + r₂ + ∠QNR = 180° ………….. (2)
From equation (1) and (2),
r₁ + r₂ = A ……………. I
Angle of deviation
δ = (i₁ – r₁) + (e – r₂) …………. (3)
Or δ = i₁ + e – A …………… (4)
At minimum deviation position i₁ = e and r₁ = r₂
and δ = δ_m by using these values
r₁ + r₂ = A
⇒ 2r = A
⇒ r = A/2 ………….. (5)
δ = i₁ + e – A = 2i₁ – A

b) Angle of incidence, I = 45°
Angle of refraction, r = 90° ⇒ i = i_c
Refractive index n₂₁ = \(\frac{1}{\sin C}=\frac{1}{\frac{1}{\sqrt{2}}}=\sqrt{2}\) = 1.414

Question 6.
Draw a neat labelled diagram of a compound microscope and explain its working. Derive an expression for its magnification.
Answer:
A compound microscope consists of two convex lenses mounted coaxially. Lens near the object is called objective. Focal length of objective is less.

Object lens forms a real, magnified image of the object. It will work as an object to eyelens.

Lens near the eye is called eye lens its focal length is high. It will form a magnified virtual final image at near point or at infinity. Final image is inverted w.r.t the original.

Ray diagram is as shown in figure. Dis-tance between objective and eye lens is called tube length ‘L’.

Eye lens will form the final image at infinity or a virtual image at near point.
Near point magnification of eye lens
m_e = (1 + \(\frac{D}{f_e}\)) …………….. (2)
When final image is at infinity Magnifcation of eye lens m_e = \(\frac{D}{f_e}\) …………… (3)
Total magnification of compound microscope m = m₀ . m_e.
∴ Total magnification
i) For final image at near point m = \(\frac{L}{f_0}\)(1+\(\frac{D}{f_e}\))
ii) For final image at infinity m = \(\frac{L}{f_0}.\frac{D}{f_e}\)
Magnification of compound microscope is very high.

Solved Problems

Question 1.
A light wave of frequency 4 × 10¹⁴ Hz and a wavelength of 5 × 10^-7m passes through a medium. Estimate the refractive index of the medium.
Answer:
Frequency (u) = 4 × 10⁴ C/S,
Wavelength (λ) = 5 × 10^-7 m, µ = ?

Question 2.
A ray of light is incident at an angle of 60 on the face of a prism of angle 30°. The emergent ray makes an angle of 30° with the incident ray. Calculate the refractive index of the material of the prism.
Answer:
Angle of incidence (i) = 60°;
Angle of prism (A) = 30°
Angle of deviation (d) = 30°
In prism i₁ + i₂ = A + d
⇒ 60 + i₂ = 30 + 30
⇒ i₂ = 0 ⇒ r₂ = 0
But r₁ + r₂ = A ⇒ r₁ + 0 = 30° or r₁ = 30°

Question 3.
Two lenses of power – 1.75D and + 2.25D respectively are placed in contact. Calculate the focal length of the combination.
Answer:
Power of 1st lens (P₁) = – 1.75 D;
Power of 2nd lens (P₂) = + 2.25 D
When in contact total power
P = P₁ + P₂ = – 1.75 + 2.25 = 0.5
Focal length of combination
f = \(\frac{100}{P}=\frac{100}{0.5}\) = 200 cm

Question 4.
Some rays falling on a converging lens are focussed 20 cm from the lens. When a diverging lens is placed in contact with the converging lens, the rays are focussed 30 cm from the combination. What is the focal length of the diverging lens?
Answer:
f_c = 20 cm
When combined with diverging lens light rays are focused at 30 cm
⇒ f_comb = 30 cm = F (say)

– ve sign indicates that it is a diverging lens.

Question 5.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism. [June ’15]
Answer:
Angle of prism (A) = 4°.
Angle of deviation (d) = 2.48°
Refractive index, n = 1 for small angled prism
d = (n₂₁ – 1) A
∴ 2.48 = (n₂₁ – 1) 4 ⇒ n₂₁ – 1 = \(\frac{2.48}{4}\)
n₂₁ = \(\frac{2.48}{4}\) + 1 = 0.62 + 1 = 1.62

Question 6.
A double convex lens of focal length 15 cm is used as a magnifying glass in order to produce an erect image which is 3 times magnified. What is the distance between the object and the lens?
Answer:
Focal length (f) = 15 cm;
Magnification (m) = 3 = v/u ⇒ v = 34

Question 7.
A compound microscope consists of an object lens of focal length 2 cm and an eyepiece of focal length 5 cm. When an object is placed at 2.2 cm from the object lens, the final image is at 25 cm from the eye lens. What is the distance between the lenses? What is the total linear magnification?
Answer:
Focal length of object lens (f₀) = 2 cm;
Object distance (u) = 2.2 cm

Question 8.
The distance between two point sources of light is 24 cm. Where should you place a converging lens, of focal length 9 cm, so that the images of both sources are formed at the same point?
Answer:
Given distance between sources = 24 cm;
Focal length of convex lens (f) = 9 cm
Both images are formed at same point i.e., image distance V is same. This will happen when one image is real and another is virtual.

Case – I: Real image let object distance

Case – II: Image is virtual then u₂ = 24 – x

⇒ x (x – 15) = (24 – x) (x – 9)
⇒ x² – 15x = 24x – 9 × 24 – x² + 9x (or) x² – 15x = – x² + 33x – 24 × 9;
⇒ 2x² – 48x + 24 × 9 = 0
∴ x² – 24x – 108 = 0 (or)
(x – 6) (x – 18) = 0
∴ x = 6 cm or x = 18 cm.

Question 9.
Find two positions of an object, placed in front of a concave mirror of focal length 15 cm, so that the image formed is 3 times the size of the object.
Answer:
Focal length of lens (f) = 15 cm;
Magnification (m) = 3 = \(\frac{v}{u}\) ⇒ v = 3u

or 15 × 4 = 60 = 45 ⇒ u = 20 cm.

Case II: Image may be virtual then v is – ve.

∴ 15 × 2 = 2u ⇒ u = 10 cm
The two positions of object are 10 cm, 20 cm.

Question 10.
When using a concave mirror, the magnification is found to be 4 times as much when the object is 25 cm from the mirror as it is with the object at 40 cm from the mirror, the image being real in each case. What is the focal length of the mirror?
Answer:
From given data, u₁ = 40 cm, u₂ = 25 cm

u₁v₁ (u₂ + v₂) = u₂v₂ (u₁ + v₁) ………… (2)
Put v₂ = 2.5 v₁ in equation (2)
∴ 40 v₁ (25 + 2.5 v₁) = 25 × 2.5 v₁ (40 + v₁)
1000 + 100 v₁ = 2500 + 62.5 v₁
⇒ (100 – 62.5) ₁ = 2500 – 1000
⇒ 37.5 ₁ = 1500 (or)

∴ Focal length of concave mirror f = 20 cm.

Question 11.
The focal length of the objective and eyepiece of a compound microscope are 4 cm and 6 cm respectively. If an object is placed at a distance of 6 cm from the objective, what is the magnification produced by the microscope?
Answer:
Focal length of objective (f₀) = 4 cm,
Focal length of eye lens (f_e) = 6 cm.
Object distance (u) = 6 cm.

In microscope generally final image is a virtual image at near point. So magnification of eye piece m_e = (l+D/f_e)
Total magnification of microscope

Intext Question And Answer

Question 1.
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
Answer:
Size of the candle (h) = 2.5 cm ;
Image size = h’
Object distance (u)= – 27 cm
Radius of curvature of the concave mirror (R) = – 36 cm
Focal length of the concave mirror,
f = \(\frac{R}{2}\) = – 18 cm;
Image distance = v
The image distance can be obtained using the mirror formula : \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)

∴ v = -54 cm

Therefore, the screen should be placed 54 cm away from the mirror to obtain a sharp image.

The magnification of the image is given as:

The height of the candle’s image is 5 cm. The negative sign indicates that the image is inverted and real.

If the candle is moved closer to the mirror, then the screen will have to be moved away from the mirror in order to obtain the image.

Question 2.
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
Answer:
Refractive index of glass (µ) = 1.55; Focal length of the double-convex lens, (f) = 20 cm Radius of curvature of one face of the lens = R₁
Radius of curvature of the other face of the lens = R₂
Radius of curvature of the double-convex lens = R
∴ R₁ = R and R₂ = – R
The value of R can be calculated as:

∴ R = 0.55 × 2 × 20 = 22 cm.
Hence, the radius of curvature of the double-convex lens is 22 cm.

Question 3.
A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm, and (b) a concave lens of focal length 16cm?
Answer:
In the given situation, the object is virtual and the image formed is real.
Object distance (u) = +12 cm
(a) Focal length of the convex lens, (f) = 20 cm Image distance = v
According to the lens formula, we have the relation:

Hence the image is formed 7.5 cm away from the lens, toward its right.

(b) Focal length of the concave lens (f) = -16 cm Image distance = v
According to the lens formula, we have the relation:

Hence, the image is formed 48 cm away from the lens, toward its right.

Question 4.
An object of size 3,0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
Answer:
Size of the object (h₁) = 3 cm;
Object distance (u) = – 14 cm
Focal length of the concave lens, (f) = – 21 cm;
Image distance = v
According to the lens formula, we have the relation :

Hence, the image is formed on the other side of the lens, 8.4 cm away from it. The negative sign shows that the image is erect and virtual.

The magnification of the image is given as:

Hence, the height of the image is 1.8 cm
If the object is moved further away from the lens, then the virtual image will move toward the focus of the lens, but not beyond it. The size of the image will decrease with the increase in the object distance.

Question 5.
What is the focal length of a convex lens of focal length 30 cm in contact with a concave lens of fqcal length 20 cm? Is the system a converging or a diverging lens? Ignore thickness of the lenses.
Answer:
Focal length of the convex lens (f₁) = 30 cm;
Focal length of the concave lens (f₂) = – 20 cm
Focal length of the system of lenses = f
The equivalent focal length of a system of two lenses in contact is given as :

Hence, the focal length of the combination of lenses is 60 cm. The negative sign indicates that the system of lenses acts as a diverging lens.

Question 6.
A small telescope has an objective lens of focal length 144 cm and an eyepiece of focal length 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?
Answer:
Focal length of the objective lens (f₀) = 144 cm
Focal length of the eyepiece (f_e) = 6.0 cm
The magnifying power of the telescope is given as : m = \(\frac{f_0}{f_e}=\frac{144}{6}\) = 24

The separation between the objective lens and the eyepiece is calculated as :
f₀ + f_e = 144 + 6 = 150 cm
Hence, the magnifying power of the telescope is 24 and the separation between the objective lens and the eyepiece is 150 cm.

Question 7.
A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
Answer:
Actual depth of the pin (d) = 15 cm
Apparent depth of the pin = d’
Refractive index of glass, (µ) = 1.5
Ratio of actual depth to the apparent depth is equal to the refractive index of glass, i.e.,
µ = \(\frac{d}{d’}\) ∴ d’ = \({\frac{d}{\mu}}=\frac{15}{1.5}\) = 10 cm.

The distance at which the pin appears to be raised = d’ – d = 15 – 10 = 5 cm.

For a small angle of incidence, this dis¬tance does not depend upon the location of the slab.

Question 8.
The image of a small electric bulb fixec on the wall of a room is to be obtained on the opposite wall 3 in away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Answer:
Distance between the object and the image (d) = 3 m
Maximum focal length of the convex lens = f_max
For real images, the maximum focal length is given as:
m_max = \(\frac{d}{4}=\frac{3}{4}\) = 0.75 m
Hence, for the required purpose, the maximum possible focal length of the convex lens is 0.75 m.

Question 9.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
Answer:
Distance between the image (screen) and the object (D) = 90 cm
Distance between two locations of the convex lens (d) = 20 cm
Focal length of the lens = f
Focal length is related to d and D as :

Therefore, the focal length of the convex lens is 21.39 cm.

Question 10.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
Answer:
The incident, refracted, and emergent rays associated with a glass prism ABC are shown in the given figure.

Angle of prism, ∠A = 60°;
Refractive index of the prism, µ = 1.524
i₁ = Incident angle;
r₁ = Refracted angle;
r₂ = Angle of incidence at the face AC
e = Emergent angle = 90°
According to Snell’s law, for face AC, we can have:

It is clear from the figure that angle
A = r₁ + r₂
∴ r₁ A – r₂ = 60 – 41 = 19°
According to Snell’s law, we have the relation:
\(\frac{\sin i_1}{\sin r_1}\)
⇒ sin i₁ = µ sin r₁ = 1.524 × sin 19° = 0.496
∴ i₁ = 29.75°
Hence, the angle of incidence is 29.75°.

Question 11.
You are given prisms made of crown glass and flint glass with a wide variety of angles. Suggest a combination of prisms which will
a) deviate a pencil of white light without much dispersion,
b) disperse (and displace) a pencil of white light without much deviation.
Answer:
a) Place the two prisms beside each other. Make sure that their bases are on the opposite sides of the incident white light, with their faces touching each other. When the white light is incident on the first prism, it will get dispersed. When this dispersed light is incident on the second prism, it will recombine and white light will emerge from the combination of the two prisms.

b) Take the system of the two prisms as suggested in answer (a). Adjust (increase) the angle of the flint-glass-prism so that the deviations due to the combination of the prisms become equal. This combination will disperse the pencil of white light without much deviation.

Question 12.
Does short sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodation? If not, what might cause these defects of vision?
Answer:
A myopic or hypermetropic person can also possess the normal ability of accommodation of the eye-lens. Myopia occurs when the eye-balls get elongated from front to back. Hypermetropia occurs when the eye-balls get shortened. When the eye-lens loses its ability of accommodation, the defect is called presbyopia.

Question 13.
A myopic person has been using spectacles of power – 1.0 dioptre for distant vision. During old age he also needs to use separate reading glass of power + 2.0 dioptres. Explain what may have happened.
Answer:
The power of the spectacles used by the myopic person (P) = – 1.0 D
Focal length of the spectacles,
f = \(\frac{1}{P}=\frac{1}{-1 \times 10^{-2}}\) = – 100cm

Hence, the far point of the person is 100 cm. He might have a normal near point of 25 cm. When he uses the spectacles, the objects placed at infinity produce virtual images at 100 cm. He uses the ability of accommodation of the eye-lens to see the objects placed between 100 cm and 25 cm. During old age, the person uses reading glasses of power, P’ = + 2D.

The ability of accommodation is lost in old age. This defect is called presbyopia. As a result, he is unable to see clearly the objects placed at 25 cm.

Question 14.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to? How is such a defect of vision corrected?
Answer:
In the given case, the person is able to see vertical lines more distincfly than horizontal lines. This means that the refracting system (cornea and eye-lens) of the eye is not working in the same way in different planes. This defect is called astigmatism. The person’s eye has enough curvature in the vertical plane. However, the curvature in the horizontal plane is insufficient. Hence, sharp images of the vertical lines are formed on the retina, but horizontal lines appear blurred. This defect can be corrected by using cylindrical lenses.

Question 15.
a) At what distance should the lens be held from the figure in Exercise 2.29 in order to view the squares distinctly with the maximum possible magnifying power?
b) What is the magnification in this case?
c) Is the magnification equal to the magnifying power in this case? Explain.
Answer:
a) The maximum possible magnification is obtained when the image is formed at the near point (d = 25 cm).
Image distance, υ = – d = – 25 cm; Focal length, f= 10 cm; Object distance = u
According to the lens formula, we have:

Hence, to view the squares distinctly, the lens should be kept 7.14 cm away from them.

Since the image is formed at the near point (25 cm), the magnifying power is equal to the magnitude of magnification.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 1st Lesson Waves Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 1st Lesson Waves

Very Short Answer Type Questions

Question 1.
What does a wave represent?
Answer:
A wave is a disturbance which moves through a medium.

Waves transmit energy without trans-mitting matter. So waves will carry energy from one place to another place.

Question 2.
Distinguish between longitudinal and transverse waves.
Answer:
Longitudinal wave :
If the particles of the medium vibrate parallel to the direction of propagation of the wave then that wave is called “longitudinal wave”.
Ex : Sound waves in air.

These waves can be produced in solids, liquids and gases.

Transverse wave :
If the particles of the medium vibrate perpendicular to the direction of propagation of the wave, then that wave is called “transverse wave”.
Ex : Waves on a stretched string.

These waves can be produced only in solids.

Question 3.
What are the parameters used to describe a progressive harmonic wave?
Answer:
For a progressive wave (y) = a sin (ωt – kx)
The parameters in the above equation
1) a = Amplitude
2) ω = Angular velocity
3) υ = Frequency
4) T = Time period
5) λ = Wavelength
6) v = Velocity (v)
7) Φ = Phase
8) K = Propagation constant.

Question 4.
Obtain an expression for the wave velocity in terms of these parameters.
Answer:
Wave velocity :
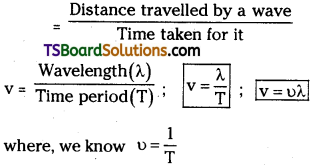
It is the distance travelled by the disturbance (energy) along the wave in one second. It is represented by V.
Wave Velocity ‘v’

Question 5.
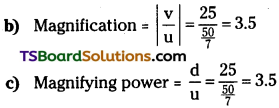
Using dimensional analysis obtain an expression for the speed of transverse waves in a stretched string.
Answer:
Speed of transverse wave in a stretched string depends on tension (T) and linear density (µ).
Let v ∝ T^a µ^b ;
Dimension of velocity (v) = LT^-1
Dimension of tension (T) = MLT^-2 ;
Linear density (p) = ML^-1
∴ v = K T^a µ^b
Where k is a dimensionless constant.
LT^-1 = K (MLT^-2)^a (ML^-1)^b
= M^a L^a T^-2a M^b L^-b
M°L¹T^-1 = M^{a + b} L^a-b T^-2a
Equating the powers of mass, length and time,
a + b = 0, a – b = 1 ⇒ – 2a = – 1

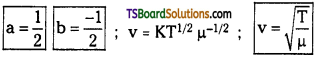
Question 6.
Using dimensional analysis obtain an ex-pression for the speed of sound waves in a medium.
Answer:
Speed of sound depends on wavelength and time period. v ∝ λ^a T^b
Dimensions of Velocity (v) = LT^-1;
Dimensions of Wavelength (λ) = L;
Dimensions of Time period (T) = T;
L¹T^-1 = L^aT^b
a = 1, b = – 1 ; v = λ¹ T^-1
v = \(\frac{\lambda}{\mathrm{T}}\)

Question 7.
What is the principle of superposition of waves?
Answer:
When two waves are pulses overlap at a point the resultant displacement is the al¬gebraic sum of displacements due to each wave. Their resultant is also a wave.
y = (y₁+ y₂)

Question 8.
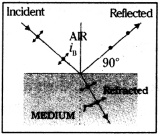
Under what conditions will a wave be reflected?
nswer:
Wave well be reflected if it falls on a rigid surface. Because at rigid surface the particles of medium does not vibrate.

If a wave falls on the interface of two different elastic media, than a Part of two different elastic media, than a part of wave is reflected and a part of incident wave will be refracted. During refraction they obey Snell’s Law.

Question 9.
What is the phase difference between the incident and reflected waves when the wave is reflected by a rigid boundary?
Answer:
At rigid boundary phase difference between the incident and reflected wave = 180° (or) (π). Because at rigid boundary a node is formed.

Question 10.
What is a stationary (or) standing wave?
Answer:
When two progressive waves having same wavelength, amplitude and frequency travelling in the medium in opposite directions superposed stationary waves are formed.

Question 11.
What do you understand by the terms ‘node’ and ‘antinode’?
Answer:
Node :
The point where the displacement is minimum (zero) of a wave is called Node.

Antinode :
The point where the displacement is maximum of a wave is called Antinode.

Question 12.
What is the distance between a node and an antinode in a stationary wave?
Answer:
The distance between a node and an antinode = \(\frac{\lambda}{\mathrm{4}}\)

Question 13.
What do you understand by ‘natural frequency’ or ‘normal mode of vibration’?
Answer:
Natural frequency :
Vibrations produced by a body with elastic properties due to application of a constant force are known as natural frequency.
Ex : For a tuning fork natural frequency depends on elastic nature of the material, the mass distribution and the dimensions of the prongs of the fork.

Question 14.
What are harmonics?
Answer:
A harmonic is defined as a ‘tone’ of sound having a frequency which is an integral multiple of the fundamental frequency.

Question 15.
A string is stretched between two rigid supports. What frequencies of vibration are possible in such a string?
Answer:
The fundamental frequency of vibration and their harmonics are possible if a string is stretched between two rigid supports. If T is the natural frequency of vibration of the string, then possible their harmonics are 2f, 3f, 4f so on.

Question 16.
The air column in a long tube, closed at one end, is set in vibration. What harmonics are possible in the vibrating air column?
Answer:
If the fundamental frequency of the air column is denoted by f, then the frequencies at which the second, third, fourth and later modes occur are 3f, 5f, 7f …………… (2n – 1) f. A closed pipe will support only odd Har-monics.

Question 17.
If the air column in a tube, open at both ends, is set in vibration; what harmonics are possible?
Answer:
If the tube is open at both the ends is set in vibration, the frequencies of the harmonics present in an open pipe are integral multiples of fundamental frequency of the air column. Let f is fundamental frequency then possible harmonics are f, 2f, 3f…. etc.

Question 18.
What are ‘beats’?
Answer:
Beats :
When two sounds of nearly equal frequency are superposed, they will create a waxing and warning intensity of sounds. This affect is called “beats”. Beats are produced due to interference of sound waves.
Beat frequency υ_beat = υ₁ – υ₂

Question 19.
Write down an expression for beat frequency and explain the terms therein.
Answer:
Beat frequency (υ_beat) = υ₁ – υ₂
Where υ₁ and υ₂ are the frequencies is of the two sound waves.

Question 20.
What is ‘Doppler effect’? Give an example.
Answer:
The apparent change in the frequency of source of sound due to relative motion between the source and observer is known as doppler’s effect.
Ex : The whistle of an approaching train appears to have high pitch. When the train is moving away pitch of its whistle decreases.

Question 21.
Write down an expression for the observed frequency when both source and observer are moving relative to each other in the same direction.
Answer:
When source and observer are moving in the same direction equation for observed
(or) apparent frequency υ = υ₀ (\(\frac{v+v_{0}}{v+v_{s}}\))

Short Answer Questions

Question 1.
What are transverse waves? Give illustrative examples of such waves.
Answer:
Transverse Waves :
In these waves, the particles of the medium vibrate perpendicular to the direction of propagation of the wave.

These waves can propagate through solids and liquids.

Let a rope or string fixed at one end. At the other end continuous periodic up and down jerks are given by a external agency then transverse waves are produced.
Example:
Vibrations in strings, ripples on water surface and electromagnetic waves.

Question 2.
What are longitudinal waves? Give illustrative examples of such waves.
Answer:
Longitudinal waves :
In these waves particles of the medium vibrate parallel to the direction of propagation of the wave.

• These waves can propagate through solids and liquids and gases.
• A longitudinal wave travels in the form of compression and rarefaction.
• These waves are also known as “Compression waves”.
• In air sound waves are longitudinal waves.

Example :
Let a long pipe filled with air has a piston at one end. If the piston is pushed and pulled continuously then a series of compressions and rare fractions are produced. It represents a longitudinal wave.

Question 3.
Write an expression for a progressive harmonic wave and explain the various parameters used in the expression.
Answer:
Equation for progressive harmonic wave towards positive x-direction.

where y = displacement at any given time
A = amplitude of wave;
ω = angular velocity
along negative x-direction
y = Asin(ωt + kx)
General expression for wave motion y = A sin (ωt ± kx)

Question 4.
Explain the modes of vibration of a stretched string with examples.
Answer:
Equation of fundamental frequency :
If the wire of length ‘l’ is stretched between points ‘A’ and ‘B’ with tension T vibrates as a single loop then the frequency of the vibrations is known as fundamental frequency and is denoted by ‘υ’.

Than length of the wire (l) = \(\frac{\lambda}{\mathrm{2}}\) ⇒ λ = 2l.
But velocity of a wave (v) = υλ ……………. (1)
In case of stretched strings
v = \(\sqrt{\frac{T}{\mu}}\) …………. (2)
where v is the velocity of transverse vibrations in the string.
T = the tension.
µ = the linear density of the string,
υλ = \(\sqrt{\frac{T}{\mu}}\) (or) υ = \(\frac{1}{\lambda}\) \(\sqrt{\frac{T}{\mu}}\) From (1)
When one loop is formed
∴ υ = \(\frac{1}{2l}\)\(\sqrt{\frac{T}{\mu}}\) (∵ λ = 2l)
If the wire vibrates for p loops, then the frequency υ_p = \(\frac{p}{2l}\)\(\sqrt{\frac{T}{\mu}}\)

Laws of Transverse vibrations in a stretched string:

I. First Law (or) Law of length :
The fundamental frequency of a vibrating string is inversely proportional to the length of the string, when the tension (T) in the string and linear density p are constant.
υ ∝ \(\frac{1}{l}\) ⇒ υl = constant
when T and ‘µ’ are constant.

II. Second law (or) Law of Tension :
The fundamental frequency of a vibrating string is directly proportional to the square root of stretching force T (Tension), when the length of the string and linear density ‘µ’ are constant.
υ ∝ √T ⇒ \(\frac{υ}{\sqrt{T}}\) = constant
when T and ‘µ’ are constant.

III. Third law (or) Law of linear density (or) Law of mass :
The fundamental frequency of a vibrating string is inversely proportional to the square root of the linear density (µ) when the length (l) and tension (T) in the string are constant.

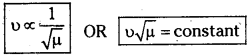
when ‘l’ and ‘T’ are constant

Examples :
An exciting tuning fork, the plucked wire of a stringed instrument, a bell struck with a hammer, a vibrating air column in a trumpet are some of examples of stretched string.

Question 5.
Explain the modes of vibration of an air column in an open pipe.
Answer:
Harmonics in open pipe: In the fundamental mode of vibration, an antinode is formed at each end with a node formed between them.
If ‘l’ is the vibrating length and λ₁ is the corresponding wavelength.
l = \(\frac{\lambda_{1}}{2}\),
The frequency of fundamental mode
(or) 1st harmonic υ₁ = \(\frac{v}{\lambda_{1}}\) ∴ υ₁ = \(\frac{v}{2l}\)

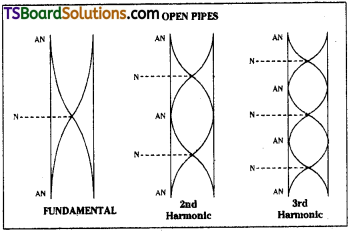
Second Harmonic (or) first overtone :
It will have three antinodes and two nodes.
If λ₂ is the corresponding wavelength

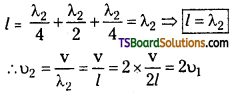
Third harmonic (or) Second overtone :
It will have four antinodes and three nodes. If λ₃ is the corresponding wavelength,

In open pipe harmonics are in the ratio of 1 : 2 : 3 …………..

Question 6.
What do you understand by ‘resonance’? How would you use resonance to deter-mine the velocity of sound in air?
Answer:
Resonance :
If the natural frequency of the body coincides with frequency periodic force impressed on it, then the body is said to be at resonance.

At resonance, the body vibrates with increasing amplitude.

Determination of velocity of sound using Resonance :
Consider a closed tube where air column length can be changed.

For the First resonance :
Length of air column is equal to = l₁ + e = \(\frac{\lambda}{4}\) → (1)

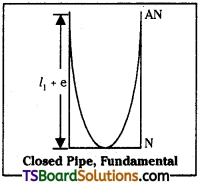
where e is endcorrection

For the Second resonance :
Length of air column is equal to = l₂ + e = \(\frac{3\lambda}{4}\) → (2)

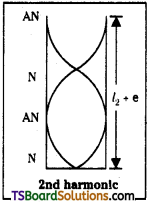
Length of the second resonating air column is approximately equal to three times the length of first resonating air column.
(2) – (1)
l₂ – l₁ = \(\frac{3\lambda}{4}-\frac{\lambda}{4}=\frac{\lambda}{2}\)
⇒ λ = 2(l₂ – l₁)

Velocity of sound in air
v = υλ
v = 2υ(l₂ – l₁)
where υ = the frequency of tuning fork, l₁, l₂ = first and second resonating lengths.

Quetion 7.
What are standing waves? Explain how standing waves may be formed in a stretched string.
Answer:
Stationary waves (or) standing waves :
When a progressive wave and reflected wave superpose with suitable phase a steady wave pattern is set up on the string or in the medium.
A standing wave is represented by y (x, t) = 2a sin kx cos ωt.

Formation of standing waves in stretched strings :
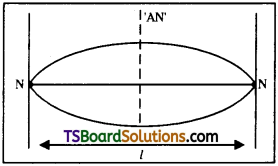
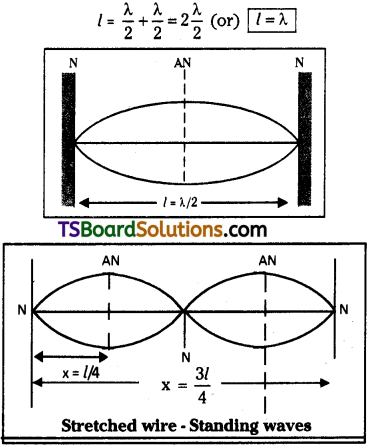
Let a wire of length V and mass’m’ is fixed between two fixed supports with some tension T.
Let the wire is plucked at the mid point then it will vibrate with maximum amplitude. So antinode (A.N) is formed at centre of wire. At the fixed ends molecules of the wire are not free to vibrate. So nodes will be formed at fixed ends as shown in figure.
Now length of wire l = \(\frac{\lambda}{2}\).
If two loops are formed,

Quetion 8.
Describe a procedure for measuring the velocity of sound in a stretched string.
Answer:
Let a wire of length ‘l’ and mass M is fixed between two rigid supports.

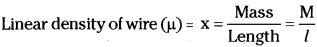
Practical method :
To measure velocity of sound in stretched strings we will adjust length of wire until stationary waves are formed in the given string by means of the tuning fork in the sonometer expt.. When
length of string (l) is equals to \(\frac{\lambda}{2}\)
l = \(\frac{\lambda}{2}\)
But υ = nλ or υ = n × 2l

Question 9.
Explain, using suitable diagrams, the formation of standing waves in a closed pipe. How may of this can be used to determine the frequency of a source of sound?
Answer:
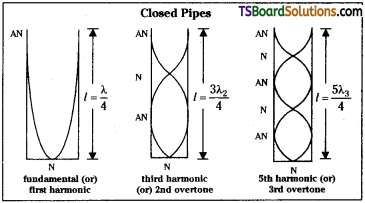
Stationary waves formed in a closed pipe :
If one end is closed and the other end is open, then it is called a ‘Closed pipe’.

Let a longitudinal wave be sent through a closed pipe. It gets reflected at the closed end. These incident and reflected waves which are of same frequency, travelling in opposite directions gets superposed along the length of the pipe. As a result of it, longitudinal stationary waves are formed. In a closed pipe
υ_n = \(\frac{(2n+1)υ}{4l}\)
For 1st harmonic, when n = 0, υ₁ = \(\frac{υ}{4l}\)
For 2nd harmonic, when n = 1, υ₂ = 3\(\frac{υ}{4l}\)
For 3rd harmonic, when n = 2, υ₂ = 5\(\frac{υ}{4l}\)
From resonating air column expt. the frequency of sound can be found by using the formula

Where l₁ ansd l₂ 1st and 2nd resonating lengths and n is the frequency of the tuning fork.

Question 10.
What are ‘beats’? When do they occur? Explain their use, if any.
Answer:
Beats :
When two sounds of nearly equal frequency are superposed, they will create a waxing and warning intensity of sounds. This effect is called “beats”.
Beats are produced due to interference of sound waves.
Beat frequency υ_beat = υ₁ – υ₂

Uses of Beats:

1. To know the frequency of an unknown tuning fork.
2. Harmful gases in a mine can be detected by using beats.

Question 11.
What is ‘Doppler effect’? Give illustrative examples.
Answer:
Doppler effect :
The apparent change in frequency heard by the observer due to the relative motion between source and the observer is called “Doppler’s effect”.

Examples of Doppler effect:

1. The frequency of sound increases as the source moves closer to the observer. Ex: Pitch of the whistle of an approaching train appears to be increased and that of a train going away decreases.
2. In astronomy, the Doppler effect was originally studied in the visible part of the electromagnetic spectrum.

Because of the inverse relationship between frequency and wavelength, we can describe the Doppler shift in terms of wavelengths. Radiation is redshifted when its wavelength increases. It indicates that the stars are moving away and universe is expanding.

Long Answer Questions

Question 1.
Explain the formation of stationary waves in stretched strings and hence deduce the equations for first, second and third harmonics and also deduce the laws of transverse waves is stretched strings. [TS Mar. 19; AP & TS May 18, 16]
Answer:
Stationary wave :
When two progressive waves of same wavelength, amplitude and frequency travelling in opposite directions and superimpose over each other stationary waves (or) standing waves are formed.

Formation of stationary wave in a stretched string:

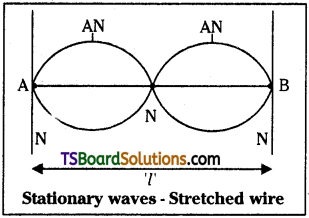
• Let us consider a string of length ‘l’ stretched at the two fixed ends ‘A’ and ‘B’.
• Now pluck the string perpendicular to its length.
• The transverse wave travel along the length of the string and get reflected at fixed ends.
• Due to superimposition of these reflected waves, stationary waves are formed in the string.

Equation of Stationary Wave :
Let two transverse progressive waves having same amplitude ‘A’, wavelength λ and frequency ‘n’; travelling in opposite direction along a stretched string be given by
y₁ = A sin (kx – ωt) and y₂ = A sin (kx + ωt)
where ω = 2πn and k = \(\frac{2 \pi}{\lambda}\)
Applying the principle of superposition of waves, the resultant wave is given by
y = y₁ + y₂
y = A sin (kx – ωt) + A sin (kx + ωt)
y = 2A sin kx cos ωt

Amplitude of resultant wave (2A sin kx) is no more constant. It depends on the
value of kx. When x = 0, \(\frac{\lambda}{2},\frac{2\lambda}{2}.\frac{3\lambda}{2}\), …………… etc.

The amplitude becomes zero.
These positions of zero amplitude are
known as “Nodes”, when x = \(\frac{\lambda}{4},\frac{3\lambda}{4}.\frac{5\lambda}{4}\), ……………. etc. The amplitude becomes 2A (Maximum).
These positions of maximum amplitude are known as “Antinodes”.

Equation of fundamental frequency :
If the wire of length ‘l’ is stretched between points ‘A’ and ‘B’ with tension T vibrates as a single loop then the frequency of the vibrations is known as fundamental frequency and is denoted by ‘υ’.
l = \(\frac{\lambda}{2}\)
But velocity of a wave v = υλ – (1)
In case of stretched strings v = \(\sqrt{\frac{T}{\mu}}\) – (2)
From (1) and (2)
υ = \(\frac{1}{\lambda}\sqrt{\frac{T}{\mu}}\)
∴ υ = \(\frac{1}{2l}\sqrt{\frac{T}{\mu}}\) (∵ λ= 2l)
If the wire vibrates for ‘p’ loops _P If
The frequency = υ_p = \(\frac{p{2l}\sqrt{\frac{T}{\mu}}\)

Formation of harmonics in stretched strings :
From above equation if the wire vibrates with one loop then p =1
Frequency of 1st harmonic υ₁ = \(\frac{1}{2l}\sqrt{\frac{T}{\mu}}\)

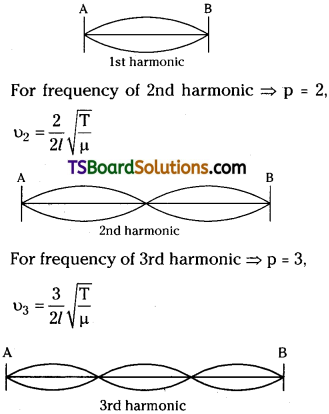
Laws of Transverse vibrations in a stretched string :
I. First Law (or) Law of length :
The fundamental frequency of a vibrating string is inversely proportional to the length of the string, when the tension (T) and its
linear density µ are constant.
υ ∝ \(\frac{1}{l}\) ⇒ υl = constant ⇒ υ₁l₁ = υ₂l₂ (∵ T, µ are constant)

II. Second law (or) Law of Tension :
The fundamental frequency of a vibrating string is directly proportional to the square root of stretching force T (Tension), when the length of the string l and linear density ‘µ’ are constant.

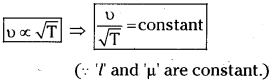
III. Third law (or) Law of linear density :
The fundamental frequency of a vibrating string is inversely proportional to the square root of the linear density (m) when the length (l) and tension (T) in the string are constant.

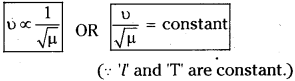
Question 2.
Explain the formation of stationary waves in an air column enclosed in open pipe. Derive the equation for the frequencies of harmonics produced. [(TS May 17, Mar. 16; AP Mar. 18, 17, 16, May 17, 14)]
Answer:
Formation of stationary wave in open pipe :
An open pipe is a cylindrical tube having air inside with both ends open.

Let a longitudinal wave pass through the organ pipe. It gets reflected at the end of the pipe. These incident and reflected waves which are of same frequency, travelling in opposite directions, get superposed along the length of the pipe.

As a result of it, longitudinal stationary waves are formed.

At the open end, the particles of the medium are free to vibrate and the incident and reflected waves will be in phase, so particles have maximum displacement, forming antinode. Thus the air column in- side a open pipe is set into vibration due to stationary waves formed in it with anti- node at each open end.

Harmonics in open pipe :
Fundamental :
In the fundamental mode of vibration, an antinode is formed at each end and a node is formed between them. The note produced is called first harmonic.

If ‘l’ is the vibrating length and λ₁ is the corresponding wavelength.

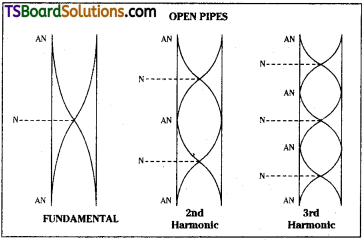
Second Harmonic (or) first overtone :
2nd harmonic consists of three antinodes and two nodes.

If λ₂ is the corresponding wavelength

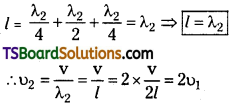
Third harmonic or Second overtone :
3rd harmonic consists of four antinodes and three nodes. If λ₃ is the corresponding wavelength,

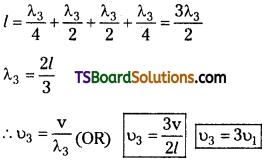
The ratio of harmonics in open pipes υ₁ : υ₂ : υ₂ : = 1 : 2 : 3 …………

Question 3.
How are stationary waves formed in closed pipes? Explain the various modes of vibrations and obtain relations for their frequencies. [T.S. Mar. ’19, ’15, May, June ’15; AP Mar. June ’15, May ’17, ’16]
Answer:
A closed pipe is a cylindrical tube having air inside, one end closed and the other is open.

Let a longitudinal wave be sent through a closed pipe. It gets reflected at the closed end of the pipe. These incident and reflected waves, which are of same frequency, trav-elling in opposite directions gets superposed as a result longitudinal stationary waves are formed.

At the closed end reflection is on a rigid surface a node is formed at closed end, at the open end antinode is formed.

I. Harmonics in a closed pipe :
Fundamental mode (or) First Harmonic :
In this one node and one antinode is formed. If ‘l’ is the vibrating length and λ₁ is the corresponding wavelength.

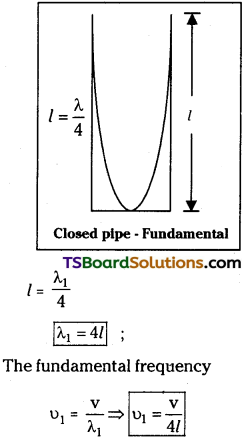
II. First overtone or Third Harmonic :

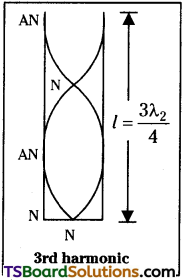
1st overtone consists of two nodes and two antinodes. If ‘l’ is the vibrating length and λ₃ is the corresponding wavelength,

as third Harmonic or first overtone.

III. Fifth Harmonic or Second overtone :
2nd overtone consists of three nodes and three antinodes.

If ‘l’ is the vibrating length, λ₅ is the corresponding wavelength,

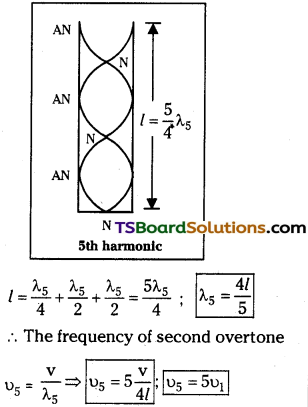
υ₅ is called fifth Harmonic.

The ratio of harmonics in closed pipe is υ₁ : υ₃ : υ₅ : = 1 : 3 : 5 : ………….

From the above, in closed pipe only odd Harmonics are formed.

Question 4.
What are beats? Obtain an expression for the beat frequency. Where and how are beats made use of?
Answer:
When two sounds of nearly (or) slightly equal frequency are superposed they will create a waxing and warning intensity of sounds. This effect is called “beats”.

Beats are produced due to interference of sound waves.

Beat frequency ubeat υ_beat = υ₁ ~ υ₂

Expression for beat frequency:

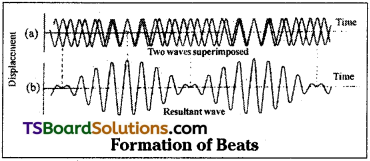
Let us consider two sound waves y₁ and y₂ of nearly equal frequency ‘υ₁‘ and ‘υ₂‘ each of amplitude a’ superpose each other then the resultant wave is given by
y = y₁ + y₂ = a sin ω₁t + a sin ω₂t.
where ω₁ = 2πυ₁ and ω₂ = 2πυ₂;
∴ y = a sin 2πυ₁t + a sin 2πυ₂t

The frequency of the resultant wave is \(\frac{υ_1+υ_2}{2}\)
The frequency of the amplitude is \(\frac{υ_1-υ_2}{2}\)

The intensity of the sound will be maximum when 2a cos 2π(\(\frac{υ_1-υ_2}{2}\)) is maximum.

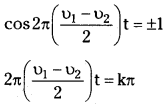
Where k = 0, 1, 2, …………. maximum sound will be heard at interval
0, \(\frac{1}{υ_1-υ_2},\frac{2}{υ_1-υ_2},\frac{3}{υ_1-υ_2}\)
The time interval between two consecutive maxima = \(\frac{1}{υ_1-υ_2}\)
or, Beat frequency = υ₁ – υ₂
The intensity of sound will be minimum when cos 2π(\(\frac{υ_1-υ_2}{2}\))t is minimum i.e., zero.
The time interval between two consecutive minima = \(\frac{1}{υ_1-υ_2}\)
The number of minima heard per second = υ₁ ~ υ₂

Importance of Beats: Beats can be used

1. in tuning musical instruments.
2. to detect dangerous gases in mines.
3. to produce special effects in cinematography.
4. to determine unknown frequency of a tuning fork.
5. in heterodyne receivers range.

Question 5.
What is Doppler effect? Obtain an expression for the apparent frequency of sound heard when the source is in motion with respect to an observer at rest. [(AP Mar. 16, 14; TS Mar. 18, 17]
Answer:
Doppler effect :
The apparent change in the frequency heard by the observer due to relative motion between the observer and the source of sound is called “Doppler effect”.

Expression for apparent frequency when source is in motion and observer at rest:
Let ‘s’ be a source of sound moving with a velocity v_s away from a stationary observer. Let the source produces a sound of frequency υ₀ and its time period is T₀.
At time t = 0 the source produces a crest.

Let the distance between source and observer is ‘L’ and velocity of sound is ‘v’.
Then time taken by observer to detect crest = t₁ = \(\frac{L}{v}\) ……… (1)
The second crest is produced after a time interval T₀.

Distance travelled by source during this time = v_sT₀. So total distance from observer = L + v_sT₀
Time taken to detect 2nd crest

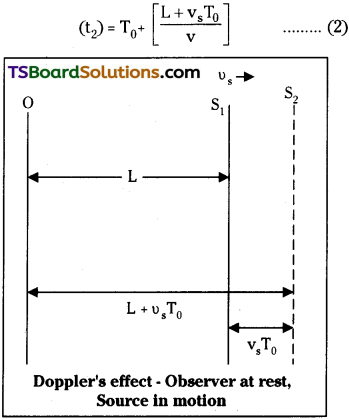
Let the source produced (n + 1)th crest at time nT₀.
Now time taken to detect that crest =

So apparent frequency υ < υ₀.
If source is moving towards observer, then v_s is -ve (as per sign convension).
∴ apparent frequency υ = υ₀ [1 – \(\frac{(-v_s)}{v}\)]
= υ₀ [1 + \(\frac{v_s}{v}\)]
When source is approaching the observer frequency heard υ = υ₀(\(\frac{v+v_s}{v}\)) OR
υ = υ₀ [1 + \(\frac{v_s}{v}\)]. In this case apparent frequency heard υ > υ₀.

Question 6.
What is Doppler shift? Obtain an expression for the apparent frequency of sound heard when the observer is in motion with respect to a source at rest. [AP June ’15]
Answer:
Doppler shift :
The difference between apparent frequency heard by observer and actual frequency produced by the source is called as “Doppler’s shift”.

Derivation of apparent frequency when source at rest and observer in motion :
Let s’ is a source at rest produces a sound of constant frequency ‘υ₀‘ Let Time Period of wave is ‘T₀‘. Let an observer is moving away from source with a velocity ‘v₀‘.

Carries a device that can count the num-ber of crests / compressions produced by source.

At time t = 0 source produces a crest. Let the distance between source and observer is L’ and velocity of sound is ‘v’.

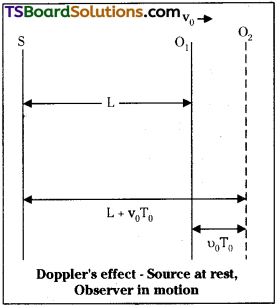
Now time taken by the observer to detect the crest t₁ = \(\frac{L}{v}\) → 1

2nd crest is produced after a time period T₀.
During this time observer moves a distance v₀T₀
time taken by observer to detect t₂ = T₀ + (\(\frac{L+T_{0}v_{0}}{v}\)) → 2
Let source produces (n + 1) th crest after a time nT₀
Time taken to detect this crest

Solved Problems

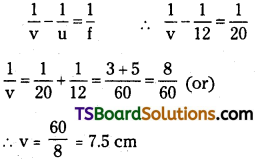
Question 1.
A stretched wire of length 0.6 m is observed to vibrate with a frequency of 30 Hz in the fundamental mode. If the string has a linear mass of 0.05 kg/m find (a) the velocity of propagation of transverse waves in the string (b) the tension in the string. [AP May 18; TS May 16]
Answer:
Vibrating length (l) = 0.6 m
For fundamental mode l = \(\frac{\lambda}{2}\)
⇒ λ = 2l = 2 × 0.6 ⇒ λ = 1.2 m
Fundamental frequency n = 30 Hz
a) Velocity of transverse wave v = nλ ;
v = 30 × 1.2 ⇒ v = 36 ms^-1

b) Linear density of the string
µ = 0.05 kg m^-1
But, v = \(\sqrt{\frac{T}{\mu}}\) (T is the tension)
T = v²µ = 36 × 36 × 0.05 = 64.8 N.

Question 2.
A steel cable of diameter 3 cm is kept under a tension of 10 kN. The density of steel is 7.8g/cm³. With what speed would transverse waves propagate along the cable?
Answer:
The density of steel is
ρ = 7.8 gm cm^-3 ⇒ 7.8 × 10³ kgm^-3
Diameter of cable D = 3 cm
⇒ r = 1.5 × 10^-2 m
Tension (T) = 10 × 10³ N.

Question 3.
Two progressive transverse waves given by y₁ = 0.07 sin π (12x – 500t) and y₂ = 0.07 sin π (12x + 500t) travelling along a stretched string form nodes and antinodes. What is the displacement at the (a) nodes (b) antinodes? (c) What is the wavelength of the standing wave?
Answer:
Equation of progressive wave is
y₁ = 0.07 sin (12πx – 500 πt) ;
y₂ = 0.07 sin (12πx + 500 πt)
a) Displacement at node = 0
b) Displacement at Antinode = 2A = 2 × 0.07 = 0.14 m.
c) Propagation constant k = 12π

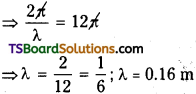
Question 4.
A string has a length of 0.4 m and a mass of 0.16 g. If the tension in the string is 70 N, what are the three lowest frequencies it produces when plucked?
Answer:
Length of string (l) = 0.4 m
Mass of the string (m) = 0.16 × 10^-3kg ;
Linear density (µ) = \(\frac{0.16}{0.4}\) = 4 × 10^-4 kg m^-1
Tension (T) = 70 N.
Fundamental frequency υ₁ = \(\frac{1}{2l}\sqrt{\frac{T}{\mu}}\) ;

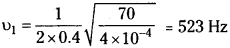
Next frequency is υ₂ = 2υ₁
= 2 × 523 = 1046 Hz

Next frequency is υ₃ = 3υ₁
= 3 × 523 = 1569 Hz

Question 5.
A metal bar when clamped at its centre, resonates in its fundamental frequency with longitudinal waves of frequency 4 kHz. If the clamp is moved to one end, what will be its fundamental resonance frequency?
Answer:
Fundamental frequency (υ) = 4 × 10³ Hz
a) If metal bar is clamped at its centre

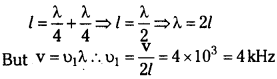
b) If metal is clamped at one end

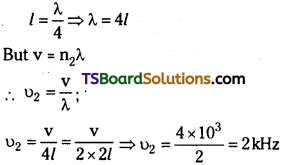
Question 6.
A closed organ pipe 70 cm long is sounded. If the velocity of sound is 331 m/s, what is the fundamental frequency of vibration of the air column? [TS Mar. ’19; AP Mar. 18, I 7, May 1 7, 14]
Answer:
Length of closed organ pipe l = 70 cm
Velocity of sound (v) = 331 ms^-1
Fundamental frequency of closed pipe

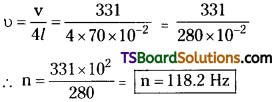
Question 7.
A vertical tube is made to stand in water so that the water level can be adjusted. Sound waves of frequency 320 Hz are sent into the top the tube. If standing waves are produced at two successive water lev-els of 20 cm and 73 cm, what is the speed of sound waves in the air in the tube?
Answer:
Frequency of sound wave (n) = 320 Hz
1st resonating length l₁ = 20 cm
2nd resonating length l₂ = 73 m
Speed of sound wave (v) = 2n (l₂ – l₁)
= 2 × 320 (73 – 20)
∴ v = 640 × 53 × 10^-2
= 33920 cm s^-1 = 339 ms^-1

Question 8.
Two organ pipes of lengths 65 cm and 70 cm respectively, are sounded simultaneously. How many beats per second will be produced between the fundamental frequencies of the two pipes? (Velocity of sound = 330 m/s).
Answer:
First open organ pipe of length (l₁) = 65 cm
Second open organ pipe of length (l₂) = 70 cm

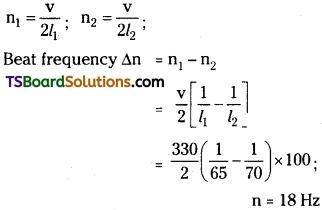
Question 9.
A train sounds its whistle as it approaches and crosses a level-crossing. An observer at the crossing measures a frequency of 219 Hz as the train approaches and a frequency of 184 Hz as it leaves. If the speed of sound is taken to be 340 m/s, in the speed of the train and the frequency of its whistle.
Answer:
a) Speed of sound (v) = 340 ms^-1 ;
Apparent frequency heard by observer when train approaches υ’ = 219 Hz

When train leaves the observer ap-parent frequency n” = 184 Hz

Question 10.
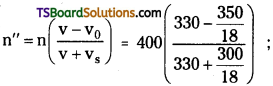
Two trucks heading in opposite directions with speeds of 60 kmph and 70 kmph respectively, approach each other. The ckiver of the first truck sounds his horn of frequency 400 Hz. What frequency does the driver of the second truck hear? (Velocity of sound = 330 m/s). After the two trucks have passed each other, what frequency does of the second truck hear?
Answer:
Speed of first truck = 60 × \(\frac{5}{18}\) = v_s
Speed of second truck = 70 × \(\frac{5}{18}\) = v₀
Frequency of first truck n = 400 Hz ;
Velocity of sound = 330 ms^-1

a) When they approach each other, frequency heard by second truck driver is

∴ Apparent frequency (n’) = 600 Hz b)

b) When they move away from each other, the frequency heard by second truck driver

∴ Apparent frequency υ” = 270 Hz

Question 11.
A rocket is moving at a speed of 200 ms^-1 towards a stationary target. While moving, it emits a wave of frequency 1000 Hz. Calculate the frequency of the sound as detected by the target. (Velocity of sound in air is 330 ms^-1) [AP Mar. ’16]
Answer:
Velocity of source (Rocket) (V_s) = 200 m/s
Velocity of sound (V) = 330 m/s.
Frequency of sound emitted (υ₀) = 1000 Hz

Frequency of sound heard by observer υ = 2540 Hz.

Question 12.
A open organ pipe 85 cm long is sounded. If the velocity of sound is 340 m/s, what is the fundamental frequency of vibration of the air column? [TS Mar. ’16]
Answer:
Length of pipe (l) = 85 cm,
Velocity of sound (V) = 340 m/s.
Fundamental frequency of open pipe = n
= \(\frac{V}{2l}\)
n = \(\frac{340 \times 100}{2 \times 85}\) = 200Hz
∴ Fundamental frequency (n) = 200 Hz.

Question 13.
A pipe 30 cm long is open at both ends. Find the fundamental frequency. Velocity of sound in air is 330 ms-1.
Answer:
Length of open pipe (l) = 30 cm;
Velocity of sound (V) = 330 ms^-1
At fundamental frequency λ = 2l.
⇒ λ = 30 × 2 = 60 cm = 0.6 m
Fundamental frequency
v = \(\frac{V}{\lambda}=\frac{330}{0.6}\) = 550 Hz.

Question 14.
If the fundamental frequency in a closed pipe is 300Hz, find the value of third har¬monic in it. [TS June ’15]
Answer:
Fundamental frequencies (v₁) = 300Hz
Frequencies of 3rd Harmonic (v₃) = 3v₁
= 300 × 3 = 900Hz
Note: In closed pipes, the harmonics are in the ratio 1:3:5 even harmonic does not exist.

Intext Question and Answer

Question 1.
A string of mass 2.50 kg is under a tension of 200 N. Then length of the stretched string is 20.0 m. If the transverse jerk is caused at one end of the string, how long does the disturbance take to reach the other end?
Answer:
Mass of the string, (M) = 2.5 kg
Tension in the string, (T) = 200 N
Length of the string (l) = 20 m
Linear density (µ) = mass per unit length = \(\frac{M}{l}=\frac{2.5}{20}\) = 0.125 kgm^-1
Velocity of transverse wave in the string is

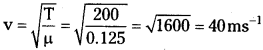
∴ Time taken by the disturbance to reach the other end, t = \(\frac{l}{v}=\frac{20}{40}\) = 0.5 s.

Question 2.
A stone dropped from the top of a tower of height 300 m splashes into the a pond of water near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 ms^-1? (g = 9.8 ms^-2)
Answer:
Height of the tower (n) = 300 m
Initial velocity (u) = 0
Acceleration due to gravity, g = 9.8 m/s²
Speed of sound = 340 ms^-1
The time (t₁) taken by the stone to strike the water in the pond can be calculated using

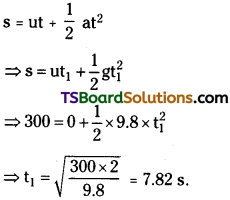
Time taken (t₂) by the sound to reach the top of the tower, t₂ = \(\frac{h}{u}=\frac{300}{340}\) = 0.88 s
∴ Total time after the splash is heard,
t = t₁ + t₂ = 7.82 + 0.88 = 8.7 s.

Question 3.
A steel wire has a length of 12 in and a mass of 2.1 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20°C = 343 ms^-1.
Answer:
Length of the wire (l) = 12 m ;
Mass of the wire (M) = 2.1 kg
Linear density (µ) = mass per unit length
= \(\frac{M}{l}=\frac{2.1kg}{12m}\) = 0.175 kgm^-1
We know that velocity of a transverse wave in a stretched string is given by
v = \(\sqrt{\frac{T}{\mu}}\) ⇒ v²µ = (343)² × 0.175
= 20588 × 575 N ≅ 2.06 × 10⁴ N.

Question 4.
A bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound? Speed of sound in air is 340 ms-1 and in water 1486 ms^-1.
Answer
a) Frequency of ultrasonic sound,
n = 1000 kHz = 10⁶ Hz
Speed of sound (v_a) = 340 ms^-1
The wavelength (λ_r) of the reflected sound is given by
λ_r = \(\frac{υ_{a}}{n}=\frac{340}{10^{6}}\) = 3.4 × 10^-4 m

b) Frequency of the ultrasonic sound,
n = 1000 kHz = 10⁶ Hz
Speed of sound in water, υ_w = 1486 ms^-1.
The wavelength (λ_r) of the reflected sound is given by
λ_r = \(\frac{υ_{w}}{n}=\frac{1486}{10^{6}}\) = 1.49 × 10^-3 m

Question 5.
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound is 1.7 kms^-1? The operating frequency of the scanner is 4.2 MHz.
Answer:
Speed of sound in the tissue,
v = 1.7 km s^-1 = 1.7 × 10³ ms^-1
Operating frequency of the scanner,
n = 4.2 MHz = 4.2 × 10⁶ Hz
The wavelength of sound in the tissue is
λ = \(\frac{\mathrm{v}}{\mathrm{n}}=\frac{1.7 \times 10^3}{4.2 \times 10^6}\) = 4.1 × 10^-4 m

Question 6.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10^-2 kg and its linear mass density is 4.0 × 10^-2 kg m^-1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
Answer:
a) Mass of the wire, M = 3.5 × 10^-2 kg m^-1

The wavelength (λ) of the stationary wave is related to the length of the wire by the relation
λ = \(\frac{2l}{n}\)
where n → no. of nodes in the wire
For fundamental node, n = 1
λ = 2l = 2 × 0.875 = 1650 m.
The speed of the transverse wave is given by
v = nλ = 4.5 × 1.75
= 78.75 ms^-1

b) The tension produced in the string is given by the formula
T = v²m = (78.75)² × 4 × 10^-2
= 248.06 N.

Question 7.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
Answer:
Length of the steel rod, l = 100 cm = 1 m.
Fundamental frequency of vibration,
n = 2.53 kHz = 2.53 × 10³ Hz

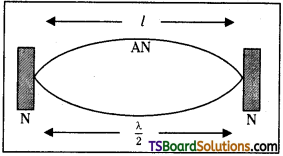
When the rod is plucked at its middle, an antinode is formed at its centre and nodes (N) are formed at its two ends as shown in the given figure.
The distance between two successive nodes is \(\frac{\lambda}{2}\).
∴ l = \(\frac{\lambda}{2}\)
⇒ λ = 2l = 2 × l = 2m
The speed of sound in steel is given by the relation:
v = nλ= 2.53 × 10³ × 2
= 5.06 × 10³ ms^-1
= 5.06 kms^-1

Question 8.
A train, standing at the outer signal of a railway station blows a whistle of freq-uency 400 Hz in still air.
i) What is the frequency of the whistle for a platform observer when the train
a) approaches the platform with a speed of 10 ms^-1,
b) recedes from the platform with a speed of 10 ms^-1?
ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 ms^-1.
Answer:
i) a) Frequency of the whistle (n) = 400 Hz
Speed of the train (v_t) = 10 ms^-1
Speed of sound (v) = 340 ms^-1
The apparent frequency (n’) of the whistle as the train approaches the platform is given by the relation

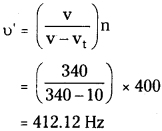
b) The apparent frequency (n’) of the whistle as the train recedes from the platform is given by the relation :

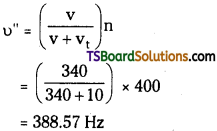
ii) The apparent change in frequency of sound is caused by the relative motions of the source and the observer. These relative motions produce no effect on the speed of sound. Therefore, the speed of sound in air in both the cases remains the same i.e., 340 ms^-1.

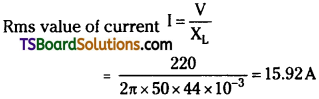
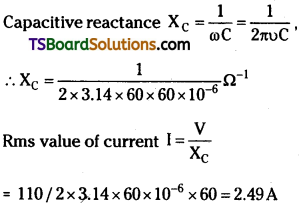
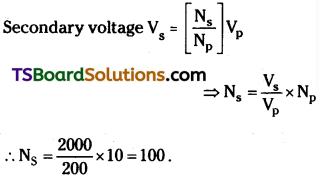
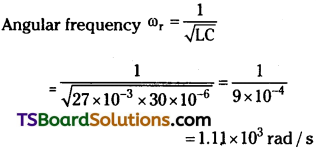
Telangana TSBIE TS Inter 2nd Year Zoology Study Material 8th Lesson Applied Biology Textbook Questions and Answers.

TS Inter 2nd Year Zoology Study Material 8th Lesson Applied Biology

Very Short Answer Type Questions

Question 1.
What factors constitute dairying?
Answer:
Breeding, feeding and management of milch animals, production, processing and marketing of their milk and milk products on economic basis constitute dairying.

Question 2.
Mention any two advantages of inbreeding.
Answer:
Two advantages of inbreeding :

1. Inbreeding increases homozygosity.
2. It helps in the accumulation of superior genes and elimination of less desirable genes.

Question 3.
Distinguish betwen out-cross and cross-breed.
Answer:
Outcrossing is the crossing of unrelated pure breeding animals of different traits with in the same breed whereas cross-breeding is the mating of animals of different breeds.

Question 4.
Define the terms layer and broiler. [Mar. ’17,’15 (A.P.)]
Answer:

1. The birds which are raised exclusively for the production of eggs are called Layers.
2. The birds which are raised only for their meat are called Broilers.

Question 5.
What is apiculture? [Mar. ’20, 17, May 17 (A.P); Mar. ’15 (T.S); Mar. ’14]
Answer:
Apiculture or Beekeeping is the maintenance of hives of honey bees for the production of honey and wax. Beekeeping is an age old cottage industry.

Question 6.
Distinguish between a drone and worker in a honey bee colony.
Answer:

1. Drones are robust, large winged small numbered, short lived and fed with bee bread by nurse workers. They are developed from unfertilized ova by arrhenotoky (male parthenogenesis).
2. Worker bees are multifaceted sterile females which develop from the fertilised eggs and peform diverse functions. They live for two or three months. They are very small in size.

Question 7.
Define the term Fishery.
Answer:
Exploitation of fish and other related aquatic organisms is called Fishery.

Question 8.
Differentiate aquaculture and pisciculture.
Answer:

1. Aquaculture or culture fishery involves rearing and management of selected aquatic organisms under regulated conditions and their subsequent harvesting after the stipulated time.
2. The term PISCICULTURE is used when the organisms cultured and exclusively fin fishes.

Question 9.
Explain the term hypophysation. [March 2015 (T.S.)]
Answer:
Hypophysation or induced breeding is followed in artificial breeding. Pituitary extracts containing FSH and LH or ovaprim are injected into brood fish to induce release of spawn for seed production.

Question 10.
List out any two Indian carps and two exotic carps. [March 2018 (A.P.); May / June 2014]
Answer:

1. Two Indian carps are catla Catla (catla) and Cirrhinus mrigala (mrigai).
2. Two exotic carps are Cyprinus carpio (Chinese carp), Tilapia (grass carp).

Question 11.
Mention any four fish by-products. [March 2019]
Answer:
Four fish by products are

1. Shark and cod liver oils containing vit A and vit D.
2. Oil from Sardine and Salmon – good source of omega – 3 fatty acids.
   (prevent cancer cel! growth, lowers blood cholesterol)
3. Fish guano – Fertiliser prepared from scrap fish.
4. Shagreen.

Question 12.
How many amino acids and polypeptide chains are present in insulin? [March 2019]
Answer:
Human insulin is made up of 51 aminoacids arranged in two polypeptide chains chain A (21 amino adds) and chian B (30 – amino acids).

Question 13.
Define the term ’vaccine’.
Answer:
The term vaccine was coined by Edward Jenner. A vaccine is a biological preparation that improves immunity to a particular disease.

Question 14.
Mention any two features of PCR.
Answer:

1. Polymerase Chain Reaction (PCR) is a powerful technique to identify many other genetic disorders such as haemophilia, phenylketonuria etc.
2. PCR helps to detect very Sow amounts of DNA by amplification of the small DNA fragment.

Question 15.
What does ADA stand for? Deficiency of ADA causes which disease?
Answer:
ADA stands for Adenosine De Aminase. ADA deficiency causes severe combined immune deficiency (SCID). It is caused by the deletion or dysfunction of the gene encoding for the enzyme ADA.

Question 16.
Define the term transgenic animal.
Answer:
Animals that have their own geneome and had their DNA manipulated to possess and express an extra gene are known as transgenic animals.

Question 17.
What is popularly called ‘Guardian Angel of Cell’s Genome’? [March 2020]
Answer:
The protein p53 plays an important role with reference to the G1 check point in the regulation of cell division cycle. It guards the integrity of the DNA. Hence it is often called the Guardian Angel of Cell’s Genome.

Question 18.
List out any four features of cancer cells. [May 2007 (A.P.)]
Answer:
Characters of cancer cells :

1. These cells are characterised by indefinite growth.
2. These cells are with out contact inhibition.
3. These cells are characterised by evading apoptosis (no death).
4. These cells a typical of parent autonomons and aggressive.

Question 19.
How do we obtain radiographs?
Answer:
A beam of X-rays is produced by an X-ray generator and is projected on the body parts. X-rays that pass through the body parts are recorded on a photographic film or observed on a fluorescent screen. Photographs developed using X-rays are known as radiographs or skiagraphs.

Question 20.
What is tomogram?
Answer:
The X-ray detector of the CT-scanner can see hundreds of different levels of density and tissues in a solid organ. The data is transmitted to a computer which builds up 3-D cross sectional picture of the part of the body and displays the picture on the screen. This recorded image is called tomogram.

Question 21.
MRI scan in harmless-justify. [March 2018 (A.P.); May/June 2014]
Answer:
MRI (Magnetic Resonance Imaging) scan is harmless because MRI does not use ionizing radiation as involved in X-rays and is generally a very safe procedure.

Question 22.
What is electrocardiography and what are the normal components of ECG? [March 2015 (A.P.)]
Answer:
Electrocardiography (ECG) is a commonly used, non invasive procedure for recording electrical changes in the heart.
A normal ECG consists 1) Waves 2) Intervals 3) Segments and 4) Complexes.

Question 23.
What does prolonged P-R interval indicate?
Answer:
Prolonged P-R interval indicates delay in conduction of impulses from S-A node to the A-V node. P-R interval is prolonged in bradycardia (slow beating of heart) and shortened in tachycardia (fast beating of heart).

Question 24.
Differentiate between primary and secondary antibodies.
Answer:

1. Primary antibodies react with the antigens of interest.
2. Secondary antibodies react with primary antibodies.

Question 25.
Which substances in a sample are detected by direct and indirect ELISA respectively? [March 2014]
Answer:
Direct ELISA – ELISA used to detect antigens.
Indirect ELISA – ELISA done to detect antibodies.

Short Answer type Questions

Question 1.
What are the various methods employed in animal breeding to improve livestock?
Answer:
Methods of animal breeding : There are broadly two methods of breeding :

1. INBREEDING
2. OUTBREEDING.

1) Inbreeding :
When crossing is done between animals of the same breed it is called inbreeding. It refers to mating of more closely related individuals within the same breed of individuals in a lineage. The breeding strategy is the identification and mating of superior males and superior females of the same breed.

Inbreeding is of two types :
1) Close breeding,
2) Line breeding.,
Close breeding is mating between male parent (sire) and female offspring and / or female (dam) with male offspring. Line breeding (cousin mating) is the selective breeding of animals for a desired feature by mating them within a closely related line (but not as close as close breeding). It leads to upgrading (to improve the quality of livestock by selective breeding for desired characteristics) of a desired commerical character.

2) Outbreeding :
Out-breeding is the breeding of the unrelated animals; it is the cross between different breeds. Out-breeding is of three types

1. Out-crossing
2. Cross-breeding
3. Interspecific hybridisation.

1. Out-crossing :
It is the practice of mating of animals within the same breed, but having no common ancestors on either side of the pedigree for 4-6 generations. The offspring of such a mating is known as an out-cross. It is the best breeding method for animals that are below average in milk production, growth rate (in beef cattle) etc. At times a single out-cross often helps to overcome inbreeding depression.

2. Cross-breeding :
In this method, superior males of one breed are mated with superior females of another breed. The offspring of such a mating is said to be a cross-breed. Cross-breeding allows the desirable qualities of two different breeds to be combined. The progeny (cross breeds) are not only used for commercial production but also inbreeding and selection to develop stable breeds which may be superior to existing breeds.

3. Interspecific hybridisation :
In this method, male and female animals of two different related species are mated. The progeny may combine desirable features of both the parents and is different from both the parents. For example when a male donkey (jack / ass) is crossed with a female horse (mare), it leads to the production of a mule.

Question 2.
Define the term ‘breed’. What are the objectives of animal breeding?
Answer:
Animal Breeding :
Animal breeding is an important aspect of animal husbandry which aims at increasing the yield of animals and improving the desirable qualities of the produce. A breed is a group of animals related by descent and similar in most characters like appearance, features, size, configuration, etc. The following are the desirable qualities for which we breed animals :

1. Disease resistance,
2. Increase in the quality and quantity of milk, meat, wool, etc.
3. Fast growth rate,
4. Enhanced productive life by improving the genetic merit of livestock,
5. Early maturity and
6. Economy of feed.

Question 3.
Explain the role of animal husbandry in human welfare.
Answer:
Animal Husbandry :
The strategies adopted for enhancing food production are bound to play a major role in meeting the requirement of food for the ever increasing world’s population in the near future. The biological principles that are applied to animal husbandry will become crucial in our efforts to increase the food production.

Animal husbandry is the agricultural practice of breeding and raising livestock (all domesticated animals reared for the benefit of man). It includes buffaloes, cows, pigs, horses, cattle, sheep, camels, goats etc. However the term livestock is often used for farm animals. If extended, it also includes poultry farming and fisheries.

Even though the estimated world’s livestock population in India and China together is more than 70%, their contribution to world’s farm produce is only 25%, i.e., the productivity per unit is very low. The average annual milk yield is about 170 liters per cow in India. Contrary to it, the average annual milk yield is about 4,100 liters per cow in Netherlands.

Because of its low productivity the Indian cow is known as ‘teacup cow’. So, newer technologies have to be applied to achieve improvement in quality and productivity. Modern methods of breeding, MOET (multiple ovulation and embryo transfer) and production of transgenic animals must be taken up on a large scale in addition to conventional practices and care.

Question 4.
List out the various steps involved in MOET.
Answer:
Multiple Ovulation and Embryo Transfer (MOET) :
The following are the steps invovled in MOET.

1. A cow is administered hormones, with FSH-like activity.
2. This induces follicular maturation and super ovulation (In super ovulation- instead of one egg, which they normally produce per cycle, they produce 6-8 eggs).
3. The animal (cow) is either mated with an elite buli or artificially inseminated.
4. The embroys are at 8-32 celled stages are recovered non-surgically and transferred to surrogate mother (an animal that develops the offspring of another animal in its womb).

Now the genetic mother is ready for another round of super ovulation.

Question 5.
Write short notes on controlled breeding experiments.
Answer:
Controlled Breeding Experiments :
They are carried out using artificial insemination and multiple ovulation and embryo transfer technology (MOET).

Artificial insemination (Al) is the technique in which semen is collected from superior bulls and introduced into the famale reproductive tract when the female is in ‘heat’. This semen can be used immediately or can be frozen and used at a later period. It can be transported in a forzen form to the place where a female is housed. In this way desirable crosses can be made. The major advantage of Al over natural mating is that it permits the dairy farmer to use top proven sires (males) for genetic improvement of his herd and control of venereal diseases. Al is also tremendous value in making optimal use of different sires and enables dairy farmer to breed individual cows to selected sires according to their breeding goals.

The breeding centre at SALON in Rae Bareli is at present the breeder and producer of top quality frozen semen of pure exotic breeds.

Multiple Ovulation and Embryo Transfer (MOET) :
The following are the steps invovled in MOET.

1. A cow is administered hormones, with FSH-like activity.
2. This induces follicular maturation and super ovulation (In super ovulation-instead of one egg, which they normally produce per cycle, they produce 6-8 eggs).
3. The animal (cow) is either mated with an elite bull or artificially inseminated.
4. The embroys are at 8-32 celled stages are recovered non-surgically and transferred to surrogate mother (an animal that develops the offspring of another animal in its womb).

Now the genetic mother is ready for another round of super ovulation.

Question 6.
Explain the important components of poultry management.
Answer:
Important Components of Poultry Management:
1) Selection of disease free and suitable breeds :
The selected breed should get acclimatised to a wide range of climatic conditions. Hybrid layers used in India are BV-300, Hyline, Poona pearls, etc. Commercial broiler strains used in India include Hubbard, Vencobb, etc.

2) Feed management (proper feed and water) :
Balanced diet is a must to maximise the yield. Brooder / chick mash, grower mash, prelayer mash and layer mash are fed to layers at different ages. Likewise pre starter mash, starter mash and finish mash are the feed given to broilers. ‘Safe water’ should be supplied through waterers at all times.

3) Health care :
Vaccination against viral diseases (Ranikhet, Marek’s, and Gumboro) and using antibiotics to treat bacterial diseases {Fowl cholera, Infectious coryza, Chronic Respiratory Disease (CRD)} make the poultry birds disease free. Fungal diseases affecting poultry are Brooder’s pneumonia. Aflatoxicosis and Thrush.

4) In addition to the above, hygiene, proper and safe farm conditions ensure better produce.

Question 7.
Discuss in brief about ‘Avian Flu’. [March 2020]
Answer:
AVIAN FLU (BIRD FLU) is an important disease affecting poultry birds and man has to be very watchful about this disease as it is very dangerous to him too. Causative organism : Bird flu is caused by an ‘avian flu virus’, the H5N1. The virus that causes the bird infection infects human too. It can start a worldwide epidemic (Pandemic disease).

Mode of infection : Infection may be spread simply by touching contaminated surfaces. Birds infected by this type of influenza, continue to release the virus as in their faeces and saliva for as long as 10 days.

Symptoms :
Infection by the avian influenza virus H5N1 in humans causes typical flu-like symptoms, which might include : cough (dry or with phlegm), diarrhoea, difficulty in breathing, fever, headache, malaise, muscle aches and sore throat.

Prevention:

1. Avoiding consumption of undercooked chicken meat reduces the risk of exposure to avian flu.
2. People who work with birds should use protective clothing and special breathing masks.
3. Complete culling of infected flock by burying or burning them.

Question 8.
Explain in brief about queen bee. [May/June 2014]
Answer:
QUEEN :
It is the individual in the colony; It is a fertile, diploid female, one per bee hive and the egg layer of the colony. She lives for about five years and her only function is to lay eggs. The queen bee during its nuptial flight receives sperms from a drone and stores in the spermatecae and lays two types of eggs, the fertilised and unfertilised. All fertilised eggs develop into females. All the larvae developing from the fertilised eggs are fed with the royal jelly (vitamin and nutrient rich secretion from the glands in the hypopharynx of the nurse workers) for the first 4 days only. Afterwards royal jelly is fed only to the bee that is bound to develop into next queen, whereas the other larvae fed on bee bread (honey and pollen) become workers (sterile females).

Question 9.
Honey bees are economically important-justify.
Answer:
Economic importance of Honey bees; The bee products like Honey, wax, propolis and bee venom are used in various ways.

1. Honey is a rich source of fructose, water, glucose, minerals and vitamins.
2. Bee’s wax is used in the preparation of cosmetics, polishes of various kinds and candles.
3. Propolis is used in the treament of inflammation and superficial burns.
4. Bee’s venom, which is extracted from the sting of worker bees, is used in the treatment of rheumatoid arthritis.
5. Pollination : Bees are the pollinators of our crop plants such as sunflower, brassica, apple and pear.

Question 10.
What are the various factors required for bee keeping?
Answer:
Factors / requirements for successful Beekeeping :

1. Knowledge of nature and habits of honey bees.
2. Selection of suitable location (termed Apiary or Bee yard) for keeping the beehives.
3. Raising a hive with the help of a queen and small group of worker bees.
4. Management of beehives during different seasons.
5. Handling and collection of honey and bee wax.

Question 11.
Fisheries have carved a niche in Indian economy-explain.
Answer:
Economic Importance of Fishery :
1. As Food :
Fish meat, in general, is a good source of proteins, vitamins (A and D), minerals and rich in iodine. Tunas, shrimps and crabs are not only edible but have export value also.

2. By-products:
A) Shark and cod liver oils are good sources of vitamins A and D. Oil from Sardine and Salmon are good sources of omega 3 fatty acids, which have multiple functions (reduce cholesterol, help prevent cancer cell growth etc.)
B) Fish guano : Fertilizer prepared from ‘scrap fish’.
C) Other fish by-products are shagreen, Isinglass (substance obtained from dried swim bladders of mostly cat fish, used in clarification of wines) etc.

Fisheries have carved a niche in the Indian economy. We now talk about ‘Blue Revolution’ as being implemented on lines similar to ‘Green Revolution’.

In addition to pisciculture, the culture of prawns, crabs and pear! oysters enable us earn foreign exchange worth millions of dollars from their exports.

Question 12.
Explain in brief structure of Insulin. [March 2015 (A.P.)]
Answer:

Structure of insulin :
Human insulin is made up of 51 amino acids arranged in two polypeptide chains – chain A (21 amino acids) and chain B (30 amino acids), which are linked together by disulphide linkages. In mammals, including humans, insulin is synthesised as a prohormone (like a pro-enzyme, which needs to be processed before it becomes fully mature and functional hormone) which contains an extra stretch called the c peptide. This c peptide is not present in the mature insulin and is removed during maturation into insulin.

The main challenge for the production of insulin in the laboratory using rDNA technique was getting insulin assembled into its mature form.

Question 13.
Define vaccine and discuss about types of vaccines.
Answer:
Vaccines :
The term ‘vaccine’ was coined by Edward Jenner. He immunised a boy against small pox by inoculating him with a relatively less dangerous cow pox virus. The technique of attenuating or weakening of a microbe was developed by Pasteur.

A vaccine is a biological preparation that improves immunity to a particular disease. A vaccine typically contains the disease causing microorganism and is often made from weakened of killed forms of the microbe. The toxins or one of the surface proteins of the microorganisms are also used in preparing vaccines.

The following are some important Biotechnologically produced vaccines.
1. Attenuated Whole Agent Vaccines :
They contain disabled (made iess virulent) live microorganisms. Mostly they are antiviral. Examples: Vaccines against yellow fever, measles, rubella, and mumps and the bacterial disease such as typhoid.

2. Inactivated Whole Agent Vaccines :
They contain “killed microbes’ (virulent before killing). Examples : Vaccines against influenza, cholera, bubonic plague, polio, hepatitis A, rabies and Sabin’s oral polio vaccine.

3. Toxoids :
They contain ‘toxoids’ which are inactivated ‘exotoxins’ of certain microbes. Examples : The vaccines against Diphtheria and Tetanus.

Thus, vaccines are used in the prevention of diseases as they induce artificially acquired active immunity.

Question 14.
Write in brief the types of gene therapy.
Answer:
Gene therapy is the insertion of genes into an individual’s cells and tissues to treat a disease such as a heriditary disease in which a deleterious mutant allele is replaced with a functional one.

Types of Gene Therapy :
Two basic types of gene therapy can be applied to humans, germ line and somatic line.

Germ line gene therapy :
In this type of therapy, functional genes (normal genes) are introduced into sperms or ova and are thus integrated into their genomes. Therefore the change or modification becomes heritable. Due to various technical and ethical reasons, the germ line gene therapy remained at the ‘infant stage’ for the time being.

Somatic line therapy :
In this type of therapy, functional genes are introduced into somatic cells of a patient. The approach is to correct a disease phenotype by treating some somatic cells in the affected person. The changes effected in this type of GT are non-heritable.

Somatic line therapy can be either ex-vivo or in vivo. In ex-vivo, cells are modified outside the body and then transplanted back. In in-vivo, genes are changed in cells, while they are still inside the body.

Question 15.
List out any four salient features of cancer cells.
Answer:
Salient features of Cancer cells :

1. These cells are characterised by indefinite growth.
2. These cells are without contact inhibition.
3. Divide eratically, with increased cell division rate.
4. These cells are characterised by evading apoptosis (no death).
5. These cells are with mutated genes.
6. These cells are atypical of parent autonomous and aggressive.
7. Antigens on the surface are abnormal.
8. These are with unusual number of chromosomes.
9. These cells are spherical due to less number of microfilaments.
10. The cells detach and exhibit metastasis as cadherins either partly or entirely missing.
11. Unlimited growth potential due to over abundance of telomerase, enzyme. [Note : You can select any 4 salient features from the given 11 points.]

Question 16.
Explain the different types of cancers. [Mar. ’18(A.P.); Mar. ’15 (T.S.); Mar. ’14]
Answer:
Types of cancers :
There are different types of cancers such as carcinomas (cancers of epithelial tissues / cells which are most common as epithelial cells divide more often), sarcomas (cancers of connective tissues), leukemias (cancers of bone marrow cells resulting in understrained production of WBC – a liquid tumor), lymphomas (cancers of the lymphatic system). Certain types of cancers are called ‘familial cancers’ (cancer that occurs in families; genetic based) and others ‘sporadic cancers’ (non-hereditary cancers occurring without any family history). Some types of cancers are caused by ‘tumor forming RNA viruses’ (oncoviruses), e.g. Rous sarcoma virus which causes ‘avian sarcoma’.

Question 17.
Write about the procedure involved in MRI. [Mar. 2017, May ’17 (A.P.)]
Answer:
MRI scan (Magnetic Resonance Imaging) is a diagnostic Radiology Technique. MRI is a non invasive medical imaging technique that helps physicians diagnose certain anatomical abnormalities or pathological conditions.

MRI scanner and procedure :
MRI scanner is a giant circular magnetic tube. The patient is placed on a movable bed that is inserted into the magnet. Human body is mainly composed of water molecules which contain two hydrogen nuclei /protons, each. The magnet creates a strong ‘magnetic field’ that makes these protons align with the direction of the magnetic field (protons are not aligned under normal conditions). A second radiofrequency electromagnetic field is then turned on for a ‘brief period’. The ‘protons’ absorb some energy from these ‘radio waves’. When this ‘second radio frequency emitting field’ is turned off, the protons release energy at a radiofrequency which can be detected by the MRI scanner (the protons return to their ‘equilibrium state’ from the ‘energized state’ at different ‘relaxation’ rates).

Question 18.
Write briefly about different waves and intervals in an ECG. [March 2019]
Answer:
Waves :
The waves in a normal record are named: P, Q, R, S, and T, in that order. A typical ECG tracing of a normal heartbeat (or cardiac cycle) consists of I. a ‘P’ wave, II. a ‘QRS complex’ of ‘waves’, III. a T wave.

P wave :
It represents the ‘atrial depolarization or atrial systole’. P wave shows that the impulse is passing through the atria. The normal duration of a P wave is -0.1 sec.

QRS complex of ‘waves’:
(Ventricular depolarization / ventricular systole) i) Q wave is a small negative wave, ii) R wave is a tall positive wave, iii) S wave is a negative wave. The normal duration of QRS complex of waves is about 0.08 – 0.1 sec.

T wave is a positive wave. It represents the ventricular repolarisation. Its duration is 0.2 sec.

Intervals:

1. P-R interval is the interval between the onset of P wave and the onset of Q wave. P-R interval is normally 0.12 – 02 sec.
2. Q-T interval is the interval between the onset of Q wave and the end of the T wave. It represents the electrical activity in the muscle of the ventricles (ventricular depolarisation). ‘QT Interval’ is dependent on the ‘heart rate’ (the ‘faster’ the ‘heart rate’ – the ‘shorter’ the interval). It lasts for about 0.4 sec.
3. R-R interval signifies the duration of one ‘cardiac cycle’ and it lasts for about 0. 8 sec. (60/72 = 0.8 sec.).

Question 19.
Discuss briefly the process of indirect ELISA.
Answer:
Indirect ELISA :
It is used to detect antibodies. The blood of the person undergoing the ‘assay’ (for example the HIV test) is allowed to clot and the cells are centrifuged out to obtain the clear serum with antibodies (called primary antibodies).

Protocol:

1. It is used to detect antibodies.
2. A known ‘antigen’ is added to the ‘well’ (adsorbed).
3. Patient’s antiserum (serum with specific antibodies) is added.
4. The ‘antibodies’ in the patient’s ‘antiserum’ (primary / complementary antibodies) bind to the antigens coated on the surface of the ‘well’.
5. Enzyme linked antihuman serum globulins (anti HISGs) are added. They bind to the antibody which is already bound to the antigen.
6. Enzyme’s substrate is added and the reaction produces a visible colour change which can be measured by a spectrophotometer.

Question 20.
Write short note on EEG.
Answer:
EEG :
Electroencephalography is the process of recording the electrical activity of the brain (graphical recording called electroencephalogram) with the help of an EEG machine and some ‘electrodes’ placed all over the scalp. Electro¬encephalograph is a very useful tool in diagnosing neurological and sleep disorders. The changed EEG patterns in the case of ‘epilepsy’ are conveniently studied with the help of an EEG. Brain shows continuous electrical activity of innumerable neurons.

The intensity and pattern of electrical activity depends on wakefulness, sleep, coma, certain pathological and phychological conditions. The main diagnostic application of EEG in neurological studies is the diagnosis of epilepsy (seizures). EEG shows distinct abnormal pattern in the case of epilepsy. EEG is also useful in the diagnosis of ‘coma’ and ‘brain death’. EEG studies are useful in analyzing sleep disorders (such as insomnia).

Waves of EEG :
The waves recorded by an EEG consist of

1. Synchronized waves which are common in normal healthy people and
2. In certain neurological conditions the waves are desynchronized (irregular wave pattern). The wave pattern can be broadly classified into ALPHA, BETA, THETA and DELTA wave patterns. The nature of the waves depends on the intensity of activity of the different parts of the cerebral cortex.

Long Answer Type Questions

Question 1.
Write in detail about out breeding.
Answer:
Out breeding :
Out-breeding is the breeding of the unrelated animals; it is the cross between different breeds. Out-breeding is of three types

1. Out-crossing
2. Cross-breeding
3. Interspecific hybridisation.

1. Out-crossing :
It is the practice of mating of animals within the same breed, but having no common ancestors on either side of the pedigree for 4-6 generations. The offspring of such a matting is known as an out-cross. It is the best breeding method for animals that are below average in milk production, growth rate (in beef cattle) etc. At times a single out-cross often helps to overcome inbreeding depression.

2. Cross-breeding :
In this method, superior males of one breed are mated with superior females of another breed. The offspring of such a mating is said to be a cross-breed. Cross-breeding allows the desirable qualities of two different breeds to be combined. The progeny (cross breeds) are not only used for commercial production but also inbreeding and selection to develoop stable breeds which may be superior to existing breeds. For example, Hisardale is a new breed of sheep developed in Punjab by crossing ‘Bikaneri ewes’ and ‘Marino rams’.

3. Interspecific hybridisation :
In this method, male and female animals of two different related species are mated. The progeny may combine desirable features of both the parents and is different from both the parents. For example when a male donkey (jack / ass) is crossed with a female horse (mare), it leads to the production of a mule (sterile). Similarly when a male horse (stallion) is crossed with a female donkey (jennet), hinny (sterile) is produced. Mules have considerable economic value.
Jack / ass X mare = mule; Stallion X Jenne thinny.

Question 2.
Explain in detail clinical inferences from ECG.
Answer:
ECG may mean electrocardiogram / electrocardiograph, but most commonly used for electrocardiogram. Electrocardiography is a commonly used, non-invasive procedure for recording electrical changes in the heart. The graphic record, which is called an electrocardiogram (ECG or EKG), shows the series of waves that relate to the electrical impulses which occur during each cardiac cycle. An electrocardiograph is a device which records the electrical activity of the heart muscle (depolarisations and repolarisations).

What is electrocardiography?
Electrocardiography is the technique by which the electrical activities of the heart are studied. Sensors (electrodes) are placed at specific parts of the body and linked to the ECG machine. ECG is recorded using 12 ‘LEADS’ (sensors from limbs and chest). Obtaining an electrocardiogram typically takes a few minutes, after which the electrodes are removed.

Clinical Inferences from ECG :

1. Enlarged P wave, indicates enlarged atria.
2. Variations in the duration, amplitude and morphology of the QRS complex indicate disorders such as bundle branch block (block of conduction of impulses through the branches of the bundle of His).
3. If the duration of the P-R interval is prolonged, it indicates delay in conduction of impulses from S-A node (pace maker) to the A-V node. P-R interval is prolonged in ‘bradycardia’ (slow beating of the heart) and shortened in ‘tachycardia’ (fast beating of the heart).
4. Prolonged Q-Tinterval indicates myocardial infarction (Ml) and hypothyroidism. Shortened Q-T interval indicates ‘hypercalcemia’.
5. Elevated S-Tsegment indicates myocardial infarction.
6. Tall T wave indicates hyperkalemia; small, flat or inverted T wave indicates hypokalemia.