TS Inter 2nd Year Physics Study Material Chapter 3 Wave Optics

Telangana TSBIE TS Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics

Very Short Answer Type Questions

Question 1.
What is Fresnel distance?
Answer:
Fresnel distance :
The term z = a²/λ is called “Fresnel distance”.

In explaining the spreading of beam due to diffraction we will use the equation z = a²/λ.

Where after travelling a distance zλ/a size of beam is comparable to size of slit (or) hole a’.

Question 2.
Give the justification for validity of ray optics.
Answer:
The wavelength of light is very small. For larger distances and objects of large size we will completely neglect the wave nature of light. In this case, we believe that light will travel in straight lines. Principles of geometry are used to explain various phenomena like reflection and refraction.

Fresnel distance z = a²/λ suggested that for distances far greater than ‘z’ ray optics is valid in the limit wavelength tends to zero.

Question 3.
What is polarisation of light?
Answer:
Polarisation :
It is a process in which vibrations of electric vectors of light are made to oscillate in a single direction.
Ex : Let a light wave is represented by y (x, t) = a sin (kx – ωt)
Here the displacement is in y – direction. So it is referred as y – polarised wave.

Question 4.
What is Malus’law? [TS May ’17]
Answer:
Mains’ Law :
Let two polaroids say P₁ and P₂ are arranged with some angle ‘0’ between their axes. Then intensity of light coming out of them is I = I₀ cos² θ

Where I₀ is intensity of polarised light after passing through 1^st polaroid P₁. This is known as Malus’ Law.

Question 5.
Explain Brewster’s law. [AP June 15; TS May 16]
Answer:
The angle of incidence i_B for which the reflected ray is plane polarised is called Brewster angle.

Explanation:
At Brewster angle i_B + r = \(\frac{\pi}{2}\)

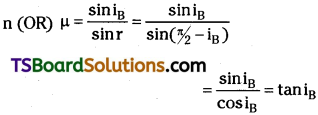
∴ The tangent of Brewster’s angle tan (i_B) is equals to refractive index. This is called “Brewster’s Law” i.e, µ = tan i_B.

Question 6.
When does a monochromatic beam of light incident on a reflective surface get completely transmitted?
Answer:
Laser beam is a monochromatic light. Let a laser beam is passed through a polariser and made to fall on a prism with Brewster’s angle. Now rotate the polariser carefully, for a particular angle of incidence we can not get reflected ray from prism. Which implies that the total light is transmitted through prism.

Short Answer Questions

Question 1.
Explain Doppler effect in light. Distinguish between red shift and blue shift. [TS Mar. 19, 16; May 15; AP Mar. 16, June 15, May 18]
Answer:
Doppler’s effect in light :
When there is relative motion between source and observer then there is a change in frequency of light received by the observer.

Red shift :
If the source moves away from the observer then frequency measured by observer is less i.e., wavelength increases As a result wave length of received light moves towards red colour. This is known as “red shift”.

Blue shift :
When source of light is approaching the observer frequency of light received decreases, i.e., wavelength of light decreases. As a result wavelength of received light will move towards blue colour. This is known as “blue shift”.

Question 2.
What is total internal reflection? Explain the phenomenon using Huygens principle.
Answer:
Total internal reflection :
When light travels from denser medium to rarer medium then for angle of incidence i > i_c i.e., (critical angle) light rays are not able to cross boundary layer between the media and simply come back into the same medium. This phenomena is known as “total internal reflection”.

Explanation :
From Huygens wave theory velocity of light in medium is high. So refracted ray will bend towards normal.

When light rays are travelling from denser medium to rarer medium they will bend away from normal.

As angle of incidence ‘i’ increases then angle of refraction ‘r’ will also increase.

For a particular value of i angle of refraction r will become 90° this angle of incidence in denser medium is called critical angle.

When angle of incidence i > i_c (critical angle) the ‘r’ is more than 90° we cannot have any refracted ray. The incident ray will simply come back into the same medium. This is called total internal reflection.

Question 3.
Derive the expression for the intensity at a point where interference of light occurs. Arrive at the conditions for maximum and zero intensity. [AP Mar. 18, 16. 15; TS May 18, Mar. 15]
Answer:
In young’s experiment two pinholes (S₁, S₂) are made on a black card board with a separation’d’ between them. Light coming from a pinhole ‘S’ will fall on these two pinholes (S₁, S₂) and spherical waves are produced. A screen (G, G₁) is placed at a distance D from the slits. This is as shown in fig.

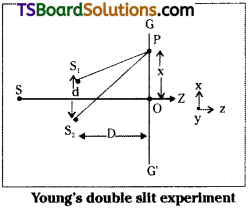
From theory of interference when the two light waves are superposed at ‘P’. We will get bright band when path difference is nλ we will get dark band when path difference is (n + \(\frac{1}{2}\))λ.

Condition for maximum intensity :
For maximum intensity path difference S₂P – S₁P = nλ
From fig . [S₂P]² – [S₁P]² =

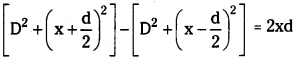
or S₂P – S₁P = 2xd /(S₂P + S₁P) …………. (1)
When D >> and D >> d then S₂P + S₁P ≅ 2D
∴ S₂P – S₁P = \(\frac{2xd}{2D}\)nλ (or) x = nλ\(\frac{D}{d}\) ………….. (2)
For dark band or zero intensity
S₂P – S₁P = (n + \(\frac{1}{2}\))λ
From eq. (1)
∴ S₂P – S₁P = 2xd/S₂P + S₁P use S₂P + S₁P = 2D
For zero intensity
S₂P – S₁P = \(\frac{2xd}{2D}\) = (n + \(\frac{1}{2}\))λ
∴ x = (n + \(\frac{1}{2}\))λ \(\frac{D}{d}\) For dark band.
Where x is distance from centre of screen and n is a ‘+Ve’ integer.

Question 4.
Does the principle of conservation of energy hold for interference and diffraction phenomena? Explain briefly. [AP May 16 ; Mar. 17. 14]
Answer:
In case of interference and diffraction we are getting a series of dark and bright bands. While forming these bands with maximum and minimum intensity law of conservation of energy holds good.

In interference and diffraction pattern energy is redistributed, i.e,, energy is reduced in one region (dark band). This energy is superposed on another region. Where it appears bright.

So in interference and diffraction pattern redistribution of energy in the regions of dark and bright bands takes place. But there is no loss of energy or creation of energy. Hence these two phenomena will obey Law of conservation of energy.

Question 5.
How do you determine the resolving power of your eye? [AP Mar. 19, 17, May 14; TS Mar. 18]
Answer:
To find resolving power of eye draw black bands of equal width say 5mm with a separation of 0.5mm between them. Gradually increase the width of gap (white strip) between to black bands form 0.5 to 1mm and 1 mm to 1.5 mm etc. after every two white bands.

Paste that paper on a wall. Wnen your distance from wall is very high – you will see only a dark band, i.e., all dark bands merged into a single band. When you are approaching the wall the bands seems to be separated into two groups with one white band between them. Now measure distance ‘D’ from wall and also spacing between black bands, (d) (i.e., width of white band)

Resolving power of eye = d/D
In this way we can find resolving power of our eye.

Question 6.
Explain polarisation of light by reflection and arrive at Brewster’s law from it. [Mar. ’15]
Answer:
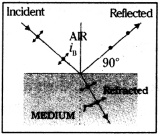
Polarisation by reflection :
When unpolarised light falls on the boundary layer separating two transparent media the reflected light is found to be partially polarised. The amount of polarisation depends on angle of incidence i.

When reflected ray and refracted ray are perpendicular the reflected ray is found to be totally plane polarised. The angle of incidence at this stage is known as Brewster angle.

Brewster’s Law :
The particular angle of incidence (i_B) for which the reflected ray is plane polarised is called “Brewster angle”.

Explanation :
At Brewster angle i_B + r = \(\frac{\pi}{2}\)

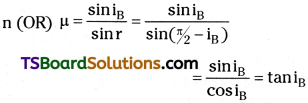
The tangent of Brewster’s angle tan (i_B) is equals to refractive index of the reflection medium. This is called “Breswter’s law”, i.e,

Question 7.
Explain polarisation by reflection with diagram and state Brewster’s law. [May ’16]
Answer:
When unpolarised light falls on the boundary of two transparent media then reflected light is found to be plane polarised. The electric vectors are vibrating perpendicular to plane of incidence.

The percentage of polarised light gradually increases with angle of incidence. For a particular angle of incidence the reflected light is totally plane polarised. This particular angle of incidence is called Brewester angle (i_B).

Brewster angle :
The angle of incidence for which the reflected light is totally plane polarised is called Brewster angle (i_B).
At Brewster angle
Refractive index n (or)

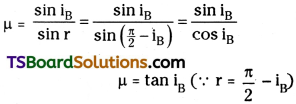
So the tangent of Brewster angle is numerically equals to refractive index of the medium on which light rays are falling. This is called “Brewster’s law”.

Question 8.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids.
Answer:
Let two polaroids say P₁ and P₂ are arranged one at the back of other. Allow unpolarised light to fall on PF first. The transmitted light through P₁ is made to fall on P₂.

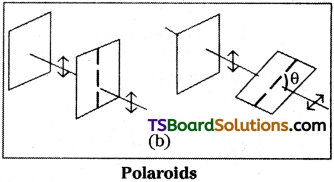
When polaroid P₁ is rotated there is no change in the intensity of transmitted light. Intensity of unpolarised light after passing through P₁ is reduced to half of initial value.

Let the pass axis of polaroid P₂ makes on angle ‘θ’ with pass axis of polariod P₁. When θ = 0 i.e., the two pass axes coincides the ail the light entered P₂ will come out.

If polaroid P₂ is gradually rotated the intensity of light coming out of P₂ gradually decreases. It becomes zero when θ = \(\frac{\pi}{2}\) i.e., the two pass axes are perpendicular to each other.

Intensity of output light through polaroid P₂ will fallow the equation I = I₀ cos² θ.

Where I₀ is intensity of light coming from P₁

This equation I = I₀ cos² θ is called Malus’Law.

Long Answer Questions

Question 1.
What is Huygens Principle? Explain the optical phenomenon of refraction using Huygens principle.
Answer:
Huygens principle :
Each point of the wave front is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave. These wavelets emanating from the wavefront are usually referred to as secondary wavelets.

From Huygens principle, every wave is a secondary wave to the preceding wave.

Wavefront :
The locus of points which oscillate in phase is called “wavefront”. (OR)
A wave front is defined as a surface of constant phase.

Refraction of a plane wave :
Let PP’ is the boundary layer between the medium 1 and 2. Let AB is a plane wave falling on the boundary layer. Draw a normal at A to the boundary. Angle between A’ A and normal angle of incidence ‘i’. Draw normal to wave-front from A. It will touch at B. Let time taken by BC to reach boundary is t. Then BC = v₁t. Now draw a circle with radius R = v₂t from A.

Draw a tangent from C on to this arc. Now CE represents the wavefront of refracted ray in the medium 2.

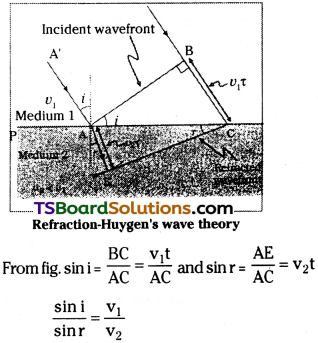
If r < i, then velocity v₂ in the medium is less and refracted ray will bend towards normal.

Let c’ is velocity of light in vacuum then n₁ = \(\frac{c}{v_1}\) and n₂ = \(\frac{c}{v_2}\). Then n₁ sin i = n₂ sin r. This is known as Snell’s Law.

If λ₁ and λ₂ represent the wavelengths, then

Hence in refraction wavelength λ and velocity v will decrease. But frequency ‘v’ is constant.

Question 2.
Distinguish between Coherent and Incoherent addition of waves. Develop the theory of constructive and destructive interferences.
Answer:
Coherent waves :
In coherent waves at a particular point in the medium, the phase difference between the displacements produced by each wave is constant.

In case of Incoherent waves the phase difference between the two waves reaching a given point in medium changes with time.

Let two waves say y₁ = a cos ωt and y₂ = a cos ωt reaches a point ‘P’ in a medium.
Then resultant displacement y = y₁ + y₂ = 2a cos ωt

Intensity I = 4I₀ (Intensity α amplitude)

Constructive interference :
For constructive interference the two waves reaching the point P must be in same phase i.e., Φ = 0 or phase difference Φ must be 2π, 4π, …………. 2πn (or) path difference must be
λ, 2λ ……….. nλ.

Let the distance travelled by the two waves in reaching a point Q is S₁Q and S₂Q
Now S₂Q – S₁Q = λ
Then y₁ = a cos ωt and y₂ = a cos (ωt – π)
= a cos ωt.
∴ Due to super position of waves y= y₁ + y₂ = a cos ωt + a cos ωt = 2 a cos ωt
Intensity I = 4a² = 4I₀
But Intensity I₀ = a² and intensity I ∝ amplitude² (a²)

Destructive interference :
For destructive interference the two waves must reach the given point with a phase of π. i.e., a path difference of λ/2.
At point Q, Path difference of the two waves is S₂Q – S₁Q = λ/2.
∴ y₁ = a cos ωt and y₂ = a cos (ωt – π)

Now the two waves will suffer destructive interference and resultant amplitude is zero.
∴ Intensity I = 0

Theory :
Let two coherent waves have a constant phase difference Φ between them.
Then y₁ = a cos cot and y₂ = a cos (ωt + Φ)
Due to super position y = y₁ + y₂ = a cos ωt + a cos (ωt + Φ)
= a [cos ωt + cos (ωt + Φ)] = 2a cos (Φ/2) cos (ωt + Φ/2)
Amplitude of new wave is 2a cos (Φ/2)

Intensity I = (2 a cos Φ/2)² = 4a² cos² (Φ/2)
When Φ = 0, 2π, 4π even multiples of π we will get I = 4a².
This is called bright band.
When Φ = π, 3π ………. odd multiples of π i.e., (2n + 1) π then I = 0
This is called dark band.
When Incoherent waves are used their phase difference changes with time i.e., Φ is not constant. So we will use average values = 4I₀ < cos² Φ/2 >
cos Φ/2 oscillates between 0 to 1. So average value is 1/2
∴ Average value of intensity = 4I₀ × \(\frac{1}{2}\) = 2I₀
So intensities will just add up.

Question 3.
Describe Young’s experiment for observing interference and hence arrive at the expression for ‘fringe width’.
Answer:
In Young’s experiment light coming from a source is allowed to pass through a pin hole s’. The light coming form is made to fall on slits S₁ and S₂ made on a black card board. Separation between the slits is d’. Since S₁ and S₂ are illuminated from the same source light waves coming from S₁ and S₂ are coherent waves with some fixed phase difference.

Let a screen GG is placed at a distance ‘D’ from the black card board to observe interference pattern.

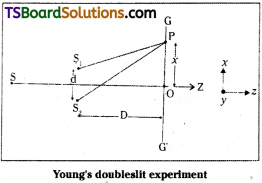
The spherical waves coming from S₁ and S₂ will interfere at a point ‘P’ on the screen. Let distance of ‘P’ from centre of screen is ‘x’.

Expression for fringe width :
To produce maximum intensity (bright band) the two light waves arriving at point P must be in phase, i.e., phase difference between them is ‘0’ or 2π, 4π ……….. This corresponds to a path difference of 0, λ, 2λ …………. nλ.
∴ Path difference = S₂P – S₁P = nλ ………… (1)
But from figure (S₂P)² – (S₁P)²

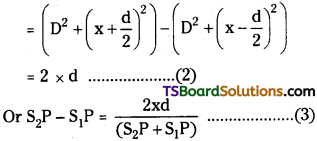
But x and d are very small when compared to distance between slit and screen D.

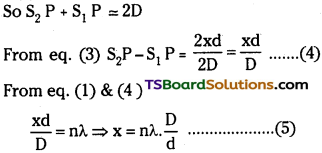
This is the condition for Bright Band.

Formation of dark band :
For formation of dark band the two light waves reaching the point ‘P’ must be out of phase i.e., Φ = π, 3π, 5π …………..
This corresponds to a path difference of λ/2, 3λ/2, 5λ/2 ………….
∴ For destructive interference path difference (\(\frac{n+1}{2}\))λ

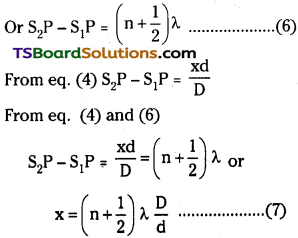
Fringe width β :
It is defined as the separation between two consecutive dark or bright bands.

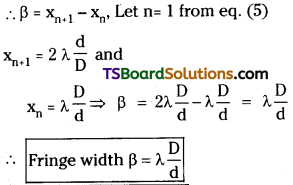
Question 4.
What is diffraction? Discuss diffraction pattern obtainable from a single slit.
Answer:
Diffraction :
Bending of light rays of sharp edges (say edge of a blade) is called “diffraction”.

Diffraction at single slit :
In young’s double slit experiment the double slit is replaced by a single narrow slit. Then on the screen a central maximum with alternate dark and bright bands of decreasing intensity are seen. These are called diffraction pattern.

Explantion :
Let LM is‘a narrow slit and a screen is placed at suitable distance. Draw a straight line through M on to the screen. It will touch the screen at C’.

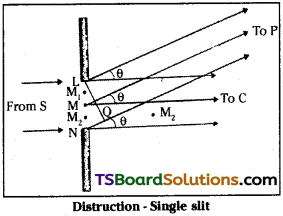
The intensity of light at any point P on screen is due to the contributions from large number of coherent sources on the slit.

Let light waves reaches the point P’ from Land N
Path difference = NP – LP = NQ = a sin θ = aθ …………… (1)
(θ is very small sin θ = θ)
At central point ‘C’ on screen θ = 0. So path difference is zero. Hence all parts of slit will contribute in phase. As a result maximum intensity is produced.

Consider the first minima :
Minimum intensity is produced when a θ = λ or θ = λ/a.

Now divide the slit into two equal parts say LM and MN. For every point M₁ in the region LM there is a point M₂ in MN region. The phase difference between M₁M₂ is 180° or π radians. So light waves reaching the point P are out of phase and we will get minimum intensity.

Consider 1^st maxima :
Maxima will occur when θ = (n + \(\frac{1}{2}\)) λ/2 For 1^st maxima
n = 1
⇒ 0 = 3 λ/2 a. Let us imagine the space between MN is divided into three equal parts. Consider first two thirds of the slit. Path difference for the two ends of this region is
\(\frac{2}{3}\)a.θ = \(\frac{2}{3}\)a × \(\frac{3\lambda}{2a}\) = λ

Now divide this \(\frac{2}{3}\)^rd region into two equal points. For ever wave coming form 1^st \(\frac{1}{3}\)^rd region on there is a wave coming from 2nd \(\frac{1}{3}\)^rd region with a phase difference of 180°. So on reaching point P their vector sum of displacements is zero. Here intensity is zero. The only light received is from 3rd \(\frac{1}{3}\)^rd part for intensity between two minima. So we will get weak bright region.

In this way we are able to explain maxima and minima formed in diffraction pattern.

Question 5.
What is resolving power of Optical Instruments? Derive the condition under which images are resolved.
Answer:
Resolving power of optical instruments :
From principles of geometrical optics, a light beam will get focussed to a point. But due to diffraction effects we are getting a spot of finite size instead of a point.

In diffraction radius of central bright region

This small value of r₀ plays a vital role in fixing the resolving power of telescopes and microscopes.

Telescopes :
In telescopes if two stars are to be resolved clearly then

Where ‘λ’ is wavelength of light used and ‘a’ is the aperture or diameter of lens used. Due to this reason we are using object lens of large diameter for better resolution.

Microscopes :
In microscopes near point magnification m = D/f = 2 tan β
For two object points to be viewed clearly their image size must be v θ = v \(\frac{1.22\lambda}{D}\)

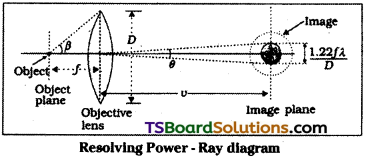
Objects with image size less than this can not be viewed clearly. So corresponding distances between them at object size

∴ Resolving power of microscope

Intext Question and Answer

Question 1.
Two slits are made 1 mm apart and the screen is placed 1 m away. What is the fringe separation when blue-green light of wavelength 500 nm is used?
Answer:
Fringe width β = \(\frac{D\lambda}{d}\). But distance of screen D = 1 m
Wave length λ = 500 nm = 5 × 10^-7 m ;
Separation between slits d = 1 mm = 1 × 10^-3 m

Question 2.
(a) The refractive index of glass is 1.5. What is the speed of light in glass? Speed of light in vacuum is 3.0 × 10⁸ m s^-1)
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Refractive index of glass, p = 1.5; Speed of light, c = 3 × 10⁸ m/s
Speed of light’in glass is given by the relation.

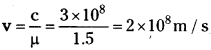
Hence, the speed of light in glass is 2 × 10⁸ m/s.

(b) The speed of light in glass is not independent of the colour of light.
The refractive index of a violet component of white light is greater than the refractive index of a red component. Hence, the speed of violet light is less than the speed of red light in glass. Hence, violet light travels slower than red light in a glass prism.

Question 3.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is λ/3?
Answer:
Let I₁ and I₂ be the intensity of the two light waves. Their resultant intensities can be obtained as:
∴ I’ = I₁ + I₂ + 2 \(\sqrt I_1I_2\) cos Φ
Where, Φ = Phase difference between the two waves
For monochromatic light waves ; Ii = I2
I’ = I₁ + I₂ + 2\(\sqrt I_1I_2\) cos Φ = 2I₁ + 2I₁ cos Φ
Phase difference = \(\frac{2 \pi}{\lambda}\) × Path difference
Since path difference = λ,; phase difference Φ = 2π
∴ I’ = 2I₁ + 2I₁ = 4I₁
Given, I = k ; ∴ I₁ = \(\frac{k}{4}\)

Question 4.
What is the Brewster angle for air to glass transition? (Refractive index of glass = 1.5.)
Answer:
Refractive index of glass µ= 1.5 ; Brewster angle = θ
Brewster angle is related to refractive index as: tan θ = µ
∴ θ = tan^-1(1.5) = 56.31°
Therefore, the Brewster angle for air to glass transition is 56.31°.

Question 5.
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
Answer:
Fresnel’s distance (z_F) is the distance for which the ray optics is a good approximation. It is given by the relation,

\(\mathrm{z}_{\mathrm{F}}=\frac{\mathrm{a}^2}{\lambda}\) ; Where, aperture width,
a = 4 mm = 4 × 10^-3 m
Wavelength’ of light, λ = 400 nm = 400 × 10^-9 m

Therefore, the distance for which the ray optics is a good approximation is 40 m.

Question 6.
In double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits?
Answer:
Wavelength of light used, 1 = 6000 nm = 600 × 10^-9 m
Angular width of a fringe θ = 0.1°
= 0.1 × \(\frac{\pi}{180}=\frac{3.14}{1800}\) rad
Angular width of a fringe is related to slit spacing (d) as:

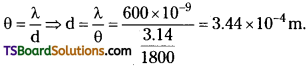
Therefore, the spacing between the slits is 3.44 × 10^-4 m.

Question 7.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of nλ/a. Justify this by suitably dividing the slit to bring out the cancellation.
Answer:
Consider that a single slit of width d is divided into n smaller slits.
Width of each slit, d’ = \(\frac{d}{n}\)
Angle of diffraction is given by the relation,

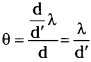
Now, each of these infinitesimally small slit sends zero intensity in direction θ. Hence, the combination of these slits will give zero intensity.