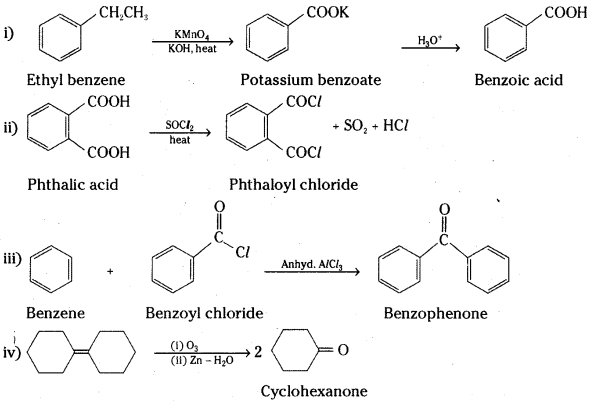
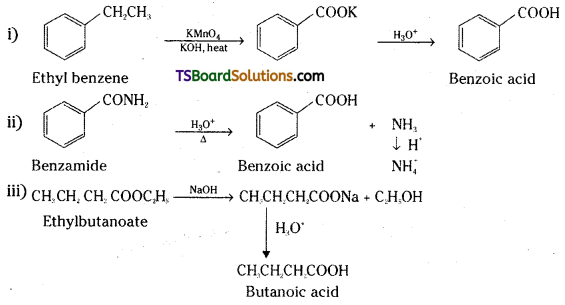
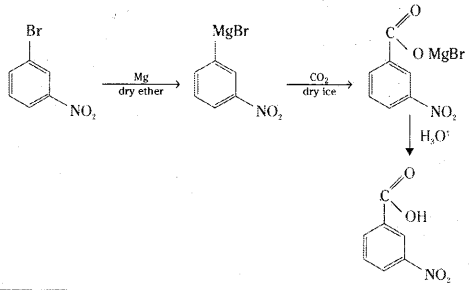
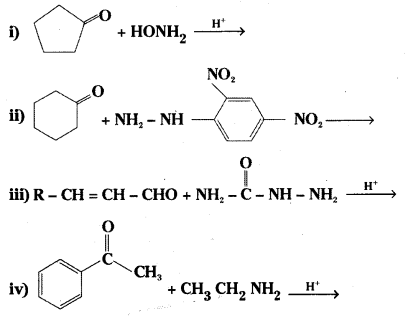
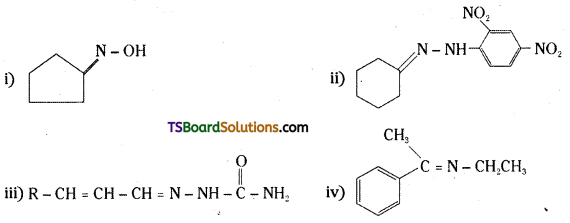
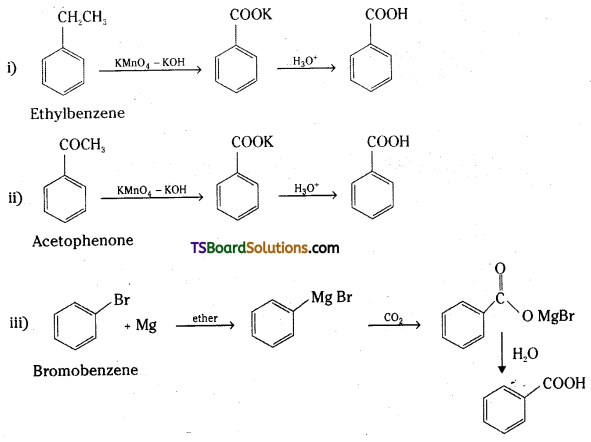
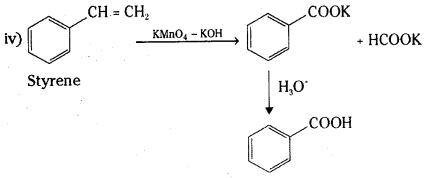
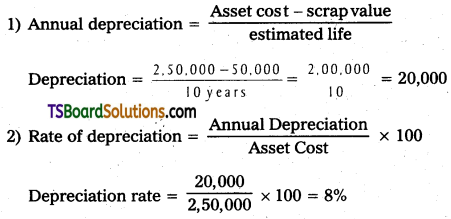
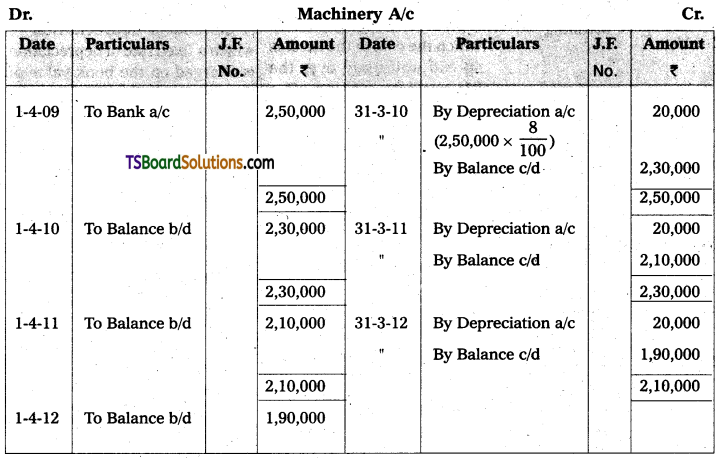
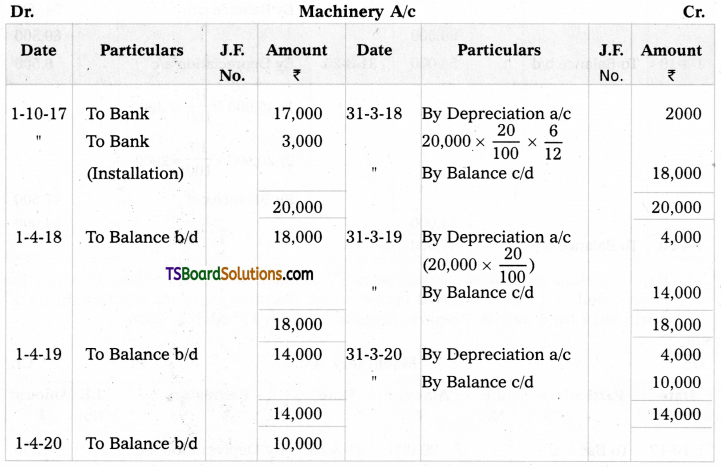
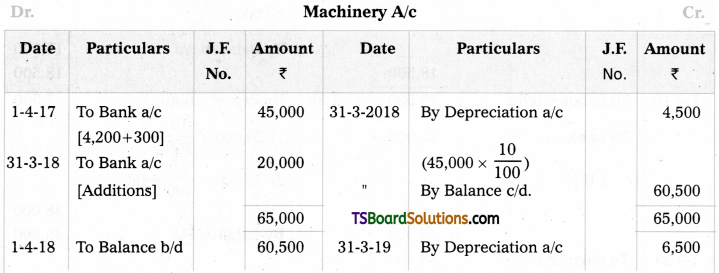
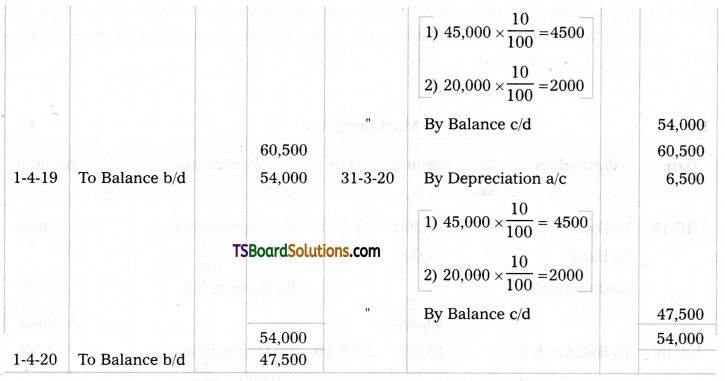
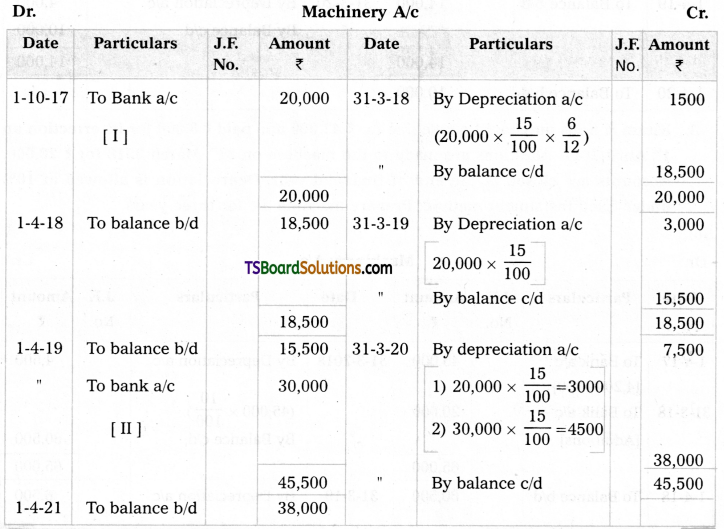
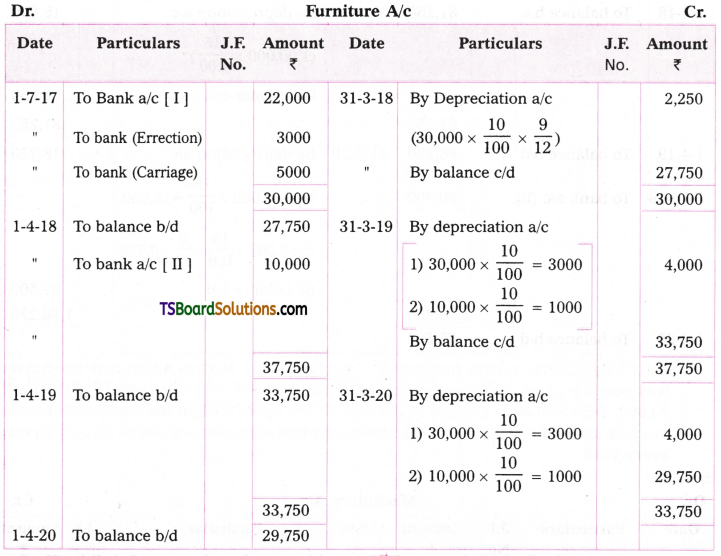
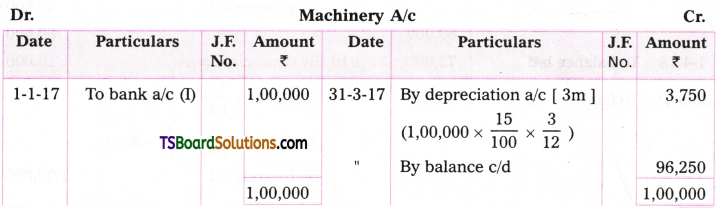
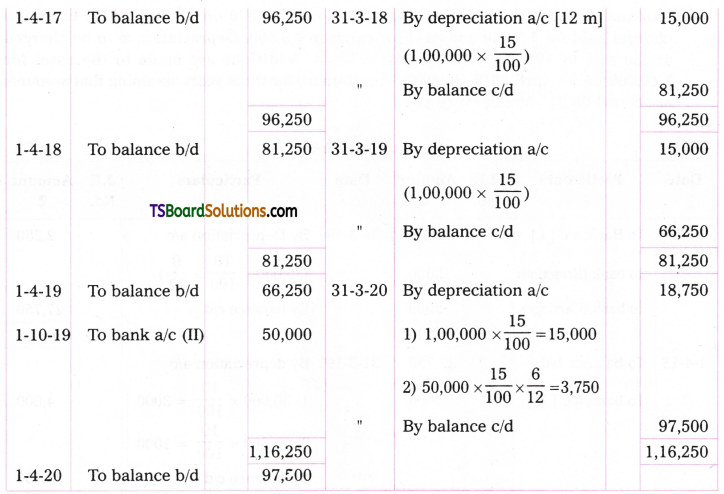
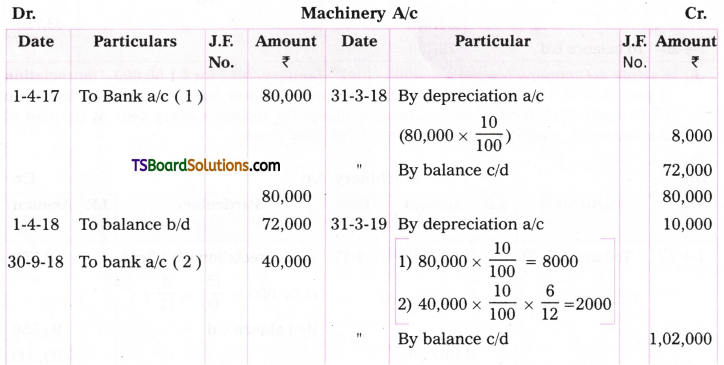
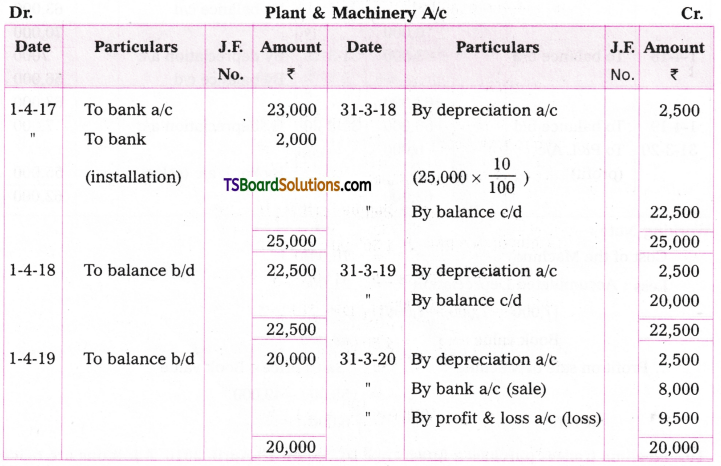
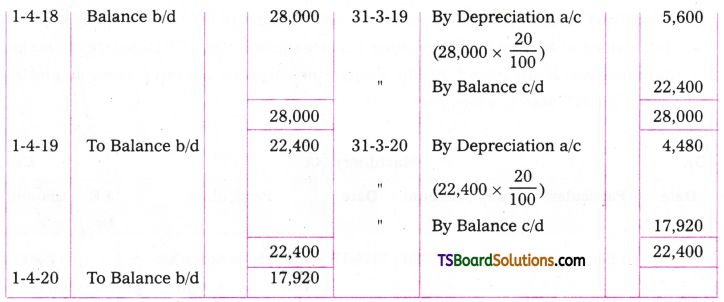
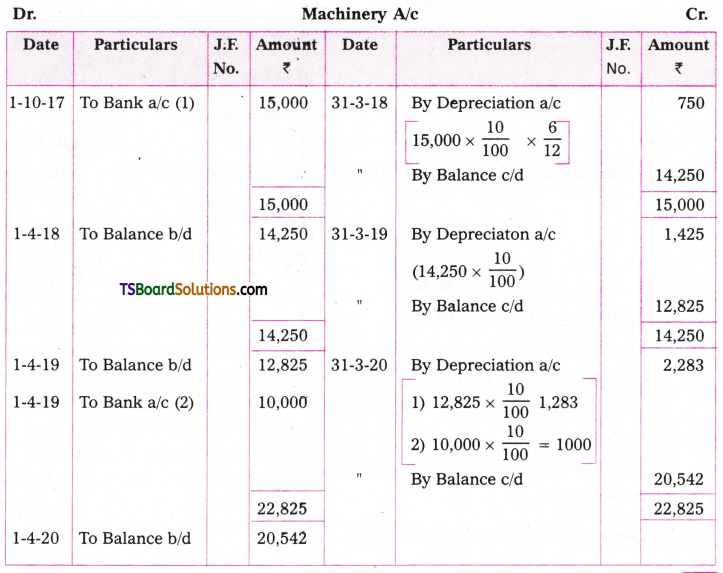
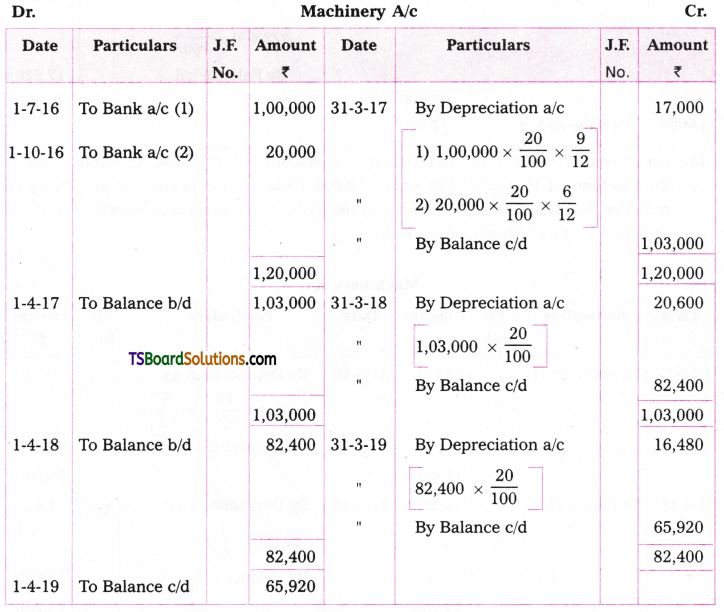
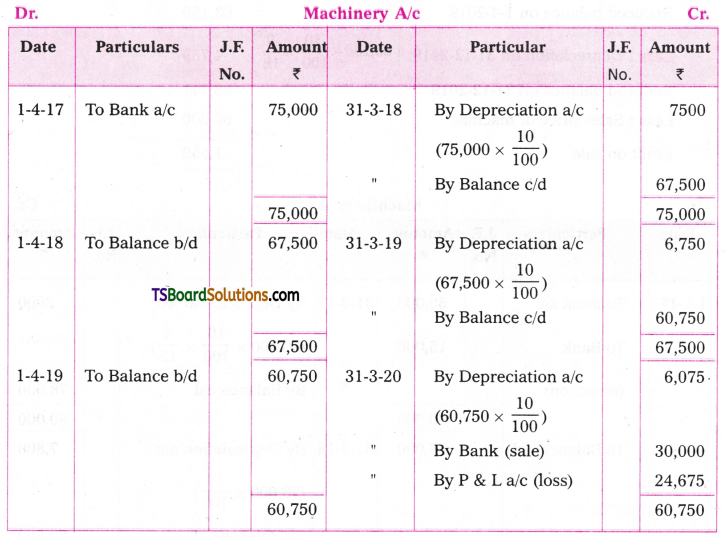
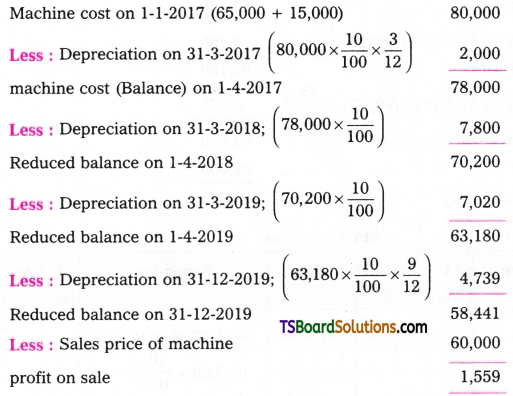
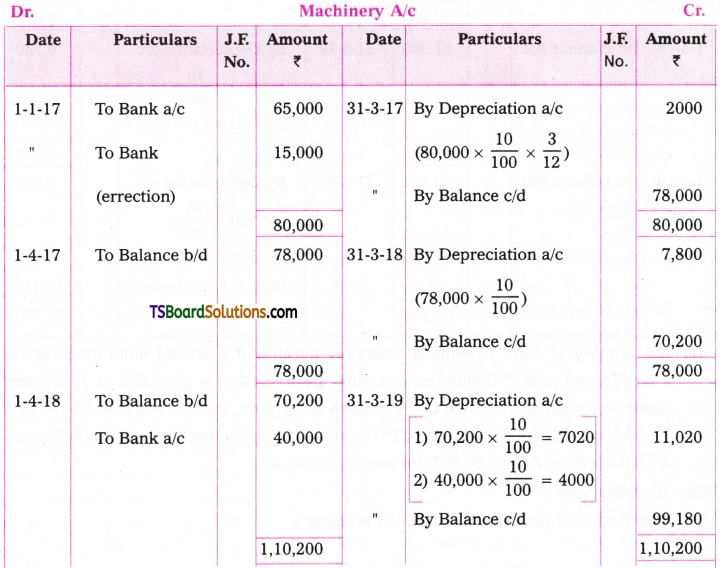
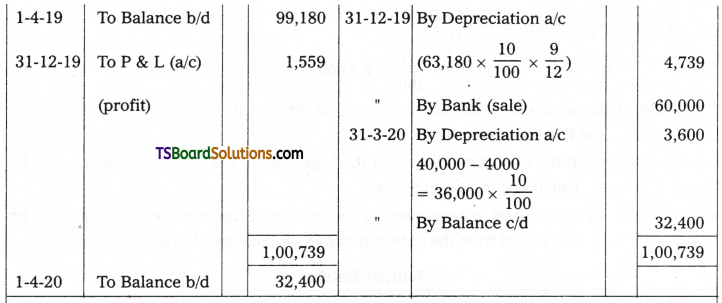
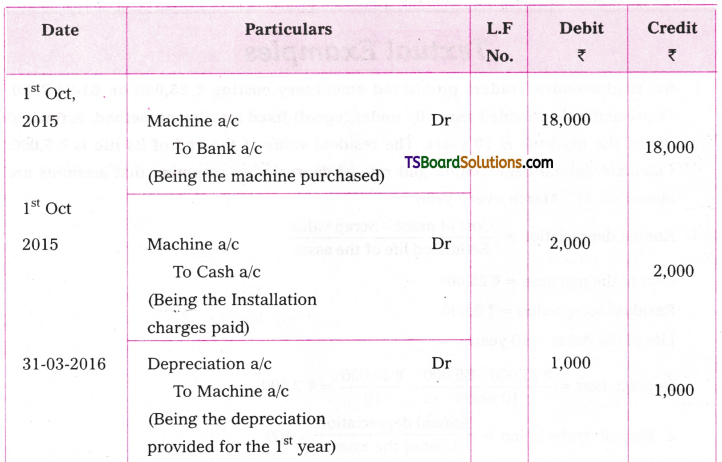
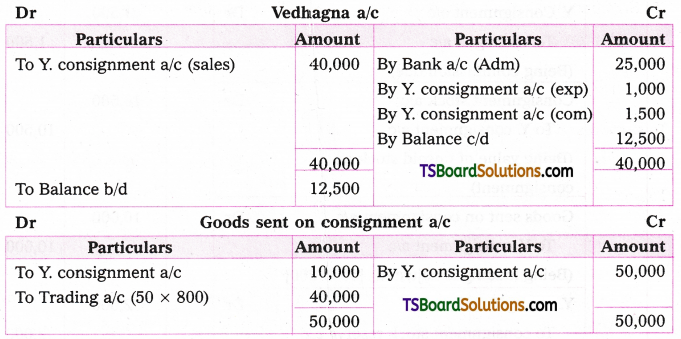
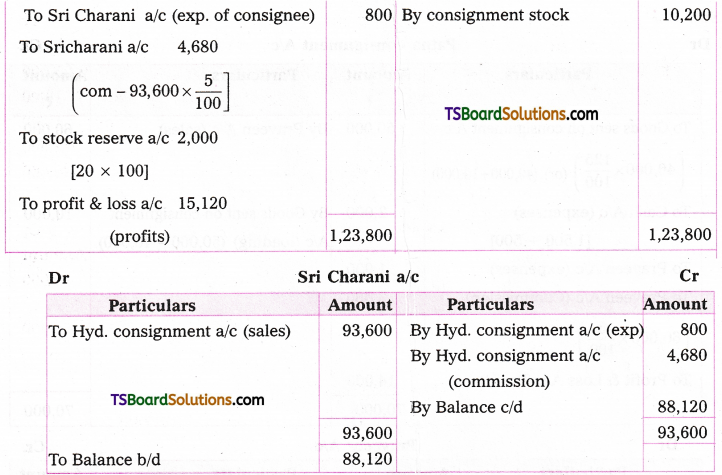
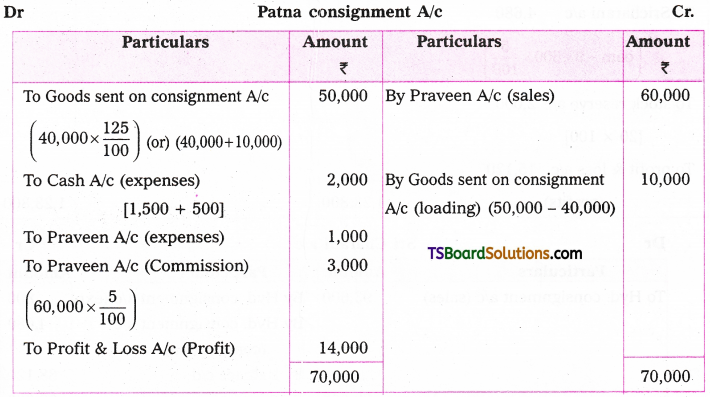
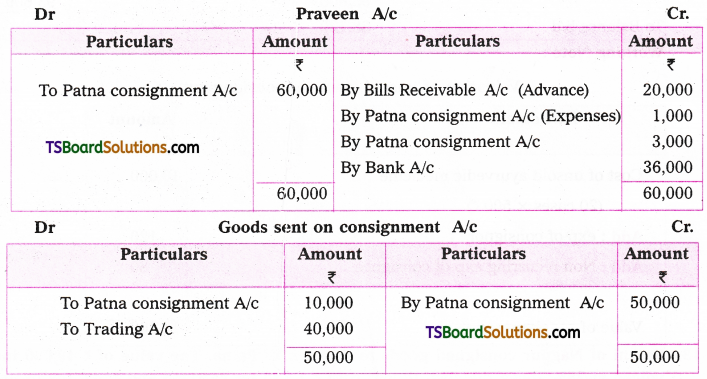
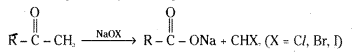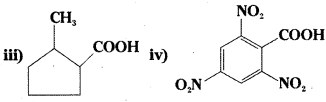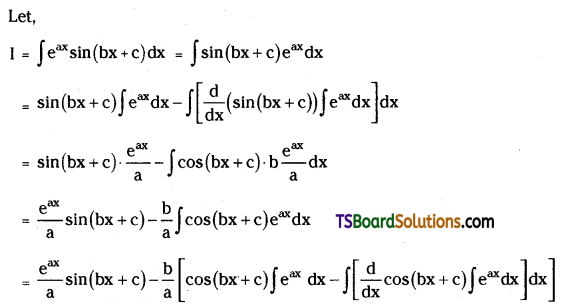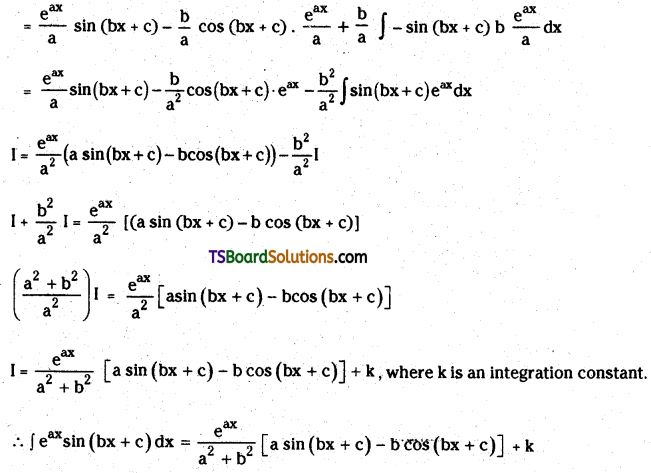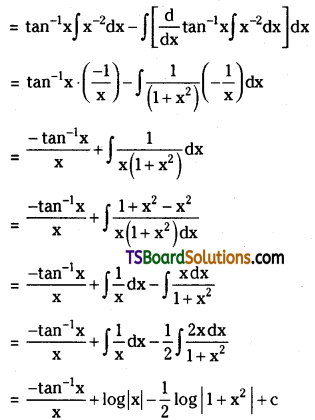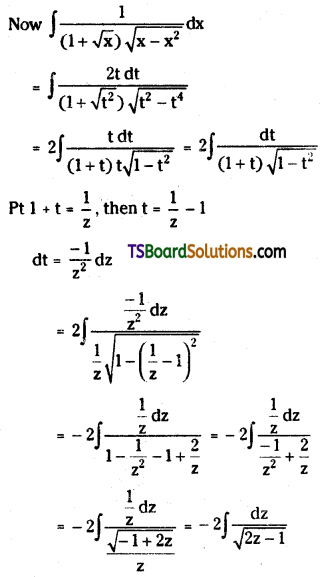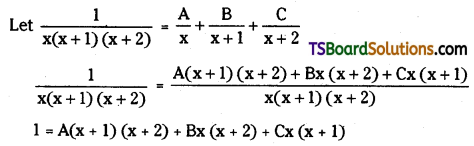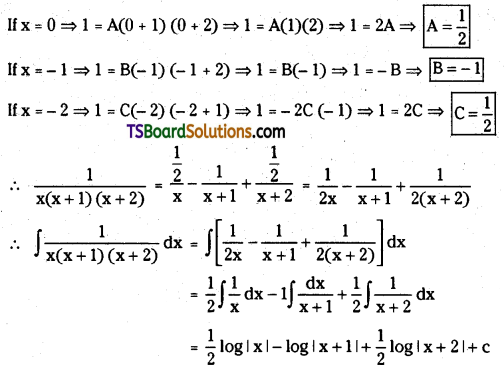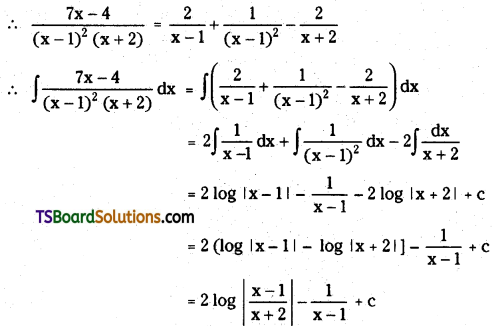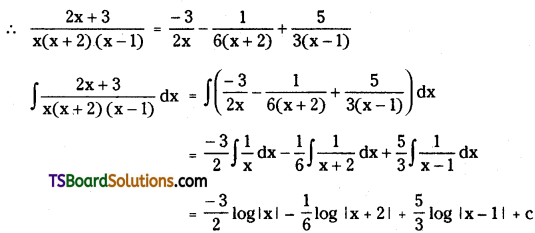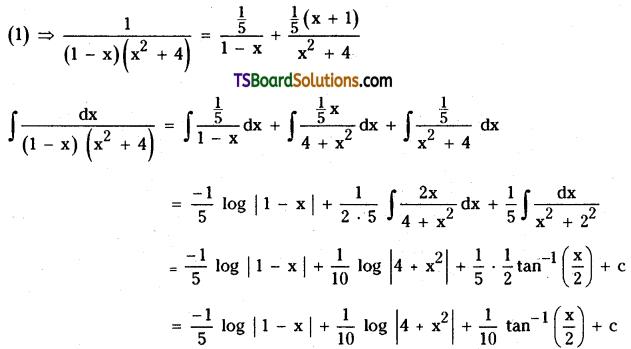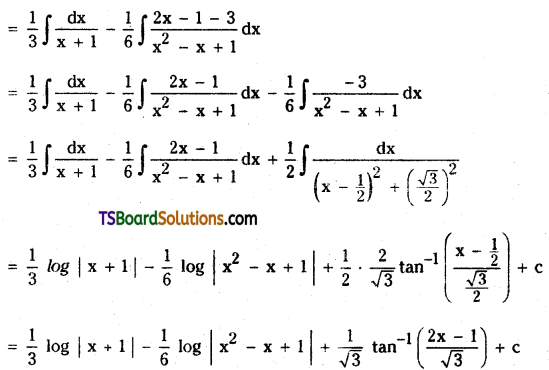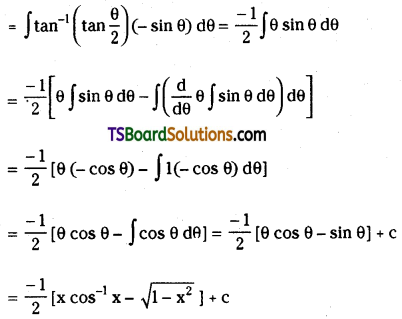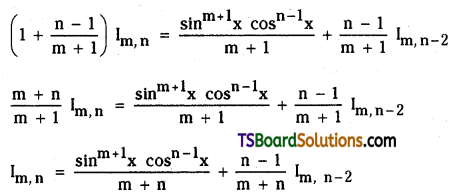Telangana TSBIE TS Inter 2nd Year Chemistry Study Material 9th Lesson Biomolecules Textbook Questions and Answers.
TS Inter 2nd Year Chemistry Study Material 9th Lesson Biomolecules
Very Short Answer Questions (2 Marks)
Question 1.
Define Carbohydrates.
Answer:
Carbohydrates are optically active polyhydroxy aldehydes or ketones or molecules which provide such units on hydrolysis.
Question 2.
Name the different types of carbohydrates on the basis of their hydrolysis. Give one example for each.
Answer:
Carbohydrates are classified into three types on the basis of their hydrolysis.
- Monosaccharides Ex: glucose
- Oligosaccharides Ex: sucrose
- Polysaccharides Ex: starch

Question 3.
Why are sugars classified as reducing and non – reducing sugars ?
Answer:
In monosaccharides, whether they are aldoses or ketoses, the functional groups are free and reduce Fehling’s solution etc. In some disaccharides such as sucrose, the reducing groups of the monosaccharides are bonded. They do not show reducing properties. On the other hand, in sugars such as maltose and lactose, the functional groups are free and reduce Fehling’s solution. Hence, sugars are classified into reducing and non – reducing sugars.
Question 4.
What do you understand from the names
a) aldopentose and
b) ketoheptose ?
Answer:
a) Aldopentose means a monosaccharide having an aldehyde group and contains five carbon atoms in its molecule.
b) Ketoheptose means a monosaccharide having a ketogroup and contains seven carbon atoms in its molecule.
Question 5.
Write two methods of preparation of glucose. [IPE 14]
Answer:
Preparation of glucose:
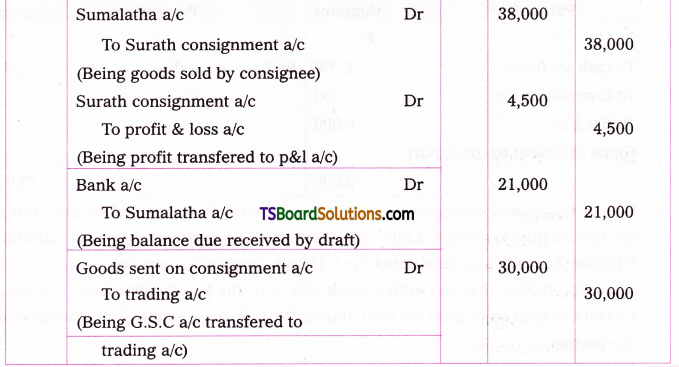
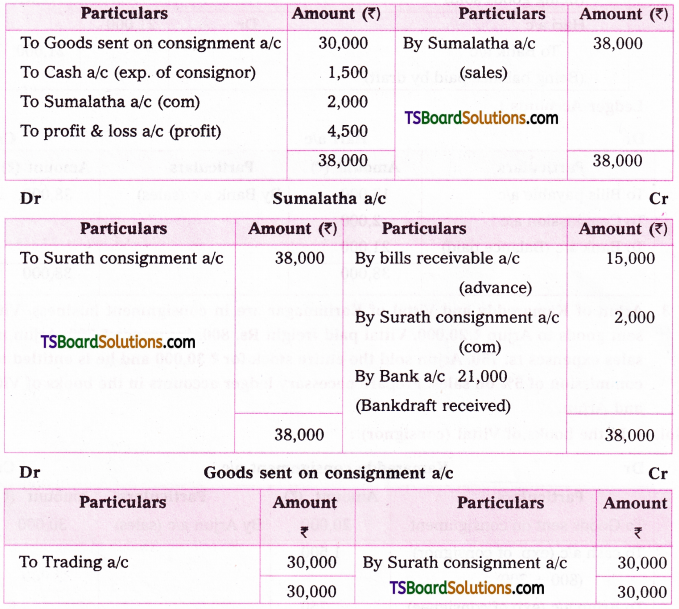
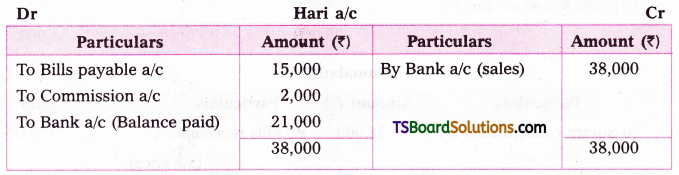
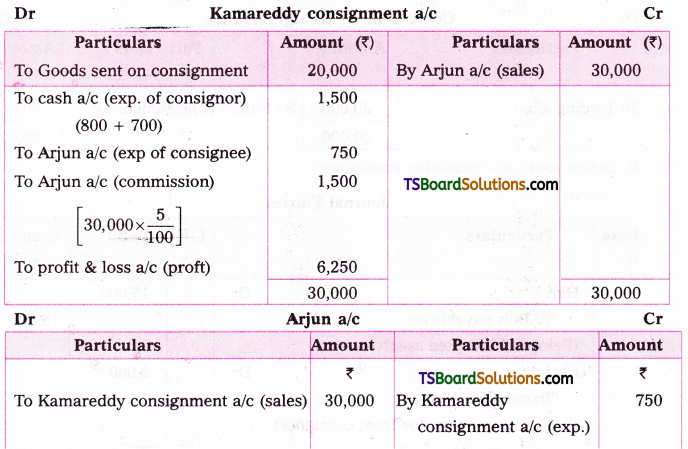
1) From sucrose (Cane sugar): Sucrose on boiling with dilute HCl or H2SO4 in alcoholic solution undergoes hydrolysis and gives equal amounts of glucose and fructose. On cooling the resulting solution, glucose being much less soluble than fructose, separates out.

2) From starch : Commercially glucose is made by the hydrolysis of starch by heat¬ing with very dilute sulphuric acid at 120°C under pressure.

Question 6.
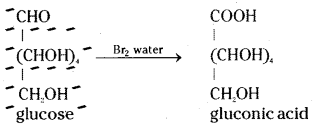
Glucose reacts with bromine water to give gluconic acid. What information do you get from this reaction about the structure of glucose ?
Answer:
Glucose is oxidised by a mild oxidising agent like bromine water to give gluconic acid, a monocarboxylic acid with molecular formula C6H12O7. This indicates the presence of an aldehyde group since only the aldehyde group can be oxidised to an acid by gaining one oxygen atom without losing any hydrogen atoms.

Question 7.
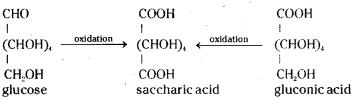
Glucose and gluconic acid on oxidation with nitric acid give saccharic acid. What information do you get from this reaction about the structure of glucose ?
Answer:
On oxidation with nitric acid, glucose as well as gluconic acid both yield a dicarboxylic acid called saccharic acid with molecular formula C6H10O8. This indicates the presence of a primary alcoholic group.
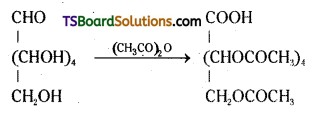
Question 8.
Glucose reacts with acetic anhydride to form penta acetate. What do you understand about the structure of glucose from his reaction ?
Answer:
Acetylation of glucose with acetic anhydride gives glucose penta acetate which confirms the presence of five -OH groups. Since it exists as a stable compound the five -OH groups should be attached to different carbon atoms.
Question 9.
Give any two reasons to understand that glucose molecule has no open chain structure.
Answer:
- Although glucose has am aldehyde group, it does not give the Schiff’s test and does not form addition product with sodium bisulphite.
- Glucose pentaacetate does not react with hydroxylamine.
These observations suggest that glucose has no open structure.
Question 10.
D – glucose means dextro rotatory glucose. Is it true ? why ?
Answer:
The letter D’ before the name of glucose does not mean dextro rotatory. ‘D’ represents relative configuration with reference to glyceraldehyde. On the other hand, ’+’ is used to represent the dextro rotatory nature of glucose.

Question 11.
What are anomers ?
Answer:
Glucose forms a six – membered ring involving the -OH at C – 5 and the -CHO group at C – 1. Thus glucose exists in two cyclic hemiacetal forms which differ in their stereo chemistry at C1, called the anomeric carbon (former aldehyde carbon). Such isomers i.e., α – form and β – form, are known as anomers.
Question 12.
Write the ring structure of D – Glucose. What are their names ?
Answer:
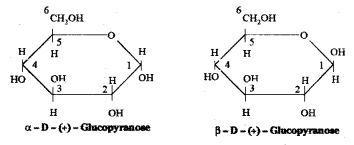
Question 13.
Write the ring structure and open chain structure of fructose.
Answer:
Ring structure and open chain structures of fructose:
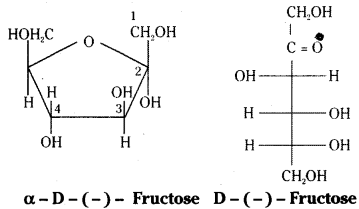
Question 14.
What do you understand by invert sugars?
Answer:
Sucrose is dextrorotatory but after hydrolysis gives an equimolar mixture of glucose which is dextrorotatory and fructose which is laevorotatory. The hydrolysis of sucrose brings about a change in the sign of rotation, from dextro (+) to laevo (-) and the product is called invert sugar.

Question 15.
What are amino acids? Give two examples.
Answer:
Compounds containing both amino (-NH2) and carboxyl (-COOH) functional groups are called amino acids.
Ex: Glycine, Alanine.
Question 16.
Write the structure of alanine and aspartic acid.
Answer:
NH2 – CH2 – COOH Alanine
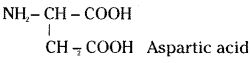
Question 17.
What do you mean by essential amino acids ? Give two examples for non – essential amino acids. [TS 16; IPE 14]
Answer:
Amino acids, which cannot be synthesised in the body and must be obtained through diet are called essential amino acids. Examples for non – essential amino acids : glycine, alanine.
Question 18.
What is Zwitter ion ? Give an example.
Answer:
In an amino acid both acidic (carboxyl group) and basic (amino group) groups are present in the same molecule. In aqueous solution, the carboxyl group can lose a proton and amino group can accept a proton, giving rise to a dipolar ion known as Zwitter ion.
Ex: H2N – CH2 – COOH ⇌ H3 \(\stackrel{+}{\mathrm{N}}\) -CH2 – \(\mathrm{CO} \overline{\mathrm{O}}\)

Question 19.
What are proteins ? Give an example.
Answer:
Proteins are polymers of α – amino acids. They are the most abundant biomolecules of the living system.
Ex : Insulin
Question 20.
What are fibrous proteins ? Give examples.
Answer:
Proteins in which the polypeptide chains run parallel and are held together by hydrogen and disulphide bonds will have fibre – like structure. Such proteins are called fibrous proteins.
Ex : Keratin (present in hair, wool, silk)
Question 21.
What are globular proteins? Give examples.
Answer:
Proteins in which the polypeptide chains coil around to give a spherical shape are called globular proteins.
Ex : Insulin
Question 22.
How are proteins classified with respect to peptide bond ?
Answer:
With respect to peptide bond, proteins are classified into dipeptides, tripeptides, tetra- peptides, pentapeptides, hexapeptides etc depending upon the number of amino acids linked by peptide bonds. When the number of amino acids is more than ten, then the products are called polypeptides.

Question 23.
What are the components of a nucleic acid?
Answer:
There are three components of a nucleic acid. They are:
- A pentose sugar
- Phosphoric acid and
- Nitrogen containing heterocyclic base.
Question 24.
Write the names of three types of RNA.
Answer:
- Messenger RNA ( m – RNA)
- Ribosomal RNA (r – RNA) and
- Transfer RNA (t – RNA)
Question 25.
Write the biological functions of nucleic acids.
Answer:
Biological functions of nucleic acids:
1) Nucleic acids control heredity at molecular level. DNA is the chemical basis of heredity. It may be regarded as the reserve of genetic information. DNA is exclusively responsible for maintaining the identity of different species of organisms over millions of years. A DNA molecule is capable of self duplication during cell division and identical DNA strands are transferred to daughter cells.
2) Nucleic acids have an important role in protein synthesis. Actually the proteins are synthesised by various RNA molecules in the cell but the message for the synthesis of a particular protein is present in DNA.

Question 26.
Name the vitamin responsible for the coagulation of blood.
Answer:
Vitamin K
Question 27.
What are monosaccharides ?
Answer:
Carbohydrates which cannot be hydrolysed into smaller units are called monosaccharides.
Question 28.
What are reducing sugars ?
Answer:
Carbohydrates which reduce Fehling’s solution and Tollen’s reagent are called reducing sugars.
Question 29.
Write two main functions of carbohydrates in plants.
Answer:
Carbohydrates mainly act as the food storage or structural materials in plants.
- Starch is the main storage polysaccharide of plants.
- Cell wall of plants is made up of cellulose.

Question 30.
Classify the following into monosaccharides and disaccharides.
i) Ribose
ii) 2 – deoxy ribose
iii) Maltose
iv) Fructose
Answer:
i) Ribose …………… Monosaccharide
ii) 2 – deoxy ribose …………… Monosaccharide
iii) Maltose …………… Disaccharide
iv) Fructose …………… Monosaccharide
Question 31.
What do you understand by the term glycosidic linkage ?
Answer:
The two monosaccharide units in a disaccharide are joined together by an oxide linkage formed by the loss of a water molecule. Such a linkage is called glycosidic linkage.
Question 32.
What is glycogen ? How is it different from starch ?
Answer:
Carbohydrates are stored in animal body as glycogen. It is also known as animal starch. The structure of glycogen is similar to amylopectin, a component of starch, but it is more highly branched.
Question 33.
What are the hydrolysis products of
i) sucrose and
ii) lactose ?
Answer:
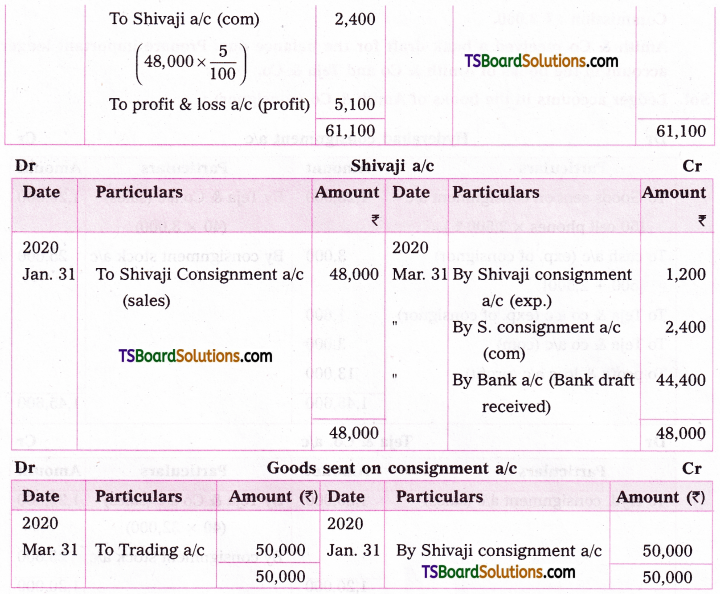
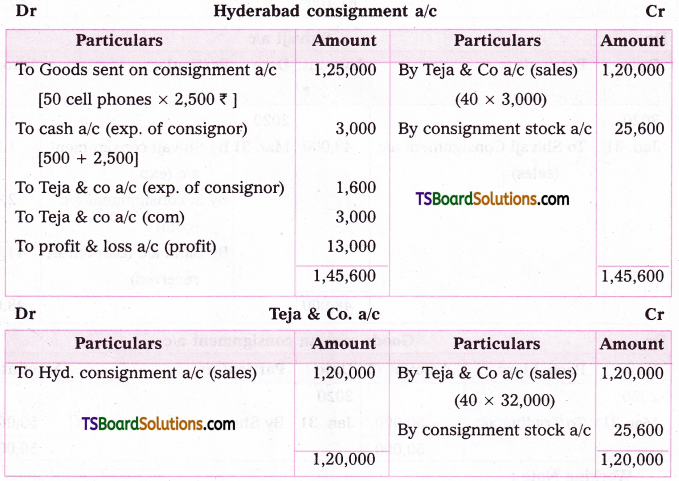
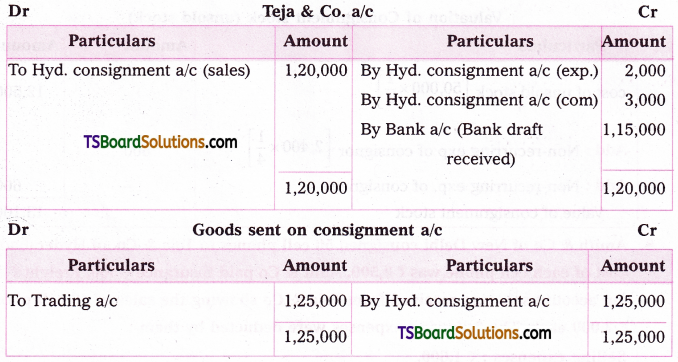
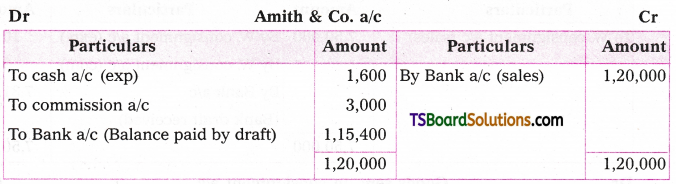
i) Sucrose on hydrolysis gives D – (+) – glucose and D – (-) – fructose.
ii) Lactose on hydrolysis gives galactose and glucose.

Question 34.
What is the basic structural difference between starch and cellulose ?
Answer:
Starch is a polymer of α – glucose. The α – D – glucose units are joined by glycosidic linkage. In amylose, which constitutes about 15 – 20% of starch, 200 -1000 α – D(+) – glucose units are held by C – 1 to C – 4 glycosidic linkage in a long unbranched chain. Amylopectin, the other component which constitutes about 80 – 85% of starch is a branched chain polymer of α – D – glucose units in which the chain is formed by C -1 to C – 4 glycosidic linkage whereas branching occurs by C -1 to C – 4.
Cellulose is a straight chain polysaccharide composed only of β – D – glucose units which are joined by glycosidic linkage between C -1 of one glucose unit and C – 4 of the next glucose unit.
Question 35.
What happens when D’- glucose is treated with the following reagents.
i) HI
ii) Bromine water
iii) HNO3
Answer:
i) On prolonged heating with HI, glucose forms n – hexane.
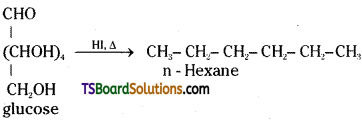
ii) When glucose is treated with bromine water it gets oxidised to gluconic acid, a monocarboxylic acid with the molecular formula, C6H12O7.
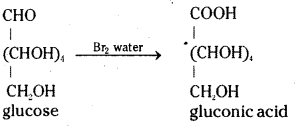
iii) On oxidation with nitric acid, glucose gives a dicarboxylic acid called saccharic acid, with molecular formula, C6H10O8.
Question 36.
Enumerate the reactions of D – glucose which cannot be explained by its open chain structure.
Answer:
The following reactions of D – glucose cannot be explained by its open chain structure.
- Glucose does not give Schiff’s test and it does not form the hydrogen sulphite addition product with NaHSO3.
- The pentaacetate of glucose doesnot react with hydroxylamine indicating the absence of free -CHO group.

Question 37.
What are essential and non – essential amino acids ? Give one example for each.
Answer:
Amino acids which cannot be synthesised in the body and must be obtained through diet are called essential amino acids.
Ex: Valine
Amino acids which are synthesised in the body are known as non – essential amino acids.
Ex: Glycine
Question 38.
Define the following as related to proteins.
i) Peptide linkage
ii) Primary structure
iii) Denaturation
Answer:
i) Peptide linkage :
Peptide linkage is an amide formed between -COOH group of one amino acid molecule and the NH2 group of another molecule of the same or different amino acid.
ii) Primary structure :
The primary structure of proteins refers to the sequence of amino acids held together by peptide linkages.
iii) Denaturation :
The loss of biological acitvity of a protein due to the destruction of the highly organized tertiary structure is called denaturation.
Ex: coagulation of egg by boiling
Question 39.
What are the common types of secondary structure of proteins ?
Answer:
The secondary structure of proteins is of two common types:
- α – helix and
- β – pleated sheet structure

Question 40.
What type of bonding helps in stabilizing the a – helix structure of proteins ?
Answer:
The spiral or α – helix is stabilized by interchain hydrogen bonding. The -NH group of each amino acid residue is hydrogen bonded to the  = O of an adjacent turn of the helix in the same chain.
= O of an adjacent turn of the helix in the same chain.
Question 41.
Differentiate between globular and fibrous proteins.
Answer:
In globular proteins the polypeptide chains coil around to give a spherical shape. These are usually soluble in water.
In fibrous proteins the polypeptide chains run parallel and are held together by hydrogen and disulphide bonds. These proteins have a fibre like structure. These are usually insoluble in water.
Question 42.
How do you explain the amphoteric behaviour of amino acids ?
Answer:
Amino acids show both acidic and basic properties. This is called amphoteric behaviour. This behaviour is due to the presence of both acidic (carboxyl group) and basic (amino group) groups in the same molecule. In aqueous solution, the carboxyl group can lose a proton and amino group can accept a proton giving rise to a dipolar ion known as zwitter ion.

Question 43.
Why are vitamin A and vitamin C essential to us ? Give their important sources.
Answer:
Vitamin A is essential tolls because its deficiency causes xerophthalmia (hardening of cornea of the eye) and night blindness.
Important sources of vitamin A : Fish liver oil, milk etc.
Vitamin C is essential to us because its deficiency causes scurvy (bleeding gums).
Sources of vitamin C: Citrus fruits, green leafy vegetables.
Question 44.
What are nucleic acids ? Mention their two important functions.
Answer:
Nucleic acids are chains of five – membered ring sugars linked by phosphate groups. The anomeric carbon of each sugar is bonded to a nitrogen of a heterocyclic compound in a β – glycosidic linkage. Functions of nucleic acids:
- DNA is the chemical basis of heredity and may be regarded as the reserve of genetic information.
- Nucleic acids have an important role in protein synthesis. Actually the proteins are synthesised by various RNA molecules in the cell but the message for the synthesis of a particular protein is present in DNA.

Question 45.
What is the difference between a nucleo-side and a nucleotide ?
Answer:
A unit formed by the attachment of a base to 1′ position of sugar is known as nucleoside.
Ex: Cytidine
When nucleoside is linked to phosphoric acid at 5′ position of sugar moity, we get a nucleotide.
Ex: Adinodine Triphosphate
Short Answer Questions (4 Marks)
Question 46.
How are the carbohydrates classified on the basis of their
a) Taste
b) Hydrolysis
c) Functional groups ?
Answer:
a) On the basis of taste carbohydrates are classified into sugars and non – sugars. Carbohydrates which are sweet to taste are called sugars while others are called non – sugars.
b) Carbohydrates are classified into three groups on the basis of their hydrolysis,
- Monosaccharides
- Oligosaccharides and
- Polysaccharides.
c) Carbohydrates are classified into
- aldoses and
- ketoses on the basis of the functional group present in them.

Question 47.
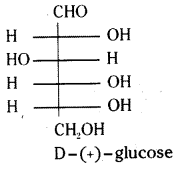
Write a brief note on the structure of glucose.
Answer:
Glucose is an aldohexose.
- The molecular formula of glucose is C6H12O6.
- On prolonged heating with HI, glucose forms n – hexane suggesting that all the carbon atoms are linked in a straight chain in its molecule.
- Glucose reacts with hydroxylamine to form an oxime and adds a molecule of HCN to give cyanohydrin. These reactions show the presence of a carbonyl group (
 = O) in glucose molecule.
= O) in glucose molecule. - Glucose on oxidation with bromine water, gives gluconic acid containing the same number of carbon atoms as in its molecule. This indicates that the carboxyl group is an aldehyde group.
- Acetylation of glucose with acetic anhydride gives glucose pentaacetate which indicates the presence of five -OH group. Since glucose is a stable compound, the five -OH groups should be present on different carbon atoms.
- Glucose, as well as gluconic acid, is oxidised with nitric acid to give saccharic acid, a dicarboxylic acid which has the same number of carbon atoms as glucose. This indicates the presence of a primary alcoholic (-OH) group in glucose.
The exact spacial arrangement of different -OH groups in glucose molecule was given by Fisher. The open chain structure of glucose is given as follows.
The above structure of glucose explained most of its properties. But it could not explain the following reactions.
1) Despite having the aldehyde group, glucose does not give Schiff’s test and does not form the addition product with sodium bisulphite.
2) The pentaacetate of glucose does not react with hydroxylamine indicating the absence of free -CHO group.
Glucose is found to exist in two different crystalline forms named as α and β. To expLain all these observations the following six membered ring structure was proposed to Glucose.
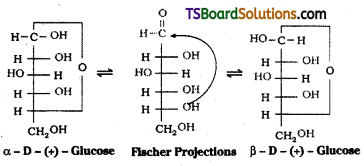
Question 48.
Write short notes on Sucrose.
Answer:
Sucrose (C12H22O11) is the most common disaccharide widely present in plants. It is mainly obtained from sugarcane or beetroot.
It is a colourless crystalline substance sweet to taste. It is dextrorotatory.
Sucrose on hydrolysis gives equimolar mixture of D – (+) – glucose and D – (-) – fructose. These two monosaccharide units are held together by a glycosidic linkage between C – 1 of α – glucose and C – 2 of β – fructose. Since the reducing groups of glucose and fructose are involved in glycosidic bond formation, sucrose is a non – reducing sugar.
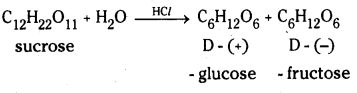

Question 49.
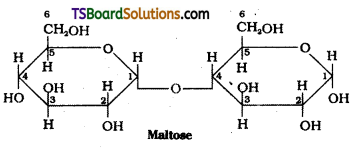
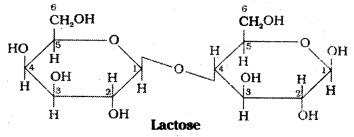
Write the structures of maltose and lactose. What are the products of hydrolysis of maltose and lactose?
Answer:
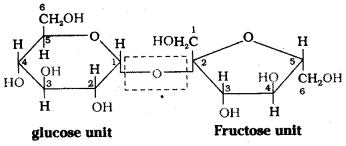
Structure of Maltose :
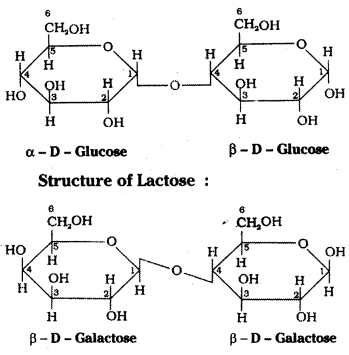
Hydrolysis products : Maltose on hydro-lysis gives α – D – glucose. Lactose on hydrolysis gives β – D – galactose and β – D – glucose.
Question 50.
Write about polysaccharides with starch and cellulose as examples.
Answer:
Carbohydrates containing large number of monosaccharide units joined together through glycosidic linkages are called polysaccharides. They act as food storages or structural materials.
Starch:
Starch is the main storage poly-saccharide of plants. It is the most important dietary source for human beings. Starch is found in cereals, roots, tubers and some vegetables. It is a polymer of α – glucose and consists of two components amylose and amylopectin. Amylose is a water soluble component which constitutes 15 – 20% of starch.
Chemically amylose is a long unbranched chain with 200-1000 α – D – (+) – glucose units held by C -1 to C – 4 glycosidic linkage. Amylopectin is insoluble in water and constitutes about 80 – 85% of starch. It is a branched chain polymer of α – D – glucose units in which the chain is formed by C -1 to C – 4 glycosidic linkage whereas branching occurs by C -1 to C – 6 glycosidic linkage.
Starch is a white amorphous powder almost insoluble in cold water but relatively more soluble in boiling water. Starch solution gives blue colour with iodine solution but the blue colour disappears on heating.
Cellulose :
Cellulose is the main structural component of vegetable matter. It is a straight chain polysaccharide composed only of β – glucose units which are joined by glycosidic link between C -1 of one glucose unit and C – 4 of the next glucose unit.

Question 51.
Write the importance of carbohydrates.
Answer:
Carbohydrates are essential for the life of both plants and animals. Honey is an instant source of energy. Carbohydrates form a major portion of our food. They are used as storage molecules as starch in plants and glycogen in animals. Cell walls of bacteria and plants are made up of cellulose.
Wood and cotton fibre contain cellulose. They provide raw materials for many important industries like textiles, paper, lacquers and breweries. D – ribose and 2 – deoxy – D – ribose are present in nucleic acids. Carbohydrates are present in biosystems in combination with many proteins and lipids.
Question 52.
Exaplain the classification of proteins as primary, secondary, tertiary and quarternary proteins with respect to their structure.
Answer:
The structure and shape of proteins can be studied at four different levels, i.e., primary, secondary, tertiary and quarternary.
i) Primary structure of proteins:
Proteins may have one or more polypeptide chains. Each polypeptide in a protein has amino acids linked with each other in a specific sequence. It is this sequence of amino acids that is said to be the primary structure. The primary structure represents the constitution of the protein.
ii) Secondary structure of proteins:
The secondary structure of proteins refers to the shape in which a long polypeptide chain can exist. These chains are found to exist in two different types of structures (1) α – helix and (2) β – pleated sheet structure. These structures arise due to the regular folding of the backbone of the polypeptide chain due to hydrogen bonding between 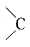 = O and -NH groups of the peptide bond.
= O and -NH groups of the peptide bond.
iii) Tertiary structure of proteins :
The tertiary structure of proteins represents overall folding of the polypeptide chains i.e., further folding of the secondary structure. It gives rise to two major molecular shapes viz. fibrous (thread like) and globular.
iv) Quarternary structure of proteins :
Some of the proteins are composed of two or more polypeptide chains referred to as sub – units. The special arrangement of these subunits with respect to each other is known as quarternary structure.

Question 53.
Explain the denaturation of proteins. [TS 16]
Answer:
When a protein in its native form, is subjected to physical change like change in temperature or chemical change like change in pH, the hydrogen bonds are disturbed. Due to this, globules unfold and helix gets uncoiled and protein loses its biological activity. This is called denaturation of protein. During denaturation, secondary and tertiary structures are destroyed but the primary structure remains intact. Coagulation of egg white on boiling is a common example of denaturation.
Question 54.
What are enzymes ? Give examples.
Answer:
Enzymes are biocatalysts which speed up reactions in biosystems. They are very specific and selective in their action and chemically all enzymes are proteins.
Ex:
1) The enzyme that catalyses the hydrolysis of maltose into glucose is named maltase.

2) An aqueous solution of sucrose is fermented by yeast to give ethyl alcohol and carbon dioxide. The enzyme invertage present in yeast converts sucrose into glucose and fructose. These sugars are then decomposed by the enzyme zymase (also present in yeast) to give ethyl alcohol and carbondioxide.
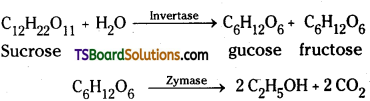
Question 55.
Explain the role of sucrose in its hydrolysis.
Answer:
Sucrose is dextrorotatory but after hydrolysis gives an equimolar mixture of glucose which is dextrorotatory and fructose which is laevorotatory. Since laevorotation of fructose (-92.4°) is more than dextrorotation of glucose (+52.5°), the mixture is laevorotatory. Thus hydrolysis of sucrose brings about a change in the sign of rotation, from dextro (+) to laevo (-) and the product is called invert sugar.

Question 56.
Write notes on vitamins.
Answer:
Vitamins are organic compounds which are required in small quantities in our diet for the maintenance of normal health. Their deficiency causes specific diseases. Plants can synthesise almost all vitamins. Vitamins are designated by alphabets A, B, C, D, E, K. Some of them are further named as subgroups e.g. B1, B2, B6, B12 etc. Excess of vitamins is also harmful.
Vitamins are classified into two groups depending upon their solubility in water or fat.
- Fat soluble vitamins: These are soluble in fat and oils but insoluble in water. Vitamins A, D, E and K are fat soluble vitamins.
- Water soluble vitamins : B group vitamins and vitamin C are soluble in water.
Some vitamins, their sources and deficiency diseases:
Vitamin A:
Sources: Fish liver oil, butter and milk. Deficiency diseases: Xerophthalmia, Night blindness.
Vitamin B1 (Thiamine):
Sources: Milk, green vegetables and cereals.
Deficiency diseases: Beri beri
Vitamin B2 (Riboflavin):
Sources: Milk, egg white, liver.
Deficiency diseases: Cheilosis
Vitamin C:
Sources: Citrus fruits, amla and green leafy vegetables.
Deficiency diseases: Scurvy
Question 57.
What do you understand by The two strands of DNA are complementary to each other” ? Explain.
Answers:
Nucleic acids have a secondary structure also besides the primary structure. DNA was given a double strand helix structure. Two nucleic acid chains are wound about each other and held together by hydrogen bonds between pairs of bases. The two strands are complementary to each other because the hydrogen bonds are formed between specific pairs of bases. Adenine forms hydrogen bonds with thymine whereas cytosine forms hydrogen bonds with guanine.

Question 58.
What are hormones ? Give one example for each. [Mar. 19, 18 ; AP & TS]
- Steroid hormones
- Poly peptide hormones and
- Amino acid derivatives.
Answer:
Hormones are molecules that act as intercellular messengers. They have several functions in the body.
- Steroid hormones:
a) Adrenal cortical hormones : Ex : Corti- coids
b) Sex hormones
a) Male sex hormones: Ex: Testosterone
b) Female sex hormones : Ex : Estrone - Poly peptide hormones : Ex : Insulin
- Amino acid derivatives: Ex: Thyroxine
Question 59.
Give the sources of the following vitamins and name the diseases caused by their deficiency (a) A (b) D (c) E and (d) K. [AP 16; 15; TS 15]
Answer:
| Name of the vitamin | Sources | Deficiency diseases |
| 1) Vitamin A | Fish liver oil, carrot, butter and milk. | Xerophthalmia, Night blindness. |
| 2) Vitamin D | Exposure to sunlight, fish and egg yolk. | Rickets and osteo – malacia. |
| 3) Vitamin E | Vegetable oils like sunflower oil. | Increased fragility of RBCs and muscular weakness. |
| 4) Vitamin K | Green leafy vegetables. | Increased blood clotting time. |
Long Answer Questions (8 Marks)
Question 60.
Explain the classification of carbohydrates.
Answers:
1) Classification on the basis of hydrolysis:
Carbohydrates are classified into three types on the basis of their hydrolysis.
- Monosaccharides
- Oligosaccharides and
- Polysaccharides.
Monosaccharides:
Carbohydrates which cannot be hydrolysed into smaller units are called monosaccharides.
Ex : Glucose, fructose, ribose etc.
Oligosaccharides:
Carbohydrates that yield two to ten monosaccharide units on hydrolysis are called oligosaccharides. They are further classified into disaccharides, trisaccharides, tetrasaccharides etc., depending upon the number of monosaccharides they provide on hydrolysis. Disaccharides, on hydrolysis, give two monosaccharide units which may be same or different.
Ex : Sucrose on hydrolysis gives one molecule of glucose and one molecule of fructose.
Maltose on hydrolysis gives two molecules of glucose only.
Polysaccharides:
Carbohydrates which yield a large number of monosaccharide units on hydrolysis are called polysaccharides. Starch, cellulose, glycogen etc., are examples for polysaccharides.
2) Classification on the basis of reducing properties:
Carbohydrates are also classified into reducing and non – reducing sugars. All those carbohydrates which reduce Fehling’s solution and Tollen’s reagent are called reducing sugars.
Ex: Glucose, fructose, maltose, lactose.
Sugars which do not reduce Fehling’s solution etc are called non – reducing sugars. For example sucrose is a non – reducing sugar.
3) Classification based on taste :
Carbo-hydrates are also classified into sugars and non – sugars on the basis of their taste. Carbohydrates such as glucose, fructose, sucrose etc., which are sweet to taste are called sugars. Polysaccharides are not sweet to taste, hence they are called non – sugars.

Question 61.
Discuss the structure of glucose on the basis of its chemical properties.
Answer:
Glucose is an aldohexose.
- The molecular formula of glucose is C6H12O6.
- On prolonged heating with HI, glucose forms n – hexane suggesting that all the carbon atoms are linked in a straight chain in its molecule.
- Glucose reacts with hydroxylamine to form an oxime and adds a molecule of HCN to give cyanohydrin. These reactions show the presence of a carbonyl group (
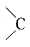 = O) in glucose molecule.
= O) in glucose molecule. - Glucose on oxidation with bromine water, gives gluconic acid containing the same number of carbon atoms as in its molecule. This indicates that the carboxyl group is an aldehyde group.
- Acetylation of glucose with acetic anhydride gives glucose pentaacetate which indicates the presence of five -OH group. Since glucose is a stable compound, the five -OH groups should be present on different carbon atoms.
- Glucose, as well as gluconic acid, is oxidised with nitric acid to give saccharic acid, a dicarboxylic acid which has the same number of carbon atoms as glucose. This indicates the presence of a primary alcoholic (-OH) group in glucose.
The exact spacial arrangement of different -OH groups in glucose molecule was given by Fisher. The open chain structure of glucose is given as follows.

The above structure of glucose explained most of its properties. But it could not explain the following reactions.
1) Despite having the aldehyde group, glucose does not give Schiff’s test and does not form the addition product with sodium bisulphite.
2) The pentaacetate of glucose does not react with hydroxylamine indicating the absence of free -CHO group.
Glucose is found to exist in two different crystalline forms named as α and β. To expLain all these observations the following six membered ring structure was proposed to Glucose.

Question 62.
Write notes on (a) fructose (b) sucrose (c) maltose (d) lactose.
Answer:
a) Fructose:
Fructose is found in fruits and honey. It is the sweetest sugar. It is obtained along with glucose by the hydrolysis of sucrose. It is an important ketohexose.
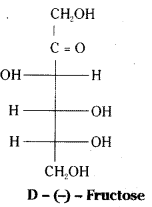
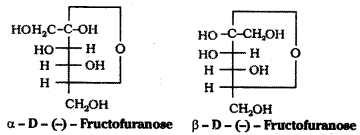
The molecular formula of fructose is C6H12O6. On the basis of its reactions it is found to contain a ketonic functional group at C2 and all she carbons in straight chain as in glucose. It is laevorotatory and belongs to D – series. Its open chain structure is Fructose also exists in two cyclic forms which are obtained by the addition of -OH at C5 to the (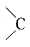 = O) group.
= O) group.
To explain all the properties of fructose, a furanose ring structure is suggested.

b) Sucrose:
Sucrose is a common disaccharide. It is obtained mainly from sugarcane or beet root. It is a colourless crystalline sweet substance. Sucrose on hydrolysis gives equimolar mixture of glucose and fructose.
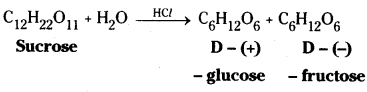
The two monosaccharide units are held together by a glycosidic linkage between C1 of α – glucose and C2 of β – fructose. Since the reducing groups of glucose and fructose are involved in glycosidic bond formation, sucrose is a non – reducing sugar. Sucrose is dextrorotatory but after hydrolysis gives a mixture of dextrorotatory glucose and laevorotatory fructose. The mixture is lae- vorotatory. The product of hydrolysis is called invert sugar.
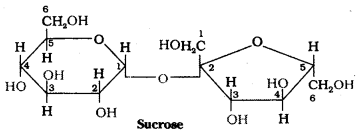
c) Maltose :
Maltose is a disaccharide. It is composed of two α – D – glucose units in which C1 of one glucose unit is linked to C4 of another glucose unit. Maltose is a reducing sugar.
d) Lactose:
Lactose occurs in milk, hence it is also known as milk sugar. On hydrolysis lactose gives β – D -galactose and β – D – glucose. The linkage is between C1 of galactose and C4 of glucose. It is a reducing sugar.
Question 63.
Write notes on (a) starch (b) cellulose (c) importance of carbohydrates.
Answer:
Carbohydrates containing large number of monosaccharide units joined together through glycosidic linkages are called polysaccharides. They act as food storages or structural materials.
Starch:
Starch is the main storage poly-saccharide of plants. It is the most important dietary source for human beings. Starch is found in cereals, roots, tubers and some vegetables. It is a polymer of α – glucose and consists of two components amylose and amylopectin. Amylose is a water soluble component which constitutes 15 – 20% of starch.
Chemically amylose is a long unbranched chain with 200-1000 α – D – (+) – glucose units held by C -1 to C – 4 glycosidic linkage. Amylopectin is insoluble in water and constitutes about 80 – 85% of starch. It is a branched chain polymer of α – D – glucose units in which the chain is formed by C -1 to C – 4 glycosidic linkage whereas branching occurs by C -1 to C – 6 glycosidic linkage.
Starch is a white amorphous powder almost insoluble in cold water but relatively more soluble in boiling water. Starch solution gives blue colour with iodine solution but the blue colour disappears on heating.
Cellulose :
Cellulose is the main structural component of vegetable matter. It is a straight chain polysaccharide composed only of β – glucose units which are joined by glycosidic link between C -1 of one glucose unit and C – 4 of the next glucose unit.
Carbohydrates are essential for the life of both plants and animals. Honey is an instant source of energy. Carbohydrates form a major portion of our food. They are used as storage molecules as starch in plants and glycogen in animals. Cell walls of bacteria and plants are made up of cellulose.
Wood and cotton fibre contain cellulose. They provide raw materials for many important industries like textiles, paper, lacquers and breweries. D – ribose and 2 – deoxy – D – ribose are present in nucleic acids. Carbohydrates are present in biosystems in combination with many proteins and lipids.

Question 64.
Write notes on amino acids.
Answer:
Compounds containing both amino (-NH2) and carboxyl (-COOH) functional groups are called amino acids.
Ex: Glycine, Alanine.
Amino acids which cannot be synthesised in the body and must be obtained through diet are called essential amino acids.
Ex: Valine
Amino acids which are synthesised in the body are known as non – essential amino acids.
Ex: Glycine
Amino acids show both acidic and basic properties. This is called amphoteric behaviour. This behaviour is due to the presence of both acidic (carboxyl group) and basic (amino group) groups in the same molecule. In aqueous solution, the carboxyl group can lose a proton and amino group can accept a proton giving rise to a dipolar ion known as zwitter ion.
Question 65.
Write notes on proteins.
Answer:
Proteins are polymers of α – amino acids. They are the most abundant biomolecules of the living system.
Ex : Insulin
Proteins in which the polypeptide chains run parallel and are held together by hydrogen and disulphide bonds will have fibre – like structure. Such proteins are called fibrous proteins.
Ex : Keratin (present in hair, wool, silk)
Proteins in which the polypeptide chains coil around to give a spherical shape are called globular proteins.
Ex : Insulin
The structure and shape of proteins can be studied at four different levels, i.e., primary, secondary, tertiary and quarternary.
i) Primary structure of proteins:
Proteins may have one or more polypeptide chains. Each polypeptide in a protein has amino acids linked with each other in a specific sequence. It is this sequence of amino acids that is said to be the primary structure. The primary structure represents the constitution of the protein.
ii) Secondary structure of proteins:
The secondary structure of proteins refers to the shape in which a long polypeptide chain can exist. These chains are found to exist in two different types of structures (1) α – helix and (2) β – pleated sheet structure. These structures arise due to the regular folding of the backbone of the polypeptide chain due to hydrogen bonding between 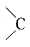 = O and -NH groups of the peptide bond.
= O and -NH groups of the peptide bond.
iii) Tertiary structure of proteins :
The tertiary structure of proteins represents overall folding of the polypeptide chains i.e., further folding of the secondary structure. It gives rise to two major molecular shapes viz. fibrous (thread like) and globular.
iv) Quarternary structure of proteins :
Some of the proteins are composed of two or more polypeptide chains referred to as sub – units. The special arrangement of these subunits with respect to each other is known as quarternary structure.
When a protein in its native form, is subjected to physical change like change in temperature or chemical change like change in pH, the hydrogen bonds are disturbed. Due to this, globules unfold and helix gets uncoiled and protein loses its biological activity. This is called denaturation of protein. During denaturation, secondary and tertiary structures are destroyed but the primary structure remains intact. Coagulation of egg white on boiling is a common example of denaturation.

Question 66.
Write notes on (a) enzymes and (b) vitamins.
Answer:
Enzymes are biocatalysts which speed up reactions in biosystems. They are very specific and selective in their action and chemically all enzymes are proteins.
Ex:
1) The enzyme that catalyses the hydrolysis of maltose into glucose is named maltase.

2) An aqueous solution of sucrose is fermented by yeast to give ethyl alcohol and carbon dioxide. The enzyme invertage present in yeast converts sucrose into glucose and fructose. These sugars are then decomposed by the enzyme zymase (also present in yeast) to give ethyl alcohol and carbondioxide.

Vitamins are organic compounds which are required in small quantities in our diet for the maintenance of normal health. Their deficiency causes specific diseases. Plants can synthesise almost all vitamins. Vitamins are designated by alphabets A, B, C, D, E, K. Some of them are further named as subgroups e.g. B1, B2, B6, B12 etc. Excess of vitamins is also harmful.
Vitamins are classified into two groups depending upon their solubility in water or fat.
- Fat soluble vitamins: These are soluble in fat and oils but insoluble in water. Vitamins A, D, E and K are fat soluble vitamins.
- Water soluble vitamins : B group vitamins and vitamin C are soluble in water.
Some vitamins, their sources and deficiency diseases:
Vitamin A:
Sources: Fish liver oil, butter and milk. Deficiency diseases: Xerophthalmia, Night blindness.
Vitamin B1 (Thiamine):
Sources: Milk, green vegetables and cereals.
Deficiency diseases: Beri beri
Vitamin B2 (Riboflavin):
Sources: Milk, egg white, liver.
Deficiency diseases: Cheilosis
Vitamin C:
Sources: Citrus fruits, amla and green leafy vegetables.
Deficiency diseases: Scurvy
| Name of the vitamin | Sources | Deficiency diseases |
| 1) Vitamin A | Fish liver oil, carrot, butter and milk. | Xerophthalmia, Night blindness. |
| 2) Vitamin D | Exposure to sunlight, fish and egg yolk. | Rickets and osteo – malacia. |
| 3) Vitamin E | Vegetable oils like sunflower oil. | Increased fragility of RBCs and muscular weakness. |
| 4) Vitamin K | Green leafy vegetables. | Increased blood clotting time. |

Question 67.
Explain the structures of DNA and RNA.
Answer:
There are three components of a nucleic acid.
i) A pentose sugar ii) Phosphoric acid and iii) Nitrogen containing amino acid.
A simplified version of nucleic acid chain is as follows.
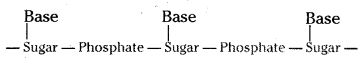
Information regarding the sequence of nucleotides in the chain of a nucleic acid is called its primary structure. Nucleic acids have a secondary structure also.
James Watson and Francis Crick proposed a double strand helix structure for DNA. Two nucleic acid chains are wound about each other and held together by hydrogen bonds between pairs of bases. The two strands are complementary to each other because the hydrogen bonds are formed between specific pairs of bases. Adenine forms hydrogen bonds with thymine whereas cytosine forms hydrogen bonds with guanine.
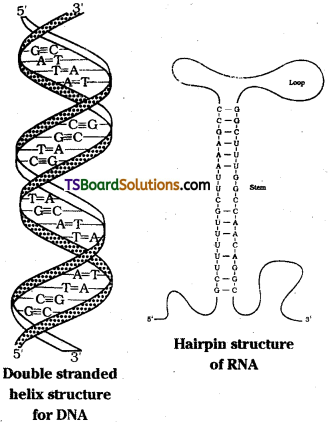
In secondary structure of RNA, helices are present but they are only single stranded. Sometimes they fold back on themselves like a hairpin thus acquiring double helix structure possesing double stranded characteristics. In double stranded arrangement guanine pairs with cytosine and adenine with uracil.
Question 68.
Write notes on the functions of different hormones in the body.
Answer:
Functions of hormones :
I. Steroid hormones:
a) Sex hormones:
i) Male sex hormones (androgens):
Test-osterone is the principal male sex hormone produced by testis. This is responsible for the development of secondary male sexual characteristics such as deep voice and facial hair.
ii) Female sex hormones (estrogens) :
Estradiol is the main female sex harmone. It is responsible for development of secondary female sex characteristics such as breast development, small voice, long hair. It also takes part in control of menstrual cycle.
iii) Pregnancy hormones progesterone) :
Progesterone is useful for preparing the uterus for the implantation of the fertilised egg. Cortico steroids (adrenal cortical hormones) are released by the adrenal cortex.
b) Cortico steroids (adrenal cortical hor-mones :
These are released by the adrenal cortex.
i) Mineralo corticoids :
These hormones control the excretion of water and salt by the kidney.
ii) Glucocorticoids :
These control the carbohydrate metabolism, modulate inflammatory reactions and are involved in reactions to stress.
If the adrenal cortex does not function properly then one of the results may be Addison’s disease. The disease is fatal unless it is treated by glucocorticoids and mineralocorticoids.

II. Non – steroidal hormones :
i) Peptide hormones:
The most important peptide hormone is insulin. It has great influence on carbohydrate metabolism. It is released in response to the rapid release in the glucose level in the blood. On the other hand the hormone glucagon tends to increase the glucose level in the blood. The two hormones together regulate the glucose level in the blood.
ii) Amino acid derivations :
These are thyroidal hormones. Thyroxine produced in the thyroid gland is an iodinated derivative of amino acid tyrosine. Abnormally low level of thyroxine leads to hypothyroidism which is characterised by Tetha- rgynea and obesity. Increased level of . thyroxine causes hyperthyroidism.
Intext Questions – Answers
Question 1.
Glucose and sucrose are soluble in water but cyclohexane and benzene (simple six membered ring compounds) are insoluble in water. Explain.
Answer:
Water is a polar solvent. Glucose and sucrose are polar compounds. Hence they are soluble in water. The partial charges of water interact with the partial charges on glucose and sucrose.
On the other hand, cyclohexane and benzene are non – polar compounds. Water molecules are not attracted to them because they have no net charge. Hence they are insoluble in water.
Question 2.
What are the expected products of hydrolysis of lactose ?
Answer:
The expected products of hydrolysis of lactose are β – D – galactose and β – D – glucose.
Question 3.
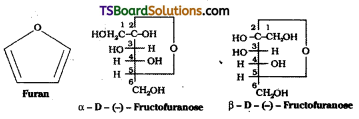
How do you explain the formation of furanose structure for fructose while glucose forms pyranose structure with the same molecular formula C6H12O6 ?
Answer:
Fructose exists in two cyclic forms which are obtained by the addition of -OH at C5 to the (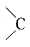 = O) group. The ring thus formed is a five membered ring and is named as furanose with analogy to the heterocyclic compound furan which has a five membered ring with one oxygen and four carbon atoms.
= O) group. The ring thus formed is a five membered ring and is named as furanose with analogy to the heterocyclic compound furan which has a five membered ring with one oxygen and four carbon atoms.
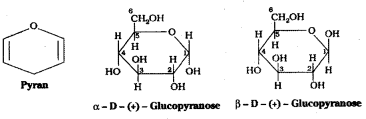
It was found that glucose forms a six – membered ring in which -OH at C5 is involved in ring formation. The -OH at C5 forms a cyclic hemiacetal structure with the -CHO group. The six membered cyclic structure of glucose is called pyranose structure in analogy with pyran.

Question 4.
The melting points and solubility of amino acids in water are generally higher than those of the corresponding halo acids. Explain.
Answer:
Amino acids are crystalline solids. They are water soluble and have high melting points. They behave like salts rather than simple amines or carboxylic acids. This behaviour is due to the presence of both acidic (carboxyl group) and basic (amino group) groups in the same molecule. In aqueous solution the carboxyl group can lose a proton and the amino group can accept a proton, giving rise to a dipolar ion known as Zwitter ion.
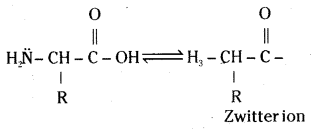
The corresponding haloacids do not show salt – like behaviour and hence their melting points and solubility in water are less.
Question 5.
Temperature and pH affect the native proteins. Explain.
Answer:
Protein found in biological system with a unique three – dimensional structure and biological activity is called as native protein. When a protein in its native form is subjected to change in temperature or pH the hydrogen bonds are disturbed. Due to this, globules unfold and helix gets uncoiled and protein loses its biological activity. This is called denaturation of protein.
Question 6.
Why can’t vitamin C be stored in our body?
Answer:
Vitamin C is a water soluble vitamin. It is readily excreted in urine and cannot be stored in our body.
Question 7.
What products would be formed when a nucleotide from DNA containing thymine is hydrolysed?
Answer:
Adenine and thymine would be formed when a nucleotide from DNA containing thymine is hydrolysis because adenine always pairs up with thymine.

Question 8.
When RNA is hydrolysed, there is no relationship among the quantities of different bases obtained. What does this fact suggest about the structure of RNA ?
Answer:
RNA molecule is a single strand complementary to only one of the two strands of a gene. Its guanine content does not necessarily be equal to its cytocine content, nor does its adenine contents to its uracil content. Hence, when RNA is hydrolysed there is no relationship among the quantities of different bases obtained.
Question 9.
What is DNA finger printing ? Mention its uses.
Answer:
Every individual has unique finger prints. These occur at the tips of fingers and have been used for identification. A sequence of bases on DNA is unique for a person and information regarding this is called DNA finger printing. It is same for every cell and can not be altered.
Importance : DNA finger printing is used
a) in forensic laboratories for identification of criminals.
b) to determine parternity of an individual.
c) to identify dead bodies in accident cases.
d) to identify racial groups to rewrite biological evolution.
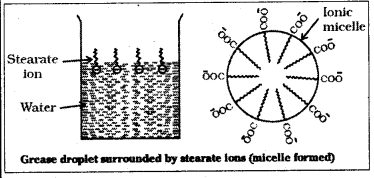
![]()
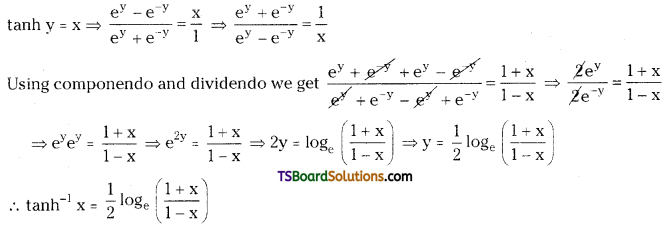
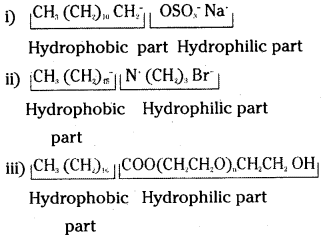
![]()
![]()

![]()
































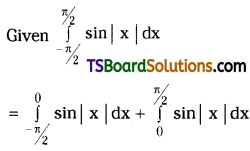


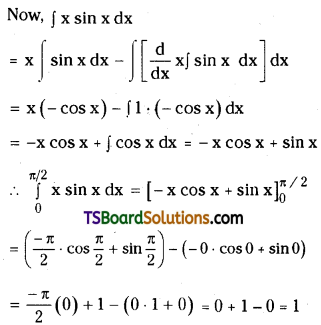



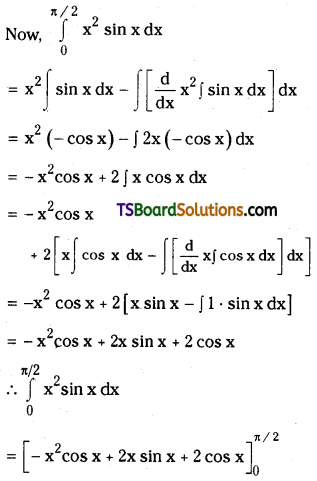
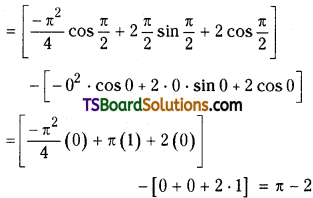


























































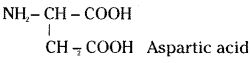















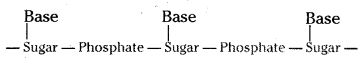



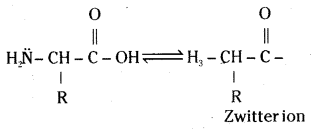




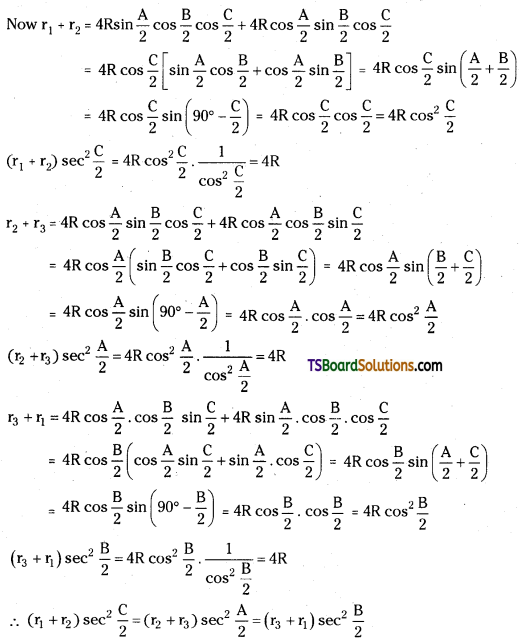
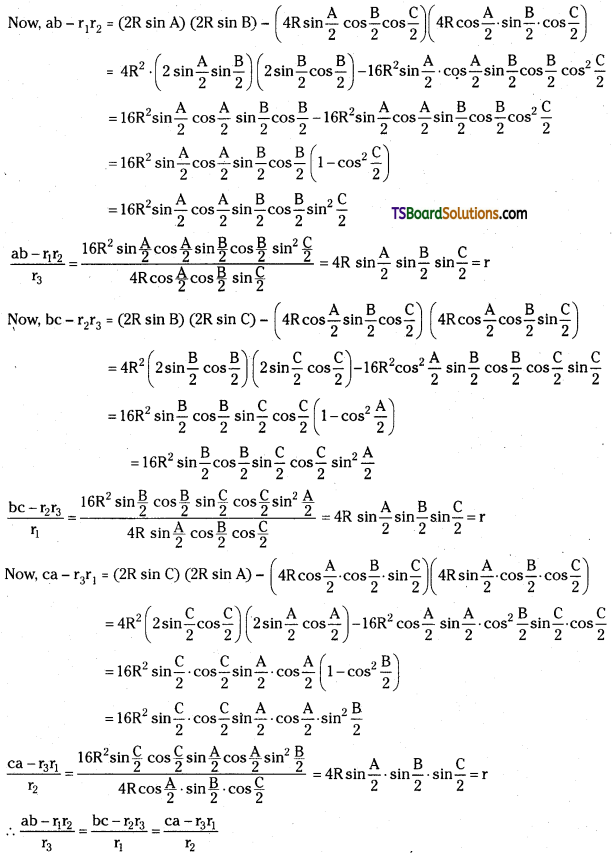






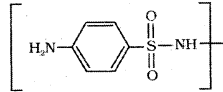
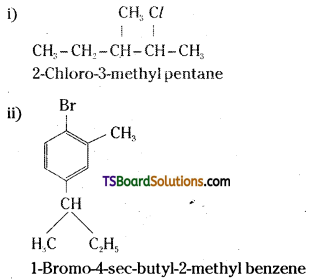
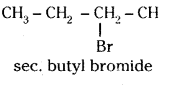
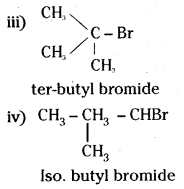
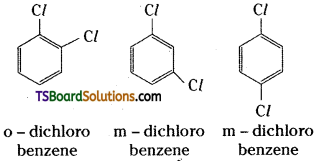
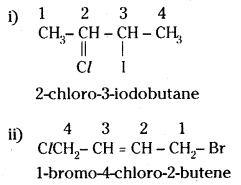
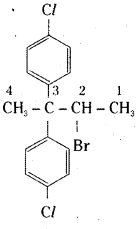
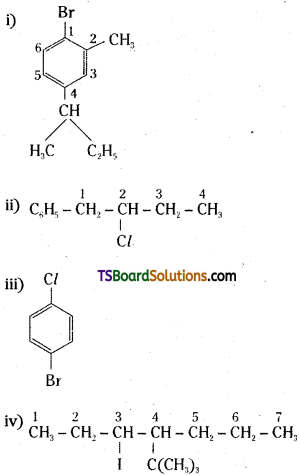
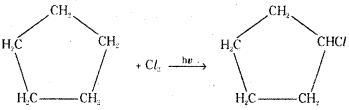
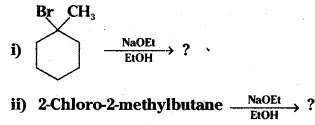
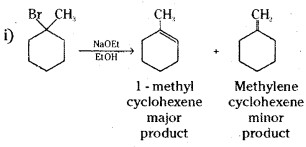
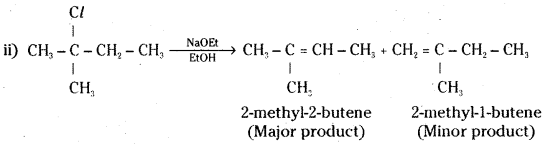
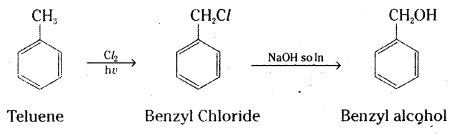
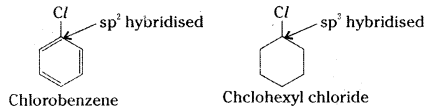
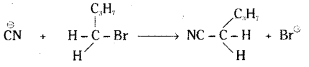
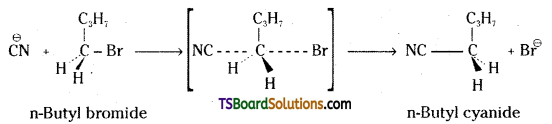
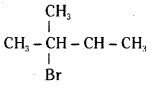
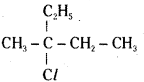
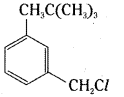
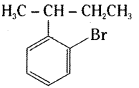
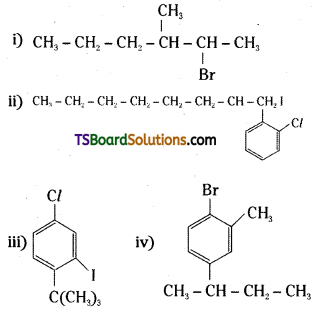

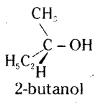
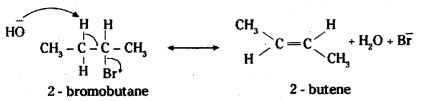

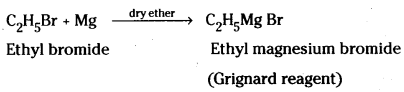
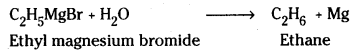
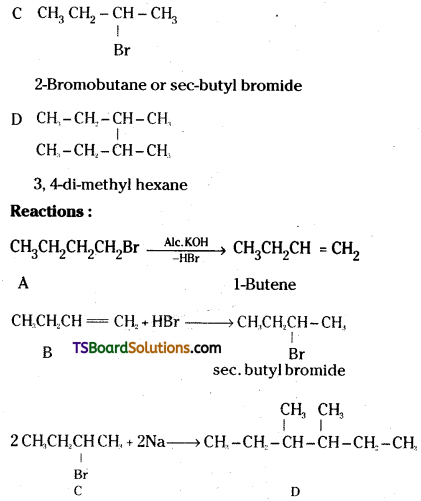
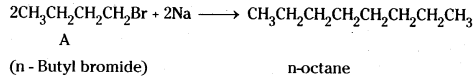



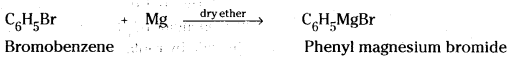
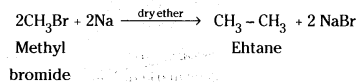
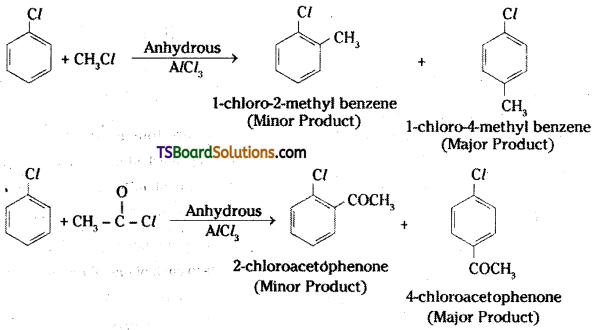
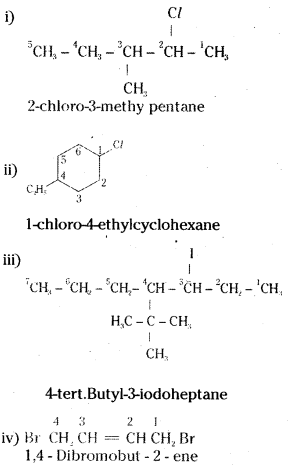
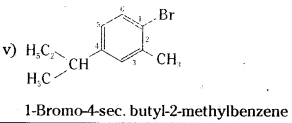
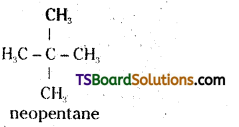
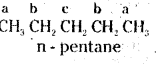
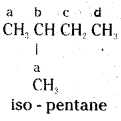
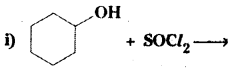
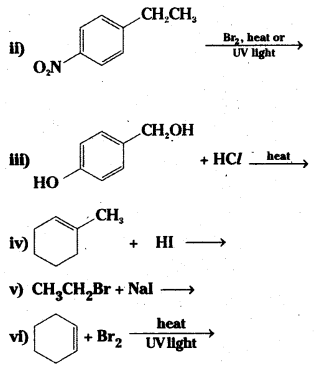
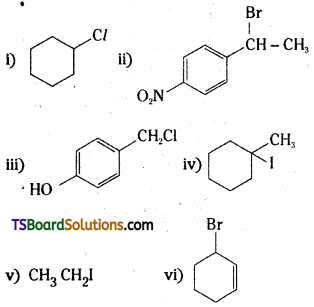
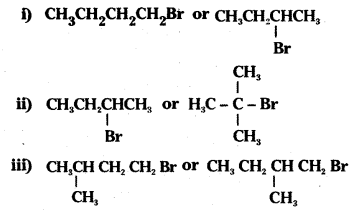
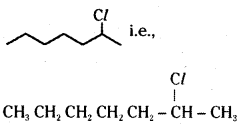
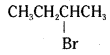 which is a secondary alkyl halide.
which is a secondary alkyl halide.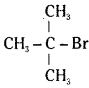 which is a tertiary alkyl halide.
which is a tertiary alkyl halide.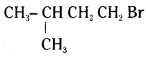 reacts more rapidly by SN2 mechanism because in the other compound
reacts more rapidly by SN2 mechanism because in the other compound 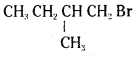 the methyl group is closer to the halogen atom and increases steric hindrance causing a decrease in the reaction rate.
the methyl group is closer to the halogen atom and increases steric hindrance causing a decrease in the reaction rate.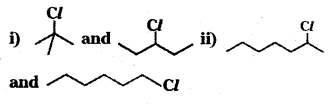



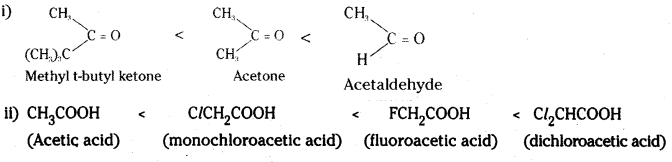


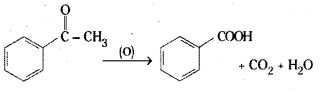

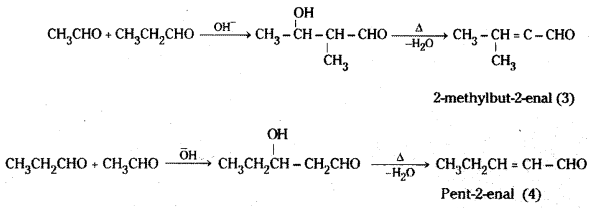
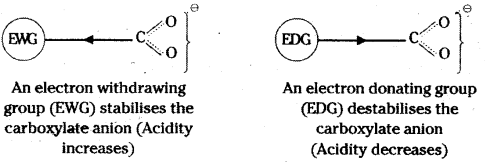

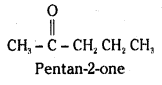
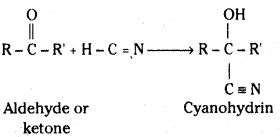

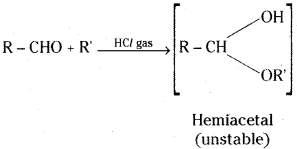
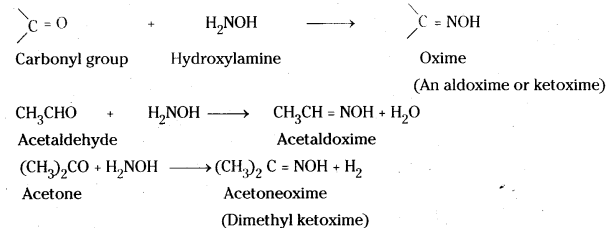
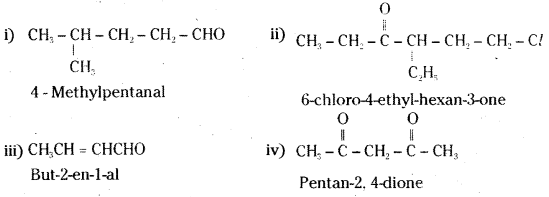
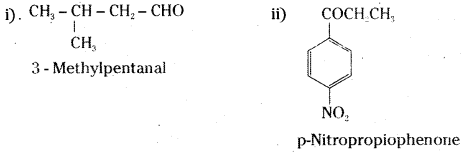
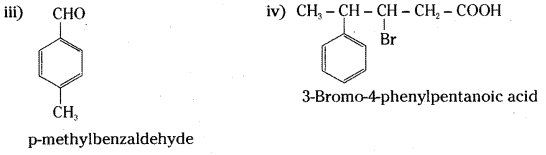
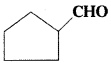
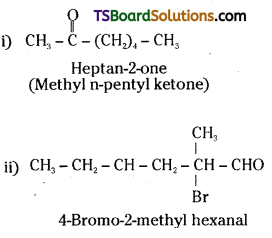
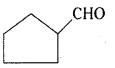
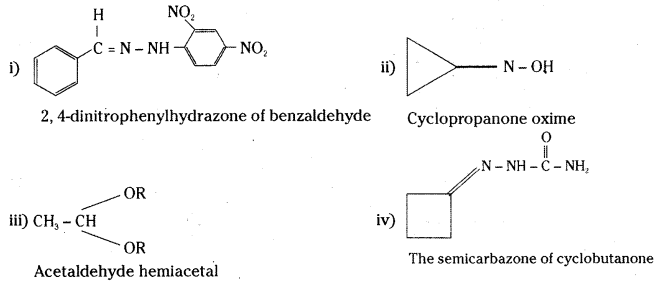
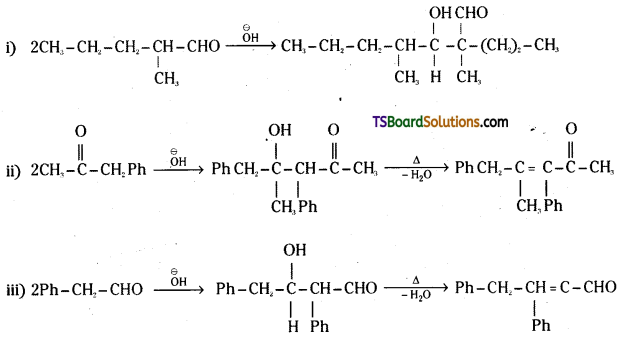
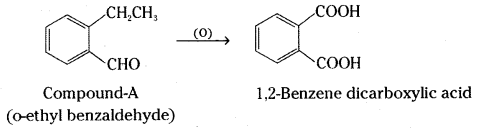
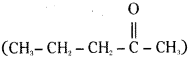 is a methylketone. It gives positive iodoform test.
is a methylketone. It gives positive iodoform test.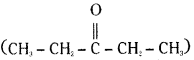 does not give iodoform.
does not give iodoform.