TS Inter Second Year Maths 2B Definite Integrals Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Definite Integrals Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Definite Integrals Important Questions Very Short Answer Type

Question 1.
Evaluate \(\int_0^a\left(a^2 x-x^3\right) d x\).
Solution:

Question 2.
Evaluate \(\int_0^4 \frac{x^2}{1+x} d x\). [(TS) May ’15]
Solution:

Question 3.
Evaluate \(\int_0^\pi \sqrt{2+2 \cos \theta} d \theta\). [(AP) May ’16, Mar. ’18. ’16]
Solution:

Question 4.
Evaluate \(\int_2^3 \frac{2 x}{1+x^2} d x\). [(TS) Mar. ’20. ’16; Mar. ’17 (AP): Mar. ’12]
Solution:

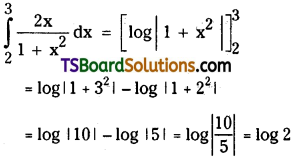
Question 5.
Evaluate \(\int_0^1 \frac{x^2}{x^2+1} d x\). [(TS) May ’18, ’10]
Solution:

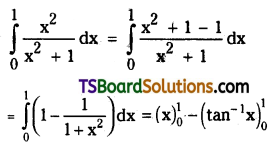
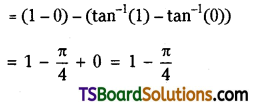
Question 6.
Evaluate \(\int_0^3 \frac{x}{\sqrt{x^2+16}} d x\). [Mar. ’17 (TS)]
Solution:
Put x² + 16 = t² then 2x dx = 2t dt
x dx = t dt
Lower limit: x = 0
⇒ t² = 16
⇒ t = 4
Upper limit: x = 3
⇒ t² = 25
⇒ t = 5

Question 7.
Evaluate \(\int_0^a \frac{d x}{x^2+a^2}\). [(TS) May ’19; (AP) ’15]
Solution:

Question 8.
Find \(\int_0^2 \sqrt{4-x^2} d x\). [Mar. ’07, May ’03]
Solution:

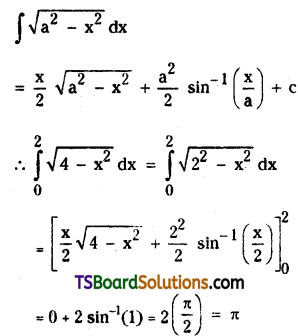
Question 9.
Evaluate \(\int_0^a \sqrt{a^2-x^2} d x\). [(TS) Mar. ’16]
Solution:
Put x = a sin θ then dx = a cos θ dθ
Lower limit: x = 0 ⇒ θ = 0
Upper limit: x = a ⇒ θ = \(\frac{\pi}{2}\)

Question 10.
Evaluate \(\int_0^1 \frac{d x}{\sqrt{3-2 x}}\). [Mar. ’19 (AP)]
Solution:
Put 3 – 2x = t² then -2 dx = 2t dt
dx = -t dt
Lower limit: x = 0
⇒ t² = 3
⇒t = √3
Upper limit: x = 1
⇒ t² = 1
⇒ t = 1

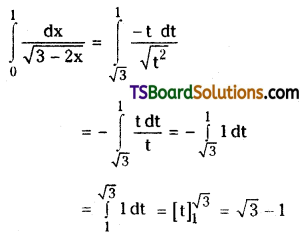
Question 11.
Evaluate \(\int_1^5 \frac{d x}{\sqrt{2 x-1}}\). [(TS) Mar. ’15]
Solution:
Put 2x – 1 = t² then 2dx = 2t dt
dx = t dt
Lower limit: x = 1
⇒ t² = 1
⇒ t = 1
Upper limit: x = 5
⇒ t² = 9
⇒ t = 3

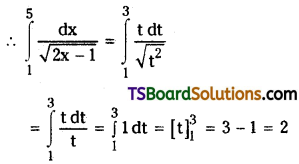
Question 12.
Evaluate \(\int_0^{\pi / 2} \frac{\sin ^5 x}{\sin ^5 x+\cos ^5 x} d x\). [(AP) May ’19, Mar. ’17; Mar. ’14]
Solution:
Let I = \(\int_0^{\pi / 2} \frac{\sin ^5 x}{\sin ^5 x+\cos ^5 x} d x\)

Question 13.
Evaluate \(\int_{\pi / 6}^{\pi / 3} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x\). [(TS) Mar. ’20, ’14]
Solution:

Question 14.
Evaluate \(\int_0^{\pi / 2} \frac{\cos ^{\frac{5}{2}} x}{\sin ^{\frac{5}{2}} x+\cos ^{\frac{5}{2}} x} d x\). [(AP) May ’15]
Solution:

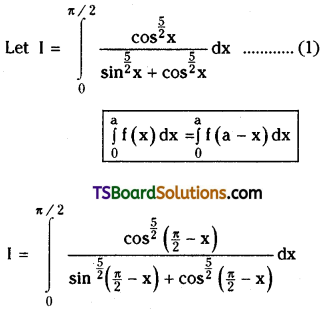
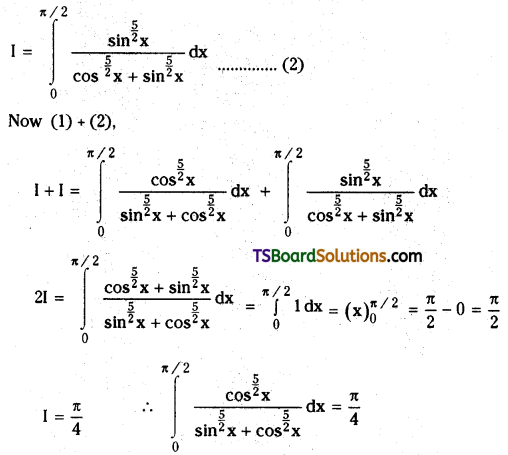
Question 15.
Evaluate \(\int_0^{\pi / 2} \frac{\sin ^2 x-\cos ^2 x}{\sin ^3 x+\cos ^3 x} d x\). [May ’12]
Solution:

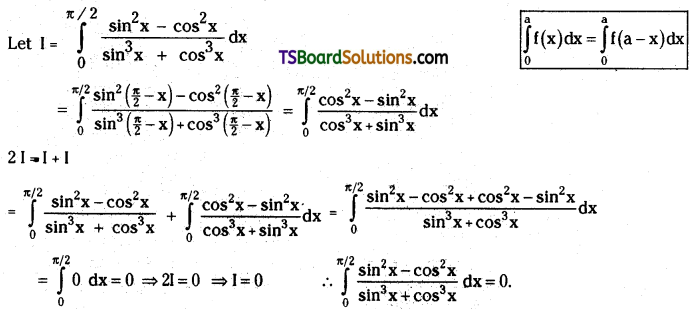
Question 16.
Evaluate \(\int_0^2|1-x| d x\). [(AP) May ’19); Mar. ’15; (TS) Mar. ’18; May ’16]
Solution:

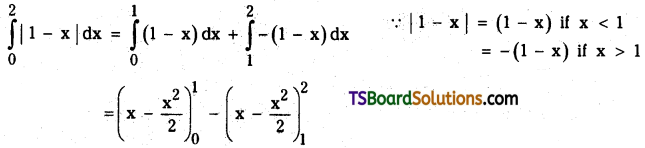
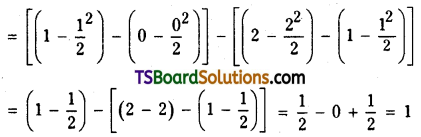
Question 17.
Evaluate \(\int_0^4|2-x| d x\). [(AP) May ’17; ’13]
Solution:

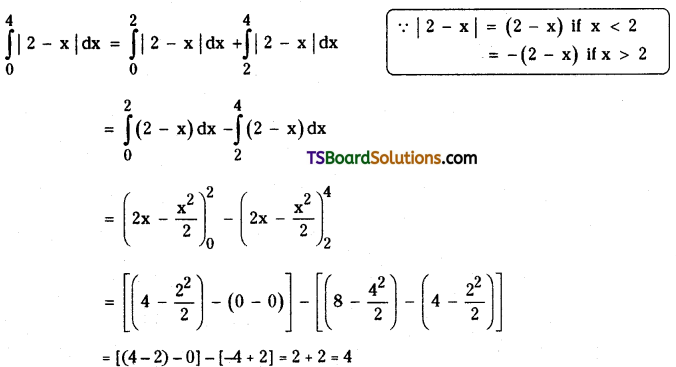
Question 18.
Find \(\int_0^{\pi / 2} \sin ^{10} x d x\)
Solution:

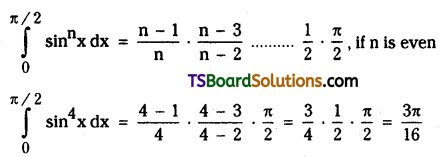
Question 19.
Find \(\int_0^{\pi / 2} \sin ^4 x d x\). [May ’06, ’02]
Solution:

Question 20.
Find \(\int_0^{\pi / 2} \cos ^{11} x d x\). [(TS) Mar. ’19]
Solution:

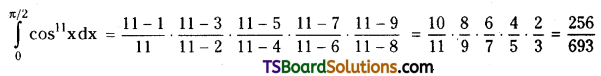
Question 21.
Find \(\int_0^{\pi / 2} \sin ^4 x \cdot \cos ^5 x d x\). [Mar. ’10]
Solution:

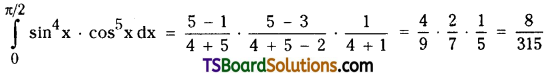
Question 22.
Find \(\int_0^{\pi / 2} \sin ^5 x \cdot \cos ^4 x d x\). [(AP) Mar. ’15]
Solution:

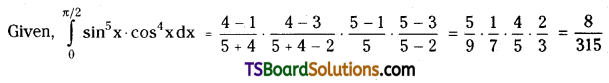
Question 23.
Find \(\int_0^{\pi / 2} \sin ^6 x \cdot \cos ^4 x d x\). [(AP) Mar. ’19; May ’16]
Solution:

Question 24.
Find \(\int_{-\pi / 2}^{\pi / 2} \sin ^2 x \cos ^4 x d x\). [(AP) Mar. ’20, ’18, ’16; May ’16 (TS); Mar. ’13]
Solution:
Let f(x) = sin²x cos⁴x
f(-x) = sin²(-x) cos⁴(-x)
= (-sin x)² (cos x)⁴
= sin²x cos⁴x
= f(x)
∴ f(x) is an even function.
We know that f(x) is even then

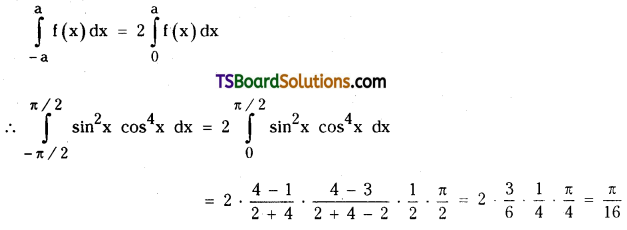
Question 25.
Find \(\int_{-\pi / 2}^{\pi / 2} \sin ^3 \theta \cos ^3 \theta d \theta\). [May ’14]
Solution:
Let, f(θ) = sin³θ . cos³θ
New, f(-θ) = sin³(-θ) cos³(-θ)
= -sin³θ . cos³θ
= -f(θ)
∴ f(θ) is an odd function.
∴ \(\int_{-\pi / 2}^{\pi / 2} \sin ^3 \theta \cos ^3 \theta d \theta\) = 0

Question 26.
Find \(\int_0^{2 \pi} \sin ^2 x \cos ^4 x d x\). [(AP) May ’18; (TS) Mar. ’15; ’14]
Solution:
Let f(x) = sin²x cos⁴x
Now f(2π – x) = sin²(2π – x) cos⁴(2π – x) = sin²x cos⁴x = f(x)
Also t(π – x) = sin²(π – x) cos⁴(π – x) = sin²x cos⁴x = f(x)
∴ \(\int_0^{2 \pi} \sin ^2 x \cos ^4 x d x=2 \int_0^\pi \sin ^2 x \cos ^4 x d x\)

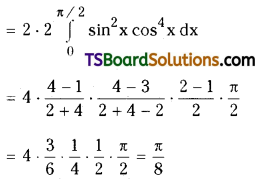
Question 27.
Find \(\int_0^\pi \sin ^3 x \cos ^3 x d x\). [(TS) May ’15]
Solution:
Let f(x) = sin³x . cos³x
Now f(π – x) = sin³(π – x) cos³(π – x)
= -sin³x cos³x
= -f(x)
∴ \(\int_0^\pi \sin ^3 x \cos ^3 x d x\) = 0

Question 28.
Find the area bounded by the parabola y = x², the X-axis, and the lines x = -1, x = 2. [(TS) May ’18, ’16; (AP) ’15]
Solution:
Given y = x², X-axis i.e., y = 0
x = -1; x = 2
y = x²

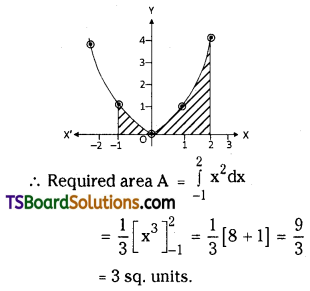
Question 29.
Find the area of the region bounded by y = x³ + 3, X-axis and x = -1, x = 2. [(TS) Mar. ’20; May ’17; Mar. ’12]
Solution:
Given y = x³ + 3, y = 0, x = -1, x = 2

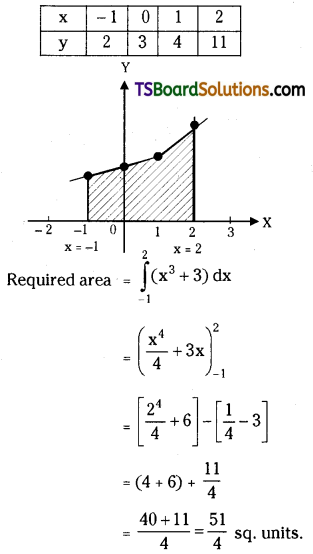
Question 30.
Find the area enclosed between the curves x = 4 – y², x = 0. [Mar. ’11, ’10]
Solution:
Given, x = 4 – y² and x = 0
Solving, 4 – y² = 0 then y = ±2
∴ y = 2 and y = -2

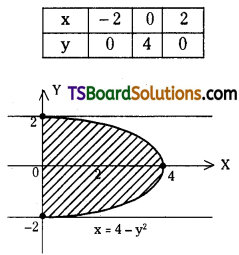
Question 31.
Find the area bounded between the curves y² – 1 = 2x and x = 0.
Solution:
Given y² – 1 = 2x and x = 0 ……..(2)
⇒ x = \(\frac{\mathrm{y}^2-1}{2}\) ……(1)

Solving (1) & (2)
o = \(\frac{\mathrm{y}^2-1}{2}\)
⇒ y² – 1 = 0
⇒ y² = 1
⇒ y = ±1

Question 32.
Find the area enclosed between the curve x² = 4y, x = 2, y = 0.
Solution:
Given x² = 4y, x = 2, y = 0
Solving, x² = 4y = 4(0) = 0

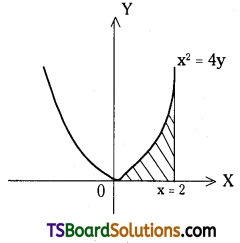
Question 33.
Find the area enclosed between the curves y = x², y = 2x. [May ’13]
Solution:
Given y = x² and y = 2x

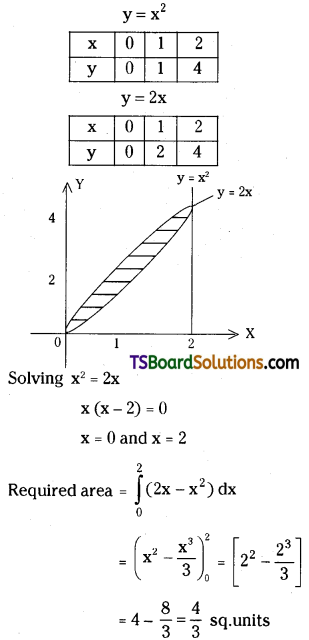
Question 34.
Find the area enclosed between the curves, y = x², y = x³. [(TS) May ’19]
Solution:
Given y = x² and y = x³

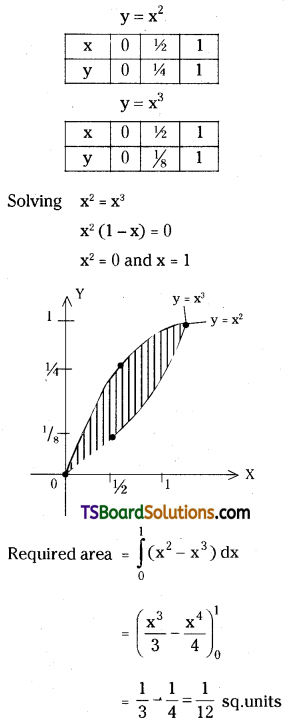
Question 35.
Evaluate \({Lim}_{n \rightarrow \infty}\left[\frac{1}{n+1}+\frac{1}{n+2}+\ldots \ldots . .+\frac{1}{6 n}\right]\)
Solution:

Question 36.
Evaluate \({Lim}_{n \rightarrow \infty} \frac{1+2^4+3^4+\ldots \ldots \ldots+n^4}{n^5}\). [(AP) Mar. ’20]
Solution:

Question 37.
Evaluate \({Lt}_{n \rightarrow \infty} \sum_{i=1}^n \frac{i}{\mathbf{n}^2+i^2}\)
Solution:

Question 38.
Find the area bounded by y = sin x, x-axis, x = 0, and x = π.
Solution:
Given curve is y = sin x, the x-axis
x = 0 and x = π

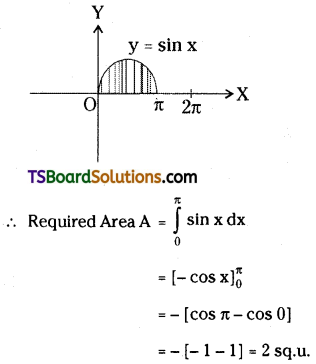
Question 39.
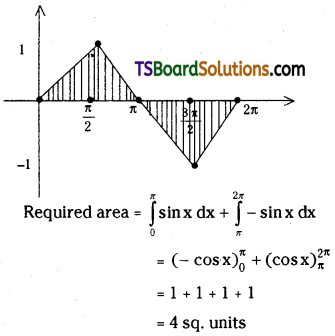
Find the area under the curve f(x) = sin x in [0, 2π]. [May ’09]
Solution:
Let y = f(x) = sin x

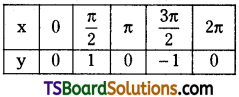
Question 40.
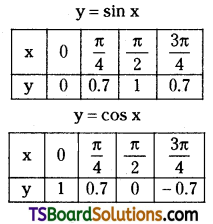
Find the area of one of the curvilinear triangles bounded by y = sin x, y = cos x, and X-axis. [Mar. ’19 (AP)]
Solution:
Given curves are
y = sin x ……..(1)
y = cos x …….(2)

Solving (1) and (2)
sin x = cos x
⇒ \(\frac{\sin x}{\cos x}\) = 1
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\)
OAB is one of the curvilinear triangles bounded by y = sin x, y = cos x and XY-axes
Required area A = \(\int_0^{\pi / 4} \sin x d x+\int_{\pi / 4}^{\pi / 2} \cos x d x\)

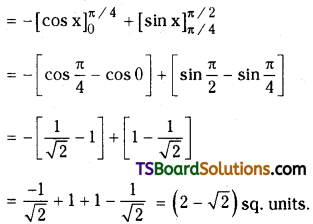
Question 41.
Find the area bounded between curves y = x², y = √x. [Mar. ’18 (TS)]
Solution:
Given curves are
y = x² …….(1)
y = √x ………(2)
From (1) and (2)
√x = x²
⇒ x = x⁴
⇒ x(1 – x³) = 0
⇒ x = 0, x³ = 1
⇒ x = 1

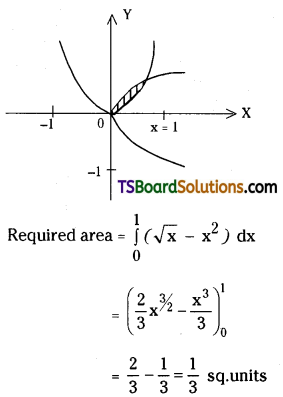
Question 42.
Evaluate \({Lt}_{n \rightarrow \infty} \frac{2^k+4^k+6^k+\ldots \ldots+(2 n)^k}{n^{k+1}}\) by using the methods of finding the definite integral of the limit of a sum. [(AP) May ’18]
Solution:

Question 43.
Evaluate \(\int_0^{\pi / 4} \sec ^4 \theta d \theta\). [May ’14]
Solution:

Question 44.
Evaluate \(\int_0^{\pi / 2} \sin ^2 \mathrm{x} d \mathbf{x}\). [May ’95]
Solution:

Question 45.
Evaluate \(\int_{-1}^1 \frac{1}{1+x^2} d x\). [May ’94, Mar. ’92]
Solution:

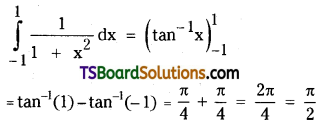
Question 46.
Evaluate \(\int_0^1 \sin ^{-1} x \mathrm{dx}\). [Mar. ’99]
Solution:

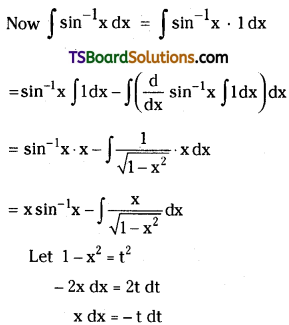
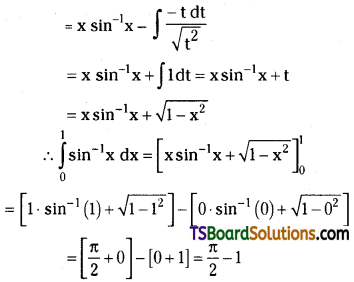
Question 47.
Evaluate \(\int_1^2 \log x d x\). [May ’98, ’94]
Solution:

Question 48.
Evaluate \(\int_0^1 \frac{d x}{e^x+e^{-x}}\). [Mar. ’06]
Solution:

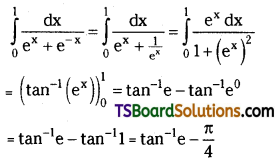
Question 49.
Evaluate \(\int_{\mathbf{a}}^{\mathbf{b}} \frac{|\mathbf{x}|}{\mathbf{x}} \mathbf{d x}\). [May ’03]
Solution:
\(\int_{\mathbf{a}}^{\mathbf{b}} \frac{|\mathrm{x}|}{\mathrm{x}} \mathrm{dx}=[|\mathrm{x}|]_{\mathrm{a}}^{\mathbf{b}}\) = |b| – |a|

Question 50.
Find \(\int_0^{\pi / 2} \cos ^8 x \mathbf{d x}\)
Solution:

Question 51.
Find \(\int_0^{\pi / 2} \sin ^7 x d x\). [Mar. ’17 (AP)]
Solution:

Question 52.
Find \(\int_0^{2 \pi} \sin ^4 x \cdot \cos ^6 x d x\). [Mar. ’19 (TS); (AP) May ’17]
Solution:

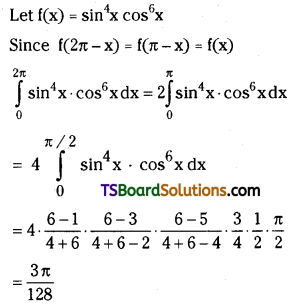
Question 53.
Find \(\int_0^\pi \sin ^3 x \cos ^6 x d x\)
Solution:
Given, Let, f(x) = sin³x cos⁶x
Now, f(π – x) = sin³(π – x) cos⁶(π – x)
= sin³x . cos⁶x
= f(x)

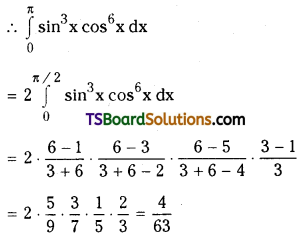
Question 54.
Evaluate \(\int_0^\pi \cos ^3 x \cdot \sin ^4 x d x\). [Mar. ’00]
Solution:
Let f(x) = cos³x sin⁴x
Then f(π – x) = cos³(π – x) sin⁴(π – x)
= -cos³x sin⁴x
= -f(x)
∴ f(x) is an odd function
∴ \(\int_0^\pi \cos ^3 x \cdot \sin ^4 x d x\) = 0

Question 55.
Evaluate \(\int_0^{\pi / 2} \frac{1}{1+\tan x} d x\). [Mar. ’02, May ’99]
Solution:

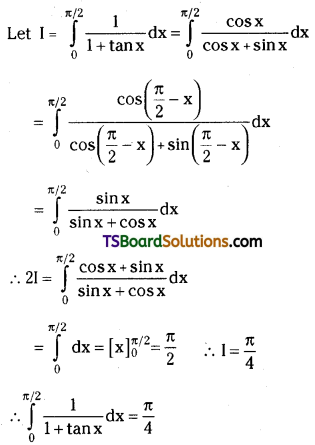
Question 56.
Find the area under the curve f(x) = cos x in [0, 2π].
Solution:
Let Y = f(x) = cos x; y = f(x) = cos x

Question 57.
Find the area enclosed between the curves y = e^x, y = x; x = 0, x = 1.
Solution:

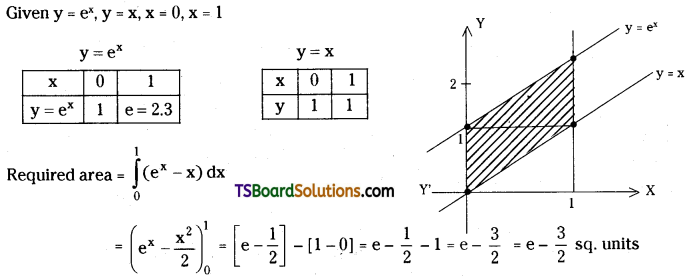
Question 58.
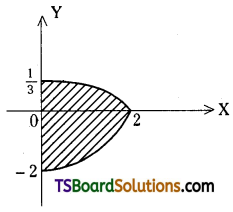
Find the area enclosed between the curves x = 2 – 5y – 3y², x = 0.
Solution:
Given x = 2 – 5y – 3y², x = 0
x = 2 – 5y – 3y²

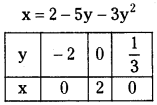
Solving, 2 – 5y – 3y² = 0
⇒ 3y² + 5y – 2 = 0
⇒ 3y² + 6y – y – 2 = 0
⇒ 3y(y + 2) – 1(y + 2) = 0
⇒ (y + 2)(3y – 1) = 0
∴ y = -2 and y = \(\frac{1}{3}\)

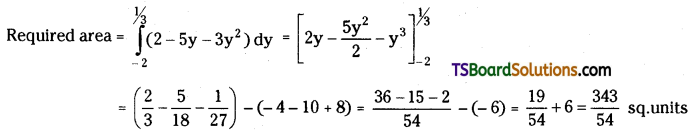
Question 59.
Find the area enclosed between the curve y² = 3x, x = 3.
Solution:
Given y² = 3x and x = 3
Solving, y² = 3(3)
y = ±3
∴ y = 3 and y = -3

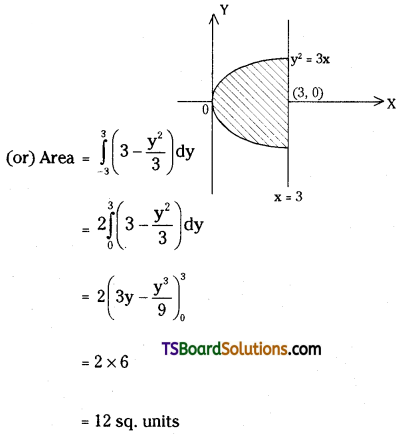
Question 60.
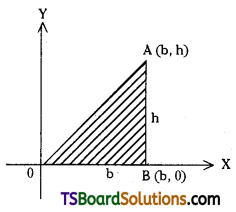
Find the area of the right-angled triangle with base b and altitude h, using the fundamental theorem of integral calculus.
Solution:
Let OAB be a right-angled triangle and ∠B = 90°.
Choose ‘O’ as the origin and OB as the +ve x-axis.
If OB = b, and AB = h then A = (b, h).
So, the equation of OA is y = (\(\frac{h}{b}\))x

Question 61.
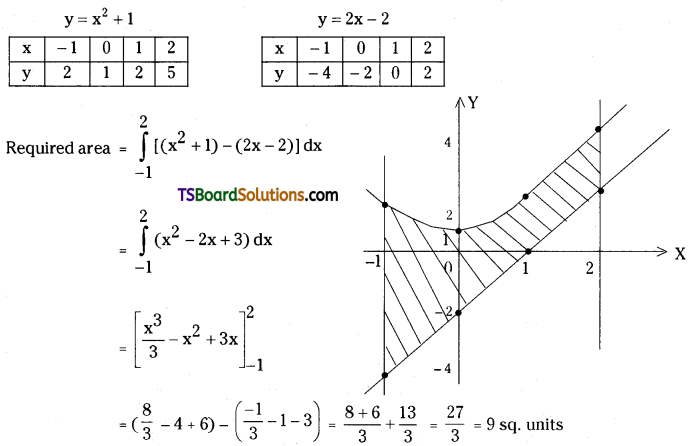
Find the area bounded between the curves y = x² + 1, y = 2x – 2, x = -1, x = 2. [(AP) May ’16]
Solution:
Given curves are y = x² + 1, y = 2x – 2
x = -1 and x = 2

Question 62.
Find the area cut off between the line y = 0 and the parabola y = x² – 4x + 3,
Solution:
Given, y = x² – 4x + 3 ……(1)
and y = o ……..(2)
Solving (1) and (2)
x² – 4x + 3 = 0
⇒ x² – 3x – x + 3 = 0
⇒ x(x – 3) – 1(2 – 3) = 0
⇒ (x – 1)(x – 3) = 0
⇒ x = 1, 3

Question 63.
Evaluate \(\int_{-\pi / 2}^{\pi / 2} \sin |\mathbf{x}| \mathbf{d x}\). [Mar. ’17 (TS)]
Solution:

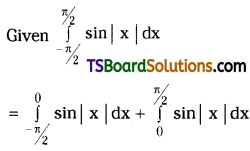
Question 64.
Show that \(\int_0^{\pi / 2} \sin ^n x d x=\int_0^{\pi / 2} \cos ^n x \mathbf{d x}\)
Solution:

Question 65.
Evaluate \(\int_0^{\pi / 2} x \sin x d x\). [Mar. ’18 (TS)]
Solution:

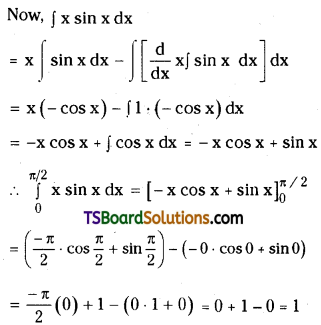
Question 66.
Evaluate \(\int_0^a(\sqrt{a}-\sqrt{x})^2 d x\). [Mar. ’19 (TS)]
Solution:

Question 67.
Evaluate \(\int_0^1 x e^{-x^2} d x\)
Solution:
Put -x² = t then -2x dx = dt
x dx = \(\frac{-\mathrm{dt}}{2}\)
Lower limit: x = 0 ⇒ t = 0
Upper limit: x = 1 ⇒ t = -1

Question 68.
Evaluate \(\int_{-1}^2 \frac{x^2}{x^2+2} d x\)
Solution:

Question 69.
Evaluate \(\int_0^{\pi / 2} x^2 \sin x d x\)
Solution:

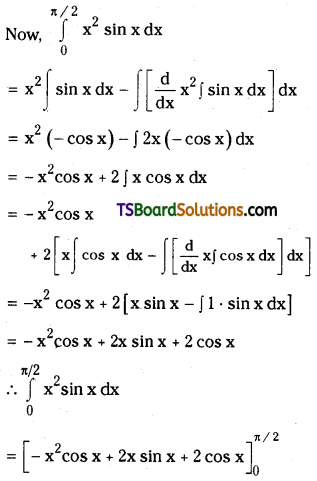
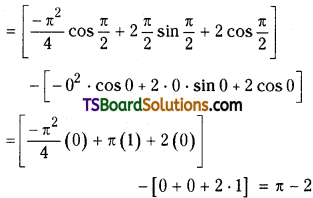
Question 70.
Evaluate \({Lt}_{n \rightarrow \infty} \frac{\sqrt{n+1}+\sqrt{n+2}+\ldots \ldots \ldots+\sqrt{n+n}}{n \sqrt{n}}\)
Solution:

Question 71.
Evaluate \(\int_0^a \mathbf{x}(\mathbf{a}-\mathbf{x})^{\mathbf{n}} \mathbf{d x}\)
Solution:

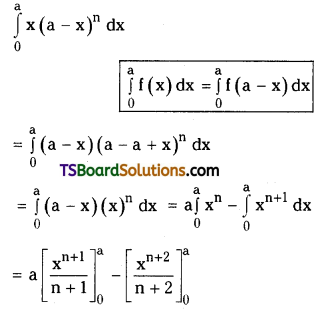
Question 72.
Evaluate \(\int_0^{\pi / 2} \tan ^5 x \cos ^8 x d x\)
Solution:

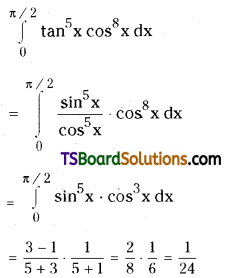
Question 73.
Find the area bounded by the curves y = sin x and y = cos x between any two consecutive points of intersection. [Mar. ’18 (AP)]
Solution:

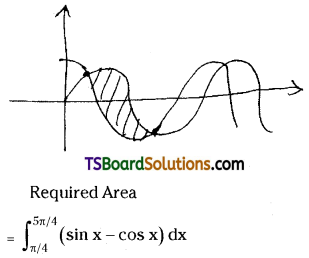
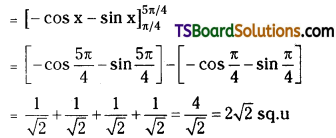
Question 74.
Evaluate \(\int_0^\pi \sin x d x\)
Solution:
\(\int_0^\pi \sin \mathrm{x} d \mathrm{x}=[-\cos \mathrm{x}]_0^\pi\)
= -[cos π – cos 0]
= -[-1 – 1]
= -(-2)
= 2

Question 75.
Evaluate \(\int_2^3 \frac{2 x}{1+x^2} d x\)
Solution:
Put 1 + x² = t, then 2x dx = dt
L.L: x = 2 ⇒ t = 5
U.L: x = 3 ⇒ t = 10

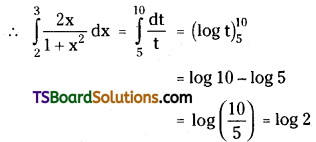
Question 76.
Evaluate \(\int_1^4 x \sqrt{x^2-1} d x\)
Solution:
Put x² – 1 = t²
⇒ 2x dx = 2t dt
⇒ x dx = t dt
L.L: x = 1 ⇒ t = 0
U.L: x = 4 ⇒ t = √15

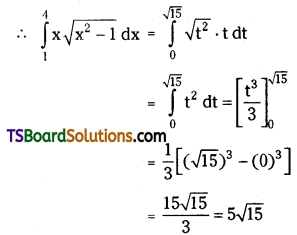
Question 77.
Evaluate \(\int_0^\pi(1+\cos x)^3 d x\)
Solution:

Question 78.
Evaluate \(\int_0^5(x+1)\) dx as a limit of a sum.
Solution:

Question 79.
Evaluate \(\int_0^4 x^2 d x\) as a limit of a sum.
Solution:

Question 80.
Find the area in sq. units bounded by the x-axis, part of the curve y = 1 + \(\frac{8}{x^2}\), and the ordinates x = 2 and x = 4.
Solution:

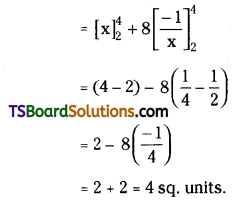
Question 81.
Find the area bounded by the curve y = log x, the x-axis, and the straight line x = e.
Solution:
Given that y = log x ………(1)
x-axis, i.e., y = 0 ……….(2)
x = e
Solve (1) & (2)
0 = log e^x
⇒ x = e⁰
⇒ x = 1

= (e log e – e) – (log 1 – 1)
= (e – e) – (0 – 1)
= 0 – (-1)
= 1 sq. units

Question 82.
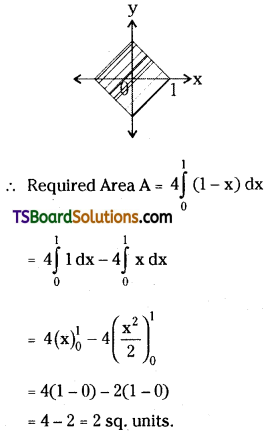
Find the area enclosed within the curve |x| + |y| = 1.
Solution:
Given curve is |x| + |y| = 1
⇒ ±x ± y = 1
Given curve represents 4 straight lines
Take x + y = 1 ⇒ y = 1 – x