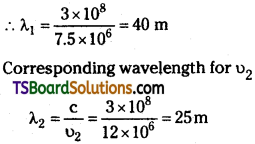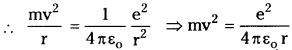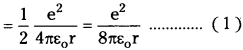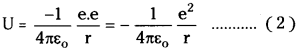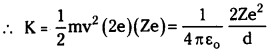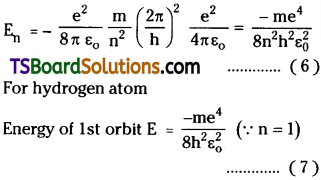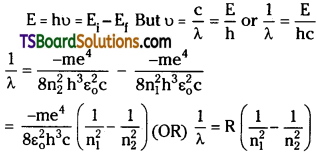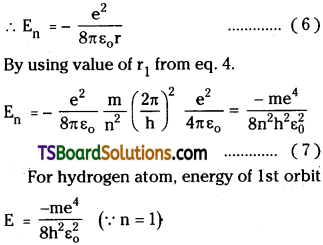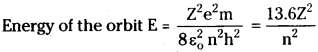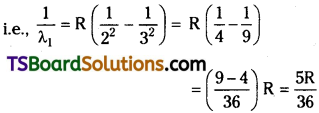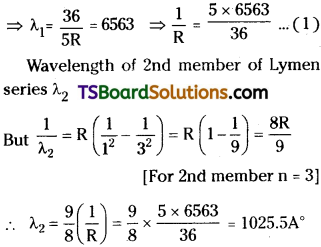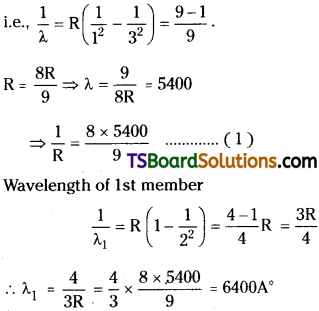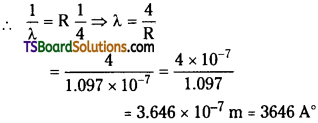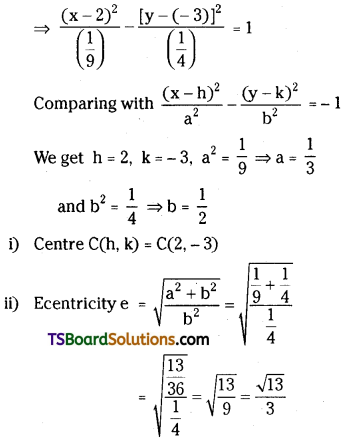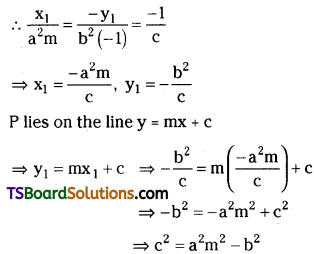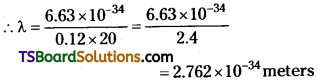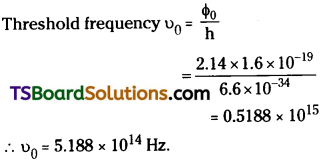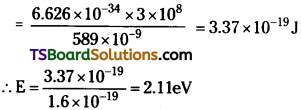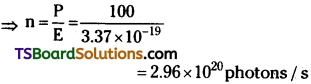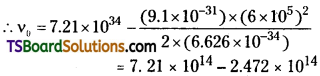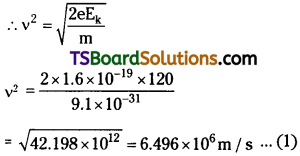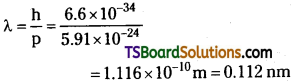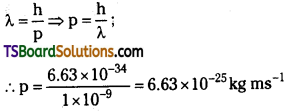TS Inter 2nd Year

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 5 Hyperbola will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Hyperbola Formulas

→ Hyperbola is a conic which is the locus of a point that moves so that the ratio of the distance from a fixed point to its distance from a fixed line is greater than 1.

→ Equation of hyperbola in the standard form is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 centre at (0, 0) and foci (±ae, 0) directrices x = ± \(\frac{a}{e}\) and eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)

→ Various fonns of the hyperbola :

Hyperbola	Conjugate hyperbola
S = \( \frac{x^2}{a^2}-\frac{y^2}{b^2} \) – 1 = 0	S’ = \( \frac{x^2}{a^2}-\frac{y^2}{b^2} \) + 1 = 0
1. Transverse axis is along * X – axis (y = 0) and its length is 2a.	1. Transverse axis is along Y – axis (x = 0) and its length is 2b.
2. Conjugate axis is along Y-axis (x = 0) and its length is 2b.	2. Conjugate axis is along X – axis (y – 0) and its length is 2a
3. Coordinates of the centre C = (0, 0).	3. Coordinates of the centre C = (0, 0).
4. Foci S = (±ae, 0)	4. Foei S’ = (0, ± be)
5. Equation of the directrices x = ±\(\frac{a}{e}\)	5. Equation of the directrices y = ±\(\frac{b}{e}\)
6. Eccentricity e = \( \sqrt{\frac{a^2+b^2}{a^2}} \)	6. Eccentricity e = \( \sqrt{\frac{a^2+b^2}{b^2}} \)

→ If the centre is at (h, k) and the axes of the hyperbola are parallel to the coordinate axis.

→ If P is any point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 and foci are S and S’ then S’P – SP = 2a.

→ Equation of rectangular hyperbola whose eccentricity is √2 is x² – y² = a².

→ The equation of auxiliary circle of the hyperbola S = 0 is x² + y² = a²,

→ x = a sec θ, y = b tan θ are the parametric equations of hyperbola.

→ The condition for a straight line y = mx + c to be a tangent to the hyperbola S = 0 is c² = a²m² – b².

→ y = mx ± \(\) is always a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 and point of contact is \(\left(-\frac{a^2 m}{c},-\frac{b^2}{c}\right)\) and \(\left(\frac{a^2 m}{c}, \frac{b^2}{c}\right)\)

→ The equation of tangent at (x₁, y₁) to S = 0 is \(\frac{x_1}{a^2}-\frac{y y_1}{b^2}\) = 1.

→ The equation of normal at (x₁, y₁) to S = 0 is \(\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}\) = a² + b²

→ Equation of tangent at the point (asec θ, btan θ) is \(\frac{x}{a}\)sec θ – \(\frac{y}{b}\)tan θ = 1.

→ Equation of normal at the point P(θ) is \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b².

→ The equation of the asymptotes of a hyperbola S = 0 are y = ±\(\frac{b}{a}\) x and the combined equation of asymptotes is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 0

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 4 Ellipse will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Ellipse Formulas

→ An ellipse is the locus of a point whose distances from a fixed point and a fixed straight line are in a constant ratio ‘e’ which is less than unity. The fixed point and the fixed straight line are called the focus and the directrix of ellipse respectively.

→ Equation of an ellipse in the standard form is – 1, (a > b). Centre = (0, 0)
Foci = (± ae, 0); Directrix, x = ±\(\frac{\mathrm{a}}{\mathrm{e}}\) and Eccentricity, e = \(\sqrt{\frac{a^2-b^2}{a^2}}\)

→ Various forms of the ellipse Form:
(i) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (a > b > 0)

(ii) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (0 < a < b)

(iii) \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 (a > b > 0)

(iv) \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 (0 < a < b)

→ If P is any point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, (a > b) and foci are S, S’, then SP + S’P = 2a.

→ The equation of the auxiliary circle of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, (a > b) is x² + y² = a².

→ Parametric equations of ellipse S = 0 are x = a cos θ, y = b sin θ and θ is called the parameter.

→ If P(x₁, y₁) is a point on the plane of the ellipse, then P lies outside, on or inside the ellipse according as Sn is positive, zero or negative.

→ The condition for the straight line y = mx + c to touch the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is (or) tangent to the ellipse is c² = a²m² + b².

→ y = mx ± \(\sqrt{a^2 m^2+b^2}\) is always a tangent to the ellipse S = 0 at \(\sqrt{a^2 m^2+b^2}\) and \(\left(\frac{a^2 m}{c}, \frac{-b^2}{c}\right)\)

→ The equation of the tangent at P (x₁, y₁)to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is \(\frac{\mathrm{x} \mathrm{x}_1}{a^2}+\frac{\mathrm{y} \mathrm{y}_1}{\mathrm{~b}^2}\) – 1 = 0

→ The equation of the normal to the ellipse at P (x₁, y₁) is \(\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}\) = a² – b²

→ Equation of the tangent at P (θ) i.e., P (a cos θ, b sin θ) to the ellipse S = 0 is \(\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}\) = 1.

→ Equation of the normal at P(θ) to the ellipse S = 0 is \(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}\) = a² – b²
where θ ≠ 0, \(\frac{\pi}{2}\), π, \(\frac{3 \pi}{2}\)

→ Eqilation of director circle of the ellipse S = 0 is x² + y² = a² + b²

→ If P(x₁, y₁) Is an external point to the ellipse S = 0, then the equation of chord of contact of P w.r.t ellipse S = 0 is \(\frac{x x_1}{a^2}+\frac{y y_1}{b^2}\) = 1.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 7 Definite Integrals will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Definite Integrals Formulas

→ If F(x) is an indefinite integral (or) anti-derivative of a function f(x) defined on [a, b] then
\(\int_a^b\)f(x) dx = F(b) – F(a) …………….. (1).
The symbol \(\int_a^b\)f (x) dx is called the definite integral of f(x) from x = a to x = b. The numbers ’a’ and ’b’ are called the limits of integration, ’a’ is called the lower limit and ’b’ is called the upper limit. If we use the notation \([\mathrm{F}(\mathrm{x})]_{\mathrm{a}}^{\mathrm{b}}\) to denote
F(b) – F(a), then from (1) \(\int_a^b\)f (x) dx = \([\mathrm{F}(\mathrm{x})]_{\mathrm{a}}^{\mathrm{b}}\) = [(F(x) at x = b) – (F(x) at x = a)].

→ Fundamental properties of definite integrals:
Property – 1 : \(\int_a^a\) f (x) dx = 0

Property-2: \(\int_a^b\) f(x)dx = \(\int_a^b\)f(t)dt

Property-3: \(\int_a^b\)f(x)dx = – \(\int_b^a\)f(x)dx

Property-4: \(\int_a^b\)f(x)dx = \(\int_a^c\)f(x)dx + \(\int_c^b\)f(x)dx, if a < c < b

Property-5: \(\int_0^a\)f (x)dx = \(\int_0^a\)f (a – x)dx

Property- 6: \(\int_{-a}^a\)f(x) dx = 2\(\int_0^a\)f(x)dx, if f(x) is even
= 0, if f(x) is odd

Property – 7: \(\int_0^{2 a}\)f(x) dx = 2\(\)f(x)dx, if f(2a – x) = f(x)
= 0, if f(2a – x) = – f(x)

Properly – 8: \(\int_a^b\)f(x)dx = \(\int_a^b\)f(a + b – x)dx

Properly-9: \(\int_0^{n a}\)f (x)dx = n\(\int_0^{a}\)f(x)dx, if f(a + x) = f(x)

Properly -10: \(\int_0^{\infty}\)f(x)dx = \({Lt}_{t \rightarrow \infty} \int_0^t\)f(x)dx and \(\int_{-\infty}^a\) f(x)dx = \({Lt}_{t \rightarrow-\infty} \int_t^a\)f(x)dx
and \(\int_{-\infty}^{\infty}\) f(x)dx = \({Lt}_{t \rightarrow \infty} \int_a^t\)f(x)dx + \({Lt}_{t \rightarrow-\infty} \int_t^a\)f(x)dx

Properly -11: |\(\int_a^b\)f(x) dx| ≤ \(\int_a^b\) |f(x)|dx

Properly -12: If f(x) ≥ 0, ∀x ∈ [a, b], then \(\int_a^b\)f(x)dx ≥ 0 and if f(x) ≥ g(x), ∀ x ∈ [a, b] then \(\int_a^b\)f(x)dx ≥ \(\int_a^b\) g(x)dx

→ Reduction Formulae:

• If I_n = \(\int_0^{\pi / 2}\)sinⁿ dx, then I_n = \(\frac{n-1}{n}\)I_n-2
• If I_n = \(\int_0^{\pi / 2}\)cosⁿ dx, then I_n = \(\frac{n-1}{n}\)I_n-2
• If I_n = \(\int_0^{\pi / 4}\)tanⁿ dx, then I_n = \(\frac{1}{n-1}\)I_n-2
• If I_n = \(\int_0^{\pi / 4}\)secⁿ dx, then I_n = \(\frac{(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = \(\int_{\pi / 4}^{\pi / 2}\)cotⁿ dx, then I_n = \(\frac{1}{n-1}\) – I_n-2
• If I_n = \(\int_{\pi / 4}^{\pi / 2}\)cosecⁿ dx, then I_n = \(\frac{-(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_m,n = \(\int_0^{\pi / 2}\)sin^mx. cosⁿxdx then I_m,n = \(\frac{-(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2

Let m and n be positive integers, then

Let n be an integer greater than or equal to 2.

Areas:
→ Let f be a continuous function on [a, b]. Then the area of the region bounded by curve y = f(x) with X – axis between the lines x = a and x = b is
(i) \(\int_a^b\)f(x)dx, if f(x) ≥ 0

(ii) –\(\int_a^b\)f(x)dx, if f(x) ≤ 0

→ Let a < c < b and if f(x) ≥ 0 on [a, cl and f(x) ≤ 0 on [b, C]. Then the area of the region bounded by the curve y = f(x) wIth X- axis between lines x = a and x = b is
\(\int_a^c\)f(x) dx – \(\int_c^b\)f(x) dx

→ The area of the region bounded by the curve x = f(y) with Y – axis between the lines y = c and y = d is
(i) \(\int_c^d\)f(y) dy, if f(y) ≥ 0

(ii) \(\int_c^d\)f(y) dy, If f(y) ≤ 0

→ Let c < e < d and If f(y) ≥ 0 on [c, e] and f(y) ≤ 0 on [e, d]. Then the area of the region bounded by the curve x = f(y) with Y-axis between the lines y = c and y =d is

\(\int_c^e\)f(y)dy – \(\int_d^e\)f(y) dy

→ The area of the region bounded by the curves y f(x), g(x) = y between the lines x = a and x = b is
(i) \(\int_a^b\)[f(x) – g(x)]dx, if f(x) ≥ g(x)

(ii) \(\int_a^b\)[g(x) – f(x)]dx; if f(x) ≤ g(x)

→ The area of the region bounded by the curves x = f(y), x = g(y) between the lines y = c and y = d is x = g(x) x = f(x)
(i) \(\int_c^d\)[f(y) – g(y)]dy, if f(y) > g(y)

(ii) \(\int_c^d\)[g(y) – f(y)]dy, if f(y) ≤ g(x)

→ Limit As A Definite Integral
Definite Integral as a limit of summation:
Definition :Let I be a continuous function on [a, b]. Divide [a, b] into ‘n’ sub Intervals ,[x₀, x₁]……….. [x_(n-1) , x_n] where a = x₀ < x₁ < x₂ < ……………… < x_n = b
Let, ξr ∈ [x_r-1, x] for r 1, 2 , ……………… n.

→ If \({Lt}_{n \rightarrow 0} \sum_{r=1}^n\) f(ξ_r) (x_r – x_r-1) exists, then f(x) is called an integrable function on [a, b] and the limit is called definite integral of f on [a, b]. It is denoted by \(\)f(x) dx
Note:
To simplify calculation we can take all sub intervals to be equal length, h
Then h = \(\frac{b-a}{n}\) and \(\int_a^b\)f(x)dx = \({Lt}_{n \rightarrow \infty} h \sum_{r=1}^n f\left(\xi_Y\right)\)

Also we take, ξ_r = x_r-1, then ξ_r = a + (r – 1)h and hence.
\(\int_a^b\)f(x)dx = \({Lt}_{n \rightarrow \infty} h \sum_{r=1}^n\)f(a +(r – 1)h] = \({Lt}_{h \rightarrow 0} h \sum_{r=1}^h\)f[a + (r – 1)h]

If a = 0, b = 1, then \(\int_0^1\)f(x)dx = \({Lt}_{n \rightarrow \infty} \frac{1}{n} \sum_{r=1}^n f\left(\frac{r-1}{n}\right)+\left(\frac{r-1}{n}\right)={Lt}_{n \rightarrow 0} \frac{1}{n} \sum_{r=0}^{n-1} f\left(\frac{r}{n}\right)\)

If a = 0, b = p then \(\int_0^P\)f(x)dx = \({Lt}_{n \rightarrow \infty} \frac{1}{n} \sum_{r=1}^{n p}\left(\left(\frac{r-1}{n}\right)\right.\)

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 8 Differential Equations will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Differential Equations Formulas

→ An equation involving one dependent variable and its derivatives with respect to one or more independent variables is called a differential equation. If the equation contains only one independent variable then it is called an ordinary differential equation and if it contains more than one independent variable then it is called a partial differential equation,

→ If the differential equation is of the form f(x) dx + g(y)dy = 0 then its solution is ∫ f(x) dx + ∫ g(y) dy = 0.

→ The order of a differential equation is the order of the highest derivative occurring in it and the largest exponent of the highest order derivative in the equation is called the degree of the differential equation.

→ By eliminating the arbitrary constants in the given equation, we can formulate the differential equation.

→ If the differential equation is of the form \(\frac{d y}{d x}=\frac{f(x, y)}{g(x, y)}\), where f and g are homogeneous functions of x and y of same degree, then we put y = vx and obtain the form Φ(υ) dυ = \(\frac{d x}{x}\) and on integration gives the solution.

→ If the differential equation is of the form
\(\frac{d y}{d x}=\frac{a x+b y+c}{a^{\prime} x+b^{\prime} y+c^{\prime}}\), where a, b, c, a, b, c are constants.

• If b = – a’ then its solution can be obtained by term by term integration after regrouping.
• If \(\frac{a}{a^{\prime}}=\frac{b}{b^{\prime}}\) = m then we put ax + by = v and bring it in the form Φ(υ) dυ = \(\frac{d x}{x}\) and then integrate.
• If \(\frac{a}{a^{\prime}} \neq \frac{b}{b^{\prime}}\), then put x = X + h, y = Y + k (h, k are obtained by solving ah + bk + c = 0 and
  a’h + b’k + c’ = 0 and bring it to the form \(\)
  Then take Y = VX and obtain Φ(V) dV = \(\frac{d X}{X}\) and then integrate.

→ If the differential equation is of the form \(\frac{d y}{d x}\) + Py = Q then the solution is
ye_∫pdx = C + ∫Q_e∫pdxdx.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 3 Parabola will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Parabola Formulas

→ The locus of a point moving on a plane such that its distance from a fixed point and a fixed straight line in the plane are in a constant ratio ‘e’ is called a conic and e is called the eccentricity of the conic. Fixed point is called focus and the fixed straight line is called the directrix. If e = 1, the conic is called a Parabola.

→ Equation of a parabola in the standard form is y2 = 4ax (a > 0) with focus (a, 0), axis y = 0, equation of directrix is x + a = 0 and length of the latus rectum is 4a.

→ Various different forms of parabola (general)
Table: 1
(i) Form: y² = 4ax
Vertex: (0, 0)
Focus: (a, 0)
Directrix: x + a = 0
Axis: y = 0

(ii) Form: x² = 4ay
Vertex: (0, 0)
Focus: (0, a)
Directrix: y + a = 0
Axis: x = 0

(iii) Form: y² = -4ax
Vertex: (0, 0)
Focus: (-a, 0)
Directrix: x – a = 0
Axis: y = 0

(iv) Form: x² = -4ay
Vertex: (0, 0)
Focus: (0, -a)
Directrix: y – a = 0
Axis: x = 0

Table: 2
(i) Form:(y – k)² = 4a(x – h)
Vertex: (h, k)
Focns: (h + a, k)
Axis: y = k
EquaffonotDlrectrlx: x – h + a = 0

(ii) Form: (y – k)² = -4a(x – h)
Vertex: (h, k)
Focus: (h – a, k)
Axis: y – k = 0
Equation of Directrix: x – h – a = 0

(iii) Form: (x – h)² = -4a(y – k)
Vertex: (h, k)
Focus: (h, k – a)
Axis: x – h = 0
Equation of Directrix : y – k -a = 0

(iv) Form : (x – h)² = 4a(y – k)
Vertex: (h, k)
Focus: (h, a + k)
Axis: x – h = 0
Equation of Directrix: y – k + a = 0

(v) Form: (x – α)² + (y – β)² = \(\frac{(l x+m y+n)^2}{l^2+m^2}\)
Vertex : Point A
Focus: (α, β)
Axis: m(x – α) – l(y – β) = 0
Equation of Directrix: lx + my + n = 0

→ The equation of parabola when its axis is parallel to X – axis is x = ly² + my + n and when axis is parallel to Y- axis is y = lx² + mx + n.

→ Focal distance of a point (x₁, y₁) on the parabola y² = 4ax is x₁ + a.

→ Parametric equations of the parabola are x = at², y = 2at.

→ P(x₁, y₁) lies outside, on or inside the parabola y² = 4ax according as S₁₁ \(\frac{\geq}{<}\) 0.

→ y = mx + c (m * 0) is a tangent to the parabola y² = 4ax when c = a/m.

→ y = mx + a/m (m ≠ 0) is always a tangent to the parabola y² = 4ax and point of contact is \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)

→ Equation of the tangent at the point (x₁, y₁) on the parabola y² = 4ax is yy₁ = 2a (x + x₁) or S₁ = 0. .

→ Equation of the normal at the point (x₁, y₁) on the parabola S = 0 is y – y₁ = \(-\frac{y_1}{2 a}\) (x – x₁).

→ Equation of tangent at a point ‘t’ i.e„ (at², 2at) on y² = 4ax is x = yt + at².

→ Equation of normal at a point ‘t’ on y² = 4ax is y + xt = 2at + at³.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 2 System of Circles will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B System of Circles Formulas

→ We denote circles by S = x² + y² + 2gx + 2fy + c = 0 and S’ = x² + y² + 2g’x + 2f’y + c’ = 0.

→ If C₁, C₂ are the centres and r₁, r₂ are radii of two intersecting circles S = 0 and S’ = 0 and C₁C₂ = d then if θ is the angle between them, then cos θ = \(\frac{d^2-r_1^2-r_2^2}{2 r_1 r_2}\)

→ If 0 is the angle between two intersecting circles S = 0 and S’ = 0, then
cos θ = \(\frac{c+c^{\prime}-2 g g^{\prime}-2 f^{\prime}}{2 \sqrt{g^2+f^2-c} \sqrt{g^2+f^2-c^{\prime}}}\)

→ Two circles S = 0 and S’ = 0 are orthogonal ⇔ 2(gg’ + ff’) = c + c’.

→ If S = 0, S’ = 0 are any two intersecting circles and λ, µ are two real numbers such that λ + µ ≠ 0 and λS + µS’ = 0 represents a circle passing through the intersection of circles S = 0, S’ = 0.

→ If S = 0, S’ = 0 are any two intersecting circles and ke R (≠ -1) then S + kS’ = 0 represents a circle passing through their point of intersection.

→ If S = 0 and a straight line L = 0 intersect, then for any real number k, S + kL = 0 represents a circle passing through their intersection.

→ The equation of common chord of two intersecting circles S = 0, S’ = 0 is S – S’ = 0.

→ The equation of common tangent at the point of contact when the circles S = 0, S’ = 0 touch each other is S – S’ = 0.

→ The radical axis of two circles is defined to be the locus of a point which moves such that its powers with respect to the two given circles are equal.

→ The radical axis of two circles S = 0, S’ = 0 is

• the common chord when the two circles intersect at two distinct points.
• the common tangent at the point of contact when the circles touch each other.

→ The radical axis of any two circles bisects the line segment joining the points of contact of the common tangent of these two circles.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 1 Circles will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Circles Formulas

→ The locus of a point in a plane such that its distance from a fixed point in the plane is always the same is called a circle. The fixed point is called “centre” and the fixed distance is called the “radius” of the circle.

→ The equation of a circle with centre (h, k) and radius ‘r’ is (x – h)² + (y – k)² = r².

→ The equation of a circle in standard form is x² + y² = r² where (0, 0) is the centre and ‘r’ is the radius.

→ The general form of equation of circle is x² + y² + 2gx + 2fy + c = 0 where (-g, -f) is the centre and \(\sqrt{g^2+f^2-c}\) is the radius.

→ The intercept made by the circle x² + y² + 2gx + 2fy + c = 0.

• on X – axis is \(2 \sqrt{g^2-c}\) if g² ≥ c.
• on Y – axis is \(2 \sqrt{f^2-c}\) if f² ≥ c.

→ Equation of circle with A(x₁, y₁) and B(x₂, y₂) as the extremities of its diameter is (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0.

→ The equation of circle passing through the three non – collinear points (x₁. y₂). (x₂, y₂) and (x₃, y₃) is

where c₁ = – (x₁² + y₁²), c₂ = – (x₂² + y₂²), c₃ = (x₃² + y₃²).

→ The centre of the above circle is

→ The parametric equations of circle with (h, k) as centre and radius (r ≥ 0) are given by x = h + r cos θ, y = k + r sin θ. 0 ≤ θ ≤ 2π.

→ Denoting S₁₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + c, a point P(x₁, y₁) is said to be an interior or an exterior or point on the circumference of the circle S = 0 according to as S₁₁ ^ 0, conversely the result is true.

→ The power of the point P(x₁, y₁) w.r.t S = 0 is S₁₁.

→ If a straight line through a point P(x₁, y₁) meets the circle S = 0 at A and B then the power of the point P is equal to PA. PB.

→ The length of the tangent from P(x₁, y₁) to a circle S = 0 is \(\sqrt{S_{11}}\).

→ If l is the perpendicular distance from the centre of the circle to the line L = 0 and ‘r’ is the radius of the circle, then the line L = 0 is said to intersects, touches or does not intersect S = 0 according to l < r, l = r or l > r.

→ The line y = mx ± r\(\sqrt{1+m^2}\) is a tangent to the circle x₂ + y₂ = r₂ for every real value of ‘m’.

→ If P(x₁, y₁) and Q(x₂, y₂) are two points on the circle S = x2 + y2 + 2gx + 2fy + c = 0 then the equation of the secant PQ is
(xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c) + (xx₂ + yy₂ + g(x + x₂) + f(y + y₂) + c)
= x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c
⇒ S₁ + S₂ = S₁₂

→ The equation of tangent at (x₁, y₁) on S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0 ⇒ S₁ = 0

→ Equation of chord joining points A ( -g + r cos θ₁, – f + r sin θ₁) and B ( -g + r cos θ₂, – f + r sin θ₂) is (x + g) cos \(\left(\frac{\theta_1+\theta_2}{2}\right)\) + (y + f)sin\(\left(\frac{\theta_1+\theta_2}{2}\right)\) = r cos \(\left(\frac{\theta_1-\theta_2}{2}\right)\)

→ Equation of the tangent at 0 of the circle S = 0 is (x + g) cos θ + (y + f) sin θ = r.

→ The equation of normal at (x₁, y₁) of the circle S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0.

→ The equation of chord of contact of a point P(x,, y,) w.r.t a circle S = 0 is S₁ = 0.

→ The equation of polar of a point P(x₁, y₁) w.r.t S = 0 is S₁ = 0.

• If P(x₁, y₁) lies on the interior of circle polar of P is S₁ = 0.
• If P(x₁, y₁) lies on the circle then the polar of P is the tangent given by S₁ =0.
• If P(x₁, y₁) lies on the exterior of circle then the polar of P is the chord of contact of P is given by S₁ = 0.

→ The pole of lx + my + n = 0 w.r.t S = 0 is (-g + \(\frac{{lr}^2}{\lg +\mathrm{mf}-\mathrm{n}}\), -f + \(\frac{m r^2}{l g+m f-n}\)) where r is the radius of the circle.

→ The pole of the line lx + my + n = 0 w.r.t the circle x² + y² = a² is

→ Two points P and Q are said to be conjugate points w.r.t S = 0 if Q lies on the polar of P and P lies on the polar of Q.

→ The two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 are conjugate w.r.t the circle S = 0 if and only if a²(l₁l₂ + m₂m₂) = n₁n₂.

→ The two lines l₁x + m₁y + n₁ = 0 and l₂x + m₂y + n₂ = 0 are said to be conjugate w.r.t. S = 0 if and only if r2 (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) where r is the radius of S = 0.

→ Two points P and Q are said to be inverse points w.r.t S = 0 if CP. CQ = r², where C is the centre and r is the radius of the circle S = 0.

→ The equation of chord having (x,. y,) as its midpoint w.r.t circle S = 0 is S₁ = S₁₁
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = x₁² + y₁² + 2gx₁ + 2fy₁ + c

→ If C₁, C₂ are the centres of two circles S = 0, S’ = 0 and r₁, r₂ are the radii of two circles then

• If C₁C₂ > r₁ + r₂ we get 4 common tangents and a non – intersecting, non-touching system.
• If C₁C₂ = r₁ + r₂ we get 3 tangents where the two circles touch externally.
• If |r₁ – r₂| < C₁C₂ < r₁ + r₂ we get 2 tangents (intersecting system).
• If C₁C₂ = |r₁ – r₂| we get one tangent and internal touching system.
• If C₁C₂ < |r₁ – r₂| we get no tangent.

→ The combined equation of the pair of tangents drawn from an external point P(x₁, y₁) to the circles = 0 is SS₁₁ = S₁².
⇒ (x² + y² + 2gx + 2fy + c) (x₁² + y₁² + 2gx₁ + 2fy₁ + c) = [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]²

→ Chord of coatact: If Pis a point outside of the circle and the tangents from P touch the circle in A and B, then the chord joining the points A and B (points of contact) is called as chord of contact of P, with respect to that circle.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 11th Lesson Electromagnetic Waves Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 11th Lesson Electromagnetic Waves

Very Short Answer Type Questions

Question 1.
What is the average wavelength of X-rays?
Answer:
Wavelength range of X-rays = 10^-8 m to 10^-13 m i.e., 1 nm to 10^-4 nm.
∴ Average wavelength of X-rays is \(\frac{1+10^{-4}}{2}\) nm = 0.5 nanometers (nearly)

Question 2.
Give any one use of infrared rays. [TS Mar. ’19; AP May ’18. ’17]
Answer:

1. Infrared detectors are used in satellites both for military purpose and to observe growth of crops.
2. Infrared radiation is responsible to keen the atmosphere warm through green house effect.

Question 3.
If the wavelength of electromagnetic radiation is doubled, what happens to die energy of photon? [TS Mar. ’16; June ’15]
Answer:
Energy of electromagnetic photon E = hυ = \(\frac{hc}{\lambda}\)

So when wavelength λ is doubled energy of photon is reduced to half.

Question 4.
What is the principle of production of electromagnetic waves?
Answer:
Electromagnetic waves are produced by accelerating charges through conductors.

Question 5.
How are Microwaves produced? [AP Mar. ’15]
Answer:
Microwaves can be produced by special type of vacuum tubes. Namely Klystrons, magnetrons and yun diodes.

Question 6.
What is sky wave propagation? [AP June ’15]
Answer:
In the frequency range from a few MHz upto about 30 MHz, long distance communication can be achieved by the ionospheric reflection of radio waves back towards the earth. This mode of propagation is called sky wave propagation and it is used by short wave broadcast services.

Question 7.
What is the ratio of speed of infrared rays and ultraviolet rays in vacuum?
Answer:
Ratio =1:1
In vacuum speed of electromagnetic waves v = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
It is applicable to whole range of electromagnetic spectrum.
∴ In vacuum velocity of UV rays = Velocity of I.R rays.

Question 8.
What is the relation between the amplitudes of the electric and magnetic fields in free space for an electromagnetic wave?
Answer:
Amplitude of Magnetic field

Relation between amplitude of Magnetic field B0 and Electric field E0 in vacuum is B₀ = \(\frac{E_0}{c}\)

Question 9.
What are the applications of microwaves? [AP Mar. 18, 17, 15; May 18, 16 , 15; June 15; TS Mar. 18, 17,15, May. 18]
Answer:

1. Microwaves are widely used in radar because of their small wavelength.
2. Microwaves are used in microwave ovens due to the frequency of microwave region is nearly equals to resonant frequency of water molecule.

Question 10.
Microwaves are used in Radars, why?
Answer:
Due to short wavelengths microwaves are suitable for the radar systems used in air craft navigation.

Question 11.
Give two uses of infrared rays. [TS Mar. ’17; May ’16; AP Mar. ’19, ’16; May ’14]
Answer:

1. Infrared detectors are used in satellites both for military purpose and to observe growth of crops.
2. Infrared radiation is responsible to keen the atmosphere warm through green house effect.

Question 12.
The charging current for a capacitor is 0.6 A. What is the displacement current across its plates?
Answer:
Charging current i = conduction current

∴ Displacement current i_d = 0.6 A across the plates.

Short Answer Questions

Question 1.
What does an electromagnetic wave consists of? On what factors does its velocity in vacuum depend?
Answer:
According to Maxwell’s theory, accelerated charges radiate electromagnetic waves.

Suppose a charge oscillates with some frequency. It produces an oscillating electric field in space. This oscillating electric field produces oscillating magnetic field. It again regenerates oscillating electric field. These electric and magnetic fields are mutually perpendicular and also perpendicular to direction of propagation. Electric field component E_x = E₀ sin (kz – ωt) Magnetic field component By = B0 sin (kz – ωt)

where k = \(\frac{2 \pi}{\lambda}\) and speed of wave v = \(\frac{\omega}{k}\)

According to Maxwell’s equations, relation between E₀ and B₀ \(\frac{E_0}{B_0}\) = c or B₀ = \(\frac{E_0}{c}\)

In vaccum velocity of electromagnetic wave c = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
∴ Velocity of electromagnetic wave in vacuum depends on permeability µ₀ and permittivity ∈₀ of vacuum.

Question 2.
What is Greenhouse effect and its contribution towards the surface temperature of earth?
Answer:
Greenhouse effect :
Infrared rays plays an important role in maintaining average temperature of earth’s atmosphere.

During daytime, earth absorbs the energy of incoming Infrared & Visible radiation from Sun. As a result earth’s surface get heated. Hot earth will reradiate energy in the form of infrared radiation.

Many molecules such as Carbon dioxide (CO₂), Ammonia (NH₃), Chloro Fluoro Carbons, Methane (CH₄), etc. will absorb the long range infrared radiation because the resonant frequency of these gases matches with infrared region. So energy reradiated by earth is trapped by these molecules as a result earth’s atmosphere is heated. This is known as “greenhouse effect”.

Effect of greenhouse gases :
When concentration of greenhouse gases such as CO₂, NH₃, CH₄ etc., increases average temperature of .earth is also gradually increase. This effect is called global warming.

Long Answer Questions

Question 1.
Give the brief history of discovery of knowledge of electromagnetic waves.
Answer:
Maxwell conducted an experiment to apply the ampere’s law to study the magnetic field at a point outside the capacitor by applying a time varying current.

Consider a point ‘P’ outside the parallel plate capacitor [See Fig (a)]. Consider a loop of radius ‘r’. Its direction is perpendicular to the conductor.
From Amperes Law B(2πr) = µ₀ i (t) → (1)

Consider another different surface [See Fig (b)]. It is a pot like dielectric surface without electrical contact with capacitor plate. But it encloses the capacitor plate.

By applying ampere’s Law LHS of eq. (1) is not changed but RHS = 0. Because there is no current flowing in the plate.
∴ B(2πr) = 0 → (2)

Consider another surface like a tiffin box [See Fig (c)] apply ampere’s circuital law with same parameters LHS of eq (1) is same. But RHS is zero
i.e. B(2πr) = 0 → (3)

From eq. (1) there is a magnetic field at ‘P’ But for the figures (b) & (c) field at ‘P’ is zero. So there is some contradiction in calculating magnetic field.

Maxwell suggested that there is some electric field E = \(\frac{Q}{Ae_0}\) between the plates
and it is perpendicular to the plates. E has some value in between the plates and vanishes outside the plate.

Electric flux between the plates Φ_E = |E|A\(\frac{Q}{\epsilon_0}\)

Charge Q on plates of capacitors changes with time as a result Φ_E changes with time.

Changing electric flux will produce the current called displacement current i_d = ∈₀\(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\).

So Maxwell suggested that source of magnetic field is not only due to conduction current i_c

but due to a total current i = i_c + i_d and

So source of magnetic field is not just conduction current, it is also produced by displacement current.

Displacement current will have same physical properties just like conduction current.

Basing on this he formulated that a time varying electric field will produce a time varying magnetic field. Similarly a time varying magnetic field will produce a time varying electric field. In this way energy oscillates between perpendicular electric and magnetic fields in an electromagnetic wave.

Question 2.
State six characteristics of electromagnetic waves. What is Greenhouse effect?
Answer:
From Maxwell’s theory

1. accelerated charges radiate electromag¬netic waves.
2. Frequency of electromagnetic wave is equal to frequency of oscillator.
3. Energy associated with the propagation of wave is obtained from oscillating source.
4. From Maxwell’s equations relation between E₀ and B₀ is \(\frac{E_0}{B_0}\) = c or B₀ = \(\frac{E_0}{c}\)
5. In vacuum velocity of electromagnetic wave c = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
6. Hertz experiments on electromagnetic waves showed that electromagnetic waves of wavelength 10 million times more than light waves could be diffracted, reflected and polarised.
   Electromagnetic waves carry energy and momentum like other waves.
7. In vacuum speed of electromagnetic waves v = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)

It is applicable to whole range of electromagnetic spectrum.

Greenhouse effect :
Infrared rays plays an important role in maintaining average temperature of earth’s atmosphere.

During daytime earth absorbs the energy of incoming Infrared & Visible radiation comming from Sun. As a result earth’s surface get heated. Hot earth will reradiate energy in the form of infrared radiation.

Many molecules such as CO₂ Ammonia (NH₃), Chloro Fluro Carbons, Methane CH₄ etc., will absorb the long range infrared radiation because the resonant frequency of these gases matches with infrared region. So energy reradiated by earth is trapped by these molecules as a result earth’s atmosphere is heated. This is known as “greenhouse effect”.

Intext Question and Answers

Question 1.
What physical quantity is the same for X- rays of wavelength 10^-10 m, red light of wavelength 6800 Å and radiowaves of wavelength 500 in?
Answer:
The speed of light (3 × 10⁸ m/s) in a vacuum is the same for all wavelengths. It is independent of the wavelength in the vacuum.

Question 2.
A plane electromagnetic wave travels in ‘ vacuum along z-direction. What can you say about the directions of its electric and magnetic field vectors? If the frequency of the wave is 30 MHz, what is its wavelength?
Answer:
The electromagnetic wave travels in a vacuum along the z-direction. The electric field (E) and the magnetic field (H) are in the x-y plane. They are mutually perpendicular.

Frequency of the wave, o = 30 MHz
= 30 × 10⁶ s^-1
Speed of light in a vacuum, c = 3 × 10⁸ m/s
Wavelength of a wave is given as, λ = \(\frac{c}{v}\)
\(\frac{3\times10^8}{30\times10^6}\) = 10 m

Question 3.
A radio can tune into any station in the 7.5 MHz to 12 MHz band. What is the corresponding wavelength band?
Answer:
A radio can tune to minimum frequency, υ₁ = 7.5 MHz = 7.5 × 10⁶ Hz
Maximum frequency, υ₂ = 12 MHz
= 12 × 10⁶ Hz ;
Speed of light, c = 3 × 10⁸m/s
Relation between λ and υ is λ₁ = \(\frac{c}{υ_1}\)

Thus the wavelength band of the ratio is 40 m to 25 m.

Question 4.
A charged particle oscillates about its mean equilibrium position with a frequency of 10⁹ Hz. What is the frequency of the electromagnetic waves produced by the oscillator?
Answer:
The frequency of an electromagnetic wave produced by the oscillator is the same as that of a charged particle oscillating about its mean position i.e., 10⁹ Hz.

Question 5.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B₀ = 510 nT. What is the amplitude of the electric field part of the wave?
Answer:
Magnetic field B₀ = 510 nT = 510 × 10^-9 T ;
Speed of light in a vacuum, c = 3 × 10⁸ m/s
Amplitude of electric field of the electromagnetic wave is given by the relation,
E = cB₀ = 3 × 10⁸ × 510 × 10^-9 = 153 N/C
Therefore, the electric field part of the wave is 153 N/C.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 13th Lesson Atoms Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 13th Lesson Atoms

Very Short Answer Type Questions

Question 1.
What is the angular momentum of electron in the second orbit of Bohr’s model of hydrogen atom?
Answer:
Angular momentum L = \(\frac{nh}{2 \pi}\)
For 2nd orbit ⇒ n = 2.
∴ Angular momentum of 2nd orbit
L₂ = \(\frac{2h}{2 \pi}=\frac{h}{\pi}\)

Question 2.
What is the expression for fine structure constant and what is its value?
Answer:
Fine structure constant a = \(\frac{2 \pi e^2}{ch}=\frac{1}{137}\)
= 7.30 × 10^-3.

Question 3.
What is the physical meaning of ‘negative energy of an electron’?
Answer:
Energy is always +ve. There is no negative energy. But negative energy of electron means it is the force of attraction with which an electron is bounded to the nucleus.

Question 4.
Sharp lines are present in the spectrum of a gas. What does this indicate?
Answer:
When gases are excited they will absorb the exact quanta of energy equals to energy level difference of the orbits.
i.e., E = hv = E_f – E_i

So electron goes to higher orbit. As a result we will see sharp lines in the spectrum of gases corresponding to that energy.

Question 5.
Name a physical quantity whose dimensions are the same as those of angular momentum.
Answer:
Angular momentum (L) = mvr,
Dimensions = ML²T^-1
Planck’s constant h has same dimensions of L.
∵ L = \(\frac{nh}{2 \pi}\), where \(\frac{n}{\pi}\) is dimensionless.

Question 6.
What is the difference between α-particle and helium atom?
Answer:
α – particle is helium nucleus. But not helium atom.

α – particle contains 2 protons and two neutrons where as helium atom contains 2 protons, two neutrons and two electrons.

Question 7.
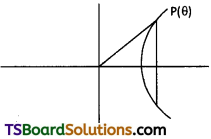
How is impact parameter related to angle of scattering?
Answer:
When impact parameter is minimum head on collision between α – particle and nucleus takes place and α- particle will be deviated by θ = π radians, when impact parameter is high or large the α – particle goes nearly undeviated.

Question 8.
Among alpha, beta and gamma radiations, which get affected by the electric field?
Answer:
α and β particles are affected by electric fields because both of them carries charge on them.

γ – ray is radiation so it is not affected by electric field.

Question 9.
What do you understand by the phrase ‘ground state atom’?
Answer:
The lowest state of the atom which is the lowest energy, with the electron revolving in the orbit of smallest radius is called the ground state.
For ground state hydrogen atom E = – 13.6 eV,

Question 10.
Why does the mass of the nucleus not have any significance in scattering in Rutherford’s experiment?
Answer:
In Rutherford experiment gold foil is used. For gold Z = 79 and its atomic weight is nearly 50 times more than α – particle. So mass of nucleus used to bombard gold atom has no significant effect.

Question 11.
The Lyman series of hydrogen spectrum line in the ultraviolet region Why?
Answer:
For Lyman series \(\frac{1}{\lambda}\) = R(\(\frac{1}{l^2}-\frac{1}{n^2}\))
n = 2, 3, 4 ….
Wavelength of 1st member of Lyman series is 1216A°. It is in ultraviolet region.

Question 12.
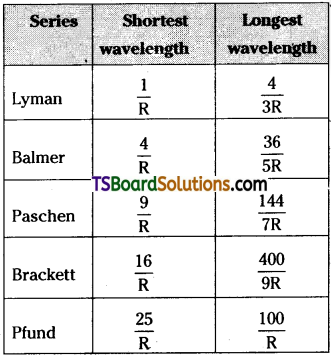
Write down a table giving longest and shortest wavelengths of different spectral series.
Answer:

Question 13.
The wavelengths of some of the spectral lines obtained in hydrogen spectrum are 1216Å, 6463 Å and 9546Å. Which one of these wavelengths belongs to the Paschen series?
Answer:
λ = 9546Å belongs to Paschen series. Paschen series is in infrared region. So wavelength λ = 9546Å is in infrared region. So it belongs to Paschen series.

Question 14.
Give two drawbacks of Rutherford’s atomic model. [TS Mar. ’19]
Answer:

1. Electron revolving around the nucleus must be continuously accelerated. An accelerating electron must lose energy continuously due to radiation and finally, atom must destroy.
2. When electron radiates energy it will spiral around nucleus. As a result its angular velocity and frequency of spectral lines must change continuously. But these two things are not taking place.

Short Answer Questions

Question 1.
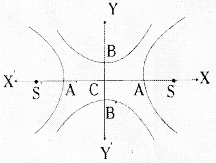
What is impact parameter and angle of scattering? How are they related to each other?
Answer:
Impact parameter :
It is the perpendicular distance of the initial velocity vector of α-particle from centre of nucleus.

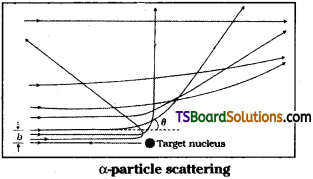
In case of head-on collision, impact parameter is minimum and α – particle rebounds back (θ = π). For a large impact parameter α – particle goes undeviated. The chance of head on collision is very small. It, in turn, suggested that mass of atom is much concentrated in a small volume.

Angle of scattering ‘0’ :
It is the angle between the direction of incident α – particle and scattered α – particle.

Relation between impact parameter and angle of scattering, when Impact parameter is less ⇒ angle of scattering is high and vice-versa.

Question 2.
Derive an expression for potential and kinetic energy of an electron in any orbit of a hydrogen atom according to Bohr’s atomic model. How does P.E. change with increasing n? [TS June 15; Mar. 15]
Answer:
According to Bohr model, electrons are revolving around the nucleus in certain permitted orbits.

For electron to revolve in orbit, the electrostatic force and centrifugal force must be equal i.e., F_c = F_e

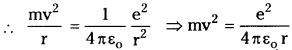
∴ Kinetic energy of electron (K) = \(\frac{1}{2}\) mv²

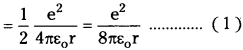
Potential energy between electron and nucleus is

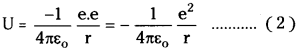
– ve sign indicates force of attraction. Relation between potential energy and radius of orbit.
From the equation (2) U ∝ \(\frac{1}{r}\) …………… (3)

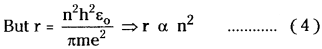
From eq. (3) & (4) potential energy
U ∝ \(\frac{1}{n^2}\)
∴ Potential energy of orbit is inversely proportional to square of number of orbit (n²).

Question 3.
What are the limitations of Bohr’s theory of hydrogen atom? [TS May 18, 17; AP Mar. 17, 14, May 17]
Answer:
Limitations of Bohr model:
i) Bohr model is applicable to hydrogen atom only. It ean not be extended even to a two electron system such as helium.

Because it involves force between + vely charged nucleus and electron.

Electrical forces between electrons are not taken into account.

ii) It is not able to explain the intensity variation in spectral lines of different frequencies and why some transitions are more preferred than others.

Question 4.
Explain the distance of closest approach and impact parameter.
Answer:
Distance of closest approach :
In α- particle scattering experiment the α – particle will move near to gold nucleus until it is just stopped.

Kinetic energy of α – particle just before stopped is equal to electrostatic potential.

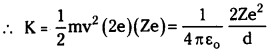
where = Z atomic number of gold, ’2e’ charge on α – particle.
distance of closest approach d = \(\frac{2 \mathrm{Ze}^2}{4 \pi \varepsilon_0 \mathrm{k}}\)

Impact parameter :
It is the perpendicular distance of the initial velocity vector of α – particle from centre of nucleus.

In case of head-on collision impact parameter is minimum and α – particle rebounds back (θ = π). For a large impact parameter α – particle goes undeviated. The chance of head on collision is very small. It in turn suggested that mass of atom is much concentrated in a small volume.

Question 5.
Give a brief account of Thomson model of atom. What are its limitations?
Answer:
J.J. Thomson Model :
J.J.Thomson thought that the positive charge of the atom is uniformly distributed through out the atom and the negatively charged electrons are embedded in it like seeds in a watermelon.

Limitations:

1. Rutherford α – particle scattering experiment showed that in an atom positive charge is concentrated at nucleus of atom.
2. In Thomson model the radiation emitted by solids and gases is due to oscillations of atoms and molecules are governed by the interactions between them.

But experiments on rarefied gases showed that hydrogen always gives rise to a set of lines with fixed wavelength.

Balmer experiments and his formula for Balmer series of wavelength of a group of lines are emitted by atomic hydrogen only. Not by interaction of atoms or molecules.

Question 6.
Describe Rutherford atom model. What are the drawbacks of this model? [AP & TS Mar. ’16]
Answer:
Rutherford’s nuclear model:

1. According to Rutherford the entire positive charge and most of the mass of the atom is concentrated at nucleus. Electrons are revolving around the nucleus as planets revolve around the sun.
2. Rutherford experiments on α – particle suggested that size of atom is about 10^-15 to 10^-14 and size of nucleus is about 10^-10 m.

Drawbacks :

1. When electron is revolving round the nucleus it is in continuously accelerated state. As per classical mechanics, it must emit energy continuously. So electron must follow spiral path instead of circular path. Finally electron must fall on nucleus i.e., + ve charge and atom will destroy which is not happening.
2. This model is not able to explain why electron in an orbit is not radiating any energy.

Question 7.
Distinguish between excitation potential and ionization potential.
Answer:
Excitation potential :

1. Generally gases or vapours are excited at low pressure by passing high current through them. For this we have to apply a very high voltage.
2. When excited atoms or molecules will absorb certain amount of energy from applied potential and gives rise to series of spectral lines called emission spectrum.

Ionisation potential :
It is the amount of minimum energy required to release an electron from the outer most orbit of the nucleus.

From Bohr’s model, energy of the orbit is the ionisation energy of electron in that orbit.
Ex: Energy of 1st orbit in hydrogen is 13.6 eV.

Practically ionisation potential of hydrogen is 13.6 eV.

Difference:
→ Excitation potential will permit electrons to transit between various energy levels whereas ionisation potential will liberate an electron from the influence of nucleus of that atom.

Question 8.
Explain the different types of spectral series of hydrogen atom.
(OR)
Write the different types of Hydrogen Spectral series. The Lyman series of Hydrogen spectrum lies in the ultraviolet region. [TS May 16, Mar. 16, AP Mar. 19, 15, May 18, 16, June 15]
Answer:
Lyman series :
When electrons are jumping from higher energy levels to the first orbit then that series of spectral lines emitted are called “Lyman series”.
In Lyman series, \(\frac{1}{\lambda}\) = R(\(\frac{1}{l^2}-\frac{1}{n^2}\))
where n = 2, 3, …………… etc.

These spectral lines are in ultraviolet region.

Balmer series :
When electrons are jumping the from higher levels to 2nd orbit then that series of spectral lines are called “Balmer series”.

For Balmer series, \(\frac{1}{\lambda}\) = R(\(\frac{1}{2^2}-\frac{1}{n^2}\))
where n = 3, 4, ………… etc.

Spectral lines of Balmer series are in visible region.

Paschen series :
When electrons are jumping on to the 3rd orbit from higher energy levels then that series of spectral lines are called “Paschen series”.
For Paschen series \(\frac{1}{\lambda}\) = R(\(\frac{1}{3^2}-\frac{1}{n^2}\))
where n = 4, 5, …………..

These spectral lines are in near infrared region.

Brackett series :
When electrons are jumping on to the 4th orbit from higher levels then that series of spectral lines are called “Brackett series”.
For Brackett series, \(\frac{1}{\lambda}\) = R(\(\frac{1}{4^2}-\frac{1}{n^2}\))
where n = 5, 6, ………… etc.

Brackett series are in middle infrared region.

Pfund series :
When electrons are jumping on to the 5th orbit from higher energy levels then that series of spectral lines are called “Pfund series”.
For Pfund series \(\frac{1}{\lambda}\) = R(\(\frac{1}{5^2}-\frac{1}{n^2}\))
n = 6, 7, ……….. etc.

These spectral lines are in far infrared region.

Reason for Lyman series in ultraviolet region :
The wavelength of Lyman series is nearly 1200 A° and less. So Lyman series is ultraviolet region.

Question 9.
Write a short note on de Broglie’s explanation of Bohr’s second postulate of quantization. [TS Mar. ’17]
Answer:
De – Broglie’s explanation for Bohr 2nd postulate :
According to de Broglie, the electron in an orbit must be seen as a particle wave. Particle waves can lead to standing waves under resonance condition.

A standing wave can be formed in a wire when length of the wire is equal to wave-length λ or integral multiple of wavelength λ (i.e., nλ). In the same way for an electron moving in a circular orbit, if its circum-ference 2πr_n is equal to nλ then standing waves will be formed in that orbit.
∴ From de-Broglie’s explanation 2πr_n = nλ
But λ = h/p = \(\frac{h}{mv_n}\)
∴ de Broglie wavelength 2πr_n = nh / mv_n
mv_nr_n = \(\frac{nh}{2 \pi}\)
Where mv_nr_n is angular momentum of electron in nth orbit.
In this way de – Broglie hypothesis provided an explanation to Bohr’s 2nd postulate.

Long Answer Questions

Question 1.
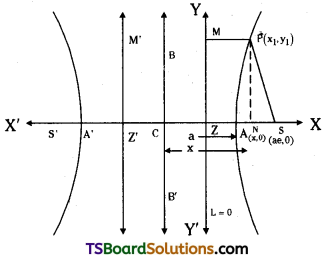
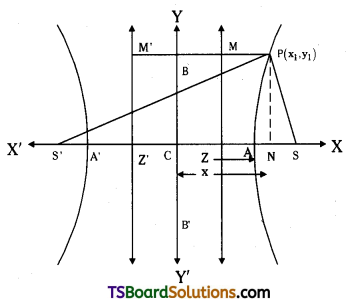
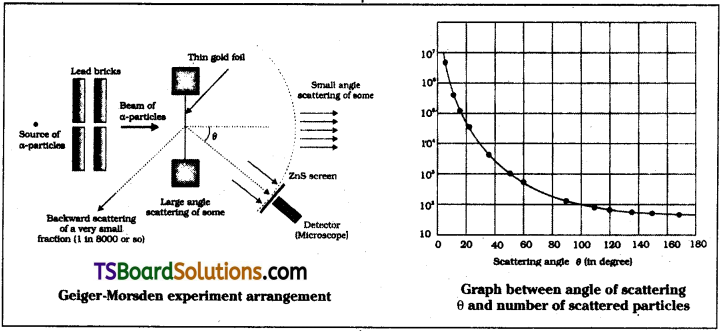
Describe Geiger – Marsden Experiment on scattering of α – particles. How is the size of the nucleus estimated in this experiment?
Answer:
Geiger – Marsden experiment :
Description :
In this experiment α – particles from ²¹⁴₈₃Bi are passed through lead blocks containing coaxial holes to emit narrow beam of α – particles. This α – particle beam falls on gold foil and scatters. The scattered α – particles are detected. By rotating the microscope at different angles (θ) number of scattered particles are measured.

Explanation :
In this experiment a beam of α – particles of energy 5.5 MeV are made to fall on gold foil.

α – particle carries 2 units of positive charge and mass is equal to that of helium nucleus.

→ Assume that the gold foil is very thin and α – particle will suffer not more than one scattering during its passage through gold foil.

For gold Z = 79. Its mass is nearly 50 times more than that of α – particle. So during collision it remains almost stationary.

Magnitude of force between α – particle and gold nuclei (F) = \(\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{r}^2}\), ‘r’ = the distance between them.

The magnitude and direction of force changes continuously as it approaches the nucleus.

Impact parameter :
It is the perpendicular distance of the initial velocity vector of α – particle from centre of nucleus.

In case of head – on collision impact parameter is minimum and α – particle rebounds back (θ = π). For a large impact parameter α – particle goes undeviated. The chance of head on collision is very small.

Estimation of size of nucleus :
In this experiment a graph is plotted between number of scattered particles (n) and angle of scattering ‘θ’. It suggested that size of nucleus is about 10^-15 to 10^-14 m. From kinetic theory size of atom is about 10^-10 m. So size of atom is 10,000 to 100,000 times more than nucleus.

Question 2.
Discuss Bohr’s theory of the spectrum of hydrogen atom. [AP Mar. ’16]
Answer:
From Bohr’s model of hydrogen atom

1. Electrons are revolving in certain per-mitted non-radiating orbits around nucleus.
2. For non-radiating orbits, orbital angular momentum L = mvr = nh / 2π.
3. Electrons may jump from one orbit to another orbit. While doing so they will emit or absorb the energy equal to diffe-rence of those orbital energies.
   E = hν = E_i – E_f

When electrons are revolving in the orbit centrifugal force and centripetal force on it are equal F_c = F_e.

For hydrogen atom n = 1
∴ r₁ = h²ε₀/π me² ……………. (5)
This is also called Bohr radius
a₀ = 5.29 × 10^-11 m
Energy of the orbit E = K + U = Kinetic energy + Potential Energy of electron.
∴ E_n = –\(\frac{e^2}{8\pi \epsilon_0 r}\)
By using value of r1 from eq. 4.

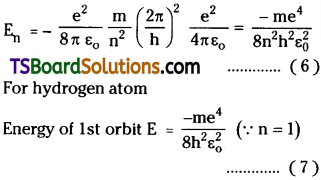
From 3rd postulate :
when electrons are jumping from higher to lower orbit.

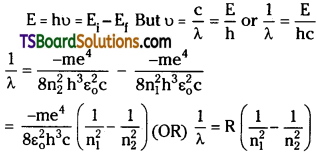
Where R = Rydberg’s constant. (∵ Electron is initially at orbit n₂ and finally at n₁)

In this way Bohr atom model successfully explained energy of the orbits and origin of spectral lines.

Question 3.
State the basic postulates of Bohr’s theory of atomic spectra. [AP Mar. ’16]
Hence obtain an expression for the radius of orbit and the energy of orbital electron in a hydrogen atom.
Answer:
Bohr’s postulates :
Bohr model of hydrogen atom consists of three main postulates.
i) Electrons in an atom could revolve in certain permitted stable orbits. Electrons revolving in these stable orbits do not emit or radiate any energy.

ii) The stable orbits are those whose orbital angular momentum is an integral multiple of h/2π.
i.e., L = nh / 2π where n = 1, 2, 3 etc. (an integer.)
These stable orbits are also called as non – radiating orbits.

iii) An electron may take a transition between non-radiating orbit.

when electron transition takes place a photon of energy equals to the energy difference between initial and final states will be radiated.
E = hν = E_i – E_f.

Bohr Model of Hydrogen atom :
When electrons are revolving in the orbit electrostatic force and centripetal force on it are equal F_c = F_e.

This is also called Bohr radius
a₀ = 5.29 × 10^-11 m
Energy of the orbit E = K + U = Kinetic energy + Potential Energy of electron.

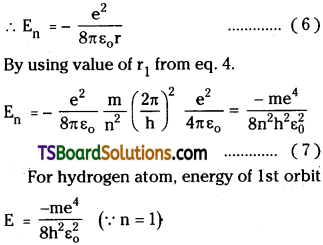
Intext Question and Answer

Question 1.
The radius of the first electron orbit of a hydrogen atom is 5.3 × 10^-11m. What is the radius of the second orbit?
Answer:
Radius of first orbit r₁ = 5.3 × 10^-11m.
Radius of Bohr orbit r =
For 2nd orbit n = 2,
∴ r = n₂ a₀ =4 × 5.3 10^-11 = 2.12 × 10^-11 m.

Question 2.
Determine the radius of the first orbit of the hydrogen atom. What would be the velocity and frequency of the electron in the first orbit ? Given: h = 6.62 × 10^-34J s, m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C, k = 9 × 10⁹ m²C.
Answer:
Given h = 6.62 × 10^-34 J,
Mass m = 9.1 × 10^-31 kg
Charge e = 1.6 × 10^-19 C;

Question 3.
The total energy of an electron in the first excited state of the hydrogen atom is – 3.4 eV. What is the potential energy of the electron in this state?
Answer:
Total energy, T.E. = – 3.4 eV.
Potential energy U = 2 x T.E. = – 3.4 × 2
= – 6.8 eV in same orbit.

Question 4.
The total energy of an electron in the first excited state of the hydrogen atom is – 3.4 eV. What is the kinetic energy of the electron in this state?
Answer:
In 1st excited state
Total energy T.E. = – 3.4 eV.
Kinetic energy in 1st excited state = T.E. – U
Where U = 2 × T.E.
∴ K = U – 2U = – U = – (-3.4) = 3.4 eV.

Question 5.
Find the radius of the hydrogen atom in its ground state. Also calculate the velocity of the electron in n = 1 orbit. Given h = 6.63 × 10^-34 Js, m = 9.1 × 10^-31kg, e = 1.6 × 10^-19 C, k = 9 × 10⁹ N m²C^-2.
Answer:
Planck’s constant h = 6.63 × 10^-34 Js.;
Mass of electron m = 9.1 × 10^-31 Kg.
Charge on electron e = 1.6 × 10^-19 C;
K = 9 × 10⁹ m²C²
a) Radius of orbit, r \(\frac{n^2h^2\epsilon_0}{\pi me^2}\) where \(\frac{h^2\epsilon_0}{\pi me^2}\) = a₀ = 5.3 × 10^-11
For 1st orbit n = 1 ⇒ r = 1 × 5.3 × 10^-11
= 5.3 × 10^-11m

Question 6.
Prove that the ionization energy of hydrogen atom is 13.6 eV.
Answer:
From Bohr atom model energy radiated when electrons are jumping from one orbit
to another orbit is E = hυ = \(\frac{m e^4}{8 \varepsilon_0^2 h^2 n^2}\) = E₁ – E₂

By definition, ionization potential is the minimum amount of energy required to remove the electron from the orbit. Now for an electron of nearest orbit n₁ = 1 and n₂ = ∞ (because electron is free from influence of nucleus).

Question 7.
Calculate the Ionization energy fora lithium atom.
Answer:

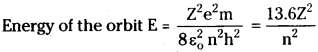
For lithium Z = 3 (But outer most orbit n = 2 in lithium)
∴ lonization energy = Energy of the orbit = \(\frac{13.6\times9}{4}\) = 30.6 eV.

Question 8.
The wavelength of the first member of Lyman series is 1216 Å. Calculate the wavelength of second member of Balmer series.
Answer:
Wavelength of 1st member of Lyman series = 1216 A°.

2nd member of Balmer series ⇒ \(\frac{1}{\lambda_2}\) = R(\(\frac{1}{2^2}-\frac{1}{4^2}\))
∵ For 2nd member of Balmer series n = 4.

Question 9.
The wavelength of first member of Balmer series is 6563 A. Calculate the wavelength of second member of Lyman series.
Answer:
Wavelength of 1 st member of Balmer series = 6563.

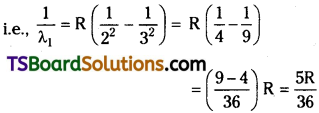
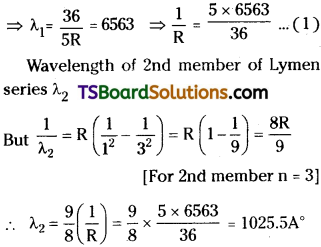
Question 10.
The second member of Lyman series in hydrogen spectrum has wavelength 5400 Å. Find the wavelength of first member.
Answer:
Wavelength of 2nd member of Lyman series λ = 5400

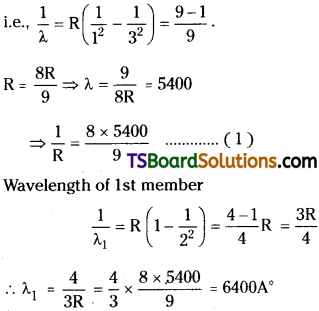
Question 11.
Calculate the shortest wavelength of Balmer series. Or Calculate the wavelength of the Balmer series limit.
Given : R = 10970000m^-1.
Answer:
Given Rydberg constant R = 10970000 m^-1
= 1.097 × 10⁷ m^-1
For Balmer series \(\frac{1}{\lambda_2}\) = R(\(\frac{1}{2^2}-\frac{1}{n^2}\))
Short wavelength ⇒ n₂ = ∞

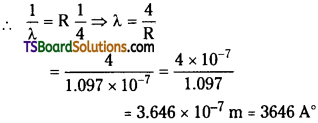
Question 12.
Using the Rydberg formula, calculate the wavelength of the first four spectral lines in the Balmer series of the hydrogen spectrum.
Answer:
For Balmer series \(\frac{1}{\lambda_2}\) = R(\(\frac{1}{2^2}-\frac{1}{n^2}\)) where
n = 2, 3, 4, 5 etc.
Rydberg constant R = 1.097 × 10⁷ m^-1


= 4102 A°

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type

Question 1.
One focus of a hyperbola is located at the point (1, -3) and the corresponding directrix is the line y = 2. Find the equation of the hyperbola if its eccentricity is \(\frac{3}{2}\).
Solution:

Given that focus S = (1, -3)
The equation of the directrix is y – 2 = 0
Eccentricity e = \(\frac{3}{2}\)
Let P(x, y) be any point on the hyperbola.
Since P(x, y) lies on the hyperbola then SP
\(\frac{SP}{PM}\) = e
SP = e . PM
⇒ \(\sqrt{(x-1)^2+(y+3)^2}=\frac{3}{2}\left|\frac{0 \cdot x+y \cdot 1-2}{\sqrt{0^2+1^2}}\right|\)
⇒ \(\sqrt{(x-1)^2+(y+3)^2}=\frac{3}{2}|y-2|\)
Squaring on both sides
⇒ (x – 1)² + (y + 3)² = \(\frac{9}{4}\)(y – 2)²
⇒ x² + 1 – 2x + y² + 9 + 6y = \(\frac{9}{4}\)(y² + 4 – 4y)
⇒ 4x² + 4 – 8x + 4y² + 24y + 36 = 9y² – 36y + 36
⇒ 4x² – 5y² – 8x + 60y + 4 = 0
∴ The equation of the hyperbola is 4x² – 5y² – 8x + 60y + 4 = 0.

Question 2.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola x² – 4y² = 4. [(AP) Mar. ’20, ’18, ’16; May ’16; (TS) Mar. ’19]
Solution:
Given the equation of the hyperbola is x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{4 y^2}{4}=1\)
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
Here a = 2, b = 1
It is a hyperbola.
Centre = (0, 0)

Question 3.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 16y² – 9x² = 144. [(AP) Mar. ’18, May ’17]
Solution:
Given the equation of the hyperbola is 16y² – 9x² = 144
⇒ \(\frac{y^2}{9}-\frac{x^2}{16}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=-1\)
Here a = 4, b = 3
It is a conjugate hyperbola.
Centre C = (0, 0)

Question 4.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 5x² – 4y² + 20x + 8y = 4.
Solution:
Given equation of the hyperbola is 5x² – 4y² + 20x + 8y = 4
⇒ (5x² + 20x) + (-4y² + 8y) = 4
⇒ 5(x² + 4x) – 4(y² – 2y) = 4
⇒ 5(x² + 2 . 2x + 2² – 2²) – 4(y² – 2 . 1 . y + 1² – 1²) = 4
⇒ 5((x + 2)² – 4) – 4((y – 1)² – 1) = 4
⇒ 5(x + 2)² – 20 – 4(y – 1)² + 4 = 4
⇒ 5(x + 2)² – 4(y – 1)² = 20

we get h = -2; k = 1; a = 2; b = √3
It is a hyperbola.
Centre C = (h, k) = (-2, 1)

⇒ x = -2 ± \(\frac{4}{3}\)
⇒ 3x = -6 ± 4
⇒ 3x = -10 or 3x = -2
⇒ 3x + 10 = 0 or 3x + 2 = 0
The length of the latus rectum

Question 5.
If the line lx + my + n = 0 is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then show that a²l² – b²m² = n². (May ’07)
Solution:

Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let the line lx + my + n = 0 ………(1)
be a tangent to the given hyperbola at P(x₁, y₁)
∴ The equation of the tangent at P(x₁, y₁) is S₁ = 0
\(\frac{\mathrm{xx}_1}{\mathrm{a}^2}-\frac{\mathrm{yy}_1}{\mathrm{~b}^2}-1=0\)
Now (1) and (2) represent the same line.

Since P(x₁, y₁) lies on line (1) then
lx₁ + my₁ + n = 0
\(l\left(\frac{-\mathrm{a}^2 l}{\mathrm{n}}\right)+\mathrm{m}\left(\frac{\mathrm{b}^2 \mathrm{~m}}{\mathrm{n}}\right)+\mathrm{n}=0\)
⇒ -a²l² + b²m² + n² = 0
⇒ n² = a²l² – b²m²
⇒ a²l² – b²m² = n²

Question 6.
Find the equations of the tangents to the hyperbola x² – 4y² = 4 which are (i) parallel (ii) perpendicular to the line x + 2y = 0. [Mar. ’19 (AP) (TS) ’15 (TS); Mar. ’14; May ’14, ’13]
Solution:
Given the equation of the hyperbola is x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
Given the equation of the straight line is x + 2y = 0
(i) The equation of the tangent parallel to the line x + 2y = 0 is x + 2y + k = 0 ………(1)
2y = -x – k
y = \(\frac{-\mathrm{x}}{2}-\frac{\mathrm{k}}{2}\)
Comparing with y = mx + c,
we get m = \(\frac{-1}{2}\), c = \(\frac{-k}{2}\)
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ \(\left(\frac{-k}{2}\right)^2=4\left(\frac{-1}{2}\right)^2-1\)
⇒ \(\frac{k^2}{4}=\frac{4}{4}-1\)
⇒ k² = 0
⇒ k = 0
Substitute the value of k in equation (1)
x + 2y + 0 = 0
⇒ x + 2y = 0
∴ No parallel tangents to x + 2y = 0.
(ii) The equation of the tangent perpendicular to line x + 2y = 0 is
2x – y + k = 0
⇒ y = 2x + k ……..(2)
Comparing with y = mx + c,
we get m = 2, c = k.
Since equation (2) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ k² = 4(2)² – (1)² = 16 – 1
⇒ k² = 15
⇒ k = ±√15
Substitute the value of k in equation (2)
y = 2x ± √15
∴ The required perpendicular tangents are y = 2x ± √15

Question 7.
Find the equations of the tangents to the hyperbola 3x² – 4y² =12 which are (i) Parallel and (ii) Perpendicular to the line y = x – 7. [(TS) Mar. ’20, May ’18, ’15; (AP) Mar. ’17, ’15, May ’16, ’15]
Solution:
Given the equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
Here a² = 4, b² = 3
Given the equation of the straight line is y = x – 7
⇒ x – y – 7 = 0
(i) The equation of the tangent parallel to the line x – y – 7 = 0 is
x – y + k = 0 ………(i)
y = x + k
Comparing with y = mx + c,
we get m = 1, c = k
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ k² = 4(1)² – 3
⇒ k² = 1
⇒ k = ±1
Substitute the value of k in equation (1)
∴ The required parallel tangents are x – y ± 1 = 0
(ii) The equation of the tangent perpendicular to the line x – y – 7 = 0 is
x + y + k = 0 …….(2)
⇒ y = -x – k
Comparing with y = mx + c,
we get m = -1, c = -k
Since equation (2) is a tangent to the given hyperbola then
c² = a²m² – b²
(-k)² = 4(-1)² – 3
⇒ k² = 4 – 3
⇒ k² = 1
⇒ k = ±1
Substitute the value of k in equation (2)
∴ The required perpendicular tangents are x + y ± 1 = 0.

Question 8.
Find the equations of the tangents drawn to the hyperbola 2x² – 3y² = 6 through (-2, 1).
Solution:
Given the equation of the hyperbola is 2x² – 3y² = 6
⇒ \(\frac{x^2}{3}-\frac{y^2}{2}=1\)
Here a² = 3, b² = 2
Let, the given point P(x, y) = (-2, 1)
Let, the equation of the tangent to the hyperbola is
y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y = mx ± \(\sqrt{3 m^2-2}\) ……..(1)
Since, this tangent passes through the point P(-2, 1)
y = m(-2) ± \(\sqrt{3 m^2-2}\)
⇒ 1 = -2m ± \(\sqrt{3 m^2-2}\)
⇒ 1 + 2m = ±\(\sqrt{3 m^2-2}\)
Squaring on both sides
(1 + 2m)² = (±\(\sqrt{3 m^2-2}\))²
⇒ 1 + 4m² + 4m = 3m² – 2
⇒ m² + 4m + 3 = 0
⇒ m² + 3m + m + 3 = 0
⇒ m(m + 3) + 1(m + 3) = 0
⇒ (m + 3)(m + 1) = 0
⇒ m + 3 = 0 (or) m + 1 = 0
⇒ m = -3 (or) m = -1
Case (i): If m = -1, then the required tangents are from (1)
y = (-1)x ± \(\sqrt{3(-1)^2-2}\)
⇒ y = -x ± \(\sqrt{3-2}\)
⇒ y = -x ± 1
⇒ x + y ± 1 = 0
Since, the point (-2, 1) does not lie on the line x + y – 1 = 0
∴ The tangent is x + y + 1 = 0
Case (ii): If m = -3, then the required tangents are from (1)
y = (-3)x ± \(\sqrt{3(-3)^2-2}\)
⇒ y = -3x ± \(\sqrt{27-2}\)
⇒ y = -3x ± √25
⇒ 3x + y ± 5 = 0
Since, the point (-2, 1) does not lie on the line 3x + y – 5 = 0
∴ The tangent is 3x + y + 5 = 0
∴ Required tangents are x + y + 1 = 0, 3x + y + 5 = 0

Question 9.
Find the equation of the hyperbola whose asymptotes are the straight lines x + 2y + 3 = 0, 3x + 4y + 5 = 0, and which passes through the point (1, -1).
Solution:
Given that the asymptotes of a hyperbola are
x + 2y + 3 = 0 ……….(1)
3x + 4y + 5 = 0 ……….(2)
Let, the given point P = (1, -1)
The equation of the hyperbola whose asymptotes are the straight lines (1) & (2) is
(x + 2y + 3) (3x + 4y + 5) + k = 0 ……….(3)
Since equation (3) passes through the point P(1, -1) then
(1 + 2(-1) + 3) (3(1) + 4(-1) + 5) + k = 0
⇒ (1 – 2 + 3) (3 – 4 + 5) + k = 0
⇒ 8 + k = 0
⇒ k = -8
Substitute the value of ‘k’ in eq. (3)
∴ The required equation of the hyperbola is (x + 2y + 3) (3x + 4y + 5) – 8 = 0
⇒ 3x² + 4xy + 5x + 6xy + 8y² + 10y + 9x + 12y + 15 – 8 = 0
⇒ 3x² + 10xy + 8y² + 14x + 22y + 7 = 0

Question 10.
Prove that the product of the perpendicular distances from any point on a hyperbola to its asymptotes is constant.
Solution:
Let S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0 be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equations of asymptotes of hyperbola S = 0 are \(\frac{x}{a}+\frac{y}{b}=0\) and \(\frac{x}{a}-\frac{y}{b}=0\)
⇒ bx + ay = 0 ……..(1)
and bx – ay = 0 ……… (2)
Let PM be the length of the perpendicular drawn from P(a sec θ, b tan θ) on line (1).
∴ PM = \(\frac{|b a \sec \theta+a b \tan \theta|}{\sqrt{a^2+b^2}}\)
Let PN be the length of the perpendicular drawn from P (a sec θ, b tan θ) on line (2).


∴ The product of the perpendicular distances from any point on a hyperbola to its asymptotes is a constant.

Question 11.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 9x² – 16y² + 72x – 32y – 16 = 0. (May ’01)
Solution:
Given equation of the hyperbola is 9x² – 16y² + 72x – 32y -16 = 0
⇒ (9x² + 72x) +(-16y² – 32y) = 16
⇒ 9(x² + 8x) – 16 (y² + 2y) = 16
⇒ 9(x² + 2 . 4 . x + 4² – 4²) – 16(y² + 2 . 1 . y + 1² – 1²) = 16
⇒ 9((x + 4)² – 16) – 16((y + 1)² – 1) = 16
⇒ 9(x + 4)² – 144 – 16(y + 1)² + 16 = 16
⇒ 9(x + 4)² – 16(y + 1)² = 144

we get h = -4, k = -1, a = 4, b = 3.
It is a hyperbola.
Centre C = (h, k) = (-4, -1)

x = -4 ± \(\frac{16}{5}\)
5x = -20 + 16 or 5x = – 20 – 16
5k = -4 or 5x = -36
5x + 4 = 0 or 5x + 36 = 0
Length of latus rectum = \(\frac{2 \mathrm{~b}^2}{\mathrm{a}}=\frac{9}{2}\)

Question 12.
Find the centre, eccentricity, foci, directrices, and the length of the latus rectum of the hyperbola 4x² – 9y² – 8x – 32 = 0.
Solution:
Given equation of the hyperbola is 4x² – 9y² – 8x – 32 = 0
⇒ (4x² – 8x) + (-9y²) = 32
⇒ 4(x² – 2x) – 9y² = 32
⇒ 4((x)² – 2 . 1 . x + 1² – 1²) – 9y² = 32
⇒ 4((x – 1)² – 1) – 9y² = 32
⇒ 4(x – 1)² – 4 – 9y² = 32
⇒ 4(x – 1)² – 9y² = 36

we get a = 3, b = 2, h = 1, k = 0
It is a hyperbola.
Centre C(h, k) = (1, 0)

Question 13.
Tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) make angles θ₁, θ₂ with transverse axis of a hyperbola. Show that the point of intersection of these tangents lies on the curve 2xy = k(x² – a²), when tan θ₁ + tan θ₂ = k. [(TS) May ’19, ’16; (AP) May ’18]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let P(x₁, y₁) be the point of intersection of the tangents

Question 14.
Prove that the point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) lies on the circle x² + y² = a² – b². [(TS) May ’17; Mar. ’16]
Solution:
Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Equation of any tangent to the hyperbola is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
Suppose P(x₁, y₁) is the point of intersection of a tangent.
Since P lies on the tangent then
y₁ = mx₁ ± \(\sqrt{a^2 m^2-b^2}\)
y₁ – mx₁ = ±\(\sqrt{a^2 m^2-b^2}\)
Squaring on both sides

This is a quadratic equation in m given the values for m say m₁ and m₂.
The tangents are perpendicular then m₁m₂ = -1

∴ P(x₁, y₁) lies on the circle x² + y² = a² – b²

Question 15.
Show that the locus of feet of the ⊥ars drawn from foci to any tangent of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is the auxiliary circle of the hyperbola.
Solution:

Let the equation of hyperbola be
S = \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\)
Let P(x₁, y₁) be the foot of the ⊥ar drawn from either of the foci to a tangent.
The equation of the tangent to the hyperbola S = 0 is
y = mx ± \(\sqrt{a^2 m^2-b^2}\) …….(1)
The equation to the ⊥ar from either focus (±ae, 0) on this tangent is
y – y₁ = \(\frac{1}{m}\)(x – x₁)


∴ P lies on x² + y² = a² which is a circle with the centre as the origin, the centre of the hyperbola.

Question 16.
Find the centre, eccentricity, foci, length of latus rectum, and equations of the directrices of the hyperbola 4(y + 3)² – 9(x – 2)² = 1. [(AP) May ’19]
Solution:
Given hyperbola is 4(y + 3)² – 9(x – 2)² = 1
⇒ \(\frac{(y+3)^2}{\frac{1}{4}}-\frac{(x-2)^2}{\frac{1}{9}}=1\)

Question 17.
Show that the equation of a hyperbola in the standard form is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). [May ’02, ’99, ’98]
Solution:
Proof: Let ‘S’ be the focus, ‘e’ be the eccentricity and L = 0 be the directrix of the hyperbola.

Let ‘P’ be a point on the hyperbola.
Let MZ be the projection of PS on the directrix L = 0 respectively.
Let ‘N’ be the projection of ‘P’ on SZ.
Since e > 1 we can divide SZ both internally and externally in the ratio e : 1.
Let A, A’ be the points of division of ‘SZ’ in the ratio e : 1 internally and externally respectively.
Let AA’ = 2a.
Let ‘C’ be the midpoint of AA’.
Points A, A’ lies on the hyperbola then
\(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
Now \(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{e}}{1}\)
SA = e AZ
CS – CA = e (CA – CZ) ……..(1)
and \(\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
SA’ = eZA’
CS + CA’ = e (CZ + CA’) ……….(2)
Now (1) + (2),
(CS – CA) + (CS + CA’) = e (CA – CZ) + e(CA’ + CZ)
CS – CA + CS + CA’ = e (CA – CZ + CZ + CA’)
2CS – CA + CA’ = e (CA + CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
2CS – CA + CA = e (CA + CA)
2CS = 2eCA
CS = e CA
CS = ae (∵ CA = a)
∴ The coordinates of focus S = (ae, 0)
Now (1) – (2),
(CS – CA) – (CS + CA’) = e(CA – CZ) – e(CA’ + CZ)
CS – CA – CS – CA’ = e(CA – CZ – CA’ – CZ) – CA – CA’ = e (CA – 2CZ – CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
-CA – CA = e(CA – 2CZ – CA)
– 2CA = -2e CZ
CA = e CZ
a = e CZ
CZ = \(\frac{a}{e}\)
∴ The equation of the directrix is x = \(\frac{a}{e}\).
Take CS, the principal axis of the hyperbola as the X-axis, and CY ⊥ CS as Y-axis.
Then S = (ae, 0) and the hyperbola is in the standard form.
Let P = (x, y)
Now, PM = ZN = CN – CZ = x – \(\frac{a}{e}\)
P lies on the hyperbola
\(\frac{SP}{PM}\) = e
SP = e PM
\(\sqrt{(x-a e)^2+(y-0)^2}=e\left(x-\frac{a}{e}\right)\)
Squaring on both sides
(x – ae)² + y² = \(\mathrm{e}^2\left(\mathrm{x}-\frac{\mathrm{a}}{\mathrm{e}}\right)^2\)

where b² = a²(e² – 1) > 0
The locus of ‘P’ is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
∴ The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

Question 18.
Show that the difference in focal distances of any point on the hyperbola is constant
(or)
The difference of the focal distances of any point on the hyperbola is constant i.e. if ‘P’ is a point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) with foci S and S’ then S’P – SP = 2a.
Solution:

Let P (x, y) be any point on the hyperbola whose centre is the origin ‘C’.
Foci are S, S’
Directrices of ZM and Z’M’.
Let PN, PM, PM’ be the perpendiculars drawn from ‘P’ upon X-axis and the two directrices respectively.
Now, \(\frac{SP}{PM}\) = e
SP = e PM
= e ZN
= e (CN – CZ)
= e (x – \(\frac{a}{e}\))
Also = \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}=\mathrm{e}\)
S’P = ePM’
= eNZ’
= e (CN + CZ’)
= e (x + \(\frac{a}{e}\))
LHS = S’P – SP
= \(e\left(x+\frac{a}{e}\right)-e\left(x-\frac{a}{e}\right)\)
= ex + a – ex + a
= 2a (constant)
∴ S’P – SP = 2a

Question 19.
Show that the condition for straight line y = mx + c to be a tangent to the hyperbola S = 0 is c² = a²m² – b². [Mar. ’03]
Solution:
Suppose y = mx + c ………(1) is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at P is
\(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1=0\) ……..(2)
Now (1) and (2) represent the same line

Question 20.
Show that the equation of the normal at P(θ) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b². [Mar. ’06]
Solution:
The equation of the tangent at P(θ) is \(\frac{x \sec \theta}{a}-\frac{y \tan \theta}{b}=1\)
Slope of tangent = \(\frac{\frac{-\sec \theta}{a}}{\frac{-\tan \theta}{b}}=\frac{b \sec \theta}{a \tan \theta}\)
Slope of normal = \(-\frac{a \tan \theta}{b \sec \theta}\)
∴ The equation of the normal at P is
y – b tan θ = \(-\frac{a \tan \theta}{b \sec \theta}\) (x – a sec θ)
⇒ by sec θ – b² sec θ tan θ = -ax tan θ + a² sec θ tan θ
⇒ ax tan θ + by sec θ = (a² + b²) sec θ tan θ
⇒ \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}=a^2+b^2\)

Question 21.
If the line lx + my = 1 is a normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then show that \(\frac{a^2}{l^2}-\frac{b^2}{m^2}=\left(a^2+b^2\right)^2\).
Solution:

Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let the line lx + my – 1 = 0 ……….(1) be normal to the given hyperbola at P(θ).
The equation of normal at P(θ) to the given hyperbola is
\(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b² …….(2)
Now (1) & (2) represent the same line.

which is the required condition.

Question 22.
Show that the equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents
(i) an ellipse if ‘c’ is a real constant less than 5.
(i) a hyperbola if ‘c’ is any real constant between 5 and 9.
(iii) Show that each ellipse in (a) and each hyperbola in (b) has foci at the two points (±2, 0), independent of the value ‘c’.
Solution:
(i) Given equation is \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\)
This equation represents an ellipse if
9 – c > 0 and 5 – c > 0
9 > c and 5 > c
c < 9 and c < 5
∴ c < 5
(ii) Given equation is \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\)
This equation represents a hyperbola if
9 – c > 0 and 5 – c < 0
9 > 0 and 5 < c
c < 9 and c > 5
∴ 5 < c < 9
(iii) In case (i): a² = 9 – c, b² = 5 – c
Now, a² – b² = (9 – c) – (5 – c)
⇒ a² – a²(1 – e²) = 9 – c – 5 + c
⇒ a²e² = 9 – 5
⇒ a²e² = 4
⇒ ae = 2
∴ foci are (±ae, 0) = (±2, 0)
In case (ii): a² = 9 – c, b² = c – 5
Now, a² + b² = 9 – c + c – 5
⇒ a² + a²(e² – 1) = 9 – 5
⇒ a²e² = 4
⇒ ae = 2
∴ foci are (±ae, 0) = (±2, 0)
These are independent of the value of ‘c’

Question 23.
A circle cuts the rectangular hyperbola xy = 1, in the points (x₁, y₁), r = 1, 2, 3, 4. Prove that x₁x₂x₃x₄ = y₁y₂y₃y₄ = 1.
Solution:
Let the circle be x² + y² = a²
Since (t, \(\frac{1}{2}\)) (t ≠ 0) lies on xy = 1
The points of intersection of the circle and the hyperbola are given by
\(t^2+\frac{1}{t^2}=a^2\)
⇒ t⁴ – a²t² + 1 = 0
⇒ t⁴ + 0 . t³ – a²t + 0 . t + 1 = 0
If t₁, t₂, t₃, t₄ are the roots of the above biquadratic, then
product of the roots t₁t₂t₃t₄ = \(\frac{1}{1}\) = 1

Telangana TSBIE TS Inter 2nd Year Physics Study Material 12th Lesson Dual Nature of Radiation and Matter Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 12th Lesson Dual Nature of Radiation and Matter

Very Short Answer Type Questions

Question 1.
What are “Cathode rays”? [TS Mar. 19; AP mar. 1 7, may 18, 14]
Answer:
Cathode rays consists of a steam of fast moving negatively charged particles.

Speed of cathode rays ranges about 0.1 to 0.2 times light velocity (3 × 10⁸m/s)

Question 2.
What important fact did Millikan’s experiment establish?
Answer:
Millikan proved the validity of Einstein’s photo electric equation and his successful explanation of photo electric effect using light quanta. He experimentally found the value of Planck’s constant ‘h’ and work function on ‘Φ’ of photo electric surface.

Question 3.
What is “work function”? [AP Mar. 19, May 16; TS Mar. 18. 17, 15]
Answer:
Work function (Φ) :
The mininum energy required by an electron to escape from metal surface is called “work function”.

Work function depends on nature of metal.

Question 4.
What is “photoelectric effect”? [AP Mar. ’18, ’17, ’15, ’14, May ’14; TS May ’17, Mar. ’18. ’16]
Answer:
Photoelectric effect :
The process of liberating an electron from the metal surface due to light energy falling on it is called “photoelectric effect”.

Question 5.
Give examples of “photosensitive substances”. Why are they called so?
Answer:

1. Metals like zinc, cadmium and magnesium will respond to ultraviolet rays.
2. Alkalimetals such as sodium, potassium, caesium and rubidium will respond to visible light.

These substances are called “photo sensitive surfaces” because they will emit electrons when light falls on them.

Question 6.
An electron, an a particle and a proton have the same kinetic energy. Which of these particles has the shortest de Broglie wavelength? [TS May, ’18, Mar. ’15]
Answer:
De-Broglie wavelength λ = \(\frac{h}{p}\); but KE = \(\frac{P^2}{2m}\)

For a particle m is more them given other particles.
So De-Broglie wavelength of a – particle is less.

Question 7.
What is Photo-electric effect? How did Einstein’s photo-electric equation explain the effects of intensity (of light) and potential on photo-electric current? [AP May 18, TS June 15]
Answer:
Photoelectric effect :
The process of emitting electron from the metal surface when light energy falling on it is called “photo-electrie effect”.

According to Einstein radiation consists of discrete units of energy called quanta of energy radiation.

Energy of quanta is called photon in light E = hυ

Maximum kinetic energy of photoelectron (K_max) is the difference of energy of incident radiation (hυ) and work function (Φ)
∴ K_max = hυ – Φ (when υ > υ₀)

Photoelectric equation can also written as

Effect of intensity :
As per Einstein’s photoelectric equation energy of photon E = hυ decides weather a photon will come out of metal surface or not. If frequency of incident light υ > υ₀ then electron will come out of that surface.

Number of electrons liberated depends on the number of photons striking the surface i.e., on intensity of light. So as per Einstein’s equation photocurrent liberated must be linearly proportional to intensity of light which is a practically proved fact.

Effect of voltage on photocurrent :
When positive potential on collector is gradually increased then photocurrent i.e., also gradually increased upto certain limit called saturation current all the photoelectrons liberated from. Photosurface reached the collector.

When υ >υ₀ photoelectron is released. The positive potential on collector will accelerate the electron. So it reaches the collector quickly. So photocurrent increases. But collector potential deals nothing with liberation of electron from photosurface.

In this way Einstein’s photoelectric equation explained the saturation of photocurrent with increasing collector +ve potential. Effect of frequency and stopping potential.

From Einstein’s photoelectric equation
K_max = hυ – Φ

i.e., kinetic energy of photoelectron is directly proportional to frequency of incident light.

Question 8.
Write down Einstein’s photoelectric equation. [AP Mar. 19, 15, May 17; TS May 18, 16]
Answer:
Maximum kinetic energy of photo electron Kmax is the difference of energy of incident radiation (hυ) and work function (Φ)
K_max= hυ – Φ (when υ > υ₀)
OR
K_max = eV₀ = hυ – Φ Or V₀ = \(\frac{h}{e}\)υ – \(\frac{\phi_{0}}{e}\)

Question 9.
Write down de Broglie’s relation and explain the terms there in. [AP & TS Mar. 18, 16; TS May 17]
Answer:
de -Broglie assumed that matter will also exhibit wave nature when it is in motion.
de – Broglie wavelength, λ = \(\frac{h}{p}=\frac{h}{mυ}\)
P = mo, momentum of the body, h = Planck’s constant, λ = wave length of moving particle.

Question 10.
State Heisenberg’s uncertainty principle. [TS Mar. 17; AP Mar. 14]
Answer:
Heisenberg’s uncertainty principle :
We cannot exactly find both momentum and position of an electron at the same time. This is called Heisenberg’s uncertainty principle.

Short Answer Questions

Question 1.
What is the effect of (i) intensity of light (ii) potential on photoelectric current? [TS Mar. ’19, June ’15]
Answer:
Effect of intensity :
The number of photo electrons liberated is directly proportional to intensity of incident radiation. So photo current increases linearly with increase of intensity of incident light.

Effect of potential :
When positive potential given to collector, photocurrent is gradually increased up to certain limit called saturation current. In this stage all the photo electrons liberated from photo surface reached the collector.

When negative potential on collector is gradually increased electrons are repelled by collector and photo current decreases.

At a particular negative voltage photo current is zero.

Stopping potential :
The minimum negative potential required by collector to stop photo current (or) becomes zero is called cut-off voltage (V₀) stopping potential.

Question 2.
How is the de-Broglie wavelength associated with an electron accelerated through a potential difference of 100 volts? [AP Mar. ’15]
Answer:
de-Broglie wavelength λ = \(\frac{h}{\sqrt{2 \mathrm{~m}} \mathrm{eV}}\)
Potential difference V = 100V; h = 6.63 × 10^-34
Mass of electron m = 9.1 × 10^-31 kg;
charge of electron e = 1.6 × 10^-19c

Question 3.
What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volt? [TS May. ’16]
Answer:
Applied potential V = 100 V.
de Broglie wavelength

∴ de Broglie wavelength 1 = 0.1227 nm.

Question 4.
Describe an experiment to study the effect of frequency of incident radiation on ‘stopping potential’.
Answer:
Experimental study of photo electric effect :
To study photo electric effect a photo sensitive surface and a metallic plate called collector are arranged on an evacuated glass tube. An arrangement is made to give required positive or negative potential to collector. By changing the filters placed in the path of incident light we will allow light rays of required frequency to fall on given photo surface.

Stopping potential :
The minimum negative potential required by collector to stop photo current or photo current to become zero is called “cut off voltage V₀“.

Effect of frequency on stopping potential are

1. Stopping potential varies linearly with frequency of incident light.
2. Every photo surface has a minimum cut off frequency υ₀ for which stopping potential V₀ = 0

Question 5.
Summarise the photon picture of electromagnetic radiation.
Answer:
Radiation consists of discrete units of energy called quanta.
Energy of quanta (E) = hυ = \(\frac{hc}{\lambda}\)

In case of light energy quanta is called photon.

Properties of photons:

1. Energy of photon E = ho Momentum ho P= \(\frac{hυ}{e}\)
2. In interaction of radiation with matter light quanta will behave like particles
3. Photons are electrically neutral. So they are not deflected by electric and magnetic fields.
4. In photons-particle collision total energy and total mometum of are conserved is in collision photon will totally loose its enery and momentum.

Question 6.
What is the deBroglie wavelength of a ball of mass 0.12Kg moving with a speed of 20ms^-1? What can we infer from this result? [AP June ’15]
Answer:
Mass of ball, m = 0.12kg ;
Speed of ball, v = 20 m/s
Plancks’ constant, h = 6.63 × 10^-34J
But de Broglie wave length λ = \(\frac{h}{p}=\frac{h}{mv}\)

∴ de Broglie wave length of given moving ball X = 2.762 × 10^-34m

Question 7.
The work function of cesium is 2.14 eV. Find the threshold frequency for cesium. (Take h = 6.6 × 10^-34Js) [IMP]
Answer:
Work function Φ₀ = 2.14 eV; h = 6.6 × 10^-34 JS

Long Answer Questions

Question 1.
How did Einstein’s photoelectric equation Explain the effect of intensity and potential on photoelectric current? How did this equation account for die effect of frequency of incident light on stopping potential?
Answer:
Einstein’s photo electric equation :
According to Einstein radiation consists of discrete units of energy called quanta of energy radiation.

Energy of quanta called photon in light E = hυ

Maximum kinetic energy of photo electron (K_max) is the difference of energy of incident radiation (hυ) and work function (Φ)
∴ K_max= hυ – Φ(when υ > υ₀)
Photo electric equation can be written as

Effect of intensity :
As per Einstein’s photo electric equation energy of photon decides weather a photon will come out (or) not from metal surface. If frequency of incident light υ > υ₀, then electron will come out from surface.

Number of electrons liberated depends on the number of photons striking the surface i.e., on intensity of light. So as per Einstein’s equation photo current liberated must be linearly proportional to intensity of light which is practically proved.

Effect of voltage on photo current :
When positive potential on collector is gradually increased then photo current i.e., also gradually increased up to certain limit called saturation current. In this stage all the photo electrons liberated from photo surface reached the collector.

When υ > υ₀ photo electron Is released. The positive potential on collector will accelerate the electron. So it reaches the collector quickly. So photo current increases. But collector potential deals nothing with liberation of electron from photo surface.

Effect of frequency and stopping potential :
⇒ Kinetic energy of photo electron is directly proportional to frequency of incident light.
From Einstein’s photo electric equation
∴ K_max= hυ – Φ

Stopping potential :
The minimum negative potential required by the collector to stop photo current is called stopping potential.

At this potential even the fastest electron (or) electron with maximum kinetic energy is prevented to reach the collector.

When frequency incident light increases then K_max of electron increases. Hence stopping potential V₀ will also increase.

∴ The graph between stopping potential V₀ and frequency o must be a straight line.

Then slope of the line is \(\frac{h}{e}\). This is experimentally proved by Millikan.

In this way Einstein’s photo electric equation successfully explained photo electric effect.

Question 2.
Describe the Davisson and Germer experiment. What did this experiment conclusively prove?
Answer:
Davisson and Germer experiment :
In this experiment, electrons are produced by heating a tungsten filament coated with barium oxide with the help of a low voltage battery.

These electrons are focussed on to a nickel target in the form of a sharp beam.

This electron beam is accelerated by the strong positive potential on nickel target.

After colliding the target electron beam will get scattered.

The scattered electron beam is collected by electron beam detector called collector.

In this experiment intensity of electron beam I for different angles of scattering is measured. A graph is plotted between angle of scattering 0 and intensity I with different target potentials of 44V to 68V.

Intensity is found to be maximum at a target potential of 54V with a scattering angle of 50°

This value coincides with the de Broglie wave length of electron.

Importance :
This experiment proved the existence of matter waves practically. It gave a strong support to de Broglie’s hypothesis of matter wave concept.

Intext Question and Amswers

Question 1.
The photoelectric cut-off voltage in a certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted?
Answer:
Photoelectric cut-off voltage, V₀ = 1.5 V ;
maximum kinetic energy K_e = eV₀
Where, e = Charge on an electron = 1.6 × 10^-19 C
∴ k_e = 1.6 × 10^-19 × 15 = 2.4 × 10^-19J
∴ The maximum kinetic energy of the photoelectrons emitted K = 2.4 × 10^-19 J.

Question 2.
The energy flux of sunlight reaching the surface of the earth is 1.388 × 10³ W/m². How many photons (nearly) per square metre are incident on the earth per second? Assume that the photons in the sunlight have an average wavelength of 550 nm.
Answer:
Energy flux of sunlight reaching the surface of earth, Φ = 1.388 × 10³ W/m²
Hence, power of sunlight per square metre, P = 1.388 × 10³W
Speed of light, c = 3 × 10⁸ m/s ; Planck’s constant, h = 6.626 × 10^-34 Js
Average wavelength of photons present in sunlight, λ = 550 nm = 550 × 10^-19 m
Number of photons per square metre incident on earth per second = n
∴ Power p = n E

∴ 3.84 × 10²¹ photons are incident per square metre / sec on earth.

Question 3.
In an experiment on photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 × 10^-15 V s. Calculate the value of Planck’s constant.
Answer:
The slope of the cut-off voltage (V) – frequency (v) graph is ; \(\frac{V}{v}\) = 4.12 × 10^-15 Vs
But hv = eV
Where, e = Charge on an electron = 1.6 × 10^-19 C; h = Planck’s constant
∴ h = e×\(\frac{V}{v}\) = 1.6 × 10^-19 × 4.12 × 10^-15
= 6.592 × 10^-34Js
∴ Planck’s constant h = 6.592 × 10^-34 Js.

Question 4.
A 100 W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is 589 nm. (a) What is the energy per photon associated with the sodium light? (b) At what rate are the photons delivered to the sphere?
Answer:
Power of the sodium lamp, P = 100 W ;
Wavelength of the emitted sodium light,
λ = 589 nm = 589 × 10^-9 m
Planck’s constant, h = 6.626 × 10^-34 Js ;
Speed of light, c = 3 × 10⁸ m/s
(a) Energy of photon E = \(\frac{hc}{\lambda}\)

(b) Number of photons delivered to the sphere = n
Power P = nE

Photons delivered per second = 2.96 × 10²⁰

Question 5.
The threshold frequency for a certain metal is 3.3 × 10¹⁴ Hz. If light of frequency 8.2 × 10¹⁴ Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission.
Answer:
Threshold frequency of the metal,
v₀ = 3.3 × 10¹⁴ Hz;
Charge on an electron, e = 1.6 × 10^-19 C ;
Frequency of light incident on the metal, v₀ = 8.2 × 10¹⁴ HZ;
Planck’s constant, h = 6.626 × 10^-34 Js
Cut-off voltage for the photoelectric emission from the metal = V₀; But eV₀ = h(υ – υ₀)

∴ The cut-off voltage for the photoelectric emission V₀ = 2.0292 V.

Question 6.
The work function for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wave-length 330 nm?
Answer:
No.
Work function of the metal, Φ₀ = 4.2 eV;
Charge on an electron, e = 1.6 × 10^-19 C
Planck’s constant, h = 6.626 × 10^-34 Js ;
Wavelength of the incident radiation,
λ = 330 nm = 330 × 10^-9 m
Speed of light, c = 3 × 10⁸ m/s ;
The energy of the incident photon E = \(\frac{hc}{\lambda}\)

Question 7.
light of frequency 7.21 × 10¹⁴ Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 10⁵ m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
Answer:
Frequency of photon, v = 488 nm
= 488 × 10^-9 m ;
Planck’s constant, h = 6.626 × 10^-34 Js
Maximum speed of the electrons, v = 6.0 × 10⁵ m/s ;
Mass of an electron, m = 9.1 × 10^-31 kg
Relation between v and K.E, \(\frac{1}{2}\) mv²
= h(ν – ν₀)⇒ ν₀ = ν –\(\frac{mv^2}{2h}\)

Threshold frequency ν₀ = 4.738 × 10⁵ Hz

Question 8.
Light of wavelength 488 nm is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut-off) potential of photoelectrons is 0.38 V. Find the work function of the material from which the emitter is made.
Answer:
Wavelength of light produced by the argon laser, λ = 488 nm = 488 × 10^-9 m
Stopping potential, V₀ = 0.38 V ;
But leV = 1.6 × 10^-19 J
∴ V₀ = \(\frac{0.38}{1.6\times10^{-19}}\)eV
Planck’s constant, h = 6.6 × 10^-34 Js ;
Charge on an electron, e = 1.6 × 10^-19 C
Speed of light, c = 3 × 10 m/s
From Einstein’s photoelectric effect,

Question 9.
Calculate the
(a) Momentum/and
(b) De Broglie wavelength of the electrons accelerated through a potential difference of 56 V.
Answer:
Potential difference, V = 56 V;
Planck’s constant, h = 6.6 × 10^-34 Js
Mass of an electron, m = 9.1 × 10^-31 kg ;
Charge on an electron, e = 1.6 × 10^-19 C

(a) At equilibrium, the kinetic energy of each electron is equal to the accelerating potential, for

The momentum of each accelerated electron
p = mv = 9.1 × 10^-31 × 4.44 × 10⁶
Momentum of each electron p
= 4.04 × 10^-24 kg m s^-1
(b)De Broglie wavelength of an electron,

Question 10.
What is the
(a) Momentum,
(b) Speed, and
(c) De Broglie wavelength of an electron with kinetic energy of 120 eV.
Answer:
Kinetic energy of the electron, E_k = 120 eV;
Planck’s constant, h = 6.6 × 10^-34 Js
Mass of an electron, m = 9.1 × 10^-31 kg ;
Charge on an electron, e = 1.6 × 10^-19 C
(a) Kinetic energy of electron E_k = \(\frac{1}{2}\)mv²
Where, υ = Speed of the electron

Momentum of the electron, p = mv
∴ P = 9.1 × 10^-31 × 6.496 × 10⁶
= 5.91 × 10^-24 kg m s^-1.
(b) Speed of the electron, v = 6.496 × 10⁶ m/s (from eq 1)

(c) De Broglie wavelength of an electron having a momentum p, is given as:

∴ de Broglie wavelength of the electron is 0.112 nm.

Question 11.
What is the de Broglie wavelength of
(a) a bullet of mass 0.040 kg travelling at the speed of 1.0 km/s,
(b) a ball of mass 0.060 kg moving at a speed of 1.0 m/s, and
(c) a dust particle of mass 1.0 × 10^-9 kg drifting with a speed of 2.2 m/s?
Answer:
(a) Mass of the bullet, m = 0.040 kg ;
Speed of the bullet, v = 1.0 km/s
= 1000 m/s
Planck’s constant, h = 6.6 × 10^-34Js
But De Broglie wavelength λ = \(\frac{h}{mv}\)

(b)Mass of the ball, m = 0.060 kg
Speed of the ball, v = 1.0 m/s
De Broglie wavelength λ = \(\frac{h}{mv}\)

(c) Mass of the dust particle, m =1 × 10^-9 kg;
Speed of the dust particle, v = 2.2 m/s
De Broglie wavelength λ = \(\frac{h}{mv}\)

Question 12.
An electron and a photon each have a wavelength of 1.00 nm. Find
(a) their momenta,
(b) the energy of the photon, and
(c) the kinetic energy of electron.
Answer:
Wavelength of an electron (λ^e) and a photon (λ^p), λ^e = λ^p = λ = 1nm = 1 × 10^-9 m
Planck’s constant, h = 6.63 × 10^-34 Js
(a) The momentum of an elementary partide is given by de Broglie relation:

(b) The energy of a photon is given by the relation:

(c) The kinetic energy (A) of an electron having momentum p,is given by the relation:
m = Mass of the electron = 9.1 × 10^-31 kg;
p = 6.63 × 10^-25 kg ms^-1

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 6 Binomial Theorem will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Binomial Theorem Formulas

→ If a, x are real numbers and n is a positive integer, then

• (x + a)ⁿ = ⁿC₀ xⁿ. a⁰ + ⁿC₁. x^n-1 . a¹ + ⁿC₂. x^n-2. a² + ………… + ⁿC_r. x^n-r. a^r + ……………. + (-1)^{r n}C_n. x⁰ . aⁿ
• (x – a)ⁿ = ⁿC₀ xⁿ. a⁰ – ⁿC₁. x^n-1 . a¹ + ⁿC₂. x^n-2. a² + ………… + ⁿC_r. x^n-r. a^r + ……………. + (-1)^{r n}C_n. x⁰ . aⁿ

→ Each of the above two expansions contain (n + 1) terms in R.H.S.

→ The general term of (x + a)ⁿ is T_r+1 = ⁿC_r x^n-r . a^r (0 ≤ r ≤ n)

→ If n is fixed we write ⁿC_r = C_r and C₀, C₁ C₂ ………….. C_n are called the binomial coefficients.

• C₀ + C₁ + C₂ …………….. + C_n = 2ⁿ
• C₀ – C₁ + C₂ – C₃ + ……………. + (-1)ⁿC_n = 0
• C₀ + C₂ + C₄ + ………….. = C₁ + C₃ + C₅ + …………… = 2^n-1

→ \(\sum_{r=0}^n\)C_r = 2ⁿ
\(\sum_{r=1}^n\)r. C_r = n. 2^n-1
\(\sum_{r=2}^n\) r(r – 1). C_r = n(n – 1).2^n-2
\(\sum_{r=1}^n\) r² .C_r = n(n + 1) 2^n-2

→ (i) If n is even then the expansion of (x + a)ⁿ has only one middle term. It is
T_{\(\frac{n}{2}\)+1} = ⁿC_{\(\frac{n}{2}\)} . x^{\(\frac{n}{2}\)}. a^{\(\frac{n}{2}\)}

(ii) If n is odd, then the expansion of (x + a)ⁿ has two middle terms. They are
T_{\(\frac{n+1}{2}\)} = nC_{\(\left(\frac{n-1}{2}\right)\)} . x^{\(\frac{n+1}{2}\)}. a^{\(\frac{n-1}{2}\)} and T_{\(\frac{n+3}{2}\)} = nC_{\(\left(\frac{n+1}{2}\right)\)} . x^{\(\frac{n-1}{2}\)} . a^{\(\frac{n+1}{2}\)}

→ Numerically greatest term in the expansion of (1 + x)” :

• If \(\frac{(\mathrm{n}+1)|\mathrm{x}|}{1+|\mathrm{x}|}\) is not an integer and if its integral part \(\left[\frac{(n+1)|x|}{1+|x|}\right]\) = r, a positive integer then T_r+1 is the numerically greatest term in the expansion of (i + x)ⁿ.
• If \(\frac{(n+1)|x|}{1+|x|}\) is positive integer, say m, then |T_m| = |T_m+1| and hence T_m and T_m+1 both are numerically greatest terms in the expansion of (1 + x)ⁿ.

→ If x is a real number such that |x| < 1 and p. q are positive integers, then

→ If n is a positive integer and x is a real number such that j x j < 1, then

• If |x| is so small that x² and higher powers of x may be neglected, then (1 + x)ⁿ = 1 + nx.
• If |x| is so small that x³ and higher powers of x may be neglected, then
  (1 + x)ⁿ = 1 + nx + \(\frac{n(n-1)}{2 !}\)x².
• if |x| is so small that x⁴ and higher powers of x may be neglected, then
  (1 + x)ⁿ = 1 + nx + \(\frac{n(n-1)}{2 !}\)x² + \(\frac{n(n-1)(n-2)}{3 !}\)x³

→ (1 + x)^p/q = 1 + \(\frac{\frac{p}{q}}{1 !}\)x + \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right)}{2 !}\)x² + \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right)\left(\frac{p}{q}-2\right)}{3 !}\)x³ + ……. + \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right) \cdots\left(\frac{p}{q}-r+1\right)}{r !}\).x^r + …………
T_r+1 = \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right)\left(\frac{p}{q}-2\right) \ldots \ldots\left(\frac{p}{q}-r+1\right)}{r !}\). x^r for r ∈ N.

→ Let n ∈ N and a, b, c ∈ R, then (a + b + c)ⁿ contains \(\frac{(\mathrm{n}+1)(\mathrm{n}+2)}{2}\) terms.
Also (a +b + c)ⁿ = \(\sum_{{0 \leq p, q, r \leq n \\ p+q+r=n}} \frac{n !}{p ! q ! r !}\) a^p . b^q. c^r