TS Inter 2nd Year Maths 2B Ellipse Formulas

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 4 Ellipse will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Ellipse Formulas

→ An ellipse is the locus of a point whose distances from a fixed point and a fixed straight line are in a constant ratio ‘e’ which is less than unity. The fixed point and the fixed straight line are called the focus and the directrix of ellipse respectively.

→ Equation of an ellipse in the standard form is – 1, (a > b). Centre = (0, 0)
Foci = (± ae, 0); Directrix, x = ±\(\frac{\mathrm{a}}{\mathrm{e}}\) and Eccentricity, e = \(\sqrt{\frac{a^2-b^2}{a^2}}\)

→ Various forms of the ellipse Form:
(i) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (a > b > 0)

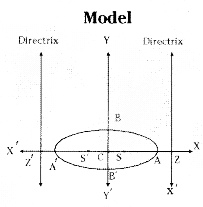
length of mayor axis (AA’)	2a
Length of minor axis	along Y axis, 2b
Centre	C = (0, 0)
Foci	S = (ae, 0) S’ = (-ae, 0)
Equation of the directrices	x = a/e x = -a/e
Eccentricity	e = \( \sqrt{\frac{a^2-b^2}{a^2}} \)

(ii) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (0 < a < b)

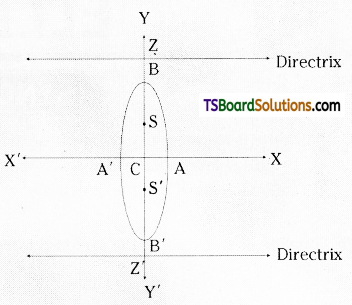
Length of major axis (BB’)	‘2b’
Length of minor axis	along X – axis, ‘2a’
Centre	C = (0, 0)
Foci	S = (0, be) S’ = (0, -be)
Equation of the directrices	y = b/e y = -b/e
Eccentricity	e = \( \sqrt{\frac{b^2-a^2}{b^2}} \)

(iii) \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 (a > b > 0)

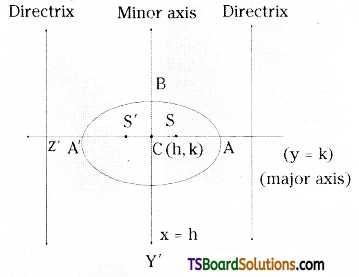
Length of major axis (AA’)	‘2a’
Length of minor axis	Along x = h, 2b
Centre	C – (h, k)
Foci	S = (h + ae, k) S’ = (h – ae, k)
Equation of the directrices	x – h + a/e x = h – a/e
Eccentricity	e = \( \sqrt{\frac{a^2-b^2}{a^2}} \)

(iv) \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 (0 < a < b)

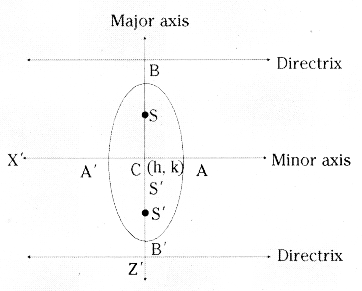
Lengtli of major axis (BB’)	‘2b’
Length of minor axis	Along y = k, ’2a’
Centre	C = (h, k)
Foci	S = (h, k + be) S ‘= (h, k – be)
Equation of the directrices	y = k + b/e y = k – b/e
Eccentricity	e = \( \sqrt{\frac{b^2-a^2}{b^2}} \)

→ If P is any point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, (a > b) and foci are S, S’, then SP + S’P = 2a.

→ The equation of the auxiliary circle of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, (a > b) is x² + y² = a².

→ Parametric equations of ellipse S = 0 are x = a cos θ, y = b sin θ and θ is called the parameter.

→ If P(x₁, y₁) is a point on the plane of the ellipse, then P lies outside, on or inside the ellipse according as Sn is positive, zero or negative.

→ The condition for the straight line y = mx + c to touch the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is (or) tangent to the ellipse is c² = a²m² + b².

→ y = mx ± \(\sqrt{a^2 m^2+b^2}\) is always a tangent to the ellipse S = 0 at \(\sqrt{a^2 m^2+b^2}\) and \(\left(\frac{a^2 m}{c}, \frac{-b^2}{c}\right)\)

→ The equation of the tangent at P (x₁, y₁)to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is \(\frac{\mathrm{x} \mathrm{x}_1}{a^2}+\frac{\mathrm{y} \mathrm{y}_1}{\mathrm{~b}^2}\) – 1 = 0

→ The equation of the normal to the ellipse at P (x₁, y₁) is \(\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}\) = a² – b²

→ Equation of the tangent at P (θ) i.e., P (a cos θ, b sin θ) to the ellipse S = 0 is \(\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}\) = 1.

→ Equation of the normal at P(θ) to the ellipse S = 0 is \(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}\) = a² – b²
where θ ≠ 0, \(\frac{\pi}{2}\), π, \(\frac{3 \pi}{2}\)

→ Eqilation of director circle of the ellipse S = 0 is x² + y² = a² + b²

→ If P(x₁, y₁) Is an external point to the ellipse S = 0, then the equation of chord of contact of P w.r.t ellipse S = 0 is \(\frac{x x_1}{a^2}+\frac{y y_1}{b^2}\) = 1.