TS Inter 2nd Year Maths 2B Definite Integrals Formulas

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 7 Definite Integrals will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Definite Integrals Formulas

→ If F(x) is an indefinite integral (or) anti-derivative of a function f(x) defined on [a, b] then
\(\int_a^b\)f(x) dx = F(b) – F(a) …………….. (1).
The symbol \(\int_a^b\)f (x) dx is called the definite integral of f(x) from x = a to x = b. The numbers ’a’ and ’b’ are called the limits of integration, ’a’ is called the lower limit and ’b’ is called the upper limit. If we use the notation \([\mathrm{F}(\mathrm{x})]_{\mathrm{a}}^{\mathrm{b}}\) to denote
F(b) – F(a), then from (1) \(\int_a^b\)f (x) dx = \([\mathrm{F}(\mathrm{x})]_{\mathrm{a}}^{\mathrm{b}}\) = [(F(x) at x = b) – (F(x) at x = a)].

→ Fundamental properties of definite integrals:
Property – 1 : \(\int_a^a\) f (x) dx = 0

Property-2: \(\int_a^b\) f(x)dx = \(\int_a^b\)f(t)dt

Property-3: \(\int_a^b\)f(x)dx = – \(\int_b^a\)f(x)dx

Property-4: \(\int_a^b\)f(x)dx = \(\int_a^c\)f(x)dx + \(\int_c^b\)f(x)dx, if a < c < b

Property-5: \(\int_0^a\)f (x)dx = \(\int_0^a\)f (a – x)dx

Property- 6: \(\int_{-a}^a\)f(x) dx = 2\(\int_0^a\)f(x)dx, if f(x) is even
= 0, if f(x) is odd

Property – 7: \(\int_0^{2 a}\)f(x) dx = 2\(\)f(x)dx, if f(2a – x) = f(x)
= 0, if f(2a – x) = – f(x)

Properly – 8: \(\int_a^b\)f(x)dx = \(\int_a^b\)f(a + b – x)dx

Properly-9: \(\int_0^{n a}\)f (x)dx = n\(\int_0^{a}\)f(x)dx, if f(a + x) = f(x)

Properly -10: \(\int_0^{\infty}\)f(x)dx = \({Lt}_{t \rightarrow \infty} \int_0^t\)f(x)dx and \(\int_{-\infty}^a\) f(x)dx = \({Lt}_{t \rightarrow-\infty} \int_t^a\)f(x)dx
and \(\int_{-\infty}^{\infty}\) f(x)dx = \({Lt}_{t \rightarrow \infty} \int_a^t\)f(x)dx + \({Lt}_{t \rightarrow-\infty} \int_t^a\)f(x)dx

Properly -11: |\(\int_a^b\)f(x) dx| ≤ \(\int_a^b\) |f(x)|dx

Properly -12: If f(x) ≥ 0, ∀x ∈ [a, b], then \(\int_a^b\)f(x)dx ≥ 0 and if f(x) ≥ g(x), ∀ x ∈ [a, b] then \(\int_a^b\)f(x)dx ≥ \(\int_a^b\) g(x)dx

→ Reduction Formulae:

• If I_n = \(\int_0^{\pi / 2}\)sinⁿ dx, then I_n = \(\frac{n-1}{n}\)I_n-2
• If I_n = \(\int_0^{\pi / 2}\)cosⁿ dx, then I_n = \(\frac{n-1}{n}\)I_n-2
• If I_n = \(\int_0^{\pi / 4}\)tanⁿ dx, then I_n = \(\frac{1}{n-1}\)I_n-2
• If I_n = \(\int_0^{\pi / 4}\)secⁿ dx, then I_n = \(\frac{(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = \(\int_{\pi / 4}^{\pi / 2}\)cotⁿ dx, then I_n = \(\frac{1}{n-1}\) – I_n-2
• If I_n = \(\int_{\pi / 4}^{\pi / 2}\)cosecⁿ dx, then I_n = \(\frac{-(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_m,n = \(\int_0^{\pi / 2}\)sin^mx. cosⁿxdx then I_m,n = \(\frac{-(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2

Let m and n be positive integers, then

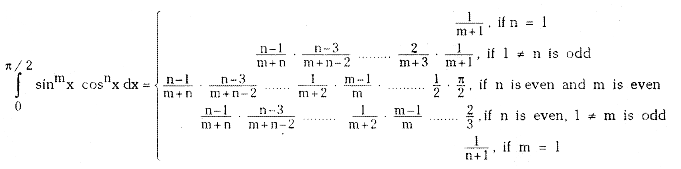
Let n be an integer greater than or equal to 2.

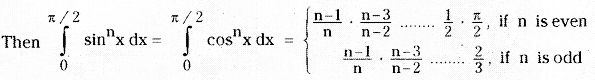
Areas:
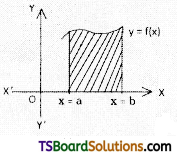
→ Let f be a continuous function on [a, b]. Then the area of the region bounded by curve y = f(x) with X – axis between the lines x = a and x = b is
(i) \(\int_a^b\)f(x)dx, if f(x) ≥ 0

(ii) –\(\int_a^b\)f(x)dx, if f(x) ≤ 0

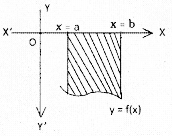
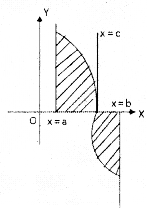
→ Let a < c < b and if f(x) ≥ 0 on [a, cl and f(x) ≤ 0 on [b, C]. Then the area of the region bounded by the curve y = f(x) wIth X- axis between lines x = a and x = b is
\(\int_a^c\)f(x) dx – \(\int_c^b\)f(x) dx

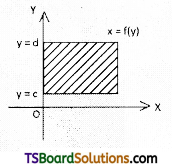
→ The area of the region bounded by the curve x = f(y) with Y – axis between the lines y = c and y = d is
(i) \(\int_c^d\)f(y) dy, if f(y) ≥ 0

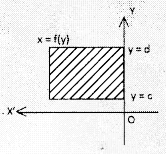
(ii) \(\int_c^d\)f(y) dy, If f(y) ≤ 0

→ Let c < e < d and If f(y) ≥ 0 on [c, e] and f(y) ≤ 0 on [e, d]. Then the area of the region bounded by the curve x = f(y) with Y-axis between the lines y = c and y =d is

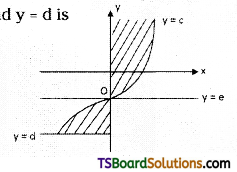
\(\int_c^e\)f(y)dy – \(\int_d^e\)f(y) dy

→ The area of the region bounded by the curves y f(x), g(x) = y between the lines x = a and x = b is
(i) \(\int_a^b\)[f(x) – g(x)]dx, if f(x) ≥ g(x)

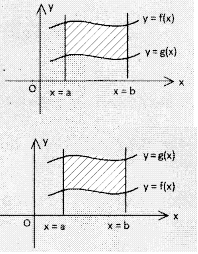
(ii) \(\int_a^b\)[g(x) – f(x)]dx; if f(x) ≤ g(x)

→ The area of the region bounded by the curves x = f(y), x = g(y) between the lines y = c and y = d is x = g(x) x = f(x)
(i) \(\int_c^d\)[f(y) – g(y)]dy, if f(y) > g(y)

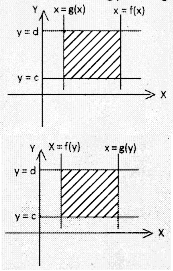
(ii) \(\int_c^d\)[g(y) – f(y)]dy, if f(y) ≤ g(x)

→ Limit As A Definite Integral
Definite Integral as a limit of summation:
Definition :Let I be a continuous function on [a, b]. Divide [a, b] into ‘n’ sub Intervals ,[x₀, x₁]……….. [x_(n-1) , x_n] where a = x₀ < x₁ < x₂ < ……………… < x_n = b
Let, ξr ∈ [x_r-1, x] for r 1, 2 , ……………… n.

→ If \({Lt}_{n \rightarrow 0} \sum_{r=1}^n\) f(ξ_r) (x_r – x_r-1) exists, then f(x) is called an integrable function on [a, b] and the limit is called definite integral of f on [a, b]. It is denoted by \(\)f(x) dx
Note:
To simplify calculation we can take all sub intervals to be equal length, h
Then h = \(\frac{b-a}{n}\) and \(\int_a^b\)f(x)dx = \({Lt}_{n \rightarrow \infty} h \sum_{r=1}^n f\left(\xi_Y\right)\)

Also we take, ξ_r = x_r-1, then ξ_r = a + (r – 1)h and hence.
\(\int_a^b\)f(x)dx = \({Lt}_{n \rightarrow \infty} h \sum_{r=1}^n\)f(a +(r – 1)h] = \({Lt}_{h \rightarrow 0} h \sum_{r=1}^h\)f[a + (r – 1)h]

If a = 0, b = 1, then \(\int_0^1\)f(x)dx = \({Lt}_{n \rightarrow \infty} \frac{1}{n} \sum_{r=1}^n f\left(\frac{r-1}{n}\right)+\left(\frac{r-1}{n}\right)={Lt}_{n \rightarrow 0} \frac{1}{n} \sum_{r=0}^{n-1} f\left(\frac{r}{n}\right)\)

If a = 0, b = p then \(\int_0^P\)f(x)dx = \({Lt}_{n \rightarrow \infty} \frac{1}{n} \sum_{r=1}^{n p}\left(\left(\frac{r-1}{n}\right)\right.\)