TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type

Question 1.
One focus of a hyperbola is located at the point (1, -3) and the corresponding directrix is the line y = 2. Find the equation of the hyperbola if its eccentricity is \(\frac{3}{2}\).
Solution:

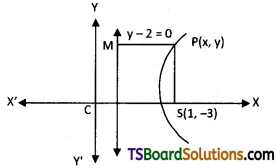
Given that focus S = (1, -3)
The equation of the directrix is y – 2 = 0
Eccentricity e = \(\frac{3}{2}\)
Let P(x, y) be any point on the hyperbola.
Since P(x, y) lies on the hyperbola then SP
\(\frac{SP}{PM}\) = e
SP = e . PM
⇒ \(\sqrt{(x-1)^2+(y+3)^2}=\frac{3}{2}\left|\frac{0 \cdot x+y \cdot 1-2}{\sqrt{0^2+1^2}}\right|\)
⇒ \(\sqrt{(x-1)^2+(y+3)^2}=\frac{3}{2}|y-2|\)
Squaring on both sides
⇒ (x – 1)² + (y + 3)² = \(\frac{9}{4}\)(y – 2)²
⇒ x² + 1 – 2x + y² + 9 + 6y = \(\frac{9}{4}\)(y² + 4 – 4y)
⇒ 4x² + 4 – 8x + 4y² + 24y + 36 = 9y² – 36y + 36
⇒ 4x² – 5y² – 8x + 60y + 4 = 0
∴ The equation of the hyperbola is 4x² – 5y² – 8x + 60y + 4 = 0.

Question 2.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola x² – 4y² = 4. [(AP) Mar. ’20, ’18, ’16; May ’16; (TS) Mar. ’19]
Solution:
Given the equation of the hyperbola is x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{4 y^2}{4}=1\)
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
Here a = 2, b = 1
It is a hyperbola.
Centre = (0, 0)

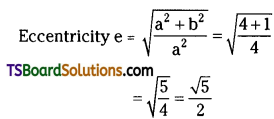
Question 3.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 16y² – 9x² = 144. [(AP) Mar. ’18, May ’17]
Solution:
Given the equation of the hyperbola is 16y² – 9x² = 144
⇒ \(\frac{y^2}{9}-\frac{x^2}{16}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=-1\)
Here a = 4, b = 3
It is a conjugate hyperbola.
Centre C = (0, 0)

Question 4.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 5x² – 4y² + 20x + 8y = 4.
Solution:
Given equation of the hyperbola is 5x² – 4y² + 20x + 8y = 4
⇒ (5x² + 20x) + (-4y² + 8y) = 4
⇒ 5(x² + 4x) – 4(y² – 2y) = 4
⇒ 5(x² + 2 . 2x + 2² – 2²) – 4(y² – 2 . 1 . y + 1² – 1²) = 4
⇒ 5((x + 2)² – 4) – 4((y – 1)² – 1) = 4
⇒ 5(x + 2)² – 20 – 4(y – 1)² + 4 = 4
⇒ 5(x + 2)² – 4(y – 1)² = 20

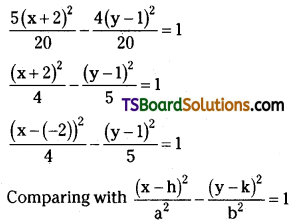
we get h = -2; k = 1; a = 2; b = √3
It is a hyperbola.
Centre C = (h, k) = (-2, 1)

⇒ x = -2 ± \(\frac{4}{3}\)
⇒ 3x = -6 ± 4
⇒ 3x = -10 or 3x = -2
⇒ 3x + 10 = 0 or 3x + 2 = 0
The length of the latus rectum

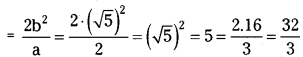
Question 5.
If the line lx + my + n = 0 is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then show that a²l² – b²m² = n². (May ’07)
Solution:

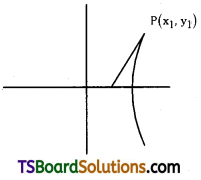
Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let the line lx + my + n = 0 ………(1)
be a tangent to the given hyperbola at P(x₁, y₁)
∴ The equation of the tangent at P(x₁, y₁) is S₁ = 0
\(\frac{\mathrm{xx}_1}{\mathrm{a}^2}-\frac{\mathrm{yy}_1}{\mathrm{~b}^2}-1=0\)
Now (1) and (2) represent the same line.

Since P(x₁, y₁) lies on line (1) then
lx₁ + my₁ + n = 0
\(l\left(\frac{-\mathrm{a}^2 l}{\mathrm{n}}\right)+\mathrm{m}\left(\frac{\mathrm{b}^2 \mathrm{~m}}{\mathrm{n}}\right)+\mathrm{n}=0\)
⇒ -a²l² + b²m² + n² = 0
⇒ n² = a²l² – b²m²
⇒ a²l² – b²m² = n²

Question 6.
Find the equations of the tangents to the hyperbola x² – 4y² = 4 which are (i) parallel (ii) perpendicular to the line x + 2y = 0. [Mar. ’19 (AP) (TS) ’15 (TS); Mar. ’14; May ’14, ’13]
Solution:
Given the equation of the hyperbola is x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
Given the equation of the straight line is x + 2y = 0
(i) The equation of the tangent parallel to the line x + 2y = 0 is x + 2y + k = 0 ………(1)
2y = -x – k
y = \(\frac{-\mathrm{x}}{2}-\frac{\mathrm{k}}{2}\)
Comparing with y = mx + c,
we get m = \(\frac{-1}{2}\), c = \(\frac{-k}{2}\)
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ \(\left(\frac{-k}{2}\right)^2=4\left(\frac{-1}{2}\right)^2-1\)
⇒ \(\frac{k^2}{4}=\frac{4}{4}-1\)
⇒ k² = 0
⇒ k = 0
Substitute the value of k in equation (1)
x + 2y + 0 = 0
⇒ x + 2y = 0
∴ No parallel tangents to x + 2y = 0.
(ii) The equation of the tangent perpendicular to line x + 2y = 0 is
2x – y + k = 0
⇒ y = 2x + k ……..(2)
Comparing with y = mx + c,
we get m = 2, c = k.
Since equation (2) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ k² = 4(2)² – (1)² = 16 – 1
⇒ k² = 15
⇒ k = ±√15
Substitute the value of k in equation (2)
y = 2x ± √15
∴ The required perpendicular tangents are y = 2x ± √15

Question 7.
Find the equations of the tangents to the hyperbola 3x² – 4y² =12 which are (i) Parallel and (ii) Perpendicular to the line y = x – 7. [(TS) Mar. ’20, May ’18, ’15; (AP) Mar. ’17, ’15, May ’16, ’15]
Solution:
Given the equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
Here a² = 4, b² = 3
Given the equation of the straight line is y = x – 7
⇒ x – y – 7 = 0
(i) The equation of the tangent parallel to the line x – y – 7 = 0 is
x – y + k = 0 ………(i)
y = x + k
Comparing with y = mx + c,
we get m = 1, c = k
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ k² = 4(1)² – 3
⇒ k² = 1
⇒ k = ±1
Substitute the value of k in equation (1)
∴ The required parallel tangents are x – y ± 1 = 0
(ii) The equation of the tangent perpendicular to the line x – y – 7 = 0 is
x + y + k = 0 …….(2)
⇒ y = -x – k
Comparing with y = mx + c,
we get m = -1, c = -k
Since equation (2) is a tangent to the given hyperbola then
c² = a²m² – b²
(-k)² = 4(-1)² – 3
⇒ k² = 4 – 3
⇒ k² = 1
⇒ k = ±1
Substitute the value of k in equation (2)
∴ The required perpendicular tangents are x + y ± 1 = 0.

Question 8.
Find the equations of the tangents drawn to the hyperbola 2x² – 3y² = 6 through (-2, 1).
Solution:
Given the equation of the hyperbola is 2x² – 3y² = 6
⇒ \(\frac{x^2}{3}-\frac{y^2}{2}=1\)
Here a² = 3, b² = 2
Let, the given point P(x, y) = (-2, 1)
Let, the equation of the tangent to the hyperbola is
y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y = mx ± \(\sqrt{3 m^2-2}\) ……..(1)
Since, this tangent passes through the point P(-2, 1)
y = m(-2) ± \(\sqrt{3 m^2-2}\)
⇒ 1 = -2m ± \(\sqrt{3 m^2-2}\)
⇒ 1 + 2m = ±\(\sqrt{3 m^2-2}\)
Squaring on both sides
(1 + 2m)² = (±\(\sqrt{3 m^2-2}\))²
⇒ 1 + 4m² + 4m = 3m² – 2
⇒ m² + 4m + 3 = 0
⇒ m² + 3m + m + 3 = 0
⇒ m(m + 3) + 1(m + 3) = 0
⇒ (m + 3)(m + 1) = 0
⇒ m + 3 = 0 (or) m + 1 = 0
⇒ m = -3 (or) m = -1
Case (i): If m = -1, then the required tangents are from (1)
y = (-1)x ± \(\sqrt{3(-1)^2-2}\)
⇒ y = -x ± \(\sqrt{3-2}\)
⇒ y = -x ± 1
⇒ x + y ± 1 = 0
Since, the point (-2, 1) does not lie on the line x + y – 1 = 0
∴ The tangent is x + y + 1 = 0
Case (ii): If m = -3, then the required tangents are from (1)
y = (-3)x ± \(\sqrt{3(-3)^2-2}\)
⇒ y = -3x ± \(\sqrt{27-2}\)
⇒ y = -3x ± √25
⇒ 3x + y ± 5 = 0
Since, the point (-2, 1) does not lie on the line 3x + y – 5 = 0
∴ The tangent is 3x + y + 5 = 0
∴ Required tangents are x + y + 1 = 0, 3x + y + 5 = 0

Question 9.
Find the equation of the hyperbola whose asymptotes are the straight lines x + 2y + 3 = 0, 3x + 4y + 5 = 0, and which passes through the point (1, -1).
Solution:
Given that the asymptotes of a hyperbola are
x + 2y + 3 = 0 ……….(1)
3x + 4y + 5 = 0 ……….(2)
Let, the given point P = (1, -1)
The equation of the hyperbola whose asymptotes are the straight lines (1) & (2) is
(x + 2y + 3) (3x + 4y + 5) + k = 0 ……….(3)
Since equation (3) passes through the point P(1, -1) then
(1 + 2(-1) + 3) (3(1) + 4(-1) + 5) + k = 0
⇒ (1 – 2 + 3) (3 – 4 + 5) + k = 0
⇒ 8 + k = 0
⇒ k = -8
Substitute the value of ‘k’ in eq. (3)
∴ The required equation of the hyperbola is (x + 2y + 3) (3x + 4y + 5) – 8 = 0
⇒ 3x² + 4xy + 5x + 6xy + 8y² + 10y + 9x + 12y + 15 – 8 = 0
⇒ 3x² + 10xy + 8y² + 14x + 22y + 7 = 0

Question 10.
Prove that the product of the perpendicular distances from any point on a hyperbola to its asymptotes is constant.
Solution:
Let S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0 be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equations of asymptotes of hyperbola S = 0 are \(\frac{x}{a}+\frac{y}{b}=0\) and \(\frac{x}{a}-\frac{y}{b}=0\)
⇒ bx + ay = 0 ……..(1)
and bx – ay = 0 ……… (2)
Let PM be the length of the perpendicular drawn from P(a sec θ, b tan θ) on line (1).
∴ PM = \(\frac{|b a \sec \theta+a b \tan \theta|}{\sqrt{a^2+b^2}}\)
Let PN be the length of the perpendicular drawn from P (a sec θ, b tan θ) on line (2).


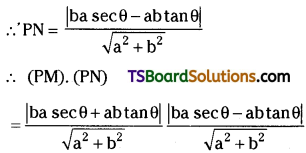
∴ The product of the perpendicular distances from any point on a hyperbola to its asymptotes is a constant.

Question 11.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 9x² – 16y² + 72x – 32y – 16 = 0. (May ’01)
Solution:
Given equation of the hyperbola is 9x² – 16y² + 72x – 32y -16 = 0
⇒ (9x² + 72x) +(-16y² – 32y) = 16
⇒ 9(x² + 8x) – 16 (y² + 2y) = 16
⇒ 9(x² + 2 . 4 . x + 4² – 4²) – 16(y² + 2 . 1 . y + 1² – 1²) = 16
⇒ 9((x + 4)² – 16) – 16((y + 1)² – 1) = 16
⇒ 9(x + 4)² – 144 – 16(y + 1)² + 16 = 16
⇒ 9(x + 4)² – 16(y + 1)² = 144

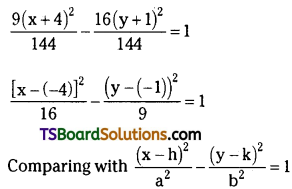
we get h = -4, k = -1, a = 4, b = 3.
It is a hyperbola.
Centre C = (h, k) = (-4, -1)

x = -4 ± \(\frac{16}{5}\)
5x = -20 + 16 or 5x = – 20 – 16
5k = -4 or 5x = -36
5x + 4 = 0 or 5x + 36 = 0
Length of latus rectum = \(\frac{2 \mathrm{~b}^2}{\mathrm{a}}=\frac{9}{2}\)

Question 12.
Find the centre, eccentricity, foci, directrices, and the length of the latus rectum of the hyperbola 4x² – 9y² – 8x – 32 = 0.
Solution:
Given equation of the hyperbola is 4x² – 9y² – 8x – 32 = 0
⇒ (4x² – 8x) + (-9y²) = 32
⇒ 4(x² – 2x) – 9y² = 32
⇒ 4((x)² – 2 . 1 . x + 1² – 1²) – 9y² = 32
⇒ 4((x – 1)² – 1) – 9y² = 32
⇒ 4(x – 1)² – 4 – 9y² = 32
⇒ 4(x – 1)² – 9y² = 36

we get a = 3, b = 2, h = 1, k = 0
It is a hyperbola.
Centre C(h, k) = (1, 0)

Question 13.
Tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) make angles θ₁, θ₂ with transverse axis of a hyperbola. Show that the point of intersection of these tangents lies on the curve 2xy = k(x² – a²), when tan θ₁ + tan θ₂ = k. [(TS) May ’19, ’16; (AP) May ’18]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let P(x₁, y₁) be the point of intersection of the tangents

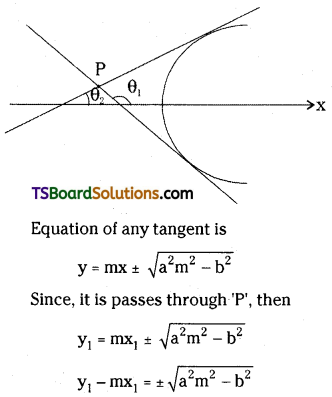
Question 14.
Prove that the point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) lies on the circle x² + y² = a² – b². [(TS) May ’17; Mar. ’16]
Solution:
Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Equation of any tangent to the hyperbola is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
Suppose P(x₁, y₁) is the point of intersection of a tangent.
Since P lies on the tangent then
y₁ = mx₁ ± \(\sqrt{a^2 m^2-b^2}\)
y₁ – mx₁ = ±\(\sqrt{a^2 m^2-b^2}\)
Squaring on both sides

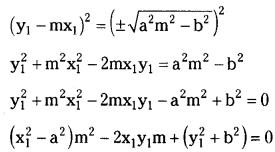
This is a quadratic equation in m given the values for m say m₁ and m₂.
The tangents are perpendicular then m₁m₂ = -1

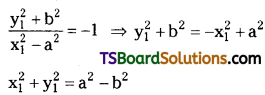
∴ P(x₁, y₁) lies on the circle x² + y² = a² – b²

Question 15.
Show that the locus of feet of the ⊥ars drawn from foci to any tangent of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is the auxiliary circle of the hyperbola.
Solution:

Let the equation of hyperbola be
S = \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\)
Let P(x₁, y₁) be the foot of the ⊥ar drawn from either of the foci to a tangent.
The equation of the tangent to the hyperbola S = 0 is
y = mx ± \(\sqrt{a^2 m^2-b^2}\) …….(1)
The equation to the ⊥ar from either focus (±ae, 0) on this tangent is
y – y₁ = \(\frac{1}{m}\)(x – x₁)


∴ P lies on x² + y² = a² which is a circle with the centre as the origin, the centre of the hyperbola.

Question 16.
Find the centre, eccentricity, foci, length of latus rectum, and equations of the directrices of the hyperbola 4(y + 3)² – 9(x – 2)² = 1. [(AP) May ’19]
Solution:
Given hyperbola is 4(y + 3)² – 9(x – 2)² = 1
⇒ \(\frac{(y+3)^2}{\frac{1}{4}}-\frac{(x-2)^2}{\frac{1}{9}}=1\)

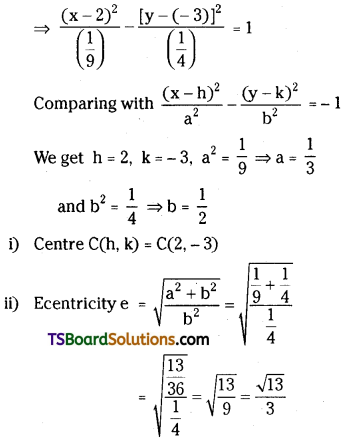
Question 17.
Show that the equation of a hyperbola in the standard form is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). [May ’02, ’99, ’98]
Solution:
Proof: Let ‘S’ be the focus, ‘e’ be the eccentricity and L = 0 be the directrix of the hyperbola.

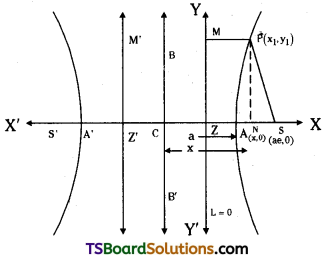
Let ‘P’ be a point on the hyperbola.
Let MZ be the projection of PS on the directrix L = 0 respectively.
Let ‘N’ be the projection of ‘P’ on SZ.
Since e > 1 we can divide SZ both internally and externally in the ratio e : 1.
Let A, A’ be the points of division of ‘SZ’ in the ratio e : 1 internally and externally respectively.
Let AA’ = 2a.
Let ‘C’ be the midpoint of AA’.
Points A, A’ lies on the hyperbola then
\(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
Now \(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{e}}{1}\)
SA = e AZ
CS – CA = e (CA – CZ) ……..(1)
and \(\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
SA’ = eZA’
CS + CA’ = e (CZ + CA’) ……….(2)
Now (1) + (2),
(CS – CA) + (CS + CA’) = e (CA – CZ) + e(CA’ + CZ)
CS – CA + CS + CA’ = e (CA – CZ + CZ + CA’)
2CS – CA + CA’ = e (CA + CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
2CS – CA + CA = e (CA + CA)
2CS = 2eCA
CS = e CA
CS = ae (∵ CA = a)
∴ The coordinates of focus S = (ae, 0)
Now (1) – (2),
(CS – CA) – (CS + CA’) = e(CA – CZ) – e(CA’ + CZ)
CS – CA – CS – CA’ = e(CA – CZ – CA’ – CZ) – CA – CA’ = e (CA – 2CZ – CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
-CA – CA = e(CA – 2CZ – CA)
– 2CA = -2e CZ
CA = e CZ
a = e CZ
CZ = \(\frac{a}{e}\)
∴ The equation of the directrix is x = \(\frac{a}{e}\).
Take CS, the principal axis of the hyperbola as the X-axis, and CY ⊥ CS as Y-axis.
Then S = (ae, 0) and the hyperbola is in the standard form.
Let P = (x, y)
Now, PM = ZN = CN – CZ = x – \(\frac{a}{e}\)
P lies on the hyperbola
\(\frac{SP}{PM}\) = e
SP = e PM
\(\sqrt{(x-a e)^2+(y-0)^2}=e\left(x-\frac{a}{e}\right)\)
Squaring on both sides
(x – ae)² + y² = \(\mathrm{e}^2\left(\mathrm{x}-\frac{\mathrm{a}}{\mathrm{e}}\right)^2\)

where b² = a²(e² – 1) > 0
The locus of ‘P’ is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
∴ The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

Question 18.
Show that the difference in focal distances of any point on the hyperbola is constant
(or)
The difference of the focal distances of any point on the hyperbola is constant i.e. if ‘P’ is a point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) with foci S and S’ then S’P – SP = 2a.
Solution:

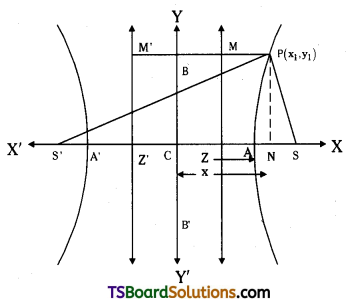
Let P (x, y) be any point on the hyperbola whose centre is the origin ‘C’.
Foci are S, S’
Directrices of ZM and Z’M’.
Let PN, PM, PM’ be the perpendiculars drawn from ‘P’ upon X-axis and the two directrices respectively.
Now, \(\frac{SP}{PM}\) = e
SP = e PM
= e ZN
= e (CN – CZ)
= e (x – \(\frac{a}{e}\))
Also = \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}=\mathrm{e}\)
S’P = ePM’
= eNZ’
= e (CN + CZ’)
= e (x + \(\frac{a}{e}\))
LHS = S’P – SP
= \(e\left(x+\frac{a}{e}\right)-e\left(x-\frac{a}{e}\right)\)
= ex + a – ex + a
= 2a (constant)
∴ S’P – SP = 2a

Question 19.
Show that the condition for straight line y = mx + c to be a tangent to the hyperbola S = 0 is c² = a²m² – b². [Mar. ’03]
Solution:
Suppose y = mx + c ………(1) is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at P is
\(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1=0\) ……..(2)
Now (1) and (2) represent the same line

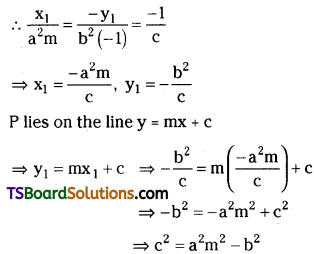
Question 20.
Show that the equation of the normal at P(θ) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b². [Mar. ’06]
Solution:
The equation of the tangent at P(θ) is \(\frac{x \sec \theta}{a}-\frac{y \tan \theta}{b}=1\)
Slope of tangent = \(\frac{\frac{-\sec \theta}{a}}{\frac{-\tan \theta}{b}}=\frac{b \sec \theta}{a \tan \theta}\)
Slope of normal = \(-\frac{a \tan \theta}{b \sec \theta}\)
∴ The equation of the normal at P is
y – b tan θ = \(-\frac{a \tan \theta}{b \sec \theta}\) (x – a sec θ)
⇒ by sec θ – b² sec θ tan θ = -ax tan θ + a² sec θ tan θ
⇒ ax tan θ + by sec θ = (a² + b²) sec θ tan θ
⇒ \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}=a^2+b^2\)

Question 21.
If the line lx + my = 1 is a normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then show that \(\frac{a^2}{l^2}-\frac{b^2}{m^2}=\left(a^2+b^2\right)^2\).
Solution:

Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let the line lx + my – 1 = 0 ……….(1) be normal to the given hyperbola at P(θ).
The equation of normal at P(θ) to the given hyperbola is
\(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b² …….(2)
Now (1) & (2) represent the same line.

which is the required condition.

Question 22.
Show that the equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents
(i) an ellipse if ‘c’ is a real constant less than 5.
(i) a hyperbola if ‘c’ is any real constant between 5 and 9.
(iii) Show that each ellipse in (a) and each hyperbola in (b) has foci at the two points (±2, 0), independent of the value ‘c’.
Solution:
(i) Given equation is \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\)
This equation represents an ellipse if
9 – c > 0 and 5 – c > 0
9 > c and 5 > c
c < 9 and c < 5
∴ c < 5
(ii) Given equation is \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\)
This equation represents a hyperbola if
9 – c > 0 and 5 – c < 0
9 > 0 and 5 < c
c < 9 and c > 5
∴ 5 < c < 9
(iii) In case (i): a² = 9 – c, b² = 5 – c
Now, a² – b² = (9 – c) – (5 – c)
⇒ a² – a²(1 – e²) = 9 – c – 5 + c
⇒ a²e² = 9 – 5
⇒ a²e² = 4
⇒ ae = 2
∴ foci are (±ae, 0) = (±2, 0)
In case (ii): a² = 9 – c, b² = c – 5
Now, a² + b² = 9 – c + c – 5
⇒ a² + a²(e² – 1) = 9 – 5
⇒ a²e² = 4
⇒ ae = 2
∴ foci are (±ae, 0) = (±2, 0)
These are independent of the value of ‘c’

Question 23.
A circle cuts the rectangular hyperbola xy = 1, in the points (x₁, y₁), r = 1, 2, 3, 4. Prove that x₁x₂x₃x₄ = y₁y₂y₃y₄ = 1.
Solution:
Let the circle be x² + y² = a²
Since (t, \(\frac{1}{2}\)) (t ≠ 0) lies on xy = 1
The points of intersection of the circle and the hyperbola are given by
\(t^2+\frac{1}{t^2}=a^2\)
⇒ t⁴ – a²t² + 1 = 0
⇒ t⁴ + 0 . t³ – a²t + 0 . t + 1 = 0
If t₁, t₂, t₃, t₄ are the roots of the above biquadratic, then
product of the roots t₁t₂t₃t₄ = \(\frac{1}{1}\) = 1