TS Inter 1st Year

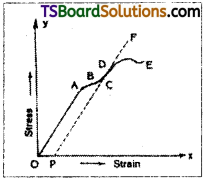
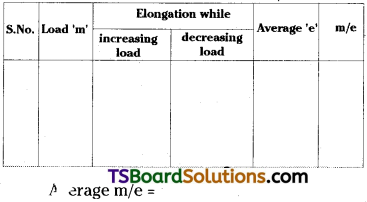
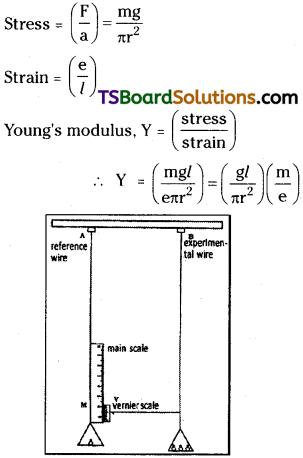
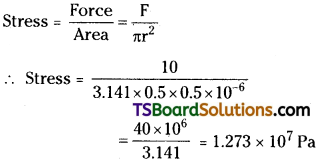
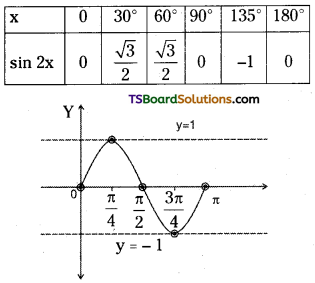
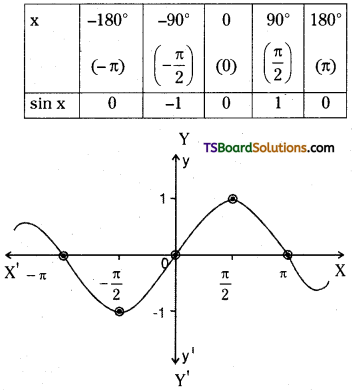
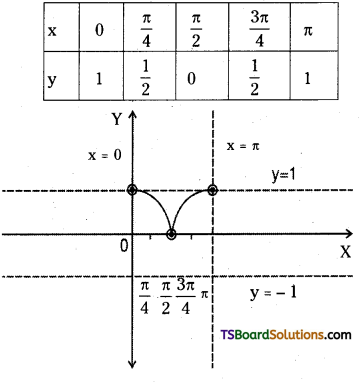
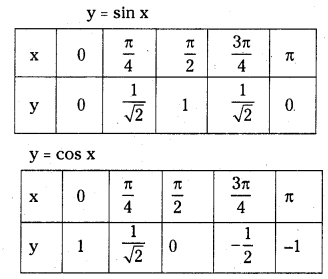
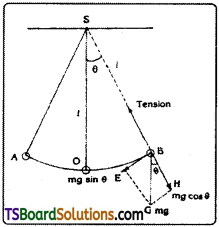
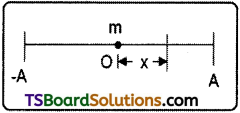
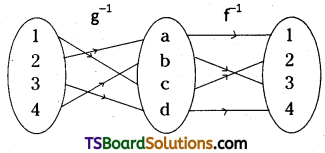
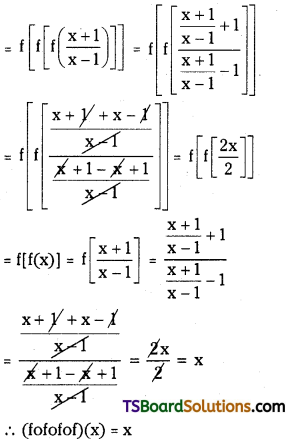
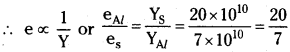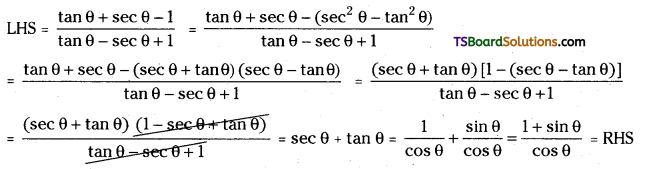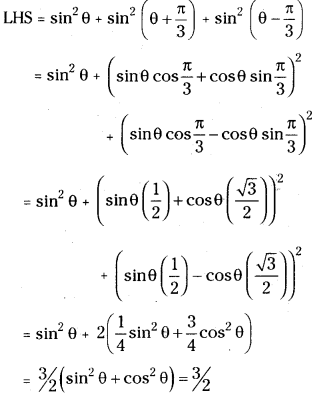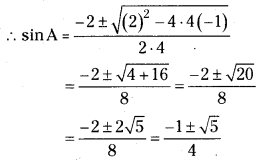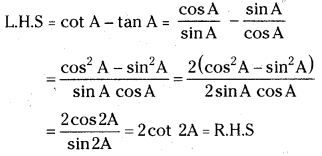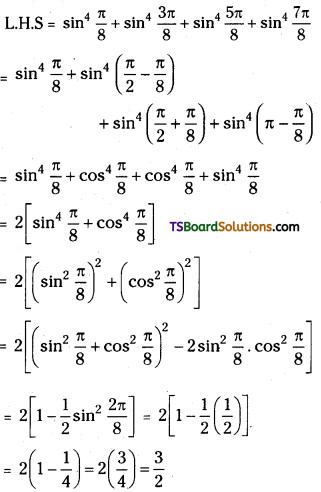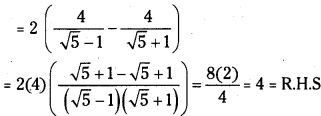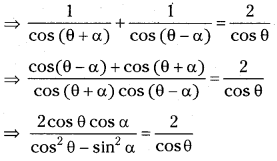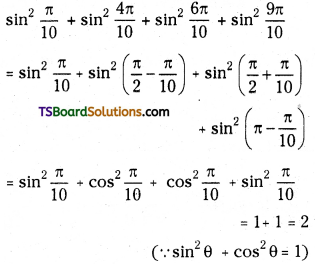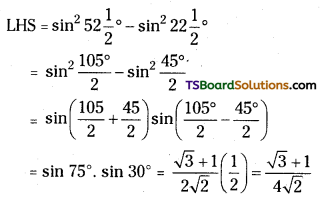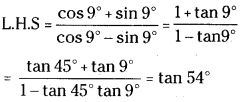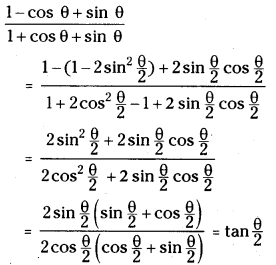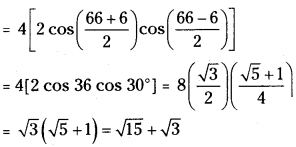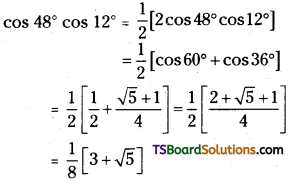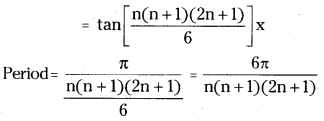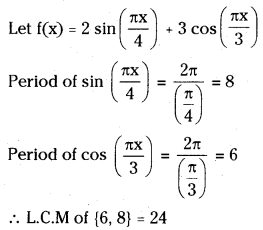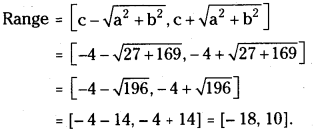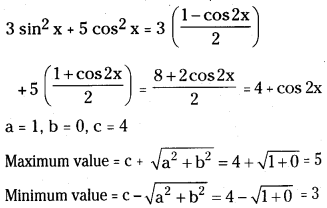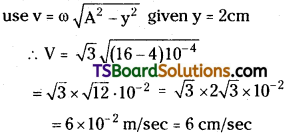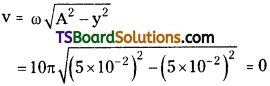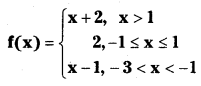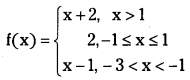Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Long Answer Type

Question 1.
If A, B, Care the angles of a triangle, prove that sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C.
Answer:
Given A + B + C = 180°
LHS = sin 2A + sin 2B + sin 2C
= 2sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + sin 2C
= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (180° – C) cos (A – B) + sin 2C
= 2 sin C cos (A – B) + 2 sin C cos C
= 2 sin C [cos (A – B) + cos C]
= 2 sin C [cos (A – B) + cos [180° – (A + B)]
= 2 sin C[cos (A – B) – cos (A + B)]
= 2 sin C (2 sin A sin B)
= 4 sin A sin B sin C = RHS

Question 2.
If A, B, C are angles of a triangle, prove that cos 2A + cos 2B + cos 2C = – 4cos A cos B cos C – 1.
Sol. Given A + B + C = 180°
LHS = cos 2A + cos 2B + cos 2C
= 2cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + cos 2C
= 2 cos (180° – C) cos (A – B) + cos 2C
= – 2 cos C cos (A – B) + 2 cos²C – 1
= – 2 cos C [cos (A – B) – cos C] – 1
= – 2 cos C [cos (A – B) – cos [180° – (A + B)]] -1
= -2 cos C [cos (A – B) + cos (A + B)] – 1
= – 2cos C (2 cos A cos B) – 1
= – 4 cos A cos B cos C – 1 = RHS

Question 3.
If A + B + C = \(\frac{3 \pi}{2}\), prove that cos 2A + cos 2B + cos 2C = 1 – 4sinA.sinB.sinC. [Mar. ’13, ’01]
Answer:
Given A + B + C = \(\frac{3 \pi}{2}\)
L.H.S. = cos 2A + cos 2B + cos 2C
= 2 cos (A + B) cos (A – B) + cos 2C
= -2 sin C cos (A – B) + 1 – 2 sin²C
[A + B = \(\frac{3 \pi}{2}\) ⇒ cos (A + B) = – sin C]
= 1 – 2 sin C [cos (A – B) + sin C]
= 1 – 2 sin C [cos (A – B) – cos (A + B)]
= 1 – 2 sin C (2 sin A sin B)
= 1 – 4 sin A sin B sin C = RHS
∴ cos 2A + cos 2B + cos 2C = 1 – 4 sin A sin B sin C

Question 4.
If A + B + C = \(\frac{3 \pi}{2}\), prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A. sin B sin C.
Answer:
Given A + B + C = 90°
LHS = cos 2A + cos 2B + cos 2C
= 2 cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + cos 2C
= 2 cos (90° – C) cos (A – B) + cos 2C
= 2 sin C cos (A – B) + 1 – 2 sin²C
= 1 + 2 sin C [cos (A – B) – sin C]
= 1 + 2 sin C [cos (A – B) – sin [90° – (A + B)]]
= 1 + 2 sin C [cos (A – B) – cos (A + B)]
= 1 + 2 sin C (2 sin A sin B)
= 1 + 4 sin A sin B sin C = RHS.

Question 5.
If A, B, C are angles in a triangle, then prove that cos A + cos B + cos C = 1 + 4 sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) sin \(\frac{C}{2}\). [Mar. ’18(AP); May ’09]
Answer:
Given A + B + C = 180°
L.H.S = cos A + cos B + cos C

Question 6.
If A, B, C are angles in a triangle, then prove that cos A + cos B – cos C = -1 + 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\). [Mar. ’19(TS); May ’06]
Answer:
Given A + B + C = 180°
L.H.S = cos A + cos B – cos C

Question 7.
If A, B, C are angles in a triangle, then prove that sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) – sin²\(\frac{C}{2}\) = 1 – 2cos \(\frac{A}{2}\). cos \(\frac{B}{2}\). sin \(\frac{C}{2}\). [Mar. ’16(AP), ’06; May ’15(TS), ’11; B.P]
Answer:
Given A + B + C = 180°
L.H.S = sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) – sin²\(\frac{C}{2}\)

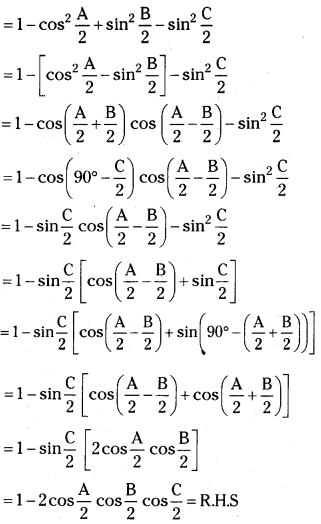
Question 8.
If A + B + C = π, then prove that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\) = 2(1 + sin \(\frac{A}{2}\). sin \(\frac{B}{2}\). sin \(\frac{C}{2}\)). [Mar. ’12, Mar. ’15(AP & TS)]
Answer:
Given A + B + C = π
L.H.S = cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\)

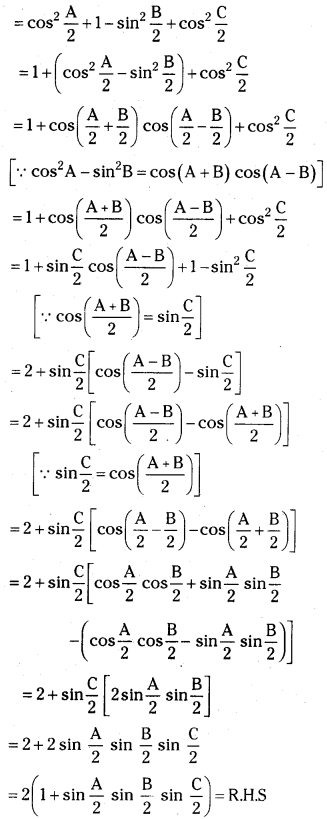
Question 9.
If A+ B + C = π, then prove that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\) = 2 cos\(\frac{A}{2}\) cos\(\frac{B}{2}\) sin\(\frac{C}{2}\). [May ’10]
Answer:
Given A + B + C = π
L.H.S = cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\)

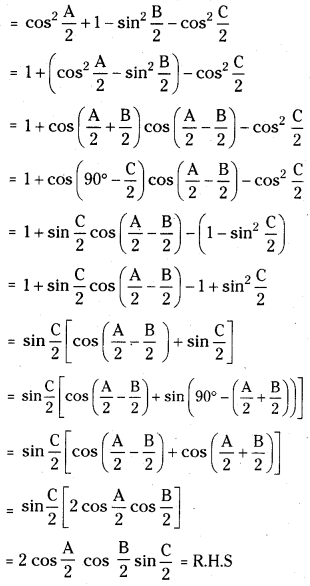
Question 10.
If A, B, C are the angles in a triangle, then prove that sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) + sin \(\frac{C}{2}\) = 1 + 4sin\(\left(\frac{\pi-A}{4}\right)\)sin\(\left(\frac{\pi-B}{4}\right)\)sin\(\left(\frac{\pi-C}{4}\right)\). [Mar. ’14, ’11, ’96]
Answer:
Given A + B + C = 180°

Question 11.
In triangle ABC, prove that cos\(\frac{1}{2}\) + cos\(\frac{B}{2}\) + cos\(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\). [Mar ’14, ’13, ’07, ’97; Mar. ’10, ’07, ’05, ’03]
Answer:
In ΔABC, A + B + C = 180°

∴ cos\(\frac{1}{2}\) + cos\(\frac{B}{2}\) + cos\(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\)

Some More Maths 1A Ratios up to Transformations Important Questions

Question 1.
If sin θ = \(\frac{4}{5}\) and θ is not in the first quadrant, find the value of cos θ.
Answer:
Given sin θ = \(\frac{4}{5}\)
Since θ is not in the first quadrant and sin θ > 0 we have 90° < θ < 180°
∴ cos θ = \(\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{16}{25}}=\frac{-3}{5}\)

Question 2.
If cosec θ + cot θ = find cos θ and determine the quadrant In which θ lies.
Answer:
We have cosec² θ – cot² θ = 1
(cosec θ + cot θ) (cosec θ – cot θ) = 1
= cosec θ – cot θ = \(\frac{1}{{cosec} \theta+\cot \theta}\) = 3
= cosec θ + cot θ = 3 …………………… (1)

Given cosec θ + cot θ = \(\frac{1}{3}\) …………………. (2)
Solving(1)& (2)
∴ 2cosec θ = 3 + \(\frac{1}{3}=\frac{10}{3}\)
⇒ cosec θ = \(\frac{5}{4}\)
⇒ sin θ = \(\frac{3}{5}\)

Also 2 cot θ = \(\frac{1}{3}\) – 3 = \(\frac{-8}{3}\)
⇒ cot θ = \(\frac{-4}{3}\)
⇒ tan θ = \(\frac{-3}{4}\)

cos θ = cot θ.sinθ = \(\left(-\frac{4}{3}\right)\left(\frac{3}{5}\right)=-\frac{4}{5}\)
sin θ is positive and cos θ is a negative
⇒ θ lies in II quadrant.

Question 3.
If sec θ + tan θ = 5, find the quadrant in which θ lies and find the value of sin θ.
Answer:
We have sec²θ – tan²θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ sec θ – tan θ = \(\frac{1}{5}\) ………….. (1)
Also given sec θ + tan θ = 5 ………………………. (2)

Adding (1) and (2), 2sec θ = 5 + \(\frac{1}{5}\) = \(\frac{26}{5}\)

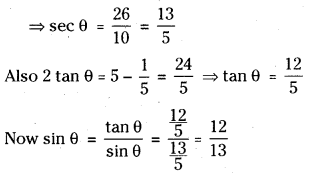
tan θ is +ve, sec θ is + ve
⇒ θ lies in first quadrant

Question 4.
Prove that cot\(\frac{\pi}{16}\).cot\(\frac{2 \pi}{16}\).cot\(\frac{3 \pi}{16}\)………………cot\(\frac{7 \pi}{16}\) = 1.
Answer:

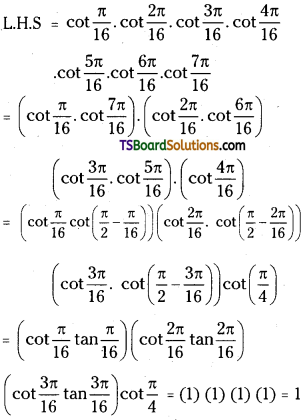
Question 5.
If a cos θ – b sin θ = c, then show that a sin θ + b cos θ = ± \(\sqrt{\mathbf{a}^2+\mathbf{b}^2-\mathbf{c}^2}\).
Answer:
Given a cos θ – b sin θ
= c and let asin θ + b cos θ = x
squaring and adding, we get
(a cos θ – b sin θ)² + (a sin θ + b cos θ) = c² + x²
a² (cos² θ + sin² θ)² + b² (sin² θ + cos² θ) = c² + x²
⇒ a² + b² = c² + x² ⇒ x² = a² + b² – c²
⇒ x = ±\(\sqrt{\mathbf{a}^2+\mathbf{b}^2-\mathbf{c}^2}\)

Question 6.
If 3 sin A + 5 cos A = 5, then show that 5 sin A – 3 cos A = ± 3.
Answer:
Given that 3 sin A + 5 cos A = 5
Let 5 sin A – 3 cos A = x
Squaring and adding, we get
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)²
⇒ 9 (sin²A + cos²A) + 25 (cos²A + sin²A) = 25 + x²
⇒ 34 = 25 + x²
⇒ x² = 9
⇒ x = ± 3
∴ 5 sin A – 3 cos A = ± 3

Question 7.
If tan 20° = p, Prove that \(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}\).
Answer:
Given that tan 20° = p, then

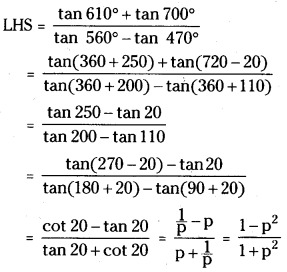
Question 8.
Evaluate sin²82\(\frac{1}{2}^{circ}\) – sin² 22\(\frac{1}{2}^{circ}\).
Answer:
sin²82\(\frac{1}{2}^{circ}\) – sin² 22\(\frac{1}{2}^{circ}\)
= sin[82\(\frac{1}{2}^{circ}\) + 22\(\frac{1}{2}^{circ}\)] + sin[82\(\frac{1}{2}^{circ}\) – 22\(\frac{1}{2}^{circ}\)]
= sin 105°. sin 60°
[∵ Use sin²A – sin²B] = sin(A +B) sin (A – B)
= sin 60° sin(60° + 45°)= sin 60°
[= sin 60° cos 45° + cos 60° sin 45°]
\(\frac{\sqrt{3}}{2}\left[\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}}\right]=\frac{\sqrt{3}(\sqrt{3}+1)}{4 \sqrt{2}}=\frac{3+\sqrt{3}}{4 \sqrt{2}}\)

Question 9.
Evaluate cos²112\(\frac{1}{2}^{circ}\) – sin²52\(\frac{1}{2}^{circ}\).
Answer:
Use cos²A – sin²B = cos(A + B) cos (A – B)
= cos²112\(\frac{1}{2}^{circ}\) – sin²52\(\frac{1}{2}^{circ}\)
= cos [112\(\frac{1}{2}^{circ}\) + 52\(\frac{1}{2}^{circ}\)] cos[112\(\frac{1}{2}^{circ}\) – 52\(\frac{1}{2}^{circ}\)]
= cos 165° . cos 60
= cos 60° cos(180 – 15) = – cos 60°. cos 15°
= \(-\frac{1}{2}\left[\frac{\sqrt{3}+1}{2 \sqrt{2}}\right]=-\frac{\sqrt{3}+1}{4 \sqrt{2}}\)

Question 10.
Prove that tan 72° = tan 18° + 2 tan 54°.
Answer:
We have cot A – tan A = \(\frac{1}{\tan A}\) – tan A
⇒ \(\frac{1-\tan ^2 \mathrm{~A}}{\tan \mathrm{A}}=\frac{2\left(1-\tan ^2 \mathrm{~A}\right)}{2 \tan \mathrm{A}}=\frac{2}{\tan 2 \mathrm{~A}}\) = 2 cot 2A
∴ cot A – tan A = 2 cot 2A
⇒ cot A = tan A + 2 cot 2A

Take A = 18°, then cot 18°
= tan 18° + 2 cot 36°
⇒ cot (90 – 72)
= tan 18° + 2 cot (90 – 54)
⇒ tan 72° = tan 18° + 2 tan 54°

Question 11.
Find the value of tan 56° – tan 11° -tan 56°. tan 11°.
Answer:
Consider 56° – 11° = 45°
⇒ tan (56° -11°) = tan 45° = 1
⇒ \(\frac{\tan 56^{\circ}-\tan 11^{\circ}}{1+\tan 56^{\circ} \tan 11^{\circ}}\) = 1
⇒ tan 56° – tan 110 – tan 56° tan 11° = 1.

Question 12.
If tan θ = \(\frac{\cos 11^{\circ}+\sin 11^{\circ}}{\cos 11^{\circ}-\sin 11^{\circ}}\) and θ is in the third quadrant, find θ.
Answer:
Given tan θ = \(\frac{\cos 11^{\circ}+\sin 11^{\circ}}{\cos 11^{\circ}-\sin 11^{\circ}}\)
= \(\frac{1+\tan 11^{\circ}}{1-\tan 11^{\circ}}\) = tan(45 + 11) = tan 56°
Since θ is in the third quadrant,
tan 56° = tan (180 + 56) = tan 236°
∴ θ = 236°

Question 13.
Show that cos 35° + cos 85° + cos 155° = 0.
Answer:
cos 35° + cos 85° + cos 155°
= cos 35° + 2cos\(\left(\frac{85+155}{2}\right)\) cos\(\left(\frac{85-155}{2}\right)\)
= cos 35° + 2 cos 120° cos (-35°)
= cos 35° – cos 35° = 0

Question 14.
Simplify cos 100°. cos 40° + sin 100°. sin 40°.
Answer:
Use cos A. cos B + sin A sin B = cos (A – B)
∴ cos 100°. cos 40° + sin 100° . sin 40°
= cos (100° – 40°) = cos 60° = \(\frac{1}{2}\)

Question 15.
Prove that sin 750°. cos 480° + cos 120°. cos 60° =\(\frac{1}{2}\)
Answer:
L.H.S = sin 750°. cos 480° + cos 120°. cos 60°
= sin [2.(360) + 30] cos [360 +120] + cos 120 cos 60
= sin 30 cos 120 + cos 120 cos 60
= \(\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{-1}{2}\)

Question 16.
Prove that \(\frac{1}{\cos 290^{\circ}}+\frac{1}{\sqrt{3} \sin 250^{\circ}}=\frac{4}{\sqrt{3}}\).
Answer:

Question 17.
Prove that √3 cosec 20° – sec 20° = 4.
Answer:
L.H.S = √3 cosec 20° – sec 20°

Question 18.
Find the period of cos (3x + 5) + 7.
Answer:
Let f(x) = cos (3x + 5) + 7
We have period of cos x is 2π ∀ x ∈ R.
∴ f (x) is periodic and period of f is \(\frac{2 \pi}{|3|}\)
\(\frac{2 \pi}{3}\) (or) f(x + p) = f(x)
⇒ cos (3x + 3p + 5) + 7 = cos (2π + 3x + 5) + 7
∴ 3x + 3p + 5 = 2π + 3x + 5
⇒ 3x = 2π
⇒ x = \(\frac{2 \pi}{3}\)

Question 19.
Find the maximum and minimum values of f(x) = 3 sin x – 4 cos x.
Answer:
Given f(x) = 3 sin x – 4 cos x
Comparing with a cos x + b sin x + c
We get a = – 4, b = 3, c = 0
Maximum value = c + \(\sqrt{a^2+b^2}\)
= 0 + \(\sqrt{16+9}=\sqrt{25}\) = 5
Minimum value = c – \(\sqrt{a^2+b^2}\)
= 0 – \(\sqrt{16+9}=\sqrt{25}\) = -5

Question 20.
Find the range of 7 cos x – 24 sin x + 5.
Answer:
Let f(x) = 7 cos x – 24 sin x + 5
a = – 24, b = 7, c = 5

Range = [c – \(\sqrt{a^2+b^2}\), c + \(\sqrt{a^2+b^2}\)]
=[5 – \(\sqrt{576+49}\), 5 + \(\sqrt{576+49}\)]
= [5 – \(\sqrt{625}\), 5 + \(\sqrt{625}\)]
= [5 – 25, 5 + 25] = [-20, 30]

Question 21.
If A – B = \(\frac{3 \pi}{4}\), then show that (1 – tan A)(1 + tan B) = 2.
Answer:
A – B = \(\frac{3 \pi}{4}\)
⇒ tan(A – B) = tan\(\frac{3 \pi}{4}\)
⇒ \(\frac{\tan A-\tan B}{1+\tan A \tan B}\) = -1
⇒ tan A – tan B = – 1 – tan A tan B
⇒ tan A – tan B + tan A tan B = -1
⇒ – tan A + tan B – tan A tan B = 1
⇒ (1 – tan A) + tan B (1 – tan A) = 1 + 1 = 2
⇒ (1 – tan A) (1 + tan B) = 2

Question 22.
If A, B, C are the angles of a triangle and if none of them is equal to \(\frac{\pi}{2}\) then prove that cot A cot B + cot B cot C + cot C cot A = 1.
Answer:
Given A + B + C = π, A + B = π – C
⇒ cot (A + B) = cot (π – C)
⇒ \(\frac{\cot A+\cot B-1}{\cot B+\cot A}\) = – cot C
⇒ cot A cot B – 1 = – cot B cot C – cot C cot A
⇒ cot A cot B + cot B cot C + cot C cot A = 1

Question 23.
If A + B + C = \(\frac{\pi}{2}\) and if none of A, B, C is n an odd multiple of \(\frac{\pi}{2}\), then prove that tan A tan B + tan B tan C + tan C tan A = 1.
Answer:
Given A + B + C = \(\frac{\pi}{2}\)
⇒ A + B = \(\frac{\pi}{2}\) – C
⇒ tan(A + B) = tan(\(\frac{\pi}{2}\) – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = cot C = \(\frac{1}{\tan C}\)
⇒ tan A tan C + tan B tan C = 1 – tan A tan B
⇒ tan A tan B + tan B tan C + tan C tan A = 1

Question 24.
Prove that cos A. cos(\(\frac{\pi}{2}\) + A) cos(\(\frac{\pi}{2}\) -A) = \(\frac{1}{4}\)cos 3A and hence deduce that cos\(\frac{\pi}{2}\)cos\(\frac{2 \pi}{2}\)cos\(\frac{3 \pi}{2}\).cos\(\frac{4 \pi}{2}\) = \(\frac{1}{16}\)
Answer:
L.H.S = cos A.cos(60 + A) cos(60 – A)
= cos A (cos² 60 – sin² A)

Question 25.
Show that cos⁴\(\frac{\pi}{8}\) + cos⁴\(\frac{3 \pi}{8}\) + ⁴\(\frac{5 \pi}{8}\) + cos⁴\(\frac{7 \pi}{8}\) = \(\frac{3}{2}\)
Answer:

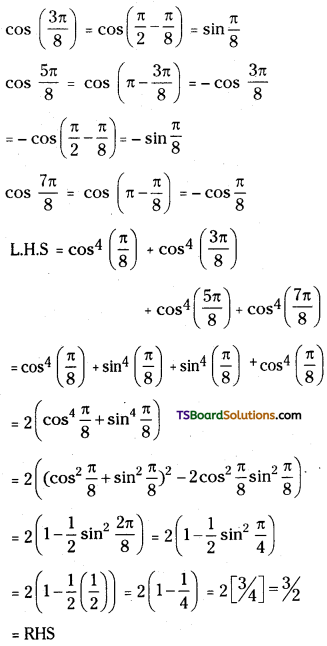
Question 26.
Prove that tan α = \(\frac{\sin 2 \alpha}{1+\cos 2 \alpha}\) and hence deduce the values of tan 15° and tan 22\(\frac{1}{2}^{\circ}\)
Answer:

Question 27.
If cos θ > θ, tan θ + sin θ = m and tan θ – sin θ = n then show that m² – n² = 4\(\sqrt{mn}\)
Answer:
Given that m = tan θ + sin θ, n = tan θ – sin θ
m + n = 2 tan θ, m – n = 2 sin θ and (m + n) (m -n)

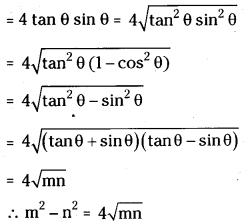
Question 28.
If 0° < A, B < 90°, cos A = \(\frac{5}{13}\) and sin B = \(\frac{4}{5}\), then find the value of sin(A+ B).
Answer:
0° < A, B < 90°, cos A = \(\frac{5}{13}\) ⇒ sin A = \(\frac{12}{13}\)
0° < A, B < 90°, sin B = \(\frac{4}{5}\) ⇒ cos B = \(\frac{3}{5}\)
∴ sin(A + B) = sin A cos B + cos A sin B
= \(\frac{12}{13} \cdot \frac{3}{5}+\frac{5}{13} \cdot \frac{4}{5}=\frac{36}{65}+\frac{20}{65}=\frac{56}{65}\)

Question 30.
If sin A = \(\frac{12}{13}\), cos B = \(\frac{3}{5}\) and neither A nor B is in the first quadrant, then find the quadrant in which A + B lies.
Answer:
Given sin A = \(\frac{12}{13}\)
A is not in the first quadrant then A lies in the Q₂.
∴ cos A = \(\frac{-5}{13}\) ⇒ cos B = \(\frac{3}{5}\)

B is not in the Q₁ then B lies in the Q₄.
∴ sin B = \(\frac{-4}{5}\)
Now sin (A + B) = sin A cos B + cos A sin B
= \(\left(\frac{12}{13}\right)\left(\frac{3}{5}\right)+\left(\frac{-5}{13}\right)\left(\frac{-4}{5}\right)=\frac{36}{65}+\frac{20}{65}=\frac{56}{65}\)

cos (A + B) = cos A . cos B – sin A sin B
= \(\left(\frac{-5}{13}\right)\left(\frac{3}{5}\right)-\left(\frac{12}{13}\right)\left(\frac{-4}{5}\right)=\frac{-15}{65}+\frac{48}{65}=\frac{33}{65}\)
sin (A + B) > 0 & cos (A + B) > 0 then A + B lies in the first quadrant.

Question 31.
Let ABC be a triangle such that cot A + cot B + cot C = √3 then prove that ABC is an equilateral triangle.
Answer:
Given that A + B + C = 180°
We have Σ cot A cot B = 1 …………………(1)
Σ(cot A – cot B)²
= Σ(cot² A + cos² B – 2 cot A cot B)
= 2 cot² A + 2 cot² B + 2 cot² C – 2 cot A cot B – 2 cot B cot C – 2 cot C cot A
= 2 [cot A + cot B + cot C]² – 6 [cot A cot B + cot B cot C + cot C cot A]
= 2 [(√3 )² ] – 6(1) = 6 – 6 = 0
∴ Σ (cot A – cot B)² = 0
⇒ cot A = cot B = cot C
⇒ cot A = cot B = cot C = \(\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}\) (∵ cot A + cot B + cot C = 73 )
⇒ A = B = C = 60°
⇒ ΔABC is an equilateral triangle.

Question 32.
Simplify tan[\(\frac{\pi}{4}\) + θ]. tan[\(\frac{\pi}{4}\) – θ]
Answer:

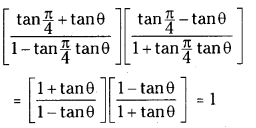
Question 33.
Simplify tan 75° + cot 75°.
Answer:
(2 + √3)(2 – √3) = 4

Question 34.
Evaluate sin²\(\left[\frac{\pi}{8}+\frac{A}{2}\right]\) – sin²\(\left[\frac{\pi}{8}-\frac{A}{2}\right]\)
Answer:
[∵ sin²A – sin²B = sin (A + B)sin(A – B)

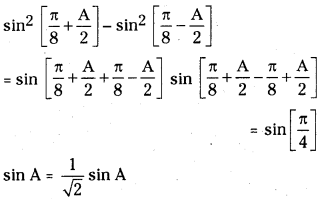
Question 35.
If A + B, A are acute angles such that sin (A + B) = \(\frac{24}{25}\) and tan A = \(\frac{3}{4}\), then find the value of cos B.
Answer:
A + B, A are acute angles ⇒ B is also acute.
Given sin (A + B) = \(\frac{24}{25}\), we have
cos (A + B) = \(\frac{7}{25}\) and tan (A + B) = \(\frac{24}{7}\)
Also tan A = \(\frac{3}{4}\)
We have tan(A + B) = \(\frac{24}{7}\)

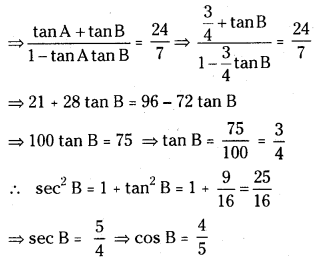
Question 36.
In a ΔABC, A is obtuse. If sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\) Bien show that sin C = \(\frac{16}{65}\).
Answer:
Given, A + B + C = 180°
⇒ A + B = 180° – C
∴ sin (A + B) = sin (180° – C) = sin C .. (1)
∴ A is obtuse angle and A lies in II quadrant.
sin A = \(\frac{3}{5}\) ⇒ cos A = –\(\frac{4}{5}\)
Also sin B = \(\frac{5}{13}\) ⇒ cos B = \(\frac{12}{13}\)
∴ sin C = sin (A + B) = sin A cos B + cos A
sin B = \(\frac{3}{5} \cdot \frac{12}{13}+\left(-\frac{4}{5}\right) \cdot \frac{5}{13}=\frac{36}{65}-\frac{20}{65}=\frac{16}{65}\)

Question 37.
Find the value of sin 22\(\frac{1}{2}^{\circ}\).
Answer:
22\(\frac{1}{2}^{\circ}\) lies in first quadrant and hence all ratios are positive.

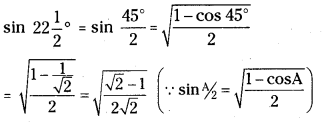
Question 38.
If cos θ = \(\frac{-5}{13}\) and \(\frac{\pi}{2}\) < θ < π find the value of sin 2θ.
Answer:
\(\frac{\pi}{2}\) < θ < π ⇒ sin θ > 0 and cos θ = \(\frac{-5}{13}\)
⇒ sin θ = \(\frac{12}{13}\)
∴ sin 2θ = 2sin θ cos θ

Question 39.
For what values of x in the first quadrant \(\frac{2 \tan x}{1-\tan ^2 x}\) is positive?
Answer:
\(\frac{2 \tan x}{1-\tan ^2 x}\) > 0 ⇒ tan 2x > 0 ⇒ 0 < 2x < \(\frac{\pi}{2}\)
⇒ 0 < x < \(\frac{\pi}{4}\)

Question 40.
If cos θ = -3/5 and π < θ < \(\frac{3 \pi}{2}\) find the value of tan \(\frac{\theta}{2}\).
Answer:

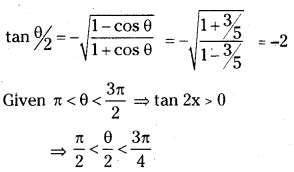
∴ \(\frac{\theta}{2}\) lies in second quadrant.

Question 41.
If 3A is not an odd multiple of \(\frac{\pi}{2}\), prove that tan A tan (60 + A) tan (60 – A) = tan 3A and hence find the value of tan 6° tan 42° tan 66° tan 78°.
Answer:
L.H.S = tan A tan (60 + A) tan (60 – A)

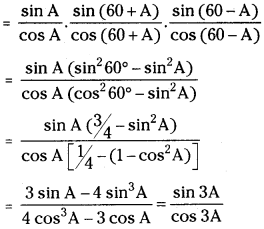
Take A = 6° in above we get tan 6° tan 66° tan 54° = tan 18°
take A = 18° in above result tan 18° tan 78° tan 42° = tan 54°
tan 6° tan 18° tan 42° tan 54° tan 66° tan 78 = tan 18° tan 54°
⇒ tan 6° tan 42° tan 66° tan 78° = 1

Question 42.
If a, b, c are non-zero real numbers and α, β are solutions of the equation a cos θ + b sin θ = c then show that
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) sin α .sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Answer:
Given a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ a² cos² θ = c² – 2bc sin θ + b² sin² θ
⇒ a² (1 – sin²θ) = c² – 2bc sin θ + b² sin² θ
⇒ (b² + a²) sin² θ – 2bc sin θ + (c² – a²) = 0
This is a quadratic equation in sin θ and suppose sin α, sin β are roots of the equation.
(∵ Given α, β are solutions of the equation)
∴ sin α + sin β = \(\frac{2 b c}{a^2+b^2}\) and sin α .sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

Question 43.
Prove that \(\frac{\sin \theta+\sin 2 \theta}{1+\cos \theta+\cos 2 \theta}\) = tan θ
Answer:

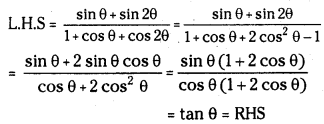
Question 44.
Prove that tan 3A tan 2A tan A = tan 3A – tan 2A – tan A.
Answer:
We have 3A = 2A + A
∴ tan 3A = tan (2A + A) = \(\frac{\tan 2 \mathrm{~A}+\tan \mathrm{A}}{1-\tan 2 \mathrm{~A} \tan \mathrm{A}}\)
⇒ tan 2A + tan A = tan 3A (1 – tan 2A tan A)
⇒ tan A tan 2A tan 3A = tan 3A – tan 2A – tan A

Question 45.
Express cos⁶A + sin⁶A in terms of sin 2A.
Answer:
cos⁶A + sin⁶A = (cos²A)³ + (sin²A)³
= (cos²A + sin²A)² – 3 cos² A sin² A (cos² A + sin² A)
= 1 – 3 cos²A sin²A ……………….(1)
= 1 – \(\frac{3}{4}\) (4 cos² A sin² A) = 1 – \(\frac{3}{4}\) sin²2A

Question 46.
If sin α = \(\frac{3}{5}\), where \(\frac{\pi}{2}\) < α < π, evaluate cos 3α.
Answer:
Given sin α = \(\frac{3}{5}\)
\(\frac{\pi}{2}\) < α < π ⇒ a lies in the Q₂

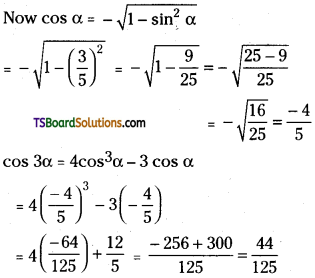
Question 47.
In a ΔABC, if tan\(\frac{A}{2}=\frac{5}{6}\) and tan \(\frac{B}{2}=\frac{20}{37}\), then show that tan \(\frac{A}{2}=\frac{2}{5}\).
Answer:
In ΔABC, A + B + C = 180°

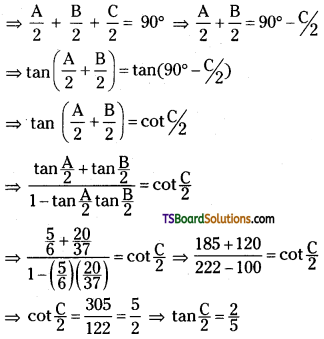
Question 48.
If cos θ = \(\frac{5}{13}\) and 270° < θ < 360°, evaluate sin\(\left(\frac{\theta}{2}\right)\) and cos\(\left(\frac{\theta}{2}\right)\)
Answer:
Given cos θ = \(\frac{5}{13}\), where 270° < θ < 360° ⇒ 135° < \(\frac{\theta}{2}\) < 180° ⇒ \(\frac{\theta}{2}\) lies in second quadrant since cos θ = \(\frac{5}{13}\)

Question 49.
Prove that cos\(\frac{2 \pi}{7}\) cos\(\frac{4 \pi}{7}\) cos\(\frac{8 \pi}{7}=\frac{1}{8}\)
Answer:
Let \(\frac{2 \pi}{7}\) = α and x = cos α cos 2α cos 4α and y = sin α sin 2α sin 4α(suppose)

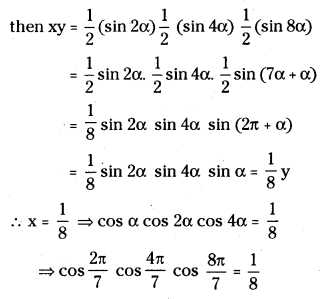
Question 50.
Prove that cos\(\frac{\pi}{11}\) cos\(\frac{2 \pi}{11}\) cos\(\frac{3 \pi}{11}\) cos\(\frac{4 \pi}{7}\) cos\(\frac{5 \pi}{7}=\frac{1}{32}\)
Answer:
Let \(\frac{\pi}{11}\) = α and x = cos α cos 2α cos 3α cos 4α cos 5α and y = sin α sin 2α sin 3α sin 4α sin 5α
xy = \(\frac{1}{2}\)(sin2α) \(\frac{1}{2}\)sin(4α) \(\frac{1}{2}\)sin(6α) \(\frac{1}{2}\)sin(8α) \(\frac{1}{2}\)sin(10α)
= \(\frac{1}{2^5}\)sin 2α sin 4α sin(11α – 5α) sin(11α – 3a) sin(11α – α)
= \(\frac{1}{2^5}\)sin 2α sin 4α sin(π – 5α) sin(π – 3a) sin(π – α)
= \(\frac{1}{2^5}\)sin α sin 2α sin 4α sin 5α = \(\frac{1}{2^5}\)y ⇒ x = \(\frac{1}{2^5}=\frac{1}{32}\)
∴ cos\(\frac{\pi}{11}\) cos\(\frac{2 \pi}{11}\) cos\(\frac{3 \pi}{11}\) cos\(\frac{4 \pi}{7}\) cos\(\frac{5 \pi}{7}=\frac{1}{32}\)

Question 51.
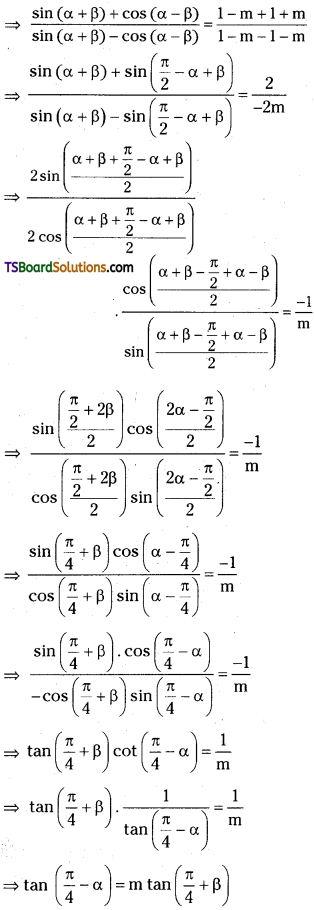
If O < A < B < \(\frac{\pi}{4}\) and sin (A + B) = \(\frac{24}{25}\) and cos(A – B) = \(\frac{4}{5}\) then find the value of tan 2A. [Mar. ’15(TS)]
Answer:
O < A < B < \(\frac{\pi}{4}\) ⇒ O < A + B < \(\frac{\pi}{2}\), –\(\frac{\pi}{2}\) < A – B < O

Question 52.
In ΔABC, prove that cos\(\frac{A}{2}\) + cos\(\frac{B}{2}\) – cos\(\frac{B}{2}\) = 4 cos\(\left(\frac{\pi+A}{4}\right)\) cos\(\left(\frac{\pi+B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\). [Mar. ’05]
Answer:
In ΔABC, A + B + C = 180°

Question 53.
In ΔABC, prove that sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) – sin\(\frac{C}{2}\) = -1 + 4cos\(\left(\frac{\pi+A}{4}\right)\)cos\(\left(\frac{\pi+B}{4}\right)\)cos\(\left(\frac{\pi-C}{4}\right)\).
Answer:
In ΔABC, A + B + C = 180° ………….(1)

Question 54.
If A + B + C = 2S, then prove that sin (S – A) + sin(S – B) + sin C = 4 cos \(\left(\frac{S-A}{2}\right)\) cos\(\left(\frac{S-B}{2}\right)\) sin\(\left(\frac{C}{2}\right)\).
Answer:
Given A + B + C = 2S
L.H.S = sin(S – A) + sin (S – B) + sin C

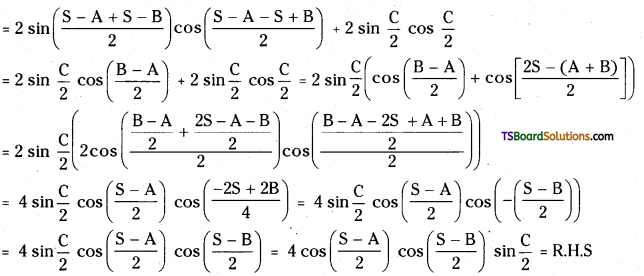
Question 55.
Eliminate ‘θ’ from x = a cos³θ, y = b sin³θ.
Answer:
Given x = a cos³θ, y = b sin³θ.
\(\frac{x}{a}\) = cos³θ, \(\frac{y}{b}\) = sin³θ

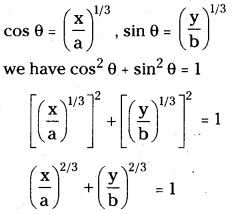
Question 56.
If none of the denominators is zero, prove that \(\left(\frac{\cos A+\cos B}{\sin A-\sin B}\right)^n+\left(\frac{\sin A+\sin B}{\cos A-\cos B}\right)^n\) = 2cotⁿ\(\left(\frac{A-B}{2}\right)\), if n is even 0, if n is odd. [Mar. ’16(TS)]
Answer:

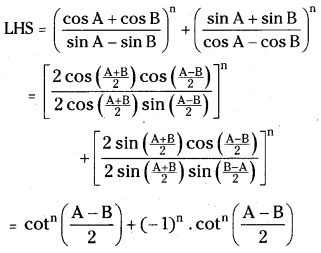
if n is odd, since (-1)ⁿ = 1
we have LHS = 0
if n is even and (- 1)ⁿ = 1
LHS = 2cotⁿ\(\left(\frac{A-B}{2}\right)\)

Question 57.
If A + B + C = 2S, then prove that cos(S – A) + cos(S – B) + cos C = 1 + 4cos\(\left(\frac{S-A}{2}\right)\) cos\(\left(\frac{S-B}{2}\right)\) cos\(\left(\frac{C}{2}\right)\). [Mar. ’17(TS)]
Answer:
Given A + B + C = 2S
L.H.S = cos(S – A) + cos(S – B) + cos C

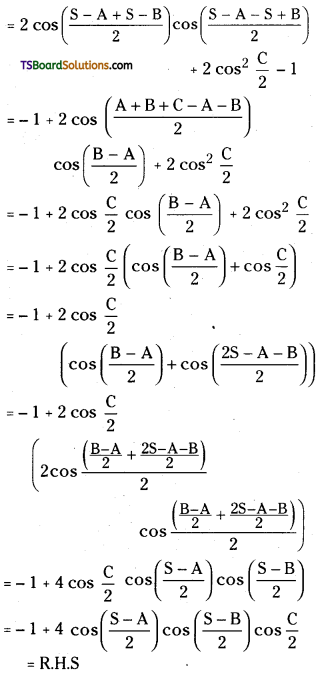
Question 58.
Prove that: sin 50° – sin 70° + sin 10° = 0
Answer:
LHS = sin 50° – sin 70° r sin 10°
= (sin 50° – sin 70°) + sin 10°
= 2 cos \(\left(\frac{50+70}{2}\right)\) sin \(\left(\frac{50-70}{2}\right)\) + sin 10°
= 2 cos 60° . sin (- 10°) + sin 10°
= – 2(\(\frac{1}{2}\)) sin 10° + sin 10° = 0

Question 59.
If A + B + C = 2s, then prove that cos(s – A) + cos (s – B) + cos (s – C) + cos s = 4 cos\(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\). [Mar. ’18(TS)]
Answer:

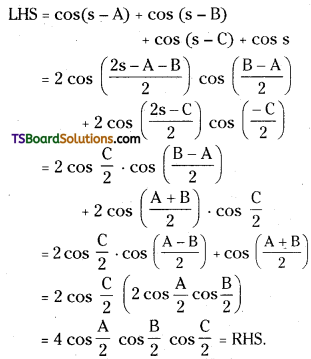
Question 60.
If A + B + C = 0, then prove that sin 2A + sin 2B + sin 2C = -4 sin A sin B sin C
Answer:
Given A + B + C = 0
LHS = sin 2A + sin 2B + sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + sin C
= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (-C) cos (A – B) + sin 2C
= -2 sin C cos (A – B) + 2 sin C cos C
= -2 sin C [cos (A-B) – cos C]
= – 2 sin C [cos (A – B) – cos [-(A + B)]]
= – 2 sin C [cos (A-B) – cos (A + B)]
= – 2 sin C [2 sin A sin B]
= -4 sin A sin B sin C = RHS.

Telangana TSBIE TS Inter 1st Year English Study Material Grammar Matching Meanings Exercise Questions and Answers.

TS Inter 1st Year English Grammar Matching Meanings

Learning means skill that improves comprehension and communication fast.

While looking up the the word in a dictionary for its accurate meaning is the best possible way, doing so is not always possible.

It is sometimes possible to ‘guess’ the meaning of a new word from the context in which it *- is used and from its composition.

Going through glossaries helps to a great extent in mastering this aspect.

In the Intermediate Public Examinations words for this question are usually picked up from the prescribed pieces. Hence, noting down the meanings of important words from the prescribed lessons will help the student score maximum possible marks allotted for this question.

Improving Vocabulary (word power) can be done in innumerable ways. These many various ways are easy to practise and enjoyable as one follows them. Some of them are presented here with one or more examples each.

1) From your regular reading, (Textbooks or general books) select five words a day that you do not clearly understand. Note them in a book, find out the meanings, take tips to use them in your own sentences from a good dictionary and start using those words in your speech or writing. Following this technique every day is very useful.

2) Try to guess the meanings of words from the context. But be sure to check whether your guess is correct or not.
Ex :
a) I saw a woman carrying a pitcher on her head and when she reached her home, she put down the pitcher. I saw water to its brims in that pitcher.
pitcher = a pot, a vessel, a container ………….. you are right.

b) Likhitha noticed her ten-month-old daughter was not closing her eyes even when she applied soap on her face. So, Likhitha took her baby to an oculist, who declared that the baby lost her power of vision and she was blind.
Oculist: guess. Yes, absolutely right: an ophthalmologist, an eye-doctor.

3) Study words with the help of their roots, parts, prefixes, suffixes, etc.
theo = god; logy = a systematic study
theology = a systematic study of god
zoo = animals; l0gy = study; zoology = study of animals
phi! = love; biblio = books; bibliophile = one who loves books
cide = kill or killing agent; or killing
pest = minute creatures; pesticide = that which kills pests

4) Study words in groups like :
a) Synonyms : words with similar (NOT THE SAME) meanings and belonging to the same parts of speech.
i) beautiful, handsome, cute, charming, pretty, attractive
ii) intelligent, brilliant, sharp, smart, bright, clever

b) Antonyms : words that have meanings opposite to one another. Like synonyms, any two antonyms should belong to the same part of speech.
i) good × bad
ii) small × big
iii) active × inactive; passive
iv) encourage × discourage
v) bright × dark; dull
vi) slow × fast

c) Homonyms : words with the same spelling; the same pronunciation but with different meanings.

1. book (n) = పుస్తకము
   book (v) = నమోదుచేయుట
   book (v) = కేటాయించుట
2. bank (n) = నీధి
   bank (v) = ఆధారపడి
   bank (n) = నదీ తీరము
3. rest = విశ్రాంతి
   rest = మిగిలిన, ఇతర
4. point = చుక్క
   point = విషయము

d) Homophones : words with different spellings and meanings but with the same pronunciation :
1 – eye; son – sun; some – sum; sight – cite – site; see – sea; seen – scene

e) Homographs : words with the same spellings but with different pronunciation and meanings :
minute (మినిట్) = నిముషము
minute (మైన్యూట్) = అతి చిన్న
live (v) (లివ్) = నివసించు
live (adj) (లైవ్) = సజీవ; ప్రతక్ష్య
And there are many more play-way methods to enrich one’s vocabulary in an entertaining way.

Special Note : Make proper use of the sections WORD STUDY and WORD GAMES in the activities part, given after lessons.

Exercises

Question 1.
Match the following words in Column A with their meanings in Column B.
Two sides of life

Answer:
i) – i
ii) – h
iii) – j
iv) – d
v) – a
vi) – g
vii) – e
viii) – b
ix) – b
x) – c

Question 2.
Match the following words in Column A with their meanings in Column B.
Father, Dear Father

Answer:
i) – i
ii) – d
iii) – f
iv) – h
v) – g
vi) – j
vii) – c
viii) – b
ix) – a
x) – e

Question 3.
Match the following words in Column A with their meanings in Column B.
The Green Champion – Thimmakka

Answer:
i) – h
ii) – f
iii) – b
iv) – j
v) – c
vi) – i
vii) – d
viii) – a
ix) – e
x) – g

Question 4.
Match the following words in Column A with their meanings in Column B.
The Green Champion – Thimmakka

Answer:
i) – e
ii) – i
iii) – h
iv) – j
v) – b
vi) – g
vii) – c
viii) – f
ix) – d
x) – a

Question 5.
Match the following words in Column A with their meanings in Column B.
Box and Cox

Answer:
i) – i
ii) – g
iii) – e
iv) – a
v) – h
vi) – j
vii) – b
viii) – f
ix) – c
x) – d

Question 6.
Match the following words in Column A with their meanings in Column B.
Two Sides of Life; Revision Test – I

Answer:
i) – h
ii) – e
iii) – j
iv) – g
v) – i
vi) – b
viii) – f
ix) – d
x) – c

Question 7.
Match the following words in Column A with their meanings in Column B.
Father, Dear Father, Revision Test – II

Answer:
i) – g
ii) – i
iii) – e
iv) – j
v) – c
vi) – a
vii) – d
viii) – b
ix) – f
x) – h

Question 8.
Match the following words in Column A with their meanings in Column B.
The Green Champion-Thimmakka; Revision Test – III

Answer:
i) – h
ii) – g
iii) – j
iv) – i
v) – a
vi) – c
vii) – e
viii) – b
ix) – f
x) – d

Question 9.
Match the following words in Column A with their meanings in Column B.
The First Four Minutes; Revision Test – IV

Answer:
i) – f
ii) – j
iii) – h
iv) – b
v) – i
vi) – d
vii) – a
viii) – e
ix) – c
x) – g

Question 10.
Match the following words in Column A with their meanings in Column B.
Box and Cox; Revision Test – V

Answer:
i) – i
ii) – e
iii) – f
iv) – g
v) – h
vi) – j
vii) – a
viii) – d
ix) – c
x) – b

Question 11.
Match the following words in Column A with their meanings in Column B.
Model Question Paper

Answer:
i) – i
ii) – f
iii) – h
iv) – j
v) – g
vi) – d
vii) – b
viii) – e
ix) – a
k) – c

Note : Go through the section “MEANINGS AND EXPLANATIONS” given at the end of all the fifteen lessons. It helps you score 28 Marks in the Public Examination. That also helps in improving your language skills.

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Matrices Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Matrices Important Questions Very Short Answer Type

Question 1.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
3 & 8 \\
7 & 2
\end{array}\right]\) and 2X + A = B, then find X. [Mar. 15 (AP); Mar. 13, 11; May 12]
Answer:

If A = \(\left[\begin{array}{ccc}
3 & 2 & -1 \\
2 & -2 & 0 \\
1 & 3 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-3 & -1 & 0 \\
2 & 1 & 3 \\
4 & -1 & 2
\end{array}\right]\) and X = A + B then find X. [Mar. 17 (TS)]
Answer:
\(\left[\begin{array}{ccc}
0 & 1 & -1 \\
4 & -1 & 3 \\
5 & 2 & 3
\end{array}\right]\)

Question 2.
If \(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]\) = \(\left[\begin{array}{cc}
5 & 2 \\
-2 & a-4
\end{array}\right]\), then find the values of x, y, z and a. [May 14, 06 Mar. 19(AP)]
Answer:
Given \(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]\) = \(\left[\begin{array}{cc}
5 & 2 \\
-2 & a-4
\end{array}\right]\)
From the equality of matrices,
x – 3 = 5
⇒ x = 8
2y – 8 = 2
2y = 10
y=5
z + 2 = – 2
z = – 4
a – 4 = 6
a = 10
∴ x = 8, y = 5, z = – 4, a = 10

If \(\left[\begin{array}{ccc}
x-1 & 2 & 5-y \\
0 & z-1 & 7 \\
1 & 0 & a-5
\end{array}\right]\) = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 4 & 7 \\
1 & 0 & 0
\end{array}\right]\) then find the values of x, y, z and ‘a’.
Answer:
2, 2, 5, 5

If \(\left[\begin{array}{ccc}
x-1 & 2 & y-5 \\
z & 0 & 2 \\
1 & -1 & 1+a
\end{array}\right]\) = \(\left[\begin{array}{ccc}
1-x & 2 & -y \\
2 & 0 & 2 \\
1 & -1 & 1
\end{array}\right]\) then find the values of x, y, z and ‘a’.
Answer:
1, \(\frac{5}{2}\), 2, 0

Question 3.
Find the trace of \(\left[\begin{array}{rrr}
1 & 3 & -5 \\
2 & -1 & 5 \\
2 & 0 & 1
\end{array}\right]\).
Answer:
Let A = \(\left[\begin{array}{rrr}
1 & 3 & -5 \\
2 & -1 & 5 \\
2 & 0 & 1
\end{array}\right]\)
∴ Tra A = 1 – 1 + 1 = 1
The elements of the principal diagonal = 1, – 1, 1

Fin the area of A if A = \(\left[\begin{array}{ccc}
1 & 2 & -1 / 2 \\
0 & -1 & 2 \\
-1 / 2 & 2 & 1
\end{array}\right]\)
Answer:
1

Question 4.
If A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
3 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\), find 3B – 2A. [Mar, 19 (TS); Mar. 12]
Answer:

If A = \(\left[\begin{array}{ccc}
0 & 1 & 2 \\
2 & 3 & 4 \\
4 & 5 & -6
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) find B – A and 4A – 5B
Answer:
\(\left[\begin{array}{ccc}
-1 & 1 & 1 \\
-2 & -2 & -4 \\
-4 & -5 & -5
\end{array}\right],\left[\begin{array}{ccc}
5 & -6 & -7 \\
8 & 7 & 16 \\
16 & 20 & -19
\end{array}\right]\)

If A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
2 & 3 & 4 \\
4 & 5 & 6
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & -2 & 0 \\
0 & 1 & -1 \\
-1 & 0 & 3
\end{array}\right]\) find A – B and 4B – 3A
Answer:
\(\left[\begin{array}{ccc}
-1 & 3 & 2 \\
2 & 2 & 5 \\
5 & 5 & 3
\end{array}\right],\left[\begin{array}{ccc}
4 & -11 & -6 \\
-6 & -5 & -16 \\
-16 & -15 & -6
\end{array}\right]\)

Question 5.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
2 & 3 & -1 \\
-3 & 1 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 1 & 2 \\
1 & 2 & 0
\end{array}\right]\) then examine whether A and B commute with respect to multiplication of matrices. [Nov, 98]
Answer:
Given A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
2 & 3 & -1 \\
-3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 1 & 2 \\
1 & 2 & 0
\end{array}\right]\)
Both A and B are square matrices of order 3.
Hence both AB and BA are defined and are matrices of order 3.

which shows that AB ≠ BA
Therefore A and B do not commute with respect to multiplication of matrices.

If A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
-4 & 2 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
2 & 3 \\
4 & 5 \\
2 & 1
\end{array}\right]\) do AB and BA exist ? If they exist find them. Do A and B commute with respect to multiplication.
Answer:
\(\left[\begin{array}{cc}
0 & -4 \\
10 & 3
\end{array}\right]\), \(\left[\begin{array}{ccc}
-10 & 2 & 21 \\
-16 & 2 & 37 \\
-2 & -2 & 11
\end{array}\right]\) & AB ≠BA

Question 6.
If A = \(\left[\begin{array}{cc}
\mathbf{i} & 0 \\
0 & -\mathbf{i}
\end{array}\right]\), then show that A² = – 1. [Mar. 16 (AP), 08]
Answer:

Find A² where A = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]\).
Answer:
\(\left[\begin{array}{rr}
14 & 10 \\
-5 & -1
\end{array}\right]\)

If A = \(\left[\begin{array}{ll}
\mathbf{i} & \mathbf{0} \\
\mathbf{0} & \mathbf{i}
\end{array}\right]\), find A².
Answer:
\(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)

Question 7.
Find \(\left[\begin{array}{ccc}
\mathbf{0} & \mathbf{c} & -\mathbf{b} \\
-\mathbf{c} & \mathbf{0} & \mathbf{a} \\
\mathbf{b} & -\mathbf{a} & \mathbf{0}
\end{array}\right]\) \(\left[\begin{array}{lll}
\mathbf{a}^2 & \mathbf{a b} & \mathbf{a c} \\
\mathbf{a b} & \mathbf{b}^2 & \mathbf{b c} \\
\mathbf{a c} & \mathbf{b c} & \mathbf{c}^2
\end{array}\right]\) [Mar. 96; May 91]
Answer:
Let A = \(\left[\begin{array}{ccc}
\mathbf{0} & \mathbf{c} & -\mathbf{b} \\
-\mathbf{c} & \mathbf{0} & \mathbf{a} \\
\mathbf{b} & -\mathbf{a} & \mathbf{0}
\end{array}\right]\), B = \(\left[\begin{array}{lll}
\mathbf{a}^2 & \mathbf{a b} & \mathbf{a c} \\
\mathbf{a b} & \mathbf{b}^2 & \mathbf{b c} \\
\mathbf{a c} & \mathbf{b c} & \mathbf{c}^2
\end{array}\right]\)
The order of matrix, A is 3 × 3
The order of matrix, B is 3 × 3
The no. of columns in A = The no. of rows in B.
∴ AB is defined.

Question 8.
If A = \(\left[\begin{array}{cc}
2 & 4 \\
-1 & k
\end{array}\right]\) and A² = 0, then find the value of k. [Mar. 17 (AP), 14, 05, May. 11, Mar. 08(TS)]
Answer:

From equality of matrices, – 2 – k = 0 ⇒ k = – 2

Question 9.
If A = \(\left[\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right]\) then find A⁴. [May 01]
Answer:

If A = \(\left[\begin{array}{ccc}
1 & 1 & 3 \\
5 & 2 & 6 \\
-2 & -1 & -3
\end{array}\right]\) then find A³.
Answer:
\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\)

Question 10.
If A = \(\left[\begin{array}{lll}
1 & 4 & 7 \\
2 & 5 & 8
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
-3 & 4 & 0 \\
4 & -2 & -1
\end{array}\right]\), then show that (A + B)’ = A’ + B’ [May. 09]
Answer:

Question 11.
If A = \(\left[\begin{array}{rrr}
-2 & 1 & 0 \\
3 & 4 & -5
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & 2 \\
4 & 3 \\
-1 & 5
\end{array}\right]\), then find A + B’. [May. 08]
Answer:

Question 12.
If A = \(\left[\begin{array}{ccc}
2 & -1 & 2 \\
1 & 3 & -4
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -2 \\
-3 & 0 \\
5 & 4
\end{array}\right]\), then verify that (AB)’ = B’A’ [Mar. 13]
Answer:

Question 13.
If A = \(\left[\begin{array}{ccc}
2 & 0 & 1 \\
-1 & 1 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & 1 & -2
\end{array}\right]\), then find (AB)’. [Mar. 19 (TS); May. 12]
Answer:

Question 14.
If A = \(\left[\begin{array}{rr}
-2 & 1 \\
5 & 0 \\
-1 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
-2 & 3 & 1 \\
4 & 0 & 2
\end{array}\right]\) then find 2A + B’ and 3B’ – A. [Mar. 10]
Answer:

Question 15.
If A = \(\left[\begin{array}{rr}
2 & -4 \\
-5 & 3
\end{array}\right]\), then find A + A’ and AA’ [May 15 (AP); May 07, 02]
Answer:

If A = \(\left[\begin{array}{cc}
-1 & 2 \\
0 & 1
\end{array}\right]\) then find AA’. Do A and A’ commute with respect to multiplication of matrices ? [Mar. 17(TS)]
Answer:
AA’ = \(\left[\begin{array}{ll}
5 & 2 \\
2 & 1
\end{array}\right]\), A’A = \(\left[\begin{array}{cc}
1 & -2 \\
-2 & 5
\end{array}\right]\); AA’ ≠ A’A

Question 16.
If A = \(\left[\begin{array}{ccc}
0 & 4 & -2 \\
-4 & 0 & 8 \\
2 & -8 & x
\end{array}\right]\) is a skew symmetric matrix, find the value of x. [Mar. 08]
Answer:

Question 17.
If A = \(\left[\begin{array}{rrr}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\) is a symmetric matrix, then find x. [Mar. 16 (AP), 05, 03, May. 15 (TS)]
Answer:

From equality of matrices, x = 6.

Question 18.
If A = \(\left[\begin{array}{rrr}
0 & 2 & 1 \\
-2 & 0 & -2 \\
-1 & x & 0
\end{array}\right]\) is a skew symmetric matrix, then find x. [May. 14, 13, 11]
Answer:
A matrix A is said to be skew symmetric if,

From the equality of matrices, x = 2.
∴ x = 2

Question 19.
Is \(\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) symmetric or skew symmetric? [Mar. 09]
Answer:

∴ A is a skew symmetric matrix since A^T = – A.

Question 20.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that AA’ = A’A = I. [Mar. 07]
Answer:

Question 21.
If ω is complex (non real) cube root of 1, then show that \(\left|\begin{array}{ccc}
1 & \omega & \omega^2 \\
\omega & \omega^2 & 1 \\
\omega^2 & 1 & \omega
\end{array}\right|\) = 0 [Mar. 14, 11; May. 92]
Answer:
1, ω, ω² are the cube roots of unity.
Then, 1 + ω + ω² = 0, ω³ = 1.

Question 22.
Find the determinant of the matrix. [May. 95]
\(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\)
Answer:
Let A = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\)
det A = \(\left|\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right|\) = 0(0 – 1) – 1 (0 – 1) + 1(1 – 0)
= 0(- 1) – 1 (- 1) + 1(1) = 0 + 1 + 1 = 2

Find the determinant of the matrix
\(\left[\begin{array}{lll}
\mathbf{a} & \mathbf{h} & \mathbf{g} \\
\mathbf{h} & \mathbf{b} & \mathbf{f} \\
\mathbf{g} & \mathbf{f} & \mathbf{c}
\end{array}\right]\).
Answer:
abc + 2fgh – af² – bg² – ch²

Find the determinant of the matrix
\(\left[\begin{array}{lll}
\mathbf{a} & \mathbf{b} & \mathbf{c} \\
\mathbf{b} & \mathbf{c} & \mathbf{a} \\
\mathbf{c} & \mathbf{a} & \mathbf{b}
\end{array}\right]\)
Answer:
3abc – a³ – b³ – c³

Question 23.
Find the determinant of the matrix \(\left[\begin{array}{ccc}
1^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right]\). [Mar. 10]
Answer:
Let A = \(\left[\begin{array}{ccc}
1^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right]=\left[\begin{array}{ccc}
1 & 4 & 9 \\
4 & 9 & 16 \\
9 & 16 & 25
\end{array}\right]\)
det A = 1(225 – 256) – 4 (100 – 144) + 9 (64 – 81)
= – 31 + 176 – 153
= 176 – 184 = – 8.

Question 24.
If A = \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\) and det A = 45, then find x. [May 09, 03, 99, 96, Mar; 07, 03]
Answer:
Given A = \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & \mathrm{x}
\end{array}\right]\) and det A = 45.
det A = 1 (3x + 24) – 0(2x – 20) + 0 (-12 – 15) = 3x + 24 – 0 + 0 = 3x + 24
Given, det A = 45 ⇒ 3x + 24 = 45 ⇒ 3x = 45 – 24 ⇒ 3x = 21 ⇒ x = 7.

Question 25.
Find the adjoint and inverse of the matrix \(\left[\begin{array}{rr}
2 & -3 \\
4 & 6
\end{array}\right]\). [Mar. 12]
Answer:
Let A = \(\left[\begin{array}{rr}
2 & -3 \\
4 & 6
\end{array}\right]\)
Cofactor of 2 is A₁ = + (6) = 6
Cofactor of 4 is A₂ = – (- 3) = 3
Cofactor of – 3 is B₁ = – (4) = – 4
Cofactor of 6 is B₂ = + (2) = 2
∴ Cofactor matrix of A is B = \(\left[\begin{array}{ll}
\mathrm{A}_1 & \mathrm{~B}_1 \\
\mathrm{~A}_2 & \mathrm{~B}_2
\end{array}\right]=\left[\begin{array}{cc}
6 & -4 \\
3 & 2
\end{array}\right]\)
Adj A = B’ = \(\left[\begin{array}{cc}
6 & 3 \\
-4 & 2
\end{array}\right]\)
det A = ad – bc = 12 – (- 12) = 12 + 12 = 24 ≠ 0
∴ A is invertiable.
A^-1 = \(\frac{{adj} A}{{det} A}=\frac{1}{24}\left[\begin{array}{rr}
6 & 3 \\
-4 & 2
\end{array}\right]\)

Find the adjoint and the Inverse of the matrix A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right]\). [Mar. 18 (AP); May 06]
Answer:
\(\left[\begin{array}{cc}
-5 & -2 \\
-3 & 1
\end{array}\right],\left[\begin{array}{cc}
\frac{5}{11} & \frac{2}{11} \\
\frac{3}{11} & \frac{-1}{11}
\end{array}\right]\)

Question 26.
Find the adjoint and inverse of the matrix A = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) [Mar. 13, 09]
Answer:
Let A = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)

Cofactor of cos α is A₁ = + (cos α) = cos α
Cofactor of sin α is A₂ = – (- sin α) = sin α
Cofactor of – sin α is B₁ = – (sin α) = – sin α
Cofactor of cos α is B₂ = + (cos α) = cos

Question 27.
Find the rank of the matrix\(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\). [Mar. 18 (TS); May 10; Mar. 08]
Answer:
Let A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\)
det A = 1(1 – 1) – 1(1 – 1) + 1 (1 – 1) = 0 – 0 + 0 = 0
Since det A = 0, Rank [A] ≠ 3
Now, \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\) is a submatrix of A, whose determinant is 1 – 1 = 0 ∴ Rank [A] ≠ 2.
Now. [1] is a submatrix of A, whose determinant is 1 ≠ 0. ∴ Rank [A] = 1

Telangana TSBIE TS Inter 1st Year Physics Study Material 10th Lesson Mechanical Properties of Solids Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 10th Lesson Mechanical Properties of Solids

Very Short Answer Type Questions

Question 1.
State Hooke’s law of elasticity.
Answer:
Hooke’s law states that within elastic limit stress is proportional to strain.

This constant is known as elastic modulus of the body.

Question 2.
State the units and dimensions of stress.
Answer:

Dimensional formula ML^-1 T^-2

Question 3.
State the units and dimensions of modulus of elasticity.
Answer:

Nm^-2 (or) pascal
Dimensional formula ML^-1 T^-2

Question 4.
State the units and dimensions of Young’s modulus.
Answer:

Dimensional formula ML^-1T²

Question 5.
State the units and dimensions of modulus of rigidity.
Answer:
Modulus of rigidity,

(or) pascal
Dimensional formula ML^-1T².

Question 6.
State the units and dimensions of Bulk modulus.
Answer:

unit is Nm^-2 (or) pascal
Dimensional formula ML^-1 T^-2

Question 7.
State the examples of nearly perfect elastic and plastic bodies.
Answer:
There is no perfectly elastic body. But behaviour of Quartz fiber is very nearer to perfectly elastic body.

Real bodies are not perfectly plastic, but behaviour of wet clay, butter etc., can be taken as examples for perfectly plastic bodies.

Short Answer Questions

Question 1.
Define Hooke’s law of elasticity, proportionality, permanent set, and breaking stress.
Answer:
Hooke’s Law :
It states that within elastic limit, stress is proportional to strain.

This constant is called elastic constant (E).

Proportionality limit:
When load is increased the elongation of the wire will also increases. The maximum load upto which the elongation is directly proportional to the load is called proportionality limit (A). The graph drawn between load and extension. It is a straight line OA’.

Permanent set :
If the load on the wire is increased beyond elastic limit, the elongation is not pro portional to load. On removal of the load the wire cannot regain its original length. The length of the wire increases permanently. In figure permanent set is given by OP. This is called permanent set.

Breaking stress :
If the load is increased beyond yield point the elongation is very rapid, even for small changes in load and wire becomes thinner and breaks. This is shown as E. The breaking force per unit area is called breaking stress.

Question 2.
Define modulus of elasticity, stress, strain and Poisson’s ratio.
Answer:
1) Stress:
Restoring force acting on unit area is called stress.

Unit: N/m² (or) pascal;
Dimensional formula: ML^-1T^-2.

2) Strain :
The change in dimension per unit original dimension of a body is called strain.

It is a ratio, so no units and dimensional formula.

3) Modulus of elasticity :
∴ From Hooke’s Law Stress x Strain or

The ratio of stress to strain is called modulus of elasticity.
Unit: N/m².
Dimensional formula: ML^-1T^-2.

4) Poisson’s ratio :
It is defined as the ratio of lateral contraction strain to longitudinal elongation strain.
Poisson’s ratio

It is a ratio, so no units and dimensional formula.

Question 3.
Define Young’s modulus, Bulk modulus, and Shear modulus.
Answer:
1) Young’s Modulus Y:
Within elastic limit, the ratio of longitudinal stress to longitudinal strain is called Young’s modulus

2. Bulk Modulus (B) :
Within elastic limit, the ratio of volumetric stress to volumetric strain is called Bulk modulus

3) Shear Modulus or Rigidity Modulus (G):
Within elastic limit, the ratio of tangential or shearing stress to shearing strain is called Shear modulus or Rigidity modulus.

Question 4.
Define stress and explain the types of stress. [AP War. 19; TS War. 16]
Answer:
Stress:
When a body is subjected to a deforming force, then restoring forces will develop inside the body. These restoring forces will oppose any sort of change in its original shape. The restoring force per unit area of the surface is called stress.

Stress:
Stress is defined as force applied per unit area.

D.F. = ML^-1T^-2 ; Unit: N/m² (or) Pascal.

Types of stress :
It is of three types. They are : 1) Longitudinal stress 2) Tangential stress (or) Shear stress 3) Volumetric stress.

Longitudinal stress:
If the force applied on a body is along its lengthwise direction then it is called longitudinal stress. It produces deformation in length.

Tangential stress (or) Shear stress:
Force applied per unit area parallel to the surface of a body trying to displace the upper layers of the body is called shearing stress.

(Parallel to the surface layers)

Volumetric stress:
If force is applied on all the sides of a body or on the volume of a body then it is called volumetric stress.

Question 5.
Define strain and explain the types of strain.
Answer:
Strain:
Strain is defined as deformation produced per unit dimension. It is a ratio. So no units.

Types of strain :
Strain is of three types. They are: 1) Longitudinal strain 2) Tangential strain or Shear strain 3) Volumetric strain.

Longitudinal strain:
The ratio of elongation to original length along length wise direction is defined as longitudinal strain.

Shearing strain :
If the force applied on a body produces a change in shape only it is called shearing force. The angle through which a plane originally perpendicular to the fixed surface shifts due to the application of shearing stress is called shearing strain or simply shear (θ).

Question 6.
Define strain energy and derive the equation for the same. [TS Mar. ’19; May ’18; AP Mar. ’14; May ’14]
Answer:
Strain energy :
The energy developed in (string) a body when it is strained is called strain energy.

Let a force F be applied on lower end of wire, fixed at the upper end. Let the extension be dl.
∴ Work done = dW = Fdl
Total work done in stretching it from 0

Question 7.
Explain why steel is preferred to copper, brass, aluminium in heavy-duty machines and in structural designs.
Answer:
For metals Young’s moduli are large. Therefore, these materials require a large force to produce small change in length. To increase the length of a thin steel wire of 0.1 cm² cross-sectional area by 0.1 %, a force of 2000 N is required. The force required to produce the same strain in aluminium, brass, and copper wire having the same cross-sectional area are 690 N, 900N, and 1100 N respectively. It means that steel is more elastic than copper, brass, and aluminium. It is for this reason that steel is preferred in heavy duty machines and in structural designs.

Question 8.
Describe the behaviour of a wire under gradually increasing load. [AP Mar. ’18, ’17, ’16, ’15, ’13, May ’16, ’13; TS Mar. 18, 17, 15; May 17,16; June 15]
Answer:
Behaviour of a wire under increasing load:
Let a wire is suspended at one end and loads are attached to the other end. When loads are gradually increased the following changes are noticed.

1) Proportionality limit (A) :
When load is increased the elongation of the wire gradually increases. The maximum load upto which the elongation is directly pro-portional to the load is called proportionality limit (A). The graph drawn between load and extension is a straight line. So point A is called proportionality limit. In this region Hooke’s Law is obeyed.

2) Elastic limit (B):
If the load is increased above the proportionality limit the elongation is not proportional to the load. Hooke’s law is not obeyed. But it exhibits elasticity which means that it regains the original length if load is removed. The maximum load on the wire upto which it exhibits elasticity is called elastic limit (B in the graph).

3) Permanent set (C) :
If the load on the wire is increased beyond elastic limit say upto C, the elongation is not proportional to load. On removal of the load, the wire does not regain its original length. Length of wire increases perma-nently. In figure permanent set is given by OP. So OP is called permanent set.

4) Point of ultimate tensile strength (D) :
If the load is further increased, upto D’ then strain increases rapidly even though there is no increase in stress.

At this stage the restoring forces seems to be subdued to then deforming forces. Elongation without increase in load is called creeping. This behaviour of metal is called yielding.

5) Fracture point (E) :
If the load is increased beyond Yield point the elongation is very rapid, even for small changes in load the wire becomes thinner and breaks. This is shown as E. The breaking force per unit area is called breaking stress.

Question 9.
Two identical solid balls, one of ivory and the other of wet clay are dropped from the same height on to the floor. Which one will rise to a greater height after striking the floor and why?
Answer:
We know that ivory ball is more elastic than wet-clay ball. Therefore, the ivory ball will tend to regain its original shape in a very short time after the collision. Due to it, there will be large energy and momentum transfer to the ivory ball in comparison to the wet-clay ball. As a result of it, the ivory ball will raise higher after the collision.

Question 10.
While constructing buildings and bridges a pillar with distributed ends is preferred to a pillar with rounded ends. Why?
Answer:
Use of pillars or columns is very common in buildings and bridges. A pillar with roun-ded-ends supports less load than that with a distributed shape at the ends. Hence, for this reason, while constructing buildings and bridges a pillar with distributed ends is preferred to a pillar with rounded ends.

Question 11.
Explain why the maximum height of a mountain on earth is approximately 10 km?
Answer:
A mountain base is not under uniform compression and this provides some shearing stress to the rocks under which they can flow. The stress due to all the material on the top should be less than the critical shearing stress at which the rocks flow.

At the bottom of a mountain of height ‘h’, the force per unit area due to the weight of the mountain is hpg where p is the density of the material of the mountain and g is the acceleration due to gravity. The material at the bottom experiences this force in the vertical direction and the sides of the mountain are free. There is a shear component, approximately hpg itself. Now the elastic limit for a typical rock is 3 × 10⁷ Nm^-2. Equating this to hpg with ρ = 3 × 10³ kg m^-3 gives
h = \(\frac{30\times10^{-7}}{3\times10^3\times10}\) = 10 km
Hence, the maximum height of a mountain on earth is approximately 10 km.

Question 12.
Explain the concept of Elastic Potential Energy in a stretched wire and hence obtain the expression for it. [AP May ’ 18, 17; AP June 15]
Answer:
When a wire is put under a tensile stress, work is done against the inter atomic forces. This work is stored in the form of “Elastic potential energy.”

Expression to elastic potential energy:
To stretch a wire, force is applied. As a result it elongates. So the force applied is useful to do some work. This work is stored in it as potential energy. When the deforming force is removed, this energy is liberated as heat. The energy developed in a body (string) when it is strained is called strain energy.

Let a force F be applied on a wire fixed at the upper end. Let the extension be dl.
∴ Work done = dW = Fdl
Total work done in stretching from

Long Answer Questions

Question 1.
Define Hooke’s law of elasticity and describe an experiment to determine the Young’s modulus of the material of a wire.
Answer:
Hooke’s Law :
Within elastic limit, stress is directly proportional to strain.
strain ∝ stress

where E constant called modulus of elasticity of the material of a body.

Determination of Young’s modulus of a wire:
The apparatus used to find Young s modulus of a wire consists of two long wires A and B of same length made with same material are used. These two wires are suspended from a rigid support and a vernier scale V’ is attached to them. Wire A is connected to the main scale (M). A fixed load is connected to this cord to keep tension in the wire. This is called reference wire. The second Wire B’ is connected to vernier scale V’. Adjustable load hanger is connected to this wire. This is called experimental wire.

Procedure :
Let a load M₁ is attached to the weight hanger at vernier. Main scale reading (M.S.R) and vernier scale reading (V.S.R) are noted. Weights are gradually increased in the steps of \(\frac{1}{2}\) kg upto a maximum load of say 3 kg. Every time M.S.R and V.S.R are noted. They are placed in tabular form.

Now loads are gradually decreased in steps of \(\frac{1}{2}\) kg. While decreasing M.S.R and V.S.R are noted for every load, values are posted in tabular form.

Let 1^st reading with mass M₁ is e₁ and 2^nd reading with mass M₂ is e₂.

Change in load M = M₂ – M₁
elongation e = e₂ – e₁
‘M’ and ‘e’ values are calculated and a graph is plotted.

Force on the wire = mg
Area of cross section of the wire = πr²
(r = radius of the wire)
Elongation = e
Original length = l

A graph is between load (m) and elongation ‘e’, is straight line passing through the origin. The slope of the graph (tan θ) gives (\(\frac{m}{e}\)). The value is substituted in the above equation to find Young’s modulus of the material of the wire.

Precautions:

1. The load applied should be much smaller than elastic limit.
2. Reading is noted only after the air bubble is brought to centre of spirit level.

Problems

Question 1.
A copper wire of 1mm diameter is stretched by applying a force of 10 N. Find the stress in the wire.
Solution:
Diameter, d = 1mm
∴ radius, r = 0.5 mm = 0.5 × 10^-3m
Force, F = 10N

Question 2.
A tungsten wire of length 20cm is stretched by 0.1cm. Find the strain on the wire.
Solution:
Length of wire, l = 20cm = 0.2m
elongation, e = 0.1cm = 1 × 10^-3m

Question 3.
If an iron wire is stretched by 1%, what is the strain on the wire?
Solution:

Question 4.
A brass wire of diameter 1mm and of length 2m is stretched by applying a force of 20N. If the increase in length is 0.51mm, find i) the stress, ii) the strain and iii) the Young’s modulus of the wire.
Solution:
Length of wire, l = 2m;
L diameter, d = 1mm = 10^-3 m
Force, F = 20N;
Increase in length, e = 0.51mm

Question 5.
A copper wire and an aluminium wire have lengths in the ratio 3: 2, diameters in the ratio 2 : 3 and forces applied in the ratio 4: 5. Find the ratio of increase in length of the two wires. (Y_Cu = 1.1 × 10¹¹ Nm^-2, Y_Al = 0.7 × 10¹¹Nm^-2)
Solution:
Ratio of lengths, l₁ : l₂ = 3 : 2;
Ratio of diameters, d₁ : d₂ = 2 : 3
Ratio of forces, F₁ : F₂ = 4 : 5
Y₁ = Y of copper = 1.1 × 10¹¹
Y₂ = Y of Aluminium = 0.7 × 10¹¹;
Ratio of elongation, e₁ : e₂ = ?

Question 6.
A brass wire of cross-sectional area 2mm² is suspended from a rigid support and a body of volume 100cm³ is attached to its other end. If the decrease in the length of the wire is 0.11mm, when the body is completely immersed in water, find the natural length of the wire.
(Y_brass = 0.91 × 10¹¹ Nm^-2, ρ_water = 10³kgm^-3)
Solution:
Area of cross section, A = 2mm = 2 × 10^-6 m²
Volume of body, V = 100 cc = 100 × 10^-6 m³
Decrease in length, e’ = 0.11mm = 0.11 × 10^-3m
Youngs modulus of brass, Y = 0.91 × 10¹¹ N/m²
Density of water, ρ = 1000 kg / m³
Use e’ = \(\frac{V\rho gl}{AY}\)

Question 7.
There are two wires of same material. Their radii and lengths are both in the ratio 1 : 2. If the extensions produced are equal, what is the ratio of the loads?
Solution:
Ratio of lengths, l₁ : l₂ = 1 : 2
Ratio of radii, r₁ : r₂ = 1 : 2
Extensions produced are equal ⇒ e₁ = e₂;
Made of same material ⇒ Y₁ = Y₂
Ratio of loads m₁ : m₂ = ?

Question 8.
Two wires of different material have same lengths and areas of cross-section. What is the ratio of their increase in length when forces applied are the same? (Y₁ = 0.90 × 10¹¹ Nm^-2, Y₂ = 3.60 × 10¹¹ Nm^-2.)
Solution:
Lengths are same ⇒ l₁ = l₂ ;
Area of cross sections are same, A₁ = A₂
Y₁ = 0.9 × 10¹¹ N/m²
Y₂ = 3.60 × 10¹¹ N/m²

Question 9.
A metal wire of length 2.5m and area of cross-section 1.5 × 10^-6 m² is stretched through 2mm. If its Young’s modulus is 1.25 × 10¹¹ Nm^-2, find the tension in the wire.
Solution:
Length of wire, l = 2.5m
Y = 1.25 × 10¹¹N/m²
Area of cross section, A = 1.5 × 10^-6 m²
Elongation, e = 2 m.m = 2 × 10^-3m
Tension, T = mg = F = ?

Question 10.
An aluminium wire and a steel wire of the same length and cross-section are joined end-to-end. The composite wire is hung from a rigid support and a load is suspended from the free end. If the increase in length of the composite wire is 1.35 mm, find the ratio of the (i) stress in the two wires and 0Q strain in the two wires. (Y_Al = 0.7 × 10¹¹ Nm^-2, Y_steel = 2 × 10¹¹m^-2)
Solution:
i) Length is same ⇒ l₁ = l₂
Area is same ⇒ A₁ = A₂
In composite wire same load will act on both wires.
∴ Ratio of stress = 1 : 1

ii) Total elongation, e = 1.35mm =e_Al + e_s
Young’s modulus of aluminium = 7 × 10¹⁰ N/m²
Y of steel = 2 × 10¹¹ N/m²
Elongation, e = \(\frac{Fl}{AY}\)
But F, l and A are same

∴ Ratio of strains in the wires is 20 : 7.

Question 11.
A 2 cm cube of some substance has its upper face displaced by 0.15cm due to a tangential force of 0.3 N while keeping the lower face fixed. Calculate the rigidity modulus of the substance.
Solution:
Side of cube, a = 2.0 cm = 2 × 10^-2 m
Area, A = 4 × 10^-4 m²
Displacement of upper layer = 0.15cm
= 0.15 × 10^-2m
Tangential force, F = 0.30N

Question 12.
A spherical ball of volume 1000 cm³ is subjected to a pressure of 10 atmosphere. The change in volume is 10^-8 cm³. If the ball is made of iron, find its bulk modulus. (1 atmosphere = 1 × 10⁵ Nm^-2)
Solution:
Volume of ball, V = 1000 cm³ = 10^-3 m³
(∵ 1M³ = 10⁶ cm³)
Pressure, P = 10 atmospheres
= 10 × 10⁵ pa ( v 1 atm = 10⁵ pascal)
Change in volume, ∆V = 10^-8 cm³

Question 13.
A copper cube of side of length 1 cm is subjected to a pressure of 100 atmosphere. Find the change in its volume if the bulk modulus of copper is 1.4 × 10¹¹ Nm^-2 (1 atm = 1 × 10⁵ Nm^-2).
Solution:
Side of cube, a’ = 1cm = 10^-2m
∴ Volume of cube = 10^-6m
Pressure, P = 100 atm = 100 × 10⁵ = 10⁷ pa
Bulk modulus, K = 1.4 × 10¹¹ N/m²;

Question 14.
Determine the pressure required to reduce the given volume of water by 2%. Bulk modulus of water is 2.2 × 10⁹ Nm^-2
Solution:

Question 15.
A steel wire of length 20 cm is stretched to increase its length by 0.2 cm. Find the lateral strain in the wire if the Poisson’s’ ratio for steel is 0.19.
Solution:
Length of wire, l = 20, cm = 0.20m,
Poisson’s ratio, σ =0.19
Increase in length, ∆l = 0.2 cm = 2 × 10^-3m
lateral strain = ?
Lateral strain = σ × longitudinal strain ‘e’

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Short Answer Type

Question 1.
Prove that \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\). [Mar. ’14]
Answer:

Question 2.
If A + B = \(\frac{\pi}{4}\), then prove that i) (1 + tan A) (1 + tan B) = 2. ii) (cot A – 1) (cot B -1) = 2. [Mar. 61′(TS), ’07 Ma
Answer:
(i) Given that A + B = 45°
⇒ tan (A + B) = tan 45°
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = 1
⇒ tan A + tan B = 1 – tan A . tan B
⇒ tan A + tan B + tan A tan B = 1

L.H.S = (1 + tan A) (1 + tan B)
= 1 + tan B + tan A + tan A tan B
= 1 + (tan A + tan B + tan A tan B)
= 1 + 1 = 2 = RHS.
∴ (1 + tan A) (1 + tan B) = 2

(ii) Given that A + B = 45°
⇒ cot (A + B) = cot 45°
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}\) = 1
⇒ cot A. cot B – 1 = cot A + cot B
⇒ cot A cot B – cot A – cot B = 1
L.H.S = (cot A – 1) (cot B – 1)
= cot A cot B – cot A – cot B + 1 = (cot A cot B – cot A – cot B) + 1 = 1 + 1=2 = RHS.
∴ (cot A – 1) (cot B – 1) = 2

Question 3.
Prove that sin²θ + sin²(θ + \(\frac{\pi}{3}\)) + sin²(θ – \(\frac{\pi}{3}\)) = \(\frac{\pi}{3}\)
Answer:

Question 4.
If A, B, C are the angles of a triangle and if none of them is equal to \(\frac{\pi}{2}\) then prove that tan A + tan B + tan C = tan A tan B tan C.
Sol. If A, B, C are the angles of a triangle then
A + B + C = 180°
⇒ A + B = 180 0 – C
⇒ tan (A + B) = tan (180° – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = – tan C
⇒ tan A + tan B = – tan C (1 – tan A tan B)
⇒ tan A + tan B = – tan C + tan A tan B tan C
⇒ tan A + tan B + tan C = tan A tan B tan C

Question 5.
If 0 < A < B < \(\frac{\pi}{4}\) and sin(A +B) = \(\frac{24}{25}\) and cos(A – B) = \(\frac{4}{5}\), then find the value of tan 2a.
Answer:
0 < A < \(\frac{\pi}{4}\) and 0 < B < \(\frac{\pi}{4}\) ⇒ 0 < A < B < \(\frac{\pi}{4}\)
∴ (A + B) lies in first quadrant.

Question 6.
If tan α – tan β = m and cot α – cot β = n, then prove that cot(α – β) = \(\frac{1}{m}-\frac{1}{n}\)
Answer:
We have tan α – tan β = m

Question 7.
If \(\frac{\sin (\alpha+\beta)}{\sin (\alpha-\beta)}=\frac{a+b}{a-b}\) then prove that a tan β = b
Answer:
Given \(\frac{\sin (\alpha+\beta)}{\sin (\alpha-\beta)}=\frac{a+b}{a-b}\)
By using componendo and dividendo, we get

Question 8.
If A + B + C = \(\frac{\pi}{2}\) and and if none of A, B, Cs an odd multiple of then prove that cot A + cot B + cot C = cot A cot B cot C.
Answer:
Given A + B + C = \(\frac{\pi}{2}\) ⇒ A + B = \(\frac{\pi}{2}\) – C
∴ cot(A + B) = c(\(\frac{\pi}{2}\) – C) = tanC = \(\frac{1}{\cot C}\)
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}=\frac{1}{\cot C}\)
⇒ cot A + cot B + cot C = cot A cot B cot C

Question 9.
Prove that sin 18° = \(\frac{\sqrt{5}-1}{4}\). [May ’10]
Answer:
Let A = 18°
5A = 90°
2A + 3A = 90°
2A = 90° – 3A
sin 2A = sin (90° – 3A)
sin 2A = cos 3A
2 sin A cos A = 4 cos³A – 3 cos A
2 sin A cos A = cos A (4 cos²A – 3)
2 sin A = 4 cos²A – 3
2 sin A = 4 (1 – sin²A) – 3
2 sin A = 4 – 4 sin²A – 3
2 sin A = 1 – 4 sin²A
4 sin²A + 2 sin A – 1 = 0
This is a quadratic equation in sin A.
Here a = 4,b = 2, c = -1

Since A = 18°, it lies in first quadrant and hence sin A > 0.
sin A = \(\frac{-1+\sqrt{5}}{4}\) ⇒ sin A = \(\frac{\sqrt{5}-1}{4}\)
∴ sin 18° = \(\frac{\sqrt{5}-1}{4}\)

Question 10.
If A is not an integral multiple of \(\frac{\pi}{2}\), prove that
(i) tan A + cot A = 2 cosec 2A,
(ii) cot A – tan A = 2 cot 2A. [B.P] [Mar. ’18(AP)]
Answer:

Question 11.
If θ is not an integral multiple of \(\frac{\pi}{2}\), prove that tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = cot θ. [Mar. ’19(AP); May ’01]
Answer:
We know that cot A – tan A = 2 cot 2A

cot A – tan A = 2 cot 2A
tan A = cot A – 2 cot 2A …………………(1)
Put A = 0 in (1)
tan θ = cot θ – 2 cot 2θ

Put A = 20 in (1)
tan 2θ = cot 2θ – 2 cot 4θ

Put A = 40 in (1)
tan 4θ = cot 4θ – 2 cot 8θ

L.H.S = tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = (cot θ – 2 cot 2θ) + 2 (cot 2θ – 2 cot 4θ) + 4 (cot 4θ – 2 cot 8θ) + 8 cot 8θ
= cot θ – 2 cot 2θ + 2 cot 2θ – 4 cot 4θ + 4 cot 4θ – 8 cot 8θ + 8 cot 8θ = cot θ = R.H.S
∴ tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = cot θ

Question 12.
Prove that sin A. sin(\(\frac{\pi}{3}\) + A) sin (\(\frac{\pi}{3}\) – A) = \(\frac{1}{4}\) sin 3A and hence deduce that sin 20°. sin 40°. sin 60°. sin 80° = \(\frac{3}{16}\). [May ’97, ’93]
Answer:

Let A = 20° ⇒ sin 20°. sin (60° + 20°) sin (60° – 20°)
= \(\frac{1}{4}\) sin 3 (20°)
⇒ sin 20° . sin 80°. sin 40° = \(\frac{1}{4}\) sin 60°

Multiply with sin 60° on both sides then we get
sin 20° . sin 40° . sin 60° . sin 80°
= \(\frac{1}{4}\)sin 60 – \(\frac{1}{4} \cdot\left(\frac{\sqrt{3}}{2}\right)^2=\frac{1}{4} \cdot \frac{3}{4}=\frac{3}{16}\)

Question 13.
Prove that sin⁴\(\frac{\pi}{8}\) + sin⁴\(\frac{5 \pi}{8}\) + sin⁴\(\frac{5 \pi}{8}\) + sin⁴\(\frac{7 \pi}{8}=\frac{3}{2}\). [Mar ’13; Mar. ’00]
Answer:

Question 14.
Show that sin A = \(\frac{\sin 3 A}{1+2 \cos 2 A}\). Hence find the value of sin 15°.
Answer:

Prove that tan α = \(\frac{\sin 2 \alpha}{1+\cos 2 \alpha}\) and hence deduce the values of tan 15° and tan 22\(\frac{1}{2}\)°
Answer:
2 – √3, √2 – 1

Question 15.
Prove that tan 9° – tan 27° – cot 27° + cot 9° = 4.
Answer:
We have tan A + cot A
= \(\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}=\frac{1}{\sin A \cos A}\) = 2 cosec 2A
Put A = 9°, we have tan 9° + cot 9° = 2 cosec 18°
Put A = 27°, we have tan 27° + cot 27° = 2 cosec 54°
L.H.S = tan 9° – tan 27° + cot 9° – cot 27° = 2 (cosec 17° – cosec 54°)

Question 16.
Prove that cos²\(\frac{\pi}{8}\) + cos²\(\frac{3 \pi}{8}\) + cos²\(\frac{5 \pi}{8}\) + cos²\(\frac{7 \pi}{8}\) = 2.
Answer:

Question 17.
Prove that sin\(\frac{\pi}{5}\). sin\(\frac{2 \pi}{8}\).sin\(\frac{3 \pi}{8}\).sin\(\frac{4 \pi}{5}=\frac{5}{16}\). [Mar. ’13]
Answer:
L.H.S = sin\(\frac{\pi}{5}\). sin\(\frac{2 \pi}{8}\).sin\(\frac{3 \pi}{8}\).sin\(\frac{4 \pi}{5}\)
= sin 36° . sin 72°. sin 108°. sin 144°
= sin 36° . sin 72°. sin (90° + 18°) sin (180° – 36°)
= sin 36° . sin (90° -18°). sin (90° +18°). sin (180° – 36°)
= sin 36° . cos 18°. cos 18°. sin 36°
= sin²36° . cos²18°
= \(\left(\frac{10-2 \sqrt{5}}{16}\right)\left(\frac{10+2 \sqrt{5}}{16}\right)\)
= \(\frac{100-20}{256}=\frac{80}{256}=\frac{5}{16}\)

Question 18.
Prove that \(\frac{1-\sec 8 \alpha}{1-\sec 4 \alpha}=\frac{\tan 8 \alpha}{\tan 2 \alpha}\).
Answer:

Question 19.
Prove that [Mar. ’19 (AP) & TS]
(1 + cos\(\frac{\pi}{10}\))(1 + cos\(\frac{3 \pi}{8}\))(1 + cos \(\frac{7 \pi}{8}\))(1 + cos\(\frac{9 \pi}{8}\)) = \(\frac{1}{16}\)
Answer:
LHS = (1 + cos\(\frac{\pi}{10}\))(1 + cos\(\frac{3 \pi}{8}\))(1 + cos \(\frac{7 \pi}{8}\))(1 + cos\(\frac{9 \pi}{8}\)
(1 + cosl8) (1 + cos 54) (1 + cos 126) (1 + cos 162)
= (1 + cos 18) (1 + sin 36) (1 – sin 36) (1 – cos 18)
= (1 + cos 18) (1 – cos 18) (1 + sin 36) (1 – sin 36)
= (1 – cos218°) (1 – sin2 36°)
= sin²18° cos²36° = \(\left(\frac{\sqrt{5}-1}{4}\right)^2\left(\frac{\sqrt{5}+1}{4}\right)^2\)
= \(\frac{(5-1)^2}{256}=\frac{16}{256}=\frac{1}{16}\)

Question 20.
If A is not an integral multiple of t, prove that cos A. cos 2A. cos 4A . cos 8A = \(\frac{\sin 16 A}{16 \sin A}\) and hence deduce that cos\(\frac{2 \pi}{15}\).cos\(\frac{4 \pi}{15}\).cos\(\frac{8 \pi}{15}\).cos\(\frac{16 \pi}{15}=\frac{1}{16}\).
Answer:
L.H.S = cos A. cos 2A. cos 4A . cos 8A

Question 21.
If \(\frac{\sin (\alpha+\beta)}{\cos (\alpha-\beta)}=\frac{1-m}{1+m}\), then prove that tan(\(\frac{\pi}{4}\) – α) = m tan(\(\frac{\pi}{4}\) + β). [Mar. ’95, ’83, ’82, ’81]
Answer:
Given \(\frac{\sin (\alpha+\beta)}{\cos (\alpha-\beta)}=\frac{1-m}{1+m}\)
By using componendo and dividendo we get

Question 22.
If sec (θ + α) + sec (θ – α) = 2 sec θ and cos α ≠ 1, then show that cos θ = ± √2 cos \(\frac{α}{2}\).
Answer:
Given sec (θ + α) + sec (θ – α) = 2 sec θ

⇒ cos²θ cos α = cos²θ – sin²α
⇒ sin²α = cos²θ – cos²θ cos α
⇒ sin²α = cos²θ (1 – cos α)
⇒ 1 – cos²α = cos²θ (1 – cos α)
⇒ (1 – cos α) (1 + cos α) = cos²θ (1 – cos α)
⇒ cos²θ = 1 cos α ⇒ cos²θ = 2 cos²\(\frac{\alpha}{2}\)
⇒ cos θ = ± √2 cos \(\frac{α}{2}\)

Question 23.
If m sin B = n sin (2A + B), then prove that (m + n)tan A = (m – n)tan (A + B). [Apr. ’85]
Answer:
Given m sin B = n sin (2A + B)
⇒ \(\frac{m}{n}=\frac{\sin (2 A+B)}{\sin B}\)
By using componendo and dividendo we get

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Mathematical Induction Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Mathematical Induction Important Questions

Question 1.
By using mathematical induction show that ∀ n ∈ N, 1² + 2² + 3² + ……………… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Answer:
Let S(n) be the statement that 1² + 2² + 3² + …………… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
If n = 1, then
LHS = n² = 1² = 1

∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ 1² + 2² + 3² + ……………… +n² = \(\frac{n(n+1)(2 n+1)}{6}\), ∀ n ∈ N.

Question 2.
By using mathematical Induction show that ∀ n ∈ N, 1³ + 2³ + 3³ + …………. + n³ = \(\frac{n^2(n+1)^2}{4}\). [May 97, 94, 93, 88, Mar. 87]
Answer:
Let S(n) be the statement that 1³ + 2³ + 3³ + ……….. + n³ = \(\frac{n^2(n+1)^2}{4}\)
If n = 1, then
L.H.S = n³ = 1³
R.H.S = \(\frac{n^2(n+1)^2}{4}\) = \(\frac{1^2(1+1)^2}{4}\) = \(\frac{1.4}{4}\) = 1
∴ L.H.S = R.H.S
∴ S(1) is true.
Assume that S(k) is true.

∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ 1³ + 2³ + 3³ + ………… + n³ = \(\frac{n^2(n+1)^2}{4}\), ∀ n ∈ N

Question 3.
By using mathematical induction show that ∀ n ∈ N, 2.3 + 3.4 + 4.5 + …………. upto n terms = \(\frac{n\left(n^2+6 n+11\right)}{3}\)
Answer:
2, 3, 4 ……………………. are in A.P.
Here a = 2, d = 3 – 2 = 1
∴ t_n = a + (n – 1)d = 2 + (n – 1)1 = 2 + n – 1 = n + 1.
3, 4, 5 …………………… are in A.P.
Here a = 3, d = 4 – 3 = 1
∴ t_n = a + (n – 1) d = 3 + (n – 1) 1 = 3 + n – 1 = n + 2.
∴ The n^th term of the given series is (n + 1) (n + 2).
Let S(n) be the statement that
2.3 + 3.4 + 4.5 + + (n + 1) (n + 2) = \(\frac{n\left(n^2+6 n+11\right)}{3}\)
If n = 1, then
LHS = (n + 1) (n + 2) = (1 + 1) (1 + 2) = 2.3 = 6
RHS = \(\frac{\mathrm{n}\left(\mathrm{n}^2+6 \mathrm{n}+11\right)}{3}\) = \(\frac{1\left(1^2+6(1)+11\right)}{3}\) = \(\frac{18}{3}\) = 6
∴ LHS = RHS
∴ S(1) is true.
Assume that S(k) is true.

Verification Method:
\(\frac{\mathrm{n}\left(\mathrm{n}^2+6 n+11\right)}{3}\)
Put n = k + 1

∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 2.3 + 3.4 + 4.5 + ……………… + (n + 1) (n + 2) = \(\frac{\mathrm{n}\left(\mathrm{n}^2+6 \mathrm{n}+11\right)}{3}\), ∀ n ∈ N

Question 4.
By using mathematical induction show that ∀ n ∈ N,
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\) [Mar. 18 May 15 (AP): May 14, 97, 92]
Answer:

Question 5.
By using mathematical induction show that ∀ n ∈ N, \(\frac{1}{1 \cdot 4}+\frac{1}{4 \cdot 7}+\frac{1}{7 \cdot 10}+\) …………….. upto n terms = \(\frac{n}{3 n+1}\).
Answer:
1, 4, 7, ………………… are in A.P.
Here, a = 1, d = 4 – 1 = 3
t_n = a + (n – 1) d = 1 + (n – 1)3 = 1 + 3n – 3 = 3n – 2
4, 7, 10, ………………. are in A.P.
Here, a = 4, d = 7 – 4 = 3
t_n = a + (n – 1) d = 4 + (n – 1)3 = 4 + 3n – 3 = 3n + 1
∴ The n^th term in the given series is \(\frac{1}{(3 n-2)(3 n+1)}\).

Question 6.
By using mathematical induction show that ∀ n ∈ N,
a + (a + d) + (a + 2d) + upto n terms = \(\frac{n}{2}\) [2a + (n – 1) d].
Answer:
a, a + d, a + 2d, ………………….. are in A.P
∴ t_n = a + (n – 1) d
∴ n th term in the given series is a + (n – 1) d.
Let S(n) be the statement that
a + (a + d) + (a + 2d) + ………………. + a + (n – 1) d = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1) d]
If n = 1 then
L.H.S = a + (n – 1)d = a + (1 – 1)d = a
R.H.S = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d] = \(\frac{1}{2}\) [2a + (1 – 1)d] = \(\frac{1}{2}\) [2a] = a
∴ L.H.S = R.H.S
∴ S(1) is true.
[a + (n – 1)d
put n = k + 1
a + (k + 1 – 1)d
= a + kd]
Assume that S(k) is true.
a + (a + d) + (a + 2d) + ………………… + [a + (k- 1) d] = \(\frac{\mathrm{k}}{2}\) [2a + (k – 1)d]
Adding (a + kd) on both sides, we get

∴ S(k + 1) is true.
By the principle of Mathematical Induction, s(n) is true, ∀ n ∈ N
∴ a + (a + d) + (a + 2d) + ….+ a + (n- 1) d = \(\frac{n}{2}\) [2a + (n – 1) d], ∀ n ∈ N

Question 7.
By using mathematical induction show that ∀ n ∈ N,
a + ar + ar² + ………. upto n terms = \(\frac{a\left(r^n-1\right)}{r-1}\), r ≠ 1. [Mar. 19 (AP); Mar. 11, 80; May 87]
Answer:
a + ar + ar² + ………. are in G.P.
∴ t_n = a . r^{n – 1}
The n th term in the given series is a . r ^{n – 1}
Let S(n) be the statement that
a + ar + ar² + …………. + a ∙ r^{n – 1} = \(\frac{a\left(r^n-1\right)}{r-1}\)
If n = 1, then
L.H.S = a ∙ r^{n – 1} = a ∙ r^{1 – 1} = a ∙ r⁰ = a ∙ 1 = a
R.H.S = \(\frac{a\left(r^n-1\right)}{r-1}=\frac{a\left(r^1-1\right)}{r-1}=\frac{a(r-1)}{r-1}\) = a
∴ L.H.S = R.H.S
∴ S(1) is true.
[a.r^{n – 1}
Put n = k + 1
a.r^{k + 1 – 1}
a.r^k]
Assume that S(k) is true.
a + ar + ar² + …….. + a.r^{k – 1} = \(\frac{a\left(r^k-1\right)}{r-1}\)
Adding ar^k on both sides we get,

∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ a + ar + ar² + ………………. + a . r^{n – 1} = \(\frac{a\left(r^n-1\right)}{r-1}\)

Question 8.
By using mathematical induction show that ∀ n ∈ N, 1.2.3 + 2.3.4 + 3.4.5 + …………………. upto n terms = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
Answer:
1, 2, 3 …………………. are in A.P.
Here a = 1, d = t₂ – t₁ = 2 – 1 = 1
t_n = a + (n – 1)d = 1 + (n – 1)1 = 1 + n – 1 = n
2, 3, 4 ………………… are in A.P.
Here a = 2, d = 3 – 2 = 1
t_n = a + (n – 1)d = 2 + (n – 1)1 = 2 + n – 1 = n + 1
3, 4, 5 …………….. are in A.P.
Here a = 3, d = 4 – 3 = 1
t_n = a + (n – 1)d = 3 + (n – 1)1 = 3 + n – 1 = n + 2
∴ The nth term in the given series is n(n + 1) (n + 2).
Let S(n) be the statement that
1.2.3 + 2.3.4 + 3.4.5 + ……………….. + n (n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
If n = 1 then
L.H.S = n(n + 1) (n + 2) = 1(1 + 1) (1 + 2) = 1.2.3 = 6
R.H.S = \(\frac{n(n+1)(n+2)(n+3)}{4}\) = \(\frac{1(1+1)(1+2)(1+3)}{4}\) = \(\frac{1.2 .3 .4}{4}\) = 6
∴ L.H.S = R.H.S
∴ S(1) is true Assume that s(k) is true
1.2.3 + 2.3.4 + 3.4.5 + ……………….. + k (k + 1) (k + 2) = \(\frac{\mathrm{k}(\mathrm{k}+1)(\mathrm{k}+2)(\mathrm{k}+3)}{4}\)
Adding (k + 1) (k + 2) (k + 3) on both sides we get
1.2.3 + 2.3.4 + 3.4.5 + …………….. + k (k + 1) (k + 2) + (k + 1) (k + 2) (k + 3)

∴ S(k + 1) is true.
∴ By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 1.2.3 + 2.3.4 + 3.4.5 + ……………… + n(n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\) ∀ n ∈ N.

Question 9.
By using mathematical induction show that ∀ n ∈ N,
\(\frac{1^3}{1}+\frac{1^3+2^3}{1+3}+\frac{1^3+2^3+3^3}{1+3+5}\) + ……………….. upto n terms = \(\frac{n}{24}\) [2n² + 9n + 13]. [Mar. 14, 07, 05]
Answer:
Numerator: n^th = 1³ + 2³ + 3³ + …………. + n³ = Σn³ = \(\frac{n^2(n+1)^2}{4}\)

Denominator: 1 + 3 + 5 + ………………. are in A.P.
Here a = 1, d = 3 – 1 = 2
t_n = a + (n – 1) d = 1 + (n – 1) 2 = 1 + 2n – 2 = 2n – 1
∴ n^th term is

∴ L.H.S = R.H.S
∴ S(1) is true.
Assume that S(k) is true.

Verification Method: \(\frac{\mathrm{n}}{24}\) [2n² + 9n + 13]
Put n = k + 1
= \(\frac{(\mathrm{k}+1)}{24}\) [2(k + 1)² + 9 (k + 1) + 13] = \(\frac{(\mathrm{k}+1)}{24}\) [2k² + 2 + 4k + 9k + 9 + 13]
= \(\frac{1}{24}\) [2k³ + 2k + 4k² + 9k² + 9k + 13k + 2k² + 2 + 4k + 9k + 9 + 13] = \(\frac{1}{24}\) [2k³ + 15k² + 37k + 24]
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.

Question 10.
By using mathematical induction show that ∀ n ∈ N, 1² + (1² + 2²) + (1² + 2² + 3²) + ……….. upto n terms = \(\frac{n(n+1)^2(n+2)}{12}\).
Answer:

Question 11.
By using mathematical induction show that ∀ n ∈ N, 2 + 3.2 + 4.2² + ……… upto n terms
Answer:
2.1 + 3.2 + 4.2² + ………………… upto n terms = n . 2ⁿ
2, 3, 4 ………….. are in A.P.
Here a = 2, d = 3 – 2 = 1
t_n = a + (n – 1)d = 2 + (n – 1)1 = 2 + n – 1 = n + 1
1, 2, 2², ……………… are in G.P.
Here a = 1, r = \(\frac{2}{1}\) = 2
t_n = a . r^{n – 1} = 1 . 2^{n – 1} = 2^{n – 1}
∴ The nth term in the given series is (n + 1) (2^{n – 1}).
Let S(n) be the statement that
2.1 + 3.2 + 4.2² + ……….. + (n + 1) 2^{n – 1} = n . 2ⁿ
If n = 1, then
L.H.S. = (n + 1)^{2n – 1} = (1 + 1) 2^{1 – 1} = 2.2⁰ = 2.1 = 2
R.H.S. = n . 2ⁿ = 1.2¹ = 2
∴ LHS = RHS
∴ S(1) is true.
[(n + 1)^{2n – 1}
put n = k + 1
(k + 1 + 1) 2^{k + 1 – 1}
(k + 2) . 2^k]
Assume that S(k) is true.
2.1 + 3.2 + 4.2² + ……….. + (k + 1)^{2k – 1} = k . 2k
Adding (k + 2) . 2^k on both sides, we get
2.1 + 3.2 + 4.2² + ………… + (k + 1) 2^{k – 1} + (k + 2) 2^k = k. 2^k + (k + 2) . 2^k = 2^k (k + k + 2)
= 2^k (2k + 2) = 2^k . 2 (k + 1) = (k + 1) . 2^{k + 1}
∴ S(k + 1) is true.
∴ By the principle of mathematical induction, S(n) is true, ∀ n ∈ N.
2.1 + 3.2 + 4. 2² + ……………… + (n + 1) 2^{n – 1} = n . 2ⁿ, ∀ n ∈ N.

Question 12.
By using mathematical induction show that ∀ n ∈ N, 49ⁿ + 16n – 1 is divisible by 64 for all positive integer n. [Mar. 18 (TS); Mar. 17 (AP); May 13, 05, 98, 93]
Answer:
Let S(n) be the statement that f(n) = 49ⁿ + 16n – 1 is divisible by 64.
If n = 1, then
f(1) = 49¹ + 16.1 – 1 = 49 + 16 – 1 = 49 + 15 = 64 = 64 × 1 is divisible by 64
∴ S(1) is true.
Assume that S(k) is true.
f(k) is divisible by 64 ⇒ 49^k + 16k – 1 is divisible by 64
⇒ 49^k + 16k – 1 = 64 M for some integer M ⇒ 49^k = 64M – 16k + 1
Now
f(k + 1) = 49^{k + 1} + 16 (k + 1) – 1 = 49^k. 49 + 16k + 16 – 1 = (64M – 16k + 1) 49 + 16k + 15
= 64.49M – 784k + 49 + 16k + 15 = 64.49M – 768k + 64
= 64(49M – 12k + 1) is divisible by 64. [ ∵ 49M – 12k + 1 is an integer]
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true ∀ n ∈ N.
∴ 49ⁿ + 16n – 1 is divisible by 64, ∀ n ∈ N.

Question 15.
By using mathematical induction show that 3 ∙ 5^{2n + 1} + 2^{3n + 1} is divisible by 17 ∀ n ∈ N. [May 12, 10, 08, 01, ’96]
Answer:
Let S(n) be the statement that f(n) = 3 . 5^{2n + 1} + 2^{3n + 1} is divisible by 17.
If n = 1, then
f(1) = 3.5^{2.1 + 1} + 2^{3.1 + 1} = 3.5³ + 24 = 3(125) + 16 = 375 + 16 = 391 = 17 × 23 is divisible by 17
∴ S(1) is true.
Assume that S(k) is true.
∴ f(k) is divisible by 17.
⇒ 3.5^{2k + 1} + 2^{3k + 1} is divisible by 17.
⇒ 3.5^{2k + 1} + 2^{3k + 1} = 17 M for some integer M.
⇒ 3.5^{2k + 1} = 17M – 2^{3k + 1}
Now f (k + 1) = 3 . 5^{2(k + 1) + 1} + 2^{3(k + 1) + 1} = 3.5^{2k + 2 + 1} + 2^{3k + 3 + 1}
= 3.5^{2k + 1} . 5² + 2^{3k + 1} . 2³
= (17M – 2^{3k + 1}) 25 + 8 . 2^{3k + 1} = 17.25 M – 25.2^{3k + 1} + 8 . 2^{3k + 1}
= 17.25 M – 17.2^{3k + 1}
= 17 (25 M – 2^{3k + 1}) is divisible by 17. [∵ 25M – 2^{3k + 1} is an integer]
∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 3 . 5^{2n + 1} + 2^{3n + 1} is divisible by 17, ∀ n ∈ N.

Question 14.
By using mathematical induction show that ∀ n ∈ N, xⁿ – yⁿ is divisible by x – y. [May 04]
Answer:
Let S(n) be the statement that f(n) = xⁿ – yⁿ is divisible by (x – y).
If n = 1 then
f(1) = x¹ – y¹ = x – y = (x – y) × 1 is divisible by (x – y)
∴ S(l) is true.
Assume that S(k) is true.
f(k) is divisible by (x – y).
⇒ x^k – y^k is divisible by (x – y)
⇒ x^k – y^k = (x – y) M, for some integer M.
⇒ x^k = (x – y) M + y^k
Now
f(k + 1) = x^{k + 1} – y^{k + 1} = x^k . x – y^k . y = [(x – y) M + y^k] x – y^k . y = (x – y) . M x + y^k . x – y^k . y
= (x – y) M x + y^k (x – y) = (x – y) [Mx + y^k] is divisible by (x – y).
[Mx + y^k] is an integer.
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ xⁿ – yⁿ is divisible by (x – y), ∀ n ∈ N.

Some More Maths 1A Mathematical Induction Important Questions

Question 1.
By using mathematical induction show that ∀ n ∈ N, 4³ + 8³+ 12³ + ……………. upto n terms = 16n² (n + 1)².
Answer:
4, 8, 12, are in A.P.
Here a = 4, d = t₂ – t₁ = 8 – 4 = 4
t_n = a + (n – 1)d = 4 + (n – 1)4 = 4 + 4n – 4 = 4n
∴ The nth term in the given series is (4n)³ = 64n³
Let S(n) be the statement that 4³ + 8³ + 12³ + …………….. + 64n³ = 16n² (n + 1)²
If n = 1, then
LHS = 64n³ = 64(1)³ = 64
RHS = 16n² (n + 1)² = 16.1² (1 +!)² = 16.1.4 = 64
∴ LHS = RHS
∴ S(1) is true.
Assume that S(k) is true.
4³ + 8³ + 12³ + ………………….. + 64k³ = 16k² (k + 1)²
Adding 64(k + 1)³ on both sides, we get
4³ + 8³ + 12³ + …………….. + 64k³ + 64(k + 1)³ = 16k² (k + 1)² + 64 (k + 1)³ = 16(k + 1)² [k² + 4 (k + 1)]
= 16(k + 1)² [k² + 4k + 4] = 16(k + 1)² (k + 2)² = 16(k + 1)² (k + 1 + 1)²
∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 4³ + 8³ + 12³ + ………………. + 64n³ = 16n² (n + 1)², ∀ n ∈ N.

Question 2.
By using mathematical induction show that ∀ n ∈ N. 2.4^{2n + 1} + 3^{3n + 1} is divisible by 11.
Answer:
Let S(n) be the statement that f(n) = 2.4^{2n + 1} + 3^{3n + 1} is divisible by 11.
If n = 1, then
f(1) = 2.4^{2.1 + 1} + 3^{3.1 + 1} = 2.4³ + 34 = 2(64) + 81
= 128 + 81 = 209 = 11 × 19 is divisible by 11.
∴ S(1) is true.
Assume that S(k) is true.
∴ f(k) is divisible by 11.
⇒ 2.4^{2k + 1} + 3^{3k + 1} is divisible by 11
⇒ 2.4^{2k + 1} + 3^{3k + 1} = 11 M, for some integer M
⇒ 2.4^{2k + 1} = 11 M – 3^{3k + 1}
Now f(k + 1) = 2.4^{2(k + 1) + 1} + 3^{3(k + 1) + 1} = 2.4^{2k + 2 + 1} + 3^{3k + 3 + 1} = 2.4^{2k + 1} . 4² + 3^{3k + 1} . 3³
= (11 M – 3^{3k + 1}) 16 + 27. 3^{3k + 1} = 11.16 M – 16. 3^{3k + 1} + 27.3^{3k + 1} = 11.16M + 11.3^{3k + 1}
= 11(16 M + 3^{3k + 1}) is divisible by 11 (∵ 16 M + 3^{3k + 1} is an integer)
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ 2.4^{2n + 1} + 3^{3n + 1} is divisible by 11, ∀ n ∈ N.

Question 3.
Using mathematical induction prove that statement for all ∀ n ∈ N,
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 n+1}{n^2}\right)\) = (n + 1)²
Answer:
Let S(n) be the statement that \(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 n+1}{n^2}\right)\) = (n + 1)²
If n = 1, then
LHS = 1 + \(\frac{2 n+1}{n^2}\) = 1 + \(\frac{2.1+1}{(1)^2}\) = 1 + \(\frac{2+1}{1}\) = 1 + 3 = 4
RHS = (n + 1)² = (1 + 1)² = (2)² = 4
∴ LHS = RHS
∴ S(1) = is true
Assume that S(k) is true

Telangana TSBIE TS Inter 1st Year Physics Study Material 9th Lesson Gravitation Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 9th Lesson Gravitation

Very Short Answer Type Questions

Question 1.
State the unit and dimension of universal gravitational constant (G).
Answer:
Units of G = N-m² / kg².
Dimensional formula = M^-1 L³ T^-2.

Question 2.
State the vector form of Newton’s law of gravitation.
Answer:
Vector form of Newton’s Law of gravitation is \(\overline{\mathrm{F}}=\frac{\mathrm{Gm}_1 \mathrm{~m}_2 \overline{\mathrm{r}}}{\overline{\mathbf{r}}^3}\)

Question 3.
If the gravitational force of the Earth on the Moon is F. What is the gravitational force of the moon on the earth? Do these forces form an action-reaction pair?
Answer:
Gravitational force between earth and moon and moon and earth are same
i-e., F_EM = – F_ME

Gravitational force between the bodies are treated as action-reaction pair.

Question 4.
What would be the change in acceleration due to gravity (g) at the surface, if the radius of Earth decreases by 2% keeping the mass of Earth constant?
Answer:
Acceleration due to gravity, g = \(\frac{GM}{R^2}\)
When mass is kept as constant and radius
is decreased by 2% then \(\frac{\Delta \mathrm{R}}{\mathrm{R}}\) × 100 = 2

From distribution of errors in multiplications and divisions \(\frac{\Delta \mathrm{g}}{\mathrm{g}}\) × 100 = -2\(\frac{\Delta \mathrm{R}}{\mathrm{R}}\) × 100

% Change in g = – 2 × 2 = – 4% – ve sign indicates that when R decreases ‘g’ increases.

Question 5.
As we go from one planet to another, how will a) the mass and b) the weight of a body change?
Answer:

1. As we go from one planet to another planet mass of the body does not change. Mass of a body is always constant.
2. As we move from one planet to another planet weight of the body gradually decreases. It become weightless. When we approaches the other planet the weight will gradually increases.

Question 6.
Keeping the length of a simple pendulum constant, will the time period to be the same on all planets? Support your answer with reason.
Answer:
Even though length of pendulum / is same the time period of oscillation T value changes from planet to planet.
Time period of pendulum, T = 2π\(\sqrt{\frac{l}{g}}\)
i.e., T depends on l and g.

Acceleration due to gravity, (g = \(\frac{GM}{R^2}\)) changes from planet to planet.

Hence Time period of pendulum changes even though length ‘l’ is same.

Question 7.
Give the equation for the value of g at a depth ‘d’ from the surface of Earth. What is the value of ‘g’ at the centre of Earth?
Answer:
Acceleration due to gravity at a depth ‘d’ below the ground is, gd = g(1 – \(\frac{D}{R}\))
Acceleration due to gravity at centre of earth is zero. (Since D = R)

Question 8.
What are the factors that make ‘g’ the least at the equator and maximum at the poles?
Answer:
‘g’ is least at equator due to
1) The equatorial radius of earth is maximum ∵ g = \(\frac{GM}{R^2}\) (∵ R = maximum)

2) Due to rotation of earth centrifugal force will act on the bodies. It opposes gravitational pull of earth on the bodies. At equator centrifugal force is maximum. So ‘g’ value is least at equator.
The g’ ⇒ maximum at poles due to

1) The polar radius of earth is minimum
(∵ g = \(\frac{GM}{R^2}\))

2) Centrifugal force due to rotation of earth is zero at poles. This centrifugal force reduces earth’s gravitational pull.

Since Centrifugal force is zero, ‘g’ value is maximum at poles.

Question 9.
“Hydrogen is in abundance around the sun but not around earth”. Explain.
Answer:
The escape velocity on the sun is very high compared to that on the earth. The gravitational pull of the sun is very large because of its larger mass compared to that of the earth. So it is very difficult for hydrogen to escape from the Sun’s atmosphere. Hence hydrogen is abundant on sun.

Question 10.
What is the time period of revolution of a geostationary satellite? Does it rotate from West to East or from East to West?
Answer:
Time period of geostationary satellite is equal to time period of rotation of earth.

∴ Time period of geostationary orbit T = 24 hours. Satellites in geostationary orbit will revolve round the earth in west to east direction in an equatorial plane.

Derive the relation between acceleration due to gravity (g) at the surface of a planet and Gravitational constant (G).

Question 11.
What are polar satellites?
Answer:
Polar satellite :
Polar satellites are low altitude satellites. They will revolve around the poles of the earth in a north-south direction. Time period of polar satellites is nearly 100 minutes.

Short Answer Questions

Question 1.
State Kepler’s Laws of planetary motion. [TS Mar. ’17]
Answer:
Kepler’s Laws :
Law of orbits (1st law):
All planets will move in elliptical orbits with the sun lies at one of its foci.

Law of areas (2nd law) :
The line that joins any planet to the sun sweeps equal areas in equal intervals of time, i.e., \(\frac{\Delta \mathrm{A}}{\Delta \mathrm{T}}\)= constant. i.e., planets will appear to move slowly when they are away from sun, and they will move fast when they are nearer to sun.

Law of periods (3rd law) :
The square of time period of revolution of a planet is proportional to the cube of the semi major axis of the ellipse traced out by the planet.
i.e., T² ∝ R³ or \(\frac{T^2}{R^3}\) = constant

Question 2.
Derive the relation between acceleration due to gravity (g) at the surface of a planet and Gravitational constant (G).
Answer:
Relation between g and G :
Each and everybody was attracted towards centre of earth with some force. This is called weight of the body,
W = mg …………. (1)

This force is due to gravitational pull on the body by the earth.

For small distances above earth from centre of earth is equal to radius of earth ‘R’.

According to Newton’s law of gravitation.

Question 3.
How does the acceleration due to gravity (g) change for the same values of height (h) and depth(d)?
Answer:
Variation of ‘g’ with altitude :
When we go to a height ‘h’ above the ground ‘g’ value decreases.
On surface of earth (g) = \(\frac{GM}{R^2}\)
At an altitude ‘h’ g(h) = \(\frac{GM}{(R+h)^{2}}\) because

R + h is the distance from centre of earth to the given point at ‘h’.
h << R ⇒ g(h) = g(1 – \(\frac{2h}{R}\))
So acceleration due to gravity decreases with height above the ground.

Variation of ‘g’ with depth :
When we go deep into the ground ‘g’ value decreases.

At a depth ‘d’ inside the ground mass of earth upto the point d from centre will exhibit force of attraction on the body. The remaining mass does not exhibit any influence. So effective radius is (R – d) only. Acceleration due to gravity ‘g’ at a depth ‘d’ is given by

So ‘g’ value decreases with depth below the ground.

Question 4.
What is orbital velocity? Obtain an expression for it. [AP Mar. 17, 14; May 18. 14]
Answer:
Orbital velocity (V₀) :
Velocity of a satellite moving in the orbit is called orbital velocityog.

Let a satellite of mass m is revolving round the earth in a circular orbit at a height ‘h’ above the ground.

Radius of the orbit = R + h where R is radius of earth.

In orbital motion is “The centrifugal and centripetal forces acting on the satellite”.

Centrifugal force = \(\frac{mV^2}{r}=\frac{mV^{2}_{0}}{R+h}\) ……… (1)
(In this case V = V₀ and r = R + h)

Centripetal force is the force acting towards the centre of the circle it is provided by gravitational force between the planet and satellite.

V₀ = \(\sqrt{gR}\) is called orbital velocity. Its value is 7.92 km/sec.

Question 5.
What is escape velocity? Obtain an expression for it. [TS Mar. ’19, ’16; AP Mar. ’19. ’18, ’15, ’13. May ’17, ’16]
Answer:
Escape speed (v₁)_min :
It is defined as the minimum velocity required by a body to overcome gravitational field of earth is known as escape velocity.

For a body of mass ‘m’ gravitational potential energy on surface of earth PE = – \(\frac{G.m.M_E}{R_E}\)

For a body to escape from gravitational field of earth its kinetic energy must be equal or more than gravitational potential energy.

Question 6.
What is a geostationary satellite? State [AP Mar. ’16, June ’15; May ’13; TS Mar. ’18, ’15, May ’18, ’16, June ’15]
Answer:
A geostationary satellite will always appears to be stationary relative to earth.

The time period of geostationary satellite is equals to time perfod of rotation of earth.

∴ Time period of geostationary orbit t = 24 hours. Satellites in geostationary orbit will revolve round the earth in west to east direction in an equatorial plane.

Uses of geostationary satellites:

1. For study of the upper layers of the atmosphere.
2. For forecasting the changes in atmosphere and weather.
3. For finding the size and shape of earth.
4. For investigating minerals and ores present in the earth’s crust.
5. For transmission of T.V. signals.
6. For study of transmission of radio waves.
7. For space research.

Question 7.
If two places are at the same height from the mean sea level; One is a mountain and other is in air. At which place will ‘g’ be greater? State the reason for your answer.
Answer:
‘g’ value on the mountain is greater than g’ value in air even though both are at same height.

For a point on mountain while deciding the ‘g’ value, mass of mountain is also considered which leads to change in ‘g’ value depending on local condition such as concentration of huge mass at a particular place. Whereas for a point in air no such effect is considered. Hence ‘g’ on the top of mountain is more.

Question 8.
The weight of an object is more at the poles than at the equator. At which of these can we get more sugar for the same weight? State the reason for your answer.
Answer:
If we are using common balance to measure sugar we will get some quantity of sugar both at equator and at poles.

Whereas if we are using spring balance to weigh sugar then weight of sugar at poles is more. So we will get less quantity.

Weight of sugar at equator is less. So we will get more quantity of sugar at equator.

Question 9.
If a nut becomes loose and gets detached from a satellite revolving around the earth, will it fall down to earth or will it revolve around earth? Give reasons for your answer.
Answer:
If a nut is detached from a satellite revolving in the orbit then its velocity is equals to orbital velocity. So it continues to revolve in the same orbit. It does not fall to earth.

Question 10.
An object projected with a velocity greater than or equal to 11.2 km.s^-1 will not return to earth. Explain the reason.
Answer:
Escape velocity of earth is 11.2 km/sec. If any body acquires a velocity of 11.2 km/ sec. or more its kinetic energy is more than gravitational potential energy. So earth is not able to stop the motion of that body. So any body with a velocity 11.2 km/s or more will escape from gravitational field of earth and never comes back to earth.

Long Answer Questions

Question 1.
Define gravitational potential energy and derive an expression for it associated with two particles of masses m₁ and m₂.
Answer:
Gravitational potential energy of a body at a point in a gravitational field of another. It is defined as the amount of work done in brining the given body from infinity to that point in the field is called Gravitational potential energy.

Expression for gravitational potential energy :
Consider two particles of masses m, and m2 are placed at the points O’ and p respectively. Let the distance between the two particles is r’ i.e., OP = r.

Let us calculate the gravitational potential energy of the particle of mass m₂ placed at point p in the gravitational field of m₁. Join OP and extended it in forward direction. Consider two points A and B on this line such that OA = x and AB = dx.

The gravitational force of attraction on the particle at A is, F = \(\frac{\mathrm{Gm_1m_2}}{\mathrm{x^2}}\)

Small amount of work done in bringing the particle without acceleration through a very small distance AB is, dW = F dx
= \(\frac{\mathrm{Gm_1m_2}}{\mathrm{x^2}}\)

Total workdone in bringing the particle from infinity to the point P is,

Since, this work done is stored in the particle as its gravitational potential energy (U). Therefore, gravitational potential energy of the particle of mass m₂ placed at point p’ in the gravitational field of particle of mass
m₁ at distance r is, U = \(\frac{\mathrm{-Gm_1m_2}}{\mathrm{r}}\)

Here, negative sign shows that the potential energy is due to attractive gravitational force between two particles.

Question 2.
Derive an expression for the variation of acceleration due to gravity (a) above and (h) below the surface of the Earth.
Answer:
Variation of acceleration due to gravity above the surface of earth :
We know ‘g’ on planet, g = \(\frac{GM}{R^2}\). But on earth g’ value changes with height above the ground h’.

Variation of ‘g’ with altitude :
For a point h’ above the earth total mass of earth seems to be concentrated at centre of earth. Now distance from centre of earth is (R + h).
Acceleration due to gravity at ‘h’ = g(h)
= \(\frac{GM_E}{(R_E+h)^2}\)

For small values of ‘h’ i.e., h << R than

Variation of acceleration due to gravity below the surface of earth :
At a depth d’ inside the ground mass of earth upto the point d from centre will exhibit force of attraction on the body. The remaining mass does not exhibit any influence.
Mass of spherical body M ∝ R³

∴ M_S/M_E = (R_E – d)³/ R³^E where M_s is mass of earth’s shell upto a depth ‘d’ from centre. Gravitational force at depth ‘d’ is

So ‘g’ value decreases with depth below the ground.

Question 3.
State Newton’s Universal Law of Gravitation. Explain how the value of the Gravitational constant (G) can be determined by Cavendish method.
Answer:
Newton’s law of gravitation :
Every body in the universe attracts every other body with a force which is directly proportional to theproduct of their masses and inversely proportional to the square of the distance between them.

This is always a force of attraction and acts along the line joining the two bodies.

Cavendish experiment to find gravitational constant ‘G’ :
Cavendish experiment consists of a long metalic rod AB to which two small lead spheres of mass ‘m’ are attached.

This rod is suspended from a rigid support with the help of a thin wire. Two heavy spheres of mass M are brought near to these small spheres in opposite direction. Then gravitational force will act between the spheres.

Force between the spheres, r = \(\frac{GMm}{d^2}\)

Two equal and opposite forces acting at the two ends of the rod AB will develop force couple and the rod will rotate through an angle ‘θ’.
∴ Torque on the rod F × L = \(\frac{GM.m}{d^2}\) → (1)
Restoring force couple = τθ → (2)
Where τ = Restoring couple per unit twist

By measuring 0 we can calculate ‘G’ value when other parameters are known. Practical value of G is 6.67 × 10^-11 Nm²/kg².

Problems

(Gravitational Constant ‘G’ = 6.67 × 10^-11 Nm²kg^-2; Radius of earth ‘R’ = 6400 km; Mass of earth ‘M_E‘ = 6 × 10²⁴ kg)

Question 1.
Two spherical balls each of mass 1 kg are placed 1 cm apart. Find the gravitational force of attraction between them.
Solution:
Mass of each ball, m = 1 kg;
Separation, r = 1 cm = 10^-2 m
Gravitational force of attraction,

Question 2.
The mass of a ball is four times the mass of another ball. When these balls are separated by a distance of 10 cm, the gravitational force between them is 6.67 × 10^-7 N. Find the masses of the two balls.
Solution:
Mass of 1st ball = m;
Mass of 2nd ball = 4m.
Separation, r = 10 cm = 0.1 m;
Mass of the 1st ball = m = ?
Gravitational force, F = 6.67 × 10^-7 N
∴ Mass of the balls are 5 kg, 20 kg.

Question 3.
Three spherical balls of masses 1 kg, 2 kg and 3 kg are placed at the corners of an equilateral triangle of side 1 m. Find the magnitude of the gravitational force exerted by the 2 kg and 3 kg masses on the 1 kg mass.
Solution:
Side of equilateral triangle, a = lm.
Masses at corners = 1 kg, 2 kg, 3 kg.
Force between 1 kg, 2g = F₁ = G.\(\frac{2\times1}{1^2}\) = 2 G
Force between I kg, 3kg = F₂ = G.\(\frac{3\times1}{1^2}\)= 3G.
Now F₁ & F₂ act with an angle of 60°
∴ Resultant force

Question 4.
At a certain height above the earth’s surface, the acceleration due to gravity is 4% of its value at the surface of the earth. Determine the height.
Solution:
Acceleration due.to gravity at a height, h = 4% of g.
Radius of earth, R = 6400K.M. = 6.4 × 10⁶m.

Question 5.
A satellite orbits the earth at a height of 1000 km. Find its orbital speed.
Solution:
Radius of earth, R = 6,400 km = 6.4 × 10⁶ m;
Mass of earth, M = 6 × 10²⁴
Height of satellite h = 1000 km;
G = 6.67 × 10¹¹ N – m² /kg²

Question 6.
A satellite orbits the earth at a height equal to the radius of earth. Find it’s (i) orbital speed and (ii) Period of revolution.
Solution:
Radius of earth, R = 6400 k.m.;
-height above earth, h = R.
Mass of earth, M = 6 × 10²⁴
G = 6.67 × 10^-11 N – m²/kg²

Question 7.
The gravitational force of attraction between two objects decreases by 36% when the distance between them is increased by 4 m. Find the original distance between them.
Solution:
Let force between the objects = F;
Distance between them = r.
For Case II distance, r₁ = (r + 4);
New force, F₁ = 36% less than F

⇒ 100 r² = 64 (r + 4)² Take square roots on both sides.
10r = 8 (r + 4) ⇒ 10 r = 8r + 32
⇒ (10 – 8) r = 2r = 32
∴ r = 16 m.

Question 8.
Four identical masses m are kept at the corners of a square of side a. Find the gravitational force exerted on one of the masses by the other masses.
Solution:
Given all masses are equal
∴ m₁ = m₂ = m₃ = m₄
Force between m₁, m₄ = F₁ = \(\frac{G.m^2}{a^2}\) ……… (1)
Force between m₄, m₃ = F₂ = \(\frac{G.m^2}{a^2}\) ……… (2)
Forces F₁ and F₂ act perpendicularly.

Their magnitudes are equal.

Now forces F_R and F₃ are like parallel. So resultant is sum of these forces.
Total force at m₄ due to other masses

Question 9.
Two spherical balls of 1 kg and 4 kg are separated by a distance of 12 cm. Find the distance of a point from the 1 kg mass at which the gravitational force on any mass becomes zero.
Solution:
Mass, m₁ = 1 kg ; Mass, m₂ = 4 kg ;
Separation, d = 12 cm
Mass of 3rd body m₃ = ?

For m₃ not to experience any force the condition is
Force between m₁, m₃ = Force between m₂, m₃.

Take square roots on both sides,
d – x = 2x ⇒ d = 3x or x = \(\frac{12}{3}\) = 4 cm
∴ Distance from 1 kg mass = 4 cm

Question 10.
Three uniform spheres each of mass m and radius R are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any one of the spheres due to the other two.
Solution:
Mass m and radius R are same for all spheres.
Force between 1, 3 spheres = F₁ = \(\frac{G.m^2}{(2R)^2}\)
Force between 1, 2 spheres = F₂ = \(\frac{G.m^2}{(2R)^2}\)

Now F₁ and F2 will act with an angle θ = 60° between them so from Parallelogram law

Question 11.
Two satellites are revolving round the earth at different heights. The ratio of their orbital speeds is 2 : 1. If one of them is at a height of 100 km what is the height of the other satellite?
Solution:
Mass of earth, m = 6 × 10²⁰ kg ;
G = 6.67 × 10^-11 N-m² / kg²
Ratio of orbital velocities V₀₁ : V₀₂ = 2 : 1;
Height of one satellite, h = 100 k.m

4R + 4h₂ = R + h₁ ⇒ h₁ = 3R + 4h₂. ;
Put h₂ = 100 km
∴ h₁ = 3 × 6400 + 400 = 19600 km.

Question 12.
A satellite is revolving round in a circular orbit with a speed of 8 km/ s^-1 at a height where the value of acceleration due to gravity is 8 m/s^-2. How high is the satellite from the Earth’s surface? (Radius of planet 6000 km.).
Solution:
Orbital velocity of satellite, V₀ = 8 km/s.
= 8 × 10³ m/s.
Acceleration due to gravity in the orbit = g
= 8 m/s²

Orbital velocity, V = \(\sqrt{gR}\)
where R is radius of the orbit and g is acceleration due to gravity in the orbit.

Height of satellite = 8000 – radius of earth ;
Radius of earth = 6000 km.
∴ Height above earth = 8000 – 6000
= 2000 km.

Question 13.
(a) Calculate the escape velocity of a body from the Earth’s surface, (b) If the Earth were made of wood, its mass would be 10% of its current mass. What would be the escape velocity, if the Earth were made of wood?
Solution:
Radius of earth, R = 6400 km = 6.4 × 10⁶ m.
Mass of earth, M = 6 × 10²⁴ kg; g = 9.8 ms^-2.
a) Escape velocity, V_e = \(\sqrt{2gR}\)
∴ V_e = \(\sqrt{2\times9.8\times6.4\times10^6}\) = 11.2 km/s

b) If earth is made of wood mass,
M₁ = 10% of M = 6 × 10²³

Additional Problems

Question 1.
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed (b) angular speed (c) angular momentum (d) kinetic energy (e) potential energy (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
Solution:
A comet while going on elliptical orbit around the Sun has constant angular momentum and total energy at all locations but other quantities vary with locations.

Question 2.
A Saturn year is 29.5 times the earth year. How far is the Saturn from the sun if the earth is 1.5 × 10⁸ km away from the sun? Solution:
Here, T_s = 29.5 T_e; R_e = 1.5 × 10⁸ km; R_s = ?

Question 3.
A body weighs 63 N on the surface of Earth. What is the gravitational force on it due to the Earth at a height equal to half the radius of the Earth?
Solution:
Weight of body = mg = 63 N
At height h, the value of g’ is given by,

Question 4.
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of earth if it weighed 250 N on the surface?
Solution:
Weight of body at a depth, d = mg’

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Very Short Answer Type

Question 1.
If cos θ = t(0 < t < 1) and θ does not lies in the first quadrant, find the values of sin θ and tan θ. [Mar. ’17(AP)]
Answer:
cos θ = t, (0< t < 1)
⇒ cos θ is positive and θ does not lie in first quadrant
⇒ θ lies in IVth quadrant
(a) sin θ = \(-\sqrt{1-\cos ^2 \theta}=-\sqrt{1-t^2}\)
(b) tan θ = \(-\sqrt{1-\cos ^2 \theta}=-\sqrt{1-t^2}\)

Question 2.
Find the value of sin²\(\frac{\pi}{10}\) + sin²\(\frac{4 \pi}{10}\) + sin²\(\frac{6 \pi}{10}\) + sin²\(\frac{9 \pi}{10}\)
Answer:

Question 3.
If sin θ = –\(\frac{1}{3}\) and θ does not lie in the third quadrant, find the value of cos θ, cot θ. [Mar. ’19(TS); Mar. ’13]
Answer:
sin θ = –\(\frac{1}{3}\) and sin θ is negative and does not lie in third quadrant, ⇒ θ lies in fourth quadrant. In IV quadrant cos θ is positive.
cos θ = \(\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{1}{9}}=\frac{2 \sqrt{2}}{3}\)
cot θ = \(\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{1}{9}}=\frac{2 \sqrt{2}}{3}\)

If sin θ = \(\frac{4}{5}\) and θ Is not In the first quadrant, find the value of cos θ. [Mar. 19 (AP): Mar. ’17 (TS)]
Answer:
\(\frac{-3}{5}\)

Question 4.
If sec θ + tan θ = \(\frac{2}{3}\), find the value of sin θ and determine the quadrant in which θ lies.
Answer:
sec θ + tan θ = \(\frac{2}{3}\) and sec²θ – tan²θ = 1
⇒ sec θ – tan θ = \(\frac{3}{2}\)
∴ 2sec θ = \(\frac{13}{6}\) ⇒ sec θ = \(\frac{13}{12}\)

Also 2 tan θ = \(\frac{2}{3}-\frac{3}{2}=-\frac{5}{6}\)
tan θ = \(-\frac{5}{6}\)

Now sin θ = \(\frac{\tan \theta}{\sec \theta}=\frac{-(5 / 12)}{13 / 12}=-\frac{5}{13}\)
Since tan θ is negative, sec is positive
∴ θ lies in fourth quadrant.

If cosec θ + cot θ = \(\frac{1}{3}\), find cos θ and determine the quadrant in which θ lies.
Answer:
\(\frac{-4}{5}\), Q₂

If sec θ + tan θ = 5, find the quadrant in which θ lies and find the value of sin θ. [May ’00]
Answer:
\(\frac{12}{13}\), Q₁

Question 5.
Show that cot\(\left(\frac{\pi}{20}\right)\).cot\(\left(\frac{3 \pi}{20}\right)\).cot\(\left(\frac{5 \pi}{20}\right)\).cot\(\left(\frac{7 \pi}{20}\right)\).cot\(\left(\frac{9 \pi}{20}\right)\) = 1. [Mar. ’05; May ’98]
Answer:
cot\(\left(\frac{\pi}{20}\right)\).cot\(\left(\frac{3 \pi}{20}\right)\).cot\(\left(\frac{5 \pi}{20}\right)\).cot\(\left(\frac{7 \pi}{20}\right)\).cot\(\left(\frac{9 \pi}{20}\right)\)
= cot 9°. cot 27°. cot 45°. cot 63°. cot 81°
= cot 9°. cot 27°. 1.cot (90 – 27) . cot (90 – 9)
= cot 9°. cot 27°. 1. tan 27°. tan 9° = 1

Question 6.
If 3 sin θ + 4 cos θ = 5, then find the value of 4sin θ – 3 cos θ. [Mar. ’12]
Answer:
Given 3 sin θ + 4 cos θ = 5 and suppose 4 sin θ – 3 cos θ = x
Squaring on adding
∴ (3sin θ + 4cosθ)² + (4sin θ – 3cosθ)² = 25 + x²
⇒ 9sin²θ + 24 sin θcos θ + 16 cos²θ + 16sin²θ – 24sinθcosθ + 9cos²θ = 25 + x²
⇒ 25 (sin²θ + cos²θ) = 25 + x
⇒ x = 0 ⇒ x = 0
∴ 4sin θ – 3cosθ = 0

Question 7.
If cos θ + sin θ = √2 cos θ , then show that cos θ – sin θ = √2 sin θ. [Mar ‘ 15(TS); May ’11; Mar. ’09, ’08]
Answer:
Given cos θ + sin θ = √2 cos θ
⇒ √2 cos θ – cos θ = sin θ
⇒ (√2 – 1)cos θ = sin θ
⇒ cos θ = \(\frac{\sin \theta}{\sqrt{2}-1}=\frac{\sqrt{2}+1}{(2-1)}\)sin θ
= (√2 + 1)sin θ = √2sin θ + sin θ
⇒ cos θ – sin θ = √2 sin θ

Question 8.
If tan 20° = λ tehn show that \(\frac{\tan 160^{\circ}-\tan 110^{\circ}}{1+\tan 160^{\circ} \tan 110^{\circ}}=\frac{1-\lambda^2}{2 \lambda}\). [Mar. ’05, Mar. ’16(AP)]
Answer:

Question 9.
Find the value of sin 330°. cos 120° + cos 210°. sin 300°. [Mar. ’18(AP)]
Answer:
sin 330° cos 120° + cos 210° sin 300°
= sin (360 – 30) cos (180 – 60) + cos (180 + 30) sin (360 – 60)
= (-sin 30°) (-cos 600) + (-cos 30°) (-sin 600)
= sin 30° cos 60° + cos 30° sin 60°
= sin (30 + 60)
= sin 90° = 1

Question 10.
If sin α + cosec α = 2, find the value of sinⁿα + cosecⁿα; n ∈ Z.
Answer:
Given sin α + cosec α = 2
Squaring on both sides sin² α + cosec² α = 2
=4 ⇒ sin²α + cosec²α = 2

Cubing of both sides
sin³ α + cosec³ α + 3 sin α cosec α (sin α cosec α) = 8
sin³α cosec³α + 3(2) = 8
⇒ sin³α + cosec³α = 2
In the same way sinⁿα + cosec³α = 2(n ∈ Z)

Question 11.
W Prove that sin 780°. sin 480° + cos 240°. cos 300° = \(\frac{1}{2}\)
Answer:
LHS = sin 780°. sin 480° + cos 240°. cos 300°
sin [2 × 360 + 60] sin [360 + 120] + cos [180 + 60] cos [360 – 60]
= sin 60 sin 120 – cos 60 cos 60
= sin 60 sin 60 – cos 60. cos 60
= \(\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2}-\frac{1}{2} \cdot \frac{1}{2}=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}\)

Question 12.
Simplify: \(\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}\)
Answer:
sin\(\left(-\frac{11 \pi}{3}\right)\) = sin(-660)
= sin(-2 × 360° + 60°) = sin 60° = \(\frac{\sqrt{3}}{2}\)

tan \(\left(\frac{35 \pi}{6}\right)\) = tan(105)
= tan(3 × 360° – 30°) = -tan 30° = \(\frac{\sqrt{3}}{2}\)

sec\(\left(-\frac{7 \pi}{3}\right)\) = sec(-420°)
= sec 420° = sec(360 + 60) = sec 60° = 2

cot\(\left(\frac{5 \pi}{4}\right)\) = cot(225°)
= (cot (180 + 45) = cot 45° = 1

cosec\(\left(\frac{7 \pi}{4}\right)\) = cosec (315°)
= cosec(270 + 45) = -sec 45° = √2

cos\(\left(\frac{17 \pi}{6}\right)\) = cos(570)
= cosec(540 + 30) = -cos 30 = –\(\frac{\sqrt{3}}{2}\)

Question 14.
If A, B, C, D are angles of a cyclic quadrilateral, then prove that cos A + cos B + cos C + cos D = 0.
Answer:
A, B, C, D are angles of a cyclic quadrilateral
⇒ A + C = 180° and B + D = 180° …………..(1)
C = 180 – A and D = 180° – B
LHS = cos A + cos B + cos C + cos D
= cos A + cos B + cos (180 – A) + cos (180 – B)
= cos A + cos B – cos A – cos B = 0 = RHS

Question 15.
Prove that cos⁴α + 2 cos²α(1 – \(\frac{1}{\sec ^2 \alpha}\)) = 1 – sin⁴α.
Answer:
LHS = cos⁴α + 2 cos²α(1 – \(\frac{1}{\sec ^2 \alpha}\))
= cos⁴α + 2cos²α(1 – cos²α)
= cos⁴α + 2 cos²α sin²α
=cos²α [cos²α + 2sin²α]
= (1 – sin2 a) [cos²α + sin²α + sin²α]
= (1 – sin²α)(1 + sin²α)= 1 – sin⁴α

Question 16.
If \(\frac{2 \sin \theta}{(1+\cos \theta+\sin \theta)}\) = x, then find the value of \(\frac{1-\cos \theta+\sin \theta}{1+\sin \theta}\)
Answer:

Question 17.
Prove that sin²52\(\frac{1}{2}^{\circ}\) + sin²22\(\frac{1}{2}^{\circ}=\frac{\sqrt{3}+1}{4 \sqrt{2}}\)
Answer:

Evaluate sin²82\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
Answer:
\(\frac{\sqrt{3}(\sqrt{3}+1)}{4 \sqrt{2}}\)

Question 18.
Evaluate cos²52\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
Answer:
[∵ cos2A – sin2B = cos(A + B) cos (A – B)]
cos²52\(\frac{1}{2}^{\circ}\) – sin²22\(\frac{1}{2}^{\circ}\)
= cos[52\(\frac{1}{2}^{\circ}\) + 22\(\frac{1}{2}^{\circ}\)]cos[52\(\frac{1}{2}^{\circ}\) – 22\(\frac{1}{2}^{\circ}\)]
= cos 75° cos 30°
= cos 30° cos(90 – 15) = cos 30° sin 15°
= \(\frac{\sqrt{3}}{2}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)=\frac{3-\sqrt{3}}{4 \sqrt{2}}\)

Evaluate cos²112\(\frac{1}{2}^{\circ}\) – sin²52\(\frac{1}{2}^{\circ}\).
Answer:
\(-\frac{\sqrt{3}+1}{4 \sqrt{2}}\)

Question 19.
Prove that tan 70° – tan 20° = 2tan 50°
Answer:

Question 20.
What is the value of tan 20° + tan 40° + √3 tan 20° tan 40°
Answer:
We have 20° + 40° = 60°
∴ tan(20° + 40°) = tan 60°
⇒ \(\frac{\tan 20^{\circ}+\tan 40^{\circ}}{1-\tan 20^{\circ} \tan 40^{\circ}}\) = √3
⇒ tan 20° + tan 40° = √3(1 – tan 20 tan 40)
⇒ tan 20° + tan 40° + √3 tan 20 tan 40) = √3

Question 21.
Prove that \(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}\) = cot 36°. [May ’15(AP); Mar. ’15(AP); Mar. ’11; N.P]
Answer:

= tan (90° – 36°) = cot 36° = RHS

Question 22.
Show that cos 42° + cos 78° + cos 162° = 0.
Answer:
L.H.S = cos 42° + cos 78° + cos 162°
= cos(60° – 18°) + cos (60° + 18°) + cos (180° – 18°)
= 2cos 60° cos 18° – cos 18°
= 2\(\left(\frac{1}{2}\right)\) cos 18° – cos 18° = cos 18° – cos 18°
= 0 = R.H.S

Question 23.
Simplify sin 1140°. cos 390° – cos 780° sin 750°.
Answer:
sin 1140°. cos 390° – cos 780° sin 750°
= sin[3(360) + 60°] cos [360 + 30°] – cos[2(360) + 60°]sin[2 × 360 + 30°]
= sin 60° cos 30° – cos 60° sin 30°
= sin(60° – 30°) = sin 30° = \(\frac{1}{2}\)

Question 24.
If sin(θ + α) = cos(θ + α), then express tan θ in terms of tan α.
Answer:
sin(θ + α) = cos(θ + α)
⇒ tan(θ + α) = 1
⇒ \(\frac{\tan \theta+\tan \alpha}{1-\tan \theta \tan \alpha}\) = 1
⇒ tan θ + tan α = 1 – tan θ tan α
⇒ tan θ + tan α + tan θ tan α = 1
⇒ tan θ[1 + tan α] = 1 – tan α
∴ tan θ = \(\frac{1-\tan \alpha}{1+\tan \alpha}\)

Question 25.
If cos θ = \(\frac{-5}{13}\) and \(\frac{\pi}{2}\) < θ < π find the value of sin 2θ.
Answer:
\(\frac{\pi}{2}\) < θ < π ⇒ sin θ > 0 and cos θ = \(\frac{-5}{13}\)
⇒ sin θ = \(\frac{12}{13}\)
∴ sin 2θ = 2sin θ cos θ
= 2\(\left(\frac{12}{13}\right)\left(-\frac{5}{13}\right)=-\frac{120}{169}\)

Question 26.
Express \(\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}\) in terms of tan\(\frac{\theta}{2}\).
Answer:

Question 27.
If 0 < θ < \(\frac{\pi}{2}\), show that \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 4 \theta}}}\) = 2cos(θ/2). [Mar. ’02]
Answer:

Question 28.
Prove that \(\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}\) = 4. [Mar. ’18(TS), Mar. ’16(AP), ’03; May ’04]
Answer:

Question 29.
If \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\), then prove that a sin 2α + b cos 2α = b. [Mar. ’10, ’01; May 05]
Answer:
Given that \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\)
⇒ b sin α = a cos α
L.H.S = a sin 2α + b cos 2α
= a(2 sinα cos α) + b(1 – 2sin²α)
= 2sin α(a cos α) + b – 2b sin²α
= 2 sin α(b sin α) + b – 2b sin²α
= 2b sin²α + b – 2b sin²α = b

Question 30.
Prove that sin 78° + cos 132° = \(\frac{\sqrt{5}-1}{4}\)
Answer:
sin 78° + cos 132° = sin 78° + cos (90 + 42)
= sin 78° – sin 42°
= 2 cos\(\left(\frac{78^{\circ}+42^{\circ}}{2}\right)\) sin\(\left(\frac{78^{\circ}-42^{\circ}}{2}\right)\)
= 2 cos 60° sin 18° = 2\(\left(-\frac{1}{2}\right)\left(\frac{\sqrt{5}-1}{4}\right)\)
= \(\frac{\sqrt{5}-1}{4}\) = R.H.S

Question 31.
Find the value of sin 34° + cos 64° – cos 4°. [May ’14]
Answer:
sin 34° + cos 64° – cos 4°
= sin 34° + 2sin \(\left(\frac{64+4}{2}\right)\) sin\(\left(\frac{4^{\circ}-64^{\circ}}{2}\right)\)
= sin 34° + 2sin 34° sin(-30°)
= sin 34° + 2sin 34°(-1/2) = 0

Question 32.
Prove that 4(cos 66° + sin 84°) = √3 + \(\sqrt{15}\). [May ’01]
Answer:
4(cos 66° + sin 84°) = 4[cos 66° + sin(90 – 6°)]
= 4[cos 66° + cod 6°]

Question 33.
Prove that cos 48° cos 12° = \(\frac{3+\sqrt{5}}{8}\).
Answer:

Question 34.
Find the period of f(x) = cos\(\left(\frac{4 x+9}{5}\right)\)
Answer:
The function f(x)
= cos x ∀ x ∈ R has the period 2π.
∴ f(x) = cos\(\left(\frac{4 x+9}{5}\right)\) is periodic and period of f is \(\frac{2 \pi}{\frac{4}{5}}=\frac{5 \pi}{2}\)

Question 35.
Find the period of f(x) = tan 5x.
Answer:
The function tan x is periodic with period π.
∴ f(x) = tan 5x is periodic and its period is \(\frac{\pi}{|5|}=\frac{\pi}{5}\)

Question 36.
Find the period of f(x) = |sin x|.
Answer:
The function sin x has period 2π ∀ x ∈ R.
But f(x) = |sin x| is periodic and its period is π.
[∵ f(x + π) = |sin(x + π)| = |- sin x| = sin x]

Question 37.
Find the period of f(x) = tan(x + 4x + 9x + …………. + n²x) (n any positive integer). [B.P. Mar ’15(AP & TS)]
Answer:
Given f(x) = tan(x + 4x + 9x + …………. + n²x)
tan(1 + 2² + 3² + …………… + n²)x

Question 38.
Find a sine function whose period is \(\frac{2}{3}\).
Answer:
\(\frac{2 \pi}{\mathrm{k}}=\frac{2}{3}\) ⇒ 3π = |k|
∴ sin kx = sin(3π x)

Question 39.
Find a cosine function whose period is 7.
Answer:
Let f(x) = cos kx
Period of cos kx = \(\frac{2 \pi}{|k|}\)
∴ \(\frac{2 \pi}{|k|}\) = 7 ⇒ |k| = \(\frac{2 \pi}{|k|}\)
∴ f(x) = cos[\(\frac{2 \pi}{|k|}\). x]

Question 40.
Find the period of cos⁴x.
Answer:

Question 41.
Find the period of 2 sin \(\left(\frac{\pi \mathbf{x}}{4}\right)\) + 3 cos \(\left(\frac{\pi \mathbf{x}}{3}\right)\).
Answer:

Question 42.
Find the minimum and maximum values of f(x) = 3 cos x + 4 sin x.
Answer:
Recall for a cos x + b sin x + c
Max value = c + \(\sqrt{a^2+b^2}\) and Min value
= c – \(\sqrt{a^2+b^2}\)
a = 3, b = 4, c = 0
∴ Max. value = \(\sqrt{9+16}\) =5
Min. value = –\(\sqrt{9+16}\) = – 5

Find the maximum and minimum values of f(x) = 3 sin x – 4 cos x.
Answer:
5, -5.

Question 43.
Find the maximum and minimum values of cos (x + \(\frac{\pi}{3}\)) + 22sin(x + \(\frac{\pi}{3}\)) – 3
Answer:
Let f(x) = cos(x + \(\frac{\pi}{3}\)) + 22sin(x + \(\frac{\pi}{3}\)) – 3
Comparing the given expression with
a sin x + b cos x + c, we get a = 2√2 , b = 1, c = – 3
∴ Maximum value of f(x) is
c + \(\sqrt{(2 \sqrt{2})^2+(1)^2}\) = -3 + \(\sqrt{(2 \sqrt{2})^2+(1)^2}\)
= -3 + \(\sqrt{8+1}\) = -3 + 3 = 0

∴ Minimum value of f(x) is
c – \(\sqrt{a^2+b^2}\) = -3 – \(\sqrt{(2 \sqrt{2})^2+(1)^2}\)
= – 3 – \(\sqrt{8+1}\) = -3 – 3 = -6

Question 44.
Find the range of 13 cos x + 3√3 sin x – 4.
Answer:
Let f(x) = 13 cos x + 3√3 sin x – 4.
a = 3√3, b = 13, c = -4

Find the range of 7 cos x – 24 sin x + 5
Answer:
[-20, 30]

Question 45.
Find the extreme values of cos 2x + cos²x.
Answer:
cos 2x + cos²x = 2cos²x – 1 + cos²x = 3cos²x – 1
and 0 ≤ cos²x ≤ 1
⇒ 0 ≤ 3 cos²x ≤ 3
⇒ -1 ≤ 3 cos²x – 1 ≤ 2

Maximum value = 2 and minimum value = -1
(or) cos 2x + cos²x = cos 2x + \(\left(\frac{1+\cos 2 x}{2}\right)\)
We have -1 ≤ cos 2x ≤ 1 ⇒ -3 ≤ 3cos 2x ≤ 3
-2 ≤ 3 cos 2x + 1 ≤ 4
-1 ≤ \(\frac{3 \cos 2 x+1}{2}\) ≤ 2

Maximum value = 2
Maximum value = -1 (or) a = \(\frac{3}{2}\), b = 0, c = \(\frac{1}{2}\)
Minimum value c – \(\sqrt{a^2+b^2}=\frac{1}{2}-\sqrt{9 / 4}\)
= \(\frac{1}{2}-\frac{3}{2}\) = -1
Maximum value : c + \(\sqrt{a^2+b^2}\) = \(\frac{1}{2}+\frac{3}{2}\) = 2

Question 46.
Find the extreme values of 3 sin²x + 5 cos² x.
Answer:

Question 47.
Sketch the graph of tan x between 0 and \(\frac{\pi}{4}\).
Answer:

Question 48.
Sketch the graph of cos 2x in the interval [0, π]
Answer:

Question 49.
Sketch the graph of sin 2x in the interval (0, π).
Answer:

Question 50.
Sketch the graph of sin x in the interval [-π, + π] taking four values on X – axis.
Answer:

Question 51.
Sketch the graph of cos²x in [0, π].
Answer:

Question 52.
Sketch the region enclosed by y = sin x, y = cos x and X – axis In the Interval [0, π].
Answer:

Telangana TSBIE TS Inter 1st Year Physics Study Material 8th Lesson Oscillations Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 8th Lesson Oscillations

Very Short Answer Type Questions

Question 1.
Give two examples of periodic motion which are not oscillatory.
Answer:

1. Motion of seconds hand of a watch.
2. Motion of fan blades which are rotating with constant angular velocity ‘w’.

For these two cases, they have constant centrifugal acceleration which does not change with rotation so it is not considered

Question 2.
The displacement in S.H.M. is given by y = a sin (20t + 4). What is the displacement when it is increased by2π/ω?
Answer:
Displacement :
Displacement remains constant ; \(\frac{2 \pi}{\omega}\) = time period T. After a time (0
period T, there is no change in equation of S.H.M.
i.e. Y = A sin (20t + 4) = Y = A sin (201 + 4 + T)
∴ There is no change in change in displacement.

Question 3.
A girl is swinging seated in a swing. What is the effect on the frequency of oscillation if she stands?
Answer:
The frequency of oscillation (n) will increase because in the standing position, the location of centre of mass of the girl shift upwards. Due to it, the effective length of the swing decreases. As n ∝ \(\frac{1}{\sqrt{l}}\), therefore, n increases.

Question 4.
The bob of a simple pendulum is a hollow sphere filled with water. How will the period of oscillation change, if the water begins to drain out of the hollow sphere?
Answer:
When water begins to drain out of the sphere, the centre of mass of the system will first move down and then will come up to the initial position. Due to this the equivalent length of the pendulum and hence time period first increases, reaches a maximum value and then decreases till it becomes equal to its initial value.

Question 5.
The bob of a simple pendulum is made of wood. What will be the effect on the time period if the wooden bob is replaced by an identical bob of aluminum?
Answer:
The time period of a simple pendulum does not change, if the wooden bob is replaced by an identical bob of aluminium because the time period of a simple pendulum is independent of the material of the bob.

Question 6.
Will a pendulum clock gain or lose time when taken to the top of a mountain?
Answer:
At higher altitudes i.e., on mountains the acceleration due to gravity is less as compared on the surface of earth. Since time period is inversely proportional to the square root of the acceleration due to gravity, the time period increases. The pendulum clock loses time on the top of a mountain.

Question 7.
What is the length of a simple pendulum which ticks seconds? (g = 9.8 ms^-2) [AP Mar. ’18: TS Mar. ’15]
Answer:
In simple pendulum T = 2π\(\sqrt{\frac{l}{g}}\) or l = \(\sqrt{\frac{gt^2}{4\pi^2}}\)
For seconds pendulum T = 2s ⇒ t² = 4
∴ = \(\frac{9.8\times4}{4\pi^2}\) = 1 m (∴ π² nearly 9.8)

Question 8.
What happens to the time period of a simple pendulum if its length is increased upto four times?
Answer:
In simple pendulum Time period T ∝ √l

From the above equation time period is doubled.

Question 9.
A pendulum clock gives correct time at the equator. Will it gain or lose time if it is taken to the poles? If so, why?
Answer:
When a pendulum clock showing correct time at equator is taken to poles then it will gain time.

Acceleration due to gravity at poles is high. Time period of pendulum T = 2π\(\sqrt{\frac{l}{g}}\).

When g increases T decreases. So number of oscillations made in the given time increases hence clock gains time.

Question 10.
What fraction of the total energy is K.E when the displacement is one half of a amplitude of a particle executing S.H.M?
Answer:
Kinetic energy is equal to three fourth (i.e.,\(\frac{3}{4}\)) of the total energy, when the displacement is one-half of its amplitude.

Question 11.
What happens to the energy of a simple harmonic oscillator if its amplitude is doubled?
Answer:
Energy of a simple harmonic oscillator,

From the above equation, energy increases by four times.

Question 12.
Can a simple pendulum be used in an artificial satellite? Give the reason
Answer:
No, this is because inside the satellite, there is no gravity, i.e., g = 0. As T = 2π\(\sqrt{\frac{l}{g}}\) where T = ∞ for g = 0. Thus, the simple pendulum will not oscillate.

Short Answer Questions

Question 1.
Define simple harmonic motion? Give two examples.
Answer:
Simple Harmonic Motion :
A body is said to be in S.H.M, if its acceleration is directly proportional to its displacement, acts opposite in direction towards a fixed point.

Examples:

1. Projection of uniform circular motion on a diameter.
2. Oscillations of simple pendulum with small amplitude.
3. Oscillations of a loaded spring.
4. Vibrations of a liquid column in U – tube.

Question 2.
Present graphically the variations of displacement, velocity and acceleration with time for a particle in S.H.M.
Answer:
The variations of displacement, velocity and acceleration with time for a particle in S.H.M can be represented graphically as shown in the figure.

From the graph

1. All quantities vary sinusoidally with time.
2. only their maxima differ and the different plots differ in phase.
3. Displacement x varies between – A to A; v(t) varies from – ωA to ωA and a (t) varies from – ω²A to ω²A.
4. With respect to displacement plot, velocity plot has a phase difference of \(\frac{\pi}{2}\) and acceleration plot has a phase difference of π.

Question 3.
What is phase? Discuss the phase relations between displacement, velocity and acceleration in simple harmonic motion.
Answer:
Phase (θ) :
Phase is defined as its state or condition as regards its position and direction of motion at that instant.
In S.H.M phase angle, θ = ωt = 2π(\(\frac{t}{T}\))

a) Phase between velocity and displacement :
In S.H.M, displacement,
y = A sin (ωt – Φ)
Velocity, V = Aω cos (ωt – Φ)
So phase difference between displacement and velocity is 90°.

b) Phase between displacement and acceleration :
In S.H.M, acceleration ‘a’ = – ω²y
or y = A sin ωt and a = – ω² A sin ωt
– ve sign indicates that acceleration and displacement are opposite.

So phase difference between displacement and acceleration is 180°.

Question 4.
Obtain an equation for the frequency of oscillation of spring of force constant k to which a mass m is attached.
Answer:
Let a spring of negligible mass is suspended from a fixed point and mass m is attached as shown. It is pulled down by a small distance ‘x’ and allowed free it will execute simple harmonic oscillations.

Displacement from mean position = x.
The restoring forces developed are opposite to displacement and proportional to ‘x’. ∴ F ∝ – x or F = – kx where k is constant of spring, (-ve sign for opposite direction)

Question 5.
Derive expressions for the kinetic energy and potential energy of a simple harmonic oscillator.
Answer:
Expression for K.E of a simple harmonic oscillator :
The displacement of the body in S.H.M., X = A sin ωt
where A = amplitude, ωt = Angular displacement.

Velocity at any instant, v = \(\frac{dx}{dt}\) = Aω cos ωt
∴ K.E = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\)mA²ω² cos² ωt

At mean position velocity is maximum and displacment x = 0
∴ K.E_max = \(\frac{1}{2}\)mA²ω²

Expression for P.E of a simple harmonic oscillator:
Let a body of mass m’ is in S.H.M with an amplitude A.

Let O is the mean position.
Equation of a body in S.H.M is given by, x = A sin ωt
For a body in S.H.M acceleration, a = – ω²Y
Force, F = ma = – mω²x
∴ Restoring force, F = mω²x

Potential energy of the body at any point say ‘x’ :
Let the body is displaced through a small distance dx
Work done, dW = F . dx = P.E.
This work done.
∴ P.E = mω²x. dx(where x is its displacement)
Total work done, W = ∫dW = \(\int_0^x m \omega^2 x\).dx
⇒ Work done, W = \(\frac{m\omega^2x^2}{2}\).
This work is stored as potential energy.
∴ P.E at any point = \(\frac{1}{2}\)mω²x²

Question 6.
How does the energy of a simple pendulum vary as it moves from one extreme position to the other during its oscillations?
Answer:
The total energy of a simple pendulum is,
E = \(\frac{1}{2}\)mA² (or) E = \(\frac{1}{2}\frac{mg}{l}\)A²

The above equation, shows that the total energy of a simple pendulum remains constant irrespective of the position at any time during the oscillation i.e., the law of conservation of energy is valid in the case of a simple pendulum. At the extreme positions P and Q the energy is completely in the form of potential energy and at the mean position 0 it is totally converted as kinetic energy.

At any other point the sum of the potential and kinetic energies is equal to the maximum kinetic energy at the mean position or maximum potential energy at the extreme position. As the bob of the pendulum moves from P to O, the potential energy decreases but appears in the same magnitude as kinetic energy. Similarly as the bob of the pendulum moves from 0 to P or Q, the kinetic energy decreases to the extent it is converted into potential energy, as shown in figure.

Question 7.
Derive the expressions for displacement, velocity and acceleration of a particle executes S.H.M.
Answer:
Displacement of a body in S.H.M.
X = A cos (ωt + Φ).

i) Displacement (x) :
At t = 0 displacement x = A i.e., at extreme position when ωt + Φ = 90° displacement x = 0 at mean position at any point x = A cos (ωt + Φ).

ii) Velocity (V): Velocity of a body in S.H.M.

When (ωt + Φ) = 0 then velocity v = 0. For points where (ωt + Φ) = 90°
Velocity V = – Aω i.e., velocity is maximum,

iii) Acceleration (a): Acceleration of a body in S.H.M. is a = \(\frac{dv}{dx}\)
= \(\frac{d}{dt}\)(-Aω sin(ωt + Φ) = -Aω²cos(ωt + Φ) = -ω²x)
a_max = -ω²A

Long Answer Questions

Question 1.
Define simple harmonic motion. Show that the motion of projection of a particle performing uniform circular motion, on any diameter is simple harmonic. [TS May 18, Mar. 16, June 15; AP Mar. ;19, 18, AP May 16, 14]
Answer:
Simple harmonic motion :
A body is said to be in S.H.M, if its acceleration is directly proportional to its displacement, acts opposite in direction towards a fixed point.

Relation between uniform circular motion and S.H.M.:
Let a particle ‘P’ is rotating in a circular path of radius ‘ω’ with a uniform angular velocity ‘P’. After time ‘t’ it goes to a new position ‘P’. Draw normals from ‘P’ on to the X – axis and on to the Y – axis. Let ON and OM are the projections on X and Y axis respectively.

As the particle is in motion it will subtend an angle θ = ωt at the centre.

From triangle OPN
ON = OP cos θ
But OP = r and θ = ωt
∴ Displacement of particle P on X – axis at any time t is
X = r cos ωt ………… (1)
From triangle OPM
OM = Y = OP sin θ
But OP = r and θ = ωt
∴ Displacement of particle P on Y- axis is
Y = r sin ωt ………… (2)

As the particle rotates in a circular path the foot of the perpendiculars OM and ON will oscillate with in the limits X to X¹ and Y to Y¹.

At any point the displacement of particle P is given by OP² = OM² = ON²
Since OM = X = r cos ωt and ON = Y = r sin ωt.

So a uniform circular motion can be treated as a combination of two mutually perpendicular simple harmonic motions.

Question 2.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. What is a seconds pendulum? [TS Mar. 18, 17, 15, May 17, 16; AP Mar. 17, 16. 15, 14, 13; AP May 18. 17. 13; June 15]
Answer:
Simple pendulum :
Massive metallic bob is suspended from a rigid support with the help of inextensable thread. This arrangement is known as simple pendulum.

So length of simple pendulum is ‘l’. Let the pendulum is pulled to a side by a small angle ‘θ’ and released it oscillate about the mean position.

Let the bob is at one extreme position B. The weight (W = mg) of body acts vertically downwards.

By resolving the weight into two perpendicular components :

1. One component mg sin θ is responsible for the to and fro motion of pendulum.
2. Other component mg cos θ will balance the tension in the string.

Force useful for motion F = mg sin θ = ma (From Newton’s 2nd Law)
From the above equations
∴ a = g sin θ

Since acceleration is proportional to displacement and acceleration is always directed towards a fixed point the motion of simple pendulum is “simple harmonic”.

Time period of simple pendulum :

Seconds pendulum :
A pendulum whose time period is 2 seconds is called “seconds pendulum.”

Question 3.
Derive the equation for the kinetic energy and potential energy of a simple harmonic oscillator and show that the total energy of a particle in simple harmonic motion is constant at any point on its path.
Answer:
Expression for K.E of a simple harmonic oscillator :
The displacement of the body in S.H.M, X = A sin ωt
where A = amplitude and ωt = Angular displacement.

Velocity at any instant, v = \(\frac{dx}{dt}\) = Aω cos ωt

At mean position velocity is maximum and displacement x = 0
∴ K.E_max = \(\frac{1}{2}\)mA²ω²

Expression for P.E of a simple harmonic oscillator :
Let a body of mass’m’ is in S.H.M with an amplitude A.

Let O is the mean position.
Equation of a body in S.H.M is given by, x = A sin ωt
For a body in S.H.M acceleration, a = – ω²Y
Force, F = ma = – mω²x
∴ Restoring force, F = mω²x

Potential energy of the body at any point say ‘x’:
Let the body is displaced through
a small distance dx
⇒ Work done, dW = F . dx
This work done = RE. in the body
∴ P.E = mω²x. dx(where x is its displacement)
Total work done, W = ∫dW = \(\int_0^x m \omega^2 x\).dx
work done, W = \(\frac{m\omega^2 x^2}{2}\)
This work is stored as potential energy.
∴ P.E at any point = \(\frac{1}{2}\)ω²x²
For conservative force total Mechanical Energy at any point = E= P.E + K.E
∴ Total energy,
E = \(\frac{1}{2}\)mω²(A² – x²) + \(\frac{1}{2}\)mω²x²
E = \(\frac{1}{2}\)mω²{A² – x² + x²} = \(\frac{1}{2}\)mω²A²

So for a body in S.H.M total energy at any point of its motion is constant and equals to \(\frac{1}{2}\)mω²A²

Problems

Question 1.
The bob of a pendulum is made of a hollow brass sphere. What happens to the time period of the pendulum, if the bob is filled with water completely? Why?
Solution:
If the hollow brass sphere is completely filled with water, then time period of simple pendulum does not change. This is because time period of a pendulum is independent of mass of the bob.

Question 2.
Two identical springs of force constant “k” are joined one at the end of the other On series). Find the effective force constant of the combination.
Solution:
When two springs of constant k each are joined together with end to end in series then effective spring constant k = \(\frac{k_1k_2}{k_1+k_2}\) in this case k_eq = \(\frac{k.k}{k+k}=\frac{k}{2}\)

In series combination, force constant of springs decreases.

Question 3.
What are the physical quantities having maximum value at the mean position in SHM?
Solution:
In S.H.M at mean position velocity and kinetic energy will have maximum values.

Question 4.
A particle executes SHM such that, the maximum velocity during the oscillation is numerically equal to half the maximum acceleration. What is the time period? [TS June ’15]
Solution:
Given maximum velocity, V_max = \(\frac{1}{2}\) maximum acceleration (a_max)
But V_max = Aw and a_max = ω² A
∴ Aω = \(\frac{1}{2}\) . Aω² ⇒ ω = 2
Time period of the body, T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{2}\)

Question 5.
A mass of 2 kg attached to a spring of force constant 260 Nm^-1 makes 100 oscillations. What is the time taken?
Solution:
Mass attached, m = 2 kg ; Force constant, k = 260 N/m
∴ Time period of loaded spring, T = 2π\(\sqrt{\frac{m}{k}}\)
= 2π\(\sqrt{\frac{2}{260}}\) = 0.5509 sec
∴ Time for 100 oscillations = 100 × 0.551
= 55.1 sec

Question 6.
A simple pendulum in a stationary lift has time period T. What would be the effect on the time period when the lift (i) moves up with uniform velocity (ii) moves down with uniform velocity (iii) moves up with uniform acceleration ‘a’ (iv) moves down with uniform acceleration ‘a’ (v) begins to fall freely under gravity?
Solution:
i) When the lift moves up with uniform velocity i.e., a = 0, there would be no change in the time period of a simple pendulum.

ii) When the lift moves down with uniform velocity i.e., a = 0, there would be no change in the time period of a simple pendulum.

iii) When lift is moving up with acceleration ‘a’ then relative acceleration = g + a
∴ Time period, T = 2 π\(\sqrt{\frac{l}{g+a}}\) so when lift is moving up with uniform acceleration time period of pendulum in it decreases.

iv) When lift is moving down with acceleration ‘a’ time period, T = 2π\(\sqrt{\frac{l}{g-a}}\)
(g – a = relative acceleration of pendulum)
So time period of pendulum in the lift decreases.

v) If the lift falls freely, a = g then the time period of a simple pendulum becomes infinite.

Question 7.
A particle executing SHM has amplitude of 4cm, and its acceleration at a distance of 1cm from the mean position is 3cms^-2. What will its velocity be when it is at a distance of 2cm from its mean position?
Solution:
Amplitude, A = 4cm = 4 × 10^-2m
Acceleration, a = 3cm/s² = 3 × 10^-2 m/s²;
Displacement, y = 1cm = 10^-2 m
∴ Angular velocity, ω = \(\sqrt{\frac{a}{y}}=\sqrt{\frac{3}{1}}=\sqrt{3}\)

To find velocity at a displacement of 2cm

Question 8.
A simple harmonic oscillator has a time period of 2s. What will be the change in the phase after 0.25 s after leaving the mean position?
Solution:
Time period, T = 2 sec; time, t = 0.25 sec
Phase difference after t sec = Φ = \(\frac{t}{T}\) × 2π
= \(\frac{0.25}{2}\) × 2π = \(\frac{2 \pi}{4}\) = 90°
For a phase of \(\frac{2 \pi}{4}\) starting from mean position the body will be at extreme position. (Phase difference between mean position and extreme position is \(\frac{2 \pi}{4}\) Rad or 90°)

Question 9.
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is (a) 5 cm (b) 3 cm (c) 0 cm.
Solution:
Given that, A = 5 cm = 5 × 10^-2m and T = 0.2 s
Angular velocity, ω = \(\frac{2 \pi}{T}=\frac{2 \pi}{0.2}\) = 10π rad s^-1

a) Displacement, y = 5 cm = 5 × 10^-2 m
i) Acceleration of the body, a = – ω²y
= -(10π)² × 5 × 10^-2 = -5π²ms^-2
ii) Velocity of the body,

b) Displacement, y = 3 cm = 3 × 10^-2 m
i) Acceleration of the body, a = – ω²y
= -(10π)² × 3 × 10^-2 = -3π²ms^-2
ii) Velocity of the body, v = ω\(\sqrt{A^2 – y^2}\)

= 10π × 4 × 10^-2 = 0.4π ms^-1

c) Displacement, y = 0 cm
i) Acceleration of the body, a = – ω²y = 0
ii) Velocity of the body, v = ω\(\sqrt{A^2 – y^2}\)
= 10π^(5xl0’2)2-(0)2\(\sqrt{(5\times10^{-2})^2-(0)^2}\)
= 10π × 5 × 10^-2 =0.5π ms^-1

Question 10.
The mass and radius of a planet are double that of the earth. If the time period of a simple pendulum on the earth is T, find the time period on the planet.
Solution:
Mass of planet, M_P = 2 M_e ;
Radius of planet, R_P = 2R_e
Time period of pendulum on earth = T ;
Time period on planet = T’

Question 11.
Calculate the change in the length of a simple pendulum of length lm, when its period of oscillation changes from 2 s to 1.5 s. [TS Mar. ’18]
Solution:
For seconds pendulum T₁ = 2 sec ;
Length l₁ = 1 m.
New time period T₂ = 1.5 sec; Length l₂ = ?

Question 12.
A freely falling body takes 2 seconds to reach the ground on a plane, when it is dropped from a height of 8m. If the period of a simple pendulum is seconds on the planet. Calculate the length of the pendulum.
Solution:
Height, h = 8m;
Time taken to reach the ground, t = 2 sec
But for a body dropped, t = \(\sqrt{\frac{2h}{g}}\)
⇒ 2 = \(\sqrt{\frac{16}{g}}\) ⇒ g = \(\frac{16}{4}\) = 4m/s² on that planet
Time period of pendulum, T = 2π\(\sqrt{\frac{l}{g}}\) = π
∴ 2\(\sqrt{\frac{l}{g}}\) = 1 or \(\frac{l}{g}=\frac{1}{4}\) ⇒ l = \(\frac{g}{4}\)
Length of pendulum = \(\frac{4}{4}\) = 1m = 100cm on that planet

Question 13.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period.
Find the length of a simple pendulum which ticks seconds, (g = 9.8 ms^-2) [AP Mar. ’18. ’16, ’15, May ’17, June ’15; TS Mar.’17, 15, May 17]
Solution:
Simple pendulum :
In a laboratory a heavy metallic bob is suspended from a rigid support with the help of a spunless thread. This arrangement is known as “simple pendulum”.

Let the length of simple pendulum is ‘l’ and the point of suspension is ‘S’. Let the pendulum is drawn to a side by a small angle ‘θ’ and allowed free to oscillate in the vertical plane. Then it will oscillate between the extreme positions A and B with a displacement say ‘x’ at any given time.

Let the bob is at one extreme position say B. The force vertically acting downwards is Weight W = mg.

By resolving the weight into two per-pendicular components:

1. The component mg sin θ is responsible for the to and fro motion of the bob.
2. The component mg cos θ will balance the tension in the string.

Force useful for motion F = mg sin θ
= ma (From Newton’s 2nd Law)
∴ a = g sin θ

Since acceleration is proportional to displacement and acceleration is always directed towards a fixed point the motion of simple pendulum is “simple harmonic”.

Time period of simple pendulum :

Problem:
In simple pendulum T = 2π\(\sqrt{\frac{l}{g}}\) or l = \(\frac{gt^2}{4\pi^2}\)
For seconds pendulum T = 2s ⇒ t² = 4
∴ l = \(\sqrt{\frac{9.8\times4}{4\pi^2}}\) = 1 m (∴ π² nearly 9.8)

Question 14.
The period of a simple pendulum is found to increase by 50% when the length of the pendulum is increased by 0.6 m. Calculate the initial length and the initial period of oscillation at a place where g = 9.8 m/s².
Solution:
a) Increase in length of pendulum = 0.6m ;
Increase in time period = 50% = 1.5T
Let original length of pendulum = 1
Original time period = T; g = 9.8 m/s².
For 1st case 9.8 = π² \(\frac{1}{T^2}\) → 1 ;
For 2nd case l₁ = (l + 0.6), T₁ = 1.5 T

But l₁ = l + 0.6 ;
∴ l + 0.6 = 2.25l ⇒ 0.6 = 1.25l
∴ Length of pendulum l = \(\frac{0.6}{1.25}\) = 0.48 m
b) Time period T = 2π\(\sqrt{\frac{l}{g}}\)
= 2 × 3.142\(\sqrt{\frac{0.48}{9.8}}\) = 6.284 × 0.2213
= 1.391 sec.

Question 15.
A clock regulated by a seconds pendulum keeps correct time. During summer the length of the pendulum increases to 1.02m. How much will the clock gain or lose in one day?
Solution:
Time period of seconds pendulum,
T = 2 sec
Length of seconds pendulum,
L = gT² / 4π² = 0. 9927 m
Length of seconds pendulum during summer = 1.02 m
∴ Error in length, ∆l = 1.02 – 1 = 0.0273
In pendulum T × √l. From principles of error

Question 16.
The time period of a body suspended from a spring is T. What will be the new time period, if the spring is cut into two equal parts and (i) the mass is suspended from one part? (ii) the mass is suspended simultaneously from both the parts?
Solution:
Time period of spring, T = 2π\(\sqrt{\frac{m}{K}}\)
When a spring is cut into two equal parts force constant of each part K₁ = 2K

ii) When mass is suspended simultaneously from two parts ⇒ they are connected in parallel. For springs in parallel K_p = K₁ – K₂ = 4K

Question 16.
What is the length of a seconds pendulum on the earth? [AP Mar. ’17, ’16; June ’15; TS Mar. ’17]
Solution:

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Functions Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Functions Important Questions Long Answer Type

Question 1.
If f : A → B, g : B → C are two bijective functions, then prove that gof : A → C is also a bijective function. [Mar. 18, 16 (AP), 09 ; May 13, 12, 10, 08, 06, 04 00, 96, 92]
Answer:
Since f: A →B is a bijective function
o f: A → B is both one-one and onto functions.
Since f: A → B is a one-one function
⇔ a₁, a₂ ∈ A, f(a₁) = f(a₂) ⇒ a₁ = a₂
Since f: A → B is a onto function ⇔ ∃ one element a ∈ A such that f(a) = b, ∀ b ∈ B.
Since g: B → C is a bijective function
⇔ g: B → C is both one-one and onto functions.
Since g: B → C is a one-one function
⇔ b₁, b₂ ∈ B, g (b₁) = g (b₂) ⇒ b₁ = b₂
Since g: B → C is an onto function ⇔ ∃ one element b e B such that g(b) = c, ∀ c ∈ C.
If f: A → B, g : B → C ⇒ gof: A → C.

To prove that gof: A → C is a one-one function:
If gof: A → C is a one-one function
⇔ a₁, a₂ ∈ A, (gof) (a₁) = (gof) (a₂) ⇒ a₁ = a₂
Now (gof) (a₁) = (gof) (a₂)
g [f(a₁)] = g [ f(a₂)] [∵ g is one-one]
f(a₁) = f(a₂) [∵ f is one-one]
a₁ = a₂
Hence, gof: A → C is a one-one function.

To prove that gof: A → C is an onto function:
Let c ∈ C
If gof: A → C is an onto function ⇔ ∃ one element a ∈ A, such that
(gof) (a) = c, ∀ c ∈ C.
Now (gof) (a) = g [f(a)] = g(b) = c
Thus for any element c ∈ C, there is an element a ∈ A such that (gof) (a) = c.
∴ gof: A → C is an onto function.
Since gof: A → C is both one-one function and onto function then
gof: A → C is a bijective function.

Question 2.
If f : A → B, g : B → C are two bijective functions, then prove that (gof)^-1 = f^-1og^-1. [Mar. ’16 (TS), 14, 11, 10, 06, 04, 02, 00, 92; May 15 (AP) 14, 11, 09, 02, 98, 94 Mar. 19 (AP) ]
Answer:
Since f: A → B, g : B → C are bijections
⇒ gof: A → C is a bijection
⇒ (gof)^-1: C → A is also a bijection
Since f: A → B is a bijective function
then f^-1: B → A is also a bijective function
Since g: B → C is a bijective function
then g^-1: C → B is also a bijective function
⇒ f^-1og^-1: C → A is also a bijection
Since the two functions (gof)^-1, f^-1og^-1 are from C → A their domains are same.
Let c ∈ C
Since f : A → B is onto ⇔ ∃ one element
a ∈ A such that
f(a) = b, ∀ b ∈ B
f(a) = b ⇒ f^-1 (b) = a
Since g : B → C is onto ⇔ ∃ one element be B such that g(b) = c, ∀ c ∈ C
g(b) = c ⇒ g^-1(c) = b
Now (gof) (a) = g[f(a)] = g (b) = c ⇒ a = (gof)^-1(c)
⇒ (gof)^-1(c) = a ………………. (1)
Also (f^-1og^-1) (c) = f^-1 [g^-1(c)] = f^-1(b) = a ……………… (2)
∴ From (1) and (2)
(gof)^-1(c) = (f^-1og^-1) (c)
∴ (gof)^-1 = f^-1og^-1.

Question 3.
Let f : A → B, is a function and I_A, I_B are identity functions on A and B respectively. Then prove that foI_A = f = I_Bof. [Mar. 18 (TS); Mar. 13, 08, 05; May 92]
Answer:
If f: A → B is a function.
If I_A and I_B are identity functions on A and B respectively.
i.e., I_A : A → B, I_B : B → B

(i) I_A: A → A, f: A → B ⇒ f o I_A : A → B
Hence, functions f o I_A and f are defined on same domain A.
Let a ∈ A
(f o I_A) (a) = f[I_A (a)] = f(a)
∴ f o I_A = f

(ii) f: A → B, I_B: B → B ⇒ I_B o f: A → B
The functions (I_B o f) and f are defined on the same domain A.
Let a ∈ A
Now (I_B o f)(a) = I_B[f(a)] = f(a)
∴ I_B o f = f ………………. (2)
From (1) and (2) we get
f o I_A = I_B o f = f

Question 4.
If f: A → B is a bijection, then prove that fof^-1 = I_B and f^-1 o f = I_A. [Mar. 17, 15 (AP); Mar. 12, 07, 03, 02; May 07, 05, 01 Mar. 19 (TS)]
Answer:

(i) Since f: A → B is a bijection ⇒ f^-1: B → A is also a bijection
I_A; f: A → B, f^-1: B → A ⇒ f^-1 o f: A → A is also bijection
Clearly I_A: A → A such that I_A(a) = a, ∀ a ∈ A
Let a ∈ A
Since f^-1: B → A is onto function ⇔ ∃ one element b ∈ B,
such that
f^-1(b) = a, ∀ a ∈ A
f^-1 (b) = a ⇒ f(a) = b
Now (f^-1of) (a) = f^-1[f(a)] = f^-1(b) = a = I_A(a)
∴ f^-1of = I_A

(ii) Since f: A → B is a bijection ⇒ f^-1: B → A is also bijection
I_B: f^-1:B → A, f: A → B = fof^-1:B → B is also a bijection
Clearly I_B: B → B such that I_B(b) = b, ∀ b ∈ B
Let b ∈ B
Since f^-1: B → A is an onto function ⇔ ∃
one element b ∈ B such that f^-1(b) = a, ∀ a ∈ A
f^-1(b) = a ⇒ f(a) = b
Now (fof^-1) (b) = f[f^-1(b)] = f(a) = b = I_B(b)
∴ fof^-1 = I_B

Question 5.
If f:A → B, g:B → A are two functions such that gof = I_A and fog = I_B, then prove that f is a bijection and g = f^-1. [May 15 (TS); Mar. 08, 01; May 03]
Answer:

(i) To prove that f is one-one
Let a₁, a₂ ∈ A and since f : A → B, f(a₁), f(a₂) ∈ B
Now f(a₁) = f(a₂ ) ⇒ g[f(a₁)] = g[f(a₂)]
⇒ (gof) (a₁) = (gof) (a₂)
⇒ I_A(a₁) = I_A(a₂)
∴ a₁ = a₂
∴ f is one-one

(ii) To prove that f is onto
Let b be an element of B
I_B (b) = (fog) (b)
⇒ b = f[g(b)] ⇒ f(g(b)) = b
i.e., there exists a pre-image g(b) ∈ A for b, under the mapping f.
∴ f is onto
Thus ‘f’ is one-one and onto hence, f^-1: B → A exists and is also one-one onto.

(iii) To prove g = f^-1
Now g:B → A and f^-1:B → A
Let a ∈ A and b be the f – image of a where b ∈ B
∴ f(a) = b ⇒ a = f^-1 (b)
Now g(b) = g[f(a)] (gof) (a) = I_AA(a) = a
⇒ a = f^-1 (b)
∴ g = f^-1

Question 6.
If f:A → B, g: B → C and h: C → D are three functions then prove that ho(gof) = (hog) of. That is composition of functions is associative. [May ‘99, ‘95]
Answer:
f:A → B, g:B → C, h:C → D be three functions.
f:A → B, and g:B → C = gof: A → C
Now gof: A → C and h:C → D ⇒ ho(gof): A → D
g:B → C and h:C → D = (hog):B → D
Now f: A → B ⇒ hog: B→D
(hog)of: A → D
Thus ho(gof) and (hog)of both exist and have the same domain A and co-domain D.
Let a ∈ A,
Hence ho(gof) = (hog) of ∈ A
Now [ho(gof)] (a) = h [(gof) (a)] = h[g(f(a))]
= (hog) [f(a)] = [(hog) of] (a)
∴ [ho(gof)] (a) = [(hog) of] (a)

Question 7.
If f: A → B, g: B → C be surjections, then show that gof: A → C is a surjection. [May 98, 97, 96, 94, 93, 91]
Answer:
Let c ∈ C
Since f: A → B is a onto ⇔ ∃ one element
a ∈ A such that f(a) = b,∀ b ∈ B
Since g: B → C is a onto ⇔ ∃ one element
b ∈ B such that g(b) = c, ∀ c ∈ C.
If f: A → B, g:B → C = gof: A → C
To prove that gof : A → C is a onto

If gof : A → C is a onto ⇔ ∃ one element a ∈ A
such that
(gof) (a) = c, ∀ c ∈ C.
Now (gof) (a) = g[f(a)] = g(b) = c
Thus for any element c € C, there is an
element a ∈ A such that (gof) (a) = c.
∴ gof: A → C is an onto function.

Question 8.
If f = ((1, a), (2, c), (4, d), (3, b)} and g^-1 = {(2, a), (4, b), (1, c), (3, d)}, then show that (gof)^-1 = f^-1og^-1. {Mar. 15 (TS); May 07, 93}
Answer:
Given
f = {(1, a), (2, c), (4, d), (3, b))
f^-1 = ((a, 1), (c, 2), (d, 4), (b, 3))
g = ((a, 2), (b, 4), (c, 1), (d, 3))
g^-1 = {(2, a), (4, b), (1, c), (3, d)}

gof:

∴ gof = {(1, 2), (2, 1), (3, 4), (4, 3)}
(gof)^-1 = {(2, 1), (1, 2), (4, 3), (3, 4)}
f^-1og^-1

f^-1og^-1 = {(1, 2), (2, 1), (3, 4), (4, 3)}
∴ (gof)^-1 = f^-1og^-1

Question 9.
If the function f is defined by

then find the values of
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(- 2)
(v) f(- 5).
Answer:
Given

(i) For x > 1; f(x) = x + 2; f(3) = 3 + 2 = 5
(ii) For – 1 ≤ x ≤ 1; f(x) = 2, f(0) = 2
(iii) For – 3 < x < – 1; f(x) = x – 1 ∴ f(- 1.5) = – 1.5 – 1 = – 2.5 (iv) For x > 1, f(x) = x + 2
f(2) = 2 + 2 = 4
For – 3 < x < – 1, f(x) = x – 1
∴ f(- 2) = – 2 – 1 = – 3
f(2) + f(- 2) = 4 – 3 = 1
(v) f(- 5) is not defined.

Question 10.
If A = {- 2, – 1, 0, 1, 2) and f: A → B is a surjection defined by f(x) = x² + x + 1 find B.
Answer:
Given, A = {- 2, – 1, 0, 1, 2)
f(x) = x² + x + 1
Since f : A → B is a surjection then f(A) = B
f(-2) = (- 2)² – 2 + 1 = 4 – 2 + 1 = 3
f(-1) = (- 1)² – 1 + 1 = 1 – 1 + 1 = 1
f(0) = 0² + 0 + 1 = 1
f(1) = 1² + 1 + 1 = 1 + 1 + 1 = 3
f(2) = 2² + 2 + 1 = 4 + 2 + 1 = 7
∴ B = f(A) = {3. 1, 7}

Question 11.
If A = {1, 2, 3, 4} and f:A → R is a function defined by f(x) = \(\frac{x^2-x+1}{x+1}\), then find the range of f.
Answer:
Given A = {1, 2, 3, 4) and f(x) = \(\frac{x^2-x+1}{x+1}\)
Since f: A → R is a function, then

Question 12.
If f: Q → Q, is defined by f(x) = 5x + 4 for all x ∈ Q, find f^-1. [Mar. 17 (TS)]
Answer:
Let y = f(x) = 5x + 4
y = f(x) ⇒ x = f^-1(y) ……………… (1)
y = 5x + 4 ⇒ y – 4 = 5x
x = \(\frac{y-4}{5}\) ………………… (2)
From (1) and (2),
f^-1(y) = \(\frac{y-4}{5}\) ⇒ f(x) = \(\frac{x-4}{5}\), ∀ x ∈ Q

Question 13.
If f(x) = \(\frac{x+1}{x-1}\) (x ≠ ± 1), then find (fofofof) (x).
Answer:
Given f(x) = \(\frac{x+1}{x-1}\) (x ≠ ± 1)
Now (fofofof) (x) = f[f[f{f(x)}]]

Question 14.
Find the domain of the real valued function f(x) = \(\sqrt{16-x^2}\).
Answer:
Given f(x) = \(\sqrt{16-x^2}\) ∈ R
⇒ 16 – x² ≥ 0
⇒ x² – 16 ≤ 0
⇒ (x + 4) (x – 4) ≤ 4
⇒ x ∈ [- 4, 4]
∴ Domain of ‘f’ is [- 4, 4]

Question 15.
Find the domain of the real valued function f(x) = \(\sqrt{9-x^2}\).
Answer:
Given f(x) = \(\sqrt{9-x^2}\) ∈ R
⇒ 9 – x² ≥ 0
⇒ x² – 9 ≤ 0
⇒ (x + 3) (x – 3) ≤ 0
⇒ x ∈ [- 3 ,3]
∴ Domain of f’ is [- 3, 3]

Question 16.
Find the domain of the real valued function f(x) = \(\frac{1}{6 x-x^2-5}\).
Answer:
Given f(x) = \(\frac{1}{6 x-x^2-5}\) ∈ R
⇒ 6x – x² – 5 ≠ 0
⇒ x² – 6x + 5 ≠ 0
⇒ x² – 5x – x + 5 ≠ 0
⇒ x(x – 5) – 1 (x – 5) ≠ 0
⇒ x – 1 ≠ 0 or x – 5 ≠ 0
⇒ x ≠ 1 or x ≠ 5
∴ x ≠ 1, 5
∴ Domain of ‘f’ is R – {1, 5}

Question 17.
Find the domain of the real valued function f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\).
Answer:
Given f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\) ∈ R
⇒ (x – 1) (x – 2) (x – 3) ≠ 0
⇒ x – 1 ≠ 0, x – 2 ≠ 0, x – 3 ≠ 0
⇒ x ≠ 1, x ≠ 2, x ≠ 3
∴ x ≠ 1, 2, 3
∴ Domain of ‘f’ is R – {1, 2, 3}

Question 18.
Find the domain of the real valued function f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\).
Answer:
Given f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\) ∈ R

⇒ 2 + x ≥ 0, 2 – x ≥ 0 and x ≠ 0
x ≥ – 2, 2 ≥ x and x ≠ 0
x ≤ 2 and x ≠ 0
⇒ x ∈ [- 2, 0) ∪ (0, 2]
∴ Domain of ‘f’ is [- 2, 0) ∪ (0, 2]

Question 19.
If f = {(1, 2), (2, – 3), (3, – 1)}, then find
(i) 2f
(ii) 2 + f
(iii) f²
(iv) √f
Answer:
Given f = {(1, 2), (2, – 3), (3, – 2)}
Domain of ‘f’ is A = {1, 2, 3}
f(1) = 2f(2) = – 3, f(3) = – 1

(i) (2f) (x) = 2f(x)
(2f) (1) = 2f(1) = 2(2) = 4
(2f) (2) = 2f(2) = 2(- 3) = – 6
(2f) (3) = 2f(3) = 2(- 1) = – 2
∴ 2f = {(1, 4), (2, – 6),(3, – 2)}

(ii) (2 + f) (x) = 2 + f(x)
(2 + f) (1) = 2 + f(1) = 2 + 2 = 4
(2 + f) (2) = 2 + f(2) = 2 – 3 = – 1
(2 + f) (3) = 2 + f(3) = 2 – 1 = 1
∴ 2 + f = {(1, 4), (2, – 1), (3, 1)}

(iii) (f²) (x) = [f(x)]²
(f²) (1) = [f(1)]² = 2² = 4
(f²) (2) = [f(2)]² = (- 3)² = 9
(f²) (3) = (f(3)]² = (- 1)² = 1
∴ f² = {(1, 4), (2, 9), (3, 1)}

(iv) (√f)(x) = √f(x)
(√f) (1) = √f(1) = √2
(√f) (2) = √f(2) = √- 3 (not valid)
(√f) (3) = √f(3) = √- 1 (not valid)
∴ √f = {(1, √2)}

Some More Maths 1A Functions Important Questions

Question 1.
If f(x) = \(\frac{\cos ^2 x+\sin ^4 x}{\sin ^2 x+\cos ^4 x}\), ∀ x ∈ R then show that f(2012) = 1.
Answer:

Question 2.
If f: R → R is defined by f(x) = \(\frac{1-x^2}{1+x^2}\), then show that f(tan θ) = cos 2θ.
Answer:
Given f: R → R, f(x) = \(\frac{1-x^2}{1+x^2}\)
LHS = f(tan θ)
= \(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\) = cos 2θ + RHS
∴ f(tan θ) = cos 2θ

Question 3.
If f: R – {±1} → R is defined by f(x) = log \(\left|\frac{1+x}{1-x}\right|\), then show that f(\(\left(\frac{2 x}{1+x^2}\right)\)) = 2f(x)
Answer:
Given f: R – {±1} → R

Question 4.
If A = {x/ – 1 ≤ x ≤ 1}, f(x) = x², g(x) = x³ which of the following are surjections?
(i) f : A → A
(ii) g: A → A
Answer:
(i) Given A = {x/ – 1 ≤ x ≤ 1}
∴ A = {- 1, 0, 1}
f(x) = x²
f(- 1) = (- 1)² = 1
f(0) = (0)² = 0
f(1) = (1)² = 1
∴ f = (- 1, 1), (0 , 0), (1, 1))

f: A → A

Range of f(A) = {0, 1) ≠ A (co-domain)
∴ f : A → A is not a surjection.

(ii) Given A = {x/ – 1 ≤ x ≤ 1}
∴ A = {- 1, 0, 1}
g(x) = x³
g(- 1) = (- 1)³ = – 1
g(0) = (0)³ = 0
g(1) = (1)³ = 1
∴ g = {(- 1, -1), (0, 0), (1, 1)}
g: A → A

Range of g(A) = {- 1, 0, 1} = A (co-domain)
∴ g is a surjection.

Question 5.
If f(x) = cos (log x) then show that
\(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\) = 0
Answer:
Given f(x) = cos (log x)
f\(\left(\frac{1}{x}\right)\) = cos\(\left(\log \frac{1}{x}\right)\) = cos (log x^-1)
= cos (- log x) = cos (log x)
Similarly f\(\left(\frac{1}{y}\right)\) = cos (log y)
f\(\left(\frac{x}{y}\right)\) = cos \(\left(\log \left(\frac{x}{y}\right)\right)\)
= cos (log x – log y)
f(xy) = cos (log xy)
= cos (log x + log y)
L.H.S: f\(\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left(f\left(\frac{x}{y}\right)+f(x y)\right)\)
= cos (log x) . cos (log y) – \(\frac{1}{2}\) [cos (log x – log y) + cos (log x + log y)]
= cos (log x) . cos (log y)

= cos (log x) . cos (log y) – cos (log x) . cos (log y) = 0
= R.H.S

Question 6.
Find the inverse function of f(x) = log₂x.
Answer:
Given f: (0, ∝) → R, f(x) = log₂x
Let y = f(x) = log₂x
y = f(x) = x = f^-1(y) ……………. (1)
y = log₂x ⇒ x = 2^y (2)
From (1) & (2)
f^-1(y) = 2y
⇒ f^-1(x) = 2x

Question 7.
If f(x) = 1 + x + x² +…….. for |x| < 1, then show that f^-1(x) = \(\frac{\mathbf{x}-1}{\mathbf{x}}\).
Answer:
Given that f(x) = 1 + x + x² + ………….
f(x) = \(\frac{1}{1-\mathrm{x}}\)

Question 8.
Find the domain of the real valued function f(x) = \(\frac{1}{\sqrt{\mathbf{x}^2-a^2}}\) (a >0). [Mar.15 (AP)]
Answer:
Given f(x) = \(\frac{1}{\sqrt{x^2-a^2}}\) ∈ R
⇒ x² – a²
⇒ (x + a) (x – a) > 0
⇒ x < – a or x > a
⇒ x ∈ (- ∝, – a) ∪ (a, ∝)
∴ Domain of f’ is (- ∝, – a) ∪ (a, ∝)

Question 9.
Find the domain of the real valued function f(x) = \(\sqrt{(\mathbf{x}-\alpha)(\beta-\mathbf{x})}\) (0 < α < β).
Answer:
Given f(x) = \(\sqrt{(\mathbf{x}-\alpha)(\beta-\mathbf{x})}\) ∈ R
⇒ (x – α) (x – β) ≥ 0
⇒ (x – α) (x – β) ≤ 0
⇒ α ≤ x ≤ β
⇒ x ∈ [α, β]
∴ Domain of ‘f’ is [α, β]

Question 10.
Find the domain of the real valued function f(x) = \(\sqrt{2-x}+\sqrt{1+x}\).
Answer:
Given f(x) = \(\sqrt{2-x}+\sqrt{1+x}\) ∈ R
⇒ 2 – x ≥ 0 and 1 + x ≥ 0
⇒ 2 ≥ x and x ≥ – 1
⇒ x ≤ 2 and x ≥ – 1
⇒ x ∈ [- 1, 2]
∴ Domain of ‘f’ is [-1, 2]

Question 11.
Find the domain of the real valued function f(x) = \(\sqrt{|\mathbf{x}|-\mathbf{x}}\)
Answer:
Given f(x) = \(\sqrt{|\mathbf{x}|-\mathbf{x}}\) ∈ R
⇒ |x| – x ≥ 0
⇒ |x| ≥ x
⇒ x ∈ R
∴ Domain of ‘f’ is ‘R.

Question 12.
Find the domain and range of the real valued function f(x) = \(\frac{2+x}{2-x}\)
Answer:
Given f(x) = \(\frac{2+x}{2-x}\) ∈ R
⇒ 2 – x ≠ 0 ⇒ x ≠ 2
Domain of T is R – { 2 }.
Let y = f(x) = \(\frac{2+x}{2-x}\)
y = \(\frac{2+x}{2-x}\)
2yx – xy = 2 + x
2y – 2 = x + xy
2y – 2 = x(1 + y)
x ∈ R – {2}, y + 1 ≠ 0
y ≠ – 1
∴ Range of ‘f’ is R – {- 1}.

Question 13.
Find the domain and range of the real valued function f(x) = \(\sqrt{9-x^2}\) [Mar. 15 (TS)]
Answer:
Given f(x) = \(\sqrt{9-x^2}\) ∈ R
⇒ 9 – x² ≥ 0
⇒ x² – 9 ≤ 0
⇒ (x + 3) (x -3) ≤ 0
⇒ x ∈ [- 3, 3]
∴ Domain of ‘f’ is [- 3, 3]
Let y = f(x) = \(\sqrt{9-x^2}\)
y = \(\sqrt{9-x^2}\)
y² = 9 – x²
x² = 9 – y²
x = \(\sqrt{9-y^2}\) ∈ R
⇒ 9 – y² ≥ 0
⇒ y² – 9 ≤ 0
⇒ (y + 3) (y – 3) ≤ 0
⇒ y ∈ [- 3, 3]
But f(x) attains only non-negative values.
∴ Range of f = [0, 3].

Question 14.
Determine whether the function f(x) = x\(\left(\frac{e^x-1}{e^x+1}\right)\) is even or odd.
Answer:

Since f(- x) = f(x) then f is an even function.

Question 15.
Determine whether the function f(x) = log(x + \(\sqrt{x^2+1}\)) is even or odd.
Answer:

Since f(- x) = – f(x) then f(x) is an odd function.

Question 16.
Find the domain of the real valued function f(x) = log [x – (x)].
Answer:
Given f(x) = log [x – (x)] ∈ R
⇒ x – (x)> 0
⇒ x > (x)
Then x is a non – integer.
∴ Domain of ‘f’ is R – Z.

Question 17.
Find the domain of the real valued function f(x) = \(\frac{1}{\log (2-x)}\).
Answer:
Given f(x) = \(\frac{1}{\log (2-x)}\) ∈ R
⇒ log (2 – x) ≠ 0 and 2 – x > 0
⇒ log (2 – x) ≠ log 1 and 2 > x
⇒ 2 – x ≠ 1 and x < 2
⇒ x ≠ 1
∴ Domain of ‘f’ is (- ∝, 1) ∪ (1, 2)

Question 18.
Find the domain of the real valued function f(x) = \(\sqrt{\mathbf{x}-[\mathbf{x}]}\).
Answer:
Given f(x) = \(\sqrt{\mathbf{x}-[\mathbf{x}]}\) ∈ R
⇒ [x] – x ≥ 0 ⇒ x ≥ [x] ⇒ x ∈ R
∴ Domain of ’f is Z.

Question 19.
Find the domain of the real valued function f(x) = \(\sqrt{[\mathbf{x}]-\mathbf{x}}\).
Answer:
Given f(x) = \(\sqrt{[\mathbf{x}]-\mathbf{x}}\) ∈ R
⇒ [x] – x ≥ 0 ⇒ [x] ≥ x ⇒ x ∈ Z
∴ Domain of ‘f’ is Z.

Question 20.
If f and g are real valued functions defined by f(x) = 2x – 1 and g(x) = x² then find
(i) (3f – 2g)(x)
(ii) (fg) (x)
(iii) \(\left(\frac{\sqrt{f}}{g}\right)\)(x)
(iv) (f + g + 2) (x)
Answer:
Given f(x) = 2x – 1 and g(x) = x²
Domain of f = domain of g R
Hence the domain of all the functions is R.
(i) (3f – 2g) (x) = 3f(x) – 2g(x)
= 3(2x – 1) – 2(x²)
= 6x – 3 – 2x²
= – 2x² + 6x – 3

(ii) (fg)(x) f(x) . g(x)
= (2x – 1)(x²) = 2x³ – x².

(iii) \(\left(\frac{\sqrt{f}}{g}\right)\) (x) = \(\frac{\sqrt{f(x)}}{g(x)}\) = \(\frac{\sqrt{2 x-1}}{x^2}\)

(iv) (f + g + 2) (x) = f(x) .g(x) + 2
= 2x – 1 + x² + 2
= x² + 2x + 1 = (x + 1)²

Question 21.
Find the domain of the real valued function f(x) = \(\sqrt{x^2-3 x+2}\).
Answer:
Given f(x)= \(\sqrt{x^2-3 x+2}\) ∈ R
⇒ x² – 3x + 2 ≥ 0
⇒ x² – 2x – x + 2 ≥ 0
⇒ x(x – 2) – 1(x – 2) ≥ 0
⇒ (x – 1) (x – 2) ≥ 0
⇒ x ≤ 1 or x ≥ 2
⇒ x ∈ (- ∝, 1] ∪ [2, ∝)
∴ Domain of ‘f’ is (- ∝, 1] ∪ [2, ∝)

Question 22.
f:R → R defined by f(x) = \(\frac{2 x+1}{3}\), then this function Is injection or not ? Justify. (Mar. 15 (TS)
Answer:
Given that f(x) = \(\frac{2 x+1}{3}\)
Let x₁, x₂ ∈ R.
Take f(x₁) = f(x₂) ⇒ \(\frac{2 x_1+1}{3}=\frac{2 x_2+1}{3}\)
⇒ 2x₁ + 1 = 2x₂ + 1 ⇒ 2x₁ = 2x₂ = x₁ = x₂
∴ f(x₁) = f(x₂) ⇒ x₁ = x₂
⇒ f is one – one.

Question 23.
If f = {(4, 5), (5, 6),(6, – 4)} and g = ((4, – 4), (6, 5), (8, 5)) then find f + g and fg. [Mar. ‘17(TS)]
Answer:
Given f = {(4, 5), (5, 6), (6, – 4)} and
g = {(4, – 4), (6, 5), (8, 5’)) then domain of f = {4, 5, 6) and Range of f = {4, 6, 8}
Domain of f + g = A ∩ B = {4, 6}
= (domain of f) ∩ (domain of g)
(i) f.g={(4, 5, – 4), (6, – 4 + 5)}
= {(4, 1), (6, 1)}

(ii) Domain of fg = (domain of f) ∩ (domain of g)
= A ∩ B = (4, 6)
= {(4, 5 × – 4).(6, – 4 × 5)}.
= {(4, – 20), (6, – 20)}

Question 24.
If f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) for all x ∈ R, are two functions, then find,
(i) (gof) (x)
(ii) (fog) (x) [Mar. 19(TS)]
Answer:
Given f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\)

(i) (gof) (x) = g[ f(x) ]
= g[2x – 1] = \(\frac{2 x-1+1}{2}\) = \(\frac{2 x}{2}\) = x

(ii) (fog) (x) = f [g(x)]
= \(f\left(\frac{x+1}{2}\right)\) = 2\(\left(\frac{\mathrm{x}+1}{2}\right)\) – 1 = x + 1 – 1 = x

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Trigonometric Equations Important Questions

Question 1.
Solve 2 cos²θ – √3 sin θ + 1 = 0. [May ’09; B.P]
Answer:
Given equation is 2 cos2 θ – √3 sin θ + 1 = 0
⇒ 2(1 – sin2 θ) – √3 sin θ + 1 = 0
⇒ 2 – 2sin2 θ – √3 sin θ + 1=0
⇒ 2 sin2 θ + √3 sin θ – 3 = 0
⇒ 2 sin2 θ + 2 √3 sin θ – √3 sin θ – 3 = 0
⇒ 2 sin θ (sin θ + √3 ) – + √3 (sin θ + √3 ) = 0
⇒ (sin θ + √3)- (2 sin θ – √3) = 0
⇒ sin θ + √3 = 0 (or) 2 sin θ – √3 = 0
⇒ sin 0θ = – J3 (or) sin θ = \(\frac{\sqrt{3}}{2}\)

Case -1: sin θ = -√3 ∉ [- 1, 1 ]
∴ There is no solution set.

Case – II : sin θ = \(\frac{\sqrt{3}}{2}\) ⇒ sin θ = sin \(\)
∴ Solution set is θ = {nπ + (-1)ⁿ α, n ∈ Z} ⇒
θ = {nπ + (-1)ⁿ\(\frac{\pi}{3}\) α, n ∈ Z}
∴ The solution of the given equation is
θ = {nπ + (-1)ⁿ\(\frac{\pi}{3}\) α, n ∈ Z}

Question 2.
Find all values of x ≠ 0 in (-π, π) satisfying the equation 8^{1+cosx+cos2x+……………..} = 4³. [Mar. ’09]
Answer:
Given 8^{1+cosx+cos2x+……………..} = 4³
8^{\(\frac{1}{1-\cos x}\)} = 4³ [∵ s_∞ = \(\frac{a}{1-r}\)]
(2³)^{\(\frac{1}{1-\cos x}\)} = 2⁶
2^{\(\frac{1}{1-\cos x}\)} = 2⁶
\(\frac{1}{1-\cos x}\) = 6
1 – cos x = \(\frac{1}{2}\)
⇒ cos x = \(\frac{1}{2}\)
⇒ x = ±\(\frac{\pi}{3}\)
∴ x = \(\frac{\pi}{3}\) (or) –\(\frac{\pi}{3}\) [∵x ∈ (-π, π)]

Question 3.
Solve tan θ + 3 cot θ = 5 sec θ. [Mar. ’02; May ’99, ’84]
Answer:
Given tan θ + 3 cot θ = 5 sec θ
⇒ \(\frac{\sin \theta}{\cos \theta}+3 \cdot \frac{\cos \theta}{\sin \theta}=\frac{5}{\cos \theta}\)
⇒ \(\frac{\sin ^2 \theta+3 \cos ^2 \theta}{\cos \theta \cdot \sin \theta}=\frac{5}{\cos \theta}\)
⇒ sin² θ + 3 cos²θ = 5 sin θ
⇒ sin² θ + 3 (1 – sin²θ) = 5 sin θ
⇒ sin² θ + 3 – 3 sin²θ = 5 sin θ
⇒ 2 sin²θ + 5 sin θ – 3 = 0
⇒ 2 sin²θ + 6 sin θ – sin θ – 3 = 0
⇒ 2 sin θ(sin θ + 3) – 1 (sin θ + 3) = 0
⇒ (sin θ + 3) (2 sin θ – 1) = 0
⇒ sin θ + 3 = 0 (or) 2 sin θ – 1 = 0
⇒ sin θ = -3 (or) sin θ = \(\frac{1}{2}\)

Case – I: sin θ = -3 ∈ [-1, 1]
There is no solution set.

Case – II: sin θ = \(\frac{1}{2}\)
⇒ sin θ = sin \(\frac{\pi}{6}\)
∴ Solution set is θ = {nπ + (-1)ⁿ α, n ∈ Z}
⇒ θ = {nπ + (-1)ⁿ \(\frac{\pi}{6}\), n ∈ Z}

∴ The solution set of the given equation is
θ = {nπ + (-1)ⁿ \(\frac{\pi}{6}\), n ∈ Z}

Question 4.
Solve 1 + sin²θ = 3sin θ. cos θ. [Mar.(AP & TS) ’17, ’11; May ’00]
Answer:
Given 1 + sin²θ = 3sin θ. cos θ
On dividing both sides with cos2θ, we get
⇒ \(\frac{1}{\cos ^2 \theta}+\frac{\sin ^2 \theta}{\cos ^2 \theta}=\frac{3 \sin \theta \cos \theta}{\cos ^2 \theta}\)
⇒ sec²θ + tan²θ = 3 tanθ
⇒ 1 + tan²θ + tan²θ = 3 tan θ
⇒ 2 tan²θ – 3 tan θ + 1 = 0
⇒ 2 tan²θ – 2 tan θ – tan θ + 1 = 0
⇒ 2 tan θ (tan θ – 1) – l(tan θ – 1) = 0
⇒ (tan θ – 1) (2 tan θ – 1) = 0
⇒ tan θ – 1=0 (or) 2 tan θ – 1 = 0
⇒ tan θ = 1 (or) 2 tan θ = \(\frac{1}{2}\)

Case – I: tan θ = 1 ⇒ tan θ = tan \(\frac{\pi}{4}\)
∴ Solution set is θ = {nπ + α, n ∈ Z}
⇒ θ = {nπ + \(\frac{\pi}{4}\), n ∈ z}

Case – II: tan θ = 1 ⇒ tan θ = 0.5
⇒ tan θ = tan 26°. 34′
Solution set is θ =
⇒ θ = {nπ + 26°.34′, n ∈ Z)
∴ The solution set of the given equation is
θ = {nπ + \(\frac{\pi}{4}\), n ∈ z} ∪ {nπ + 26°.34′, n ∈ Z}

Question 5.
Solve √2(sin x + cos x) = √3. [Mar. ’16(AP), Mar. 15(AP); May ’12, ’08]
Answer:
Given equation is √2(sin x + cos x) = √3
⇒ sin x + cos x = \(\frac{\sqrt{3}}{\sqrt{2}}\)
On dividing Both sides with \(\sqrt{a^2+b^2}\)
= \(\sqrt{1^2+1^2}\) = , we get
⇒ \(\frac{1}{\sqrt{2}}\)sin x + \(\frac{1}{\sqrt{2}}\)cos x = \(\frac{1}{\sqrt{2}}\)
⇒ cos x.cos\(\frac{\pi}{4}\) + sin x sin\(\frac{\pi}{4}=\frac{\sqrt{3}}{2}\)
⇒ cos(x – \(\frac{\pi}{4}\)) = cos\(\frac{\pi}{6}\)

∴ Solution set is θ = {2nπ ± α, n ∈ Z}
⇒ x – \(\frac{\pi}{4}\) = {2nπ + \(\frac{\pi}{6}\), n ∈ Z}

Case – I: x – \(\frac{\pi}{4}\) = 2nπ + \(\frac{\pi}{6}\), n ∈ Z
x = 2nπ + \(\frac{\pi}{6}\) + \(\frac{\pi}{4}\)
x = 2nπ + \(\frac{5\pi}{12}\)
x = {(24n + 5)\(\frac{\pi}{12}\)}, n ∈ Z

Case – II: x – \(\frac{\pi}{4}\) = 2nπ – \(\frac{\pi}{6}\), n ∈ Z
x = 2nπ – \(\frac{\pi}{6}\) + \(\frac{\pi}{4}\)
x = 2nπ + \(\frac{\pi}{12}\)
x = {(24n + 1)\(\frac{\pi}{12}\)}, n ∈ Z

∴ The solution set of the given equation is
x = {(24n + 5)\(\frac{\pi}{12}\)} ∪ {(24n + 1)\(\frac{\pi}{12}\)}, n ∈ Z

Question 6.
If θ₁, θ₂ are solutions of the equation a cos 2θ + b sin 2θ = c, tan θ₁ ≠ tan θ₂ and a + c ≠ 0, then find the values of
(i) tan θ₁ + tan θ₂
(ii) tan θ₁. tan θ₂.
Answer:
Given equation is a cos 2θ + b sin 2θ = c
⇒ a\(\left[\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right]\) + b\(\left[\frac{2 \tan \theta}{1+\tan ^2 \theta}\right]\) = c
⇒ \(\frac{\mathrm{a}-\mathrm{a} \tan ^2 \theta+2 b \tan \theta}{1+\tan ^2 \theta}\) = c
⇒ a – a tan²θ + 2b tan θ = c + c tan²θ
⇒ c + c tan²θ – a + a tan²θ – 2b tan θ = 0
⇒ (a + c) tan²θ – 2b tan θ + (c – a) = 0 ……… (1)
This is a quadratic equation in tan θ since θ₁, θ₂ are the roots of the given equation.

tan θ₁, tan θ₂ are the roots of the equation (1).
i) Sum of the roots = tan θ₁ + tan θ₂
= \(\frac{-b}{a}=\frac{-(-2 b)}{a+c}\)
tan θ₁ + tan θ₂ = \(\frac{2 b}{a+c}\)

ii) Product of the roots = tan θ₁ . tan θ₂
= \(\frac{c}{a}=\frac{c-a}{a+c}\)
tan θ₁ . tan θ₂ = \(\frac{c}{a}=\frac{c-a}{a+c}\)

Question 7.
Solve : 4 sin x. sin 2x. sin 4x = sin 3x.
Answer:
Given sin 3x = 4 sin x . sin 2x. sin 4x
= 2 sin x (2 sin 2x sin 4x)
= 2 sin x (cos 2x – cos 6x)
⇒ sin 3x = 2 cos 2x sin x – 2 cos 6x sin x
⇒ sin 3x = sin 3x – sin x – 2 cos 6x sin x
⇒ 2 cos 6x sin x + sin x = 0
⇒ sin x (2 cos 6x + 1) = 0
⇒ sin x = 0 or cos 6x = – \(\frac{1}{2}\)

Case (1): sin x = 0 ⇒ x = nπ, n ∈ Z is the general solution.

Case (2): cos 6x = –\(\frac{1}{2}\)
Principal solution is α = \(\frac{2 \pi}{3}\)
General solution is 6x = 2nπ ± \(\frac{2 \pi}{3}\)
⇒ x = \(\frac{\mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z.
∴ The solution set of the given equation is x = {nπ, n ∈ Z} ∪ {\(\frac{\mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z}

Question 8.
If θ < 0 < π, solve cos θ cos 2θ cos 3θ = \(\frac{1}{4}\).
Answer:
Given equation is cos θ cos 2θ cos 3θ = \(\frac{1}{4}\)
⇒ 4 cos θ cos 2θ cos 3θ = 1
⇒ 2 cos 2θ (2 cos 3θ cosθ) = 1
⇒ 2 cos 2θ [cos (3θ + θ) + cos(3θ – θ)] = 1
⇒ 2 cos 2θ (cos 4θ + cos 2θ) = 1
⇒ 2 cos 4θ cos 2θ + 2 cos2 2θ – 1 = 0
⇒ 2 cos 4θ cos 2θ + cos 4θ = 0
⇒ cos 4θ (2 cos 2θ + 1) = 0
⇒ cos4θ = 0 (or) ⇒ 2 cos 2θ + 1 = 0
cos 2θ = –\(\frac{1}{2}\)

Case – I: cos 4θ = 0

∴ The solutions of the case – I in (0, π) are \(\frac{\pi}{8}, \frac{3 \pi}{8}, \frac{5 \pi}{8}, \frac{7 \pi}{8}\)

Case – II: cos 2θ = –\(\frac{1}{2}\)

∴ The solutions of the case – II in (0, π) are \(\frac{\pi}{3}, \frac{2 \pi}{3}\)
∴ The solutions of the given equation in (0, π) are \(\frac{\pi}{8}, \frac{\pi}{3}, \frac{3 \pi}{8}, \frac{5 \pi}{8}, \frac{2 \pi}{3} \frac{7 \pi}{8}\)

Question 9.
Solve sin 2x – cos 2x = sin x – cos x [Mar. ’99]
Answer:
Given equation is
(sin 2x – sin x) – (cos 2x – cos x) = 0

Case – I: sin\(\left(\frac{x}{2}\right)\) = 0
Solution set is θ = {nπ, n ∈ Z}
\(\frac{x}{2}\) = {nπ, n ∈ Z}
x = {2nπ, n ∈ Z}

Case – II: tan\(\left(\frac{3 \mathrm{x}}{2}\right)\) = -1
tan\(\left(\frac{3 \mathrm{x}}{2}\right)\) = tan\(\left(\frac{-\pi}{4}\right)\)
∴ The solution set is θ = {nπ + α, n ∈ Z}
\(\frac{3 x}{2}\) = {n – \(\frac{\pi}{4}\), n ∈ Z}
x = {\(\frac{2 n \pi}{3}-\frac{\pi}{6}\), n ∈ Z}
∴ The solution set of the given equation is x = {2nπ, n ∈ Z} ∪ {\(\frac{2 n \pi}{3}-\frac{\pi}{6}\), n ∈ Z}

Question 10.
Solve 2 cos²θ + 11 sin θ = 7.
Answer:
Given equation is 2 cos²θ + 11 sin θ = 7
⇒ 2(1 – sin² θ) + 11 sin θ = 7
⇒ -2 sin² θ + 11 sin θ = 5
⇒ 2 sin² θ – 11 sin θ + 5 = 0
⇒ 2 sin² θ – 10 sin θ – sin θ + 5 = 0
⇒ 2 sin θ (sin θ – 5) – 1 (sin θ – 5) = 0
⇒ (2 sin θ – 1) (sin θ – 5) = 0

If sin θ – 5 = 0 then sin θ = 5 is not admissible.
If 2 sin θ – 1 = 0 ⇒ sin θ = \(\frac{1}{4}\) and the principal solution is α = \(\frac{\pi}{6}\)
∴ General solution is θ = nπ + (-1)ⁿ\(\frac{\pi}{6}\), n ∈ Z.

Question 11.
Solve sin x + √3 cos x = √2. [Mar. ’18(TS); Mar. ’10; May ’98, ’93]
Answer:
Given equation is sin x + √3 cos x = √2
On dividing both sides with \(\sqrt{a^2+b^2}\)

Hence the solution set of the given equation is x = {2nπ + \(\frac{5\pi}{12}\), n ∈ Z} ∪ {2nπ – \(\frac{\pi}{12}\), n ∈ Z}

Question 12.
Solve cot 2x – (√3 + 1)cot x + √3 = 0. [Mar. ’14, ’12]
Answer:
Given cot 2x – (√3 + 1)cot x + √3 = 0
⇒ cot 2x – √3 cot x – cot x + √3 = 0
⇒ cot x(cot x – √3) – 1(cot x – √3) = 0
⇒ (cot x – √3) (cot x – 1) = 0
⇒ cot x – √3=0 (or) cot x – 1 = 0
⇒ cot x = √3 (or) cot x = 1
⇒ cot x = cot 30° (or) cot x = cot 45°
⇒ x = 30° (or) x = 45°

General solutions:
x = nπ + 30°, n ∈ Z
Let n = 0 ⇒ x = 30°

General solution:
x = nπ + 45°, n ∈ Z
Let n = 0 ⇒ x = 45°
∴ Solutions set = {30°, 45°}

Question 13.
If x + y = \(\frac{2 \pi}{3}\) and sin x + sin y = \(\frac{3}{2}\), find x and y. [Mar. ’97]
Answer:
Given x + y = \(\frac{2 \pi}{3}\) …………(1)
sin x + sin y = \(\frac{3}{2}\)

Some More Maths 1A Trigonometric Equations Important Questions

Question 1.
If x is acute and sin (x + 10°) = cos (3x – 68°) find x in degrees.
Answer:
Given sin (x + 10°) = cos (3x – 68°)
⇒ sin(x + 10°) = sin[90° + (3x – 68°)]
= sin (22° + 3x)
⇒ x + 10°= nπ + (-1)ⁿ (22° + 3x)

If n = 2k (even) k ∈ Z then
x + 10° = 2k7t + (-1)” (22° + 3x)
⇒ 2kπ + (-1)2k (22° + 3x) = 2kπ + 22° + 3x
⇒ 2x = -k(2π) – 12°
⇒ x = \(θ\) = -k(180°) – 6°

If n = 2k + 1 then
x + 10° = (2k + 1) 180° – (22° + 3x)
⇒ 4x = (2k +1) 180° – 32°
⇒ x = (2k + 1)45° – 8°
When k = 0 we get x = 37°
If we take k = 1, 2, ………… the value of x is not acute.
Hence the value of x is 37°.

Question 2.
Solve 5 cos²θ + 7 sin²θ = 6.
Answer:
Given 5 cos²θ + 7 sin²θ = 6
Dividing by cos²θ we get,
5 + 7 tan²θ = 6 sec²θ
⇒ 5 + 7 tan²θ = 6(1 + tan²θ)
⇒ tan²θ – 1 = 0 ⇒ tan²θ = 1 ⇒ tan θ = ±1
θ = nπ ± \(\frac{\pi}{4}\),n ∈ Z is the general solution.

Question 3.
Solve 2 sin²θ – 4 = 5 cos θ.
Answer:
2 sin²θ – 4 = 5 cos θ
⇒ 2(1 – cos²θ) – 5 cos θ – 4 = 0
⇒ 2cos²θ + 5cos θ + 4-2 = 0
⇒ 2cos²θ + 5cos θ + 2 = 0
⇒ 2cos²θ + 4cos θ + cos θ + 2 = 0
⇒ 2cos θ(cos θ + 2) + 1(cos θ + 2) = 0
⇒ (cos θ + 2)(2cos θ + 1) = 0
cos θ + 2 = 0 is not admissible.
Consider 2cos θ + 1 = 0 ⇒ cos θ = –\(\frac{1}{2}\), the principal solution is α = \(\frac{2 \pi}{3}\)
∴ General solution is θ = 2nπ ± \(\frac{2 \pi}{3}\),n ∈ Z.

Question 4.
Solve 4cos²θ + √3 = 2(√3 + 1)cos θ.
Answer:
4cos²θ – 2(√3 + 1)cosθ + √3 = 0
⇒ 4cos²θ – 2√3cos θ – 2cos θ + √3 =0
⇒ 2cosθ(2cosθ – √3)- 1(2cos θ – √3) = 0
⇒ (2cosθ – 1)(2cosθ – √3) = 0
If cos θ = \(\frac{1}{2}\) then θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z is the general solution.
If 2cos θ – √3 = 0 then cos θ = \(\frac{\sqrt{3}}{2}\)
Hence the general solution in this case is
θ = 2nπ ± \(\frac{\pi}{6}\) ,n ∈ Z.

Question 5.
Solve √3 sin θ – cos θ = √2. [May ’14, Mar. ’18(AP)]
Answer:
Given √3 sin θ – cos θ = √2
Divide both sides by
\(\sqrt{3+1}\) = 2, \(\frac{\sqrt{3}}{2}\)sin θ – \(\frac{1}{2}\)cos θ = \(\frac{1}{\sqrt{2}}\)

∴ The principal solution for θ – \(\frac{\pi}{6}\) is α = \(\frac{\pi}{4}\)
∴General soIutio is θ – \(\frac{\pi}{6}\) = nπ + (-1)ⁿ \(\frac{\pi}{4}\)
⇒ θ = \(\frac{\pi}{6}\) + nπ + (-1)ⁿ \(\frac{\pi}{4}\)

Question 6.
Solve cos 2θ + cos 8θ = cos 5θ.
Answer:
Given cos 2θ + cos 8θ = cos 5θ
⇒ 2 cos 5θ cos 3θ = cos 5θ
⇒ cos 5θ(2 cos 3θ – 1) = 0
Case (i): cos 5θ = 0
⇒ 5θ = (2n + 1)\(\frac{\pi}{2}\) ⇒ θ = (2n + 1)\(\frac{\pi}{10}\), n ∈ Z

Case (ii): 2cos 3θ – 1 = 0 ⇒ cos 3θ = \(\frac{1}{2}\)
Principal solution is α = \(\frac{\pi}{3}\)

∴ General Solution is
3θ = 2nπ ± \(\frac{\pi}{3}\) ⇒ θ = \(\frac{2 \mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z

∴ General Solutions are
{(2n + 1)\(\frac{\pi}{10}, \frac{2 \mathrm{n} \pi}{3} \pm \frac{\pi}{9}\), n ∈ Z}

Question 7.
Solve cos θ – cos 7θ = sin 4θ.
Answer:
2sin\(\left(\frac{\theta+7 \theta}{2}\right)\) sin\(\left(\frac{7 \theta-\theta}{2}\right)\) = sin 4θ
⇒ 2sin4θ sin 3θ = sin 4θ
⇒ sin 4θ(2 sin 3θ – 1) = 0

Case (i): sin 4θ = 0 ⇒ 4θ = nθ ⇒ \(\frac{\mathrm{n} \pi}{4}\), n ∈ Z

Case (ii): 2sin 3θ – 1 = 0 ⇒ sin 3θ = \(\frac{1}{2}\)
Principal solution is α = \(\frac{\pi}{6}\)

∴ General solution is 3θ = nπ + (-1)ⁿ\(\frac{\pi}{6}\)
⇒ θ = \(\frac{\mathrm{n} \pi}{3}\) + (-1)ⁿ\(\frac{\pi}{18}\), n ∈ Z

Question 8.
If tan(π cos θ) = cot (π sin θ), then prove that cos(θ – \(\frac{\pi}{4}\)) = ±\(\frac{1}{2 \sqrt{2}}\). [Mar ’15(TS)]
Answer:
Given that tan(π cos θ)
= cot(π sin θ) = tan(\(\frac{\pi}{2}\) – π cos θ)
∴ π cos θ = ±\(\frac{\pi}{2}\) – π sin θ
⇒ cos θ = ±\(\frac{1}{2}\) – sin θ ⇒ cos θ + sin θ = ±\(\frac{1}{2}\)
⇒ cos θ\(\frac{1}{\sqrt{2}}\) + sin θ\(\frac{1}{\sqrt{2}}=\pm \frac{1}{2 \sqrt{2}}\)
⇒ cos θ cos\(\frac{\pi}{4}\) + sin θ sin\(\frac{\pi}{4}\) = \(\pm \frac{1}{2 \sqrt{2}}\)

Question 9.
If α, β are the solutions of the equation a cos θ + b sin θ = c, where a, b, c ∈ R and if a² + b² > 0, cos α ≠ cos β and sin α ≠ sin β then show that
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α. cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α. sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Answer:
Given acos θ + bsin θ = c ⇒ acos θ = c – bsin θ ⇒ a²cos2θ = c² – 2bcsinθ + b²sin²θ
⇒ a² (1 – sin²θ) = c² – 2bcsinθ + b² sin²θ
⇒ (a² + b²)sin²θ – 2bcsinθ + (c² – a²) = 0
This is a quadratic equation in sin θ and let the roots be sin α and sin β. Then
sin α + sin β = \(\frac{2 b c}{a^2+b^2}\); sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Also b sin θ = c – acos θ ⇒ b²sin²θ = c² -2accos θ + a²cos²θ
⇒ b²(1 – cos²θ) = c² – 2ac cosθ + a² cos²θ
⇒ (b² + a²)cos²θ – 2ac cosθ + (c² – b²) =0
This is a quadratic equation in cos θ and let cos α, cos β be the roots. Then
cos α + cos β = \(\frac{2 a c}{a^2+b^2}\) and cos α. cos β = \(\frac{c^2-b^2}{a^2+b^2}\)

Hence from above we have
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α. cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

Question 10.
Give p ≠ ± q, show that the solutions of cos p0 + cos q0 = 0 form two series each of which is in A.P. Also find the common difference of each A.P. [Mar. ’19(AP)]
Answer:
Given equation is cos pθ + cos qθ = 0

which are two A.P.’s is with common differences

Telangana TSBIE TS Inter 1st Year Physics Study Material 7th Lesson Systems of Particles and Rotational Motion Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 7th Lesson Systems of Particles and Rotational Motion

Very Short Answer Type Questions

Question 1.
Is it necessary that a mass should be present at the centre of mass of any system? [AP May. ’16; May ’14]
Answer:
No. It is not necessary to present some mass at centre of mass of the system.
Ex: At the centre of ring (or) bangle, there is no mass present at centre of mass.

Question 2.
What is the difference in the positions of a girl carrying a bag in one of her hands and another girl carrying a bag in each of her two hands?
Answer:
i) a) When she carries a bag in one hand her centre of mass will shift to the side of the hand that carries the bag.
b) When a bag is in one hand some unbalanced force will act on her and it is difficult to carry.

ii) If she carries two bags in two hands then her centre of mass remains unchanged. Force on two hands are equal i.e. balanced so it is easy to carry the bags.

Question 3.
Two rigid bodies have same moment of inertia about their axes of symmetry. Of the two, which body will have greater kinetic energy?
Answer:
Relation between angular momentum and kinetic energy is, KE = \(\frac{L^2}{2I}\)

Because moment of inertia is same the body with large angular momentum will have larger kinetic energy.

Question 4.
Why are spokes provided in a bicycle wheel? [AP May ’14]
Answer:
The spokes of cycle wheel increase its moment of inertia. The greater the moment of inertia, the greater is the opposition to any change in uniform rotational motion. As a result the cycle runs smoother and speeder. If the cycle wheel had no spokes, the cycle would be driven in jerks and hence unsafe.

Question 5.
We cannot open or close the door by applying force at the hinges. Why? [AP May ’16]
Answer:
To open or close a door, we apply a force normal to the door. If the force is applied at the hinges the perpendicular distance of force is zero. Hence, there will be no turning effect however large force is applied.

Question 6.
Why do we prefer a spanner of longer arm as compared to the spanner of shorter arm?
Answer:
The turning effect of force, τ = \(\overline{\mathrm{r}}\times\overline{\mathrm{F}}\). When arm of the spanner is long, r is larger. Therefore smaller force (F) will produce the same turning effect. Hence, the spanner of longer arm is preferred as compared to the spanner of shorter arm.

Question 7.
By spinning eggs on a table top, how will you distinguish an hard boiled egg from egg? [AP Mar. ’13]
Answer:
To distinguish between a hard boiled egg and a raw egg, we spin each on a table top. The egg which spins at a slower rate shall be a raw egg. This is because in a raw egg, liquid matter inside tries to get away from the axis of rotation. Therefore, its moment of inertia ‘I’ increases. As τ = Iα = constant, therefore, α decreases i.e., raw egg will spin with smaller angular acceleration.

Question 8.
Why should a helicopter necessarily have two propellers?
Answer:
If the helicopter had only one propeller, then due to conservation of angular momen¬tum, the helicopter itself would turn in the opposite direction. Hence, the helicopter should necessarily have two propellers.

Question 9.
If the polar ice caps of the earth were to melt, what would the effect of the length of the day be?
Answer:
Earth rotates about its polar axis. When ice of polar caps of earth melts, mass concen¬trated near the axis of rotation spreads out. Therefore, moment of inertia ‘I’ increases.

As no external torque acts, L = Iω = I(\(\frac{2 \pi}{T}\)) = constant

with increase of I, T will increase i.e., length of the day will increase.

Question 10.
Why is it easier to balance a bicycle in motion?
Answer:
A bicycle in motion is in rotational equilibrium. From principles of Dynamics of rotational bodies is that the forces that are perpendicular to the axis of rotation will try to turn the axis of rotation but necessary forces will arise it cancel these forces due to inertia of rotation and fixed position of axis is maintained. So it is easy to balance a rotating body.

Short Answer Questions

Question 1.
Distinguish between centre of mass and centre of gravity. [AP Mar. 18, 17, 16, 15, 14, 13, May 17; June 15 : TS Mar. 16. 15, May 18, 17]
Answer:

Question 2.
Show that a system of particles moving under the influence of an external force, moves as if the force is applied at its centre of mass. [AP May ’18]
Answer:
Consider a system of particles of masses m₁, m₂, ……….. mn moves with velocity

But Force (F) = ma, so total force on the body is
F = Ma_C.M = m₁a₁ + m₂a₂ + m₃a₃ + ……….. + m_n a_n
or Total Force F = Ma_C.M = F₁ + F₂ + F₃ + ……… + F_n

Hence, total force on the body is the sum of forces on individual particles and it is equals to force on centre of mass of the body.

Question 3.
Explain about the centre of mass of earth-moon system and its rotation around the sun.
Answer:
The interaction of earth and moon does not effect the motion of centre of mass of earth and moon system around the sun. The gravitational force between earth and moon is internal force. Internal forces cannot change the position of centre of mass.

The external force acting on the centre of mass of earth and moon system is force between the sun and C.M. of earth, moon system. Motion of centre of mass depends on external force. Hence, earth moon system continues to move in an elliptical path around the sun. It is irrespective of rotation of moon around earth.

Question 4.
Define vector product. Explain the properties of a vector product with two examples. [AP Mar. ’17, ’15 ; TS Mar. ’17, ’16, ’15; APMay ’18. ’17; TS May ’18. ’16]
Answer:
Vector product (or) cross product :
If the product of two vectors (say \(\overline{\mathrm{A}}\) and \(\overline{\mathrm{B}}\)) gives a vector then that multiplication of vectors is called cross product or vector product of vectors.

Properties of cross product:
1. Cross product is not commutative i.e.

2. Cross product obeys distributive law i.e.,

3. If any vector is represented by the combination of \(\overline{\mathrm{i}},\overline{\mathrm{j}}\) and \(\overline{\mathrm{k}}\) then cross product will obey right hand screw rule.
4. The product of two coplanar perpendicular unit vectors will generate a unit vector perpendicular to that plane

5. Cross product of parallel vectors is zero

Examples of cross product:
1) Torque (or) moment of force (\(\overline{\mathrm{\tau}}\)) :
It is defined as the product of force and perpendicular distance from the point of application.
∴ Torque τ = \(\overline{\mathrm{r}}\times\overline{\mathrm{F}}\)

2) Angular momentum and angular velocity :
For a rigid body in motion, Angular momentum (\(\overline{\mathrm{L}}\)) = radius (\(\overline{\mathrm{r}}\)) x momentum (\(\overline{\mathrm{P}}\))
∴ Angular momentum (\(\overline{\mathrm{L}}\)) = \(\overline{\mathrm{r}}\) × (m\(\overline{\mathrm{v}}\)) = m(\(\overline{\mathrm{r}}\times\overline{\mathrm{v}}\))

Question 5.
Define angular velocity. Derive v = r ω. [TS Mar. 19,’ 17, 16; AP Mar. 19, May. 16; May 14]
Answer:
Angular velocity (ω) :
Rate of change of angular displacement is called angular velocity.

Relation between linear velocity (v) and angular velocity (ω) :
Let a particle P is moving along circumference of a circle of radius r1 with uniform speed v. Let it is initially at the position A, during a small time ∆t it goes to a new position say C from B. Angle subtended during this small interval is say dθ.

By definition angular velocity,

Question 6.
State the principle of conservation of angular momentum. Give two examples.
Answer:
Law of conservation of angular momentum:
When no external torque is acting on a body then the angular momentum of that rota-ting body is constant.
i.e., I₁ω₁ = I₂ω₂ (when τ = 0)

Example -1:
A boy stands over the centre of a horizontal platform which is rotating freely with a speed ω₁ (n₁revolutions/sec.) about a vertical axis passing through the centre of the platform and straight up through the boy. He holds two bricks in each of his hands close to his body. The combined moment of inertia of the system is say I₁. Let the boy stretches his arms to hold the masses far away from his body. In this position the moment of inertia increases to I₂ and let ω₂ is his angular speed.

Here ω₂ < ω₁ because moment of inertia increases.

Example – 2 :
An athlete diving off a high spring board can bring his legs and hands close to the body and performs Somersault about a horizontal axis passing through his body in the air before reaching the water below it. During the fall his angular momentum remains constant.

Question 7.
Define angular acceleration and torque. Establish the relation between angular acceleration and torque. [TS Mar. ’18, ’17; TS May ’17, June ’15; AP Mar. ’19, June ’15]
Answer:
Angular acceleration (α) :
Rate of change of angular velocity is called angular acceleration.

Torque :
It is defined as the product of the force and the perpendicular distance of the point of application of the force from that point.

Relation between angular acceleration and Torque:
We know that, L = Iω

On differentiating the above expression with respect to time ‘t’

But \(\frac{dL}{dt}\) is the rate of change of angular momentum called ‘Torque (τ)”.

and \(\frac{d \omega}{dt}\) is the rate of change of angular velocity called “angular acceleration (α)”

∴ The relation between Torque and angular acceleration is, τ = lα

Question 8.
Write the equations of motion for a particle rotating about a fixed axis.
Answer:
Equations of rotational kinematics :
If ‘θ’ is the angular displacement, Wj is the initial angular velocity, ω_f is the final angular velocity after a time ‘t’ seconds and ‘α’ is the angular acceleration, then the equations of rotational kinematics can be written as,

Question 9.
Derive expressions for the final velocity and total energy of a body rolling without slipping.
Answer:
A rolling body has both translational kinetic energy and rotational kinetic energy. So the total K.E energy of a rolling body is,

Long Answer Questions

Question 1.
(a) State and prove parallel axis theorem.
(b) For a thin flat circular disk, the radius of gyration about a diameter as axis is k. If the disk is cut along a diameter AB as shown into two equal pieces, then find the radius of gyration of each piece about AB.

Answer:
a) Parallel axis theorem :
The moment of inertia of a rigid body about an axis passing through a point is the sum of moment of inertia about parallel axis passing through centre of mass (I_G) and mass of the body multiplied by Square of distance (MR²) between the axes i.e.,
I = I_G + MR²

Proof :
Consider a rigid body of mass M with ‘G’ as its centre of mass. Iq the moment of inertia about an axis passing through centre of mass. I = The moment of inertia about an axis passing through the point ’O’ in that plane.

Let perpendicular distance between the axes is OG = R (say)

Consider point P in the given plane. Join OP and GP. Extend the line OG and drop a normal from ’P’ on to it as shown in figure.

The moment of inertia about the axis passing through centre of mass G.
(I_G) = ∑mGP² ……….. (1)

M.O.I. of the body about an axis passing through ‘O’ (I) = ∑mOP² ………… (2)
From triangle OPD
OP² = OD² + DP²
⇒ OD = OG + GD
∴ OD² = (OG + GD)² = OG² + GD² + 2OG. GD ………….. (3)
From Equations (2) and (3)
I = ∑mOP² = Em [ (OG² + GD² + 2OG. GD) + DP²]
∴ I = ∑m {GD² + DP² + OG² + 20G. GN}
But GD² + DP² = GP²
∴ I = ∑m {GP² + OG² + 20G. GD}
∴ I = ∑m GP² + ∑mOG² + 20G ∑mGD ………. (4)

But the terms ∑mGP² = I_G
∑mOG² = MR² (∵ ∑m = M and OG = R)
The term 20G ∑mGD = 0. Because it represents sum of moment of masses about centre of mass. Hence its value is zero.
∴ I = I_G + MR²

Hence parallel axis theorem is proved.

b) Moment of inertia of a disc of mass ‘M’ and radius ‘R’ about its diameter is,
I = \(\frac{MR^2}{4}\)

If ‘k’ is radius of gyration of disc then, I = Mk²
∴ Mk² = \(\frac{MR^2}{4}\) ⇒ k = R/2

After cutting along the diameter, mass M of each piece = \(\frac{M}{2}\)
Moment of inertia of each piece,

Question 2.
(a) State and prove perpendicular axis theorem.
(b) If a thin circular ring and a thin flat circular disk of same mass have same moment of inertia about their respective diameters as axis. Then find the ratio of their radii.
Answer:
a) Perpendicular axis theorem :
The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moment of inertia about two perpendicular axis concurrent with perpendicular axis and lying in the plane of the body.
∴ I_z = I_x + I_y

Proof :
Consider a rectangular plane lamina. X and Y are two mutually perpendicular axis in the plane. Choose another perpendicular axis Z passing through the point ‘O’.

Consider a particle P in XOY plane.
Its co-ordinates are (x, y).
Moment of inertia of particle about
X-axis is I_X = ∑my².
M.O.I about Y-axis is I_Y = ∑mx²
M.O.I about Z axis is I_Z = ∑ m . OP²
From triangle OAP,
OP² = OA² + AP² = y² + x²
∴ Iz = ∑ mOP² = ∑ m (y² + x²)
∴ Iz = X my² + ∑ mx²
But ∑ my² = I_x and ∑ mx² = I_y

∴ Moment of Inertia about a perpendicular axis passing through ‘O’ is I_Z = I_X + I_Y
Hence perpendicular axis theorem is proved.

b) Moment of inertia of a thin circular ring about its diameter is, I₁ = m₁ R²₁

Moment of inertia of a flat circular disc about its diameter is, I₂ = \(\frac{m_2R^{2}_{2}}{2}\)
Given that two objects having same moment of inertia i.e., I₁ = I₂

Question 3.
State and prove the principle of conservation of angular momentum. Explain the principle of conservation of angular momentum with examples. [AP Mar. ’16]
Answer:
Law of conservation of angular momentum: When no external torque is acting on a body then the angular momentum of that rotating body is constant.
i.e., I₁ω₁ = I₂ω₂ (when τ = 0)

Explanation:
Here I₁ and I₂ are moment of inertia of rotating bodies and ω₁ and ω₂ are their initial and final angular velocities. If

Example -1 :
A boy stands over the centre of a horizontal platform which is rotating freely with a speed ω₁ (n₁ revolutions/sec.) about a vertical axis passing through the centre of the platform and straight up through the boy. He holds two bricks in each of his hands close to his body. The combined moment of inertia of the system is say I₁. Let the boy stretches his arms to hold the masses far away from his body. In this position the moment of inertia increases to I₂ and let ω₂ is his angular speed.

Here ω₂ < ω₁ because moment of inertia increases.

Example – 2 :
An athlete diving off a high spring board can bring his legs and hands close to the body and performs Somersault about a horizontal axis passing through his body in the air before reaching the water below it. During the fall his angular momentum remains constant.

Position of centre of mass of some symmetrical bodies :

Comparison of translatory and rotatory motions :

Problems

Question 1.
Show that a • (b × c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors a, b and c. (IMP)
Solution:
Let a parallelopiped be formed on three

Now \(\hat{a}\) • (\(\hat{b}\times\hat{c}\) x c) = \(\hat{a}\) • be \(\hat{n}\) = (a) (be) cos 0° – abc

Which is equal in magnitude to the volume of parallelopiped.

Question 2.
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope ? Assume that there is no slipping.
Soution:
Here M = 3 kg ; R = 40 cm = 0.4 m
Moment of inertia of the hollow cylinder about its axis, I = MR² = 3(0.4)² = 0.48 kg m²
Force applied, F = 30 N
∴ Torque, τ = F × R = 30 × 0.4 = 12 N – m

If α is angular acceleration produced, then from τ = Iα

Linear acceleration, a = Ra = 0.4 × 25
= 10 ms^-2.

Question 3.
A coin is kept a distance of 10 cm from the centre of a circular turn table. If the coefficient of static friction between the table and the coin is 0.8. Find the frequency or rotation of the disc at which the coin will just begin to slip.
Solution:
Distance of coin = r = 10 cm = 0.1 m.
Coefficient of friction µ = 0.8.
Frequency of rotation = number of rotations per second.

Question 4.
Find the torque of a force \(\mathbf{7} \overrightarrow{\mathbf{i}}+\mathbf{3} \overrightarrow{\mathbf{j}}-5 \overrightarrow{\mathbf{k}}\) about the origin. The force acts on a particle whose position vector is \(\overrightarrow{\mathbf{i}}-\overrightarrow{\mathbf{j}}+\overrightarrow{\mathbf{k}}\). [AP Mar. ’14, ’13; May ’13]
Answer:

Question 5.
Particles of masses 1g, 2g, 3g….., 100g are kept at the marks 1 cm, 2 cm, 3 cm…, 100 cm respectively on a meter scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the meter scale.
Solution:
Given Masses of 1g, 2g, 3g 100 g are 1, 2, 3 ……….. 100 cm on a scale.

i) Sum of masses 2m = \(\sum_{i=1}^n\)ni
Sum of n natural numbers S

∴ Total mass M = 5051 gr = 5.051 kg → (1)

ii) Centre of mass of all these masses is given by

iii) M.O.I. = I

Sum of cubes of 1st n natural numbers is

M.O.I. about C.M. = I_G = I – MR²
= 2.550 – 5.05 × 0.67 × 0.67 = 2.550 – 2.267 = 0.283 kg.m2

iv) Perpendicular bisector is at 50 CM.
So shift M.O.I from centre of mass to
x₁ = 50cm point from x = 67 CM
∴ Distance between the axis
R = 67 – 50 = 17cm = 0.17M
M.O.I. about this axis I = I_G + MR²
= 0.283 + 5.05 × 0.17 × 0.17
= 0.283 + 0.146 = 0.429 kgm²
∴ M.O.I. about perpendicular bisector of scale = 0.429 kg – m²

Question 6.
Calculate the moment of inertia of a fly wheel, if its angular velocity is increased from 60 r.p.m. to 180 r.p.m. when 100 J of work is done on it. [TS May ’16]
Solution:
W = 100 J, ω₁ = 60 RPM = 1 R.P.S = 2π Rad.
ω₂ = 180 R.P.M. = 3 R.P.S = 6π Rad.

Question 7.
Three particles each of mass 100 g are placed at the vertices of an equilateral triangle of side length 10 cm. Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
Solution:
Mass of each particle m = 100 g; side of equilateral triangle = 10 cm.
In equilateral triangle height of angular bisector CD = \(\frac{\sqrt{3}}{2}\)l

Centroid will divide the angular bisector in a ratio 2 : 1

So X distance of each mass from vertex to centroid is 2.\(\frac{\sqrt{3}}{2}\)l = \(\frac{\sqrt{3}}{2}\)l
Moment of Inertia of the system

Question 8.
Four particles each of mass 100g are placed at the corners of a square of side 10 cm. Find the moment of inertia of the system about an axis passing through the centre of the square and perpendicular to its plane. Find also the radius of gyration of the system.
Solution:
Mass of each particle, m = 100 g = 0.1 kg.
Length of side’of square, a = 10 cm = 0.1 m
In square distance of corner from centre of square = \(\frac{1}{2}\) diagonal = \(\frac{\sqrt{2}a}{2}=\frac{a}{\sqrt{2}}\)

∴ Total moment of Inertia

Question 9.
Two uniform circular discs, each of mass 1 kg and radius 20 cm, are kept in contact about the tangent passing through the point of contact. Find the moment of inertia of the system about the tangent passing through the point of contact.
Solution:
Mass of disc = M = 1 kg.
Radius of disc = 20 cm = 0.2 m

They are in contact as shown.
M.O.I of a circular disc about a tangent parallel to its plane = \(\frac{5}{4}\) MR²
Total M.O.I. of the system

Question 10.
Four spheres each diameter 2a and mass ‘m’ are placed with their centres on the four corners of a square of the side b. Calculate the moment of inertia of the system about any side of the square.
Solution:
Diameter of sphere = 2a ⇒ radius = a.
Side of square = b.
For spheres 1 and 2 axis of rotation is same and passing through diameters. M.O.I. of solid sphere about any diameter = \(\frac{2}{5}\)MR² (put M = m and R = a)

Transfer this M.O.I. on to the axis using
Parallel axis theorem.

Total M.O.I. of the system

Question 11.
To maintain a rotor at a uniform angular speed or 200 rad s^-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine? (Note : uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
Solution:
Given uniform angular speed (ω) = 200 rad s^-1
Torque, τ = 180 N – m ; But power p = τω
∴ P =180 × 200 = 36000 watt = 36 kW

Question 12.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
Solution:
Let m be the mass of the stick concentrated at C, the 50 cm mark

For equilibrium
about C’, i.e. at the 45 cm mark,
10g (45 – 12) = mg (50 – 45)
10g × 33 = mg × 5
m = \(\frac{10\times33}{5}\) = 66 grams

Question 13.
Determine the kinetic energy of a circular disc rotating with a speed of 60 rpm about an axis passing through a point on its circumference and perpendicular to its plane. The circular disc has a mass of 5 kg and radius 1 m.
Solution:
Mass of disc, M = 5 kg; Radius R = 1 m.
Angular velocity, co = 60 RPM = \(\frac{60\times 2\pi}{60}\) = 2πRad/sec

M.O.I. of disc about a point passing through circumference and perpendicular to the plane.

Question 14.
Two particles, each of mass m and speed u, travel in opposite directions along para¬llel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momemtum is taken.
Solution:
Angular momentum, L = mvr
Choose any axis say ‘A’
Let at any given time distance between m₁ & m₂ = L = L₁ + L₂
About the axis ‘A’ both will rotate in same direction See fig.

∴ Total angular momentum
L = L₁ + L₂ = muL₁ + muL₂ = mu (L₁ + L₂) = muL

about any new axis say B distance of m₁ and m₂
are say L’₁ and L’₂
Total angular momentum,
L = mu L’₁ + mu L’₂
or L = mu(L’₁ + L’₂) = muL (∵ L’₁ + L’₂ = L)
Hence, total angular momentum of the system is always constant.

Question 15.
The moment of inertia of a fly wheel making 300 revolutions per minute is 0.3 kgm². Find the torque required to bring it to rest in 20s.
Solution:
M.O.I, I = 0.3 kg. ; time, t = 20 sec.,
ω₁ = 300 R.P.M. = \(\frac{300}{60}\) = 5. R.P.S.; ω₂ = 0

Torque, τ = Iα = 0.3 × \(\frac{5\times 2\pi}{20}\) = 0.471 N – m.

Question 16.
When 100J of work is done on a fly wheel, its angular velocity is increased from 60 rpm to 180 rpm. What is the moment of inertia of the wheel?
Solution:
W=100J, ω₁ = 60 RPM = 1 R.PS = 2π Rad.
ω₂ =180 R.P.M. = 3 R.P.S = 6π Rad.

Question 17.
Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are lOOg, 150g and 200g respectively. Each side of the equilateral triangle is 0.5 m long, lOOg mass is at origin and 150g mass is on the X-axis. [TS Mar. 18, June 15; AP Mar. ’18]
Solution:
Mass at A = 100g ; Coordinates = 0, 0
Mass at B = 150 g; Coordinates = (0.5, 0)
Mass at C = 200g; Coordinates (0.25,0.25 √3 )
Coordinates x_cm