TS Inter 1st Year Maths 1A Mathematical Induction Important Questions

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Mathematical Induction Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Mathematical Induction Important Questions

Question 1.
By using mathematical induction show that ∀ n ∈ N, 1² + 2² + 3² + ……………… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Answer:
Let S(n) be the statement that 1² + 2² + 3² + …………… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
If n = 1, then
LHS = n² = 1² = 1

∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ 1² + 2² + 3² + ……………… +n² = \(\frac{n(n+1)(2 n+1)}{6}\), ∀ n ∈ N.

Question 2.
By using mathematical Induction show that ∀ n ∈ N, 1³ + 2³ + 3³ + …………. + n³ = \(\frac{n^2(n+1)^2}{4}\). [May 97, 94, 93, 88, Mar. 87]
Answer:
Let S(n) be the statement that 1³ + 2³ + 3³ + ……….. + n³ = \(\frac{n^2(n+1)^2}{4}\)
If n = 1, then
L.H.S = n³ = 1³
R.H.S = \(\frac{n^2(n+1)^2}{4}\) = \(\frac{1^2(1+1)^2}{4}\) = \(\frac{1.4}{4}\) = 1
∴ L.H.S = R.H.S
∴ S(1) is true.
Assume that S(k) is true.

∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ 1³ + 2³ + 3³ + ………… + n³ = \(\frac{n^2(n+1)^2}{4}\), ∀ n ∈ N

Question 3.
By using mathematical induction show that ∀ n ∈ N, 2.3 + 3.4 + 4.5 + …………. upto n terms = \(\frac{n\left(n^2+6 n+11\right)}{3}\)
Answer:
2, 3, 4 ……………………. are in A.P.
Here a = 2, d = 3 – 2 = 1
∴ t_n = a + (n – 1)d = 2 + (n – 1)1 = 2 + n – 1 = n + 1.
3, 4, 5 …………………… are in A.P.
Here a = 3, d = 4 – 3 = 1
∴ t_n = a + (n – 1) d = 3 + (n – 1) 1 = 3 + n – 1 = n + 2.
∴ The n^th term of the given series is (n + 1) (n + 2).
Let S(n) be the statement that
2.3 + 3.4 + 4.5 + + (n + 1) (n + 2) = \(\frac{n\left(n^2+6 n+11\right)}{3}\)
If n = 1, then
LHS = (n + 1) (n + 2) = (1 + 1) (1 + 2) = 2.3 = 6
RHS = \(\frac{\mathrm{n}\left(\mathrm{n}^2+6 \mathrm{n}+11\right)}{3}\) = \(\frac{1\left(1^2+6(1)+11\right)}{3}\) = \(\frac{18}{3}\) = 6
∴ LHS = RHS
∴ S(1) is true.
Assume that S(k) is true.

Verification Method:
\(\frac{\mathrm{n}\left(\mathrm{n}^2+6 n+11\right)}{3}\)
Put n = k + 1

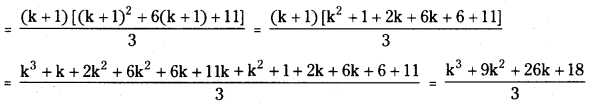
∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 2.3 + 3.4 + 4.5 + ……………… + (n + 1) (n + 2) = \(\frac{\mathrm{n}\left(\mathrm{n}^2+6 \mathrm{n}+11\right)}{3}\), ∀ n ∈ N

Question 4.
By using mathematical induction show that ∀ n ∈ N,
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\) [Mar. 18 May 15 (AP): May 14, 97, 92]
Answer:

Question 5.
By using mathematical induction show that ∀ n ∈ N, \(\frac{1}{1 \cdot 4}+\frac{1}{4 \cdot 7}+\frac{1}{7 \cdot 10}+\) …………….. upto n terms = \(\frac{n}{3 n+1}\).
Answer:
1, 4, 7, ………………… are in A.P.
Here, a = 1, d = 4 – 1 = 3
t_n = a + (n – 1) d = 1 + (n – 1)3 = 1 + 3n – 3 = 3n – 2
4, 7, 10, ………………. are in A.P.
Here, a = 4, d = 7 – 4 = 3
t_n = a + (n – 1) d = 4 + (n – 1)3 = 4 + 3n – 3 = 3n + 1
∴ The n^th term in the given series is \(\frac{1}{(3 n-2)(3 n+1)}\).

Question 6.
By using mathematical induction show that ∀ n ∈ N,
a + (a + d) + (a + 2d) + upto n terms = \(\frac{n}{2}\) [2a + (n – 1) d].
Answer:
a, a + d, a + 2d, ………………….. are in A.P
∴ t_n = a + (n – 1) d
∴ n th term in the given series is a + (n – 1) d.
Let S(n) be the statement that
a + (a + d) + (a + 2d) + ………………. + a + (n – 1) d = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1) d]
If n = 1 then
L.H.S = a + (n – 1)d = a + (1 – 1)d = a
R.H.S = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d] = \(\frac{1}{2}\) [2a + (1 – 1)d] = \(\frac{1}{2}\) [2a] = a
∴ L.H.S = R.H.S
∴ S(1) is true.
[a + (n – 1)d
put n = k + 1
a + (k + 1 – 1)d
= a + kd]
Assume that S(k) is true.
a + (a + d) + (a + 2d) + ………………… + [a + (k- 1) d] = \(\frac{\mathrm{k}}{2}\) [2a + (k – 1)d]
Adding (a + kd) on both sides, we get

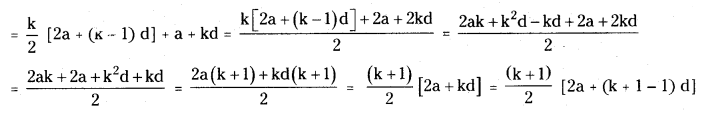
∴ S(k + 1) is true.
By the principle of Mathematical Induction, s(n) is true, ∀ n ∈ N
∴ a + (a + d) + (a + 2d) + ….+ a + (n- 1) d = \(\frac{n}{2}\) [2a + (n – 1) d], ∀ n ∈ N

Question 7.
By using mathematical induction show that ∀ n ∈ N,
a + ar + ar² + ………. upto n terms = \(\frac{a\left(r^n-1\right)}{r-1}\), r ≠ 1. [Mar. 19 (AP); Mar. 11, 80; May 87]
Answer:
a + ar + ar² + ………. are in G.P.
∴ t_n = a . r^{n – 1}
The n th term in the given series is a . r ^{n – 1}
Let S(n) be the statement that
a + ar + ar² + …………. + a ∙ r^{n – 1} = \(\frac{a\left(r^n-1\right)}{r-1}\)
If n = 1, then
L.H.S = a ∙ r^{n – 1} = a ∙ r^{1 – 1} = a ∙ r⁰ = a ∙ 1 = a
R.H.S = \(\frac{a\left(r^n-1\right)}{r-1}=\frac{a\left(r^1-1\right)}{r-1}=\frac{a(r-1)}{r-1}\) = a
∴ L.H.S = R.H.S
∴ S(1) is true.
[a.r^{n – 1}
Put n = k + 1
a.r^{k + 1 – 1}
a.r^k]
Assume that S(k) is true.
a + ar + ar² + …….. + a.r^{k – 1} = \(\frac{a\left(r^k-1\right)}{r-1}\)
Adding ar^k on both sides we get,

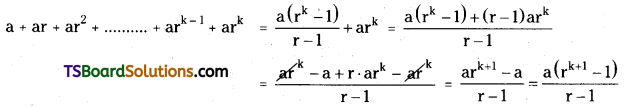
∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ a + ar + ar² + ………………. + a . r^{n – 1} = \(\frac{a\left(r^n-1\right)}{r-1}\)

Question 8.
By using mathematical induction show that ∀ n ∈ N, 1.2.3 + 2.3.4 + 3.4.5 + …………………. upto n terms = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
Answer:
1, 2, 3 …………………. are in A.P.
Here a = 1, d = t₂ – t₁ = 2 – 1 = 1
t_n = a + (n – 1)d = 1 + (n – 1)1 = 1 + n – 1 = n
2, 3, 4 ………………… are in A.P.
Here a = 2, d = 3 – 2 = 1
t_n = a + (n – 1)d = 2 + (n – 1)1 = 2 + n – 1 = n + 1
3, 4, 5 …………….. are in A.P.
Here a = 3, d = 4 – 3 = 1
t_n = a + (n – 1)d = 3 + (n – 1)1 = 3 + n – 1 = n + 2
∴ The nth term in the given series is n(n + 1) (n + 2).
Let S(n) be the statement that
1.2.3 + 2.3.4 + 3.4.5 + ……………….. + n (n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
If n = 1 then
L.H.S = n(n + 1) (n + 2) = 1(1 + 1) (1 + 2) = 1.2.3 = 6
R.H.S = \(\frac{n(n+1)(n+2)(n+3)}{4}\) = \(\frac{1(1+1)(1+2)(1+3)}{4}\) = \(\frac{1.2 .3 .4}{4}\) = 6
∴ L.H.S = R.H.S
∴ S(1) is true Assume that s(k) is true
1.2.3 + 2.3.4 + 3.4.5 + ……………….. + k (k + 1) (k + 2) = \(\frac{\mathrm{k}(\mathrm{k}+1)(\mathrm{k}+2)(\mathrm{k}+3)}{4}\)
Adding (k + 1) (k + 2) (k + 3) on both sides we get
1.2.3 + 2.3.4 + 3.4.5 + …………….. + k (k + 1) (k + 2) + (k + 1) (k + 2) (k + 3)

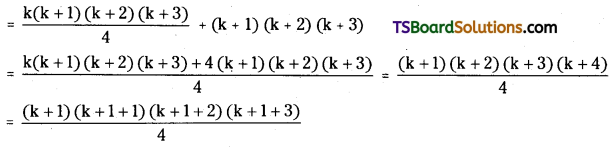
∴ S(k + 1) is true.
∴ By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 1.2.3 + 2.3.4 + 3.4.5 + ……………… + n(n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\) ∀ n ∈ N.

Question 9.
By using mathematical induction show that ∀ n ∈ N,
\(\frac{1^3}{1}+\frac{1^3+2^3}{1+3}+\frac{1^3+2^3+3^3}{1+3+5}\) + ……………….. upto n terms = \(\frac{n}{24}\) [2n² + 9n + 13]. [Mar. 14, 07, 05]
Answer:
Numerator: n^th = 1³ + 2³ + 3³ + …………. + n³ = Σn³ = \(\frac{n^2(n+1)^2}{4}\)

Denominator: 1 + 3 + 5 + ………………. are in A.P.
Here a = 1, d = 3 – 1 = 2
t_n = a + (n – 1) d = 1 + (n – 1) 2 = 1 + 2n – 2 = 2n – 1
∴ n^th term is

∴ L.H.S = R.H.S
∴ S(1) is true.
Assume that S(k) is true.

Verification Method: \(\frac{\mathrm{n}}{24}\) [2n² + 9n + 13]
Put n = k + 1
= \(\frac{(\mathrm{k}+1)}{24}\) [2(k + 1)² + 9 (k + 1) + 13] = \(\frac{(\mathrm{k}+1)}{24}\) [2k² + 2 + 4k + 9k + 9 + 13]
= \(\frac{1}{24}\) [2k³ + 2k + 4k² + 9k² + 9k + 13k + 2k² + 2 + 4k + 9k + 9 + 13] = \(\frac{1}{24}\) [2k³ + 15k² + 37k + 24]
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.

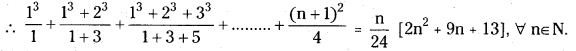
Question 10.
By using mathematical induction show that ∀ n ∈ N, 1² + (1² + 2²) + (1² + 2² + 3²) + ……….. upto n terms = \(\frac{n(n+1)^2(n+2)}{12}\).
Answer:

Question 11.
By using mathematical induction show that ∀ n ∈ N, 2 + 3.2 + 4.2² + ……… upto n terms
Answer:
2.1 + 3.2 + 4.2² + ………………… upto n terms = n . 2ⁿ
2, 3, 4 ………….. are in A.P.
Here a = 2, d = 3 – 2 = 1
t_n = a + (n – 1)d = 2 + (n – 1)1 = 2 + n – 1 = n + 1
1, 2, 2², ……………… are in G.P.
Here a = 1, r = \(\frac{2}{1}\) = 2
t_n = a . r^{n – 1} = 1 . 2^{n – 1} = 2^{n – 1}
∴ The nth term in the given series is (n + 1) (2^{n – 1}).
Let S(n) be the statement that
2.1 + 3.2 + 4.2² + ……….. + (n + 1) 2^{n – 1} = n . 2ⁿ
If n = 1, then
L.H.S. = (n + 1)^{2n – 1} = (1 + 1) 2^{1 – 1} = 2.2⁰ = 2.1 = 2
R.H.S. = n . 2ⁿ = 1.2¹ = 2
∴ LHS = RHS
∴ S(1) is true.
[(n + 1)^{2n – 1}
put n = k + 1
(k + 1 + 1) 2^{k + 1 – 1}
(k + 2) . 2^k]
Assume that S(k) is true.
2.1 + 3.2 + 4.2² + ……….. + (k + 1)^{2k – 1} = k . 2k
Adding (k + 2) . 2^k on both sides, we get
2.1 + 3.2 + 4.2² + ………… + (k + 1) 2^{k – 1} + (k + 2) 2^k = k. 2^k + (k + 2) . 2^k = 2^k (k + k + 2)
= 2^k (2k + 2) = 2^k . 2 (k + 1) = (k + 1) . 2^{k + 1}
∴ S(k + 1) is true.
∴ By the principle of mathematical induction, S(n) is true, ∀ n ∈ N.
2.1 + 3.2 + 4. 2² + ……………… + (n + 1) 2^{n – 1} = n . 2ⁿ, ∀ n ∈ N.

Question 12.
By using mathematical induction show that ∀ n ∈ N, 49ⁿ + 16n – 1 is divisible by 64 for all positive integer n. [Mar. 18 (TS); Mar. 17 (AP); May 13, 05, 98, 93]
Answer:
Let S(n) be the statement that f(n) = 49ⁿ + 16n – 1 is divisible by 64.
If n = 1, then
f(1) = 49¹ + 16.1 – 1 = 49 + 16 – 1 = 49 + 15 = 64 = 64 × 1 is divisible by 64
∴ S(1) is true.
Assume that S(k) is true.
f(k) is divisible by 64 ⇒ 49^k + 16k – 1 is divisible by 64
⇒ 49^k + 16k – 1 = 64 M for some integer M ⇒ 49^k = 64M – 16k + 1
Now
f(k + 1) = 49^{k + 1} + 16 (k + 1) – 1 = 49^k. 49 + 16k + 16 – 1 = (64M – 16k + 1) 49 + 16k + 15
= 64.49M – 784k + 49 + 16k + 15 = 64.49M – 768k + 64
= 64(49M – 12k + 1) is divisible by 64. [ ∵ 49M – 12k + 1 is an integer]
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true ∀ n ∈ N.
∴ 49ⁿ + 16n – 1 is divisible by 64, ∀ n ∈ N.

Question 15.
By using mathematical induction show that 3 ∙ 5^{2n + 1} + 2^{3n + 1} is divisible by 17 ∀ n ∈ N. [May 12, 10, 08, 01, ’96]
Answer:
Let S(n) be the statement that f(n) = 3 . 5^{2n + 1} + 2^{3n + 1} is divisible by 17.
If n = 1, then
f(1) = 3.5^{2.1 + 1} + 2^{3.1 + 1} = 3.5³ + 24 = 3(125) + 16 = 375 + 16 = 391 = 17 × 23 is divisible by 17
∴ S(1) is true.
Assume that S(k) is true.
∴ f(k) is divisible by 17.
⇒ 3.5^{2k + 1} + 2^{3k + 1} is divisible by 17.
⇒ 3.5^{2k + 1} + 2^{3k + 1} = 17 M for some integer M.
⇒ 3.5^{2k + 1} = 17M – 2^{3k + 1}
Now f (k + 1) = 3 . 5^{2(k + 1) + 1} + 2^{3(k + 1) + 1} = 3.5^{2k + 2 + 1} + 2^{3k + 3 + 1}
= 3.5^{2k + 1} . 5² + 2^{3k + 1} . 2³
= (17M – 2^{3k + 1}) 25 + 8 . 2^{3k + 1} = 17.25 M – 25.2^{3k + 1} + 8 . 2^{3k + 1}
= 17.25 M – 17.2^{3k + 1}
= 17 (25 M – 2^{3k + 1}) is divisible by 17. [∵ 25M – 2^{3k + 1} is an integer]
∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 3 . 5^{2n + 1} + 2^{3n + 1} is divisible by 17, ∀ n ∈ N.

Question 14.
By using mathematical induction show that ∀ n ∈ N, xⁿ – yⁿ is divisible by x – y. [May 04]
Answer:
Let S(n) be the statement that f(n) = xⁿ – yⁿ is divisible by (x – y).
If n = 1 then
f(1) = x¹ – y¹ = x – y = (x – y) × 1 is divisible by (x – y)
∴ S(l) is true.
Assume that S(k) is true.
f(k) is divisible by (x – y).
⇒ x^k – y^k is divisible by (x – y)
⇒ x^k – y^k = (x – y) M, for some integer M.
⇒ x^k = (x – y) M + y^k
Now
f(k + 1) = x^{k + 1} – y^{k + 1} = x^k . x – y^k . y = [(x – y) M + y^k] x – y^k . y = (x – y) . M x + y^k . x – y^k . y
= (x – y) M x + y^k (x – y) = (x – y) [Mx + y^k] is divisible by (x – y).
[Mx + y^k] is an integer.
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ xⁿ – yⁿ is divisible by (x – y), ∀ n ∈ N.

Some More Maths 1A Mathematical Induction Important Questions

Question 1.
By using mathematical induction show that ∀ n ∈ N, 4³ + 8³+ 12³ + ……………. upto n terms = 16n² (n + 1)².
Answer:
4, 8, 12, are in A.P.
Here a = 4, d = t₂ – t₁ = 8 – 4 = 4
t_n = a + (n – 1)d = 4 + (n – 1)4 = 4 + 4n – 4 = 4n
∴ The nth term in the given series is (4n)³ = 64n³
Let S(n) be the statement that 4³ + 8³ + 12³ + …………….. + 64n³ = 16n² (n + 1)²
If n = 1, then
LHS = 64n³ = 64(1)³ = 64
RHS = 16n² (n + 1)² = 16.1² (1 +!)² = 16.1.4 = 64
∴ LHS = RHS
∴ S(1) is true.
Assume that S(k) is true.
4³ + 8³ + 12³ + ………………….. + 64k³ = 16k² (k + 1)²
Adding 64(k + 1)³ on both sides, we get
4³ + 8³ + 12³ + …………….. + 64k³ + 64(k + 1)³ = 16k² (k + 1)² + 64 (k + 1)³ = 16(k + 1)² [k² + 4 (k + 1)]
= 16(k + 1)² [k² + 4k + 4] = 16(k + 1)² (k + 2)² = 16(k + 1)² (k + 1 + 1)²
∴ S(k + 1) is true.
By the principle of mathematical induction, S(n) is true ∀ n ∈ N.
∴ 4³ + 8³ + 12³ + ………………. + 64n³ = 16n² (n + 1)², ∀ n ∈ N.

Question 2.
By using mathematical induction show that ∀ n ∈ N. 2.4^{2n + 1} + 3^{3n + 1} is divisible by 11.
Answer:
Let S(n) be the statement that f(n) = 2.4^{2n + 1} + 3^{3n + 1} is divisible by 11.
If n = 1, then
f(1) = 2.4^{2.1 + 1} + 3^{3.1 + 1} = 2.4³ + 34 = 2(64) + 81
= 128 + 81 = 209 = 11 × 19 is divisible by 11.
∴ S(1) is true.
Assume that S(k) is true.
∴ f(k) is divisible by 11.
⇒ 2.4^{2k + 1} + 3^{3k + 1} is divisible by 11
⇒ 2.4^{2k + 1} + 3^{3k + 1} = 11 M, for some integer M
⇒ 2.4^{2k + 1} = 11 M – 3^{3k + 1}
Now f(k + 1) = 2.4^{2(k + 1) + 1} + 3^{3(k + 1) + 1} = 2.4^{2k + 2 + 1} + 3^{3k + 3 + 1} = 2.4^{2k + 1} . 4² + 3^{3k + 1} . 3³
= (11 M – 3^{3k + 1}) 16 + 27. 3^{3k + 1} = 11.16 M – 16. 3^{3k + 1} + 27.3^{3k + 1} = 11.16M + 11.3^{3k + 1}
= 11(16 M + 3^{3k + 1}) is divisible by 11 (∵ 16 M + 3^{3k + 1} is an integer)
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.
∴ 2.4^{2n + 1} + 3^{3n + 1} is divisible by 11, ∀ n ∈ N.

Question 3.
Using mathematical induction prove that statement for all ∀ n ∈ N,
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 n+1}{n^2}\right)\) = (n + 1)²
Answer:
Let S(n) be the statement that \(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left(1+\frac{2 n+1}{n^2}\right)\) = (n + 1)²
If n = 1, then
LHS = 1 + \(\frac{2 n+1}{n^2}\) = 1 + \(\frac{2.1+1}{(1)^2}\) = 1 + \(\frac{2+1}{1}\) = 1 + 3 = 4
RHS = (n + 1)² = (1 + 1)² = (2)² = 4
∴ LHS = RHS
∴ S(1) = is true
Assume that S(k) is true