TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Long Answer Type

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Ratios up to Transformations Important Questions Long Answer Type

Question 1.
If A, B, Care the angles of a triangle, prove that sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C.
Answer:
Given A + B + C = 180°
LHS = sin 2A + sin 2B + sin 2C
= 2sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + sin 2C
= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (180° – C) cos (A – B) + sin 2C
= 2 sin C cos (A – B) + 2 sin C cos C
= 2 sin C [cos (A – B) + cos C]
= 2 sin C [cos (A – B) + cos [180° – (A + B)]
= 2 sin C[cos (A – B) – cos (A + B)]
= 2 sin C (2 sin A sin B)
= 4 sin A sin B sin C = RHS

Question 2.
If A, B, C are angles of a triangle, prove that cos 2A + cos 2B + cos 2C = – 4cos A cos B cos C – 1.
Sol. Given A + B + C = 180°
LHS = cos 2A + cos 2B + cos 2C
= 2cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + cos 2C
= 2 cos (180° – C) cos (A – B) + cos 2C
= – 2 cos C cos (A – B) + 2 cos²C – 1
= – 2 cos C [cos (A – B) – cos C] – 1
= – 2 cos C [cos (A – B) – cos [180° – (A + B)]] -1
= -2 cos C [cos (A – B) + cos (A + B)] – 1
= – 2cos C (2 cos A cos B) – 1
= – 4 cos A cos B cos C – 1 = RHS

Question 3.
If A + B + C = \(\frac{3 \pi}{2}\), prove that cos 2A + cos 2B + cos 2C = 1 – 4sinA.sinB.sinC. [Mar. ’13, ’01]
Answer:
Given A + B + C = \(\frac{3 \pi}{2}\)
L.H.S. = cos 2A + cos 2B + cos 2C
= 2 cos (A + B) cos (A – B) + cos 2C
= -2 sin C cos (A – B) + 1 – 2 sin²C
[A + B = \(\frac{3 \pi}{2}\) ⇒ cos (A + B) = – sin C]
= 1 – 2 sin C [cos (A – B) + sin C]
= 1 – 2 sin C [cos (A – B) – cos (A + B)]
= 1 – 2 sin C (2 sin A sin B)
= 1 – 4 sin A sin B sin C = RHS
∴ cos 2A + cos 2B + cos 2C = 1 – 4 sin A sin B sin C

Question 4.
If A + B + C = \(\frac{3 \pi}{2}\), prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A. sin B sin C.
Answer:
Given A + B + C = 90°
LHS = cos 2A + cos 2B + cos 2C
= 2 cos\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + cos 2C
= 2 cos (A + B) cos (A – B) + cos 2C
= 2 cos (90° – C) cos (A – B) + cos 2C
= 2 sin C cos (A – B) + 1 – 2 sin²C
= 1 + 2 sin C [cos (A – B) – sin C]
= 1 + 2 sin C [cos (A – B) – sin [90° – (A + B)]]
= 1 + 2 sin C [cos (A – B) – cos (A + B)]
= 1 + 2 sin C (2 sin A sin B)
= 1 + 4 sin A sin B sin C = RHS.

Question 5.
If A, B, C are angles in a triangle, then prove that cos A + cos B + cos C = 1 + 4 sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) sin \(\frac{C}{2}\). [Mar. ’18(AP); May ’09]
Answer:
Given A + B + C = 180°
L.H.S = cos A + cos B + cos C

Question 6.
If A, B, C are angles in a triangle, then prove that cos A + cos B – cos C = -1 + 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\). [Mar. ’19(TS); May ’06]
Answer:
Given A + B + C = 180°
L.H.S = cos A + cos B – cos C

Question 7.
If A, B, C are angles in a triangle, then prove that sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) – sin²\(\frac{C}{2}\) = 1 – 2cos \(\frac{A}{2}\). cos \(\frac{B}{2}\). sin \(\frac{C}{2}\). [Mar. ’16(AP), ’06; May ’15(TS), ’11; B.P]
Answer:
Given A + B + C = 180°
L.H.S = sin²\(\frac{A}{2}\) + sin²\(\frac{B}{2}\) – sin²\(\frac{C}{2}\)

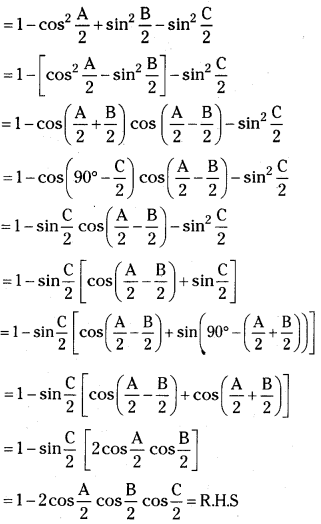
Question 8.
If A + B + C = π, then prove that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\) = 2(1 + sin \(\frac{A}{2}\). sin \(\frac{B}{2}\). sin \(\frac{C}{2}\)). [Mar. ’12, Mar. ’15(AP & TS)]
Answer:
Given A + B + C = π
L.H.S = cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\)

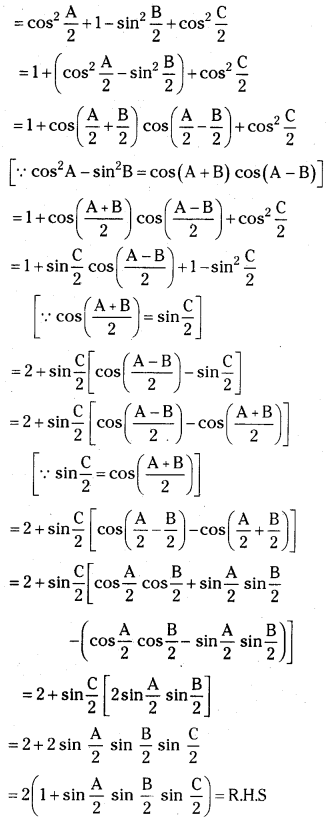
Question 9.
If A+ B + C = π, then prove that cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\) = 2 cos\(\frac{A}{2}\) cos\(\frac{B}{2}\) sin\(\frac{C}{2}\). [May ’10]
Answer:
Given A + B + C = π
L.H.S = cos²\(\frac{A}{2}\) + cos²\(\frac{B}{2}\) – cos²\(\frac{C}{2}\)

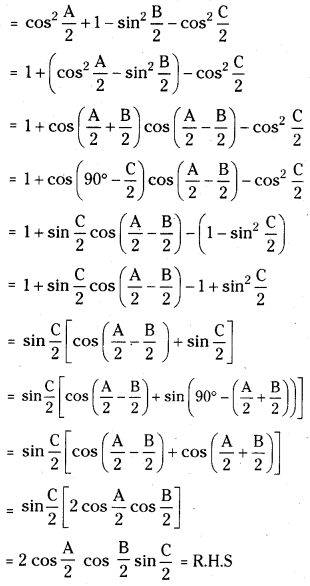
Question 10.
If A, B, C are the angles in a triangle, then prove that sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) + sin \(\frac{C}{2}\) = 1 + 4sin\(\left(\frac{\pi-A}{4}\right)\)sin\(\left(\frac{\pi-B}{4}\right)\)sin\(\left(\frac{\pi-C}{4}\right)\). [Mar. ’14, ’11, ’96]
Answer:
Given A + B + C = 180°

Question 11.
In triangle ABC, prove that cos\(\frac{1}{2}\) + cos\(\frac{B}{2}\) + cos\(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\). [Mar ’14, ’13, ’07, ’97; Mar. ’10, ’07, ’05, ’03]
Answer:
In ΔABC, A + B + C = 180°

∴ cos\(\frac{1}{2}\) + cos\(\frac{B}{2}\) + cos\(\frac{C}{2}\) = 4 cos\(\left(\frac{\pi-A}{4}\right)\) cos\(\left(\frac{\pi-B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\)

Some More Maths 1A Ratios up to Transformations Important Questions

Question 1.
If sin θ = \(\frac{4}{5}\) and θ is not in the first quadrant, find the value of cos θ.
Answer:
Given sin θ = \(\frac{4}{5}\)
Since θ is not in the first quadrant and sin θ > 0 we have 90° < θ < 180°
∴ cos θ = \(\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{16}{25}}=\frac{-3}{5}\)

Question 2.
If cosec θ + cot θ = find cos θ and determine the quadrant In which θ lies.
Answer:
We have cosec² θ – cot² θ = 1
(cosec θ + cot θ) (cosec θ – cot θ) = 1
= cosec θ – cot θ = \(\frac{1}{{cosec} \theta+\cot \theta}\) = 3
= cosec θ + cot θ = 3 …………………… (1)

Given cosec θ + cot θ = \(\frac{1}{3}\) …………………. (2)
Solving(1)& (2)
∴ 2cosec θ = 3 + \(\frac{1}{3}=\frac{10}{3}\)
⇒ cosec θ = \(\frac{5}{4}\)
⇒ sin θ = \(\frac{3}{5}\)

Also 2 cot θ = \(\frac{1}{3}\) – 3 = \(\frac{-8}{3}\)
⇒ cot θ = \(\frac{-4}{3}\)
⇒ tan θ = \(\frac{-3}{4}\)

cos θ = cot θ.sinθ = \(\left(-\frac{4}{3}\right)\left(\frac{3}{5}\right)=-\frac{4}{5}\)
sin θ is positive and cos θ is a negative
⇒ θ lies in II quadrant.

Question 3.
If sec θ + tan θ = 5, find the quadrant in which θ lies and find the value of sin θ.
Answer:
We have sec²θ – tan²θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ sec θ – tan θ = \(\frac{1}{5}\) ………….. (1)
Also given sec θ + tan θ = 5 ………………………. (2)

Adding (1) and (2), 2sec θ = 5 + \(\frac{1}{5}\) = \(\frac{26}{5}\)

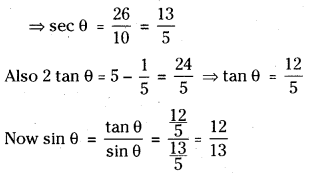
tan θ is +ve, sec θ is + ve
⇒ θ lies in first quadrant

Question 4.
Prove that cot\(\frac{\pi}{16}\).cot\(\frac{2 \pi}{16}\).cot\(\frac{3 \pi}{16}\)………………cot\(\frac{7 \pi}{16}\) = 1.
Answer:

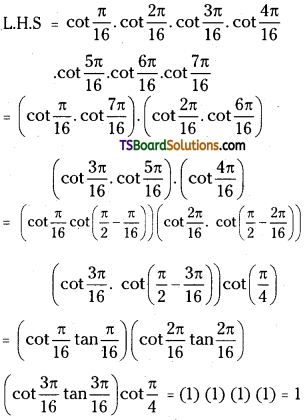
Question 5.
If a cos θ – b sin θ = c, then show that a sin θ + b cos θ = ± \(\sqrt{\mathbf{a}^2+\mathbf{b}^2-\mathbf{c}^2}\).
Answer:
Given a cos θ – b sin θ
= c and let asin θ + b cos θ = x
squaring and adding, we get
(a cos θ – b sin θ)² + (a sin θ + b cos θ) = c² + x²
a² (cos² θ + sin² θ)² + b² (sin² θ + cos² θ) = c² + x²
⇒ a² + b² = c² + x² ⇒ x² = a² + b² – c²
⇒ x = ±\(\sqrt{\mathbf{a}^2+\mathbf{b}^2-\mathbf{c}^2}\)

Question 6.
If 3 sin A + 5 cos A = 5, then show that 5 sin A – 3 cos A = ± 3.
Answer:
Given that 3 sin A + 5 cos A = 5
Let 5 sin A – 3 cos A = x
Squaring and adding, we get
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)²
⇒ 9 (sin²A + cos²A) + 25 (cos²A + sin²A) = 25 + x²
⇒ 34 = 25 + x²
⇒ x² = 9
⇒ x = ± 3
∴ 5 sin A – 3 cos A = ± 3

Question 7.
If tan 20° = p, Prove that \(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}\).
Answer:
Given that tan 20° = p, then

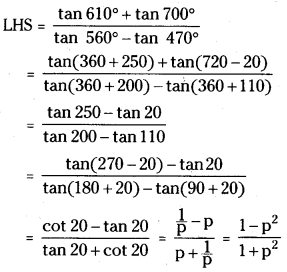
Question 8.
Evaluate sin²82\(\frac{1}{2}^{circ}\) – sin² 22\(\frac{1}{2}^{circ}\).
Answer:
sin²82\(\frac{1}{2}^{circ}\) – sin² 22\(\frac{1}{2}^{circ}\)
= sin[82\(\frac{1}{2}^{circ}\) + 22\(\frac{1}{2}^{circ}\)] + sin[82\(\frac{1}{2}^{circ}\) – 22\(\frac{1}{2}^{circ}\)]
= sin 105°. sin 60°
[∵ Use sin²A – sin²B] = sin(A +B) sin (A – B)
= sin 60° sin(60° + 45°)= sin 60°
[= sin 60° cos 45° + cos 60° sin 45°]
\(\frac{\sqrt{3}}{2}\left[\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}}\right]=\frac{\sqrt{3}(\sqrt{3}+1)}{4 \sqrt{2}}=\frac{3+\sqrt{3}}{4 \sqrt{2}}\)

Question 9.
Evaluate cos²112\(\frac{1}{2}^{circ}\) – sin²52\(\frac{1}{2}^{circ}\).
Answer:
Use cos²A – sin²B = cos(A + B) cos (A – B)
= cos²112\(\frac{1}{2}^{circ}\) – sin²52\(\frac{1}{2}^{circ}\)
= cos [112\(\frac{1}{2}^{circ}\) + 52\(\frac{1}{2}^{circ}\)] cos[112\(\frac{1}{2}^{circ}\) – 52\(\frac{1}{2}^{circ}\)]
= cos 165° . cos 60
= cos 60° cos(180 – 15) = – cos 60°. cos 15°
= \(-\frac{1}{2}\left[\frac{\sqrt{3}+1}{2 \sqrt{2}}\right]=-\frac{\sqrt{3}+1}{4 \sqrt{2}}\)

Question 10.
Prove that tan 72° = tan 18° + 2 tan 54°.
Answer:
We have cot A – tan A = \(\frac{1}{\tan A}\) – tan A
⇒ \(\frac{1-\tan ^2 \mathrm{~A}}{\tan \mathrm{A}}=\frac{2\left(1-\tan ^2 \mathrm{~A}\right)}{2 \tan \mathrm{A}}=\frac{2}{\tan 2 \mathrm{~A}}\) = 2 cot 2A
∴ cot A – tan A = 2 cot 2A
⇒ cot A = tan A + 2 cot 2A

Take A = 18°, then cot 18°
= tan 18° + 2 cot 36°
⇒ cot (90 – 72)
= tan 18° + 2 cot (90 – 54)
⇒ tan 72° = tan 18° + 2 tan 54°

Question 11.
Find the value of tan 56° – tan 11° -tan 56°. tan 11°.
Answer:
Consider 56° – 11° = 45°
⇒ tan (56° -11°) = tan 45° = 1
⇒ \(\frac{\tan 56^{\circ}-\tan 11^{\circ}}{1+\tan 56^{\circ} \tan 11^{\circ}}\) = 1
⇒ tan 56° – tan 110 – tan 56° tan 11° = 1.

Question 12.
If tan θ = \(\frac{\cos 11^{\circ}+\sin 11^{\circ}}{\cos 11^{\circ}-\sin 11^{\circ}}\) and θ is in the third quadrant, find θ.
Answer:
Given tan θ = \(\frac{\cos 11^{\circ}+\sin 11^{\circ}}{\cos 11^{\circ}-\sin 11^{\circ}}\)
= \(\frac{1+\tan 11^{\circ}}{1-\tan 11^{\circ}}\) = tan(45 + 11) = tan 56°
Since θ is in the third quadrant,
tan 56° = tan (180 + 56) = tan 236°
∴ θ = 236°

Question 13.
Show that cos 35° + cos 85° + cos 155° = 0.
Answer:
cos 35° + cos 85° + cos 155°
= cos 35° + 2cos\(\left(\frac{85+155}{2}\right)\) cos\(\left(\frac{85-155}{2}\right)\)
= cos 35° + 2 cos 120° cos (-35°)
= cos 35° – cos 35° = 0

Question 14.
Simplify cos 100°. cos 40° + sin 100°. sin 40°.
Answer:
Use cos A. cos B + sin A sin B = cos (A – B)
∴ cos 100°. cos 40° + sin 100° . sin 40°
= cos (100° – 40°) = cos 60° = \(\frac{1}{2}\)

Question 15.
Prove that sin 750°. cos 480° + cos 120°. cos 60° =\(\frac{1}{2}\)
Answer:
L.H.S = sin 750°. cos 480° + cos 120°. cos 60°
= sin [2.(360) + 30] cos [360 +120] + cos 120 cos 60
= sin 30 cos 120 + cos 120 cos 60
= \(\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)+\left(-\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{-1}{2}\)

Question 16.
Prove that \(\frac{1}{\cos 290^{\circ}}+\frac{1}{\sqrt{3} \sin 250^{\circ}}=\frac{4}{\sqrt{3}}\).
Answer:

Question 17.
Prove that √3 cosec 20° – sec 20° = 4.
Answer:
L.H.S = √3 cosec 20° – sec 20°

Question 18.
Find the period of cos (3x + 5) + 7.
Answer:
Let f(x) = cos (3x + 5) + 7
We have period of cos x is 2π ∀ x ∈ R.
∴ f (x) is periodic and period of f is \(\frac{2 \pi}{|3|}\)
\(\frac{2 \pi}{3}\) (or) f(x + p) = f(x)
⇒ cos (3x + 3p + 5) + 7 = cos (2π + 3x + 5) + 7
∴ 3x + 3p + 5 = 2π + 3x + 5
⇒ 3x = 2π
⇒ x = \(\frac{2 \pi}{3}\)

Question 19.
Find the maximum and minimum values of f(x) = 3 sin x – 4 cos x.
Answer:
Given f(x) = 3 sin x – 4 cos x
Comparing with a cos x + b sin x + c
We get a = – 4, b = 3, c = 0
Maximum value = c + \(\sqrt{a^2+b^2}\)
= 0 + \(\sqrt{16+9}=\sqrt{25}\) = 5
Minimum value = c – \(\sqrt{a^2+b^2}\)
= 0 – \(\sqrt{16+9}=\sqrt{25}\) = -5

Question 20.
Find the range of 7 cos x – 24 sin x + 5.
Answer:
Let f(x) = 7 cos x – 24 sin x + 5
a = – 24, b = 7, c = 5

Range = [c – \(\sqrt{a^2+b^2}\), c + \(\sqrt{a^2+b^2}\)]
=[5 – \(\sqrt{576+49}\), 5 + \(\sqrt{576+49}\)]
= [5 – \(\sqrt{625}\), 5 + \(\sqrt{625}\)]
= [5 – 25, 5 + 25] = [-20, 30]

Question 21.
If A – B = \(\frac{3 \pi}{4}\), then show that (1 – tan A)(1 + tan B) = 2.
Answer:
A – B = \(\frac{3 \pi}{4}\)
⇒ tan(A – B) = tan\(\frac{3 \pi}{4}\)
⇒ \(\frac{\tan A-\tan B}{1+\tan A \tan B}\) = -1
⇒ tan A – tan B = – 1 – tan A tan B
⇒ tan A – tan B + tan A tan B = -1
⇒ – tan A + tan B – tan A tan B = 1
⇒ (1 – tan A) + tan B (1 – tan A) = 1 + 1 = 2
⇒ (1 – tan A) (1 + tan B) = 2

Question 22.
If A, B, C are the angles of a triangle and if none of them is equal to \(\frac{\pi}{2}\) then prove that cot A cot B + cot B cot C + cot C cot A = 1.
Answer:
Given A + B + C = π, A + B = π – C
⇒ cot (A + B) = cot (π – C)
⇒ \(\frac{\cot A+\cot B-1}{\cot B+\cot A}\) = – cot C
⇒ cot A cot B – 1 = – cot B cot C – cot C cot A
⇒ cot A cot B + cot B cot C + cot C cot A = 1

Question 23.
If A + B + C = \(\frac{\pi}{2}\) and if none of A, B, C is n an odd multiple of \(\frac{\pi}{2}\), then prove that tan A tan B + tan B tan C + tan C tan A = 1.
Answer:
Given A + B + C = \(\frac{\pi}{2}\)
⇒ A + B = \(\frac{\pi}{2}\) – C
⇒ tan(A + B) = tan(\(\frac{\pi}{2}\) – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = cot C = \(\frac{1}{\tan C}\)
⇒ tan A tan C + tan B tan C = 1 – tan A tan B
⇒ tan A tan B + tan B tan C + tan C tan A = 1

Question 24.
Prove that cos A. cos(\(\frac{\pi}{2}\) + A) cos(\(\frac{\pi}{2}\) -A) = \(\frac{1}{4}\)cos 3A and hence deduce that cos\(\frac{\pi}{2}\)cos\(\frac{2 \pi}{2}\)cos\(\frac{3 \pi}{2}\).cos\(\frac{4 \pi}{2}\) = \(\frac{1}{16}\)
Answer:
L.H.S = cos A.cos(60 + A) cos(60 – A)
= cos A (cos² 60 – sin² A)

Question 25.
Show that cos⁴\(\frac{\pi}{8}\) + cos⁴\(\frac{3 \pi}{8}\) + ⁴\(\frac{5 \pi}{8}\) + cos⁴\(\frac{7 \pi}{8}\) = \(\frac{3}{2}\)
Answer:

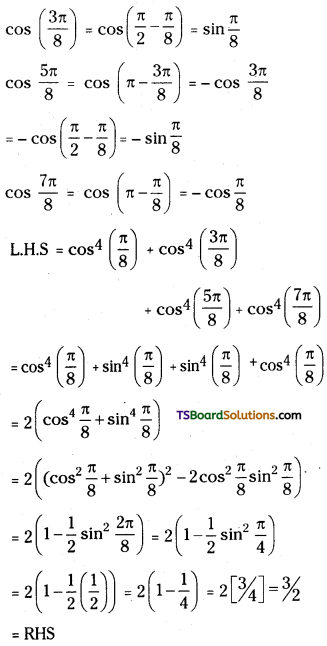
Question 26.
Prove that tan α = \(\frac{\sin 2 \alpha}{1+\cos 2 \alpha}\) and hence deduce the values of tan 15° and tan 22\(\frac{1}{2}^{\circ}\)
Answer:

Question 27.
If cos θ > θ, tan θ + sin θ = m and tan θ – sin θ = n then show that m² – n² = 4\(\sqrt{mn}\)
Answer:
Given that m = tan θ + sin θ, n = tan θ – sin θ
m + n = 2 tan θ, m – n = 2 sin θ and (m + n) (m -n)

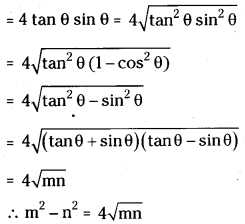
Question 28.
If 0° < A, B < 90°, cos A = \(\frac{5}{13}\) and sin B = \(\frac{4}{5}\), then find the value of sin(A+ B).
Answer:
0° < A, B < 90°, cos A = \(\frac{5}{13}\) ⇒ sin A = \(\frac{12}{13}\)
0° < A, B < 90°, sin B = \(\frac{4}{5}\) ⇒ cos B = \(\frac{3}{5}\)
∴ sin(A + B) = sin A cos B + cos A sin B
= \(\frac{12}{13} \cdot \frac{3}{5}+\frac{5}{13} \cdot \frac{4}{5}=\frac{36}{65}+\frac{20}{65}=\frac{56}{65}\)

Question 30.
If sin A = \(\frac{12}{13}\), cos B = \(\frac{3}{5}\) and neither A nor B is in the first quadrant, then find the quadrant in which A + B lies.
Answer:
Given sin A = \(\frac{12}{13}\)
A is not in the first quadrant then A lies in the Q₂.
∴ cos A = \(\frac{-5}{13}\) ⇒ cos B = \(\frac{3}{5}\)

B is not in the Q₁ then B lies in the Q₄.
∴ sin B = \(\frac{-4}{5}\)
Now sin (A + B) = sin A cos B + cos A sin B
= \(\left(\frac{12}{13}\right)\left(\frac{3}{5}\right)+\left(\frac{-5}{13}\right)\left(\frac{-4}{5}\right)=\frac{36}{65}+\frac{20}{65}=\frac{56}{65}\)

cos (A + B) = cos A . cos B – sin A sin B
= \(\left(\frac{-5}{13}\right)\left(\frac{3}{5}\right)-\left(\frac{12}{13}\right)\left(\frac{-4}{5}\right)=\frac{-15}{65}+\frac{48}{65}=\frac{33}{65}\)
sin (A + B) > 0 & cos (A + B) > 0 then A + B lies in the first quadrant.

Question 31.
Let ABC be a triangle such that cot A + cot B + cot C = √3 then prove that ABC is an equilateral triangle.
Answer:
Given that A + B + C = 180°
We have Σ cot A cot B = 1 …………………(1)
Σ(cot A – cot B)²
= Σ(cot² A + cos² B – 2 cot A cot B)
= 2 cot² A + 2 cot² B + 2 cot² C – 2 cot A cot B – 2 cot B cot C – 2 cot C cot A
= 2 [cot A + cot B + cot C]² – 6 [cot A cot B + cot B cot C + cot C cot A]
= 2 [(√3 )² ] – 6(1) = 6 – 6 = 0
∴ Σ (cot A – cot B)² = 0
⇒ cot A = cot B = cot C
⇒ cot A = cot B = cot C = \(\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}\) (∵ cot A + cot B + cot C = 73 )
⇒ A = B = C = 60°
⇒ ΔABC is an equilateral triangle.

Question 32.
Simplify tan[\(\frac{\pi}{4}\) + θ]. tan[\(\frac{\pi}{4}\) – θ]
Answer:

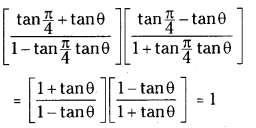
Question 33.
Simplify tan 75° + cot 75°.
Answer:
(2 + √3)(2 – √3) = 4

Question 34.
Evaluate sin²\(\left[\frac{\pi}{8}+\frac{A}{2}\right]\) – sin²\(\left[\frac{\pi}{8}-\frac{A}{2}\right]\)
Answer:
[∵ sin²A – sin²B = sin (A + B)sin(A – B)

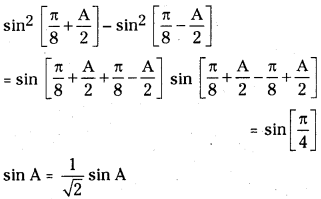
Question 35.
If A + B, A are acute angles such that sin (A + B) = \(\frac{24}{25}\) and tan A = \(\frac{3}{4}\), then find the value of cos B.
Answer:
A + B, A are acute angles ⇒ B is also acute.
Given sin (A + B) = \(\frac{24}{25}\), we have
cos (A + B) = \(\frac{7}{25}\) and tan (A + B) = \(\frac{24}{7}\)
Also tan A = \(\frac{3}{4}\)
We have tan(A + B) = \(\frac{24}{7}\)

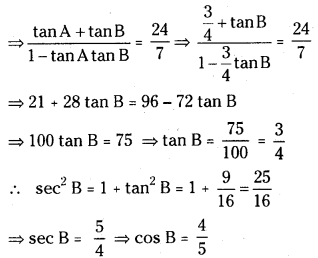
Question 36.
In a ΔABC, A is obtuse. If sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\) Bien show that sin C = \(\frac{16}{65}\).
Answer:
Given, A + B + C = 180°
⇒ A + B = 180° – C
∴ sin (A + B) = sin (180° – C) = sin C .. (1)
∴ A is obtuse angle and A lies in II quadrant.
sin A = \(\frac{3}{5}\) ⇒ cos A = –\(\frac{4}{5}\)
Also sin B = \(\frac{5}{13}\) ⇒ cos B = \(\frac{12}{13}\)
∴ sin C = sin (A + B) = sin A cos B + cos A
sin B = \(\frac{3}{5} \cdot \frac{12}{13}+\left(-\frac{4}{5}\right) \cdot \frac{5}{13}=\frac{36}{65}-\frac{20}{65}=\frac{16}{65}\)

Question 37.
Find the value of sin 22\(\frac{1}{2}^{\circ}\).
Answer:
22\(\frac{1}{2}^{\circ}\) lies in first quadrant and hence all ratios are positive.

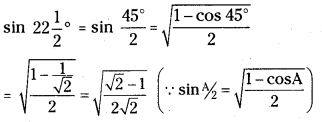
Question 38.
If cos θ = \(\frac{-5}{13}\) and \(\frac{\pi}{2}\) < θ < π find the value of sin 2θ.
Answer:
\(\frac{\pi}{2}\) < θ < π ⇒ sin θ > 0 and cos θ = \(\frac{-5}{13}\)
⇒ sin θ = \(\frac{12}{13}\)
∴ sin 2θ = 2sin θ cos θ

Question 39.
For what values of x in the first quadrant \(\frac{2 \tan x}{1-\tan ^2 x}\) is positive?
Answer:
\(\frac{2 \tan x}{1-\tan ^2 x}\) > 0 ⇒ tan 2x > 0 ⇒ 0 < 2x < \(\frac{\pi}{2}\)
⇒ 0 < x < \(\frac{\pi}{4}\)

Question 40.
If cos θ = -3/5 and π < θ < \(\frac{3 \pi}{2}\) find the value of tan \(\frac{\theta}{2}\).
Answer:

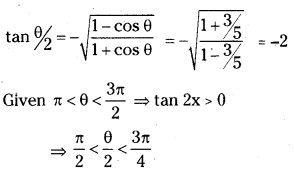
∴ \(\frac{\theta}{2}\) lies in second quadrant.

Question 41.
If 3A is not an odd multiple of \(\frac{\pi}{2}\), prove that tan A tan (60 + A) tan (60 – A) = tan 3A and hence find the value of tan 6° tan 42° tan 66° tan 78°.
Answer:
L.H.S = tan A tan (60 + A) tan (60 – A)

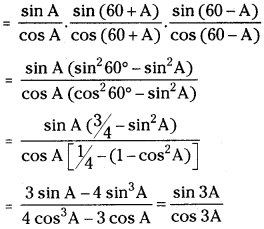
Take A = 6° in above we get tan 6° tan 66° tan 54° = tan 18°
take A = 18° in above result tan 18° tan 78° tan 42° = tan 54°
tan 6° tan 18° tan 42° tan 54° tan 66° tan 78 = tan 18° tan 54°
⇒ tan 6° tan 42° tan 66° tan 78° = 1

Question 42.
If a, b, c are non-zero real numbers and α, β are solutions of the equation a cos θ + b sin θ = c then show that
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) sin α .sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Answer:
Given a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ a² cos² θ = c² – 2bc sin θ + b² sin² θ
⇒ a² (1 – sin²θ) = c² – 2bc sin θ + b² sin² θ
⇒ (b² + a²) sin² θ – 2bc sin θ + (c² – a²) = 0
This is a quadratic equation in sin θ and suppose sin α, sin β are roots of the equation.
(∵ Given α, β are solutions of the equation)
∴ sin α + sin β = \(\frac{2 b c}{a^2+b^2}\) and sin α .sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

Question 43.
Prove that \(\frac{\sin \theta+\sin 2 \theta}{1+\cos \theta+\cos 2 \theta}\) = tan θ
Answer:

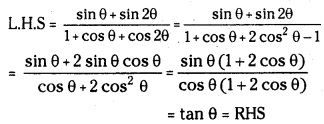
Question 44.
Prove that tan 3A tan 2A tan A = tan 3A – tan 2A – tan A.
Answer:
We have 3A = 2A + A
∴ tan 3A = tan (2A + A) = \(\frac{\tan 2 \mathrm{~A}+\tan \mathrm{A}}{1-\tan 2 \mathrm{~A} \tan \mathrm{A}}\)
⇒ tan 2A + tan A = tan 3A (1 – tan 2A tan A)
⇒ tan A tan 2A tan 3A = tan 3A – tan 2A – tan A

Question 45.
Express cos⁶A + sin⁶A in terms of sin 2A.
Answer:
cos⁶A + sin⁶A = (cos²A)³ + (sin²A)³
= (cos²A + sin²A)² – 3 cos² A sin² A (cos² A + sin² A)
= 1 – 3 cos²A sin²A ……………….(1)
= 1 – \(\frac{3}{4}\) (4 cos² A sin² A) = 1 – \(\frac{3}{4}\) sin²2A

Question 46.
If sin α = \(\frac{3}{5}\), where \(\frac{\pi}{2}\) < α < π, evaluate cos 3α.
Answer:
Given sin α = \(\frac{3}{5}\)
\(\frac{\pi}{2}\) < α < π ⇒ a lies in the Q₂

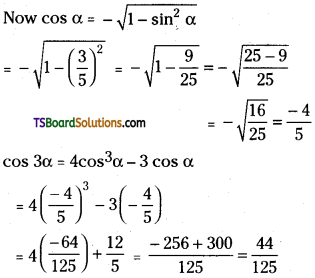
Question 47.
In a ΔABC, if tan\(\frac{A}{2}=\frac{5}{6}\) and tan \(\frac{B}{2}=\frac{20}{37}\), then show that tan \(\frac{A}{2}=\frac{2}{5}\).
Answer:
In ΔABC, A + B + C = 180°

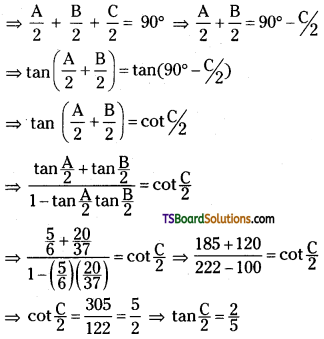
Question 48.
If cos θ = \(\frac{5}{13}\) and 270° < θ < 360°, evaluate sin\(\left(\frac{\theta}{2}\right)\) and cos\(\left(\frac{\theta}{2}\right)\)
Answer:
Given cos θ = \(\frac{5}{13}\), where 270° < θ < 360° ⇒ 135° < \(\frac{\theta}{2}\) < 180° ⇒ \(\frac{\theta}{2}\) lies in second quadrant since cos θ = \(\frac{5}{13}\)

Question 49.
Prove that cos\(\frac{2 \pi}{7}\) cos\(\frac{4 \pi}{7}\) cos\(\frac{8 \pi}{7}=\frac{1}{8}\)
Answer:
Let \(\frac{2 \pi}{7}\) = α and x = cos α cos 2α cos 4α and y = sin α sin 2α sin 4α(suppose)

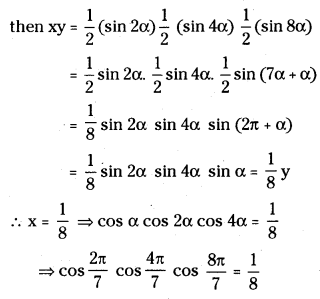
Question 50.
Prove that cos\(\frac{\pi}{11}\) cos\(\frac{2 \pi}{11}\) cos\(\frac{3 \pi}{11}\) cos\(\frac{4 \pi}{7}\) cos\(\frac{5 \pi}{7}=\frac{1}{32}\)
Answer:
Let \(\frac{\pi}{11}\) = α and x = cos α cos 2α cos 3α cos 4α cos 5α and y = sin α sin 2α sin 3α sin 4α sin 5α
xy = \(\frac{1}{2}\)(sin2α) \(\frac{1}{2}\)sin(4α) \(\frac{1}{2}\)sin(6α) \(\frac{1}{2}\)sin(8α) \(\frac{1}{2}\)sin(10α)
= \(\frac{1}{2^5}\)sin 2α sin 4α sin(11α – 5α) sin(11α – 3a) sin(11α – α)
= \(\frac{1}{2^5}\)sin 2α sin 4α sin(π – 5α) sin(π – 3a) sin(π – α)
= \(\frac{1}{2^5}\)sin α sin 2α sin 4α sin 5α = \(\frac{1}{2^5}\)y ⇒ x = \(\frac{1}{2^5}=\frac{1}{32}\)
∴ cos\(\frac{\pi}{11}\) cos\(\frac{2 \pi}{11}\) cos\(\frac{3 \pi}{11}\) cos\(\frac{4 \pi}{7}\) cos\(\frac{5 \pi}{7}=\frac{1}{32}\)

Question 51.
If O < A < B < \(\frac{\pi}{4}\) and sin (A + B) = \(\frac{24}{25}\) and cos(A – B) = \(\frac{4}{5}\) then find the value of tan 2A. [Mar. ’15(TS)]
Answer:
O < A < B < \(\frac{\pi}{4}\) ⇒ O < A + B < \(\frac{\pi}{2}\), –\(\frac{\pi}{2}\) < A – B < O

Question 52.
In ΔABC, prove that cos\(\frac{A}{2}\) + cos\(\frac{B}{2}\) – cos\(\frac{B}{2}\) = 4 cos\(\left(\frac{\pi+A}{4}\right)\) cos\(\left(\frac{\pi+B}{4}\right)\) cos\(\left(\frac{\pi-C}{4}\right)\). [Mar. ’05]
Answer:
In ΔABC, A + B + C = 180°

Question 53.
In ΔABC, prove that sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) – sin\(\frac{C}{2}\) = -1 + 4cos\(\left(\frac{\pi+A}{4}\right)\)cos\(\left(\frac{\pi+B}{4}\right)\)cos\(\left(\frac{\pi-C}{4}\right)\).
Answer:
In ΔABC, A + B + C = 180° ………….(1)

Question 54.
If A + B + C = 2S, then prove that sin (S – A) + sin(S – B) + sin C = 4 cos \(\left(\frac{S-A}{2}\right)\) cos\(\left(\frac{S-B}{2}\right)\) sin\(\left(\frac{C}{2}\right)\).
Answer:
Given A + B + C = 2S
L.H.S = sin(S – A) + sin (S – B) + sin C

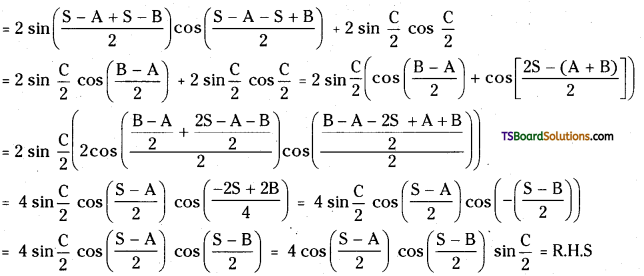
Question 55.
Eliminate ‘θ’ from x = a cos³θ, y = b sin³θ.
Answer:
Given x = a cos³θ, y = b sin³θ.
\(\frac{x}{a}\) = cos³θ, \(\frac{y}{b}\) = sin³θ

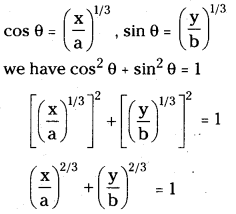
Question 56.
If none of the denominators is zero, prove that \(\left(\frac{\cos A+\cos B}{\sin A-\sin B}\right)^n+\left(\frac{\sin A+\sin B}{\cos A-\cos B}\right)^n\) = 2cotⁿ\(\left(\frac{A-B}{2}\right)\), if n is even 0, if n is odd. [Mar. ’16(TS)]
Answer:

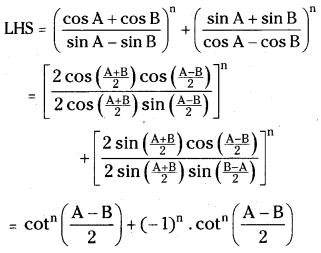
if n is odd, since (-1)ⁿ = 1
we have LHS = 0
if n is even and (- 1)ⁿ = 1
LHS = 2cotⁿ\(\left(\frac{A-B}{2}\right)\)

Question 57.
If A + B + C = 2S, then prove that cos(S – A) + cos(S – B) + cos C = 1 + 4cos\(\left(\frac{S-A}{2}\right)\) cos\(\left(\frac{S-B}{2}\right)\) cos\(\left(\frac{C}{2}\right)\). [Mar. ’17(TS)]
Answer:
Given A + B + C = 2S
L.H.S = cos(S – A) + cos(S – B) + cos C

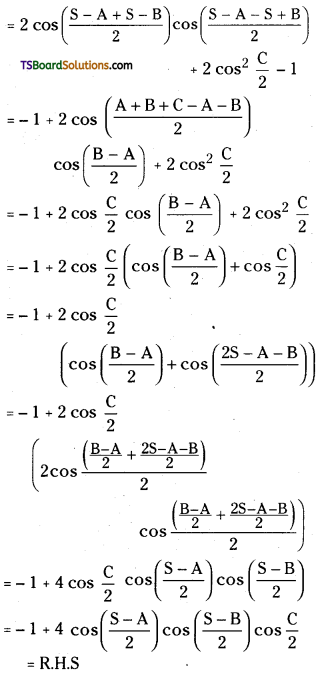
Question 58.
Prove that: sin 50° – sin 70° + sin 10° = 0
Answer:
LHS = sin 50° – sin 70° r sin 10°
= (sin 50° – sin 70°) + sin 10°
= 2 cos \(\left(\frac{50+70}{2}\right)\) sin \(\left(\frac{50-70}{2}\right)\) + sin 10°
= 2 cos 60° . sin (- 10°) + sin 10°
= – 2(\(\frac{1}{2}\)) sin 10° + sin 10° = 0

Question 59.
If A + B + C = 2s, then prove that cos(s – A) + cos (s – B) + cos (s – C) + cos s = 4 cos\(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\). [Mar. ’18(TS)]
Answer:

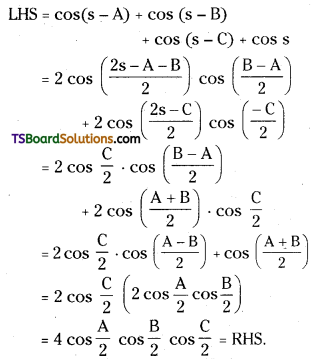
Question 60.
If A + B + C = 0, then prove that sin 2A + sin 2B + sin 2C = -4 sin A sin B sin C
Answer:
Given A + B + C = 0
LHS = sin 2A + sin 2B + sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + sin C
= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (-C) cos (A – B) + sin 2C
= -2 sin C cos (A – B) + 2 sin C cos C
= -2 sin C [cos (A-B) – cos C]
= – 2 sin C [cos (A – B) – cos [-(A + B)]]
= – 2 sin C [cos (A-B) – cos (A + B)]
= – 2 sin C [2 sin A sin B]
= -4 sin A sin B sin C = RHS.