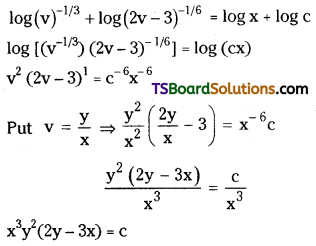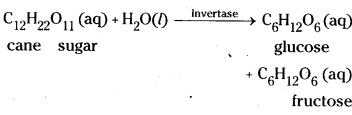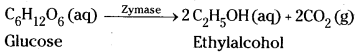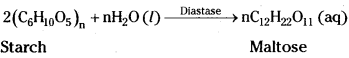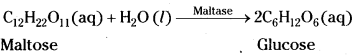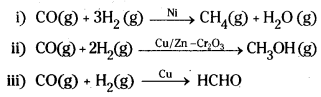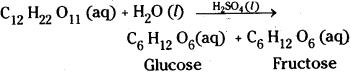Mahesh

Telangana TSBIE TS Inter 2nd Year English Study Material Grammar Idioms and Phrases Exercise Questions and Answers.

TS Inter 2nd Year English Grammar Idioms and Phrases

Q.No. 12 (4 Marks)

Do you have any idea of what an idiom is?
Let us read this conversation.

Anitha  :  Hi, Akhila… seem to be over the moon!
Akhila  :  Yeah…Don’t you know? The Inter results are music to my ears. What about you?
Anitha  :  Ah! I had to eat humble pie.
Akhila  :  Why… ? You burnt the midnight oil… I think.
Anitha  :  Nevertheless, I failed in one subject.
Akhila  :  Don’t cry your eyes out. Pull up your socks. Prepare we for the next exam.
Anitha  :  It’s OK. But my father doesn’t have belief in my ability, often says, “Don’t tell me cock and bull stories”.
Akhila  :  Come on Anitha. Don’t cry over spilt milk. Keep bad company at bay. You will succeed. Cheer up…
Anitha  :  Thank you Akhila. You have been a pillar of support.
Akhila  :  It’s alright. See you

Have you gone through the groups of words in italics ? What do they mean? What can you get from the words in isolation? Don’t they sound strang Yes, they are called idioms.

What is an idiom ?
An idiom is an artistic expression whose meaning is unpredictable from the usual meaning of its component words. Use of idioms adds glamour to the language, and finds a place in everyday use of language as well.

Now, let’s look at some idiomatic expressions and their usage.

1. once in a blue moon: happen very rarely
He attends classes once in a blue moon.

2. an arm and a leg: very expensive
It cost me an arm and a leg to study in the USA.

3. a piece of the cake: very easy
Batting is a piece of cake for Virat these days.

4. a drop in the ocean: a tiny part of something much bigger
The small donation was just a drop in the ocean.

5. bite one’s tongue: want to say something but stop oneself
Sitara wanted to speak out about the unfair decision. But she bit her tongue.

6. go the extra mile: doing much more than required
My father always goes the extra mile to help the needy.

7. get ducks in a row: to get one’s affairs in order or organized
I can’t hope to do well at my job until I get my ducks in a row.

8. let the cat out of the bag: reveal a secret accidentally
Joel let the cat out of the bag about my surprise birthday party.

9. working against the clock: not having enough time to do something
I am really working against the clock now. I must hurry.

10. flogging a dead horse: attempting to continue with something that is over We are flogging a dead horse. Our present business is making no money.
So, let’s do something else.

11. on cloud nine: very happy
Rahul is on cloud nine since he got a good job.

12. bolt from the blue: something happened unexpectedly
The results of the recent polls were a bolt from the blue to many parties.

13. storm in a tea cup: making unnecessary fuss/ getting excited about something unimportant
There was a storm in a tea cup over who should be the Chief Guest on Hostel Day.

14. make hay while the sun shines : to take advantage of a good situation that may not last long
Our boss is on vacation. Let’s make hay while the sun shines and relax.

15. beat black and blue: covered with bruise marks caused by being hit
Kiran was beaten black and blue by the violent crowd.

16. fight an uphill battle: struggle against very unfavourable circumstances
The Kings XI Punjab must fight an uphill battle to win the IPL title.

17. donkey’s years: a long time .
I have been teaching grammar for donkey’s years.

18. at the eleventh hour: at the last possible moment
If you want to do your best, don’t do things at the eleventh hour.

19. bee in one’s bonnet: an idea that constantly occupies one’s thoughts
Our English teacher has a bee in her bonnet about correct pronunciation.

20. cook someone’s goose: spoil someone’s plans or chances of success
This year’s severe drought cooked Ramaiah’s goose.

21. feather in one’s cap: the achievement of which one can be proud of
Bahubali’s success is a feather in Rajamouli’s cap.

22. rags to riches: start offbeing very poor and become very rich and successful
Dhirubhai Ambani’s life is a story of rags to riches.

23. in the blink of an eye: happen fast and instantaneously
The announcement of intermediate results reached every come” in the blink of an eye.

24. in/by leaps and bounds: make rapid or spectacular progress
Our business flourished in leaps and bounds.

25. risk life and limb: in danger of death or severe injury
Don’t risk your life and limb by participating in reality shows.

26. save one’s neck/skin: escape from death, punishment, etc. especially by leaving others in an extremely difficult situation
Satish got his friends into trouble to save his skin.

27. birds of a feather flock together: similar in many ways, so spend time together
Arun and Varan are sports enthusiasts and are often found together. So, our friends usually speak of them as birds of a feather (flock together).

29. bite off more than you can chew: try to manage something too difficult
Actor Shireesh bit off more than he could chew in his debut movie.

30. take the bull by the horns: act decisively to deal with a complex problem
I want to take the bull by the horns by deciding to swim across the fiver.

31. leave no stone unturned: try everything possible to achieve something
President Kalam left no stone unturned to motivate the youth.

32. no spring chicken: one is quite old or well past one’s youth
I am no spring chicken, you know. How can I dance?

33. beyond wildest dreams: better than you imagined for
Last year’s rainfall was beyond our wildest dreams.

34. keep your nose to the grindstone: concentrate on working or studying hard (informal)
In the Intermediate class, my daughter has to keep her nose to the grindstone. No time for games or music.

35. paddle your own canoe: do something without the help of others
Sonu refused all help as he believed in paddling his owm canoe.

36. have a bone to pick: annoyed with somebody and talk to them about it
Lakshmi has a bone to pick with Revati as she was not invited to the marriage.

37. give a tongue-lashing: scold someone severely
The teacher gave the lazy boy a tongue-lashing when he called Rani a lazy girl.

38. dressed up to the nines: wearing bright or glamorous clothes
Actors often dress up to the nines for public functions.

39. make one’s ears burn: embarrassed by hearing something being said about you
The discussion about my childhood pranks made my ears burn.

40. turn a deaf ear: refuse to listen to somebody
Our boss turned a deaf ear to our request to change the meeting venue.

41. back to the salt mines: returning to work with some reluctance
After the vacation, the students had to go back to the salt mines.

42. nuts and bolts: detailed facts and the practical aspects (informal)
Unless I get to know the nuts and bolts of the business, I can’t venture into it.

43. step into someone’s shoes: take over a job / a position held by someone before you
When the manager retires, I’ll step into his shoes.

44. catch-22: a frustrating situation that will lead to further frustration
In big cities, if you don’t have a place to live in, you can’t get a job, and with no job, you can’t get a place to live in! Thus, it’s a catch-22 situation.

45. at the drop of a hat: do it immediately without hesitation
The wealthy socialite throws parties at the drop of a hat.

46. wild goose chase: a search for something that is impossible for you to find or that does not exist, that makes you waste a lot of time
Without a proper address or phone number, it would be a wild goose chase to locate someone in Hyderabad.

47. taste your own medicine: have the same bad treatment that you have given to others
The evil-minded will taste their own medicine sooner or later.

48. blow one’s horn: to praise oneself; to boast
People avoid her as she constantly blows her horn.

49. burn the midnight oil: to work very late into the night
I have to present this report by tomorrow. So, I must bum the midnight oil tonight.

50. thrilled to bits: extremely pleased about something
I was thrilled to bits when I received a fancy gift.

51. a bed of roses: something which is easy
Life is not always a bed of roses.

52. a white elephant: expensive but not that useful
His new car has become a white elephant.

53. hit the nail on the head: say something correctly
She hit the nail on the head with her response.

54. spill the beans: to reveal a secret
They were afraid he would spill the beans.

55. hot cakes: fastselling
The new model cars are selling like hot cakes.

56. face the music: accept unpleasant consequences
Having lost his character, he has to face the music.

57. judge a book by its cover: judge something primarily on appearance
You can’t judge a book by its cover. Just because he looks strange, that doesn’t mean . he is not a nice person.

58. Achilles heel: a weak (vulnerable) spot
Maths has always been my Achilles heel.

59. by a whisker: by a very small amount/margin
Finally, our team lost by a whisker and I was disappointed.

60. every cloud has a silver lining: every misfortune has some positive aspect
If we hadn’t missed the plane, we wouldn’t have met you. It is rightly said every cloud has a silver lining.

61. part and parcel: an essential or fundamental element
Don’t get disheartened at losing your form. It’s part and parcel of being a professional.

62. a thick skin: an ability to not be upset by criticism
A politician needs a thick skin.

63. a sea change: a complete change in someone’s attitude or behavior
There is a sea change in the behavior of the culprit after his release from the prison.

64. in a nutshell: briefly; in essence
Let me explain the proceedings in a nutshell.

65. get the nod: to receive permission from someone to start something
Rahul got the nod after a lengthy discussion among the members.

66. take the rap: to be blamed or punished, especially for something you have not done
She was prepared to take the rap for the shoplifting, though it had been her sister’s idea.

67. dark horse: one who is previously unknown and is now prominent
The Gujarat Titans has proved to be a dark horse in the recent IPL.

68. a hot potato: controversial and sensitive issue
Racism is currently a hot potato in the international cricket.

69. a square meal: a large, filling, nutritious meal
The soldiers are very tired. They haven’t had a square eat for four days.

70. by fair means or foul: by any possible method
They never gave up trying to recover their property by fair means or foul.

71. a labour of love: a task that you do for pleasure without expecting payment
Preparing this book is clearly a labour of love.

72. keep the pot boiling: keep going on actively
I threw in a question just to keep the pot boiling while my brain caught up.

73. tie the knot: to get married
The couple tied the knot last year.

74. from top to bottom: very thoroughly
I would clean my room from top to bottom every Sunday.

Exercises

I. Fill in the blanks ITI the following sentences with suitable idiomatic expressions given below. Make necessary changes in the idioms if needed.

take the rap
in a nut shell
a sea change
by a whisker
get the nod
a thick skin

1. Finally, our team lost _____________ and I was disappointed.
2. A politician needs _____________
3. There is _____________ in the behavior of the culprit after his release from the prison.
4. Let me explain the proceedings _____________
5. Rahul _____________ after a lengthy discussion among the members.
6. She was prepared to _____________ for the shoplifting, though it had been her sister’s idea.
Answers:
1. by a whisker
2. a thick skin
3. a sea change
4. in a nutshell
5. go the nod
6. take the rap

II. Fill in the blanks in the following sentences with suitable idiomatic expressions given below. Make necessary changes in the idioms if needed.

on cloud nine
tie the knot
go the extra mile
apiece of cake
turn a deaf ear
hot cakes

1. The new model cars are selling like _____________
2. My father always _____________ since he got a good job.
3. Rahul is _____________ for Virat these days.
4. The couple _____________ last year.
5. Our boss _____________ to our request to change the meeting venue.
Answers:
1. hot cakes
2. goes the extra mile
3. on cloud nine
4. a piece of cake
5. tied the knot
6. turned a deaf ear

Telangana TSBIE TS Inter 2nd Year Accountancy Study Material 4th Lesson Partnership Accounts Textbook Questions and Answers.

TS Inter 2nd Year Accountancy Study Material 4th Lesson Partnership Accounts

Very Short Answer Questions

Question 1.
What is partnership?
Answer:

1. According to section 4, the Partnership Act 1932, partnership means “The relationship between persons who have agreed to share profits of the business carried on by all or any one of them acting for all”.
2. The persons who have entered into partnership business are called individually as “partners” and collectively as “a firm” and the name under which their business is carried on is called the name of the firm.

Question 2.
What is a partnership deed?
Answer:

1. It is a document that defines the rights and liabilities of partners of the firm besides containing other matters pertaining to the conduct and management of the firm.
2. Partnership deed is signed by all the partners.

Question 3.
State the methods of preparing partners’ capital accounts.
Answer:
There are methods of preparing partners’ capital accounts.
They are: A) Fixed capital method; and B) Fluctuating capital method.

Question 4.
What is the fixed capital method?
Answer:

1. Under fixed capital method, we prepare two accounts partner capital account and partners current account.
2. All the adjustments such as drawings, interest on capital, salary or commission, share of profits will be recorded in a partners current account, and the partners capital account is remains unchanged. Because of this, it is called fixed capital method.

Question 5.
What is fluctuating capital method?
Answer:

1. Under this method, all transactions relating to a partner such as capital contributed by partner, interest on capital, drawings, interest on drawings, salary, commission to partner, share of profit or loss are recorded in capital account only.
2. Because of this, the balance in capital account keeps on changing every year. Hence, it is called fluctuating capital method.

Question 6.
What is partnership? State its features.
Answer: Definition: According to section 4, Partnership Act 1932, partnership means “The relationship between persons who have agreed to share profits of the business carried on by all or any one of them acting for all”.
Features:

• Agreement: The partnership is formed to make profits. It is an agreement entered between/among all the partners.
• Business: It must be of a lawful business. It includes trade, vocation and profession.
• Profit sharing: The partners share the profit and losses of the business as per the
  agreement.
• Management: Partnership business may be managed or carried on by all the partners or any one of the partners acting on behalf of all the other partners, f) Unlimited liability: The liability of a partner in partnership firm is not only unlimited, but also joint and several.

Question 7.
What is partnership deed? State its contents.
Answer:
Partnership deed; It is a document which defines the rights and liabilities of partners of the firm besides containing other matters pertaining to the conduct and management of the firm.
Contents of partnership deed: The written agreement can contain as much, or as little, as partners want. The law does not say what it must contain. The usual contents of partnership deed are listed as here under.

1. Name of the partnership firm.
2. Names, addresses and occupation of all the partners.
3. Nature, object and duration of business.
4. Amount of capital to be contributed by each partner.
5. Drawings if any, allowed for private purposes.
6. Sharing of profits and losses.
7. Rate of interest on capital and drawings.
8. Rights, duties and liabilities of each partner.
9. Method of keeping books of accounts and audit.
10. Mode of payment to retired partner’s share.

Question 8.
What is Profit and Loss appropriation account?
Answer:

1. Profit and Loss appropriation account is prepared after ascertaining the net profit (or) loss through profit and loss account.
2. Profit and Loss appropriation account is a normal account. It is an extension of profit and loss account.
   This account is debited with interest on capital of partners, salary, commission remuneration to the partners, if allowed and profit transfer to general reserve and credited with the net profit, interest on drawings.
3. The balance if any, may be net profit or loss and will be distributed to the partners as per their profit sharing ratio.

Question 9.
State the provisions of partnership act in the absence of partnership deed,
Answer:
It is to be noted that if there is no partnership deed all the partners should abide by the provisions of partnership Act 1932.
In the absence of partnership deed, the partnership Act states that:

• All the profits and losses are to be shared equally.
• No interest is to be provided on capital.
• No interest is to be charged on drawings.
• No salary or commission is payable to managing partner.
• The partners who provided loan to firm are entitled to get interest @ 6% p.a. on the loan.
• Every partner shall take part in management of the business.

Textual Problems

Question 1.
A, B and C are partners sharing profits and loss equally with share capital of Rs. 50,000, Rs. 40,000 and t 30,000 respectively. The profit for the year ended 31st March 2015 amounted to Rs. 56,000 before allowing interest on capital @ 8% p.a. and salary to A Rs. 6,000 and commission to C Rs. 4,000.
Prepare profit and loss appropriation account.
Answer:
Profit & Loss appropriation a/c

Question 2.
X,Y and Z are partners sharing profits and losses in the ratio of 2: 2: 1. Each partner withdraws the fixed sum of Rs. 4,000 per month for their personal use.
Mr. X, withdraws on 1st day of every month, Mr. Y withdraws on the last day of every month and Mr. Z withdraws on middle of every month. Calculate interest on drawings. Rate of interest is 6% p.a.
Answer:
Calculation of Interest on Drawings:
Total drawings 4000 x 12 = 48,000
Rate of interest 6%

Question 3.
A and B are partners sharing profits and loss in the ratio of 3: 2 respectively. A contributed Rs. 2,00,000 and B contributed Rs. 1,50,000 towards their capital at the beginning of the year. Their drawings during the jfear amounted to Rs. 10,000 and 12,000 respectively. Mr. A is entitled to a salary of Rs. 8,000 and Mr. B to be given a commission of Rs. 10,000. Interest on capital to be provided @ 10% p.a. Interest on drawings amounted to t 500 for A and 1600 for B. Net profit before above adjustments amounted to Rs. 62,000.
Prepare profit or loss appropriation account and partners capital accounts under fluctuating capital method.
Answer:
Profit & Loss appropriation a/c

Fluctuation capital method

Question 4.
Sitha and Githa are partners sharing profits and losses in the ratio of 2: 3. Their capital accounts showed a balance of Rs. 1,00,000 and Rs. 1,50,000 respectively as on 1st April 2014. During the year, Sitha and Githa withdraw Rs. 5,000 and Rs. 7,000 respectively for personal use. Interest on capital to be provided @ 8% p.a. Interest on drawings amounted to Rs. 500 and Rs. 700 respectively. Profit for the year ended 31st March 2015, before making above adjustments amounted to Rs. 75,000.
Prepare: (a) Profit & Loss Appropriation account, (b) Partners capital accounts under (i) Fixed capital method, (ii) Fluctuation capital method.
Answer:
Profit & Loss appropriation a/c

Fixed capital method:

Fluctuations capital method:

Question 5.
Ramu and Robert are partners sharing profits and losses in the ratio of 5: 3. Give journal entries for the following and give capital accounts of Ramu and Robert.
(a) Capital introduced by Ramu Rs. 50,000 and Robert Rs. 80,000.
(b) Drawings by Ramu Rs. 5,000 and Robert Rs. 6,000.
(c) Interest on capital: Ramu Rs. 2,500 and Robert Rs. 4,000.
(d) Interest on drawings Ramu Rs. 300 and Robert Rs. 400.
(e) Profit transferred to General Reserve Rs. 9,000.
(f) Salary to Ramu Rs. 10,000 and Commission to Robert Rs. 7,000.
Answer:
Journal entries in the books of Ram and Robert

Question 6.
X and Y are partners sharing profits and losses in the ratio of 3: 2. Their trial balance as on 31 March, 2020 was as under.

You are required to prepare Trading, Profit and loss account, Profit and loss appropration account for the year ended 31 March 2020 and balance sheet as on that date after considering the following.
a) Closing stock value at t 48,000.
b) Interest on capital allowed at 6% p.a.
c) X is allowed a salary of Rs. 600 per month.
d) Depreciate machinery by 5% and Furniture by 8%.
e) Provide for bad debts @ 5% on debtors.
f) Transfer of general Reserve Rs. 5,000.
Answer:
Trading & Profit and loss a/c of X & Y for the year ended 31.03.2020

Balance Sheet of X & Y as on 31-03-2020

Question 7.
The following is the trial balance of Rarnesh and Suresh as on 31 March 2019. They share profit and losses in the ratio of 1: 3 respectively.


Prepare final accounts after taking into account the following.
a) Stock on March 2019 valued at Rs. 13,000.
b) Wages due Rs. 1,000
c) Taxes paid in advance Rs. 500
d) Provide for bad debts @ 6% on debtors.
e) Interst on capital allowed at 8%.
f) Interest on drawings @ 6% p.a.
g) Ramesh is allowed a salary of Rs. 7,000.
h) Depriciate buildings by Rs. 3,000, write off goodwill Rs. 2,000 and furniture by Rs. 800.
Answer:
Trading & Profit and loss a/c of Ramesh & Suresh for the year ended 31.03.2019

Balance Sheet of Ramesh & Suresh as on 31-03-2019

Question 8.
Ganga and Yamuna carrying on partnership business sharing profits and losses equally. Their trial balance as on 31 March 2020 was as under.

Additional information:
a) Closing Stock valued at Rs. 17,000.
b) Salaries payable Rs. 2,000.
c) Provide for bad debts @ 6% on debtors.
d) Interest on Loan to be provided.
e) Depreciate Fixed assets by 3% and furniture by Rs. 500.
f) Interest allowed on capital at 6%. No interest required on current accounts.
g) Interest on drawings Ganga Rs. 250, Yamuna Rs. 150.
h) Transfer to general Reserve Rs. 6,000.
Answer:



Balance Sheet of Ganga & Yamuna as on 31-03-2020

Textual Examples

Question 1.
Mr. Ram withdraws Rs. 1000 per month for his personal use. The rate of interest islO % per annum. Calculate interest on drawings in the following cases;
(a) When the amount (drawings) is taken on 1st day of every month.
(b) When the amount is drawn on last day of every month.
(c) When the amount is drawn in the middle of every month.
Answer:
Ram’s total drawings for the year Rs. 12,000
(12 months @ Rs. 1000 per month)
Rate of interest 10% per annum.

Question 2.
Mr. Ravi and Mohan are partners in a firm on 1st April 2019 with a capital of Rs. 1,50,000 and Rs. 2,00,000 respectively. On 1st July 2014 Mr. Ravi introduced Rs. 50,000 as an additional capital. Rate of it interest on capital is 10% p.a. Calculate interest on capital. Books are closed on 31st March, 2020.
Answer:
Calculation of interest on Capital On Ram’s capital
On Rs. 1,50,000 for one year @ 10% p.a.
(1 – 4-2019 to 31 – 3-2020)

On Mohan’s capital
On Rs. 2,00,000 @ 10% p.a. for one year
(1-4-2019 to 31 -3 – 2020)

Question 3.
Ram, Laxman and Hanuman are partners in a firm sharing profits and loss in the ratio of 2: 2: 1 respectively. Ram withdraw Rs. 5,000 per month on 1st day of every month. Laxman withdraw Rs. 4,000 per month on last day of every month. Hanuman withdraw^ Rs. 3,000 per month at the middie of every month. Rate of interest on drawings is 6% per annum. Calculate interest on drawings.
Answer:
Calculation of interest on Drawings:
Total drawings for the year;
Ram: 12 months @ t 5,000 per month = Rs. 60,000
Laxman: 12 months @ Rs. 4,000 per month = Rs. 48,000
Hanuman: 12 months @ Rs. 3,000 per month = Rs. 36,000
Interest on drawings = Total drawings x Rate of interest x Time

Note: (Student may follow product method. It take more time to calculate. For example in case of Ram’s Drawings interest is to calculated for 12 times, i.e., on 1st Rs. 5,000 drawn, interest is for 12 months and 2nd Rs. 5,000 drawn, interest is for 11 months so on. If we take average of this we get 6.5 months (time). So, calculate interest for 6.5 months on total drawings for the year. Therefore, student is advised to remember the above formula for each mode of drawings).

Question 4.
Ram and Rahim commenced a business on 1st April 2019. Ram brings in Rs. 20,000 in cash and Furniture worth Rs. 5,000 towards his capital. Mr. Rahim brings Rs. 10,000 in cash and Rs. 15,000 worth of building and creditors Rs. 5,000 towards his capital. Give journal entries and capital account of Ram and Rahim.
Answer:
Journal Entries


Ledger Accounts:

Question 5.
Mr. A and B are partners sharing profits and losses in the ratio of 2:1 have contributed Rs.1,00,000 and Rs. 60,000 respectively towards their capital. The partnership agreement provides that;
(a) Interest is allowed on capital @ 8% per annum.
(b) Mr. A is allowed a salary of Rs. 20,000 p.a.
(c) During the year A takes t 10,000 and B takes Rs. 5,000 towards personal use.
(d) Interest on drawings amounted to Rs. 1,000 for A and Rs. 500 for B.
(e) Partners decided to transfer Rs. 8,000 to general reserve a/c.
Net profit of the firm before above adjustments amounted to Rs. 45,000 for the year ended 31st March 2020.
You are required to give journal entries and profit and loss appropriation account and partners capital accounts (Fluctuating capital method).
Answer:
Journal entries

Note: Capital accounts may be prepared separately for A and B.

Question 6.
P, Q and R are partners sharing profits and losses in the ratio of 4: 3: 3. On 1st April 2019, their capital accounts showed a balance Rs. 80,000, Rs. 60,000 and Rs. 60,000 respectively. P is entitled to a salary of Rs.15,000 and Q is to get a commission of Rs. 8,000. Interest on capital is allowed @ 5% per annum. Their drawings during the year ended 31st March 2020, amounted to Rs. 4,000, Rs. 3,000 and Rs. 3,000 respectively for P,Q and R.

The interest on drawing amounted to Rs. 200, Rs. 150 and Rs. 150 respectively They decided to transfer Rs. 10,000 to general reserve. The profit earned for the year ended 31 March, 2020 amounted to Rs. 60,000 before making above adjustments.
Give profit & loss appropriation account and partners capital accounts under
(a) Fixed capital method
(b) Fluctuation capital method,
Answer:

Note: The balance of profit available is Rs. 17,500 i.e., Rs. 60,500 – Rs. 43,000. It- is distributed among P, Q and R in the ratio of 4: 3: 3. P gets Rs. 7,000: Q gets Rs. 5,250 and R gets Rs. 5,250.
(a) Fixed capital method:

(b) Fluctuating capital method:

Question 7.
Ram and Rahim are partners sharing profits and losses in the ratio of 3: 2 respectively. The following trail balance is extracted from their books as on 31 March 2020. You are required to prepare Trading, profit and loss account, profit and loss appropriation account and balance sheet as on that date.

The following and additional Informations is provided:
a) Closing stock valued at T 50,000.
b) Depreciate Machinery by 10%, Furniture by 8%, Buildings by 5%.
c) Provide for outstanding wages Rs. 6,000 and salaries Rs. 8,000.
d) Insurance paid in advance Rs. 500.
e) Provide for doubtful debts at 5% on debtors.
f) Interest on capital is allowed @ 6% p.a.
g) Interest on drawings: Ram Rs. 300, Rahim Rs. 180.
h) Transfer to general Reserve t 10,000.
i) Salary allowed to Ram Rs. 8,000 and commission allowed to Rahim Rs. 6,000.
Answer:
Trading & Profit and loss a/c of Ram and Rahim for the year ended 31 March, 2020

Note: Profit is Rs. 1,00,500 (ie., 1,30,500 – 30,000) transferred to capital accounts of Ram 3/5 of 1,00,500 ie., Rs. 60,300 and to Rahim 2/5 of 1,00,500 ie., 40,200.

Balance Sheet of Ram and Rahim as on 31st March, 2020


Note: Capital accounts age maintained under fluctuating capital method. Hence, all adjustments relating to interest on capital, drawings, salary and commission to partners, drawings, general reserve are recorded in capital accounts of partners concerned.

Question 8.
A and B are partners sharing profits and losses in the ratio of their capital. Their trial balance as on 31 March, 2020 is as follows.

You are required to prepare financial statements for the year ending 31 March 2020 after taking into account the following adjustments.
a) Closing stock valued at Rs. 28,000.
b) Salaries due Rs. 4,000.
c) Depreciate buildings by 2%, Machinery by 10%.
d) Interest due on investments Rs. 2,500.
e) Provide for bad debts at 5% on debtors.
f) Interest on capital is allowed at 8% p.a. No interest allowed on current account balances.
g) Interest on drawings: A – Rs. 80 and B – Rs. 40.
h) Salary allowed to B * Rs. 6,000.
i) Transfer to general Reserve Rs. 15,000.
Answer:





Balance Sheet of A and B as on 31 March, 2020

Telangana TSBIE TS Inter 2nd Year English Study Material Grammar One-word Substitutes Exercise Questions and Answers.

TS Inter 2nd Year English Grammar One-word Substitutes

Q.No.11 (4 Marks)

A single word that can be used in the place of many words is usually referred to as a one-word substitute. Knowing the meanings and usage of as many one-word substitutes as possible is very helpful in note-making and precis writing. It also improves one’s insight into the functioning of the language.

One h Ipful way to understand and remember the meaning of longer words is to know the r anings of their parts. ‘Telephone’, for example, is a combination of two parts ire. t ie (= distance) and ph?ne (= sound). Now think of the meanings of telescope (vision), telegram (writing), pbonedcs etc. ‘Autobiography’ is made up of three parts i. e. auto (= self), bio (=life) and graphy (= writing). Now you can easily understand and remember the meanings of words like automatic, automobile, biology, biometric, geography. Another way of acquiring quick command of one-word substitutes is to study them in groups, for example, of words pertaining to various fields of knowledge, referring to persons, etc. But the time – tested method is to have constant practice in knowing the meanings first arid then using them in sentences.

One – word substitutes
We can master our vocabulary by learning one-word subsdtutes. A one-word substitute, as its name indicates, is a word that replaces a group of words. The knowledge of one-word substitutes not only saves time while writing but also helps you in scoring good marks in competitive examinations.
To have a clearer understanding of one-word substitutes, read the following two passages. Pay special attention to the words or groups of words in bold.

(a) Here is my cousin Saraswathi. She is a person who loves books very much. Whatever book she S:il:n lay h~r hands on, she loves it and reads it. Recently shehas developed a keen interest in books dealing with the study of human mind. Yesterday, at a seminar, she explained how some people suffer from a morbid fear of water. She also discussed how some . people exhibit obsessive devotion to their own people. Later, she talked about the study of gods. Participants in the seminar appreciated her as a person with total knowledge in the topic she discusses. But, she humbly admitted that she was just like anyone of them there,

(b) Here is my cousin Saraswathi. She is a blbUophlle. Whatever ~ book she can lay her hands on, she loves it and reads it. Recently she bas developed a keen interest in books dealing with psychology. Yesterday, at a seminar, she explained how some people suffer from hydrophobia or aquaphobia. She also discussed how some people exhibit ethnomanla. Later, she talked about theology. Participants in the seminar appreciated her as omniscient in the topic she discusses. But she humbly admitted that she was just like anyone of them there.

Have you noticed how one-word substitutes (in Passage (b)) replaced groups of words (in Passage (a))? Between passages (a) and (b), which do you like better? Yes, you are right! One-word substitutes lend brevity (the soul of wit), variety (the spice of life), beauty (a joy forever) and clarity (the soul of communication) to language. They help one enhance one’s understanding of the mechanism that governs the formation of words. Keeping in view the multiple advantages of learning as many one-word substitutes as possible, keep on acquiring a few one-word substitutes a week like a hobby (culture).

Activity

Fill in the blanks in the following sentences with one word substitutes. Choose the right word from the list given in the box below

anaemia
benefactor
chronicle
debut
ecology
germicide
infanticide
misanthrope
optimist
panacea

1. Repeated and reckless use of a ______________ results in irreparable damage because of the side effects of the chemicals.
2. The sage says that his view of life is his ______________ to every problem one encounters in one’s life.
3. The present pandemic has very effectively emphasized the importance of preserving and protecting ______________
4. Severe fever for a few months left my mother with ______________
5. My uncle is such an ______________ that he sees opportunities even in dreaded difficulties!
6. Swami Vivekananda said that one who extends spiritual knowledge to others is the best ______________
7. Srilekha invited loud applause with her melodies in her very ______________
8. Some people resort to ______________ when a girl child is born in their homes, which is inhuman.
9. Our teachers always encourage us to stay updated. For that, they advise us to go through a ______________ a day and be in touch with all major historical events.
10. You can never find a miserable ______________ as this gentleman. Introduce to him
Answer:
1. germicide
2. panacea
3. ecology
4. anaemia
5. optimist
6. benefactor
7. debut
8. infanticide
9. chronicle
10. misanthrope

Given below is a list of words to enrich your vocabulary.

1. agends  :  a list of things to be discussed at a meeting
2. agnostic  :  a person who claims neither faith nor dis-belief in the existence of God
3. altruism  :  unselfish interest in the welfare of others
4. amateur  :  one who engages in an activity as a pastime rather than as a profession
5. ambidextrous  :  able to use both hands equally well
6. ambiguous  :  having more than one meaning and so, is unclear
7. amphibious  :  living on land as well as in water
8. anarchist  :  one who rebels against authority or established order
9. anarchy  :  the absence of government or control in a society
10. annihilation  :  complete destruction of something
13. anonymous  :  (a person) not identified by name, of unknown name
12. anthology  :  a collection of poems or stories
13. antidote  :  a substance that’can act against the effect of poison
14. antiseptic  :  a medicine that prevents infection
15. archaeology  :  study of life and culture of ancient people through the excavation of sites
16. atheist  :  a person who does not believe in the existence of god.
17. audience  :  a number of people listening to a lecture or a concert
18. autobiography  :  the life history of a person written by him self/herself
19. autonomous  :  (a person or an insurute) that can take decisions independently
20. bacteriology  :  a scientific study of bacteria
21. benefactor  :  one who gives money or help to another person or cause
22. bibliophile  :  a person who loves reading and keeping books
23. biography  :  a story of someone’s life written by another person
24. biosphere  :  the totality of living organisms and their environemnt
25. bouquet  :  a bunch of flowers tied together to be given as a present or to welcome someone

26. brunch  :  a late morning meal eaten instead of breakfast and lunch
27. calligraphy  :  the art of good handwriting
28. cannibal  :  a person who eats human flesh
29. cantonment  :  a permanent station for soldiers, garrison
30. cardiologist  :  a doctor who treats heart diseases
31. celibacy  :  the state of remaining unmarried
32. centennial  :  (centenary) the hundredth anniversary of an event
33. chef  :  a professional cook, typically the head cook in a restaurant
34. chronicle  :  a record of historical events
35. colleagues  :  people who work in the same organization
36. contemporary  :  living or occurring at the same time
37. cosmopolitan  :  an outlook that is influenced by people from all over the world
38. den  : the home of lions
39. dermatologist  :  a doctor who treats skin diseases
40. drought  :  prolonged period of abnormally low rain- fall
41. edible  :  fit to be eaten as food by humans
42. egoist (egotist)  :  a selfish person who talks and thinks of himself/herself
42. egoist (egotist)  :  a selfish person who talks and thinks of himself/herself
43. encyclopedia  :  a book of information covering all subjects (disease) regularly found in a particular
44. endemic  :  area or among particular people
45. ephemeral  :  that which has a short life
46. epidemic  :  the spread of an infectious disease in a very short time in a place
47. epitaph  : a short text written on a tombstone
48. epitome  :  the perfect example of something
49. etiquette  :  the rules of accepted polite behaviour in a society
50. etymology  :  the study of the origin and history of words
51. geocentric  :  having the earth at the centre
52. glutton  :  one who eats excessively

53. graphophobia  :  fear of writing
54. gregarious  :  (of people) who love the company of others
55. gymnasium  :  a room that has equipment for physical exercises
56. hematophobia  :  fear of blood
57. herbarium  :  a collection of dried plants
58. hydrosphere  :  all the water of the earth
59. iconoclast  :  one who attacks established and cherished beliefs; idol breaker
60. imminent  :  about to happen in the immediate future
61. immune  :  resistant to a particular disease or toxin
62. incorrigible  :  (of people) who cannot be corrected or changed
63. indefatigable  :  able to work for a long time without becoming tired
64. indelible  :  (a mark) that cannot be erased easily
65. inevitable  :  that which will happen and cannot be avoided
66. infallible  :  incapable of making mistakes
67. inflammable  :  catching tire quickly
68. insolvent  :  unable to pay debts
69. invincible  :  too strong to be defeated
70. invisible  :  that which cannot be seen
71. irrevocable  :  something that cannot be changed
72. kennel  :  a house or shelter for a dog
73. lethal  :  designed to cause death
74. loquacious  :  talking a lot or too much
75. maxim  :  a short statement expressing the rule of conduct
76. mercenary  :  concerned with making money at the expense of ethics
77. misogynist  :  a man who hates women
78. mortuary  :  a place where dead bodies are kept until cremation
79. notorious  :  well known for some bad quality
80. novice  :  one who is inexperienced or new to a job

81. nuance  :  a slight difference in meaning that is difficult to detect
82. obsolete  :  something which is out of date
83. omnipotent  :  having unlimited power
84. omniscient  :  having complete or unlimited knowledge
85. opaque  :  that which cannot be seen through, not transparent
86. optician  :  a person whose job is to examine people’s eyes and to recommend and sell glasses
87. optimist  :  one who looks at the bright side of things
88. ornithology  :  a scientific study of birds
89. orthopaedician  :  one who treats conditions involving the musculo-skeletal system / bone specialist
90. paediatrician  :  a doctor who treats diseases of children
91. palindrome  :  a word or phrase that reads the same backwards or forwards Example: madam
92. pantheism  :  the belief that God is present in all things
93. patent  :  sole right to produce or sell an invention
94. pedestrian  :  a person walking on a street
95. penchant  :  strong taste or liking for something
96. perennial  :  lasting for a long time, continually recurring
97. peregrination  :  a long slow journey, especially on foot
98. pessimist  :  one who looks at the dark side of things
99. philanthropist  :  a person who helps the needy
100. physician  :  one who attends to sick people and prescribes medicines
101. pilgrimage  :  a journey to a holy place for religious reasons
102. polyglot  :  one who can speak many languages
103. professional  :  a person with proven practical knowledge in a field
104. psychology  :  the study of human mind and behaviour
105. quarantine  :  confinement to one place to prevent the spread of infection
106. seismograph  :  an instrument for detecting earthquakes
107. somnambulism  :  the habit or activity of walking in sleep
108. spendthrift  :  a person who wastes money
109. stalwart  :  a loyal supporter of an organization

110. stoic  :  one who is indifferent to pleasure or pain
111. teetotaller  :  one who never takes alcoholic drinks
112. theist  :  a person who believes in the existence of God
113. verbose  :  using more words than required
114. veteran  :  someone who has a lot of experience in a field
115. web  :  the home of spiders

Exercises

Match the following word in Column A with their meanings / definitions in Column B.

Question 1.

Answer:
i) d
ii) e
iii) a
iv) g
v) b
vi) c

Question 2.

Answer:
i) f
ii) g
iii) e
iv) c
v) b
vi) a

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Differential Equations Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Differential Equations Important Questions Short Answer Type

Model I – Problems on Variables Separable Method

Question 1.
Solve \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x-y + x² (e^-y). [(AP) May ’18, (TS) ’17]
Solution:

Question 2.
Solve (e^x + 1) y dy + (y + 1) dx = 0. [May ’10, mar. ’04]
Solution:

Question 3.
Solve tan y sec²x dx + tan x sec²y dy = 0.
Solution:
Given D.E is tan y sec²x dx + tan x sec²y dy = 0
⇒ \(\frac{\sec ^2 x d x}{\tan x}+\frac{\sec ^2 y d y}{\tan y}=0\)
⇒ \(\int \frac{\sec ^2 x}{\tan x} d x+\int \frac{\sec ^2 y}{\tan y} d y=c\)
⇒ log|tan x| + log|tan y| = c
⇒ log|tan x| + log|tan y| = log c
⇒ log|tan x tan y| = log c
⇒ tan x tan y = c

Question 4.
Solve (xy² + x) dx + (yx² + y) dy = 0. [(TS) Mar. ’20, (AP) ’15; May ’13]
Solution:

Question 5.
Solve \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\). [Mar. ’05]
Solution:

Question 6.
Solve \(\frac{d y}{d x}=\frac{-\left(y^2+y+1\right)}{\left(x^2+x+1\right)}\). [May ’08, Mar. ’03]
Solution:


which is the required general solution.
(where k = √3c = constant)

Question 7.
Solve \(\sin ^{-1}\left(\frac{d y}{d x}\right)\) = x + y. [(TS) Mar. ’20; May ’07]
Solution:

⇒ ∫sec²t dt – ∫tan t sec t dt = x + c
⇒ tan t – sec t = x + c
⇒ tan(x + y) – sec(x + y) = x + c
which is the required general solution.

Question 8.
Solve \(\frac{d y}{d x}\) = tan²(x + y).
Solution:

Question 9.
Solve \(\frac{d y}{d x}\) – x tan(y – x) = 1. [(TS) May ’15]
Solution:
Put y – x = z, then
\(\frac{d y}{d x}-1=\frac{d z}{d x}\)
⇒ \(\frac{d y}{d x}=1+\frac{d z}{d x}\)

∴ The solution is sin(y – x) = \(c \mathrm{e}^{\mathrm{x}^2 / 2}\), where c is an arbitrary constant.

Question 10.
Solve (x + y + 1) \(\frac{d y}{d x}\) = 1
Solution:

⇒ x + y + 1 – log(1 + x + y + 1) = x + c
⇒ y + 1 – log(x + y + 2) = c
⇒ y – log(x + y + 2) = c
Which is the required solution.

Question 11.
Solve \(\sqrt{1+x^2} d x+\sqrt{1+y^2} d y=0\). [Mar. ’09]
Solution:

Question 12.
Solve y(1 + x) dx + x(1 + y) dy = 0. [(AP) Mar. ’20]
Solution:
Given D.E. is y(1 + x) dx + x(1 + y) dy = 0
y(1 + x) dx = -x(1 + y) dy
\(\frac{1+x}{x} d x=\frac{-(1+y)}{y} d y\)
\(\left(\frac{1}{x}+1\right) d x=\left(\frac{-1}{y}-1\right) d y\)
Now, Integrating on both sides, we get
\(\int\left(\frac{1}{x}+1\right) d x=\int\left(\frac{-1}{y}-1\right) d y\)
\(\int \frac{1}{x} d x+\int 1 d x=-\int \frac{1}{y} d y-\int 1 d y\)
log x + x = -log y – y + c
log x + x + log y + y = c
x + y + log xy = c
Which is the required solution.

Question 13.
Solve \(\frac{d y}{d x}=\frac{x y+y}{x y+x}\). [(TS) May ’16]
Solution:

Question 14.
Solve \(\frac{d y}{d x}\) = sin(x + y) + cos(x + y)
Solution:
Given D.E. is \(\frac{d y}{d x}\) = sin(x + y) + cos(x + y)
Put x + y = z
differential w.r.t ‘x’
\(1+\frac{d y}{d x}=\frac{d z}{d x}\)
⇒ \(\frac{d y}{d x}=\frac{d z}{d x}-1\)
(1) ⇒ \(\frac{\mathrm{dz}}{\mathrm{d} \mathrm{x}}\) – 1 = sin z + cos z

Question 15.
Solve \(\frac{d y}{d x}\) = (3x + y + 4)²
Solution:
Given D.E. is \(\frac{d y}{d x}\) = (3x + y + 4)² …….(1)
Put 3x + y + 4 = z
differential w.r.t ‘x’
\(3+\frac{d y}{d x}=\frac{d z}{d x}\)
⇒ \(\frac{d y}{d x}=\frac{d z}{d x}-3\)

Question 16.
Find the equation of the curve whose slope, at any point (x, y) is \(\frac{y}{x^2}\) and which satisfies the condition y = 1, when x = 3.
Solution:
We know that the slope at any point (x, y) on the curve is m = \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
Given that, slope of at any point (x, y) on the curve is m = \(\frac{y}{x^2}\)

Question 17.
Solve (y² – 2xy) dx + (2xy – x²) dy = 0. [May ’01]
Solution:

Question 18.
Solve \(\frac{d y}{d x}=\frac{y^2-2 x y}{x^2-x y}\). [Mar. ’19 (AP)]
Solution:
Given D.E is \(\frac{d y}{d x}=\frac{y^2-2 x y}{x^2-x y}\) ……..(1)
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 2.
Now, put y = vx
Diff. w.r. to x, we get



This is the required general solution of the given equation.

Question 19.
Find the equation of a curve whose gradient is \(\frac{d y}{d x}=\frac{y}{x}-\cos ^2 \frac{y}{x}\), where x > 0, y > 0 and which passes through the point (1, \(\frac{\pi}{4}\)). [(AP) May ’19, ’16, (TS) ’16]
Solution:
Given D.E. is \(\frac{d y}{d x}=\frac{y}{x}-\cos ^2 \frac{y}{x}\) ………(1)
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 1.
Put y = vx
diff. w.r.t ‘x’ on both sides

Question 20.
Give the solution of \(x \sin ^2\left(\frac{y}{x}\right) d x=y d x-x d y\) which passes through the point (1, \(\frac{\pi}{4}\)). [Mar. ’14]
Solution:
Given differential equation is

The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 1.
Put y = vx
Diff. w.r. to ‘x’ on both sides


which is the required particular solution.

Model II – Problems on Homogeneous D.E.

Question 21.
Solve (x² – y²) dx – xy dy = 0. [(AP) May ’17; Mar. ’09]
Solution:

Question 22.
Solve \(\frac{d y}{d x}=\frac{(x+y)^2}{2 x^2}\). [Mar. ’05]
Solution:

Question 23.
Solve (x² – y²) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy
Solution:
Given D.E. is (x – y ) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy
\(\frac{d y}{d x}=\frac{x y}{x^2-y^2}\) ………(1)
This is a homogeneous equation since both the nr and dr are homogeneous functions of degree 2.
Let y = vx

⇒ -x² = 2y² log(cy)
⇒ x² + 2y² log(cy) = 0
Which is the required general solution.

Question 24.
Solve (x² + y²) dx = 2xy dy. [(AP) Mar. ’20, Mar. ’17, ’16]
Solution:
Given diff. equation is \(\frac{d y}{d x}=\left(\frac{2 x y}{x^2+y^2}\right)^{-1}\) …….(1)
Clearly, it is a homogeneous diff. equation of degree zero.

which is the required general solution.

Question 25.
Solve y² dx + (x² – xy + y²) dy = 0.
Solution:
Given D.E is y² dx + (x² – xy + y²) dy = 0
(x² – xy + y²) dy = -y² dx


Which is the required general solution.

Question 26.
Solve \(\frac{d y}{d x}+\frac{y}{x}=\frac{y^2}{x^2}\)
Solution:

Question 27.
Solve x dy = \(\left(y+x \cos ^2 \frac{y}{x}\right) d x\). [Mar. ’13, ’11]
Solution:
Given diff. equation is
x dy = \(\left(y+x \cos ^2 \frac{y}{x}\right) d x\)
\(\frac{d y}{d x}=\frac{y+x \cos ^2 \frac{y}{x}}{x}=\frac{y}{x}+\cos ^2 \frac{y}{x}\) …….(1)
Clearly, it is a homogeneous differential equation of degree zero.
Let y = vx then v + x \(\frac{d v}{d x}=\frac{d y}{d x}\)
From (1), x \(\frac{\mathrm{dv}}{\mathrm{dx}}\) = v + cos²v – v = cos²v
sec²v dv = \(\frac{\mathrm{dx}}{\mathrm{x}}\)
Integrating on both sides
∫sec²v dv = ∫\(\frac{\mathrm{dx}}{\mathrm{x}}\)
tan v = log x + c
⇒ tan(\(\frac{y}{x}\)) = log x + c
Which is the required general solution.

Question 28.
Solve (2x – y) dy = (2y – x) dx. [Mar. ’12]
Solution:
Given diff. equation is \(\frac{d y}{d x}=\frac{2 y-x}{2 x-y}\) …….(1)
Clearly, it is a homogeneous diff. equation of degree zero.

Which is the required general solution.

Question 29.
Solve xy² dy – (x³ + y³) dx = 0. [(TS) May ’18]
Solution:
Given D.E. is xy² dy – (x³ + y³) dx = 0
xy² dy = (x³ + y³) dx
\(\frac{d y}{d x}=\frac{x^3+y^3}{x y^2}\) ……(1)
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 3.
Put y = vx
diff. w.r.t ‘x’ on both sides

Which is the general solution of the given equations.

Question 30.
Solve (x³ – 3xy²) dx + (3x²y – y³) dy = 0. [(AP) May ’18; May ’14]
Solution:
Given D.E is (x³ – 3xy²) dx + (3x²y – y³) dy = 0
(3x²y – y³) dy = -(x³ – 3xy²) dx
\(\frac{d y}{d x}=\frac{-\left(x^3-3 x y^2\right)}{3 x^2 y-y^3}\)
\(\frac{d y}{d x}=\frac{3 x y^2-x^3}{3 x^2 y-y^3}\) ……..(1)
It is a homogeneous equation since both nr and dr are homogeneous functions of degree 3.
Put y = vx
Then diff. w.r. t. x



Which is the required solution of the given equation.

Question 31.
Solve (x²y – 2xy²) dx = (x³ – 3x²y) dy. [Mar. ’18 (AP)]
Solution:

Question 32.
Solve \(\frac{d y}{d x}=\frac{2 x-y+1}{x+2 y-3}\)
Solution:
Given D.E. is \(\frac{d y}{d x}=\frac{2 x-y+1}{x+2 y-3}\) …….(1)
Comparing (1) with \(\frac{d y}{d x}=\frac{a x+b y+c}{a^1 x+b^1 y+c^1}\)
We get a = 2, b = -1, c = 1
a’ = 1, b’ = 2, c’ = -3
Now b = -1 = -(1) = -a’
∴ b = -a’
Now (x + 2y – 3) dy = (2x – y + 1) dx
⇒ x dy + 2y dy – 3dy = 2x dy – y dx + dx
⇒ x dy + 2y dy – 3 dy – 2x dx + y dx – dx = 0
⇒ (x dy + y dx) + 2y dy – 3 dy + 2x dx – dx = 0
⇒ d(xy) + 2y dy – 3 dy + 2x dx – dx = 0
By integrating, we get
∫d(xy) + 2∫y dy – 3 ∫1 dy + 2 ∫x dx – ∫dx = c
xy + 2 . \(\frac{y^2}{2}\) – 3y + 2 . \(\frac{x^2}{2}\) – x = c
xy + y² – 3y + x² – x = c
Which is the required solution.

Model III – Problems on non-homogeneous D.E.

Question 33.
Solve \(\frac{d y}{d x}=\frac{-3 x-2 y+5}{2 x+3 y+5}\)
Solution:
Given diff. equation is \(\frac{d y}{d x}=\frac{-3 x-2 y+5}{2 x+3 y+5}\) …….(1)
Comparing it with \(\frac{d y}{d x}=\frac{a x+b y+c}{a^{\prime} x+b^{\prime} y+c^{\prime}}\)
We get a = -3, b = -2, c = 5, a’ = 2, b’ = 3, c’ = 5
Then, we can solve equation (1) by the case (i)
∴ b = -a’
\(\frac{d y}{d x}=\frac{-3 x-2 y+5}{2 x+3 y+5}\)
⇒ dy (2x + 3y + 5) = dx (-3x – 2y + 5)
⇒ 2x dy + 3y dy + 5 dy + 3x dx + 2y dx – 5 dx = 0
⇒ 2(x dy + y dy) + 3y dy + 5 dy + 3x dx – 5 dx = 0
⇒ 2d(xy) + 3y dy + 5 dy + 3x dx – 5 dx = 0
Integrating on both sides, we get
2∫d(xy) + 3∫y dy + 5∫dy + 3∫x dx – 5∫dx = c
⇒ 2xy + 3 \(\frac{y^2}{2}\) + 5y + 3 \(\frac{x^2}{2}\) – 5x = c
⇒ 4xy + 3y² + 10y + 3x² – 10x = 2c = k
(k = constant)
Which is the required general solution.

Question 34.
Solve 2(x – 3y + 1) \(\frac{d y}{d x}\) = 4x – 2y + 1
Solution:
Given D.E is 2(x – 3y + 1) \(\frac{d y}{d x}\) = 4x – 2y + 1
\(\frac{d y}{d x}=\frac{4 x-2 y+1}{2 x-6 y+2}\) …….(1)
Comparing (1) with \(\frac{d y}{d x}=\frac{a x+b y+c}{a^{\prime} x+b^{\prime} y+c^{\prime}}\)
We get a = 4, b = -2, c = 1
a’ = 2, b’ = -6, c’ = 2
Now, b = -2 = -(2) = -a’
∴ b = -a’
Hence we can solve by the case (1).
(2x – 6y + 2) dy = (4x – 2y + 1) dx
⇒ 2x dy – 6y dy + 2 dy = 4x dx – 2y dx + 1 dx
⇒ 2x dy – 6y dy + 2 dy – 4x dx + 2y dx – 1 dx = 0
⇒ 2(x dy + y dx) – 6y dy – 4x dx + 2dy – 1 dx = 0
⇒ 2d(xy) – 6y dy – 4x dx + 2 dy – dx = 0
By integrating we get,
2∫d(xy) – 6∫y dy – 4∫x dx + 2∫dy – ∫dx = c
⇒ 2(xy) – 6(\(\frac{y^2}{2}\)) – 4(\(\frac{x^2}{2}\)) + 2y – x = 0
⇒ 2xy – 3y² – 2x² + 2y – x = c
Which is the required solution.

Question 35.
Solve x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 2y = log x
Solution:
Given D.E. is x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 2y = log x
dividing on both sides by ‘x’
\(\frac{d y}{d x}+\frac{2 y}{x}=\frac{\log x}{x}\)
Which is in the form \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + Py = Q
It is linear in y.

Model IV(a) – Problems on L.D.E in y

Question 36.
Solve x log x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = 2 log x. [(AP) Mar. ’20; May ’14]
Solution:

Question 37.
Solve (1 + x²) \(\frac{d y}{d x}\) + y = \(e^{\tan ^{-1} x}\). [(AP) Mar. ’18, ’16; May ’16, (TS) Mar. ’15 (TS); May ’13]
Solution:

Question 38.
Solve \(\frac{d y}{d x}\) = y tan x + e^x sec x. [(TS) May ’19; Mar. ’09]
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) – y tan x = e^x sec x ……..(1)
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
We get P = -tan x, Q = e^x sec x
I.F. = e^2∫Pdx
= e^{-∫tan x dx}
= e^{log|cos x|}
= cos x
The solution of (1) is,
y (I.F) = ∫Q(I.F) dx + c
y (cos x) = ∫e^x sec x (cos x) dx + c = ∫e^x + c
y (cos x) = e^x + c
Which is the required solution.

Question 39.
Solve \(\frac{d y}{d x}\) + y sec x = tan x. [May ’10]
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) + y sec x = tan x
It is a linear diff. equation in y.
It compared with \(\frac{d y}{d x}\) + Py = Q
We get P = sec x, Q = tan x
I.F. = e^∫Pdx
= e^{∫sec x dx}
= e^{log|sec x + tan x|}
= sec x + tan x
The solution of (1) is,
y (I.F) = ∫Q(I.F) dx + c
y(sec x + tan x) = ∫tan x (sec x + tan x) dx + c
= ∫sec x tan x dx + ∫tan²x dx + c
= ∫sec x tan x dx + ∫(sec²x – 1) dx + c
= sec x + tan x – x + c
Which is the required solution.

Question 40.
Solve \(\frac{d y}{d x}\) + y tan x = sin x. [(TS) Mar. ’16, ’12]
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) + y tan x = sin x ……..(1)
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
Where P = tan x, Q = sin x
I.F = e^∫Pdx
= e^{∫tan x dx}
= sec x
The solution of (1) is,
y(I.F) = ∫Q(I.F) dx + c
y sec x = ∫sin x . sec x dx + c
y sec x = ∫tan x dx + c
y sec x = log|sec x| + c
Which is the required solution.

Question 41.
Solve \(\frac{d y}{d x}\) + y tan x = cos³x. [(AP) May ’19, ’18; Mar. ’17]
Solution:
Given diff. equation is \(\frac{d y}{d x}\) + + y tan x = cos³x
It is a linear diff. equation in y of the first order.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
we get P = tan x, Q = cos³x

Which is the required solution.

Question 42.
Solve cos x . \(\frac{d y}{d x}\) + y sin x = sec²x. [Mar. ’19 (TS); Mar. ’14]
Solution:
Given differential equation is
cos x . \(\frac{d y}{d x}\) + y sin x = sec²x
Dividing on both sides by cos x, we get
\(\frac{d y}{d x}\) + y tan x = sec³x
Which is in the form of \(\frac{d y}{d x}\) + Py = Q
It is linear in ‘y’
Here, P = tan x, Q = sec³x
IF = e^∫Pdx
= e^{∫tan x dx}
= e^{log|sec x|}
= sec x
∴ Solution is y(I. F) = ∫Q(I. F) dx + c
y sec x = ∫sec²x . sec²x dx + c
= ∫sec⁴x dx + c
= ∫sec²x . sec²x dx + c
= ∫(1 + tan²x) sec²x dx + c
= ∫(1 + t²) dt + c
Put tan x = t ⇒ sec²x dx = dt
= ∫1 dt + ∫t² dt + c
= t + \(\frac{\mathrm{t}^3}{3}\) + c
y sec x = tan x + \(\frac{1}{3}\) tan³x + c

Question 43.
Solve (1 + x²) \(\frac{d y}{d x}\) + y = tan^-1x. [(AP) May ’16]
Solution:

Question 44.
Solve (1 + x²) \(\frac{d y}{d x}\) + 2xy – 4x² = 0. [Mar. ’06]
Solution:
Given diff. equation is
\(\frac{d y}{d x}+\frac{2 x y}{1+x^2}=\frac{4 x^2}{1+x^2}\) …….(1)
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q

Which is the required solution.

Question 45.
Solve \(\frac{d y}{d x}+y\left(\frac{4 x}{1+x^2}\right)=\frac{1}{\left(1+x^2\right)^2}\). [(AP) May ’17]
Solution:

Question 46.
Solve \(\frac{d y}{d x}+\frac{3 x^2}{1+x^3} y=\frac{1+x^2}{1+x^3}\)
Solution:

Question 47.
Solve \(\frac{1}{x} \frac{d y}{d x}+y e^x=e^{(1-x) e^x}\). [(AP) May ’18]
Solution:

Question 48.
Solve x(x – 1) \(\frac{d y}{d x}\) – y = x³(x – 1)³. [(AP) Mar. ’19]
Solution:

Model IV(b) – Problems on L.D.E in x

Question 49.
Solve (1 + y²) dx = (tan^-1y – x) dy. [Mar. ’18 (TS); May; Mar. ’15 (AP); May ’15 (TS)]
Solution:

Question 50.
Solve (x + 2y³) \(\frac{d y}{d x}\) = y. [May ’12]
Solution:

Question 51.
Solve (x + y + 1) \(\frac{d y}{d x}\) = 1. [Mar. ’17 (TS); Mar. ’13]
Solution:
Given diff. equation is \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{1}{\mathrm{x}+\mathrm{y}+1}\)
\(\frac{d x}{d y}\) – x = y + 1 ……..(1)
It is a linear diff. equation in x.
Comparing it with \(\frac{d x}{d y}\) + Px = Q
Where P = -1, Q = y + 1
I.F. = e^∫Pdy = e^{∫(-1) dy} = e^-y
The solution of (1) is
x(I.F) = ∫Q(I.F) dy + c

Which is the required general solution.

Model V – Problems on Bernoulli’s D.E.

Question 52.
Solve \(\frac{d y}{d x}\) (x²y³ + xy) = 1. [Mar. ’11]
Solution:

Telangana TSBIE TS Inter 2nd Year English Study Material Grammar Punctuation Exercise Questions and Answers.

TS Inter 2nd Year English Grammar Punctuation

(Symbols- .,,) to be used out of 10 necessary

Q.No. 10 (8 × 1/2 = 4 Marks)

Communication is not simply uttering words. It’s just one aspect of it. Communication is an art that only a few people truly understand. It includes signs we may convey indirectly, such as body language. Many people believe it is a more effective medium of communication. Body language is influenced by where we stop, the words we focus on, and our facial expressions.

However, you cannot use body language when writing. Despite this, many people are able to express themselves beautifully through this medium. Punctuation serves as body language in written form, empowering our emotions. This is made up of wordplay, pauses, exclamations, and introspection.

Here, we’ll become acquainted with the various types of punctuation marks used in the English language. They all serve a different purpose, and their proper use can improve the meaning of a sentence. They not only give your words more substance, but also the kind of depth that can only be conveyed verbally. We’ll take a quick look at all of these punctuation marks and how they’re used in written communication.

We’ll break them down for you so you don’t have any doubts.

Punctuations are an important part of written communication, and learning about them will help you understand how to use them correctly in sentences. To grasp Punctuation knowledge, re-read the content you write and try to check whether you are using Punctuation correctly or not, as this is the most common mistake we all make at times. You’ll be surprised by the results. It’s a fascinating experiment that everyone should try.

Play with punctuation

Let us understand and relish the following sets of sentences.

1. Stop, not hang him.
Stop not, hang him.
(A comma kills a man. Punctuation matters!)

2. Woman, without her man, is nothing.
(Woman is nothing unless there is a man.)
Woman! Without her, man is nothing.
(Man is nothing unless there is a woman.)

3. Let’s eat Grandpa.
(Grandpa is going to be eaten!)
Let’s eat, Grandpa.
(inviting grandpa to eat)

4. Akbar said Ashoka was a great warrior.
(Ashoka was a great warrior.)
“Akbar”, said Ashoka, “was a great warrior.”
(Akbar was a great warrior.)

5. This section consists of seven- year-old children.
(The children are aged seven.)
This section consists of seven year-old children.
(There are seven children who are one-year old.)

6. These are my employees.
(These people are my employees.)
These are my employee’s.
(These things belong to my employee.)
These are my employees’.
(These things belong to my employees;)

The above sentences clearly indicate how punctuation marks are helpful in conveying the correct meaning.

Punctuation marks, like traffic signals, are visual indicators used in written/ printed texts to make texts meaningful.

Types of punctuation: There are three types of punctuation. They are:

Now, let us look at their specific functions in detail.

A. End punctuation
1. Full stop (.)
It indicates the most extended pause and is always placed at the end of a sentence. It is used
i) at the end of declarative and imperative sentences.
Naveen is a university student.
Come here.

ii) after most abbreviations and initials.
M.A. (Master of Arts), B.Sc. (Bachelor of Science),
a.m. (ante meridian)

iii) to separate hour from minute and date from month and year.
The class begins at 7.45 a.m. daily.
Vanitha was born on 15.12.2015.

Note: Full stops are omitted (NOT used)
i) in acronyms (abbreviations pronounced as complete words).
NATO, UNESCO, VAT

ii) when the capital letter in the abbreviation doesn’t stand for a complete word.
TV (Television), TB (Tuberculosis)

iii) in newspaper headlines.
Art is more than unbroken lines
Heat wave condition persists until May

2. Question mark (?)
It is used
i) at the end of an interrogative sentence.
Do you like sweets?

ii) after question tags or similar words.
He likes music, doesn’t he? This is your car, right?

iii) after el I iptical questions. .
Doing well? In trouble?
Note: A question mark is not used at the end of an indirect question.
The principal asked me where I had gone

3. Exclamation mark (!)
It is used .
i) after an emotional expression of joy/sorrow/surprise/shock/anger, etc.
How fabulous the movie is!
What an awful experience it was!

ii) after an interjection or one-word exclamation.
Pity! She lost her father.
Hurrah! We won the match.

iii) after an imperative sentence when it is charged with feeling (a strong : command).
Shut up! Go and bring your notebook.
Get lost! I need no explanation.

Excercise 

I. Use appropriate end punctuation marks (full stop question mark / exclamation mark) with the following sentences.

Questions:
1) Will you show me the book
2) How intelligent you are
3) You like English, don’t you
4) Stop the bus for me
5) It is raining now
6) What an idea
7) Was the meal nourishing
8) Hold me I am going to faint
9) The dam burst Run for your lives
10) Watch out A car is coming
Answers:
1) Will you show me the book?
2) How intelligent you are!
3) You like English, don’t you?
4) Stop the bus for me.
5) It is raining now.
6) What an idea!
7) Was the meal nourishing ?
8) Hold me! I am going to faint.
9) The dam burst! Run for your lives.
10) Watch out! A car is coming.

II. Read the following paragraph and use appropriate end punctuation marks (full stop/ question mark/exclamation mark) wherever necessary.

Once upon a time there lived a duck and a kangaroo They were friends One day the duck asked the Kangaroo, ‘Dear friend, “How do you jump” The Kangaroo replied, “Ah it is very easy Do you love it” The duck said, “Oh is it I love to jump like you then The Kangaroo said, “Sit on my back I will take you round the world”
Answer:
Once upon a time there lived a duck and a kangaroo. They were friends. One day the duck asked the kangaroo, “Dear friend, How do you jump?” The Kangaroo replied, “Ah! It is very easy. Do you love it ?” The duck said, “Oh! Is it ? I love to jump like you then. The kangaroo said, “Sit on my back. I will take you round the world.”

Exercise

1. Use appropriate internal punctuation marks (semicolon / colon /comma/ quotation marks / ellipses) in the following sentences.

Questions:
1. The monsoon failed this year too and the country is in the grip of a famine.
2. I wasn’t just annoyed I was absolutely furious
3. Sumit said, Where are you going?
4. She worked hard she failed.
5. August 151947. It was the day on which we won independence.
6. The man said I wasn’t wounded.
7. He was not stupid just passive.
8. The grand tour usually included Paris France Vienna Austria Rome and Italy
Answers:
1. The monsoon failed this year too: and the country is in the grip of a famine.
2. I wasn’t just annoyed; I was absolutely furious
3. Sumit said, “Where are you going?
4. She worked hard: she failed.
5. August 151947-It was the day on which we won independence.
6. The man said, “I wasn’t wounded.
7. He was not stupid just passive.
8. The grand tour usually included Paris France,Vienna, Austria, Rome, and Italy.

Excercise – A

I. Use appropriate word punctuation marks (apostrophe / hyphen/capitals) in the following sentences.ellipses) in the following sentences.

Questions:
1. this is my cousins car,
2. gandhiji led the non violent movement
3. there are forty-six boys in the class.
4. these are my father in laws clothes.
5. we have semi-skilled workers
6. iam a member of the officers club.
7. he wants an up to date account
8. they prefer sugar free sweet.
Answers:
1. This is my cousins car,
2. Gandhiji led the non violent movement
3. There are forty-six boys in the class.
4. These are my father in laws clothes.
5. We have semi-skilled workers
6. I am a member of the officers club.
7. He wants an up to date account
8. They prefer sugar free sweet.

II. Read the following paragraph and use appropriate word punctuation marks (apostrophe / hyphen / capitals) wherever necessary.

there was an old owl. everyday he used to see some incidents happening around him. yesterday he saw a boy helping his mother-in-law. today he saw him shouting at her. the boys father in law was kind and gentle, the boy shouted at his father in law was kind and gentle, the boy shouted at his father in law too. the owls curiosity grew more and more to know about the boy.
Answer:
There was an old owl. Everyday he used to see some incidents happening around him. Yesterday he saw a boy helping his mother-in-law. today he saw him shouting at her. The boys father in law was kind and gentle. The boy shouted at his father in law too. The owls curiosity grew more and more to know about the boy.

Exercises – B

I. Punctuate the following letter.

24-7/A
bank street
hyderabad
27 October 2015,

To
the editor
box no 128
the hindu
Hyderabad

dear sir,
with reference to your advertisement in todays newspaper for the post of an incharge of ads section i would like to apply for it before that let me be known of the details of the interview like date time and venue.

yours faithfully,
manisharma,
Answer:
24-7/A
Bank street,
Hyderabad
27 October 2015,

To
The editor
box no 128
The hindu
Hyderabad

Dear sir,

with reference to your advertisement in today’s newspaper for the post of an incharge of ads section i would like to apply for it before that let me be known of the details of the interview like date time and venue.

yours faithfully,
manisharma.

II. Punctuate the following dialogue.

Iasya ………… hai kavya how are you
kavya ………… fine what about you not seen for a week
Iasya ………… ive been to my grandmas village for vacation
kavya ………… oh how did you feel there
Iasya ………… fabulous what a pleasant life it was greenery cool breeze everywhere
kavya ………… you are right but we are living in towns noting but concrete
Iasya ………… but why dont we concentrate on planting
kavya ………… good idea why dent we start first
Iasya ………… ok lets meet here tomorrow again
kavya ………… ok bye see you
Answer:
Iasya ………… Hai Kavya. How are you?
kavya ………… Fine. What about you? Not seen for a week?
Iasya ………… I’ve been to my grandma’s village for vacation.
kavya ………… Oh! How did you feel there?
Iasya ………… Fabulous! What a pleasant life it was! Greenery, cool breeze everywhere
kavya ………… You are right. But we are living in towns. Nothing but concrete jungles!
Iasya ………… But, why shouldn’t we concentrate on planting?
kavya ………… Good idea! Why shouldn’t we start first?
Iasya ………… OK. Let’s meet here tomorrow again,
kavya ………… OK. Bye! See you.

III. There should be ten punctuation marks in the following paragraph. Try to insert at least eight of them.

two weeks ago i was amused when a friend who couldnt bear to sleep alone, woke me up close to midnight at the hotel into which we had checked in. can we hire a double room im
totally spooked, she said
Answer:
Two weeks ago, I was amused when a lriend who couldn’t bear to sleep alone, woke me up close to midnight, at the hotel into which we had checked in. “Can we hire a double room? I’m totally spooked,” she said.

Exercise(From the prescribed prose Lesssons)

Rewrite the following sentence / sentences using punctuation marks where necessary.

Question 1.
aristotle could have aooided the mistake of thinking that women have fewer teeth than men by the simple device ot asking mrs aristotle to keep her mouth open while he counted
Answer:
Aristotle could have avoided the mistake of thinking that women have fewer teeth than men by the simple device of asking Mrs. Aristotle to keep her mouth open while he counted.

Question 2.
if someone maintains that two and two are five or that Iceland is on the equator you feel pity rather than anger unless you know so little of arithmetic or geography that his opinion shakes your own contrary conviction
Answer:
If someone maintains that two and two are five or that Iceland is on the equator, you feel pity rather than anger unless you know so little of arithmetic or geography that his opinion shakes your own contrary conviction.

Question 3.
When i was young I lived much outside my own country in france germany italy and the united states.
Answer:
When I was young, I lived much outside my own country in France, Germany, Italy, and the United States.

Question 4.
mahatma gandhi deplores railways and steam boats and machinery he would like to. undo the whole of the Industrial Revolution you may never have an opportunity of actually meeting anyone who holds this opinion because in western countries most people take advantage of modern techniques forgranted
Answer:
Mahatma Gandhi deplores railways and steamboats, and machinery; he would like to undo the whole of the Industrial Revolution. You may never have an opportunity of actually meeting anyone who holds this opinion because, in Western countries, most people take advantage of modem techniques for granted.

Question 5.
be very wary of opinions thatflatteryourselfesteem both men and women, nine times out of ten are firmly convinced of the superior excellence of their own sex
Answer:
Be very wary of opinions that flatter your self-streern. Both men and women, nine times out of ten, are firmly convinced of the superior excellence of their own sex.

Question 6.
from the earliest days there had been many notable women in India poets scholars capable administrators and leaders of religious movements
Answer:
From the earliest days there had been many notable women in India – poets, scholars, capable administrators and leaders of religious movements.

Question 7.
women all over india came forward defying all social taboos sacrificing physical comforts and denying the validity of all restrictions which had been enforced against them to take up every kind of work connected with national movement
Answer:
Women all over India came forward, defying all social taboos, sacrificing physical comforts, and denying the validity of all restrictions which had been enforced against them, to take up every kind of work connected with national movement.

Question 8.
It was a matter of surprise to the outside world that independent india should have appointed women to the highest posts so freely as members of the cabinet as governors of provinces as ambassadors and as leaders of delegations to international conferences for in an oriental country such as india women are presumed to be held in subjection and therefore all this seemed to be unnatural.
Answer:
It was a matter of surprise to the outside world that independent India should have appointed women to the highest posts so freely, as members of the Cabinet, as Governors ofProvinces, as Ambassadors and as leaders of delegations to international conferences, for in an oriental country such as India, women are presumed to be held in subjection and therefore all this seemed to be unnatural.

Question 9.
originally he seems to have been uncertain of the response or at least of the kind of work that women could do in the national movement for t hough he was a passionate believer in the equality of women he seems to have been doubtful whether the women of india
Answer:
Originally, he seems to have been uncertain of the response, or at least of the kind of work that women could do in the national movement, for though he was a passionate believer in the equality of women, he seems to have been doubtful whether the women of India….

Question 10.
what the gandhian movement did was to release women from the social bandages that custom had imposed and conservatism had upheld
Answer:
What the Gandhian movement did was to release women from the social bond ages that custom had imposed and conservatism had upheld.

Question 11.
after the citys rain fed potholes the transition to smooth roads within the campus of the thiagarajar college of engineering is more than a treat the man behind the tar topped tracks is known as Madurai’s Plastic Road Man.
Answer:
After the city’s rain-fed potholes, the transition to smooth roads within the campus of the Thiagarajar College of Engineering (fCE) is more than a treat. T.he man behind the tar-topped tracks is known as Madurai’s Plastic Road Man.

Question 12.
The day we met Dr Vasudevan he was waving a special gazette notification of the ministry of environment & forests dated 4th February 2011 directing all municipal authorities across the country to encourage use of plastic waste by adopting suitable technology” such as in road construction.
Answer:
The day we met Dr. Vasudevan, he was waving a special gazette notification of the Ministry of Environment & Forests, dated 4th February, 2011, directing all municipal authorities across the country to “encourage the use of plastic waste by adopting suitable technology such as in road construction…”

Question 13.
dr kalams words proved prophetic with full support from the college correspondent Dr.oasudeoan laid the first 60 feet long plastic road within the campus
Answer:
Dr. Kalam’s words proved prophetic. With full support from the College Correspondent, Dr. Vasudevan laid the first 60 feet long plastic road within the campus.

Question 14.
the jamshedpur utilities and services company a tata enterprise approached Dr. Vasudevan last november for using plastic waste in laying roads in jamshedpur.
Answer:
The Jamshedpur Utilities and Services Company, a Tata enterprise approached Dr. Vasudevan for using plastic in laying roads in Jamshedpur,

Question 15.
the view of this world which india has taken is summed up in one compound Sanskrit word sacchidananda the meaning is that reality which is essentially one has three phases.
Answer:
The view of this world which India has taken is summed up in one compound Sanskrit word, Sacchidananda. The meaning is that Reality, which is essentially one, has three phases.

Question 16.
The first is sat it is the simple fact that things are the fact which relates us to all things through the relationship of common. existence The second is chit it is the fact that we know which relates us to all things, through the relation ship of knowledge the third is ananda it is the fact that we enjoy which unites us with all things through the relationship of love.
Answer:
The first is sat: it is the simple fact that things are, the fact which relates us to all things through the relationship of common existence. The second is chit: it is the fact that we know, which relates us to all things through the relationship of knowledge. The third is ananda: it is the fact that we enjoy, which unites us with all things through the relationship of love.

Question 17.
In kalidasas drama shakuntala the hermitage which dominates the play overshadowing the kings palace has the same idea running through it – the
recognition of the kinship of man with conscious and unconscious creation alike
Answer:
In Kalidasa’s drama, Stiakuntala, the hermitage, which dominates the play, ” overshadowing the king’s palace, has the same idea running through it – – the recognition of the kinship of man with conscious and unconscious creation alike.

Question 18.
in the west era dramas human characters drown our attention in the vortex of their passions nature occasionally peeps out but she is almost always a trespasser who has to offer excuses or bow apologetically and depart
Answer:
In the Western dramas, human characters drown our attention in the vortex of their passions. Nature occasionally peeps out, but she is almost always a trespasser, who has to offer excuses, or bow apologetically and depart.

Question 19.
but in all our dramas which still retain their fame such as Mrit- Shakatika Shakuntala Uttara ramachatita nature stands on her own right proving that she has her great function to impart, the peace of the eternal to human emotions
Answer:
But in all our dramas which still retain their fame, such as Mrit-Shakatika, Shakuntala, Uttara-Ramacharita, Nature stands on her own right, proving that she has her great function, to impart the peace of the eternal to human emotions.

Question 20.
yes mrs moore (opens door and talks loudly) come right in
Answer:
Yes, Mrs. Moore! (Opens door and talks lougly.) Come right in.

Question 21.
yes it was months and months before he had any sort of a job i worried a bit you know i was afraid he would get so discouraged he would
Answer:
Yes, it was months and months before he had any sort of a job. I worried a bit, you know, 1 was afraid he would get so discouraged…. he would….

Question 22.
no firm is going to smile and say forget it my boy no they dont do things that way these days
Answer:
No firm is going to smile .and say, ‘Forget it, my boy’ no, they don’t do things that way these days.

Question 23.
mr van king had brought it down to his office intending to have it reset – and put it in his office safe and forgot it imagine forgetting a diamond heirLoom worth a fabuLous fortune
Answer:
Mr Van King had broughtit down to his office, intending to have it re-set – – and put it in his office safe, and -forgot it! Imagine forgetting a diamond heirloom worth a fabulous fortune!

Question 24.
dont worry not a souL saw us wait ill get it (10)
Answer:
Don’t worry. Not a soul saw us! Wait, I’ll get it.

Question 25.
are you surejim that you put itthere oh oh… i see (laughs) you have it
Answer:
Are you sure Jim, that you put it there?… Oh, oh…. I see… You have it!

Question 26.
yes but you keep out of this youll never get the diamond jim poor Larry wiLson was sentenced to ten years in jail today… I” stealing.
Answer:
Yes! But you keep out of this, you’ll never get the diamond! Jim, poor Larry Wilson was sentenced to ten years in jail today… stealing.

Question 27.
JIM: ma you dont think i stoLe that diamond
MA: what eLse am i to think
Answer:
Jim: Ma! You don’t think I stole that diamond?
Ma: What else am I to think?

Question 28.
just what are you going to do with the diamond no jim keep quiet a moment mrs ryan what are you going to do with that diamond
Answer:
Just what are you going to do with the diamond? No. Jim, keep quiet a moment. Mrs. Ryan, what are you going to do with that diamond?

Question 29.
I promise but jitn i i (tries not to cry) ill never forget this night never(J0)
Answer:
I promise. But Jim, I…. I…. (tries not to cry) I’ll never forget this night, never.

Question 30.
a) King dilipa with Queen sudakshina has entered upon the the life of the forest the great monarch is busy tending the cattle of the hermitage [Model Question Paper]
Answer:
King Dilipa, with Queen Sudakshina, has entered upon the life of the forest. The great monarch is busy tending the cattle of the hermitage.

b) Sum it said where are you going [Model Question Paper] .
Answer:
Sumit said, “Where are you going ?”

Question 31.
It is more difficult to deal with the self esteem of man as a man because we cannot argue out the matter unth some non-human mind, the only way i know of dealing with this general human conceit is to remind ourselves that man is a brief episode in the life of a small planet in a little corner of the universe and that for aught we know other parts of the cosmos may contain beings as superior to ourselves as we are to jellyfish. [REVISION TEST-I]
Answer:
It is more difficult to deal with the self-esteem of man as a man because we cannot argue out the matter with some non- human mind. The only way I know of dealing with this general human conceit is to remind ourselves that man is a brief episode in the life of a small planet in a little corner of the universe and that, for aught we know, other parts of the cosmos may contain beings as superior to ourselves as we are to jellyfish.

Question 32.
The brahmo samaj led the movement for emancipation the ancient rules of purdah were broken and brahmo women moved freely in society: but this was but a false dawn as it was far in advance of popular opinion. [REVISION TEST-II]
Answer:
The Brahmo Samaj led the movement for emancipation. The ancient rules of purdah – were broken and Brahmo women moved freely in society: but this was but a false dawn as it was far in advance of popular opinion.

Question 33.
after a decades hard work and persistent efforts’ his simple invention of a technology ” to use – plastic waste to lay roads patented by TCE finally got a shot in the arm last month with the centre approving its wider application. [REVISION TEST-III]
Answer:
After a decade’s hard work and persistent efforts, his invention of a simple technology to use plastic waste to lay roads, patented by TCE, finally got a shot in the arm with the Centre approving its wider application.

Question 34.
a) King dilipa with Queen sudakshina has entered upon the the life of the forest the great monarch is busy tending the cattle of the hermitage [Model Question Paper]
Answer:
King Dilipa, with Queen Sudakshina, has entered upon the life of the forest. The great monarch is busy tending the cattle of the hermitage.

b) Sum it said where are you going [Model Question Paper]
Answer:
Sumit said, “Where are you going ?”

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Measures of Dispersion Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Measures of Dispersion Important Questions Very Short Answer Type

Question 1.
Find the mean deviation from the mean of the discrete data 6, 7, 10, 12, 13, 4, 12, 16. [TS – May 2016, Mar. ’14]
Solution:
Given data is 6, 7, 10, 12, 13, 4, 12, 16
The arithmetic mean of the given data is
\(\overline{\mathrm{x}}=\frac{\text { Sum of the observations }}{\text { No. of observations }}\)
= \(\frac{\Sigma x}{n}=\frac{6+7+10+12+13+4+12+16}{8}\)
\(\bar{x}=\frac{80}{8}\) = 10
The deviations of the respective observations from the mean are 6 – 10, 7 – 10, 10 – 10, 12 – 10, 13 – 10, 4 – 10, 12 – 10, 16 – 10 = – 4, – 3, 0, 2, 3, – 6, 2, 6
The absolute values of the deviations are 4, 3, 0, 2, 3, 6, 2, 6.
∴ The required mean deviation about mean is
M.D = \(=\sum_{i=1}^n \frac{\left|x_i-\bar{x}\right|}{n}=\sum_{i=1}^8 \frac{\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{4+3+0+2+3+6+2+6}{8}\)
= \(\frac{26}{8}=\frac{13}{4}\) = 3.25.

Question 2.
Find the mean deviation about mean for the data 38, 70, 48, 40, 42, 55, 63, 46, 54, 44. [AP – May 2015].
Solution:
Given data is 38, 70, 48, 40, 42, 35, 63, 46, 54, 44
The arithmetic mean of the given data is
\(\overline{\mathrm{x}}=\frac{\text { Sum of the observations }}{\text { No. of observations }}\)
= \(\frac{\Sigma \mathrm{x}}{\mathrm{n}}\)
= \(\frac{38+70+48+40+42+55+63+46+54+44}{10}\)
= \(\frac{500}{10}\) = 50
The deviations of the respective observations from the mean are 38 – 50, 70 – 50, 48 – 50, 40 – 50, 42 – 50, 55 – 50, 63 – 50, 46 – 50, 54 – 50, 44 – 50 = – 12, 20, – 2, – 10, – 8, 5, 13, – 4, 4, – 6
The absolute values of the deviations are 12, 20, 2, 10,8, 5, 13, 4, 4, 6.
∴ The required mean deviation about mean is
M.D. = \(\sum_{i=1}^n \frac{\left|x_i-\bar{x}\right|}{n}=\sum_{i=1}^{10} \frac{\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{12+20+2+10+8+5+13+4+4+6}{10}\)
= \(\frac{84}{10}\) = 8.4.

Question 3.
Find the mean deviation about mean for the data 3, 6, 10, 4, 9, 10.
[AP – Mar. ’18, May ’16; TS – Mar. ’17; May ’14]
Solution:
Given data is 3, 6, 10, 4, 9, 10
The arithmetic mean of the given data is
\(\overline{\mathrm{x}}=\frac{\text { Sum of the observations }}{\text { No. of observations }}\)
= \(\frac{\Sigma \mathrm{x}}{\mathrm{n}}=\frac{3+6+10+4+9+10}{6}\)
= \(\frac{42}{6}\) = 7
The deviations of the respective observations from the mean are 3 – 7, 6 – 7, 10 – 7, 4 – 7, 9 – 7, 10 – 7
= – 4, – 1, 3, – 3, 2, 3
The absolute values of the deviations are 4, 1, 3, 3, 2, 3.
The required mean deviation about mean is
MD = \(\sum_{i=1}^n \frac{\left|x_i-\bar{x}\right|}{n}=\sum_{i=1}^6 \frac{\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{4+1+3+3+2+3}{6}\)
= \(\frac{16}{6}\) = 2.666 = 2.7.

Question 4.
Find the mean deviation about median for the data 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17. [AP – Mar. 2016]
Sol.
Given data is 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
The ascending order of the observations in the given data is
10, 11, 11, 12, 13,13, 16,16, 17, 17, 18
Median of one given data is M = 13.
The deviations of the respective observations from the median i.e., x_i – M are
13 – 13, 17 – 13, 16 – 13, 11 – 13, 13 – 13, 10 – 13, 16 – 13, 11 – 13, 18 – 13, 12 – 13, 17 – 13
= 0, 4.3, – 2, 0, – 3, 3, – 2, 5, – 1, 4
The absolute values of the deviations are
0, 4, 3, 2, 0, 3, 3, 2, 5, 14.
∴ The required mean deviation about median is
M.D = \(\sum_{i=1}^n \frac{\left|x_i-M\right|}{n}=\sum_{i=1}^{11} \frac{\left|x_i-M\right|}{n}\)
= \(\frac{0+4+3+2+0+3+3+2+5+1+4}{11}\)
= \(\frac{27}{11}\) = 2.45.

Question 5.
Find the mean deviation about median for the data 4,6, 9, 3, 10,13,2. [TS – Mar. ‘18, ’15, May ’15; AP-Mar. ‘19, ’17]
Solution:
Given data is 4, 6, 9, 3, 10, 13, 2
The ascending order of the observations in given data is
2, 3, 4. 6, 9, 10, 13
Median of given data is M = 6
The deviations of the respective observations from the median i.e., x_i – M are
2 – 6, 3 – 6, 4 – 6, 6 – 6, 9 – 6, 10 – 6, 13 – 6 = – 4, – 3, – 2, 0, 3, 4, 7
The absolute values of the deviations are 4, 3, 2, 0, 3, 4, 7.
∴ The required mean deviation about median is
M.D = \(\sum_{i=1}^n \frac{\left|x_i-M\right|}{n}=\sum_{i=1}^7 \frac{\left|x_i-M\right|}{n}\)
= \(\frac{4+3+2+0+3+4+7}{7}\)
= \(\frac{23}{7}\) = 3.29.

Question 6.
Find the mean deviation about median for the data 6, 7, 10, 12, 13, 4, 12, 16.
Solution:
Given data is 6, 7, 10, 12, 13, 4, 12, 16
The ascending order of the observations in the given data is
4, 6, 7, 10, 12, 12, 13, 16
Median of one given data is M = \(\frac{10+12}{2}\)
= \(\frac{22}{2}\) = 11
The deviations of the respective observations from the median i.e., x_i – M are
6 – 11, 7 – 11, 10 – 11, 12 – 11, 13 – 11, 4 – 11, 12 – 11, 16 – 11 = – 5, – 4,- 1, 1, 2, – 7, 1, 5
The absolute values of the deviations are 5, 4, 1, 1, 2, 7, 1, 5.
∴ The required mean deviation about median is
M.D = \(\sum_{i=1}^n \frac{\left|x_i-M\right|}{n}=\sum_{i=1}^8 \frac{\left|x_i-M\right|}{n}\)
= \(\frac{5+4+1+1+2+7+1+5}{8}\)
= \(\frac{26}{8}=\frac{13}{4}\) = 3.25.

Question 7.
Find the mean deviation about mean for the following data. [AP – Mar. 2019]

Solution:
We can form the following table for the given data:

Here, Σf_i = 40
Σf_ix_i = 320
∴ Mean of the given data is \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{320}{40}\) = 8
From the table, Σf_i |x_i – \(\overline{\mathrm{x}}\)| = 140
Mean deviation about mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\widetilde{\mathrm{x}}\right|}{\mathrm{N}}=\frac{140}{40}\) = 3.5.

Question 8.
Find the mean deviation about mean for the following data.

Solution:
We can form the following table for the given data:

Here, N = Σf_i = 45
Σf_ix_i = 534
∴ Mean of the given data is \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{534}{45}\) = 11.8
From the table, Σf_i |x_i – x| = 33.0
Mean deviation about mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|}{\mathrm{N}}\)
= \(\frac{33}{45}\) = 0.73.

Question 9.
Find the mean deviation about mean for the following data.

Solution:

Here, N = Σf_i = 80
Σf_ix_i = 4000
∴ Mean of the given data is \(\bar{x}=\frac{\Sigma f_i x_i}{N}=\frac{4000}{80}\) = 50
From the table, Σf_i |x_i – \(\bar{x}\)| = 1280
Mean deviation about mean \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|}{\mathrm{N}}=\frac{1280}{80}\) = 16.

Question 10.
Find the mean deviation about median for the following data. [May ‘14]

Solution:
We can form the following table for the given data:

Median = \(\frac{N^{\text {th }}}{2}\) observation
= \(\frac{30}{2}\) = 15th observation = 13.
Mean deviation about median, M.D = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{N}}=\frac{149}{30}\) = 4.966 = 4.97.

Question 11.
Find the mean deviation about median for the following data.

Solution:
We can form the following table for the given data:

Median = \(\frac{N^{\text {th }}}{2}\) observation
= \(\frac{26}{2}\) = 13th observation = 7.
Mean deviation about median, M.D = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{N}}=\frac{84}{26}\) = 3.23.

Question 12.
Find the variance and standard deviation for the discrete data: 5, 12, 3, 18, 6, 8, 2, 10. [AP – Mar. 2015; TS – Mar. 2019]
Solution:
Given data is 5, 12, 3, 18. 6, 8, 2, 10
The mean of the given data is \(\overline{\mathrm{x}}=\frac{\sum \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}\)
= \(\frac{5+12+3+18+6+8+2+10}{8}=\frac{64}{8}\) = 8
To find the variance we construct the following table:

Here, Σ(x_i – \(\bar{x}\)) = 194
∴ Variance, \(\sigma^2=\frac{1}{n} \sum_{i=1}^8\left(x_i-\bar{x}\right)^2=\frac{194}{8}\) = 24.25
Standard deviation, a = \(\sqrt{\text { variance }}\)
= \(\sqrt{24.25}\)= 4.92 (approxi.)

Question 13.
Find the variance for the discrete data : 6, 7, 10, 12, 13, 4, 8, 12.
Solution:
Given data is 6, 7, 10, 12, 13, 4, 8, 12
The mean of the given data is \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}\)
= \(\frac{6+7+10+12+13+4+8+12}{8}=\frac{72}{8}\) = 9
To find the variance we construct the following table:

Here, Σ(x_i – \(\bar{x}\))² = 74
∴ variance, \(\sigma^2=\frac{1}{n} \sum_{\mathrm{i}=1}^8\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^2=\frac{74}{8}\) = 9.25.

Question 14.
Find the variance for the discrete data: 350, 361, 370, 373, 376, 379, 385, 387, 394, 395.
Solution:
Given data is 350, 361, 370, 373, 376, 379, 385, 387, 394, 395
The mean of the given data is
\(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}=\frac{350+361+370+373+376+379+385+387+394+395}{10}=\frac{3770}{10}\) = 377
To find the variance we construct the following table:

Here, Σ(x_i – x) = 1832
∴ Variance \(\frac{1}{n} \sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2\)
= \(\frac{1832}{10}\) = 183.2.

Question 15.
The variance of 20 observations is 5. If each of the observations is multiplied by 2. Find the variance of the resulting observations. [Board Paper]
Solution:
Let the given observations be x₁, x₂, x₃, …………… x₂₀
Mean, \(\bar{x}=\sum_{i=1}^{20} x_i \times \frac{1}{n}\)
Given that, n = 20 and variance = 5
\(\frac{1}{n} \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\) = 5
\(\frac{1}{20} \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\) = 5
\(\sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\) = 100
If each observation is multiplied by 2 then the new observations are 2x₁, 2x₂, 2x₃, …………….., 2x₂₀
i.e., y₁, y₂, y₃, ……………, y₂₀
y_i = 2x₁
The mean of the new observations
\(\overline{\mathrm{y}}=\frac{1}{\mathrm{n}} \sum_{\mathrm{i}=1}^{20} \mathrm{y}_{\mathrm{i}}\)
= \(\frac{1}{20} \sum_{\mathrm{i}=1}^{20} 2 \mathrm{x}_{\mathrm{i}}=2\left[\frac{1}{20} \sum_{\mathrm{i}=1}^{20} \mathrm{x}_{\mathrm{i}}\right]=2 \overline{\mathrm{x}}\)
⇒ \(\overline{\mathrm{x}}=\frac{\overline{\mathrm{y}}}{2}\)
Substituting the values of \(\bar{x}_{\mathbf{i}}\) and \(\overline{\mathbf{x}}\) in (1), we get
\(\sum_{\mathrm{i}=1}^{20}\left(\frac{\mathrm{y}_{\mathrm{i}}}{2}-\frac{\overline{\mathrm{y}}}{2}\right)^2\) = 100
\(\frac{1}{4} \sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2\) = 100
\(\sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2\) = 400
∴ The variance of the new observations = \(\frac{1}{n} \sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2\)
= \(\frac{1}{20}\) (400) = 20 = 2² . 5

Note:
If each observation is multiplied by a constant ‘k’, the variance of the resulting observation becomes k² times the original variance.

Question 16.
If each of the observation x₁, x₂, ………………, x_n is increased by k, where k is a positive or negative number, then show that the variance remains unchanged.
Solution:
Let, \(\overline{\mathrm{x}}\) be the mean of x₁, x₂, …………….., x_n then
variance, \(\sigma^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2\)
\(\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i\)
1f k is added to each observat ion then the new observations will be x₁ + k₁, x₂ + k, x₃ + k, ………………….. x_n + k i.e., y₁, y₂, y₃, …………., y_n.
Now, y_i = x_i+ k,
For i = 1, 2, 3 …………… n
Let \(\overline{\mathrm{y}}\) be the mean of the new observations then
\(\bar{y}=\frac{1}{n} \sum_{i=1}^n y_i=\frac{1}{n} \sum_{i=1}^n x_i+k\)
= \(\frac{1}{n} \sum_{i=1}^n x_i+k=\frac{1}{n} \sum_{i=1}^n x_i+\frac{1}{n} \sum_{i=1}^n k\)
= \(\overline{\mathrm{x}}+\frac{1}{\mathrm{n}} \mathrm{nk}=\overline{\mathrm{x}}+\mathrm{k}\).

Variance of the new observations
\(\sigma_y^2=\frac{1}{n} \sum_{i=1}^n\left(y_i-\bar{y}\right)^2\)
= \(\frac{1}{n} \sum_{i=1}^n\left(x_i+k-\bar{x}-k\right)^2\)
= \(\frac{1}{n} \sum_{i=1}^n\left(x_i-\vec{x}\right)^2\) = σ²
∴ The variance of new observations is same that of the original observations.

Note :
If each observation is added by a number ‘a’ then the variance remains unchanged.

Question 17.
The coefficient of variation of two distributions are 60 and 70 and their standard deviations are 21 and 16 respectively. Find their arithmetic means.
Solution:
I distribution:
Let \(\overline{\mathbf{x}}_1\) and σ₁ be the mean and standard deviation of I distribution.
Given that, Coefficient of variation, C.V = 60
Standard deviation, σ₁ = 21
∴ CV = \(\frac{\sigma_1}{x_1}\) × 100
60 = \(\frac{21}{\overline{\mathrm{x}}_1}\) × 100
\(\overline{\mathrm{x}}_1=\frac{21}{60} \times 100\)
\(\overline{\mathrm{x}}_1\) = 35

II distribution:
Let \(\overline{\mathrm{x}}_2\) and σ₂ be the mean and standard deviation of II distribution.
Given that, C.V = 70
Standard deviation, σ₂ = 16
∴ CV = \(\frac{\sigma_2}{\overline{\mathrm{x}}_2}\) × 100
70 = \(\frac{16}{\bar{x}_2}\) × 100
\(\overline{\mathrm{x}}_2\) = \(\frac{16}{70}\) × 100
= \(\frac{160}{7}\) = 22.85.

Question 18.
The mean of 5 observations is 4.4. Their variance is 8.24. If three of the observations are 1, 2 and 6, find the other two observations.
Solution:
Let, the remaining 2 observations be x, y.
∴ The series is 1, 2, 6, x, y.
Given that, mean, \(\overline{\mathbf{x}}\) = 4.4
\(\frac{1+2+6+\mathrm{x}+\mathrm{y}}{5}\) = 4.4
9 + x + y = 22
x + y = 13 ……………….(1)
Given that, σ² = 8.24
\(\frac{\sum_{i=1}^n x_i^2}{n}-(\bar{x})^2\) = 8.24
\(\frac{1+4+36+x^2+y^2}{5}\) = (4.4)² = 8.24
\(\frac{41+x^2+y^2}{5}\) = 8.24 + 19,36
\(\frac{41+x^2+y^2}{5}\) = 27.6
41 + x² + y² = 138
x² + y² = 138 – 41
x² + y² = 97 ……………..(2)
From(1), y = 13 – x
From (2), x² + (13 – x)² = 97
x² + 169 + x² – 26x – 97 = 0
2x² – 26x + 72 = 0
x² – 13x + 36 = 0
x² – 9x – 4x + 36 0
x(x – 9) – 4 (x – 9) = 0
(x – 9) (x – 4) = 0
x = 9 or x = 4
If x = 4 then y = 13 – 4 = 9
If x = 9 then y = 13 – 9 = 4
∴ The remaining two observations are 4 and 9.

Question 19.
The arithmetic mean and standard deviation of a set of 9 items are 43 and 5 respectively. If an item of value 63 is added to that set, find the new mean and standard deviation of 10 item set given.
Solution:
Given that, number of items, n = 9
Mean, \(\overline{\mathrm{x}}\) = 43
\(\frac{1}{n} \sum_{i=1}^9 x_i\)= 43
\(\frac{1}{9} \sum_{i=1}^9 x_i\) = 43
\(\sum_{i=1}^9 x_i\) = 387
Now, given 10th item = 63
∴ Sum of the 10 observations \(\sum_{i=1}^9 x_i\) + 63 = 387 + 63 = 450
The mean of the new observations \(\frac{1}{n} \sum_{i=1}^{10} x_i\) = \(\frac{1}{10}\) (450) =
Given that, standard deviation, σ = 5
σ² = 25
\(\frac{1}{n} \sum_{i=1}^9 x_i^2-(\bar{x})^2\) = 25
\(\frac{1}{9} \sum_{i=1}^9 x_i^2-(43)^2\) = 25
\(\frac{1}{9} \sum_{i=1}^9 x_i^2\) – x = 25 + (43)²
= 25 + 1849 = 1874
\(\frac{1}{9} \sum_{i=1}^9 x_i^2\) = 1874 × 9 = 16866
Given that, 10th item = 63
∴ \(\frac{1}{9} \sum_{i=1}^10 x_i^2\) = \(\frac{1}{9} \sum_{i=1}^9 x_i^2\) + (63)²
= 16866 + 3969 = 20835
The variance of new observations = \(\frac{1}{n} \sum_{i=1}^{10} x_i^2-\bar{x}^2\)
= \(\frac{1}{10}\) (20835) – (45)²
= 2083.5 – 2025 = 58.5
∴ Standard deviation = √58.5 = 7.64.

Telangana TSBIE TS Inter 2nd Year Chemistry Study Material 4th Lesson Surface Chemistry Textbook Questions and Answers.

TS Inter 2nd Year Chemistry Study Material 4th Lesson Surface Chemistry

Very Short Answer Questions (2 Marks)

Question 1.
What is an interface ? Give one example.
Answer:
The boundary that separate the two bulk phases is called surface or interface, e.g. Solid-liquid or solid/liquid.

Question 2.
What is adsorption ? Give one example.
Answer:
Accumulation of molecular species at the surface rather than in bulk of a solid or liquid is known as adsorption.
Eg : Aqueous solution of raw sugar when passed over animal charcoal becomes colourless due to the removal of colouring matter of sugar by adsorption on animal charcoal.

Question 3.
What is absorption? Give one example.
Answer:
Absorption is a process of distribution of the molecules of a substance uniformly in the bulk of another substance e.g: when a sponge or chalk piece is dipped in water, water is distributed throughout the sponge or chalk piece.

Question 4.
Distinguish between adsorption and absorption. Give one example.
Answer:

Eg : when a chalk piece is dipped in ink the colouring matter is retained only on the surface due to adsorption while the solvent of the ink goes deeper into the stick.

Question 5.
The moist air becomes dry in the presence of silica gel. Give reason for this.
Answer:
The moist air becomes dry in the presence of silica gel because water molecules get adsorbed on the surface of silica gel.

Question 6.
Methylene blue solution when shaken with animal charcoal gives a colourless filtrate on filtration. Give the reason.
Answer:
When animal charcoal is added to a solu¬tion of methylene blue solution and shaken the molecules of methylene blue are adsorbed on the surface of animal charcoal and are removed from solution. So the filtrate becomes colourless.

Question 7.
A small amount of silica gel and a small amount of anhydrous calcium chloride are placed separately in two corners of a vessel containing water vapour. What phenomena will occur ?
Answer:
Water vapour is absorbed by anhydrous calcium chloride but it is adsorbed on silica gel.

Question 8.
What is desorption ?
Answer:
The process of removal of an adsorbed substance from the surface is called desorption.

Question 9.
What is sorption ?
Answer:
If adsorption and absorption takes place simultaneously it is known as sorption.

Question 10.
Amongst adsorption, absorption which is a surface phenomena and why ?
Answer:
Adsorption is surface phenomenon. In this process molecular species accumulates at the surface rather than in the bulk.

Question 11.
What is the name given to the phenomenon when both adsorption and absorption take place together ?
Answer:
The name sorption is given to the phenomenon when both adsorption and absorption take place together.

Question 12.
Chalk stick dipped in an ink solution exhibits the following.
a) The surface of the stick retains the colour of the ink.
b) Breaking the chalk stick, it is found still white from inside.
Explain the above observations.
Answer:
a) The colouring matter is retained only on the surface due to adsorption. So the surface of the stick retains the colour.
b) Only the solvent of the ink goes deeper into the stick but not colouring matter. So it is still white inside.

Question 13.
What are the factors which influence the adsorption of a gas on a solid ?
Answer:

1. Nature of the gas
2. Nature of the adsorbent
3. Specific area of the solid
4. Pressure of the gas
5. Temperature
6. Activation of adsorbent

Question 14.
Why is adsorption always exothermic ?
Answer:
During adsorption there is always a decrease in residual forces of the surface i.e., there is decrease in surface energy which appears as heat. So adsorption is always exothermic.

Question 15.
Give the signs of AH and AS when ammonia gas gets adsorbed on charcoal.
Answer:
When ammonia gas is adsorbed on charcoal heat is liberated. So AH of adsorption is always negative (∆H = -Ve). When ammonia gas is adsorbed on charcoal the freedom of its molecules become restricted. So entropy decreases (∆S = -Ve).

Question 16.
How many types of adsorption are known? What are they?
Answer:
There are mainly two types of adsorption.
a) Physical adsorption or physisorption.
b) Chemical adsorption or chemisorption.

Question 17.
What types of forces are involved in physisorption of a gas on solid ?
Answer:
Only weak van der Waal’s forces are involved in physisorption of a gas on solid.

Question 18.
What type of interaction occuring between gas molecules and a solid surface is responsible for chemisorption of the gas on solid?
Answer:
Chemical bonds occur between gas molecules and a solid surface during chemisorption of the gas on solid. The chemical bonds may be ionic or covalent in nature.

Question 19.
Why chemisorption is called activated adsorption ?
Answer:
The chemical adsorption involves a high energy of activation. So it is called activated adsorption.

Question 20.
What is the difference between physisorption and chemisorption ?
Answer:
Physisorption is due to weak van der Waal’s forces between the gas molecules and the solid surface. Chemisorption is due to chemical bonds such as covalent or ionic between gas molecules and solid surface.

Question 21.
Out of physisorption and chemisorption, which can be reversed ?
Answer:
Physisorption can be reversed. By increasing the pressure more gas is adsorbed and by decreasing the pressure the adsorbed gas is removed. By decreasing the temperature more gas is adsorbed while by increasing the temperature the adsorbed gas is removed.

Question 22.
How is adsorption of a gas related to its critical temperature ? ,
Answer:
Easily liquefiable gases which have high critical temperatures are readily adsorbed since the van der Waal’s forces are stronger near the critical temperatures.

Question 23.
The critical temperature of SO₂ is 630K and that of CH₄ is 190K. Which one is adsorbed easily on actived charcoal ?
Answer:
Activated charcoal adsorbs more SO₂ since it has more critical temperature than methane.

Question 24.
Easily liquifiable gases are readily adsorbed on solids. Why ?
Answer:
Easily liquifiable gases are readily adsorbed on solids because van der Waal’s forces are stronger near the critical temperature.

Question 25.
Amongst SO₂, H₂ which will be adsorbed more readily on the surface of charcoal and why ?
Answer:
SO₂ is adsorbed more readily on the surface of charcoal compared to H₂ because its critical temperature is more, as van der Waal’s forces are stronger near critical temperature.

Question 26.
Compare the enthalpy of adsorption for physisorption and chemisorption.
Answer:
The enthalpy of adsorption is low in physisorption (20 – 40 kJ mol^-1) but in chemisorption it is high (80 – 240 kJ mol^-1).

Question 27.
What is the magnitude of enthalpy of physical adsorption ? Give reason for this magnitude.
Answer:
The magnitude of enthalpy of physical adsorption is low i.e., about 20 -40 kJ mol^-1. This is because the attraction between gas molecules and solid surface is only due to weak van der Waal’s forces.

Question 28.
What is the magnitude of enthalpy of chemisorption ? Give reason for this magnitude.
Answer:
The enthalpy of chemisorption is high 80 – 240 KJ mol^-1 as it involves chemical bond formation.

Question 29.
Give any two applications of adsorption.
Answer:

1. Gas masks containing activated charcoal or mixture of adsorbents used by coal miners adsorb poisonous gases during breathing.
2. Due to the difference in degree of adsorption of gases by charcoal a mixture of noble gases can be separated by adsorption on coconut charcoal at different temperatures.

Question 30.
Why physisorption suffers from lack of specificity ?
Answer:
Since van der Waal’s forces are universal, a given surface of an adsorbent does not show any preference for a particular gas. So physisorption suffers from lack of specificity.

Question 31.
What is an adsorption isotherm ? Write the equation of Freundlich adsorption isotherm.
Answer:
The variation in the amount of gas adsorbed by the adsorbent with pressure at constant temperature can be shown as a curve termed as adsorption isotherm.
Freundlich adsorption isotherm is
\(\frac{\mathrm{x}}{\mathrm{m}}\) = k . p^1/n (n > 1) m
where x is the mass of the gas adsorbed on mass ‘m’ of the adsorbent at pressure p. k and n are constants.

Question 32.
In the Freundlich adsorption isotherm mention the conditions under which following graph will be true ?

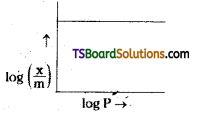
Answer:
When \(\frac{\mathrm{1}}{\mathrm{n}}\) = 0 in Freundlich adsorption isontherm, \(\frac{\mathrm{x}}{\mathrm{m}}\) = constant, the adsorption is m independent of pressure.

Question 33.
What role does adsorption play in heterogeneous catalysis ?
Answer:
Adsorption of reactants on solid surface of the catalysts increase the rate of reaction. There are many gaseous reactions of industrial importance involving use of solid catalysts.

Question 34.
What is the role of MnO₂ in the preparation of O₂ from KClO₃ ?
Answer:
In the preparation of O₂ from KClO₃, MnO₂ acts as catalyst and the decomposition of KClO₃ takes place at considerably low temperatures.

Question 35.
Define “promoters” and “poisons” in the phenomenon of catalysis ?
Answer:
Promoters are the substances that enhances the activity of catalyst. Poisons are the substances which decrease the catalytic activity of a catalyst.

Question 36.
What is homogeneous catalysis ? How is different from heterogeneous catalysis ?
Answer:
If the reactants and the catalysts are in the same phase, the process is said to be homogeneous catalysis. In heterogeneous catalysis the reactants and catalysts are in different phases.

Question 37.
Give two examples for homogeneous catalytic reactions.
Answer:
1) Oxidation of SO₂ to SO₃ with O₂ in the presence of oxides of N₂ as catalyst in the lead chamber process.
2SO₂(g) + O₂ (g) 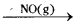> SO₃ (g)
Reactants and catalysts are gases

2) Acid catalysed hydrolysis of ester
CH₃ COOC₂H₅(l) + H₂O 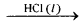CH₃COOH(aq) + C₂H₅ – OH(aq)
Reactants and catalysts are liquids

Question 38.
Give two examples for heterogeneous catalysis.
Answer:
1) Oxidation of sulphur dioxide into sulphur trioxide in the presence of Pt
2 SO₂(g) + O₂(g) 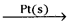2SO₃
Reactants are gases while the catalyst Pt is solid.

2) Manufacture of ammonia by Haber’s process involves the combination of N₂ and H₂ in the presence of iron powder.
N₂(g) + 3H₂(g) 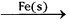2NH₃ (g)
Reactants are gases catalyst is solid.

Question 39.
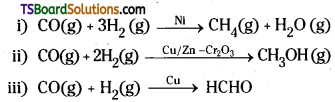
Give two examples which indicate the selectivity of heterogeneous catalysis.
Answer:
Selectivity of a catalyst is its ability to direct a reaction to from specific products.

Question 40.
Why zeolites are treated as shape selective catalysts ?
Answer:
Zeolites are good shape selective catalysts because of their honeycomb like structures.
The reactions taking place in zeolites depend upon the size and shape of reactant and product molecules as well as upon the pores and cavities of the zeolites.

Question 41.
Which zeolite catalyst is used to convert alcohols directly into gasoline ?
Answer:
ZSM-5 converts alcohols directly into gasoline (petrol) by dehydrating them to give a mixture of hydrocarbons.

Question 42.
What are enzymes ?What is their role in human body ?
Answer:
Enzymes are biochemical catalysts and the phenomenon of catalysis is called biochemical catalysis. These are complex nitrogenous organic compounds. They are protein molecules of higher molecular mass and form collidal solutions in water. Enzymes catalyse the life process in human body.

Question 43.
Can catalyst increase the yield of reaction?
Answer:
No. A catalyst will increase the rates of forward and backward reactions equally. So the yield of reaction do not change.

Question 44.
Name any two enzyme catalysed reactions. Give the reasons.
Answer:
i) Inversion of sugar: The enzyme invertase converts cane sugar into glucose and fructose.

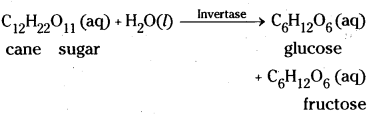
ii) Conversion of glucose into ethyl alcohol:
The enzyme zymase converts glucose into ethyl alcohol and carbon dioxide.

Question 45.
Name the enzymes obtained from soya-beans source.
Answer:
Urease which converts urea into ammonia and carbon dioxide.

Question 46.
Name the used in
a) Decomposition of urea into ammonia.
b) Conversion of proteins into peptides in stomach.
Answer:
a) Decomposition of urea of into ammonia is catalysed by urease.
NH₂CONH₂ (aq) → 2NH₃(g) + CO₂(g)
b) Pepsin converts proteins into peptides in stomach.

Question 47.
What enzymes are obtained from yeast ?
Answer:

1. Invertase which converts sugar into glucose and fructose,
2. Zymase which converts glucose into ethyl alcohol and carbondioxide.

Question 48.
At what ranges of temperature and pH, enzymes are active ?
Answer:
The optimum temperature range for enzymatic activity is 298 – 310K.
The pH range for enzymatic activity is 5-7.

Question 49.
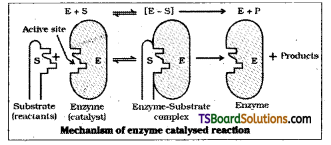
Represent diagramatically the mechanism of enzyme catalysis.
Answer:

Question 50.
Name any two industrially important heterogeneous catalytic reactions mentioning the catalysts used.
Answer:

1. In Haber’s process for the manufacture of ammonia, catalyst is iron powder mixed with molybdenum as promoter.
2. In Contact process for the manufacture of sulphuric acid, catalyst is platinised asbestos or vanadium pentoxide.

Question 51.
What is a colloidal solution ? How is it different from a true solution with respect to dispersed particle size and homogeneity ?
Answer:
A colloidal solution is a heterogeneous sys-tem in which one substance is dispersed (dispersed phase) as large particles in another substance (dispersion medium) Colloidal particles are larger than simple molecules of a true solution. Their size range between 1 and 1000 nm (10^-9 to 10^-6m).

Question 52.
Name the dispersed phase and dispersion medium in the following colloidal system i) fog ii) smoke iii) milk.
Answer:

1. Fog : Dispersed phase : Liquid
   Dispersed medium : Gas
2. Smoke : Dispersed phase : Solid
   Dispersed medium : Gas
3. Milk : Dispersed phase : Fat
   Dispersed medium : Water

Question 53.
What are lyophilic and lyophobic sols ? Give one example for each type.
Answer:
Colloids in which there is affinity between dispersed phase and dispersion medium are called lyophilic sols.
Ex : Starch sol, Gelatin. ,
Colloids in which there is very little affinity between the dispersion medium, and dispersed phase are called lyophobic sols.
Ex : Smoke, Gold sol.

Question 54.
Explain the terms with suitable examples.
i) aerosol
ii) hydrosol
Answer:
i) Aerosol is a colloidal system in which dispersed phase is liquid and dispersion medium is gas. e.g : fog, smoke.
ii) Hydrosol is the colloidal system that consists of water as dispersion medium. e.g : Starch in water, milk.

Question 55.
Explain why lyophilic colloids are relatively more stable than lyophobic colloids.
Answer:
Lyophilic colloids are more stable than lyophobic colloids because lyophilic colloids are extensively solvated. The colloidal particles are covered by a sheath of the dispersion medium in which they are dispersed.

Question 56.
Give two examples of colloidal solutions of liquids dispersed in solid. What is the name given to colloidal solution ?
Answer:

1. Butter
2. Cheese
   Liquids dispersed in solid type colloids are named as gels.

Question 57.
What is the difference between multimolecular and macromolecular colloids ? Give one example for each.
Answer:
In multimolecular colloids large number of atoms or small molecules of the dispersed phase aggregate together to form species in the colloidal range. e.g.: Gold sol, sulphur sol.
In macromolecular colloids the size of individual macromolecules are in the colloidal range.
e.g.: Starch, proteins etc.

Question 58.
What are micelles ? Give one example.
Answer:
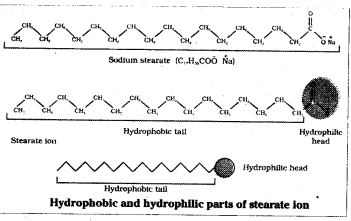
The substances which behave as electrolytes at low concentration but at higher concentrations exhibit colloidal behaviour due to formation of aggregates are called micelles and the colloids formed are called associated colloids. They contain a hydrophobic long hydrocarbon chain as one end and a hydrophilic polar group as another end. e.g.: Sodium stearate R COO^– Na⁺.

Question 59.
How do micelles differ from a normal collodial solutions ?
Answer:
Micelles contain a long hydrocarbon part which is hydrophobic tail and a polar hydrophilic head. These are absent in normal colloidal solution.
eg. Sodium stearate C₁₇H^–₃₅COO^–Na⁺ contain long hydrocarbon part stearate radical (C₁₇H₃₅^–) is hydrophobic tail while COO^– part is hydrophilic head.

Question 60.
Give two examples of associated colloids.
Answer:

1. Soaps dissolved in water
2. Detergents dissolved in water.

Question 61.
Can the same substance act both as colloid and crystalloid ?
Answer:
Yes. The same substance can act both as colloid and crystalloid.
e.g.: Common salt
(NaCl) a typical crystalloid in an aqueous solution behave as a colloid in the benzene medium.

Question 62.
Give two examples of lyophobic sols.
Answer:

1. Metal colloids like gold sol.
2. Collids of metal sulphides such as AS₂S₃.

Question 63.
Give examples of colloidal system of
i) Liquid in solid
ii) gas in solid.
Answer:
i) Example for liquid in solid is cheese or butter.
ii) Example for gas in liquid is froth or soap lather.

Question 64.
What type of substances form lyophobic sols?
Answer:
Substances like metals, and their sulphides form lyophobic sols.

Question 65.
What is Critical Micelle Concentration (CMC) and Kraft temperature ?
Answer:
The formation of micelle takes place above certain temperature called Kraft temperature and above a particular concentration called Critical Micelle Concentration.

Question 66.
Why lyophobic colloids are called irreversible colloids ?
Answer:
Lyophobic sols are readily precipitated on the addition of small amounts of electrolytes or by heating or by shaking. The precipitates does not give back the collodial sol by simple addition of the dispersion medium to it. So they are called irreversible colloids.

Question 67.
How a colloidal sol of arsenous sulphide is prepared ?
Answer:
Arsenous sulphide sol can be prepared by ; double decomposition method of arsenous i oxide and hydrogen sulphide.
AS₂O₃ + 3H₂ S → AS₂S₃ (sol) + 3H₂O

Question 68.
What is peptization ?
Answer:
Peptization is a process of converting a precipitate into colloidal sol by shaking it with the dispersion medium in the presence of a small amount of electrolyte. The electrolyte used for this purpose is called peptizing agent.

Question 69.
What is dialysis ? How is dialysis can be made feat ?
Answer:
Dialysis is a process of removing of dissolved substance from a collodial solution using a suitable membrane. Dialysis can be made fast by applying emf if the dissolved substance in impure colloidal solution is an electrolyte i.e., electrodialysis.

Question 70.
What is collodion solution ?
Answer:
Collodion is a 4% solution of nitro – cellulose in a mixture of alcohol and ether.

Question 71.
How an ultrafilter paper is prepared from ordinary filter paper ?
Answer:
Ultra filter paper is prepared by soaking the filter paper in collodion solution hardening by formaldehyde and then finally drying it.

Question 72.
What is Tyndall effect ?
Answer:
Colloidal particles scatter light in all directions in space. The scattering of light illuminates the path of beam in the colloidal dispersion. This is known as Tyndall effect.

Question 73.
Under what conditions is Tyndall effect observed ?
Answer:
Tyndall effect is observed only when the following two conditions are satisfied.

1. The diameter of the dispersed particles is not much smaller than the wavelength of the light used.
2. The refractive indices of the dispersed phase and the dispersion medium differ greatly in magnitude.

Question 74.
Can Tyndall effect be used to distinguish between a collodial solution and a true solution ? Explain.
Answer:
Tyndall effect is used to distinguish between a colloidal solution and a true solution. When an intense beam of light is focussed on the collodial solution contained in a glass vessel, the focus of light can be observed with a microscope kept at right angles to the beam. Individual colloidal particles appear as bright stars.

Question 75.
Sky appears blue in colour. Explain.
Answer:
Dust particles along with water vapour suspended in air, scatter blue light which reaches our eyes and hence the sky looks blue.

Question 76.
What is Brojvnian movement ?
Answer:
The zig-zag motion of colloidal particles all over the field of view in a collodial solution is called Brownian movement.

Question 77.
What is the main cause for charge on a colloidal solution ?
Answer:
Preferential adsorption of ions is the main cause for charge on a colloidal particle. The sol particles acquire positive or negative charge by preferential adsorption of positive or negative ions.

Question 78.
What is electrokinetic potenital or zeta potential ?
Answer:
The potential difference between the fixed layers and the diffused layer of opposite charge in a colloidal solution is called the electrokinetic potential or zeta potential.

Question 79.
Write the formula of positively charged and negatively charged hydrated ferric oxide collodial solutions.
Answer:
If FeCl₃ solution is added to hot water a positively charged sol of hydrated ferric oxide is formed due to adsorption of Fe³⁺ ions. However when ferric chloride solution is added to NaOH solution taken in excess, a negatively charged sol is obtained with adsorption of OH^– ions.
Fe₂O₃ . xH₂O / Fe ³⁺
Positively charged
Fe₂O₃ . xH₂O /OH^–
Negatively charged

Question 80.
Give the order of coagulating power of Cl^–, SO₄^2-, PO₄^3- in the coagulation of positive sols.
Answer:
PO₄^3- > SO₄^2- > Cl^–
More the charge on anion more is the coagulating power.

Question 81.
Amongst Na⁺, Ba²⁺, Al³⁺ which coagulates negative sol readily and why ?
Answer:
According to Hardy – Schulze rule more the charge on ion more is the coagulating power of the oppositely charged colloid. Since Al carry more charge coagulates negative sol readily.

Question 82.
A colloidal solution of AgI is positively charged when prepared from a solution containing excess of Ag⁺ ions and negatively charged when prepared solution containing excess of I^– ions. Explain.
Answer:
A collodial particle adsorb the ion from solution which is common to it. When AgI colloid is prepared from a solution containing excess Ag⁺ ions, the colloidal particle adsorb Ag⁺ ion and thus get positive charge. If Agl colloid is prepared from solution containing excess I^– ions, the colloidal particle adsorb I^– ions and thus get negative charge.

Question 83.
What is electrophoresis ?
Answer:
The movement of colloidal particles under an applied emf is called electrophoresis.

Question 84.
What is electro osmosis ?
Answer:
If the movement of colloidal particles is arrested by some suitable means, the dispersion medium moves in opposite direction under the applied emf. This phenomenon is called electro osmosis.

Question 85.
What is coagulation ?
Answer:
The process of settling down of colloidal particles is called coagulation or precipitation or flocculation of the sol.

Question 86.
Define flocculation value.
Answer:
The minimum concentration of an electrolyte in millimoles per litre required to cause coagulation of a sol in two hours is called flocculation value.

Question 87.
State Hardy – Schulze rule.
Answer:
Greater the valence (charge) of the coagu-lating ion added greater is its power to cause coagulation. This is known as Hardy-Schulze rule.

Question 88.
Coagulation takes place when sodium chloride solution is added to a colloidal solution of hydrated ferric oxide. Explain.
Answer:
When sodium chloride solution added to a colloidal solution of hydrated ferric oxide, the Na⁺ ions neutralize the negative charge on colloidal particles then colloidal particles come close, combine forming bigger particles and thus coagulated.

Question 89.
How are lyophobic solutions protected from phenomenon of coagulation ?
Answer:
Lyophobic colloids are protected from coagulation by adding lyophilic colloids to lyophobic colloid. The lyophilic colloid form a protective layer around lyophobic particles and thus protect the lyophobic colloid from the action of electrolytes.

Question 90.
What is protective colloid ?
Answer:
When lyophilic colloid is added to lyophobic colloid, the lyophilic colloid form a protective layer around lyophobic colloid and thus protect the lyophobic colloid from the action of electrolytes. So the lyophilic colloids are called protective colloids.

Question 91.
What is an emulsion ? Give two examples.
Answer:
Emulsions are liqud – liquid colloidal systems in which finely divided droplets of one liquid dispersed in another. If a mixture of two immiscible or partially miscible liquids is shaken a coarse dispersion of one liquid in the other called enjulsion is obtained.
Ex : Milk and Vanishing cream.

Question 92.
How emulsions are classified ? Give one example for each type of emulsion. [Mar. 2018 . TS]
Answer:
Emulsions are two types.

1. Oil dispersed in water or oil/water (o/w) type eg. Milk, Vanishing cream.
2. Water dispersed in oil (water / oil) (w/o) type. eg. Butter, cream.

Question 93.
What is an emulsifying agent ?
Answer:
For stablisation of an emulsion, the third component added to emulsion is called emulsifying agent. Eg (Proteins and soaps are emulsifying agent for o/w emulsions.

Question 94.
What is demulsification ? Name two demulsifiers.
Answer:
Separation of an emulsion into consituent liquids is called demulsification. Demulsification can be carried by heating, freezing, centrifusing etc.

Question 95.
How is artifical rain produced ?
Answer:
Artificial rain can be produced by throwing electrified sand or spraying a sol carrying charge opposite to the one on clouds from an aeroplane.

Question 96.
Bleeding from fresh cat can be stopped by applying alum. Give reasons.
Answer:
Blood is a colloidal solution of alluminoid substances. The styptic action of alum is due to coagulation of blood forming a clot which stops further bleeding.

Question 97.
Deltas are formed at the points where river enters the sea. Why ?
Answer:
River water is a colloidal solution of clay. Sea water contains a number of electrolytes. When river water meets the sea water, the electrolytes of sea water coagulates the colloidal solution of clay resulting in its deposition of clay with formation of delta.

Question 98.
Name any two applications of colloidal solutions.
Answer:

1. Purification of drinking water : Water from natural sources contain collodial impurities. When alum is added the colloidal particles in water coagulates and the water becomes fit for drinking.
2. Several medicines are used as colloi-dal solutions : Colloidal medicines are more effective due to their large surface area and are therefore easily assimilated.

Question 99.
How can aerial pollution by colloidal particles of smoke be prevented ? Explain.
Answer:
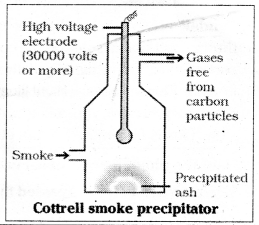
Smoke is a colloidal solution of solid particles such as carbon, arsenic compounds, dust etc. The smoke is made to pass through a precipitator called Cottrell precipitator. Before coming out of chimney the precipitator contain plates carrying opposite charge to that carried by smoke particles. The particles on coming in contact with these plates lose their and get precipitated.

Question 100.
Alum is used to purify water obtained from natural soruces. Explain.
Answer:
Water from natural sources contain colloidal impurities. When alum is added, the colloidal particles in water coagulates and the water becomes fit for drinking.

Question 101.
Why medicines are more effective in colloidal state ?
Answer:
Medicines in colloidal state are more effective due to their large surface area and are therefore easily assimilated.

Question 102.
How rubber is obtained from latex ?
Answer:
Plant latex is a colloidal solution of rubber particles which are negatively charged. Rubber is obtained from latex by coagulation on adding electrolytes.

Question 103.
Name the type of emulsion to which milk belongs.
Answer:
Milk is an emulsion of oil dispersed in water (o/w) type.

Short Answer Questions (4 Marks)

Question 104.
What is adsorption? Discuss the mechanism of adsorption of gases on solids.
Answer:
The accumulation of molecular species at the surface rather than in the bulk of a solid or liquid is known as adsorption.

Mechanism of adsorption :
Adsorption arises due to the fact that the surface particles of the adsorbent are not in the same environment as the particles inside the bulk. The particle inside the bulk is surrounded by other particles in all directions and all the forces acting between the particles are mutually balanced.

But the particle on the surface have no particles of its own above it and contain only below to it. So these unbalanced residual attractive forces are responsible for attracting the adsorbate molecules on its surface.

Question 105.
What are different types of adsorption ? Give any four differences between characteristics of these different types. [TS Mar. 19; (AP & TS 15)]
Answer:
Adsorption is two types, i) Physical adsor-ption and 2) Chemical adsorption.

Homogeneous catalysis: When the rea­ctants and the catalyst are in the same phase i.e., either liquid or gas the process is said to be homogeneous catalysis.

Question 106.
What do you understand by the terms given below ?
a) Absorption
b) Adsorption
c) Adsorbent and adsorbate
Answer:
a) Absorption: Uniform distribution of the substance throughout the bulk of a solid is absorption.
b) Adsorption: Accumulation of molecular species at the surface rather than in the bulk of solid or liquid is known as adsorption.
c) The substance which concentrates or accumulates on the surface is termed as adsorbate and the material on the surface of which the adsorption takes place is called adsorbent.

Question 107.
Adsorption of a gas on the surface of solid is generally accompanied by decrease in entropy. Still it is a spontaneous process. Explain.
Answer:
During adsorption there is always decrease in surface energy which appears as heat. So adsorption is always exothermic and ∆H of adsorption is always negative. But during adsorption entropy of the gas decreases due to decrease in the movement of gas molecules.

Thus entropy of adsorption AS is also negative. For the process of adsorption ∆G must be negative at a constant temperature on the basis of equation ∆G = ∆H – T∆S. In the equation ∆G = ∆H – T∆S, ∆G can be negative if ∆H has sufficiently more negative value and -T∆S is positive. The combination of these two factors makes ∆G negative. So adsorption process becomes spontaneous.

As the adsorption proceeds ∆H become less negative and becomes equal to T∆S and ∆G become zero. At this state equilibrium is attained.

Question 108.
How can the constants k and n of the Freundlich adsorption equation be calculated ?
Answer:
Freundlich adsorption isotherm is
\(\frac{\mathrm{x}}{\mathrm{m}}\) – k . p^1/n (n > 1) ……………… (1)
Where x is the mass of gas adsorbed
m is the mass of adsorbent
p is the pressure
Taking logarithms of equation (1)
log \(\frac{\mathrm{x}}{\mathrm{m}}[/latex = logk + [latex]\frac{\mathrm{1}}{\mathrm{n}}[/latex log p

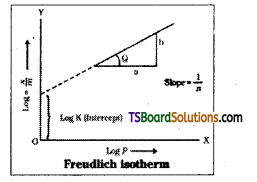
A graph is plotted by taking [latex]\frac{\mathrm{x}}{\mathrm{m}}\) on Y – axis and log p on X – axis. This gives a straight line the slope of the straight line gives the value of \(\frac{\mathrm{1}}{\mathrm{n}}\) . The intercept on the Y – axis n gives the value of log k.

Question 109.
How does the extent of adsorption depend upon
a) Increasing the surface area per unit mass of adsorbent
b) Increasing temperature of the system
c) Increasing pressure of the gas.
Answer:
a) The surface area available for adsorption per unit mass of adsorbent is known as specific area. Greater the specific area of the solid, greater would be its adsorbent power. Because of this reason porous or finely divided forms of adsorbents adsorb more extensively.

b) The adsorption at a surface initially increases till a saturation point is achieved. At this juncture an equilibrium is established.
Adsorption ⇌ Desorption ; ∆H = +Ve Since adsorption is accompanied by evolution of heat, according to Le-Chateliers principle the magnitude of adsorption will decrease with rise in temperature.

c) The adsorption of gas generally increases the increase of pressure at constant temperature. Adsorption of gas on solid resuits in the decrease of pressure, therefore according to Le-Chatelier’s principle increase in pressure increase the extent of adsorption.

Question 110.
What is catalysis? How is catalysis classified ? Give two examples for each type of catalysis [AP 16; TS 15; IPE ’14]
Answer:
Substances which accelerate the rate of a slow chemical reaction but whose chemical nature and mass remain unchanged after the reaction are known as catalysts and the phenomenon is known as catalysis.
Catalysis is mainly two types.
i) Homogeneous catalysis: When the reactants and the catalyst are in the same phase i.e., either liquid or gas the process is said to be homogeneous catalysis.
e-g

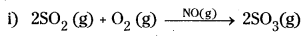
Reactants SO₂ and O₂ and the catalyst NO are all gases and in the same phase.

ii) CH₃COOCH₃ (l) + H₂O 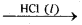CH₃COOH (aq) + C₂H₅OH (aq)
The reactants and catalysts are in the same liquid phase.

2) Heterogeneous catalysis: The catalytic process in which the reactants and the catalyst are in different phases is known as heterogeneous catalysis.

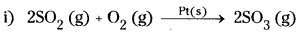
The reactants are in gaseous state while that catalyst is solid.

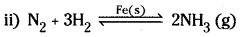
Reactants are gases, catalyst is solid.

Question 111.
Discuss the mechanism involved in adsorption theory of heterogeneous catalysis.
Answer:
As per old theory the reactant molecules in the gaseous state or in solutions are adsorbed on the surface of the solid catalyst. The increase in concentration of the reactants on the surface increase the rate of reaction. The heat liberated during adsorption is also utilised in increasing the rate of reaction. According to modern theory,

1. Reactant molecules diffuse on to the surface of catalyst.
2. The reactant molecules adsorb on the surface of the catalyst.
3. Chemical reaction takes place between adsorbed reactant molecules through formation of an intermediate.
4. The product molecules adsorb from the catalyst surface making the surface available for more reaction to occur.
5. The product molecules diffuse away from the surface of the catalyst for the adsorption of fresh reactant molecules.

Question 112.
Discuss some features of catalysis by zeolites.
Answer:
The catalytic reactions which depend on the structure of the pores of catalyst and the size of the molecules of reactants and products is called shape – selective catalysis.

Zeolites are good shape- selective catalysts, because of their honey comb like structure. Zeolites are microporous alumino silicates with three dimensional network of silicates. The reactions taking place in zeolites are shape – selective catalytic reactions.

Zeolites are widely used as catalysts in photo chemical industries for cracking and isomerisation of hydrocarbons. Eg: ZSM – 5 converts alcohols directly into petrol by dehydrating them.

Question 113.
Give brief account of mechanism of enzyme catalysis with suitable diagrams.
Answer:

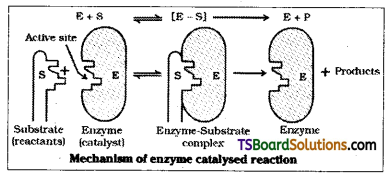
Colloidal enzyme particles contain large number of cavities which have characteristic shape. They possess active groups such as -NH₂, -COOH, -SH, -OH etc. These are active centres on the surface of the enzyme particles. The molecules of the reactant which have a complimentary shape that can fit into these cavities just like a key fit into a lock.

The active groups combine with reactant molecule forming an activated complex which then decompose into products.

The enzyme catalysed reactions may be considered to proceed in two steps.

1. Binding of substrate to enzyme to form an activated complex (ES#).
   E + S → ES#
2. Activated complex decomposes to give product.
   ES → E + P

Question 114.
Discuss the factors that influence the catalytic activity of enzymes.
Answer:
The catalytic activity of enzymes will be influenced by
1) Temperature: The rate of enzyme catalysed reaction is maximum at a definite temperature called the optimum temperature. The optimum range is 298 – 310K. On either side of the optimum temperature the enzyme activity decreases.

2) pH : The rate of an enzyme – catalysed reaction is maximum at a particular pH called optimum pH which lies between 5-7.

3) Activators and Co-enzymes: The enzymatic activity is increased in the presence of certain substances known as Co-enzymes e.g. If a small non-protein vitamin is present along with an enzyme the catalytic activity is enhanced considerably.
Activators are generally metal ions Na⁺, Mn²⁺, CO²⁺, Cu²⁺ etc. When these are bonded to enzyme molecules their catalytic activity increases.
e.g. Catalytic activity of amylase combined with Na+ is very high.

4) Inhibitors or poisons : The substance which decrease the catalytic activity of enzymes are called inhibitors or poisons. These interact with the active functional groups and reduce the catalytic activity of the enzyme.

Question 115.
Name any six enzyme catalysed reactions.
Answer:

1. Inversion of cane sugar into glucose and fructose in the presence of enzyme invertase.
   
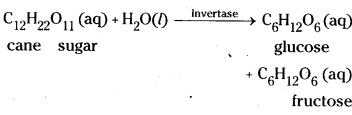
2. Conversion of glucose into ethyl alcohol in the presence of zymase.
   
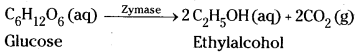
3. Conversion of starch into maltose in the presence of diastase.
   
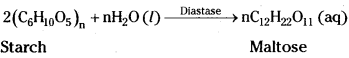
4. Conversion of maltose into glucose in the presence of maltase.
   
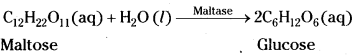
5. Conversion of proteins into peptides in intestine in the presence of enzyme trypsin.
6. Conversion of milk into curd in the presence of enzyme lacto bacilli.

Question 116.
What do you mean by activity and selectivity of catalysts ?
Answer:
Activity :
The ability of a catalyst in increasing the rate of reaction is defined as its activity. The activity of the catalyst depends upon the strength of chemisorption. When the reactant molecules are adsorbed on the surface of catalyst they become reactive.

Selectivity:
The selectivity of a catalyst is its ability to direct a reaction to form specific products. Eg. Different products are formed from H₂ and CO by using different catalysts.

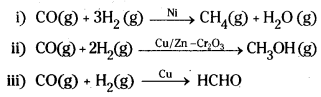
These reactions indicate that a given substance can act as catalyst only in a particular reaction and not in all reactions.

Question 117.
How are colloids classified on the basis of physical states of components ?
Answer:
Depending on the physical states of components the colloids are classified into eight types

Question 118.
How are colloids classified on the basis of nature of the dispersion medium ?
Answer:
Dispersion medium may be a solid, liquid or gas. Thus depending on the nature of dispersion medium the colloids are three types.

1. Dispersion medium is solid: Dispersion phase may be solid or liquid or gas.
2. Dispersion medium is liquid: Dispersion phase may be solid or liquid of gas.
3. Dispersion medium is gas: Dispersion phase may be solid or liquid.
4. Solid in liquids are called sols, liquid in liquid are called emulsions, liquid in solids are called gels. If the dispersion medium is water, the sol is called aquasol or hydrosol and if the dispersion medium is alcohol it is called alcohol and so on.

Question 119.
How are colloids classified on the basis of interaction between dispersed phase and dispersion medium ?
Answer:
Depending upon the nature of interaction between the dispersed phase and dispersion medium the colloidal sols are classified into two types.
1) Lyophilic colloids:
If there is attraction between the dispersion medium and dispersed phase, the colloids are called as lyophilic colloids. Lyophilic means solvent loving or solvent attracting. These can be prepared by direct mixing and can be separated from one another by evaporating. These sols are reversible, so called reversible sols. These are stable and cannot be easily coagulated.

2) Lyophobic colloids :
If there is repulsion between dispersion medium and dispersed phase, the colloids are called lyophobic colloids. Lyophobic means solvent hating. This type of colloids cannot be prepared simply by mixing. They have to be prepared by special methods. These sols are readily precipitated by the addition of small amounts of electrolytes or by heating. The precipitate does not give back the colloidal sol by simple addition of the dispersion medium to it. So these are known as irreversible sols. Lyophobic sols need stabilising agents for their preservation.
If water is the dispersion medium these are called hydrophilic and hydrophobic colloids.

Question 120.
What Is the difference between a colloidal sol, gel, emulsion and a foam ?
Answer:
When the dispersed phase is solid and the dispersion medium is liquid the colloid is called sol. Ex: Paints.
If the dispersed phase is liquid and the dispersion medium is solid, the colloid is called gel. Ex: Cheese, butter.
If one liquid is dispersed in another liquid, the colloid is called emulsion. Ex: Milk
If the dispersed phase is gas and dis-persed medium is liquid, the colloid is called foam. Ex : Froth, soap lather.

Question 121.
What are lyophilic and lyophobic sols ? Compare two terms interms of stability and reversibility.
Answer:
Depending upon the nature of interaction between the dispersed phase and dispersion medium the colloidal sols are classified into two types.
1) Lyophilic colloids:
If there is attraction between‘the dispersion medium and dispersed phase, the colloids are called as lyophilic colloids. Lyophilic means solvent loving or solvent attracting. These can be prepared by direct mixing and can be separated from one another by evaporating. These sols are reversible, so called reversible sols. These are stable and cannot be easily coagulated.

2) Lyophobic colloids:
If there is repulsion between dispersion medium and dispersed phase, the colloids are called lyophobic colloids. Lyophobic means solvent hating. This type of colloids cannot be prepared simply by mixing. They have to be prepared by special methods.

These sols are readily precipitated by the addition of small amounts of electrolytes or by heating. The precipitate does not give back the colloidal sol by simple addition of the dispersion medium to it. So these are known as irreversible sols. Lyophobic sols need stabilising agent for their preservation.

If water is the dispersion medium these are called hydrophilic and hydrophobic colloids.

Question 122.
Name a substance whose molecules consist of lyophilic as well as lyophobic parts. Give its use in our dally life.
Answer:
Micells contain both lyophilic as well as lyophobic parts eg. soap. Soap is sodium or potassium salt of higher fatty acid and may be represented as R COO^– Na⁺. Sodium stearate is CH₃ (CH₂)₁₆ COO^– Na⁺ is a major component of many soaps when dissolved in water it dissociates into CH₃ (CH₂)₁₆ COO^– and Na⁺ ions. The CH₃(CH₂)₁₆ COO^– consists of two parts, the long non polar hydrocarbon chain CH₃(CH₂)₁₆ is water repelling and it is hydrophobic end. The polar COO^– group is water attracting and is hydrophilic end.

In our daily life when we use soap, the hydrophobic part of soap ion penetrates into the oil droplet and the hydrophilic part project out of the oil droplet.

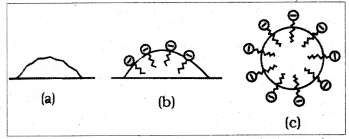
Since the polar group can interact with water, the oil droplet surrounded hydrocarbon part is pulled into water and is removed from the dirty surface. Thus soap emulsifies the oil and washes it out.

Question 123.
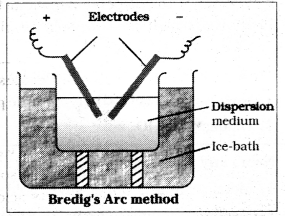
Describe Bredig’s arc method of preparation of colloids with a neat diagram.
Answer:
This process involves dispersion as well as condensation. In this method Electric arc is struck between electrodes of the metal immersed in the dispersion medium. The intense heat produced vapourises the metal which then condenses to form particles of colloidal size. Colloidal sols of metals such as gold, silver, platinum, etc. are prepared by this method.

Question 124.
Name any four examples of colloids by chemical methods with necessary chemical equations.
Answer:

1. AS₂S₃ sol can be prepared by double decomposition method.
   AS₂O₃ + 3H₂S AS₂S₃ (sol) + 3H₂O
2. Sulphur sol can be prepared by oxidation method.
   SO₂ + 2H₂S 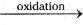3S_(sol) + 2H₂O
3. Gold sol can be prepared by reduction method.
   2AuCl₃ + 3HCH0 + 3H₂O 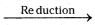2Au (sol) + 3HCOOH + 6HCl
4. Ferric hydroxide sol can be prepared by hydrolysis method.
   FeCl₃ + 3H₂O 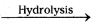Fe(OH₃) + 3 HCl

Question 125.
Describe the purification of colloidal solutions by the phenomenon of dialysis with a neat diagram.
Answer:

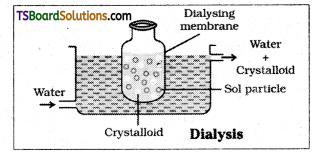
Dialysis is a process of removing a dissolved substance from a colloidal solution using a suitable membrane. The apparatus used for this purpose is called dialyser. A bag of suitable membrane containing the colloidal solution is suspended in a vessel containing a continous flow of water. The bag made with animal membrane, or parchment paper or cellophane sheet allow the molecules or ions to diffuse through it into the water and pure colloidal solution is left behind in the bag.

Question 126.
Explain the formation of micelles with a neat sketch.
Answer:
Certain substances behave as strong electrolytes at low concentrations but at higher concentrations exhibit colloidal behaviour due to the formation of aggregates. These aggregated particles are called micelles or associated colloids.

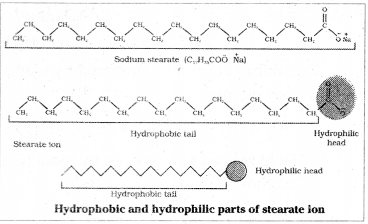
For example soap is a sodium or potassium salt of higher fatty acid and may be represented as RCOO^– Na⁺ eg. sodium stearate CH₃ (CH₂)]₆ COO^– Na⁺, It dissociates into RCOO^– and Na⁺ ions when dissolved in water. The RCOO^– ions consists of two parts. The long hydrocarbon chain R (also called non polar tail) which is hydrophobic (water repelling) and a polar group COO^– which is hydrophilic.

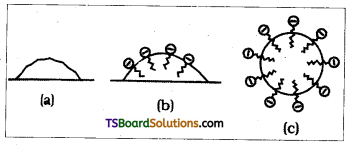
The RCOO^– ions are therefore present with their COO^– group into water and hydrocarbon chains (R) staying away from it and remain at the surface. At critical micelle concentration the COO^– Ions are pulled into the bulk of the solution and are aggregated to form spherical shape with their hydrocarbon chain pointing towards the centre of sphere with COO^– part remaining outward on the surface of the sphere. The aggregate thus formed is known as ionic micelle.

Question 127.
Action of soap is due to emulsification and micelle formation. Comment.
Answer:
The cleansing action of soap is due to the fact that soap molecules form a micelle around the oil droplet in such away that hydrophobic part of the stearate ions is in the oil droplet and hydrophilic part projects out of the grease droplet.

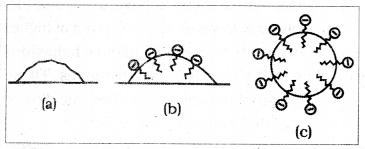
Since the polar groups can interact with water, the oil droplet surrounded by stearate ions is now pulled into water and is removed from the dirty surface. Thus soap helps in emulsification and washing away of oils and fats.

Question 128.
Explain the phenomenon of Brownian movement giving reasons for the occurrence of this phenomena.
Answer:
The colloidal particles in a colloid are in continuous zig-zag motion all over the field of view. This continous zig-zag motion of colloidal particles in a colloid is called as Brownian movement.

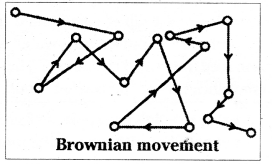
The Brownian movement is due to the bombardment of the molecules of dispersion medium on colloidal particles (dispered phase). The motion is independent of the nature of the colloid but depends on the size of the particles and viscosity of the solution.

Question 129.
Name any four positively charged sols.
Answer:
Positively charged sols.

1. Hydrated metallic oxide sols e.g: Al₂O₃ . X H₂O, CrO₃ . X H₂O and Fe₂O₃ . X H₂O
2. Basic dye stuffs eg. methylene blue sol
3. Haemoglobin (blood)
4. Oxides e.g : TiO₂ sol

Question 130.
Name any four negatively charged sols.
Answer:

1. Metal sols e.g.: Copper, silver, gold sols.
2. Metallic sulphide sols e.g: AS₂S₃, Sb₂S₃, Cds etc.
3. Acid dye stuff sols, e.g: eosin congo red sols.
4. Sols of starch, gum, gelatin, clay, charcoal etc.

Question 131.
Explain the terms Helmholtz electrical double layer and zeta potential. What are their significances in the colloidal solutions ?
Answer:
In a colloid the colloidal particles acquire positive or negative charge by selective adsorption of ions on the surface of the colloidal particle. This positive or negative charge on colloidal particle attracts ions of opposite charge from the medium forming a second layer as shown below.
Agl/I^– K⁺
AgI/Ag⁺ I^–
The combination of the two layers of opposite charges around the colloidal particle is called Helmholtz electrical double layer. The first layer of ions is firmly held and is known as fixed layer while the second layer is mobile and is known as diffused layer. Between these two layers of opposite charges there develops a potential difference called electrokinetic potential or zeta potential.

The presence of equal and similar charges on colloidal particles is responsible for the stability of collodial solution. The repulsion between the colloidal particles having same charge keep them away and preventing them to come closer and coagulate.

Question 132.
Explain with a neat sketch the phenomenon of electrophoresis.
Answer:

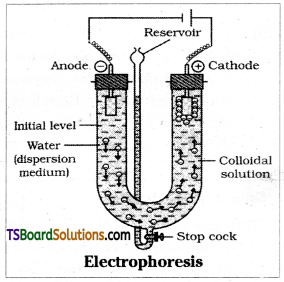
When electric potential is applied across two platinum electrodes dipping in a colloidal solution the colloidal particles move towards one or the other electrode. The movement of colloidal particles under the applied emf is called electrophoresis postively charged particles move towards the cathode while negatively charged particles move towards the anode.

Question 133.
Explain the following terms.
i) Electrophoresis
ii) Coagulation
iii) Tyndall effect
Answer:
i) Electrophoresis:
When electric potential is applied across two platinum electrodes dipping in a colloidal solution the colloidal particles move towards one or the other electrode. The movement of colloidal particles under the applied emf is called electrophoresis. Positively charged particles move towards the cathode while negatively charged particles move towards the anode.

ii) Coagulation:
The process of setting down of colloidal particles is called coagulation or precipitation or flocculation of the sol. When the charge on colloidal particles is neutralised, the colloidal particles come nearer to form aggregates and settles down under the force of gravity.

iii) Tyndall effect :
When light is passed through a colloidal solution the colloidal particles scatter the light in all directions in space. This scattering of light illuminates the path of beam in the colloidal dispersion. This is known as Tyndall effect.

Question 134.
Explain the phenomenon observed,
i) When a beam of light is passed through a colloidal sol.
ii) An electrolyte, NaCl is added to hydrated ferric oxide.
iii) An electric current is passed through a colloidal solution.
Answer:
i) When a beam of light is passed through a colloidal sol the colloidal particles scatter light in all directions in space. This scattering of light illuminates the path of beam in the colloidal dispersion. This is known as Tyndall effect.

ii) When NaCl is added, the colloidal particles are precipitated. This is because that colloidal particles interact with ions carrying opposite charge to that present on themselves. Then neutralisation of charges on colloidal particles takes place leading to their coagulation.

iii) When electric current is passed through a colloidal solution the colloidal particles move towards oppositely charged electrodes, get discharged and finally precipitated.

Question 135.
Describe Cottrell smoke precipitator with a neat diagram.
Answer:
Smoke is a colloidal solution of solid particles such as carbon, arsenic compounds, dust etc. in air. The smoke before coming out of chimney is passed through a precipitator containing plates having a charge opposite to that carried by smoke particles. The particles on coming in contact with these plates lose their charge and get precipitated. The particles thus settle down on the floor of the chamber. The precipitator is called Cottrell precipitator.

Question 36.
Among NaCl, Na₂SO₄ Na₃ PO₄ electrolytes which is more effective for coagulation of hydrated ferric oxide sol and why ?
Answer:
Hydrated ferric oxide sol carry positive charge. So it can be coagulated by adding an electrolyte that can neutralise the positive charge. Among NaCl, Na₂SO₄ and Na₃PO₄, Na₃PO₄ is more effective for coagulation because from Na₃PO₄ the PO₄^3- ion formed can neutralize effectively. This is according to Hardy Schulze law which states that greater the valence of coagulating ion added the greater is its power to cause coagulation.

Question 137.
Discuss how a lyophilic colloid protect a lyophobic colliod.
Answer:
Lyophilic sols are more stable than lyophobic sols. In lyophilic colloids the particles are extensively solvated and covered by a layer of the dispersion medium. When a lyophilic colloid is added to a lyophobic sol the lyophilic particles form a protective layer around lyophobic particles and thus protect the latter from the action by electrolytes. Lyophilic colloids used for this purpose are called protective colloids.

Question 138.
Discuss the use of colloids in
i) Purification of drinking water
ii) Tanning
iii) Medicines
Answer:
i) Purification of drinking water :
Water obtained from natural sources contain colloidal particles. Alum is added to such water to coagulate the colloidal impurities and make water fit for drinking purposes.

ii) Tanning :
Animal skins are colloidal in nature. When the skin containing positively charged particles is soaked in tannin that contain negatively charged colloidal particles, mutual coagulation takes place. This makes the skin hard and the process is called Tanning.

iii) Medicines :
Most of the medicines are colloidal in nature. Colloidal medicines are more effective because they have large surface area and are therefore easily assimilated, e.g : Argyrol is a silver sol used as an eye lotion. Colloidal antimony is used in curing Kala azar.

Question 139.
Define Gold number.
Answer:
The protective power of protective colloids (lyophilic colloids) is measured by gold number. It is defined as “the mass in mill-grams which protects the coagulation of 10 ml of a gold sol on adding 1 ml of 10% NaCl solution”.

Question 140.
How do emulsifiers stabilize emulsion ? Name two emulsifiers.
Answer:
Emulsions are unstable. For stablisation of emulsion, a third component called emulsifying agent is usually added. The emulsifiying agent forms an interfacial film between suspended particles and the medium.

1. Proteins are emulsifying agent for o/w type emulsions.
2. Heavy metal salts of fatty acids, long chain alcohols, lamp black, etc. are emulsifying agents for w/o type emulsion.

Long Answer Questions (8 Marks)

Question 141.
Explain the terms absorption, adsorption and sorption. Describe the different types of absorption. [AP ’15]
Answer:
Absorption :
Uniform distribution of a substance through out the bulk of the solid is called absorption. For example, when a sponge or chalk piece is dipped in water, it distributes uniformly throughout the sponge or chalk piece due to absorption.

Adsorption:
The accumulation of molecular species at the surface rather than in the bulk of a solid or liquid is termed as adsorption. The substance which accumulates on the surface is called adsorbate and the material oh which the adsorption take place is called adsorbent.

Sorption :
If adsorption and absorption takes place simultaneously, it is known as sorption.

Adsorption is two types 1) Physical adsorption or physisorption and 2) Chemical adsorption or chemisorption.
Physisorption:

1. It is due to the adsorption of a gas on a solid surface due to weak van der Waal’s forces.
2. It is universal and lacks of specificity.
3. The gases which have high critical temperatures adsorb easily.
4. It is reversible and increases with increase in pressure and decrease in temperature.
5. The enthalpy of physisorption is low.

Chemisorption:

1. If the adsorption of a gas on a solid surface takes due to chemical bonds, it is called chemisorption.
2. It involves high energy of activation.
3. Physical adsorption at low temperature may convert into chemical adsorption at high temperature.
4. It is highly specific in nature and is irreversible in nature.
5. The enthalpy of chemisorption is high since it involves chemical bond formation.

Question 142.
Discuss the characteristics of physical adsorption.
Answer:
Characteristics of physical adsorption.
i) Lack of specificity:
Since Van der Waal’s forces are universal thefe is no specificity for physical adsorption. Any gas can be absorbed on any solid.

ii) Nature of adsorbate :
The amount of gas adsorbed by a solid depends on the nature of gas. Easily liquefiable gases which have high critical temperatures are readily adsorbed. This is because van der Waal’s forces are stronger near the critical temperature.

iii) Reversibilty :
Physical adsorption of a gas by a solid is generally reversible. With increase in pressure and decrease in te’mperatue adsorption increases. This is because adsorption decreases the volume of gas and adsorption is exothermic. With decrease in pressure and increase in temperature adsorption decreases. This is accroding to Le chatelier’s principle.

iv) Surface area of adsorbent:
More the surface area more is adsorption. Finely divided metals and porous substances having more surface area adsorbs more amount of gases.

v) Enthalpy of adsorption:
Since van der Waal’s forces are weak the enthalpy of physical adsorption is quite low (20 – 40 kJ mol^-1).

Question 143.
Discuss the characteristics of chemisorption.
Answer:
Characteristics of Chemisorption :
i) High specificity :
Chemisorption is highly specific. It will occur only if there is possibility for the formation of chemical bonds between adsorbate and adsorbent.

ii) Irreversibility:
The chemical adsorption is due to compound formation i.e., due to chemical reaction. It is slow at low temperatures but increases with increase in temperature because the chemical reaction between adsorbent and adsorbate requires some energy of activation.
The physical adsorption taking place at low temperature may convert into chemical adsorption at a high temperature usually high pressures are favourable for chemisorption.

iii) Surface area:
With increase in surface area chemical adsorption increases.

iv) Enthalpy of adsorption :
Since chemisorption involves chemical bond formation, the enthalpy of chemisorption is also high (80 – 240 kJ mol^-1).

Question 144.
Compare and contrast the phenomenon of physisorption and chemisorption.
Answer:

Question 145.
What is an adsorption isotherm ? Discuss the phenomenon of adsorption of gases on solids with the help of Freundlich adsorption isotherm.
Answer:
The variation in the amount of gas adsorbed by the adsorbent with pressure at constant temperature can be expressed by means of a curve called as adsorption isotherm.

Freundlich adsorption isotherm :
It gives the empirical relationship between the quantity of gas adsorbed by unit mass of solid adsorbent and pressure at a particular temperature. The relationship can be expressed as
\(\frac{\mathrm{x}}{\mathrm{m}}\) = k . p^1/n (n > 1) ……………….. (1)

where x is the mass of gas adsorbed
m is the mass of adsorbent
p is pressure
k and n are constants which depend on the nature of gas and the adsorbent at a particular temperature.

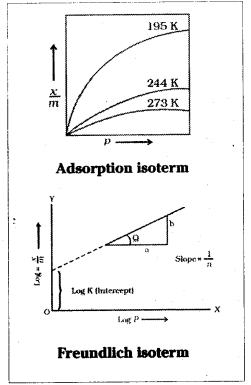
The curves in the graph indicate that at constant pressure, there is decrease in physical adsorption with increase in pressure.
Taking logarithms of equation (1)
log \(\frac{\mathrm{x}}{\mathrm{m}}\) = log k + \(\frac{\mathrm{1}}{\mathrm{n}}\) log p …………… (2)
on plotting log \(\frac{\mathrm{x}}{\mathrm{m}}\) on y – axis and log p on x axis if a straight line is obtained Freundlich isotherm is valid. The slope of the straight line gives the value of \(\frac{\mathrm{1}}{\mathrm{n}}\). The intercept on n the y – axis give the value of log k.

The factor \(\frac{\mathrm{1}}{\mathrm{n}}\) can have values 0 and 1. Thus equation 2 holds good over a limited range of pressures when \(\frac{\mathrm{1}}{\mathrm{n}}\) = 0, \(\frac{\mathrm{x}}{\mathrm{m}}\) = constant
the adsorption is independent of pressure,
when \(\frac{\mathrm{1}}{\mathrm{n}}\) = 1, \(\frac{\mathrm{x}}{\mathrm{m}}\) = k.p i.e, \(\frac{\mathrm{x}}{\mathrm{m}}\) ∝ p. The adsorption varies directly with pressure. Freundlich adsorption isotherm fails at high pressures.

Question 146.
Give a detailed account of applications of adsorption.
Answer:
The adsorption phenomenon have a number of applications.

1. Production of high vacuum: The traces of air remained in a vessel after evacuation by a vacuum pump can be removed by adsorbing on charcoal to give high vacuum.
2. Gas masks : Gas masks consisting of activated charcoal or mixture of adsorbents adsorb poisonous gases during breathing. These are mainly used by coal miners.
3. Control of humidity : The mositure in air can be decreased by adsorbing it on silica gel or alumina gel thus the humidity in a room can be controlled.
4. Removal of coloured substances: Animal charcoal removes colours of impure coloured solution by adsorbing impurities.
5. Heterogeneous catalysis : Reactant molecules adsorb on the solid catalyst and decrease to activation energy. Thus the reaction proceed fastly.
6. Separation of Inert gases : The inert gases can be separated by adsorbing them on coconut charcoal at different tempe-ratures. This process depends on the difference in the degree of adsorption of gases.
7. In curing diseases : Several drugs kill germs by adsorbing on germs.
8. Froth floatation process: Sulphide ores are concentrated by this method.

Question 147.
What is catalysis ? How is catalysis classified ? Give four examples for each type of catalysis.
Answer:
Substances which accelerate the rate of a slow chemical reaction but whose chemical nature and mass remain unchanged after the reaction are known as catalysts and the phenomenon is known as catalysis.

Catalysis can be broadly divided into two groups.
I) Homogeneous catalysis: When the reactants and the catalyst are in the same phase, i.e., either in liquid or in gas phase, the process is said to be homogeneous catalysis.
Examples:
1) Oxidation of SO₂ to SO₃ in the presence of oxides of nitrogen.

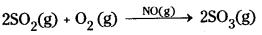
SO₂, O₂ and the catalyst NO are all gases and are in same phase.

2) Hydrolysis of methyl acetate catalysed by H⁺.
CH₃COOCH₃CO + H₂O (l) 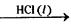CH₃ COOH (aq) + CH₃OH (aq)
Both reactants and the catalyst are in same liquid phase.

3) Hydrolysis of sugar catalysed by H⁺.

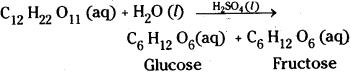
4) In the oxidation of oxalic acid with aqueous KMnO₄ in acid medium Mn²⁺ ion formed during the reaction act as catalyst.
2KMnO₄ (aq) + 3H₂SO₄ (aq) + 3H₂C₂O₄ (aq) →K₂SO₄ (aq) + 2MnSO₄ (aq) + 8H₂O (l) + 10CO₂ (g)

II) Heterogeneous catalysis: The catalytic process in which the reactants and the catalyst are in different phases is known as heterogeneous catalysis.
Examples:
1) Oxidation of SO₂ to SO₃ in the presence of Pt.

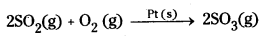
2) Synthesis of ammonia by the reaction of N₂ gas and H₂ gas in the presence of solid iron powder catalyst in Haber’s process.

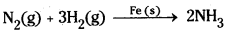
3) Oxidation of ammonia to nitric oxide in the platinum gauze.

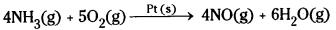
4) Hydrogenation of vegetable oils in the presence of solid nickel as catalyst.

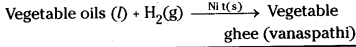
Question 148.
Discuss the mechanism of heterogeneous catalysis.
Answer:
As per old theory the reactant molecules in the gaseous state or in solutions are adsorbed on the surface of the solid catalyst. The increase in concentration of the reactants on the surface increase the rate of reaction. The heat liberated during adsorption is also utilised in increasing the rate of reaction.
According to modern theory.

1. Reactant molecules diffuse on to the surface of catalyst.
2. The reactant molecules adsorb on the surface of the catalyst.
3. Chemical reaction takes place between adsorbed reactant molecules through formation of an intermediate.
4. The product molecules desorb from the catalyst surface making the surface available for more reaction to occur.
5. The product molecules diffuse away from the surface of the catalyst for the adsorption of fresh reactant molecules.

Question 149.
What are enzymes ? Explain in detail the enzyme catalysis with necessary examples.
Answer:
Enzymes are complex nitrogeneous organic . compounds which are produced by living plants and animals. They are mainly protein molecules of high molecular mass and form ‘ colloidal solutions in water. These catalyse numerous reactions that occurs in plants and animals. So they are termed as bio-chemical catalysts and the phenomenon is known as biochemical catalysis.
Mechanism of enzyme catalysed reaction :

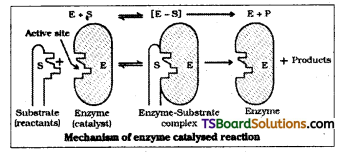
There are a number of cavities present on the surface of colloidal particles of enzymes. These cavities are of characteristic shape and possess active groups such as -NH₂, – COOH, -SH -OH etc. These are the active centres on the surface of enzyme particles. The molecules of the reactant which have complimentary shape fit into these cavities just like a key fits into a lock. The reactant molecule combine with active groups forming an activated complex which decomposes into the products. These reactions may be considered to proceed in two steps.

1. To form an activated complex
   E + S → ES#
2. Decomposition of activated complex to give the product
   ES# → E + P

Examples:
1) Inversion of cane sugar in the presence of invertase.

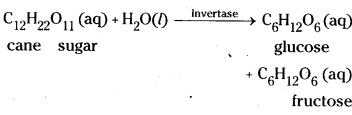
2) Conversion of glucose into ethyl alcohol in the presence of zymase.

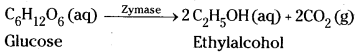
Question 150.
What are colloidal solutions ? How they are classified ? Give examples.
Answer:
A colloidal solution is a heterogeneous system in which one substance is dispersed (dispersed phase) as large particles in another substance (dispersion medium).

Colloids are classified on the basis of the following criteria.
i) Physical states of the dispersed phase and the dispersion medium.

ii) Nature of the interaction between the dispersed phase and the dispersion medium.
Depending upon the nature of interaction between the dispersed phase and dispersion medium the colloidal sols are classified into two types.
a) Lyophilic colloids:
If there is attraction between the dispersion medium and dispersed phase, the colloids are called as lyophilic colloids. Lyophilic means solvent loving or solvent attracting. These can be prepared by direct mixing and can be separated from one another by evaporating. These sols are reversible, so called reversible sols. These are stable and cannot be easily coagulated.

b) Lyophobic colloids :
If there is repulsion between dispersion medium and dispersed phase, the colloids are called lyophobic colloids. Lyophobic means solvent hating. This type of colloids cannot be prepared simply by mixing. They have to be prepared by special methods. These sols are readily precipitated by the addition of small amounts of electrolytes or by heating. The precipitate does not give back the colloidal sol by simple addition of the dispersion medium to it. So these are known as irreversible sols. Lyophobic sols need stabilising agents for their preservation.

If water is the dispersion medium these are called hydrophilic and hydrophobic colloids.

iii) Type of particles of the dispersed phase: :
Depending upon the type of the particles of the dispersed phase colloids are classified as multimolecular, macro. molecular and associated colloids.
a) Multimolecular colloids contain aggregates of atoms or molecules of dispersed phase to from particles of colloidal size, eg: Sulphur sol.

b) Macromolecular colloids contain dispersed phase of macromolecules of colloidal range. e.g. : Starch, cellulose, proteins and enzymes etc.

c) Associated colloids contain aggregates of long non polar hydrocarbon chain along with polar groups such as COOHSO₃H. The hydrocarbon chain is hydrophylic end and polar group is hydrophobic end. These aggregated particles formed are called micelles and also known as associated colloid.

Question 151.
How are colloids classified on the basis of the nature of interaction between a dispersed phase and a dispersion medium ? Describe an important characteristic of each class. Which of the sols need stabilising agents for preservation ?
Answer:
Nature of the interaction between the dis-persed phase and the dispersion medium.
Depending upon the nature of inter-action between the dispersed phase and dispersion medium the colloidal sols are classified into two types.
a) Lyophilic colloids:
If there is attraction between the dispersion medium and dispersed phase, the colloids are called as lyophilic colloids. Lyophilic means solvent loving or solvent attracting. These can be prepared by direct mixing and can be separated from one another by evaporating. These sols are reversible, so called reversible sols. These are stable and cannot be easily coagulated.

b) Lyophobic colloids :
If there is repulsion between dispersion medium and dispersed phase, the colloids are called lyophobic colloids. Lyophobic means solvent hating. This type of colloids cannot be prepared simply by mixing. They have to be prepared by special methods.

These sols are readily precipitated by the addition of small amounts of electrolytes or by heating. The precipitate does not give back the colloidal sol by simple addition of the dispersion medium to it. So these are known as irreversible sols. Lyophobic sols need stabilising agents for their preservation.

If water is the dispersion medium these are called hydrophilic and hydrophobic colloids.

Question 152.
What are micelles ? Discuss the mechanism of micelle formation and cleaning action of soap.
Answer:
Micelles and Mechanisim of micelle for-mation : Certain substances behave as strong electrolytes at low concentrations but at higher concentrations exhibit colloidal behaviour due to the formation of aggregates. These aggregated particles are called micelles or associated colloids.

For example soap is a sodium or potassium salt of higher fatty acid and may be represented as RCOC^– Na⁺ eg. sodium stearate CH₃ (CH₂)₁₆ COO^– Na⁺. It dissociates into RCOO^– and Na⁺ ions when dissolved in water. The RCOO^– ions consists of two parts. The long hydrocarbon chain R (also called non polar tail) which is hydrophobic (water repelling) and a polar group COO^– which is hydrophilic.

The RCOO^– ions are therefore present with their COO^– group into water and hydrocarbon chains (R) staying away from it and remain at the surface. At critical micelle concentration the COO^– Ions are pulled into the bulk of the solution and are aggregated to form spherical shape with their hydrocarbon chain pointing towards the centre of sphere with COO^– part remaining outward on the surface of the sphere. The aggregate thus formed is known as ionic micelle.

Cleaning Action:
The cleansing action of soap is due to the fact that soap molecules form a micelle around the oil droplet in such away that hydrophobic part of the stearate ions is in the oil droplet and hydrophilic part projects out of the grease droplet.

Since the polar groups can interact with water, the oil droplet surrounded by stearate ions is now pulled into water and is removed from the dirty surface. Thus soap helps in emulsification and washing away of oils and fats.

Question 153.
Describe the properties of colloids with necessary diagrams wherever necessary.
Answer:
1) Colligative properties:
Since the colloidal particles are aggregates of small particles, the number of particles in colloidal solution is comparatively less than those in true solution. So the values of colligative properties such as lowering of vapour pressure, elevation in boiling point, depression in freezing point and osmotic pressure are lesser than those shown by true solution at same concentration.

2) Optical properties :
When a beam of light is passed through a colloidal solution the colloidal particles scatter the light in all directions. This scattering of light illuminates the path of beam in colloidal dispersion. This is known as tyndall effect. The bright cone of the light is called Tyndall cone.

Tyndall effect is observed only when the following two conditions are satisfied.

1. The diameter of the colloidal particle should not be much smaller than the wave length of the light used.
2. The refractive indices of the dispersed phase and the dispersion medium should differ greatly in magnitude.
   

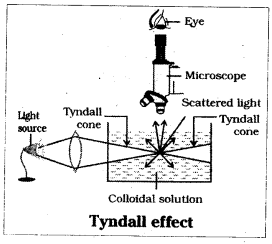
3) Colour :
Colour of colloidal solution depends on the wavelength of light scattered by the colloidal particles. The wavelength depends on the size and shape of the colloidal particle. Large particles scatter shorter wavelength light and vice versa. Spherical particles scatter red light and disc like particles scatter blue light.
The colour of the colloid changes from the direction it is viewed.

4) Kinetic property:
The colloidal particles are in continous zig-zag motion due to bombardment of the molecules of the dispersion medium on collodial particles.

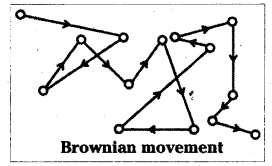
The motion of colloidal particle is independent of the nature of the colloid but depends on the size of the particles and viscosity of the solution.

5) Electrical properties:
Colloidal particles. always carry an electric charge. The charge on the colloidal particle is considered as a fixed layer. It attracts the opposite charge in the solution which forms a second diffused layer. Between these two oppositely charged layers a potential difference arises. This is known as electrokinetic or zeta potential.

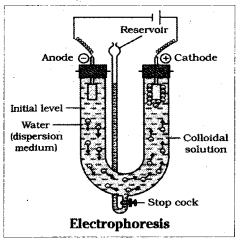
When an emf is applied the colloidal particles move towards cathode or anode depending on the charge present on it. It is known as electrophoresis.
If the movement of colloidal particles is arrested by some suitable means, the dispersion medium moves in the opposite direction. This is known as electro-osmosis.

6) Coagulation or precipitation :
If the charge on the colloidal particles is neutralised by adding a suitable oppositely charged ion, the colloidal particles coagulates or precipitates.

Question 154.
What are emulsions ? How are they classified ? Describe the applications of emulsions. [AP ’17 ; TS ’16]
Answer:
Emulsions are liquid – liquid colloidal system. The dispersion of finely divided droplets in another liquid emulsion. The emulsions are two types.

1. Oil dispersed in water (o/w)
2. Water dispersed in oil (w/o)

a) In o/w type emulsions water is the dispersion medium and oil is dispersion phase eg. milk and vanishing cream.
b) In w/o type emulsions oil is the dispersion medium and water is dispersion phase, eg ; butter

Applications of emulsions:
Emulsions are useful
(a) in the digestion of fats in intestines
(b) in washing processes of clothes and crockery
(c) in the preparation of lotions, creams, ointments in pharmaceuticals and cosmotics
(d) in the extraction of metals
(e) in the conversion of cream into butter by churning.

Intext Questions – Answers

Question 1.
Write any two characteristics of chemisorption.
Answer:

1. Chemisorption is highly specific. It will occur only when there is possibility of chemical bonding between adsorbent and adsorbate.
2. Enthalpy of chemisorption is high (80 – 240 kJmol^-1) since it involves bond formation.

Question 2.
Why does physisorption decrease with increase in temperature ?
Answer:
Adsorption is exothermic process. So according to Le-Chatelier’s principle physical adsorption occurs readily at low temperature and decreases with increasing temperature.

Question 3.
Why are finely powdered substances more effective adsorbents than their non powdered crystal forms ?
Answer:
The extent of adsorption increases with the increase of surface area of the adsorbent. Thus finely divided metals and porous substances having large surface areas are good adsorbents.

Question 4.
Hydrogen used in Haber’s process is obtained by reacting methane with steam in presence of NiO as catalyst. The process is known as steam reforming. Why is it necessary to remove CO formed in steam reforming when ammonia is obtained by Haber’s process ?
Answer:
The CO present in hydrogen act as poison to the molybdenum acting as promoter for iron which is used as catalyst. So it is necessary to remove CO from H₂ obtained by steam reforming during the manufacture of ammonia by Haber’s process.

Question 5.
Why is ester hydrolysis slow in the beginning but is fast after sometime ?
Answer:
Ester hydrolysis is slow in the beginning and becomes faster after sometime. This is because of the formation of acetic acid during the reaction which act as catalyst.

Question 6.
What is the role of desorption in the process of adsorption catalysts ?
Answer:
Desorption of reaction products from the surface of catalyst and there by making the surface available again for adsorption of reactants. Thus more reactions takes place.

Question 7.
What modification can you suggest in the Hardy – Schulze law ?
Answer:
Hardy-Schulze law states that greater the valence of the coagulating ion added, greater is its power to cause coagulation. Instead of valence by using charge we can say greater the charge on the coagulating ion added more is its coagulating power.

Question 8.
Why is it essential to wash the precipitate in gravimetric chemical analysis with wash liquid before drying and weighing it quantitatively ?
Answer:
The ions present in the solution will be adsorbed on the solid precipitate in gravimetric chemical analysis. This gives erronious results. On washing the precipitate with wash liquid before drying and weighing it quantitatively the adsorbed ions will be removed.

Telangana TSBIE TS Inter 2nd Year Chemistry Study Material 5th Lesson General Principles of Metallurgy Textbook Questions and Answers.

TS Inter 2nd Year Chemistry Study Material 5th Lesson General Principles of Metallurgy

Very Short Answer Questions (2 Marks)

Question 1.
What is the role of depressant in froth floatation ?
Answer:
It is possible to separate a mixture of two sulphide ores by adjusting proportion of oil to water or by using depressants in froth floatation process. For example, in the case of an ore containing ZnS and PbS, the depresent used is NaCN. It selectively prevents ZnS from coming to the froth but allows PbS to come with froth. NaCN forms a layer of Na₂ [Zn(CN)₄] on the surface of ZnS.

Question 2.
Between C and CO, which is a better reducing agent at 673K ?
Answer:
At 673K, CO is a better reducing agent than C.

Question 3.
Name the common elements present in the anode mud in the electrolytic refining of copper.
Answer:
Impurities from the blister copper deposit as anode mud which contains antimony, selenium, tellurium, silver, gold and platinum.
These elements are so present because they are less basic and less reactive.

Question 4.
State the role of silica in the metallurgy of copper. [IPE ’14]
Answer:
Silica removes FeO present as an impurity in the form of slag FeSiO₃.

Question 5.
Explain “poling”. [AP ’16, ’15]
Answer:
Poling is a metal refining process. The molten metal is stirred with logs (poles) of green wood. The impurities are removed as gases. Blister copper is purified by this method. The reducing gases evolved from the wood, prevent the oxidation of copper.

Question 6.
Describe a method for the refining of nickel.
Answer:
Nickel is refined by vapour phase refining.
Mond’s process: In this process, nickel is heated in a stream of carbon monoxide forming a volatile complex, nickel tetra carbonyl.

The carbonyl is subjected to higher temperature so that it is decomposed giving the pure metal.

Question 7.
How is cast iron different from pig iron ?
Answer:
The iron obtained from blast furnace contains about 4% carbon and many impurities in smaller amount (eg : S, P, Si, Mn). This is known as pig iron.

Cast iron is different from pig iron and is made by melting pig iron with scrap iron and coke using hot air blast. It has slightly lower carbon content (about 3%) and is extremely hard and brittle.

Question 8.
What is the difference between a mineral and an ore ?
Answer:
Minerals are naturally occurring chemical compounds in the earth’s crust. Out of many minerals of the metal, only a few minerals are chemically and commercially viable, to be used as sources for the extraction of the metal. Such minerals are known as ores.

Question 9.
Why copper matte is put in silica lined converter?
Answer:
Iron is converted to slag by heating copper ore with silica. Iron silicate and copper are produced in the form of copper matte. This contains Cu₂S and FeS.
When O₂ is passed it converts the FeS into FeO.
2FeS + 3O₂ → 2FeO + 2SO₂
Silica is used to remove FeO as iron silicate slag.
FeO + SiO₂ → Fe SiO₃

Question 10.
What is the role of cryolite in the metallurgy of aluminium? [TS ’16, ’15]
Answer:
The role of cryolite is to

1. increase electrical conductivity,
2. to dissolve alumina,
3. to lower the melting point of alumina.

Question 11.
How is leaching carried out in the case of low grade copper ores ?
Answer:
Copper is extracted by hydrometallurgy from low grade ores. It is leached out using acid or bacteria. The solution containing Cu⁺² is treated with scrap iron (or) H₂.
Cu⁺²_(aq) + H_2(g) → Cu_(s) + 2H⁺_(aq)

Question 12.
Why is zinc not extracted from zinc oxide through reduction using CO ?
Answer:
Zinc is not extracted from zinc oxide through reduction by using CO because ∆G value for the reduction reaction is + ve.
2ZnO + 2CO → 2Zn^– + 2CO₂, ∆G = + 200 kJ

Question 13.
Give the composition of the following alloys. [AP & TS Mar. 19; (Mar. 2018/1 7; IPE 14)]
a) Brass
b) Bronze
c) German silver
Answer:
a) Brass contains Cu 60% and Zn 40%.
b) Bronze contains Cu 60-80% and Sn 20-40%.
c) German silver contains Cu 25-40%, Zn 25-35%, Ni 40-50%.

Question 14.
Explain the terms gangue and slag.
Answer:
Ore is usually contaminated with earthy materials and undesired chemical compounds. These are collectively known as gangue or matrix.
Flux reacts with gangue forming slag. Slag can be removed in the liquid form as it has lower melting point than gangue.
eg: Flux + gangue → slag
FeO + SiO₂ → FeSiO₃

Question 15.
How is Ag or Au obtained by leaching from the respective ores ?
Answer:
In the metallurgy of silver and that of gold, the respective metals are leached with a dilute solution of NaCN or KCN in the presence of air. From the leached solution, the metal is obtained through displacement by zinc.

Question 16.
What are the limitations of Ellingham diagram ?
Answer:
Ellingham diagram normally consists of plots of ∆_fG° vs T for formation of oxides of elements. Such diagrams help us in predicting the feasibility of thermal reduction of an ore.
Limitations:

1. The graph simply indicates whether a reaction is possible or not. i.e., the tendency of reduction with a reducing agent is indicated. It does not say about the kinetics of the reduction process.
2. The interpretation of ∆G^⊖ is based on K. (∆G^⊖ = – RT In K). Thus it is presumed that the reactants and products are in equilibrium. This is not always true because the reactant / product may be solid.

Question 17.
Write any two ores with formulae of the following metals: [TS ’15; IPE ’14]
a) Aluminium
b) Zinc
c) Iron
d) Copper
Answer:

Question 18.
What is matte ? Give its composition. [AP ’15]
Answer:
During the extraction of copper from copper pyrites, the product of blast furnace consists of Cu₂S and a little of FeS. This product is known as matte. This contains Cu₂S and FeS.

Question 19.
What is blister copper? Why is it so called? [Mar. 2018 – TS]
Answer:
During the extraction of copper from copper pyrites, when the matte formed is subjected to Bessemerisation, a liquid solution of copper is formed.
2Cu₂O + Cu₂S → 6Cu + SO₂.
It has blistered appearance due to evolution of SO₂ and so it is called blister copper.

Question 20.
Explain magnetic separation of impurities from an ore.
Answer:

If either the ore or the gangue is capable of being attracted by a magnetic roller, magnetic separation is carried out. The powdered ore is carried on a conveyer belt which passes over a magnetic roller. The magnetic substance collects near the magnetic roller while non-magnetic material will collect away from the roller.
Ex : Haematite containing tin stone impurity is purified by this method.

Question 21.
What is flux ? Give an example.
Answer:
During metallurgical operations, a foreign substance is added to the ore to remove the gangue. This substances called flux. This can be removed with the help of perforated ladder.
Flux + gangue → slag
In the extraction of copper SiO₂ is used as a flux to remove FeO.

Question 22.
Give two uses each of the following metals:
a) Zinc
b) Copper
c) Iron
d) Aluminium
Answer:
Uses:
a) Zinc :

1. Zinc is used for galvanising iron.
2. Zinc is used as reducing agent in the manufacture of paints, dye-stuff’s etc.
3. Used in large quantities in batteries.

b) Copper:

1. Used in several alloys, eg : Brass (Cu and Zinc)
2. Making wires in electrical industry.

c) Iron:

1. Cast iron is used for casting stoves, railway sleepers, etc.
2. Wrought iron is used making wires, bolts, agricultural implements.

d) Aluminium :

1. Aluminium foils are used as wrapers for chocolates.
2. Aluminium is used in the extraction of chromium and manganese from their oxides.
3. Aluminium wires are used as electrical conductors.

Question 23.
Between C and CO, which is a better reducing agent for ZnO ?
Answer:
Coke is a better reducing agent for ZnO and not CO.

Question 24.
Give the uses of
a) Cast iron
b) Wrought iron
c) Nickel steel
d) Stainless steel
Answer:
a) Cast iron is used for casting stoves, railway sleepers, gutter pipes, toys etc.
It is used in the manufacture of wrought iron and steel.
b) Wrought iron is used in making anchors, wires, bolts, chains and agricultural implements.
c) Nickel steel is used for making cables, automobiles and aeroplane parts, pendulum and measuring tapes.
d) Stainless steel is used for cycles, auto-mobiles, utensils, pens etc.

Question 25.
How is aluminium useful in the extraction of chromium and manganese from their oxides ?
Answer:
Aluminium is a reducing agent because of its electropositive character, in the extraction of chromium and manganese from their oxides
Cr₂O₃ + 2Al → Al₂O₃ + 2Cr + heat
3Mn₃O₄ + 8 Al → 4Al₂O₃ + 9 Mn + heat

Short Answer Questions (4 Marks)

Question 26.
Copper can be extracted by hydrometallurgy but not zinc – explain.
Answer:
Zinc cannot be extracted by hydrometallurgy as it is a highly electropositive metal.

The E° value of Cu²⁺ / Cu is more than that of hydrogen while E° value of Zn⁺²/ Zn is less than that of H₂. Therefore, Cu⁺² can be reduced to Cu by H₂ but not zinc.
Cu⁺⁺; (aq) + H₂(g) → Cu(s) + 2H⁺ (aq)

Question 27.
Why is the extraction of copper from pyrites more difficult than that from its oxide ore through reduction ?
Answer:
Pyrites cannot be reduced by carbon (or) hydrogen because the ∆G⁰ of Cu₂S is greater than ∆G⁰ of Cu₂O. Hence the sulphide ore is first converted into oxide and then reduced.
Copper pyrites contains iron as impurity. The iron can be removed only by using silica with which it forms a slag.
FeO + SiO₂ → FeSiO₃

Question 28.
Explain Zone refining.
Answer:
Zone refining is based on the principle that the impurities are more soluble in the melt s than in the solid state of the metal.

A circular mobile heater is fixed at one end of a rod of the impure metal. The molten zone moves along with the heater which is moved forward. As the heater moves for-ward, the pure metal crystallises out of the rnetal and impurities pass on into the adjacent molten zone.

As this process is repeated, the impurities get concentrated at one end. This end is cut off. This method is very useful for producing semiconductor grade metals of very high purity, eg : germanium, silicon, boron.

Question 29.
Write down the chemical reactions taking place in the extraction of zinc from zinc blende.
Answer:
Zinc blende
Concentrated by froth floatation
↓
Concentrated ore
Roasting in air – The concentrated ore is roasted in the presence of excess air at about 1200k to form zinc oxide
↓

Reduction of ZnO with coke at in a fire clay retort to zinc.metal.
↓

Purification by fractional distillation or electrolysis using impure zinc as anode, white sheet of pure zinc as cathode and ZnSO₄ solution acidified with dil. H₂SO₄ as electrolyte
↓
Pure zinc metal

Question 30.
Write down the chemical reactions taking place in different zones in the blast furnace during the extraction of iron.
Answer:
Oxide ores of iron are mixed with limestone and coke and fed into a blast furnace from its top.

Hot air is blown from the bottom of the furnace and burnt to give temperature upto 2200 K in the lower portion itself. In upper part, the temperature is lower, and the iron oxides coming from top are reduced in steps to FeO.
At 500 – 800 K (lower temp, range upper part of blast furnace)
3 Fe₂O₃ + CO → 2Fe₃O₄ + CO₂
Fe₃O₄ + 4CO → 3Fe + 4CO₂
Fe₂O₃ + CO → 2FeO + CO₂
At 900 – 1500 K (higher temp. range)
C + CO₂ → 2CO
FeO + CO →Fe + CO₂
CaCO₃ → CaO + CO₂
CaO + SiO₂ → CaSiO₃
Limestone is decomposed to CaO which removes silicate impurity of the ore as CaSiO₃ slag.

Question 31.
How is alumina separated from silica in the bauxite ore associated with silica ? Give equations. [TS ’15]
Answer:
Bauxite ore associated with silica impurity is called white bauxite. It is purified by serpeck’s process. In this process the bauxite is mixed with coke and heated in the presence of N₂ at 2075 K . Silica is reduced to silicon and escapes as vapour.
Al₂O₃ + 3C + N₂ → 2AlN + 3CO

The AlN is hydrolysed to form aluminium hydroxide.
AlN + 3H₂O → Al(OH)₃ + NH₃
The Al(OH)₃ ppt is filtered, washed, dried and ignited then pure alumina is formed.
2Al(OH)₃ → Al₂O₃ + 3H₂O

Question 32.
Giving examples to differentiate roasting and calcination. [AP & TS ’16 ; IPE ’14] [Mar. 19, ’18 – TS]
Answer:
i) Calcination involves heating of the ore in the absence of air just below its fusion temperature. Volatile matter escapes leaving behind the metal oxide. Calcination makes the ore porous and is made in reverberatory furnace.
Fe₂O₃ . xH₂O (S) Fe₂O₃(s) + xH₂O (g)
ZnCO₃ (s) ZnO (s) + CO₂ (g)
CaCO₃ . MgCO₃ (s) CaO(s) + MgO (s) + 2CO₂ (g)

ii) Roasting :
In roasting, the ore is heated in a regular supply of air in a furnace, at a temperature, below the melting point of the metal.
The ore loses sulphur as its oxide leaving behind oxide of the metal. Roasting is done in reverberatory or blast furnace.
2 ZnS + 3O₂ → 2ZnO + 2SO₂
2 PbS + 3O₂ → 2PbO + 2SO₂

Question 33.
The value of ∆G° for the formation of Cr₂O₃ is – 540 kJmol^-1 and that of Al₂O₃ is -827 kJ mol^-1. Is the reduction of Cr₂O₃ possible with Al ?
Answer:
The height of the line in an Ellingham diagram indicates instability of the oxide since the higher the line, more positive the ∆G, the less spontaneous the formation of the oxide.
Cr₂O₃ + 2Al → 2Cr + Al₂O₃
2Cr(s) + \(\frac{3}{2}\) O₂(g) → Cr₂O₃(s)
2Al(s) + \(\frac{3}{2}\) O₂ (g) → Al₂O₃ (s)
The line for oxidation of Cr is above that of Al. This means Cr₂O₃ is less stable than Al₂O₃ at all temperatures and Al will be able to reduce Cr₂O₂ to Cr. Thus, the lower the ∆G, line on the Ellingham diagram, the more stable is the compound. Hence reduction of Cr₂O₃ by Al is energetically favourable.

Question 34.
What is the role of graphite rod in the electrometallurgy of aluminium ?
Answer:
In the electrometallurgy of aluminium, a fused mixture of alumina, cryolite and fluorspur is electrolysed using graphite rod as anode and graphite lined iron as cathode.

During electrolysis, Al is liberated at cathode and CO, CO₂ are liberated at anode.

If some other metal is used as anode, instead of graphite then O₂ liberated will not only oxidise the metal of the electrode but could also convert some of the Al liberated at cathode back to Al₂O₃.

So the role of graphite rod in the electrometallurgy of aluminium is to prevent the liberation of O₂ at anode which may oxidise some of the liberated aluminium back to Al₂O₃.

Question 35.
Outline the principles of refining of metals by the following methods.
a) Zone refining
b) Electrolytic refining
c) Poling
d) Vapour phase refining
Answer:
a) Zone refining :
Impurities are more soluble in the melt than in the solid state of the metal. A circular mobile heater is fixed at one end of a rod of the impure metal. The molten zone moves along with the heater which is moved forward. As the heater moves forward the pure metal crystallises out of the metal and impurities pass on into the adjacent molten zone. The process is repeated several times and the heater is moved in the same direction from one end to the other end. At one end, impurities get concentrated. This end is cut off. Ex : Germanium.

b) Electrolytic refining :
Impure metal is used as anode. A strip of the same metal in pure form is used as cathode. They are put in a suitable electrolytic bath containing soluble salt of the same metal. The required metal gets deposited on the cathode in the pure form. The metal, constituting the impurity goes as the anode mud.

c) Poling :
In this method, the molten metal is stirred with logs of green wood. Then, the impurities are removed either as gases or they get oxidised and form Scum over the surface of the molten metal.
Ex : Blister copper is purified by this method. The reducing gases, evolved from the wood, prevent the oxidation of copper.

d) Vapour phase refining:
In this method, the metal is converted into its volatile compound and collected elsewhere. It is then decomposed to give pure metal.
Mond process for refining nickel: In this process, nickel is heated in a stream of carbon monoxide forming a volatile complex, nickel tetra carbonyl.

The carbonyl is subjected to higher temperature so that it is decomposed giving the pure metal.

Question 36.
Predict the conditions under which Al might be expected to reduce MgO.
Answer:
Aluminium can reduce MgO to Mg only at temperature above 1350°C. Only at T > 1350°C, AG’f becomes more than ∆G°f of Al₂O₃ as per Ellingham diagram used as cathode. Electrolyte is the acidified solution of the salt of the same metal. The required metal gets deposited on the cathode in the pure form. The metal, constituting the impurity goes as the anode mud.
Anode : M → Mⁿ⁺ + ne^–
Cathode : Mⁿ⁺ + ne^– → M (Pure metal)
Copper is refined using electrolytic method. Anodes are of impure copper and pure copper. Copper strips are taken as cathode. Acidified copper sulphate solution is the electrolyte. Result of electrolysis is the transfer of copper in pure form from anode to the cathode.
Anode : Cu → Cu⁺⁺ + 2e^–
Cathode : Cu⁺⁺ + 2e → Cu

Question 37.
Explain the purification of sulphide ore by froth floatation method. [ Mar. ’18 AP] [AP Mar. 19; (AP ‘ 17, 15; TS ‘ 15)]
Answer:
In this process ore is powdered and made into a slurry with water. A rotating paddle is used to agitate the suspension in presence of an oil. Froth is formed which carries mineral particles. To this slurry froth collectors and stabilisers are added. Collectors (pine oil, xanthate) enhance non – wettability of the mineral particles. Froth stabilisers (e.g. cresols, aniline) stabilise the froth. The mineral particles become wet by oils while gangue particles become wet by water. The froth is light and is skimmed off. The ore particles are then obtained from the froth.

Question 38.
Explain the process of leaching of alumina from bauxite.
Answer:
Leaching often used if the ore alone but not the gangue is soluble in same suitable solvent.

Bauxite is usually contains SiO₂, iron oxides, and Titanium oxide as impurity. The powdered ore is digested with a concentrated solution of NaOH at 473 – 523 K and 35 – 36 bar pressure. Al₂O₃ is leached out as sodium aluminate leaving the other impurities behind.
Al₂O₃ (S) + 2NaOH + 3 H₂O (l) → 2Na[Al(OH)₄] (aq)
The aluminate is alkaline in nature and is neutralised by passing CO₂ gas and hydrated Al₂O₃ is precipitated.

At this stage freshly precipitated hydrated Al₂O₃ is added. Precipitation of Al₂O₃. xH₂O is obtained.
2Na[Al(OH)₄] (aq) + CO₂(g) → Al₂O₃ . x H₂O (s) + 2NaHCO₃ (aq)
The sodium silicate remains in solution and the insoluble hydrated alumina is filtered; dried and heated to give pure Al₂O₃.
Al₂O₃. x H₂O (s) Al₂O₃(S) + xH₂O(g)

Question 39.
What is Ellingham diagram ?
What information can be known from this in the reduction of oxides ?
Answer:
a) Ellingham diagram consists of plots of \(\Delta \mathrm{G}_{\mathrm{f}}^{\mathrm{o}}\) vs T for formation of oxides of elemens.
2 x M (s) + O₂ (s) → 2 M_xO
In this reaction, the gaseous amount is decreasing from left to right due to the consumption of gases leading to negative value of ∆S which changes the value of ∆G in the equation ∆G = ∆H – T∆S subsequently shifts towards higher side despite rising T.

b) Each plot is a staright line except when some change in phase (s → liq or liq → g) takes place. The temperature at which such change occurs is indicated by an increase in the slope on +ve side.

c) There is a point in a curve below which ∆G is negative. So M_xO is stable. Above this point M_xO decomposes on its own.

d) The height of the line in Ellingham diagram indicates instability of the oxide.

Uses : Ellingham diagram provides a basis for considering the choice of reducing agent in the reduction of oxides such diagram helps in predicting the feasibility of thermal reduction of an ore.

Question 40.
How is copper extracted from copper pyrites ?
Answer:
In the Ellingham diagram, the 4 Cu + O₂ → 2 Cu₂O line is at the top. So it is quite easy to reduce Cu₂O to Cu directly by heating with coke.
Most of the Cu ores are sulphides and some contain iron.
Ores :

1. Copper iron pyrites Cu FeS₂
2. Copper glance Cu₂S

First stage : Sulphide ores are purified by froth floatation.

Second stage :
Roasting of the sulphide ore.
2Cu₂S + 3O₂ → 2Cu₂O + 2SO₂
2FeS + 3O₂ → 2FeO + 2SO₂
In actual practice, the ore is heated in a reverberatory furnace after mixing with silica. FeO is removed by using silica as flux.
FeO + SiO₂ → FeSiO₃
Copper is produced in the form of copper matte. This contains Cu₂S and FeS.

Third stage :
Copper matte is then charged into silica lined convertor. Hot air is blown and some silica is added. FeS is converted to FeO. Cu₂S / Cu₂0 is converted to metallic copper.
2FeS + 3O₂ → 2FeO + 2SO₂
2Cu₂S + 3O₂ → 2Cu₂O + 2SO₂
2Cu₂0 + Cu₂S → 6 Cu + SO₂
The solidified copper has blister appearance due to evolution of SO₂. Hence it is called blister copper.

Fourth stage :
Copper is refined using electrolytic method. Anodes are of impure copper and pure copper strips are taken as cathode. Electrolysis is carried out using acidified CuSO₄ solution.
Anode : Cu → Cu⁺⁺ + 2e^–
Cathode : Cu⁺⁺ + 2e → Cu
Flow diagram :
Copper pyrites CuFeS₂
Froth floatation
↓
Concentrated ore
Roasting (volatile impurities escape) Formation of Cu₂S and FeS.
↓
Roasted ore
Mixed with coke and sand
FeS eliminated as FeSiO₃
↓
Matte Cu₂S + FeS
Hot air and sand
Cu₂O and Cu₂S give copper
↓
Blister copper
Refining poling and electrolysis
↓
Pure copper metal.

Question 41.
Explain the extraction of zinc from zinc blende.
Answer:
Ores :

1. Zinc blende ZnS
2. Calamine ZnCO₃

Zinc blende is purified by froth floatation. Now the concentrated ore is subjected to roasting.
2ZnS + 3O₂ → 2ZnO + 2SO₂
Zinc oxide is reduced with coke.

The metal is distilled and collected by rapid chilling. Very pure zinc is obtained by electrolysis. Acidified CuSO₄ solution is taken as electrolyte. Impure zinc is taken as anode and pure zinc is taken as anode. On passing current pure zinc gets deposited on the cathode.
Extraction of Zinc :.
Zinc blende ZnS
Cone, by froth floatation
↓
Concentrated ore
Roasting in air
↓
ZnO
Reduction with coke at 1673 K
↓
Zinc
Purification by fractional distillation / electrolysis
↓
Pure zinc metal

Question 42.
Explain smelting process in the extraction of copper.
Answer:
The copper pyrites is heated in a reverberatory furnace after mixing with silion the furnace, iron oxide slags as iron silicate and copper is produced in the form of copper matte. This Contains Cu₂S and FeS.
FeO + SiO₂ → FeSiO₃ (Slag)
Copper matte is then charged into silica lined converter. Some silica is also added and hot air blast is blown to convert remaining FeS to FeO and Cu₂S / Cu₂O to the metallic copper.
2FeS + 3O₂ →2FeO + 2SO₂
2 Cu₂S + 3O₂ → 2 Cu₂O + 2SO₂
FeO + SiO₂ → FeSiO₃
2Cu₂0 + Cu₂S → 6 Cu + SO₂

Question 43.
ExplaIn electrometallurgy with an example.
Answer:
Electrometallurgy :
Metallurgy involving
the use of electric are furnace, electrolysis and other electrical operations is called electrometallurgy.

Electrolytic reduction of alumina :
Al₂O₃ is mixed with Na₃AlF₆ and fluorspar CaF₂. The function cryolite is to lower the melt ing point of Al₂O₃ and CaF₂ increases electrical conductivity. Electrolysis is carried out in an iron take lines inside with graphite which acts as cathode. A number of carbon rods, suspended in the electrolyte acts as anode. The temperature is maintained at 1175 to 1225 K and current is passed. Following reactions takes place.
Na₃AlF₆ → 3 NaF₃ + AlF₃
4 AlF₃ → 4 Al⁺³ + 12F^–
At cathode : 4Al⁺³ + 12e → 4 Al
At anode: 12F^– → 6F₂ + 12e
F₂ formed at anode reacts with alumina and form AlF₃.
2 Al₂O₃ + 6F₂ → 4 AlF₃ + 3O₂
Anode : Graphite
Cathode : Steel
At anode : C + O^2- → CO(g) + 2e^–
C (s) + 2O^2- → CO₂ (g) + 4e^–
At cathode : Al³⁺ (melt) + 3e^– → Al (l)
The oxygen liberated at anode reacts with the carbon of anode producing CO and CO₂.
Therefore, anode has to be replaced periodically.

The overall reaction is
2 Al₂O₃ + 3C → 4 Al + 3CO₂
This process is known as Hall – Heroult process.

Question 44.
Explain briefly the extraction of aluminium from bauxite.
Answer:
1) Bauxite is digested with hot cone. NaOH at 523K. Al₂O₃ dissolves. Impurities are filtered off.
Al₂O₃ + 2 NaOH + 3H₂O (l) → 2Na [Al(OH)₄] aq
The aluminate is alkaline in nature and is neutralised by passing CO₂ gas. Al₂O₃ is precipitated.
2Na [Al (OH)₄] (aq) + CO₂ (g) → Al₂O₃. x H₂O + 2NaHCO₃.
The sodium silicate remains in the solution and the insoluble hydrated alumina is filtered, dried and heated to give pure Al₂O₃.
Al₂O₃. X H₂O Al₂O₃ (s) + xH₂O(g)

2) The purified Al₂O₃ is mixed with Na₃ AlF₆ or CaF₂ which lower the melting point of the mix and also increases conductivity. The fused matrix is electrolysed.

Steel vessel with lining of carbon acts as cathode and graphite anode is used. The overall reaction may be 2Al₂O₃ + 3C → 4Al + 3CO₂.
Reactions: At cathode Al³⁺ (melt) + 3e^– → Al
At anode C(s) + O^2- (melt) → CO (g) + 2e^–
C(s) + 2O^2- (melt) → CO₂ (g) + 4e^–
Flow Diagram :
Bauxite Al₂O₃ . 2H₂O digested with hot cone. NaOH Al₂O₃ dissolves – impurities eliminated
Na [Al (OH)₄]
CO₂ bubbled
Al (OH)₃ PPt
heated at 1473K
Pure alumina
electrolysis of alumina mixed with molten cryolite or
CaF₂ at 1200 K using carbon lining of cell – cathode
carbon rods – anode.
Pure aluminium metal.

Long Answer Questions (8 Marks)

Question 45.
The choice of a reducing agent in a particular case depends on thermodynamic factor. Explain with two examples.
Answer:
Consider the reduction of Cr₂O₃ by Al.
Cr₂O₃ + 2 Al → 2 Cr + Al₂O₃
2Cr (s) + \(\frac{3}{2}\) O₂(g) → Cr₂O₃ (s)
and 2 Al (s) + \(\frac{3}{2}\) O₂ (s) → Al₂O₃(s)
The line for oxidation of Cr is above that of Al. This means Cr₂O₃ is less stable than Al₂O₃ at all temperatures and Al will be able to reduce Cr₂O₃ to Cr. Thus, the lower the ∆G line on the Ellingham diagram, the more stable the compound. Hence, reduction of Cr₂O₃ by Al is energetically favourable.

Ex : 2 – The lower the line in Ellingham diagram, the more stable the oxide. Hence if Mg is heated with ZnO, it will reduce to zinc, but the reverse redaction does not occur.
Mg + ZnO → MgO + Zn

Question 46.
Discuss the extraction of zinc from zinc blende.
Answer: R
Ores :

1. Zinc blende ZnS
2. Calamine ZnCO₃

Zinc blende is purified by froth floatation. Now the concentrated ore is subjected to roasting.
2ZnS + 3O₂ → 2ZnO + 2SO₂
Zinc oxide is reduced with coke.

The metal is distilled and collected by rapid chilling. Very pure zinc is obtained by electrolysis. Acidified CuSO₄ solution is taken as electrolyte. Impure zinc is taken as anode and pure zinc is taken as anode. On passing current pure zinc gets deposited on the cathode.
Extraction of Zinc :.
Zinc blende ZnS
Cone, by froth floatation
↓
Concentrated ore
Roasting in air
↓
ZnO
Reduction with coke at 1673 K
↓
Zinc
Purification by fractional distillation / electrolysis
↓
Pure zinc metal

Question 47.
Explain the reactions occurring in the blast furnance in the extraction of iron.
Answer:
In the Blast furnace, reduction of iron oxides takes place in different temperature ranges. Oxides ores of iron are mixed with limestone and coke and fed into blast furnace from its top. Hot air is blown from the bottom of the furnace and coke is burnt to give temperature upto about 2200 K in the lower portion itself. The CO and heat moves to upper part of the furnace.

At 500 – 800 K:-
3 Fe₂O₃ + CO → 2Fe₃O₄ + CO₂
Fe₃O₄ + 4CO → 3Fe + 4CO₂
Fe₂O₃ + CO → 2FeO + CO₂

At 900- 1500K:-
C + CO₂ → 2CO
FeO + CO → Fe + CO₂
Limestone is also decomposed to CaO which removes silicate impurity as slag.
CaCO₃ → CaO + CO₂
CaO + SiO₂ → CaSiO₃ (slag)
The slag is in molten state and separates and from iron. This contains 4% C, and impurities (eg : P, S, Si, Mn). This is known as pig iron.

Flow Chart:
Haematite Fe₂O₃
Crushed ore is washed with stream of water.
↓
Concentrated ore
Roasting in air / calcination moisture and volatile impurities are w eliminated FeO changes to Fe₂O₃
↓
Calcinated ore
Calcincated ore, coke and limestone in 8 : 4 : 1 reduced by CO in blast 4, furnace SiO₂ remove as CaSiO₃
↓
Pigiron

Question 48.
Discuss the extraction of copper from copper pyrites.
Answer:
In the Ellingham diagram, the 4 Cu + O₂ → 2 Cu₂O line is at the top. So it is quite easy to reduce Cu₂O to Cu directly by heating with coke.
Most of the Cu ores are sulphides and some contain iron.
Ores :

1. Copper iron pyrites Cu FeS₂
2. Copper glance Cu₂S

First stage : Sulphide ores are purified by froth floatation.

Second stage :
Roasting of the sulphide ore.
2Cu₂S + 3O₂ → 2Cu₂O + 2SO₂
2FeS + 3O₂ → 2FeO + 2SO₂
In actual practice, the ore is heated in a reverberatory furnace after mixing with silica. FeO is removed by using silica as flux.
FeO + SiO₂ → FeSiO₃
Copper is produced in the form of copper matte. This contains Cu₂S and FeS.

Third stage :
Copper matte is then charged into silica lined convertor. Hot air is blown and some silica is added. FeS is converted to FeO. Cu₂S / Cu₂0 is converted to metallic copper.
2FeS + 3O₂ → 2FeO + 2SO₂
2Cu₂S + 3O₂ → 2Cu₂O + 2SO₂
2Cu₂0 + Cu₂S → 6 Cu + SO₂
The solidified copper has blister appearance due to evolution of SO₂. Hence it is called blister copper.

Fourth stage :
Copper is refined using electrolytic method. Anodes are of impure copper and pure copper strips are taken as cathode. Electrolysis is carried out using acidified CuSO₄ solution.
Anode : Cu → Cu⁺⁺ + 2e^–
Cathode : Cu⁺⁺ + 2e → Cu
Flow diagram :
Copper pyrites CuFeS₂
Froth floatation
↓
Concentrated ore
Roasting (volatile impurities escape) Formation of Cu₂S and FeS.
↓
Roasted ore
Mixed with coke and sand
FeS eliminated as FeSiO₃
↓
Matte Cu₂S + FeS
Hot air and sand
Cu₂O and Cu₂S give copper
↓
Blister copper
Refining poling and electrolysis
↓
Pure copper metal.

Question 49.
Explain the various steps involved in the extraction of aluminium from bauxite.
Answer:
1) Bauxite is digested with hot cone. NaOH at 523K. Al₂O₃ dissolves. Impurities are filtered off.
Al₂O₃ + 2 NaOH + 3H₂O (l) → 2Na [Al(OH)₄] aq
The aluminate is alkaline in nature and is neutralised by passing CO₂ gas. Al₂O₃ is precipitated.
2Na [Al (OH)₄] (aq) + CO₂ (g) → Al₂O₃. x H₂O + 2NaHCO₃.
The sodium silicate remains in the solution and the insoluble hydrated alumina is filtered, dried and heated to give pure Al₂O₃.
Al₂O₃. X H₂O Al₂O₃ (s) + xH₂O(g)

2) The purified Al₂O₃ is mixed with Na₃ AlF₆ or CaF₂ which lower the melting point of the mix and also increases conductivity. The fused matrix is electrolysed.

Steel vessel with lining of carbon acts as cathode and graphite anode is used. The overall reaction may be 2Al₂O₃ + 3C → 4Al + 3CO₂.
Reactions: At cathode Al³⁺ (melt) + 3e^– → Al
At anode C(s) + O^2- (melt) → CO (g) + 2e^–
C(s) + 2O^2- (melt) → CO₂ (g) + 4e^–
Flow Diagram :
Bauxite Al₂O₃ . 2H₂O digested with hot cone. NaOH Al₂O₃ dissolves – impurities eliminated
Na [Al (OH)₄]
CO₂ bubbled
Al (OH)₃ PPt
heated at 1473K
Pure alumina
electrolysis of alumina mixed with molten cryolite or
CaF₂ at 1200 K using carbon lining of cell – cathode
carbon rods – anode.
Pure aluminium metal.

Intext Questions – Answers

Question 1.
Which ores can be separated by magnetic separation ?
Answer:
Ores in which one of the components is .agnetic can be concentrated eg : ores containing iron.
Ex : Haematite Fe₂O₃
Magnetite Fe₃O₄
Siderite FeCO₃
Iron pyrites FeS₂

Question 2.
What is the significance of leaching in the extraction of aluminium ?
Answer:
Leaching is significant as it helps in removing impurities like SiO₂, Fe₂O₃ etc. from bauxite ore.

Question 3.
Suggest a condition under winch magnesium could reduce alumina.
i) \(\frac{4}{3}\)Al + O₂ → 2/3 Al₂O₃
ii) 2 Mg + O₂ → 2MgO
Answer:
In the Ellingham diagram at the point of inter-section of Al₂O₃ and MgO, the ∆G^O becomes zero for the reaction.
2/3 Al₂O₃ + 2 Mg → 2 MgO + 4/3 Al.
Below that point, magnesium can reduce alumias.

Question 4.
The reaction Cr₂O₃ + 2Al → Al₂O₃ + 2Cr is thermodynamically feasible. Why does it not take place at room temperature.
Answer:
Certain amount of activation energy is essential even for such reactions which are thermodynamically feasible, therefore heating is required.

Question 5.
Is it true that under certain conditions, Mg can reduce Al₂O₃ and A1 can reduce MgO. What are those conditions ?
Answer:
Yes, below 1350°C Mg can reduce Al₂O₃ and above 1350°C, Al can reduce MgO. This can be inferred from ∆G^O vs T plots.

Question 6.
At a site, low grade copper ores are available and zinc and iron scraps are available. Which of the two scraps would be more suitable for reducing leached copper ore and why ?
Answer:
Zinc being above in electrochemical series, the reduction will be fast if zinc is used. But zinc is costlier than iron. So using iron scraps will be advisable and advantageous.

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Differential Equations Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Differential Equations Important Questions Very Short Answer Type

Question 1.
Find the order and degree of the differential equation \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\). [(TS) May ’18; May ’13]
Solution:
Given differential equation is \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\)
Cubing on both sides we get,
\(\left(\frac{d^2 y}{d x^2}\right)^3=\left[1+\left(\frac{d y}{d x}\right)^2\right]^5\)
∴ Order = Order of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2
Degree = The degree of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 3

Question 2.
Find the order and degree of \(1+\left(\frac{d^2 y}{d x^2}\right)^2=\left[2+\left(\frac{d y}{d x}\right)^2\right]^{3 / 2}\)
Solution:
Given differential equation is \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\)
Cubing on both sides,
\(\left(\frac{d^2 y}{d x^2}\right)^3=\left[1+\left(\frac{d y}{d x}\right)^2\right]^5\)
The given equation is a polynomial equation in \(\frac{d^2 y}{d x^2}, \frac{d y}{d x}\)
Hence, \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) is the highest derivative occurring in the equation.
Its order = 2
The degree = 3

Question 3.
Find the order and degree of \(\left[\left(\frac{d y}{d x}\right)^{1 / 2}+\left(\frac{d^2 y}{d x^2}\right)^{1 / 3}\right]^{1 / 4}=0\). [May ’12]
Solution:
Given differential equation is

∴ Order = Order of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2
Degree = The degree of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2

Question 4.
Find the order and degree of \(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\). [May ’14]
Solution:
Given differential equation is \(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\)
It is a polynomial equation in \(\frac{d^3 y}{dx^3}, \frac{d y}{d x}\)
Hence, \(\frac{\mathrm{d}^3 \mathrm{y}}{\mathrm{dx}^3}\) is the highest derivative occurring in the equation.
Its order = 3
degree = 2

Question 5.
Find the order and degree of \(x^{1 / 2}\left(\frac{d^2 y}{d x^2}\right)^{1 / 3}+x \frac{d y}{d x}+y=0\). [(AP) Mar. ’18, (TS) ’15]
Solution:

It is a polynomial equation in \(\frac{d^2 y}{d x^2} \& \frac{d y}{d x}\)
Hence \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) is the highest derivative occurring in the equation.
Order = 2
Degree = 1

Question 6.
Find the order and degree of \(\left[\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3\right]^{6 / 5}=6 y\). [(TS) May ’17, ’15; (AP) Mar. ’16, May ’15]
Solution:
Given differential equation is
\(\left[\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^3\right]^{6 / 5}=6 y\)
\(\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3=(6 y)^{5 / 6}\)
∴ Order = Order of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2
Degree = The degree of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 1

Question 7.
Form the differential equation corresponding to y = cx – 2c², where c is a parameter. [Mar. ’19 (AP) ’12]
Solution:
The given equation is y = cx – 2c², where ‘c’ is a parameter. ……..(1)
Differentiating with respect to x on both sides
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = c – 0
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = c ……..(2)
From (1) and (2),
y = \(x\left(\frac{d y}{d x}\right)-2\left(\frac{d y}{d x}\right)^2\)
which is the required differential equation.

Question 8.
Form the differential equation corresponding to y = A cos 3x + B sin 3x, where A and B are parameters. [(TS) Mar. ’20, May ’16; (AP) Mar. ’15; May ’14]
Solution:
The given equation is y = A cos 3x + B sin 3x where A, B are parameters. …….(1)
Differentiate with respect to ‘x’ on both sides
y1 = A (-sin 3x) 3 + B (cos 3x) 3 = -3A sin 3x + 3B cos 3x
Again differentiate with respect to ‘x’ on both sides
y2 = -3A (cos 3x) 3 + 3B (-sin 3x) 3
= -9A cos 3x – 9B sin 3x
= -9 (A cos 3x + B sin 3x)
= -9y (from (1))
∴ \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) + 9y = 0 or y² + 9y = 0
which is the required differential equation.

Question 9.
Form the differential equation corresponding to y = a cos(nx + b), where a, b are parameters. [(AP) May ’17]
Solution:
Given y = a cos(nx + b) ……..(1)
(a, b are parameters)
Diff. (1) w.r. to x on both sides we get,
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a[-sin(nx + b) (n)] = -an sin(nx + b) ……….(2)
Again diff. (2) w.r.to x on both sides we get,
\(\frac{d^2 y}{d x^2}\) = -an [cos(nx + b) n]
= -an² cos(nx + b)
= -n²y (from (1))
Required D.E is \(\frac{d^2 y}{d x^2}\) + n2y = 0

Question 10.
Find the order and degree of the differential equation of the family of all circles with their centres at the origin. [(TS) Mar. ’17, ’11]
Solution:
Equation of the family of circles with their centres at the origin is x² + y² = r²
Differentiate with respect to ‘x’ we get,
2x + 2y \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
⇒ x + y \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
∴ Order = Order of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1
Degree = The degree of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1

Question 11.
Obtain the differential equation which corresponds to the rectangular hyperbolas which have the coordinate axes as asymptotes.
Solution:
The equation of the family of the rectangular hyperbolas which have the coordinate axes as asymptotes are xy = c² …….(1)
where c is a parameter
Diff. (1) w.r. t. x on both sides, we get
x \(\frac{d y}{d x}\) + y = 0
∴ Required D.E is x \(\frac{d y}{d x}\) + y = 0

Question 12.
Find the general solution of x + y \(\frac{d y}{d x}\) = 0. [(AP) May ’16]
Solution:
Given D.E is x + y \(\frac{d y}{d x}\) = 0
x dx + y dy = 0
Integrating on both sides we get
∫x dx + ∫y dy = c
\(\frac{x^2}{2}+\frac{y^2}{2}\) = c
x² + y² = 2c
Which is the required solution of D.E.

Question 13.
Find the general solution of \(\frac{d y}{d x}=\frac{2 y}{x}\). [(TS) Mar. ’19, (AP) ’17]
Solution:
Given D.E. is \(\frac{d y}{d x}=\frac{2 y}{x}\)
⇒ \(\frac{1}{y} d y=\frac{2}{x} d x\)
⇒ \(\int \frac{1}{y} d y=\int \frac{2}{x} d x\)
⇒ log y = 2 log x + log c
⇒ log y = log x² + log c
⇒ log y = log(x²c)
⇒ y = cx² is the required D.E

Question 14.
Find the general solution of \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x+y. [(TS) Mar. ’18]
Solution:
Given \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x+y
⇒ \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x . e^y
⇒ e^-y dy = e^x dx
⇒ ∫e^-y dy = ∫e^x dx
⇒ -e^-y = e^x + c
⇒ e^x + e^-y = c

Question 15.
Find the general solution of \(\sqrt{1-x^2} d y+\sqrt{1-y^2} d x=0\)
Solution:
Given D.E is \(\sqrt{1-x^2} d y+\sqrt{1-y^2} d x=0\)

sin^-1(y) = -sin^-1(x) + c
sin^-1(x) + sin^-1(y) = c
Which is the required general solution.

Question 16.
Solve \(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\). [(TS) May ’19]
Solution:
Given differential equation is
\(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
⇒ \(\frac{d y}{1+y^2}=\frac{d x}{1+x^2}\)
Integrating on both sides
\(\int \frac{d y}{1+y^2}=\int \frac{d x}{1+x^2}\)
tan^-1(y) = tan^-1(x) + c
Which is the required solution.

Question 17.
Solve \(\frac{\mathbf{d y}}{\mathbf{d x}}\) + 1 = e^x+y
Solution:

Question 18.
Form the differential equation corresponding to the family of circles passing through the origin and having centres on the Y-axis.
Solution:
The equation of the family of circles passing through the origin and having centres on the Y-axis is x² + y² + 2fy = 0 …….(1)
where f is a parameter.
Diff. (1) w.r. to ‘x’ on both sides, we get

Question 19.
Find the order of the differential equation corresponding to y = Ae^x + Be^3x + Ce^5x. (A, B, C being parameters)
Solution:
Given equation is y = Ae^x + Be^2x + Ce^5x, (A, B, C are parameters)
Here, no. of arbitrary constants = 3
∴ The order of D.E = 3

Question 20.
Form the differential equation corresponding to xy = ae^x + be^-x where a, b are parameters. [(AP) May ’19]
Solution:
Given xy = ae^x + be^-x ……..(1)
(a, b are parameters)
Diff. (1) with respect to x on both sides, we get

Question 21.
Obtain the differential equation which corresponds to the ellipses with centres at the origin and having coordinate axes as axes.
Solution:
The equation of the family of ellipses with centres at the origin and having coordinate axes as axes is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ……..(1)
(a, b are arbitrary constants)
Diff. (1) w.r. t. x on both sides, we get

Which is the required solution.

Question 22.
Find the I.F of (cos x) \(\frac{d y}{d x}\) + y sin x = tan x.
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) + y tan x = sec x . tan x
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q,
where P = tan x, Q = sec x tan x
I.F = e^{∫P dx}
= e^{∫tan x dx}
= e^{log|sec x| x}
= sec x

Question 23.
Find I.F of x \(\frac{d y}{d x}\) – y = 2x² sec²2x.
Solution:
Given diff. equation is x \(\frac{d y}{d x}\) – y = 2x² sec²2x
Dividing with x on both sides we get,
\(\frac{\mathrm{dy}}{\mathrm{dx}}-\frac{\mathrm{y}}{\mathrm{x}}\) = 2x sec²2x
\(\frac{d y}{d x}+\left(\frac{-1}{x}\right) y\) = 2x sec²2x
It is a linear diff. equation in y of the first order.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
We get P = \(\frac{-1}{x}\), Q = 2x sec²2x

Question 24.
Find the order of the differential equation obtained by eliminating the arbitrary constants b and c from xy = ce^x + be^-x + x².
Solution:
Given equation is xy = ce^x + be^-x + x²
order of the differential equation = number of arbitary constants = 2.

Question 25.
Form the differential equation of the family of curves y = (a + bx) e^kx where a, b are parameters.
Solution:
Given equation is y = (a + bx) e^kx ……..(1)
a, b are arbitrary constants
differentiating (1) w.r.t ‘x’ on both sides, we get

Again differentiating (2) w.r.t ‘x’ on both sides

Which is the required differential equation.

Question 26.
Form the differential equation of the family of curves y = ax² + bx, where a, b are parameters.
Solution:
Given equation is y = ax² + bx ……..(1)
a, b are arbitrary constants
differentiating (1) w.r.t ‘x’ on both sides
\(\frac{d y}{d x}\) = a(2x) + b(1)
\(\frac{d y}{d x}\) = 2ax + b …….(2)
Again differentiating (2) w.r.t ‘x’ on both sides


Which is the required differential equation.

Question 27.
Form the differential equation of the family of curves ax² + by² = 1, where a, b are parameters.
Solution:
Given equation is ax² + by² = 1 …….(1)
a, b are parameters
differentiating (1) w.r.t ‘x’ on both sides

Again differentiating (2) w.r.t ‘x’ on both sides

Which is the required differential equation.

Question 28.
Form the differential equation of the family of curves xy = ax² + \(\frac{b}{x}\), where a, b are parameters.
Solution:
Given equation is xy = ax² + \(\frac{b}{x}\)
xy = \(\frac{a x^3+b}{x}\)
x²y = ax³ + b …….(1)
a, b are parameters
differentiating (1) w.r.t ‘x’ on both sides
x² \(\frac{d y}{d x}\) + y . 2x = a . 3x² + 0
x² \(\frac{d y}{d x}\) + 2xy = 3ax² ……..(2)
Again differentiating (2) w.r.t ‘x’ on both sides

Substitute the value of ‘a’ in (2)

Which is the required D.E.

Question 29.
Find the differential equation of the family of circles that touch the y-axis at the origin.
Solution:
The equation of the family of circles that touch the y-axis at the origin is x² + y² + 2gx = 0 …….(1)
g is a parameter.
differentiating (1) w.r.t ‘x’ on both sides, we get
2x + 2y \(\frac{d y}{d x}\) + 2g = 0
x + y \(\frac{d y}{d x}\) + g = 0
∴ g = -x – y \(\frac{d y}{d x}\)
Substitute the value of ‘g’ in (1)
x² + y² + 2x[-x – y \(\frac{d y}{d x}\)] = 0
x² + y² – 2x² – 2xy \(\frac{d y}{d x}\) = 0
y² – x² – 2xy \(\frac{d y}{d x}\) = 0
Which is the required D.E.

Question 30.
Obtain the D.E. corresponding to the parabolas each of which has a latus rectum 4a and whose axis is parallel to the x-axis.
Solution:
The equation of the family of parabolas each of which has a latus rectum 4a and whose axis is parallel to the x-axis is
(y – k)² = 4a(x – h) ……..(1)
h, k are parameters differentiating (1) w.r.t ‘x’ on both sides, we get
2(y – k) \(\frac{d y}{d x}\) = 4a(1 – 0)
\(\frac{d y}{d x}\) . 2(y – k) = 4a
\(\frac{d y}{d x}\) (y – k) = 2a …….(2)
Again differentiating (2) w.r. t ‘x’ on both sides, we get


Which is the required D.E.

Question 31.
Obtain the D.E. corresponding to the parabolas having their focus at the origin and axis along the x-axis.
Solution:
The equation of the family of parabolas having their foci at the origin and axis along the x-axis is
y² = 4a(x + a) ……..(1), ‘a’ is a parameter
differentiating (1) w.r.t ‘x’ on both sides


Which is the required D.E.

Question 32.
Express the D.E. \(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\) of f(x) dx + g(y) dy = 0.
Solution:
Given differential equation is \(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
\(\frac{d y}{1+y^2}=\frac{d x}{1+x^2}\)
\(\frac{d x}{1+x^2}-\frac{d y}{1+y^2}=0\)
This is of the form f(x) dx + g(y) dy = 0

Question 33.
Express the D.E. y – x \(\frac{d y}{d x}\) = a(y² + \(\frac{d y}{d x}\)) in the form of f(x) dx + g(y) dy = 0.
Solution:
Given D.E. is y – x \(\frac{d y}{d x}\) = a(y² + \(\frac{d y}{d x}\))

This is of the form f(x) dx + g(y) dy = 0.

Question 34.
Express the D.E. \(\frac{d y}{d x}\) = e^x-y + x² e^-y in the form of f(x) dx + g(y) dy = 0.
Solution:
Given D.E. is \(\frac{d y}{d x}\) = e^x-y + x² e^-y
⇒ \(\frac{d y}{d x}\) = e^x . e^-y + x² e^-y
⇒ \(\frac{d y}{d x}\) = e^-y (e^x + x²)
⇒ \(\frac{d y}{e^{-y}}\) = (e^x + x²) dx
⇒ e^y dy = (e^x + x²) dx
⇒ (e^x + x²) dx – e^y dy = 0
This is of the form f(x) dx + g(y) dy = 0

Question 35.
Express the D.E. \(\frac{d y}{d x}\) + x² = x² e^3y in the form of f(x) dx + g(y) dy = 0.
Solution:
Given D.E. is \(\frac{d y}{d x}\) + x² = x² e^3y
⇒ \(\frac{d y}{d x}\) = x² e^3y – x²
⇒ \(\frac{d y}{d x}\) = x² (e^3y – 1)
⇒ \(\frac{\mathrm{dy}}{\mathrm{e}^{3 \mathrm{y}}-1}\) = x² dx
⇒ x² dx – \(\frac{\mathrm{dy}}{\mathrm{e}^{3 \mathrm{y}}-1}\) = 0
This is of the form f(x) dx + g(y) dy = 0.

Question 36.
Show that f(x, y) = 4x²y + 2xy² is a homogeneous function of degree 3.
Solution:
Given f(x, y) = 4x²y + 2xy²
Now, f(kx, ky) = 4(kx)² (ky) + 2(kx) (ky)²
= 4k² . x² . ky + 2kx . k²y²
= k³ (4x²y + 2xy²)
= k³ f(x, y)
∴ f(x, y) is a homogeneous function of degree 3.

Question 37.
Show that g(x, y) = \(x y^{1 / 2}+y x^{1 / 2}\) is a homogeneous function of degree 3/2.
Solution:
Given g(x, y) = \(x y^{1 / 2}+y x^{1 / 2}\)

∴ g(x, y) is a homogeneous function of degree 3/2.

Question 38.
Show that h(x, y) = \(\frac{x^2+y^2}{x^3+y^3}\) is a homogeneous function of degree = 1.
Solution:
Given h(x, y) = \(\frac{x^2+y^2}{x^3+y^3}\)

∴ h(x, y) is a homogeneous function of degree -1.

Question 39.
Show that f(x, y) = 1 + e^x/y is a homogeneous function of x and y.
Solution:
Given f(x, y) = 1 + e^x/y
Now f(kx, ky) = 1 + \(e^{\left(\frac{k x}{k y}\right)}\)
= 1 + e^x/y
= k⁰ f(x, y)
Hence, f(x, y) is a homogeneous function of degree ‘0’.

Question 40.
Show that f(x, y) = \(x \sqrt{x^2+y^2}-y^2\) is a homogeneous function of x and y.
Solution:
Given f(x, y) = \(x \sqrt{x^2+y^2}-y^2\)

Hence f(x, y) is a homogeneous function of degree 2.

Question 41.
Show that f(x, y) = x – y log y + y log x is a homogeneous function of x and y.
Solution:
Given f(x, y) = x – y log y + y log x
Now f(kx, ky) = kx – ky log (ky) + (ky) log (kx)
= kx – ky (log k + log y) + ky (log k + log x)
= kx – ky log y – ky log k + ky log k + ky log x
= kx – ky log y + ky log x
= k(x – y log y + y log x)
= k f(x, y)
Hence, f(x, y) is a homogeneous function of degree 1.

Question 42.
Express \(\left(1+e^{x / y}\right) d x+e^{x / y}\left(1-\frac{x}{y}\right) d y=0\) in the form of \(\frac{\mathbf{d x}}{\mathbf{d y}}=\mathbf{F}\left(\frac{\mathbf{x}}{\mathbf{y}}\right)\).
Solution:

Which is the required form.

Question 43.
Express \(\frac{\mathbf{d y}}{\mathbf{d x}}=\frac{\mathbf{y}}{x+y \cdot e^{\frac{-2 x}{y}}}\) in the form \(\frac{\mathbf{d x}}{\mathbf{d y}}=\mathbf{F}\left(\frac{x}{\mathbf{y}}\right)\).
Solution:

Which is the required form.

Question 44.
Express x dy – y dx = \(\sqrt{x^2+y^2}\) in the form \(F\left(\frac{y}{x}\right)=\frac{d y}{d x}\).
Solution:
Given equation is x dy – y dx = \(\sqrt{x^2+y^2}\) dx

Which is in the required form.

Question 45.
Express \(\left(x-y \tan ^{-1} \frac{y}{x}\right) d x+x \tan ^{-1} \frac{y}{x} d y=0\) in the form \(F\left(\frac{y}{x}\right)=\frac{d y}{d x}\).
Solution:
Given equation is

Which is in the required form.

Question 46.
Express x \(\frac{d y}{d x}\) = y(log y – log x + 1) in the form \(F\left(\frac{y}{x}\right)=\frac{d y}{d x}\).
Solution:
Given equation is x \(\frac{d y}{d x}\) = y(log y – log x + 1)
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{y}}{\mathrm{x}}\left[\log \left(\frac{\mathrm{y}}{\mathrm{x}}\right)+1\right]=\mathrm{F}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\)
Which is in the required form.

Question 47.
Transform the D.E. x log x \(\frac{d y}{d x}\) + y = 2 log x.
Solution:
Given D.E. is x log x \(\frac{d y}{d x}\) + y = 2 log x
dividing both sides by x log x, we get
\(\frac{d y}{d x}+\frac{y}{x \log x}=\frac{2 \log x}{x \log x}\)
\(\frac{\mathrm{dy}}{\mathrm{dx}}+\frac{\mathrm{y}}{x \log x}=\frac{2}{\mathrm{x}}\)
Which is in the form \(\frac{d y}{d x}\) + Py = Q
It is linear in y.
Here P = \(\frac{1}{x \log x}\), Q = \(\frac{2}{\mathrm{x}}\)

Question 48.
Transform the D.E. (x + 2y³) \(\frac{\mathrm{dy}}{\mathrm{d} x}\) = y
Solution:
Given D.E. is (x + 2y³) \(\frac{\mathrm{dy}}{\mathrm{d} x}\) = y

Which is in the form \(\frac{\mathrm{dx}}{\mathrm{d} y}\) + Px = Q
It is linear in x.
Here P = \(\frac{-1}{y}\), Q = 2y².

Question 49.
Find the I.F of the D.E. (2x – 10y³) \(\frac{d y}{d x}\) + y = 0 by transforming it into a linear form.
Solution:
Given D.E. is (2x – 10y³) \(\frac{d y}{d x}\) + y = 0
(2x – 10y³) \(\frac{d y}{d x}\) = -y

Question 50.
Find the I.F of the D.E. y . \(\frac{\mathrm{dx}}{\mathrm{dy}}\) – x = 2y³ by transforming it into linear form.
Solution:
Given D.E. is y . \(\frac{\mathrm{dx}}{\mathrm{dy}}\) – x = 2y³
dividing both sides by ‘y’ we get
\(\frac{\mathrm{dx}}{\mathrm{dy}}-\frac{\mathrm{x}}{\mathrm{y}}\) = 2y²
Which is in the form \(\frac{\mathrm{dx}}{\mathrm{dy}}\) + Px = Q
It is linear in x.
Here P = \(\frac{-1}{y}\), Q = 2y²

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Partial Fractions Important Questions to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Partial Fractions Important Questions

Question 1.
Resolve \(\frac{5 x+1}{(x+2)(x-1)}\) into partial fractions. [May 2000]
Solution:
Let \(\frac{5 x+1}{(x+2)(x-1)}=\frac{A}{x+2}+\frac{B}{x-1}\)
= \(\frac{A(x-1)+B(x+2)}{(x+2)(x-1)}\)
⇒ 5x + 1 = A (x – 1) + B (x + 2)
Put x = – 2 then 5 (- 2) + 1 = A (- 2 – 1)
⇒ – 3A = – 9
⇒ A = 3
Put x = 1 then 5(1) + I = B(1 + 2)
⇒ 3B = 6
⇒ B = 2
∴ \(\frac{5 x+1}{(x+2)(x-1)}=\frac{3}{x+2}+\frac{2}{x-1}\).

Question 2.
Resolve \(\frac{3 x+7}{x^2-3 x+2}\) into partial fractions. [May ’14]
Solution:
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-1)(x-2)}\)
Let \(\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\)
= \(\frac{A(x-2)+B(x-1)}{(x-1)(x-2)}\)
3x + 7 = A (x – 2) + B (x – 1)
Put x = 1 then 3(1) + 7 = A (1 – 2)
⇒ 3 + 7 = A (- 1)
⇒ 10 = – A
⇒ A = – 10
Put x = 2 then 3(2) + 7 = B(2 – 1)
⇒ 6 + 7 = B(1)
⇒ B = 13
∴ \(\frac{3 x+7}{(x-1)(x-2)}=\frac{-10}{x-1}+\frac{13}{x-2}\).

Question 3.
Resolve \(\frac{x+4}{\left(x^2-4\right)(x+1)}\) into partial fractions. [Mar. ‘14]
Solution:

Question 4.
Resolve \(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}\) into partial fractions. [March 2008].
Solution:

Put x = – 3
⇒ C (- 6 + 3) = 9 – 39 + 15
⇒ C(- 3) = – 15
⇒ C = 5
Now, comparing the coefficients of x² in equation (1), we get
A + 2B = 1
⇒ – 1 + 2B = 1
⇒ 2B = 2
⇒ B = 1
∴ \(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}=\frac{-1}{2 x+3}+\frac{1}{x+3}+\frac{5}{(x+3)^2}\).

Question 5.
Resolve \(\frac{1}{(x-1)^2(x-2)}\) into partial fractions. [May 2013].
Solution:
Let \(\frac{1}{(x-1)^2(x-2)}\) = \(\frac{A}{(x-1)}+\frac{B}{(x-1)^2}+\frac{C}{(x-2)}\)
⇒ \(\frac{1}{(x-1)^2(x-2)}\) = \(\frac{A(x-1)(x-2)+B(x-2)+C(x-1)^2}{(x-1)^2(x-2)}\)
⇒ A (x – 1) (x – 2) + B (x – 2) + C (x – 1)² = 1 …………….(1)
If x = 1
⇒ B(- 1) = 1
⇒ B = – 1
If x = 2
⇒ C(1) = 1
⇒ C = 1
Now, comparing the coefficients of x² in equation (1) we get,
A + C = 0
⇒ A = – 1
∴ \(\frac{1}{(x-1)^2(x-2)}=\frac{(-1)}{x-1}+\frac{(-1)}{(x-1)^2}+\frac{1}{x-2}\).

Question 6.
Resolve \(\frac{2 x^2+2 x+1}{x^3+x^2}\) into partial fractions. [TS – MAr. 2017]
Solution:
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}\)
Let \(\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
\(\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A x(x+1)+B(x+1)+C\left(x^2\right)}{x^2(x+1)}\)
⇒ Ax (x + 1) + B (x + 1) + Cx² = 2x² + 2x + 1 …………….(1)
If x = 0
⇒ B(1) = 1
⇒ B = 1
If x = – 1
⇒ C(- 1)² = 2(1)² – 2 + 1
⇒ C = 1.
Now, comparing the coeff. of x² on both sides of (1) we get,
A+ C = 2
⇒ A + 1 = 2
⇒ A = 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\).

Question 7.
Resolve \(\frac{3 x-18}{x^3(x+3)}\) into partial fractions.
Solution:
Let \(\frac{3 x-18}{x^3(x+3)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+3}\)
\(\frac{3 x-18}{x^3(x+3)}\) = \(\frac{\mathrm{Ax}^2(\mathrm{x}+3)+\mathrm{Bx}(\mathrm{x}+3)+\mathrm{C}(\mathrm{x}+3)+\mathrm{Dx}^3}{\mathrm{x}^3(\mathrm{x}+3)}\)
⇒ Ax² (x + 3) + Bx (x + 3) + C (x + 3) + D(x³) = 3x – 18 ………………(1)
If x = 0
⇒ C(3) = – 18
⇒ C = – 6
If x = – 3
⇒ D (- 27) = – 9 – 18
⇒ D = 1
Now, comparing the coeff. of x³ in (1) we get,
A + D = 0
⇒ A + 1 = 0
⇒ A = – 1
Now, comparing the coeff. of x² in (1) we get,
3A + B = 0
⇒ 3(- 1) + B = 0,
⇒ B = 3
∴ \(\frac{3 x-18}{x^3(x+3)}=\frac{(-1)}{x}+\frac{3}{x^2}+\frac{(-6)}{x^3}+\frac{1}{x+3}\).

Question 8.
Resolve \(\frac{3 x^2-8 x^2+10}{(x-1)^4}\) into partial fractions. [March 2006]
Solution:
Let x – 1 = y
⇒ x = y + 1

Question 9.
Resolve \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\) into partial fractions. [March ’11, 2007, June ’11, TS – Mar. ’18, AP – MAr. 2015; MAy ’12, ’01]
Solution:
Let \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\)
\(\frac{\mathrm{A}\left(\mathrm{x}^2+2\right)+(\mathrm{Bx}+\mathrm{C})(\mathrm{x}-1)}{(\mathrm{x}-1)\left(\mathrm{x}^2+2\right)}=\frac{2 \mathrm{x}^2+3 \mathrm{x}+4}{(\mathrm{x}-1)\left(\mathrm{x}^2+2\right)}\)
A(x² + 2) + (Bx + C) (x – 1) = 2x² + 3x + 4 ……………….(1)
Put x = 1
⇒ A (1 + 2) = 2 + 3 + 4
⇒ A(3) = 9
⇒ A = 3.
From (1),
⇒ 2x² + 3x + 4 = Ax² + 2A + Bx² – Bx + Cx – C
Now, comparing the coefficients of x2 we get,
A + B = 2
⇒ 3 + B = 2
⇒ B = – 1
Comparing coefficients of x we get,
⇒ – B + C = 3
⇒ 1 + C = 3
⇒ C = 2
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{(-1) x+2}{x^2+2}\)
= \(\frac{3}{x-1}+\frac{-x+2}{x^2+2}\).

Question 10.
Resolve \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\) into partial fractions. [May ‘09, ‘07, Mar. ‘12, ‘09, ‘05]
[AP – Mar. ‘17, ’16. May ’16; Board Paper].
Solution:
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\)
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A\left(x^2+1\right)+(B x+C)(x+2)}{(x+2)\left(x^2+1\right)}\)
A (x² + 1) + (Bx + C) (x + 2) = x – 3 ……………….(1)
If x = – 2
⇒ A (4 + 1) = 4 – 3
⇒ A = \(\frac{1}{5}\)
From (1),
⇒ Ax² + A + Bx² + 2Bx + Cx + 2C = x² – 3
Now, comparing coeff. of x² on both sides of (1) we get,
A + B = 1
⇒ \(\frac{1}{5}\) + B = 1
⇒ B = 1 – \(\frac{1}{5}\)
⇒ B = \(\frac{4}{5}\)
Comparing coeff. of x on both sides of (1) we get
2B + C = 0
⇒ \(\frac{8}{5}\) + C = O
⇒ C = \(\frac{-8}{5}\)
∴ \(\frac{x^2-3}{(z+2)\left(x^2+1\right)}=\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\).

Question 11.
Resolve \(\frac{2 x^2+1}{x^3-1}\) into partial fractions.
Solution:
\(\frac{2 x^2+1}{x^3-1}=\frac{2 x^2+1}{(x-1)\left(x^2+x+1\right)}\)
Let \(\frac{2 x^2+1}{(x-1)\left(x^2+x+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+x+1}\)
\(\frac{2 x^2+1}{(x-1)\left(x^2+x+1\right)}=\frac{A\left(x^2+x+1\right)+(B x+C)(x-1)}{(x-1)\left(x^2+x+1\right)}\)
A (x² + x + 1) + (Bx + C) (x – 1) = 2x² + 1 ……………….(1)
If x = 1
⇒ A (3) = 3
⇒ A = 1
From (1),
⇒ Ax² + Ax + A + Bx² – Bx + Cx – C = 2x² + 1
Now comparing coeff. of x² on both sides of (1) we get,
A + B = 2
⇒ 1 + B = 2
⇒ B = 1
Now, comparing coeff. of x on both sides of (1) we get, —-
A – B + C = 0
⇒ 1 – 1 + C = 0
⇒ C = 0
∴ \(\frac{2 x^2+1}{x^3-1}=\frac{1}{x-1}+\frac{x}{x^2+x+1}\).

Question 12.
Resolve \(\frac{\mathbf{x}^3}{(\mathbf{x}-\mathbf{a})(\mathbf{x}-\mathbf{b})(\mathbf{x}-\mathbf{c})}\) into partial fractions. [TS – MAy ’16, ’15, May ’08] [TS – Mar. 2019]
Solution:

Question 13.
Resolve \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\) into partial fractions.
Solution:
Let \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\)
= \(\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{x+2}+\frac{C}{x-3}\)
= \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\)
= \(\frac{(2 \mathrm{x}-1)(\mathrm{x}+2)(\mathrm{x}-3)+2 \mathrm{~A}(\mathrm{x}+2)(\mathrm{x}-3)+2 B(2 \mathrm{x}-1)(\mathrm{x}-3)+2 \mathrm{C}(2 \mathrm{x}-1)(\mathrm{x}+2)}{2(2 \mathrm{x}-1(\mathrm{x}+2)(\mathrm{x}-3)}\)
2x³ = (2x – 1) (x + 2) (x -3) + 2A (x + 2) (x – 3) + 2B (2x – 1) (x – 3) + 2C (2x – 1) (x + 2)
If x = \(\frac{1}{2}\)
⇒ 2A(\(\frac{1}{2}\) + 2) (\(\frac{1}{2}\) – 3) = 2 . \(\frac{1}{8}\)
⇒ 2A . \(\frac{5}{2}\) . \(\frac{-5}{2}\) = \(\frac{1}{4}\)
A = \(-\frac{1}{50}\)
If x = – 2
⇒ 2B (2 (- 2) – 1) (- 2 – 3) = – 2 (8)
⇒ 2B (- 5) (- 5) = – 16
B = \(\frac{-8}{25}\)
If x = 3
⇒ 2C (6 – 1) (3 + 2) = 2 (27)
⇒ 2C (5) (5) = 2(27)
C = \(\frac{27}{25}\)
∴ \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\) = \(\frac{1}{2}+\frac{\frac{-1}{50}}{2 x-1}+\frac{\left(\frac{-8}{25}\right)}{x+2}+\frac{\frac{27}{25}}{x-3}\)
= \(\frac{1}{2}-\frac{1}{50(2 x-1)}-\frac{8}{25(x+2)}+\frac{27}{25(x-3)}\).

Question 14.
Resolve \(\frac{x^4}{(x-1)(x-2)}\) into partial fractions. [TS – Mar. ’16, Mar. ’13, ’10]
Solution:

15x – 14 = A (x – 2) + B (x – 1)
If x = 1
⇒ A(1 – 2) = 15 – 14
⇒ A = – 1
If x = 2
⇒ B(2 – 1) = 15 (2) – 14
⇒ B = 30 – 14
⇒ B = 16
∴ \(\frac{x^4}{(x-1)(x-2)}\) = x² + 3x + 7 – \(\frac{1}{(x-1)}+\frac{16}{(x-2)}\).

Question 15.
Find the coefficient of x⁴ in the expansion \(\frac{3 x}{(x-2)(x+1)}\) of in powers of x. [Mar. ’89, ’97]
Solution:
Let \(\frac{3 x}{(x-2)(x+1)}=\frac{A}{x-2}+\frac{B}{x+1}\)
\(\frac{3 x}{(x-2)(x+1)}=\frac{A(x+1)+B(x-2)}{(x-2)(x+1)}\)
⇒ A(x + 1) + B(x – 2) = 3x
If x = 2
⇒ A(3) = 6
⇒ A = 2
If x = – 1
⇒ B (- 3) = -3
⇒ B = 1

Question 16.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x-4}{x^2-5 x+6}\) specfying the region in which the expansion is valid. [May 2010]
Solution:
Given, \(\frac{x-4}{x^2-5 x+6}=\frac{x-4}{(x-3)(x-2)}\)
Let \(\frac{x-4}{(x-3)(x-2)}=\frac{A}{(x-3)}+\frac{B}{(x-2)}\)
\(\frac{\mathrm{x}-4}{(\mathrm{x}-3)(\mathrm{x}-2)}=\frac{\mathrm{A}(\mathrm{x}-2)+\mathrm{B}(\mathrm{x}-3)}{(\mathrm{x}-3)(\mathrm{x}-2)}\)
⇒ A(x – 2) + B (x – 3) = x – 4
If x = 3
⇒ A(1) = – 1
⇒ A = – 1
If x = 2
⇒ B (- 1) = – 2
⇒ B = 2
∴ \(\frac{x-4}{(x-3)(x-2)}=\frac{(-1)}{x-3}+\frac{2}{x-2}\)
Now, \(\frac{-1}{x-3}+\frac{2}{x-2}=\frac{-1}{-3\left(1-\frac{x}{3}\right)}+\frac{2}{(-2)\left(1-\frac{x}{2}\right)}\)
= \(\frac{1}{3}\) (1 – \(\frac{x}{3}\))^-1 – (1 – \(\frac{x}{2}\))^-1 ………….(1)
Now, (1 – \(\frac{x}{3}\))^-1 expansion is valid when
|\(\frac{x}{3}\)| < 1
⇒ |x| < 3
(1 – \(\frac{x}{3}\))^-1 expansion is valid when
|\(\frac{x}{2}\)| < 1
⇒ |x| < 2
Thus, if |x| < 2, both the above expansions are valid.
Hence, we get from (1)
\(\frac{-1}{x-3}+\frac{2}{x-2}\) = \(\frac{1}{3}\left[1+\frac{x}{3}+\left(\frac{x}{3}\right)^2+\ldots \ldots+\left(\frac{x}{3}\right)^n+\ldots \ldots\right]\) – \(\left[1+\frac{\mathrm{x}}{2}+\left(\frac{\mathrm{x}}{2}\right)^2+\ldots \ldots\left(\frac{\mathrm{x}}{2}\right)^{\mathrm{n}}+\ldots .\right]\)
∴ Coeff. of xⁿ = \(\frac{1}{3 \cdot 3^n}-\frac{1}{2^n}=\frac{1}{3^{n+1}}-\frac{1}{2^n}\).

Some More Maths 2A Partial Fractions Important Questions

Question 1.
Resolve \(\frac{2 x+3}{5(x+2)(2 x+1)}\) into partial fractions.
Solution:

Question 2.
Resolve \(\frac{13 x+43}{2 x^2+17 x+30}\) into partial fractions.
Solution:
We have 2x² + 17x + 30 = (2x + 5) (x + 6)
∴ \(\frac{13 x+43}{2 x^2+17 x+30}=\frac{13 x+43}{(2 x+5)(x+6)}\)
Now, let
\(\frac{13 x+43}{(2 x+5)(x+6)}=\frac{A}{2 x+5}+\frac{B}{x+6}\)
∴ 13x + 43 = A(x + 6) + B(2x + 5)
= (A + 2B)x + (6A + 5B)
Comparing the coefficients of like powers of x, we have
A + 2B = 13 and 6A + 5B = 43
Solving these two equations,
we get A = 3 and B = 5
∴ \(\frac{13 x+43}{2 x^2+17 x+30}=\frac{3}{2 x+5}+\frac{5}{x+6}\).

Question 3.
Resolve \(\frac{x^2-x+1}{(x+1)(x-1)^2}\) into partial fractions.
Solution:
Let \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A}{(x+1)}+\frac{B}{(x-1)}+\frac{C}{(x-1)^2}\)
\(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A(x-1)^2+B(x+1)(x-1)+C(x+1)}{(x+1)(x-1)^2}\)
⇒ A(x – 1)² + B(x + 1) (x – 1) + C(x + 1) = x2 – x + 1 …………….(1)
If x = – 1
⇒ A(4) = 3
⇒ A = \(\frac{3}{4}\)
If x = 1
⇒ C(2) = 1
⇒ C = \(\frac{1}{2}\)
Now, comparing the coeff. of x² in equation (1)
We get A + B = 1
⇒ \(\frac{3}{4}\) + B = 1
⇒ B = 1 – \(\frac{3}{4}\)
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\).

Question 4.
Resolve \(\frac{x-1}{(x+1)(x-2)^2}\) into partial fractions.
Solution:

Question 5.
Resolve \(\frac{1}{x^3(x+a)}\) into partial fractions.
Solution:
Let \(\frac{1}{x^3(x+a)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+a}\)
\(\frac{1}{x^3(x+a)}=\frac{\mathrm{Ax}^2(\mathrm{x}+\mathrm{a})+\mathrm{Bx}(\mathrm{x}+\mathrm{a})+\mathrm{C}(\mathrm{x}+\mathrm{a})+\mathrm{D}\left(\mathrm{x}^3\right)}{\mathrm{x}^3(\mathrm{x}+\mathrm{a})}\)
⇒ Ax² (x + a) + Bx (x + a) + C (x + a) + D(x³) = 1 ……………..(1)
If x = 0
⇒ C(a) = 1
⇒ C = \(\frac{1}{a}\)
If x = – a = 1
⇒ D(- a³) = 1
⇒ D = \(\frac{-1}{a^3}\)
Now, comparing the coeff. of x³ in (1) we get
A + D = 0
⇒ A – \(\frac{1}{a^3}\) = 0
⇒ A = \(\frac{1}{a^3}\)
Now, comparing the coeff. of x² in (1) we get
Aa + B = 0
⇒ a \(\frac{1}{a^3}\) + B = 0
⇒ B = \(-\frac{1}{a^2}\)
∴ \(\frac{1}{x^3(x+a)}=\frac{\frac{1}{a^3}}{x}+\frac{\frac{-1}{a^2}}{x^2}+\frac{\frac{1}{a}}{x^3}+\frac{\frac{-1}{a^3}}{x+a}\)
= \(\frac{1}{a^3 x}+\frac{(-1)}{a^2 x^2}+\frac{1}{a^3}+\frac{(-1)}{a^3(x+a)}\)

Question 6.
Resolve \(\frac{x^2+5 x+7}{(x-3)^3}\) into partial fractions.
Solution:
Let y = x – 3
⇒ x = y + 3
Now,

Question 7.
Resolve \(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\) into partial fractions.
Solution:

If x = 1
⇒ B(3) = 3
⇒ B = 1.
From (1)
⇒ Ax³ – A + Bx² + Bx + B + Cx³ + Cx – 2Cx² + Dx² + D – 2Dx = x³ + x² + 1
Now, comparing coeffi. of x³ we get,
A + C = 1 ……………….(2)
Comparing coeff. of x² we get,
B – 2C + D = 1
⇒ 1 – 2C + D = 1
⇒ – 2C + D = 0 ……………(3)
Comparing coeff. of x we get,
B + C – 2D = 0
⇒ C – 2D = – 1 …………….(4)
Comparing constants we get,
– A + B + D = 1
⇒ – A + D = 0 …………….(5)
Solving (3) and (4)

From (5)
⇒ – A + D = 0
⇒ A + \(\frac{2}{3}\) = 0
⇒ A = \(\frac{2}{3}\)
∴ \(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}=\frac{2}{3(x-1)}+\frac{1}{(x-1)^2}+\frac{x+2}{3\left(x^2+x+1\right)}\).

Question 8.
Resolve \(\frac{x^2}{(x-1)(x-2)}\) into partial fractions.
Solution:
Let \(\frac{x^2}{(x-1)(x-2)}=1+\frac{A}{x-1}+\frac{B}{x-2}\)
\(\frac{x^2}{(x-1)(x-2)}=\frac{(x-1)(x-2)+A(x-2)+B(x-1)}{(x-1)(x-2)}\)
x² = (x – 1) (x – 2) + A (x – 2) B (x – 1)
If x = 1
⇒ A (1 – 2) = 1
⇒ A (- 1) = 1
⇒ A = – 1
If x = 2
⇒ B (2 – 1) = 4
⇒ B (1) = 4
⇒ B = 4
∴ \(\frac{x^2}{(x-1)(x-2)}=1+\frac{(-1)}{x-1}+\frac{4}{x-2}\)
= 1 – \(\frac{1}{(x-1)}+\frac{4}{(x-2)}\).

Question 9.
Resolve \(\frac{x^3}{(2 x-1)(x-1)^2}\) into partial fractions.
Solution:
Let \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{(x-1)}+\frac{C}{(x-1)^2}\)
⇒ \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{(2 \mathrm{x}-1)(\mathrm{x}-1)^2+\mathrm{A}(2)(\mathrm{x}-1)^2+2 B(2 x-1)(x-1)+2 C(2 x-1)}{2(2 x-1)(x-1)^2}\)
⇒ 2x³ = (2x – 1) (x – 1)² + 2A (x – 1)² + 2B(2x – 1) (x – 1) + 2C (2x – 1)
If x = \(\frac{1}{2}\)
⇒ 2A (\(\frac{1}{2}\) – 1)² = 2(\(\frac{1}{2}\))³
⇒ 2A (\(\frac{1}{4}\)) = 2 . \(\frac{1}{8}\)
⇒ A =\(\frac{1}{2}\)
If x = 1
⇒ 2C (2 – 1) = 2
⇒ C = i
Comparing the coefficients of x², we get
2A + 4B – 5 = 0
2 (\(\frac{1}{2}\)) + 4B – 5 = 0
⇒ 4B = 4
⇒ B = 1.
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{\frac{1}{2}}{2 x-1}+\frac{(+1)}{x-1}+\frac{1}{(x-1)^2}\)
= \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{x-1}+\frac{1}{(x-1)^2}\).

Question 10.
Resolve \(\frac{x^3}{(x-1)(x+2)}\) into partial fractions. [Ap – Mar. 2019]
Solution:
Let (x – 1) (x + 2) = x² + 2x – x – 2 = x

A(x + 2) + B(x – 1) = 3x – 2
If x = 1
⇒ A (1 + 2) = 3 – 2
⇒ A = \(\frac{1}{3}\)
If x = – 2
⇒ B (- 2 – 1) = 3 (- 2) – 2
B (- 3) = – 8
⇒ B = \(\frac{8}{3}\)
∴ \(\frac{x^3}{(x-1)(x+2)}\) = x – 1 + \(\frac{\frac{1}{3}}{x-1}+\frac{\frac{8}{3}}{x+2}\)
= x – 1 + \(\frac{1}{3(x-1)}+\frac{8}{3(x+2)}\).

Question 11.
Find the coefficient of x³ in the power series expansion of \(\frac{5 x+6}{(x+2)(1-x)}\) specifying the region in which the expansion is valid.
Solution:

Question 12.
Resolve \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) into partial fractions.
Solution:
Let \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}=\frac{A x+B}{x^2+2}+\frac{C x+D}{x^2+3}\)
\(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) = \(\frac{(\mathrm{Ax}+\mathrm{B})\left(\mathrm{x}^2+3\right)+(\mathrm{Cx}+\mathrm{D})\left(\mathrm{x}^2+2\right)}{\left(\mathrm{x}^2+2\right)\left(\mathrm{x}^2+3\right)}\)
(Ax + B) (x² + 3) + (Cx + D) (x² + 2) = x³ + x² + 1
Ax³ 3Ax + Bx² + 3B + Cx³ + 2Cx + Dx² + 2D = x³ + x² + 1
Now, comparing the coefficients of x3 we get,
⇒ A + C = 1 ………………(1)
Comparing the coefficients of x2 we get,
⇒ B + D = 1 ………………(2)
Comparing the coefficients of x, we get,
⇒ 3A + 2C = 0 ……………..(3)
Comparing the constant terms we get,
⇒ 3B + 2D = 1 …………….(4)
Solve (1) and (3)

Question 13.
Resolve \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}\) into partial fractions.
Solution:
Let \(\frac{3 x^3-2 x^2-1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\) = x⁴ + 2x² + 1 – x²
= (x² + 1)² – x²
= (x² + x + 1) (x² – x + 1)
= \(\frac{A x+B}{x^2+x+1}+\frac{C x+D}{x^2-x+1}\)
\(\frac{3 x^3-2 x^2-1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\) = \(\frac{(A x+B)\left(x^2-x+1\right)+(C x+D)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
(Ax + B) (x² – x + 1) + (Cx + D) (x² + x + 1) = 3x³ – 2x² – 1
AX³ – Ax² + Ax + Bx² – Bx + B + Cx³ + Cx² + Cx + Dx² + Dx + D = 3x³ – 2x² – 1
Now, comparing the coeff. of x³ on both sides we get
⇒ A + C = 3 …………….(1)
Comparing the coefi. of x² on both sides,
we get
⇒ – A + B + C + D = – 2 ……………..(2)
Comparing the coeff. of xon both sides, we get
A – B + C + D = 0
⇒ 3 – B + D = 0
⇒ B – D = 3 ………………..(3)
Comparing constants on both sides we get,
B + D = – 1 ……………(4)
From (3) and (4),
⇒ B – D = 3
B + D = – 1
2B = 2
B = 1
from B – D = 3
1 – D = 3
D = – 2
From (2)
⇒ – A + B + C + D = – 2
⇒ – A + 1 + C – 2 = – 2
– A + C = – 1 ……………(5)
Solving (1) and (5)
A + C = 3
– A + C = – 1
2C = + 2
C = + 1
from A + C = 3
A + 1 = 3
A = 2
∴ \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{2 x+1}{x^2+x+1}+\frac{x-2}{x^2-x+1}\).

Question 14.
Resolve \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) into partial fractions.
Solution:
Let \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) = \(\frac{A}{1-x}+\frac{B}{(1-x)^2}+\frac{C x+D}{1+x^2}\)
\(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) = \(\frac{A(1-x)\left(1+x^2\right)+B\left(1+x^2\right)+(C x+D)(1-x)^2}{(1-x)^2\left(1+x^2\right)}\)
⇒ A (1 – x) (1 + x²) + B (1 + x²) + (Cx + D) (1 – x)² = x + 3 ………………(1)
If x = 1
⇒ B(1 + 1) = 1 + 3
⇒ B(2) = 4
⇒ B = 2.
From (1)
⇒ A(1 + x² – x – x³) + B (1 + x²) + (Cx + D) (1 + x² – 2x) = x + 3
⇒ A + Ax² – Ax – Ax³ + B + Bx² + Cx + Cx³ – 2Cx² + D + Dx² – 2Dx = x + 3
Now, comparing the coefficients of x³ on both sides we get,
⇒ – A + C = 0
⇒ A – C = 0 ……………..(2)
Corn paring the coefficients of x² we get,
A + B – 2C + D = 0
A + 2 – 2C + D = 0
⇒ A – 2C + D = – 2 ………………(3)
Comparing coefficients of x we get,
– A + C – 2D = 1
⇒ 0 – 2D = 1
⇒ D = \(-\frac{1}{2}\)
Comparing constants we get,
A + B + D = 3 ………………(4)
From (4)
⇒ A + 2 – \(\frac{1}{2}\) = 3
⇒ A = \(\frac{3}{2}\)
From (2)
⇒ \(\frac{3}{2}\) – C = 0
C = \(\frac{3}{2}\)
∴ \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) = \(\frac{\frac{3}{2}}{(1-x)}+\frac{2}{(1-x)^2}+\frac{\frac{3}{2} x-\frac{1}{2}}{1+x^2}\)
= \(\frac{3}{2(1-x)}+\frac{2}{(1-x)^2}+\frac{3 x-1}{2\left(1+x^2\right)}\).

Question 15.
Resolve \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\) into partial fractions.
Solution:
Let \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\) = \(\frac{A x+B}{1-x+x^2}+\frac{C}{x+2}\)
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{(A x+B)(x+2)+C\left(1-x+x^2\right)}{\left(1-x+x^2\right)(x+2)}\)
(Ax + B) (x + 2) + C (1 – x + x²) = 3x – 1 …………….(1)
If x = – 2
⇒ C (1 + 2 + 4) = – 6 – 1
⇒ C(7) = – 7
⇒ C = – 1
From (1)
⇒ Ax² + 2Ax+ Bx + 2B + C – Cx + Cx² = 3x – 1
Now. comparing coeff. of x² we get,
⇒ A + C = 0
⇒ A – 1 = 0
⇒ A = 1
Comparing coeff. of x we get,
2A + B – C = 3
⇒ 2 + B + 1 = 3
⇒ B + 3 = 3
⇒ B = 0
∴ \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{x}{1-x+x^2}+\frac{(-1)}{x+2}\).

Question 16.
Resolve \(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\) into partial fractions.
Solution:

A (x – 1) (x² + x + 1) + B (x² + x + 1) + (Cx + D) (x – 1)² = x³ + x² + 1 ………………(1)
II x = 1
⇒ B(3) = 3
⇒ B = 1
From (1)
⇒ Ax³ + Ax² + Ax – Ax² – Ax – A + Bx² + Bx + B + Cx³ + Cx – 2Cx² + Dx² + D – 2Dx = x³ + x² + 1
Now, comparing coefficients of x³ we get,
A + C = 1 ………….(2)
Comparing coeff. of x² we get,
B – 2C + D = 1
⇒ 1 – 2C + D = 1
⇒ – 2C + D = 0 …………….(3)
Comparing coeff. of x we get,
B + C – 2D = 0
⇒ C – 2D = – 1
Comparing constants we get,
⇒ – A + B + D = 1
⇒ – A + D = 0 ………….(5)
Solving (3) and (4)

Question 17.
Resolve \(\frac{x^3}{(2 x-1)(x-1)^2}\) into partial fractions.
Solution:

If x = 1
⇒ 2C (2 – 1) = 2
⇒ C = 1
Comparing the coefficients of x we get,
2A + 4B – 5 = 0
2(\(\frac{1}{2}\)) + 4B – 5 = o
⇒ B = 1
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{\frac{1}{2}}{2 x-1}+\frac{(+1)}{x-1}+\frac{1}{(x-1)^2}\)
= \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{x-1}+\frac{1}{(x-1)^2}\)

Question 18.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x}{(x-1)^2(x-2)}\) specifying the region In which the expansion is valid. [AP – May 2015].
Solution:
Let \(\frac{x}{(x-1)^2(x-2)}\) = \(\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x-2}\)
\(\frac{x}{(x-1)^2(x-2)}\) = \(\frac{A(x-1)(x-2)+B(x-2)+C(x-1)^2}{(x-1)^2(x-2)}\)
A(x – 1) (x – 2) + B (x – 2) + C(x – 1)² = x ……………….(1)
If x = 1
⇒ B (- 1) = 1
⇒ B = – 1
If x = 2
⇒ C(1) = 2
⇒ C = 2
Now comparing coefficients of x² on both sides of (1)
A + C = 0
⇒ A + 2 = 0
⇒ A = – 2
∴ \(\frac{x}{(x-1)^2(x-2)}=\frac{(-2)}{x-1}+\frac{(-1)}{(x-1)^2}+\frac{2}{(x-2)}\).

Telangana TSBIE TS Inter 2nd Year Chemistry Study Material Lesson 6(d) Group-18 Elements Textbook Questions and Answers.

TS Inter 2nd Year Chemistry Study Material Lesson 6(d) Group-18 Elements

Very Short Answer Questions (2 Marks)

Question 1.
What inspired Bartlett for carrying out reaction between Xe and PtF₆?
Answer:
Neil Bartlett, first prepared a red compound which is formulated as Q₂⁺ PtF₆^–. He, then realised that the first ionisation enthalpy of molecular oxygen was almost identical with that of Xenon. He then made another red colour compound XePtF₆ by mixing PtF₆ and Xenon.

Question 2.
Which of the following does not exist?
a) XeOF₄
b) NeF₂
c) XeF₂
d) XeF₆
Answer:
NeF₂ does not exist.

Question 3.
Why do noble gases have comparatively large atomic sizes?
Answer:
The atomic radii of the noble gas elements are all very large. Because these have van der Waals radii which Is larger than Ionic and covalent radii.

Question 4.
List out the uses of neons. [Mar. 18 – A.P.]
Answer:

1. Neon is used in discharge tubes and fluorescent bulbs for advertisement display purposes.
2. Neon bulbs are used in botanical gardens and in green houses.

Question 5.
Write any two uses of argon.
Answer:

1. Argon is used to provide an inert atmosphere in high temperature metallurgical processes.
2. For filling electric bulbs.
3. Used in laboratory for handling substances that are air sensitive.

Question 6.
In modern diving apparatus, a mixture of He and O₂ is used. Why? [AP ’16]
Answer:
Helium has very low solubility in blood. So it is used as a diluent for oxygen in modern diving apparatus.

Question 7.
Helium is heavier than hydrogen. Yet helium is used (instead of H₂) in filling balloons for meteorological observations. Why?
Answer:
Helium is non-inflammable and light gas. Hence it is used in filling balloons for mete-orological observations.

Question 8.
How is XeO₃ prepared ?
Answer:
XeO₃ is prepared by the hydrolysis of XeF₆.
XeF₆ + 3H₂O → XeO₃ + 6HF

Question 9.
Give the preparation of
a) XeOF₄
b) XeO₂F₂
Answer:
Partial hydrolysis of XeF₆ gives oxyfluorides.
a) XeF₆ + H₂O → XeOF₄ + 2HF
b) XeF₆ + 2H₂O → XeO₂F₂ + 4HF

Question 10.
Explain the structure of XeO₃. [TS ’16 ; IPE ’14]
Answer:
Xe undergoes sp³ hybridisation.

Unpaired electrons in d-orbital form dπ – pπ bonds with oxygen, sp³ orbitals form 3σ bonds with oxygen atoms. Because of the presence of lone pair, the molecule assumes pyramidal shape with a bond angle of 103°.

Question 11.
Noble gases are inert- Explain.
Answer:
The inertness to chemical reactivity is due to –

1. The noble gases except helium (1 s²) have completely filled ns²np⁶ electronic configuration in their valence shell.
2. They have high ionisation enthalpy and high positive electron gain enthalpy.

Question 12.
Write the name and formula of the first noble gas compound prepared by Bertlett.
Answer:
Xe⁺ [PtF₆]^–
Xenon hexa fluoro platinate

Question 13.
Explain the shape of XeF₄ on the basis of use VSEPR theory. [Mar. 2018 – AP]
Answer:
XeF₄ [Xenon tetrafluoride]:
shape is octahedral. But due to the presence of two lone pairs, the molecule assumes square planar structure.

Total number of electron pairs is 6. The Xe atom undergoes sp³d² Hybridisation. Hence shape is octahedral. But due to the presence of two lone pairs, the molecule assumes square planar structure.

Question 14.
Give the outer electronic configuration of noble gases.
Answer:
ns²np⁶

Question 15.
Why do noble gases form compounds with fluorine and oxygen only?
Answer:
Because fluorine and oxygen are highly electronegative, they can form compounds with noble gases.

Question 16.
How is XeOF₄ prepared? Describe its molecular shape.
Answer:
Partial hydrolysis of XeF₆ gives oxyfluorides
XeF₆ + H₂O → XeOF₄ + 2HF
XeOF₄ has square pyramidal.

Question 17.
What is the major source of helium?
Answer:
Natural gas

Question 18.
Which noble gas is radioactive? How is it formed?
Answer:
Radon. Radon is obtained as a decay product of Ra²²⁶.
\({ }_{88}^{226} \mathrm{Ra}\) → \({ }_{86}^{222} \mathrm{Rn}\) + \({ }_2^4 \mathrm{He}\)

Question 19.
Name the following.
a) most abundant noble gas in atmosphere
b) radioactive noble gas
c) noble gas with least boiling point
d) noble gas forming large number of compounds
e) noble gas not present in atmosphere.
Answer:
a) Argon
b) Radon
c) Helium
d) Xenon
e) Radon

Short Answer Questions (4 Marks)

Question 20.
How are xenon fluorides XeF₂, XeF₄ and XeF₆ obtained ? [AP ’17 ; IPE ’14] [Mar. 2018 – TS]
Answer:
Xenon fluorides are obtained by the direct combination of elements under appropriate conditions.

Question 21.
How are XeO₃ and XeOF₄ prepared?
Answer:
Hydrolysis of XeF₄ and XeF₆ gives XeO₃.
XeF₆ + 3H₂O → XeO₃ + 6HF
Partial hydrolysis of XeF₆ gives XeOF₄
XeF₆ + H₂O → XeOF₄ + 2HF

Question 22.
Give the formulae and describe the struc-tures of noble gas sp>ecies, isoelectronic with
a) ICl₄
b) IBr₂^–
c) BrO₃^–
Answer:
a) XeF₄
b) XeF₂
c) XeF₆

a) ICl₄ is isoelectronic with XeF₄. XeF₄ is square planar in which Xe undergoes sp³d² hybridisation. If has two lone pairs.

Structure of XeF₄: Square planar.

b) IBr₂^– is isoelectronic with XeF₂. XeF₂ is linear. Xe undergoes sp³d hybridisation. Three lone pairs occupy three vertices of triangle.

c) BrO₃^– is isoelectronic with XeF₆. In XeF₆, Xe undergoes sp³d³ hybridisation. XeF₆ has seven electron pairs (6 bonding pairs and one lone pair) XeF₆ thus has a distorted octahedral structure

Question 23.
Explain the reaction of the following with water. [AP ’15 ; IPE ’14]
a) XeF₂
b) XeF₄
c) XeF₆
Answer:
a) XeF₂ reacts with water and give Xe, HF and O₂
2XeF₂ + 2H₂O → 2Xe + 4HF + O₂

b) XeF₄ reacts with water and give Xe, XeO₃, HF and O₂
6XeF₄ + 12H₂O → 4 Xe + 2XeO₃ + 24 HF + 3O₂

c) XeF₆ reacts with water and give XeO₃, HF
XeF₆ + 3H₂O → XeO₃ + 6 HF

Question 24.
Explain the structures of [(AP ’17) (Mar. 2018 – T.S)]
a) XeF₂ and
b) XeF₄
Answer:
a) In XeF₂, Xe undergoes sp3d hybridisation.

There are three bond pairs and two lone pairs. The two bond pairs overlap end-end with 2p_z orbitals of two F atoms. Thus XeF₂ molecule has linear structure.

b) XeF₄ is square planar. Xe undergoes sp³d² hybridisation. [Mar. 2018 – A.P.]

There are two lone pairs and four bond pairs. The four bond pairs overlap end-end with 2p_z orbitals of four F atoms.

Question 25.
Explain the structure of [TS ’15]
a) XeF₆ and
b) XeOF₄.
Answer:
a) XeF₆ has distorted octohedral shapes. XeF₆ has seven electron pairs. (6 bonding and one lone pair). It has a distorted octahedral structure in the gas phase.

b) XeOF₄ has square pyramidal structure.

Xe in excited state undergoes sp³d² hybridisation. One hybrid orbital is occupied by a lone pair. Other five orbitals are occupied by unpaired electrons. Five orbitals form five σ bonds. The unpaired electrons in unhybridised’d’ orbital forms a π bond with oxygen. As the lone pair occupies axial position, XeOF₄ assumes square pyramidal structure.

Question 26.
Complete following:
a) XeF₂ + H₂O →
b) XeF₂ + PF₅ →
c) XeF₄ + SbF₅ →
d) XeF₆ + AsF₅ →
e) XeF₄ + O₂F₂ →
f) NaF + XeF₆ →
(Hint: NaF + XeF₆ → Na⁺[XeF₇]^–)
Answer:
a) XeF₂ is hydrolysed to give Xe, HF and O₂.
2XeF₂(s) + 2H₂O (l) → 2Xe (g) + 4HF (aq) + O₂(g)

b) Xenon fluorides react with fluoride ion acceptors to form cationic species.
XeF₂ + PF₅ → [XeF]⁺ [PF₆]^–

c) Xenon tetrafluoride reacts with fluoride ion to form cationic species.
XeF₄ + SbF₅ → [XeF₃]⁺ [SbF₆]^–

d) XeF₆ + ASF₅ → [XeF₅]⁺ [AsF₆]^–

e) XeF₆ is prepared by the interaction of XeF₆ and O₂F₂ at 143 K.
XeF₄ + O₂F₂ → XeF₆ + O₂

f) XeF₆ reacts with fluoride ion donors to form fluoroanions.
XeF₄ + NaF → Na⁺ [XeF₇]^–

Question 27.
How are XeF₂ and XeF₄ prepared? Give their structures. [AP ’17]
Answer:
Xenon fluorides are obtained by the direct combination of elements under appropriate conditions.

Hydrolysis of XeF₄ and XeF₆ gives XeO₃.
XeF₆ + 3H₂O → XeO₃ + 6HF
Partial hydrolysis of XeF₆ gives XeOF₄
XeF₆ + H₂O → XeOF₄ + 2HF

Long Answer Questions (8 Marks)

Question 28.
How are XeF₂, XeF₂. Explain their reaction with water. Discuss their structures.
Answer:
XeF₂ is prepared by heating Xenon and Fluorine in a seated Nickel tube in the ratio 1 : 2 at 673K for 8hrs.

Reaction with water:
XeF₂ is hydrolysed to give Xe, HF and O₂
2XeF₂ (s) + 2H₂O (l) → 2Xe(g) + 4HF (aq) + O₂(g)

Structure:
Xe in the first excited state

Xe undergoes sp³d hybridisation. The sp³d orbitals assume trigonal bipyramidal geometry. Two fluorine atoms form 2π bonds with Xe.

The bond pairs occupy axial positions. XeF₄: XeF₄ is formed when Xe and F₂ mixed in the ratio 1 : 5, heated to 873K at 7 bar.

Reaction with water: XeF₄ hydrolysed with water to XeO₃.
6XeF₄ + 12H₂O → 4Xe + 2XeO₃ + 24HF + 3O₂
Structure of XeF₄ : XeF₄ is square planar Xe in the second excited state

Xe undergoes sp³ d² hybridisation. Xe forms four o bonds with 4 fluorine atoms. Two lone pairs occupy axial positions. The four fluorine atoms occupy corners of a square.

Additional Questions – Answers

Question 1.
Why are the elements of group 18 known as noble gases?
Answer:
The group 18 elements have completely filled s and p orbitals in their valence shell. They react with a few elements only under certain conditions. Therefore they are known as noble gases.

Question 2.
Noble gases have very low boiling points. Why?
Answer:
Noble gases are monoatomic. There are no inter atomic forces except weak dispersion forces. Hence they are liquified at very low temperatures. Hence they have low boiling points.

Question 3.
Does the hydrolysis of XeF₆ lead to a redox reaction?
Answer:
No, the products of hydrolysis are XeF₄ and XeO₂F₂ where the oxidation states of all the elements remain the same.

Intext Questions – Answers

Question 1.
Why is Helium used in diving apparatus ?
Answer:
Helium acts as a diluent for oxygen. Hence it is used in diving apparatus.

Question 2.
Balance the following equation.
XeF₆ + H₆O > XeO₂ F₂ + HF
Answer:
XeF₆ + 2H₂O > XeO₂F₂ + 4HF

Question 3.
Why has it been difficult to study the chemistry of Radon?
Answer:
Radon is radioactive element with very short Half-life period. Hence its study is difficult.