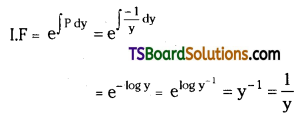TS Inter Second Year Maths 2B Differential Equations Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Differential Equations Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Differential Equations Important Questions Very Short Answer Type

Question 1.
Find the order and degree of the differential equation \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\). [(TS) May ’18; May ’13]
Solution:
Given differential equation is \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\)
Cubing on both sides we get,
\(\left(\frac{d^2 y}{d x^2}\right)^3=\left[1+\left(\frac{d y}{d x}\right)^2\right]^5\)
∴ Order = Order of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2
Degree = The degree of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 3

Question 2.
Find the order and degree of \(1+\left(\frac{d^2 y}{d x^2}\right)^2=\left[2+\left(\frac{d y}{d x}\right)^2\right]^{3 / 2}\)
Solution:
Given differential equation is \(\frac{d^2 y}{d x^2}=\left[1+\left(\frac{d y}{d x}\right)^2\right]^{5 / 3}\)
Cubing on both sides,
\(\left(\frac{d^2 y}{d x^2}\right)^3=\left[1+\left(\frac{d y}{d x}\right)^2\right]^5\)
The given equation is a polynomial equation in \(\frac{d^2 y}{d x^2}, \frac{d y}{d x}\)
Hence, \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) is the highest derivative occurring in the equation.
Its order = 2
The degree = 3

Question 3.
Find the order and degree of \(\left[\left(\frac{d y}{d x}\right)^{1 / 2}+\left(\frac{d^2 y}{d x^2}\right)^{1 / 3}\right]^{1 / 4}=0\). [May ’12]
Solution:
Given differential equation is

∴ Order = Order of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2
Degree = The degree of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2

Question 4.
Find the order and degree of \(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\). [May ’14]
Solution:
Given differential equation is \(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\)
It is a polynomial equation in \(\frac{d^3 y}{dx^3}, \frac{d y}{d x}\)
Hence, \(\frac{\mathrm{d}^3 \mathrm{y}}{\mathrm{dx}^3}\) is the highest derivative occurring in the equation.
Its order = 3
degree = 2

Question 5.
Find the order and degree of \(x^{1 / 2}\left(\frac{d^2 y}{d x^2}\right)^{1 / 3}+x \frac{d y}{d x}+y=0\). [(AP) Mar. ’18, (TS) ’15]
Solution:

It is a polynomial equation in \(\frac{d^2 y}{d x^2} \& \frac{d y}{d x}\)
Hence \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) is the highest derivative occurring in the equation.
Order = 2
Degree = 1

Question 6.
Find the order and degree of \(\left[\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3\right]^{6 / 5}=6 y\). [(TS) May ’17, ’15; (AP) Mar. ’16, May ’15]
Solution:
Given differential equation is
\(\left[\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^3\right]^{6 / 5}=6 y\)
\(\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3=(6 y)^{5 / 6}\)
∴ Order = Order of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 2
Degree = The degree of \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = 1

Question 7.
Form the differential equation corresponding to y = cx – 2c², where c is a parameter. [Mar. ’19 (AP) ’12]
Solution:
The given equation is y = cx – 2c², where ‘c’ is a parameter. ……..(1)
Differentiating with respect to x on both sides
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = c – 0
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = c ……..(2)
From (1) and (2),
y = \(x\left(\frac{d y}{d x}\right)-2\left(\frac{d y}{d x}\right)^2\)
which is the required differential equation.

Question 8.
Form the differential equation corresponding to y = A cos 3x + B sin 3x, where A and B are parameters. [(TS) Mar. ’20, May ’16; (AP) Mar. ’15; May ’14]
Solution:
The given equation is y = A cos 3x + B sin 3x where A, B are parameters. …….(1)
Differentiate with respect to ‘x’ on both sides
y1 = A (-sin 3x) 3 + B (cos 3x) 3 = -3A sin 3x + 3B cos 3x
Again differentiate with respect to ‘x’ on both sides
y2 = -3A (cos 3x) 3 + 3B (-sin 3x) 3
= -9A cos 3x – 9B sin 3x
= -9 (A cos 3x + B sin 3x)
= -9y (from (1))
∴ \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) + 9y = 0 or y² + 9y = 0
which is the required differential equation.

Question 9.
Form the differential equation corresponding to y = a cos(nx + b), where a, b are parameters. [(AP) May ’17]
Solution:
Given y = a cos(nx + b) ……..(1)
(a, b are parameters)
Diff. (1) w.r. to x on both sides we get,
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a[-sin(nx + b) (n)] = -an sin(nx + b) ……….(2)
Again diff. (2) w.r.to x on both sides we get,
\(\frac{d^2 y}{d x^2}\) = -an [cos(nx + b) n]
= -an² cos(nx + b)
= -n²y (from (1))
Required D.E is \(\frac{d^2 y}{d x^2}\) + n2y = 0

Question 10.
Find the order and degree of the differential equation of the family of all circles with their centres at the origin. [(TS) Mar. ’17, ’11]
Solution:
Equation of the family of circles with their centres at the origin is x² + y² = r²
Differentiate with respect to ‘x’ we get,
2x + 2y \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
⇒ x + y \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
∴ Order = Order of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1
Degree = The degree of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1

Question 11.
Obtain the differential equation which corresponds to the rectangular hyperbolas which have the coordinate axes as asymptotes.
Solution:
The equation of the family of the rectangular hyperbolas which have the coordinate axes as asymptotes are xy = c² …….(1)
where c is a parameter
Diff. (1) w.r. t. x on both sides, we get
x \(\frac{d y}{d x}\) + y = 0
∴ Required D.E is x \(\frac{d y}{d x}\) + y = 0

Question 12.
Find the general solution of x + y \(\frac{d y}{d x}\) = 0. [(AP) May ’16]
Solution:
Given D.E is x + y \(\frac{d y}{d x}\) = 0
x dx + y dy = 0
Integrating on both sides we get
∫x dx + ∫y dy = c
\(\frac{x^2}{2}+\frac{y^2}{2}\) = c
x² + y² = 2c
Which is the required solution of D.E.

Question 13.
Find the general solution of \(\frac{d y}{d x}=\frac{2 y}{x}\). [(TS) Mar. ’19, (AP) ’17]
Solution:
Given D.E. is \(\frac{d y}{d x}=\frac{2 y}{x}\)
⇒ \(\frac{1}{y} d y=\frac{2}{x} d x\)
⇒ \(\int \frac{1}{y} d y=\int \frac{2}{x} d x\)
⇒ log y = 2 log x + log c
⇒ log y = log x² + log c
⇒ log y = log(x²c)
⇒ y = cx² is the required D.E

Question 14.
Find the general solution of \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x+y. [(TS) Mar. ’18]
Solution:
Given \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x+y
⇒ \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x . e^y
⇒ e^-y dy = e^x dx
⇒ ∫e^-y dy = ∫e^x dx
⇒ -e^-y = e^x + c
⇒ e^x + e^-y = c

Question 15.
Find the general solution of \(\sqrt{1-x^2} d y+\sqrt{1-y^2} d x=0\)
Solution:
Given D.E is \(\sqrt{1-x^2} d y+\sqrt{1-y^2} d x=0\)

sin^-1(y) = -sin^-1(x) + c
sin^-1(x) + sin^-1(y) = c
Which is the required general solution.

Question 16.
Solve \(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\). [(TS) May ’19]
Solution:
Given differential equation is
\(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
⇒ \(\frac{d y}{1+y^2}=\frac{d x}{1+x^2}\)
Integrating on both sides
\(\int \frac{d y}{1+y^2}=\int \frac{d x}{1+x^2}\)
tan^-1(y) = tan^-1(x) + c
Which is the required solution.

Question 17.
Solve \(\frac{\mathbf{d y}}{\mathbf{d x}}\) + 1 = e^x+y
Solution:

Question 18.
Form the differential equation corresponding to the family of circles passing through the origin and having centres on the Y-axis.
Solution:
The equation of the family of circles passing through the origin and having centres on the Y-axis is x² + y² + 2fy = 0 …….(1)
where f is a parameter.
Diff. (1) w.r. to ‘x’ on both sides, we get

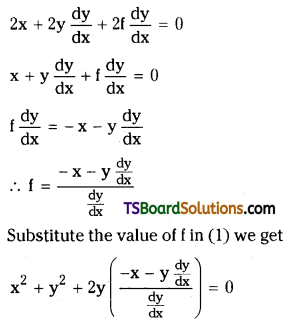
Question 19.
Find the order of the differential equation corresponding to y = Ae^x + Be^3x + Ce^5x. (A, B, C being parameters)
Solution:
Given equation is y = Ae^x + Be^2x + Ce^5x, (A, B, C are parameters)
Here, no. of arbitrary constants = 3
∴ The order of D.E = 3

Question 20.
Form the differential equation corresponding to xy = ae^x + be^-x where a, b are parameters. [(AP) May ’19]
Solution:
Given xy = ae^x + be^-x ……..(1)
(a, b are parameters)
Diff. (1) with respect to x on both sides, we get

Question 21.
Obtain the differential equation which corresponds to the ellipses with centres at the origin and having coordinate axes as axes.
Solution:
The equation of the family of ellipses with centres at the origin and having coordinate axes as axes is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ……..(1)
(a, b are arbitrary constants)
Diff. (1) w.r. t. x on both sides, we get

Which is the required solution.

Question 22.
Find the I.F of (cos x) \(\frac{d y}{d x}\) + y sin x = tan x.
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) + y tan x = sec x . tan x
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q,
where P = tan x, Q = sec x tan x
I.F = e^{∫P dx}
= e^{∫tan x dx}
= e^{log|sec x| x}
= sec x

Question 23.
Find I.F of x \(\frac{d y}{d x}\) – y = 2x² sec²2x.
Solution:
Given diff. equation is x \(\frac{d y}{d x}\) – y = 2x² sec²2x
Dividing with x on both sides we get,
\(\frac{\mathrm{dy}}{\mathrm{dx}}-\frac{\mathrm{y}}{\mathrm{x}}\) = 2x sec²2x
\(\frac{d y}{d x}+\left(\frac{-1}{x}\right) y\) = 2x sec²2x
It is a linear diff. equation in y of the first order.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
We get P = \(\frac{-1}{x}\), Q = 2x sec²2x

Question 24.
Find the order of the differential equation obtained by eliminating the arbitrary constants b and c from xy = ce^x + be^-x + x².
Solution:
Given equation is xy = ce^x + be^-x + x²
order of the differential equation = number of arbitary constants = 2.

Question 25.
Form the differential equation of the family of curves y = (a + bx) e^kx where a, b are parameters.
Solution:
Given equation is y = (a + bx) e^kx ……..(1)
a, b are arbitrary constants
differentiating (1) w.r.t ‘x’ on both sides, we get

Again differentiating (2) w.r.t ‘x’ on both sides

Which is the required differential equation.

Question 26.
Form the differential equation of the family of curves y = ax² + bx, where a, b are parameters.
Solution:
Given equation is y = ax² + bx ……..(1)
a, b are arbitrary constants
differentiating (1) w.r.t ‘x’ on both sides
\(\frac{d y}{d x}\) = a(2x) + b(1)
\(\frac{d y}{d x}\) = 2ax + b …….(2)
Again differentiating (2) w.r.t ‘x’ on both sides


Which is the required differential equation.

Question 27.
Form the differential equation of the family of curves ax² + by² = 1, where a, b are parameters.
Solution:
Given equation is ax² + by² = 1 …….(1)
a, b are parameters
differentiating (1) w.r.t ‘x’ on both sides

Again differentiating (2) w.r.t ‘x’ on both sides

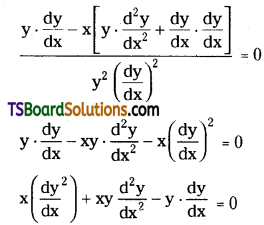
Which is the required differential equation.

Question 28.
Form the differential equation of the family of curves xy = ax² + \(\frac{b}{x}\), where a, b are parameters.
Solution:
Given equation is xy = ax² + \(\frac{b}{x}\)
xy = \(\frac{a x^3+b}{x}\)
x²y = ax³ + b …….(1)
a, b are parameters
differentiating (1) w.r.t ‘x’ on both sides
x² \(\frac{d y}{d x}\) + y . 2x = a . 3x² + 0
x² \(\frac{d y}{d x}\) + 2xy = 3ax² ……..(2)
Again differentiating (2) w.r.t ‘x’ on both sides

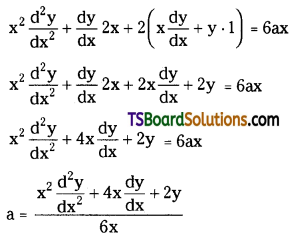
Substitute the value of ‘a’ in (2)

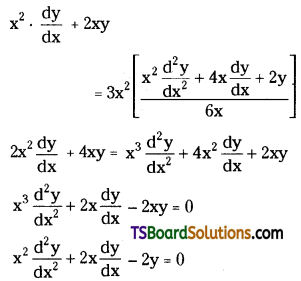
Which is the required D.E.

Question 29.
Find the differential equation of the family of circles that touch the y-axis at the origin.
Solution:
The equation of the family of circles that touch the y-axis at the origin is x² + y² + 2gx = 0 …….(1)
g is a parameter.
differentiating (1) w.r.t ‘x’ on both sides, we get
2x + 2y \(\frac{d y}{d x}\) + 2g = 0
x + y \(\frac{d y}{d x}\) + g = 0
∴ g = -x – y \(\frac{d y}{d x}\)
Substitute the value of ‘g’ in (1)
x² + y² + 2x[-x – y \(\frac{d y}{d x}\)] = 0
x² + y² – 2x² – 2xy \(\frac{d y}{d x}\) = 0
y² – x² – 2xy \(\frac{d y}{d x}\) = 0
Which is the required D.E.

Question 30.
Obtain the D.E. corresponding to the parabolas each of which has a latus rectum 4a and whose axis is parallel to the x-axis.
Solution:
The equation of the family of parabolas each of which has a latus rectum 4a and whose axis is parallel to the x-axis is
(y – k)² = 4a(x – h) ……..(1)
h, k are parameters differentiating (1) w.r.t ‘x’ on both sides, we get
2(y – k) \(\frac{d y}{d x}\) = 4a(1 – 0)
\(\frac{d y}{d x}\) . 2(y – k) = 4a
\(\frac{d y}{d x}\) (y – k) = 2a …….(2)
Again differentiating (2) w.r. t ‘x’ on both sides, we get


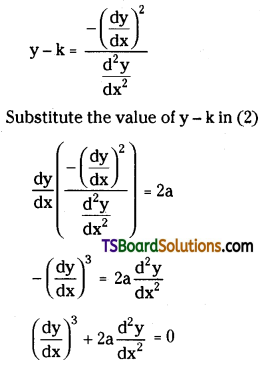
Which is the required D.E.

Question 31.
Obtain the D.E. corresponding to the parabolas having their focus at the origin and axis along the x-axis.
Solution:
The equation of the family of parabolas having their foci at the origin and axis along the x-axis is
y² = 4a(x + a) ……..(1), ‘a’ is a parameter
differentiating (1) w.r.t ‘x’ on both sides


Which is the required D.E.

Question 32.
Express the D.E. \(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\) of f(x) dx + g(y) dy = 0.
Solution:
Given differential equation is \(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
\(\frac{d y}{1+y^2}=\frac{d x}{1+x^2}\)
\(\frac{d x}{1+x^2}-\frac{d y}{1+y^2}=0\)
This is of the form f(x) dx + g(y) dy = 0

Question 33.
Express the D.E. y – x \(\frac{d y}{d x}\) = a(y² + \(\frac{d y}{d x}\)) in the form of f(x) dx + g(y) dy = 0.
Solution:
Given D.E. is y – x \(\frac{d y}{d x}\) = a(y² + \(\frac{d y}{d x}\))

This is of the form f(x) dx + g(y) dy = 0.

Question 34.
Express the D.E. \(\frac{d y}{d x}\) = e^x-y + x² e^-y in the form of f(x) dx + g(y) dy = 0.
Solution:
Given D.E. is \(\frac{d y}{d x}\) = e^x-y + x² e^-y
⇒ \(\frac{d y}{d x}\) = e^x . e^-y + x² e^-y
⇒ \(\frac{d y}{d x}\) = e^-y (e^x + x²)
⇒ \(\frac{d y}{e^{-y}}\) = (e^x + x²) dx
⇒ e^y dy = (e^x + x²) dx
⇒ (e^x + x²) dx – e^y dy = 0
This is of the form f(x) dx + g(y) dy = 0

Question 35.
Express the D.E. \(\frac{d y}{d x}\) + x² = x² e^3y in the form of f(x) dx + g(y) dy = 0.
Solution:
Given D.E. is \(\frac{d y}{d x}\) + x² = x² e^3y
⇒ \(\frac{d y}{d x}\) = x² e^3y – x²
⇒ \(\frac{d y}{d x}\) = x² (e^3y – 1)
⇒ \(\frac{\mathrm{dy}}{\mathrm{e}^{3 \mathrm{y}}-1}\) = x² dx
⇒ x² dx – \(\frac{\mathrm{dy}}{\mathrm{e}^{3 \mathrm{y}}-1}\) = 0
This is of the form f(x) dx + g(y) dy = 0.

Question 36.
Show that f(x, y) = 4x²y + 2xy² is a homogeneous function of degree 3.
Solution:
Given f(x, y) = 4x²y + 2xy²
Now, f(kx, ky) = 4(kx)² (ky) + 2(kx) (ky)²
= 4k² . x² . ky + 2kx . k²y²
= k³ (4x²y + 2xy²)
= k³ f(x, y)
∴ f(x, y) is a homogeneous function of degree 3.

Question 37.
Show that g(x, y) = \(x y^{1 / 2}+y x^{1 / 2}\) is a homogeneous function of degree 3/2.
Solution:
Given g(x, y) = \(x y^{1 / 2}+y x^{1 / 2}\)

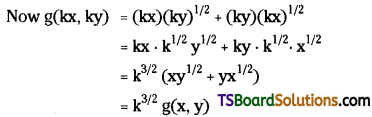
∴ g(x, y) is a homogeneous function of degree 3/2.

Question 38.
Show that h(x, y) = \(\frac{x^2+y^2}{x^3+y^3}\) is a homogeneous function of degree = 1.
Solution:
Given h(x, y) = \(\frac{x^2+y^2}{x^3+y^3}\)

∴ h(x, y) is a homogeneous function of degree -1.

Question 39.
Show that f(x, y) = 1 + e^x/y is a homogeneous function of x and y.
Solution:
Given f(x, y) = 1 + e^x/y
Now f(kx, ky) = 1 + \(e^{\left(\frac{k x}{k y}\right)}\)
= 1 + e^x/y
= k⁰ f(x, y)
Hence, f(x, y) is a homogeneous function of degree ‘0’.

Question 40.
Show that f(x, y) = \(x \sqrt{x^2+y^2}-y^2\) is a homogeneous function of x and y.
Solution:
Given f(x, y) = \(x \sqrt{x^2+y^2}-y^2\)

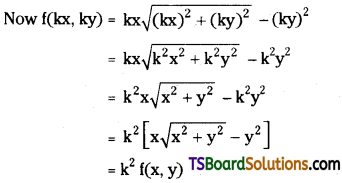
Hence f(x, y) is a homogeneous function of degree 2.

Question 41.
Show that f(x, y) = x – y log y + y log x is a homogeneous function of x and y.
Solution:
Given f(x, y) = x – y log y + y log x
Now f(kx, ky) = kx – ky log (ky) + (ky) log (kx)
= kx – ky (log k + log y) + ky (log k + log x)
= kx – ky log y – ky log k + ky log k + ky log x
= kx – ky log y + ky log x
= k(x – y log y + y log x)
= k f(x, y)
Hence, f(x, y) is a homogeneous function of degree 1.

Question 42.
Express \(\left(1+e^{x / y}\right) d x+e^{x / y}\left(1-\frac{x}{y}\right) d y=0\) in the form of \(\frac{\mathbf{d x}}{\mathbf{d y}}=\mathbf{F}\left(\frac{\mathbf{x}}{\mathbf{y}}\right)\).
Solution:

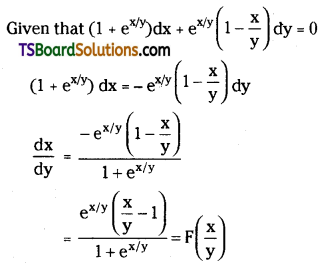
Which is the required form.

Question 43.
Express \(\frac{\mathbf{d y}}{\mathbf{d x}}=\frac{\mathbf{y}}{x+y \cdot e^{\frac{-2 x}{y}}}\) in the form \(\frac{\mathbf{d x}}{\mathbf{d y}}=\mathbf{F}\left(\frac{x}{\mathbf{y}}\right)\).
Solution:

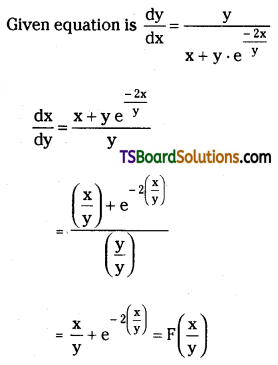
Which is the required form.

Question 44.
Express x dy – y dx = \(\sqrt{x^2+y^2}\) in the form \(F\left(\frac{y}{x}\right)=\frac{d y}{d x}\).
Solution:
Given equation is x dy – y dx = \(\sqrt{x^2+y^2}\) dx

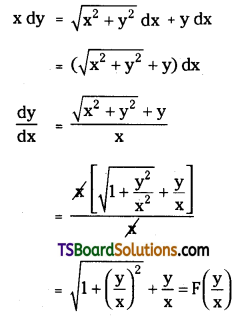
Which is in the required form.

Question 45.
Express \(\left(x-y \tan ^{-1} \frac{y}{x}\right) d x+x \tan ^{-1} \frac{y}{x} d y=0\) in the form \(F\left(\frac{y}{x}\right)=\frac{d y}{d x}\).
Solution:
Given equation is

Which is in the required form.

Question 46.
Express x \(\frac{d y}{d x}\) = y(log y – log x + 1) in the form \(F\left(\frac{y}{x}\right)=\frac{d y}{d x}\).
Solution:
Given equation is x \(\frac{d y}{d x}\) = y(log y – log x + 1)
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{y}}{\mathrm{x}}\left[\log \left(\frac{\mathrm{y}}{\mathrm{x}}\right)+1\right]=\mathrm{F}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\)
Which is in the required form.

Question 47.
Transform the D.E. x log x \(\frac{d y}{d x}\) + y = 2 log x.
Solution:
Given D.E. is x log x \(\frac{d y}{d x}\) + y = 2 log x
dividing both sides by x log x, we get
\(\frac{d y}{d x}+\frac{y}{x \log x}=\frac{2 \log x}{x \log x}\)
\(\frac{\mathrm{dy}}{\mathrm{dx}}+\frac{\mathrm{y}}{x \log x}=\frac{2}{\mathrm{x}}\)
Which is in the form \(\frac{d y}{d x}\) + Py = Q
It is linear in y.
Here P = \(\frac{1}{x \log x}\), Q = \(\frac{2}{\mathrm{x}}\)

Question 48.
Transform the D.E. (x + 2y³) \(\frac{\mathrm{dy}}{\mathrm{d} x}\) = y
Solution:
Given D.E. is (x + 2y³) \(\frac{\mathrm{dy}}{\mathrm{d} x}\) = y

Which is in the form \(\frac{\mathrm{dx}}{\mathrm{d} y}\) + Px = Q
It is linear in x.
Here P = \(\frac{-1}{y}\), Q = 2y².

Question 49.
Find the I.F of the D.E. (2x – 10y³) \(\frac{d y}{d x}\) + y = 0 by transforming it into a linear form.
Solution:
Given D.E. is (2x – 10y³) \(\frac{d y}{d x}\) + y = 0
(2x – 10y³) \(\frac{d y}{d x}\) = -y

Question 50.
Find the I.F of the D.E. y . \(\frac{\mathrm{dx}}{\mathrm{dy}}\) – x = 2y³ by transforming it into linear form.
Solution:
Given D.E. is y . \(\frac{\mathrm{dx}}{\mathrm{dy}}\) – x = 2y³
dividing both sides by ‘y’ we get
\(\frac{\mathrm{dx}}{\mathrm{dy}}-\frac{\mathrm{x}}{\mathrm{y}}\) = 2y²
Which is in the form \(\frac{\mathrm{dx}}{\mathrm{dy}}\) + Px = Q
It is linear in x.
Here P = \(\frac{-1}{y}\), Q = 2y²