TS Inter Second Year Maths 2A Partial Fractions Important Questions

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Partial Fractions Important Questions to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Partial Fractions Important Questions

Question 1.
Resolve \(\frac{5 x+1}{(x+2)(x-1)}\) into partial fractions. [May 2000]
Solution:
Let \(\frac{5 x+1}{(x+2)(x-1)}=\frac{A}{x+2}+\frac{B}{x-1}\)
= \(\frac{A(x-1)+B(x+2)}{(x+2)(x-1)}\)
⇒ 5x + 1 = A (x – 1) + B (x + 2)
Put x = – 2 then 5 (- 2) + 1 = A (- 2 – 1)
⇒ – 3A = – 9
⇒ A = 3
Put x = 1 then 5(1) + I = B(1 + 2)
⇒ 3B = 6
⇒ B = 2
∴ \(\frac{5 x+1}{(x+2)(x-1)}=\frac{3}{x+2}+\frac{2}{x-1}\).

Question 2.
Resolve \(\frac{3 x+7}{x^2-3 x+2}\) into partial fractions. [May ’14]
Solution:
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-1)(x-2)}\)
Let \(\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\)
= \(\frac{A(x-2)+B(x-1)}{(x-1)(x-2)}\)
3x + 7 = A (x – 2) + B (x – 1)
Put x = 1 then 3(1) + 7 = A (1 – 2)
⇒ 3 + 7 = A (- 1)
⇒ 10 = – A
⇒ A = – 10
Put x = 2 then 3(2) + 7 = B(2 – 1)
⇒ 6 + 7 = B(1)
⇒ B = 13
∴ \(\frac{3 x+7}{(x-1)(x-2)}=\frac{-10}{x-1}+\frac{13}{x-2}\).

Question 3.
Resolve \(\frac{x+4}{\left(x^2-4\right)(x+1)}\) into partial fractions. [Mar. ‘14]
Solution:

Question 4.
Resolve \(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}\) into partial fractions. [March 2008].
Solution:

Put x = – 3
⇒ C (- 6 + 3) = 9 – 39 + 15
⇒ C(- 3) = – 15
⇒ C = 5
Now, comparing the coefficients of x² in equation (1), we get
A + 2B = 1
⇒ – 1 + 2B = 1
⇒ 2B = 2
⇒ B = 1
∴ \(\frac{x^2+13 x+15}{(2 x+3)(x+3)^2}=\frac{-1}{2 x+3}+\frac{1}{x+3}+\frac{5}{(x+3)^2}\).

Question 5.
Resolve \(\frac{1}{(x-1)^2(x-2)}\) into partial fractions. [May 2013].
Solution:
Let \(\frac{1}{(x-1)^2(x-2)}\) = \(\frac{A}{(x-1)}+\frac{B}{(x-1)^2}+\frac{C}{(x-2)}\)
⇒ \(\frac{1}{(x-1)^2(x-2)}\) = \(\frac{A(x-1)(x-2)+B(x-2)+C(x-1)^2}{(x-1)^2(x-2)}\)
⇒ A (x – 1) (x – 2) + B (x – 2) + C (x – 1)² = 1 …………….(1)
If x = 1
⇒ B(- 1) = 1
⇒ B = – 1
If x = 2
⇒ C(1) = 1
⇒ C = 1
Now, comparing the coefficients of x² in equation (1) we get,
A + C = 0
⇒ A = – 1
∴ \(\frac{1}{(x-1)^2(x-2)}=\frac{(-1)}{x-1}+\frac{(-1)}{(x-1)^2}+\frac{1}{x-2}\).

Question 6.
Resolve \(\frac{2 x^2+2 x+1}{x^3+x^2}\) into partial fractions. [TS – MAr. 2017]
Solution:
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}\)
Let \(\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
\(\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A x(x+1)+B(x+1)+C\left(x^2\right)}{x^2(x+1)}\)
⇒ Ax (x + 1) + B (x + 1) + Cx² = 2x² + 2x + 1 …………….(1)
If x = 0
⇒ B(1) = 1
⇒ B = 1
If x = – 1
⇒ C(- 1)² = 2(1)² – 2 + 1
⇒ C = 1.
Now, comparing the coeff. of x² on both sides of (1) we get,
A+ C = 2
⇒ A + 1 = 2
⇒ A = 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\).

Question 7.
Resolve \(\frac{3 x-18}{x^3(x+3)}\) into partial fractions.
Solution:
Let \(\frac{3 x-18}{x^3(x+3)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+3}\)
\(\frac{3 x-18}{x^3(x+3)}\) = \(\frac{\mathrm{Ax}^2(\mathrm{x}+3)+\mathrm{Bx}(\mathrm{x}+3)+\mathrm{C}(\mathrm{x}+3)+\mathrm{Dx}^3}{\mathrm{x}^3(\mathrm{x}+3)}\)
⇒ Ax² (x + 3) + Bx (x + 3) + C (x + 3) + D(x³) = 3x – 18 ………………(1)
If x = 0
⇒ C(3) = – 18
⇒ C = – 6
If x = – 3
⇒ D (- 27) = – 9 – 18
⇒ D = 1
Now, comparing the coeff. of x³ in (1) we get,
A + D = 0
⇒ A + 1 = 0
⇒ A = – 1
Now, comparing the coeff. of x² in (1) we get,
3A + B = 0
⇒ 3(- 1) + B = 0,
⇒ B = 3
∴ \(\frac{3 x-18}{x^3(x+3)}=\frac{(-1)}{x}+\frac{3}{x^2}+\frac{(-6)}{x^3}+\frac{1}{x+3}\).

Question 8.
Resolve \(\frac{3 x^2-8 x^2+10}{(x-1)^4}\) into partial fractions. [March 2006]
Solution:
Let x – 1 = y
⇒ x = y + 1

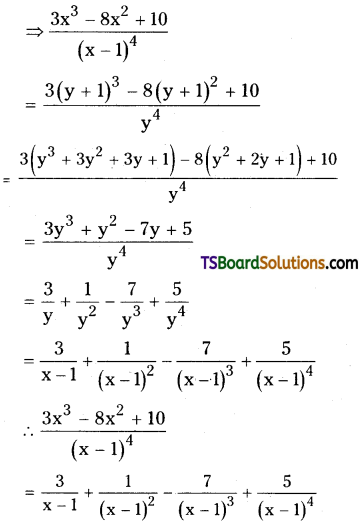
Question 9.
Resolve \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\) into partial fractions. [March ’11, 2007, June ’11, TS – Mar. ’18, AP – MAr. 2015; MAy ’12, ’01]
Solution:
Let \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\)
\(\frac{\mathrm{A}\left(\mathrm{x}^2+2\right)+(\mathrm{Bx}+\mathrm{C})(\mathrm{x}-1)}{(\mathrm{x}-1)\left(\mathrm{x}^2+2\right)}=\frac{2 \mathrm{x}^2+3 \mathrm{x}+4}{(\mathrm{x}-1)\left(\mathrm{x}^2+2\right)}\)
A(x² + 2) + (Bx + C) (x – 1) = 2x² + 3x + 4 ……………….(1)
Put x = 1
⇒ A (1 + 2) = 2 + 3 + 4
⇒ A(3) = 9
⇒ A = 3.
From (1),
⇒ 2x² + 3x + 4 = Ax² + 2A + Bx² – Bx + Cx – C
Now, comparing the coefficients of x2 we get,
A + B = 2
⇒ 3 + B = 2
⇒ B = – 1
Comparing coefficients of x we get,
⇒ – B + C = 3
⇒ 1 + C = 3
⇒ C = 2
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{(-1) x+2}{x^2+2}\)
= \(\frac{3}{x-1}+\frac{-x+2}{x^2+2}\).

Question 10.
Resolve \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\) into partial fractions. [May ‘09, ‘07, Mar. ‘12, ‘09, ‘05]
[AP – Mar. ‘17, ’16. May ’16; Board Paper].
Solution:
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\)
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A\left(x^2+1\right)+(B x+C)(x+2)}{(x+2)\left(x^2+1\right)}\)
A (x² + 1) + (Bx + C) (x + 2) = x – 3 ……………….(1)
If x = – 2
⇒ A (4 + 1) = 4 – 3
⇒ A = \(\frac{1}{5}\)
From (1),
⇒ Ax² + A + Bx² + 2Bx + Cx + 2C = x² – 3
Now, comparing coeff. of x² on both sides of (1) we get,
A + B = 1
⇒ \(\frac{1}{5}\) + B = 1
⇒ B = 1 – \(\frac{1}{5}\)
⇒ B = \(\frac{4}{5}\)
Comparing coeff. of x on both sides of (1) we get
2B + C = 0
⇒ \(\frac{8}{5}\) + C = O
⇒ C = \(\frac{-8}{5}\)
∴ \(\frac{x^2-3}{(z+2)\left(x^2+1\right)}=\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\).

Question 11.
Resolve \(\frac{2 x^2+1}{x^3-1}\) into partial fractions.
Solution:
\(\frac{2 x^2+1}{x^3-1}=\frac{2 x^2+1}{(x-1)\left(x^2+x+1\right)}\)
Let \(\frac{2 x^2+1}{(x-1)\left(x^2+x+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+x+1}\)
\(\frac{2 x^2+1}{(x-1)\left(x^2+x+1\right)}=\frac{A\left(x^2+x+1\right)+(B x+C)(x-1)}{(x-1)\left(x^2+x+1\right)}\)
A (x² + x + 1) + (Bx + C) (x – 1) = 2x² + 1 ……………….(1)
If x = 1
⇒ A (3) = 3
⇒ A = 1
From (1),
⇒ Ax² + Ax + A + Bx² – Bx + Cx – C = 2x² + 1
Now comparing coeff. of x² on both sides of (1) we get,
A + B = 2
⇒ 1 + B = 2
⇒ B = 1
Now, comparing coeff. of x on both sides of (1) we get, —-
A – B + C = 0
⇒ 1 – 1 + C = 0
⇒ C = 0
∴ \(\frac{2 x^2+1}{x^3-1}=\frac{1}{x-1}+\frac{x}{x^2+x+1}\).

Question 12.
Resolve \(\frac{\mathbf{x}^3}{(\mathbf{x}-\mathbf{a})(\mathbf{x}-\mathbf{b})(\mathbf{x}-\mathbf{c})}\) into partial fractions. [TS – MAy ’16, ’15, May ’08] [TS – Mar. 2019]
Solution:

Question 13.
Resolve \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\) into partial fractions.
Solution:
Let \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\)
= \(\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{x+2}+\frac{C}{x-3}\)
= \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\)
= \(\frac{(2 \mathrm{x}-1)(\mathrm{x}+2)(\mathrm{x}-3)+2 \mathrm{~A}(\mathrm{x}+2)(\mathrm{x}-3)+2 B(2 \mathrm{x}-1)(\mathrm{x}-3)+2 \mathrm{C}(2 \mathrm{x}-1)(\mathrm{x}+2)}{2(2 \mathrm{x}-1(\mathrm{x}+2)(\mathrm{x}-3)}\)
2x³ = (2x – 1) (x + 2) (x -3) + 2A (x + 2) (x – 3) + 2B (2x – 1) (x – 3) + 2C (2x – 1) (x + 2)
If x = \(\frac{1}{2}\)
⇒ 2A(\(\frac{1}{2}\) + 2) (\(\frac{1}{2}\) – 3) = 2 . \(\frac{1}{8}\)
⇒ 2A . \(\frac{5}{2}\) . \(\frac{-5}{2}\) = \(\frac{1}{4}\)
A = \(-\frac{1}{50}\)
If x = – 2
⇒ 2B (2 (- 2) – 1) (- 2 – 3) = – 2 (8)
⇒ 2B (- 5) (- 5) = – 16
B = \(\frac{-8}{25}\)
If x = 3
⇒ 2C (6 – 1) (3 + 2) = 2 (27)
⇒ 2C (5) (5) = 2(27)
C = \(\frac{27}{25}\)
∴ \(\frac{x^3}{(2 x-1)(x+2)(x-3)}\) = \(\frac{1}{2}+\frac{\frac{-1}{50}}{2 x-1}+\frac{\left(\frac{-8}{25}\right)}{x+2}+\frac{\frac{27}{25}}{x-3}\)
= \(\frac{1}{2}-\frac{1}{50(2 x-1)}-\frac{8}{25(x+2)}+\frac{27}{25(x-3)}\).

Question 14.
Resolve \(\frac{x^4}{(x-1)(x-2)}\) into partial fractions. [TS – Mar. ’16, Mar. ’13, ’10]
Solution:

15x – 14 = A (x – 2) + B (x – 1)
If x = 1
⇒ A(1 – 2) = 15 – 14
⇒ A = – 1
If x = 2
⇒ B(2 – 1) = 15 (2) – 14
⇒ B = 30 – 14
⇒ B = 16
∴ \(\frac{x^4}{(x-1)(x-2)}\) = x² + 3x + 7 – \(\frac{1}{(x-1)}+\frac{16}{(x-2)}\).

Question 15.
Find the coefficient of x⁴ in the expansion \(\frac{3 x}{(x-2)(x+1)}\) of in powers of x. [Mar. ’89, ’97]
Solution:
Let \(\frac{3 x}{(x-2)(x+1)}=\frac{A}{x-2}+\frac{B}{x+1}\)
\(\frac{3 x}{(x-2)(x+1)}=\frac{A(x+1)+B(x-2)}{(x-2)(x+1)}\)
⇒ A(x + 1) + B(x – 2) = 3x
If x = 2
⇒ A(3) = 6
⇒ A = 2
If x = – 1
⇒ B (- 3) = -3
⇒ B = 1

Question 16.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x-4}{x^2-5 x+6}\) specfying the region in which the expansion is valid. [May 2010]
Solution:
Given, \(\frac{x-4}{x^2-5 x+6}=\frac{x-4}{(x-3)(x-2)}\)
Let \(\frac{x-4}{(x-3)(x-2)}=\frac{A}{(x-3)}+\frac{B}{(x-2)}\)
\(\frac{\mathrm{x}-4}{(\mathrm{x}-3)(\mathrm{x}-2)}=\frac{\mathrm{A}(\mathrm{x}-2)+\mathrm{B}(\mathrm{x}-3)}{(\mathrm{x}-3)(\mathrm{x}-2)}\)
⇒ A(x – 2) + B (x – 3) = x – 4
If x = 3
⇒ A(1) = – 1
⇒ A = – 1
If x = 2
⇒ B (- 1) = – 2
⇒ B = 2
∴ \(\frac{x-4}{(x-3)(x-2)}=\frac{(-1)}{x-3}+\frac{2}{x-2}\)
Now, \(\frac{-1}{x-3}+\frac{2}{x-2}=\frac{-1}{-3\left(1-\frac{x}{3}\right)}+\frac{2}{(-2)\left(1-\frac{x}{2}\right)}\)
= \(\frac{1}{3}\) (1 – \(\frac{x}{3}\))^-1 – (1 – \(\frac{x}{2}\))^-1 ………….(1)
Now, (1 – \(\frac{x}{3}\))^-1 expansion is valid when
|\(\frac{x}{3}\)| < 1
⇒ |x| < 3
(1 – \(\frac{x}{3}\))^-1 expansion is valid when
|\(\frac{x}{2}\)| < 1
⇒ |x| < 2
Thus, if |x| < 2, both the above expansions are valid.
Hence, we get from (1)
\(\frac{-1}{x-3}+\frac{2}{x-2}\) = \(\frac{1}{3}\left[1+\frac{x}{3}+\left(\frac{x}{3}\right)^2+\ldots \ldots+\left(\frac{x}{3}\right)^n+\ldots \ldots\right]\) – \(\left[1+\frac{\mathrm{x}}{2}+\left(\frac{\mathrm{x}}{2}\right)^2+\ldots \ldots\left(\frac{\mathrm{x}}{2}\right)^{\mathrm{n}}+\ldots .\right]\)
∴ Coeff. of xⁿ = \(\frac{1}{3 \cdot 3^n}-\frac{1}{2^n}=\frac{1}{3^{n+1}}-\frac{1}{2^n}\).

Some More Maths 2A Partial Fractions Important Questions

Question 1.
Resolve \(\frac{2 x+3}{5(x+2)(2 x+1)}\) into partial fractions.
Solution:

Question 2.
Resolve \(\frac{13 x+43}{2 x^2+17 x+30}\) into partial fractions.
Solution:
We have 2x² + 17x + 30 = (2x + 5) (x + 6)
∴ \(\frac{13 x+43}{2 x^2+17 x+30}=\frac{13 x+43}{(2 x+5)(x+6)}\)
Now, let
\(\frac{13 x+43}{(2 x+5)(x+6)}=\frac{A}{2 x+5}+\frac{B}{x+6}\)
∴ 13x + 43 = A(x + 6) + B(2x + 5)
= (A + 2B)x + (6A + 5B)
Comparing the coefficients of like powers of x, we have
A + 2B = 13 and 6A + 5B = 43
Solving these two equations,
we get A = 3 and B = 5
∴ \(\frac{13 x+43}{2 x^2+17 x+30}=\frac{3}{2 x+5}+\frac{5}{x+6}\).

Question 3.
Resolve \(\frac{x^2-x+1}{(x+1)(x-1)^2}\) into partial fractions.
Solution:
Let \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A}{(x+1)}+\frac{B}{(x-1)}+\frac{C}{(x-1)^2}\)
\(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A(x-1)^2+B(x+1)(x-1)+C(x+1)}{(x+1)(x-1)^2}\)
⇒ A(x – 1)² + B(x + 1) (x – 1) + C(x + 1) = x2 – x + 1 …………….(1)
If x = – 1
⇒ A(4) = 3
⇒ A = \(\frac{3}{4}\)
If x = 1
⇒ C(2) = 1
⇒ C = \(\frac{1}{2}\)
Now, comparing the coeff. of x² in equation (1)
We get A + B = 1
⇒ \(\frac{3}{4}\) + B = 1
⇒ B = 1 – \(\frac{3}{4}\)
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\).

Question 4.
Resolve \(\frac{x-1}{(x+1)(x-2)^2}\) into partial fractions.
Solution:

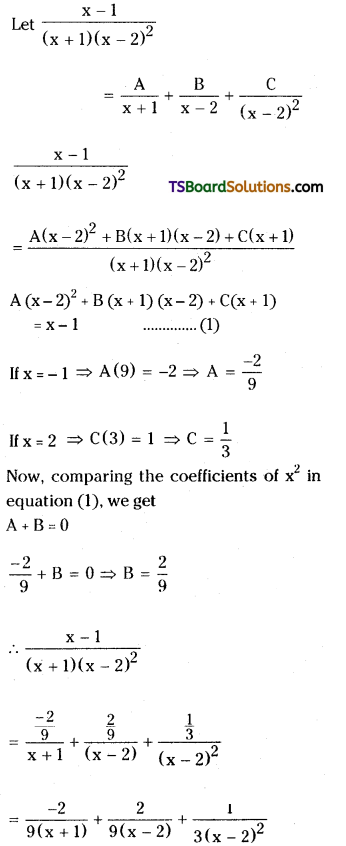
Question 5.
Resolve \(\frac{1}{x^3(x+a)}\) into partial fractions.
Solution:
Let \(\frac{1}{x^3(x+a)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+a}\)
\(\frac{1}{x^3(x+a)}=\frac{\mathrm{Ax}^2(\mathrm{x}+\mathrm{a})+\mathrm{Bx}(\mathrm{x}+\mathrm{a})+\mathrm{C}(\mathrm{x}+\mathrm{a})+\mathrm{D}\left(\mathrm{x}^3\right)}{\mathrm{x}^3(\mathrm{x}+\mathrm{a})}\)
⇒ Ax² (x + a) + Bx (x + a) + C (x + a) + D(x³) = 1 ……………..(1)
If x = 0
⇒ C(a) = 1
⇒ C = \(\frac{1}{a}\)
If x = – a = 1
⇒ D(- a³) = 1
⇒ D = \(\frac{-1}{a^3}\)
Now, comparing the coeff. of x³ in (1) we get
A + D = 0
⇒ A – \(\frac{1}{a^3}\) = 0
⇒ A = \(\frac{1}{a^3}\)
Now, comparing the coeff. of x² in (1) we get
Aa + B = 0
⇒ a \(\frac{1}{a^3}\) + B = 0
⇒ B = \(-\frac{1}{a^2}\)
∴ \(\frac{1}{x^3(x+a)}=\frac{\frac{1}{a^3}}{x}+\frac{\frac{-1}{a^2}}{x^2}+\frac{\frac{1}{a}}{x^3}+\frac{\frac{-1}{a^3}}{x+a}\)
= \(\frac{1}{a^3 x}+\frac{(-1)}{a^2 x^2}+\frac{1}{a^3}+\frac{(-1)}{a^3(x+a)}\)

Question 6.
Resolve \(\frac{x^2+5 x+7}{(x-3)^3}\) into partial fractions.
Solution:
Let y = x – 3
⇒ x = y + 3
Now,

Question 7.
Resolve \(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\) into partial fractions.
Solution:

If x = 1
⇒ B(3) = 3
⇒ B = 1.
From (1)
⇒ Ax³ – A + Bx² + Bx + B + Cx³ + Cx – 2Cx² + Dx² + D – 2Dx = x³ + x² + 1
Now, comparing coeffi. of x³ we get,
A + C = 1 ……………….(2)
Comparing coeff. of x² we get,
B – 2C + D = 1
⇒ 1 – 2C + D = 1
⇒ – 2C + D = 0 ……………(3)
Comparing coeff. of x we get,
B + C – 2D = 0
⇒ C – 2D = – 1 …………….(4)
Comparing constants we get,
– A + B + D = 1
⇒ – A + D = 0 …………….(5)
Solving (3) and (4)

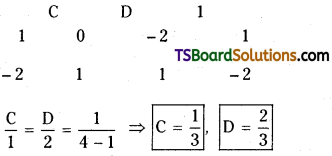
From (5)
⇒ – A + D = 0
⇒ A + \(\frac{2}{3}\) = 0
⇒ A = \(\frac{2}{3}\)
∴ \(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}=\frac{2}{3(x-1)}+\frac{1}{(x-1)^2}+\frac{x+2}{3\left(x^2+x+1\right)}\).

Question 8.
Resolve \(\frac{x^2}{(x-1)(x-2)}\) into partial fractions.
Solution:
Let \(\frac{x^2}{(x-1)(x-2)}=1+\frac{A}{x-1}+\frac{B}{x-2}\)
\(\frac{x^2}{(x-1)(x-2)}=\frac{(x-1)(x-2)+A(x-2)+B(x-1)}{(x-1)(x-2)}\)
x² = (x – 1) (x – 2) + A (x – 2) B (x – 1)
If x = 1
⇒ A (1 – 2) = 1
⇒ A (- 1) = 1
⇒ A = – 1
If x = 2
⇒ B (2 – 1) = 4
⇒ B (1) = 4
⇒ B = 4
∴ \(\frac{x^2}{(x-1)(x-2)}=1+\frac{(-1)}{x-1}+\frac{4}{x-2}\)
= 1 – \(\frac{1}{(x-1)}+\frac{4}{(x-2)}\).

Question 9.
Resolve \(\frac{x^3}{(2 x-1)(x-1)^2}\) into partial fractions.
Solution:
Let \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{(x-1)}+\frac{C}{(x-1)^2}\)
⇒ \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{(2 \mathrm{x}-1)(\mathrm{x}-1)^2+\mathrm{A}(2)(\mathrm{x}-1)^2+2 B(2 x-1)(x-1)+2 C(2 x-1)}{2(2 x-1)(x-1)^2}\)
⇒ 2x³ = (2x – 1) (x – 1)² + 2A (x – 1)² + 2B(2x – 1) (x – 1) + 2C (2x – 1)
If x = \(\frac{1}{2}\)
⇒ 2A (\(\frac{1}{2}\) – 1)² = 2(\(\frac{1}{2}\))³
⇒ 2A (\(\frac{1}{4}\)) = 2 . \(\frac{1}{8}\)
⇒ A =\(\frac{1}{2}\)
If x = 1
⇒ 2C (2 – 1) = 2
⇒ C = i
Comparing the coefficients of x², we get
2A + 4B – 5 = 0
2 (\(\frac{1}{2}\)) + 4B – 5 = 0
⇒ 4B = 4
⇒ B = 1.
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{\frac{1}{2}}{2 x-1}+\frac{(+1)}{x-1}+\frac{1}{(x-1)^2}\)
= \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{x-1}+\frac{1}{(x-1)^2}\).

Question 10.
Resolve \(\frac{x^3}{(x-1)(x+2)}\) into partial fractions. [Ap – Mar. 2019]
Solution:
Let (x – 1) (x + 2) = x² + 2x – x – 2 = x

A(x + 2) + B(x – 1) = 3x – 2
If x = 1
⇒ A (1 + 2) = 3 – 2
⇒ A = \(\frac{1}{3}\)
If x = – 2
⇒ B (- 2 – 1) = 3 (- 2) – 2
B (- 3) = – 8
⇒ B = \(\frac{8}{3}\)
∴ \(\frac{x^3}{(x-1)(x+2)}\) = x – 1 + \(\frac{\frac{1}{3}}{x-1}+\frac{\frac{8}{3}}{x+2}\)
= x – 1 + \(\frac{1}{3(x-1)}+\frac{8}{3(x+2)}\).

Question 11.
Find the coefficient of x³ in the power series expansion of \(\frac{5 x+6}{(x+2)(1-x)}\) specifying the region in which the expansion is valid.
Solution:

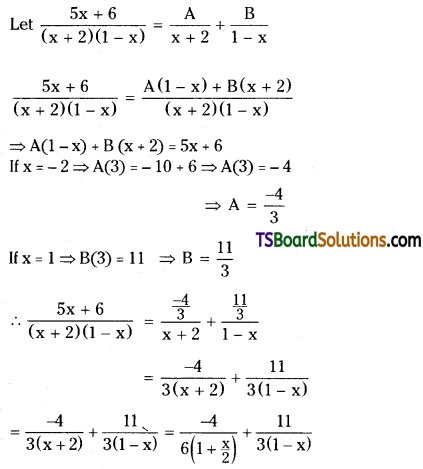
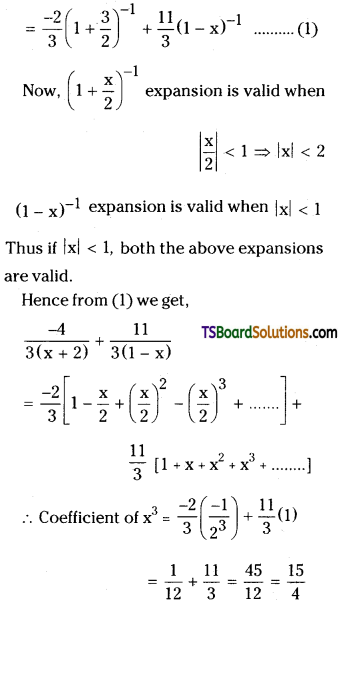
Question 12.
Resolve \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) into partial fractions.
Solution:
Let \(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}=\frac{A x+B}{x^2+2}+\frac{C x+D}{x^2+3}\)
\(\frac{x^3+x^2+1}{\left(x^2+2\right)\left(x^2+3\right)}\) = \(\frac{(\mathrm{Ax}+\mathrm{B})\left(\mathrm{x}^2+3\right)+(\mathrm{Cx}+\mathrm{D})\left(\mathrm{x}^2+2\right)}{\left(\mathrm{x}^2+2\right)\left(\mathrm{x}^2+3\right)}\)
(Ax + B) (x² + 3) + (Cx + D) (x² + 2) = x³ + x² + 1
Ax³ 3Ax + Bx² + 3B + Cx³ + 2Cx + Dx² + 2D = x³ + x² + 1
Now, comparing the coefficients of x3 we get,
⇒ A + C = 1 ………………(1)
Comparing the coefficients of x2 we get,
⇒ B + D = 1 ………………(2)
Comparing the coefficients of x, we get,
⇒ 3A + 2C = 0 ……………..(3)
Comparing the constant terms we get,
⇒ 3B + 2D = 1 …………….(4)
Solve (1) and (3)

Question 13.
Resolve \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}\) into partial fractions.
Solution:
Let \(\frac{3 x^3-2 x^2-1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\) = x⁴ + 2x² + 1 – x²
= (x² + 1)² – x²
= (x² + x + 1) (x² – x + 1)
= \(\frac{A x+B}{x^2+x+1}+\frac{C x+D}{x^2-x+1}\)
\(\frac{3 x^3-2 x^2-1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\) = \(\frac{(A x+B)\left(x^2-x+1\right)+(C x+D)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
(Ax + B) (x² – x + 1) + (Cx + D) (x² + x + 1) = 3x³ – 2x² – 1
AX³ – Ax² + Ax + Bx² – Bx + B + Cx³ + Cx² + Cx + Dx² + Dx + D = 3x³ – 2x² – 1
Now, comparing the coeff. of x³ on both sides we get
⇒ A + C = 3 …………….(1)
Comparing the coefi. of x² on both sides,
we get
⇒ – A + B + C + D = – 2 ……………..(2)
Comparing the coeff. of xon both sides, we get
A – B + C + D = 0
⇒ 3 – B + D = 0
⇒ B – D = 3 ………………..(3)
Comparing constants on both sides we get,
B + D = – 1 ……………(4)
From (3) and (4),
⇒ B – D = 3
B + D = – 1
2B = 2
B = 1
from B – D = 3
1 – D = 3
D = – 2
From (2)
⇒ – A + B + C + D = – 2
⇒ – A + 1 + C – 2 = – 2
– A + C = – 1 ……………(5)
Solving (1) and (5)
A + C = 3
– A + C = – 1
2C = + 2
C = + 1
from A + C = 3
A + 1 = 3
A = 2
∴ \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{2 x+1}{x^2+x+1}+\frac{x-2}{x^2-x+1}\).

Question 14.
Resolve \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) into partial fractions.
Solution:
Let \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) = \(\frac{A}{1-x}+\frac{B}{(1-x)^2}+\frac{C x+D}{1+x^2}\)
\(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) = \(\frac{A(1-x)\left(1+x^2\right)+B\left(1+x^2\right)+(C x+D)(1-x)^2}{(1-x)^2\left(1+x^2\right)}\)
⇒ A (1 – x) (1 + x²) + B (1 + x²) + (Cx + D) (1 – x)² = x + 3 ………………(1)
If x = 1
⇒ B(1 + 1) = 1 + 3
⇒ B(2) = 4
⇒ B = 2.
From (1)
⇒ A(1 + x² – x – x³) + B (1 + x²) + (Cx + D) (1 + x² – 2x) = x + 3
⇒ A + Ax² – Ax – Ax³ + B + Bx² + Cx + Cx³ – 2Cx² + D + Dx² – 2Dx = x + 3
Now, comparing the coefficients of x³ on both sides we get,
⇒ – A + C = 0
⇒ A – C = 0 ……………..(2)
Corn paring the coefficients of x² we get,
A + B – 2C + D = 0
A + 2 – 2C + D = 0
⇒ A – 2C + D = – 2 ………………(3)
Comparing coefficients of x we get,
– A + C – 2D = 1
⇒ 0 – 2D = 1
⇒ D = \(-\frac{1}{2}\)
Comparing constants we get,
A + B + D = 3 ………………(4)
From (4)
⇒ A + 2 – \(\frac{1}{2}\) = 3
⇒ A = \(\frac{3}{2}\)
From (2)
⇒ \(\frac{3}{2}\) – C = 0
C = \(\frac{3}{2}\)
∴ \(\frac{x+3}{(1-x)^2\left(1+x^2\right)}\) = \(\frac{\frac{3}{2}}{(1-x)}+\frac{2}{(1-x)^2}+\frac{\frac{3}{2} x-\frac{1}{2}}{1+x^2}\)
= \(\frac{3}{2(1-x)}+\frac{2}{(1-x)^2}+\frac{3 x-1}{2\left(1+x^2\right)}\).

Question 15.
Resolve \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\) into partial fractions.
Solution:
Let \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\) = \(\frac{A x+B}{1-x+x^2}+\frac{C}{x+2}\)
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{(A x+B)(x+2)+C\left(1-x+x^2\right)}{\left(1-x+x^2\right)(x+2)}\)
(Ax + B) (x + 2) + C (1 – x + x²) = 3x – 1 …………….(1)
If x = – 2
⇒ C (1 + 2 + 4) = – 6 – 1
⇒ C(7) = – 7
⇒ C = – 1
From (1)
⇒ Ax² + 2Ax+ Bx + 2B + C – Cx + Cx² = 3x – 1
Now. comparing coeff. of x² we get,
⇒ A + C = 0
⇒ A – 1 = 0
⇒ A = 1
Comparing coeff. of x we get,
2A + B – C = 3
⇒ 2 + B + 1 = 3
⇒ B + 3 = 3
⇒ B = 0
∴ \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{x}{1-x+x^2}+\frac{(-1)}{x+2}\).

Question 16.
Resolve \(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\) into partial fractions.
Solution:

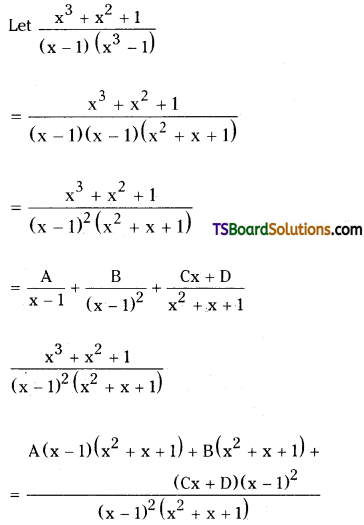
A (x – 1) (x² + x + 1) + B (x² + x + 1) + (Cx + D) (x – 1)² = x³ + x² + 1 ………………(1)
II x = 1
⇒ B(3) = 3
⇒ B = 1
From (1)
⇒ Ax³ + Ax² + Ax – Ax² – Ax – A + Bx² + Bx + B + Cx³ + Cx – 2Cx² + Dx² + D – 2Dx = x³ + x² + 1
Now, comparing coefficients of x³ we get,
A + C = 1 ………….(2)
Comparing coeff. of x² we get,
B – 2C + D = 1
⇒ 1 – 2C + D = 1
⇒ – 2C + D = 0 …………….(3)
Comparing coeff. of x we get,
B + C – 2D = 0
⇒ C – 2D = – 1
Comparing constants we get,
⇒ – A + B + D = 1
⇒ – A + D = 0 ………….(5)
Solving (3) and (4)

Question 17.
Resolve \(\frac{x^3}{(2 x-1)(x-1)^2}\) into partial fractions.
Solution:

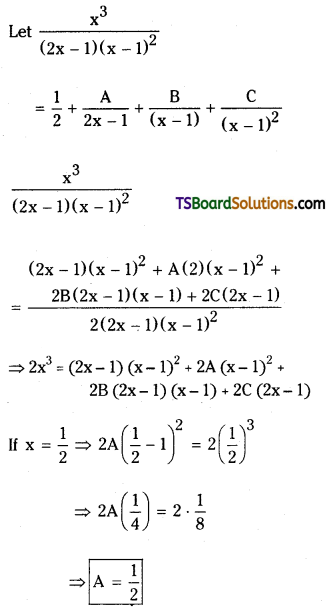
If x = 1
⇒ 2C (2 – 1) = 2
⇒ C = 1
Comparing the coefficients of x we get,
2A + 4B – 5 = 0
2(\(\frac{1}{2}\)) + 4B – 5 = o
⇒ B = 1
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{\frac{1}{2}}{2 x-1}+\frac{(+1)}{x-1}+\frac{1}{(x-1)^2}\)
= \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{x-1}+\frac{1}{(x-1)^2}\)

Question 18.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x}{(x-1)^2(x-2)}\) specifying the region In which the expansion is valid. [AP – May 2015].
Solution:
Let \(\frac{x}{(x-1)^2(x-2)}\) = \(\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x-2}\)
\(\frac{x}{(x-1)^2(x-2)}\) = \(\frac{A(x-1)(x-2)+B(x-2)+C(x-1)^2}{(x-1)^2(x-2)}\)
A(x – 1) (x – 2) + B (x – 2) + C(x – 1)² = x ……………….(1)
If x = 1
⇒ B (- 1) = 1
⇒ B = – 1
If x = 2
⇒ C(1) = 2
⇒ C = 2
Now comparing coefficients of x² on both sides of (1)
A + C = 0
⇒ A + 2 = 0
⇒ A = – 2
∴ \(\frac{x}{(x-1)^2(x-2)}=\frac{(-2)}{x-1}+\frac{(-1)}{(x-1)^2}+\frac{2}{(x-2)}\).