TS Inter Second Year Maths 2B Differential Equations Important Questions Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Differential Equations Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Differential Equations Important Questions Short Answer Type

Model I – Problems on Variables Separable Method

Question 1.
Solve \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = e^x-y + x² (e^-y). [(AP) May ’18, (TS) ’17]
Solution:

Question 2.
Solve (e^x + 1) y dy + (y + 1) dx = 0. [May ’10, mar. ’04]
Solution:

Question 3.
Solve tan y sec²x dx + tan x sec²y dy = 0.
Solution:
Given D.E is tan y sec²x dx + tan x sec²y dy = 0
⇒ \(\frac{\sec ^2 x d x}{\tan x}+\frac{\sec ^2 y d y}{\tan y}=0\)
⇒ \(\int \frac{\sec ^2 x}{\tan x} d x+\int \frac{\sec ^2 y}{\tan y} d y=c\)
⇒ log|tan x| + log|tan y| = c
⇒ log|tan x| + log|tan y| = log c
⇒ log|tan x tan y| = log c
⇒ tan x tan y = c

Question 4.
Solve (xy² + x) dx + (yx² + y) dy = 0. [(TS) Mar. ’20, (AP) ’15; May ’13]
Solution:

Question 5.
Solve \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\). [Mar. ’05]
Solution:

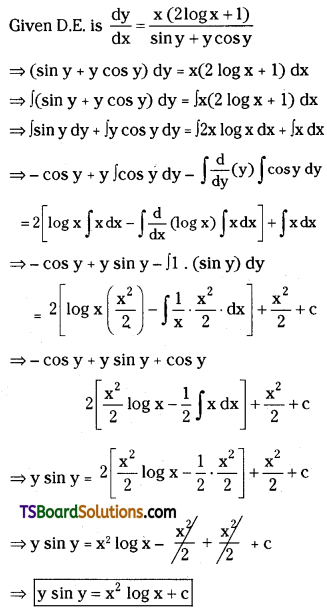
Question 6.
Solve \(\frac{d y}{d x}=\frac{-\left(y^2+y+1\right)}{\left(x^2+x+1\right)}\). [May ’08, Mar. ’03]
Solution:


which is the required general solution.
(where k = √3c = constant)

Question 7.
Solve \(\sin ^{-1}\left(\frac{d y}{d x}\right)\) = x + y. [(TS) Mar. ’20; May ’07]
Solution:

⇒ ∫sec²t dt – ∫tan t sec t dt = x + c
⇒ tan t – sec t = x + c
⇒ tan(x + y) – sec(x + y) = x + c
which is the required general solution.

Question 8.
Solve \(\frac{d y}{d x}\) = tan²(x + y).
Solution:

Question 9.
Solve \(\frac{d y}{d x}\) – x tan(y – x) = 1. [(TS) May ’15]
Solution:
Put y – x = z, then
\(\frac{d y}{d x}-1=\frac{d z}{d x}\)
⇒ \(\frac{d y}{d x}=1+\frac{d z}{d x}\)

∴ The solution is sin(y – x) = \(c \mathrm{e}^{\mathrm{x}^2 / 2}\), where c is an arbitrary constant.

Question 10.
Solve (x + y + 1) \(\frac{d y}{d x}\) = 1
Solution:

⇒ x + y + 1 – log(1 + x + y + 1) = x + c
⇒ y + 1 – log(x + y + 2) = c
⇒ y – log(x + y + 2) = c
Which is the required solution.

Question 11.
Solve \(\sqrt{1+x^2} d x+\sqrt{1+y^2} d y=0\). [Mar. ’09]
Solution:

Question 12.
Solve y(1 + x) dx + x(1 + y) dy = 0. [(AP) Mar. ’20]
Solution:
Given D.E. is y(1 + x) dx + x(1 + y) dy = 0
y(1 + x) dx = -x(1 + y) dy
\(\frac{1+x}{x} d x=\frac{-(1+y)}{y} d y\)
\(\left(\frac{1}{x}+1\right) d x=\left(\frac{-1}{y}-1\right) d y\)
Now, Integrating on both sides, we get
\(\int\left(\frac{1}{x}+1\right) d x=\int\left(\frac{-1}{y}-1\right) d y\)
\(\int \frac{1}{x} d x+\int 1 d x=-\int \frac{1}{y} d y-\int 1 d y\)
log x + x = -log y – y + c
log x + x + log y + y = c
x + y + log xy = c
Which is the required solution.

Question 13.
Solve \(\frac{d y}{d x}=\frac{x y+y}{x y+x}\). [(TS) May ’16]
Solution:

Question 14.
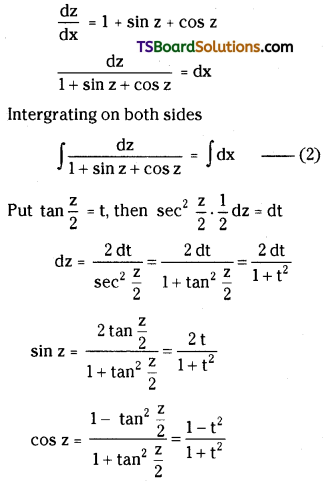
Solve \(\frac{d y}{d x}\) = sin(x + y) + cos(x + y)
Solution:
Given D.E. is \(\frac{d y}{d x}\) = sin(x + y) + cos(x + y)
Put x + y = z
differential w.r.t ‘x’
\(1+\frac{d y}{d x}=\frac{d z}{d x}\)
⇒ \(\frac{d y}{d x}=\frac{d z}{d x}-1\)
(1) ⇒ \(\frac{\mathrm{dz}}{\mathrm{d} \mathrm{x}}\) – 1 = sin z + cos z

Question 15.
Solve \(\frac{d y}{d x}\) = (3x + y + 4)²
Solution:
Given D.E. is \(\frac{d y}{d x}\) = (3x + y + 4)² …….(1)
Put 3x + y + 4 = z
differential w.r.t ‘x’
\(3+\frac{d y}{d x}=\frac{d z}{d x}\)
⇒ \(\frac{d y}{d x}=\frac{d z}{d x}-3\)

Question 16.
Find the equation of the curve whose slope, at any point (x, y) is \(\frac{y}{x^2}\) and which satisfies the condition y = 1, when x = 3.
Solution:
We know that the slope at any point (x, y) on the curve is m = \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
Given that, slope of at any point (x, y) on the curve is m = \(\frac{y}{x^2}\)

Question 17.
Solve (y² – 2xy) dx + (2xy – x²) dy = 0. [May ’01]
Solution:

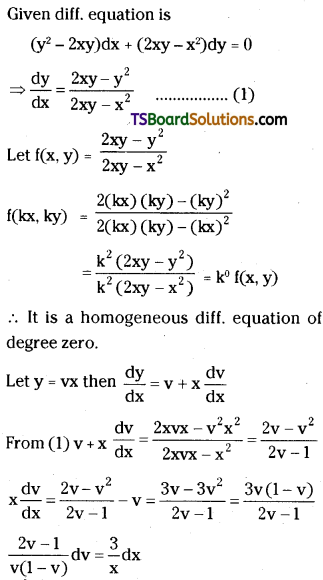
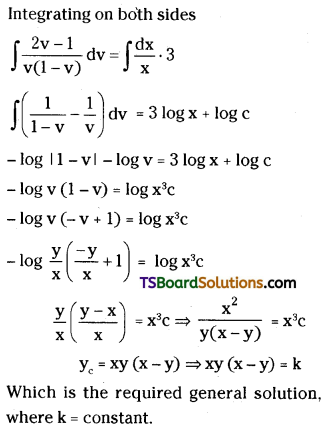
Question 18.
Solve \(\frac{d y}{d x}=\frac{y^2-2 x y}{x^2-x y}\). [Mar. ’19 (AP)]
Solution:
Given D.E is \(\frac{d y}{d x}=\frac{y^2-2 x y}{x^2-x y}\) ……..(1)
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 2.
Now, put y = vx
Diff. w.r. to x, we get



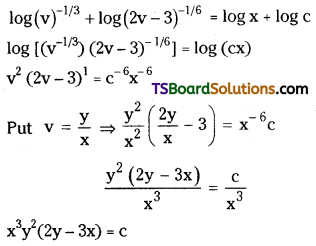
This is the required general solution of the given equation.

Question 19.
Find the equation of a curve whose gradient is \(\frac{d y}{d x}=\frac{y}{x}-\cos ^2 \frac{y}{x}\), where x > 0, y > 0 and which passes through the point (1, \(\frac{\pi}{4}\)). [(AP) May ’19, ’16, (TS) ’16]
Solution:
Given D.E. is \(\frac{d y}{d x}=\frac{y}{x}-\cos ^2 \frac{y}{x}\) ………(1)
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 1.
Put y = vx
diff. w.r.t ‘x’ on both sides

Question 20.
Give the solution of \(x \sin ^2\left(\frac{y}{x}\right) d x=y d x-x d y\) which passes through the point (1, \(\frac{\pi}{4}\)). [Mar. ’14]
Solution:
Given differential equation is

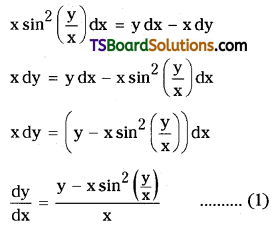
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 1.
Put y = vx
Diff. w.r. to ‘x’ on both sides


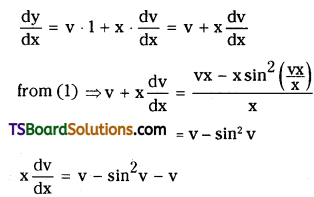
which is the required particular solution.

Model II – Problems on Homogeneous D.E.

Question 21.
Solve (x² – y²) dx – xy dy = 0. [(AP) May ’17; Mar. ’09]
Solution:

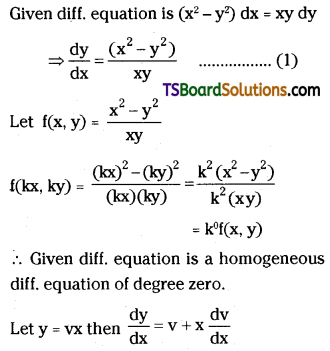
Question 22.
Solve \(\frac{d y}{d x}=\frac{(x+y)^2}{2 x^2}\). [Mar. ’05]
Solution:

Question 23.
Solve (x² – y²) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy
Solution:
Given D.E. is (x – y ) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy
\(\frac{d y}{d x}=\frac{x y}{x^2-y^2}\) ………(1)
This is a homogeneous equation since both the nr and dr are homogeneous functions of degree 2.
Let y = vx

⇒ -x² = 2y² log(cy)
⇒ x² + 2y² log(cy) = 0
Which is the required general solution.

Question 24.
Solve (x² + y²) dx = 2xy dy. [(AP) Mar. ’20, Mar. ’17, ’16]
Solution:
Given diff. equation is \(\frac{d y}{d x}=\left(\frac{2 x y}{x^2+y^2}\right)^{-1}\) …….(1)
Clearly, it is a homogeneous diff. equation of degree zero.

which is the required general solution.

Question 25.
Solve y² dx + (x² – xy + y²) dy = 0.
Solution:
Given D.E is y² dx + (x² – xy + y²) dy = 0
(x² – xy + y²) dy = -y² dx


Which is the required general solution.

Question 26.
Solve \(\frac{d y}{d x}+\frac{y}{x}=\frac{y^2}{x^2}\)
Solution:

Question 27.
Solve x dy = \(\left(y+x \cos ^2 \frac{y}{x}\right) d x\). [Mar. ’13, ’11]
Solution:
Given diff. equation is
x dy = \(\left(y+x \cos ^2 \frac{y}{x}\right) d x\)
\(\frac{d y}{d x}=\frac{y+x \cos ^2 \frac{y}{x}}{x}=\frac{y}{x}+\cos ^2 \frac{y}{x}\) …….(1)
Clearly, it is a homogeneous differential equation of degree zero.
Let y = vx then v + x \(\frac{d v}{d x}=\frac{d y}{d x}\)
From (1), x \(\frac{\mathrm{dv}}{\mathrm{dx}}\) = v + cos²v – v = cos²v
sec²v dv = \(\frac{\mathrm{dx}}{\mathrm{x}}\)
Integrating on both sides
∫sec²v dv = ∫\(\frac{\mathrm{dx}}{\mathrm{x}}\)
tan v = log x + c
⇒ tan(\(\frac{y}{x}\)) = log x + c
Which is the required general solution.

Question 28.
Solve (2x – y) dy = (2y – x) dx. [Mar. ’12]
Solution:
Given diff. equation is \(\frac{d y}{d x}=\frac{2 y-x}{2 x-y}\) …….(1)
Clearly, it is a homogeneous diff. equation of degree zero.

Which is the required general solution.

Question 29.
Solve xy² dy – (x³ + y³) dx = 0. [(TS) May ’18]
Solution:
Given D.E. is xy² dy – (x³ + y³) dx = 0
xy² dy = (x³ + y³) dx
\(\frac{d y}{d x}=\frac{x^3+y^3}{x y^2}\) ……(1)
The given equation is a homogeneous equation since both the numerator and denominator are homogeneous functions of degree 3.
Put y = vx
diff. w.r.t ‘x’ on both sides

Which is the general solution of the given equations.

Question 30.
Solve (x³ – 3xy²) dx + (3x²y – y³) dy = 0. [(AP) May ’18; May ’14]
Solution:
Given D.E is (x³ – 3xy²) dx + (3x²y – y³) dy = 0
(3x²y – y³) dy = -(x³ – 3xy²) dx
\(\frac{d y}{d x}=\frac{-\left(x^3-3 x y^2\right)}{3 x^2 y-y^3}\)
\(\frac{d y}{d x}=\frac{3 x y^2-x^3}{3 x^2 y-y^3}\) ……..(1)
It is a homogeneous equation since both nr and dr are homogeneous functions of degree 3.
Put y = vx
Then diff. w.r. t. x



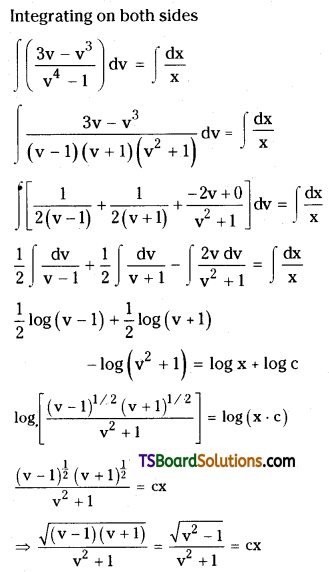
Which is the required solution of the given equation.

Question 31.
Solve (x²y – 2xy²) dx = (x³ – 3x²y) dy. [Mar. ’18 (AP)]
Solution:

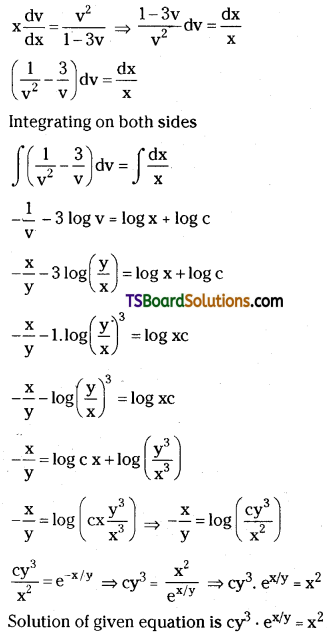
Question 32.
Solve \(\frac{d y}{d x}=\frac{2 x-y+1}{x+2 y-3}\)
Solution:
Given D.E. is \(\frac{d y}{d x}=\frac{2 x-y+1}{x+2 y-3}\) …….(1)
Comparing (1) with \(\frac{d y}{d x}=\frac{a x+b y+c}{a^1 x+b^1 y+c^1}\)
We get a = 2, b = -1, c = 1
a’ = 1, b’ = 2, c’ = -3
Now b = -1 = -(1) = -a’
∴ b = -a’
Now (x + 2y – 3) dy = (2x – y + 1) dx
⇒ x dy + 2y dy – 3dy = 2x dy – y dx + dx
⇒ x dy + 2y dy – 3 dy – 2x dx + y dx – dx = 0
⇒ (x dy + y dx) + 2y dy – 3 dy + 2x dx – dx = 0
⇒ d(xy) + 2y dy – 3 dy + 2x dx – dx = 0
By integrating, we get
∫d(xy) + 2∫y dy – 3 ∫1 dy + 2 ∫x dx – ∫dx = c
xy + 2 . \(\frac{y^2}{2}\) – 3y + 2 . \(\frac{x^2}{2}\) – x = c
xy + y² – 3y + x² – x = c
Which is the required solution.

Model III – Problems on non-homogeneous D.E.

Question 33.
Solve \(\frac{d y}{d x}=\frac{-3 x-2 y+5}{2 x+3 y+5}\)
Solution:
Given diff. equation is \(\frac{d y}{d x}=\frac{-3 x-2 y+5}{2 x+3 y+5}\) …….(1)
Comparing it with \(\frac{d y}{d x}=\frac{a x+b y+c}{a^{\prime} x+b^{\prime} y+c^{\prime}}\)
We get a = -3, b = -2, c = 5, a’ = 2, b’ = 3, c’ = 5
Then, we can solve equation (1) by the case (i)
∴ b = -a’
\(\frac{d y}{d x}=\frac{-3 x-2 y+5}{2 x+3 y+5}\)
⇒ dy (2x + 3y + 5) = dx (-3x – 2y + 5)
⇒ 2x dy + 3y dy + 5 dy + 3x dx + 2y dx – 5 dx = 0
⇒ 2(x dy + y dy) + 3y dy + 5 dy + 3x dx – 5 dx = 0
⇒ 2d(xy) + 3y dy + 5 dy + 3x dx – 5 dx = 0
Integrating on both sides, we get
2∫d(xy) + 3∫y dy + 5∫dy + 3∫x dx – 5∫dx = c
⇒ 2xy + 3 \(\frac{y^2}{2}\) + 5y + 3 \(\frac{x^2}{2}\) – 5x = c
⇒ 4xy + 3y² + 10y + 3x² – 10x = 2c = k
(k = constant)
Which is the required general solution.

Question 34.
Solve 2(x – 3y + 1) \(\frac{d y}{d x}\) = 4x – 2y + 1
Solution:
Given D.E is 2(x – 3y + 1) \(\frac{d y}{d x}\) = 4x – 2y + 1
\(\frac{d y}{d x}=\frac{4 x-2 y+1}{2 x-6 y+2}\) …….(1)
Comparing (1) with \(\frac{d y}{d x}=\frac{a x+b y+c}{a^{\prime} x+b^{\prime} y+c^{\prime}}\)
We get a = 4, b = -2, c = 1
a’ = 2, b’ = -6, c’ = 2
Now, b = -2 = -(2) = -a’
∴ b = -a’
Hence we can solve by the case (1).
(2x – 6y + 2) dy = (4x – 2y + 1) dx
⇒ 2x dy – 6y dy + 2 dy = 4x dx – 2y dx + 1 dx
⇒ 2x dy – 6y dy + 2 dy – 4x dx + 2y dx – 1 dx = 0
⇒ 2(x dy + y dx) – 6y dy – 4x dx + 2dy – 1 dx = 0
⇒ 2d(xy) – 6y dy – 4x dx + 2 dy – dx = 0
By integrating we get,
2∫d(xy) – 6∫y dy – 4∫x dx + 2∫dy – ∫dx = c
⇒ 2(xy) – 6(\(\frac{y^2}{2}\)) – 4(\(\frac{x^2}{2}\)) + 2y – x = 0
⇒ 2xy – 3y² – 2x² + 2y – x = c
Which is the required solution.

Question 35.
Solve x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 2y = log x
Solution:
Given D.E. is x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 2y = log x
dividing on both sides by ‘x’
\(\frac{d y}{d x}+\frac{2 y}{x}=\frac{\log x}{x}\)
Which is in the form \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + Py = Q
It is linear in y.

Model IV(a) – Problems on L.D.E in y

Question 36.
Solve x log x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = 2 log x. [(AP) Mar. ’20; May ’14]
Solution:

Question 37.
Solve (1 + x²) \(\frac{d y}{d x}\) + y = \(e^{\tan ^{-1} x}\). [(AP) Mar. ’18, ’16; May ’16, (TS) Mar. ’15 (TS); May ’13]
Solution:

Question 38.
Solve \(\frac{d y}{d x}\) = y tan x + e^x sec x. [(TS) May ’19; Mar. ’09]
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) – y tan x = e^x sec x ……..(1)
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
We get P = -tan x, Q = e^x sec x
I.F. = e^2∫Pdx
= e^{-∫tan x dx}
= e^{log|cos x|}
= cos x
The solution of (1) is,
y (I.F) = ∫Q(I.F) dx + c
y (cos x) = ∫e^x sec x (cos x) dx + c = ∫e^x + c
y (cos x) = e^x + c
Which is the required solution.

Question 39.
Solve \(\frac{d y}{d x}\) + y sec x = tan x. [May ’10]
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) + y sec x = tan x
It is a linear diff. equation in y.
It compared with \(\frac{d y}{d x}\) + Py = Q
We get P = sec x, Q = tan x
I.F. = e^∫Pdx
= e^{∫sec x dx}
= e^{log|sec x + tan x|}
= sec x + tan x
The solution of (1) is,
y (I.F) = ∫Q(I.F) dx + c
y(sec x + tan x) = ∫tan x (sec x + tan x) dx + c
= ∫sec x tan x dx + ∫tan²x dx + c
= ∫sec x tan x dx + ∫(sec²x – 1) dx + c
= sec x + tan x – x + c
Which is the required solution.

Question 40.
Solve \(\frac{d y}{d x}\) + y tan x = sin x. [(TS) Mar. ’16, ’12]
Solution:
Given diff. equation is
\(\frac{d y}{d x}\) + y tan x = sin x ……..(1)
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
Where P = tan x, Q = sin x
I.F = e^∫Pdx
= e^{∫tan x dx}
= sec x
The solution of (1) is,
y(I.F) = ∫Q(I.F) dx + c
y sec x = ∫sin x . sec x dx + c
y sec x = ∫tan x dx + c
y sec x = log|sec x| + c
Which is the required solution.

Question 41.
Solve \(\frac{d y}{d x}\) + y tan x = cos³x. [(AP) May ’19, ’18; Mar. ’17]
Solution:
Given diff. equation is \(\frac{d y}{d x}\) + + y tan x = cos³x
It is a linear diff. equation in y of the first order.
Comparing it with \(\frac{d y}{d x}\) + Py = Q
we get P = tan x, Q = cos³x

Which is the required solution.

Question 42.
Solve cos x . \(\frac{d y}{d x}\) + y sin x = sec²x. [Mar. ’19 (TS); Mar. ’14]
Solution:
Given differential equation is
cos x . \(\frac{d y}{d x}\) + y sin x = sec²x
Dividing on both sides by cos x, we get
\(\frac{d y}{d x}\) + y tan x = sec³x
Which is in the form of \(\frac{d y}{d x}\) + Py = Q
It is linear in ‘y’
Here, P = tan x, Q = sec³x
IF = e^∫Pdx
= e^{∫tan x dx}
= e^{log|sec x|}
= sec x
∴ Solution is y(I. F) = ∫Q(I. F) dx + c
y sec x = ∫sec²x . sec²x dx + c
= ∫sec⁴x dx + c
= ∫sec²x . sec²x dx + c
= ∫(1 + tan²x) sec²x dx + c
= ∫(1 + t²) dt + c
Put tan x = t ⇒ sec²x dx = dt
= ∫1 dt + ∫t² dt + c
= t + \(\frac{\mathrm{t}^3}{3}\) + c
y sec x = tan x + \(\frac{1}{3}\) tan³x + c

Question 43.
Solve (1 + x²) \(\frac{d y}{d x}\) + y = tan^-1x. [(AP) May ’16]
Solution:

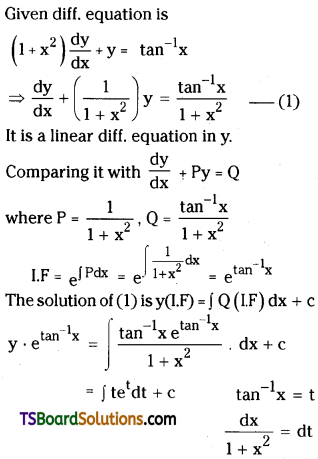
Question 44.
Solve (1 + x²) \(\frac{d y}{d x}\) + 2xy – 4x² = 0. [Mar. ’06]
Solution:
Given diff. equation is
\(\frac{d y}{d x}+\frac{2 x y}{1+x^2}=\frac{4 x^2}{1+x^2}\) …….(1)
It is a linear diff. equation in y.
Comparing it with \(\frac{d y}{d x}\) + Py = Q

Which is the required solution.

Question 45.
Solve \(\frac{d y}{d x}+y\left(\frac{4 x}{1+x^2}\right)=\frac{1}{\left(1+x^2\right)^2}\). [(AP) May ’17]
Solution:

Question 46.
Solve \(\frac{d y}{d x}+\frac{3 x^2}{1+x^3} y=\frac{1+x^2}{1+x^3}\)
Solution:

Question 47.
Solve \(\frac{1}{x} \frac{d y}{d x}+y e^x=e^{(1-x) e^x}\). [(AP) May ’18]
Solution:

Question 48.
Solve x(x – 1) \(\frac{d y}{d x}\) – y = x³(x – 1)³. [(AP) Mar. ’19]
Solution:

Model IV(b) – Problems on L.D.E in x

Question 49.
Solve (1 + y²) dx = (tan^-1y – x) dy. [Mar. ’18 (TS); May; Mar. ’15 (AP); May ’15 (TS)]
Solution:

Question 50.
Solve (x + 2y³) \(\frac{d y}{d x}\) = y. [May ’12]
Solution:

Question 51.
Solve (x + y + 1) \(\frac{d y}{d x}\) = 1. [Mar. ’17 (TS); Mar. ’13]
Solution:
Given diff. equation is \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{1}{\mathrm{x}+\mathrm{y}+1}\)
\(\frac{d x}{d y}\) – x = y + 1 ……..(1)
It is a linear diff. equation in x.
Comparing it with \(\frac{d x}{d y}\) + Px = Q
Where P = -1, Q = y + 1
I.F. = e^∫Pdy = e^{∫(-1) dy} = e^-y
The solution of (1) is
x(I.F) = ∫Q(I.F) dy + c

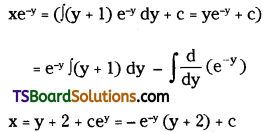
Which is the required general solution.

Model V – Problems on Bernoulli’s D.E.

Question 52.
Solve \(\frac{d y}{d x}\) (x²y³ + xy) = 1. [Mar. ’11]
Solution: