TS Inter Second Year Maths 2A Measures of Dispersion Important Questions Very Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Measures of Dispersion Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Measures of Dispersion Important Questions Very Short Answer Type

Question 1.
Find the mean deviation from the mean of the discrete data 6, 7, 10, 12, 13, 4, 12, 16. [TS – May 2016, Mar. ’14]
Solution:
Given data is 6, 7, 10, 12, 13, 4, 12, 16
The arithmetic mean of the given data is
\(\overline{\mathrm{x}}=\frac{\text { Sum of the observations }}{\text { No. of observations }}\)
= \(\frac{\Sigma x}{n}=\frac{6+7+10+12+13+4+12+16}{8}\)
\(\bar{x}=\frac{80}{8}\) = 10
The deviations of the respective observations from the mean are 6 – 10, 7 – 10, 10 – 10, 12 – 10, 13 – 10, 4 – 10, 12 – 10, 16 – 10 = – 4, – 3, 0, 2, 3, – 6, 2, 6
The absolute values of the deviations are 4, 3, 0, 2, 3, 6, 2, 6.
∴ The required mean deviation about mean is
M.D = \(=\sum_{i=1}^n \frac{\left|x_i-\bar{x}\right|}{n}=\sum_{i=1}^8 \frac{\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{4+3+0+2+3+6+2+6}{8}\)
= \(\frac{26}{8}=\frac{13}{4}\) = 3.25.

Question 2.
Find the mean deviation about mean for the data 38, 70, 48, 40, 42, 55, 63, 46, 54, 44. [AP – May 2015].
Solution:
Given data is 38, 70, 48, 40, 42, 35, 63, 46, 54, 44
The arithmetic mean of the given data is
\(\overline{\mathrm{x}}=\frac{\text { Sum of the observations }}{\text { No. of observations }}\)
= \(\frac{\Sigma \mathrm{x}}{\mathrm{n}}\)
= \(\frac{38+70+48+40+42+55+63+46+54+44}{10}\)
= \(\frac{500}{10}\) = 50
The deviations of the respective observations from the mean are 38 – 50, 70 – 50, 48 – 50, 40 – 50, 42 – 50, 55 – 50, 63 – 50, 46 – 50, 54 – 50, 44 – 50 = – 12, 20, – 2, – 10, – 8, 5, 13, – 4, 4, – 6
The absolute values of the deviations are 12, 20, 2, 10,8, 5, 13, 4, 4, 6.
∴ The required mean deviation about mean is
M.D. = \(\sum_{i=1}^n \frac{\left|x_i-\bar{x}\right|}{n}=\sum_{i=1}^{10} \frac{\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{12+20+2+10+8+5+13+4+4+6}{10}\)
= \(\frac{84}{10}\) = 8.4.

Question 3.
Find the mean deviation about mean for the data 3, 6, 10, 4, 9, 10.
[AP – Mar. ’18, May ’16; TS – Mar. ’17; May ’14]
Solution:
Given data is 3, 6, 10, 4, 9, 10
The arithmetic mean of the given data is
\(\overline{\mathrm{x}}=\frac{\text { Sum of the observations }}{\text { No. of observations }}\)
= \(\frac{\Sigma \mathrm{x}}{\mathrm{n}}=\frac{3+6+10+4+9+10}{6}\)
= \(\frac{42}{6}\) = 7
The deviations of the respective observations from the mean are 3 – 7, 6 – 7, 10 – 7, 4 – 7, 9 – 7, 10 – 7
= – 4, – 1, 3, – 3, 2, 3
The absolute values of the deviations are 4, 1, 3, 3, 2, 3.
The required mean deviation about mean is
MD = \(\sum_{i=1}^n \frac{\left|x_i-\bar{x}\right|}{n}=\sum_{i=1}^6 \frac{\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{4+1+3+3+2+3}{6}\)
= \(\frac{16}{6}\) = 2.666 = 2.7.

Question 4.
Find the mean deviation about median for the data 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17. [AP – Mar. 2016]
Sol.
Given data is 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
The ascending order of the observations in the given data is
10, 11, 11, 12, 13,13, 16,16, 17, 17, 18
Median of one given data is M = 13.
The deviations of the respective observations from the median i.e., x_i – M are
13 – 13, 17 – 13, 16 – 13, 11 – 13, 13 – 13, 10 – 13, 16 – 13, 11 – 13, 18 – 13, 12 – 13, 17 – 13
= 0, 4.3, – 2, 0, – 3, 3, – 2, 5, – 1, 4
The absolute values of the deviations are
0, 4, 3, 2, 0, 3, 3, 2, 5, 14.
∴ The required mean deviation about median is
M.D = \(\sum_{i=1}^n \frac{\left|x_i-M\right|}{n}=\sum_{i=1}^{11} \frac{\left|x_i-M\right|}{n}\)
= \(\frac{0+4+3+2+0+3+3+2+5+1+4}{11}\)
= \(\frac{27}{11}\) = 2.45.

Question 5.
Find the mean deviation about median for the data 4,6, 9, 3, 10,13,2. [TS – Mar. ‘18, ’15, May ’15; AP-Mar. ‘19, ’17]
Solution:
Given data is 4, 6, 9, 3, 10, 13, 2
The ascending order of the observations in given data is
2, 3, 4. 6, 9, 10, 13
Median of given data is M = 6
The deviations of the respective observations from the median i.e., x_i – M are
2 – 6, 3 – 6, 4 – 6, 6 – 6, 9 – 6, 10 – 6, 13 – 6 = – 4, – 3, – 2, 0, 3, 4, 7
The absolute values of the deviations are 4, 3, 2, 0, 3, 4, 7.
∴ The required mean deviation about median is
M.D = \(\sum_{i=1}^n \frac{\left|x_i-M\right|}{n}=\sum_{i=1}^7 \frac{\left|x_i-M\right|}{n}\)
= \(\frac{4+3+2+0+3+4+7}{7}\)
= \(\frac{23}{7}\) = 3.29.

Question 6.
Find the mean deviation about median for the data 6, 7, 10, 12, 13, 4, 12, 16.
Solution:
Given data is 6, 7, 10, 12, 13, 4, 12, 16
The ascending order of the observations in the given data is
4, 6, 7, 10, 12, 12, 13, 16
Median of one given data is M = \(\frac{10+12}{2}\)
= \(\frac{22}{2}\) = 11
The deviations of the respective observations from the median i.e., x_i – M are
6 – 11, 7 – 11, 10 – 11, 12 – 11, 13 – 11, 4 – 11, 12 – 11, 16 – 11 = – 5, – 4,- 1, 1, 2, – 7, 1, 5
The absolute values of the deviations are 5, 4, 1, 1, 2, 7, 1, 5.
∴ The required mean deviation about median is
M.D = \(\sum_{i=1}^n \frac{\left|x_i-M\right|}{n}=\sum_{i=1}^8 \frac{\left|x_i-M\right|}{n}\)
= \(\frac{5+4+1+1+2+7+1+5}{8}\)
= \(\frac{26}{8}=\frac{13}{4}\) = 3.25.

Question 7.
Find the mean deviation about mean for the following data. [AP – Mar. 2019]

Solution:
We can form the following table for the given data:

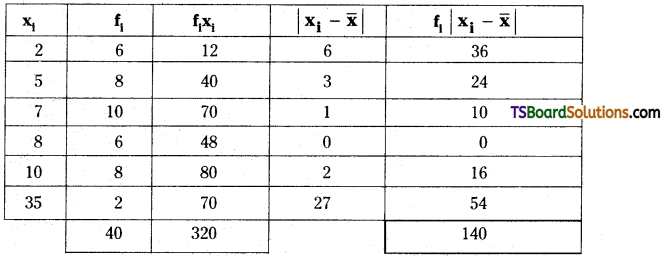
Here, Σf_i = 40
Σf_ix_i = 320
∴ Mean of the given data is \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{320}{40}\) = 8
From the table, Σf_i |x_i – \(\overline{\mathrm{x}}\)| = 140
Mean deviation about mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\widetilde{\mathrm{x}}\right|}{\mathrm{N}}=\frac{140}{40}\) = 3.5.

Question 8.
Find the mean deviation about mean for the following data.

Solution:
We can form the following table for the given data:

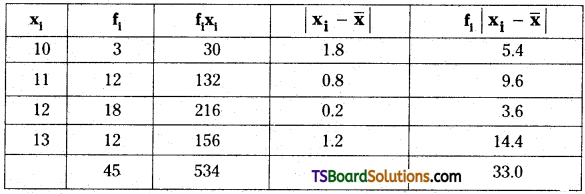
Here, N = Σf_i = 45
Σf_ix_i = 534
∴ Mean of the given data is \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{534}{45}\) = 11.8
From the table, Σf_i |x_i – x| = 33.0
Mean deviation about mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|}{\mathrm{N}}\)
= \(\frac{33}{45}\) = 0.73.

Question 9.
Find the mean deviation about mean for the following data.

Solution:

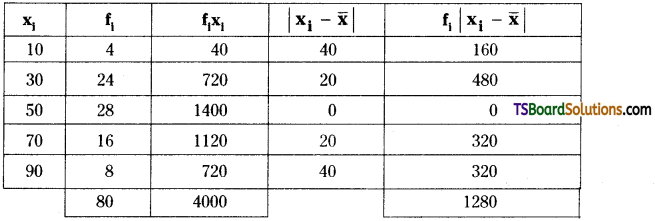
Here, N = Σf_i = 80
Σf_ix_i = 4000
∴ Mean of the given data is \(\bar{x}=\frac{\Sigma f_i x_i}{N}=\frac{4000}{80}\) = 50
From the table, Σf_i |x_i – \(\bar{x}\)| = 1280
Mean deviation about mean \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|}{\mathrm{N}}=\frac{1280}{80}\) = 16.

Question 10.
Find the mean deviation about median for the following data. [May ‘14]

Solution:
We can form the following table for the given data:

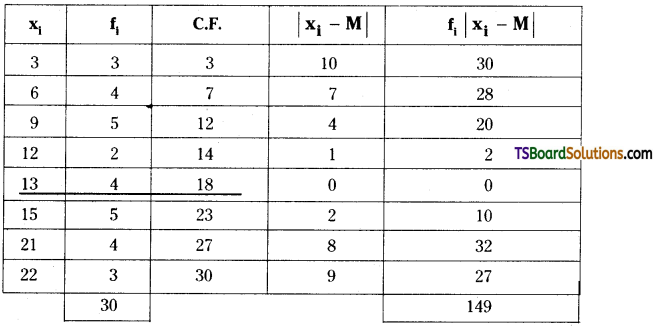
Median = \(\frac{N^{\text {th }}}{2}\) observation
= \(\frac{30}{2}\) = 15th observation = 13.
Mean deviation about median, M.D = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{N}}=\frac{149}{30}\) = 4.966 = 4.97.

Question 11.
Find the mean deviation about median for the following data.

Solution:
We can form the following table for the given data:

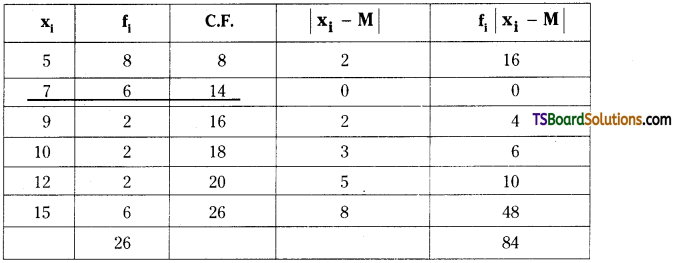
Median = \(\frac{N^{\text {th }}}{2}\) observation
= \(\frac{26}{2}\) = 13th observation = 7.
Mean deviation about median, M.D = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{N}}=\frac{84}{26}\) = 3.23.

Question 12.
Find the variance and standard deviation for the discrete data: 5, 12, 3, 18, 6, 8, 2, 10. [AP – Mar. 2015; TS – Mar. 2019]
Solution:
Given data is 5, 12, 3, 18. 6, 8, 2, 10
The mean of the given data is \(\overline{\mathrm{x}}=\frac{\sum \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}\)
= \(\frac{5+12+3+18+6+8+2+10}{8}=\frac{64}{8}\) = 8
To find the variance we construct the following table:

Here, Σ(x_i – \(\bar{x}\)) = 194
∴ Variance, \(\sigma^2=\frac{1}{n} \sum_{i=1}^8\left(x_i-\bar{x}\right)^2=\frac{194}{8}\) = 24.25
Standard deviation, a = \(\sqrt{\text { variance }}\)
= \(\sqrt{24.25}\)= 4.92 (approxi.)

Question 13.
Find the variance for the discrete data : 6, 7, 10, 12, 13, 4, 8, 12.
Solution:
Given data is 6, 7, 10, 12, 13, 4, 8, 12
The mean of the given data is \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}\)
= \(\frac{6+7+10+12+13+4+8+12}{8}=\frac{72}{8}\) = 9
To find the variance we construct the following table:

Here, Σ(x_i – \(\bar{x}\))² = 74
∴ variance, \(\sigma^2=\frac{1}{n} \sum_{\mathrm{i}=1}^8\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^2=\frac{74}{8}\) = 9.25.

Question 14.
Find the variance for the discrete data: 350, 361, 370, 373, 376, 379, 385, 387, 394, 395.
Solution:
Given data is 350, 361, 370, 373, 376, 379, 385, 387, 394, 395
The mean of the given data is
\(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}=\frac{350+361+370+373+376+379+385+387+394+395}{10}=\frac{3770}{10}\) = 377
To find the variance we construct the following table:

Here, Σ(x_i – x) = 1832
∴ Variance \(\frac{1}{n} \sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2\)
= \(\frac{1832}{10}\) = 183.2.

Question 15.
The variance of 20 observations is 5. If each of the observations is multiplied by 2. Find the variance of the resulting observations. [Board Paper]
Solution:
Let the given observations be x₁, x₂, x₃, …………… x₂₀
Mean, \(\bar{x}=\sum_{i=1}^{20} x_i \times \frac{1}{n}\)
Given that, n = 20 and variance = 5
\(\frac{1}{n} \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\) = 5
\(\frac{1}{20} \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\) = 5
\(\sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\) = 100
If each observation is multiplied by 2 then the new observations are 2x₁, 2x₂, 2x₃, …………….., 2x₂₀
i.e., y₁, y₂, y₃, ……………, y₂₀
y_i = 2x₁
The mean of the new observations
\(\overline{\mathrm{y}}=\frac{1}{\mathrm{n}} \sum_{\mathrm{i}=1}^{20} \mathrm{y}_{\mathrm{i}}\)
= \(\frac{1}{20} \sum_{\mathrm{i}=1}^{20} 2 \mathrm{x}_{\mathrm{i}}=2\left[\frac{1}{20} \sum_{\mathrm{i}=1}^{20} \mathrm{x}_{\mathrm{i}}\right]=2 \overline{\mathrm{x}}\)
⇒ \(\overline{\mathrm{x}}=\frac{\overline{\mathrm{y}}}{2}\)
Substituting the values of \(\bar{x}_{\mathbf{i}}\) and \(\overline{\mathbf{x}}\) in (1), we get
\(\sum_{\mathrm{i}=1}^{20}\left(\frac{\mathrm{y}_{\mathrm{i}}}{2}-\frac{\overline{\mathrm{y}}}{2}\right)^2\) = 100
\(\frac{1}{4} \sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2\) = 100
\(\sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2\) = 400
∴ The variance of the new observations = \(\frac{1}{n} \sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2\)
= \(\frac{1}{20}\) (400) = 20 = 2² . 5

Note:
If each observation is multiplied by a constant ‘k’, the variance of the resulting observation becomes k² times the original variance.

Question 16.
If each of the observation x₁, x₂, ………………, x_n is increased by k, where k is a positive or negative number, then show that the variance remains unchanged.
Solution:
Let, \(\overline{\mathrm{x}}\) be the mean of x₁, x₂, …………….., x_n then
variance, \(\sigma^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2\)
\(\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i\)
1f k is added to each observat ion then the new observations will be x₁ + k₁, x₂ + k, x₃ + k, ………………….. x_n + k i.e., y₁, y₂, y₃, …………., y_n.
Now, y_i = x_i+ k,
For i = 1, 2, 3 …………… n
Let \(\overline{\mathrm{y}}\) be the mean of the new observations then
\(\bar{y}=\frac{1}{n} \sum_{i=1}^n y_i=\frac{1}{n} \sum_{i=1}^n x_i+k\)
= \(\frac{1}{n} \sum_{i=1}^n x_i+k=\frac{1}{n} \sum_{i=1}^n x_i+\frac{1}{n} \sum_{i=1}^n k\)
= \(\overline{\mathrm{x}}+\frac{1}{\mathrm{n}} \mathrm{nk}=\overline{\mathrm{x}}+\mathrm{k}\).

Variance of the new observations
\(\sigma_y^2=\frac{1}{n} \sum_{i=1}^n\left(y_i-\bar{y}\right)^2\)
= \(\frac{1}{n} \sum_{i=1}^n\left(x_i+k-\bar{x}-k\right)^2\)
= \(\frac{1}{n} \sum_{i=1}^n\left(x_i-\vec{x}\right)^2\) = σ²
∴ The variance of new observations is same that of the original observations.

Note :
If each observation is added by a number ‘a’ then the variance remains unchanged.

Question 17.
The coefficient of variation of two distributions are 60 and 70 and their standard deviations are 21 and 16 respectively. Find their arithmetic means.
Solution:
I distribution:
Let \(\overline{\mathbf{x}}_1\) and σ₁ be the mean and standard deviation of I distribution.
Given that, Coefficient of variation, C.V = 60
Standard deviation, σ₁ = 21
∴ CV = \(\frac{\sigma_1}{x_1}\) × 100
60 = \(\frac{21}{\overline{\mathrm{x}}_1}\) × 100
\(\overline{\mathrm{x}}_1=\frac{21}{60} \times 100\)
\(\overline{\mathrm{x}}_1\) = 35

II distribution:
Let \(\overline{\mathrm{x}}_2\) and σ₂ be the mean and standard deviation of II distribution.
Given that, C.V = 70
Standard deviation, σ₂ = 16
∴ CV = \(\frac{\sigma_2}{\overline{\mathrm{x}}_2}\) × 100
70 = \(\frac{16}{\bar{x}_2}\) × 100
\(\overline{\mathrm{x}}_2\) = \(\frac{16}{70}\) × 100
= \(\frac{160}{7}\) = 22.85.

Question 18.
The mean of 5 observations is 4.4. Their variance is 8.24. If three of the observations are 1, 2 and 6, find the other two observations.
Solution:
Let, the remaining 2 observations be x, y.
∴ The series is 1, 2, 6, x, y.
Given that, mean, \(\overline{\mathbf{x}}\) = 4.4
\(\frac{1+2+6+\mathrm{x}+\mathrm{y}}{5}\) = 4.4
9 + x + y = 22
x + y = 13 ……………….(1)
Given that, σ² = 8.24
\(\frac{\sum_{i=1}^n x_i^2}{n}-(\bar{x})^2\) = 8.24
\(\frac{1+4+36+x^2+y^2}{5}\) = (4.4)² = 8.24
\(\frac{41+x^2+y^2}{5}\) = 8.24 + 19,36
\(\frac{41+x^2+y^2}{5}\) = 27.6
41 + x² + y² = 138
x² + y² = 138 – 41
x² + y² = 97 ……………..(2)
From(1), y = 13 – x
From (2), x² + (13 – x)² = 97
x² + 169 + x² – 26x – 97 = 0
2x² – 26x + 72 = 0
x² – 13x + 36 = 0
x² – 9x – 4x + 36 0
x(x – 9) – 4 (x – 9) = 0
(x – 9) (x – 4) = 0
x = 9 or x = 4
If x = 4 then y = 13 – 4 = 9
If x = 9 then y = 13 – 9 = 4
∴ The remaining two observations are 4 and 9.

Question 19.
The arithmetic mean and standard deviation of a set of 9 items are 43 and 5 respectively. If an item of value 63 is added to that set, find the new mean and standard deviation of 10 item set given.
Solution:
Given that, number of items, n = 9
Mean, \(\overline{\mathrm{x}}\) = 43
\(\frac{1}{n} \sum_{i=1}^9 x_i\)= 43
\(\frac{1}{9} \sum_{i=1}^9 x_i\) = 43
\(\sum_{i=1}^9 x_i\) = 387
Now, given 10th item = 63
∴ Sum of the 10 observations \(\sum_{i=1}^9 x_i\) + 63 = 387 + 63 = 450
The mean of the new observations \(\frac{1}{n} \sum_{i=1}^{10} x_i\) = \(\frac{1}{10}\) (450) =
Given that, standard deviation, σ = 5
σ² = 25
\(\frac{1}{n} \sum_{i=1}^9 x_i^2-(\bar{x})^2\) = 25
\(\frac{1}{9} \sum_{i=1}^9 x_i^2-(43)^2\) = 25
\(\frac{1}{9} \sum_{i=1}^9 x_i^2\) – x = 25 + (43)²
= 25 + 1849 = 1874
\(\frac{1}{9} \sum_{i=1}^9 x_i^2\) = 1874 × 9 = 16866
Given that, 10th item = 63
∴ \(\frac{1}{9} \sum_{i=1}^10 x_i^2\) = \(\frac{1}{9} \sum_{i=1}^9 x_i^2\) + (63)²
= 16866 + 3969 = 20835
The variance of new observations = \(\frac{1}{n} \sum_{i=1}^{10} x_i^2-\bar{x}^2\)
= \(\frac{1}{10}\) (20835) – (45)²
= 2083.5 – 2025 = 58.5
∴ Standard deviation = √58.5 = 7.64.