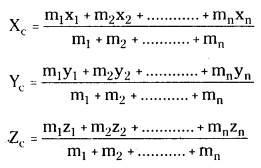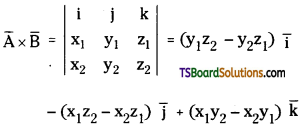Here students can locate TS Inter 1st Year Physics Notes 7th Lesson Systems of Particles and Rotational Motion to prepare for their exam.
TS Inter 1st Year Physics Notes 7th Lesson Systems of Particles and Rotational Motion
→ Rigid body: A rigid body is a body with perfectly definite and unchanging shape. The distance between all the pair of particles of such body do not change.
Note: There is no real body that is truely rigid. All real bodies deform under the influence of forces. But in many cases this deformation is negligible.
→ Translational motion: In translational motion the body will move as a whole from one place to another place.
In pure translational motion all the particles of the body will have same velocity at any instant of time.
→ Axis of rotation: To prevent translational motion a rigid body has to be fixed along a straight line. Then the only possible motion is rotation about that fixed line. This fixed line is called axis of rotation.
→ Rotation: In rotation every particle of a rigid body moves in a circle which lies in a plane perpendicular to the axis of rotation. The rotating body has a centre on the axis.
→ Centre of mass: For a rigid body or system of particles the total mass seems to be concentrated at a particular point is called centre of mass.
Such point will behave as if it is the representative of whole translational motion of that body.
→ Centre of gravity: It is a point in the body where the total weight of the body seems to be concentrated.
If we apply an equal and opposite force to weight of the body (W = mg) the body will be in mechanical equilibrium (i.e. both in translational and rotational equilibrium).

→ Co-ordinates of centre of mass:
1. For symmetric bodies when origin is taken at geometric centre then centre of mass is also at geometric centre. Ex: Thin rod, disc, sphere etc.
2. Let two bodies of masses say m1 and m2 are at distances say x1 and x2, from origin then centre of mass = xc = \(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
So we can assume that position centre of mass is the ratio of sum of moment of masses and total mass of the body.
Note:
1. Let two bodies of equal masses m and m are separated by a distance x then centre of mass of that svstem is at \(\frac{x}{2}\).
2. If three equal masses are at the corners of a triangle then centre of mass is at centroid of that triangle.
3. Let a system of particles say m1, m2, m3 ………….. mn are in a plane or in space then co-ordinates of centre of mass will have x, y for plane and X, Y and Z for space where
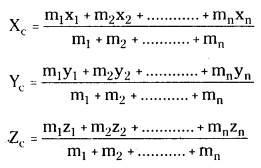
→ Characteristics of centre of mass:
- Total mass of the body seems to be concentrated at centre of mass.
- The total external force (Fext) applied on a body seems to be applied at centre of mass. Fext = M ac where ‘a’ is acceleration of centre of mass.
- Internal forces cannot change the motion of centre of mass.
- A complex motion is a combination of translational and rotational motions. In complex motion centre of mass represents the entire translational motion of the whole body.
- The momentum of a body is the product of mass of the body and velocity of centre of mass P̅ = MVc
- Co-ordinates of centre of mass do not depend on the co-ordinate system chosen.
→ Motion of centre of mass:
1. Motion of centre of mass represents the translational motion of the whole body.
2. Velocity of centre of mass
Vc = \(\frac{m_1 v_1+m_2 v_2+\ldots \ldots \ldots+m_n v_n}{\Sigma m_i}\)
i.e., velocity of centre of mass is the ratio of sum of momentum of all particles to total mass of the body.
3. Momentum of centre of mass P̅c is the sum of momentum of all the particles of the body.
P̅c = MV̅c = m1v1 + m2v2 + ……………… + mnvn
4. External force acting on centre of mass ^
F = M Ac = m1a1 + m2a2 ………………+ mnan or
F = MAc = F1 + F2 + …………….. + Fn
Where a1, a2,…….. an are accelerations of individual particles of masses m1, m2 …. mn
→ Explosion of a shell in mid air: Let a shell moves along a parabolic trajectory explodes in mid air and divided into number of fragments. Still then centre of mass of that system of fragments will follow “the same parabolic path”.
Explanation: Explosion is due to internal forces. Internal forces cannot change the momentum of a body. So algebraic sum of momentum of all fragments is constant. So velocity of centre of mass is constant.
Hence centre of mass will follow the same parabolic path.

→ Cross product or vector product of vectors:
If the multiplication of two vectors generates a vector then that vector multiplication is called cross product. Mathematically
A̅ × B̅ = |A̅||B̅|sin θ n̂
Where n is a unit vector perpendicular to the plane of A̅ and B̅.
Note: The new vector generated is always perpendicular to both A̅ and B̅ i.e., perpendicular to the plane containing A̅ and B̅.
Properties of cross product:
- Cross product is not commutative i.e., A̅ × B̅ ≠ B̅ × A̅ But A̅ × B̅ = -B̅ × A̅
- Cross product obeys distributive law i.e., A̅ × (B̅ + C̅) = (A̅ × B̅) + (A̅ × C̅)
- If any vector is represented by the combination of i̅, j̅ and k̅ then cross product will obey right hand screw rule.
- The product of two coplanar perpendicular unit vectors will generate a unit vector perpendicular to that plane i.e. i̅ × j̅ = k̅, j̅ × k̅ = i̅ and k̅ × i̅ = j̅
- Cross product of parallel vectors is zero
i. e. i̅ × i̅ = j̅ × j̅ = k̅ × k̅ =0
→ Angular displacement (θ): The angle subtended by a body at the centre when it is in angular motion is called angular dis-placement. Unit: Radian.
→ Angular velocity (ω): Rate of change in angular displacement is called angular velocity.
Let angular displacement is Δθ over a time interval Δt then average angular velocity
ω = \(\frac{\Delta \theta}{\Delta t}\), Unit = Radian / sec
Note:
- Relation between angular velocity and linear velocity is v = rω
- For a body in rotatory motion all the particles will have same angular velocity ‘ω’. But linear velocity ‘v’ changes.
→ Angular acceleration (α): The rate of change of angular velocity is defined as angular acceleration.
Angular acceleration α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)
Unit: Radian /sec2
→ Moment of force couple or torque (τ): The moment of force is called torque or moment of force couple.
Let a force F̅ is applied on a point P’.
The position vector of P from origin is r then
Torque τ = r̅ × F̅ = |r̅ | × |F̅ |sin θ . n̂
It is a vector. Its direction is perpendicular to both r̅ and F̅ (or) it is perpendicular to the plane containing r̅ and F̅.
Unit: Newton metre (N – m) ; D.F: ML2 T-2
Note:
1. Torque is the product of force F and perpendicular distance between force (F) and point of application (i.e. r sin θ).
2. Torque represents the energy with which a body is rotated. So units of torque and energy are same.
→ Angular momentum (L): Let a particle of mass m’ has a linear momentum P and its position vector is r from origin then angular momentum of that particle is defined as
L = r̅ × p̅ = |r̅||p̅|sin θ n̂
Angular momentum is a vector. L is perpendicular to the plane containing r and P .
Unit: Kg – metre2 and D.F.: ML2
Note: Angular momentum is the product of momentum P̅ and perpendicular distance (r sin θ) from origin. It is also written as L = Iω
→ Torque and angular momentum: The time rate of change of the angular momentum of a particle is equal to torque acting on it.
Torque τ = \(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}=\overline{\mathrm{r}} \cdot \frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}\)
Note:
The time rate of change of the angular momentum of a system of particles about a point is equal to the sum of external torque i.e.,
\(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}\) = τext lust like \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}\) = Fext
→ Law of conservation of angular momentum:
When external torque (τext) is zero, the total angular momentum of a system is conserved i. e., it remains constant.
When τext, = 0 then \(\frac{\mathrm{d} \overline{\mathrm{L}}}{\mathrm{dt}}\) = 0 i.e. angular momentum L̅ is constant, i.e. I1ω1 + I2ω2 = constant
Note:
1. For a system of particles when τext = 0 then \(\mathrm{d} \overline{\mathrm{L}}_1+\mathrm{d} \overline{\mathrm{L}}_2+\ldots \ldots+\mathrm{d} \overline{\mathrm{L}}_{\mathrm{n}}=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{d} \overline{\mathrm{L}}_{\mathrm{i}}\) = 0.
2. Law of conservation of angular momentum is similar to law of conservation of linear momentum in linear motion.
→ Equilibrium of a rigid body: A rigid body is said to be in mechanical equilibrium if both its linear momentum and angular momentum are not changing with time. Then the body has neither linear acceleration nor angular acceleration.
(or)
1. The vector sum of all the forces acting on a rigid body must be zero.
i.e. F1 + F2 + ……………. + Fn = \(\sum_{i=1}^n F_i\) = 0
This condition provides translational equilibrium of the body.
2. The vector sum of all the torques acting on a rigid body must be zero i.e.,
τ1 + τ2 + ……………. + τn = \(\sum_{i=1}^n \tau_i\) = 0
This condition provides rotational equilibrium of the body.
→ Couple (or) Force couple: A pair of equal and opposite forces with different lines of action is known as couple.
A couple produces rotation without translation.

→ Moments or moment of force: It is defined as the product of force and perpendicular distance between force and its point of application.
→ Principles of moments: For a lever to be in mechanical equilibrium let R is the reaction of the support at fulcrum. It is directed upwards and F1, and F2 are the forces then
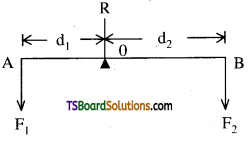
1. For translational equilibrium R – F1 – F2 = 0 i.e. algebraic sum of forces must be zero.
2. For rotational equilibrium d1F1 = d2F2 = 0. i.e. algebraic sum of moments must be zero.
→ Lever: An ideal lever is a light rod pivoted at a point along its length. This point is called “fulcrum”. In levers d1F1 = d2F2 i.e .
Load arm × load = Force arm × Force
Mechanical advantage (M.A) = \(\frac{\mathrm{F}_1}{\mathrm{~F}_2}=\frac{\mathrm{d}_2}{\mathrm{~d}_2}\)
If effort arm d2 is larger than load arm then M.A > 1 i.e. we can lift greater loads with less effort.
→ Moment of Inertia (I): The inertia of a rotating body is called moment of inertia.
Mathematically, Moment of Inertia, I = \(\sum_{i=1}^n\) m1r12 = MR2
→ Radius of gyration (k): Radium of gyration of a body about an axis may be defined as the distance from the axis of a mass point whose mass is equal to whole mass of the body and whose moment of inertia is equal to moment of inertia of the whole body about that axis.
Fly wheel: Fly wheel is a metalic body with large moment of inertia.
It is used in rotational motion of engines like automobiles. It allows a gradual change in speed and prevents jerky motion.
→ Perpendicular axis theorem: The moment of inertia of a plane body (lamina) about an axis perpendicular to its plane is equal to the sum of its moment of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body, i.e., Iz = Ix + Iy
→ Parallel axis theorem: The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through the centre of mass and the product of its mass and square of the distance between the two parallel axes, i.e., I = IG + MR2
→ Rolling motion: Rolling motion is a combination of translational motion and rotatory motion.
→ Kinetic energy of a rolling body: When a body is rolling on a body without slipping then it will have translational kinetic energy (\(\frac{1}{2}\)mv2) and rotational kinetic energy (\(\frac{1}{2}\)Iω2).
Total kinetic energy of rolling body
K.ER = \(\frac{1}{2}\)mv2 + \(\frac{1}{2}\)Iω>2
→ For two particle system of masses m1 and m2 with positions x1 and x2.
(a) Coordinates of centre of mass,
xc = \(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
(b) If coordinate system coincides with m1 then xc = \(\frac{\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\) or xc = \(\frac{\mathrm{m}_2 \mathrm{~d}}{\mathrm{~m}_1+\mathrm{m}_2}\) where d is distance between m1 and m2.
(c) Ratio of distances from centre of mass is = \(\frac{\mathrm{d}_1}{\mathrm{~d}_2}=\frac{\mathrm{m}_2}{\mathrm{~m}_1}\)
→ For many particle system

→ Cross product: A̅ × B̅ is defined as |A̅||B̅| sin θ. n̅ where n̅ is a unit vector perpendicular to the plane of A̅ and B̅.

→ In cross product i̅ × i̅ = j̅ × j̅ = k̅ × k̅ = 0 i.e., cross product of parallel vectors is zero.
→ In cross product i̅ × j̅ = k̅, j̅ × k̅ = i̅ and k̅ × i̅ = j̅ cross product of two heterogeneous unit vectors will generate third unit vector taken in clockwise direction.
→ If A̅ = x1 i̅ + y1 j̅ + z1 k̅ and B̅ = x2 i̅ + y2 j̅ + z2 k̅ then
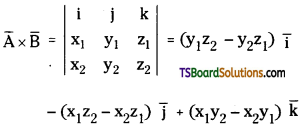
→ Angular velocity
ω = \(\frac{\text { angular displacement }}{\text { time }}=\frac{\theta}{t}\)
ω = \(\frac{\theta}{t}\)
For small quantities, ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)
Unit : Radian/sec
ω = \(\frac{\theta}{t}\) or ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) or ω = \(\frac{2 \pi \mathrm{n}}{\mathrm{t}}\) (n = number of rotations)
→ Angular acceleration,
α = \(\frac{\text { change in angular velocity }}{\text { time }}\)
α = \(\frac{\omega_2-\omega_1}{t}\) or α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)
Unit: Radian/sec2
→ Relation between v and ω is v = rω
→ Relation between a and α is a = rα
→ Centripetal acceleration, ac = rω = vω = \(\frac{v^2}{r}\)
→ Centrifugal force = \(\frac{\mathrm{mv}^2}{\mathrm{r}}\) = mrω2
→ When a coin is placed on a gramphone disc or on a circular turn table or for a vehicle is moving in a curved path limiting friction,
μs = \(\frac{f_s}{N}=\frac{r \omega^2}{g}\)
→ When a vertically hanging body M’ is balanced by a rotating body m in horizontal planp then at equilibrium
Mg = mrω2 or Angular velocity required for balance is ω = \(\sqrt{\frac{\mathrm{Mg}}{\mathrm{mr}}}\)
→ Torque, τ = r̅ × F̅ = |r̅| |F̅| sin θ. It represents the energy with which a body is turned.
→ Moment of force couple = one of the force in couple × distance between the directions of forces.
→ Moment of inertia, I = \(\sum_{i=1}^n\)m1r12 or I = MR2
→ If moment of inertia, I = MR2 = MK2 then K is called radius of gyration.

→ From parallel axis theorem moment of inertia about any parallel axis to the axis passing through centre of mass is, I = IG + MR2.
→ From perpendicular axis theorem M.O.I. about a perpendicular axis to the plane
Iz = Ix + Iy
→ Moment of inertia of a thin rod of length l.
(a) M.O. I of thin rod about its axis and perpendicular to length, I = \(\frac{\mathrm{M} l^2}{12}\); K = \(\frac{l}{\sqrt{12}}\)
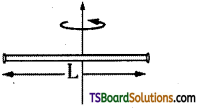
(b) M.O.I. of thin rod about one end of the rod and perpendicular to length,
l = \(\frac{\mathrm{m} l^2}{3}\); K = \(\frac{l}{\sqrt{3}}\)

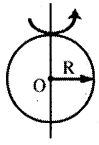
→ Moment of Inertia of a circular ring of radius R
a) M. O.O of a circular ring about an axis pass¬ing through the centre and perpendicular to its plane I = MR2, K = R
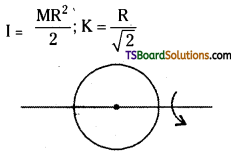
b) M.O.I. of a circular ring about any diameter,
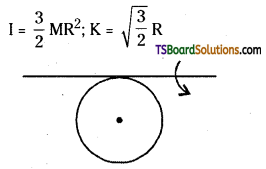
c) M.O.I. about any tangent and parallel to the diameter
→ Moment of Inertia of a disc of radius R
(a) M.O.I about an axis passing through centre and perpendicular to the plane,
I = \(\frac{\mathrm{MR}^2}{2}\); K = \(\frac{\mathrm{R}}{\sqrt{2}}\)
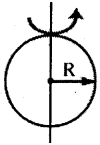
(b) MOI. about any diameter,
I = \(\frac{\mathrm{MR}^2}{4}\); K = \(\frac{\mathrm{R}}{2}\)
(c) MOI about any rangent,
I = \(\frac{5}{4}\)MR2; K = \(\frac{\sqrt{5}}{2}\)R
→ Moment of inertia of a rectangular plane lamina
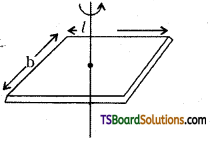
(a) about the centre and perpendicular to the plane
I = M\(\frac{\left(l^2+b^2\right)}{12}\); K = \(\sqrt{\frac{l^2+b^2}{12}}\)
(b) about the axis parallel to length,
I = \(\frac{\mathrm{Mb}^2}{12}\); K = \(\frac{\mathrm{b}}{\sqrt{12}}\)
(c) about any axis parallel to breadth,
I = \(\frac{\mathrm{b}}{\sqrt{12}}\); K = \(\frac{l}{\sqrt{12}}\)
→ Moment of inertia oía solid sphere
(a) about an axis passing through diameter
I = \(\frac{2}{3}\)MR2; K = \(\sqrt{\frac{2}{5}}\)R
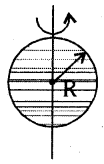
(b) about any tangent, I = \(\frac{7}{5}\)MR2; K = \(\sqrt{\frac{7}{5}}\)R
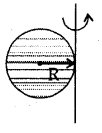
→ Moment of inertia of a hollow sphere
(a) about any diameter, I = \(\frac{2}{3}\)MR2; K = \(\sqrt{\frac{2}{3}}\)R
(b) about any tangent I = \(\frac{5}{3}\)MR2; K = \(\sqrt{\frac{5}{3}}\)R

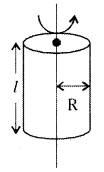
→ Moment of inertia of a solid cylinder of length l and radius R
a) M.O.I. about natural axis of cylinder,
I = \(\frac{\mathrm{MR}^2}{2}\); K = \(\frac{\mathrm{R}}{\sqrt{2}}\)
b) M.O.I. about an axis perpendicular to length and passing through centre,
I = M\(\left(\frac{l^2}{12}+\frac{\mathrm{R}^2}{4}\right)\); K = \(\sqrt{\frac{l^2}{12}+\frac{\mathrm{R}^2}{4}}\)
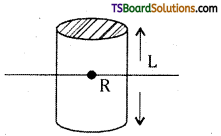
→ M. O.I. of a hollow cylinder of length / and radius R
a) about the natural axis, I = MR2; K = R
b) about an axis perpendicular to length and passing through centre
I = \(\left(\frac{l^2}{12}+\frac{\mathrm{R}^2}{2}\right)\); K = \(\sqrt{\frac{l^2}{12}+\frac{\mathrm{R}^2}{2}}\)
→ Angular momentum, L = Iω
→ Relation between angular momentum (L) and torque (τ) is, τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}=\frac{\mathrm{L}_2-\mathrm{L}_1}{\mathrm{t}}\)
→ Relation between τ and α is τ = Iα
→ From law of conservation of angular momentum
I1ω1 + I2ω2 = constant (When no external torque acts on the body)
![]()