Here students can locate TS Inter 1st Year Physics Notes 8th Lesson Oscillations to prepare for their exam.
TS Inter 1st Year Physics Notes 8th Lesson Oscillations
→ Periodic motion: A motion that repeats itself at regular intervals of time is called periodic motion.
→ Oscillations or vibrations: When a small displacement is given to a body at rest position (i. e. its mean position) then a force will come into play and tries to bring back the body to its rest position or equilibrium position by executing to and fro motion about mean position. These are called vibrations or oscillations.
→ Time period (T): In periodic motion the smallest time interval after which the motion is repeated is called its time period.
→ Displacement: For a body in periodic motion the displacement changes with time, so displacement is given by x(t) (or)
f(t) = A cos ωt
→ Frequency: The reciprocal of time period (T) gives the number of repetitions that occur for unit time. It is called frequency (o).
υ = \(\frac{1}{T}\) = 1/Time period
→ Fourier theory: According to Fourier “any periodic function can be expressed as a super position of sine and cosine functions of different time periods with suitable coefficients.”
→ Simple harmonic motion (explanation of equation): In simple harmonic motion displacement is a sinusoidal function of time. i.e. x(t) = A cos(ωt ± Φ)
The particle will oscillate back and forth about the origin on X-axis within the limits + A and -A where A is amplitude, ω and Φ are constants.
(a) Amplitude A of simple harmonic motion (S.H.M.) is the magnitude of maximum displacement of the particle. Displacement of particle varies from +A to -A.
(b) Phase of motion (or) Argument: For a body in S.H.M the position of a particle or state of motion of a particle at any time t’ is determined by the argument (wt + Φ). The term (wt + Φ) is called argument or phase of motion.
(c) Phase constant (or) phase angle: The value of phase of motion at time t = 0 is called”phase constant Φ” or”phase angle”.
(d) Simple harmonic motion is represented with a cosine function. It has a periodicity of 2n. The function repeats after a time period T.
![]()
→ Reference circle: Let a particle p’ moves uniformly on a circle. The projection of p on any diameter of the circle will execute S.H.M.
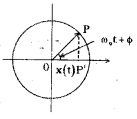
The particle ‘p’ is called “reference parti-cle” and the circle on which the particle moves is called “reference circle”.
→ Velocity of a body on S.H.M.: For a body in uniform circular motion speed v = coA. The direction of velocity v̅, at any time is along the tangent to the circle at that instantaneous point. Mathematically velocity of the body v̅(t) = -ωAsin(ωt + Φ) or v(t) = \(\frac{d}{d t}\)x(t) = \(\frac{d}{d t}\)Acos(ωt + Φ)
= -ωAsin(ωt + Φ)
→ Acceleration (a): For a body in S.H.M the instantaneous acceleration of the particle is a(t) = -ω2 A cos(wt + Φ) = -ω2 x(t)
or a(t) = \(\frac{d}{d t}\)v(t) = \(\frac{d}{d t}\)[-A ω sin(ωt + Φ)]
= -A(ω2cos(ωt + Φ))
Note:
a(t) implies the acceleration of the body is a function of time.
Maximum acceleration of the body amM = – co2A. Note: -ve sign indicates that acceleration and displacement are in opposite direction.
→ Force on a body in S.H.M:
Acceleration a(t) = – ω2x(t)
Force F = m a
∴ Force on a body in S.H.M
F(t) = ma = m(-ω2xt) = – K x(t)
Where K = mω2 and m = mass of the body
→ Energy of a body in S.H.M: For a body in S.H.M both kinetic energy and potential energy will change with time. These values will vary between zero and their maximum value.
Kinetic energy K = \(\frac{1}{2}\)mv
= \(\frac{1}{2}\)mω2 A2 sin2 (ωt + Φ)
= \(\frac{1}{2}\)kA2 sin2 (ωt + Φ)
Potential energy U = \(\frac{1}{2}\)kx
= \(\frac{1}{2}\)kA2 cos2 (ωt + Φ)
→ Springs:
- In case of springs for smaller displace-ments when compared with length of the spring Hooke’s law will hold good.
- The small oscillations of a block of mass m’ connected to a spring can be taken as simple harmonic.
- In case of springs the restoring force acting on the block of mass m is F(x) = – k (x)
- Spring constant k is defined as the force required for unit elongation.
Unit: newton/metre, K= force/displacement ⇒ K = \(\frac{-F}{x}\) = ve sign indicates that force and displacement are opposite in direction. For a stiff spring k is high. For a soft spring k is less. - Angular frequency of a loaded spring ω = \(\sqrt{\frac{K}{m}}\)
Time period of oscillation T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)
Where m is load attached and k is constant of spring.
→ Simple pendulum:
Time period of oscillation T = 2π\(\sqrt{l / \mathrm{g}}\)
→ Damped oscillations: In damped oscillations the energy of the system is dissipated continuously
When damping is very small the oscillations will remain approximately periodic. Eg: Oscillations of simple pendulum.
Damping force depends on nature of medium.
→ Free oscillations: When a system is displaced from its equilibrium position and allowed free to oscillate then oscillations made by die body are known as free oscillations.
Frequency of vibration is known as natural frequency of that body.
→ Forced or driven oscillations: If a body is made to oscillate under the influence of an external periodic force (say ω0) then those oscillations are called forced oscillations.
→ Resonance: The phenomenon of increase in amplitude of vibrating body when driving force frequency ‘ω0‘ is equal to or very close to natural frequency ‘ω’ of the oscillator is called resonance.
Note: When driving frequency is very close to natural frequency of vibrating body then also resonance will occur. Due to this reason damage to building is caused in earthquake effected area.
→ Displacement of a body in S.H.M
Y = A sin (ωt ± Φ)
→ Velocity of a body in S.H.M is
V = \(\frac{d y}{d t}=\frac{d}{d t}\) (A sin ωt)
V = Aω cos ωt ( where Y = A sin ωt)
or V = ω\(\sqrt{A^2-Y^2}\)
Maximum velocity, Vmax = Aω
![]()
→ Acceleration of a body in S.H.M
a = -ω2 A sin ωt or a = -ω2Y .
(where Y = A sin ωt)
(- ve sign shows that acceleration and displacement are opposite to each other) Maximum acceleration, amax = ω2A
→ Angular velocity ω of a body in S.H.M:
∝ – Y or a = – ω2Y ( – ve sign for opposite direction only )
∴ ω = \(\frac{a}{Y}\) or ω = \(\sqrt{\frac{a}{Y}}\)
∴ Angular velocity of a body in S.H.M,
ω = \(\sqrt{\frac{\text { acceleration }}{\text { displacement }}}\)
→ Time period of a body in S.H.M: The time taken for one complete oscillation is called “time period”.
Time Period,
(T) = \(\frac{\text { Angular displacement for one rotation }}{\text { Angular velocity }}=\frac{2 \pi}{\omega}\)
∴ T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{Y}{\mathrm{a}}}=2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}\)
→ Frequency (υ) is the number of vibrations (or) rotations per second.
Frequency, υ = \(\frac{1}{\mathrm{~T}}=\frac{1}{2 \pi} \sqrt{\frac{\mathrm{a}}{\mathrm{Y}}}\),
⇒ υ = \(\frac{\omega}{2 \pi}\) or ω = /7io 2n
→ Springs:
- In springs force constant is defined as the ratio of Force to displacement.
Spring constant, (K) = \(\frac{F}{Y}\) - Time period, T = \(\sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\) = 2π.\(\sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)
- If mass of the spring mj is also taken into account then time period,
T1 = 2π\(\frac{\sqrt{\left(m+\frac{m_1}{3}\right)}}{K}\)(For real spring ) - Frequency of vibration, n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{m}}\)
For Real spring, n = \(\frac{1}{2 \pi} \sqrt{\frac{K}{\left(m+\frac{m_1}{3}\right)}}\) - When a spring is divided into ‘n’ parts then its force constant (k) will increase.
New force constant k1 = nk
where n number of parts and k = original spring constant.
→ Simple Pendulum:
- In simple pendulum component of weight of the bob useful for to and fro motion is F = mg sin θ
- Time period, T = 2π\(\sqrt{\frac{l}{g}}\) ⇒ g = 4π\(\frac{l}{\mathrm{~T}^2}\)
- When a simple pendulum is placed in a lift moving with some acceleration then its time period changes.
- When lift moves up with an acceleration ‘a’ its time period decreases, T = 2π\(\sqrt{\frac{l}{g+a}}\)
- When lift moves down with an acceleration ‘a’ its time period increases, T = 2π\(\sqrt{\frac{l}{g-a}}\)
- For seconds pendulum time period, T = 2 sec
Length of seconds pendulum on earth = 100 cm = 1 m ( nearly ) - In simple pendulum L – T2 graph is a straight line passing through origin.