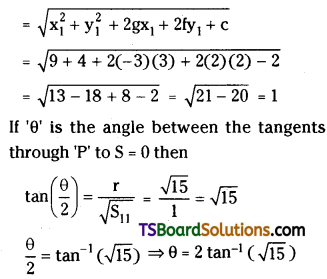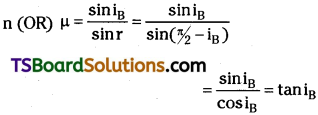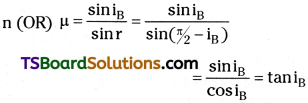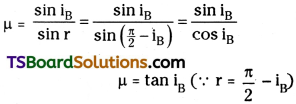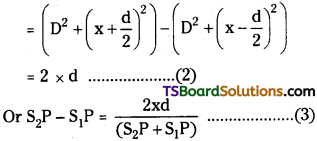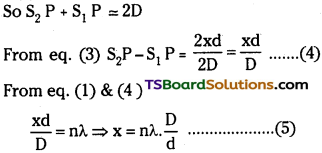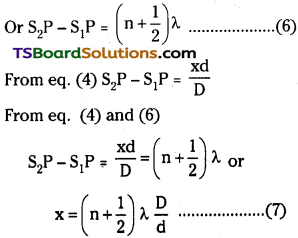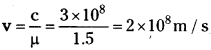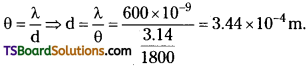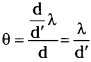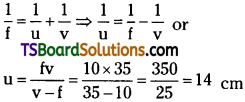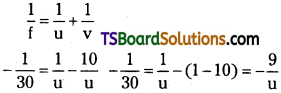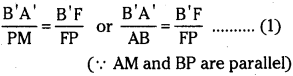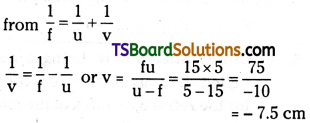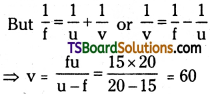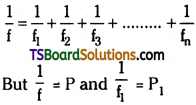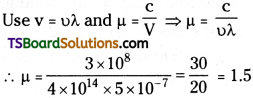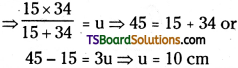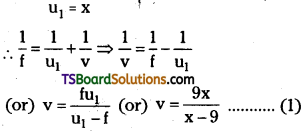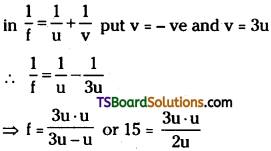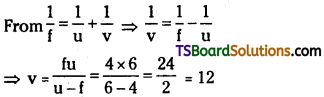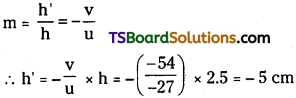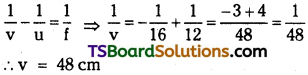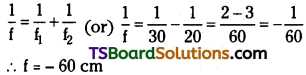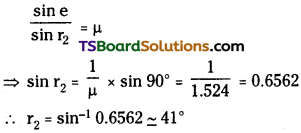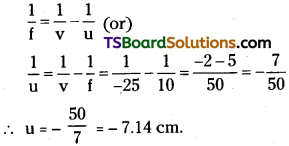TS Inter 2nd Year

Here students can locate TS Inter 2nd Year Physics Notes 12th Lesson Dual Nature of Radiation and Matter to prepare for their exam.

TS Inter 2nd Year Physics Notes 12th Lesson Dual Nature of Radiation and Matter

→ Cathode rays: Cathode rays are produced in a discharge tube at a pressure of 0.001 mm and at a potential of 10,000V.

• Cathode rays consists of a steam of fast moving negatively charged particles.
• Speed of cathode rays ranges about 0.1 to 0.2 times light velocity (3 × 10⁸m/s)
• From Millikan’s oil drop experiment charge on electron was found to be 1.602 × 10^-19C.

→ Electron emission: A free electron is held inside a metal surface due to attractive forces of ions.
An electron can come out of the metal surface only if it has got sufficient energy to overcome the attractive force.

→ Work function (Φ) : The minimum energy required by an electron to escape from metal surface is called “work function”.
Work function depends on nature of metal.

Note:
In metals, work function of platinum is highest Φ_p = 5.65 eV,
Work function of caesium is lowest Φ_p = 2.14.

→ Electron volt (eV): One electron volt is the energy acquired by an electron when it is accelerated through a potential of 1 volt.
1 eV= 1.602 × 10¹⁹ joules

→ Thermionic emission: In thermionic emission electrons (metal surfaces) are heated to gain sufficient thermal energy to leave the metal surface.

→ Field emission: In field emission strong electric field is applied on metal so that electrons can be pulled out of the metal.

→ Photo-electric emission: When metal surfaces are illuminated with light waves of suitable energy electrons are emitted from metal surface. This process is called”photo electric emission”.

→ Photo electric effect: The process of libe-rating an electron from the metal surface due to light energy falling on it is called “photo electric effect”.

→ Hallwach’s and Lenard’s observations:
I. Lenard allowed ultraviolet light to fall on metal electrodes placed in an evacuated glass tube. He observed that current is flow¬ing in the circuit. When ultraviolet radiations were stopped immediately current flow was also stopped.

II. Hallwach’s conducted experiments on zinc plates exposed to ultraviolet radiation.

• When a negatively charged zinc plate is exposed to U.V. radiation it lost negative charge.
• When a positively charged zinc plate is exposed to U.V. radiation its positive charge increased.
  From above observations he concluded that
  • Negatively charged particles are emitted from zinc plate under the action of U.V. rays.
  •  When frequency of incident light is lesser than a certian value called thres¬hold frequency electrons are not liberated from zinc surface.

→ Stopping potential: The minimum negative potential required by collector to stop photo current (or) becomes zero is called “cut off voltage (v₀)”
K_max = ev₀ (or) \(\frac{1}{2}\)mV_max = ev₀

→ Effect of frequency on stopping potential:

• Stopping potential varies linearly with frequency of incident light.
• Every photo surface has a minimum cut off frequency for which stopping potential V₀ = 0

→ Laws of photo electric emission

• Photo electric emission is an instanta¬neous process where time delay is 10^-9 seconds or even less
• Every photo surface has a minimum cut of frequency v₀ called threshold frequency. Photo emission takes place when frequency of incident radiation υ > υ₀
• For frequency υ > υ₀ photo current is directly proportional to intensity of incident light.
• When frequency of incident light υ > υ₀ kinetic energy of photo electron is directly proportional to frequency υ.
  i. e., KE ∝ υ (i.e., υ > υ₀)

→ Photo electric effect: Wave theory of light As per wave theory photo electric emission must follow the following rules.

• When intensity of light is high energy absorbed by electrons is also high so liberation of electron and its kinetic energy must depend on intensity of light.
• Threshold frequency limit should not exist.
• Energy absorption by electrons from incident light waves is a slow process. Explicit calculations estimated that it may take hours together to liberate electrons from given metal surface. Practically photo electric effect is not at all obeying any prediction from wave theory of light.

→ Einstein’s photo electric equation: According to Einstein radiation consists of discrete units of energy called quanta of energy radiation.
Energy of quanta called photon in light E = hυ
Maximum kinetic energy of photo electron K_max is the difference of energy of incident radiation (hυ) and its work function (t)>).
K_max = hυ – Φ (when υ > υ₀)
or \(\frac{1}{2}\)V_max = h(υ – υ₀)
Work function Φ₀ = hυ₀

→ Millikan’s verification of photo electric equation : Millikan practically verified Einstein’s photo electric equation and found slope of v₀ – υ graph is \(\frac{h}{e}\). He calculated h value from \(\frac{h}{e}\) value obtained from υ₀ – υ graph. It coincides with h’ value obtained by other scientists.

→ Particle nature of light: In photo electric effect energy of quanta interacted with electrons. Energy of quanta E = hυ, momentum p = \(\frac{\mathrm{hv}}{\mathrm{c}}\)
Since energy quanta has momentum p and a fixed value of energy it is treated as particle. Energy quanta of light is called photon.

→ Properties of photons:

• Energy of photon E = hυ, momentum p = \(\frac{\mathrm{hv}}{\mathrm{c}}\)
• In interaction of radiation with matter light quanta will behave like particles.
• Photons are electrically neutral. So they are not deflected by electric and magnetic fields.
• In photon – particle collision total energy and total mometum are conserved. On collision photon will totally loose its enery and momentum.
  Note : In collision between photon and particles total number of photons may not be conserved.

→ Dual nature of light : Light shows wave nature in physical phenomena like interference, diffraction and polarisation.
Light shows particle nature in explaining the phenomena like photo electric effect and compton effect.
So we will consider either wave nature or particle nature depending on the experiment.
Ex:- In case of human eye light gathering by eye lens is explained with wave nature. Where as absorption of energy by rods and cones in retina are explained by particle nature of light.

→ de – Broglie hypothesis: Radiation has dual nature i.e., energy can exist as a wave or as a particle. He assumed that like energy matter will also have dual nature, i.e., matter will have energy and wave nature.
Wave length associated with moving particle λ = \(\frac{h}{p}=\frac{h}{m v}\) = is called de – Broglie wave length.
Experimental results proved wave nature of matter.

→ Heisenberg’s uncertainty principle: According to Heisenberg’s uncertainty principle we cannot exactly find both momentum and position of an electron at the same time.

→ Davisson and Germer experiment: It verified de-Broglie hypothesis.

→ Photo cell: A photo cell will convert light energy into electrical energy. In these cells intensity variation of light is converted into charges in electrical current. They are widely used in recording and reproduction of sound, automatic switches and in automatic counters.

→ Energy of photon E = hυ ⇒ E = \(\frac{\mathrm{hc}}{\lambda}\)
Maximum kinetic energy of photo electron K_max = eV₀

→ Work function Φ₀ = hυ₀ ‘ υ₀ = \(\frac{\phi_0}{\mathrm{~h}}\)
Einsteins’s photo electric equation
K_max = hυ – Φ₀ or eV₀ = hυ – Φ₀
Where V₀ = Stopping potential.

→ de – BrogUe wave length, λ = \(\frac{h}{p}=\frac{h}{m v}\) or \(\frac{h}{p}=\frac{c}{v}\) = λ

→ Kinetic energy of electron in electric field K = eV
Wavelength, λ = \(\frac{h}{p}=\frac{h}{\sqrt{2 m k}}=\frac{h}{\sqrt{2 m e V}}\)

Here students can locate TS Inter 2nd Year Physics Notes 13th Lesson Atoms to prepare for their exam.

TS Inter 2nd Year Physics Notes 13th Lesson Atoms

→ J.J. Thomson thought that the positive charge of the atom is uniformly distributed through out the volume of the atom and the negatively charged electrons are embedded in it like seeds in a watermelon.

→ According to Rutherford the entire positive charge and most of the mass of the atom is concentrated in a small volume called nucleus. Electrons are revolving around the nucleus at some distance just as planets revolve around the sun.

→ Alpha particle scattering experiments on gold foil showed that size of nucleus is about 10^-14 to 10^-15 m and size of atom is nearly 10^-10 m.

→ Most of the atom is empty space. The electrons would be moving in certain orbits with some distance from nucleus just like planets around the sun.

→ Alpha particle scattering experiment :
Magnitude of force between α – particle and gold nuclie is F = \(\frac{1}{4 \pi \epsilon_o} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{r}^2}\) Where ‘r’ is the distance between α – particle and nucleus.
The magnitude and direction of force changes continuously as it approaches the nucleus.

→ Impact Parameter: It is the perpendicular distance of the initial velocity vector of a particle from centre of nucleus.
In case of head on collision impact parameter is minimum and α – particle rebounds back (θ = π). For a large impact parameter α – particle goes undeviated. The chance of head on collision is very small. It in turn suggested that mass of atom is much concentrated in a small volume.

→ Bohr postulates : Bohr model of hydrogen atom consists of three main postulates.

• Electrons in an atom could revolve in certain permitted stable orbits. Electrons revolving in these stable orbits do not emit or radiate any energy.
• The stable orbits are those whose orbital angular momentum is an integral multiple of h/ 2π.
  i. e., L = nh / 2π where n = 1, 2, 3, ……………… etc. (an integer.)
  These stable orbits are also called as non – radiating orbits.
• An electron may take a transition between non-radiating orbits. When electron transition takes place a photon of energy equals to the energy difference between initial and final states will be radiated.
  E = hv = E_i– E_j

→ Bohr radius (a₀): According to Bohr theory radius of the orbit, r = \(\frac{\mathrm{n}^2 \mathrm{~h}^2 \epsilon_0}{\pi \mathrm{me}^2}\) when n = 1. It is called first orbit. Radius of 1st orbit r₁ = \(\frac{h^2 \epsilon_0}{\pi \mathrm{me}^2}\) = 5.29 × 10^-11 m. This is called Bohr orbit a₀.
a₀ = \(\frac{h^2 \epsilon_0}{\pi \mathrm{me}^2}\) = 5.29 × 10^-11 m = 0.529 Å

→ Energy of orbit: From Bohr theory energy of the orbit E = –\(\frac{m e^4}{8 n^2 h^2 \epsilon_o^2}\)
Where – ve sign indicates the force of attraction between electron and nucleus.
For 1st orbit n = 1.
Its energy E₁ = -2.18 × 10^-18 J or
E₁ = – 13.6 eV.
For all other orbits their energy E = \(\frac{13.6}{n^2}\) eV
Note: The energy of an atom is least (i.e., it has maximum – ve value) when electron is revolving with n = 1 orbit. This energy state (n = 1) is called lowest state of the atom or ground state. For ground state of hydrogen atom E = – 13.6 eV.

→ Spectral series: From Bohr model electrons are permitted to transit between the energy levels while doing so they will absorb or release the exact amount of energy difference of the initial and final states.
∴ Energy absorbed or released E = hv = E_i – E_f
E = hv = \(\frac{\mathrm{hc}}{\lambda}=\frac{m \mathrm{e}^4}{8 \varepsilon_{\mathrm{o}} \mathrm{h}^2}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right]\) or
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right]\) where R is Rydberg’s constant R = 1.03 × 10⁷ / m

→ Lyman series: When electrons are jumping on to the first orbit from higher energy levels then that series of spectral lines emitted are called ”lyman series”.
In Lyman series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{n^2}\right]\) where n = 2, 3, …… etc

→ Balmer series : When electrons are jumping on to the second orbit from higher levels then that series of spectral lines are called “Balmer series”.
For Balmer series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{\mathrm{n}^2}\right]\) where n = 3,4,………. Spectral lines of Balmer series are in visible region.

→ Paschen series : When electrons are jump¬ing on to the 3rd orbit from higher energy levels then that series of spectral lines are called “Paschen series”.
For Paschen series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{\mathrm{n}^2}\right]\)
n = 4, 5………….. These spectral lines are in near infrared region.

→ Brackett series: When electrons are jump¬ing on to the 4th orbit from higher levels then that series of spectral lines are called “Brackett series”.
For Brackett series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{4^2}-\frac{1}{n^2}\right]\) where n = 5, 6, …………….
Brackett series are in middle infrared region.

→ Pfund series: When electrons are jumping on to the 5th orbit from higher energy levels then that series of spectral lines are called
“pfund series”.
For pfund series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{5^2}-\frac{1}{\mathrm{n}^2}\right]\)
where n = 6, 7, ………… These spectral lines are in far infrared region.

Note : In spectral lines \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right]\)R
But \(\frac{1}{\lambda}\) = v/c

Frequency of spectral line v = Rc\(\left[\frac{1}{n_i^2}-\frac{1}{n_f^2}\right]\)

→ Ionisation potential : It is the amount of minimum energy required to release an ele-ctron from the outer most orbit of the nucleus.
From Bohr’s model energy of the orbit is the ionisation energy of electron in that orbit.
Ex: Energy of 1st orbit in hydrogen is 13.6 eV.
Practically ionisation potential of hydro-gen is 13.6 eV.
Note : The success of Bohr atom model is in the prediction of ionisation energy of orbits.

→ Force between ‘a’ particle and positively charged nucleus
F = \(\frac{1}{4 \pi \varepsilon_o} \frac{2 \mathrm{e}(\mathrm{Ze})}{\mathrm{r} 2}=\frac{\mathrm{Ze}^2}{2 \pi \varepsilon_0 r^2}\)

→ Kinetic energy of α – particle,
K = \(\frac{2 Z \mathrm{e}^2}{4 \pi \varepsilon_{\mathrm{o}} \mathrm{d}}=\frac{Z \mathrm{e}^2}{2 \pi \varepsilon_{\mathrm{o}} \mathrm{d}}\)

→ Distance of closest approach d = \(\frac{\mathrm{Ze}^2}{2 \pi \varepsilon_0 \mathrm{k}}\)

→ For an electron moving in the orbit of hydrogen atom = \(\frac{m v^2}{r}=\frac{1}{4 \pi \varepsilon_o} \frac{Z^2}{r^2}\)

→ For an atom of atomic number ‘Z’, \(\frac{\mathrm{mv}^2}{\mathrm{r}}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{Ze}^2}{\mathrm{r}^2}\)

→ Relation between orbit radius and velocity in hydrogen atom is r = e² / 4πε₀
mv² = \(\frac{1}{4 \pi \varepsilon_o}\) where k = \(\frac{1}{4 \pi \varepsilon_o}\) = 9 × 10⁹

→ In hydrogen atom .
(1) Kinetic energy K = \(\frac{1}{2}\)mv²

(ii) Potential energy U = \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_o \mathrm{r}}=\frac{m \mathrm{e}^4}{8 \mathrm{n}^2 \mathrm{~h}^2 \varepsilon_o^2}\)
= \(-\frac{e^2}{4 \pi \varepsilon_o r}\) (-ve sigh for force of attraction)

(iii) Total energy E = K + U
= \(-\frac{e^2}{8 \pi \varepsilon_o r}=\frac{-m e^4}{8 n^2 h^2 \varepsilon_o^2}\)

(iv) Velocity of electron in orbit v = e/\(\sqrt{4 \pi \varepsilon_o \mathrm{mr}}\)

→ Spectral series: Wavelengths of spectral series are given by \(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)\)
where n₁ and n₂ are the number of orbits between which electron transition takes place.
Energy radiated In transition E = hv = E₂ – E₁
In Bohr atom model.
Angular momentum of orbital L = mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
radius of nth orbit r_n = \(\frac{\mathrm{nh}}{2 \pi}\)

Velocity of electron in nth orbit
V_n = e/\(\sqrt{4 \pi \varepsilon_o m r_n}\)
or v_n = \(\frac{1}{\mathrm{n}} \frac{\mathrm{e}^2}{4 \pi \varepsilon_{\mathrm{o}}} \frac{1}{(\mathrm{~h} / 2 \pi)}\)
or
r_n = \(\frac{\mathrm{n}^2 \mathrm{~h}^2 \varepsilon_0}{\pi \mathrm{me}^4}\)
Bohr radius a₀ = \(\frac{h^2 \varepsilon_o}{\pi m e^4}\) = 5.29 × 10^-11 m

Energy of nth orbit
E_n = \(\frac{-\mathrm{me}^4}{8 \mathrm{n}^2 \mathrm{~h}^2 \varepsilon_{\mathrm{o}}^2}=\frac{-2.18 \times 10^{-18}}{\mathrm{n}^2}\)J = \(\frac{-13.6}{n^2}\)eV
Rydberg’s constant R = \(\frac{m \mathrm{e}^4}{8 \varepsilon_o^2 h^3 \mathrm{c}}\)
= 1.03 × 10⁷ m^-1

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Circles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Circles Important Questions Short Answer Type

Question 1.
If a point P is moving such that the lengths of tangents drawn from P to the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 are in the ratio 2 : 3, then find the equation of the locus of P. [(AP) Mar. ’19, (TS) ’17]
Solution:
Let P(x₁, y₁) be a point on the locus and S = x² + y² – 4x – 6y – 12 = 0
S’ = x² + y² + 6x + 18y + 26 = 0 be the given circles.

Question 2.
If a point P is moving such that the lengths of tangents drawn from P to x² + y² – 2x + 4y – 20 = 0 and x² + y² – 2x – 8y + 1 = 0 are in the ratio 2 : 1, then show that the equation of locus of P is x² + y² – 2x – 12y + 8 = 0.
Solution:
Let P(x, y) be a point on the locus and
S = x² + y² – 2x + 4y – 20 = 0
S’ = x² + y² – 2x – 8y + 1 = 0 be the given circles.
Length of tangent from P to S = 0 is
PA = \(\sqrt{S_{11}}=\sqrt{x^2+y^2-2 x+4 y-20}\)
Length of tangent from P to S’ = 0 is
PB = \(\sqrt{\mathrm{S}_{11}^{\prime}}=\sqrt{\mathrm{x}^2+\mathrm{y}^2-2 \mathrm{x}-8 \mathrm{y}+1}\)
Given condition is PA : PB = 2 : 1
\(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{2}{1}\)
⇒ PA = 2PB
⇒ \(\sqrt{x^2+y^2-2 x+4 y-20}\) = \(2 \sqrt{x^2+y^2-2 x-8 y+1}\)
squaring on both sides
⇒ x² + y² – 2x + 4y – 20 = 4(x² + y² – 2x – 8y + 1)
⇒ x² + y² – 2x + 4y – 20 – 4x² – 4y² + 8x + 32y – 4 = 0
⇒ -3x² – 3y² + 6x + 36y – 24 = 0
⇒ x² + y² – 2x – 12y + 8 = 0
The equation of locus of P is x² + y² – 2x – 12y + 8 = 0.

Question 3.
Find the equations of the tangent to the circle x² + y² – 4x + 6y – 12 = 0 which are parallel to x + y – 8 = 0. (Mar. ’01)
Solution:
Given equation of the circle is x² + y² – 4x + 6y – 12 = 0

Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -2, f = 3, c = -12
Centre C = (-g, -f) = (2, -3)
Radius r = \(\sqrt{g^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{4+9+12}\) = 5
Given equation of the straight line is x + y – 8 = 0
The equation of the tangent parallel to x + y – 8 = 0 is
x + y + k = 0 ……….(1)
Since eq. (1) is a tangent to the given circle then r = d.
r = \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)
⇒ 5 = \(\frac{|1(2)+1(-3)+\mathbf{k}|}{\sqrt{(1)^2+(1)^2}}\)
⇒ 5 = \(\frac{|2-3+\mathbf{k}|}{\sqrt{2}}\)
⇒ 5√2 = |k – 1|
⇒ k – 1 = ±5√2
⇒ k = 1 ± 5√2
Substitute the value of ‘k’ in eq. (1)
x + y + 1 ± 5√2 = 0

Question 4.
Show that x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0 and find its point of contact.
Solution:
Given equation of the circle is x² + y² – 3x + 7y + 14 = 0

Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we get

Given the equation of the line is x + y + 1 = 0.
Now, d = The perpendicular distance from the centre C\(\left(\frac{3}{2}, \frac{-7}{2}\right)\) to the line x + y + 1 = 0.

Since r = d then, the line x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0.
Let P(h, k) be the point of contact.
Now, P(h, k) is the foot of the perpendicular drawn from C = \(\left(\frac{3}{2}, \frac{-7}{2}\right)\) to the line x + y + 1 = 0

∴ The point of contact is P(2, -3).

Question 5.
Show that the points (1, 1), (-6, 0), (-2, 2), and (-2, -8) are concyclic and find the equation of the circle on which they lie. [(AP) Mar. ’19; May ’17]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since, (1) passes through point (1, 1)
1² + 1² + 2g(1) + 2f(1) + c = 0
2 + 2g + 2f + c = 0
2g + 2f + c = -2 ……(2)
Since, (1) passes through the point (-6, 0)
(-6)² + 0² + 2g(-6) + 0 + c = 0
36 + c – 12g = 0
-12g + c = -36 …….(3)
Since, (1) passes through the point (-2, 2)
(-2)² + (2)² + 2g(-2) + 2f(2) + c = 0
4 + 4 – 4g + 4f + c = 0
-4g + 4f + c = -8 ……..(4)
From (2) and (3)

From (3) and (4)

Solving (5) and (6)

g = 2, f = 3
Substitute the values of g, f in (2)
2(2) + 2(3) + c = -2
4 + 6 + c = -2
10 + c = -2
c = -12
Now, substitute the values of g, f, c in (1)
∴ The equation of the required circle is
x² + y² + 2(2) x + 2(3) y – 12 = 0
x² + y² + 4x + 6y – 12 = 0 ………(7)
Now, substituting the point (-2, -8) in (7)
(-2)² + (-8)² + 4(-2) + 6(-8) – 12 = 0
4 + 64 – 8 – 48 – 12 = 0
68 – 68 = 0
0 = 0
∴ Given points are concyclic.
∴ Required equation of the circle is x² + y² + 4x + 6y – 12 = 0

Question 6.
Find the equations of the tangents to the circle x² + y² + 2x – 2y – 3 = 0 which are perpendicular to 3x – y + 4 = 0.
Solution:
Given equation of the circle is x² + y² + 2x – 2y – 3 = 0

Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = 1, f = -1, c = -3,
Centre of the circle C(-g, -f) = (-1, 1)
The radius of the circle
r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(-1)^2+(1)^2+3}\)
= √5
Given the equation of the straight line is 3x – y + 4 = 0
The equation of the straight line perpendicular to 3x – y + 4 = 0 is
x + 3y + k = 0 ……..(1)
Since (1) is the tangent to the given circle then r = d
√5 = \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)

The equations of the tangents are from (1),
x + 3y – 2 ± 5√2 = 0

Question 7.
Show that the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0 and finds its point of contact. (May ’10)
Solution:
Given equation of the circle is x² + y² – 4x – 8y + 7 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
we get g = -2, f = -4, c = 7
Let the given point P(x₁, y₁) = (-1, 2)
The equation of the tangent is S1 = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-1) + y(2) – 2(x – 1) – 4(y + 2) + 7 = 0
⇒ -x + 2y – 2x + 2 – 4y – 8 + 7 = 0
⇒ -3x – 2y + 1 = 0
⇒ 3x + 2y – 1 = 0

Given equation of the circle is x² + y² + 4x + 6y = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = 2, f = 3, c = 0
Centre C(-g, -f) = (-2, -3)
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9}\)
= √13
Now d = The perpendicular distance from the centre C = (-2, -3) to the line 3x + 2y – 1 = 0

Since r = d, the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0.
Let Q(h, k) be the point of contact.
Now, Q(h, k) is the foot of the perpendicular drawn from centre C(-2, -3) to the line 3x + 2y – 1 = 0.

∴ The point of contact Q(h, k) = (1, -1).

Question 8.
Find the angle between the tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0. (Mar. ’12)
Solution:
Given the equation of the circle is x² + y² – 6x + 4y – 2 = 0.

Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -3, f = 2, c = -2
Radius r = \(\sqrt{9+4+2}=\sqrt{15}\)
Let the given point P(x₁, y₁) = (3, 2)
Length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

Question 9.
Find the locus of ‘P’ where the tangent is drawn from ‘P’ to x² + y² = a² are perpendicular to each other.
Solution:
Given the equation of the circle is x² + y² = a²
Radius r = a

Let P(x₁, y₁) be any point on the locus.
Length of the tangent = \(\sqrt{\mathrm{S}_{11}}\) = \(\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2-\mathrm{a}^2}\)
Given that angle between the tangents θ = 90°
If ‘θ’ is the angle between the tangents through ‘P’ to the given circle then
\(\tan \left(\frac{\theta}{2}\right)=\frac{r}{\sqrt{S_{11}}}\)

Question 10.
Find the chord length intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0. [(TS) Mar. ’16]
Solution:
Given equation of the circle is x² + y² – 8x – 2y – 8 = 0

Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -4, f = -1, c = -8
Centre of the circle C = (-g, -f) = (4, 1)
Radius r =\(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(-4)^2+(-1)^2+8}\)
= 5
Given equation of the straight line is x + y + 1 = 0
Now d = perpendicular distance from the centre C(4, 1) to the chord x + y + 1 = 0

Question 11.
Find the chord length intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3. [(TS) Mar. ’20; (AP) Mar. ’18, May ’16, Mar. ’13]
Solution:
Given equation of the circle is x² + y² – x + 3y – 22 = 0

Question 12.
Find die length of the chord formed by x² + y² = a² on the line x cos α + y sin α = P. [(TS) Mar. ’16]
Solution:
Given equation of the circle is x² + y² – a² = 0

Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 0, f = 0, c = -a²
Centre of the circle C(-g, -f) = (0, 0)
Radius of the circle r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(0)^2+(0)^2+a^2}\)
= a
Given the equation of the straight line is x cos α + y sin α – P = 0
Now d = perpendicular distance from the centre C(0,0) to the chord x cos α + y sin α – P = 0

Question 13.
Find the equation of the circle with centre (-2, 3) cutting a chord length 2 units on 3x + 4y + 4 = 0. (Mar. ’11)
Solution:
Given that centre C(h, k) = (-2, 3)
Given the equation of the straight line is 3x + 4y + 4 = 0
Now d = The perpendicular distance from the centre C(-2, 3) to the line 3x + 4y + 4 = 0.

Given that the length of the chord = 2
\(2 \sqrt{\mathrm{r}^2-\mathrm{d}^2}\) = 2
⇒ \(\sqrt{\mathrm{r}^2-\mathrm{d}^2}\) = 1
⇒ r² – d² = 1
⇒ r² – 2² = 1
⇒ r² – 4 = 1
⇒ r² = 5
⇒ r = √5
The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x + 2)² + (y- 3)² = (√5)²
⇒ x² + 4 + 4x + y² + 9 – 6y = 5
⇒ x² + y² + 4x – 6y + 8 = 0

Question 14.
Find the area of the triangle formed by the normal at (3, -4) to the circle x² + y² – 22x – 4y + 25 = 0 with the coordinate axis. [Mar. ’18 (TS)]
Solution:
Given circle is x² + y² – 22x – 4y + 25 = 0
Compare with x² + y² + 2gx + 2fy + c = 0 then
we get 2g = -22 ⇒ g = -11
2f = -4 ⇒ f = -2, c = 25
centre c(-g, -f) = c(11, 2)

The area of the triangle formed by the normal with the coordinate axis = \(\frac{c^2}{2|a b|}\)
= \(\frac{(-25)^2}{2|3(-4)|}\)
= \(\frac{625}{24}\) sq units

Question 15.
Find the mid point of the chord intercepted by x² + y² – 2x – 10y + 1 = 0 on the line x – 2y + 7 = 0.
Solution:
Given equation of the circle is x² + y² – 2x – 10y + 1 = 0

Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
we get, g = -1, f = -5, c = 1
Centre of the circle, C = (-g, -f) = (1, 5)
Given equation of the straight line is x – 2y + 7 = 0
Comparing this equation with ax + by + c = 0,
we get a = 1, b = -2, c = 7
Let P(h, k) is the midpoint of the chord x – 2y + 7 = 0
Now P(h, k) is the foot of the perpendicular from centre C(1, 5) on the chord x – 2y + 7 = 0

Question 16.
Show that the area of the triangle formed by the two tangents through P(x₁, y₁) to the circle S = x² + y² + 2gx + 2fy + c = 0 and the chord of contact of ‘P’ with respect to S = 0 is \(\frac{\mathbf{r}\left(\mathbf{S}_{11}\right)^{3 / 2}}{\mathbf{S}_{11}+\mathbf{r}^2}\), where ‘r’ is the radius of the circle.
Solution:
If θ is the angle between the tangents ‘P’ to S = 0, then
\(\tan \left(\frac{\theta}{2}\right)=\frac{r}{\sqrt{S_{11}}}\)

Let Q, R be the chord of the contact from ‘P’ to the circle.
Let PA be the ⊥r from P to QR.

Question 17.
Find the pole of the line x + y + 2 = 0 w.r.t the circle x² + y² – 4x + 6y – 12 = 0. [(AP) Mar. ’17, May ’15]
Solution:
Given equation of the circle x² + y² – 4x + 6y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = 3, c = -12
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9+12}\)
= 5
Given equation of the straight line is x + y + 2 = 0
Comparing this equation with lx + my + n = 0,
we get l = 1, m = 1, n = 2
The pole of lx + my + n = 0 w.r.t x² + y² + 2gx + 2fy + c = 0 is

Question 18.
Find the pole of the line 3x + 4y – 45 = 0 w.r.t the circle x² + y² – 6x – 8y + 5 = 0. [(AP) Mar. ’16]
Solution:
Given equation of the circle x² + y² – 6x – 8y + 5 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -3, f = -4, c = 5
Radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{9+16-5}\)
= √20
Given the equation of the straight line is 3x + 4y – 45 = 0
Comparing the given equation with lx + my + n = 0,
we get l = 3, m = 4, n = -45
The pole of lx + my + n = 0 w.r.t x² + y² + 2gx + 2fy + c = 0 is

Question 19.
Show that the lines 2x + 3y + 11 = 0, 2x – 2y – 1 = 0 are conjugate w.r.t the circle x² + y² + 4x + 6y + 12 = 0.
Solution:
Given equation of the circle x² + y² + 4x + 6y + 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 2, f = 3, c = 12
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9-12}\)
= 1
Given equations of the straight lines are
2x + 3y + 11 = 0 …….(1)
2x – 2y – 1 = 0 ………(2)
Comparing (1) with l₁x + m₁y + n₁ = 0
we get l₁ = 2, m₁ = 3, n₁ = 11
Comparing (2) with l₂x + m₂y + n₂ = 0
we get l₂ = 2, m₂ = -2, n₂ = -1
Now (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
= [2(2) + 3(3) – 11] [2(2) + 3(-2) + 1]
= (4 + 9 – 11) (4 – 6 + 1)
= 2(-1)
= -2
r² (l₁l₂ + m₁m₂) = (1)² [2(2) + 3(-2)]
= 1(4 – 6)
= -2
∴ (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = r² (l₁l₂ + m₁m₂)
∴ Given lines are conjugate w.r.t given circle.

Question 20.
Find the value of ‘k’ if x + y – 5 = 0 and 2x + ky – 8 = 0 are conjugate with respect to the circle x² + y² – 2x – 2y – 1 = 0. [(TS) May ’18]
Solution:
Given equation of the circle is x² + y² – 2x – 2y – 1 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -1, f = -1, c = -1
Radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{1+1+1}\)
= √3
Given equations of the straight lines are
x + y – 5 = 0 ………(1)
2x + ky – 8 = 0 ……..(2)
Comparing (1) with l₁x + m₁y + n₁ = 0
we get l₁ = 1, m₁ = 1, n₁ = -5
Comparing (2) with l₂x + m₂y + n₂ = 0
we get l₂ = 2, m₂ = k, n₂ = -8
Since given lines are conjugate w.r.t given circle, then
(l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = r² (l₁l₂ + m₁m₂)
⇒ [1(-1) + 1(-1) + 5] [2(-1) + k(-1) + 8] = (√3)2 [1(2) + 1(k)]
⇒ (-1 – 1 + 5)(-2 – k + 8) = 3(2 + k)
⇒ 3(-k + 6) = 3(k + 2)
⇒ -k + 6 = k + 2
⇒ 2k = 4
⇒ k = 2

Question 21.
Find the condition that the tangents drawn from (0, 0) to S = x² + y² + 2gx + 2fy + c = 0 be perpendicular to each other. [(TS) May ’16]
Solution:
Given equation of the circle is S = x² + y² + 2gx + 2fy + c = 0

Centre, C = (-g, -f)
Radius, r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
Let, the given point P(x₁, y₁) = (0, 0)
The angle between the tangents, θ = 90°
The length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

Question 22.
If the abscissae of points A, B are the roots of the equation x² + 2ax – b² = 0 and ordinates of A, B are roots of y² + 2py – q² = 0, then find the equation of a circle for which \(\overline{\mathbf{A B}}\) is a diameter. (Mar. ’14)
Solution:
Let A (x₁, y₁)( B (x₂, y₂) are the two given points.
Since x₁, x₂ are the roots of the quadratic equation x² + 2ax – b² = 0 then
sum of the roots = \(\frac{-b}{a}\)
x₁ + x₂ = \(\frac{-2 \mathrm{a}}{1}\) = -2a
Product of the roots = \(\frac{c}{a}\)
x₁x₂ = \(\frac{-b^2}{1}\) = -b²
Since y₁, y₂ are the roots of the quadratic equation y² + 2py – q² = 0 then
sum of the roots = \(\frac{-b}{a}\)
y₁ + y₂ = \(\frac{-2 p}{1}\) = -2p
Product of the roots = \(\frac{c}{a}\)
y₁y₂ = \(\frac{-\mathrm{q}^2}{1}\) = -q²
The equation of a circle for which \(\overline{\mathbf{A B}}\) is a diameter is
(x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ x² – xx₂ – xx₁ + x₁x₂ + y² – yy₁ – yy₂ + y₁y₂ = 0
⇒ x² – x(x₁ + x₂) + x₁x₂ + y² – y(y₁ + y₂) + y₁y₂ = 0
⇒ x² – x(-2a) + (-b2) + y² – y(-2p) + (-q2) = 0
⇒ x² + y² + 2ax + 2py – b² – q² = 0

Question 23.
Find the equation of the circle which touches the x-axis at a distance of 3 from the origin and make an intercept of length 6 on the y-axis.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)

Since (1) meets the x-axis at A(3, 0)
∴ Point A(3, 0) lies on the circle (1), then
(3)² + (0)² + 2g(3) + 2f(0) + c = 0
⇒ 9 + 6g + c = 0
⇒ 6g + c = -9 ……..(2)
Since, the circle (1) touches the x-axis, then
g² = c …….(3)
From (2) and (3)
6g + g² = – 9
⇒ g² + 6g + 9 = 0
⇒ (g + 3)² = 0
⇒ g + 3 = 0
⇒ g = -3
Now, substitute the value of g in (3), and we get
(-3)² = c
⇒ c = 9
Given that the intercept on the y-axis made by (1) is 6
\(2 \sqrt{f^2-c}\) = 6
⇒ \(\sqrt{\mathrm{f}^2-\mathrm{c}}\) = 3
⇒ \(\sqrt{\mathrm{f}^2-9}\) = 3
⇒ f² – 9 = 9
⇒ f² = 18
⇒ f = ±3√2
Substitute the values of g, f, c in (1)
∴ The required equation of the circle is x² + y² + 2(-3)x + 2(±3√2)y + 9 = 0
⇒ x² + y² – 6x ± 6√2y + 9 = 0

Question 24.
Find the equation of the circle passing through (0, 0) and making intercepts 4, 3 on the x, y-axis respectively.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through the point (0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
∴ c = 0
Given that the intercept on the x-axis made by (1) = 4

Now, substitute the values of g, f, c in (1)
The equation of the required circle is
x² + y² + 2(±2)x + 2(±\(\frac{3}{2}\))y + 0 = 0
⇒ x² + y² ± 4x ± 3y = 0

Question 25.
Show that the locus of the point of intersection of the lines x cos α + y sin α = a, x sin α – y cos α = b (α is a parameter) is a circle.
Solution:
Given equations of the straight lines are
x cos α + y sin α = a …….(1)
x sin α – y cos α = b …….(2)
Now (1)² + (2)²
⇒ (x cos α + y sin α)² + (x sin α – y cos α)² = a² + b²
⇒ x² cos²α + y² sin²α + 2xy sin α cos α + x² sin²α + y² cos²α – 2xy sin α cos α = a² + b²
⇒ x² (cos²α + sin²α) + y² (sin²α + cos²α) = a² + b²
⇒ x² (1) + y² (1) = a² + b²
∴ x² + y² = a² + b²
∴ The locus of the point of intersection of the given line is x² + y² = a² + b²
It represents a circle.

Question 26.
If y = mx + c and x² + y² = a²
(i) Intersect at A and B
(ii) AB = 2λ, then show that c² = (1 + m²) (a² – λ²)
Solution:
Given the equation of the circle is x² + y² = a²

Comparing this equation with x² + y² = r², then centre of the circle C = (0, 0)
The radius of the circle r = a
Given the equation of the straight line is mx – y + c = 0
Now, d = the perpendicular distance from the centre C(0, 0) to the line mx – y + c = 0

Question 27.
Find the equation of the circle with centre (2, 3) and touch the line 3x – 4y + 1 = 0.
Solution:
Given, centre C(h, k) = (2, 3)

Given the equation of the straight line is 3x – 4y + 1 = 0
Since, the line 3x – 4y + 1 = 0 touches the required circle, then the line 3x – 4y + 1 = 0 is a tangent to the required circle.
∴ Radius r = The perpendicular distance from the centre C(2, 3) to the tangent 3x – 4y + 1 = 0

∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = (1)²
⇒ x² + 4 – 4x + y² + 9 – 6y = 1
⇒ x² + y² – 4x – 6y + 12 = 0

Question 28.
Find the equation of the tangent at the point 30° (parametric value of θ) of the circle x² + y² + 4x + 6y – 39 = 0.
Solution:
Given equation of the circle is x² + y² + 4x + 6y – 39 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
We get g = 2, f = 3, c = -39
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(2)^2+(3)^2+39}\)
= 2√13
The given point θ = 30°
∴ The equation of the tangent at the point θ of the given circle is (x + g) cos θ + (y + f) sin θ = r
⇒ (x + 2) cos 30° + (y + 3) sin 30° = 2√13
⇒ (x + 2) . \(\frac{\sqrt{3}}{2}\) + (y + 3) . \(\frac{1}{2}\) = 2√13
⇒ √3x + 2√3 + y + 3 = 4√13
⇒ √3x + y + 2√3 + 3 – 4√13 = 0

Question 29.
Find the equation of the tangent to x² + y² – 2x + 4y = 0 at (3, -1). Also, find the equation of tangent parallel to it. [(TS) May ’17]
Solution:
Given equation of the circle is x² + y² – 2x + 4y = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = -1, f = 2, c = 0
The given point P(x₁, y₁) = (3, -1)
∴ The equation of the tangent at P is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(-1) – 1(x + 3) + 2(y – 1) + 0 = 0
⇒ 3x – y – x – 3 + 2y – 2 = 0
⇒ 2x + y – 5 = 0
Centre of the circle, C = (-g, -f) = (1, -2)

Radius of the circle, r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(-1)^2+(2)^2+0}\)
= √5
The equation of the straight line parallel to the tangent 2x + y – 5 = 0 is
2x + y + k = 0 …….(1)
If (1) is a tangent to the given circle when r = d

The equations of tangents to the circle are from (1)
2x + y ± 5 = 0
One of these equations namely 2x + y – 5 = 0 is the tangent at (3, -1).
The tangent parallel to 2x + y – 5 = 0 is 2x + y + 5 = 0.

Question 30.
If 4x – 3y + 7 = 0 is a tangent to the circle represented by x² + y² – 6x + 4y – 12 = 0 then find the point of contact.
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get, g = -3, f = 2, c = -12
Centre of the circle, C = (-g, -f) = (3, -2)
Given equation of the tangent is 4x – 3y + 7 = 0
Let the point of contact be P = (h, k)

Now, P(h, k) is the foot of the perpendicular from the centre, C(3, -2) to the tangent 4x – 3y + 7 = 0

Question 31.
Find the equation of the normal to the circle x² + y² – 4x – 6y + 11 = 0 at (3, 2). Also, find the other point where the normal meets the circle.
Solution:
Given equation of the circle is x² + y² – 4x – 6y + 11 = 0

Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -3, c = 11
Given point P(x₁, y₁) = (3, 2)
Centre of the circle C(-g, -f) = (2, 3)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) + (- 2) (x + 3) – 3(y + 2) + 11 = 0
⇒ 3x + 2y – 2x – 6 – 3y – 6 + 11 = 0
⇒ x – y – 1 = 0
Slope of the tangent at P is m = \(\frac{-1}{-1}\) = 1
Slope of the normal at P is \(\frac{-1}{m}=\frac{-1}{1}\) = -1
∴ The equation of the normal at P is
y – y₁ = \(\frac{-1}{m}\) (x – x₁)
⇒ y – 2 = -1(x – 3)
⇒ y – 2 = -x + 3
⇒ x + y – 5 = 0
Other point of the normal Q = (x, y)
The centre of the circle is the midpoint of P and Q (point of intersection of normal and circle)
∴ C(2, 3) = Midpoint of PQ

∴ The normal at (3, 2) meets the circle at (1, 4).

Question 32.
Find the equation of the normal to the circle x² + y² – 10x – 2y + 6 = 0 at (3, 5). Also, find the other point where the normal meets the circle.
Solution:
Given equation of the circle is x² + y² – 10x – 2y + 6 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -5, f = -1, c = 6
The given point P(x₁, y₁) = (3, 5)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(5) + (-5) (x + 3) + (-1) (y + 5) + 6 = 0
⇒ 3x + 5y – 5x – 15 – y – 5 + 6 = 0
⇒ -2x + 4y – 14 = 0
⇒ x – 2y + 7 = 0
The slope of the tangent at P is m = \(\frac{-\mathrm{a}}{\mathrm{b}}=\frac{-1}{-2}=\frac{1}{2}\)
The slope of the normal at P is \(\frac{-1}{\mathrm{~m}}=\frac{-1}{\frac{1}{2}}\) = -2
∴ The equation of the normal at P(3, 5) is
\(\mathrm{y}-\mathrm{y}_1=\frac{-1}{\mathrm{~m}}\left(\mathrm{x}-\mathrm{x}_1\right)\)
⇒ y – 5 = -2(x – 3)
⇒ y – 5 = -2x + 6
⇒ 2x + y – 1 = 0

Question 33.
Find the locus of P, where the tangents drawn from P to x² + y² = a² include an angled α.
Solution:
Given the equation of the circle is x² + y² = a²

Comparing this equation with x² + y² = r²
We get r = a
Let P(x₁, y₁) be a point on the locus.
The length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

Question 34.
If ax + by + c = 0 is polar of (1, 1) w.r.t x² + y² – 2x + 2y + 1 = 0 and HCF of a, b, c is equal to one, then find a² + b² + c².
Solution:
Given equation of the circle is x² + y² – 2x + 2y + 1 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0,
We get g = -1, f = 1, c = 1
Let, the given point P(x₁, y₁) = (1, 1)
The equation of polar of (1, 1) w.r. t to the given circle is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(1) – 1(x + 1) + 1(y + 1) + 1 = 0
⇒ x + y – x – 1 + y + 1 + 1 = 0
⇒ 2y + 1 = 0
Given equation of the polar is ax + by + c = 0, then
a = 0, b = 2, c = 1
The H.C.F of a, b, c is equal to ‘1’.
Now a² + b² + c² = (0)² + (2)² + (1)²
= 0 + 4 + 1
= 5

Question 35.
If the polar of the points on the circle x² + y² = a² with respect to the circle x² + y² = b² touches the circle x² + y² = c², then prove that a, b, c are in Geometric Progression.
Solution:
Given the equation of the first circle is x² + y² = a²

Let P(x₁, y₁) be any point on the circle x² + y² = a², then
\(\mathrm{x}_1^2+\mathrm{y}_1^2=\mathrm{a}^2\) ……….(1)
The equation of the second circle is x² + y² = b²
The polar of P(x₁, y₁) w.r.t the second circle x² + y² = b² is S₁ = 0
xx₁ + yy₁ – b² = 0 ……..(2)
The equation of the third circle is x² + y² = c²
Centre C = (0, 0); Radius r = c
Since (2) is a tangent to the circle x² + y² = c² then r = d
c = \(\frac{\left|\mathrm{x}_1(0)+\mathrm{y}_1(0)-\mathrm{b}^2\right|}{\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2}}\)
⇒ c = \(\frac{\left|-b^2\right|}{\sqrt{a^2}}\)
⇒ c = \(\frac{\mathrm{b}^2}{\mathrm{a}}\)
⇒ b² = ac
∴ a, b, c are in geometric progression.

Question 36.
Find the slope of the polar of (1, 3) with respect to the circle x² + y² – 4x – 4y – 4 = 0. Also, find the distance from the centre of it.
Solution:
Given equation of the circle is x² + y² – 4x – 4y – 4 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -2, c = -4
Centre of the circle C = (-g, -f) = (2, 2)
Let the given point be P(x₁, y₁) = (1, 3)
The equation of polar of (1, 3) w.r.t the given circle is S1 = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(3) – 2(x + 1) – 2(y + 3) – 4 = 0
⇒ x + 3y – 2x – 2 – 2y – 6 – 4 = 0
⇒ -x + y – 12 = 0
⇒ x – y + 12 = 0
The slope of the polar is m = \(\frac{-\mathrm{a}}{\mathrm{b}}=\frac{-1}{-1}\) = 1
The perpendicular distance from the centre C(2, 2) to the polar x – y + 12 = 0 is

Question 37.
Show that, four common tangents can be drawn for the circles given by x² + y² – 14x + 6y + 33 = 0 and x² + y² + 30x – 2y + 1 = 0 and find the internal and external centres of similitude. [(TS) Mar. ’19]
Solution:
Given equations of the circles are
x² + y² – 14x + 6y + 33 = 0 ……..(1)
x² + y² + 30x – 2y + 1 = 0 ………(2)
For the circle (1), Centre C₁ = (7, -3)

Now r₁ + r₂ = 5 + 15 = 20 = √400
∴ C₁C₂ > r₁ + r₂
∴ The given circles are each circle lies completely outside the other circle.
∴ No.of common tangents = 4

The internal centre of similitude A₁ internally divides C₁C₂ in the ratio r₁ : r₂ (5 : 15 = 1 : 3).
∴ The internal centre of similitude

The external centre of similitude A₂ divides C₁C₂ in the ratio r₁ : r₂ (5 : 15 = 1 : 3) externally.

∴ The external centre of similitude

Question 38.
If a point P is moving such that the lengths of the tangent drawn from ‘P’ to the circle x² + y² + 8x + 12y + 15 = 0 and x² + y² – 4x – 6y – 12 = 0 are equal, then find the equation of the locus of P. (Mar. ’09)
Solution:
Given equations of the circles are
x² + y² + 8x + 12y + 15 = 0
x² + y² – 4x – 6y – 12 = 0

Let P(x₁, y₁) be any point on the locus.
PA, PB be the lengths of the tangent from P to the circles (1) & (2) respectively.
Given condition is PA = PB

The equation of the locus of ‘P’ is 12x + 18y + 27 = 0
⇒ 4x + 6y + 9 = 0

Question 39.
Find the inverse point of (-2, 3) with respect to the circle x² + y² – 4x – 6y + 9 = 0.
Solution:
Given equation of the circle is x² + y² – 4x – 6y + 9 = 0

Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get, g = -2, f = -3, c = 9
Let, the given point P(x₁, y₁) = (-2, 3)
Now, the polar of P(-2, 3) w.r.t. the given circle is S₁ = 0.
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-2) + y(3) – 2(x – 2) – 3(y + 3) + 9 = 0
⇒ -2x + 3y – 2x + 4 – 3y – 9 + 9 = 0
⇒ -4x + 4 = 0
⇒ x – 1 = 0
Let Q(h, k) be the inverse point of P(-2, 3) w.r.t. the circle x² + y² – 4x – 6y + 9 = 0.
Now, Q(h, k) is the foot of the perpendicular from P(-2, 3) w.r.t. x – 1 = 0

∴ The inverse point of (-2, 3) is (1, 3).

Here students can locate TS Inter 2nd Year Physics Notes 14th Lesson Nuclei to prepare for their exam.

TS Inter 2nd Year Physics Notes 14th Lesson Nuclei

→ Nearly 99.9% of mass of atom is concentrated in a small volume called Nucleus.

→ Radius of atom is nearly 10,000 times more than radius of nucleus.

→ Volume of nucleus is nearly 10^-12 times less than volume of atom.

→ Atomic mass unit (1u): 1 /12th mass of ¹²₆C atom is taken as “atomic mass unit”.
1.u = \(\frac{1.992647 \times 10^{-26}}{12}\) = 1.660539 x 10^-27

Energy equivalent of 1u = 931.5 MeV.

→ Isotopes: The nuclei having the same atomic number (Z) but different mass number (A) are called “isotopes”. Ex: ₈O¹⁶, ₈O¹⁷, ₈O¹⁸.

→ Isobars: The nuclei having the same mass number (A) but different atomic numbers (Z) are called “isobars”. Ex: ¹⁴₆C, ¹⁴₇N

→ Isotones : The nuclei having same neutron number (N) but different atomic number (Z) are called “isotones”. Ex: ₈₀Hg¹⁹⁸, ₇₉¹⁹⁷Au.

→ Isomers : Nuclei having the same atomic number (Z) and mass number (A) but with different nuclear properties such as radio-active decay and magnetic moments are called “isomers”.
Ex: I₃₅⁸⁰ Br^m, ⁸⁰₃₅Br^g . Here ‘m’ denotes metastable state and ‘g’ denotes ground state.

→ Positive charge of nucleus is due to protons.

→ Toted charge of electrons in an atom is (- Ze) and that of protons is (+ Ze). Where Z is atomic number.

→ Neutron is a chargeless particle. Mass of neutron and mass of proton are almost equal.

→ A free neutron is unstable when it is outside the nucleus. Its mean life period is 1000 sec.

→ Inside nucleus neutron is stable.

→ Number of neutrons in an atom is (A – Z) where A is mass number and Z is “atomic number”.

→ Volume of nucleus is proportional to mass number V ∝ A (OR) \(\frac{4}{3}\)πR³ ∝ A ⇒ R = R₀A^1/3 where RQ is a constant. R₀ = 1.2 × 10^-15 m.

→ Density of nuclear matter is almost cons-tant. It is independent of mass number A.

→ Density of nuclear matter ρ_n = 2.3 × 10¹⁷ kg/m³.

→ Einstein mass .energy equation: From theory of relativity mass is treated as another form of energy. Relation between mass and energy is E = mc². Where c = Velocity of light = 3 × 10⁸ m/s.

→ In a nuclear reaction Law of conservation of energy states that the initial energy and, final energy are equal provided the energy associated with mass is also taken into account.

→ Mass defect: In every nucleus the theore-tical mass (M_T) is always less than practical mass (M). The difference of mass of nucleus and its constituents is known as “mass defect”. Mass defect Δm = [Zm_p + (A – Z) m_n] – M.

→ Binding energy : When a certain number of protons and neutrons are brought together to form a nucleus the certain amount of energy E_b is released.
The energy released while forming a nucleus is called “Binding energy E_b“. Binding energy = Δmc².
Note : We have to supply an amount of energy equals to E_b from outside to divide a nucleus into its constituents.

→ Nuclear force:

• A nuclear force is much stronger than the coulomb1 force between the charges or the gravitational force between masses.
• Nuclear force between two nucleons is distance dependent.
• From potential energy graph of a pair of nucleons these forces are found to be attractive forces when separation between nucleons is 0.8 Fermi or more. These forces are found to be repulsive forces when separation between nucleons is less than 0.8 Fermi.
• Nuclear forces are saturated forces.
• Nuclear forces does not depend on charge. So nuclear force between proton-proton, proton – neutron and neutron – neutron are equal.

→ Radioactive decay : The spontaneous disintegration of unstable nucleus is referred as “radioactivity or radioactive decay”.
When a nucleus undergoes radioactive decay three types of radioactive decay takes place.

• α – decay : In this process ₂⁴He nuclei are emitted.
• β – deay : In this process electrons or positrons are emitted.
• γ – decay : In this process high energy photons (E.M. Waves) are liberated.

→ Law of radioactive decay : Let N is the number of nuclei in a sample. The number of nuclei (ΔN) undergoing radioactive decay during the time ‘Δt’ is given by
\(\frac{\Delta \mathrm{N}}{\Delta \mathrm{t}}\) N or \(\frac{\Delta \mathrm{N}}{\Delta \mathrm{t}}\) = λN

Where λ is disintegration constant or decay constant.

→ Decay rate (R) or Activity: The total decay rate of a sample is the number of nuclei disintegrating per unit time.
∴ Total decay rate R = – \(\frac{\mathrm{dN}}{\mathrm{dt}}\) (OR)
R = R₀e^λt (or) R = λN (activity )
Total decay rate is also called activity.

→ Half – life period (T_1/2): The half-life period of a radioactive nuclide is the time taken for the number of nuclei (N) to become half of initial nuclei (N_o) i.e., N = \(\frac{\mathrm{N}_{\mathrm{o}}}{2}\).

→ Average life time : In a radioactive substance some nuclei may live for a long time and some nuclei may live for a short time. So we are using average life time T.

→ Becquerel (Bq): Becquerel is a unit to mea-sure radioactivity of a substance.
If a radioactive substance ungergoes 1 disintegration or decay per second then it is called Becquerel.

→ Curie: It is a unit to measure radioactivity of a substance.
If a radioactive substance undergoes 3.7 × 10¹⁰ decays per second then radioactivity of that substance is called curie.

Note:

• Curie is a very big unit. So generally millicurie is used to measure radioactivity,
• 1 Curie = 3.7 × 10¹⁰ Bq (Becquerel)

→ Alpha decay : In α – decay ₂He⁴ nuclie is emitted from given radioactive substance. So mass number of product nucleus (called daughter nucleus) is decreased by four units and atomic number is decreased by two units. Equation of α – decay is
^A_ZX → ^A-4_Z-2X + ⁴₂He (a-particle)

→ Average life time τ = \(\frac{\mathrm{T}}{0.693}=\frac{\text { Half }-\text { life period }}{0.693}\)

→ Power of nuclear reactor P = \(\frac{\text { Number of fission } \times \text { Energy per fission }}{\text { time }}\)
Or
P = \(\frac{n}{t}\) × E

Here students can locate TS Inter 2nd Year Physics Notes 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits to prepare for their exam.

TS Inter 2nd Year Physics Notes 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits

→ Classification of solids (based on resistance or conductivity)

→Metals : Solids with low resistivity (ρ) or high conductivity (σ) are called metals.
Resistivity (ρ) of metals is 10^-2 – 10^-8 ohm – m.
Conductivity (σ) of metals is 10² to 10⁸ S m^-1.

→ Semiconductors: For semiconductors the resistivity (ρ) and conductivity (σ) are in intermediate range.
Resistivity (ρ) is 10^-5 to 10⁶ Ω m ;
Conductivity (σ) is 10⁵ to 10^-6 S m^-1.

→ Insulators : For insulators the resistivity (ρ) is very high and conductivity (σ) is very less.
Resistivity (ρ) is 10¹¹ to 10¹⁹ Ω m ;
Conductivity (σ) is 10^-11 to 10^-19 Sm^-1.
Note: Resistivity is not the only criteria to classify solids. Many other factors are also taken into account.

→ Semiconductors :

• In semiconductor devices the supply and flow of charge carriers are within the solid itself.
• Semiconductors are again divided into two types.
  • Elemental semiconductors : Elements such as Germanium (Ge) and Silicon (Si) are called “elemental semiconductors”
  • Compound semiconductors: These are again two types.
    • Inorganic semiconductors such as CdS, GaAs, CdSe, InP etc.
    • Organic semiconductors such as anthracene, doped pthalocyanlnes etc. and
      Organic polymers such as polypyrrole, polyaniline etc.

→ Energy Bands:

• According to Bohr theory in an isolated atom the energy of any electron is decided by the orbit in which it revolves.
• When atoms come together to form a solid these energy levels will come close together or even they may overlap. As a result an electron will have different energy levels with continuous variation of energy, which leads to the concept of energy bands.
• Valence band: The energy band which incl-udes all the energy levels of valence electrons is called “valence band”.

→ Conduction band: The energy level above valence band is called “conduction band”.
If there is some gap between valence band and conduction band then electrons in valence band will be bounded and there are no free electrons in conduction band. Note : If the lowest energy level of conduction band coincides with highest energy level of valence band or if lowest energy level of conduction band is less than highest energy level of valence band then electrons can freely go to conduction band with no external energy this is the case with most of the solids.

→ Forbidden band : The energy gap between valence band and conduction band where we cannot see any electrons is called “for-bidden band”.
Note: In case of semiconductors forbidden band width is less than 3 eV. (For Germanium it is 0.7eV and for Silicon it is 1.1 eV). Because of this small gap even at room temperatures some electrons from valence band can acquire enough energy they will cross the forbidden gap and goes to conduction band due to this reason resistance of semiconductors is less.

→ Intrinsic semiconductors: Semiconductors with ultra high pure state are called “intrinsic semiconductors”.
In pure Germanium (Ge) or Silicon(Si) crystal every Germanium or Silicon atom forms four covalent bonds with neighbouring Ge/Si crystal.
At very low temperature, intrinsic semi-conductors are insulators when temperature increases electrons absorbs more thermal energy and it may become a free electron and that atom will become positive.
A free electron leaves a positive site called hole. Le., thermal energy effectively ionises a few atoms. •
In intrinsic semiconductors number of free electrons (n^ is equal to number of holes (n^) and current contribution by electrons (7J and holes (1^) is same.
∴ In an intrinsic semiconductor n_e = n_h = n₁
Total current I = I_e + I_h

→ Extrinsic semiconductors: A suitable amount of impurity is added to intrinsic semiconductor to promote its conductivity. Such type of semiconductors are called “extrinsic semiconductors” or “impure semi-conductors”.

→ Doping: The process of deliberate addition of impurities to intrinsic semiconductor to promote conductivity is called “doping”.

→ n – type semiconductors: When pentavalent impurities such as phosphorous (P), arsenic (As), antimony (Sb) are added to intrinsic semiconductors then they are called “n-type semiconductors”.
In these semiconductors current flows through negative charges (electrons) so they are called n-type.
Note : In n-type semiconductors majority charge carriers are “electrons”, minority charge carriers are “holes”.

→ p-type semiconductors : When trivalent impurities such as Boron (B), Aluminium (Al), Galium (Ga), Indium (In) etc. are added to intrinsic semiconductor then it is called “p type semiconductor”.
In these semiconductors current flows through positive charges called holes. So they are called p-type semiconductors.
Note : In p-type semiconductors majority charge carriers are “holes” and minority charge carriers are “electrons”.

→ p-n junction : A p-n junction is formed by adding a small quantity of pentavalent impurities in a highly controlled manner to a p-type silicon/germanium wafer.

→ During the formation of p-n junction diffusion and drift of charge carriers takes place.

→ In a p-n junction concentration of holes is high at p – side and concentration of electrons is high at n-side. Due to the concentration gradient between p-type and n-type regions holes diffuse to n-region and electrons diffuse to p-region. This leads to diffusion current.

→ Due to diffusion of electron an ionised donor is developed at n-region and due to diffusion of holes to n- region an ionised acceptor will develop at p-region. These ions are immobile. So some – ve charge is developed in p-region and positive charge is developed in n-region. This space charge prevents further motion of electrons and holes near junction.

→ Depletion layer : Both the negative and positive space charge regions near junction are called “depletion region”.

→ Drift: The motion of charge carriers due to the electric field is called drift. Current flowing due to drift of charges is called “drift current*.
Note : In a p-n junction total current is the sum of diffusion current and drift current. The direction of drift current is opposite to diffusion current.

→ In a p-n junction initially diffusion current is large and drift current is small.

→ In a p-n junction under equilibrium conduction there is no net current.

→ p-n junction forward bias: When external voltage ‘V is applied to a p-n junction such thatp-region is connected to ‘+ ve’ terminal and n region is connected to ‘-ve’ terminal then it is called “forward bias”.

→ p-n junction reverse bias : When external voltage V is applied to a p-n junction such that p – region is connected to ‘- ve’ terminal and n-region is connected to ‘+ve’ terminal then it is called “reverse bias”.

→ Rectifier : The process of converting alternating current (a.c) into direct current (d.c) is called “rectification”. Instruments used for rectification is called “rectifier”.
Note : A p-n junction diode can be used as a rectifier because it allows current to flow in one direction only. i.et, in forward bias it will conduct current whereas in reverse bias it does not allow current to pass through it.

→ Zener diode : A zener diode is a highly doped p-n junction with sharp break down voltage. Generally zener is operated in reverse bias condition.
Note: In forward bias condition zener diode will also act as ordinary p-n junction.

→ Transistor : A transistor is a three layered electronic device.
These layers are called emitter, base and collector.
Transistors are two types 1) p-n-p 2) n-p-n

→ Emitter: Emitter region is of moderate size. It is heavily doped. It supplies large number of majority charge carriers for the current flow through transistor.

→ Base : Width of base region is very less. It is lightly doped nearly with 3 to 5% impurity concentration of emitter.

→ Collector: Size of collector region is larger than emitter. It is moderately doped (i.e., impurity concentration is less than emitter).

→ Biasing of transistor : In a transistor for transistor action to takes place

• Emitter base region must be forward biased,
• Base collector region must be reverse biased,
• Forward bias emitter base potential V_EB must be Jess than reverse bias collector base potential V_CB.
• If a transistor is biased as above than the transistor is said to be in active state.

→ In a transistor emitter current (I_E) = Base current (I_B) + Collector current (I_C)
I_E = I_B + I_C
Hence transistor is a current controlled device.

→ Input resistance (r₁): It is defined as the ratio of change in emitter base voltage (ΔV_BE) to change in base current (AI_g) when collector-emitter voltage is constant.
Input resistance, r_i = \(\left[\frac{\Delta \mathrm{V}_{\mathrm{BE}}}{\Delta \mathrm{I}_{\mathrm{B}}}\right]_{\mathrm{V}_{\mathrm{CE}}}\)

→ Output resistance (r₀): It is defined as the ratio of change in collector- emitter voltage (ΔV_CE) to change in collector current (I_c) when base current (I_B) is constant.
Output resistance, r₀ = \(\left[\frac{\Delta \mathrm{V}_{\mathrm{CE}}}{\Delta \mathrm{I}_{\mathrm{C}}}\right]_{\mathrm{I}_{\mathrm{B}}}\)

→ Current amplification factor (β): It is defined as the ratio of change in collector current (I_c) to change in base current (I_B) when collector – emitter voltage (V_CE) is constant.
Current amplification, β = \(\left[\frac{\Delta \mathrm{I}_{\mathrm{C}}}{\Delta \mathrm{I}_{\mathrm{B}}}\right]_{\mathrm{V}_{\mathrm{CE}}}=\frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{B}}}\)

→ Transistor as a switch : By changing the emitter base potential a transistor can be operated as a switch. For a transistor when input emitter-base potential is less than 0.6 V it is in cut off mode i.e., output current is zero. If input V_i is more than 0.6V transistor is in active state and we will get output current.
This property of output voltage V₀ is high or low is used in switches.

→ Transistor as an amplifier: A transistor can be used as an amplifier in its active region. In this region output voltage v₀ increases drastically even for a small change in input voltage V_i.
In transistor amplifier the mid point of active region is taken as operating point (also called.lnput potential) on which varying signal voltage is superposed. This vanat ion is magnified at output side by a factor equak to amplification factor β.

→ Voltage amplification factor A_v: ¡fis defined as the ratio of output signal voltage (V₀) to in put signal voltage (V_i).
Voltage amplification, A_v = \(\left[\frac{v_0}{v_i}\right]_{v_{B B}}=\beta \frac{R_C}{R_B}\)
Note : Generally voltage amplification is given at common emitter configuration VBB is emitter – base voltage in common emitter configuration.

→ Feedback amplifier : When a part of the output of an amplifier is fed as input in emitter base circuit then it is called “feed back amplifier”.
Note : Generally feedback is achieved by inductive coupling or LC or RC networks.

→ Transistor oscillator: A transistor oscillator is also a feedback amplifier with a suitable value of inductance (L) and capacitor (C) at output side. A part of output of L.C circuit is given as feedback to emitter base circuit.

Frequency of oscillation, υ = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)

→ NOT gate : It has one input terminal and one output terminal. The output of NOT gate is the opposite of input i.e., if input is ‘O’ then output is T. If input is T then output is ‘0’.

→ OR gate: It consists of two input terminals and one output terminal. In this gate if any one input terminal is high then the output is also high as shown in truth table.

→ AND gate : It consists of two input terminals and one output terminal. In AND gate if both input signals are high (say A and B) then only output is high truth table is as shown.

→ NAND gate: It consists of two input terminals and one output terminal. NAND gate is a combination of AND gate and NOT gate. If any one of input signal (A or B) is ‘O’ we will get T as output.

→ NOR gate : It consists of two input terminals and one output terminal. NOR gate is a combination of OR gate and NOT gate. The output is the negative of OR gate as shown in truth table.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics

Very Short Answer Type Questions

Question 1.
What is Fresnel distance?
Answer:
Fresnel distance :
The term z = a²/λ is called “Fresnel distance”.

In explaining the spreading of beam due to diffraction we will use the equation z = a²/λ.

Where after travelling a distance zλ/a size of beam is comparable to size of slit (or) hole a’.

Question 2.
Give the justification for validity of ray optics.
Answer:
The wavelength of light is very small. For larger distances and objects of large size we will completely neglect the wave nature of light. In this case, we believe that light will travel in straight lines. Principles of geometry are used to explain various phenomena like reflection and refraction.

Fresnel distance z = a²/λ suggested that for distances far greater than ‘z’ ray optics is valid in the limit wavelength tends to zero.

Question 3.
What is polarisation of light?
Answer:
Polarisation :
It is a process in which vibrations of electric vectors of light are made to oscillate in a single direction.
Ex : Let a light wave is represented by y (x, t) = a sin (kx – ωt)
Here the displacement is in y – direction. So it is referred as y – polarised wave.

Question 4.
What is Malus’law? [TS May ’17]
Answer:
Mains’ Law :
Let two polaroids say P₁ and P₂ are arranged with some angle ‘0’ between their axes. Then intensity of light coming out of them is I = I₀ cos² θ

Where I₀ is intensity of polarised light after passing through 1^st polaroid P₁. This is known as Malus’ Law.

Question 5.
Explain Brewster’s law. [AP June 15; TS May 16]
Answer:
The angle of incidence i_B for which the reflected ray is plane polarised is called Brewster angle.

Explanation:
At Brewster angle i_B + r = \(\frac{\pi}{2}\)

∴ The tangent of Brewster’s angle tan (i_B) is equals to refractive index. This is called “Brewster’s Law” i.e, µ = tan i_B.

Question 6.
When does a monochromatic beam of light incident on a reflective surface get completely transmitted?
Answer:
Laser beam is a monochromatic light. Let a laser beam is passed through a polariser and made to fall on a prism with Brewster’s angle. Now rotate the polariser carefully, for a particular angle of incidence we can not get reflected ray from prism. Which implies that the total light is transmitted through prism.

Short Answer Questions

Question 1.
Explain Doppler effect in light. Distinguish between red shift and blue shift. [TS Mar. 19, 16; May 15; AP Mar. 16, June 15, May 18]
Answer:
Doppler’s effect in light :
When there is relative motion between source and observer then there is a change in frequency of light received by the observer.

Red shift :
If the source moves away from the observer then frequency measured by observer is less i.e., wavelength increases As a result wave length of received light moves towards red colour. This is known as “red shift”.

Blue shift :
When source of light is approaching the observer frequency of light received decreases, i.e., wavelength of light decreases. As a result wavelength of received light will move towards blue colour. This is known as “blue shift”.

Question 2.
What is total internal reflection? Explain the phenomenon using Huygens principle.
Answer:
Total internal reflection :
When light travels from denser medium to rarer medium then for angle of incidence i > i_c i.e., (critical angle) light rays are not able to cross boundary layer between the media and simply come back into the same medium. This phenomena is known as “total internal reflection”.

Explanation :
From Huygens wave theory velocity of light in medium is high. So refracted ray will bend towards normal.

When light rays are travelling from denser medium to rarer medium they will bend away from normal.

As angle of incidence ‘i’ increases then angle of refraction ‘r’ will also increase.

For a particular value of i angle of refraction r will become 90° this angle of incidence in denser medium is called critical angle.

When angle of incidence i > i_c (critical angle) the ‘r’ is more than 90° we cannot have any refracted ray. The incident ray will simply come back into the same medium. This is called total internal reflection.

Question 3.
Derive the expression for the intensity at a point where interference of light occurs. Arrive at the conditions for maximum and zero intensity. [AP Mar. 18, 16. 15; TS May 18, Mar. 15]
Answer:
In young’s experiment two pinholes (S₁, S₂) are made on a black card board with a separation’d’ between them. Light coming from a pinhole ‘S’ will fall on these two pinholes (S₁, S₂) and spherical waves are produced. A screen (G, G₁) is placed at a distance D from the slits. This is as shown in fig.

From theory of interference when the two light waves are superposed at ‘P’. We will get bright band when path difference is nλ we will get dark band when path difference is (n + \(\frac{1}{2}\))λ.

Condition for maximum intensity :
For maximum intensity path difference S₂P – S₁P = nλ
From fig . [S₂P]² – [S₁P]² =

or S₂P – S₁P = 2xd /(S₂P + S₁P) …………. (1)
When D >> and D >> d then S₂P + S₁P ≅ 2D
∴ S₂P – S₁P = \(\frac{2xd}{2D}\)nλ (or) x = nλ\(\frac{D}{d}\) ………….. (2)
For dark band or zero intensity
S₂P – S₁P = (n + \(\frac{1}{2}\))λ
From eq. (1)
∴ S₂P – S₁P = 2xd/S₂P + S₁P use S₂P + S₁P = 2D
For zero intensity
S₂P – S₁P = \(\frac{2xd}{2D}\) = (n + \(\frac{1}{2}\))λ
∴ x = (n + \(\frac{1}{2}\))λ \(\frac{D}{d}\) For dark band.
Where x is distance from centre of screen and n is a ‘+Ve’ integer.

Question 4.
Does the principle of conservation of energy hold for interference and diffraction phenomena? Explain briefly. [AP May 16 ; Mar. 17. 14]
Answer:
In case of interference and diffraction we are getting a series of dark and bright bands. While forming these bands with maximum and minimum intensity law of conservation of energy holds good.

In interference and diffraction pattern energy is redistributed, i.e,, energy is reduced in one region (dark band). This energy is superposed on another region. Where it appears bright.

So in interference and diffraction pattern redistribution of energy in the regions of dark and bright bands takes place. But there is no loss of energy or creation of energy. Hence these two phenomena will obey Law of conservation of energy.

Question 5.
How do you determine the resolving power of your eye? [AP Mar. 19, 17, May 14; TS Mar. 18]
Answer:
To find resolving power of eye draw black bands of equal width say 5mm with a separation of 0.5mm between them. Gradually increase the width of gap (white strip) between to black bands form 0.5 to 1mm and 1 mm to 1.5 mm etc. after every two white bands.

Paste that paper on a wall. Wnen your distance from wall is very high – you will see only a dark band, i.e., all dark bands merged into a single band. When you are approaching the wall the bands seems to be separated into two groups with one white band between them. Now measure distance ‘D’ from wall and also spacing between black bands, (d) (i.e., width of white band)

Resolving power of eye = d/D
In this way we can find resolving power of our eye.

Question 6.
Explain polarisation of light by reflection and arrive at Brewster’s law from it. [Mar. ’15]
Answer:
Polarisation by reflection :
When unpolarised light falls on the boundary layer separating two transparent media the reflected light is found to be partially polarised. The amount of polarisation depends on angle of incidence i.

When reflected ray and refracted ray are perpendicular the reflected ray is found to be totally plane polarised. The angle of incidence at this stage is known as Brewster angle.

Brewster’s Law :
The particular angle of incidence (i_B) for which the reflected ray is plane polarised is called “Brewster angle”.

Explanation :
At Brewster angle i_B + r = \(\frac{\pi}{2}\)

The tangent of Brewster’s angle tan (i_B) is equals to refractive index of the reflection medium. This is called “Breswter’s law”, i.e,

Question 7.
Explain polarisation by reflection with diagram and state Brewster’s law. [May ’16]
Answer:
When unpolarised light falls on the boundary of two transparent media then reflected light is found to be plane polarised. The electric vectors are vibrating perpendicular to plane of incidence.

The percentage of polarised light gradually increases with angle of incidence. For a particular angle of incidence the reflected light is totally plane polarised. This particular angle of incidence is called Brewester angle (i_B).

Brewster angle :
The angle of incidence for which the reflected light is totally plane polarised is called Brewster angle (i_B).
At Brewster angle
Refractive index n (or)

So the tangent of Brewster angle is numerically equals to refractive index of the medium on which light rays are falling. This is called “Brewster’s law”.

Question 8.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids.
Answer:
Let two polaroids say P₁ and P₂ are arranged one at the back of other. Allow unpolarised light to fall on PF first. The transmitted light through P₁ is made to fall on P₂.

When polaroid P₁ is rotated there is no change in the intensity of transmitted light. Intensity of unpolarised light after passing through P₁ is reduced to half of initial value.

Let the pass axis of polaroid P₂ makes on angle ‘θ’ with pass axis of polariod P₁. When θ = 0 i.e., the two pass axes coincides the ail the light entered P₂ will come out.

If polaroid P₂ is gradually rotated the intensity of light coming out of P₂ gradually decreases. It becomes zero when θ = \(\frac{\pi}{2}\) i.e., the two pass axes are perpendicular to each other.

Intensity of output light through polaroid P₂ will fallow the equation I = I₀ cos² θ.

Where I₀ is intensity of light coming from P₁

This equation I = I₀ cos² θ is called Malus’Law.

Long Answer Questions

Question 1.
What is Huygens Principle? Explain the optical phenomenon of refraction using Huygens principle.
Answer:
Huygens principle :
Each point of the wave front is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave. These wavelets emanating from the wavefront are usually referred to as secondary wavelets.

From Huygens principle, every wave is a secondary wave to the preceding wave.

Wavefront :
The locus of points which oscillate in phase is called “wavefront”. (OR)
A wave front is defined as a surface of constant phase.

Refraction of a plane wave :
Let PP’ is the boundary layer between the medium 1 and 2. Let AB is a plane wave falling on the boundary layer. Draw a normal at A to the boundary. Angle between A’ A and normal angle of incidence ‘i’. Draw normal to wave-front from A. It will touch at B. Let time taken by BC to reach boundary is t. Then BC = v₁t. Now draw a circle with radius R = v₂t from A.

Draw a tangent from C on to this arc. Now CE represents the wavefront of refracted ray in the medium 2.

If r < i, then velocity v₂ in the medium is less and refracted ray will bend towards normal.

Let c’ is velocity of light in vacuum then n₁ = \(\frac{c}{v_1}\) and n₂ = \(\frac{c}{v_2}\). Then n₁ sin i = n₂ sin r. This is known as Snell’s Law.

If λ₁ and λ₂ represent the wavelengths, then

Hence in refraction wavelength λ and velocity v will decrease. But frequency ‘v’ is constant.

Question 2.
Distinguish between Coherent and Incoherent addition of waves. Develop the theory of constructive and destructive interferences.
Answer:
Coherent waves :
In coherent waves at a particular point in the medium, the phase difference between the displacements produced by each wave is constant.

In case of Incoherent waves the phase difference between the two waves reaching a given point in medium changes with time.

Let two waves say y₁ = a cos ωt and y₂ = a cos ωt reaches a point ‘P’ in a medium.
Then resultant displacement y = y₁ + y₂ = 2a cos ωt

Intensity I = 4I₀ (Intensity α amplitude)

Constructive interference :
For constructive interference the two waves reaching the point P must be in same phase i.e., Φ = 0 or phase difference Φ must be 2π, 4π, …………. 2πn (or) path difference must be
λ, 2λ ……….. nλ.

Let the distance travelled by the two waves in reaching a point Q is S₁Q and S₂Q
Now S₂Q – S₁Q = λ
Then y₁ = a cos ωt and y₂ = a cos (ωt – π)
= a cos ωt.
∴ Due to super position of waves y= y₁ + y₂ = a cos ωt + a cos ωt = 2 a cos ωt
Intensity I = 4a² = 4I₀
But Intensity I₀ = a² and intensity I ∝ amplitude² (a²)

Destructive interference :
For destructive interference the two waves must reach the given point with a phase of π. i.e., a path difference of λ/2.
At point Q, Path difference of the two waves is S₂Q – S₁Q = λ/2.
∴ y₁ = a cos ωt and y₂ = a cos (ωt – π)

Now the two waves will suffer destructive interference and resultant amplitude is zero.
∴ Intensity I = 0

Theory :
Let two coherent waves have a constant phase difference Φ between them.
Then y₁ = a cos cot and y₂ = a cos (ωt + Φ)
Due to super position y = y₁ + y₂ = a cos ωt + a cos (ωt + Φ)
= a [cos ωt + cos (ωt + Φ)] = 2a cos (Φ/2) cos (ωt + Φ/2)
Amplitude of new wave is 2a cos (Φ/2)

Intensity I = (2 a cos Φ/2)² = 4a² cos² (Φ/2)
When Φ = 0, 2π, 4π even multiples of π we will get I = 4a².
This is called bright band.
When Φ = π, 3π ………. odd multiples of π i.e., (2n + 1) π then I = 0
This is called dark band.
When Incoherent waves are used their phase difference changes with time i.e., Φ is not constant. So we will use average values = 4I₀ < cos² Φ/2 >
cos Φ/2 oscillates between 0 to 1. So average value is 1/2
∴ Average value of intensity = 4I₀ × \(\frac{1}{2}\) = 2I₀
So intensities will just add up.

Question 3.
Describe Young’s experiment for observing interference and hence arrive at the expression for ‘fringe width’.
Answer:
In Young’s experiment light coming from a source is allowed to pass through a pin hole s’. The light coming form is made to fall on slits S₁ and S₂ made on a black card board. Separation between the slits is d’. Since S₁ and S₂ are illuminated from the same source light waves coming from S₁ and S₂ are coherent waves with some fixed phase difference.

Let a screen GG is placed at a distance ‘D’ from the black card board to observe interference pattern.

The spherical waves coming from S₁ and S₂ will interfere at a point ‘P’ on the screen. Let distance of ‘P’ from centre of screen is ‘x’.

Expression for fringe width :
To produce maximum intensity (bright band) the two light waves arriving at point P must be in phase, i.e., phase difference between them is ‘0’ or 2π, 4π ……….. This corresponds to a path difference of 0, λ, 2λ …………. nλ.
∴ Path difference = S₂P – S₁P = nλ ………… (1)
But from figure (S₂P)² – (S₁P)²

But x and d are very small when compared to distance between slit and screen D.

This is the condition for Bright Band.

Formation of dark band :
For formation of dark band the two light waves reaching the point ‘P’ must be out of phase i.e., Φ = π, 3π, 5π …………..
This corresponds to a path difference of λ/2, 3λ/2, 5λ/2 ………….
∴ For destructive interference path difference (\(\frac{n+1}{2}\))λ

Fringe width β :
It is defined as the separation between two consecutive dark or bright bands.

Question 4.
What is diffraction? Discuss diffraction pattern obtainable from a single slit.
Answer:
Diffraction :
Bending of light rays of sharp edges (say edge of a blade) is called “diffraction”.

Diffraction at single slit :
In young’s double slit experiment the double slit is replaced by a single narrow slit. Then on the screen a central maximum with alternate dark and bright bands of decreasing intensity are seen. These are called diffraction pattern.

Explantion :
Let LM is‘a narrow slit and a screen is placed at suitable distance. Draw a straight line through M on to the screen. It will touch the screen at C’.

The intensity of light at any point P on screen is due to the contributions from large number of coherent sources on the slit.

Let light waves reaches the point P’ from Land N
Path difference = NP – LP = NQ = a sin θ = aθ …………… (1)
(θ is very small sin θ = θ)
At central point ‘C’ on screen θ = 0. So path difference is zero. Hence all parts of slit will contribute in phase. As a result maximum intensity is produced.

Consider the first minima :
Minimum intensity is produced when a θ = λ or θ = λ/a.

Now divide the slit into two equal parts say LM and MN. For every point M₁ in the region LM there is a point M₂ in MN region. The phase difference between M₁M₂ is 180° or π radians. So light waves reaching the point P are out of phase and we will get minimum intensity.

Consider 1^st maxima :
Maxima will occur when θ = (n + \(\frac{1}{2}\)) λ/2 For 1^st maxima
n = 1
⇒ 0 = 3 λ/2 a. Let us imagine the space between MN is divided into three equal parts. Consider first two thirds of the slit. Path difference for the two ends of this region is
\(\frac{2}{3}\)a.θ = \(\frac{2}{3}\)a × \(\frac{3\lambda}{2a}\) = λ

Now divide this \(\frac{2}{3}\)^rd region into two equal points. For ever wave coming form 1^st \(\frac{1}{3}\)^rd region on there is a wave coming from 2nd \(\frac{1}{3}\)^rd region with a phase difference of 180°. So on reaching point P their vector sum of displacements is zero. Here intensity is zero. The only light received is from 3rd \(\frac{1}{3}\)^rd part for intensity between two minima. So we will get weak bright region.

In this way we are able to explain maxima and minima formed in diffraction pattern.

Question 5.
What is resolving power of Optical Instruments? Derive the condition under which images are resolved.
Answer:
Resolving power of optical instruments :
From principles of geometrical optics, a light beam will get focussed to a point. But due to diffraction effects we are getting a spot of finite size instead of a point.

In diffraction radius of central bright region

This small value of r₀ plays a vital role in fixing the resolving power of telescopes and microscopes.

Telescopes :
In telescopes if two stars are to be resolved clearly then

Where ‘λ’ is wavelength of light used and ‘a’ is the aperture or diameter of lens used. Due to this reason we are using object lens of large diameter for better resolution.

Microscopes :
In microscopes near point magnification m = D/f = 2 tan β
For two object points to be viewed clearly their image size must be v θ = v \(\frac{1.22\lambda}{D}\)

Objects with image size less than this can not be viewed clearly. So corresponding distances between them at object size

∴ Resolving power of microscope

Intext Question and Answer

Question 1.
Two slits are made 1 mm apart and the screen is placed 1 m away. What is the fringe separation when blue-green light of wavelength 500 nm is used?
Answer:
Fringe width β = \(\frac{D\lambda}{d}\). But distance of screen D = 1 m
Wave length λ = 500 nm = 5 × 10^-7 m ;
Separation between slits d = 1 mm = 1 × 10^-3 m

Question 2.
(a) The refractive index of glass is 1.5. What is the speed of light in glass? Speed of light in vacuum is 3.0 × 10⁸ m s^-1)
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Refractive index of glass, p = 1.5; Speed of light, c = 3 × 10⁸ m/s
Speed of light’in glass is given by the relation.

Hence, the speed of light in glass is 2 × 10⁸ m/s.

(b) The speed of light in glass is not independent of the colour of light.
The refractive index of a violet component of white light is greater than the refractive index of a red component. Hence, the speed of violet light is less than the speed of red light in glass. Hence, violet light travels slower than red light in a glass prism.

Question 3.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is λ/3?
Answer:
Let I₁ and I₂ be the intensity of the two light waves. Their resultant intensities can be obtained as:
∴ I’ = I₁ + I₂ + 2 \(\sqrt I_1I_2\) cos Φ
Where, Φ = Phase difference between the two waves
For monochromatic light waves ; Ii = I2
I’ = I₁ + I₂ + 2\(\sqrt I_1I_2\) cos Φ = 2I₁ + 2I₁ cos Φ
Phase difference = \(\frac{2 \pi}{\lambda}\) × Path difference
Since path difference = λ,; phase difference Φ = 2π
∴ I’ = 2I₁ + 2I₁ = 4I₁
Given, I = k ; ∴ I₁ = \(\frac{k}{4}\)

Question 4.
What is the Brewster angle for air to glass transition? (Refractive index of glass = 1.5.)
Answer:
Refractive index of glass µ= 1.5 ; Brewster angle = θ
Brewster angle is related to refractive index as: tan θ = µ
∴ θ = tan^-1(1.5) = 56.31°
Therefore, the Brewster angle for air to glass transition is 56.31°.

Question 5.
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
Answer:
Fresnel’s distance (z_F) is the distance for which the ray optics is a good approximation. It is given by the relation,

\(\mathrm{z}_{\mathrm{F}}=\frac{\mathrm{a}^2}{\lambda}\) ; Where, aperture width,
a = 4 mm = 4 × 10^-3 m
Wavelength’ of light, λ = 400 nm = 400 × 10^-9 m

Therefore, the distance for which the ray optics is a good approximation is 40 m.

Question 6.
In double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits?
Answer:
Wavelength of light used, 1 = 6000 nm = 600 × 10^-9 m
Angular width of a fringe θ = 0.1°
= 0.1 × \(\frac{\pi}{180}=\frac{3.14}{1800}\) rad
Angular width of a fringe is related to slit spacing (d) as:

Therefore, the spacing between the slits is 3.44 × 10^-4 m.

Question 7.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of nλ/a. Justify this by suitably dividing the slit to bring out the cancellation.
Answer:
Consider that a single slit of width d is divided into n smaller slits.
Width of each slit, d’ = \(\frac{d}{n}\)
Angle of diffraction is given by the relation,

Now, each of these infinitesimally small slit sends zero intensity in direction θ. Hence, the combination of these slits will give zero intensity.

Here students can locate TS Inter 2nd Year Physics Notes 16th Lesson Communication Systems to prepare for their exam.

TS Inter 2nd Year Physics Notes 16th Lesson Communication Systems

→ Communication is the act of transmission of information.

→ Electronic communication refers to faithful transfer of information or message in the form of electrical voltage or current from one point to another point.

→ World Wide Web (WWW) : Tim Berners – Lee invented the World Wide Web.
WWW may be regarded as the mammoth encyclopedia of knowledge accessible to everyone round the clock throughout the year.

→ Essentials of communication system: Every communication system has three essential elements. They are

• Transmitter
• Medium or Channel and
• Receiver.

→ In communication system transmitter and receiver are located at different places. Channel is the physical medium that connects them. Channel may consists of wires or optical fibres or even without wires called wireless transmission.

→ Purpose of transmitter is to convert the message signal produced by source into a form suitable for transmission through channel.

→ Receiver will convert the signals received through channel into a recognisable form of the original message signal.

→ Types of Communication: Communication is of two types.

• Point to point communication: Here one transmitter and one receiver are connected directly, signals can be exchanged between both of them. Ex: Telephone.
• Broadcast: In broadcast one transmitter is connected to many receivers. Here signals are unidirectional i.e., from transmitter to receiver only. Ex: Radio signals or Radio broadcasting.

→ Transducer: Any device that converts one form of energy into another form can be termed as “transducer”.
Ex : Microphone which converts sound waves into electrical signals.

→ Signal: It contains information in electrical form and suitable for transmitting through medium or channel.
Signals are two types :

• Analog signals which contains continuous variation of voltage or current.
• Digital signals con-tains two discrete states namely high (1) and low (0) out puts corresponds to 0, 1′ in binary system.

→ Noise: Noise is referred as unwanted signal present in the signal received.

→ Attenuation : The loss of strength of signal while propagating through a medium is known as “attenuation”.

→ Amplification: It is a process in which the strength of signal is increased i.e., ampli-tude of signal is increased.
Note : Amplification is necessary to com-pensate attenuation of signal in medium.

→ Range : It is defined as the maximum dis-tance between source and receiver upto which the signal can be received with sufficient strength.

→ Modulation: The process of superimposing a low frequency signal onto a high frequency carrier wave is known as “modulation”.
Note : Modulation is necessary for long range transmission of signals.

→ Demodulation: The process of recovering the superimposed signal from modulated carrier wave is called demodulation.

→ Repeater: A repeater is a combination of a receiver and transmitter. If receives signals through medium. Strength of signal is increased by amplification and again it will transmit the signals. Repeaters are highly useful to increase the range of transmission. Note : A repeater will retransmit the signals either with same carrier frequency equal to that of received signals or it may retransmit with some other carrier frequency.

→ Band width : It is the frequency difference between lowest and highest frequencies used.
Ex : Speech signals contains frequencies between 300 Hz to 3100 Hz. So band width of speech signal is 3100 – 300 = 2800.

→ Various band widths of transmission medium:

• Band width of coaxial cable is nearly 750 MHz. They are suitable for transmission upto 18 GHz frequency.
• Frequency range of transmission in optical fibre is 1 THz to 1000 THz. Band width of signals that can be transmitted is more than 100 GHz.

→ Propagation of E.M waves in space : The energy of a signal produced by transmitter is given to an antenna. Antenna will radiate the energy into space in the form of electromagnetic waves. Propagation of E.M waves in space is through different types.

→ Ground waves: For ground wave propagation attenuation on surface of earth is high. The magnitude of attenuation is proportional to frequency. Due to very high energy absorption of ground the ground wave propagation is limited to few kilometers from transmitting antenna. Range of ground wave propagation mainly depends on

• Strength or energy of transmitted signals
• Frequency of radiated signals.

→ Ionosphere: The upper part of our atmosphere is called ionosphere. At greater altitudes density of gases is less. The high energy radiation coming from sun ionizes the gas molecules in that region. Depending on ion concentration ionosphere is divided into many layers.

→ Troposphere: This region is nearly about 10 km from ground. It is formed during daytime and night-time also. It is suitable for propagation of V.H.F (Very High Frequencies).

→ D – layer: It is nearly at a height of 65 to 75 km. It is formed during daytime only. This zone will reflect L.F. signals, absorbs M.F and H.F signals to some extent.

→ E-layer: It is nearly at a height of 100 km above the earth. It is formed during day-time only. It helps for surface waves and reflects H.F waves.
Note : D-layer and E- layer zone is called stratosphere. The height of D and E layers depends on intensity of sun’s radiation.

→ Space wave: T.V. transmitting antennas are preferred to construct at elevated height such as hills or mountains and receiving antennas are placed at the top of buildings.

→ Antenna and its size: Trans miss ion of low frequency of voice signals (frequency range 20 Hz to 20,000 Hz) to longer distances is not possible because

• Energy associated with low frequency signals is less.
• For longer wavelength signals (low frequency) say voice signals of 20 kHz, the size of antenna is in the range of 15 km which is practically impossible.

Here students can locate TS Inter 2nd Year Physics Notes 8th Lesson Magnetism and Matter to prepare for their exam.

TS Inter 2nd Year Physics Notes 8th Lesson Magnetism and Matter

→ Earth behaves as a huge magnet with magnetic field pointing approximately along geographic north and south directions.

→ Every magnet has two poles namely North pole and South pole. Magnetic monopole is an imaginary concept.

→ Like poles will repel and unlike poles will attract

→ When a magnet is divided into two parts they will behave as two separate weak magnets.

→ Magnets can be made with iron and its alloys.

→ A bar magnet consists of north pole and south pole is also called magnetic dipole. Its behaviour is similar to an electric dipole of a positive and negative charge.

→ Magnetic field lines: The path followed by a free magnetic needle will represent a magnetic line of force.
Properties:

• Magnetic field lines are closed curves.
• The tangent to the field line at a given point represents the direction of net magnetic field (B) at that point.
• For a strong magnet or in a strong magnetic field these lines are denser. Around a weak magnet they are less in number.
• These lines donot intersect.

→ Bar magnet: Every bar magnet has north & south poles.

• Magnetic field lines of a bar magnet are similar to that of a solenoid of dipole moment M = NIA.
• Magnetic field for a far point on the axis of a bar magnet (B) = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{\mathrm{r}^3}\).
• On equatorial line of bar magnet
  B_E = \(\frac{\mu_0}{4 \pi}\left(\frac{M}{r^3}\right)\)
• e- For a magnetic dipole in a uniform magnetic field torque τ = m̅ x B̅ = mB sin θ.
  x = I\(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) = mB sin θ for small angles sin θ = 0.
  τ = mBθ; Time period of oscillation T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{mB}}}\)

→ Magnetic potential energy (U_m) : It is the work done by an external field to bring the magnetic poles to the given location or configuration from infinite distance.

• Magnetic potential energy U_m = -mB cos θ = m̅. B̅
• Magnetic potential energy U_m = -mB when θ = 0°.
• U_m is minimum (stable equilibrium). Magnetic potential energy Um is maximum when 0 = 180°.
• U_m maximum = mB (unstable equilibrium).

→ Gauss’s Law for magnetism : Gauss law states that the net magnetic flux through any closed surface is zero.

→ Earth’s magnetism: The magnetic field of earth is believed to arise due to electrical currents produced by convective motion of metallic fluids in outer core of earth. This effect is also known as the dynamo effect.

• The magnetic north pole of earth is at a latitude at 79.74° N and at a longitude of 71.8° W. It is some where in North Canada.
• The magnetic south pole of earth is at 79.74° S and 108.22° E in the Antarctica.

→ Magnetic declination (D) :
The magnetic meridian at a given place makes some angle (D) with true geographic north and south directions.

The angle between true geographic north to the north shown by magnetic compass is called “mag¬netic declination (or) simply declination (D).”
Note: Declination is more at poles and less at equator.

→ Angle of dip (or) inclination (I) : It is the angle of total magnetic field at a given place with the surface of earth.
Note: At a given place horizontal component of earth’s magnetic field H_E = B_E cos I.
Vertical component of earth’s magnetic field Z_E = B_E sin I.
Tangent of dip tan I = \(\frac{\mathrm{Z}_{\mathrm{E}}}{\mathrm{H}_{\mathrm{E}}}\).

→ Magnetisation (I) : It is the ratio of net magnetic moment per unit volume.
I = \(\frac{m_{\text {net }}}{V}\); Where m_net = the vectorial sum of magnetic moments of atoms in bulk material and V = volume of the given material.
Magnetic intensity is a vector, dimensions L^-1A.
Unit: Ampere/metre : A m^-1.

→ Magnetic intensity (H) : The ratio of magnetic field (B₀) to the permeability of free space (µ₀) is called “magnetic intensity”.
Magnetic intensity H = \(\frac{B_0}{\mu_0}\).

→ Solenoid, magnetic intensity and magnetic field B:
For a solenoid with the interior material of zero magnetisation material B₀ = µ₀nl. or H = \(\frac{B_0}{\mu_0}\) = nl.

→ If solenoid is filled with a material of non¬zero magnetisation material then
B = B₀ + B_m Where B_m = magnetic field due to core material. ‘
B_m = µ₀g M then H = \(\frac{\mathrm{B}}{\mu_0}\) – M

→ Magnetic susceptibility (χ) : Susceptibility is a measure for the response of magnetic materials to an external field.
χ = \(\frac{\mathrm{I}}{\mathrm{H}}=\frac{\text { Magnetic intensity }}{\text { Magnetisation }}\)
It is a dimensionless quantity.
Note : Relative permeability µ_r = 1 + χ

→ Relation between µ, µ_r and χ:
In magnetism the three quantities µ, µ_r and χ are connected with the relation
µ = µ_r(1 + χ)

→ Magnetic properties of matter : All substances are magnetically divided into three types depending on the property susceptibility (χ).
I If χ is -ve ⇒ it is dia-magnetic substance.
If χ is positive and very small ⇒ it is paramagnetic substance.
I If χ is positive and large ⇒ it is ferro-magnetic substance.

→ Diamagnetic substances:

• For these substances susceptibility x is -ve.
• In a magnetic field they will tend to travel from strong field to weak field.
• They seems to be repelled by magnets.
• For diamagnetic substances the resultant angular momentum of atoms is zero.
• Superconductors are most exotic dia-magnetic substances. For super conductors χ = -1 and µ_r = 0.
  Ex: Bismuth, Copper, Lead, Silicon etc. Note : The phenomenon of perfect diamagnetism in superconductors is called Meissner effect.

→ Paramagnetism:

• These substances are feebly attracted by magnets.
• The susceptibility (χ) of these substances is +ve and nearly equals to one.
• In a magnetic field these substances will move from weak field to strong field.
• Individual atoms posses permanent magnetic dipole moment. But due to random thermal motion of atoms net magnetic moment is zero.
• Magnetisation of paramagnetic substance is given by M = C\(\frac{B_0}{T}\) and χ = C\(\frac{\mu_0}{\mathrm{~T}}\)
  where ‘C’ = Curie constant.
  Ex : Aluminium, Sodium and Calcium etc.

→ Ferromagnetism:

• Ferromagnetic substances are strongly attracted by magnets.
• The susceptibility (χ) is +ve and very large.
• Individual atoms of these substances will spontaneously align in a common direction over a small volume called domain.
• Size of domain is nearly 1 mm³ or a domain may contain nearly 10¹¹ atoms.
• In these substances magnetic field lines are very crowded.
• Every ferromagnetic substance will transform into paramagnetic substance at a temperature called Curie Tempe¬rature (Tc).
  Ex: Manganese, Iron, Cobalt, Nickel etc.

→ Hysteresis loop : Magnetic hysteresis loop is a graph between magnetic field (B) and magnetic intensity (M) of a ferromagnetic substance.

→ Retentivity or Remanence : The magnetic intensity (H) of a material at applied magnetic field B = 0 is called retentivity. In hysteresis loop value of H on +ve Y-axis i.e., at B = 0 gives retentivity.

→ Coercivity: The -ve value of’magnetic field – (B) applied (i.e., in opposite direction of magnetisation) at which the magnetic intensity (H) inside the sample is zero is called “coercivity”. In hysteresis diagram the value of B on -ve X-axis gives coercivity.

Telangana TSBIE TS Inter 2nd Year Physics Study Material 2nd Lesson Ray Optics and Optical Instruments Textbook Questions and Answers.

TS Inter 2nd Year Physics Study Material 2nd Lesson Ray Optics and Optical Instruments

Very Short Answer Type Questions

Question 1.
Define focal length and radius of curvature of a concave lens.
Answer:
Focal length (f) :
The distance between centre of lens and principle focus is called “focal length (f)”

Radius of curvature :
The distance between centre of lens to centre of curvature is called “Radius of curvature” (R).

Question 2.
What do you understand by the terms ‘focus’ and ‘principal focus’ in the context of lenses?
Answer:
Principal focus :
When a paraxial beam of light making small angle with principal axis falls on a lens, after refraction the refracted rays will converge at a point or they appear to diverge from a point on principal axis. This point is called “principal focus”.

Focus :
When parallel rays making some angle with principal axis passes through a lens then after refraction they will converge at a point in a plane passing through F and perpendicular to principal axis called focal plane.

This point of convergence or divergence in a focal plane is called focus. If the focus is on principal axis it is called principal focus.

Question 3.
What is optical density and how is it different from mass density?
Answer:
An optically denser medium is one in which velocity of light is less.

An optically rarer medium may have less mass density.
Ex: Mass density of turpentine is less than water but optical density of turpentine is more than water.

Question 4.
What are the laws of reflection through curved mirrors?
Answer:
Laws of reflection :

1. Angle of reflection is equais to angle of incidence (∠r = ∠i).
2. The incident ray, the reflected ray and normal to the reflecting surface lie in the same plane.

Question 5.
Define ‘power’ of a convex lens. What is [TS Mar., May 16; AP Mar. ’17, May 16]
Answer:
Power of a lens (P) :
Power of a lens is defined as the tangent of the angle by which it converges or diverges a beam of light falling at unit distance from the optical centre, i.e.
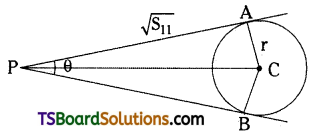
tan δ = \(\frac{h}{f}\), h = 1, δ = \(\frac{h}{f}\)
Power P = \(\frac{1}{f}\) unit: dioptre. Here f is in metre.

Question 6.
A concave mirror of focal length 10 cm is placed at a distance 35 cm from a wall. How far from the wall should an object be placed so that its real image is formed on the wall? [TS May ’19]
Answer:
Focal length (f) = 10 cm.
Image distance (v) = 35 cm
Position of object (u) = ?

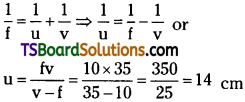
Object distance is from pole of mirror.
From wall the distance of the object
d = 35 – 14 = 21 cm.

Question 7.
A concave mirror produces an image of a long vertical pin, placed 40 cm from the mirror at the position of the object. Find the focal length of the mirror.
Answer:
Given the object and image are at a distance of 40 cm i.e., v = u = 40 cm
In concave mirror when object is at 2f then image is also at 2f ⇒ 2f = 40 cm
∴ Focal length of concave mirror = 20 cm.

Question 8.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism. [AP Mar. 19, 18, June 15]
Answer:
Angle of prism A = 4°.
Angle of deviation, d = 2.48°
Refractive index, n = 1 for small angled prism d = (n – 1) A
∴ 2.48 = (n – 1) 4
⇒ n – 1 = \(\frac{2.48}{4}\) n = \(\frac{2.48}{4}\) + 1 = 0.62 + 1 = 1.62
∴ n = 1.62.

Question 9.
What is ‘dispersion’? Which colour gets relatively more dispersed? [Mar., May ’14]
Answer:
Dispersion :
The phenomenon of splitting of light into its component colours is known as dispersion.

Dispersion takes place due to change in refractive index of medium for different wave lengths.

Bending of violet component of white light is maximum due to its short wavelength.

Question 10.
The focal length of a concave lens is 30 cm. Where should an object be placed so that its image is 1/10 of its size?
Answer:
Here f = – 30 cm, u = ? (For a concave lens)
m = \(\frac{v}{u}=\frac{1}{10}\)
v is – ve because virtual image is formed

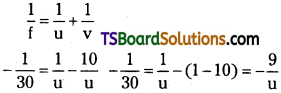
∴ u = 9 × 30 = 270 cm

Question 11.
What is myopia? How can it be corrected? [TS May 17, Mar. 17, 15, June 15; AP Mar., June ’15]
Answer:
Hypermyopia :
It is an eye defect. Where light rays coming from distant object are converged at a point infront of retina. This defect is called “short sightendness or Hyper myopia”, This defect can be compensated by using a concave lens.

Question 12.
What is hypermetropia? How can it be corrected? [AP May 17, Mar.’ 16; TS Mar. 18]
Answer:
Hypermetropia :
It is an eye defect. In this defect, eye lens focuses the incoming light at a point behind the retina. This is called “far sightedness or Hypermetropia”. This defect can be compensated by using a convex lens.

Short Answer Questions

Question 1.
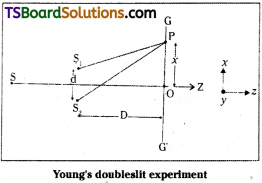
A light ray passes through a prism of angle A in a position of minimum deviation. Obtain an expression for (a) the angle of incidence in terms of the angle of the prism and the angle of minimum devia¬tion (b) the angle of refraction in terms of the refractive index of the prism.
Answer:
a) Let a light ray PQ enters the prism with angle of incidence i and emerges out with an angle ‘e’. When it is at minimum deviation position.
from quadrilateral AQNR
∠A + ∠QNR = 180° …………… (1)
In triangle QNR,
r₁ + r₂ + ∠QNR = 180° …………… (2)
From equation (1) and (2);
r₁ + r₂ = A ……………. (3)

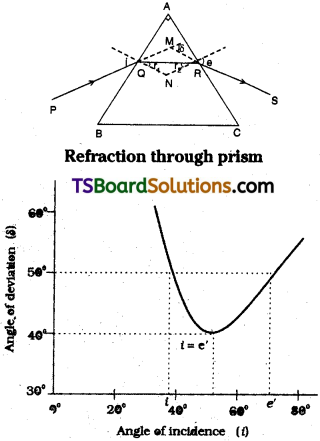
Deviation δ = (i₁ – r₁) + (i₂ – r₂)
= (i₁ + i₂) – r₁ + r₂
At minimum deviation position
i₁ = i₂ = p and r₁ = r₂ = r
∴ δ = i₁ + i₂ – A ⇒ 2i = A + δ
∴ i = \(\frac{A+\delta}{2}\) ……….. (4)

b) From equation (3) r₁ + r₂ = A.
∴ r₁ + r₂ = 2r = A ⇒ r = \(\frac{A}{2}\)

Question 2.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length. [AP Mar. ’19, ’17. May ’18, ’16]
Answer:
Focal length (f) :
The distance between principal focus and pole of mirror is called “focal length” (f).

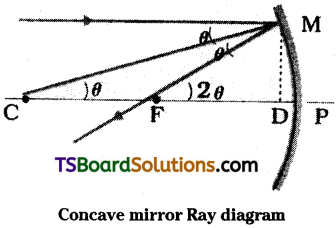
R = 2f proof:
Let ‘C’ be the centre of curvature of a concave mirror, ‘P’ be its pole and F be the principal focus. Line passing through P and F is called principal axis. Consider a ray parallel to principal axis falls on the mirror at ‘M’. After reflection, it passes through principal focus ‘F’. Join CM. It is perpendicular to mirror at M. Let angle of incidence is 0 and MD is the perpendicular at M. From principles of geometry

∠MCP = θ and ∠MFP = 2θ
Now tan θ = \(\frac{MD}{CD}\) = θ ………….. (1)
(∵ when θ is small tan θ = θ)
and tan 2θ = \(\frac{MD}{FD}\) = 2θ ………… (2)
From equation (1) and (2); FD = CD/2 ………….. (3)
But when D is very close to ‘P’
FD = FP & and CD = CP
∴ f = \(\frac{R}{2}\) ⇒ R = 2f
⇒ Radius of curvature R = 2 × focal length.

Question 3.
A mobile phone lies along the principal axis of a concave mirror longitudinally. Explain why the magnification is not uniform.
Answer:
Let a mobile phone is placed along the principal axis of a concave mirror longitudinally then magnification is not uniform.
Explanation :
Let the mobile phone is placed on principal axis as shown.

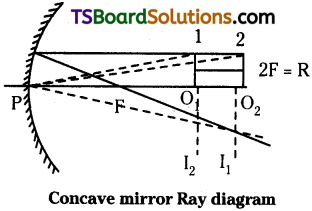
Let the points 1 and 2 will represent the two ends of mobile phone. For the end 1 object distance is PO₁ = u₁. For the end ‘2’ object distance is PO₂ = u₂. Light rays coming from nearer end will form more magnified image I₁ and light rays coming from remote point will form less magnified image I₂.

Because in mirrors \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Since f is same. When u increases v will decrease. So v₁ > v₂.

But linear magnification m = \(\frac{v}{u}\)
In first case m₁ = \(\frac{v_1}{u_1}\) and
in second casern m<₂ = \(\frac{v_2}{u_2}\)
Here v₁ > v₂ and u₁ < u₂ as a result m₁ > m₂.
So magnification of mobile phone placed longitudinally is not uniform.

Question 4.
Explain the Cartesian sign convention for mirrors.
Answer:
Cartesian sign convention :

1. All distances must be measured from the pole of the mirror (centre of Jens).
2. The distances measured along the direction of the incident ray are taken as positive and against the direction of incident ray are taken as negative.
3. Distances (heights) above the principal axis of mirror or lens are taken as positive and below are taken as ve’.

Question 5.
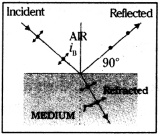
Define critical angle. Explain total internal reflection using a neat diagram. [AP Mar. 15. May 14; TS Mar. ’18. ’15, May 17]
Answer:
Critical Angle :
When the light travels from denser to rarer medium, for which angle of incidence, the angle of refraction is 90° is called critical angle of denser medium.

Explanation :
Consider two transparent media say 1 and 2. Where medium 1 is denser medium and medium 2 is a rarer medium.

Let light rays are starting from point A in denser medium. For angle of incidence i₁ they will strike the boundary layer say at ‘O₁‘. Draw normal at ‘O₁‘ when light rays are travelling from denser medium to they will bend away from normal so angle of refraction (r₁) greater than i₁.

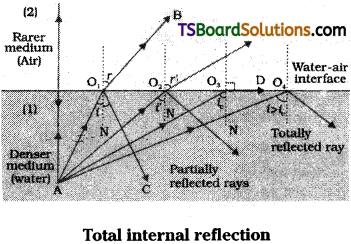
When angle of incidence is gradually increased then angle of refraction r₂ will also increase. For a particular angle of incidence ic angle of refraction r = 90° it is called critical angle.

For angle of incidence i > i_c there is no refracted ray in medium two. At this stage light rays are not able to penetrate the boundary layer so they will come back into 1st medium. This is called total internal reflection.

Question 6.
Explain the formation of a mirage. [TS Mar. 19, May 18; AP Mar. 16]
Answer:
Mirage are formed on hot summer days. On a hot summer day earth is heated due to heat radiation from sun. So air near the earth is heated its density will decrease and hot air goes up density. In this process, we will get a special atmosphere where low density air is near earth and its density gradually increases while going up.

Now light rays coming from sun will travel from denser air layers to less dense region (rarer medium). So they will continuously bend away from normal and undergoes total internal reflection.

As a result we will get inverted images of tall objects and an illusion as if there are ponds on high ways even though there is no wet surface. This type of illusion is called mirages.

Question 7.
Explain the formation of a rainbow.
Answer:
Rainbow :
Rainbow is due to dispersion of white light through water drops.

Condition to set Rainbow are 1) Sun should be shining at one side and rain should be at the other side of sky. Formation of rainbow is at least a three step process i.e., refraction – reflection and refraction i.e., light rays entering the water drop should suffer total internal reflection and comes out of the drop through refraction.

Explanation :
Sun lightis first refracted as it enters a rain drop. This causes the different wave lengths of white light to separate. Longer wavelengths (red colour) will bend less and shorter wavelengths (blue and violet colours) will bend more. These component rays will suffer total internal reflection inside the water drop at water – air boundary and again they will travel in water drop and finally they will come out of water drop after refraction.

In this way we will get rainbow on a rainy day when sun is shining at other end.

Question 8.
Why does the setting sun appear red? [AP Mar.’ 14, June ‘ 15; TS Mar.’ 17; May 15]
Answer:
Setting sun appears red due to scattering.

The amount of scattering is inversely proportional to fourth power of the wavelength. i.e, Amount of scattering αλ⁴. This is called Rayleigh’s formula.

Light of shorter wavelengths will scatter much more than light of longer wavelength. Due to this reason, blue light will scatter more than red light.

Rayleigh formula will hold good when size of the particles << λ. For particles of large size i.e., at water droplets, large dust particles etc., visible light of all wavelengths will scatter equally.

At sun set or at sun rise light rays will pass through a longer distances through atmosphere. In this process light of shorter wavelength is removed and light of longer wave length (Red) will suffer less scattering reaches our eye. As a result at sunrise and of sunset sun will appear red.

Question 9.
With a neat labelled diagram explain the formation of image in a simple microscope. [AP Mar. 18, 16, 15. May ’16. June 15; TS Mar., May 16]
Answer:
A single convex lens is used in a simple microscope. Here object distance is adjusted to be less than focal length of the convex lens used i.e., u < f. By proper adjustment of object distance final virtual image is made to form either at near point or at infinity.

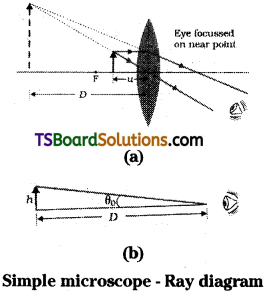
Angular magnification (m) = tan θ₀ = \(\frac{h}{d}\)
Where h’ is say height of image and ‘d’ is ‘d’ near point distance.
For maximum clarity eye will form image of parallel rays at near point.

When image is at near point:
Linear magnification m = \(\frac{v}{u}\) = 1 + \(\frac{D}{f}\) because final image is at near point D.

Question 10.
What is the position of the object for a simple microscope? What is the maximum magnification of a simple micro-scope for a realistic focal length?
Answer:
In simple microscope, object is placed in between centre of lens (C) and its principal focus (f). As a result a magnified virtual image is made to form either at near point or at infinity with suitable object distance ‘u’.

In simple microscope near point magnification m = (1 + D/f) when image is at infinity magnification m = D/f.

Magnification – Limits :
Theoretically, we can achieve very high magnification m’ for simple microscope. But due to practical consideration, we can not increase magnification beyond a limit.
Ex : For a magnification of 5 at for point focal length of convex lens
f = \(\frac{D}{m}=\frac{25}{5}\) = 5 cm
with this focal length thickness of lens is high, so dispersion takes place and chromatic aberration will come into account.

Even with a very careful design of convex lens we can not get a magnification of more than ten with simple microscope. Magnification of m = 5 to 10 is the possible limit.

Long Answer Questions

Question 1.
a) What is the cartesian sign convention? Applying this convention and using a neat diagram, derive an expression for finding the image distance using the mirror equation.
b) An object of 5 cm height is placed at a distance of 15 cm from a concave mirror of radius of curvature 20 cm. Find the size of the image.
Answer:
a) Cartesian sign convention :

1. All distances must be measured from the pole of the mirror (or) the optical centre of lens.
2. The distances measured along the direction of the incident ray are taken as positive and against the direction of incident ray are taken as negative.
3. The distances (heights) measured above the principal axis of mirror or lens are taken as positive and below are taken as ve’.

Mirror equation :
The relation \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\) is known as “mirror equation”.

Derivation of equation for image distance :

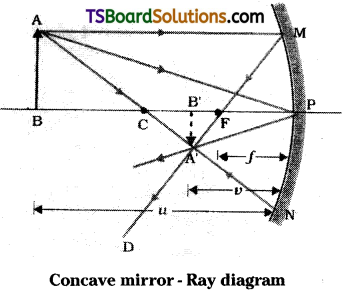
Let an object is placed infront of a con-cave mirror beyond centre of curvature then a real image is formed between f and c as shown in figure.

As per sign convention all distances must be measured from pole of mirror P.

∴ Focal length f = PF it is against to direction of incident ray so f is – ve.

Image distance from pole of mirror is v = PB’. It is measured against direction of incident ray so image distance v is – ve.

By applying sign convention to mirror equation \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\) becomes

b) Height of object (h) = 5 cm;
Object distance (u) = 15 cm
Radius of curvature (R) = 2f = 20 cm ⇒ f = 10 cm

Question 2.
a) Using a neat labelled diagram derive the mirror equation Define linear magnification.
b) An object is placed at 5 cm from a con¬vex is the position and nature of the image?
Answer:
a) Let an object AB is placed in front of a concave mirror beyond radius of curvature C’, The parallel ray comming from object after reflection at mirror (M) will pass through principal focus (F). The ray passing through centre of curvature falls normally on mirror at N. Intersection of these two rays will give position of image A’B’. This is as shown in figure.

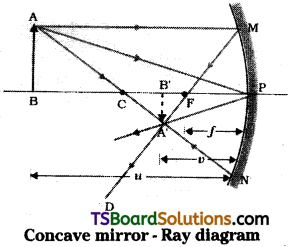
In figure Triangle A’B’ P and MPF are similar triangles by comparing ratio of sides

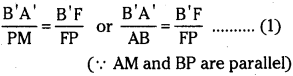
But triangles A ‘ B’ P and BAP are also similar.

In this equation
B’P Image distance B’P = v, FP = Focal length and BP = object distance = u.
∵ These distances measured from pole ‘P’ are against to direction of incident ray v is – ve, f is – ve and u is – ve.
By using these values in equation (3),

This is known as “mirror equation”.

Linear magnification :
The ratio of height of image (h’) to height of object (h) is called “linear magnification”.

Linear magnification, m = \(\frac{h’}{h}=\frac{-v}{u}\).

b) Object distance u = 5 cm; Focal length of convex lens f = 15 cm
Image distance v = ?

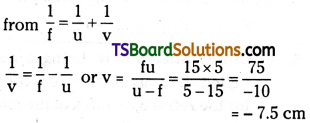
– ve sign indicates image is virtual image.
∴ Position of image is 7.5 cm infront of the lens.

3. a) Derive an expression for a thin double convex lens. Can you apply the same to a double concave lens too?
b) An object is placed at a distance of 20 cm from a thin double convex iens of focal length 15 cm, Find the position and magnification of the image.
Answer:
a) Refraction through double convex lens :
Refraction through double convex lens is studied in two steps.

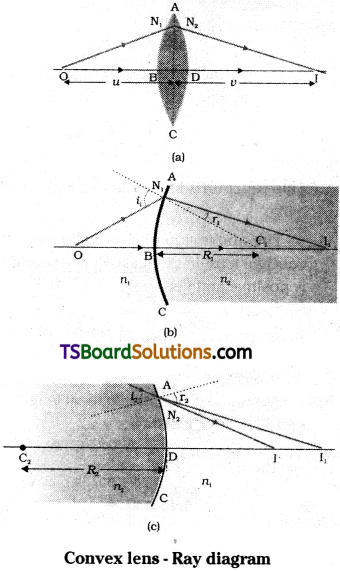
1st step :
Let the first surface will form the image of object ‘O’ at I₁ for this case
\(\frac{\mathrm{n}_1}{\mathrm{OB}}+\frac{\mathrm{n}_2}{\mathrm{BI}_1}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{BC}_1}\) ………. (1)
In 2nd step the second surface will form image at I where 1st image Ij will act as virtual object for 2nd surface,
∴ \(-\frac{\mathrm{n}_2}{\mathrm{DI_1}}+\frac{\mathrm{n}_1}{\mathrm{DI}}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{DC_2}}\) ………. (2)
For thin lens thickness, BD is small
so BI = D₁
By adding equaion (1) and (2)
\(\frac{n_1}{OB}+\frac{n_1}{DI}\) = (n₂ – n₁ [latex]\frac{1}{BC_1}+\frac{1}{DC_2}[/latex] …………… (3)
If point object is at infinity then OB = ∞ and DI = focal length f.

The distance BC₁ = + R₁ and DC₂ = – R₂ by using these values in equation (3)
\(\frac{n_1}{f}\) = (n₂ – n₁) (\(\frac{1}{R_1}-\frac{1}{R_2}\))

Here refraction is from air to glass so n₁ = 1 and n₂ = n₂₁
∴ \(\frac{1}{f}\) = (n₂₁ – 1) (\(\frac{1}{R_1}-\frac{1}{R_2}\))

This equation is known as lens makers formula.
The above equation is valid even for concave lens. In that case, R₁ is – ve and R₂ is positive and f is – ve.
So \(\frac{1}{f}\) = (n₂₁ – 1) (\(\frac{1}{R_1}-\frac{1}{R_2}\)) is vaild even for concave lens.

b) Object distance u = 20 cm; focal length f = 15 cm. Image distance v = ?

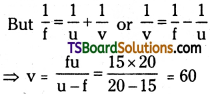
∴ Image distance v = 60 cm.
Magnification m = \(\frac{v}{u}=-\frac{60}{20}\) = 3

Question 4.
Obtain an expression for the combined focal length for two thin convex lenses kept in contact and hence obtain an expression for the combined power of the combination of the lenses.
Answer:
Let two thin lenses A, B with focal lengths f₁ and f₂ are in contact. Let ‘O’ is a point object on the principal axis. The first lens will form the image I₁ of the object

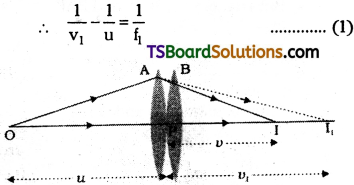
This first image I₁ will act as an object to second lens and final image I is produced.
∴ \(\frac{1}{v}-\frac{1}{v_1}=\frac{1}{f_2}\) ………….. (2)
by adding equation (1) and (2)
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_1}+\frac{1}{f_2}\).
But \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
Here the lens system is regarded as equivalent to a single lens of focal length ‘f’.
∴ \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
If there are n lenses in contact then equivalent focal length is given by

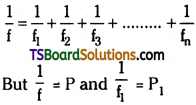
So interms of power,
P = P₁ + P₂ + P₃ + …………. + P_n
Equivalent focal length of lenses in contact is \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}+\frac{1}{f_3}+………….+\frac{1}{f_n}\)

Equivalent power of lens combination is
P = P₁ + P₂ + …………. + P_n.

Question 5.
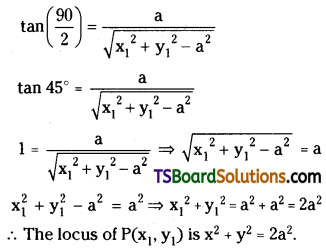
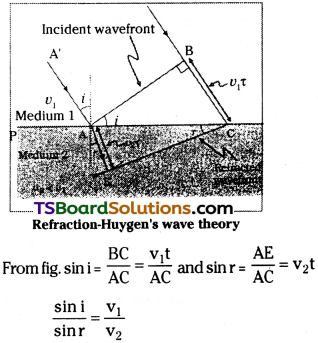
a) Define Snell’s Law. Using a neat la¬belled diagram derive an expression for the refractive index of the material of an equilateral prism.
b) A ray of light, after passing through a medium, meets the surface separating the medium from air to an angle of 45° and is just not refracted. What is the refractive index of the medium?
Answer:
a) Snell’s Law :
The ratio of sine of angle of incidence to sine of angle of refraction is constant for a given pair of media. i.e., sin i / sin r = n₂₁.
where n₂₁ is refractive index of 2nd medium w.r.to 1st medium.

Derivation of refractive index of prism :
Let ABC is the cross-section of a prism. AB and AC are refracting surfaces. ∠A is angle of prism. Let a light ray PQ falls on AB with angle of incidence i₁. After refraction path of light ray QR is parallel to prism base. RS is emergent ray with angle of emergence ‘e’. When PQ and RS are extended they will meet at M. Angle of deviation is δ. They are as show in figure.

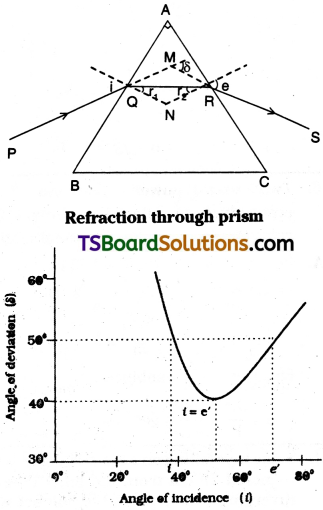
In figure, ∠A + ∠QNR = 180° …………. (1)
In triangle QNR,
r₁ + r₂ + ∠QNR = 180° ………….. (2)
From equation (1) and (2),
r₁ + r₂ = A ……………. I
Angle of deviation
δ = (i₁ – r₁) + (e – r₂) …………. (3)
Or δ = i₁ + e – A …………… (4)
At minimum deviation position i₁ = e and r₁ = r₂
and δ = δ_m by using these values
r₁ + r₂ = A
⇒ 2r = A
⇒ r = A/2 ………….. (5)
δ = i₁ + e – A = 2i₁ – A

b) Angle of incidence, I = 45°
Angle of refraction, r = 90° ⇒ i = i_c
Refractive index n₂₁ = \(\frac{1}{\sin C}=\frac{1}{\frac{1}{\sqrt{2}}}=\sqrt{2}\) = 1.414

Question 6.
Draw a neat labelled diagram of a compound microscope and explain its working. Derive an expression for its magnification.
Answer:
A compound microscope consists of two convex lenses mounted coaxially. Lens near the object is called objective. Focal length of objective is less.

Object lens forms a real, magnified image of the object. It will work as an object to eyelens.

Lens near the eye is called eye lens its focal length is high. It will form a magnified virtual final image at near point or at infinity. Final image is inverted w.r.t the original.

Ray diagram is as shown in figure. Dis-tance between objective and eye lens is called tube length ‘L’.

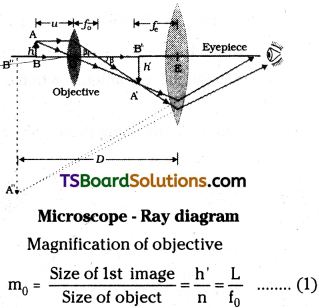
Eye lens will form the final image at infinity or a virtual image at near point.
Near point magnification of eye lens
m_e = (1 + \(\frac{D}{f_e}\)) …………….. (2)
When final image is at infinity Magnifcation of eye lens m_e = \(\frac{D}{f_e}\) …………… (3)
Total magnification of compound microscope m = m₀ . m_e.
∴ Total magnification
i) For final image at near point m = \(\frac{L}{f_0}\)(1+\(\frac{D}{f_e}\))
ii) For final image at infinity m = \(\frac{L}{f_0}.\frac{D}{f_e}\)
Magnification of compound microscope is very high.

Solved Problems

Question 1.
A light wave of frequency 4 × 10¹⁴ Hz and a wavelength of 5 × 10^-7m passes through a medium. Estimate the refractive index of the medium.
Answer:
Frequency (u) = 4 × 10⁴ C/S,
Wavelength (λ) = 5 × 10^-7 m, µ = ?

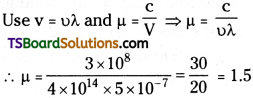
Question 2.
A ray of light is incident at an angle of 60 on the face of a prism of angle 30°. The emergent ray makes an angle of 30° with the incident ray. Calculate the refractive index of the material of the prism.
Answer:
Angle of incidence (i) = 60°;
Angle of prism (A) = 30°
Angle of deviation (d) = 30°
In prism i₁ + i₂ = A + d
⇒ 60 + i₂ = 30 + 30
⇒ i₂ = 0 ⇒ r₂ = 0
But r₁ + r₂ = A ⇒ r₁ + 0 = 30° or r₁ = 30°

Question 3.
Two lenses of power – 1.75D and + 2.25D respectively are placed in contact. Calculate the focal length of the combination.
Answer:
Power of 1st lens (P₁) = – 1.75 D;
Power of 2nd lens (P₂) = + 2.25 D
When in contact total power
P = P₁ + P₂ = – 1.75 + 2.25 = 0.5
Focal length of combination
f = \(\frac{100}{P}=\frac{100}{0.5}\) = 200 cm

Question 4.
Some rays falling on a converging lens are focussed 20 cm from the lens. When a diverging lens is placed in contact with the converging lens, the rays are focussed 30 cm from the combination. What is the focal length of the diverging lens?
Answer:
f_c = 20 cm
When combined with diverging lens light rays are focused at 30 cm
⇒ f_comb = 30 cm = F (say)

– ve sign indicates that it is a diverging lens.

Question 5.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism. [June ’15]
Answer:
Angle of prism (A) = 4°.
Angle of deviation (d) = 2.48°
Refractive index, n = 1 for small angled prism
d = (n₂₁ – 1) A
∴ 2.48 = (n₂₁ – 1) 4 ⇒ n₂₁ – 1 = \(\frac{2.48}{4}\)
n₂₁ = \(\frac{2.48}{4}\) + 1 = 0.62 + 1 = 1.62

Question 6.
A double convex lens of focal length 15 cm is used as a magnifying glass in order to produce an erect image which is 3 times magnified. What is the distance between the object and the lens?
Answer:
Focal length (f) = 15 cm;
Magnification (m) = 3 = v/u ⇒ v = 34

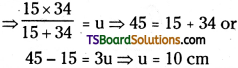
Question 7.
A compound microscope consists of an object lens of focal length 2 cm and an eyepiece of focal length 5 cm. When an object is placed at 2.2 cm from the object lens, the final image is at 25 cm from the eye lens. What is the distance between the lenses? What is the total linear magnification?
Answer:
Focal length of object lens (f₀) = 2 cm;
Object distance (u) = 2.2 cm

Question 8.
The distance between two point sources of light is 24 cm. Where should you place a converging lens, of focal length 9 cm, so that the images of both sources are formed at the same point?
Answer:
Given distance between sources = 24 cm;
Focal length of convex lens (f) = 9 cm
Both images are formed at same point i.e., image distance V is same. This will happen when one image is real and another is virtual.

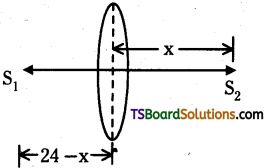
Case – I: Real image let object distance

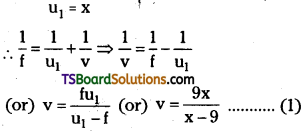
Case – II: Image is virtual then u₂ = 24 – x

⇒ x (x – 15) = (24 – x) (x – 9)
⇒ x² – 15x = 24x – 9 × 24 – x² + 9x (or) x² – 15x = – x² + 33x – 24 × 9;
⇒ 2x² – 48x + 24 × 9 = 0
∴ x² – 24x – 108 = 0 (or)
(x – 6) (x – 18) = 0
∴ x = 6 cm or x = 18 cm.

Question 9.
Find two positions of an object, placed in front of a concave mirror of focal length 15 cm, so that the image formed is 3 times the size of the object.
Answer:
Focal length of lens (f) = 15 cm;
Magnification (m) = 3 = \(\frac{v}{u}\) ⇒ v = 3u

or 15 × 4 = 60 = 45 ⇒ u = 20 cm.

Case II: Image may be virtual then v is – ve.

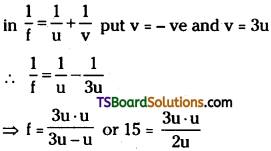
∴ 15 × 2 = 2u ⇒ u = 10 cm
The two positions of object are 10 cm, 20 cm.

Question 10.
When using a concave mirror, the magnification is found to be 4 times as much when the object is 25 cm from the mirror as it is with the object at 40 cm from the mirror, the image being real in each case. What is the focal length of the mirror?
Answer:
From given data, u₁ = 40 cm, u₂ = 25 cm

u₁v₁ (u₂ + v₂) = u₂v₂ (u₁ + v₁) ………… (2)
Put v₂ = 2.5 v₁ in equation (2)
∴ 40 v₁ (25 + 2.5 v₁) = 25 × 2.5 v₁ (40 + v₁)
1000 + 100 v₁ = 2500 + 62.5 v₁
⇒ (100 – 62.5) ₁ = 2500 – 1000
⇒ 37.5 ₁ = 1500 (or)

∴ Focal length of concave mirror f = 20 cm.

Question 11.
The focal length of the objective and eyepiece of a compound microscope are 4 cm and 6 cm respectively. If an object is placed at a distance of 6 cm from the objective, what is the magnification produced by the microscope?
Answer:
Focal length of objective (f₀) = 4 cm,
Focal length of eye lens (f_e) = 6 cm.
Object distance (u) = 6 cm.

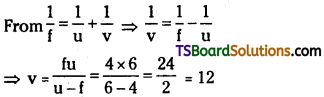
In microscope generally final image is a virtual image at near point. So magnification of eye piece m_e = (l+D/f_e)
Total magnification of microscope

Intext Question And Answer

Question 1.
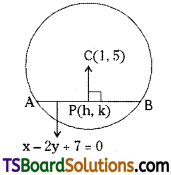
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
Answer:
Size of the candle (h) = 2.5 cm ;
Image size = h’
Object distance (u)= – 27 cm
Radius of curvature of the concave mirror (R) = – 36 cm
Focal length of the concave mirror,
f = \(\frac{R}{2}\) = – 18 cm;
Image distance = v
The image distance can be obtained using the mirror formula : \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)

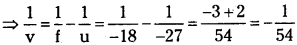
∴ v = -54 cm

Therefore, the screen should be placed 54 cm away from the mirror to obtain a sharp image.

The magnification of the image is given as:

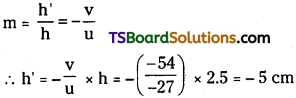
The height of the candle’s image is 5 cm. The negative sign indicates that the image is inverted and real.

If the candle is moved closer to the mirror, then the screen will have to be moved away from the mirror in order to obtain the image.

Question 2.
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
Answer:
Refractive index of glass (µ) = 1.55; Focal length of the double-convex lens, (f) = 20 cm Radius of curvature of one face of the lens = R₁
Radius of curvature of the other face of the lens = R₂
Radius of curvature of the double-convex lens = R
∴ R₁ = R and R₂ = – R
The value of R can be calculated as:

∴ R = 0.55 × 2 × 20 = 22 cm.
Hence, the radius of curvature of the double-convex lens is 22 cm.

Question 3.
A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm, and (b) a concave lens of focal length 16cm?
Answer:
In the given situation, the object is virtual and the image formed is real.
Object distance (u) = +12 cm
(a) Focal length of the convex lens, (f) = 20 cm Image distance = v
According to the lens formula, we have the relation:

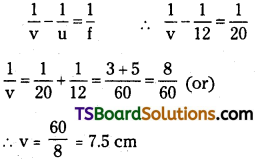
Hence the image is formed 7.5 cm away from the lens, toward its right.

(b) Focal length of the concave lens (f) = -16 cm Image distance = v
According to the lens formula, we have the relation:

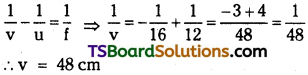
Hence, the image is formed 48 cm away from the lens, toward its right.

Question 4.
An object of size 3,0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
Answer:
Size of the object (h₁) = 3 cm;
Object distance (u) = – 14 cm
Focal length of the concave lens, (f) = – 21 cm;
Image distance = v
According to the lens formula, we have the relation :

Hence, the image is formed on the other side of the lens, 8.4 cm away from it. The negative sign shows that the image is erect and virtual.

The magnification of the image is given as:

Hence, the height of the image is 1.8 cm
If the object is moved further away from the lens, then the virtual image will move toward the focus of the lens, but not beyond it. The size of the image will decrease with the increase in the object distance.

Question 5.
What is the focal length of a convex lens of focal length 30 cm in contact with a concave lens of fqcal length 20 cm? Is the system a converging or a diverging lens? Ignore thickness of the lenses.
Answer:
Focal length of the convex lens (f₁) = 30 cm;
Focal length of the concave lens (f₂) = – 20 cm
Focal length of the system of lenses = f
The equivalent focal length of a system of two lenses in contact is given as :

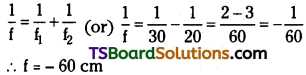
Hence, the focal length of the combination of lenses is 60 cm. The negative sign indicates that the system of lenses acts as a diverging lens.

Question 6.
A small telescope has an objective lens of focal length 144 cm and an eyepiece of focal length 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?
Answer:
Focal length of the objective lens (f₀) = 144 cm
Focal length of the eyepiece (f_e) = 6.0 cm
The magnifying power of the telescope is given as : m = \(\frac{f_0}{f_e}=\frac{144}{6}\) = 24

The separation between the objective lens and the eyepiece is calculated as :
f₀ + f_e = 144 + 6 = 150 cm
Hence, the magnifying power of the telescope is 24 and the separation between the objective lens and the eyepiece is 150 cm.

Question 7.
A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
Answer:
Actual depth of the pin (d) = 15 cm
Apparent depth of the pin = d’
Refractive index of glass, (µ) = 1.5
Ratio of actual depth to the apparent depth is equal to the refractive index of glass, i.e.,
µ = \(\frac{d}{d’}\) ∴ d’ = \({\frac{d}{\mu}}=\frac{15}{1.5}\) = 10 cm.

The distance at which the pin appears to be raised = d’ – d = 15 – 10 = 5 cm.

For a small angle of incidence, this dis¬tance does not depend upon the location of the slab.

Question 8.
The image of a small electric bulb fixec on the wall of a room is to be obtained on the opposite wall 3 in away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Answer:
Distance between the object and the image (d) = 3 m
Maximum focal length of the convex lens = f_max
For real images, the maximum focal length is given as:
m_max = \(\frac{d}{4}=\frac{3}{4}\) = 0.75 m
Hence, for the required purpose, the maximum possible focal length of the convex lens is 0.75 m.

Question 9.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
Answer:
Distance between the image (screen) and the object (D) = 90 cm
Distance between two locations of the convex lens (d) = 20 cm
Focal length of the lens = f
Focal length is related to d and D as :

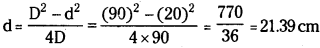
Therefore, the focal length of the convex lens is 21.39 cm.

Question 10.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
Answer:
The incident, refracted, and emergent rays associated with a glass prism ABC are shown in the given figure.

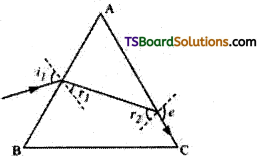
Angle of prism, ∠A = 60°;
Refractive index of the prism, µ = 1.524
i₁ = Incident angle;
r₁ = Refracted angle;
r₂ = Angle of incidence at the face AC
e = Emergent angle = 90°
According to Snell’s law, for face AC, we can have:

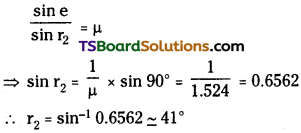
It is clear from the figure that angle
A = r₁ + r₂
∴ r₁ A – r₂ = 60 – 41 = 19°
According to Snell’s law, we have the relation:
\(\frac{\sin i_1}{\sin r_1}\)
⇒ sin i₁ = µ sin r₁ = 1.524 × sin 19° = 0.496
∴ i₁ = 29.75°
Hence, the angle of incidence is 29.75°.

Question 11.
You are given prisms made of crown glass and flint glass with a wide variety of angles. Suggest a combination of prisms which will
a) deviate a pencil of white light without much dispersion,
b) disperse (and displace) a pencil of white light without much deviation.
Answer:
a) Place the two prisms beside each other. Make sure that their bases are on the opposite sides of the incident white light, with their faces touching each other. When the white light is incident on the first prism, it will get dispersed. When this dispersed light is incident on the second prism, it will recombine and white light will emerge from the combination of the two prisms.

b) Take the system of the two prisms as suggested in answer (a). Adjust (increase) the angle of the flint-glass-prism so that the deviations due to the combination of the prisms become equal. This combination will disperse the pencil of white light without much deviation.

Question 12.
Does short sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodation? If not, what might cause these defects of vision?
Answer:
A myopic or hypermetropic person can also possess the normal ability of accommodation of the eye-lens. Myopia occurs when the eye-balls get elongated from front to back. Hypermetropia occurs when the eye-balls get shortened. When the eye-lens loses its ability of accommodation, the defect is called presbyopia.

Question 13.
A myopic person has been using spectacles of power – 1.0 dioptre for distant vision. During old age he also needs to use separate reading glass of power + 2.0 dioptres. Explain what may have happened.
Answer:
The power of the spectacles used by the myopic person (P) = – 1.0 D
Focal length of the spectacles,
f = \(\frac{1}{P}=\frac{1}{-1 \times 10^{-2}}\) = – 100cm

Hence, the far point of the person is 100 cm. He might have a normal near point of 25 cm. When he uses the spectacles, the objects placed at infinity produce virtual images at 100 cm. He uses the ability of accommodation of the eye-lens to see the objects placed between 100 cm and 25 cm. During old age, the person uses reading glasses of power, P’ = + 2D.

The ability of accommodation is lost in old age. This defect is called presbyopia. As a result, he is unable to see clearly the objects placed at 25 cm.

Question 14.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to? How is such a defect of vision corrected?
Answer:
In the given case, the person is able to see vertical lines more distincfly than horizontal lines. This means that the refracting system (cornea and eye-lens) of the eye is not working in the same way in different planes. This defect is called astigmatism. The person’s eye has enough curvature in the vertical plane. However, the curvature in the horizontal plane is insufficient. Hence, sharp images of the vertical lines are formed on the retina, but horizontal lines appear blurred. This defect can be corrected by using cylindrical lenses.

Question 15.
a) At what distance should the lens be held from the figure in Exercise 2.29 in order to view the squares distinctly with the maximum possible magnifying power?
b) What is the magnification in this case?
c) Is the magnification equal to the magnifying power in this case? Explain.
Answer:
a) The maximum possible magnification is obtained when the image is formed at the near point (d = 25 cm).
Image distance, υ = – d = – 25 cm; Focal length, f= 10 cm; Object distance = u
According to the lens formula, we have:

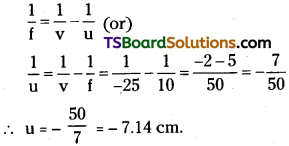
Hence, to view the squares distinctly, the lens should be kept 7.14 cm away from them.

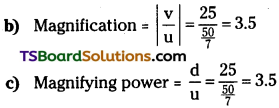
Since the image is formed at the near point (25 cm), the magnifying power is equal to the magnitude of magnification.

Here students can locate TS Inter 2nd Year Physics Notes 6th Lesson Current Electricity to prepare for their exam.

TS Inter 2nd Year Physics Notes 6th Lesson Current Electricity

→ Ohm’s Law: At constant temperature current (I) flowing through a conductor is proportional to the potential difference between the ends of that conductor.
V ∝ I ⇒ V = RI where R = constant called resistance. Unit: Ohm (Ω).

→ Conductors – Resistance:
Resistance: The obstruction created by a conductor for the mobility of charges through it is known as “resistance”.

• The resistance of a conductor (R) is proportional to length; R ∝ l → (1)
• and Inversely proportional to area of cross section of the conductor.
  R ∝ l → (2)
  From eq. (1) & (2) R ∝ \(\frac{l}{\mathrm{~A}}\) ⇒ R = \(\frac{\rho l}{\mathrm{~A}}\)
  ⇒ ρ = \(\frac{\mathrm{RA}}{l}\)
  where p = resistivity of the conductor.

→ Current density (J):
The ratio of current through a conductor to its area of cross-sec¬tion is called “current density (j).”
Current density (j) = \(\frac{\text { Current }}{\text { Area }}=\frac{I}{A}\)

Note:

• Potential V = IR = I\(\frac{\rho \cdot l}{\mathrm{~A}}\) = jρl
• Potential V = E.I. (Intensity of electric field x distance)
  ∴ EI = JpI or E = jp or j = \(\frac{E}{\rho}\) = Eσ
  where σ Is conductivity of the material.

→ Drift velocity (v_d): The speed with which an electron gets drifted in a metallic conductor under the application of external electric field is called “drift velocity (v_d).”

→ Drift Velocity v_d = \(\frac{-\mathrm{eE}}{\mathrm{m}}\)τ. Where τ = the average time between two successive collisions.
Note: Current density j = \(\frac{\mathrm{ne}^2}{\mathrm{~m}}\)τE and Conductivity = σ = \(\frac{\mathrm{ne}^2}{\mathrm{~m}}\)τ.

→ Mobility (μ): It is defined as the mag-nitude of drift velocity per unit electric field.
μ = \(\frac{\left|\mathrm{v}_{\mathrm{d}}\right|}{\mathrm{E}}\) But vd = \(\frac{\mathrm{e} \mathrm{E}}{\mathrm{m}}\) ⇒ μ = \(\frac{v_d}{E}=\frac{e \tau}{m}\)

→ Resistivity: Resistivity of a substance
ρ = \(\frac{\mathrm{RA}}{\ell}\)
It is defined as the resistance of a unit cube between its opposite parallel surfaces.
Resistivity depends on the nature of substance but not on its dimensions.
Unit: Ohm – metre (Ωm).

→ Temperature coefficient of resistivity:
The resistivity of a substance changes with temperature. ρ_T = ρ₀ [l + α(T – T₀)].
Where α = temperature coefficient of resistivity.
α = \(\)/°C

Note:

• For metals a Increases with temperature.
• For semiconductors and insulators a decreases with temperature.

→ Colour code: Carbon resistors have a set of coaxial coloured rings on them. It gives the value of that resistor along with tole¬rable limit.
On every carbon resistor four colour bands are printed. In some cases only Three colour bands are printed.
1st two bands from left to right gives the numerical values of that resistor.
3rd band gives number of zero’s to be put after first two digits.
Fourth band gives maximum allowed variation limit of that resistor called “tolerance”.

→ Colour code – Values:

• Black → 0;
• Brown → 1;
• Red → 2
• Orange → 3;
• Yellow → 4
• Green → 5
• Blue → 6;
• Violet → 7;
• Gray → 8;
• White → 9

→ Tolerance: Gold band – 5 %; Silver band -10 %. If there is no 4th band tolerance is 20%. Ex: A carbon resistor consists of Orange, green, green bands then its value is
1st orange = 3. 2nd band green = 5,
3rd green = 5
No Fourth band ⇒ tolerance is 20%
So for that resistor the value is 35 followed by five zero’s.
∴ Resistance of resistor is 3500000 Q
i. e., R = 3.5 Mega ohms with 20% tolerance.

→ Electrical Power (P): Energy dissipated per unit time is “power”.
In a conductor of resistance R’ while carrying a current I, this power produces heat in that conductor.
Power P = I²R = VI = V²/R. Unit: Watt.

→ Transmission power loss (P_c): Power wasted in transmitting lines P . While supplying electrical power from generator to consumer is P_c = I²R_c => P_c = \(\frac{\mathrm{P}^2 \mathrm{R}_{\mathrm{c}}}{\mathrm{V}^2}\)
i. e., power wasted in a line is inversely proportional to the square of voltage of line. P = total power to be transmitted.
∵ P_c ∝ \(\frac{1}{\mathrm{~V}^2}\) we are prefering high voltage transmission lines to reduce transmission power losses.

→ Resistors in series: When resistances are connected in series (1) Same current flows through all resistors.
Effective resistance (R_eff) is the sum of individual resistances i.e., R_eff = R₁ + R₂ + R₃ + ……………..
ii) Effective resistance R_eff is greater than the greatest value of resistor in that combination.

→ Resistors in parallel:

• When resistors are connected in parallel potential difference across all resistors is same.
• Effective resistance is given by \(\frac{1}{R_{\text {efl }}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)
• Effective resistance is less than least resistor in that combination.

→ Cells emf and Internal resistance: emf of a cell (ε):
The open circuit voltage between negative and positive terminals of a cell is called “emf of that cell”.

→ Internal resistance of cell (r):
In a cell current flows through electrolyte. Every electrolyte has some finite resistance.
The resistance offered by the cell for the flow of current through it is called “internal resistance of the cell (r).
Note: When a cell is connected in a circuit then potential difference across terminals is V = ε – ir
Current in the circuit i = ε/(R + r)
Where E = emf of cell, r = internal resis-tance and R = resistance of the circuit.

→ Cells in series:
Let two cells of emf ε₁ and ε₂ with internal resistance r₁, and r₂ are connected in series then
i. e., power wasted in a line is inversely proportional to the square of voltage of line. P = total power to be transmitted.
∵ P_c ∝ \(\frac{1}{\mathrm{~V}^2}\) we are prefering high voltage transmission lines to reduce transmission power losses.

→ Resistors in series: When resistances are connected in series (1) Same current flows through all resistors.
Effective resistance (R_eff) is the sum of individual resistances i.e., R_eff = R₁ + R₂ + R₃ + …………
ii) Effective resistance R_eff is greater than the greatest value of resistor in that combination.

→ Resistors in parallel:

• When resistors are connected in parallel potential difference across all resistors is same.
• Effective resistance is given by
  \(\frac{1}{\mathrm{R}_{\mathrm{efl}}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)
• Effective resistance is less than least resistor in that combination.

→ Cells emf and Internal resistance : emf of a cell (ε) : The open circuit voltage between negative and positive terminals of a cell is called “emf of that cell”.

→ Internal resistance of cell (r) : In a cell current flows through electrolyte. Every electrolyte has some finite resistance.
The resistance offered by the cell for the flow of current through it is called “internal resistance of the cell (r).”
Note: When a cell is connected in a circuit then potential difference across terminals is V = ε – ir
Current in the circuit i = ε/(R + r)
Where E = emf of cell,
r = internal resistance and
R = resistance of the circuit.

→ Cells in series: Let two cells of emf ε₁ and ε₂ with internal resistance r₁, and r₂ are

• total emf ε = ε₁ + ε₂
• total p.d across them
  V = ε₁ + ε₂ – i(r₁ + r₂)
• equivalent resistance r_eq = r₁ + r₂
• current in circuit I = \(\frac{\varepsilon_1+\varepsilon_2}{R+r_1+r_2}\)
• Due to series combination potential difference in the circuit increases.

Note : If n identical cells are connected in series emf ε = nε₁, I = nI₁, r_eff = n .r .
Where ε₁ = emf of single cell,
I₁ = current given by single cell in circuit
r = internal resistance of each cell.

→ Parallel combination of cells: Let two cells of emf ε₁ and ε₂ are connected parallel then

• Equivalent emf ε_eq = \(\frac{\varepsilon_1 \mathbf{r}_2+\varepsilon_2 r_1}{r_1+r_2}\)
• Equivalent resistance \(\left(\frac{1}{r_{\mathrm{eq}}}\right)=\frac{1}{r_1}+\frac{1}{r_2}\)
  ⇒ r_eq = \(\frac{r_1 r_2}{r_1+r_2}\)
• Current in circuit I = I₁ + I₂
• P.D in circuit V = \(\frac{\varepsilon_1 r_2+\varepsilon_2 r_1}{r_1+r_2}-I\left[\frac{r_1 r_2}{r_1+r_2}\right]\)
  ⇒ V_eq = ε_eq – Ir_eq
• Due to parallel combination current in the circuit increases.

Note: When n identical batteries are connected in parallel.

• emf ε₁ = ε
• Current I = nI₁
• effective internal resistance of combination r_eff = \(\frac{r}{n}\)

→ Kirchhoff s Laws:

• Junction rule : At any junction sum of currents towards the junction is equals to sum of currents away from the junction. (OR) Algebraic sum of currents around a junction is zero.
• Loop rule : Algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.

→ Wheatstone’s principle : In a balanced Wheatstone’s bridge ratio of resistances in adjacent arms is constant.
i.e \(\frac{P}{Q}=\frac{R}{S}\Rightarrow \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\mathrm{R}_3}{\mathrm{R}_4}\)
⇒ \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l}{(100-l)}\)

→ Average current I = \(\frac{\Delta q}{\Delta t}\); Instantaneous current i = \(\frac{\mathrm{dq}}{\mathrm{dt}}\); Current density j = i/A Unit : Amp/rn2

→ Resistance R = \(\frac{V}{i}\); Resistance R = \(\frac{\rho l}{\mathrm{~A}}=\frac{\rho l}{\pi \mathrm{r}^2}\); Conductance G = \(\frac{1}{R}\).

→ AcceleratIon of electron In electric field a = \(\frac{\mathrm{eE}}{\mathrm{m}}\)

→ Drift velocity of electron (v_d) = \(\frac{i}{\text { neA }}\), V_d = \(\frac{e \tau E}{m}\); mobility (μ) = \(\frac{\mathrm{e \tau}}{\mathrm{m}}\) where τ average time between two successive collisions.

→ ResIstivity (or) specific resistance
ρ = \(\frac{\mathrm{RA}}{l}=\frac{\mathrm{R} \pi \mathrm{r}^2}{l}\); Conductance σ = \(\frac{1}{\rho}\)

→ Temperature coefficient of resistivity
α = \(\frac{\rho_2-\rho_1}{\rho_1\left(t_2-t_1\right)}\)/°C ⇒ α = \(\frac{\mathrm{d} \rho}{\rho \mathrm{dt}}\)/°C

→ Temperature coefficient of resistance
α = \(\frac{\mathrm{R}_{\mathrm{t}}-\mathrm{R}_0}{\mathrm{R}_0\left(\mathrm{t}_2-\mathrm{t}_1\right)}\)/°C
α = \(\frac{\mathrm{dR}}{\mathrm{Rdt}}\) (or) α = \(\frac{\mathrm{R}_2-\mathrm{R}_1}{\mathrm{R}_1\left(\mathrm{t}_2-\mathrm{t}_1\right)}\)/°C
R_t = R₀[1 + α(t₂ – t₁)]

→ If two wires are made of same material then
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{l_1}{l_2} \frac{\mathrm{A}_2}{\mathrm{~A}_1} \Rightarrow \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{l_1 \mathrm{r}_2^2}{l_2 \mathrm{r}_1^2}\)

→ In series combination of resistors:

• R_eq = R₁ + R₂ + …………. + R_n
• Same current will flow through all resistors.
• Potential drop on resistors V₁ = i R₁, V₂ = i R₂ etc.
• Total potential drop V = V₁ + V₂ + ……………. etc.
• Current of circuit I = \(\frac{\text { Total Potential }}{\text { Total Resistance }}=\frac{V}{R_{e q}}\)

→ In parallel combination of resistors:

• \(\frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}+\ldots \ldots \ldots+\frac{1}{R_n}\)
• For two resistors (R_eg) = \(\frac{\mathrm{R}_1 \mathrm{R}_2}{\mathrm{R}_1+\mathrm{R}_2}\)
• Same potential difference is applied on all resistors.
• Total current I = I₁ + I₂ + I₃ + ……… i.e., sum of individual currents through each resistor.
  I = \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{eq}}}=\mathrm{V}\left(\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\ldots .+\frac{1}{\mathrm{R}_{\mathrm{n}}}\right)\)

→ In cells

• While discharging, termina! voltage V = E – ir
• While charging. terminal voltage V = E + ir
• Current in circuIt i = \(\frac{E}{R+r}\)
  r = Internal resistance of battery;
  R = Resistance in circuit.

→ Electrical energy W = Vit = i²Rt = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)t

→ Electric power P = Vi = i²R = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)t; Power wasted in transmission lines P_c = P²R_c/V² where P = Power transmitted ;
R_c = Resistance of line

→ 1 kilo watt hour = 36 × 10⁵ J or 3.6 × 10⁶ J.

→ At balance condition in Wheatstone’s bridge \(\frac{P}{Q}=\frac{R}{S}\)

→ If capacitors are used in balanced Wheat stone’s bridge \(\frac{C_1}{C_2}=\frac{C_3}{C_4}\)

→ In meter bridge at balance condition \(\frac{\mathrm{R}}{\mathrm{S}}=\frac{l_1}{l_2}\)
Unknown resistance x = R\(\frac{l_1}{l_2}\)
where I₂ = (100 – I₁)

→ In potentiometer,
In comparison of emf of two cells \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2}\)

→ In determination of internal resistance
r = R\(\left[\frac{l_1-l_2}{l_2}\right]\)

Here students can locate TS Inter 2nd Year Physics Notes 5th Lesson Electrostatic Potential and Capacitance to prepare for their exam.

TS Inter 2nd Year Physics Notes 5th Lesson Electrostatic Potential and Capacitance

→ Coulomb force between two stationary charges is also a conservative force, i.e., work done in moving a test charge depends only on initial and final positions but not on the path.

→ Potential due to a point charge q’ at a distance ‘r’ V(r) = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r}\)

→ Potential due to a system of charges :
Consider a system of charges q₁, q₂, q₃, ………… q_n then potential at a point P = the algebraic sum of individual potentials at that point.
V = V₁ + V₂ + V₃ + ……….. + V_n
or
V = \(\frac{1}{4 \pi \varepsilon_0}\left(\frac{\mathrm{q}_1}{\mathrm{r}_1}+\frac{\mathrm{q}_2}{\mathrm{r}_2}+\frac{\mathrm{q}_3}{\mathrm{r}_3}+\ldots \ldots+\frac{\mathrm{q}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}}\right)\)

→ Potential on a conducting sphere :
When a charge q’ is given to a conducting sphere it will be uniformly distributed over the sphere of radius R’.
(a) Potential at a distance ‘r’
(V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\). (r > R)
(b) For a point inside the shell the potential is constant V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{R}\)

→ Equipotential surface :
An equipotential surface has a constant potential at all points on that surface.
Ex: Potential at a distance V from charge q’
(V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\). Now a circle of radius r from q’ will have same potential i.e., that
circle represents an equipotential circle.
Note Work done in moving a charge q’ on an equipotential surface is zero.

→ Potential energy due to a system of charges:
Consider two charges say q₁ and q₂ placed at positions r₁ and r₂ from origin. Then distance between them = r₁₂.

(a) Potential energy of the system of two charges
U = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}\)

(b) If a system has three charges say q₁ q₂ and q₃ at positions r₁, r₂ and r₃ then potential energy of that system = the alzebraic sum of potential energy between every two charges.
∴ Potential energy of system U = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{r_{12}}+\frac{q_2 q_3}{r_{23}}+\frac{q_3 q_1}{r_{13}}\right]\)

→ Potential energy of a dipole in an electric field :
When an electric dipole is placed in a uniform electric field. Net force on the charges are Eq and – Eq. So resultant force is zero. But dipole will experience some torque τ on it. So it will rotate say from position θ1 to θ2 with the field (E). Torque τ = workdone by external field E
W = PE (cos θ₀ – cos θ₁) where
p = dipolemoment.

→ Electrostatic potential is constant through out the volume of the conductor and has same value equal to that on the surface.

→ Electric field at the surface of a charged a conductor E = \(\frac{\sigma}{\varepsilon_0}\)n .

→ Dielectrics : Dielectrics are the substances which does not conduct electricity.

→ Dielectric constant is defined as the ratio of force between two charges in vacuum to force between the same charges with a dielectric between them when distance is constant.
K = \(\frac{\mathrm{F}_1}{\mathrm{~F}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2} / \frac{1}{4 \pi \varepsilon} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\)
K = \(\frac{\varepsilon}{\varepsilon_0}\) = ε_r
where k = relative permittivity (or) dielectric constant.

→ Polar dielectrics: A dielectric molecule in which + ve and – ve charges are polarised into two groups without application of electric field is called polar dielectric field.

→ Non-polar dielectrics : A dielectric molecule in which the centres of all positive charges and all negative charges coincide when there is no electric field is called non polar dielectric.

→ In external electric field E’ behaviour of polar and non-polar dielectrics is same.

→ When a dielectric of constant k’ is introduced in an electric field ‘E’ then intensity of electric field inside the dielectric is reduced to E/K i.e., E_d = E/K.

→ Electric susceptibility (χ) : It is defined as the ratio of dipolemoment per unit volume to Electric field E
χ = \(\frac{P}{E}\) where P is polarisation i.e., dipole moment per unit volume.

→ Capacity (Q : It is defined as the ratio of charge Q’ to potential (V) of a conductor.
Capacity (C) = \(\frac{\text { Charge }(Q)}{\text { Potential }(V)}\) unit: Farad
Note: Capacity of a conductor depends on its geometrical shape and medium between the plates.

→ Parallel plate capacitor: It consists of two metallic plates separated by some distance ’d’ and one plate is connected to earth.
Capacity of parallel plate capacitor s0A
C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) (with vacuum between the plates)
C = K \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) (with a dielectric K filled between the plates).

→ Energy stored in a capacitor (U) : When a capacitor is charged to a potential ‘V’ it will store some electrical charge in it. While dis-charging the capacitor this electric charge is capable of doing some work. So while charging the work done to charge the capa-citor is stored in the form of potential energy in it.
Energy stored in a capacitor
U = \(\frac{1}{2}\)CV² = \(\frac{\mathrm{QV}}{2}=\frac{\mathrm{Q}^2}{2 \mathrm{C}}\)

→ Energy density (OR) Energy stored per unit volume : It is defined as the ratio of energy stored in a capacitor to the total volume between the plates of a capacitor.
Energy density U = \(\frac{1}{2}\)ε₀E²
Where E is intensity of electric field between the plates.

→ Van deGraaff generator: It is used to produce very high voltages such as 1 million volts.

→ Force between two charges in free space is
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\)

→ Relative permittivity ε_r = \(\frac{\varepsilon}{\varepsilon_0}\)
\(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ N – m²/C²
ε₀ = 8.854 × 10^-12 F/m or \(\frac{c^2}{N-m^2}\)

→ From the superposition principle, the resultant force on a given charge due to multiple charges is \(\overline{\mathrm{F}}_{\mathrm{R}}=\overline{\mathrm{F}}_1+\overline{\mathrm{F}}_2 \ldots \ldots \ldots \overline{\mathrm{F}}_{\mathrm{n}}\) (Vector sum of forces)

→ Intensity of electric field E = \(\frac{\mathrm{F}}{\mathrm{q}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}\)

→ Force experienced by a charge q in electric field E is F = Eq.

→ Potential due to a point charge is V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)

→ Relation between Intensity of electric field E̅ and potential V is E = \(\frac{V}{d}\).

→ Workdone to move a charge q through a potential V is W = qV.

→ Electrostatic potential due to a system of charges is
V_R = V₁ + V₂ + V₃ + ……….. + V_n
(algebraic sum of individual potentials.)

→ Dipoles: A dipole consists of two equal and opposite charges separated by a distance 2a.

• Dipolemoment (p) = q2a = 2qa.
• Potential due to a dipole at any point
  V = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{qa} \cos \theta}{\mathrm{r}^2}=\frac{\mathrm{p} \cos \theta}{4 \pi \varepsilon_0 \mathrm{r}^2}=\frac{\overline{\mathrm{p}} \cdot \overline{\mathrm{r}}}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
  where r̅ is a unit vector along the line joining centre of dipole and given point.
• Torque on dipole in uniform electric field E is τ = p̅. E̅ = |p̅||E̅| sin θ
• Work done to rotate a dipole from angle θ₁ to θ₂ in electric field W = potential energy stored U(θ) = PE (cos θ₁ – cos θ₂)

→ Total electric flux through given area
\(\oint_E=\oint_s \bar{E} \cdot \overline{d s}=\oint_s\) E ds cos θ
From Gauss’s theorem \(\oint_E=\oint_s \bar{E} \cdot \overline{d s}\)E̅.ds̅ = \(\frac{\mathrm{q}}{\varepsilon_0}\)
Linear charge density λ = \(\frac{\mathrm{dq}}{\mathrm{dl}}\) where dq is charge on the infinitesimal length dl.

→ For an infinitely long straight charged conductor:
(a) Intensity at any perpendicular point is E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)
(b) Potential at any perpendicular point is V = \(\frac{\lambda}{2 \pi \varepsilon_0}\)log_e r + K

→ For a charged infinite plane sheet:
Intensity of electric field at a distance r from the plane is E = \(\frac{\sigma}{2 \varepsilon_0}\)

→ For a charged spherical shell : Surface charge density σ = \(\frac{\mathrm{dQ}}{\mathrm{dS}}\) or
σ = \(\frac{\text { Charge } \mathrm{q}}{\text { Surface area } \mathrm{S}}\)
(i) For points outside the shell
(a) Intensity of electric field E = \(\frac{\sigma}{s_0} \frac{\mathrm{R}^2}{\mathrm{r}^2}\)
(b) Potential V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\) + K where K is a constant of Integration.

(ii) For points on the surface of the sphere
(a) Intensity of electnc field E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{R}^2}\)
(b) Potential V = \(=\frac{1}{4 \pi \varepsilon_0} \frac{q}{R}\)

(iii) For points inside the shell
(a) Intensity of electric field E = O;
(b) Potential V = \(=\frac{1}{4 \pi \varepsilon_0} \frac{q}{R}\)

→ Capacity C = \(\frac{\text { Charge q }}{\text { Potential V }}\)
C = \(\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) =KC₀ with dielectric of constant K.

→ By placing a dielectric between the plates of a capacitor

• Intensity of electric field E_M = \(\frac{\mathrm{E}_0}{\mathrm{~K}}\)
• Capacity C = KC₀
• Potential V_M = \(\frac{\mathrm{V}_0}{\mathrm{~K}}\)

→ When a dielectric is partially introduced between the plates of a capacitor then its capacity
C = \(\frac{\varepsilon_0 A}{d-t+\frac{t}{K}}\) or C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}-t\left(1-\frac{1}{\mathrm{~K}}\right)}\)
decrease in distance = d – t\(\left(1-\frac{1}{\mathrm{~K}}\right)\) and ‘t’ is the thickness of the dielectric slab.

→ In parallel combination of capacitors, the resultant capacity C = C₁ + C₂ + C₃ + ……… etc.

→ When capacitors are connected in series, the resultant capacity is given by
\(\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)….or C = \(\frac{\mathrm{C}_1 \mathrm{C}_2}{\mathrm{C}_1+\mathrm{C}_2}\)

→ Energy stored in a capacitor
U = \(\frac{1}{2}\)CV² = \(\frac{\mathrm{Q}^2}{2 \mathrm{C}}=\frac{\mathrm{QV}}{2}\)

→ Effect of dielectric on a capacitor :
1. When charging battery is continued
(a) Potential V = V₀;
(b) Capacity C = KC₀
(c) Charge Q = KQ₀;
(d) Energy stored U = KU₀
where V₀, C₀, Q₀ and U₀ are values without dielectric.

2. When charging battery is removed from circuit
(a) Potential V = \(\frac{\mathrm{V}_0}{\mathrm{~K}}\);
(b) Capacity C = KC₀
(c) Charge on capacitor q = q₀
(d) Energy stored U = \(\frac{\mathrm{U}_0}{\mathrm{~K}}\)

Here students can locate TS Inter 2nd Year Physics Notes 4th Lesson Electric Charges and Fields to prepare for their exam.

TS Inter 2nd Year Physics Notes 4th Lesson Electric Charges and Fields

→ Electrical charges given to conductors will flow from one end to other end. Charges moving through conductors leads to flow of current.

→ Electrical charges are two types

• positive charge,
• negative charge.

→ In the process of electrification we will remove or add electrons to substances with some techniques. Substance that looses electrons will become positive substance that gains electrons will become negative.

→ Quantisation of charge: Electric charge ‘Q ’ on a substance is an integral multiple of fundamental charge of electron, i.e., Q = ne. It is called Quantisation of charge.

→ Law of conservation of charge : The total charge of an isolated system is always con-stant. i.e., charge can not be created or des-troyed. This is known as “law of conservation of charge”.

→ Charge on electron e = 1.602 × 10^-19 C it is taken as fundamental charge.

→ Coulomb’s Law:
Force attraction (or) repulsion between the charges is proportional to product of charges and inversely proportional to the square of the distance between them.
∴ From Coulomb’s law F ∝ q₁q₂ and F ∝ 1/r²
F ∝ \(\frac{q_1 q_2}{r^2}\) (OR) F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
Where \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ N-m² / C² is a constant.
ε₀ is permittivity of free space.
Its value is 8.85 × 10^-12 farad/metre.

→ Force on a given charge (q) due to multiple charges is the vector sum of all the forces acting on the given charge.
\(\overline{\mathrm{F}_{\mathrm{R}}}=\overline{\mathrm{F}}_1+\overline{\mathrm{F}}_2+\overline{\mathrm{F}}_3\) ……….
Where F₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q^q q_2}{r_1^2}\) etc
Note : To find resultant force we must use principles of vector addition i.e., parallelogram law or triangle law.

→ Electric field : Every charged particle (q) will produce an electric field everywhere in the surrounding. It is a vector. It follows inverse square law.

→ Intensity of electric field (or) electric field strength (E̅) : Intensity of electric field or electric field at a point in space is the force experienced by a unit positive charge placed at that point.
F = Eq (or) E = (F/q), SI unit: Vm^-1

→ Electric field lines of force : Electric field lines represent electric field E due to a charge ‘q’ in a pictorial manner. When E is strong field lines are move nearer or crowded. In a weak field electric field lines are less dense.

→ Electric flux (Φ): The number of electric field line passing through unit area placed normal to the field at a given point is called “electric flux”. It is a measure for the strength of electric field at that point.

→ Electric dipole: Two equal and opposite charges separated by some distance will constitute an “electric dipole”.

→ Dipole moment (p̅): The product of one of the charge in dipole and separation between the charges is defined as “dipole moment (P̅)”.
Dipole moment (p̅) = q. 2a (or) p = 2aq
It is a vector. It acts along the direction of -q to q.
Unit: coulomb – metre.

→ Dipole in a uniform electric field : Let an electric dipole is placed in an electric field of intensity E. Then F = Eq
Torque on dipole τ = p̅ x E̅
Let p̅ and E̅ are in the plane of the paper then torque τ will act perpendicularly to the plane of the paper.

→ Linear charge density (λ) :
It is defined as the ratio of charge (Q) to length of the conductor (L).
Linear charge density
λ = \(\frac{\text { Charge }}{\text { Length }} \frac{(\mathrm{Q})}{(\mathrm{L})}\)
⇒ λ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{L}}\)
Unit: Coulomb / metre.

→ Surface charge density (σ) : W
It is defined as the ratio of charge (Q) to surface area of (A) of that conductor.
Surface charge density
σ = \(\frac{\text { Charge }}{\text { Area }} \frac{(\mathrm{Q})}{(\mathrm{A})}\)
⇒ σ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{A}}\)
Unit: Coulomb / metre²

→ Volume charge density (ρ):
It is defined as the ratio of charge on the conductor ‘Q’ to volume of the conductor.
Volume charge density
ρ = \(\frac{\text { Charge }}{\text { Volume }} \frac{(Q)}{(V)}\)
⇒ ρ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{V}}\)
Unit: Coulomb / m³.

→ Gauss law : The total electrical flux (Φ) through a closed surface (s) is 1/ε₀ times more than the total charge (Q) enclosed by that surface.
From Gauss law (Φ) = \(\frac{1}{\varepsilon_0}\) Q

→ Important conclusions from Gauss’s law:

• Gauss law is applicable to any closed surface irrespective of its shape.
• The term Q refers to sum of all the charges inside the gaussian surface.
• A gaussian surface is that surface for which we choosed to apply gauss law.
• It is not necessary to consider any charges out side the gaussian surface to find the flux (Φ) coming out of it.
• Gauss law is very useful in the calculations to find electric field when the system (gaussian surface) has some symmetry.

→ Charge Q = ne. Where e = charge on electron = 1.6 × 10^-19 C.

→ Force between two charges F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)

→ Force between multiple charges : In a system of charges say q₁ q₂, q₃ ………. q_n.
Force on charge qj is say F₁ = F₁₂ + F₁₃ + F₁₄ ………….. F_1n
(OR) Total force on q₁ say
F₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{r_{21}^2}+\frac{q_1 q_3}{r_{13}^2}+\ldots . .+\frac{q_1 q_n}{r_{1 n}^2}\right]\)

→ Electric field due to a point charge q’ at a point r is E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}^2}\) (OR) E̅ = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}^2}\)r̅

→ Electric flux Φ = E.Δs = E Δs cos θ.
Where θ is the angle between electric field E̅ and area vector Δs .

→ Dipole moment p = q.2a. Where q is one of the charge on dipole and ‘2a’ is separation between the charges.

→ Electric field at any point on the axis of a dipole
E_axial = \(\frac{\mathrm{q}}{4 \pi \varepsilon_0} \frac{4 \mathrm{ar}}{\left[\mathrm{r}^2-\mathrm{a}^2\right]^2}=\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{pr}}{\left(\mathrm{r}^2-\mathrm{a}^2\right)^2}\)
where r > > a then E_axial = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{p}}{\mathrm{r}^3}\)
When r is the distance of given point from centre of dipole.

→ Electric field of any point on the equatorial line of a dipole.
E_eq = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{qa}}{\left[\mathrm{r}^2+\mathrm{a}^2\right]^{3 / 2}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{p}}{\left[\mathrm{r}^2+\mathrm{a}^2\right]^{3 / 2}}\)
When r >> a then E_eq = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{p}}{\mathrm{r}^3}\)
Note : E_axial and E_eq will act along the line joining the given point ’p’ and centre of dipole ‘O’.

→ Torque on a dipole when placed in a uniform electric field E is τ̅ = p̅ x E̅ = pE sin θ.
Where θ is the angle between P̅ and E̅.

→ Charge distribution on conductors:
Charge (Q) given to a conductor will uniformly spread on the entire conductor.
(a) Linear charge density λ = \(\frac{\text { Charge }}{\text { Length }} \frac{\mathrm{Q}}{\mathrm{L}}\) unit: C/m
(b) Surface charge density σ = \(\frac{\text { Charge }}{\text { Surface area }} \frac{Q}{A}\) unit / C/m²
(c) Volume charge density ρ = \(\frac{\text { Charge }}{\text { Volume }} \frac{Q}{V}\) unit: C/m³

→ Gauss’s law : The total electric flux (Φ) coming out of a closed surface is \(\frac{1}{\varepsilon_0}\) times greater than the total charge (Q) enclosed by that surface.
Φ = \(\frac{Q}{\varepsilon_0}\)

→ Electric field due to an infinitely long straight uniformly charged wire E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)n̅.
(∵ n̅ = 1) or, E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)

→ Field due to a uniformly charged infinite plane sheet is E = \(\frac{\sigma}{2 \varepsilon_0}\)n̅.
or. E = \(\frac{\sigma}{2 \varepsilon_0}\), (∵ n̅ = 1)

→ Field due to a uniformly charged thin spherical shell:
(a) At any point out side the shell is
E = \(\frac{\mathrm{Q}}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
(b) Inside the shell electric field E = 0.