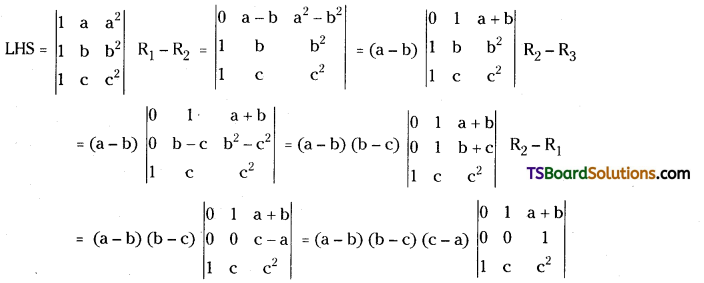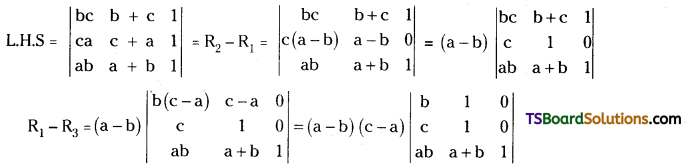Telangana TSBIE TS Inter 2nd Year English Study Material 6th Lesson How to Avoid Foolish Opinions Textbook Questions and Answers.
TS Inter 2nd Year English Study Material 6th Lesson How to Avoid Foolish Opinions
Annotations (Section A, Q.No. 1, Marks: 4)
Annotate the following in about 100 words each.
a) If someone maintains that two and two are five or that Iceland is on the equator, you feel pity rather than anger…….. (Revision Test – I)
Introduction: These beautiful lines are taken from the thought-provoking essay, “How to Avoid Foolish Opinions” written by Bertrand Russell. His clarity of thought and fluency of expression lend beauty to his style.
Context and Meanings: Russell gives us tips on how to avoid foolish opinions. He says that there are many ways to avoid being dramatic. To avoid foolish opinions, no super human or genius is required. Many matters are less easily brought to the test of experience. If we hear views opposite to our opinions, it makes us angry. It is a sign that we actually have no good reason for our opinion. If someone has very stupid and wrong opinions, we feel pity rather than anger. So, we must carefully reconsider our ideas.
Critical Comment: Though the article discusses many mistakes mankind is prove to make, it ends with a lively ray of hope.
కవి పరిచయం : బెర్ట్రాండ్ రస్సెల్ చే రచింపబడిన “మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి” అను ఆలోచనను రేకెత్తించే వ్యాసం నుండి ఈ అందమైన పంక్తులు తీసుకొనబడినవి. ఇతని యొక్క స్పష్టమైన ఆలోచన మరియు ధారాళమైన అభిప్రాయం ఇతని శైలికి అందాన్ని ఇస్తున్నాయి.
సందర్భ౦ మరియు అర్థం : మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి అనే దాని మీద రస్సెల్ మనకు సూచనలు ఇస్తున్నారు. మూర్ఖంగా వ్యవహరించడాన్ని నిరోధించుటకు అనేక మార్గాలున్నాయి. అనేక విషయాలు అనుభవం యొక్క పీక్షకు చాలా సులువుగా తీసుకురాబడతాయి. మన అభిప్రాయంకు వ్యతిరేఖంగా మనం అభిప్రాయాలు వింటే, అది మనకు కోపం తెప్పిస్తుంటే, అది మన అభిప్రాయానికి వాస్తవంగా సరైన కారణం లేదనే ఒక సూచిక. ఎవరైనా చాలా తెలివి తక్కువ మరియు తప్పుడు అభిప్రాయాలను కలిగిఉంటే, కోపం కంటే మనం జాలి చూపుతాము. కావున, మనం జాగ్రత్తగా మన అభిప్రాయాలను నిర్ధారించుకోవాలి.
విమర్శ : మానవాళి అనేక తప్పులు చేయటానికి అవకాశం ఉందని ఈ వ్యాసం చర్చించినప్పటికీ ఇది చక్కటి ఆశీకిరణంతో ముగుస్తుంది.
b) Persecution is used in the theology not in arithmetic because, there is knowledge, but in theology, there is only opinion. (Revision Test – I)
Introduction: These lines are taken from the thought provoking essay, “How to Avoid Foolish Opinion” written by Bertrand Russell. His clarity of thought and fluency of expression lend beauty to his style.
Context and Meanings: Russell gives us tips on how to avoid foolish opinion. Here, he tells us about controversies. The worst controversies are about matters which have no gcoa ev de ne either way. If you can not observe an issue, think about any biases you might have about it. This is because belief can go beyond facts. Persecution means annoying others deliberately all the time, the theology is required belief where as arithmetic is require facts and figures. Hence, persecution is not used in arithmetic but in theology – the study of God and religion.
Critical Comment: The author says that belief can go beyond facts.
కవి పరిచయం : బెర్ట్రాండ్ రస్సెల్ చే రచింపబడిన “మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి” అనే ఆలోచనను రేకెత్తించే వ్యాసం నుండి ఈ పంక్తులు తీసుకొనబడినవి. ఇతని యొక్క స్పష్టమైన ఆలోచన మరియు ధారాళమైన అభిప్రాయాలు ఇతని శైలికి అందాన్ని ఇస్తున్నాయి.
సందర్భ౦ మరియు అర్థం : మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి అనే దాని గురించి రస్సెల్ మనకు సూచనలు ఇస్తున్నారు. ఇతను మనకు వివాదాలు గురించి చెప్తున్నాడు. మంచి సాక్ష్యాలు లేని విషయాలు గురించి చెత్త వివాదాలు ఉన్నాయి. ఒక విషయాన్ని పరిశీలించలేకపోతే దాని గురించి మీకు ఏదైనా పక్షపాతాలు ఉన్నాయా లేదా ఆలోచించండి. ఎందుకంటే విశ్వాసం వాస్తవాలను అధిగమించగలదు. పీడించడం, చికాకు పెట్టడం అంటే ఇతరులను ఉద్దేశ్య పూర్వకంగా అన్ని వేళలా చూపించడం, చికాకు పెట్టడం. వేదాంతానికి నమ్మకం అవసరం, ఇక్కడ అంకగణితానికి వాస్తవాలు మరియు గణాంకాలు అవసరం. అందువల్ల, వేధింపు, చికాకు అనేది అంకగణితంలో ఉపయోగించబడదు కానీ వేదాంతశాస్త్రంతలో – దేవుని అధ్యయనంలో ఉపయోగిస్తారు.
విమర్శ: నమ్మకం వాస్తవాలకు అతీతంగా ఉంటుందని రచయిత చెప్పారు.
![]()
c) I have frequently found myself growing less dogmatic and cocksure through realising the possible reasonableness of a hypothetical opponent.
Introduction: These lines are taken from the thought provoking essay, “How to Avoid Foolish Opinions” written by Bertrand Russell. His clarity of thought and fluency of expression lend beauty to his style.
Context and Meanings: The writer advises us to argue with an imaginary character who has a different point of view. It is a good plan to test our arguments. Imaginary dialogues through psychological imagination serve a great purpose. Continue Conversation with that person hypothetically. You end up with reversing your ideas wherever necessary. He says that he has done the some experiment.
Critical Comment: Here, the author offers us hypothetical opponent to avoid foolish opinions and to become a less dogmatic.
కవి పరిచయం : బెర్ట్రాండ్ రస్సెల్ చే రచింపబడిన “మూర్ఖపు ఆలోచనలను ఎలా నివారించాలి” అనే ఆలోచనను రేకెత్తించే వ్యాసం నుండి ఈ పంక్తులు తీసుకొనబడినవి. ఇతని యొక్క స్పష్టమైన ఆలోచన మరియు అబిప్రాయ ధారాళం ఇతని శైలికి అందాన్ని చేకూర్చుతున్నాయి.
సందర్భ౦ మరియు అర్థం : మూర్ఖపు ఆలోచనలను ఎలా నివారించాలనే దానిపై తస్సెల్ మునకు సూచనలు ఇస్తున్నారు. ఇక్కడ అభిప్రాయ భేదం ఉన్న ఊహాజనిత పాత్రతో వాదించమని రచయిత మనకు సలహా ఇస్తున్నాడు. మన సంభాషణను పరీక్షించుకొనుటకు ఇది మంచి ప్రణాళిక. మన ఊహాశక్తితో కల్పిత సంభాషణల సృష్టి గొప్ప ఫలితాలను ఇస్తుంది. మీ అభిప్రాయాలకు వ్యతిరేఖ ఆలోచనలు గల వ్యక్తిని మీ ఎదురుగా ఉన్నట్లు భావించండి. వారితో కల్పిత సంభాషణలను కొనసాగించండి. దీని తుది ఫలితం అవసరమైన చోటల్లా మీ అభిప్రాయాలను సరిచేసుకొని మెరుగుపరుచుకొంటారు. రచయిత ఇదే ప్రయోగం చేశానని చెప్తున్నారు.
విమర్శ: ఇక్కడ, మూర్ఖపు అభిప్రాయాలను నివారించుటకు మరియు మొండిగా ఉండకుఁ డా ఉండుటకు, రచయిత ఒక ఊహాజనితపాత్రను చూస్తున్నాడు.
d) Be very way of opinions that flatter your self esteem.
Introduction: These lines are taken from the thought provoking essay, “How to Avoid Foolish Opinions” written by Bertrand Russell. This clarity of thought and fluency of expression lend beauty to his style.
Context and Meaning: In this essay, Russell give us tips on how to avoid foolish opinions. He cautions us against comments that boost one’s ego. This problem is tough to solve because everyone is sure of his/her supremacy. He advises a healthy dose of modesty and common sense. Our principles should not be dramatic. Other’s standards and ideals should equally be respected. He adds that dealing with a man’s self-esteem is challenging the only solution is to remind people of the episodic human life on a small planet.
Critical Comment: Though the essay discusses many mistakes mankind is prone to make, it ends with a lively ray of hope.
కవి పరిచయం : బెర్ట్రాండ్ రస్సెల్ చే రచింపబడిన “మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి” అనే ఆలోచనను రేకెత్తించే వ్యాసం నుండి ఈ పంక్తులు తీసుకొనబడినవి. ఇతని ఆలోచన స్పష్టత మరియు వ్యక్తీకరణ యొక్క పటిమ అతని శైలికి అందాన్ని ఇస్తుంది.
సందర్భ౦ మరియు అర్థం : ఈ వ్యాసంలో రస్సెల్ తెలివి తక్కువ అభిప్రాయాలను ఎలా నివారించలో మనకు చిట్కాలు ఇస్తున్నారు. ఒకరి అహాన్ని పెంచే వ్యాఖ్యలకు వ్యతిరేఖంగా తనకు మనల్ని హెచ్చరిస్తున్నాడు. ప్రతి ఒక్కరూ తమ ఆధిపత్యాన్ని ఖచ్చితంగా కలిగిఉంటారు కాబట్టి ఈ సమస్యను పరిష్కరించడం చాలా కష్టం. అతను నమ్రత మరియు ఇంగితజ్ఞానం యొక్క ఆరోగ్యకరమైన మోతాదును సూచించాడు. మన సూత్రాలు పిడివాదంగా ఉండకూడదు. ఇతరుల యొక్క ప్రమాణాలు మరియు ఆదర్శాలను సముద్రంగా గౌరవించాలి. మనిషి యొక్క ఆత్మగౌరవంతో వ్యవహరించడం సవాలుతో కూడుకున్నదని అతను చెప్పాడు. ఒక చిన్న గ్రహం మీద ఎపిసోడ్ మాపైన జీవితాన్ని ప్రజలకు గుర్తు చేయడము ఏకైక పరిష్కారం.
విమర్శ : మానవజాతి చేయవలసిన అనేక తప్పులను వ్యాసం చర్చిస్తున్నప్పటికీ, ఇది సజీవమైన ఆశతో ముగుస్తుంది.
Paragraph Questions & Answers (Section A, Q.No.3, Marks: 4)
Answer the following Questions in about 100 words
a) How can we prevent developing a dogmatic attitude as per Russell’s suggestion ? (Revision Test – I)
Answer:
The thought provoking essay, “How to Avoid Foolish Opinion’s” is written by Bertrand Russell. In this essay, he says that there are many ways to avoid being dogmatic. Making a keen observation where it can settle the bias is the first way. Next to know what other people think.
One has to be aware of what they think. This can be done by going on vacation and talking to people with different ideas. The third is arguing with an imaginary character. The fourth one is to deal with one’s sense of self worth. To overcome conceit, we must remember that we live for a short while on a small planet in vast cosmos.
ఆలోచనను రేకెత్తించు వ్యాసం ‘మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి’ అను వ్యాసం బెర్ట్రాండ్ రస్సెల్ చే రచింపబడింది. ఈ వ్యాసంలో, మొండిగా మాట్లాడాన్ని నివారించుటకు అనేక మార్గాలు ఉన్నాయని ఇతను చెప్తున్నారు. అందులో మొదటి మార్గం స్పష్టమైన పరిశీలన. రెండవది, ఇతరులు ఏమి ఆలోచిస్తున్నారో తెలుసుకోవటానికి, ముందు వారు ఏమనుకుంటున్నారో అవగాహన ఉండాలి. భిన్న అభిప్రాయాలు గల వ్యక్తులతో మాట్లాడటం మరియు సెలవుల యాత్రకు వెళ్ళటం వలన ఇది సాధ్యమౌతుంది. కల్పితపాత్రతో వాదించటం మరియు సంచరించటం మూడవ మార్గం. ఒకరి యొక్క ఆత్మ విలువ గౌరవం పరీక్షించుట నాల్గవ మార్గం. అహంను జయించుటకు, సువిశాల ప్రపంచంలో అణుమాత్రం కూడా ఉండని మన స్థానాన్ని గుర్తించటం. మన జీవితం క్షణకాలం మాత్రమే అని తెలుసుకోవటం.
![]()
b) Travel is an excellent educator. Explain with reference to Russell’s essay,”How to Avoid Foolish Opinions”.
Answer:
The thougnt provoking essay, How to Avoid Foolish Opinions” is written by Bertrand Russell. In this essay, he gives us tips on how to avoid foolish opinions and being dogmatic. Great and eminent people believe that fraud is an excellent educator. It gives travelers a lot of knowledge. It gives after the information about culture, custom, costumes, crops, climate and food habit of the people or area concerned.
It can explain all the details in elaborate manner. In the present essay, Russel also explains the importance of visiting, foreign countries. One can become aware of opinions held in different people. Talking to different people with different ideas, makes one know what other people think. Such type of observation teaches us to avoid foolish opinions. The writer personally experienced the benefits of living outside his own country.
‘మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి’ అనే ఆలోచనను రేకెత్తించు వ్యాసం బెర్ట్రాండ్ రస్సెల్ చే రచింపబడింది. ఈ వ్యాసంలో అతను మూర్ఖపు అభిప్రాయాలను మరియు పిడివాదాన్ని ఎలా నివారించాలో మనకు చిట్కాలు ఇచ్చాడు. గొప్ప మరియు ప్రముఖ వ్యక్తులు ప్రయాణం ఒక అద్భుతమైన విద్యావేత్త అని నమ్ముతారు. ఇది ప్రయాణికులకు చాలా జ్ఞానాన్ని ఇస్తుంది. ఇది వారికి సంబంధించిన సంస్కృతి, ఆచారం, దుస్తులు పంటలు, వాతావరణం మరియు ఆహారపు అలవాట్ల గురించి సమాచారాన్ని అందిస్తుంది. ఇది అన్ని వివరాలను విస్తృతమైన పద్ధతిలో వివరించగలదు.
ప్రస్తుత వ్యాసంలో రీస్సెల్ విదేశాలను సందర్శించడం యొక్క ప్రాముఖ్యతను కూడా వివరించుట. వివిధ వ్యక్తులలో ఉన్న అభిప్రాయాల గురించి తెలుసుకోవచ్చు. విభిన్న ఆలోచనలతో ఉన్న విభిన్న వ్యక్తులతో మాట్లాడటం వలన ఇతర వ్యక్తులు ఏమనుకుంటున్నారో తెలుస్తుంది అటువంటి పరిశీలన మూర్ఖపు అభిప్రాయాలను నివారించేందుకు మనకు బోధిస్తుంది. రచయిత అని సొంత దేశం వెలుపల నివసించడం వల్ల కలిగే ప్రయోజనాలను వ్యక్తిగతంగా వివరించాడు.
c) According to Russell, what is the only way to tackle self pride?
Answer:
The thought provoking essay, How to Avoid Foolish Opinions” is written by Bertrand Russell. In this essay, he gives us tips on how to avoid foolish opinions and being dogmatic. Great and eminent people believe that travel is our excellent educator. It gives travellors a lot of knowledge. It gives them the information about culture, custom, costumes, crops, climate and food habit of the people or are concerned.
It can explain all the details in elaborate manner. In the present essay, Russell also explains the importance of visiting. Foreign countries once can become aware off opinions held in different people. Talking to different people with different ideas makes one know what other people think. Such type of observation teaches us to avoid foolish opinions. The wroter personally expressing
‘మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి’ అనే ఆలోచనను రేకెత్తించు వ్యాసం బెర్ట్రాండ్ రస్సెల్ చే రచింపబడింది. ఈ వ్యాసంలో అతను మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలో మనకు చిట్కాలు మరియు ఇంగితజ్ఞానం యొక్క ఆరోగ్యకరమైన మోతాదును సూచించాడు. ఎందుకంటే అహంను వ్యవహరించడం చాలా కష్టం. కాబట్టి, మన సూత్రాలు పిడివాదంగా ఉండకూడదు.
ఇతరుల యొక్క ఆత్మగౌరవంతో వ్యతిరేకించడం సవాలుతో కూడుకున్నరని రచయిత చెప్పాడు. ఒక చిన్న గ్రహం మీద ఎపిసోడ్ జీవితాన్ని వారికి గుర్తు చేయటమే ఏకైక పరిష్కారం. అప్పుడు, అహం చితికిపోతుంది మరియు మూర్ఖపు అభిప్రాయాలు అంతరించిపోతాయి.
d) what does bertrand Russell say about a person getting angry about a difference of opinion.
Answer:
The thought provoking essay,”How to Avoid Foolish Opinions” is written by Bertrand Russell. In this essay, he gives us tips on how to avoid foolish opinions and being dogmatic. He advises us to identify our weak points and reconsider our opinions. when we hear views opposite to our opinions. It makes us angry. It is a clear sign of something wrong with our beliefs. then we must carefully reconsider our ideas. We have to be aware of what other people think. Thus, we can avoid such problem.
‘మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి’ అనే ఆలోచనను రేకెత్తించు వ్యాసం బెర్ట్రాండ్ రస్సెల్ చే రచింపబడింది. ఈ వ్యాసంలో అతను మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలో మనకు చిట్కాలు ఇచ్చాడు. సున్నిత పరిశీలన ద్వారా విషయాలను ధృవీకరించుకోవడం మంచిదని సలహాఇస్తున్నాడు. మన బలహీనతలను గుర్తించి మన ఆలోచనలను పునఃపరిశీలించడం మంచిదని మనకు సలహా ఇస్తున్నాడు.
మన నమ్మకాలకు వ్యతిరేక అభిప్రాయాలు విన్నప్పుడు మనకు కోపం వచ్చిందంటే అది మన లోపభూయిష్ట ఆలోచనకు స్పష్ట సంకేతం. అప్పుడు మన అభిప్రాయాలను మనం జాగ్రత్తగా తిరిగి పరీక్షించుకోవాలి. ఇతరులు ఏమి ఆలోచిస్తున్నారో మనం అవగాహన కలిగి ఉండాలి. అలా అలాంటి సమస్యను మాత్రం నివారించగలము.
How to Avoid Foolish Opinions Summary in English
About Author
img 1
Bertrand Arthur William Russell, 3rd Earl Russell OM FRS[66] (18 May 1872 February 1970) was a British philosopher, logician, and public intellectual.
Few of his notable works in English:
1896. German Social Democracy. London: Longmans, Green
1903. A Free man’s worship, and other essays.
1905. On Denoting, Mind, Vol. 14. ISSN 0026-4423. Basil Blackwell
1910. Philosophical Essays. London: Longmans, Green
1916. Why Men Fight. New York: The Century Co
1927. The Analysis of Matter. London: Kegan Paul, Trench, Trubner
1969. Dear Bertrand Russell… A Selection of his Correspondence with the General Public
1950-1968, edited by Barry Feinberg and Ronald Kasrils. London: George Allen and Unwin
Bertrand Russell’s essay, “How to Avoid Foolish Opinions” is a thought-provoking essay the author talks about people’s opinions and how we might avoid the foolish ones. He tells us to keep our beliefs in check, and elaborates about controversies and customs. He also mentions things that affect people’s opinions, such as self-esteem and Foolish opinions and how we might get past them.
To avoid foolish opinions, no superhuman genius is required. A few simple rules will keep us from silly error. If the matter can be settled by observation, we must make the observation ourselves. Aristotle could have avoided thinking, women have fever teeth than man. If he told Mrs. Aristotle to keep her mouth open while he counted, thinking that we know something when in fact we don’t is a big mistake. Many matters are less easily brought to the test of experience. If an opinion opposite to our own makes us angry, it is sign that we actually have no good reason for our opinion. If someone has very stupid and wrong opinions, we feel pity rather than anger.
The worst controversies are about matters which have no good evidence either way. A good way of ridding ourselves of certain kinds of rigid beliefs is to become aware of opinions held in social circles different from our own. If we cannot travel, we should find people with whom we disagree and read newspapers belonging to a party that is not ours. But becoming aware of foreign customs does not always have benefits.
For those with good imagination, it is a good plan to imagine an argument with a person having a different opinion. Mahatma Gandhi disliked railways and stem boats and machinery and would have liked to undo the industrial revolution. In western countries most people take the advantage of modern technology for granted. So it is rare to find someone with this opinion. But to make sure we are right, disagreeing with this opinion, it is a good plan to test the arguments by considering what Gandhi might have said to them.
We should be very wary of opinions that halter our self-steem. Both man and women are very convinced of the excellence of their own “Sex”. there is abundant evidence on both sides. The question actually can not be solved, but self-esteem hides this from most people. All people are convinced that their own nation is the best. Again there is no right answer to the question about the best nation. The only way of dealing with this general human vanity is to remind ourselves that man is a short episode in the life of small planet in a little corner of universe, and other parts of cosmos may contain beings much superior.
We must avoid blindly believing anything without concrete reason. We should confirm the things that we can with observation and hear out the opinions of other people regarding controversial topics. Self-esteem greatly affects opinion but it can be checked by remaining ourselves of our place in the universe.
![]()
How to Avoid Foolish Opinions Summary in Telugu
Note: This summary is only meant for Lesson Reference, not for examination purpose
బెర్ట్రాండ్ రస్సెల్ యొక్క వ్యాసం “మూర్ఖపు అభిప్రాయాలను ఎలా నివారించాలి” అనేది ఆలోచనను రేకెత్తించే వ్యాసం. రచయిత ప్రజల అభిప్రాయాల గురించి మరియు మనం తెలివితక్కువ వాటిని ఎలా నివారించవచ్చో మాట్లాడతాడు. అతను మన నమ్మకాలను అదుపులో ఉంచుకోమని చెప్పాడు మరియు వివాదాల గురించి మరియు ఆచారాల గురించి వివరిస్తాడు. ఆత్మగౌరవం మరియు మూర్ఖపు అభిప్రాయాలు మరియు మనం వాటిని ఎలా అధిగమించగలం వాటి వ్యక్తుల అభిప్రాయాలను ప్రభావితం చేసే విషయాలను కూడా అతను పేర్కొన్నాడు.
మూర్ఖపు అభిప్రాయాలను నివారించడానికి, మానవాతీత మేధాశక్తి అవసరం లేదు. కొన్ని సాధారణ నియమాలు చిన్న వెర్రి లోపం నుండి మనల్ని కాపాడతాయి. పరిశీలన ద్వారా సమస్యను పరిష్కరించగల్గితే మనమే పరిశీలన చేసుకోవాలి. అరిస్టాటిల్ తాను లెక్కపెట్టే సమయంలో నోరు తెరచి ఉంచమని మిసెస్ అరిస్టాటిల్కు చెబితే పురుషులకంటే స్త్రీలకు దంతాలు తక్కువగా ఉంటాయని భావించకుండా ఉంటాడు. వాస్తవానికి మనకు తెలియనప్పుడు మనకు తెలుసు అని ఆలోచించడం పెద్ద తప్పు. చాలా విషయాలు అనుభవం యొక్క పరీక్షకూ చాలా సులభంగా తీసుకోబడతాయి. మన అభిప్రాయానిక వ్యతిరేఖమైన అభిప్రాయం మనకు కోపం తెప్పిస్తే అది మన అభిప్రాయానికి సరైన కారణం లేదని సూచిస్తుంది. ఎవరైనా చాలా తెలివితక్కువ మరియు తప్పుడు అభిప్రాయాలను కలిగి ఉంటే, కోపం కంటే మనం జాలి చూపుతాము.
మంచి సాక్ష్యాలు లేని విషయాలు గురించి చెత్త వివాదాలు ఉన్నాయి. కొన్ని రకాల మొండి నమ్మకాలను వదిలించుకోవడానికి ఒక మంచి మార్గం, మన స్వంత అభిప్రాయాల కంటే భిన్నమైన సామాజిక వర్గాల్లో ఉన్న అభిప్రాయాలు గురించి తెలుసుకోవడం. మనం ప్రయాణం చేయలేకపోతే, మనం విభేదించే వ్యక్తులను కనుగొని, మనది కాని పార్టీకి సంబంధించిన వార్తాపత్రికలను చదవాలి. కానీ విదేశీ ఆచారాల గురించి తెలుసుకోవడం ఎల్లప్పుడూ ప్రయోజనాలను కలిగిఉండదు.
మంచి ఊహ ఉన్న వారికి భిన్నమైన అభిప్రాయాన్ని కలిగిఉన్న వ్యక్తితో వాదనను ఊహించుకోవడం మంచి ప్రణాళిక. మహాత్మాగాంధీ రైల్వేలుస్టీమ్ బోట్లను మరియు యంత్రాలను ఇష్టపడలేదు. మరియు పారిశ్రామిక విప్లవాన్ని రద్దుచేయడానికి ఇష్టపడేవారు. పాశ్చాత్య దేశాలలో చాలా మంది ప్రజలు ఆధునిక సాంకేతిక పరిజ్ఞానాన్ని సద్వినియోగం చేసుకుంటారు. కాబట్టి ఈ అభిప్రాయం ఉన్నవారు చాలా అరుదు. కానీ, మనము ఈ అభిప్రాయంతో ఏకీభవిస్తున్నామని నిర్ధారించుకోవడానికి, గాంధీ వారితో ఏమి చెప్పారో పరిశీలించడం ద్వారా వాదనలను పరీక్షించడం మంచి ప్రణాళిక.
మన ఆత్మగౌరవాన్ని దెబ్బతీసే అభిప్రాయాల పట్ల మనం చాలా జాగ్రత్తగా ఉండాలి. స్త్రీ, పురుషులు ఇరువురు వారివారి అహంపట్ల అనుకూలంగా ఉంటారు. ఇరువురి పట్ల ధారళమైన సాక్ష్యం ఉంది. వాస్తవానికి ఈ ప్రశ్న పరిష్కరించలేము. కానీ, ఆత్మగౌరవం ఈ విషయాన్ని చాలా మంది నుండి దాస్తుంది. అందరూ వారి జాతే గొప్ప అని ఒప్పించబడతారు. గొప్ప జాతి గురించి సరైన సమాధానం లేదు. ఇందులో నుంచి బయటపడే మార్గం విశాలవిశ్వం యొక్క విస్తృతితో పోల్చుకున్నప్పుడు ఆణుమాత్రం కూడా ఉండదని మన స్థానాన్ని గుర్తించడం అహం చితికిపోతుంది. మూర్ఖపు అభిప్రాయాలు అంతరించిపోతాయి.
సరైన కారణం లేకుండా ఏదైనా గుడ్డిగా నమ్మటాన్ని మనం నివారించాలి. మన పరిశీలన ద్వారా మనం చేయు విషయాలను ఋజువు చేసుకోవాలి మరియు ఎదైనా సమస్యలకు సంబంధించి ఇతరుల అభిప్రాయాల్ని తెలుసుకోవాలి. ఆత్మగౌరవం దీన్ని చాలా ప్రభావితం చేస్తుంది. కానీ మనకు ఈ విశ్యంలో మన పాత్రను గుర్తుచేసుకొని వీటి పరిశీలన చేసుకోగలగాలి.
![]()
How to Avoid Foolish Opinions Summary in Hindi
Note: This summary is only meant for Lesson Reference, not for examination purpose
बट्रेंड रसेल निबंध ‘मूर्खतापूर्ण विचारों से कैसे बचे एक विचारोत्तेजक निबंध है । हम मुर्खों से कैसे बच सकते हैं। वे हमें अपने विश्वासों को नियंत्रण में रखने के लिए कहते हैं और विवादों – रीति-रिवाजों के बारे में विस्तार से बताते हैं । वे उन चीजों का भी उल्लेख करते हैं जो लोगों की राय को प्रभावित करती हैं, जैसे कि आत्मसम्मान और मूर्खतापूर्ण राय और हम उनसे कैसे पार सकते हैं ।
मूर्खतापूर्ण विचारों से बचने के लिए किसी अतिमानवीय प्रतिभा की आवश्यकता नहीं है । कुछ सरल नियम हमें मूर्खतापूर्ण त्रुटि से बचाते हैं । यदि मामले को अवलोकन से सुलभाया जा सकता है, तो हमें स्वयं अवलोकन करना चाहिए । अरस्तू ने यह नहीं सोचा होगा कि महिलाओं के दाँत पुरुषों की तुलना में कम होते हैं यदि उन्होंने श्रीमती अरस्तू से कहा कि जब वह गिनों तो अपना मुँह खुला रखें । यह सोचना एक बड़ी भूल है कि हम जानते हैं कि वास्तव में हम कब नहीं जानते | कई चीजें बहुत आसानी से अनुभव की परीक्षा के अधीन होती हैं, अगर वृभारी विरोधी राय हमें गुस्सा दिलाती है, तो इसका मतलब है कि हमारी राय जायज नहीं है । अगर किसी के पास बहुत बेवकूफ और गलत विचार है । हम क्रोध के बजाय दया दिखाते हैं ।
सबसे खराब विवाद उन मामलों के बारे में हैं, जिन के पास किसी भी तरह से कोई अच्छा सबूत नहीं है । कुछ प्रकार के कठोर विश्वासों से खुद को मुक्त कनने का एक अच्छा तरीका सामाजिक मंडल में हमारे अपने से अलग राय के बारे में जागरूक होना है । अगर हम यात्रा नहीं कर सकते हैं, तो हम ऐसे लोगों को ढूँढना चाहिए जिन से हमें असमत है और उस पार्टी से संबंधित समाचार पत्र पढ़ना चाहिए, जो हमारी नहीं है । लेकिन विदेशी रीति-रिवाजों से अवगत होने से हमेशा लाभ नहीं होता है ।
अच्छी कल्पना वाले लोगों के लिए, एक अलग राय रखनेवाले व्यक्ति के साथ तर्क की कल्पना करना एक अच्छी योजना है। महात्मा गाँधी रेलवे और स्टीम बोट और मशीनरी को नापसंद करते थे और औद्योगिक क्रांति को पूर्ववत् करना पसंद करते थे । पश्चिमी देशों में ज्यादावर लोग आधुनिक तकनीक का फायदा उठा लेते हैं । तो इस राय होनेवाले व्यक्ति बहुत कम हैं । लेकिन यह सुनिश्चित करने के लिए कि हम इस राय से सही सहमत हैं, गाँधीजी ने दूसरों से क्या कहा होगा, इसपर विचार करके तर्कों का परीक्षण करता एक अच्छी योजना है ।
हमें उन विचारों से बहुत सावधान रहना चाहिए जो खयं की उत्कृष्टता के प्रति अश्वस्त हों, सेक्स के दोनों पक्षों में प्रचुर प्रमाण हैं । प्रश्न वास्तव में हल नहीं किया जा सकता है । लेकिन आत्मसम्मान इसे ज्यादावर लोगों से छुपाता है । सभी लोग आश्वस्त हैं कि उनका अपना राष्ट्र सर्वश्रेष्ठ है । फिर से सर्वश्रेष्ठ राष्ट्र रै प्रश्न का कोई सही उत्तर नहीं है । इस सामान्य मानवीय घमड से निपटाने का एकमात्र तरीका यह है कि हम खुद को याद दिलाएँ कि मनुष्य ब्रह्मांड के एक छोटे से कोने में छोटे ग्रह के जीवन में एक छोटी सी घटना है और लागत के अन्य हिस्सों में प्राणी बहुत बेहतर हो सकते हैं ।
हमें बिना ठोस कारण के किसी भी बात पर आँख मूँधकर विश्वास करने से बरना चाहिए । हमें उन चीजों की पहचान करनी चाहिए जो हम अवलोकन के साथ कर सकते हैं और विवादास्पद् विषयों के बारे में उनके लोगों की राय सुन सकते हैं, आत्म सम्मान राय को बहुत प्रभावित करता है । लेकिन ब्रह्मांड में अपने स्थान से खुद को बचाकर इसकी जाँच की जा सकती है ।
Meanings and Explanations
fatal (adj) / (ఫె ఇట్ ల్)/ ‘feɪ.təl/ : causing failure or disaster, వైఫల్యాన్ని, వైపరీత్యాన్ని కలిగించగల, विफलता या आपदा के कारण होना
prone (adj)/(ప్రఉన్)/prəʊn : liable; likely to do something bad; తప్పు చేసే లక్షణము, అవకాశము కల, करने की भावना
hedgehogs (n,pl) /(హెడ్జ్ హొగ్ జ్)/ ‘hedʒ.hɒgz : small brown nocturnal animals with needle like spikes on their backs,
చిన్న గోధుమ ఛాయలో ఉండే నిశాచర జంతువులు, వీపుపై సూదుల వంటి తీగలు ఉంటాయి
छोटे भूरे रंग के निशाचर जानवर जिनकी पीठ पर सुई की तरह कीले होती हैं ।
beetles (n, pl) / (బీట్ ల్ స్) /’bi.təls : large, black insects with hard case over their backs, వీపుపై పెంకులాంటి కప్పు ఉండే పెద్ద, నల్లటి కీటకములు, पीठ पर कठोर डिब्बेनाले बड़े, काले कीड़े निश्चित रूप से कहना
commit (v) / (కమిట్)//kə’mɪt : say definitely, give an opinion, ఖచ్చితమని పెప్పుట, అభిప్రాయము ప్రకటించుట, राय देना
unicorn (n,pl) / (యూనికో(ర్)న్)// ‘ju:.nɪ.kɔ:n : an imaginary white horse like animal with a long horn, పొడవైన కొమ్ము కల గుర్రంలాంటి తెల్ల కల్పిత జంతువు, एक लंबे सींग वाला एक काल्पनिक सफेद घोड़ा जैसा जानवर; लंबे सींगवाले घोड़े की तरह एक सफेद पौराणिक जानवर
salamanders (n,pl) / (స్యాలమండ(ర్)జ్) / ‘sæl.ə.mæn.dər : animals like lizards with short legs and long tails,
పొట్టి కాళ్ళు, పొడుగుతోక ఉండే బల్లుల లాంటి జంతువులు, छोटे पैर और लंबी पूँछ वाले छिपकली जैसे जानवर
dogmatic (n) /(డొ గ్ మ్యాటిక్)/ dɒg’mæt.ɪk : being certain that one’s beliefs are right and others should accept them without considering other opinions or evidence ఇతరుల అభిప్రాయాలు, ఆధారాలు పట్టించుకోకుండా తమ నమ్మకమే సరియైనది, ఇతరులు దానిని ఆమోదించాలి అని ఖచ్చితంగా అనుకునే
दूसरों की राय या आधार को ध्यान में रखे बिना, निश्चित होना कि किसी के विश्वास सही हैं और दूसरों को उन्हें स्वीकार करना चाहिए ।
passionate (adj) / (ప్యాషనట్) / ‘pæʃ.ən.ət /: strong opinions; మంచి ఉత్సాహము కల, उत्साह की तीव्र भावनाओं का होना या दिखाना
savage (adj) / (స్యావిజ్)/’sæv.ɪdʒ / : causing great harm, అత్యంత హానికర, बहुत नुकसान पहुँचा रहा हैं
persecutions(n) /(ప (ర్)సి క్యూషన్) /p3:.sɪ’kju:ʃən : annoying others deliberately all the time: అన్ని వేళలా ఉద్దేశ్య పూర్వకంగా చికాకు పెట్టటం, हर समय जान बूझकर परेशान करना
theology (n)/(థియోలజి)/ θi’ɒl.ə.dʒi : the study of religion, మత, దైవ అధ్యయన శాస్త్రము, धर्म का अध्ययन
warrants (v) /(వొరంట్ స్) / ‘wɒr.ənt : Justifies, సమర్థిస్తున్న, సరియైనదని తెలుపు, समर्थ करना, सही है कहना
diminishing (v+ing-adj)/(డిమినిషింగ్)/dɪ’mɪn.ɪʃın : decreasing, తగ్గుతున్న, हासमान / घटना
intensity (n)/(ఇంటెన్స టి)/ ɪn’ten.sə.ti : huge quantity; great degree, పెద్ద మొత్తం, ఎక్కువ స్థాయి, तीव्रता / बड़ीमात्रा
![]()
insular (adj)/(ఇన్ స్య ల(ర్)) /in.sjə.lər : only interested in one’s own opinions, తమ అభిప్రాయాలపట్ల మాత్రమే ఆసక్తిగల, केवल अपनी राय में दिल चस्पी है।
prejudice (n)/(ప్రెజుడిస్)/ ‘predʒ.ə.dɪs : an unreasonable liking or dislike without sensible base, దురభిప్రాయములు, ఆధార రహిత ఆసక్తి లేదా వ్యతిరేకత, युक्तियुक्त आधार के बिना अकारण और अनुचित प संद या नापसंद
perverse (adj)/(ప(ర్)వ(ర్)స్) / pə’v3:s : deliberately and determinedly doing what others think is wrong, ఇతరులు తప్పు అని భావించేదానిని కావాలని గట్టి పట్టుదలతో చేసే, जानबूझकर और निर्णायक रूप से वही करना जो दूसरे गलत समझते हैं ।
reflection (n) /(రిఫ్లెక్షన్)/ ri’flek.ʃən : careful thought, పరిశీలించి చేసిన ఆలోచన, सावधान विचार
Manchus (n prop); (మ్యాంసూచ్)/ mæn’tʃʊ : people who are originally living in Manchuria, who formed the last imperial dynasty in China (1644-1912) ; స్వతహాగా మంచూరియ దేశీయులు, 1644 నుండి 1912 వరకు చైనాను పాలించిన చివరి సామ్రాజ్యా ధినేతలు, सावधान विचार लोग जो मूल रूप मे मंचूरिया में रह रहे हैं, जिन्होंने चीन में अंतिम राजवंश का गठन किया (1644-1912)
pigtail (n)/(పిగ్ టె ఇల్) / ‘pɪg.teɪl : : hair bunched into a plait, జడ, बालों को एक चोटी के रूप में बाँधा गया
dominion (డమినిఅన్)/ də’mɪn.jən : authority to rule, పాలనాధికారము, शासन करने का अधिकार
deplores (v) /(డిప్లో(ర్)జ్)/ dɪ’plɔ:r : criticises strongly and publicly, బహిరంగంగా, తీవ్రంగా విమర్శించుట, कड़ी और खुलेआम आलोचना करना
refutation (n) /(రెఫ్యు టె ఇసన్) / ref.ju’teɪ.ʃən : proof that something is wrong, ఇతరులకు విసుగు కలిగేంచేంతగా అతి విశ్వాసముతో, ( पुनरावृत्ति) प्रमाण है कि यह गलत है
cocksure (adj)/(కొక్ షు ఆ(ర్))/kɒk’∫ɔ:r : confident that annoys, ఇతరులకు విసుగు కలిగేంచేంతగా అతి విశ్వాసముతో, दूसरों को परेशान करने की हद तक अति आविश्वास से
abundant (adj) /(అబండంట్)/o’bʌn.dənt : plentiful, పెద్ద మొత్తాలలో ఉన్న, बड़ी मात्रा में
inherently (adv)/(ఇన్ హి అరంట్లి)/ ɪn’her.ənt.li : in a way as a natural part of something, అంతర్లీనంగా, సహజంగా భాగమై ఉన్న, एक तरह से किसी चीज के प्राकृतिक भाग के रूप में
conceals (v)/(కన్ సీల్ జ్)/ kən’si:l : hides, wepe, छुपाना
persuaded (v,pt)/(ప(ర్)స్వె ఇడిడ్) / pə’sweɪd : made some one believe something is correct సరియైనది అని నమ్మేలా చేసేను,
किसी को विश्वास दिलाया कि कुछ सही है
trivial (adj) /(ట్రివిఆల్)/ ‘trɪv.i.əl : not important, ప్రాధాన్యత లేని, तुच्छ, महत्वपूर्ण नहीं
demonstrably (డిమొన్ స్ట్రబ్ లి)/ dɪ’mon.strə.bli : in a way that can be proved, నిరూపణకు వీలైన రీతిలో, एक तरह से जिसे साबित किया जा सकता है, एक सत्यापन योग्य तरीके से
aught (n)/(ఓట్)/ɔ:t/ : the smallest part, అతి చిన్న భాగము, सबसे छोटा हिस्सा
reflection (n) /(రిఫ్లెక్షన్) / rɪflek.ʃən : careful thought, పరిశీలించి చేసిన ఆలోచన, सावधान विचार
Manchus (n-prop)/(మ్యాంచూస్)/mæn’tʃʊ : people who are originally living in Manchuria, who formed the last imperial dynasty in China, (1644 – 1912) స్వతహాగా మంచూరియ దేశీయులు, 1644 నుండి 1912 వరకు చైనాను పాలించిన చివరి సామ్రాజ్యా ధినేతలు
सावधान विचार लोग जो मूल रूप मे मंचूरिया में रह रहे हैं, जिन्होंने चीन में अंतिम राजवंश का गठन किया (1644-1912)
pigtail (n) ⁄(పిగ్ టె ఇల్) / ‘pɪg.teɪl : hair bunched into a plait, జడ, बालों को एक चोटी के रूप में बाँधा गया
dominion (n) /(డమినిఅన్)/ də’mɪn.jən : authority to rule, పాలనాధికారము, शासन करने का अधिकार
deplores (v) /(డిప్లో(ర్)జ్)/dɪ’plɔ:r : criticises strongly and publicly, బహిరంగంగా, తీవ్రంగా విమర్శించుట, कड़ी और खुलेआम आलोचना करना
refutation (n) /(రెఫ్యు టెఇసన్)/ ref.ju’teı.ʃən : proof that something is wrong, ఇతరులకు విసుగు కలిగేంచేంతగా అతి విశ్వాసముతో, ( पुनरावृत्ति) प्रमाण है कि यह गलत है
cocksure (adj)/(కొక్ షు (అర్))/kɒk’ʃɔ:r : confident that annoys, ఇతరులకు విసుగు కలిగేంచేంతగా అతి విశ్వాసముతో, दूसरों को परेशान करने की हद तक अति आविश्वास से
abundant (adj) (అబండంట్)/ ɔ’bʌn.dənt : plentiful, పెద్ద మొత్తాలలో ఉన్న, बड़ी मात्रा में
inherently (adv)/(ఇన్ హిఅరంట్లి)/ ɪn’her.ənt.li : in a way as a natural part of something, అంతర్లీనంగా, సహజంగా భాగమై ఉన్న, एक तरह से किसी चीज के प्राकृतिक भाग के रूप में
conceals (v)/(కన్ సీల్ జ్)/ kən’si:l : hides, దాచిపెట్టుట, छुपाना
![]()
persuaded (v,pt)/(ప(ర్)స్వెఇడిడ్) / pə’sweɪd : made some one believe something is correct సరియైనది అని నమ్మేలా చేసేను, किसी को विश्वास दिलाया कि कुछ सही है
trivial (adj) (ట్రివిఆల్)/’trɪv.i.əl : not important, ప్రాధాన్యత లేని, तुच्छ, महत्वपूर्ण नहीं
(demonstrably /(డిమొన్ స్ట్రబ్ లి)/ dɪ’mɒn.strə.bli : in a way that can be proved, నిరూపణకు వీలైన రీతిలో, एक तरह से जिसे साबित किया जा सकता है, एक सत्यापन योग्य तरीके से
aught (n) : (ఓట్) : ɔ:t : the smallest part, అతి చిన్న భాగము, सबसे छोटा हिस्सा

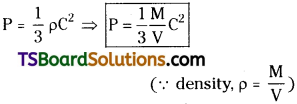
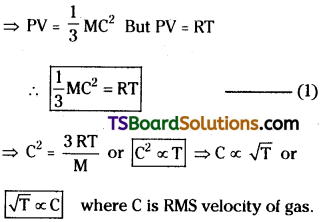

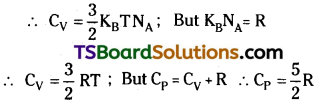


















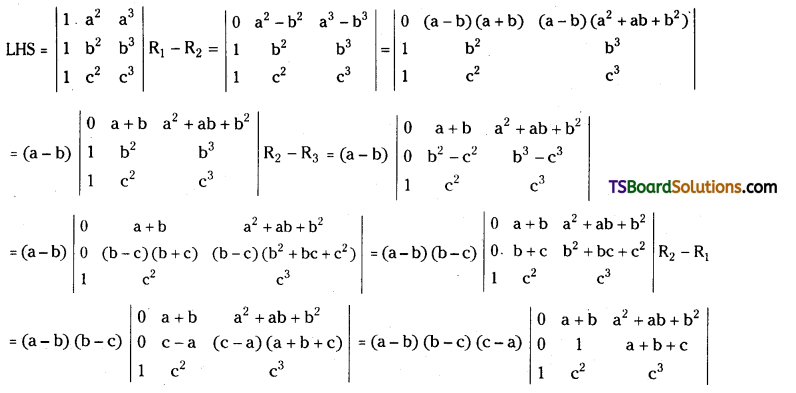
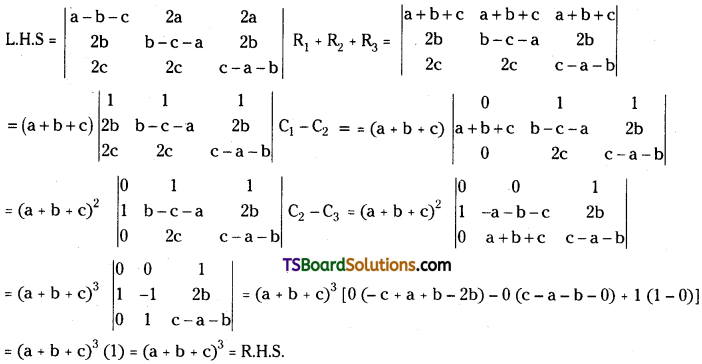
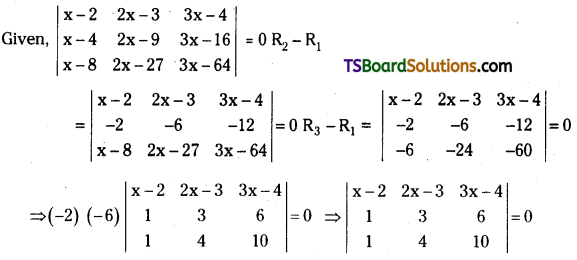
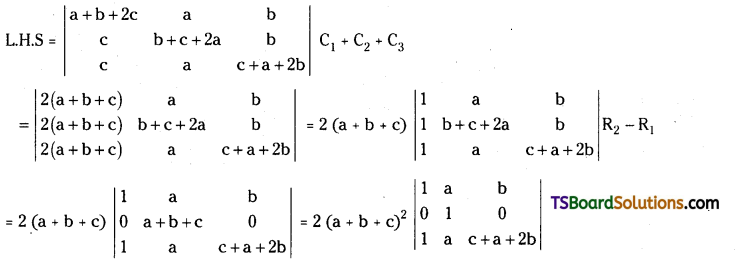 = 2 (a + b + c)2 [1{(c + a + 2b) – 0} – a (0 – 0) + b (0 – 1)]
= 2 (a + b + c)2 [1{(c + a + 2b) – 0} – a (0 – 0) + b (0 – 1)]