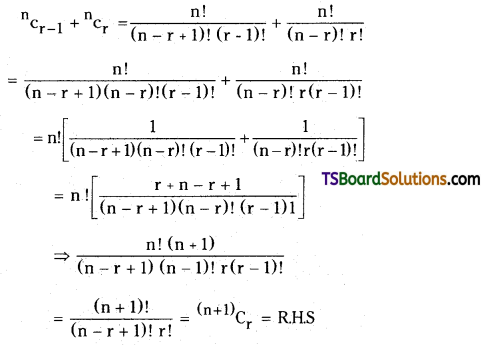Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Short Answer Type to help strengthen their preparations for exams.
TS Inter Second Year Maths 2A Permutations and Combinations Important Questions Short Answer Type
Question 1.
If the letters of the word PRlSON are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the rank of the word
i) PRISON.
ii) SIPRON [Mar. ‘14, May’ 13, AP – Mar. 2017]
Solution:
i) The alphabetical order of the letters of the given word is I, N, O, P, R, S.
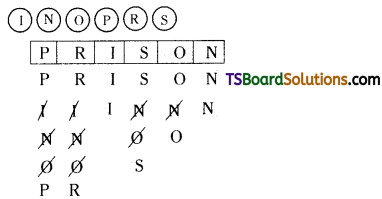
The no. of words begin with I is 5! = 120
The no. of words begin with N is 5! = 120
The no. of words begin with O is 5! = 120
The no. of words begin with Pl is 4! = 24
The no. of words begin with PN is 4! = 24
The no. of words begin with PN is 4! = 24
The no. of words begin with PRlN is 2! = 2
The no, of words begin with PRIO is 2! = 2
The no. of words begin with PRISN is 1! = 1
The next word is PRISON = 1
∴ Rank of the word, PRISON = 120 + 120 + 120 + 24 + 24 + 24 + 2 + 2 + 1 + 1 = 438.
ii) The alphabetical order of the letters of the given word is I, N, O, P, R, S.

The no. of words begin with L is 5! = 120
The no. of words begin with N is 5! = 120
The no. of words begin with Ois 5! = 120
The no. of words begin with P is 5! = 120
The no. of words begin with R is 5! = 120
The no. of words begin with SIN is 3! 6
The no. ol words begin with SlO is 3! = 6
The no. of words begin with SIPN is 2! = 2
The no. of words begin with SIPO is 2! = 2
The no. of wor(ls begin with SIPRN is 1! = 1
The next word is SIPRON = 1
∴ The Rank of SIPRON is 120 + 120 + 120 + 120 + 120 + 6 + 6 + 2 + 2 + 1 + 1 = 618.

Question 2.
If the letters of the word MASTER are permuted In all possible ways and the words thus formed are arranged in the dictionary order, then find the ranks of the word REMAST. [March ‘08, Board Paper].
Solution:

The alphabetical order of the letters of the given word is A, E. M, R, S, T.
The no. of words begin with A is 5! = 120
The no. of words begin with E is 5! = 120
The no. of words begin with M is 5! = 120
The no. of words begin with RA is 4! = 24
The no. of words begin with REA is 3! = 6
The next word is REMAST = 1
∴ The Rank of the word, REMAST = 120 + 120 + 120 + 246 + 1 = 391.
Question 3.
If the letters of the word MASTER are permuted in all possible ways and the words thus fonned are arranged in the dictionary order, then find the ranks f the word MASTER. [AP & TS – Mar. 2019] [May ‘11, ‘10, ‘07,’06; March ‘11,’09, ‘08, TS – Mar. 2016; AP – Mar., May 2015].
Solution:
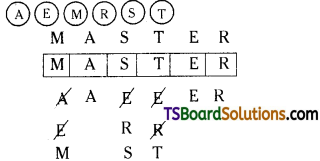
The alphabetical order of the letters of thi given word is A, E, M, R, S, T.
The no. of words begin with A is 5! = 120
The no. of words begin with E is 5! = 120
The no. of words begin with MAE is 3! = 6
The no. of words begin with MAR is 3! = 6
The no. of words begin with MASE is 2! = 2
The no. of words begin with MASR is 2! = 2
The next word is MASTER = 1
The Rank of the word, MASTER = 120 + 120 + 6 + 6 + 2 + 2 + 1 = 257.
Question 4.
Find the sum of all 4-digit numbers that can be formed using the digits 1, 3, 5, 7, 9. [AP & TS – Mar. 18; May ‘14, Mar.13]
Solution:
The no. of four digited number formed by using the digits 1, 3, 5, 7, 9 without repetition = \({ }^n P_r={ }^5 P_4\)
= 5 . 4. 3 . 2 = 120.
Out of these 120 numbers, \({ }^n P_r={ }^5 P_4\) number contain 1 in units place.
\({ }^4 \mathrm{P}_3\) numbers contain 1 in Ten’s place.
\({ }^4 \mathrm{P}_3\) numbers contain 1 in hundred’s place.
\({ }^4 \mathrm{P}_3\) numbers contain 1 in thousand’s place.
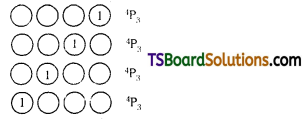
∴ The value obtained by adding (1) in all the numbers = \({ }^4 \mathrm{P}_3\) × 1 × 1 + \({ }^4 \mathrm{P}_3\) × 1 × 10 + \({ }^4 \mathrm{P}_3\) × 1 × 100 + \({ }^4 \mathrm{P}_3\) × 1 × 1000
= \({ }^4 \mathrm{P}_3\) × 1 + \({ }^4 \mathrm{P}_3\) × 10 + \({ }^4 \mathrm{P}_3\) × 100 + \({ }^4 \mathrm{P}_3\) × 1000
= \({ }^4 \mathrm{P}_3\) × 1 [1 + 10 + 100 + 1000]
= \({ }^4 \mathrm{P}_3\) × 3 × (1111)
Similarly the value obtained by adding (3) is \({ }^4 \mathrm{P}_3\) × 3 × 1111
The value obtained by adding (5) is \({ }^4 \mathrm{P}_3\) × 5 × 1111
The value obtained by adding (7) is \({ }^4 \mathrm{P}_3\) × 7 × 1111
The value obtained by adding (9) is \({ }^4 \mathrm{P}_3\) × 9 × 1111
The sum of all the numbers = \({ }^4 \mathrm{P}_3\) × 1 × (1111) + \({ }^4 \mathrm{P}_3\) × 3 × (1111) + \({ }^4 \mathrm{P}_3\) × 5 × (1111) + \({ }^4 \mathrm{P}_3\) × 7 × (1111) + \({ }^4 \mathrm{P}_3\) × 9 × (1111)
= \({ }^4 \mathrm{P}_3\) (1111) [1 + 3 + 5 + 7 + 9]
= 24 (1111) (25) = 6,66,600.

Question 5.
Find the sum of aIl 4 digited numbers that can be formed using the digits 1, 2, 4, 5, 6 without repetition. [March ’10]
Solution:
The number of 4 digited numbers formed by using the digits 1, 2, 4, 5, 6 without repetition = \({ }^5 \mathrm{P}_4\)
= 5 . 4 . 3 . 2 = 120
Out of these 120 numbers,
\({ }^4 \mathrm{P}_3\) numbers contain 1 in units places
\({ }^4 \mathrm{P}_3\) numbers contain 1 in ten’s place
\({ }^4 \mathrm{P}_3\) numbers contain 1 in hundred’s place
\({ }^4 \mathrm{P}_3\) numbers contain 1 in thousand’s place

∴ The value obtained by adding (1) in all the numbers
= \({ }^4 \mathrm{P}_3\) × 1 × 1 + \({ }^4 \mathrm{P}_3\) × 1 × 10 + \({ }^4 \mathrm{P}_3\) × 1 × 100 + \({ }^4 \mathrm{P}_3\) × 1 × 1000
= \({ }^4 \mathrm{P}_3\) × 1 [1 + 10 + 100 + 1000]
= \({ }^4 \mathrm{P}_3\) × 1 × 1111
Similarly the value obtained by adding (2) is \({ }^4 \mathrm{P}_3\) × 2 (1111)
The value obtained by adding (4) is \({ }^4 \mathrm{P}_3\) × 4 (1111)
The value obtained by adding (5) is \({ }^4 \mathrm{P}_3\) × 5 (1111)
The value obtained by adding (6) is \({ }^4 \mathrm{P}_3\) × 6 (1111)
∴ The sum of all the numbers = \({ }^4 \mathrm{P}_3\) x 1×1111 + \({ }^4 \mathrm{P}_3\) x2(1111) + \({ }^4 \mathrm{P}_3\) x4(1111) + \({ }^4 \mathrm{P}_3\) x5(1111)+ \({ }^4 \mathrm{P}_3\)x6(1111)
= \({ }^4 \mathrm{P}_3\) (1111) + (1 + 2 + 4 + 5 + 6)
= \({ }^4 \mathrm{P}_3\) (1111) (18)
= 4 . 3 . 2 (1111) (18)
= 24 (1111) 18
= 479952.
Question 6.
Find the number of numbers that are greater than 4000 which can be formed using the digits 0, 2, 4,6, 8 without repetition. [May ‘09]
Solution:
From the given digits, 0 cannot be placed in the first place. So, 1st place can be filled with the remaining four digits.
All the numbers of five digits are greater than 4000.
4 digit numbers:
In four digit numbers the number starting 4 with 4 or 6 or 8 are greater than 4000.
The number of 4 digit numbers which begin with 4 or 6 or 8 = 3 . \({ }^4 \mathrm{P}_3\)
= 3 . 4 . 3 . 2 = 72
5 digit numbers:

The number of five digit numbers = 4 . \({ }^4 \mathrm{P}_4\)
= 4 . 4 . 3 . 2 . 1 = 96
∴ The number of numbers greater than 4000 = 72 + 96 = 168.
Question 7.
Find the number of ways of arranging 5 different mathematics hooks, 4 different physics books and 3 different chemistry books such that the books of the same subject are together.
Solution:
The number of ways of arranging three bundles of Maths, Physics and Chemistry books is \({ }^3 \mathrm{P}_3\) = 3!.
5 different Mathematics books in the bundle are arranged among themselves in 5! ways.
4 different Physics books in the bundle are arranged among themselves in 4! ways.
3 different Chemistry books in the bundle are arranged among themselves in 3! ways.
∴ The required number of arrangements = 3! . 5! . 4! . 3!
= 6 . 120 . 24 . 6 = 103684.

Question 8.
Find the number of ways of arranging 7 gents and 4 ladies around a circular table if no two ladles wish to sit together. [May ‘07]
Solution:
First arrange 7 gents around a circle in (7 – 1)! = 6! ways.

Now arrange 4 ladies in 7 positions in \({ }^7 \mathrm{P}_4\) ways.
∴ The required number of arrangements = 6! . \({ }^7 \mathrm{P}_4\)
= 6 . 5 . 4 . 3 . 2 . 1 . 7 . 6 . 5 . 4 = 604800.
Question 9.
Find the number of ways of arranging the letters of word SINGING so that
i) they begin and end with I
ii) the two G’s come together.
Solution:
The given word has 7 letters ¡n which there are 21’s are alike, 2N’s are alike. 2G’s are alike, 1S is different.
i) They begin and end with I:

First we fill the first and last places with I’s in \(\frac{2 !}{2 !}\) ways.
Now, we fill the remaining 5 places with the remaining 5 letters in \(\frac{5 !}{2 ! 2 !}\) ways.
∴ The number of required arrangments is \(\frac{5 !}{2 ! 2 !} \cdot \frac{2 !}{2 !}=\frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 2}\) = 30.
ii) The 2 G’s come together:
Treat the 2Gs as one unit.
Then we have 6 letters in which there are 2I’s and 2N’s.
They can be arranged in \(\frac{6 !}{2 ! 2 !}\) ways.
Now, the 2G’s can be arranged among themselves in \(\frac{2 !}{2 !}\).
∴ The number of required arrangments is \(\frac{6 !}{2 ! 2 !} \cdot \frac{2 !}{2 !}\) = 180.
Question 10.
If the letters of the word EAMCET are permuted in all possible ways and 1f the words they formed are arranged In the dictionary order, find the rank of the word EAMCET. [TS – May 2015; Mar. ‘12] [AP – May, Mar. 2016; TS – Mar. 2017, May ’16]
Solution:
Given word EAMCET,
The alphabetical order of the letters of the, ACEEMT.
The no. of words begin with A = \(\frac{5 !}{2 !}\) = 60
The no. of words begin with C = \(\frac{5 !}{2 !}\) = 60
The no. of words begin with EAC = 3! = 6
The no. of words begin with EAE = 3! = 6
The next word is EAMCET = 1
Rank of word EAMCET = 60 + 60 + 6 + 6 + 1 = 133.

Question 11.
If 1 ≤ r ≤ n,then show that \({ }^n C_{r-1}+{ }^n C_r={ }^{(n+1)} C_r\). [March’11, May ‘9]
Solution:
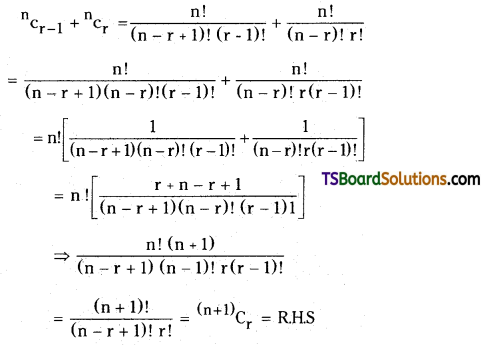
Question 12.
Prove that 3 ≤ r ≤ n, \({ }^{(n-3)} C_r+3 \cdot{ }^{(n-3)} C_{(r-1)}+3 \cdot{ }^{(n-3)} C_{(r-2)}\) + \({ }^{(n-3)} C_{(r-3)}={ }^n C_r\). [May ’12, ’09]
Solution:

Question 13.
Simplify \({ }^{34} C_5+\sum_{r=0}^4(38-r) C_4\). [AP – Mar. ’19, ’17, ’16; March ’12, May ’11].
Solution:


Question 14.
Find the number of ways of selecting 3 girls and 3 boys out of 7 girls and 6 boys. [May ’09]
Solution:
The no. of ways of selecting 3 girls and 3 boys out of 7 girls and 6 boys = \({ }^7 \mathrm{C}_3 \cdot{ }^6 \mathrm{C}_3\)
= \(\frac{7 \cdot 6 \cdot 5}{1 \cdot 2 \cdot 3} \cdot \frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1}\) = 700
Question 15.
Find the number of ways of selecting 3 vowels and 2 consonants from the letters of the word EQUATION. [May ’11, March ’07]
Solution:
The word EQUATION contains 5 vowels and 3 consonants.
The 3 vowels can be selected from 5 vowels in \({ }^5 \mathrm{C}_3\) ways.
The 2 consonants can be selected from 3 consonants in \({ }^3 \mathrm{C}_2\) ways.
∴ The required no. of ways of selecting 3 vowels and 2 consonants = \({ }^5 \mathrm{C}_3 \cdot{ }^3 \mathrm{C}_2\)
= \(\frac{5 \cdot 4 \cdot 3}{3 \cdot 2 \cdot 1} \cdot \frac{3 \cdot 2}{2 \cdot 1}\) = 30.
Question 16.
Prove that \(\frac{{ }^{4 n} C_{2 n}}{{ }^{2 n} C_n}=\frac{1 \cdot 3 \cdot 5 \ldots \ldots(4 n-1)}{\{1 \cdot 3 \cdot 5 \ldots \ldots(2 n-1)\}^2}\). [TS – Mar. ’19, May ’08, 2000, Mart. ’98] [AP – Mar. 2017, 2015, TS – May 2015].
Solution:


Question 17.
Find the number of ways of selecting a cricket team of 11 players from 7 batsmen and 6 bowlers such that there will be atleast 5 bowlers in the team. [May ’14, ’10, March ’05, Board Paper AP – May 2016; TS – Mar. 18, May 2016]
Solution:
Total number of players in the team = 11.

1) 6 Batsmen, 5 bowlers:
The no. of ways of selecting a cricket team = \({ }^7 \mathrm{C}_6 \cdot{ }^6 \mathrm{C}_5\)
= 7 . 6 = 42
2) 5 Batsmen, 6 bowlers:
The no. of ways of selecting cricket team = \({ }^7 \mathrm{C}_5 \cdot{ }^6 \mathrm{C}_6\)
= \(\frac{7 \cdot 6}{2 \cdot 1}\) . 1
= 7 . 3 = 21.
Question 18.
Find the number of ways of forming a committee of 5 members out of 6 Indians and 5 Americans so that always the Indians will be in majority in the committee. [TS – Mar. 2015; March ‘13. ’09, ’08]
Solution:
Since, the committee must contain always the Indians will be in majority, the members of the committee may be the following.
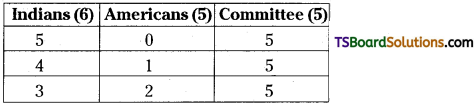
i) 5 Indians, 0 Americans.
The no. of ways of selecting committee = \({ }^6 \mathrm{C}_5 \cdot{ }^5 \mathrm{C}_0\)
=6×1 = 6
ii) 4 Indians, 1 American:
The no. of ways of selecting committee = \({ }^6 \mathrm{C}_4 \cdot{ }^5 \mathrm{C}_1\)
= \(\frac{6 \cdot 5}{2 \cdot 1}\) . 5 = 75
iii) 3 Indians, 2 Americans.
The no. of ways of selecting committee = \({ }^6 \mathrm{C}_3 \cdot{ }^5 \mathrm{C}_2\)
= \(\frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} \cdot \frac{5 \cdot 4}{2 \cdot 1}\) = 200
The required no. of ways of selecting j committee = 6 + 75 + 200 = 281.

Some More Maths 2A Permutations and Combinations Important Questions
Question 19.
If \({ }^n \mathrm{P}_3\) = 1320, find n. [May ’08, March ’10, ’07]
Solution:
Given \({ }^n \mathrm{P}_3\) = 1320 = 12 . 11 . 10
\({ }^n P_3={ }^{12} P_3\)
⇒ n = 12.
Question 20.
If \((n+1) P_5:{ }^n P_6\) = 2 : 7, find n.
Solution:
Given \(\frac{(n+1)}{{ }^n P_5}=\frac{2}{7}\)
\(\frac{(n+1) n(n-1)(n-2)(n-3)}{n(n-1)(n-2)(n-3)(n-4)(n-5)}=\frac{2}{7}\)
\(\frac{(n+1)}{(n-4)(n-5)}=\frac{2}{7}\)
7n + 7 = 2 (n2 – 5n – 4n + 20)
7n + 7 = 2n2 – 18n + 40
2n2 – 18n – 7n + 40 – 7 = 0
2n2 – 25n + 33 = 0
2n2 – 22n – 3n + 33 = 0
2n (n – 11) – 3 (n – 11) = 0
(n – 11) (2n – 3) = 0
n = 11; n = \(\frac{3}{2}\)
Since, n is a integer then n = 11.
Question 20.
If \({ }^{18} P_{(r-1)}:{ }^{17} P_{(r-1)}\) = 9 : 7, find ‘r’.
Solution:
Given, \({ }^{18} \mathrm{P}_{\mathrm{r}-1}:{ }^{17} \mathrm{P}_{\mathrm{r}-1}\) = 9 : 7

Question 21.
Find the number of different chains that can be prepared using 7 dIfferent coloured beads.
Solution:
Total number of beads n = 7
The no. of different chains that can be prepared using 7 different coloured beads is = \(\frac{(7-1) !}{2}=\frac{6 !}{2}\) = 360.

Question 22.
Prove that \({ }^{25} C_4+\sum_{r=0}^4(29-r) C_3={ }^{30} C_4\). [AP – Mar. 2018]
Solution:

Question 23.
Find the number of ways of arranging 5 boys and 4 girls in a row so that the row begins and ends with boys.
Solution
The total no. of persons is 9. (5 boys + 4 girls)
Let us take 9 blank’s,
First, we fill the first and last places with boys.
This can be done in \({ }^5 \mathrm{P}_2\) ways.
Now, we have to fill up the remaining 7 places with the remaining 7 persons (3 boys + 4 girls) In 7! ways.
The required no. of arrangements is = \({ }^5 \mathrm{P}_2\) . 7!
= 20 × 5040 = 100800.
Question 24.
In how many ways 9 mathematics papers can be arranged so that the best and the worst (i) may come together (ii) may not come together?
Solution:
i) If the best and worst papers are treated as one unit, then we have 9 – 2 + 1 = 7 + 1 = 8 papers.
Now these can be arranged in (7 + 1)! ways and the best and worst papers between themselves can be permuted in 2! ways.
Therefore the number of arrangements in which best and worst papers come twet her is 8! 2!.
ii) Total number of ways of arranging 9 mathematics papers is 9!.
The best and worst papers come together in 8! . 2! ways.
Therefore the number of ways they may not come together is
9! – 8! 2! = 8! (9 – 2) 8! × 7.

Question 25.
Find the number of ways of arrangIng 6 boys and 6 girls ¡n a row. In how many of these arrangements
i) all the girls are together
ii) no two girls are together
iii) boys and girls come alternately?
Solution:
6 boys + 6 girls = 12 persons.
They can be arranged in a row in (12)! ways.
i) Treat the 6 girls as one unit. Then we have 6 boys + 1 unit of girls.
They can be arranged in 7! ways.
Now, the 6 girls among themselves can be permuted in 6! ways.
Hence, by the fundamental principle, the number of arrangements in which all 6 girls are together 7! x 6!.
ii) First we arrange 6 boys in a row in 6! ways.
The girls can be arranged in the 7 gaps between the boys.
These gaps are shown below by the letter X.

Now, the girls can be arranged in these 7 gaps in \({ }^7 \mathrm{P}_6\) ways.
Hence, by the fundamental principle, the number of arrange ments in which no two girls corner together is 6! × 7P6
= 6! × 7!
= 7 × 6! × 6!.
iii) Let us take 12 places. The row may begin with either a boy or a girl. That is, 2 ways.
If it begins with a boy, then all odd places (1, 3, 5, 7, 9, 11) will be occupied by boys and the even places (2, 4, 6, 8, 10, 12) by girls.
The 6 boys can be arranged in the 6 odd places in 6! ways and the 6 girls can be arranged in the 6 even places in 6! ways.
Thus the number of arrangements in which boys and girls come alternately is 2 x 6! x 6!.
Note :
In the above, one may think that questions (ii) and (iii) are same. But they are not (as evident from the answers).
In Question (ii), after arranging 6 boys, we found 7 gaps and 6 girls are arranged in these 7 gaps.
Hence one place remains vacant.
It can be any one of the 7 gaps. But in Question (iii), the vacant place should either be at the beginning or at the ending but not in between.
Thus, only 2 choices for the vacant place.
Question 26.
Find the number of 4 letter words that can be formed using the letters of the word MIRACLE. How many of them
i) begin with an vowel
ii) begin and end with vowels
iii) end with a consonant ?
Solution:
The word MIRACLE has 7 letters. Hence the number of 4 letter words that can be formed using these letters is \({ }^7 \mathrm{P}_4\) = 7 × 6 × 5 × 4 = 840.
Let us take 4 blanks.

i) We can fill the first place with one of the 3 vowels (I, A, E) in \({ }^3 \mathrm{P}_1\) = 3 ways.
Now, the remaining 3 places can be filled using the re¬maining 6 letters in \({ }^6 \mathrm{P}_3\) = 120 ways.
Thus the number of 4 letter words that begin with an vowel is 3 × 120 = 360.
ii) Fill the first and last places with 2 vowels in \({ }^3 \mathrm{P}_2\) = 6 ways.
The remaining 2 places can be filled with the remaining 5 letters in \({ }^5 \mathrm{P}_2\) = 20 ways.
Thus the number of 4 letter words that begin and end with vowels is 6 × 20 = 120.
iii) We can fill the last place with one of the 4 consonants (M, R, C, L) in \({ }^4 \mathrm{P}_1\) = 4 ways.
The remaining 3 places can be filled with the letters in \({ }^6 \mathrm{P}_3\) ways.
Thus the number of 4 letter words that end with an vowel is 4 × \({ }^6 \mathrm{P}_3\) = 4 × 120 = 480.

Question 27.
Find the number of ways of permuting the letters of the word PICTURE so that
i) all vowels come together
ii) no two vowels come together.
iii) the relative positions of vowels and consonants are not disturbed.
Solution:
The word PICTURE has 3 vowels (I, U, E) and 4 consonants (P, C, T, R).
i) Treat the 3 vowels as one unit. Then we can arrange 4 consonants + 1 unit of vowels in 5! ways. Now the 3 vowels among themselves can be permuted in 3! ways. Hence the number of per¬mutations in which the 3 vowels come together is 5! × 3! = 720.
ii) First arrange the 4 consonants in 4! ways. Then in between the vowels, in the beginning and in the ending, there are 5 gaps as shown below by the letter X.
In these 5 places we can arrange the 3 vowels \({ }^5 \mathrm{P}_3\) ways.
Thus the number of words in which no two vowels come together is 4! × \({ }^5 \mathrm{P}_3\)
= 24 × 60 = 1440.
iii) The three vowels can be arranged in their relative positions in 3! ways and the 4 consonants can be arranged in their relative positions in 4! ways.

The required number of arrangements is 3! . 4! = 144.
Note :
In the above problem, from (i) we get that the number of permutations in which the vowels do not come together is
= Total number of permutations – number of permutations in which 3 vowels come together.
= 7! – 5! . 3!
= 5040 – 720 = 4320.
But the number of permutations in which no two vowels come together is only 1440.
In the remaining 2880 permutations two vowels come together and third appears away from these.
Question 28.
Find the number of 4-digit numbers that can be formed using the digits 2, 3, 5, 6, 8 (without repetition). How many of them are divisible by
i) 2
ii) 3
iii) 4
iv) 5
v) 25
Solution:
The number of 4 digit numbers that can be formed using the 5 digits 2, 3, 5, 6, 8 is \({ }^5 \mathrm{P}_4\) = 120.
i) divisible by 2 :
A number is divisible by 2, when its unit place must be filled with an even digits (2 or 6 or 8) from among the given integers. This can be done in three ways.
Now, the remaining three places can be filled with remaining four digits in \({ }^4 P_3\) = 4 . 3 . 2 = 24 ways.
∴ The no. of 4 digited numbers divisible by 2 = 3 . 24 = 72

ii) Divisible by 3:
A number is divisible by 3 only when sum of the digits in that number is a multiple of 3.
Sum of the given 5 digits = 2 + 3 + 5 + 6 + 8 = 24.
The 4 digits such that, their sum is a multiple of 3 from the given digits are 2, 3, 5, 8 (or) 2, 5, 6, 8.
In each case, we can permute (arrange) in 4! ways.
∴ The no. of 4 digited numbers divisible by 3 = 2 . 4!
= 2 . 4 . 3 . 2 . 1 = 48.
∴ The no. of 4 digited numbers divisible by 3 = 48.
iii) Divisible by 4 :
A number is divisible by 4.
Hence, the last two places should be filled with one of the following 28, 32, 36, 52, 56, 68.
Thus, the last two places can be filled in 6 ways.
The remaining two places can be filled by remaining three digits in \({ }^3 \mathrm{P}_2\) = 3 . 2 = 6 ways.
The number of 4 digited number divisible by 4 = 6 × 6 = 36.
iv) Divisible by 5 :
A number is divisible by 5 when its units place must be filled by 5 from the given integers 2, 3, 5, 6, 8.
This can be done in one way.
The remaining three places can be filled with remaining 4 digits in 4P3 ways = 4 . 3 . 2 = 24 ways.
∴ The number of 4 digited number divisible by 5 = 1 × 24 = 24.
v) Divisible by 25 :
A number is divisible by 25, when its last two places are filled with 25.
Thus, the last two places can be filled in one way.
The remaining two places from the remaining 3 digits can be filled in \({ }^3 \mathrm{P}_2\) = 6 ways.
∴ The number of 4 digited number divisible by 25 = 1 × 6 = 6.
Question 29.
If the letters of the word BRING are per-muted in all possible ways and the words thus formed are arranged in the dictionary order, then find the 59th word.
Solution:
Given word is BRING.
∴ The alphabetical order of the letters is B, G, I, N, R.
In the dictionary order, first we write all words beginning with B.
Clearly the number of words beginning with B are 4! = 24.
Similarly the number of words begin with G are 4! = 24.
Since the words begin with B and G sum to 48, the 59th word must start with I.
Number of words given with IB = 3! = 6
Hence the 59th word must start with IG. Number of words begin with IGB = 2! = 2
Number of words begin with IGN = 2! = 2
∴ Next word is 59th = IGRBN.
Question 30.
Find the number of 5-letter words that can be formed using the letters of the word MIXTURE which begin with an vowel when repetitions are allowed.
Solution:
We have to fill up 5 blanks using the letters of the word MIXTURE having 7 letters among which there are 3 vowels. Fill the first place with one of the vowels (I or U or E) in 3 ways as shown below.

Each of the remaining 4 places can be filled in 7 ways (since we can use all 7 letters each time).
Thus the number of 5 letter words is 3 × 7 × 7 × 7 × 7 = 3 × 74.

Question 31.
Find the number of 4 – digit numbers that can be formed using the digits 1, 2, 3, 4, 5, 6, that are divisible by
i) 2
ii) 3 when repetition is allowed.
Solution:
i) Numbers divisible by 2:
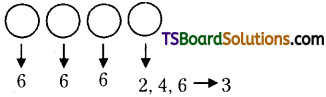
For a number to be divisible by 2.
The units place should be filled with an even digit (2 or 4 or 6).
This can be done in 3 ways.
Now, each of the remaining 3 places can be filled in 6 ways.
∴ The number of 4 digit numbers that are divisible by 2 is 8.
ii) Numbers divisible by 3 :
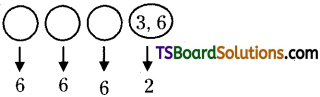
Fill the first three places with the given 6 digits in 63 ways.
Now, after filling up the first three places with three digits if we fill up the unit’s place in 6 ways we get 6 consecutive positive integers.
Out of any six consecutive integers exactly two are divisible by 3.
Hence, the unit’s place can be filled in two ways.
∴ The number of 4 digit numbers divisible by 3 is
2 . 63 = 2 . 216 = 432.
Question 32.
Find the number of 5 – letter words that! can be formed using the letters of the word EXPLAIN that begin and end with a vowel when repetitions are allowed.
Solution:
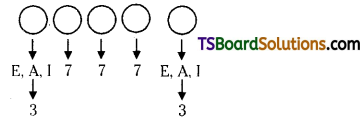
We can fill the first and last places with vowels each in 3 ways (E, A, I).
Now, each of the remaining three places can be filled in 7 ways (when repetitions are allowed).
∴ The number of 5 letter words which begin and end with vowels is 32 . 73
= 9 . 343 = 3087.

Question 33.
Find the number of ways of arranging 8 persons around a circular table if two particular persons were to sit together.
Solution:
Treat the two particular persons as one unit.
Then we have 6 + 1 = 7 things.
They can be arranged around a circular table in (7 – 1) ! = 6!
Now, the two particular persons can be arranged among themselves in 2! ways.
∴ The number of required arrangements is 6! – 2! = 6 . 5 . 4 . 3 . 2 . 1 . 2 = 1440.
Question 34.
Find the number of ways of arranging 8 men and 4 women around a circular table. In how many of them
i) all the women come together
ii) no two women come together.
Solution:
Total number of persons = 12 [8M + 4W]
∴ The number of ways of arranging these 12 persons around a circular table = (12 – 1)1 = 11!
i) All the women come together :
Treat the four women as one unit then we have 8 men + 1 unit of women then we have 9 entries.
They can be arranged around a circular table in (9 – 1) ! = 8! ways.
Now, the four women among themselves can be arranged in 4! ways.
The required number of arrangements is 8! . 4!.
ii) No two women come together :
First we arrange 8 men around the circular table in (8 – 1) ! = 7 ! ways.
There are 8 places in between them.
Now, we can arrange the four women in these 8 places in \({ }^8 \mathrm{P}_4\) ways.
The required number of arrangements is 7 ! . \({ }^8 \mathrm{P}_4\).
Question 35.
Find the number of ways of seating 5 Indians, 4 Americans and 3 Russians at a round table so that
i) all Indians sit together
ii) no two Russians sit together
iii) persons of same nationality sit together.
Solution:
i) All Indians sit together :
Treat the five Indians as one unit.
Then we have 4 Americans + 3 Russians + 1 unit of Indians = 8 entries.
They can be arranged at a round table in (8 – 1) ! = 7 ! ways.
Now, the five Indians among themselves can be arranged in 5! ways.
∴ The required number of arrangements is 7! – 5!.
ii) Now two Russians sit together :
First we arrange the 5 Indians + 4 Americans around the table in (9 – 1)! = 8! ways.
Now, there are 9 gaps in between 9 persons.
The 3 Russians can be arranged in the 9 gaps in \({ }^9 P_3\).
∴ The required number of arrangements is 8! . \({ }^9 P_3\).
Persons of same nationality sit together:
Treat the 5 Indians as one unit, the four Americans as one unit and the 3 Russians as one unit.
These 3 units can be arranged at round table in (3 – 1)1 = 2! ways.
Now, the 5 Indians among themselves can be arranged in 5! ways.
The four Americans among themselves can be arranged in 4! ways.
The 3 Russians among themselves can be arranged in 3! ways.
The required number of arrangements = 2! . 5! . 3! . 4!.

Question 36.
Find the number of ways of arranging the letters of the word SPECIFIC. In how many of them
i) the two ‘C’, ‘S’ come together,
ii) the two I’s do not come together.
Solution:
The given word has eight letters in which there are 2 I’s are alike and 2 C’s are alike and rest are different.
They can be arranged in \(\frac{8 !}{2 ! 2 !}\) ways.
\(\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 2}\) = 10080.
i) the two C’s come together:
Treat the 2 C’s as one unit.
Then we have 6 + 1 = 7 letters.
In which 2 I’s are alike.
Now, they can be arranged in \(\frac{7 !}{2 !}\) ways.
The 2 C’s can be arranged among themselves in \(\frac{2 !}{2 !}\) ways.
∴ The number of required arrangements = \(\frac{7 !}{2 !} \cdot \frac{2 !}{2 !}\) = 2520.
ii) The 2I’s do not come together:
Since, the 2 I’s do not come togeter, then first arrange the remaining six letters in \(\frac{6 !}{2 !}\) ways.
Among these 6 letters we find 7 gaps.
Now, the 2 I’s can be arranged in these 7 gaps in \(\frac{{ }^7 \mathrm{P}_2}{2 !}\) ways.
∴ The number of required arrangements = \(\frac{6 !}{2 !} \cdot \frac{{ }^7 \mathrm{P}_2}{2 !}\)
= \(\frac{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2} \cdot \frac{7 \cdot 6}{2}\) = 7560
Question 37.
Find the number of 5- digit numbers that can be formed using the digits 1, 1, 2, 2, 3. How many of them are even?
Solution:
In the given 5 digits there are two 1’s and two 2’s.
They can be arranged in \(\frac{5 !}{2 ! 2 !}\) ways
= \(\frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 2}\) = 30
Now, the remaining 4 places can be arranged using the remaining digits 1, 1, 2, 3 in \(\frac{4 !}{2 !}\) ways = 12.
The number of 5 digit even numbers that can be formed using the digits 1, 1, 2, 2, 3 is 12.
Question 38.
Find the number of ways of arranging the letters of the words if
i) SINGING
ii) PERMUTATION
iii) COMBINATION
Solution:
i) SINGING: Given word is ‘SINGING’.
The word SINGING contains 7 letters in which there are 2 I’s are alike, 2 N’s are alike and 2G’s are alike, and rest are different.
∴ The number of required arrangements = \(\frac{7 !}{2 ! 2 ! 2 !}\).
ii) PERMUTATION:
Given word is ‘PERMUTATION’.
The word ‘PERMUTATION’ contains 11 letters in which there are 2 T’s are alike and rest are different.
∴ The number of required arrangements = \(\frac{11 !}{2 !}\)
iii) COMBINATION:
Given word is COMBINATiON.
The word ‘COMBiNATION’ contains 11 letters in which there are 2 O’s are alike, 2 I’s are alike, 2 N’s are alike and rest are different.
∴ The number of required arrangements = \(\frac{11 !}{2 ! 2 ! 2 !}\).

Question 39.
If the letters of the word AJANTA are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the ranks of the words
(i) AJANTA
(ii) JANATA.
Solution:
The alphabetical order of the letters of the given word is AAAJNT.
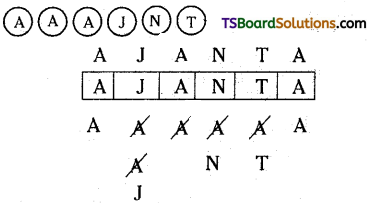
The no. of words begin with AA is 4! = 24
The no. of words begin with AJAA is 2! = 2
The no. of words begin with AJANA is 1! = 1
The next word is AJANTA = 1
Rank of the word, AJANTA = 24 + 2 + 2 + 1 + 1 = 28.
ii) The alphabetical order of the letters of the given word is AAAJNT.
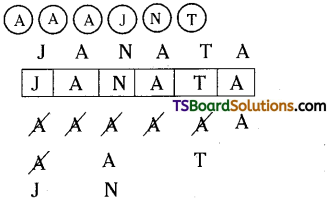
The no. of words begin with A is \(\frac{5 !}{2 !}\) = 60
The no. of words begin with JAA is 3! = 6
The no. of words begin with JANAA is 1! = 1
The next word ¡s JANATA = I
∴ Rank of the word, JANATA = 60 + 6 + 1 + 1 = 68.
Question 40.
Find the number of ways of forming a committee of 4 members out of 6 boys and 4 girls such that there is atleast one girl in the committee.
Solution:

Since, the committee must contain at least one girl, the numbers of committee will be as follows:
i) 3 boys and one girl :
The number of ways of selecting committee = \({ }^6 \mathrm{C}_3 \cdot{ }^4 \mathrm{C}_1=\frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} \cdot 4\) = 80.
ii) 2 boys and 2 girls :
The number of ways of selecting committee = \({ }^6 \mathrm{C}_2 \cdot{ }^4 \mathrm{C}_2=\frac{6 \cdot 5}{2 \cdot 1} \cdot \frac{4 \cdot 3}{2 \cdot 1}\) = 90.
iii) One boy and 3 girls :
The number of ways of selecting committee = \({ }^6 \mathrm{C}_1 \cdot{ }^4 \mathrm{C}_3\) = 6 . 4 = 24
iv) 0 boys and 4 girls: The number of ways of selecting committee = \({ }^6 \mathrm{C}_0 \cdot{ }^4 \mathrm{C}_4\) = 1
∴ The required number of ways of selecting a committee is = 80 + 90 + 24 + 1 = 195.

Question 41.
Find the number of ways of selecting 11 member cricket team from 7 batsmen, 6 bowlers and 2 wicket keepers so that the team contains 2 wicket keepers and atleast 4 bowlers. [March ‘14]
Solution:
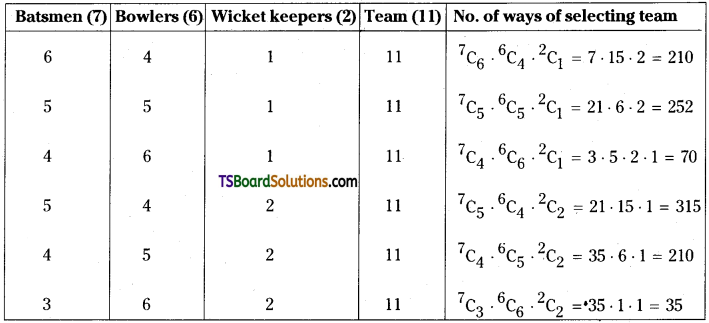
The number of ways of selecting the required cricket team = 210 + 252 + 70 + 315 + 210 + 35 = 1092.
Question 42.
If 2 ≤ r ≤ n, then show that \({ }^n C_{(r-1)}+2 \cdot{ }^n C_{(r-1)}+{ }^n C_r={ }^{(n+2)} C_r\).
Solution:
L.H.S:
\({ }^n C_{(r-1)}+2 \cdot{ }^n C_{(r-1)}+{ }^n C_r\)
= \({ }^n C_{r-2}+{ }^n C_{r-1}+{ }^n C_{r-1}+{ }^n C_r\)
= \({ }^{(n+1)} C_{r-1}+{ }^{(n-1)} C_r={ }^{(n+2)} C_r\) = R.H.S
Question 43.
14 persons are seated at a round table. Find the number of ways of selecting two persons out of them who are not seated
adjacent to each other. [AP – May 2015]
Solution:
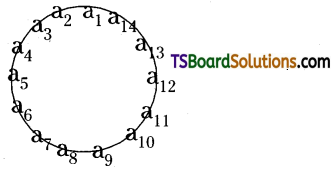
14 persons at the round table.
Selecting 2 persons from 14 persons to be seated on a circular table = \({ }^{14} C_2=\frac{14 \cdot 13}{1 \cdot 2}\) = 91 ways.
The number of ways of selecting 2 adjacent persons 14 (a1a2, a2a3, a3a4 ………………….. a14a1)
∴ The number of required selections = 91 – 14 = 77.

Question 44.
Find the number of ways of selecting a committee of 6 members out of 10 members always including a specified number.
Solution:
Since, a specified member always includes in a committee.
Remaining 5 members can be selected from 9 members in \({ }^9 \mathrm{C}_5\) ways.
∴ Required number of ways of selecting a committee C = \({ }^9 \mathrm{C}_5=\frac{9 \cdot 8 \cdot 7 \cdot 6 \cdot 5}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 126.
Question 45.
If a set A has 12 elements, find the num¬ber of subsets of A having
i) 4 elements
ii) Atleast 3 elements
iii) Atmost 3 elements.
Solution:
Number of elements in set A = 12
i) Number of subsets of A with exactly four elements = \({ }^{{ }^n} \mathrm{C}_{\mathrm{r}}={ }^{12} \mathrm{C}_4\)
= \(\frac{12 \cdot 11 \cdot 10 \cdot 9}{4 \cdot 3 \cdot 2 \cdot 1}\) = 495.
ii) Number of subsets of A with exactly zero elements is \({ }^{12} \mathrm{C}_0\).
Number of subsets of A with exactly one elements is \({ }^{12} \mathrm{C}_1\).
Number of subsets of A with exactly two elements is \({ }^{12} \mathrm{C}_2\).
Total number of subsets of A formed = 2n = 212.
Number of subsets of A with atleast 3 elements = Total number of subsets – number of subsets contains 0 or 1 or 2 elements.
= 212 – [latex]{ }^{12} \mathrm{C}_0+{ }^{12} \mathrm{C}_1+{ }^{12} \mathrm{C}_2[/latex]
= 4096 – 1 – 12 – \(\frac{12 \cdot 11}{2 \cdot 1}\)
= 4096 – 1 – 12 – 66
= 4096 – 79 = 4017.
iii) The required subsets contain atmost 3 elements i.e., it may contain 0 or 1 or 2 or 3 elements.
Number of subsets of A with exactly one element is \({ }^{12} \mathrm{C}_1\).
Number of subsets of A with exactly two elements is \({ }^{12} \mathrm{C}_2\).
Number of subsets of A with exactly three elements is \({ }^{12} \mathrm{C}_3\).
:. Number of subsets of A with atmost 3 elements = \({ }^{12} \mathrm{C}_0+{ }^{12} \mathrm{C}_1+{ }^{12} \mathrm{C}_2+{ }^{12} \mathrm{C}_3\)
= 1 + 12 + 66 + \(\frac{12 \cdot 11 \cdot 10}{3 \cdot 2 \cdot 1}\)
= 79 + 220 = 299
Question 46.
In 5 vowels and 6 consonants are given, then how many 6 letter words can be formed with 3 vowels and 3 consonants.
Solution:
Given 5 vowels and 6 consonants.
6 letter word is formed with 3 vowels and 3 consonants.
Number of ways of selecting 3 vowels from 5 vowels is \({ }^5 \mathrm{C}_3\).
Number of ways of selecting 3 consonants is from 6 consonants is \({ }^6 \mathrm{C}_3\).
∴ Total number of ways of selecting = \({ }^5 \mathrm{C}_3 \times{ }^6 \mathrm{C}_3\)
These letters can be arranged themselves in 6! ways.
∴ Number of 6 letter words formed = \({ }^5 \mathrm{C}_3 \times{ }^6 \mathrm{C}_3\) × 6!.

Question 47.
A question paper is divided into 3 sections A, B, C containing 3, 4, 5 questions respectively. Find the number of ways of attempting 6 questions choosing atleast one from each section.
Solution:
A question paper contains 3 sections A, B, C containing 3, 4, 5 questions respectively.
Number of ways of selecting 6 questions out of these 12 questions = \({ }^{12} \mathrm{C}_6\)
Number of ways of selecting 6 questions from sections B and C (i.e., from 9 questions) = \({ }^9 \mathrm{C}_6\)
Number of ways of selecting 6 questions from sections A and C (i.e., from 8 questions) = \({ }^8 \mathrm{C}_6\)
Number of ways of selecting 6 questions from sections A and B (i.e., 7 questions) = \({ }^7 \mathrm{C}_6\)
∴ Number of ways of selecting 6 questions choosing atleast one from each section = \({ }^{12} \mathrm{C}_6-{ }^7 \mathrm{C}_6-{ }^8 \mathrm{C}_6-{ }^9 \mathrm{C}_6\) = 805.
Question 48.
Find the sum of all 4-digit numbers that can be formed using the digits 0, 2, 4, 7, 8 without repetition.
Solution:
The number of 4 digited numbers formed by the using the digits 0, 2, 4, 7 8 = \(\) (∵ 0 is present).
= 5 × 4 × 3 × 2 – 4 × 3 × 2
= 120 – 24 = 96
The sum of r-digited numbers formed with n distinct non-zero digits (when ’0′ is present).
= \({ }^{(n-1)} P_{(r-1)}\) × (Sum of ’n’ digits) × (111 …………….. 1)r times – \({ }^{(n-2)} \mathrm{P}_{(\mathrm{r}-2)}\) × (Sum of n digits) × (111 …………. 1)r – 1 times
= \((5-1)_{P_{(4-1)}}\) × (0 + 2 + 4 + 7 + 8) × 1111 – \((5-2)_{P_{(4-2)}}\) × (0 + 2 + 4 + 7 + 8) × 111
= \({ }^4 \mathrm{P}_3\) × 21 × 1111 – \({ }^3 \mathrm{P}_2\) × 21 × 111
= 24 × 21 × 1111 – 6 × 21 × 111 = 5,45,958.
![]()