Learning these TS Inter 1st Year Maths 1A Formulas Chapter 8 Inverse Trigonometric Functions will help students to solve mathematical problems quickly.
TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Formulas
→ sin-1(sin θ) = θ, if θ ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
→ sin (sin-1x) = x, if x ∈ [-1, 1]
→ cos-1(cos θ) = θ, if θ ∈ [0, π]
→ cos (cos-1x) = x, if x ∈ [-1, 1]
→ tan-1(tan θ) = θ, if θ ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
→ tan(tan-1x) = x, if x ∈ R
→ cot-1(cot θ) = θ, if θ ∈ (0, π)
→ cot(cot-1x) = x, if x ∈ R
→ sin-1 (- x) = – sin-1 x if x ∈ [-1, 1]
→ cos-1(- x) = π – cos-1 x if x ∈ [-1, 1]
→ tan-1 (- x) = – tan-1 x, if x ∈ R
→ cot-1 (- x) = π – cot-1 x if x ∈ R
→ sin-1 x – cos 1 x = \(\frac{\pi}{2}\) , if x ∈ [-1, 1]
→ tan-1x + cot-1x = \(\frac{\pi}{2}\), for any x ∈ R
→ sec-1x + cosec-1x = \(\frac{\pi}{2}\) , if x ∈ (-∞, -1] ∪ [1, ∞)
![]()
→ sin-1x = cosec-1\(\left(\frac{1}{x}\right)\) for x ∈ [-1, 0) ∪[1, ∞)
→ cos-1x = sec-1\(\left(\frac{1}{x}\right)\) for x ∈ [-1, 0) ∪(0, 1]
→ cot-1x = tan-1\(\frac{1}{x}\) if x > 0
→ cot-1x = + tan-1\(\frac{1}{x}\) , if x < 0
→ sin-1x + sin-1y = sin-1 (x\(\sqrt{1-y^2}\) + y\(\sqrt{1-x^2}\)) if x, y ∈ [0, 1] and x2 + y2 < 1
→ sin-1x + sin-1 y = π – sin-1 (x\(\sqrt{1-y^2}\) + y\(\sqrt{1-x^2}\)) if x, y ∈ [0, 1] and x2 + y2 > 1
→ sin-1x – sin-1y = sin-1(x\(\sqrt{1-y^2}\) – y\(\sqrt{1-x^2}\)) if x. y ∈ [0, 1]
→ cos-1x + cos-1y = cos-1(xy – \(\sqrt{1-x^2} \sqrt{1-y^2}\)) if x, y ∈ [0, 1 ]
→ cos-1x – cos-1y = cos-1(xy + \(\sqrt{1-x^2} \sqrt{1-y^2}\)) if 0 ≤ x ≤ y ≤ 1
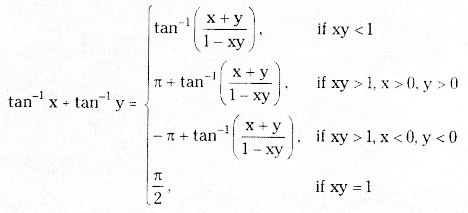
→ tan-1x – tan-1y = tan-1\(\left(\frac{x-y}{1+x y}\right)\) if x > 0, y >0 (or) x < 0, y < 0
→ 2sin-1x = sin-1 (2x\(\sqrt{1-\mathrm{x}^2}\))
→ 2cos-1x = cos-1(2x2 – 1)
![]()
→ 2tan-1x = tan-1\(\left(\frac{2 x}{1-x^2}\right)\)
→ 3sin-1x = sin-1(3x -4x3)
→ 3cos-1x = cos-1(4x3 – 3x)
→ 3tan-1x = tan-1\(\left(\frac{3 x-x^3}{1-3 x^2}\right)\)