TS Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Formulas

Learning these TS Inter 1st Year Maths 1A Formulas Chapter 6 Trigonometric Ratios up to Transformations will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Formulas

→ sin θ, cos θ, tan θ, cot θ, cosec θ and sec θ are called trigonometric functions. The reciprocals of sin θ, cos θ, tan θ are cosec θ, sec θ and cot θ respectively.

→ The main identities are sin²θ + cos²θ =1, sec²θ – tan²θ = 1 and cosec²θ – cot²θ = 1.

→ The bounds for sin θ, cos θ and sec θ are |sin θ| ≤ 1, |cosec θ| ≤ 1 and |sec θ| ≥ 1.

→ The three main tables are given by
Table 1 :

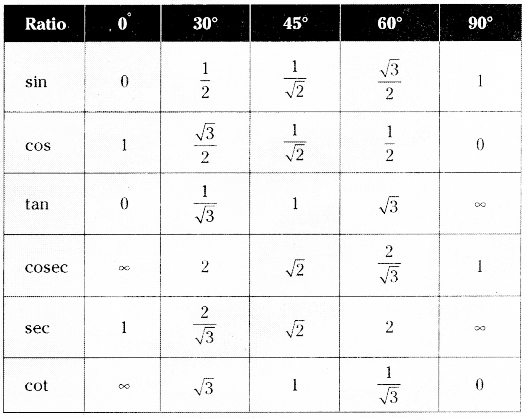
→ Using “All Silver Tea Cups”, the following tables may be comitted to memory.
Table 2:

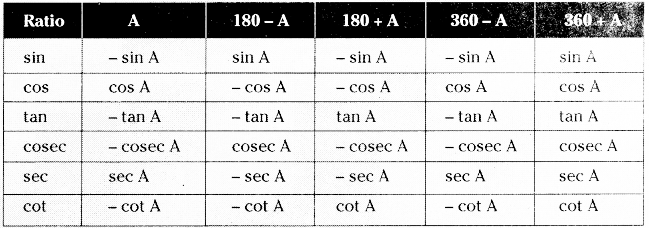
Table 3:

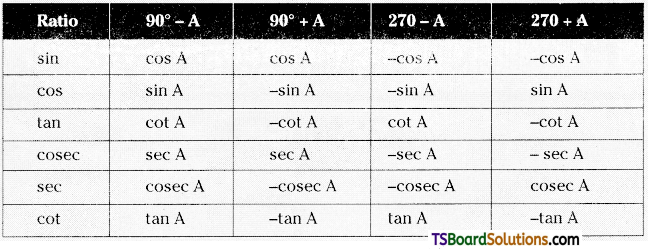
→ sin 0° = 0 = cos 90°

• sin 15° = \(\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)\) = cos 75°, sin 18° = \(\left(\frac{\sqrt{5}-1}{4}\right)\) = cos 72°
• sin 36° = \(\left(\frac{\sqrt{10}-2 \sqrt{5}}{4}\right)\) = cos 54°, sin 54° = \(\left(\frac{\sqrt{5}+1}{4}\right)\) = cos 36°
• sin 72° = \(\left(\frac{\sqrt{10+2 \sqrt{5}}}{4}\right)\) = cos 18°
• sin 75° = \(\left(\frac{\sqrt{3}+1}{2 \sqrt{2}}\right)\) = cos 15°
• tan 15° = 2 – √3 , tan 75° = 2 + √3

→ Any non constant function f: R → R is said to be Periodic” if there exists a real number p (* 0) such that f (x + p) = f(x) for each x e R. The least positive value of p with this period is called the “Period of f”.

→ (a) If f (x) is a periodic function with period p then f(ax +b) is also a periodic function with period \(\left(\frac{p}{|a|}\right)\)
(b) If y = f(x), y = g(x) are periodic functions with l, m as the periods respectively then h(x) = a f(x) + b g(x) where a, b R is a periodic function and LCM of {l, m} if exist is a period of h.
(c) The period of sin x, cosec x, cos x and sec x is 2π.
(d) The period of tan x and cot x is π.

→ (a) Range of a sin x + b cos x is \(\left[-\sqrt{a^2+b^2}, \sqrt{a^2+b^2}\right]\)
(b) Range of a sin x + b cos x + c is \(\left[c-\sqrt{a^2+b^2}, c+\sqrt{a^2+b^2}\right]\)

→ (a) sin(A ± B) = sin A cos B ± cos A sin B
(b) cos(A ± B) = cos A cos B ∓ sin A sin B
(c) tan (A ± B) = \(\frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}\)
(d) cot (A ± B) = \(\frac{\cot A \cot B \pm 1}{\cot B \mp \cot A}\)
(e) sin (A + B) sin (A – B) = sin²A – sin²B = cos²B – cos²A
(f) cos (A + B) cos (A – B) = cos2A – sin’B = cos2B – sin2A

→ (a) sin (A + B + C) = sin A cos B cos C + cos A sin B cos C + cos A cos B sin C – sin A sin B sin C
(b) cos (A + B + C) = cos A cos B cos C + cos A sin B sin C – sin A cos B sin C – sin A sin B cos C
(c) tan (A + B + C) = \(\frac{\sum \tan A-\pi \tan A}{1-\sum \tan A \tan B}\)

→ (a) sin 2A = 2 sinA cos A, sinA = 2 sin\(\frac{\mathrm{A}}{2}\) cos \(\frac{\mathrm{A}}{2}\)
(b) cos 2A = cos²A – sin²A = 1 – 2 sin²A = 2 cos²A – 1
cos A = cos² \(\frac{\mathrm{A}}{2}\) – sin² \(\frac{\mathrm{A}}{2}\) = 1 – 2 sin²\(\frac{\mathrm{A}}{2}\) = 2 cos² \(\frac{\mathrm{A}}{2}\) – 1
(c) tan 2A = \(\frac{2 \tan A}{1-\tan ^2 A}\), tan A = \(\frac{2 \tan \frac{A}{2}}{1-\tan ^2 \frac{A}{2}}\) (\(\frac{A}{2}\), A are not odd multiples of \(\frac{\pi}{2}\))
(d) cot 2A = \(\frac{\cot ^2 A-1}{2 \cot A}\), cot A = \(\frac{\cot ^2 \frac{A}{2}-1}{2 \cot \frac{A}{2}}\) (A is not an integral multiple of π)
(e) sin 2A = \(\frac{2 \tan A}{1+\tan ^2 A}\), sin A = \(\frac{2 \tan \frac{A}{2}-1}{1+\tan ^2 \frac{A}{2}}\) (\(\frac{A}{2}\) is not an integral multiple of \(\frac{\pi}{2}\))
(f) cos 2A = \(\frac{1-\tan ^2 \mathrm{~A}}{1+\tan ^2 \mathrm{~A}}\), cos A = \(\frac{1-\tan ^2 \frac{A}{2}}{1+\tan ^2 \frac{A}{2}}\)

→ (a) sin 3A = 3 sin A – 4 sin³A
(b) cos 3A = 4cos³A – 3 cos A
(c) tan 3A = \(\frac{3 \tan A-\tan ^3 A}{1-3 \tan ^2 A}\)
(d) cot 3A = \(\frac{3 \cot A-\cot ^3 A}{1-3 \cot ^2 A}\)

→ Sums into formulae:
(a) sin (A + B) + sin (A – B) = 2 sin A cos B
(b) sin(A + B) – sin (A – B) = 2 cos A sin B
(c) cos (A + B) – cos (A – B) = 2 cos A cos B
(d) cos (A – B) – cos (A + B) = 2 sin A sin B

→ (a) sin C + sin D = 2 sin \(\left(\frac{C+D}{2}\right)\) cos \(\left(\frac{C-D}{2}\right)\)
(b) sin C – sin D = 2 cos\(\left(\frac{C+D}{2}\right)\) sin \(\left(\frac{C-D}{2}\right)\)
(c) cos C + cos D = 2 cos\(\left(\frac{C+D}{2}\right)\) cos \(\left(\frac{C-D}{2}\right)\)
(d) cos C – cos D = 2 sin \(\left(\frac{C+D}{2}\right)\) sin \(\left(\frac{D-C}{2}\right)\)

→ (a) sin A = ±\(\sqrt{\frac{1-\cos 2 A}{2}}\)
(b) cos A = ±\(\sqrt{\frac{1+\cos 2 A}{2}}\)
(c) tan A = ±\(\pm \sqrt{\frac{1-\cos 2 A}{1+\cos 2 A}}\), if A is not an odd multiple of \(\frac{\pi}{2}\)

→ (a) sin \(\frac{A}{2}=\pm \sqrt{\frac{1-\cos A}{2}}\)
(b) cos \(\frac{A}{2}=\pm \sqrt{\frac{1+\cos A}{2}}\)
(c) tan\(\frac{A}{2}=\pm \sqrt{\frac{1-\cos A}{1+\cos A}}\), if A is not an odd mutiple of π.

→ (a) sin x and cos x are continuous functions on IR.
(b) tan x is discontinuous at x = (2n – 1) \(\frac{\pi}{2}\), n ∈ Z
(c) sec x is discontinuous at x = (2x + 1) \(\frac{\pi}{2}\), n ∈ Z
(d) cosec x is discontinuous at x = nπ, n ∈ Z