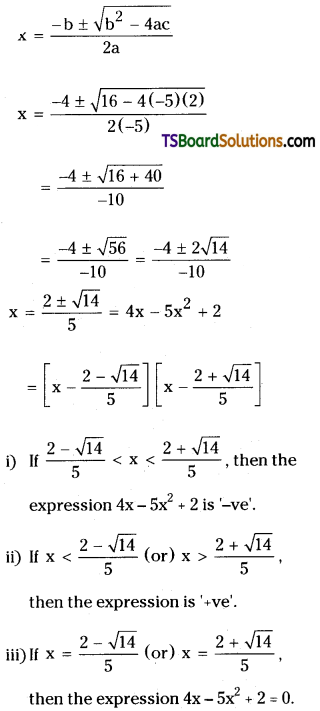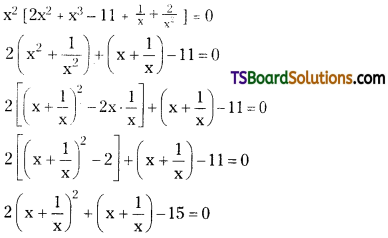Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type to help strengthen their preparations for exams.
TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Short Answer Type
Question 1.
Find the range of \(\frac{x^2+x+1}{x^2-x+1}\). [Mar.’10. ’04, May ’10]
Solution:
Let y = \(\frac{x^2+x+1}{x^2-x+1}\)
⇒ y(x2 – x + 1) = x2 + x + 1
⇒ yx2 – yx + y – x2 – x – 1 = 0
⇒ (y – 1)x2 + (- y – 1) x + y – 1 = 0
x is real;
⇒ discriminant ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ (- y – 1)2 – 4 (y – 1) (y – 1) ≥ 0
⇒ y2 + 1 + 2y – 4 (y2 – y – y + 1) ≥ 0
⇒ y2 + 1 + 2y – 4y2 + 8y – 4 ≥ 0
⇒ – 3y2 + 10y – 3 ≥ 0
⇒ 3y2 – 10y + 3 ≤ 0
⇒ 3y2 – 9y – y + 3 ≤ 0
⇒ 3y (y – 3) – 1 (y – 3) ≤ 0
⇒ \(\frac{1}{3}\) ≤ y ≤ 3
∴ y lies between \(\frac{1}{3}\) and 3.
∴ Range = [\(\frac{1}{3}\), 3]
Question 2.
Find the range of \(\frac{x+2}{2 x^2+3 x+6}\). [AP – May ’16; Mar ’13, ’08, Mar. 2000, B.P]
Solution:
Let y = \(\frac{x+2}{2 x^2+3 x+6}\)
⇒ 2x2y + 3xy + 6y = x + 2
⇒ (2y)x2 + (3y – 1)x + (6y – 2) = 0
x is real;
⇒ Discriminant ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ (3y – 1)2 – 4(2y) (6y – 2) ≥ 0
⇒ 9y2 + 1 – 6y – 48y2 + 16y ≥ 0
⇒ – 39y2 + 10y + 1 ≥ 0
⇒ 39y2 – 10y – 1 ≤ 0
⇒ 39y2 – 13y + 3y – 1 ≤ 0
⇒ 13y (3y – 1) + (3y – 1) ≤ 0
⇒ (13y + 1) (3y – 1) ≤ 0
⇒ \(\frac{-1}{13} \leq y \leq \frac{1}{3}\)
y lies between \(\frac{-1}{13}\) and \(\frac{1}{3}\).
∴ Range = [\(\frac{-1}{13}\), \(\frac{1}{3}\)].

Question 3.
Find the range of \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\). [Mar. ’09, ’98].
Solution:
Let y = \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\)
⇒ x2y – 3xy + 2y = 2x2 – 6x + 5
⇒ x2y – 3xy + 2y – 2x2 + 6x – 5 = 0
⇒ (y – 2)x2 +(- 3y+ 6)x + 2y – 5 = 0
x is real ;
⇒ Discriminant ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ (- 3y + 6)2 – 4(y – 2) (2y – 5) ≥ 0
⇒ 9y2 + 36 – 36y – 4(2y2 – 5y – 4y + 10) ≥ 0
⇒ 9y2 + 36 – 36y – 8y2 + 20y + 16y – 40 ≥ 0
⇒ y2 – 4 ≥ 0
⇒ (y – 2) (y + 2) ≥ 0
⇒ y ≤ – 2 (or) y ≥ 2 y ≤ – 2 y ≥ 2
∴ y does not lies between – 2, 2.

∴ Range = (- ∞, – 2] u [2, ∞).
Question 4.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real. [TS – Mar. ’18, ’16, May ’12, March ’11, ’05; AP – Mar. ’17, ’16, ’15].
Solution:
Let y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
(3x + 1) (x + 1) y = x + 1 + 3x + 1 – 1
⇒ y[3x2 + 4x + 1] = 4x + 1
⇒ 3x2y + 4xy . y – 4x – 1 = 0
⇒ (3y)x2 + (4y – 4) x + (y – 1) = 0
If x is real ;
⇒ Discriminant ≥ 0
b2 – 4ac ≥ 0
⇒ (4y – 4)2 – 4 (3y) (y – 1) ≥ 0
⇒ 16y2 + 16 – 32y – 12y2 + 12y ≥ 0
⇒ 4y2 – 20y + 16 ≥ 0
⇒ 4 (y2 – 5y + 4) ≥ 0
⇒ y2 – 4y – y + 4 ≥ 0
⇒ (y -4) – 1 (y – 4) ≥ 0
⇒ =(y – 1) (y – 4) ≥ 0
⇒ y ≤ 1 (or) y ≥ 4

∴ y does not lies between 1 and 4.
∴ Range is (- ∞, 1] [4, ∞)

Question 5.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between and 1. [TS – May 2016] [May ‘11, ‘07, March ‘14, ’13, ‘08, ‘02] [AP – Mar. 2019]
Solution:
Let y = \(\frac{x}{x^2-5 x+9}\)
⇒ x2 – 5xy + 9y = x
⇒ y . x2 + (- 5y – 1) x + 9y = 0
If x is real
⇒ Discriminant, b2 – 4ac ≥ 0
⇒ (- 5y – 1)2 – 4 . y . 9y ≥ 0
⇒ 25y2 + 1 + 10y – 36y2 ≥ 0
⇒ – 11y2 + 10y + 1 ≥ 0
⇒ 11y2 – 10y – 1 ≤ 0
⇒ 11y (y – 1) + 1 (y – 1) ≤ 0
⇒ (11y + 1) (y – 1) ≤ 0
⇒ \(\frac{-1}{11}\) ≤ y ≤ 1
∴ y lies between \(\frac{-1}{11}\) and 1.
Question 6.
If the expression \(\frac{x-p}{x^2-3 x+2}\) takes all real values for x ∈ R, then find the bounds for p. [May ‘09, ‘06. March ‘06] [TS & AP – May 2015].
Solution:
Let y = \(\frac{x-p}{x^2-3 x+2}\)
⇒ yx2 – 3xy + 2y = x – p
⇒ y . x2 + (- 3y – 1) x + (2y + p) = 0
x is real
⇒ Discriminant ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ (- 3y – 1)2 – 4y (2y + p) ≥ 0
⇒ 9y2 + 1 + 6y – 8y2 – 4py ≥ 0
⇒ y2 + (6 – 4p) y + 1 ≥ 0
⇒ y is real then, y2 + (6 – 4p) y + 1 ≥ 0
The roots of y2 + (6 – 4p) y + 1 = 0 are real and equal or lmaginary.
Then discriminant ≤ 0
⇒ b2 – 4ac ≤ 0
⇒ (6 – 4p)2 – 4(1)(1) ≤ 0
⇒ 36 + 16p2 – 48p – 4 ≤ 0
⇒ 16p2 – 48p + 32 ≤ 0
⇒ p2 – 3p + 2 ≤ 0
⇒ p2 – 2p – p + 2 ≤ 0
⇒ p(p – 2) – 1(p – 2) ≤ 0
⇒ (p – 1) (p – 2) ≤ 0
⇒ 1 ≤ p ≤ 2
If p = 1 (or) p = 2 then \(\frac{x-p}{x^2-3 x+2}\) is not defined.
∴ 1 < p < 2.

Question 7.
Show that none of the values of the function \(\frac{x^2+34 x-71}{x^2+2 x-7}\) over R lies between 5 and 9. [March ‘12. ‘07]
Solution:
Let y = \(\frac{x^2+34 x-71}{x^2+2 x-7}\)
⇒ y(x2 + 2x – 7) = x2 + 34x – 71 = 0
⇒ yx2 + 2xy – 7y – x2 – 34x + 71 = o
⇒ (y – 1)x2 + (2y – 34) x – 7y + 71 = 0
If x is real ;
= Discriminant ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ (2y – 34)2 -4 (y – 1) (- 7y + 71) ≥ 0
⇒ 4y2 + 1156 – 136y – 4 (- 7y2 + 71y + 7y – 71) ≥ 0
⇒ 4y2 + 1156 – 136y + 28y2 – 284y – 28y + 284 ≥ 0
⇒ 32y2 – 448y + 1440 ≥ 0
⇒ y2 – 14y + 45 ≥ 0
⇒ y2 – 9y – 5y + 45 ≥ 0
⇒ y (y – 9) – 5(y – 9) ≥ 0
⇒ (y – 5) (y – 9) ≥ 0
⇒ y ≤ 5 (or) y ≥ 9
∴ y does not Lies between 5 and 9.
Hence, none of the values of given function over R lies between 5 and 9.
Question 8.
Find the maximum and minimum values of the function \(\frac{x^2+14 x+9}{x^2+2 x+3}\) over R. [AP – March 2018; May ’14, ‘05].
Solution:
Let y = \(\frac{x^2+14 x+9}{x^2+2 x+3}\)
⇒ yx2 + 2xy + 3y – x – 14x – 9 = 0
⇒ (y – 1)x2 + (2y – 14)x + 3y – 9 = 0
If x is real
⇒ Discriminant, b2 – 4ac ≥ O
⇒ (2y – 14)2 – 4(y – 1)(3y – 9) ≥ 0
⇒ 24y2 + 196 – 56y – 4[3y2 – 9y – 3y + 9]≥ 0
⇒ 4y2 + 196 – 56y – 12y2 + 36y. 12y – 36 ≥ 0
⇒ – 8y2 – 8y + 160 ≥ 0
⇒ y2 + y – 20 ≤ 0
⇒ y2 + 5y – 4y – 20 ≤ 0
⇒ y(y + 5) – + 5) ≤ 0
⇒ (y + 5) (y – 4) ≤ 0
⇒ – 5 ≤ y ≤ 4
⇒ y lies between – 5 and 4.
Minimum value = – 5, Maximum value = 4
Range = [- 5, 4].

Question 9.
If c2 ≠ ab and the roots of (c2 – ab) x2 – 2 (a2 – bc) x + (b2 – ac) = 0 are equal, then show that a3 + b3 + c3 = 3abc or a = 0. [May ’01] [TS – Mar. ’19].
Solution:
Given quadratic equation is (c2 – ab) x2 – 2 (a2 – bc)x + b2 – ac = 0 ……………(1)
Comparing this equation with
ax2 + bx +c = 0, we have
⇒ a = c2 – ab, b = – 2 (a2 – bc), c = b2 – ac
Since (1) has equal roots.
⇒ b2 – 4ac = 0
⇒ [- 2 (a2 – bc)]2 – 4 (c2 – ab) (b2 – ac)= 0
⇒ 4 [a4 + b2c2 – 2a2bc] – 4[b2c2 – ⇒ ac3 – ab3 – a2bc] = 0
⇒ 4a4 + 4b2c2 – 8a2bc – 4b2c2 + ⇒ 4ac3 + 4ab3 – 4a2bc = 0
⇒ 4a[a3 – 3abc + c3 + b3] = 0
⇒ a = 0 (or)a3 + b3 + c3 = 3abc.
Question 10.
Let a, b, c ∈ R and a ≠ 0 then the roots of ax2 + bx + c = 0 are non-real complex numbers If and only If ax2 + bx + c and a have the same sign for all x ∈ R. [May ’98. ‘93. Mar.’99]
Solution:
The roots of the quadratic equation ax2 + bx + c = 0 are imaginary then
b2 – 4ac < 0
4ac – b2 > 0.
Now, ax2 + bx + c = a [x2 + \(\frac{b}{a} x+\frac{c}{a}\)]
\(\frac{a x^2+b x+c}{a}\) = x2 + \(\frac{b}{a} x+\frac{c}{a}\)
= x2 + 2 . x . \(\frac{b}{2 a}\) + \(\left(\frac{b}{2 a}\right)^2-\left(\frac{b}{2 a}\right)^2+\frac{c}{a}\)
= \(\left(x+\frac{b}{2 a}\right)^2+\frac{c}{a}-\frac{b^2}{4 a^2}\)
= \(\left(x+\frac{b}{2 a}\right)^2+\frac{4 a c-b^2}{4 a^2}\) > 0
∴ \(\frac{a x^2+b x+c}{a}\) > 0
∴ For x ∈ R, ax2 + bx + c and a have the same sign.
Question 11.
Let a, b, c ∈ R and a 0 such that the equation ax2 + bx + c = 0 has real roots α and β with α < β, then
i) for α < x <, ax2 + bx + c and a have opposite signs.
ii) for x < α or x > β, ax2 + bx + c and a have the same sign.
Solution:
α, β are the roots of ax2 + bx + c = 0.
Then ax2 + bx + c = a (x – α) (x – β)
\(\frac{a x^2+b x+c}{a}\) = (x – α) (x – β) ……………(1)
i) Suppose x ∈ R, α < x < β x > α, x – β < 0 (x – α) > 0
(x – α) (x – β) < 0
From (1),
⇒ \(\frac{a x^2+b x+c}{a}\) < 0
∴ ax2 + bx + c, a have opposite sign.
ii) Suppose x ∈ R, x < α Suppose x ∈ R, x > β
x < α < β.
x< α x < β
x – α < 0 x – β < 0 x- β > 0 x – α > 0
(x – α) (x – β) >0
from (1)
\(\frac{a x^2+b x+c}{a}\) > 0
ax2 + bx + c, a have same sign.
x > β > α
x > β x > α
x – β > 0 x – α > 0
(x – α) (x – β) > 0
from (1)
\(\frac{a x^2+b x+c}{a}\) > 0
ax2 + bx + c, a have same sign.
∴ x ∈ R, x < α (or) x > β then ax2 + bx + c and a have the same sign.

Question 12.
Suppose that a, b, c ∈ R, a ≠ 0 and f(x) = ax2 + bx + c
i) If a > 0, then f(x) has absolute minimum at x = \(\frac{-b}{2 a}\) and the minimum value is \(\frac{4 a c-b^2}{4 a}\).
ii) If a < 0, then f(x) has absolute maximum at x = \(\frac{-b}{2 a}\) and the maximum value is \(\frac{4 a c-b^2}{4 a}\).
Solution:
f(x) = ax2 + bx + c
f’(x) =2ax + b
⇒ For f(x) has max. or min.
then f’(x) = 0
⇒ 2ax + b = 0
⇒ x = \(\frac{-b}{2 a}\)
Now, f”(x) = 2a
i) If a >0 then f”(x) > 0 and hence f has min. value at x = \(\frac{-b}{2 a}\)
Minimum of f = f(\(\frac{-b}{2 a}\))
= \(a\left(\frac{-b}{2 a}\right)^2+b\left(\frac{-b}{2 a}\right)+c\)
= \(a \frac{b^2}{4 a^2}-\frac{b^2}{2 a}+c\)
= \(\frac{b^2-2 b^2+4 a c}{4 a}=\frac{4 a c-b^2}{4 a}\)
ii) If a < 0 then f”(x) < 0 and hence f has max. value at x = \(\frac{-b}{2 a}\)
Maximum of f = f(\(\frac{-b}{2 a}\))
= \(a\left(\frac{-b}{2 a}\right)^2+b\left(\frac{-b}{2 a}\right)+c\)
= \(a \cdot \frac{b^2}{4 a^2}-\frac{b^2}{2 a}+c\)
= \(\frac{b^2-2 b^2+4 a c}{4 a}=\frac{4 a c-b^2}{4 a}\).
Question 13.
If x1, x2 are the roots of the quadratic equation ax2 + bx + c = 0 and c ≠ 0, find
the value of (ax1 + b) + (ax2 + b) in terms of a, b, c. [TS – Mar. 2017]
Solution:
Given that x1, x2 are the roots of ax2 + bx + c = 0
⇒ x1 + x2 = – b/a, x1x2 = c/a
also ax12 + bx1 + c = 0,
ax22 + bx2 + c = 0
⇒ x1 (ax1 + b) = – c,
x2(ax2 + b) = – c
⇒ (ax1 + b) = – c/x1,
(ax2 + b) = – c/x2
Now (ax1 + b)-2 + (ax2 + b)-2 = \(\left(\frac{-c}{x_1}\right)^{-2}+\left(\frac{-c}{x_2}\right)^{-2}=\frac{x_1^2}{c^2}+\frac{x_2^2}{c^2}=\frac{x_1^2+x_2^2}{c^2}\)
= \(\frac{\left(x_1+x_2\right)^2-2 x_1 x_2}{c^2}\)
= \(\frac{\left(\frac{-b}{a}\right)^2-2 \cdot \frac{c}{a}}{c^2}=\frac{b^2-2 a c}{c^2 a^2}\).

Some More Maths 2A Quadratic Expressions Important Questions
Question 1.
Find the roots of the equation 6√5 x2 – 9x – 3√5 = 0.
Solution:
Given quadratic equation is
6√5x2 – 9x – 3√5 = 0
Comparing this with ax2 + bx + c = 0, we have
a = 6√5, b = – 9, c = – 3√5
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
are the roots of quadratic equation.
x = \(\frac{9 \pm \sqrt{81+360}}{12 \sqrt{5}}=\frac{9 \pm \sqrt{441}}{12 \sqrt{5}}=\frac{9 \pm 21}{12 \sqrt{5}}\)
= \(\frac{9+21}{12 \sqrt{5}} \text { (or) } \frac{9-21}{12 \sqrt{5}}\)
= \(\frac{30}{12 \sqrt{5}} \text { (or) } \frac{-12}{12 \sqrt{5}}=\frac{\sqrt{5}}{2} \text { (or) } \frac{-1}{\sqrt{5}}\)
∴ The roots of the quadratic equation are \(\frac{\sqrt{5}}{2} \text { (or) } \frac{-1}{\sqrt{5}}\).
Question 2.
Form a quadratic equation whose roots are 2√3 – 5 and – 2√3 – 5.
Solution:
Let a = 2√3 – 5, p = – 2√3 – 5
Now, a+ = 2√3 – 5 – 2√3 – 5 = – 10
= (2√3 – 5) (- 2√3 – 5) = – (12 – 25) = 13
The quadratic equation whose roots are α, β is x2 – (α + β) + αβ = 0
⇒ x2 + 10x + 13 = 0
Question 3.
Form a quadratic equation whose roots are \(\frac{\mathbf{m}}{\mathbf{n}}, \frac{-\mathbf{n}}{\mathbf{m}}\), (m ≠ 0, n ≠ 0).
Solution:
Let α = \(\frac{m}{n}\), β = \(\frac{-\mathrm{n}}{\mathrm{m}}\)
Now, α + β = \(\frac{m}{n}-\frac{n}{m}=\frac{m^2-n^2}{m n}\)
αβ = \(\frac{m}{n} \cdot \frac{-n}{m}\) = – 1
The quadratic equation whose roots are α, β is x2 – (α + β)x + αβ = 0
x2 – \(\frac{\left(m^2-n^2\right)}{m n}\)x – 1 = 0
mnx2 – (m2 – n2)x – mn = 0.

Question 4.
If α, β are the roots of ax2 + bx + c = 0 then find α3 + β3.
Solution:
Since a, are the roots of ax2 + bx + c = 0
α + β = – \(\frac{b}{a}\), αβ = \(\frac{c}{a}\)
α3 + β3 = (α + β)3 – 3αβ(α + β)
= \(\left(\frac{-b}{a}\right)^3-3 \cdot \frac{c}{a}\left(\frac{-b}{a}\right)\)
= \(\frac{-b^3}{a^3}+\frac{3 b c}{a^2}\)
⇒ \(\frac{3 a b c-b^3}{a^3}\).
Question 5.
For what values of m, x2 + (m + 3) x + (m + 6) = 0 will have equa roots?
Solution:
Given quadratic equation is x2 + (m + 3) x + (m + 6) = 0 ……………(1)
Comparing this with ax2 + bx c = 0 we get
a = 1, b = m + 3, c = m + 6
Since (1) have equal roots
⇒ b2 – 4ac = 0
⇒ [m + 3]2 – 4(1)(m + 6) = 0
⇒ m2 + 9 + 6m – 4m – 24 = 0
⇒ m2 + 2m – 15 = 0
⇒ m2 + 5m – 3m – 15 = 0
⇒ m (m + 5) – 3 (m + 5) = 0
⇒ (m – 3) (m + 5) = 0
⇒ m = 3 (or) m = – 5
The values of m are 3, – 5.
Question 6.
For what values of m, x2 – 2 (1 + 3m) x + 7(3 + 2m) = 0 will have equal roots?
Solution:
Given quadratic equation is
x2 – 2 (1 + 3m) x + 7 (3 + 2m) = 0 …………….(1)
Comparing this with ax2 + bx + c = 0,
we get a = 1, b = – 2 (1 + 3m), c = 7 (3 + 2m)
Since (1) have equal roots
⇒ b2 – 4ac = 0
⇒ [- 2 (1 + 3m)]2 – 4(1) . 7 . (3 + 2m) = 0
⇒ 4 (1 + 9m2 + 6m) – 28 (3 + 2m) = 0
⇒ 9m2 + 6m + 1 – 21 – 14m = 0
⇒ 9m2 – 8m – 20 = 0
⇒ 9m2 – 18m + 10m – 20 = 0
⇒ 9m (m – 2) + 10(m – 2) = 0
⇒ (9m + 10) (m – 2) = 0
m = \(\frac{-10}{9}\) (or) m = 2
The values of m are \(\frac{-10}{9}\), 2.

Question 7.
For what values of m, (2m + 1) x2 + 2(m + 3) x + (m + 5) = 0 will have equal roots?
Solution:
Given quadratic equation is (2m + 1) x2 + 2(m + 3) x + (m + 5) = 0
Comparing this with ax2 + bx + c = 0,
we get a = 2m + 1, b = 2 (m + 3), c = m + 5
SInce (1) have equal roots
⇒ b2 – 4ac = 0
⇒ (2 (m + 3))2 – 4(2m + 1) (m + 5) = 0
⇒ 4(m2 + 9 + 6m) – 4[2m2 + 10m + m + 5] = 0
⇒ m2 + 9 + 6m – 2m2 – 11m + 5 = 0
⇒ – m2 – 5m + 4 = 0
⇒ m2 + 5m -4 = 0
m = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-5 \pm \sqrt{25-4(1)(-4)}}{2(1)}\)
= \(\frac{-5 \pm \sqrt{25+16}}{2}=\frac{-5 \pm \sqrt{41}}{2}\)
Question 8.
Show that the roots of the equation x2 – 2px + p2 – q2 + 2qr – r2 = 0 are rational, where p, q, r are rational.
sol.
Given that, p, q, r are rational.
Given quadratic equation is
x2 – 2px + p2 – q2 + 2qr – r2 = 0
Comparing this with ax2 + bx + c = 0 we get
a = 1, b = – 2p, c = p2 – q2 + 2qr – r2
b2 – 4ac = 4p2 – 4(1) (p2 – q2 + 2qr – r2)
= 4p2 – 4p2 + 4q2 – 8qr + 4r2
= 4q2 – 8qr + 4r2
= 4 (q2 – 2qr + r2) = 4 (q – r)2 = [2 (q – r)]2 ≥ 0
Since b2 – 4ac ≥ 0 then the roots of the given equation are rational.
Question 9.
Find the quadratic equation, the sum of whose roots is 7 and sum of the squares of the roots is 25.
Solution:
Let α and β be the roots of a required equation.
Given that the sum of roots = 7
α + β = 7
The sum of squares of the roots = 25
αβ = 25
We know that, (α + β)2 = α2 + β2 + 2αβ
72 = 25 + 2αβ
2αβ = 49 – 25 = 24
αβ = 12
The quadratic equation whose roots are α, β is x2 – (α + β)x + αβ = 0
x2 – 7x + 12 = 0.

Question 10.
Solve the equation 31 + x + 31 – x = 10.
Solution:
Given equation is 3 . 3x + \(\frac{3}{3^x}\) = 10
Let 3x = a
⇒ 3a + \(\frac{3}{a}\) = 10
⇒ 3a2 – 10a + 3 = 0
⇒ a2 – 9a – a + 3 = 3 = 0
⇒ 3a (a – 3) – 1 (a – 3) = 0
⇒ (a – 3) (3a – 1) = 0
⇒ a = 3 (or) a = \(\frac{1}{3}\)
Case-1 :
If a = 3
⇒ 3 = 3x
⇒ x = 1
Case – 2 :
If a = \(\frac{1}{3}\)
⇒ \(\frac{1}{3}\) = 3x
⇒ 3x = 3– 1
⇒ x = – 1.
∴ The solution set of the given equation is {- 1, 1}.
Question 11.
Solve 71+x + 71-x = 50 for real x.
Solution:
Given equation is 71+x + 71-x = 50
7 . 7x + \(\frac{7}{a}\) = 50 ……………..(1)
Let 7x = a
⇒ 7a + \(\frac{7}{a}\) = 50
⇒ 7a2 – 50a + 7 = 0
⇒ 7a2 – 49a – a + 7 = 0
⇒ 7a (a – 7) – 1(a – 7) = 0
⇒ (a – 7) (7a – 1) = 0
⇒ a = 7 (or) \(\frac{1}{7}\)
Case – 1:
If a = 7
⇒ 7x = 7
⇒ x = 1
Case – 2:
If a = \(\frac{1}{7}\)
⇒ 7x = 7-1
x = – 1
Hence the solution set of the given equation is {- 1, 1}.

Question 12.
If x2 – 6x + 5 = 0 and x2 – 3ax + 35 = 0 have a common root, then find a.
Solution:
Given quadratic equations are x2 – 6x + 5 = 0
Comparing with a1x2 + b1x + c1 = 0, we get
a1 = 1, b1 = – 6, c1 = 5
Now, x2 – 3ax + 35 = 0
Comparing with a2x2 + b2x + c2 = 0
we get, a2 = 1, b2 = – 3a c2 = 35
The condition for two quadratic equation. to have a common root is
(c1a2 – c2a11)2 = (a1b2 – a2b1) (b1c2 – b2c1)
⇒ (5(1) – 35(1))2 = (1 – 3a) – (1) – 6) (- 6(35) – (- 3a) 5)
⇒ (5 – 35)2 = (- 3a + 6) (- 210 + 15a)
⇒ 900 = 3(- a + 2) 5 (- 42 + 3a)
⇒ 900 = 15(- a + 2) (- 42 + 3a)
⇒ 42a – 3a2 – 84 + 6a = 60
⇒ 3a2 – 48a+ 144 = 0
⇒ a2 – 16a + 48 = 0
⇒ a – 12a – 4a + 48 = 0
⇒ a(a – 12) – 4(a – 12) = 0
⇒ (a – 4) (a – 12) = 0
⇒ a = 4 (or) a = 12.
Question 13.
For what values of x, the expression x2 – 5x + 14 is positive?
Solution:
Given expression is x2 – 5x + 14
The roots of x2 – 5x + 14 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{5 \pm \sqrt{25-4 \cdot 1(14)}}{2(1)}\)
= \(\frac{5 \pm \sqrt{25-56}}{2}=\frac{5 \pm \mathrm{i} \sqrt{31}}{2}\)
which are not real.
∴ For all x ∈ R, the expression x2 – 5x + 14 is + ve.

Question 14.
For what values of x, the expression 3x2 + 4x + 4 is positive?
Solution:
The given quadratic expression is 3x2 + 4x + 4
The roots of 3x2 + 4x + 4 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{-4 \pm \sqrt{16-48}}{2(3)}\)
= \(\frac{-4 \pm \sqrt{-32}}{6}\)
= \(\frac{-2 \pm i \sqrt{8}}{3}=\frac{-2 \pm 2 \mathrm{i} \sqrt{2}}{3}\)
which are complex numbers (non real).
∴ For all x ∈ R, the expression 3x2 + 4x + 4 is + ve.
Question 15.
For what values of x, the expression x2 – 7x + 10 is negative?
Solution:
Given expression is x2 – 7x + 10
= x2 – 5x – 2x + 10
= x (x – 5) – 2 (x – 5)
= (x – 2) (x – 5)
i) If 2 < x < 5, then the expression x2 – 7x + 10 is ‘- ve’.
ii) If x < 2 (or) x > 5, then the expression x2 – 7x + 10 is ’+ve’.
iii) If x = 2 (or) x = 5, then the expression : x2 – 7x + 10 = 0.
Question 16.
For what values of x, the expression 15 + 4x – 3x2 is negative?
Solution:
Given expression is 15 + 4x – 3x2
= – 3x2 + 9x – 5x + 15 = 3x (- x + 3) + 5(- x + 3)
= (3x + 5) (- x + 3)
i) If \(\frac{-5}{3}\) < x < 3, then the expression is 15 + 4x – 3×2 is ‘+ ve’.
ii) If x < \(\frac{-5}{3}\) (or) x > 3, then the expression is 15 + 4x – 3x2 is ‘- ve’.
iii) If x = \(\frac{-5}{3}\) (or) x = 3,then the expression 15 + 4x – 3x2 = 0.

Question 17.
Find the changes in the sign of 4x – 5x2 + 2 for x ∈ R.
Solution:
Given quadratic expression is 4x – 5x2 + 2
The roots of given expression are
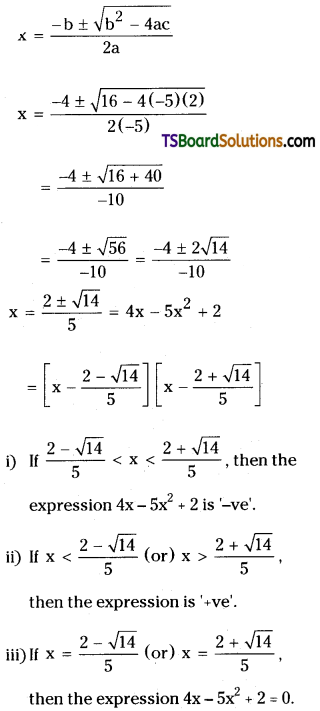
Questi0n 18.
Find the roots of the equation 4x2 – 4x + 17 = 3x2 – 10x – 17.
Solution:
Given equation can be rewritten as x2 + 6x + 34 = 0.
The roots of the quadratic equation, ax2 + bx + c = 0 are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
Here a = 1, b = 6 and c = 34.
Therefore the roots of the given equation are \(\frac{-6 \pm \sqrt{(6)^2-4(1)(34)}}{2(1)}\)
= \(\frac{-6 \pm \sqrt{-100}}{2}\)
= \(\frac{-6 \pm 10 \mathrm{i}}{2}\) (since i2 = – 1)
= – 3 + 5i, – 3 – 5i
Hence the roots of the given equation are – 3 + 5i and – 3 – 5i.

Questi0n 19.
Solve, \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\).
Solution:
Given equation is \(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\)
Let \(\sqrt{\frac{x}{1-x}}\) = a
\(\sqrt{\frac{1-x}{x}}=\frac{1}{a}\)
a + \(\frac{1}{a}=\frac{13}{6}\)
⇒ 6a2 + 6 = 13a
⇒ 6a2 – 13a + 6 = 0
⇒ 6a2 – 9a – 4a + 6 = 0
⇒ 3a (2a – 3) – 2 (2a – 3) = 0
⇒ 2a – 3 = 0, 3a – 2 = 0
⇒ 3a = 2
⇒ a = \(\frac{2}{3}\)
⇒ a = \(\frac{2}{3}\)
Case – 1:
If a = \(\frac{2}{3}\)
⇒ \(\sqrt{\frac{x}{1-x}}=\frac{2}{3}\)
⇒ \(\frac{x}{1-x}=\frac{4}{9}\)
9x = 4 – 4x
13x = 4
x = \(\frac{4}{13}\)
Case-2: .
If a = \(\frac{2}{3}\)
⇒ \(\sqrt{\frac{x}{1-x}}=\frac{3}{2}\)
⇒ \(\frac{x}{1-x}=\frac{9}{4}\)
⇒ 4x = 9 – 9x
⇒ 13x = 9
⇒ x = \(\frac{9}{13}\)
∴ The solution set of given equation is {\(\frac{9}{13}\), \(\frac{4}{13}\)}
Question 20.
Find the numbers which exceed their square root by 12.
Solution:
Let ‘x’ be any number.
Given that, x = √x + 12 ………….(1)
x – 12 = √x
⇒ squaring on both sides
⇒ x2 + 144 – 24x = x
⇒ x2 + 144 – 25x = 0
⇒ x2 – 16x – 9x + 144= 0
⇒ x (x – 16) – 9 (x – 16) = 0
⇒ (x – 9) (x – 16) = 0
⇒ x = 9 (or) x = 16.
But x = 9 does not satisfy (1) whilex = 16 satisfy.
∴ The required number is 16.

Question 21.
Prove that there is a unique pair of con-secutive positive odd Integers such that the sum of their squares is 290 and find it.
Solution:
Since two consecutive odd integers differ by 2.
Let a pair of consecutive .ve odd integers are x, x + 2.
Given that, the sum of their squares is 290
⇒ x2 + (x + 2)2 = 290 ………………..(1)
⇒ x2 + x2 + 4 + 4x = 290
⇒ 2x2 + 4x – 286 = 0
⇒ x2 + 2x- 143 = 0
⇒ x2 + 13x – 11x – 143 = 0
⇒ x (x + 13) – 11 (x + 13) = 0
⇒ (x – 11) (x + 13) = 0
⇒ x = 11 (or) x = – 13
Since x is positive, x = 11
Hence 11 is the only +ve odd integer satisfying equation (1).
∴ A pair of consecutive +ve odd integers are x, x + 2 = 11, 13.
∴ (11, 13) is the unique pair of integers which satisfy the given condition.
Question 22.
If α, β are the roots of the equation ax2 + bx + c = 0, find the values of the following expressions in terms of a, b, c.
i) α4 β7 + α7 β4
ii) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\)
iii) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\)
Solution:
Since α, β are the roots of the equation ax2 + bx + c = 0 then
α + β = \(\frac{-b}{a}\); αβ = \(\frac{c}{a}\)
i) α4 β7 + α7 β4 = α4β4 (β3 + α3)
= α4β4 (α3 + β3)
= α4β4 [(α + β)3 – 3αβ(α + β)]
= \(\left(\frac{c}{a}\right)^4\left[\left(\frac{-b}{a}\right)^3-3 \cdot \frac{c}{a} \cdot \frac{-b}{a}\right]\)
= \(\frac{c^4}{a^4}\left(\frac{-b^3}{a^3}+\frac{3 b c}{a^2}\right)\)
= \(\frac{c^4}{a^4} \frac{\left(-b^3+3 a b c\right)}{a^3}=\frac{c^4\left(3 a b c-b^3\right)}{a^7}\)
ii) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^2\), if c ≠ 0.

iii) \(\frac{\alpha^2+\beta^2}{\alpha^{-2}+\beta^{-2}}\) if c ≠ 0.
= \(\frac{\alpha^2+\beta^2}{\frac{1}{\alpha^2}+\frac{1}{\beta^2}}=\frac{\alpha^2+\beta^2}{\frac{\alpha^2+\beta^2}{\left(\alpha^2 \beta^2\right)}}\)
= (αβ)2 = \(\frac{c^2}{a^2}\).

Question 23.
If x2 + 4ax + 3 = 0 and 2x2 + 3ax – 9 = 0 have a common root, then find the values of ‘a’ and the common roots.
Solution:
Given quadratic equations are x2 + 4ax + 3 = 0
Comparing this equation with
a1x2 + b1x + c1 = 0
a1 = 1, b1 = 4a, c1 = 3
Now 2x2 + 3ax – 9 = 0
Comparing this equation with
a2x2 + b2x + c2 = 0
a2 = 2, b2 = 3a, c2 = 9
The condition for two quadratic equations
a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0
to have a common root is
(c1a2 – c2a1)2 = (a1b2 – b1a2) (b1c2 – c1b2)
⇒(3 . 2 – (- 9)(1))2 = (1 . 3a – 2 . 4a) (4a (- 9) – 3a (3))
⇒ (6 + 9)2 = (3a – 8a)(- 36a – 9a)
⇒ 152 = (- 5a) (- 45a)
⇒ 225 = 225a2
⇒ a2 = 1
⇒ a = ± 1
Case – I:
If a = 1 then the given equation reduces to
x2 + 4x + 3 = 0
x2 + 3x + x + 3 = 0
x (x + 3) + 1 (x + 3) = 0
(x + 3) (x + 1) = 0
x = – 1, x = – 3
2x2 + 3x – 9 = 0
2x2 + 6x – 3x – 9 = 0
2x (x + 3) – 3 (x + 3) = 0
(x + 3) (2x – 3) = 0
2x = 3, x = – 3
x = \(\frac{3}{2}\)
∴ The roots of the given equation are respectively – 1, – 3 and \(\frac{3}{2}\), – 3.
In this case the common root of the given equation is – 3.
Case – II:
If a = – 1 then the given equation reduces to
x2 – 4x + 3 = 0,
x2-3x-x.3 = 0
x (x – 3) – 1(x – 3) = 0
(x – 3) (x – 1) = 0
x = 3, x = 1
2x2 – 3x – 9 = 0
2x2 – 6x + 3x – 9 = 0
2x (x – 3) + 3 (x – 3) = 0
(x – 3)(2x + 3)=0
x = 3, 2x = – 3
x = \(\frac{-3}{2}\)
∴ The roots of the given equation are respectively 3, 1 and 3
In this case the common root of the given equation is 3.
Question 24.
Discuss the signs of the expression x2 + x + 1 for x ∈ R.
Solution:
Given quadratic expression is x2 + x + 1
The roots of x2 + x + 1 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{-1 \pm \sqrt{1-4}}{2(1)}\)
= \(\frac{-1 \pm i \sqrt{3}}{2}\)
which are complex roots (non real)
for all x ∈ R, the expression x2 + x + 1 is positive.

Question 25.
For what values of x the expression x2 – 5x + 14 is positive?
Solution:
Given expression is x2 – 5x + 14 = 0
The roots of x2 – 5x + 14 = 0 are
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{5 \pm \sqrt{25-4 \cdot 1(14)}}{2(1)}\)
= \(\frac{5 \pm \sqrt{25-56}}{2}\)
= \(\frac{5 \pm i \sqrt{31}}{2}\)
which are non real.
∴ For all x ∈ R, the expression x2 – 5x + 1 is +ve.
Question 26.
For what values of x the expression – 6x2 + 2x – 3 is negative?
Solution:
Given quadratic expression is – 6x2 + 2x -3
The roots of – 6x2 + 2x – 3 = 0 is

which are non real.
Here the coefficient of x2 is – ve’.
∴ x ∈ R, the expression – 6x2 + 2x – 3 is ‘-ve’.
Question 26.
Find the value of x at which the following expressions have maximum or minimum?
i) x2 + 5x + 6
ii) 2x – x2 + 7
Solution:
i) x2 – 5x – 6
Given quadratic expression is x2 + 5x + 6
Comparing this expression with ax2 + bx + c
We have a = 1, b = 5, c = 6
Here a = 1 > 0. x2 + 5x + 6 has minimum at
x = \(\frac{-\mathrm{b}}{2 \mathrm{a}}\)
x = \(\frac{-5}{2(1)}=\frac{-5}{2}\)
ii) 2x – x2 + 7
Given quadratic expression is – x2 + 2x + 7
Comparint. this expression with ax2 + bx + c
we get. a = – 1, b = 2, c = 7
Here, a = – 1 < 0 – x2 + 2x + 7 has absolute maximum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(-1)}\) = 1.
Question 27.
Solve 2x4 + x3 – 11x2 + x + 2 = 0. [TS – Mar. 2015]
Solution:
Given equation is 2x4 + x3 – 11x2 + x + 2 = 0
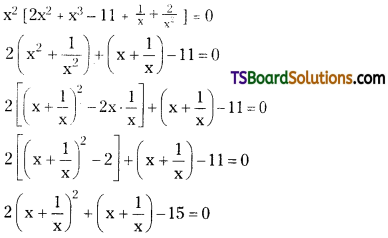
Let x + \(\frac{1}{x}\) = t
⇒ 2t2 + t – 15 = 0
⇒ 2t2 + 6t – 5t – 15 = 0
⇒ 2t (t + 3) – 5 (t + 3) = 0
⇒ (t + 3) (2t – 5) = 0
⇒ t + 3 = 0
⇒ x + \(\frac{1}{x}\) + 3 = 0
⇒ \(\frac{x^2+1+3 x}{x}\) = 0
⇒ x2 + 3x + 1 = 0
⇒ x = \(\frac{-3 \pm \sqrt{9-4}}{2}\)
∴ x = \(\frac{-3 \pm \sqrt{5}}{2}\)
⇒ 2t – 5 = 0
⇒ 2 (\(\left(x+\frac{1}{x}\right)\)) – 5 = 0
⇒ \(\frac{2 x^2+2-5 x}{x}\) = 0
= 2x2 – 5x + 2 = 0
2x2 – 4x – x + 2 = 0
2x (x – 2) – 1 (x – 2) = 0
(x – 2) (2x – 1) = 0
∴ x = 2, ½
∴ Solution set = \(\left\{\frac{-3 \pm \sqrt{5}}{2}, 2 . \frac{1}{2}\right\}\).

Question 28.
For what values of x the expression x2 – 5x – 14 is positive. [AP-Mar. 2018]
Solution:
x2 – 5x – 14 = (x + 2) (x – 7)
The roots of x2 – 5x – 14 = 0 are – 2, 7.
Here coeff. x2 is 1. This is positive.
So x < – 2 or x > 7 then x2 – 5x – 14 is positive.
Question 29.
Find the set of solutions of x2 + x – 12 ≤ 0 by algebraic method. [TS – Mar. 2019]
Solution:
Algebraic method:
x2 + x – 12 = 0
⇒ x2 + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4) (x -3) = 0
⇒ x = – 4 or 3
⇒ x2 + x – 12 ≤ 0
⇒ – 4 ≤ x ≤ 13
![]()
![]()
![]()