Here students can locate TS Inter 1st Year Physics Notes 11th Lesson Mechanical Properties of Fluids to prepare for their exam.
TS Inter 1st Year Physics Notes 11th Lesson Mechanical Properties of Fluids
→ Pressure : It is defined as the normal force acting per unit area.
Pressure (P) = Force/Area.
Unit: Nm-2 (or) pascal
D.F: ML-1 T-2
It is a “scalar quantity”.
Note : Common unit of pressure is atmosphere. 1 atmosphere = 1.013 × 105 pascal.
→ Density (ρ):
The ratio of mass to volume of a body or mass per unit volume.
Density (ρ) : \(\frac{\text { mass }}{\text { volume }} \frac{\mathrm{m}}{\mathrm{v}}\)
Unit: kg m-3, D.F: ML-3
→ Relative density: The ratio of the density of the body to the density of water at 4 °C is called Relative density.
→ Pascal’s law: The pressure in a fluid at rest is the same at all the points if they are at the same height in the liquid.
Note : If the pressures were not equal in different parts of the fluid then some resultant force must act on it and the fluid will flow. Since the fluid is assumed to be at rest then pressure must be same every where.
→ Gauge pressure : The excess of pressure P – Pa at a depth h’ is called gauge pressure where P’ is the pressure at given point and Pa’ is atmospheric pressure.
→ Hydrostatic paradox:
- In a liquid the pressure at all the points of same height is equal.
- The pressure difference depends on vertical height only. From these two concepts “whatever is the shape and mass of liquid in the container, it will have same pressure difference when h is same”. This is called “hydrostatic paradox”.
→ Mercury barometer : Mercury barometer is used to measure atmospheric pressure.
It consists of one metre long glass tube with one side closed. It is filled with mercury and inverted into a trough con-taining mercury. Height of mercury column above mean level gives atmospheric pressure.
→ Manometer: Manometer is useful to measure pressure difference. It consists of a ‘U’ tube. One arm of ‘U’ tube is connected to the vessel where pressure is to be measured. The other long arm filled with mercury is open to atmospheric pressure. Gauge pressure = P – Pa.
Note: To measure small pressure differences we will use Torr . 1 Torr = 1 m.m of Hg = 133 pascal (Pa)
1 Atmospheric pressure = 1 Bar = 105 Pa
Note : Hydraulic lifts and hydraulic brakes will work on principle of Pascal’s law.
→ Hydraulic lift : It consists of two cylinders with different areas of cross section. Both are separated and connected through a liquid. Let force F( is applied on small piston of area A, then pressure P = F1/A1 will be transmitted to large piston of area
From Pascal’s law
P = \(\frac{F_2}{A_2}=\frac{F_1}{A_1}\) ⇒ F2 = F1\(\frac{\mathrm{A}_2}{\mathrm{~A}_1}\)
Where A2/A1 is called mechanical advantage. In hydraulic lifts force applied on small piston F1, multiplied by a factor A2/A1, at large piston and it will lift heavy loads with small force.
→ Hydraulic brakes : In hydraulic brakes a small force is applied on a master cylinder filled with fluid through brake pedal. It is transmitted through brake oil to other cylinders attached to four wheels. As a result brake linings of all the wheels will expand with uniform force and braking is very smooth.
![]()
→ Fluid dynamics: It is a branch of physics which deals about the study of fluids in motion.
→ Steady flow: The flow of the fluid is said to be “steady” if at any given point the velocity of each passing fluid particle remains constant in time.
→ Stream line: The path taken by a fluid particle under a steady flow is called stream line.
Note: The tangent drawn at any point gives the direction of velocity of fluid particle at that point.
→ Equation of continuity: It states that the volume flux (or) flow rate remains constant throughout the pipe of flow.
Mathematical form of equation of continuity is AV = constant (or) A1V1 = A2V2
Note : Equation of continuity is a consequence of law of conservation of mass of an incompressible fluid in motion.
→ Bernoulli’s principle: For a fluid in stream line flow the sum of pressure energy (p), kinetic energy \(\left(\frac{\rho V^2}{2}\right)\) and potential energy (ρgh) per unit volume remains constant.
i. e., P + \(\frac{1}{2}\)ρV2 + ρgh
or P1 + \(\frac{1}{2}\)ρV12 + ρgh1 = P2 + —ρV22 + ρgh2
→ Limitations of Bernoulli’s principle :
- The fluids must be non viscous, be-cause in the derivation we assumed that no energy is lost due to friction.
- The fluids must be uncompressible, because in the derivation elastic energy of the fluid is not taken into account.
→ Speed of efflux (Torricelli’s Law) :
- Speed of efflux from an open tank V = \(\sqrt{2 \mathrm{gh}}\)
- Speed of efflux from a closed tank V = \(\sqrt{2 g h+\frac{2\left(P-P_a\right)}{\rho}}\)
Where P’ pressure on fluid in closed tank and Pa is atmosphere pressure.
→ Venturi meter: Venturimeter is used to measure the flow speed of uncompressible liquids.
It consists of a tube with broader diameter ‘A’ with a small constriction of area ‘a’ at middle. When liquids flow through this tube pressure difference (h) will develop due to high velocity at constriction.
Velocity of fluid V = \(\sqrt{\left(\frac{2 \rho_m g h}{\rho}\right)}\left[\left(\frac{A}{a}\right)^2-1\right]^{-1 / 2}\)
Where ρ = density of liquid and ρm = density of mercury.
→ Dynamic lift: Dynamic lift is the force that acts on a body moving through a fluid. Ex : Hydro foil, Aeroplane wing, spinning ball.
When a body is moving through a fluid due to its shape or motion some pressure difference (P2 – P1) will develop at top and bottom layers of the body.
Dynamic lift = (P2 – P1) × Area (A)
→ Magnus effect : The dynamic lift due to spinning of a body is called magnus effect.
→ Viscosity: The resistance to the flow of liquid between different layers is called viscosity.
(or)
Friction between liquid layers in motion is called viscosity.
→ Coefficient of viscosity (η): It is defined as the ratio of shearing stress to shearing strain rate.
S.I unit of viscosity is poiseiulle (PI) or NS m-2.
Dimensional formula: ML-1 T Note : Poise is C.G.S unit of viscosity. 1 poise = 10-1 poiseiulle (PI)
→ Strain rate : For a flowing liquid strain increases continuously with time. So rate of
change of strain is called “strain rate”.
Strain rate = \(\frac{\text { strain }}{\text { time }}=\frac{\Delta \mathrm{x} / l}{\Delta \mathrm{t}}=\frac{\mathrm{V}}{l}\) (∵ \(\frac{\Delta x}{\Delta t}\) = V)
→ Variation of viscosity of fluids with temperature :
1. Viscosity of liquids will decrease with temperature.
In liquids when temperature increases separation between molecules increases and cohesive force between molecules decreases. So viscosity decreases.
2. In case of gases viscosity increases with temperature.
In gases when temperature increases velocity of gases increases and exchange of momentum due to collision of gas molecules increases. So resistance to flow of gas molecules (viscosity) increases.
→ Stoke’s Law: From Stoke’s law for a smooth spherical body falling through a fluid :
- Force due to viscosity is proportional to velocity of the body. It acts in opposite direction of velocity F ∝ – V.
- Force due to viscosity is proportional to viscosity of the fluid F ∝ η.
- Force due to viscosity is proportional to radius of the body (a) i.e., F ∝ a
From Stoke s law force due to viscosity F ∝ – aηV, magnitude of force F = 6π a ηV
→ Terminal velocity : When a body is falling through a fluid after sometime the body will attain a constant speed V called “terminal velocity”.
At terminal velocity force due to viscosity (Fv) and force due to buoyancy (Fb) are equal to weight of the body (mg).
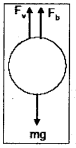
Terminal velocity of a body
VY = \(\frac{2}{9} \frac{r^2 g\left(\rho-\rho_0\right)}{\eta}\)
→ Reynolds number (Re): Reynolds number represents the ratio of internal force to viscous force of a flowing liquid.
Internal force = ρAV2,
Force due to viscosity = \(\frac{\eta \mathrm{AV}}{\mathrm{d}}\)
Reynolds number = \(\frac{\text { Internal force }}{\text { Forcedue to viscosity }}\)
= \(\frac{\rho \mathrm{AV}^2}{\eta \mathrm{AV} / \mathrm{d}}=\frac{\rho \mathrm{Vd}}{\eta}\)
Note : For steady or laminor flow Re < 1000
For turbulent flow Re > 2000
→ Critical Reynolds number: For every fluid in motion the laminor flow will become turbulent flow for R = 1000 to 2000.
The velocity of the fluid where laminor flow becomes turbulent is called “critical velocity”. Reynolds number corresponding to critical velocity is called “critical Reynold’s number”.
→ Critical velocity (V): The maximum velocity of a fluid in a tube for which the flow remains streamlined is called critical velocity.
Critical velocity Vc = Re η/pd.
→ Surface energy: In a liquid molecules near the surface are pulled down due to cohes’ive forces of liquid molecules. As a result these surface molecules will have some negative potential energy.
Energy possessed by the surface molecules of a liquid is known as “surface energy.”
Note : Due to surface energy liquid layers tends to have least surface area.
![]()
→ Surface tension (S) : Surface tension is the force per unit length acting in the plane of the interface between the plane of the liquid and any other substance.
Unit: newton/metre. D.F = MT-2
→ Surface energy & surface tension: Surface energy per unit area of the liquid interface is equal to “surface tension.”
Surface tension (S) : \(\frac{\text { Surface energy }}{\text { Area of liquid surface }}\)
→ Angle of contact (θ): The angle between the tangent to the liquid surface at the point of contact and solid surface inside the liquid is called “angle of contact ‘θ’.”
→ Drops and bubbles:
- Rain drops and soap bubbles are sphe-rical because of negative surface energy. Liquid surface tries to occupy minimum possible area. Among all geometrical shapes sphere has least surface area. So drops and bubbles are spherical.
- Excess pressure inside a liquid drop is P = \(\frac{2 \mathrm{~S}_{\mathrm{T}}}{\mathrm{r}}\)
r = radius of the drop - Excess pressure inside a bubble is P = \(\frac{4 \mathrm{~S}_{\mathrm{T}}}{\mathrm{r}}\)
→ Capillary rise: The rise or fall of a liquid in a capillary tube above or below mean level is called capillary rise. Capillary rise is due to surface tension of liquids.
Note :
- When angle of contact θ < 90° then capillary rise takes place.
- When angle of contact θ > 90° capillary depression takes place.
→ Wetting agents: Substances which decrease angle of contact between the liquid and solid molecules are known as “wetting agents”.
Wetting agents are used in dyeing fabrics. Note : Due to wetting agents force of attraction between the solid and liquid molecules (SSA) is more than force due to surface tension force of liquid (SLi)
→ Water proof agents : Substances which increase the angle of contact between the liquid and solid molecules are known as “Water proof agents.”
Water proof agents are used in marine paints and in soaps and detergents.
Note : Due to water proof agents force of attraction between liquid and solid molecules (Ssa) is less than force of attraction between liquid molecules due to surface tension (SLi).
→ Detergent action: Molecules of detergents are hair pin shaped. One end is attached to water molecule and the other end to dirt particles or grease particles etc. Detergent molecules will also reduce the surface tension of water drastically. As a result force between dirt particles and liquid molecules is reduced. Due to strong force between dirt molecules and detergent molecules thej* can be easily removed.
→ Average pressure, Pav = \(\frac{\mathrm{F}}{\mathrm{A}}\)
→ Hydrostatic pressure of a liquid, P = hρg
ρ = density of liquid; h = height of liquid
→ Pressure at any point in a liquid at a depth of ‘h’ is, P = P0 + h dg
where P0 = atmospheric pressure.
→ Pressure energy per unit volume = P = hydrostatic pressure
→ Upward force due to buoyancy = Vρg
= weight of liquid displaced by the body
→ Fraction of volume of a body submersed in a liquid = \(\frac{\text { density of object }}{\text { density of fluid }}\)
→ From equation of continuity A1V1 = A2V2 i.e., At steady flow volume flux is constant.
→ Critical Velocity, Vc = \(\frac{R \cdot \eta}{d \rho}\) or number, R = \(\frac{V_c d \rho}{\eta}\)
d = diameter of tube;
ρ = density of fluid,
η = coefficient of viscosity.
→ Bernoulli’s theorem states that total energy of a fluid at any point in that fluid is constant.
P + \(\frac{1}{2}\)ρv2 + ρgh = a constant
→ At horizointal points or fluid is flowing horizontally then \(\frac{P_1}{\rho_1}+\frac{v_1^2}{2}=\frac{P_2}{\rho_2}+\frac{v_2^2}{2}\)
→ Aero – dynamic lift on wing of aeroplane p ressure difference × Area of wing
Dynamic lift = (P2 – P1) A
→ Velocity gradient, \(\frac{\Delta v}{\Delta x}\)
= \(\frac{\text { Change in velocity }}{\text { Perpendicular distance between layers }}\)
→ Coefficient of viscosity, η = \(\frac{\mathrm{F}}{\mathrm{A}} \frac{\Delta \mathrm{x}}{\Delta v}\) or
η = \(\frac{\pi \mathrm{Pa}^2}{8 \mathrm{Ql}}\) (Poiseuille’s equation)
(where Q = volume of liquid flowing per second, r = radius of tube, l = length of tube and P = pressure difference)
→ Torricelli’s formula : Velocity of liquid through a hole, v = \(\sqrt{2 g h}\)
(h = height of liquid above centre of hole.)
→ Stake’s Law : Viscous force on a smooth spherical body, F = 6π η av
![]()
→ Terminal velocity is the constant velocity with which the body is falling through the fluid.
Terminal velocity, vt = \(\frac{2}{9} a^2 \frac{g\left(\rho-\rho_0\right)}{\eta}\)
ρ = density of the body,
ρ0 = density of fluid,
η = coefficient of viscosity of fluid.
→ Surface tension = \(\frac{\text { Force }}{\text { Length }}\) ⇒ S = \(\frac{\mathrm{F}}{l}\)
→ Surface Tension, S = \(\frac{\mathrm{rdg}\left(\mathrm{h}+\frac{\mathrm{r}}{3}\right)}{2 \cos \theta}=\frac{\mathrm{rhdg}}{2 \cos \theta}\)
For water θ = 0°
S = \(\frac{\text { rhdg }}{2}\)
→ Height of liquid h ∝ S, h ∝ \(\frac{1}{r}\). This is called “Jurin’s law”.
→ When a capillary tube is tilted by an angle a’ with vertical then vertical height of liq¬uid is same. But length of liquid in capillary tube increases.
h1 = \(\frac{\mathrm{h}}{\cos \alpha}\)
Ratio of lengths for two different angles is
\(\frac{\mathrm{h}_1}{\mathrm{~h}_2}=\frac{\cos \alpha_2}{\cos \alpha_1}\)
→ If a capillary tube of insufficient length is placed in a liquid, then liquid will rise upto top of capillary tube but angle of contact 0 will increase.
\(\frac{\mathrm{h}_1}{\cos \theta_1}=\frac{\mathrm{h}_2}{\cos \theta_2}\) or h1cos θ2 = h2 cos θ1
→ Excess of pressure inside a soap bubble,
P = \(\frac{4 \mathrm{~S}}{\mathrm{r}}\)
→ Excess of pressure inside a liquid drop,
P = \(\frac{2 \mathrm{~S}}{\mathrm{r}}\)
→ Work done to blow a soap bubble from soap solution, w = 8πr2S
→ Work done to increase the radius of a soap bubble from r1 to r2 is, w = 8πS (r22 – r12)
(where r2 > r1)
→ Work done to divide a large drop of liquid into ‘n’ small droplets, w = 4πr2S (n\(\frac{1}{3}\) – 1)
→ Energy released when ‘n’ small droplets are combined to form a large bubble is,
w = 4πr2S (n\(\frac{2}{3}\) – 1)